Fuzzy Multi-Attribute Group Decision-Making Method Based on Weight Optimization Models

Abstract

For interval-valued intuitionistic fuzzy sets featuring complementary symmetry in evaluation relations, this paper proposes a novel, complete fuzzy multi-attribute group decision-making (MAGDM) method that optimizes both expert weights and attribute weights. First, an optimization model is constructed to determine expert weights by minimizing the cumulative difference between individual evaluations and the overall consistent evaluations derived from all experts. Second, based on the Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS), the improved closeness index for evaluating each alternative is obtained. Finally, leveraging entropy theory, a concise and interpretable optimization model is established to determine the attribute weight. This weight is then incorporated into the closeness index to enable the ranking of alternatives. Integrating these features, the complete fuzzy MAGDM algorithm is formulated, effectively combining the strengths of subjective and objective weighting approaches. To conclude, the feasibility and effectiveness of the proposed method are thoroughly verified and compared through detailed examination of two real-world cases.

1. Introduction

Multi-attribute group decision-making is a process wherein multiple decision-makers define the decision scope surrounding the decision goal and subsequently propose methodologies to evaluate, rank, and select alternatives [1]. This process primarily addresses problems of evaluation and selection, with its theories and methods finding wide application in engineering, technology, economics, management, and other fields. In this paper, the term “experts” refers to decision-makers.

MAGDM processes employ diverse methodologies such as the ELimination and Choice Translating REality (ELECTRE) method [2], the Preference Ranking Organization METhod for Enrichment Evaluations (PROMETHEE) [3], and the Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) [4]. Regardless of the method selected, three critical issues must be addressed: handling fuzzy information, determining expert weights, and assigning attribute weights. First, as economic and social complexity intensifies, decision-making problems have become increasingly intricate. On one hand, the inherent fuzziness of certain attributes impedes their quantification. Decision-makers consequently struggle to obtain precise information, leading to ambiguous evaluations. On the other hand, even quantifiable attributes may yield inaccurate assessments due to subjective and objective factors—such as cognitive limitations or incomplete information—that influence decision-makers’ judgments. These observations underscore that fuzziness pervades nearly all decision-making processes, highlighting why fuzzy multi-attribute decision making (FMADM) has garnered widespread scholarly attention. The FMADM methodology integrates fuzzy theory into multi-attribute decision making to enhance scientific rigor and practical applicability. By leveraging fuzzy sets, this approach not only provides a nuanced description of alternatives’ attributes but also mitigates evaluation inaccuracies arising from subjective biases or contextual constraints.

Secondly, determining both expert weights and attribute weights is critical in MAGDM, as different weights may lead to divergent decision outcomes, a point that has garnered significant scholarly attention. Weight determination methods fall into three categories: subjective, objective, and combined subjective–objective weighting methods. Subjective weighting methods assign weights by comparing and evaluating the importance of decision-makers or attributes. While these methods align with the perceived significance of decision elements, their reliance on human judgment introduces subjectivity and demands substantial resources. Common techniques include the Analytic Hierarchy Process (AHP) [5] and the Delphi method. Objective weighting methods derive weights directly from data, leveraging mathematical rigor to ensure strong objectivity. However, they often overlook decision-makers’ intentions, potentially leading to results misaligned with practical contexts. Representative approaches include the entropy weighting method [6] and the deviation maximization method. Combined subjective–objective methods integrate the strengths of both paradigms; they incorporate decision-makers’ preferences while respecting inherent patterns in objective data [7]. This synergy enhances result reliability and alignment with real-world scenarios. A typical example is the goal programming method. In practice, combined weighting methods are preferred for determining expert and attribute weights, as they produce more credible and robust decision outcomes.

To resolve increasingly complex decision-making problems more effectively, scholars have conducted extensive research on fuzzy multi-attribute group decision-making methods. In the intuitionistic fuzzy context, Sina et al. [8] directly assigned expert weights via subjective weighting, determined attribute weights by integrating two objective methods—Criteria Importance Through Intercriteria Correlation (CRITIC) and Ideal Point—and ranked alternatives using combined Additive Ratio ASsessment (ARAS) and Evaluation based on Distance from Average Solution (EDAS) for construction project selection. Shi-fang et al. [9] derived expert weights through an Intuitionistic Fuzzy Weighted Averaging (IFWA) operator, aggregated multi-expert decision matrices, determined attribute weights via intuitionistic fuzzy entropy, and solved personnel selection problems with Grey Relational Analysis (GRA). Behnam et al. [10] calculated expert weights using IFWA, determined attribute weights through subjective weighting combined with IFWA, and addressed manufacturing system upgrades via ELECTRE. In interval-valued intuitionistic fuzzy settings, Ting-Yu et al. [11] assigned expert weights subjectively, optimized attribute weights through a weight model, and ranked treatment plans using TOPSIS, while Feifei et al. [12] directly assigned expert weights subjectively, determined attribute weights via continuous weighted entropy, and applied TOPSIS for emergency risk management. For interval-valued hesitant fuzzy sets (IVHFS), Gitinavard et al. [13] determined attribute weights by combining expert assignments with extended maximum deviation, extended IVHFS-TOPSIS for expert weights, and solved location/supplier selection with their proposed IVHFS-Multi-Criteria Weighting and Ranking (MCWR) model. Cross-domain innovations include Jebadass et al.’s [14] low-light enhancement framework using three-level fuzzy transformation (clear→blurred→intuitionistic blurred→interval-valued intuitionistic blurred images) to dynamically quantify pixel uncertainty via interval-valued intuitionistic fuzzy sets with entropy-driven parameter optimization, outperforming seven benchmarks on entropy, absolute mean brightness error, and contrast improvement in 500-image tests; Alolaiyan et al. [15] developed an interval-valued intuitionistic fuzzy similarity measure integrating hesitation functions with proven mathematical properties (symmetry, boundedness, triangular inequality) that outperformed benchmarks in software quality assessment and production strategy selection; and Kavitha et al. [16] established the mathematical framework of self-centered interval-valued intuitionistic fuzzy graphs (IVIFG) with rigorous proofs of necessary/sufficient conditions and embedding properties, whose security deployment model quantifying illegal inter-city communication correlations significantly outperformed traditional fuzzy graphs in eccentricity calculations.

When addressing complex problems via fuzzy multi-attribute group decision making, conventional approaches that determine expert weights or attribute weights solely through subjective or objective weighting methods fail to simultaneously capture the internal patterns of data and incorporate expert insights. Consequently, these methods often lack the capacity to establish a comprehensive framework for multi-attribute group decision making. To overcome this limitation, this paper proposes interpretable and concise optimization models derived from objective data to determine expert weights and attribute weights, respectively. Decision-makers can introduce subjective opinions regarding these weights based on practical requirements, thereby integrating appropriate constraints into the optimization models. This synergistic approach leverages the strengths of both subjective and objective weighting methodologies. Furthermore, by enhancing the closeness index through the inclusion comparison possibility of interval-valued intuitionistic fuzzy sets [9], the TOPSIS method is refined. The innovations of this work are thus summarized as follows.

• In the environment of interval-valued intuitionistic fuzzy sets, we extend the method in [17] to establish a new expert weight optimization model. When the distance between the individual expert evaluation result and the expert group evaluation result is closer, we should give it a higher weight, and it is verified by numerical experiments that the expert weight will be inversely proportional to the corresponding distance.
• Based on integration of the subjective opinions of decision makers into entropy theory, a new optimization model is established to determine attribute weight. It overcomes the disadvantage of the entropy weight method, which is completely objective. Compared with the attribute weight optimization model in [9], it is simpler in form and more efficient in computation.
• A complete set of fuzzy multi-attribute group decision-making methods is formed.

While the general framework of the method in this paper aligns with that of [9], it introduces three key innovations. First, regarding expert weight determination, this paper establishes an optimization model objective based on consistency to integrate the strengths of both subjective and objective weighting methods—a significant departure from the direct subjective weighting approach used in [9]. Second, for attribute weight determination, we leverage entropy theory to formulate the optimization model objective, contrasting with the closeness maximization objective in [9]. This approach not only provides a stronger theoretical foundation but also exhibits a concise form and accelerated solution speed. Third, in case studies, we first validate the feasibility of the proposed algorithm through a simple real-world problem (mobile phone purchase), then conduct an in-depth analysis and comparison using the classical case from [9] to comprehensively demonstrate the method’s effectiveness and superiority.

This paper is structured as follows. Section 2 presents foundational theories of interval-valued intuitionistic fuzzy sets. Section 3 details the extended methodology for determining expert weights and attribute weights, integrates the extended TOPSIS framework based on inclusion comparison possibility [9], and ultimately formulates a comprehensive fuzzy multi-attribute group decision-making algorithm. Section 4 validates the method’s efficacy through two decision-making case studies, followed by comparative analysis and discussion of results. The paper concludes with a summary of key contributions and findings.

2. Preliminaries

Fuzzy set theory serves as a fundamental methodology for processing uncertain information. Initially proposed by Zadeh in 1965 [18], fuzzy sets established a mathematical framework to characterize and manipulate imprecise data in decision-making contexts. To address limitations in representing complex human hesitancy, Atanassov et al. extended this theory in 1986 by introducing intuitionistic fuzzy sets (IFSs) [19], which simultaneously model decision-makers’ support, opposition, and neutrality through membership, non-membership, and hesitation degrees. This advancement significantly enhanced the handling of uncertain decision information. Later, Gehrke et al. (1996) developed interval-valued fuzzy sets [20] to resolve the rigidity of single-value membership assignments, representing membership degrees as closed subintervals within [0,1]. Further addressing hesitation in evaluations, Torra et al. (2009) conceived hesitant fuzzy sets (HFSs) [21], permitting multiple possible membership values. Building on IFS and HFS, Zhu et al. (2012) synthesized dual hesitant fuzzy sets (DHFSs) [22], which incorporate multiple non-membership values alongside multi-valued memberships. Subsequently, Yager (2013) formulated Pythagorean fuzzy sets (PFSs) [23] by relaxing the membership–nonmembership constraint of IFS to allow broader uncertainty representation. These foundational theories have spurred further extensions, including interval-valued intuitionistic fuzzy sets [24], collectively enriching the paradigm for modeling sophisticated uncertainty in decision systems.

The multi-attribute group decision-making algorithm proposed in this paper is discussed in the environment of interval-valued intuitionistic fuzzy sets, so we will list the related theories of interval-valued intuitionistic fuzzy sets.

Definition 1.

X is a non-empty set and the interval-valued intuitionistic fuzzy set is as follows:

$$A=\left\{<x,({\mu }_A\left(x\right),v_A\left(x\right))>|x\in X\right\}.$$

(1)

where ${\mu }_A\left(x\right)$ and $v_A\left(x\right)$ represent the membership interval-valued and non-membership interval-valued of $x\in X$, respectively. They can be expressed by the interval-valued as:

$${\mu }_A\left(x\right)=[{\mu }_A^{-}\left(x\right),{\mu }_A^{+}\left(x\right)],v_A\left(x\right)=[v_A^{-}\left(x\right),v_A^{+}\left(x\right)],$$

(2)

and they satisfy ${\mu }_A\left(x\right)\subseteq [0,1]$, $v_A\left(x\right)\subseteq [0,1]$ and $0\le {\mu }_A^{+}\left(x\right)+v_A^{+}\left(x\right)\le 1$. When ${\mu }_A^{-}\left(x\right)={\mu }_A^{+}\left(x\right)$ and $v_A^{-}\left(x\right)=v_A^{+}\left(x\right)$, interval-valued intuitionistic fuzzy sets degenerate into intuitionistic fuzzy sets. At the same time, for $\forall x\in X$, its hesitation interval-valued can be expressed as:

$${\pi }_A\left(x\right)=[{\pi }_A^{-}\left(x\right),{\pi }_A^{+}\left(x\right)]=[1-{\mu }_A^{+}\left(x\right)-v_A^{+}\left(x\right),1-{\mu }_A^{-}\left(x\right)-v_A^{-}\left(x\right)].$$

(3)

Definition 2.

If

$$\begin{array}{c}\hfill A_x=<{\mu }_A\left(x\right),v_A\left(x\right)>=<[{\mu }_A^{-}\left(x\right),{\mu }_A^{+}\left(x\right)],[v_A^{-}\left(x\right),v_A^{+}\left(x\right)]>,\\ \hfill B_x=<{\mu }_B\left(x\right),v_B\left(x\right)>=<[{\mu }_B^{-}\left(x\right),{\mu }_B^{+}\left(x\right)],[v_B^{-}\left(x\right),v_B^{+}\left(x\right)]>,\end{array}$$

are any two interval-valued intuitionistic fuzzy sets, λ is any real number greater than 0, then there are the following operation rules [9]:

1. 

$A_x\oplus B_x=<[{\mu }_A^{-}\left(x\right)+{\mu }_B^{-}\left(x\right)-{\mu }_A^{-}\left(x\right)·{\mu }_B^{-}\left(x\right),{\mu }_A^{+}\left(x\right)+{\mu }_B^{+}\left(x\right)-{\mu }_A^{+}\left(x\right)·{\mu }_B^{+}\left(x\right)],[v_A^{-}\left(x\right)·v_B^{-}\left(x\right),v_A^{+}\left(x\right)·v_B^{+}\left(x\right)]>;$

2. 

$A_x\otimes B_x=<[{\mu }_A^{-}\left(x\right)·{\mu }_B^{-}\left(x\right),{\mu }_A^{+}\left(x\right)·{\mu }_B^{+}\left(x\right)],[v_A^{-}\left(x\right)+v_B^{-}\left(x\right)-v_A^{-}\left(x\right)·v_B^{-}\left(x\right),v_A^{+}\left(x\right)+v_B^{+}\left(x\right)-v_A^{+}\left(x\right)·v_B^{+}\left(x\right)]>;$

3. 

$\lambda ·A_x=<[1-{(1-{\mu }_A^{-}\left(x\right))}^{\lambda },1-{(1-{\mu }_A^{+}\left(x\right))}^{\lambda }],[{\left(v_A^{-}\left(x\right)\right)}^{\lambda },{\left(v_A^{+}\left(x\right)\right)}^{\lambda }]>;$

4. 

${\left(A_x\right)}^{\lambda }=<[{\left({\mu }_A^{-}\left(x\right)\right)}^{\lambda },{\left({\mu }_A^{+}\left(x\right)\right)}^{\lambda }],[1-{(1-v_A^{-}\left(x\right))}^{\lambda },1-{(1-v_A^{+}\left(x\right))}^{\lambda }]>.$

Definition 3.

If

$$\begin{array}{c}\hfill A_x=<{\mu }_A\left(x\right),v_A\left(x\right)>=<[{\mu }_A^{-}\left(x\right),{\mu }_A^{+}\left(x\right)],[v_A^{-}\left(x\right),v_A^{+}\left(x\right)]>,\\ \hfill B_x=<{\mu }_B\left(x\right),v_B\left(x\right)>=<[{\mu }_B^{-}\left(x\right),{\mu }_B^{+}\left(x\right)],[v_B^{-}\left(x\right),v_B^{+}\left(x\right)]>,\\ \hfill C_x=<{\mu }_C\left(x\right),v_C\left(x\right)>=<[{\mu }_C^{-}\left(x\right),{\mu }_C^{+}\left(x\right)],[v_C^{-}\left(x\right),v_C^{+}\left(x\right)]>,\end{array}$$

are any two interval-valued intuitionistic fuzzy sets, then the lower bound $p^{-}(A_x\supseteq B_x)$ of the inclusion comparison possibility [9,25] of $A_x$ and $B_x$ is defined as:

$$p^{-}(A_x\supseteq B_x)=max\left\{1-max\left\{{\displaystyle \frac{(1-v_B^{-}\left(x\right))-{\mu }_A^{-}\left(x\right)}{(1-{\mu }_A^{-}\left(x\right)-v_A^{+}\left(x\right))+(1-{\mu }_B^{+}\left(x\right)-v_B^{-}\left(x\right))}},0\right\},0\right\}.$$

(4)

And the upper bound $p^{+}(A_x\supseteq B_x)$ of the inclusion comparison possibility of $A_x$ and $B_x$ is defined as:

$$p^{+}(A_x\supseteq B_x)=max\left\{1-max\left\{{\displaystyle \frac{(1-v_B^{+}\left(x\right))-{\mu }_A^{+}\left(x\right)}{(1-{\mu }_A^{+}\left(x\right)-v_A^{-}\left(x\right))+(1-{\mu }_B^{-}\left(x\right)-v_B^{+}\left(x\right))}},0\right\},0\right\}.$$

(5)

Then the inclusion comparison possibility $p(A_x\supseteq B_x)$ of $A_x$ and $B_x$ is defined as:

$$p(A_x\supseteq B_x)={\displaystyle \frac{1}{2}}(p^{-}(A_x\supseteq B_x)+p^{+}(A_x\supseteq B_x)),$$

(6)

and thus, the degree that $A_x$ is not smaller than $B_x$ is $p(A_x\supseteq B_x)$. Then $p(A_x\supseteq B_x)$ has the following properties:

1. 

$0\le p(A_x\supseteq B_x)\le 1;$

2. 

$p(A_x\supseteq B_x)+p(A_x\subseteq B_x)=1;$

3. 

$p(A_x\supseteq B_x)\ge 0.5$ if $p(A_x\supseteq C_x)\ge 0.5$ and $p(C_x\supseteq B_x)\ge 0.5$.

So $p(A_x\supseteq B_x)$ satisfies complementary symmetry.

Definition 4.

If

$$A_x=\left\{<x_i,[{\mu }_A^{-}\left(x_i\right),{\mu }_A^{+}\left(x_i\right)],[v_A^{-}\left(x_i\right),v_A^{+}\left(x_i\right)]>|x_i\in X\right\},$$

is any interval intuitionistic fuzzy set, Cui-Ping et al. [26] defined its fuzzy entropy as:

$$E\left(A\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{2-\left|{\mu }_A^{-}\left(x_i\right)-v_A^{-}\left(x_i\right)\right|-\left|{\mu }_A^{+}\left(x_i\right)-v_A^{+}\left(x_i\right)\right|+{\pi }_A^{-}\left(x_i\right)+{\pi }_A^{+}\left(x_i\right)}{2+\left|{\mu }_A^{-}\left(x_i\right)-v_A^{-}\left(x_i\right)\right|+\left|{\mu }_A^{+}\left(x_i\right)-v_A^{+}\left(x_i\right)\right|+{\pi }_A^{-}\left(x_i\right)+{\pi }_A^{+}\left(x_i\right)}},$$

(7)

obviously $0\le E\left(A\right)\le 1$.

3. Improved Fuzzy Multi-Attribute Group Decision-Making Method

3.1. Fuzzy Multi-Attribute Group Decision-Making Problem

Given the increasing complexity of decision-making environments and challenges, fuzzy multi-attribute group decision-making (FMAGDM) methods for addressing evaluation and selection problems have garnered significant scholarly attention. Although diverse FMAGDM methodologies exist, they invariably entail three core phases: fuzzification processing to model uncertain information, assignment of expert weights to integrate multi-source judgments, and determination of attribute weights to quantify criterion importance. When addressing MAGDM problems, the following assumptions may be adopted:

1.

l decision makers;

2.

m alternatives;

3.

n indicators of each alternative.

Expertsneed to evaluate each index of each alternative semantically, among which the k-th decision maker is marked as $D_k$, the i-th alternative is marked as $A_i$, and the j-th indicator is marked as $x_j$. The following Figure 1 shows the process of solving the fuzzy multi-attribute group decision-making problem.

Building upon the enhanced TOPSIS method in [9], this work formalizes semantic evaluations of the i-th alternative’s j-th attribute by the k-th expert using interval-valued intuitionistic fuzzy sets, denoted as $A_{ij}^k=<[{\mu }_{ij}^{k-},{\mu }_{ij}^{k+}],[v_{ij}^{k-},v_{ij}^{k+}]>$. Optimization models subsequently determine expert and attribute weights, with constraints incorporable per practical requirements. This dual-weighting approach integrates objective data utilization while incorporating subjective intentions, ultimately enabling alternative ranking to form a complete fuzzy multi-attribute group decision-making method for resolving complex MAGDM problems.

Consider the following real-world multi-attribute group decision-making scenario. Jack seeks to purchase a new mobile phone but cannot immediately decide among numerous market brands. He therefore convenes a decision group comprising himself ($D_1$), his father ($D_2$), mother ($D_3$), sister ($D_4$), and friend Ahn ($D_5$) to conduct semantic evaluations of three alternative models ($A_1$, $A_2$, $A_3$). Evaluations are performed across five attributes: battery life ($x_1$), design ($x_2$), price ($x_3$), camera functionality ($x_4$), and performance ($x_5$), where price ($x_3$) is the sole cost criterion, while all others are benefit criteria. Ultimately, Jack selects the alternative with the highest aggregated evaluation.

3.2. Determination of Expert Weight Based on Optimization Model

Liu et al. [17] assert that experts vary considerably in their domain expertise and knowledge, necessitating differential weighting where greater weight is assigned to those with extensive experience and comprehensive understanding of decision contexts. Specifically, experts whose evaluations demonstrate higher consistency with the collective assessment provide more valuable references, thus warranting greater weight allocation. Building on this principle, we establish an optimization model incorporating decision-makers’ subjective inputs as constraints, enabling expert weight determination through integrated subjective–objective methodology. Consider the decision matrix $A_{\left(i\right)}$ for the i-th alternative:

$$A_{\left(i\right)}=\left(\begin{array}{cccc}{A}_{\left(i\right)}^1& A_{\left(i\right)}^2& \dots & A_{\left(i\right)}^l\end{array}\right),$$

(8)

Let $A_{\left(i\right)}^k={\left(\begin{array}{cccc}{A}_{i1}^k& A_{i2}^k& \dots & A_{in}^k\end{array}\right)}^T$ represent the k-th expert’s evaluation of the i-th alternative, with corresponding expert weights $\mathit{w}={\left(\begin{array}{cccc}{w}_1& w_2& \dots & w_l\end{array}\right)}^T$. Each alternative’s consistent score is derived from a linear combination of all l expert evaluations. Given the interval-valued intuitionistic fuzzy representation $A_{ij}^k=<[{\mu }_{ij}^{k-},{\mu }_{ij}^{k+}],[v_{ij}^{k-},v_{ij}^{k+}]>$ for the k-th expert’s assessment of the i-th alternative’s j-th attribute, we extend Liu et al.’s optimization model [17] to this framework. Since each $A_{ij}^k$ comprises four distinct values, decomposing the interval-valued intuitionistic fuzzy sets results in a fourfold increase in dimensionality for the evaluation column vector of the k-th expert’s assessment of the i-th alternative.

$$A_{\left(i\right)}^k={\left(\begin{array}{cccccccccccc}{\mu }_{i1}^{k-}& \dots & {\mu }_{in}^{k-}& {\mu }_{i1}^{k+}& \dots & {\mu }_{in}^{k+}& v_{i1}^{k-}& \dots & v_{in}^{k-}& v_{i1}^{k+}& \dots & v_{in}^{k+}\end{array}\right)}^T.$$

(9)

Then the consistent score point corresponding to the i-th alternative can be expressed as:

$${\mathit{b}}_{\left(i\right)}=\sum _{k=1}^l{w}_k·A_{\left(i\right)}^k=\left(\begin{array}{c}\sum _{k=1}^l{w}_k·{\mu }_{i1}^{k-}\\ ⋮\\ \sum _{k=1}^l{w}_k·{\mu }_{in}^{k-}\\ \sum _{k=1}^l{w}_k·{\mu }_{i1}^{k+}\\ ⋮\\ \sum _{k=1}^l{w}_k·{\mu }_{in}^{k+}\\ \sum _{k=1}^l{w}_k·v_{i1}^{k-}\\ ⋮\\ \sum _{k=1}^l{w}_k·v_{in}^{k-}\\ \sum _{k=1}^l{w}_k·v_{i1}^{k+}\\ ⋮\\ \sum _{k=1}^l{w}_k·v_{in}^{k+}\end{array}\right),$$

(10)

which reflects the overall evaluation results of experts on the i-th alternative.

And all alternatives are treated equally, so the decision matrix $A_{\left(i\right)}$ corresponding to each alternative can be assembled into an overall decision matrix

$$A={\left(\begin{array}{cccc}{A}_{\left(1\right)}& A_{\left(2\right)}& \dots & A_{\left(m\right)}\end{array}\right)}^T,$$

with determining the expert weight, where the k-th column $A^{\left(k\right)}$ of A represents the evaluation results of all alternatives by the k-th expert. Then the overall consistent score point is $\mathit{b}={\left(\begin{array}{cccc}{\mathit{b}}_{\left(1\right)}& {\mathit{b}}_{\left(2\right)}& \dots & {\mathit{b}}_{\left(m\right)}\end{array}\right)}^T$, and thus, the distance from the evaluation results $A^{\left(k\right)}$ of all alternatives by the k-th expert to the overall consistent score point $\mathit{b}$ is:

$$d_{\left(k\right)}={∥A^{\left(k\right)}-\mathit{b}∥}_2.$$

Finally, we can establish an optimization model as follows:

$$\begin{array}{cc}\hfill & \underset{\mathit{w}}{min}Q\left(\mathit{w}\right)=\sum _{k=1}^l{d}_{\left(k\right)}\hfill \\ \hfill & s.t.\left\{\begin{array}{c}\sum _{k=1}^l{w}_k=1,\hfill \\ 0\le w_k\le 1,1\le k\le l.\hfill \end{array}\right.\hfill \end{array}$$

(11)

The optimization model establishes that expert weights are inversely proportional to the distance between individual evaluations and the overall consistent score—experts with evaluations closer to the consensus receive higher weights. For instance, Figure 2 demonstrates that the resulting expert weights after optimization follow $w_4>w_2>w_1>w_5>w_3$.

Furthermore, additional constraints can be incorporated into the optimization model, such as assigning maximum weight to authoritative experts. This approach demonstrates that expert weights are mathematically inversely proportional to their evaluation’s distance from the consistent score—the closer an expert’s assessment aligns with the consensus, the higher their assigned weight.

Example 1.

Here are four experts evaluating two alternatives, each of which has three indicators. See

Table 1. Example 1.

Alternatives	Indicators	Decision Makers
		Expert 1	Expert 2	Expert 3	Expert 4
Alternative 1	Indicator 1	H	M	H	VH
	Indicator 2	M	H	M	L
	Indicator 3	L	VH	M	H
Alternative 2	Indicator 1	M	H	VH	M
	Indicator 2	H	VH	M	L
	Indicator 3	L	M	H	VL

for details.

Table 2. Linguistic evaluation and corresponding interval-valued intuitionistic fuzzy sets [9].

Linguistic Evaluation	Interval-Valued Intuitionistic Fuzzy Sets
Very high (VH)	$<[0.75,0.95],[0.00,0.05]>$
High (H)	$<[0.50,0.70],[0.05,0.25]>$
Medium (M)	$<[0.30,0.50],[0.20,0.40]>$
Low (L)	$<[0.05,0.25],[0.50,0.70]>$
Very low (VL)	$<[0.00,0.05],[0.75,0.95]>$

shows the interval-valued intuitionistic fuzzy sets corresponding to different linguistic evaluations.

The optimization model (11) yields results presented in

Table 3. Results.

Decision Maker	Expert 1	Expert 2	Expert 3	Expert 4
Weight	0.29501	0.21857	0.30683	0.17959
Distance to overall consistent score point	0.78239	1.05610	0.75226	1.28546
Corresponding product	0.23081	0.23082	0.23082	0.23085

, demonstrating that expert weights are mathematically inversely proportional to the distance between individual evaluations and the overall consistent score. Experts whose evaluations align more closely with the consensus receive higher weights, validating the model’s intended design.

3.3. Improved TOPSIS Method

While [9] developed an improved TOPSIS method for multi-attribute group decision making, they assigned expert weights directly without detailing their derivation methodology. This work extends their framework by calculating expert weights through our newly proposed method. Subsequently, integrating these weights with the enhanced TOPSIS approach from [9] enables comprehensive resolution of multi-attribute group decision problems. The complete procedure unfolds as follows.

Firstly, after obtaining the expert weight $\mathit{w}$ according to the optimization model, we can weight the evaluation $A_{ij}^k$ of the j-th indicator of the i-th alternative by the k-th decision-maker to get ${\underset{·}{A}}_{ij}^k$:

$${\underset{·}{A}}_{ij}^k=l·w_k·A_{ij}^k\triangleq <[{\underset{·}{\mu }}_{ij}^{k-},{\underset{·}{\mu }}_{ij}^{k+}],[{\underset{·}{v}}_{ij}^{k-},{\underset{·}{v}}_{ij}^{k+}]>.$$

(12)

Secondly, according to [9], the optimal membership degree $p\left({\underset{·}{A}}_{ij}^k\right)$ of ${\underset{·}{A}}_{ij}^k$ can be calculated according to the following formula:

$$p\left({\underset{·}{A}}_{ij}^k\right)={\displaystyle \frac{1}{l(l-1)}}(\sum _{k^{\prime }=1}^{l}p({\underset{·}{A}}_{ij}^k\supseteq {\underset{·}{A}}_{ij}^{k^{\prime }})+{\displaystyle \frac{l}{2}}-1).$$

(13)

According to the above calculation, the interval-valued intuitionistic fuzzy order weighted average (IIOWA) operator [27,28] can be extended to get the comprehensive decision matrix D. The specific steps are as follows:

• Reorder $\left(\begin{array}{cccc}1& 2& \dots & l\end{array}\right)$ to $\left(\begin{array}{cccc}\sigma \left(1\right)& \sigma \left(2\right)& \dots & \sigma \left(l\right)\end{array}\right)$, which satisfies $p\left({\underset{·}{A}}_{ij}^{\sigma (k-1)}\right)\ge p\left({\underset{·}{A}}_{ij}^{\sigma \left(k\right)}\right)$;
• Calculate the weight vector $\mathit{\tau }={\left(\begin{array}{cccc}{\tau }_1& {\tau }_2& \dots & {\tau }_l\end{array}\right)}^T$ of IIOWA operator:

  $${\tau }_k={\displaystyle \frac{e^{-({(k-u_l)}^2/2·t_l^2)}}{{\sum }_{k^{\prime }=1}^l{e}^{-({(k^{\prime }-u_l)}^2/2·t_l^2)}}},$$

  (14)

  where $u_l$ is the average value of $1,2,\dots ,l$ and $t_l$ is the corresponding standard deviation.
• Using IIOWA operator to calculate the element $A_{ij}$ in row i and column j of the comprehensive decision matrix D:

  $$A_{ij}=<{[1-\prod _{k=1}^1{(1-{\underset{·}{\mu }}_{ij}^{\sigma (k)-})}^{{\tau }_k},1-\prod _{k=1}^1{\underset{·}{\mu }}_{ij}^{\sigma (k)+})}^{{\tau }_k}],[\prod _{k=1}^1{({\underset{·}{v}}_{ij}^{\sigma (k)-})}^{{\tau }_k},\prod _{k=1}^1{({\underset{·}{v}}_{ij}^{\sigma (k)+})}^{{\tau }_k}]>,$$

  which represents the comprehensive evaluation of the j-th indicator of the i-th alternative by all experts, and is abbreviated as $A_{ij}=<[{\mu }_{ij}^{-},{\mu }_{ij}^{+}],[v_{ij}^{-},v_{ij}^{+}]>$.

The synthesized decision matrix D simultaneously captures the differential importance of experts while preserving the collective consistency of their evaluations. Subsequently, the positive and negative ideal solutions for interval-valued intuitionistic fuzzy sets are derived from D:

$$\begin{array}{c}\hfill A_{+}=\left\{<x_j,([{\mu }_{+j}^{-},{\mu }_{+j}^{+}],[v_{+j}^{-},v_{+j}^{+}])>|x_j\in X,j=1,2,\dots ,n\right\},\end{array}$$

(15)

$$\begin{array}{c}\hfill A_{-}=\left\{<x_j,([{\mu }_{-j}^{-},{\mu }_{-j}^{+}],[v_{-j}^{-},v_{-j}^{+}])>|x_j\in X,j=1,2,\dots ,n\right\},\end{array}$$

(16)

where

$$\begin{array}{c}\hfill [{\mu }_{+j}^{-},{\mu }_{+j}^{+}]=[(\left(\underset{i}{max}{\mu }_{ij}^{-}\right|x_j\in X_b),\left(\underset{i}{min}{\mu }_{ij}^{-}\right|x_j\in X_c)),(\left(\underset{i}{max}{\mu }_{ij}^{+}\right|x_j\in X_b),\left(\underset{i}{min}{\mu }_{ij}^{+}\right|x_j\in X_c))],\\ \hfill [v_{+j}^{-},v_{+j}^{+}]=[(\left(\underset{i}{min}{v}_{ij}^{-}\right|x_j\in X_b),\left(\underset{i}{max}{v}_{ij}^{-}\right|x_j\in X_c)),(\left(\underset{i}{min}{v}_{ij}^{+}\right|x_j\in X_b),\left(\underset{i}{max}{v}_{ij}^{+}\right|x_j\in X_c))],\\ \hfill [{\mu }_{-j}^{-},{\mu }_{-j}^{+}]=[(\left(\underset{i}{min}{\mu }_{ij}^{-}\right|x_j\in X_b),\left(\underset{i}{max}{\mu }_{ij}^{-}\right|x_j\in X_c)),(\left(\underset{i}{min}{\mu }_{ij}^{+}\right|x_j\in X_b),\left(\underset{i}{max}{\mu }_{ij}^{+}\right|x_j\in X_c))],\\ \hfill [v_{-j}^{-},v_{-j}^{+}]=[(\left(\underset{i}{max}{v}_{ij}^{-}\right|x_j\in X_b),\left(\underset{i}{min}{v}_{ij}^{-}\right|x_j\in X_c)),(\left(\underset{i}{max}{v}_{ij}^{+}\right|x_j\in X_b),\left(\underset{i}{min}{v}_{ij}^{+}\right|x_j\in X_c))].\end{array}$$

Also, $X_b$ represents the benefit indicator, and $X_c$ represents the cost indicator in the indicator. Finally, assuming that the attribute weight is $\overline{\mathit{w}}={\left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)}^T$, we can improve the closeness index of the i-th alternative to be $CC\left(A_i\right)$:

$$\begin{array}{cc}\hfill CC\left(A_i\right)=& \sum _{j=1}^{n}p\left((A_{ij}\supseteq A_{-j}\mid x_j\in X_b),(A_{-j}\supseteq A_{ij}\mid x_j\in X_c)\right){\overline{w}}_j·\hfill \\ \hfill & \{\sum _{j=1}^n[\left(p(A_{+j}\supseteq A_{ij})+p(A_{ij}\supseteq A_{-j})\mid x_j\in X_b\right),\hfill \\ \hfill & \left(p(A_{ij}\supseteq A_{+j})+p(A_{-j}\supseteq A_{ij})\mid x_j\in X_c\right)]{\overline{w}}_j{\}}^{-1},\hfill \end{array}$$

(17)

where $0\le CC\left(A_i\right)\le 1(i=1,2,\dots ,m)$. For the j-th indicator of the i-th alternative, if it belongs to the benefit indicator, the inclusion comparison possibility $p(A_{ij}\supseteq A_{-j})$ with $A_{ij}$ not less than $A_{-j}$ and the inclusion comparison possibility $p(A_{+j}\supseteq A_{ij})$ with $A_{ij}$ not greater than $A_{+j}$ are calculated. At this time, if there is a higher possibility that $A_{ij}$ is better than $A_{+j}$ and a lower possibility that $A_{ij}$ is worse than $A_{-j}$, then the j-th indicator of the i-th alternative has a good performance. And the same is true for the cost indicator. Therefore, we can sort the closeness index $CC\left(A_i\right)$ and choose the alternative with the largest index value as the optimal alternative.

3.4. Optimization Model for Determination of Attribute Weight

While the initial two components propose a novel expert weighting method integrated with the improved TOPSIS approach from [9]—enabling multi-attribute group decision resolution through enhanced closeness indices $CC\left(A_i\right)$—they do not address attribute weight determination. Although Ting-Yu [9] established attribute weights by maximizing alternative closeness values when weights are unknown, our work advances a more interpretable and concise optimization model for attribute weight derivation. The methodology proceeds as follows.

When attribute weights are unknown, entropy theory dictates that attributes exhibiting low fuzzy entropy across alternatives provide greater discriminative information for decision making and should consequently receive higher weights. Conversely, attributes with high entropy are typically deemed less significant by decision-makers and warrant minimal weighting [29,30]. The entropy weight $w_j^E$ for attribute $x_j$ is then calculated as follows:

$$w_j^E={\displaystyle \frac{1-E\left(x_j\right)}{{\sum }_{i=1}^{n}1-E\left(x_j\right)}},$$

(18)

Here $E\left(x_j\right)$ denotes the entropy value of attribute $x_j$. However, as the entropy weighting method operates purely objectively—considering only data patterns while disregarding expert opinions and project-specific requirements—we establish the following entropy-based optimization model:

$$\begin{array}{cc}\hfill & max\sum _{j=1}^n{\overline{w}}_j·(1-E\left(x_j\right))\hfill \\ \hfill & s.t.\left\{\begin{array}{c}\sum _{j=1}^n{\overline{w}}_j=1,\hfill \\ {\overline{w}}_j\ge 0,j=1,2,\dots ,n.\hfill \end{array}\right.\hfill \end{array}$$

(19)

and

$${\Gamma }_0=\left\{\left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)|\sum _{j=1}^n{\overline{w}}_j=1,{\overline{w}}_j\ge 0,j=1,2,\dots ,n\right\}.$$

(20)

Solving the optimization model yields attribute weights $\left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)=\left(\begin{array}{ccccccc}0& \dots & 0& 1& 0& \dots & 0\end{array}\right)$, assigning unit weight solely to the attribute with minimal fuzzy entropy while zeroing others. This impractical outcome stems from the model’s failure to incorporate expert knowledge and project-specific constraints. Consequently, practitioners typically impose weight restrictions based on expert judgment, expressible through five constraint forms: weak ranking, strict ranking, ranking differences, interval boundaries, or proportional boundaries. Given the inherent variability in expert opinions, we introduce non-negative deviation variables:

$$e_{\left(1\right)j_1{j}_2}^{-},e_{\left(2\right)j_1{j}_2}^{-},e_{\left(3\right)j_1{j}_2{j}_3}^{-},e_{\left(4\right)j_1}^{-},e_{\left(4\right)j_1}^{+},e_{\left(5\right)j_1{j}_2}^{-}(j_1\ne j_2\ne j_3),$$

(21)

which can be added to the five types of constraints to become the relaxed five types of constraints.

• Relaxed weak ranking:

  $${\Gamma }_1=\left\{\left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)\in {\Gamma }_0|{\overline{w}}_{j_1}+e_{\left(1\right)j_1{j}_2}^{-}\ge {\overline{w}}_{j_2},j_1\in {{\rm Y}}_1,j_2\in {\Lambda }_1\right\},$$

  where ${{\rm Y}}_1$ and ${\Lambda }_1$ are two disjoint subsets in index set $N=\left\{1,2,\dots ,n\right\}$.
• Relaxed strict ranking:

  $${\Gamma }_2=\left\{\left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)\in {\Gamma }_0|{\overline{w}}_{j_1}-{\overline{w}}_{j_2}+e_{\left(2\right)j_1{j}_2}^{-}\ge {\delta }_{j_1{j}_2}^{\prime },j_1\in {{\rm Y}}_2,j_2\in {\Lambda }_2\right\},$$

  where ${\delta }_{j_1{j}_2}^{\prime }$ is a constant and ${\delta }_{j_1{j}_2}^{\prime }\ge 0$, ${{\rm Y}}_2$ and ${\Lambda }_2$ are two disjoint subsets in index set N.
• Relaxed ranking of differences:

  $${\Gamma }_3=\left\{\left[\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right]\in {\Gamma }_0|\begin{array}{cc}\hfill & {\overline{w}}_{j_1}-2{\overline{w}}_{j_2}+{\overline{w}}_{j_3}+e_{\left(3\right)j_1{j}_2{j}_3}^{-}\ge 0,\hfill \\ \hfill & j_1\in {{\rm Y}}_3,j_2\in {\Lambda }_3,j_3\in {\Omega }_3\hfill \end{array}\right\}$$

  (22)

  where ${{\rm Y}}_3$, ${\Lambda }_3$ and ${\Omega }_3$ are three disjoint subsets in index set N.
• Relaxed interval-valued boundary:

  $${\Gamma }_4=\left\{\left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)\in {\Gamma }_0|{\overline{w}}_{j_1}+e_{\left(4\right)j_1}^{-}\ge {\delta }_{j_1},{\overline{w}}_{j_1}-e_{\left(4\right)j_1}^{+}\le {\delta }_{j_1}+{\epsilon }_{j_1},j_1\in {{\rm Y}}_4\right\},$$

  where ${\delta }_{j_1}$ and ${\epsilon }_{j_1}$ are constants, which satisfy ${\delta }_{j_1}\ge 0$, ${\epsilon }_{j_1}\ge 0$, $0\le {\delta }_{j_1}\le {\delta }_{j_1}+{\epsilon }_{j_1}\le 1$, ${{\rm Y}}_4$ is a subset in index set N.
• Relaxed proportional boundary:

  $${\Gamma }_5=\left\{\left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)\in {\Gamma }_0|{\displaystyle \frac{{\overline{w}}_{j_1}}{{\overline{w}}_{j_2}}}+e_{\left(5\right)j_1{j}_2}^{-}\ge {\delta }_{j_1{j}_2}^{\prime \prime },j_1\in {{\rm Y}}_5,j_2\in {\Lambda }_5\right\},$$

  where ${\delta }_{j_1{j}_2}^{\prime \prime }$ is a constant and $0\le {\delta }_{j_1{j}_2}^{\prime }\le 1$, ${{\rm Y}}_5$ and ${\Lambda }_5$ are two disjoint subsets in index set N.

And let $\Gamma$ be the sum of the five kinds of relaxed constraints: $\Gamma ={\Gamma }_1\cup {\Gamma }_2\cup {\Gamma }_3\cup {\Gamma }_4\cup {\Gamma }_5$.

Evidently, minimizing expert input during attribute weight constraint specification facilitates more conclusive weight determination. Consequently, we aim to minimize these non-negative deviation variables. Augmenting the preceding optimization model with this objective yields the refined formulation:

$$\begin{array}{cc}\hfill & max\sum _{j=1}^n{\overline{w}}_j·(1-E\left(x_j\right))\hfill \\ \hfill & min\left\{\sum _{j_1,j_2,j_3\in N}(e_{\left(1\right)j_1{j}_2}^{-}+e_{\left(2\right)j_1{j}_2}^{-}+e_{\left(3\right)j_1{j}_2{j}_3}^{-}+e_{\left(4\right)j_1}^{-}+e_{\left(4\right)j_1}^{+}+e_{\left(5\right)j_1{j}_2}^{-})\right\}\hfill \\ \hfill & s.t.\left\{\begin{array}{c}\left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)\in \Gamma .\hfill \\ e_{\left(1\right)j_1{j}_2}^{-}\ge 0,j_1\in {{\rm Y}}_1,j_2\in {\Lambda }_1.\hfill \\ e_{\left(2\right)j_1{j}_2}^{-}\ge 0,j_1\in {{\rm Y}}_2,j_2\in {\Lambda }_2.\hfill \\ e_{\left(3\right)j_1{j}_2{j}_3}^{-}\ge 0,j_1\in {{\rm Y}}_3,j_2\in {\Lambda }_3,j_3\in {\Omega }_3.\hfill \\ e_{\left(4\right)j_1}^{-}\ge 0,e_{\left(4\right)j_1}^{+}\ge 0,j_1\in {{\rm Y}}_4.\hfill \\ e_{\left(5\right)j_1{j}_2}^{-}\ge 0,j_1\in {{\rm Y}}_5,j_2\in {\Lambda }_5.\hfill \end{array}\right.\hfill \end{array}$$

(23)

In order to facilitate the solution, the above model can be transformed into a single-objective optimization model by using the max–min operator of Zimmermann and Zysno [31]:

$$\begin{array}{cc}\hfill & max\vartheta \hfill \\ \hfill & s.t.\left\{\begin{array}{c}\sum _{j=1}^n{\overline{w}}_j·(1-E\left(x_j\right))\ge \vartheta ,\hfill \\ -\sum _{j_1,j_2,j_3\in N}(e_{\left(1\right)j_1{j}_2}^{-}+e_{\left(2\right)j_1{j}_2}^{-}+e_{\left(3\right)j_1{j}_2{j}_3}^{-}+e_{\left(4\right)j_1}^{-}+e_{\left(4\right)j_1}^{+}+e_{\left(5\right)j_1{j}_2}^{-})\ge \vartheta ,\hfill \\ \left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)\in \Gamma .\hfill \\ e_{\left(1\right)j_1{j}_2}^{-}\ge 0,j_1\in {{\rm Y}}_1,j_2\in {\Lambda }_1.\hfill \\ e_{\left(2\right)j_1{j}_2}^{-}\ge 0,j_1\in {{\rm Y}}_2,j_2\in {\Lambda }_2.\hfill \\ e_{\left(3\right)j_1{j}_2{j}_3}^{-}\ge 0,j_1\in {{\rm Y}}_3,j_2\in {\Lambda }_3,j_3\in {\Omega }_3.\hfill \\ e_{\left(4\right)j_1}^{-}\ge 0,e_{\left(4\right)j_1}^{+}\ge 0,j_1\in {{\rm Y}}_4.\hfill \\ e_{\left(5\right)j_1{j}_2}^{-}\ge 0,j_1\in {{\rm Y}}_5,j_2\in {\Lambda }_5.\hfill \end{array}\right.\hfill \end{array}$$

(24)

Integrating entropy theory with expert insights, we formulate an optimization model distinguished by strong interpretability and structural simplicity. This approach incorporates both objective data patterns and subjective expert judgments, enabling the derivation of practically significant attribute weights for multi-attribute group decision resolution. Additionally, supplementary constraints reflecting project-specific requirements may be incorporated to further refine attribute weighting.

3.5. The Complete Algorithm

This paper systematically integrates four key methodologies: interval-valued intuitionistic fuzzy sets, expert weight determination via optimization modeling, enhanced TOPSIS decision making, and attribute weight optimization. Our novel integration framework comprehensively resolves multi-attribute group decision-making problems, enabling final decision formulation. The complete methodological architecture is illustrated in Figure 3.

Figure 3 illustrates the integrated methodology. Semantic evaluations are first fuzzified using interval-valued intuitionistic fuzzy sets; an optimization model then determines expert weights; subsequently, the enhanced closeness index $CC\left(A_i\right)$ is derived via TOPSIS; attribute weights are next established through an entropy-based optimization model; finally, incorporating these weights into $CC\left(A_i\right)$ enables alternative ranking. Crucially, both optimization models leverage objective data patterns while incorporating subjective decision-maker inputs, maintaining strong interpretability and computational efficiency throughout. The complete algorithmic implementation is presented in Algorithm 1.

Algorithm 1 The complete algorithm.

Input:  Semantic evaluation of n indicators of m alternatives by l experts. Output:  The ranking of m alternatives.   1: The collected semantic evaluation is transformed into interval-valued intuitionistic fuzzy set $A_{ij}^k(i=1,2,\dots ,m;j=1,2,\dots ,n;k=1,2,\dots ,l)$.   2: Calculate the distance $d_{\left(k\right)}={∥A^{\left(k\right)}-\mathit{b}∥}_2$, where $A^{\left(k\right)}$ is the evaluation result of all alternatives by the k-th expert $(k=1,2,\dots ,l)$ and $\mathit{b}$ is the overall consistent score point.   3: Establish the optimization model (11) and get the expert weight $\mathit{w}={\left(\begin{array}{cccc}{w}_1& w_2& \dots & w_l\end{array}\right)}^T$.   4: Weight the evaluation $A_{ij}^k$ to get ${\underset{·}{A}}_{ij}^k$, and calculate the optimal membership $p\left({\underset{·}{A}}_{ij}^k\right)$ of ${\underset{·}{A}}_{ij}^k$.   5: The comprehensive decision matrix D is obtained by using the extension IIOWA operator.   6: Find the positive and negative ideal solutions, and assume that the attribute weight is $\overline{\mathit{w}}={\left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)}^T$ to get the closeness index $CC\left(A_i\right)$ of the i-th alternative.   7: Establish the optimization model (24) and get the attribute weight $\overline{\mathit{w}}={\left(\begin{array}{cccc}{\overline{w}}_1& {\overline{w}}_2& \dots & {\overline{w}}_n\end{array}\right)}^T$.   8: According to the closeness index $CC\left(A_i\right)$, m alternatives can be ranked.

4. Case Study

This section validates the proposed methodology through two multi-attribute group decision-making case studies. First, we resolve the mobile phone selection problem introduced in Section 3.5 using Algorithm 1, demonstrating its practical feasibility and implementation efficiency. Second, we replicate the case study from [9] and conduct comparative analysis to substantiate the enhanced effectiveness and advantages of our algorithm.

4.1. Case 1

For the mobile phone purchase case study in Section 3.5, semantic evaluations of alternatives $A_1$, $A_2$, and $A_3$ are collected from Jack ($D_1$), his father ($D_2$), mother ($D_3$), sister ($D_4$), and friend Ahn ($D_5$). The optimal purchasing decision is then determined through our proposed algorithm.

• We collect the linguistic evaluations of three alternatives from five decision makers across five indicators, as shown in

  Table 4. Linguistic evaluation (Case 1).

  Alternatives	Indicators	Decision Makers
  		${\mathit{D}}_{\mathbf{1}}$	${\mathit{D}}_{\mathbf{2}}$	${\mathit{D}}_{\mathbf{3}}$	${\mathit{D}}_{\mathbf{4}}$	${\mathit{D}}_{\mathbf{5}}$
  $A_1$	$x_1$	VH	H	VH	VH	VH
  	$x_2$	L	M	VL	M	VL
  	$x_3$	M	L	VH	M	L
  	$x_4$	L	H	H	H	M
  	$x_5$	L	H	M	M	VH
  $A_2$	$x_1$	M	VL	H	M	VH
  	$x_2$	L	L	M	L	M
  	$x_3$	VH	VH	H	VH	M
  	$x_4$	VL	M	VL	H	H
  	$x_5$	L	H	VH	M	VH
  $A_3$	$x_1$	L	H	M	L	H
  	$x_2$	L	VH	M	M	VH
  	$x_3$	VH	M	L	L	M
  	$x_4$	M	H	L	VH	VH
  	$x_5$	VH	M	VH	M	M

  , and convert them into interval-valued intuitionistic fuzzy sets according to Table 2.
• Decomposing interval-valued intuitionistic fuzzy sets quadruples the dimensionality of the evaluation column vector for the k-th expert’s assessment of the i-th alternative. The consistent score vector ${\mathit{b}}_{\left(i\right)}$ for the i-th alternative is computed as the linear combination of all l expert evaluations. Subsequently, we aggregate evaluations across alternatives and calculate the distance between each expert’s evaluation matrix $A^k$ and the global consistent score vector $\mathit{b}$.
• Establish the expert weight optimization model:

  $$\begin{array}{cc}\hfill & \underset{\mathit{w}}{min}Q\left(\mathit{w}\right)=\sum _{k=1}^5{d}_{\left(k\right)}\hfill \\ \hfill & s.t.\left\{\begin{array}{c}\sum _{k=1}^5{w}_k=1,\hfill \\ 0\le w_k\le 1,1\le k\le 5.\hfill \end{array}\right.\hfill \end{array}$$

  (25)
  It can be obtained that the weight of three decision makers is

  $$\mathit{w}={\left(\begin{array}{ccccc}0.154362& 0.218228& 0.170675& 0.277186& 0.179549\end{array}\right)}^T.$$
• Through the expert weights obtained above, the evaluation $A_{ij}^k$ is weighted by (12) to get ${\underset{·}{A}}_{ij}^k$, and the optimal membership $p\left({\underset{·}{A}}_{ij}^k\right)$ of ${\underset{·}{A}}_{ij}^k$ is calculated by (13). For example, ${\underset{·}{A}}_{11}^1=<[0.6570,0.9010],[0,0.0990]>$, $p({\underset{·}{A}}_{11}^1\supseteq {\underset{·}{A}}_{11}^2)=0.6788$, $p({\underset{·}{A}}_{11}^1\supseteq {\underset{·}{A}}_{11}^3)=0.4672$ and $p\left({\underset{·}{A}}_{11}^1\right)=0.1958$.
• A comprehensive decision matrix D is obtained by using the extension IIOWA (whose weighted vector is $\tau ={\left(\begin{array}{ccccc}0.1117& 0.2365& 0.3036& 0.2365& 0.1117\end{array}\right)}^T$):

  $$D=\left(\begin{array}{ccc}<[0.7005,0.9234],[0,0.0749]>& \dots & <[0.4198,0.6561],[0,0.2838]>\\ ⋮& \ddots & ⋮\\ <[0.2386,0.4478],[0.2378,0.4832]>& \dots & <[0.5524,0.8163],[0,0.1625]>\end{array}\right).$$
• Use (15) and (16) to find the positive and negative ideal solutions of interval-valued intuitionistic fuzzy solutions corresponding to the comprehensive decision matrix D, and calculate the closeness of each alternative through (17).
• Establish the attribute weight optimization model:

  $$\begin{array}{c}max\vartheta \hfill \\ s.t.\left\{\begin{array}{c}\begin{array}{c}(1-0.4247)·{\overline{w}}_1+(1-0.3804)·{\overline{w}}_2+\hfill \\ (1-0.4508)·{\overline{w}}_3+(1-0.3959)·{\overline{w}}_4+(1-0.5823)·{\overline{w}}_5\ge \vartheta ,\hfill \\ -(e_{\left(1\right)14}^{-}+e_{\left(2\right)52}^{-}+e_{\left(3\right)324}^{-}+e_{\left(4\right)4}^{-}+e_{\left(4\right)4}^{+}+e_{\left(5\right)23}^{-})\ge \vartheta ,\hfill \\ {\overline{w}}_1+e_{\left(1\right)12}^{-}\ge {\overline{w}}_2,{\overline{w}}_5-{\overline{w}}_3+e_{\left(2\right)53}^{-}\ge 0.03,{\overline{w}}_1-2{\overline{w}}_4+{\overline{w}}_3+e_{\left(3\right)143}^{-}\ge 0,\hfill \\ {\overline{w}}_3+e_{\left(4\right)3}^{-}\ge 0.10,{\overline{w}}_3-e_{\left(4\right)3}^{+}\le 0.20,{\displaystyle \frac{{\overline{w}}_4}{{\overline{w}}_5}}+e_{\left(5\right)45}^{-}\ge 0.5,\hfill \\ (e_{\left(1\right)12}^{-}\ge 0,e_{\left(2\right)53}^{-}\ge 0,e_{\left(3\right)143}^{-}\ge 0,e_{\left(4\right)3}^{-}\ge 0,e_{\left(4\right)3}^{+}\ge 0,e_{\left(5\right)45}^{-}\ge 0),\hfill \\ {\overline{w}}_1+{\overline{w}}_2+{\overline{w}}_3+{\overline{w}}_4+{\overline{w}}_5=1,\hfill \\ {\overline{w}}_j\ge 0,j=1,2,\dots ,5.\hfill \end{array}\hfill \end{array}\right.\hfill \end{array}$$

  (26)
  Then the weight of five attributes is $\overline{\mathit{w}}={\left(\begin{array}{ccccc}0.1695& 0.1615& 0.1968& 0.1575& 0.3148\end{array}\right)}^T$.
• Substitute the attribute weights obtained in step 7 into the closeness index to obtain $CC\left(A_1\right)=0.522389$, $CC\left(A_2\right)=0.4553813$, $CC\left(A_3\right)=0.5745725$. According to the closeness, the ranking of each alternative is $A_3>A_1{A}_2$; thus, the optimal alternative is $A_3$.

4.2. Case 2

This section addresses a multi-attribute group decision-making problem using the proposed methodology, replicating the clinical case from [9] for comparative validation. The case involves treatment selection for an 82-year-old hypertensive patient with basilar artery occlusion. Three adult children $\{D_1,D_2,D_3\}$ conduct linguistic evaluations of four treatment alternatives $\{A_1,A_2,A_3,A_4\}$—intravenous thrombolysis, intra-arterial thrombolysis, antiplatelet therapy, and heparinization—across five clinical indicators $\{x_1,x_2,x_3,x_4,x_5\}$: survival rate, complication severity, cure probability, cost, and recurrence risk. Benefit criteria $\{x_1,x_3\}$ and cost criteria $\{x_2,x_4,x_5\}$ are distinguished, with the algorithm enabling final treatment selection.

The algorithm proposed in this paper can be used to make the decision:

• Collect the linguistic evaluation and convert them into interval-valued intuitionistic fuzzy sets according to Table 2, as shown in

  Table 5. Linguistic evaluation (Case 2) [9].

  Alternatives	Indicators	Decision Makers
  		${\mathit{D}}_{\mathbf{1}}$	${\mathit{D}}_{\mathbf{2}}$	${\mathit{D}}_{\mathbf{3}}$
  $A_1$	$x_1$	VH	VH	H
  	$x_2$	M	M	L
  	$x_3$	M	M	H
  	$x_4$	M	M	L
  	$x_5$	M	L	M
  $A_2$	$x_1$	H	H	VH
  	$x_2$	M	H	M
  	$x_3$	VH	H	VH
  	$x_4$	VH	VH	H
  	$x_5$	L	L	VL
  $A_3$	$x_1$	M	L	M
  	$x_2$	L	L	M
  	$x_3$	VL	VL	L
  	$x_4$	L	VL	VL
  	$x_5$	H	VH	VH
  $A_4$	$x_1$	M	H	H
  	$x_2$	VL	M	L
  	$x_3$	L	M	L
  	$x_4$	M	H	L
  	$x_5$	VH	H	VH
  $A_5$	$x_1$	VH	VH	H
  	$x_2$	M	M	L
  	$x_3$	M	M	H
  	$x_4$	M	M	L
  	$x_5$	M	L	M

  .
• Assemble the evaluation results of all alternatives and calculate the distance from the evaluation results $A^k$ of the k-th expert to the overall consistent score point $\mathit{b}$.
• Establish the expert weight optimization model:

  $$\begin{array}{cc}\hfill & \underset{\mathit{w}}{min}Q\left(\mathit{w}\right)=\sum _{k=1}^3{d}_{\left(k\right)}\hfill \\ \hfill & s.t.\left\{\begin{array}{c}\sum _{k=1}^3{w}_k=1,\hfill \\ 0\le w_k\le 1,1\le k\le 3.\hfill \end{array}\right.\hfill \end{array}$$

  (27)
  It can be obtained that the weight of three decision makers is

  $$\mathit{w}={\left(\begin{array}{ccc}0.455887& 0.268183& 0.275930\end{array}\right)}^T.$$
• Through the expert weights obtained above, the evaluation $A_{ij}^k$ is weighted by (12) to get ${\underset{·}{A}}_{ij}^k$, and the optimal membership $p\left({\underset{·}{A}}_{ij}^k\right)$ of ${\underset{·}{A}}_{ij}^k$ is calculated by (13). For example, ${\underset{·}{A}}_{11}^1=<[0.8498,0.9834],[0,0.0166]>$, $p({\underset{·}{A}}_{11}^1\supseteq {\underset{·}{A}}_{11}^2)=0.6638$, $p({\underset{·}{A}}_{11}^1\supseteq {\underset{·}{A}}_{11}^3)=0.9207$ and $p\left({\underset{·}{A}}_{11}^1\right)=0.4308$.
• A comprehensive decision matrix D is obtained by using the extension IIOWA (whose weighted vector is $\tau ={\left(\begin{array}{ccc}0.2429& 0.5142& 0.2429\end{array}\right)}^T$):

  $$D=\left(\begin{array}{ccc}<[0.6907,0.9160],[0,0.0810]>& \dots & <[0.2445,0.4410],[0.2580,0.4657]>\\ ⋮& \ddots & ⋮\\ <[0.4088,0.6190],[0.0983,0.3649]>& \dots & <[0.6946,0.9184],[0,0.0788]>\end{array}\right).$$
• Use (15) and (16) to find the positive and negative ideal solutions of interval-valued intuitionistic fuzzy solutions corresponding to the comprehensive decision matrix D, and calculate the closeness of each alternative through (17).
• Establish the attribute weight optimization model, in which the constraints of experts on attribute weight are the same as that used in [9]:

  $$\begin{array}{c}max\vartheta \hfill \\ s.t.\left\{\begin{array}{c}\begin{array}{c}(1-0.5324)·{\overline{w}}_1+(1-0.6909)·{\overline{w}}_2+\hfill \\ (1-0.4400)·{\overline{w}}_3+(1-0.5452)·{\overline{w}}_4+(1-0.4530)·{\overline{w}}_5\ge \vartheta ,\hfill \\ -(e_{\left(1\right)14}^{-}+e_{\left(2\right)52}^{-}+e_{\left(3\right)324}^{-}+e_{\left(4\right)4}^{-}+e_{\left(4\right)4}^{+}+e_{\left(5\right)23}^{-})\ge \vartheta ,\hfill \\ {\overline{w}}_1+e_{\left(1\right)14}^{-}\ge {\overline{w}}_4,{\overline{w}}_5-{\overline{w}}_2+e_{\left(2\right)52}^{-}\ge 0.04,{\overline{w}}_3-2{\overline{w}}_2+{\overline{w}}_4+e_{\left(3\right)324}^{-}\ge 0,\hfill \\ {\overline{w}}_4+e_{\left(4\right)4}^{-}\ge 0.08,{\overline{w}}_4-e_{\left(4\right)4}^{+}\le 0.15,{\displaystyle \frac{{\overline{w}}_2}{{\overline{w}}_3}}+e_{\left(5\right)23}^{-}\ge 0.4,\hfill \\ (e_{\left(1\right)14}^{-}\ge 0,e_{\left(2\right)52}^{-}\ge 0,e_{\left(3\right)324}^{-}\ge 0,e_{\left(4\right)4}^{-}\ge 0,e_{\left(4\right)4}^{+}\ge 0,e_{\left(5\right)23}^{-}\ge 0),\hfill \\ {\overline{w}}_1+{\overline{w}}_2+{\overline{w}}_3+{\overline{w}}_4+{\overline{w}}_5=1,\hfill \\ {\overline{w}}_j\ge 0,j=1,2,\dots ,5.\hfill \end{array}\hfill \end{array}\right.\hfill \end{array}$$

  (28)
  Then the weight of five attributes is $\overline{\mathit{w}}={\left(\begin{array}{ccccc}0.1497& 0.2022& 0.2554& 0.1497& 0.2429\end{array}\right)}^T$.
• Substitute the attribute weights obtained in step 7 into the closeness index to obtain $CC\left(A_1\right)=0.5406708$, $CC\left(A_2\right)=0.5449616$, $CC\left(A_3\right)=0.4323463$, $CC\left(A_4\right)=0.4570640$. According to the closeness, the ranking of each alternative is $A_2>A_1>A_4>A_3$; thus, the optimal alternative is $A_2$.

4.3. Comparison and Discussion

In this paper, we mainly improve the optimization models for determining expert weight and attribute weight. In this part, we compare them with the expert weights and attribute weights in [9], and discuss the differences of the case results.

4.3.1. Comparison of Expert Weights

Compared with [9] which directly assigns expert weights subjectively without methodological justification, this paper develops an optimization model (27) for expert weight determination that integrates subjective preferences with objective data patterns, possessing rigorous mathematical foundations. The case study solves this model to derive expert weights, while

Table 6. Expert weight comparison.

Method	Decision Maker	${\mathit{D}}_1$	${\mathit{D}}_2$	${\mathit{D}}_3$
Method 1 Optimization model (27)	Weight	0.45588704	0.26818322	0.27592974
	Distance	0.7149089	1.2154090	1.1810347
	Product	0.325917724	0.325952299	0.325882607
Method 2 Direct subjective weighting method [9]	Weight	0.4	0.35	0.25
	Distance	0.7972884	1.0807029	1.2472645
	Product	0.318915349	0.378246014	0.311816127
Method 3 Averaging method	Weight	0.33333333	0.33333333	0.33333333
	Distance	0.8760708	1.1343133	1.1184066
	Product	0.2920236	0.3781044	0.372802

compares three methods—our optimization approach, [9]’s direct assignment, and averaging—presenting (1) weights of three decision makers, (2) their distances to the overall consistent score, and (3) weight–distance products.

Through observation Table 6, we find the following:

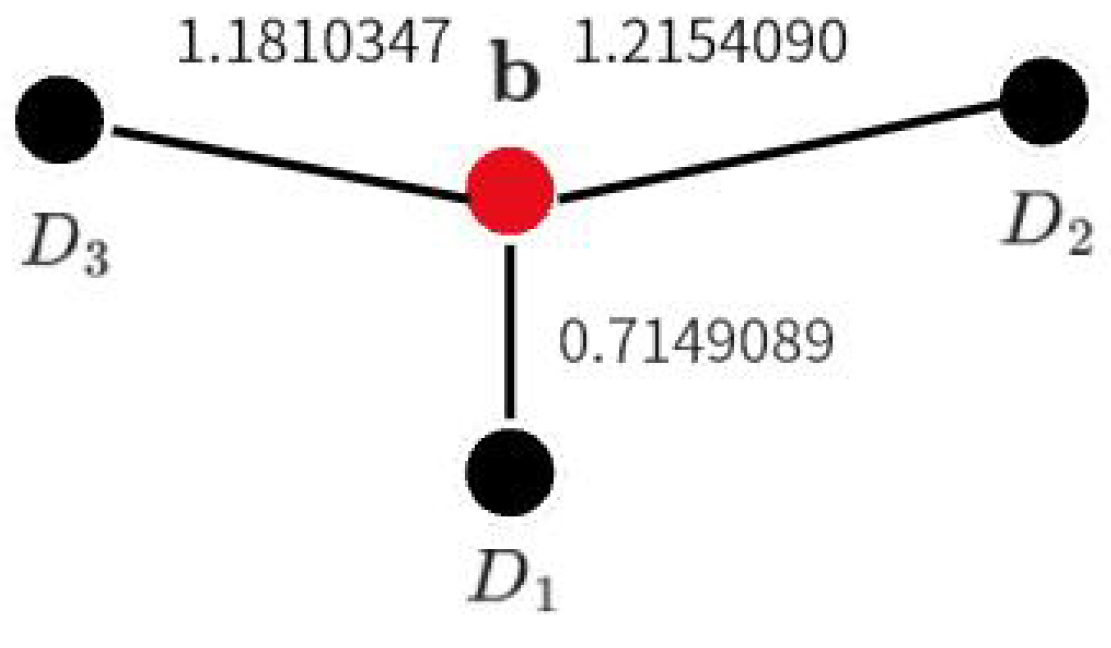
• From the numerical point of view, comparing the results of method 1 and method 2, the weight of $D_1$ is always the largest; the weights of $D_2$ and $D_3$ obtained by method 1 are very close, and the weight of $D_3$ is a little larger; however, in method 2, the weight of $D_2$ is obviously larger than the weight of $D_3$.
• From Figure 4, the evaluation point of $D_1$ is between $D_2$ and $D_3$; thus, the overall consistent score point $\mathit{b}$ is closest to $D_1$. Meanwhile, the distances of evaluation point $D_2$ to $\mathit{b}$ and $D_3$ to $\mathit{b}$ are very close, so the weights of $D_2$ and $D_3$ are also close.
• The summed distances across three methods are, respectively, 3.1113526, 3.1252558, and 3.17907, indicating Method 1’s optimality through minimal distance. For Method 1, the near-equality of each decision-maker’s weight–distance product ($w\times d$) demonstrates strict inverse proportionality between weights and distances to the consistent score. Although Method 2 exhibits negative weight–distance correlation, it fails to establish strict inverse proportionality. Conversely, under averaging weights (lacking empirical/data-driven foundations), unequal distances reveal no systematic weight–distance relationship.

4.3.2. Comparison of Attribute Weights

Unlike [9]’s closeness maximization approach, this paper establishes an interpretable entropy-based optimization model for attribute weight determination. After deriving expert weights via both [9]’s subjective method and our optimization model (27),

Table 7. Results by using expert weight in [9].

		The Original Data in [9]	Optimization Model in [9]	Optimization Model (24)	Entropy Weight Method
Attribute weight	${\overline{w}}_1$	0.2759844	0.2460	0.1497	0.2052
	${\overline{w}}_2$	0.1056329	0.1703	0.2022	0.1271
	${\overline{w}}_3$	0.2031062	0.2674	0.2554	0.2260
	${\overline{w}}_4$	0.1440145	0.0827	0.1497	0.1931
	${\overline{w}}_5$	0.2712621	0.2335	0.2429	0.2486
Closeness index	$CC\left(A_1\right)$	0.5540084	0.5504545	0.5348309	0.5436584
	$CC\left(A_2\right)$	0.5615795	0.5669940	0.5450698	0.5461983
	$CC\left(A_3\right)$	0.4072068	0.4012777	0.4312377	0.4284350
	$CC\left(A_4\right)$	0.4458253	0.4576273	0.4605085	0.4507837
Ranking of alternatives		$A_2>A_1>A_4>A_3$	$A_2>A_1>A_4>A_3$	$A_2>A_1>A_4>A_3$	$A_2>A_1>A_4>A_3$
Optimal decision		$A_2$	$A_2$	$A_2$	$A_2$
Efficiency		–	14,322 steps 396 s	13,813 steps 331 s	–

and

Table 8. Results by using expert weight (27).

		The Original Data in [9]	Optimization Model in [9]	Optimization Model (24)	Entropy Weight Method
Attribute weight	${\overline{w}}_1$	0.2759844	0.2460	0.1497	0.2000
	${\overline{w}}_2$	0.1056329	0.1703	0.2022	0.1322
	${\overline{w}}_3$	0.2031062	0.2674	0.2554	0.2395
	${\overline{w}}_4$	0.1440145	0.0827	0.1497	0.1945
	${\overline{w}}_5$	0.2712621	0.2335	0.2429	0.2339
Closeness index	$CC\left(A_1\right)$	0.5540084	0.5543304	0.5406708	0.5480974
	$CC\left(A_2\right)$	0.5615795	0.5685524	0.5449616	0.5460672
	$CC\left(A_3\right)$	0.4041474	0.4323463	0.4312377	0.4328601
	$CC\left(A_4\right)$	0.4458253	0.4532379	0.4570640	0.4478981
Ranking of alternatives		$A_2>A_1>A_4>A_3$	$A_2>A_1>A_4>A_3$	$A_2>A_1>A_4>A_3$	$A_1>A_2>A_4>A_3$
Optimal decision		$A_2$	$A_2$	$A_2$	$A_1$
Efficiency		–	14,322 steps 393 s	13,813 steps 325 s	–

present three attribute weighting approaches: (1) closeness maximization optimization, (2) our entropy theory optimization, and (3) entropy weighting. The alternatives’ closeness values are then calculated and compared with [9]’s baseline. For optimization models (1) and (2), we employ Python’s differential_evolution method with initial conditions (Python 3.7 and scipy 1.7.3): $\vartheta =0$, $\overline{\mathit{w}}={(0.2,0.2,0.2,0.2,0.2)}^T$, $e_{\left(1\right)14}^{-}=e_{\left(2\right)52}^{-}=e_{\left(3\right)324}^{-}=e_{\left(4\right)4}^{-}=e_{\left(4\right)4}^{+}=e_{\left(5\right)23}^{-}=0$, using fixed random seed initialization.

By comparing Table 7 and Table 8, it is found that:

• Regarding attribute weight determination, both optimization-based weighting approaches exhibit minimal sensitivity to variations in expert weights—the attribute weights remain largely unchanged despite minor expert weight adjustments. In contrast, entropy-based weighting demonstrates significantly greater sensitivity to such expert weight fluctuations.
• From the view of closeness index, for all methods, the closeness of alternative $A_1$ is close to $A_2$, while closeness of alternative $A_3$ is close to $A_4$, and closeness of $A_1$ and $A_2$ is obviously larger than that of alternatives $A_3$ and $A_4$.
• Tabular results in Table 7 and Table 8 demonstrate consistent alternative rankings across all attribute weighting methods when applying [9]’s expert weights. When substituting our optimized expert weights, all methods except entropy weighting—which disregards expert opinions due to its exclusive reliance on objective data—produce identical rankings consistent with [9]. This indicates the final rankings’ robustness to variations in both expert and attribute weights, while closeness index values reveal nuanced distinctions between alternatives.
• Regarding final alternative selection, only the combination of expert weight optimization model (11) with entropy-based attribute weighting selects $A_1$ as optimal; all other configurations select $A_2$, aligning with the optimal choice in [9].
• From the view of efficiency, the optimization model (24) proposed in this paper is more efficient, which shortens the solving time by about 17% compared with the attribute weight optimization model in [9].
• Compared to the pure entropy weight method, optimization model (24) integrates expert subjective insights with entropy theory, thereby addressing entropy’s fundamental limitation of relying exclusively on objective data patterns while disregarding expert judgment.
• Combining data from Table 7 and Table 8 with comparative analysis against [9] yields

  Table 9. Influence of weight on closeness index.

  		Expert Weight in [9] Attribute Weight (24)	Expert Weight in [9] Attribute Weight (18)	Expert Weight (11) Attribute Weight in [9]	Expert Weight (11) Attribute Weight (24)	Expert Weight (11) Attribute Weight (18)
  Expert weight	$\Delta w_1$	0	0	0.05588704	0.05588704	0.05588704
  	$\Delta w_2$	0	0	−0.08181678	−0.08181678	−0.08181678
  	$\Delta w_3$	0	0	0.02592974	0.02592974	0.02592974
  	${\parallel \Delta \mathit{w}\parallel }_2^2$	0	0	0.01048970	0.01048970	0.01048970
  Attribute weight	$\Delta {\overline{w}}_1$	−0.1262844	−0.0707844	−0.0299844	−0.1262844	−0.0759844
  	$\Delta {\overline{w}}_2$	0.0965671	0.0214671	0.0646671	0.0965671	0.0265671
  	$\Delta {\overline{w}}_3$	0.0522938	0.0228938	0.0642938	0.0522938	0.0363938
  	$\Delta {\overline{w}}_4$	0.0056855	0.0490855	−0.0613145	0.0056855	0.0504855
  	$\Delta {\overline{w}}_5$	−0.0283621	−0.0226621	−0.0377621	−0.0283621	−0.0373621
  	$\parallel \Delta \overline{\mathit{w}}{\parallel }_2^2$	0.02884433	0.008918351	0.014400035	0.02884433	0.011748661
  Closeness index	$\Delta CC\left(A_1\right)$	−0.0191775	−0.01035	0.000322	−0.0133376	−0.005911
  	$\Delta CC\left(A_2\right)$	−0.0165097	−0.0153812	0.0069729	−0.0166179	−0.0155123
  	$\Delta CC\left(A_3\right)$	0.0240309	0.0212282	0.0281989	0.0270903	0.0287127
  	$\Delta CC\left(A_4\right)$	0.0146832	0.0049584	0.0074126	0.0112387	0.0020728

  , which examines the influence of expert and attribute weights on closeness indices. While variations in either weight category alter closeness values, Table 9 reveals that attribute weights exert disproportionate influence on these indices.

5. Conclusions

Within the interval-valued intuitionistic fuzzy environment, this paper integrates the TOPSIS method with dual optimization models to establish a comprehensive fuzzy multi-attribute group decision-making methodology:

• This paper first establishes an interpretable optimization model for expert weight determination. Empirical verification demonstrates that expert weights increase as their evaluations approach the overall consistent score, with weights exhibiting strict inverse proportionality to evaluation distance. Furthermore, the model accommodates custom constraints incorporable per practical requirements, thereby achieving a subjective–objective weighting synergy.
• Second, this paper proposes an interpretable, concise optimization model for attribute weight determination that integrates entropy theory with decision-maker inputs. Compared to purely objective entropy weighting, this approach significantly enhances the integration of subjective preferences.
• This paper validates the proposed method’s feasibility through two case studies. First, resolution of the mobile phone selection problem demonstrates practical implementability. Second, application to the treatment alternative decision-making problem from [9] yields identical optimal alternatives when compared with their results, confirming methodological effectiveness. Concurrently, our attribute weight optimization model achieves approximately 17% higher computational efficiency than [9]’s counterpart.

Future research directions include (1) extending the framework to advanced fuzzy sets beyond interval-valued intuitionistic fuzzy environments, such as interval Pythagorean fuzzy sets and inverse fuzzy sets [32,33]; (2) comparing aggregation operator efficacy, particularly contrasting IIOWA with alternatives like IVIFWA; (3) implementing computational approximation techniques in fundamental operators to enhance efficiency [34].