Formal Verification of Solidity Smart Contracts via Automata Theory
Abstract
1. Introduction
- Formal Modeling and Transformation of Smart Contracts: We propose an innovative method to convert Solidity-based smart contracts into the formal language Promela, using a finite state machine (FSM) model that captures the symmetry in contract control flow and state transitions. This provides a structured framework for systematic verification of smart contracts.
- Comprehensive Verification Method Expansion: Our approach extends beyond security analysis to include the verification of key properties such as fairness and liveness, ensuring the correctness, ideal behavior, and expected outcomes of contracts in decentralized environments. This expansion broadens the scope of smart contract verification, addressing not only protection against attacks but also the fairness and final goals of contract execution.
- Blockchain Smart Contract Security Assurance: We introduce a rigorous formal verification mechanism to ensure the security and correctness of smart contracts in decentralized blockchain environments. By formally modeling and verifying the contract execution process, potential logical errors and security vulnerabilities can be effectively identified, preventing deviations from expected behaviors during contract execution and ensuring the transparency and controllability of the contract.
- Model Checking and Verification: We utilize the Spin tool to verify the Promela-modeled smart contracts, employing both manually and automatically generated Linear Temporal Logic (LTL) formulas for comprehensive validation. This ensures the correctness of the contract logic, identifies potential errors and design flaws, and enhances the robustness and trustworthiness of the smart contract.
2. Related Works
2.1. Formal Modeling of Smart Contracts
2.2. Verification of Smart Contracts
2.3. Checking Correctness and Safety Properties
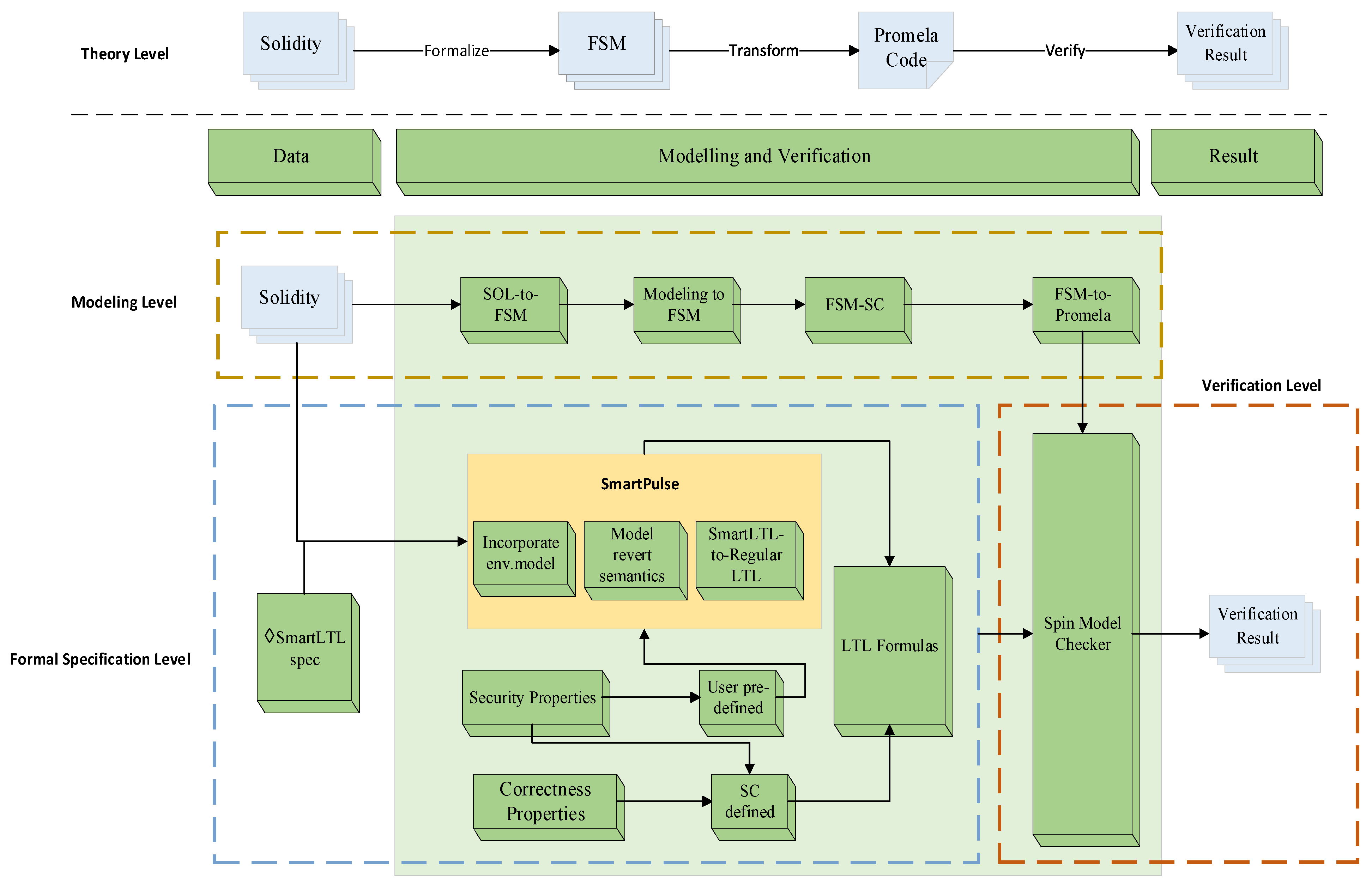
3. Materials and Methods
3.1. Formal Description of Smart Contracts
- is a finite set of states that represents the different stages of the contract.
- is a finite set of events.
- is a finite set of variables.
- is the deterministic transition relation (where , and ).
- is the initial state set, which assigns initial values to the contract’s variables and states, .
- is the final state set.
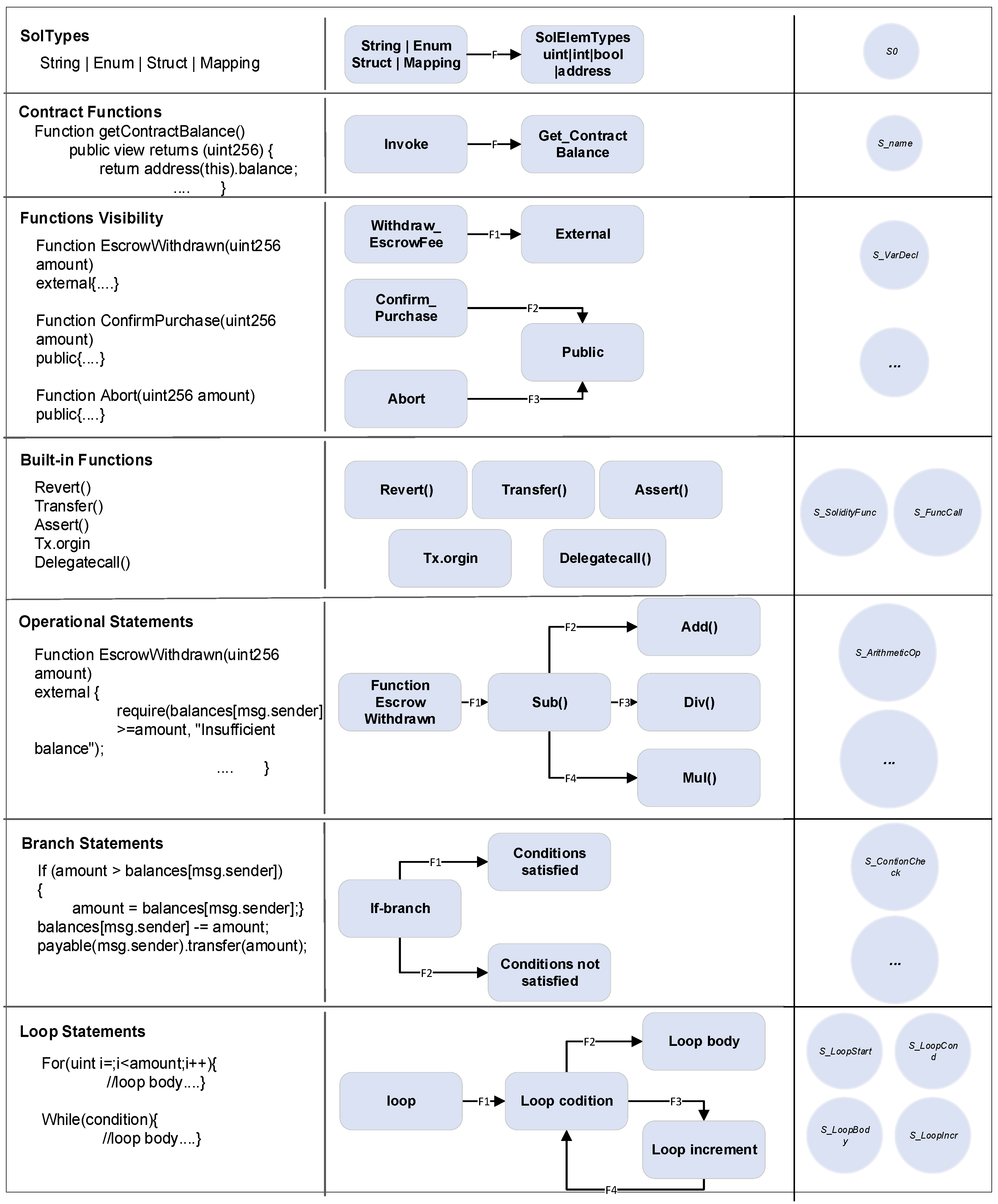
3.2. Converting Smart Contracts to FSM
| Algorithm 1: CREATEStateMachine (,,,,,) |
| Call Algorithm 2 and 3 to construct state machine Input: Solidity Source Code Output: SRP Model (,,,,,) Initialization 1: Initialize state set with initial states Σ* 2: Initialize event set 3: Initialize variable set 4: Initialize transition function 5: Initialize end state set Algorithm 2 Expressions Transformation Algorithm 6: Solidity Statements ← Expressions Algorithm 3 Statements Transformation Algorithm 7: SRP Model ← Function statements 8: return SRP Model |
| Algorithm 2: Transform Statements to SRP |
| Input: Solidity Statements Output: SRP Model (,,,,,) 1: if Contract variable declarations or constructor exists then 2: Add initial state S0 to ; 3: Add state S0 to ; 4: Add transition (S0, S0) to ; 5: Add event related to contract declarations to ; 6: for Each function declaration do 7: Add state S_name to ; 8: Add transition (S0, S_name) to ; 9: Add event related to function declaration to ; 10: for Each function statement do 11: if Variable declaration then 12: Add state S_VarDecl to ; 13: Add transition from previous state to S_VarDecl; 14: Add variable to ; 15: Add event related to variable declaration to ; 16: if Built-in functions Revert(), Transfer(), Assert(), Tx.origin, Delegatecall() then 17: Add state S_SolidityFunc to ; 18: Add transition from previous state to S_SolidityFunc; 19: Add event related to Solidity function call to ; 20: if Function calls then 21: Add state S_FuncCall to ; 22: Add transition from previous state to S_FuncCall; 23: Add event related to function calls to ; 24: if Arithmetic operations Add(a + b), Sub(a - b) then 25: Add state S_ArithmeticOp to ; 26: Add transition from previous state to S_ArithmeticOp; 27: Add event related to arithmetic operations to ; 28: if Conditional statements switch(condition), if(condition) then 29: Add state S_ConditionCheck to ; 30: Add transition from previous state to S_ConditionCheck; 31: Add event related to condition checks to ; 32: if Loop statements for(int i, condition, i++) then 33: Add states S_LoopStart, S_LoopCond, S_LoopBody, S_LoopIncr to ; 34: Add transition from previous state to S_LoopStart; 35: Add transition from S_LoopStart to S_LoopCond; 36: Add transition from S_LoopCond to S_LoopBody; 37: Add transition from S_LoopBody to S_LoopIncr; 38: Add transition from S_LoopIncr back to S_LoopCond; 39: Add event related to loops to ; 40: Add final states to ; 41: return SRP Model |
- Expressions with Variables (): These are expressions that contain at least one local variable. For such expressions (lines 3–13), the FSM introduces a state for each expression , with transitions to handle conditional checks and loops, replicating complex execution paths.
- Expressions with Function Calls (): These are expressions containing at least one function call, in this case (lines 14–23). The algorithm sets up states and transitions to manage function call sequences and any Ether-sending operations, accurately reflecting interactions within the smart contract.
- Explicit Expressions (): These are straightforward expressions without any variables or function calls. The algorithm (lines 24–36) handles arithmetic operations, conditional checks, and loops with constant bounds by creating corresponding states and transitions to maintain logical accuracy in the FSM.
Algorithm 3: Convert Expressions to Statements Input: Expressions where i =1…N
Output: State machine representation of expressions
1: for Every expression and i = 1..N do
2: if Expression is of type (with variables) then
3: Add state Si for expression ;
4: Add transition Ti from S_visibility to Si;
5: if Expression involves conditional checks then
6: Add state S_Condition;
7: Add transition Ti from Si to S_Condition;
8: if Expression involves loops then
9: Add state S_Loop, S_Loop_condition, S_Loop_increment;
10: Add transition Ti from Si to S_Loop;
11: Add transition Ti+1 from S_Loop to S_Loop_condition with guard(condition);
12: Add transition Ti+2 from S_Loop_condition to S_Loop_increment;
13: Add transition Ti+3 from S_Loop_increment back to
S_Loop_condition with guard(!condition);
14: if Expression is of type (with function calls) then
15: Add state Si for function calls in ;
16: Add transition Ti from S_visibility to Si;
17: if Expression involves sending ether then
18: Add state S_Sending_ether;
19: Add transition Ti from Si to S_Sending_ether;
20: if Expression involves internal/external function calls then
21: Add state S_Call_function, S_External_call_function;
22: Add transition Ti from Si to S_Call_function;
23: Add transition Ti+1 from Si to S_External_call_function;
24: if Expression is of type (explicit expression) then
25: if Expression involves simple arithmetic then
26: Add state S_Arithmetic;
27: Add transition Ti from S_visibility to S_Arithmetic;
28: if Expression involves conditional checks without variables then
29: Add state S_Condition;
30: Add transition Ti from S_Arithmetic to S_Condition;
31: if Expression involves loops with constant bounds then
32: Add state S_Loop, S_Loop_condition, S_Loop_increment;
33: Add transition Ti from S_Arithmetic to S_Loop;
34: Add transition Ti+1 from S_Loop to S_Loop_condition with guard(condition);
35: Add transition Ti+2 from S_Loop_condition to S_Loop_increment;
36: Add transition Ti+3 from S_Loop_increment to S_Loop_condition with guard(!condition);
37: return SRP model
3.3. Modeling Promela Through FSM
4. Experiments
4.1. Sculpting Promela Models Using LTL
4.2. Generating LTL with Smart Pulse
4.3. Model Checking of Smart Contracts
4.4. Simulation
4.5. Verification
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Analysis Method | Tool | Target |
|---|---|---|
| Symbolic Execution/Static Analysis | Oyente | EVM bytecode + Ethereum global state |
| Zeus | Solidity source → LLVM | |
| Mythril | Solidity source + EVM bytecode | |
| VERX | Solidity + properties → symbolic automata | |
| SOLC-VERIFY | Solidity source with annotations | |
| Slither | Solidity source → SlithIR | |
| Model Checking | SPIN | Solidity → Promela (FSM model + LTL) |
| UPPAAL | Solidity with timing constraints | |
| NuSMV | Solidity modeled via transition systems | |
| Smart Pulse | Solidity → FSM → Smart LTL properties | |
| VERISOL | Solidity (Boogie-based) | |
| Theorem Proving | Coq | Solidity modeled manually in Coq |
| Isabelle/HOL | EVM bytecode → Lem language | |
| KEVM | EVM bytecode → K framework | |
| KEVMVER | KEVM-based property verifier with specification language |
Appendix B
| Vulnerability | Cause | Potential Impact |
|---|---|---|
| Reentrancy | External calls are made before completing internal state updates, allowing repeated entry | Repeated unauthorized fund withdrawals; exemplified by the DAO attack where the contract was drained |
| Disorder | Contract functions depend on a specific execution order but can be called out of sequence | Unauthorized access, unintended state transitions, or disruption of contract logic |
| Timestamp Dependency | Reliance on block timestamps for critical logic which can be influenced by miners | Time-based conditions may be manipulated to gain unfair advantages |
| Block Number Dependency | Use of block numbers in key logic, which miners can slightly influence | Fairness or correctness of time- or randomness-related operations may be compromised |
| Stack Overflow | Excessive recursion or deeply nested calls exceed the EVM’s stack limit | Contract failure or erratic behavior, possibly leading to service disruption |
| Denial of Service (DoS) | Resource exhaustion, such as excessive gas consumption or blocked execution paths | Contract becomes unresponsive, leading to loss of functionality or availability |
| Integer Overflow | Arithmetic operations exceed variable limits, causing numeric wraparound | Inaccurate computations, balance manipulation, or faulty contract logic |
| Race Condition | Contract behavior is influenced by transaction timing, which can be manipulated concurrently | Double-spending, inconsistent states, or unexpected execution outcomes |
References
- Yaga, D.; Mell, P.; Roby, N.; Scarfone, K. Blockchain technology overview. arXiv 2019, arXiv:1906.11078. [Google Scholar] [CrossRef]
- Gavin, W. Ethereum: A Secure Decentralised Generalised Transaction Ledger. 2019. Available online: https://mholende.win.tue.nl/seminar/references/ethereum_yellowpaper.pdf (accessed on 12 June 2025).
- Etherscan. The Ethereum Blockchain Explorer. 2025. Available online: https://etherscan.io (accessed on 12 June 2025).
- Szabo, N. The idea of smart contracts. Nick Szabo’s Pap. Concise Tutor. 1997, 6, 199. [Google Scholar]
- Andreas, M.; Gavin, W. Mastering Ethereum: Building Smart Contracts and Dapps; O’Reilly Media: Sebastopol, CA, USA, 2018. [Google Scholar]
- BlockCAT. On the Parity Multi-Sig Wallet Attack. 2017. Available online: https://medium.com/blockcat/on-the-parity-multi-sig-wallet-attack-83fb5e7f4b8c (accessed on 12 June 2025).
- Pretrov, S. Another Parity Wallet Hack Explained. 2017. Available online: https://medium.com/@Pr0Ger/another-parity-wallet-hack-explained-847ca46a2e1c (accessed on 12 June 2025).
- Wikipedia. Poly Network Exploit. 2025. Available online: https://en.wikipedia.org/wiki/Poly_Network_exploit (accessed on 12 June 2025).
- Hildenbrandt, E.; Saxena, M.; Rodrigues, N.; Zhu, X.; Daian, P.; Guth, D.; Moore, B.; Park, D.; Zhang, Y.; Stefanescu, A.; et al. KEVM: A complete formal semantics of the Ethereum virtual machine. In Proceedings of the 2018 IEEE 31st Computer Security Foundations Symposium (CSF), Oxford, UK, 9–12 July 2018; pp. 204–217. [Google Scholar] [CrossRef]
- Kalra, S.; Goel, M.; Dhawan, M.; Sharma, S. Zeus: Analyzing safety of smart contracts. In Proceedings of the Network and Distributed System Security Symposium (NDSS), San Diego, CA, USA, 18–21 February 2018; pp. 1–12. [Google Scholar]
- Permenev, A.; Dimitrov, D.; Tsankov, P.; Drachsler-Cohen, D.; Vechev, M. Verx: Safety verification of smart contracts. In Proceedings of the 2020 IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 18–21 May 2020; pp. 18–20. [Google Scholar]
- Holzmann, G.J. The model checker SPIN. IEEE Trans. Softw. Eng. 1997, 23, 279–295. [Google Scholar] [CrossRef]
- Hamdaqa, M.; Met, L.A.P.; Qasse, I. iContractML 2.0: A domain-specific language for modeling and deploying smart contracts onto multiple blockchain platforms. Inf. Softw. Technol. 2022, 144, 106762. [Google Scholar] [CrossRef]
- Jurgelaitis, M.; Butkien e, R. Solidity Code Generation from UML State Machines in Model-Driven Smart Contract Development. IEEE Access 2022, 10, 33465–33481. [Google Scholar] [CrossRef]
- Ethereum. Solidity Documentation. 2022. Available online: https://docs.soliditylang.org/en/v0.8.11 (accessed on 12 June 2025).
- Dolev, S.; Wang, Z. Sodsmpc: Fsm based anonymous and private quantumsafe smart contracts. In Proceedings of the 2020 IEEE 19th International Symposium on Network Computing and Applications (NCA), Cambridge, MA, USA, 24–27 November 2020; pp. 1–10. [Google Scholar]
- Volland, F. State Machine: A Compilation of Patterns and Best Practices for the Smart Contract Programming Language.2024. Available online: https://fravoll.github.io/solidity-patterns/state_machine.html (accessed on 12 June 2025).
- Mavridou, A.; Laszka, A. Designing secure ethereum smart contracts: A finite state machine based approach. In Proceedings of the International Conference on Financial Cryptography and Data Security, Nieuwpoort, Curacao, 26 February–2 March 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 523–540. [Google Scholar]
- Mavridou, A.; Laszka, A.; Stachtiari, E.; Dubey, A. Verisolid: Correct-by-design smart contracts for Ethereum. In Proceedings of the Financial Cryptography and Data Security-23rd International Conference (FC 2019), Frigate Bay, Saint Kitts and Nevis, 18–22 February 2019; Revised Selected Papers. pp. 446–465. [Google Scholar] [CrossRef]
- Liao, Z.; Hao, S.; Nan, Y.; Zheng, Z. Smartstate: Detecting state-reverting vulnerabilities in smart contracts via fine-grained state-dependency analysis. In Proceedings of the 32nd ACM SIGSOFT International Symposium on Software Testing and Analysis, Seattle, WA, USA, 17–21 July 2023; pp. 980–991. [Google Scholar]
- Luo, H.; Lin, Y.; Yan, X.; Hu, X.; Wang, Y.; Zeng, Q.; Wang, H.; Jiang, J. Guiding LLM-based Smart Contract Generation with Finite State Machine. arXiv 2025, arXiv::2505.08542. [Google Scholar] [CrossRef]
- Ladleif, J.; Weske, M. A unifying model of legal smart contracts. In Proceedings of the International Conference on Conceptual Modeling, Vienna, Austria, 3–6 November 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 323–337. [Google Scholar]
- Hirai, Y. Defining the ethereum virtual machine for interactive theorem provers. In Financial Cryptography and Data Security; Brenner, M., Ed.; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Roșu, G.; Șerbănută, T.F. An overview of the K semantic framework. J. Log. Algebr. Program. 2010, 79, 397–434. [Google Scholar] [CrossRef]
- Bhargavan, K.; Delignat-Lavaud, A.; Fournet, C.; Gollamudi, A.; Gonthier, G.; Kobeissi, N.; Kulatova, N.; Rastogi, A.; Sibut-Pinote, T.; Swamy, N.; et al. Formal verification of smart contracts: Short paper. In Proceedings of the 2016 ACM Workshop on Programming Languages and Analysis for Security, Vienna, Austria, 24 October 2016; pp. 91–96. [Google Scholar]
- Nehai, Z.; Piriou, P.Y.; Daumas, F. Model-checking of smart contracts. In Proceedings of the 2018 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Halifax, NS, Canada, 30 July–3 August 2018; pp. 980–987. [Google Scholar]
- Bai, X.; Cheng, Z.; Duan, Z.; Hu, K. Formal Modeling and Verification of Smart Contracts. In Proceedings of the 2018 7th International Conference on Software and Computer Applications, Kuantan, Malaysia, 8–10 February 2018. [Google Scholar]
- Wang, Y.; Lahiri, S.; Chen, S.; Pan, R.; Dillig, I.; Born, C.; Naseer, I.; Ferles, K. Formal verification of workflow policies for smart contracts in azure blockchain. In Verified Software. Theories, Tools, and Experiments, Proceedings of the 11th International Conference, VSTTE 2019, New York, NY, USA, 13–14 July 2019; Revised Selected Papers; Springer Nature: Heidelberg, Germany, 2019; p. 87. [Google Scholar]
- Hajdu, A.; Jovanovic, D. solc-verify: A modular verifier for solidity smart contracts. In Verified Software. Theories, Tools, and Experiments, Proceedings of the 11th International Conference, VSTTE 2019, New York, NY, USA, 13–14 July 2019; Chakraborty, S., Navas, J.A., Eds.; Revised Selected Papers, Volume 12031 of Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; pp. 161–179. [Google Scholar]
- Park, D.; Zhang, Y.; Saxena, M.; Daian, P.; Roşu, G. A formal verification tool for ethereum vm bytecode. In Proceedings of the 2018 26th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Lake Buena Vista, FL, USA, 4–9 November 2018; p. 912915. [Google Scholar]
- Stephens, J.; Ferles, K.; Mariano, B.; Lahiri, S.; Dillig, I. SmartPulse: Automated Checking of Temporal Properties in Smart Contracts. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 555–571. [Google Scholar] [CrossRef]
- Bartoletti, M.; Galletta, L.; Murgia, M. A minimal core calculus for Solidity contracts. In Data Privacy Management, Cryptocurrencies and Blockchain Technology; Pérez-Solà, C., Navarro-Arribas, G., Biryukov, A., Garcia-Alfaro, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 233–243. [Google Scholar]
- Crafa, S.; Di Pirro, M.; Zucca, E. Is Solidity solid enough? In Financial Cryptography and Data Security; Bracciali, A., Clark, J., Pintore, F., Rønne, P.B., Sala, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 138–153. [Google Scholar]
- Ahrendt, W.; Bubel, R. Functional verification of smart contracts via strong data integrity. In Leveraging Applications of Formal Methods, Verification and Validation: Applications; Margaria, T., Steffen, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 9–24. [Google Scholar]
- Rosu, G.; Chen, F.; Ball, T. Synthesizing monitors for safety properties: This time with calls and returns. In International Workshop on Runtime Verification, RV; Leucker, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 51–68. [Google Scholar]
- Baresi, L.; Mehdi, M.; Kallehbasti, P.; Rossi, M. Efficient scalable verification of LTL specifications. In Proceedings of the ACM/IEEE International Conference on Software Engineering (ICSE), Florence, Italy, 16–24 May 2015; pp. 711–721. [Google Scholar]
- Brockschmidt, M.; Cook, B.; Ishtiaq, S.; Khlaaf, H.; Piterman, N. T2: Temporal property verification. In Tools and Algorithms for the Construction and Analysis of Systems, Proceedings of the TACAS, Eindhoven, The Netherlands, 2–8 April 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 387–393. [Google Scholar]
- Beyene, T.A.; Popeea, C.; Rybalchenko, A. Solving existentially quantified horn clauses. In Computer Aided Verification (CAV); Springer: Berlin/Heidelberg, Germany, 2013; pp. 869–882. [Google Scholar]
- Strom, R.E.; Typestate, S. A programming language concept for enhancing software reliability. IEEE Trans. Softw. Eng. 1986, SE-12, 157–171. [Google Scholar] [CrossRef]
- Browne, M.C.; Clarke, E.M.; Grümberg, O. Characterizing finite Kripke structures in propositional temporal logic. Theor. Comput. Sci. 1988, 59, 115–131. [Google Scholar] [CrossRef]
- Wang, M.; Tian, C.; Zhang, N.; Duan, Z. Verifying full regular temporal properties of programs via dynamic program execution. IEEE Trans. Reliab. 2018, 68, 1101–1116. [Google Scholar] [CrossRef]
- Cook, B.; Gotsman, A.; Podelski, A.; Rybalchenko, A.; Vardi, M.Y. Proving that programs eventually do something good. In Proceedings of the 34th ACM SIGPLANSIGACT Symposium on Principles of Programming Languages, Proceedings of the POPL 2007, Nice, France, 17–19 January 2007; Hofmann, M., Felleisen, M., Eds.; ACM: New York, NY, USA, 2007; pp. 265–276. [Google Scholar]
- Dietsch, D.; Heizmann, M.; Langenfeld, V.; Podelski, A. Fairness modulo theory: A new approach to ltl software model checking. In International Conference on Computer Aided Verification; Springer: Cham, Switzerland, 2015; pp. 49–66. [Google Scholar]
- Garfatta, I.; Klai, K.; Graïet, M.; Gaaloul, W. Model checking of vulnerabilities in smart contracts: A solidity-to-CPN approach. In Proceedings of the 37th ACM/SIGAPP Symposium on Applied Computing, Brno, Czech Republic, 25–29 April 2022; pp. 316–325. [Google Scholar]
- Sergey, I.; Nagaraj, V.; Johannsen, J.; Kumar, A.; Trunov, A.; Hao, K.C.G. Safer smart contract programming with scilla. Proc. ACM Program. Lang. 2019, 3, 185:1–185:30. [Google Scholar] [CrossRef]
- Coquand, T.; Huet, G.P. The calculus of constructions. Inf. Comput. 1988, 76, 95–120. [Google Scholar] [CrossRef]
- Vardi, M.Y. Automata-theoretic model checking revisited. In VMCAI 2007. LNCS; Cook, B., Podelski, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4349, pp. 137–150. [Google Scholar] [CrossRef][Green Version]
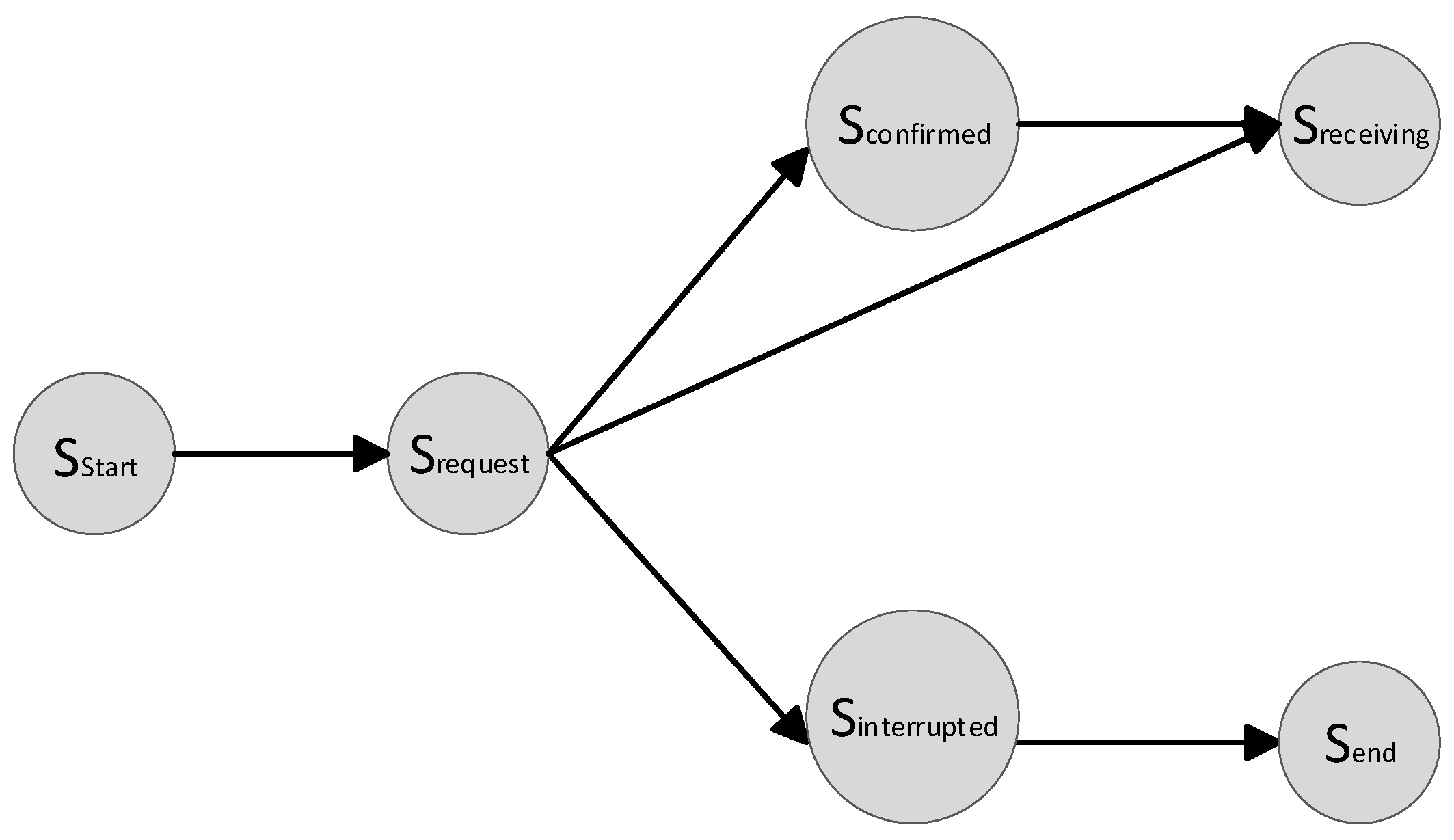

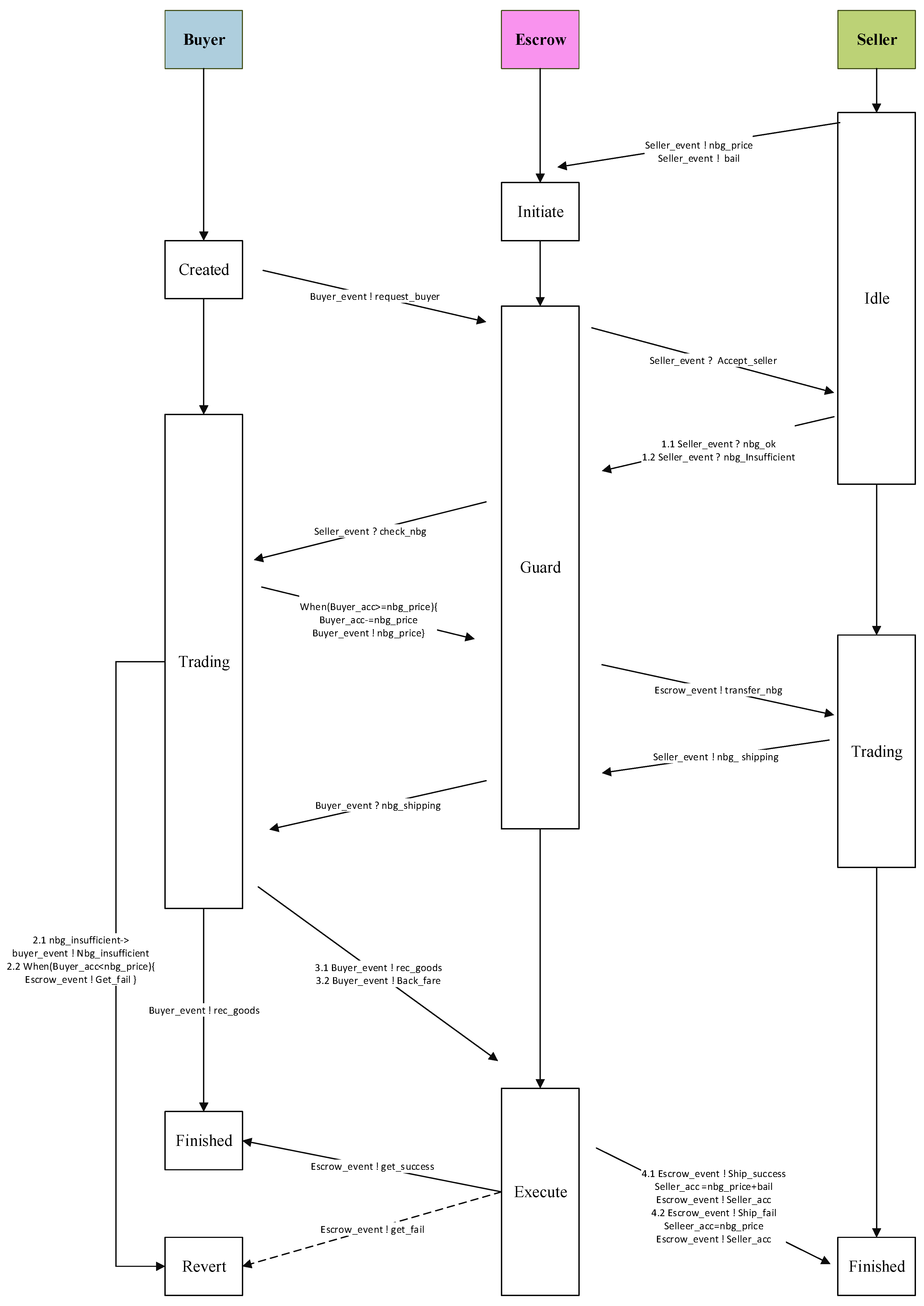
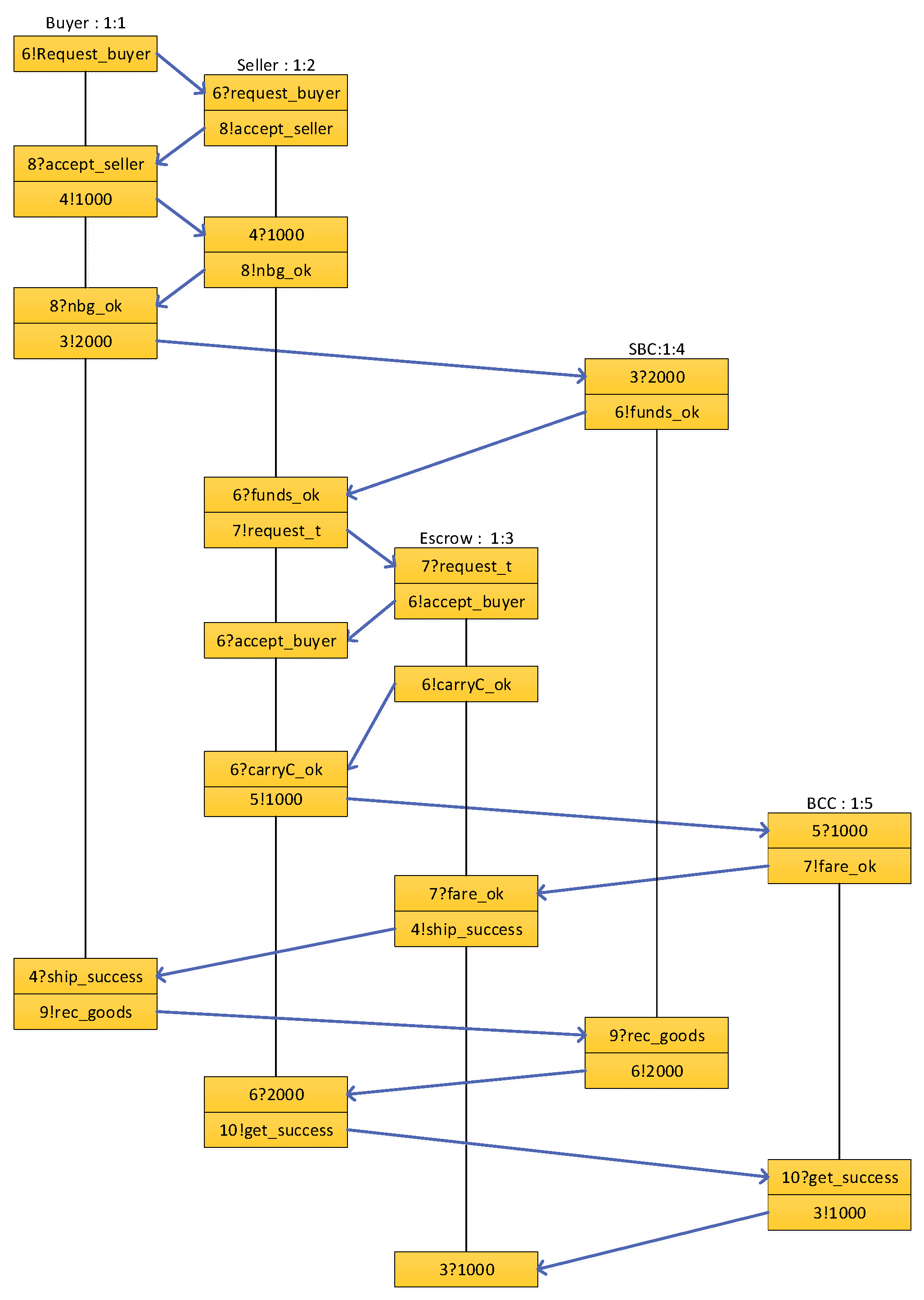

| State | Meaning of Each State |
|---|---|
| Start | |
| Buyer Requests to purchase goods | |
| Buyer pays for goods | |
| Buyer refund or suspension of transaction | |
| Buyer receiving | |
| Transaction completed |
| State | Meaning of Each State |
|---|---|
| Start | |
| Seller accepting buyer requests | |
| Seller refuses to deal without goods | |
| Seller confirms money in escrow | |
| Seller’s refusal or buyer’s refund | |
| Transaction completed |
| Event | Event Types for Smart Contracts |
|---|---|
| a | Initialize transactions between smart contracts |
| b1 | Buyer makes payment |
| b2 | Buyers cancel transactions with sellers |
| b3 | Sellers cancel transactions with buyers |
| c1 | Call revert when entering an error state |
| c2 | Fulfillment of orders |
| revert | Solidity error-handling functions |
| RefundEscrow | If a user withdraws funds after refunds are enabled, they will eventually be sent the sum of their deposits. | []((finished(EscrowVault.enableRefunds)) ==>(<>(finished(send(from,to, amt),(to==user&&amt== fsum(EscrowVault.deposit(payee),2, payee==user)))))) |
| If the beneficiary withdraws after the escrow is ended, they will eventually be sent the sum of all deposits. | []( !(finished(Seller.withdraw) && finished(Buyer.requestRefund)) ) | |
| EscrowVault | If a user requests a refund after refunds are enabled, they will eventually be sent the sum of their deposits. | <>(finished(EscrowVault.deposit)) && <>(finished(EscrowVault.close, (ben==this.beneficiary))) |
| If the escrow is closed, the beneficiary will only be sent the sum of all deposits. | <>(finished(EscrowVault.deposit)) && <>(finished(EscrowVault.close, (ben==this.beneficiary))) |
| Property | Description | Detects | Main Vulnerabilities |
|---|---|---|---|
| After the transaction ends, the sum of all account balances equals the initial total balance. | Prevents fund misallocation, loss or creation of value. | Integer overflow | |
| If the seller receives returned goods, the buyer must eventually receive a refund. | Ensures liveness and prevents funds being locked. | DoS | |
| Ensures correct operation sequence: return → refund → pickup, and payment before pickup. | Enforces control flow and prevents early/illegal function access. | TOD | |
| Upon successful transaction, seller and buyer balances are updated as per protocol; escrow remains unchanged. | Detects incorrect state updates, faulty fund transfers. | Funds leakage | |
| Once the buyer confirms receipt, refund action must never occur. | Prevents double refunds, ensures finality of transaction. | Reentrancy | |
| Once refund function is triggered, the buyer will eventually receive a refund equal to the original deposit. | Ensures full refund delivery and prevents inconsistency between deposit and refund. | Invariant violation | |
| : | Prevents simultaneous execution of seller withdrawal and buyer refund request. | Prevents race conditions and conflicting fund flows. | Race condition/state inconsistency |
| Before the transaction is closed, the seller must be specified and the seller’s shipping operation completed. | Ensures correct sequencing and state validation before contract closure. | Improper finalization | |
| Every user’s deposit and refund will eventually be completed; the contract must not block any user’s progress. | Guarantees progress of user interactions and avoids indefinite locking. | DOS |
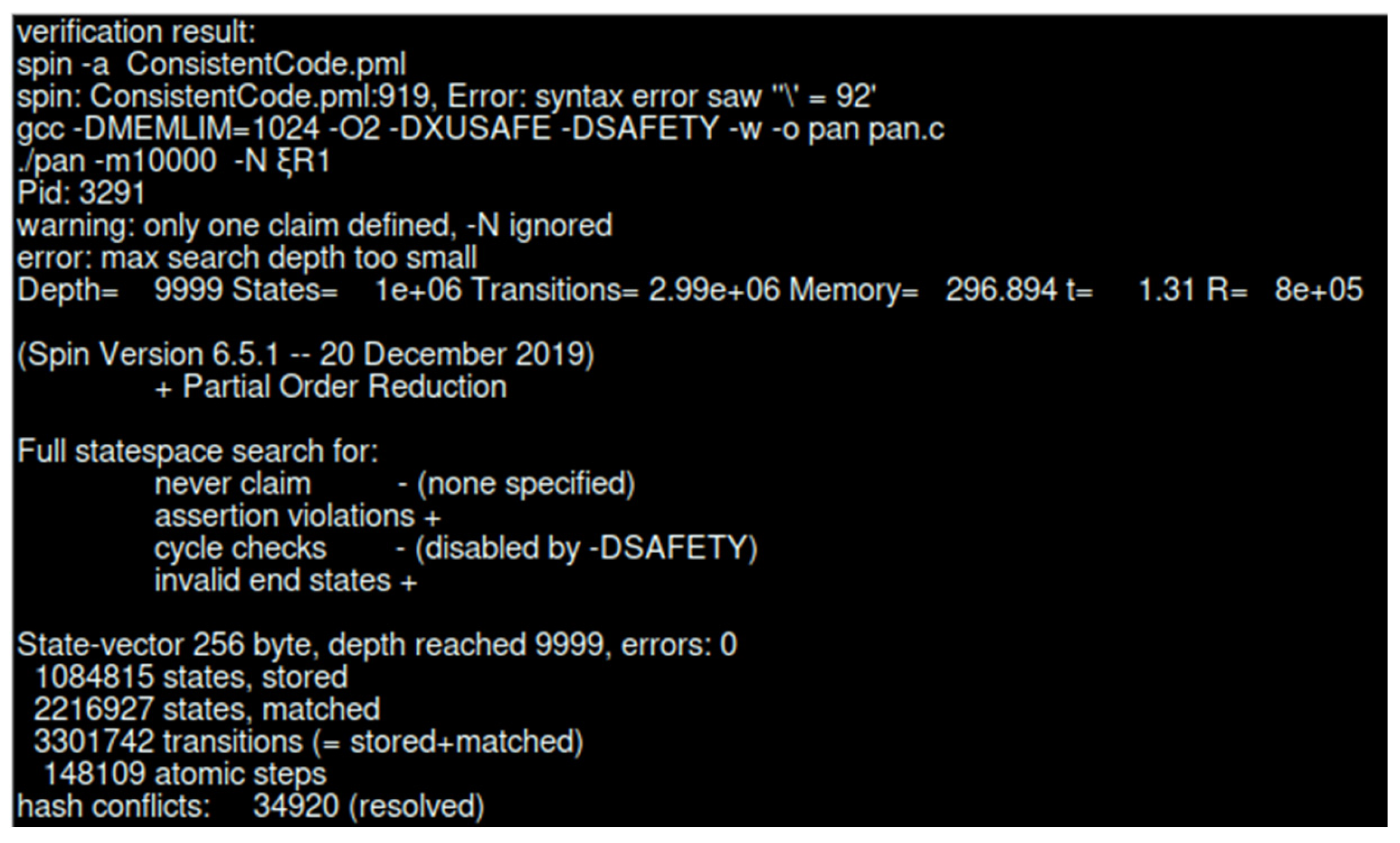
| LTL Property | Type | States | Transitions | Memory (MB) | Verified |
|---|---|---|---|---|---|
| Invariance | 1,084,815 | 3,301,742 | 311.151 | √ | |
| Response | 967,856 | 2,869,858 | 313.397 | √ | |
| Safety | 1,124,427 | 3,532,446 | 311.022 | √ | |
| Liveness | 963,291 | 2,737,076 | 272.362 | √ | |
| Safety | 1,145,663 | 3,598,231 | 315.210 | √ | |
| Liveness | 980,453 | 2,810,925 | 276.030 | √ | |
| : | Safety | 1,132,450 | 3,543,678 | 310.711 | √ |
| Fairness | 1,169,783 | 3,669,054 | 319.409 | √ | |
| Liveness | 970,873 | 2,756,332 | 273.862 | √ |
| Project | Properties | Type | Contracts | LOC | Verified |
|---|---|---|---|---|---|
| Crowdsale | 23 | Crowdsale | 20 | 1198 | 18 |
| Parity-wallet | 10 | Wallet | 2 | 200 | 8 |
| Secure-auction | 12 | Auction | 3 | 149 | 9 |
| ICO | 31 | ICO | 14 | 686 | 27 |
| ERC20 | 24 | Token | 6 | 599 | 22 |
| Brickblock | 10 | Token | 9 | 549 | 8 |
| blockking | 8 | Game | 1 | 100 | 7 |
| MRV | 12 | Token | 7 | 832 | 10 |
| Verx | KEVM | Smart Pulse | Zeus | Our Work | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Benchmark | Tests | TP | TN | FN | FP | TP | TN | FN | FP | TP | TN | FN | FP | TP | TN | FN | FP | TP | TN | FN | FP |
| Reentrancy | 17 | 9 | 5 | 2 | 1 | 2 | 2 | 9 | 4 | 13 | 1 | 2 | 0 | 8 | 4 | 4 | 1 | 14 | 2 | 1 | 0 |
| Disorder | 20 | 6 | 10 | 4 | 0 | 4 | 5 | 6 | 6 | 11 | 5 | 3 | 1 | 7 | 9 | 4 | 0 | 15 | 2 | 3 | 0 |
| DOS | 11 | 5 | 2 | 3 | 1 | 2 | 2 | 2 | 5 | 8 | 2 | 1 | 0 | 6 | 2 | 2 | 1 | 10 | 1 | 0 | 0 |
| Race Condition | 8 | 4 | 1 | 2 | 1 | 3 | 1 | 1 | 3 | 6 | 1 | 1 | 0 | 5 | 1 | 2 | 0 | 7 | 1 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, M.; Xu, Y.; Zhang, Y.; Yang, K.; Yan, S.; Cen, L. Formal Verification of Solidity Smart Contracts via Automata Theory. Symmetry 2025, 17, 1275. https://doi.org/10.3390/sym17081275
Xiao M, Xu Y, Zhang Y, Yang K, Yan S, Cen L. Formal Verification of Solidity Smart Contracts via Automata Theory. Symmetry. 2025; 17(8):1275. https://doi.org/10.3390/sym17081275
Chicago/Turabian StyleXiao, Meihua, Yangping Xu, Yongtuo Zhang, Ke Yang, Sufen Yan, and Li Cen. 2025. "Formal Verification of Solidity Smart Contracts via Automata Theory" Symmetry 17, no. 8: 1275. https://doi.org/10.3390/sym17081275
APA StyleXiao, M., Xu, Y., Zhang, Y., Yang, K., Yan, S., & Cen, L. (2025). Formal Verification of Solidity Smart Contracts via Automata Theory. Symmetry, 17(8), 1275. https://doi.org/10.3390/sym17081275





