Symmetry-Oriented Dynamic Routing Planning Algorithm for Reliable Map Fusion in Distributed UAV Communication Networks

Abstract

To enable distributed target searches by unmanned aerial vehicle (UAV) swarms, it is essential to collaboratively process multi-source sensing data and construct a globally consistent map. In response to the challenges posed by constrained communication and multi-hop transmission delays, this paper proposes a symmetry-oriented dynamic routing planning algorithm for reliable map fusion. The algorithm introduces a framework for the transmission and fusion of local perception maps, formulating routing tasks as an integer programming problem to determine latency-minimized transmission paths. When packet loss occurs, a dynamic re-routing strategy is triggered to ensure the continued reliability of the fusion process. The routing design preserves latency symmetry, aiming to keep transmission delays under packet loss conditions close to those under ideal, lossless scenarios. To improve scalability in large-scale UAV swarms, an approximate algorithm based on L-step forward prediction is further introduced to reduce computational complexity. The simulation results demonstrate that the proposed algorithm achieves low latency, strong robustness, and stable performance under varying communication conditions.

1. Introduction

Due to various factors such as environment, terrain, and interference, unmanned aerial vehicle (UAV) communication networks often experience degraded signal quality or even communication failure for certain UAVs [1]. In such communication-constrained scenarios, ensuring inter-UAV information exchange and reliable map fusion remains one of the core challenges for multi-UAV collaborative search tasks [2]. Before planning coordinated search routes, each UAV must obtain target state information of the search area. This requires UAVs to share environmental sensing data via multi-hop routing and collaboratively construct a consistent environmental map [3]. However, in complex and dynamic environments, unstable communication links and high-latency multi-hop transmissions significantly hinder the timeliness of information sharing and the reliability of map fusion, posing substantial challenges for reliable and low-latency routing in multi-UAV networks [4]. Moreover, to support time-sensitive collaborative perception and decision-making, it is desirable for the routing system to exhibit delay symmetry, that is, maintain similar latency performance in both ideal and adverse communication conditions.

During multi-UAV collaborative searches, due to variations in observation angles, locations, and sensor performance, the environmental information collected by each UAV tends to differ, resulting in inconsistent local maps. Effective cooperative planning among UAVs relies on consistent and reliable environmental awareness, which requires not only robust map fusion algorithms but also the stable transmission of mapping data across the network to enable timely updates and seamless information sharing [5,6].

Traditional map fusion approaches largely depend on full-map broadcasting and fusion among neighboring nodes. For instance, Bhuvana et al. [7] employed a distributed Kalman filter based on multi-target tracking to derive global target states by fusing inter-UAV communication data. Zheng et al. [8] investigated the influence of multi-source information on UAV path planning by analyzing the characteristics of shared environmental data. These studies typically assume ideal communication conditions where each UAV can receive complete shared information, which is unrealistic in practice due to constraints such as limited transmission range, latency, and packet loss. Under limited communication range, UAVs can only interact with their immediate neighbors and thus cannot access global information. To address this, Khan et al. [9] proposed a smoothed occupancy grid map for distributed fusion, incorporating timestamp mechanisms to prevent redundant fusion in multi-hop networks. Saadaoui et al. [10,11] proposed two optimized strategies for information sharing and merging during cooperative search where only information received from neighboring UAVs is eligible for fusion. Yao et al. [12] introduced a consensus algorithm with a state predictor that enables UAVs to achieve agreement on the environmental map with only local neighbor communications. In addition, communication errors may occur due to perception inaccuracies or transmission bit errors. Cheng et al. [13] proposed a distributed consensus algorithm that allows the UAV swarm to compute globally consistent results even when some UAVs have erroneous sensing outputs. UAV communication links are vulnerable to noise and fading, leading to data loss during transmission and the potential failure of distributed information fusion. To tackle this, Li et al. [14] addressed partial grid data loss during probabilistic map exchange and proposed a least squares-based method for missing data recovery, followed by an uncertainty-weighted consensus algorithm to achieve distributed agreement. Zhang et al. [15], under a similar modeling framework, employed radial basis function neural networks to restore missing information, enhancing the quality of recovered data and achieving more stable fusion outcomes.

The aforementioned methods only enable map information to be transmitted between single-hop neighbors, requiring multiple rounds of update and fusion to propagate perception data to multi-hop UAVs. As a result, the convergence speed of map consistency is relatively slow. Routing algorithms in UAV self-organized networks, known as Flying ad hoc Networks (FANETs) [16], can provide reliable multi-hop information transmission capabilities, thereby ensuring both robust and fast-converging map fusion. FANET routing algorithms are primarily categorized into topology-based routing and position-based routing. Topology-based routing algorithms utilize network topology information to design data transmission paths, establishing an efficient end-to-end route from the source to the destination before data transmission. Classic Mobile ad hoc Network (MANET) routing protocols such as Ad hoc On-Demand Distance Vector (AODV) [17], Optimized Link State Routing (OLSR) [18], and Destination-Sequenced Distance Vector (DSDV) [19] have been adapted and widely applied in FANETs. For instance, Pu et al. [20] proposed Link-Quality and Traffic-Load Aware (LTA)-OLSR, which introduces received signal strength and Media Access Control (MAC)-layer queue length to evaluate link quality and node load, thereby selecting transmission paths with better link conditions. Song et al. [21] developed an enhanced OLSR based on mobility prediction and delay prediction (OLSR-PMD) by predicting node positions and latency to optimize the selection of multipoint relay nodes, enhancing link and route stability. Tu et al. [22] presented the application of the Destination Sequenced Distance Vector (DSDV) scheme by combining the hop count and signal-to-noise ratio (SNR), which made routing decisions more scientific and effective, thus improving both data transmission efficiency and quality of service (QoS). Usman et al. [23] introduced Reliable Link and Position Routing (RLPR), which augments the traditional AODV protocol with position and link reliability information. By restricting broadcast range and applying energy thresholds, RLPR alleviates the broadcast storm problem and effectively extends network lifetime. Position-based routing algorithms, on the other hand, rely on the geographic location information of the node and its neighbors to forward data. Greedy Perimeter Stateless Routing (GPSR) [24] is a representative position-based protocol. However, due to the highly dynamic nature and 3D spatial characteristics of FANETs, its performance often falls short, prompting researchers to propose various enhancements. Rodrigues et al. [25] proposed GPSR with Position Prediction and Uncertainty (GPSR-PPU), which incorporates position prediction and uncertainty handling mechanisms to improve next-hop selection, though link stability remains a concern. Kumar et al. [26] developed Stability Factor-based Geographic Routing (SF-GeoR), which introduces a stability factor combining the node proximity ratio and residual energy to select more stable relay nodes, improving message delivery success rate and latency performance, albeit with insufficient consideration for link quality and noise interference. In a further refinement, Kumar et al. [27] proposed Utility Function (UF)-GPSR, which uses a utility function that integrates residual energy, movement direction, link risk, distance, and speed to reduce link disruption in dynamic environments. However, its reliance on predefined safe zones introduces limitations. Hosseinzadeh et al. [28] proposed GPSR+, which adapts to rapidly changing network conditions by employing a position prediction strategy and adjusting the Hello message interval. It also utilizes a spherical exclusion technique to construct a candidate node set for selecting the most stable next hop. Despite its improvements, the performance of this scheme is still constrained by the accuracy of position prediction.

Current routing algorithms primarily focus on point-to-point data transmission and do not consider the coordinated routing optimization required when information from multiple sources is transmitted concurrently across the network for map fusion. To enhance inter-UAV collaboration efficiency, it is necessary to design a multi-hop routing planning algorithm specifically oriented toward reliable map fusion, while also maintaining delay symmetry between communication scenarios with and without packet loss.

To address the above challenges, this paper proposes a dynamic routing planning algorithm for reliable map fusion, built upon a three-layer “Modeling–Planning–Compensation” architecture to enable cross-layer collaborative optimization. First, we modeled the UAV communication transmission process based on Rayleigh fading channels and propose a local-perception-map-based information fusion framework. This framework requires the routing planning of local perception maps during the fusion process to ensure that data packets are transmitted reliably to the entire network with minimal delay. Next, we designed an integer programming-based routing planning algorithm to solve for the minimum-delay routing paths. To manage computational complexity, an upper-bound estimation method was introduced. To cope with potential packet loss, a dynamic re-routing algorithm was developed to restore missing data through rerouting compensation. The overall routing strategy was designed to minimize the difference in latency between ideal and lossy communication conditions, thereby achieving symmetry in routing performance. Furthermore, to address the complexity challenge arising from the increasing number of UAVs, we propose a fixed-step forward prediction approximation algorithm to reduce computation while maintaining routing effectiveness.

2. System Model

2.1. Communication Model

Assume that there are $N_U$ UAVs in the swarm, denoted as $V_1,V_2,\dots ,V_{N_U}$, each functioning as a communication node. The wireless channel gain between any two distinct nodes is denoted by $G_{ij}$, where $i\ne j$. When node i acts as the transmitter, it transmits with power $P_i$; as the receiver, it observes an average noise power of ${\sigma }_j^2$. We assume that the UAVs have sufficient bandwidth resources and operate on different frequency bands, so inter-UAV interference can be neglected [29]. The SNR at the receiving end for communication from UAV $V_i$ to UAV $V_j$ is given by

$${\mathsf{\Gamma }}_{ij}={\displaystyle \frac{P_i{G}_{ij}}{{\sigma }_j}}.$$

(1)

We consider performing target searches in environments without line-of-sight paths, such as urban areas or forests. The channel gain can be modeled using the Rayleigh fading model, expressed as

$$G_{ij}={\displaystyle \frac{C_{ij}{\left|h_{ij}\right|}^2}{d_{ij}^{\alpha }}},$$

(2)

where $C_{ij}$ is a constant that accounts for antenna gain and propagation obstacles (such as shadow fading), $h_{ij}$ represents the effect of multipath fading on the channel gain, $d_{ij}$ is the distance between UAV $V_i$ and UAV $V_j$, and $\alpha$ is the path loss exponent.

To maintain the connectivity of a communication link, the packet loss rate must remain within an acceptable range. This requires the link to maintain a sufficiently high received SNR. We assume that a data packet is successfully transmitted if the received SNR exceeds a certain threshold. Let $\gamma$ denote the minimum SNR threshold required for successful transmission. Assuming that the channel experiences fast Rayleigh fading, the small-scale fading coefficient $h_{ij}$ follows a complex Gaussian distribution with zero mean and unit variance. Based on Equations (1) and (2), the probability of successful communication between UAV $V_i$ and UAV $V_j$ can be calculated as

$$P_{ij}({\mathsf{\Gamma }}_{ij}\ge \gamma )=exp\left(-{\displaystyle \frac{{\sigma }_j^2\gamma d_{ij}^{\alpha }}{C_{ij}{P}_i}}\right).$$

(3)

Equation (3) represents the long-term statistical success probability, averaged over fast fading events. Based on practical system requirements, a link establishment threshold $\delta$ is defined to evaluate link validity. Specifically, if $P_{ij}\ge \delta$, the communication link between UAVs $V_i$ and $V_j$ is considered effective and reliable. Otherwise, the link is regarded as unavailable. This threshold $\delta$ effectively serves as a density threshold, constraining the sparsity of the resulting communication network.

In summary, the key parameters governing network initialization and link establishment include the following:

• $\gamma$: Minimum SNR threshold for reliable transmission.
• $\delta$: Communication success probability threshold defining link existence.
• $d_{ij}$: Inter-node distance, reflecting spatial distribution.
• $\alpha$: Path loss exponent.
• $C_{ij}$: Constant representing antenna gain and environmental attenuation.

Using the above link establishment criterion, the adjacency matrix $\mathbf{N}\in {\mathbb{R}}^{N_U\times N_U}$ is constructed, where each element $N_{ij}=1$ indicates the existence of a valid bidirectional communication link between UAVs $V_i$ and $V_j$. Since $P_{ij}=P_{ji}$, the adjacency matrix $\mathbf{N}$ is symmetric. The resulting UAV communication network is deemed connected if every UAV node can reach any other node via direct links or multi-hop paths.

In this study, it was assumed that the initial UAV deployment satisfies the network connectivity condition based on the above parameters. This connected communication network provided the foundation for subsequent routing planning and multi-source map fusion.

2.2. Map Model

We constructed a grid-based map model of the mission area with reference to [30]. The mission area S was assumed to be a two-dimensional square plane, which was discretized into $S_x\times S_y$ equally sized grid cells, where $S_x$ and $S_y$ denote the number of rows and columns, respectively. This discretized grid map model was mathematically tractable and maintained generalization capabilities as it could be extended to irregular terrains through adaptive grid partitioning. Suppose that there are $N_T$ targets in the mission area whose motion states are unknown and move independently. We adopt a probabilistic grid map to describe the UAV’s perception of the mission area. Each grid cell $c=(x,y)$ is associated with a probability $b\left(c\right)$, representing the likelihood that a target exists in that cell. The probabilities across all grid cells satisfy the normalization condition ${\sum }_{c\in S}b\left(c\right)=N_T$.

Assume that each UAV is equipped with a sensor of sensing radius $R_S$. A grid cell is considered observable by a UAV if its distance to the UAV is less than $R_S$. The observable region of UAV $V_i$ at time step k is defined as $o_{i,k}=\{c\mid d(c,V_i)<R_S\}$, where $d(c,V_i)$ represents the distance between grid cell c and UAV $V_i$. At each time step k, the sensor performs an independent observation over the grid and produces a detection result $o_{i,k}\left(c\right)\in \{0,1\}$. Specifically, $o_{i,k}\left(c\right)=0$ indicates that UAV $V_i$ does not detect a target in grid cell c, while $o_{i,k}\left(c\right)=1$ indicates that a target is detected in cell c. Due to limitations in sensor detection capabilities, observation errors may occur. Let $p_d$ denote the probability that the sensor gives a correct detection; then, the error probability is $1-p_d$.

Given the probability distribution map $b_k$ and the observation result $o_k\left(c\right)$ at the previous time step, the updated probability distribution map at time step $k+1$, denoted by $b_{k+1}$, can be obtained using the Bayesian update method. The update rule for the probability map is

$$b_{k+1}\left(c\right)={\displaystyle \frac{p(o_k\left(c\right)\mid {\theta }_c=1)b_k\left(c\right)}{p(o_k\left(c\right)\mid {\theta }_c=1)b_k\left(c\right)+p(o_k\left(c\right)\mid {\theta }_c=0)(1-b_k\left(c\right))}},$$

(4)

where ${\theta }_c=1$ denotes the event that a target exists in grid cell c and ${\theta }_c=0$ indicates that there is no target in the cell. If $o_k\left(c\right)=1$, then $p(o_k\left(c\right)\mid {\theta }_c=1)=p_d$; otherwise, it equals $1-p_d$.

In this study, the UAVs were assumed to be randomly distributed across the mission area prior to map fusion, representing their initial sensing positions after completing local exploration. The subsequent map fusion process focused on the reliable transmission and integration of local observation maps under constrained communication conditions, rather than on UAV trajectory planning. Although UAV movement patterns may impact the completeness of local sensing data, this work did not explicitly model or optimize UAV flight paths. The proposed routing planning algorithm and map fusion framework assumed that each UAV had collected its initial observation map and emphasized the reliable dissemination and fusion of this information within the communication network. Future research may consider the joint optimization of UAV mobility and map fusion to enhance overall mapping completeness and system performance.

3. Map Fusion

The proposed map fusion framework operates under the assumption that UAVs have completed their initial environmental sensing and generated their respective local observation maps. Their subsequent positions during the map fusion process are considered fixed for the purposes of communication and data sharing. This assumption decoupled UAV mobility planning from the routing and fusion tasks addressed in this work. While UAV flight paths directly affect the spatial distribution and completeness of sensing data, the current study focused exclusively on ensuring the efficient and reliable sharing of the collected local maps.

Common distributed map fusion algorithms can be classified into two main types. One approach is to transmit a globally updated probability map (obtained using Equation (4)) to neighboring UAVs for map fusion. The other approach involves transmitting and fusing the local observation map $o_k\left(c\right)$ [9]. In UAV target search tasks, the sensing range of a UAV is usually much smaller than the overall mission area, so transmitting local observation maps can significantly reduce the communication overhead. Based on this consideration, we adopted the method of transmitting local observation maps for map fusion.

Specifically, at each time step k, each UAV performed environmental sensing and obtained a local observation map $o_{i,k}$. Each UAV then shared its local observation map with the others and received local maps from all other UAVs. As a result, every UAV held the complete set of local observation maps at time k, which could be combined into a global observation map $O_k={\bigcup }_i{o}_{i,k}$. It should be noted that although the global observation map $O_k$ was computed in a distributed manner, the fact that each UAV held all local maps ensured that the result was consistent across the network. Therefore, each UAV obtained a distributed but consistent global observation map $O_k$. Based on this, the local observation result $o_k\left(c\right)$ in Equation (4) could be replaced by the globally consistent observation map $O_k$, enabling the calculation of a globally consistent probability distribution map $b_{k+1}$.

We assumed that all UAVs performed sensing and generated their local observation maps synchronously, meaning that data transmission started simultaneously across the network. The ultimate goal of the UAV network was to ensure that each local observation map $o_{i,k}$ was delivered to all UAVs. To achieve this, UAVs formed a multi-hop network and transmitted the data using a broadcast-based approach.

As shown in Figure 1, the time axis was divided into a series of fixed-length time frames. Each time frame consisted of a preceding relay interval and a subsequent listening interval. During the relay interval, UAVs broadcasted and forwarded their local observation maps according to the scheduled routing plan. During the listening interval, UAVs received and buffered local observation maps transmitted by other UAVs.

Each relay interval was defined as a short time unit in which only one data transmission could be completed, while the listening interval was defined as a time unit capable of receiving all data sent within the same time frame. Since the communication model assumed sufficient frequency resources among UAVs and no mutual interference, it was feasible to assume that multiple UAVs could transmit simultaneously and that the receiving UAV could process all of them during the listening interval. A time frame was a very short duration, during which the channel condition was assumed to remain constant [31]. For instance, under the 802.11n protocol, the total delay for transmitting a 1 KB data packet was approximately 0.2 ms. Even when accounting for contention and data rate fluctuations, the duration of a single time frame could still be considered less than 1 ms.

Let $M\in {\{0,1\}}^{(T+1)\times N_U\times N_U}$ be the storage matrix of the UAVs, where each element $M_{i,j}^t\in \{0,1\}$ is a binary variable indicating whether UAV $V_i$ has cached the local observation map $o_{j,k}$ after transmission during the t-th time frame. A value of 1 indicates that UAV $V_i$ has cached the local map $o_{j,k}$, while 0 means that it has not. The storage matrices at the initial and terminal time frames are predefined. At the initial time, $M^0=I$, which is an identity matrix, indicating that each UAV only possesses its own local observation map from onboard sensing and has not yet exchanged information with others. At the terminal time, $M^T=\mathbf{1}$, which is a matrix of all ones, indicating that by the end of the task, each UAV has obtained all local observation maps from every other UAV.

We formulated the UAV relay routing planning task as the following 0-1 integer programming problem:

$$\begin{array}{}\mathrm{(5a)}& {\displaystyle \underset{S,M}{min}}T\hfill \mathrm{(5b)}& \mathrm{s}.\mathrm{t}.{\displaystyle \sum _j}{S}_{ij}^t\le 1,i\in [1,N_U],t\in [1,T],\hfill \mathrm{(5c)}& \hspace{1em}\hspace{1em}\hspace{1em}{S}_{ij}^t\le M_{ij}^t,i\in [1,N_U],j\in [1,N_U],t\in [1,T],\hfill \mathrm{(5d)}& \hspace{1em}\hspace{1em}\hspace{1em}{M}_{ij}^t=max\left(M_{ij}^{t-1},{\displaystyle \sum _k}{N}_{ik}{S}_{kj}^t\right),i\in [1,N_U],j\in [1,N_U],t\in [1,T],\hfill \mathrm{(5e)}& \hspace{1em}\hspace{1em}\hspace{1em}{M}^0=I^{N_U\times N_U},\hfill \mathrm{(5f)}& \hspace{1em}\hspace{1em}\hspace{1em}{M}^T={\mathbf{1}}^{N_U\times N_U},\hfill \end{array}$$

where $S\in {\{0,1\}}^{T\times N_U\times N_U}$ is the UAV relay routing matrix, where each element $S_{i,j}^t\in \{0,1\}$ is a binary variable. A value of 1 indicated that UAV $V_i$ broadcasts and forwards the local observation map $o_{j,k}$ during the t-th time interval. The objective in Equation (5a) was to minimize the total time required to complete the task. Equation (5b) ensured that each UAV could transmit at most one data packet per time frame, which aligned with our assumption about the relay interval. Equation (5c) enforced the forwarding constraint, stating that UAV $V_i$ could only forward data from UAV $V_j$ if it had already stored that data. Equation (5d) defined the state transition of the storage matrix. The value $M_{ij}^t=1$ held if at least one of the following conditions was satisfied: (1) the previous time frame already had $M_{ij}^{t-1}=1$ or (2) during the current time frame, UAV $V_i$ received the j-th data packet from a neighboring UAV. Equation (5e,f) specified the initial and terminal conditions of the storage matrix.

4. Dynamic Routing Planning Algorithm

4.1. Routing Planning Solution

The routing planning problem defined in Equation (5) involves optimizing the number of time frames, which is tightly coupled with the terminal condition constraints and the number of optimization variables S and M. As a result, it is difficult to solve the problem directly. One possible approach is to perform a binary search over the time frame count T to find the minimal T that satisfies all constraints. However, this requires solving the integer programming problem multiple times, which leads to very high computational complexity. To address this, we reformulated the problem into the following alternative form:

$$\begin{array}{}\mathrm{(6a)}& {\displaystyle \underset{S,M,y}{max}}{\displaystyle \sum _t}{y}_t\hfill \mathrm{(6b)}& \mathrm{s}.\mathrm{t}.{\displaystyle \sum _j}{S}_{ij}^t\le 1,i\in [1,N_U],t\in [1,T],\hfill \mathrm{(6c)}& \hspace{1em}\hspace{1em}\hspace{1em}{S}_{ij}^t\le M_{ij}^t,i\in [1,N_U],j\in [1,N_U],t\in [1,T],\hfill \mathrm{(6d)}& \hspace{1em}\hspace{1em}\hspace{1em}{M}_{ij}^t=max\left(M_{ij}^{t-1},{\displaystyle \sum _k}{N}_{ik}{S}_{kj}^t\right),i\in [1,N_U],j\in [1,N_U],t\in [1,T],\hfill \mathrm{(6e)}& \hspace{1em}\hspace{1em}\hspace{1em}{M}^0=I^{N_U\times N_U},\hfill \mathrm{(6f)}& \hspace{1em}\hspace{1em}\hspace{1em}{y}_t\left(N_U^2-{\displaystyle \sum _{i,j}}{M}_{ij}^t\right)=0,t\in [1,T].\hfill \end{array}$$

In Equation (6), we introduced a binary auxiliary variable $y\in {\{0,1\}}^T$ and modified both the objective function and the terminal condition in Equation (5f). The objective was changed to maximizing the sum of the auxiliary variables. Note that Equation (6f) imposed a constraint on $y_t$, such that either $y_t=0$ or $N_U^2-{\sum }_{i,j}{M}_{ij}^t=0$ or both. Here, $N_U^2-{\sum }_{i,j}{M}_{ij}^t$ could be regarded as an indicator of task completion as its value became zero only when $M^t={\mathbf{1}}^{N_U\times N_U}$. This implied that $y_t$ acted as an indicator variable representing whether the task had been completed at time frame t, and it could take the value of 1 only if the task was complete. By summing $y_t$, we could determine how many time frames corresponded to the completed task status out of the total T frames. This allowed us to optimize routing performance under a fixed value of T. In the following, we explain the relationship between the fixed T and the optimal routing time.

Assume that the optimal solution to the routing problem in Equation (5) is $T^{*}$. The state transition equation for the storage matrix in Equation (6d) ensures that for any time frame $t\ge T^{*}$, we have $M^t={\mathbf{1}}^{N_U\times N_U}$. Therefore, in the optimal solution of the problem (Equation (6)), the last $T-T^{*}+1$ time frames will have $y_t=1$. This implies that the optimal routing time of the routing planning problem can be expressed as

$$T^{*}=T-\sum _t{y}_t^{*}+1.$$

(7)

4.2. Upper Bound Estimation for Routing Time

In Equation (6), both the terminal condition and the number of optimization variables were fixed and did not change during the optimization process, allowing the problem to be solved using an integer programming solver. However, it was important to ensure that the task could be completed within the total number of time frames T, i.e., $T\ge T^{*}$; otherwise, the optimal time frame count computed via Equation (7) would not reflect the true optimal routing time. This required us to set T as an upper bound in the optimization problem.

In the routing planning problem, the number of optimization variables increased linearly with the total number of time frames. Therefore, setting an overly conservative upper bound could lead to excessive computational time. To address this, we aimed to determine a tight upper bound for the total number of time frames. In this section, we provide such an upper bound along with its proof.

Theorem 1.

For any connected spanning subgraph of a connected graph, the corresponding optimal routing time $T_{sub}^{*}$ is always greater than or equal to the optimal routing time of the original graph, i.e., $T_{sub}^{*}\ge T^{*}.$

Proof of Theorem 1. 

Let the adjacency matrix of the original communication graph be N and let the adjacency matrix of its spanning subgraph be $N^{\prime }$. Since the edges of the spanning subgraph must be a subset of those in the original graph, we have $N_{ij}\ge N_{ij}^{\prime }\mathrm{for}\mathrm{all}i,j$. Assume that the optimal routing time for the subgraph is $T_{\mathrm{sub}}^{*}$, with corresponding forwarding routing matrix $S^{\prime }$ and storage matrix $M^{\prime }$. If the same routing matrix $S^{\prime }$ is used for forwarding scheduling in the original graph, then the following inequality holds: ${\sum }_k{N}_{ik}{S}_{kj}^t\ge {\sum }_k{N}_{ik}^{\prime }{S}_{kj}^t$, which implies that the state transitions of the storage matrix in the original graph must satisfy

$$M_{ij}^t=max\left(M_{ij}^{t-1},\sum _k{N}_{ik}{S}_{kj}^t\right)\ge max\left(M_{ij}^{t-1},\sum _k{N}_{ik}^{\prime }{S}_{kj}^t\right)={\left(M_{ij}^{\prime }\right)}^t.$$

(8)

At time step $T_{\mathrm{sub}}^{*}$, the above inequality still holds. Since the storage matrix of the spanning subgraph is the all-ones matrix at this time, the storage matrix of the original graph must also be the all-ones matrix. This indicates that there exists at least one forwarding strategy by which the original graph can complete the forwarding task within $T_{\mathrm{sub}}^{*}$ time frames. Therefore, the optimal routing time $T^{*}$ of the original graph cannot be greater than $T_{\mathrm{sub}}^{*}$, which completes the proof.    □

This theorem only proves that there exists at least one case where $T^{*}=T_{\mathrm{sub}}^{*}$. The inequality $T^{*}\le T_{\mathrm{sub}}^{*}$ can be easily demonstrated with a simple example, for instance, a fully connected graph with three nodes and a connected spanning subgraph formed by removing any one edge. Their optimal routing times are 1 and 3, respectively. Communication connectivity graphs can have highly diverse topologies, and finding a common optimal upper bound that applies to all such topologies is very challenging. However, Theorem 1 tells us that the optimal routing time of any connected spanning subgraph provides a valid upper bound for the original graph. This naturally leads us to consider using the minimal connected spanning subgraph as an upper bound estimator. The minimum spanning tree (MST) of a graph is the smallest connected spanning subgraph that satisfies the connectivity requirement. Removing any edge from the MST results in a disconnected graph. Moreover, every connected graph has at least one minimum spanning tree. Therefore, our goal becomes finding the optimal routing time of the minimum spanning tree.

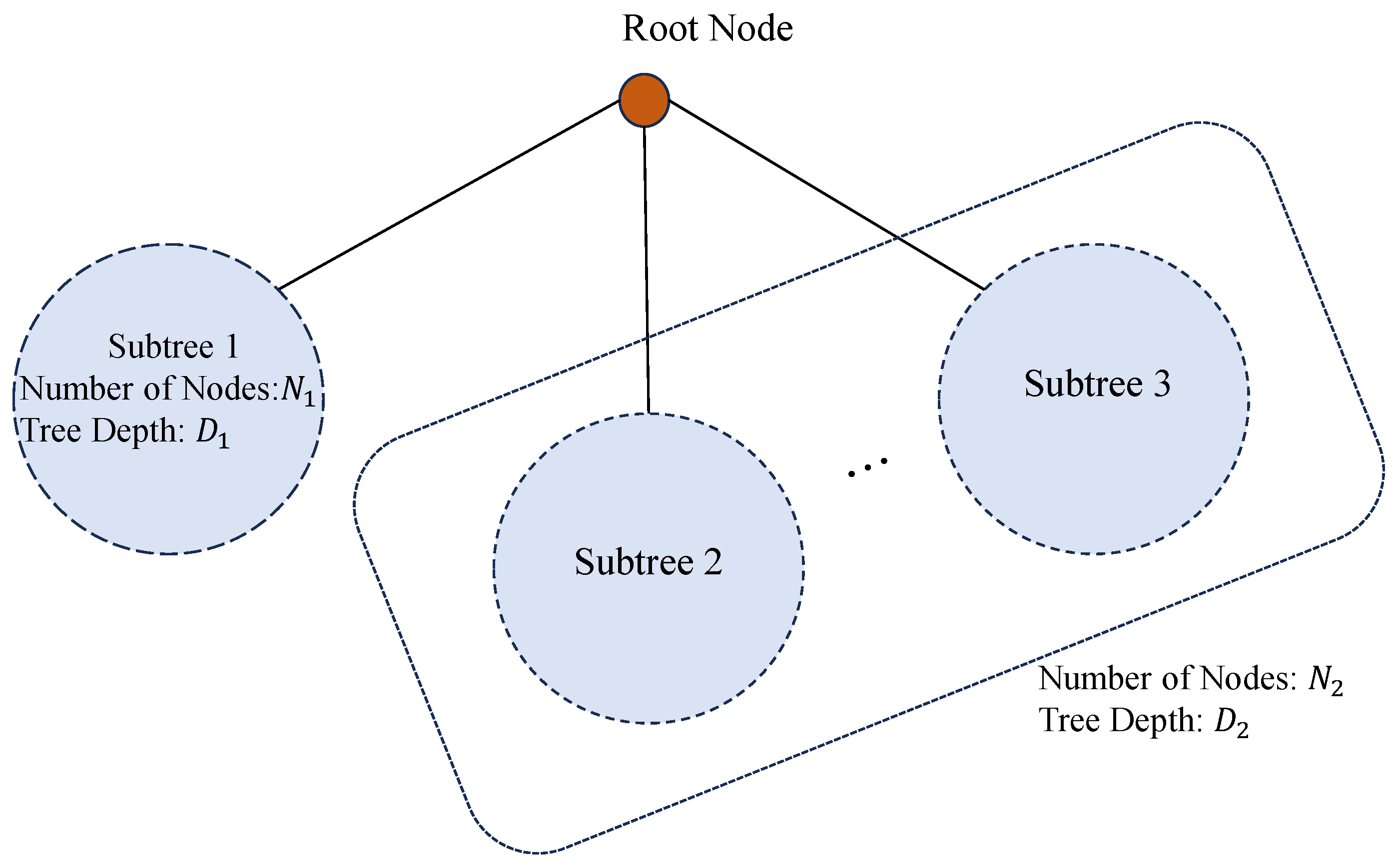
Theorem 2.

The optimal routing time of a tree-structured communication network is given by $T^{*}=N_U+⌊{\displaystyle \frac{D}{2}}⌋-1$, where $N_U$ is the number of nodes in the tree, D is the diameter of the tree (defined as the maximum path length between any two nodes), and $⌊·⌋$ represents the floor operation.

Proof of Theorem 2. 

The total routing time consists of two parts: forwarding time and scheduling time. The forwarding time refers to the total time each node needs to forward its own data, which equals $N_U$, since each of the $N_U$ nodes must transmit once.

To analyze the scheduling time, we consider any non-leaf node p in the tree as the root (see Figure 2). Node p connects multiple subtrees. Let Subtree 1 be the deepest subtree with depth $D_1$ and node count $N_1$, and let Subtrees 2 to n together have node count $N_2$ and maximum depth $D_2$. Since all data transmissions between these subtrees must pass through node p, p serves as a critical relay. After p finishes forwarding all data packets in $N_U$ time frames, additional scheduling time is required for packets to reach the leaf nodes of its subtrees.

If the last forwarded packet belongs to Subtrees 2 to n, the remaining intra-subtree broadcast delay is at least $D_1-1$. Conversely, if the last forwarded packet belongs to Subtree 1, the remaining delay is $D_2-1$, where $D_2\le D_1$. Therefore, to minimize delay, node p should forward the data destined for Subtree 1 last, ensuring that the scheduling time is $D_2-1$. Consequently, the total routing time considering node p as the relay is $N_U+D_2-1$.

To obtain the routing time for the entire tree, we maximize over all possible relay nodes p. Let the leaf nodes corresponding to depths $D_1$ and $D_2$ be u and v, respectively. The path between u and v must pass through p and has length $D_1+D_2$, which is bounded by the tree’s diameter, i.e., $D_1+D_2\le D$. Assuming $D_1\ge D_2$, the maximum possible value of $D_2$ is $⌊{\displaystyle \frac{D}{2}}⌋$. Substituting this into the previous expression, we conclude that the optimal routing time for the tree is $T^{*}=N_U+⌊{\displaystyle \frac{D}{2}}⌋-1$.    □

It is important to note that in Theorem 2, we derived the theoretical maximum value of $D_2$. In fact, this value can be achieved in any tree by simply selecting the root node p as the central point of the path corresponding to the tree’s diameter. This theorem tells us that the optimal routing time of any tree-structured communication network is a fixed value.

Theorem 3.

For any connected communication network, the tight upper bound of its optimal routing time is $N_U+⌊{\displaystyle \frac{D}{2}}⌋-1,$ and this bound is achieved when the communication network is a tree.

Proof of Theorem 3. 

For any connected communication network, we can identify its minimum spanning tree $N_{\mathrm{mst}}$, whose corresponding optimal routing time is $T_{\mathrm{mst}}^{*}$. The minimum spanning tree is a connected spanning subgraph of the original graph. According to Theorem 1, we have $T^{*}\le T_{\mathrm{mst}}^{*}.$ From Theorem 2, we know that $T_{\mathrm{mst}}^{*}=N_U+⌊{\displaystyle \frac{D}{2}}⌋-1.$ Thus, the theorem is proven.    □

4.3. Packet Loss Replanning Algorithm

Under low SNR conditions, communication links between UAVs may experience packet loss. When packet loss occurs, the actual storage matrix deviates from the optimal storage matrix estimated during the initial routing planning. This discrepancy may cause the forwarding matrix in subsequent time frames to become invalid. In such cases, it is necessary to replan the forwarding routing matrix. Assume that packet loss occurs at time frame $t_l$ and that the actual storage matrix at that moment is $M_s$. Note that due to packet loss, this storage matrix differs from the originally planned storage matrix $M^{t_l}$. If no packet loss had occurred, the forwarding task would have required $T^{*}-t_l$ additional time frames to complete. In the worst case, one extra time frame is needed for retransmission, after which the forwarding resumes as planned. Therefore, the upper bound on the new routing time becomes $T=T^{*}-t_l+1.$ The replanning optimization problem is defined as follows:

$$\begin{array}{}\mathrm{(9a)}& {\displaystyle \underset{S,M,y}{max}}{\displaystyle \sum _t}{y}_t\hfill \mathrm{(9b)}& \mathrm{s}.\mathrm{t}.{\displaystyle \sum _j}{S}_{ij}^t\le 1,i\in [1,N_U],t\in [1,T],\hfill \mathrm{(9c)}& \hspace{1em}\hspace{1em}\hspace{1em}{S}_{ij}^t\le M_{ij}^t,i\in [1,N_U],j\in [1,N_U],t\in [1,T],\hfill \mathrm{(9d)}& \hspace{1em}\hspace{1em}\hspace{1em}{M}_{ij}^t=max\left(M_{ij}^{t-1},{\displaystyle \sum _k}{N}_{ik}{S}_{kj}^t\right),i\in [1,N_U],j\in [1,N_U],t\in [1,T],\hfill \mathrm{(9e)}& \hspace{1em}\hspace{1em}\hspace{1em}{M}^0=M_s,\hfill \mathrm{(9f)}& \hspace{1em}\hspace{1em}\hspace{1em}{y}_t\left(N_U^2-{\displaystyle \sum _{i,j}}{M}_{ij}^t\right)=0,t\in [1,T].\hfill \end{array}$$

4.4. Fixed-Step Forward Prediction Algorithm

The aforementioned algorithm performs forwarding route planning across all time steps in one shot. While it can obtain the globally optimal routing plan, its computational complexity is high. Moreover, when packet loss occurs, the replanning process still requires recomputing the entire routing schedule. To reduce computational overhead, we propose an approximate algorithm based on multi-step forward prediction. The multi-step prediction with single-step execution strategy, inspired by Model Predictive Control (MPC), allows the algorithm to escape the local optimum of step-by-step decision-making and find higher-quality solutions by forecasting future behavior. Following the MPC approach, we apply multi-step forward prediction to UAV forwarding route planning and execute only the predicted decision for the first time frame. Assuming the prediction horizon is $T=L$, the problem can be reformulated as follows:

$$\begin{array}{}\mathrm{(10a)}& {\displaystyle \underset{S,M}{max}}{\displaystyle \sum _i}{\displaystyle \sum _j}{M}_{ij}^L\hfill \mathrm{(10b)}& \mathrm{s}.\mathrm{t}.\left(9\mathrm{b}\right)–\left(9\mathrm{e}\right).\hfill \end{array}$$

The objective of the above problem is designed to maximize the sum of all UAVs’ storage matrices after L steps of transmission, effectively aiming to disseminate data packets to as many neighboring UAVs as possible. This approximate solution performs an L-step forward routing prediction at each time frame. In the event of packet loss, the prediction is recalculated at every time frame, which inherently accounts for the impact of the loss. Therefore, there is no need to separately design an additional routing replanning algorithm.

Summarizing Section 4.1–Section 4.4, the overall pseudocode of the proposed map fusion-based routing planning algorithm is presented in Algorithm 1.

Algorithm 1 Dynamic Routing Planning Algorithm for Reliable Map Fusion
1:	Initialization: Time step $t=1$, replanning flag $replan=\mathrm{True}$;
2:	while task is not completed do
3:	if $N_U$ < quantity threshold $N_0$ then
4:	if $replan=\mathrm{True}$ then
5:	Compute upper bound of routing time $T_{\mathrm{upper}}$;
6:	Use the routing planner or replanning algorithm to solve global forwarding schedule S;
7:	$replan\leftarrow \mathrm{False}$;
8:	$t\leftarrow 1$;
9:	end if
10:	Execute the t-th forwarding step in S;
11:	if packet loss occurs then
12:	$replan\leftarrow \mathrm{True}$;
13:	end if
14:	else
15:	// L-step forward prediction algorithm:
16:	At current time step t, use the current storage matrix $M^t$ as initial state;
17:	Set prediction horizon L;
18:	Prediction Generation:
19:	Solve the following optimisation over horizon L: Maximise Equation (10a) after L steps, subject to constraints (9b)–(9e), using $M^t$ as $M^0$;
20:	Obtain L-step predicted forwarding schedule $S=\{S^1,S^2,\dots ,S^L\}$;
21:	Predict future storage matrices $M^1,M^2,\dots ,M^L$ using storage update rules;
22:	Execution and Update:
23:	Execute the first step $S^1$ of the predicted schedule;
24:	Update the actual storage matrix to reflect successful transmissions and any packet loss;
25:	end if
26:	$t\leftarrow t+1$;
27:	end while

5. Simulation

This study considered a scenario in which multiple UAVs performed distributed map fusion, forming a connected communication network. The parameters used in the communication model followed the settings in [29]. The UAV transmit power was fixed at $P_i=100\mathrm{mW}$, the average noise power was ${\sigma }_j^2=-70\mathrm{dBm}$, and the minimum SNR threshold was $\gamma =10\mathrm{dB}$. The constant accounting for antenna gain and shadow fading was set to $C_{ij}=20$ and the path loss exponent was $\alpha =3$. With the transmit power fixed, the communication success probability defined in Equation (3) was only affected by the distance between UAVs. When the distance $d_{ij}=500\mathrm{m}$, the calculated communication success probability was $P_{ij}=93.9\%$. We used this value as the connectivity threshold—if the communication success probability between two UAVs exceeded this value, the communication link was considered connected. All subsequent experiments were conducted under this parameter setting.

5.1. Map Fusion Algorithm Experiments

We first compared four different map fusion algorithms: consensus-based fusion [12], averaging [9], uncertainty-based fusion [14], and our local map fusion.

In a square area of $4000\mathrm{m}\times 4000\mathrm{m}$, we deployed multiple UAVs to perform map fusion. The mission area was discretized into a $40\times 40$ grid with a spatial resolution of $100\mathrm{m}$. The initial probability distribution map was set as uniform, meaning that the probability of a target being present was equal across all grid cells. The UAVs were randomly distributed throughout the environment, each independently sensing the map once before starting the fusion process. We evaluated the performance of each map fusion algorithm based on the degree of difference between the maps held by different UAVs. The evaluation metric was calculated as

$$F_{\mathrm{diff}}={\displaystyle \frac{1}{N_U}}\sum _{i=1}^{N_U}\sum _c\mathrm{abs}\left(b_i\left(c\right)-\overline{b}\left(c\right)\right),$$

(11)

where $\overline{b}\left(c\right)$ represents the average value of cell c across the maps of all $N_U$ UAVs. This metric reflected the absolute deviation of each UAV’s resulting map from the average map.

The results of map deviation after fusion are shown in Figure 3a. We compared the map differences after fusion for different algorithms under 4, 8, 16, 32, 64, and 128 UAVs. As shown in the figure, regardless of the algorithm used, the map deviation increased as the number of UAVs grew. This indicated that achieving consistent map fusion became more difficult with larger UAV swarms. Among the evaluated methods, the uncertainty-based fusion algorithm performed the worst, while the averaging algorithm and consensus-based fusion yielded similar results. Our proposed method outperformed all others. The reason lies in the fact that the three baseline algorithms all performed fusion based on the global probability map. In each update step, the detected target information could only be propagated to neighboring UAVs and could not spread across the entire network. This resulted in delayed information transmission over multi-hop UAV links. As the network size increased, the map inconsistency between UAVs also became larger. Compared to the uncertainty-based fusion algorithm, both the consensus and averaging algorithms tended to converge the detected grid probabilities toward the mean. Since the initial probability map was uniformly distributed (i.e., all grid cells had the same initial probability), the probability differences between UAVs after detection remained small, and the spread of detection events among neighbors was more gradual. In contrast, our proposed method broadcasted the local observation map across the entire network, so that in a single update step, all UAVs could access global information. This enabled the network to achieve globally consistent map fusion, demonstrating the superiority of our method in maintaining consistent situational awareness. The communication overhead for each algorithm is shown in Figure 3b. We assumed that each data point was encoded as a 32 bit, single-precision, floating-point number. Only the communication cost for transmitting maps was considered, while the fixed overhead of communication protocols was ignored.

Since all three baseline algorithms performed fusion based on the global map, their communication data volumes were the same: equal to the number of edges in the UAV network multiplied by the size of the global map. In this experiment, this could be expressed as $\mathcal{O}\left(E{S}_x{S}_y\right)$, where E is the number of edges in the UAV communication network. In contrast, our proposed method was based on broadcasting local observation maps throughout the network, resulting in a communication data volume of $\mathcal{O}\left(R^{2}SE{N}_U\right)$, where $R^{2}S$ represents the size of the local observation map and $N_U$ is the number of UAVs. Since the local observation maps were significantly smaller than the global map in our experiments, the communication overhead of our method remained relatively low. However, because each local map needed to be broadcast across the entire network, the communication data volume in our method grew quadratically with the number of UAVs, while that of the global map-based methods grew linearly. This trend is also reflected in the figure, showing that the communication data volume of our method increased more rapidly with the number of UAVs. This suggests that our proposed method is more suitable for map fusion in small-scale UAV swarms.

It should be noted that although the overhead of packet headers in communication protocols was not explicitly considered in this study, in practice, each data packet consists of the local observation map data along with its attached header. The header primarily includes metadata such as the source node ID, timestamp, and fragment index, typically accounting for approximately 5–10% of the total packet size. In addition, during the dynamic routing process, the bandwidth overhead caused by protocol control messages—such as neighbor state broadcasts and re-routing trigger signals—remains relatively small. The communication volume of these control messages accounts for approximately 8–12% of the total overhead, increasing slightly as the network scale grows, but not constituting a significant bottleneck. Therefore, the overall communication overhead is still dominated by the broadcasting of local observation map data, while the additional bandwidth consumption introduced by protocol mechanisms can be regarded as a lightweight and controllable overhead.

5.2. Routing Planning Experiments

To evaluate the performance of the proposed routing planning algorithm, we compared the fusion delays of different algorithms within the local observation map fusion framework presented in this paper. Each local observation map only contained the offset parameters along two axes and the grid data within the sensing range, resulting in a data size of less than 1 KB. Therefore, we assumed that each time frame corresponded to 1 ms. We ignored the algorithm’s processing time and defined fusion delay as the product of the optimal number of routing time frames and the duration of a single time frame.

In this section, six algorithms are compared:

(1)

L-forward: An approximate forwarding routing algorithm based on L-step forward prediction. The algorithm used L-step prediction and executed only the first step in each time frame. The prediction horizon was set to $L=2$.

(2)

Greedy1: Furthest-first scheduling. Each UAV prioritized forwarding the data packet it stored that was furthest from its destination.

(3)

Greedy2: Greedy broadcast. Each UAV prioritized broadcasting the data that was missing from the largest number of its neighbors.

(4)

Flooding: Global broadcast of local observation data using the flooding method.

(5)

OLSR [32]: Optimized Link State Routing with multipoint relay (MPR), used to optimize the flooding-based forwarding process.

(6)

Plan: The dynamic routing planning algorithm proposed in this paper. The initial routing was planned using our algorithm and, in the event of packet loss, the forwarding schedule was recomputed using the proposed replanning algorithm to ensure transmission reliability.

The experimental setup was the same as in the previous subsection. UAVs were randomly initialized within a fixed-size area of $4000\times 4000$ meters, and packet routing experiments were conducted with different numbers of UAVs (4, 8, 16, and 32). The number of edges in the randomly generated connected communication graphs for each network scale is listed in

Table 1. Number of edges in connected graphs.

Number of UAVs	4	8	16	32
Number of Edges	5	13	38	105

. The corresponding map fusion delays are shown in Figure 4.

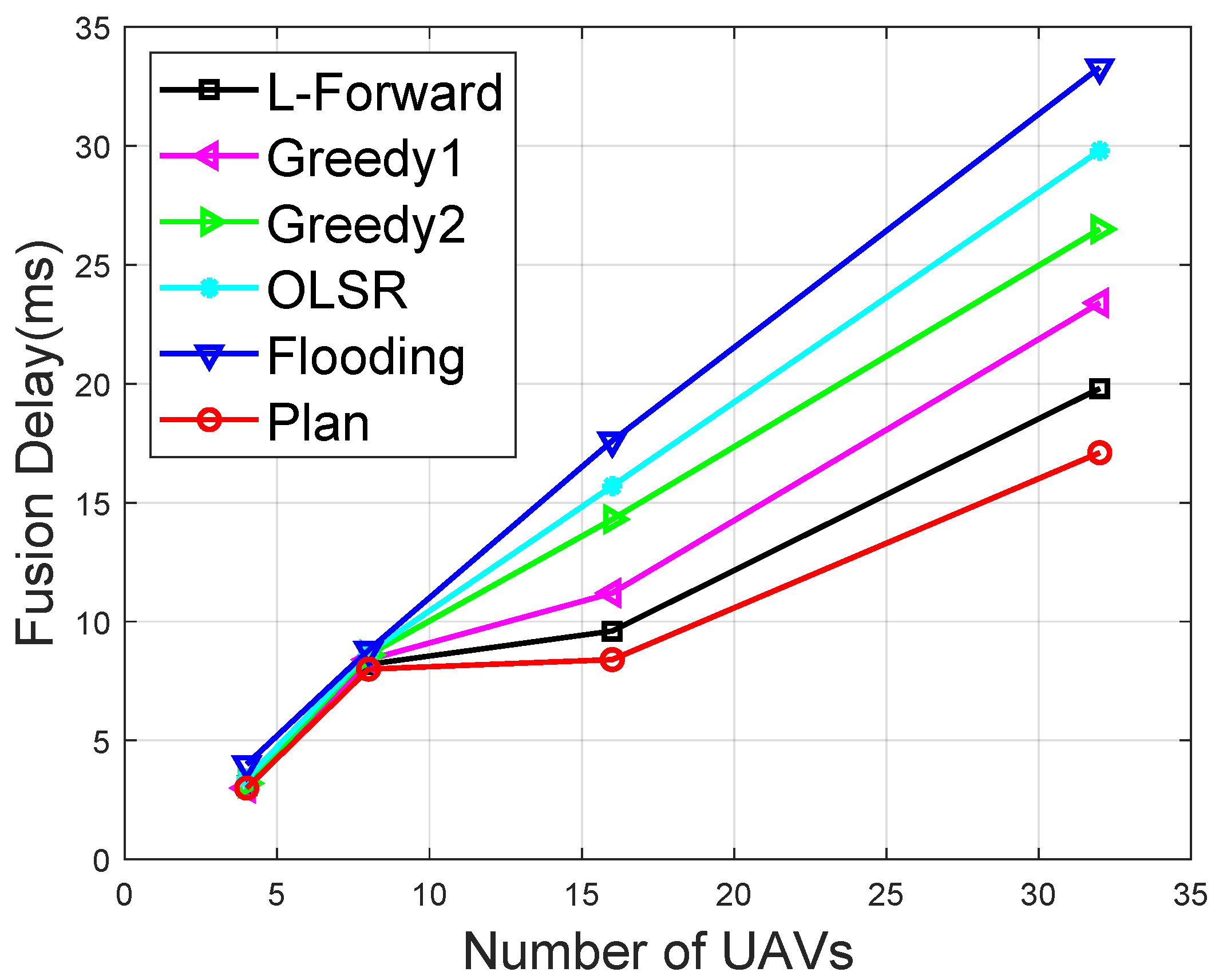
It can be observed that when the number of UAVs was small, all methods were able to complete map fusion with similar delays. This was because with fewer UAVs, the structure of the communication graph was relatively simple, making it easy to route all messages throughout the network. As the number of UAVs in the swarm increased, the performance of OLSR and flooding gradually degraded, and the performance of the greedy algorithms also became noticeably inferior to the planning-based methods. The L-step forward prediction-based planning algorithm performed second best, only behind the replanning-based algorithm. This was due to the increasing complexity of the UAV communication network topology as the swarm grew larger. Routing based on greedy algorithms and flooding tended to result in redundant transmissions. Furthermore, decision-making that did not consider future inter-node dependencies often fell into suboptimal solutions. Therefore, algorithms that lacked global coordination generally performed poorly. In contrast, the L-step forward prediction planning algorithm achieved relatively good performance because it incorporated foresight into future decisions over a fixed number of steps, helping to avoid the limitations of myopic, single-step greedy strategies. However, its performance still slightly lagged behind that of the full global planning algorithm, which could find the globally optimal solution by considering multi-step coordination among UAVs and achieving the most efficient collaboration. Nevertheless, the total planning horizon of the global planning algorithm increased linearly with the number of UAVs, causing the computational complexity to grow exponentially. The L-step forward prediction method, by fixing the prediction horizon, managed to control the problem complexity, offering a good balance between solution quality and planning efficiency.

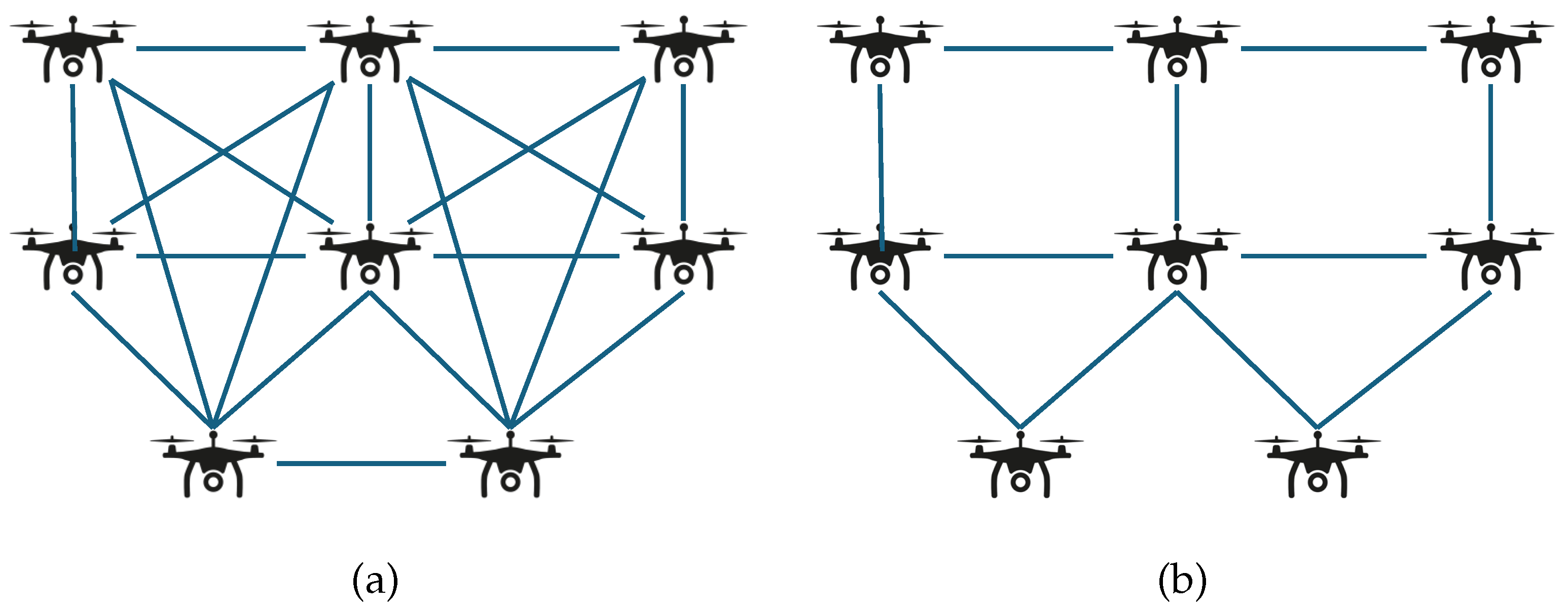
We further conducted experiments on networks with different connectivity densities. In this experiment, we varied the node density when randomly generating UAV positions, resulting in different levels of sparsity in the resulting connected graphs. The number of edges in networks with varying connectivity densities is shown in

Table 2. Number of edges in connected graphs with different network densities.

Number of UAVs	4	8	16	32
Dense Connectivity Graph	6	20	53	186
Sparse Connectivity Graph	4	11	26	57

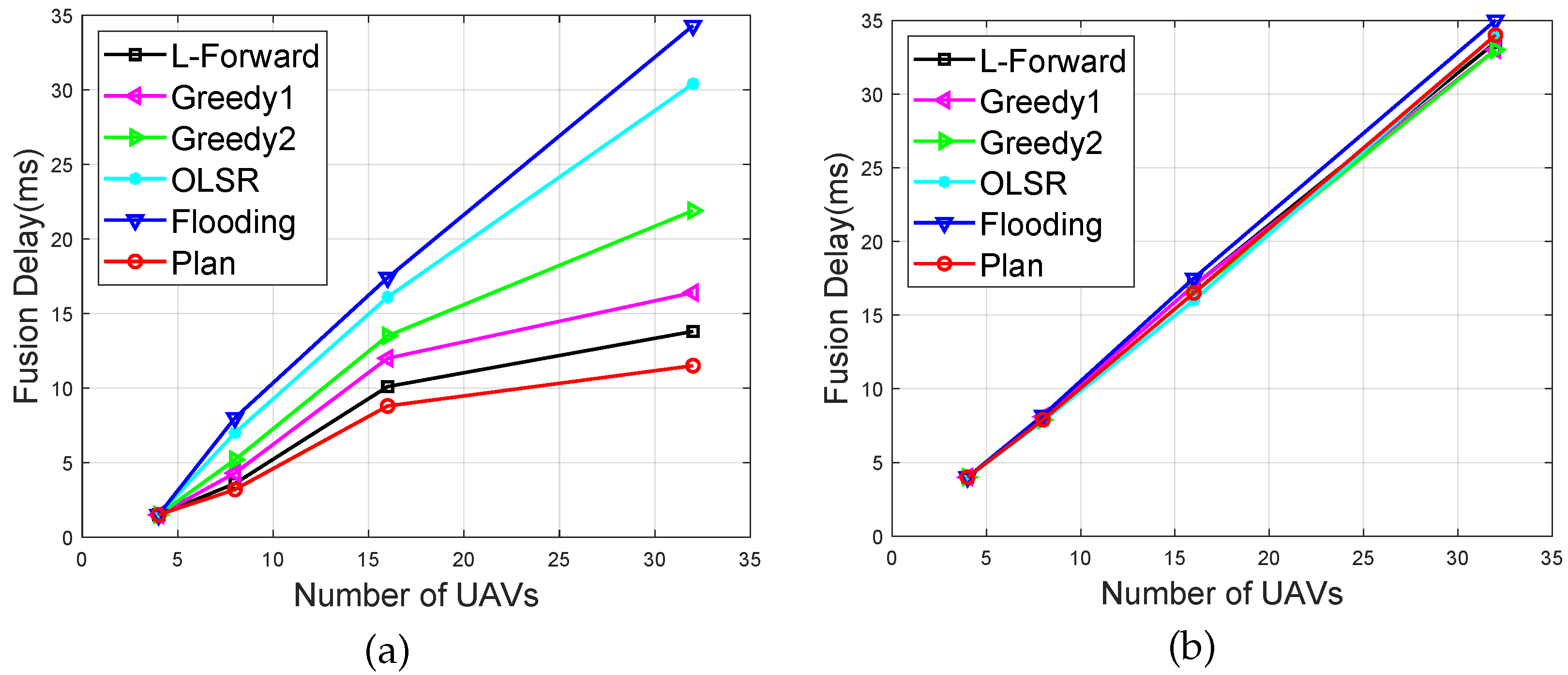
and the typical network topology diagrams under different connectivity densities with eight UAVs are shown in Figure 5. The comparison of fusion delays are presented in Figure 6. In densely connected networks (Figure 6a), the proposed dynamic routing algorithm significantly reduced map fusion delay compared to the baseline algorithms, and the performance improvement became more pronounced as the number of UAVs increased. This was because densely connected networks typically contained multiple distinct routing paths for data transmission, which placed higher demands on cooperative routing among nodes. Algorithms such as OLSR and flooding did not account for cooperative forwarding between nodes, leading to poor performance. Greedy algorithms partially considered cooperative routing but only made single-step optimal decisions, lacking the capability for multi-step prediction, which limited their effectiveness.In contrast, the L-forward approximation algorithm considered node cooperation within a limited prediction horizon, which helped reduce fusion delay to some extent. However, in sparsely connected networks (Figure 6b), our proposed algorithm did not significantly improve map fusion delay. This was because in sparse networks, some node pairs were connected by only a single unique routing path. The nodes along these paths became critical and formed performance bottlenecks. In such cases, complex cooperative routing is unnecessary, and even simple strategies can produce reasonably good forwarding schedules, resulting in similar fusion delays. Overall, our dynamic routing planning algorithm for reliable map fusion is more suitable for networks with relatively dense communication connectivity, under which the algorithm achieves better symmetry in fusion latency between lossless and lossy transmission scenarios.

5.3. Replanning Experiments

We conducted ablation experiments to assess the effectiveness of the proposed routing replanning algorithm under communication packet loss scenarios. Three methods were compared:

(1)

Without replan: When packet loss occurred, the system relied on repeated retransmissions without adjusting the routing plan.

(2)

Static routing: Routing paths were predetermined before the mission and remained fixed throughout the map fusion process, regardless of any packet loss or link failures.

(3)

Replan: Dynamic routing replanning was employed, which adaptively recalculated transmission paths in real time to respond to link failures and maintain efficient data dissemination.

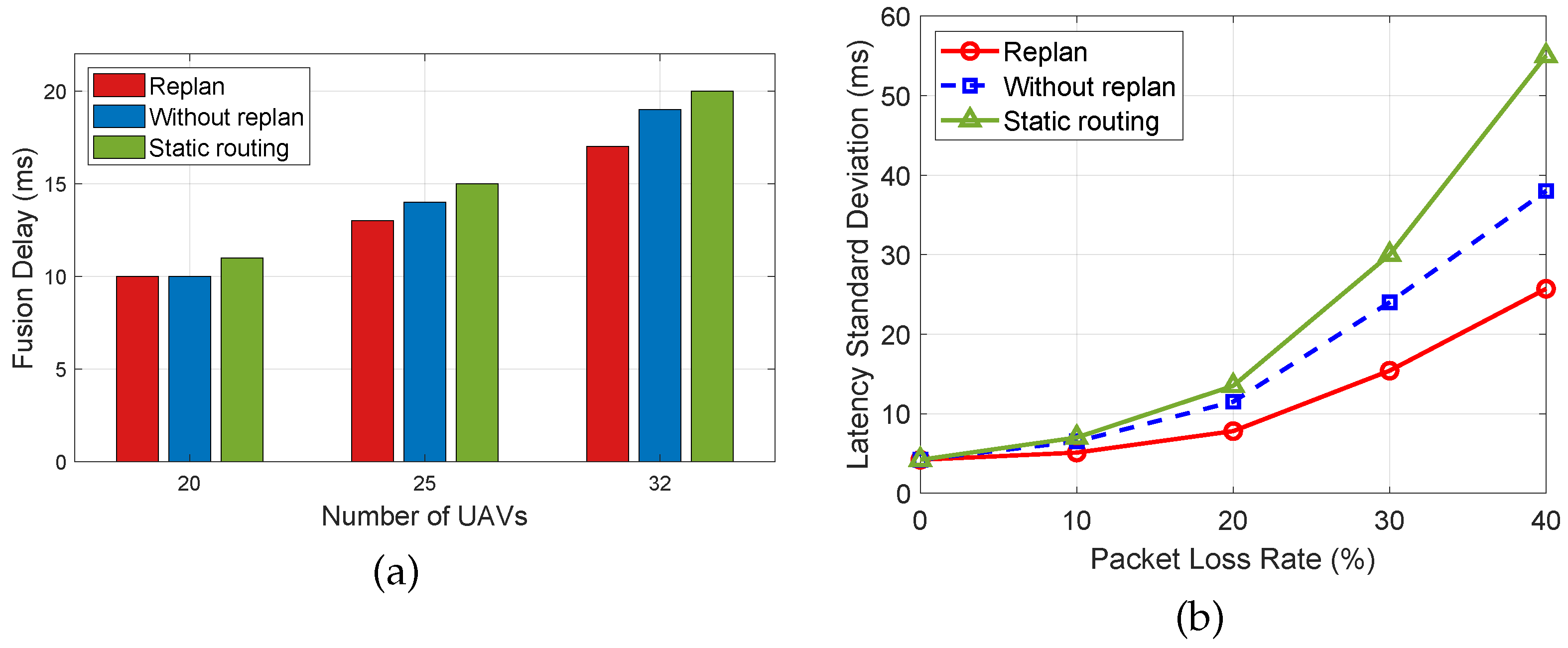
The experimental results are shown in Figure 7a. In this experiment, the packet loss rate was set at 6.1%. Under this relatively low packet loss condition, the overall differences among the three methods were modest. However, our routing replanning algorithm consistently achieved the shortest fusion delay. As the number of UAVs increased, the likelihood of packet loss naturally grew, yet the network remained generally stable at this loss rate. In the baseline method without replanning, reliance on repeated retransmissions led to progressively higher fusion delays as the network expanded. The static routing baseline performed even worse: its inability to adapt routing paths to local link failures or network congestion caused delays to accumulate rapidly as the network size increased. In contrast, our dynamic routing replanning approach continuously adjusted transmission paths based on real-time network conditions. This allowed UAVs to collaboratively discover alternative routes, effectively mitigating the impact of packet loss on transmission scheduling. As a result, robust and efficient map fusion was achieved even in the presence of communication disruptions.

In addition to overall fusion delay, we further analyzed latency symmetry among UAVs by calculating the standard deviation of node-level transmission completion times under different conditions. Specifically, the latency standard deviation (${\sigma }_T$) was computed using the following formula:

$${\sigma }_T=\sqrt{{\displaystyle \frac{1}{N_U}}\sum _{i=1}^{N_U}{(T_i-{\mu }_T)}^2}$$

(12)

where $N_U$ is the number of UAVs, $T_i$ represents the transmission completion time of UAV node i, and ${\mu }_T$ is the mean transmission completion time across all UAVs.

The results, shown in Figure 7b, were obtained under a more challenging condition, with the UAV swarm size increased to 32 nodes. The findings reveal that the proposed dynamic routing replanning method consistently achieved the lowest latency standard deviation, indicating superior delay symmetry and load balancing across the network. In contrast, the static routing baseline exhibited significantly worse performance in terms of latency symmetry. Although it showed slightly more stable transmission delays compared to the non-replanning baseline under low packet loss conditions, its lack of adaptability under high-loss and large-scale network conditions led to severe degradation, with certain UAV nodes experiencing extreme delays due to fixed paths being blocked or congested. As a result, the latency standard deviation increased sharply, indicating poor load balancing.

Overall, these results confirm that our dynamic routing replanning algorithm not only reduces the average map fusion delay but also ensures a more uniform distribution of transmission delays across UAV nodes, especially in large-scale UAV networks operating under non-ideal communication environments. This highlights its advantages in both efficiency and network stability over static routing and non-replanning methods.

5.4. Forward Prediction Step Analysis

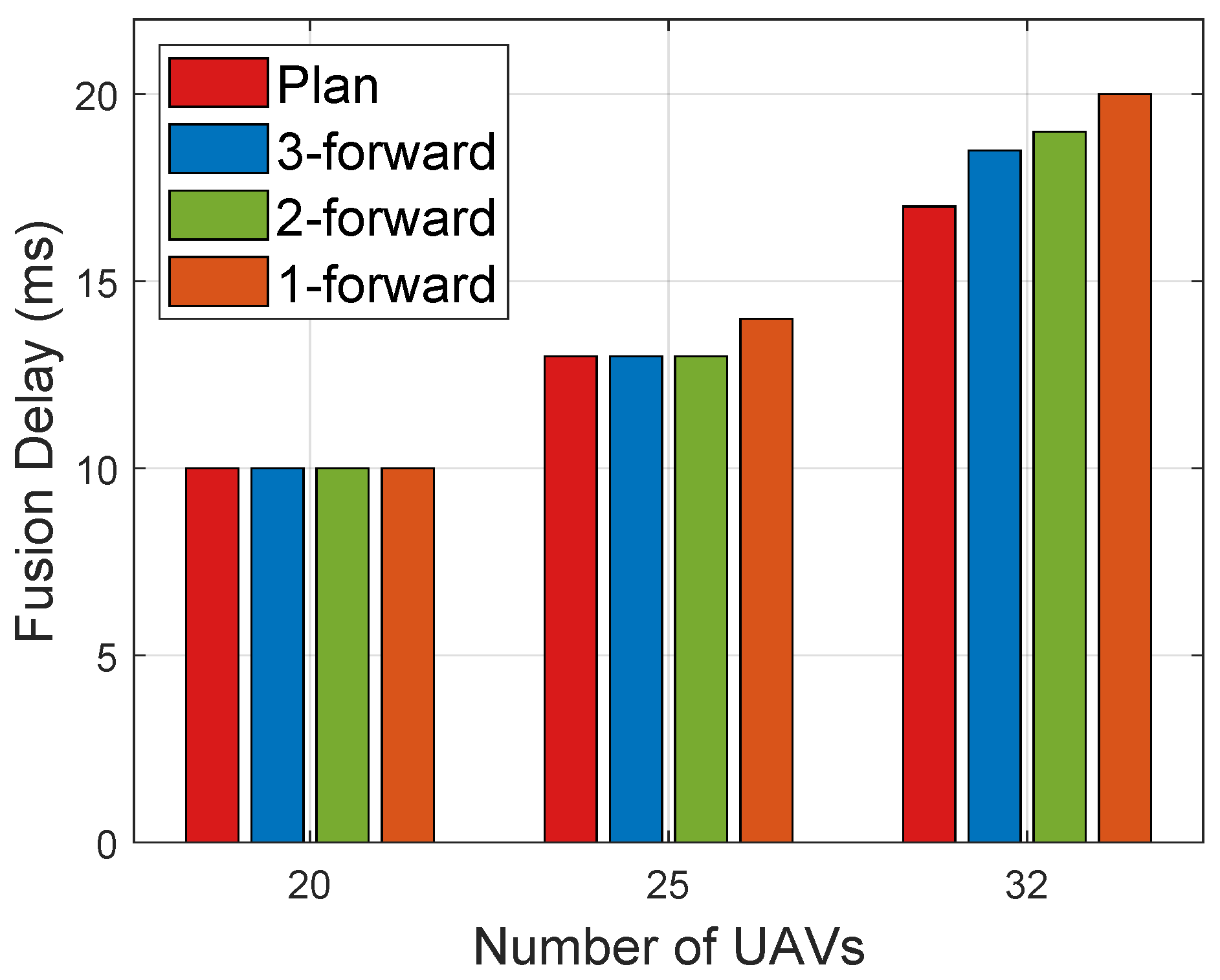
The L-step forward prediction algorithm requires manual configuration of the prediction horizon L, which impacts both solution quality and computational time. We conducted experiments to evaluate how different prediction step sizes affect the performance of the L-step forward prediction algorithm. Specifically, we tested the routing time of the approximate algorithm for $L=1,2,3$, and the results are shown in Figure 8.

When the number of UAVs was 20, the approximate algorithm achieved the same performance as the optimal routing planning algorithm. This indicated that when the network was relatively small and simple, the L-step forward prediction algorithm could produce high-quality results while significantly reducing the computational complexity of routing planning. When the number of UAVs increased to 25, the performance of the single-step prediction algorithm ($L=1$) was worse than that of the optimal routing algorithm, whereas the two-step and three-step prediction algorithms ($L=2,3$) still matched the performance of the optimal method. However, when the number of UAVs increased to 32, all fixed-step forward prediction algorithms performed worse than the optimal routing algorithm. This suggested that as the network became more complex, the approximation introduced by fixed-step prediction without global coordination led to performance degradation, and the shorter the prediction horizon, the more noticeable the degradation. Nevertheless, even in the 32-UAV scenario, the performance drop of the approximate algorithm compared to the optimal solution was not significant and remained better than that of the greedy algorithms. This demonstrates that the L-step forward prediction approach is indeed capable of achieving reasonably high-quality solutions while greatly reducing the computational burden of routing planning.

6. Conclusions

This paper proposed a symmetry-oriented dynamic routing planning algorithm for reliable map fusion in distributed multi-UAV systems. We introduced a map fusion framework based on local observation maps, under which the problem of minimum-delay routing for disseminating local maps within the UAV network was formulated as an integer programming problem. Mathematical analysis provided a tight upper bound for the routing planning problem, which was used to guide both the routing computation and the dynamic re-routing process in the presence of packet loss, thereby achieving approximate latency symmetry between fusion under lossy and lossless conditions. To address the computational complexity challenges of routing planning in large-scale UAV swarms, we proposed an approximate algorithm based on L-step forward prediction. Extensive comparative experiments demonstrated that the proposed algorithm achieves favorable performance in terms of both fusion reliability and delay in distributed map fusion scenarios.

Future work will explore integrating UAV mobility planning with the proposed routing and fusion framework, enabling the joint optimization of flight paths and map dissemination strategies. This integration aims to maximize area coverage and sensing completeness while maintaining efficient map fusion performance.