Research on Load Forecasting Prediction Model Based on Modified Sand Cat Swarm Optimization and SelfAttention TCN

Abstract

The core structure of modern power systems reflects a fundamental symmetry between electricity supply and demand, and accurate load forecasting is essential for maintaining this dynamic balance. To improve the accuracy of short-term load forecasting in power systems, this paper proposes a novel model that combines a Multi-Strategy Improved Sand Cat Swarm Optimization algorithm (MSCSO) with a Self-Attention Temporal Convolutional Network (SA TCN). The model constructs efficient input features through data denoising, correlation filtering, and dimensionality reduction using UMAP. MSCSO integrates Uniform Tent Chaos Mapping, a sensitivity enhancement mechanism, and Lévy flight to optimize key parameters of the SA TCN, ensuring symmetrical exploration and stable convergence in the solution space. The self-attention mechanism exhibits structural symmetry when processing each position in the input sequence and does not rely on fixed positional order, enabling the model to more effectively capture long-term dependencies and preserve the symmetry of the sequence structure—demonstrating its advantage in symmetry-based modeling. Experimental results on historical load data from Panama show that the proposed model achieves excellent forecasting accuracy (RMSE = 24.7072, MAE = 17.5225, R² = 0.9830), highlighting its innovation and applicability in symmetrical system environments.

1. Introduction

As critical operational data and a key indicator of power systems, power load plays a significant role in understanding electricity usage patterns and formulating future power generation plans [1]. The task of power load forecasting has emerged in this context. In recent years, with the widespread deployment of sensor technologies and intelligent perception devices, a large volume of environmental and operational data can be collected in real time and utilized for modeling and analysis, providing a rich data foundation for power load forecasting. Sensor-acquired data, as a major source of model input, plays a vital role in improving the timeliness and accuracy of forecasting models. Accurate short-term power load forecasting is crucial for various aspects, including enhancing economic efficiency of electricity use, ensuring the safety and reliability of power systems, optimizing operational dispatching, promoting renewable energy integration, and achieving energy conservation and emission reduction. Precise short-term load forecasting serves as a fundamental guarantee for the economic, safe, and clean operation of power systems [2].

Research on short-term power load forecasting can be classified from both spatial and temporal dimensions [3]. From the spatial perspective, depending on the geographical scope of the forecasting target, it is generally divided into regional load forecasting, substation load forecasting, and user-level load forecasting. From the temporal perspective, based on forecasting time spans, it includes ultra-short-term forecasting (ranging from several minutes to 24 h), short-term forecasting (1 to 7 days), medium-term forecasting (monthly to yearly), and long-term forecasting (multiple years to decades). With the continuous enhancement of “sensing–computing–control” capabilities in modern power grids, load forecasting methods integrated with sensor data have become an essential component in building intelligent power systems.

From the perspective of technical approaches, power load forecasting is mainly divided into three categories: classical statistical forecasting methods, machine learning methods, and deep learning methods. Classical statistical forecasting methods were the earliest applied techniques [4], primarily including models such as autoregressive integrated moving average (ARIMA) [5] and Autoregressive conditional heteroskedasticity (ARCH) [6]. ARIMA achieves forecasting through differencing and an autoregressive moving average; ARCH models the relationship between conditional variance and residuals. Although these methods are simple and easy to use, it is difficult for them to handle complex nonlinear relationships and they can no longer meet practical needs in modern power systems.

Machine learning methods have emerged with the development of computer technology and mainly include models such as Support Vector Machines (SVM) [7] and Random Forests [8]. SVM utilizes kernel functions and optimal separating hyperplanes for forecasting; Random Forest improves forecasting stability by integrating multiple decision trees. These methods overcome the limitations of traditional approaches, offering a strong generalization ability and robustness, but they require substantial domain expertise.

Deep learning methods are advanced technologies that have developed rapidly in recent years, mainly including models such as Recurrent Neural Networks (RNNs) [9] and Long Short-Term Memory (LSTM) networks [10]. RNN processes sequential data through recurrent structures; LSTM effectively captures long-term dependencies using gating mechanisms. With powerful feature extraction and nonlinear mapping capabilities, deep learning methods exhibit excellent forecasting performance and adaptability, and are becoming the most promising technical approach in this field.

In the field of short-term power load forecasting, extensive research has been conducted by scholars both domestically and internationally. Among them, ChengMing Lee developed a method utilizing biorthogonal wavelets, which was embedded into the ARIMA model as an enhancement scheme to improve forecasting accuracy [11]. Aasim proposed a hybrid model that combines Wavelet Transform (WT) and Support Vector Machine to forecast power load [12]. Grzegorz Dudek constructed an optimized Random Forest model based on seven input patterns and three training modes for short-term load forecasting [13]. Heng Shi proposed a pooling-based deep RNN, which addresses the overfitting problem through pooling operations, for forecasting highly volatile household electricity loads [14]. Ali Parizad introduced a gated recurrent unit (GRU) model with a two-step hyperparameter optimization process using Grid Search and Random Search, applied to long-term power load forecasting, and implemented parallel distributed computing on a high-performance computing cluster [15]. Yi Yang developed a combined forecasting model integrating gated recurrent unit (ELM), RNN, and SVM, with parameters optimized by the Multi-Objective Particle Swarm Optimization (MOPSO) algorithm to perform power load forecasting [16].

The short-term power load forecasting model proposed in this paper, based on MSCSO and SA TCN, possesses at least four significant and novel advantages. First, the use of UMAP technology to reconstruct high-dimensional time series data reduces data dimensionality and computational burden while effectively capturing the intrinsic feature relationships, contributing to improved forecasting accuracy during the data preparation stage. Second, the Uniformization Tent Chaos Mapping, Sand Cat sensitivity improvement, and Lévy flight strategy in MSCSO enhance each stage of the algorithm’s optimization process, significantly improving solution quality. Third, the self-attention mechanism strengthens the forecasting model’s capability to extract long-range information from time series data. The proposed SwishPlus activation function enhances the model’s nonlinear capability and expands the activation range of neurons. Fourth, MSCSO performs the crucial parameter setting for SA TCN, reducing instability and performance suppression caused by manual intervention.

In summary, the proposed MSCSO–SA TCN model demonstrates theoretical innovation and has been experimentally validated in terms of forecasting accuracy, offering insights for future research. It is worth noting that the model’s multi-source input features—including temperature, humidity, wind speed, and other environmental variables—are collected in real time by automated sensors deployed in the operational environment of the power system. Integrating sensor data not only provides the model with rich spatiotemporal information and high-frequency features but also enhances its adaptability and generalization under dynamic grid conditions. This enables more responsive and accurate forecasting of real-world grid operations, highlighting the practical applicability and deployment potential of the proposed approach in smart grid scenarios.

2. Materials and Methods

2.1. UMAP

The factors influencing power load are diverse, including natural factors and human factors. These influencing factors exhibit nonlinear and nonstationary characteristics. Although the original dataset contains rich information, it is challenging to analyze and forecast directly in a high-dimensional space. The relatively low forecasting accuracy of previous power load forecasting models has been greatly limited by this problem.

To effectively handle the complex feature structure of high-dimensional power load data, this paper employs Uniform Manifold Approximation and Projection [17] for data reconstruction and dimensionality reduction. UMAP is a dimensionality reduction method based on manifold learning and algebraic topology theory. By constructing a fuzzy topological representation of data samples and optimizing the low-dimensional embedding space, UMAP can achieve efficient dimensionality reduction while preserving the topological structure of the data. Compared with traditional dimensionality reduction methods, UMAP not only effectively maintains the global structure and local neighborhood relationships of the data but also offers advantages such as fast convergence and strong scalability. Additionally, UMAP demonstrates lower computational complexity and better data structure preservation than t-distributed Stochastic Neighbor Embedding (t-SNE) when processing large-scale datasets. The dimensionality reduction process of UMAP mainly includes the following steps:

Step 1: Construct a weighted k-neighbor graph:

Let the input dataset be $X=\left\{x_1,\dots ,x_N\right\}$, with a dissimilarity measure.

$d:X\times X\to ℝ\ge 0$; define ${\rho }_i$ and ${\sigma }_i$ for each $x_i$:

${\rho }_i$ expresses the constraint of local connectivity:

$${\rho }_i=\min \{d(x_i,x_j)\left|1\le j\right.\le k,d(x_i,x_j)>0\}$$

(1)

${\sigma }_i$ serves as the corresponding normalization factor and is calculated by the following formula:

$${\displaystyle \sum _{j=1}^k\exp (\frac{-\max (0,d(x_i,x_j)-{\rho }_i)}{{\sigma }_i})}={\log }_2^k$$

(2)

Step 2: Calculate the weight function $v_{j\left|i\right.}$:

$$v_{j\left|i\right.}=\exp ({\displaystyle \frac{-\max (0,d(x_i,x_j)-{\rho }_i)}{{\sigma }_i}})$$

(3)

Step 3: Calculate the weight $v_{ij}$ between the i-th data point and the j-th data point in the original space:

$$v_{ij}=(v_{j\left|i\right.}+v_{i\left|j\right.})-v_{j\left|i\right.}\cdot v_{i\left|j\right.}$$

(4)

Step 4: Calculate the symmetric weight $w_{ij}$ between the i-th data point and the j-th data point in the original space:

$$w_{ij}={\displaystyle \frac{1}{1+a{d}_{ij}^{2b}}}$$

(5)

where $a$ and $b$ are hyperparameters, and $d_{ij}^{2b}$ is the distance between data points $x_i$ and $x_j$.

Step 5: Calculate the UMAP cost function $C_{UMAP}$:

$$C_{UMAP}={\displaystyle \sum _{ij}\left[v_{ij}\log (\frac{v_{ij}}{w_{ij}})+(1-v_{ij})\log (\frac{1-v_{ij}}{1-w_{ij}})\right]}$$

(6)

Step 6: Take the positions of the data points in the optimized low-dimensional space as the final result, given by the following formula:

$$x_i=(x_i^{(1)},x_i^{(2)},\dots ,x_i^{(d)})$$

(7)

Here, $x_i^{\left(1\right)},x_i^{\left(2\right)},\dots ,x_i^{\left(d\right)}$ represent the coordinates of the data point $x_i$ in each dimension of the low-dimensional space.

In Formulas (1) and (2), ${\rho }_i$ and ${\sigma }_i$ represent the local connectivity constraint and normalization factor, respectively, which are used to determine the connection range between data points.

In Formulas (3)–(5), the conditional probability of data points in the high-dimensional space $v_{j\left|i\right.}$, the asymmetric weight $v_{ij}$, and the symmetric weight $w_{ij}$ are calculated, respectively, in order to construct the topological structure of the data.

The cost function $C_{UMAP}$ in Formula (6) is used to evaluate the degree to which the topological structure is preserved before and after dimensionality reduction—the smaller the value, the better the dimensionality reduction performance.

Formula (7) provides the coordinate representation of the data points after dimensionality reduction, where $x_i^{\left(1\right)},x_i^{\left(2\right)},\dots ,x_i^{\left(d\right)}$ indicate the positions in each dimension of the new space.

2.2. MSCSO

The Sand Cat Swarm Optimization (SCSO) algorithm [18] achieves model parameter optimization by simulating the unique predatory behavior of sand cat swarms. SCSO mainly consists of two stages: exploration and exploitation. In the initial phase, the population is initialized using a random generation method, which results in an inability to ensure the quality and diversity of the initial population. As the number of iterations increases, the search mechanism in the exploration stage demonstrates low development efficiency. Due to the sensitivity settings, the algorithm is prone to falling into local optima traps. Although the algorithm has a simple structure and few parameters, the exploration range of population individuals in the search space decreases as the iterations proceed, which can lead to search stagnation and a reduction in the global search performance of the algorithm. The implementation details of SCSO are as follows:

Step 1: Generate an initial matrix of size $n\times d$ randomly within the given interval.

$$\left[\begin{array}{l}{X}_1\\ ⋮\\ X_i\\ ⋮\\ X_n\end{array}\right]=\left[\begin{array}{lllll}{x}_{11}& \dots & x_{1j}& \dots & x_{1d}\\ ⋮& & ⋮& & ⋮\\ x_{i1}& \dots & x_{ij}& \dots & x_{id}\\ ⋮& & ⋮& & ⋮\\ x_{n1}& \dots & x_{nj}& \dots & x_{nd}\end{array}\right]$$

(8)

Here, $X_i$ is the i-th sand cat individual, and $x_{ij}$ represents the position of the i-th sand cat in the j-th dimension of the space.

Step 2: The position update equation in the exploration phase is as follows:

$$P_{(t+1)}=r\cdot (P_{bc(t)}-rand\cdot P_{c(t)})$$

(9)

$P_{bc\left(t\right)}$ represents the best candidate position of the sand cat individual at the current iteration, and $P_{c\left(t\right)}$ is the current position of the sand cat.

Here, $rand$ is a random number in the range (0, 1), and $r$ denotes the sensitivity of the sand cat individual.

$$r=rand\cdot r_g$$

(10)

Here, $r_g$ represents the general formula for sand cat sensitivity, as follows:

$$r_g=s_M-({\displaystyle \frac{s_M\times t}{T}})$$

(11)

In Formula (11), $s_M$ is set to a fixed value of 2, $t$ is the current iteration number, and $T$ is the maximum number of iterations.

Step 3: The position update equation in the exploitation phase is as follows:

$$P_{rnd}=\left|rand\cdot P_b(t)-P_c(t)\right|$$

(12)

$$P(t+1)=P_b(t)-r\cdot P_{rnd}\cdot \cos (\theta )$$

(13)

In the above equation, $P_{rnd}$ represents a random position that ensures the sand cat is close to the prey, $P_b\left(t\right)$ is the best position of the sand cat in the t-th iteration, and $P\left(t+1\right)$ is the updated position of the sand cat. $\theta$ is a random angle within the range [0, 360].

The transition formula between the exploration phase and the exploitation phase is as follows:

$$P(t+1)=\left\{\begin{array}{l}r\cdot (P_{bc}(t)-rand\cdot P_c(t)),\left|R\right|>1;\mathit{exploration}\\ P_b(t)-r\cdot P_{rnd}\cdot \cos (\theta ),\left|R\right|\le 1;\mathit{exploitation}\end{array}\right.$$

(14)

$$R=2\times rand\times r_g-r_g$$

(15)

In Formula (15), the parameter $R$ controls the phase switching of the sand cat.

In Formula (8), $X_i$ represents the i-th sand cat individual, and $x_{ij}$ denotes the position of that individual in the j-th dimension of the space, used for initializing the population distribution.

In Formulas (9)–(11), $P\left(t+1\right)$ represents the new position of the sand cat in the exploration phase, $P_{bc}\left(t\right)$ is the current best candidate position, and $P_c\left(t\right)$ is the current position.

$r$ and $r_g$ represent the individual sensitivity and the general sensitivity formula, respectively, where $s_M$ is set to a fixed value of 2, $t$ is the current iteration number, and $T$ is the maximum number of iterations.

In Formulas (12)–(15), $P_{rnd}$ represents a random position that ensures the sand cat is close to the prey, $P_b\left(t\right)$ is the current best sand cat position, $P\left(t+1\right)$ is the updated position, $\theta$ is a rand angle within the range [0, 360], $R$ is the parameter that controls the phase switching, and $rand$ is a random number in the range (0, 1).

2.2.1. UTCM

The SCSO algorithm possesses some of the advantages mentioned earlier; however, its shortcomings are also evident. First, the initial population generated by the random generation method cannot ensure consistently high-quality populations. Second, due to the sensitivity settings, the algorithm is prone to falling into local optima traps, with the possibility of finding suboptimal solutions. Third, the search mechanism in the exploration phase demonstrates low development efficiency and is also prone to getting stuck in local optima, which is unfavorable for global exploration.

The initial population of SCSO is generated using a random generation method, which may result in the presence of low-quality individuals within the initial population. Moreover, the random generation method tends to produce individuals in similar regions, limiting the diversity of the population. To address this problem, this paper innovatively improves the Tent Chaos Mapping [19] and proposes the Uniformization Tent Chaos Mapping (UTCM) to increase the diversity of individuals within the initial population. Incorporating UTCM into the population generation stage enhances diversity among individuals, achieves uniform distribution, and improves the overall quality of the sand cat population. The specific formulas are as follows:

Map the input value $x$ to the interval [0, 1] using the following formula:

$$x^{\prime }={\displaystyle \frac{x-B_l}{B_u-B_l}}$$

(16)

Here, $B_l$ and $B_u$ represent the lower and upper bounds of the sand cat population, respectively. Apply the Tent mapping function for uniform mapping using the following formula:

$$x^{″}=\left\{\begin{array}{l}{\displaystyle \frac{x^{\prime }}{0.3}},x^{\prime }<0.3\\ {\displaystyle \frac{1-x^{\prime }}{1-0.3}},x^{\prime }>0.3\end{array}\right.$$

(17)

Remap the mapped value back to the original interval $\left[B_l,B_u\right]$ using the following formula:

$$x_{UTCM}=x^{″}\cdot (B_u-B_l)+B_l$$

(18)

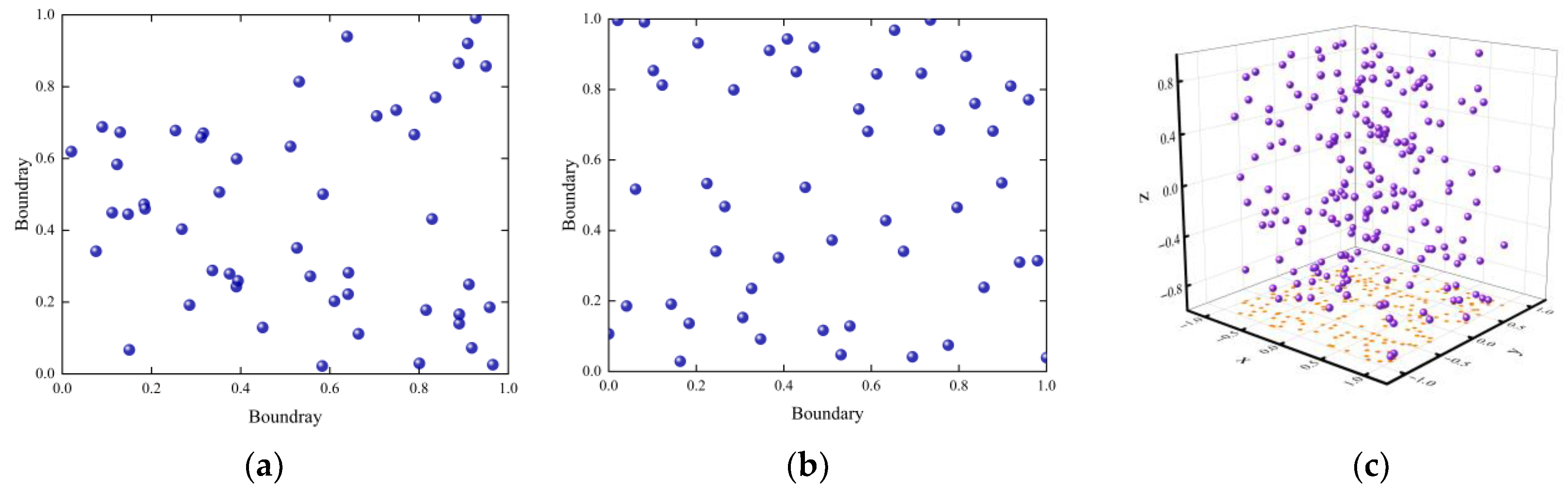
The population distributions of the sand cat populations generated by random initialization and by UTCM are shown, respectively, in Figure 1.

As shown in Figure 1, although the population generated using the random generation method exhibits strong randomness, it is not uniformly distributed and presents a phenomenon of regional clustering. In contrast, the population generated using the UTCM method is more evenly distributed and exhibits significant diversity, which helps the algorithm avoid local optima traps and enhances the possibility of exploring the global optimum. The chaotic nature of UTCM makes it sensitive to slight changes in initial conditions, thereby improving the robustness of the algorithm.

2.2.2. Sensitivity Improvement

The sensitivity of sand cat individuals determines their responsiveness to environmental changes or the ability to acquire information from other individuals during the optimization process. Sensitivity affects their decision-making and movement within the search space. The sensitivity defined by SCSO has limitations; the fixed sensitivity used during iterations lacks adaptability throughout the optimization process, which may result in a suboptimal exploration–exploitation trade-off and premature convergence into local optima traps. MSCSO proposes a dynamic cyclic pattern sensitivity variation mechanism that enhances the diversity of sand cat individuals while allowing the algorithm to gradually transition from the exploration phase to the exploitation phase, thereby improving the quality of solutions. Additionally, because the new sensitivity mechanism incorporates randomness, it facilitates better exploration of the search space and helps escape local optima traps.

The sensitivity variation trend of SCSO with the number of iterations, calculated according to Equations (10) and (11), is shown in Figure 2. Although the sensitivity exhibits good nonlinearity, it is evident that the sensitivity is positive in the first half and negative in the second half, which limits the global exploration capability. Therefore, a cosine evolution adaptive factor is introduced to improve the sensitivity, as expressed by the following formula:

$$\delta =\cos (t^{\tau }-{\displaystyle \frac{\pi }{2}})$$

(19)

Here, $\delta$ is the cosine-evolution adaptive factor, and $\tau$ is the adaptive coefficient, which achieves optimal performance when $\tau =3$. $r^{\prime }$ is the improved sensitivity, and Figure 3 shows the variation trend of $r^{\prime }$ during the iteration process:

Figure 2. Sensitivity of SCSO.

Figure 2. Sensitivity of SCSO.

As shown in Figure 3, the sensitivity maintains a relatively high value throughout the entire iteration process, overcoming the shortcomings of a small exploration range and significant variation between the early and later stages of the iteration. This improvement enhances the algorithm’s global exploration capability during the middle and later stages of the iteration.

2.2.3. Introduction of the Lévy Flight Strategy to Optimize the Exploitation Phase

Since the exploration range of population individuals in the position update mechanism decreases as the number of iterations increases, the exploitation range of the algorithm also gradually shrinks. This approach tends to cause the optimal solution to converge toward a particular location, which may lead the algorithm into search stagnation and subsequently into local optima traps. To address this limitation, the Lévy flight [20] is introduced, and its formula is as follows:

$$num=(1+\beta )!\cdot \sin ({\displaystyle \frac{\pi \beta }{2}})$$

(20)

$$den=({\displaystyle \frac{1+\beta }{2}})!\cdot \beta \cdot 2^{({\displaystyle \frac{\beta -1}{2}})}$$

(21)

$$\sigma ={({\displaystyle \frac{num}{den}})}^{{\displaystyle \frac{1}{\beta }}}$$

(22)

$$u=randn(1,population)\cdot \sigma$$

(23)

$$v=randn(1,population)$$

(24)

$$z={\displaystyle \frac{u}{{\left|v\right|}^{\frac{1}{\beta }}}}$$

(25)

Here, $\beta$ is a fixed value of 1.05, $\sigma$ is the standard deviation of the Lévy flight step size, and $z$ is the step size of the Lévy flight.

The position update equation in the exploration phase after introducing Lévy flight is as follows:

$$P(t+1)=P_b(t)-a\cdot z\cdot r\cdot {\mathrm{P}}_{rnd}\cdot \cos \theta$$

(26)

Here, $a$ is the adjustment coefficient, with a value of 0.13.

The introduction of Lévy flight enhances the global search capability of the algorithm, providing a strong ability to escape when encountering local optima traps. The heavy-tailed step length allows the algorithm to occasionally perform large jumps, enabling it to traverse distant regions and increasing the likelihood of discovering better solutions. This facilitates more effective exploration of the search space.

2.2.4. MSCSO Algorithm Testing

To verify the effectiveness and stability of the MSCSO algorithm, Schwefel’s 2.26 function (f₁(x)) and the Shekel function (f₂(x)) were selected to test the optimization capabilities of each algorithm on multimodal problems and fixed-dimension multimodal test functions (the function plots are shown in Figure 4 and Figure 5, and the specific formulas of the test functions are as follows. The specific parameters of the Shekel function are listed in

Table 1. Detailed parameters of the f₂(x) function.

$i$	$a_{ij},j=1,\dots ,4$				$c_i$
1	4	4	4	4	0.1
2	1	1	1	1	0.2
3	8	8	8	8	0.3
4	6	6	6	6	0.4
5	7	7	7	7	0.4
6	2	9	2	9	0.6
7	5	5	3	3	0.3
8	8	1	8	1	0.7
9	6	2	6	2	0.5
10	7	3.6	7	3.6	0.5

). The standard SCSO, Snake Optimization (SO) algorithm [21], and Sparrow Search Algorithm (SSA) [22] were selected for comparison to evaluate the performance of the MSCSO algorithm. In this section, all experiments were conducted using MATLAB 2023a.

All algorithms used an initial population size of 50 and 300 iterations. The experimental results are detailed in

Table 2. Performance of four optimization algorithms on the f₁(x) function.

	MSCSO	SCSO	SO	SSA
Optimum value	−12,569.4866	−12,569.4817	−12,466.3157	−11,951.0455
Average value	−12,511.7415	−11,751.6299	−10,622.1787	−9824.0811
Standard deviation	673.4711	1410.7477	1791.4764	2437.5102

and

Table 3. Performance of four optimization algorithms on the f₂(x) function.

	MSCSO	SCSO	SO	SSA
Optimum value	−10.5364	−10.5364	−10.5363	−10.5364
Average value	−10.4978	−10.2461	−10.0963	−10.0902
Standard deviation	0.5752	1.3372	1.6964	1.3865

, and the iterative optimization processes for the two functions are shown in Figure 6 and Figure 7.

$$f_1(x)=-{\displaystyle \sum _{i=1}^n-x_{{}_i}\sin (\sqrt{\left|x_i\right|})}$$

(27)

$$f\left(x\right)=-{\displaystyle {\sum }_{i=1}^m{\left[\left(x-a_i\right){\left(x-a_i\right)}^T+c_i\right]}^{-1}}$$

(28)

Figure 4 and Figure 5 illustrate the graphical representations of the Schwefel’s 2.26 function and the Shekel function, respectively. As shown by the function plots, the Schwefel’s 2.26 function contains multiple extreme points, exhibiting a complex high-dimensional structure with numerous local optima. This makes optimization algorithms prone to becoming trapped in local optima, especially when the search space is large or the strategy is not sufficiently comprehensive. The Shekel function represents a fixed-dimension multimodal optimization problem, containing multiple local minima and one global minimum, presenting a relatively complex multimodal structure. Therefore, it places high demands on the global search capability of the algorithm.

As shown in Figure 6, the proposed MSCSO, through ingenious strategy improvements, effectively enhanced global search capability, successfully overcame local optima traps, and was able to quickly find the global optimum. In contrast, although the SCSO algorithm possesses a certain ability to escape local optima and can find the global optimum within 300 iterations, its convergence speed is slow, and its performance lags significantly behind that of the proposed MSCSO.

Additionally, while the SO algorithm has some capacity to escape local optima, its search strategy is designed to expand the search range only after more than half of the total iterations, resulting in a longer time required to escape local optima. Moreover, the SO algorithm clearly failed to find the global optimum, indicating insufficient local optima escape capability. Therefore, when dealing with complex high-dimensional optimization problems, the SO algorithm shows poor stability, and its optimization results are not necessarily the global optimum.

The SSA algorithm’s single search strategy revealed its weakness in global search capability. When handling high-dimensional complex functions, it is prone to becoming trapped in local optima. Especially in optimization problems with multimodal or complex structures, the SSA algorithm’s search efficiency drops significantly, exhibiting a strong tendency toward premature convergence.

Figure 7 illustrates the performance differences of each algorithm on the Shekel function. Since the number of iterations required by each algorithm to find the optimal solution was less than 300, only the first 150 iteration curves are plotted in Figure 7 for ease of observation. Similarly to Figure 6, Figure 7 also highlights the clear differences among the algorithms in terms of solution quality, convergence speed, global search capability, and stability.

Although both the SO algorithm and the SSA algorithm found the global optimum, their convergence speeds were relatively slow. During the iteration process, both algorithms repeatedly became trapped in local optima, resulting in significant fluctuations. These fluctuations not only consumed more time during the optimization process but also affected the robustness of the algorithms. The SO algorithm frequently fell into local optima and required excessive iterations throughout the optimization process. Additionally, the SO algorithm exhibited large fluctuations during optimization, making it unsuitable for complex search spaces. The SSA algorithm encountered the same issue observed in Figure 6, where its poor global search strategy led to a tendency for premature convergence. Compared with SO and SSA, the SCSO demonstrated stronger local optima escape capability and faster convergence speed, but its performance was still far inferior to that of MSCSO.

The MSCSO algorithm, leveraging its flexible global search strategy and local exploitation mechanism, was able to quickly find the global optimum with the fewest iterations while achieving the highest convergence speed. This advantage primarily stems from the multi-strategy integration mechanism adopted by the MSCSO algorithm, which not only achieves high optimization speed but also balances global exploration and local exploitation, effectively avoiding local optima traps.

Based on the above analysis of Figure 6 and Figure 7, the MSCSO algorithm demonstrates the advantages of a fast convergence speed and high solution accuracy in complex optimization problems. In contrast, the SCSO, SO, and SSA algorithms each exhibit issues such as a slow convergence speed or insufficient stability when applied to high-dimensional complex problems.

Table 2 and Table 3 list the optimal solutions obtained by each algorithm on the f₁(x) and f₂(x) functions, as well as the average value and standard deviation of the best values calculated in each of the 300 iterations. These evaluation metrics can intuitively reflect the performance differences among the algorithms.

In terms of the optimal solution, both the MSCSO and SCSO algorithms successfully found the global optimum for both functions. The SO algorithm did not reach the global optimum of the f₁(x) function but found a solution closer to the global optimum than that obtained by the SSA algorithm. In this metric, the MSCSO algorithm, benefiting from its strong global search capability, clearly outperformed the SSA and SO algorithms.

Average value serves as another important metric that can offset the occasional bias that may arise when evaluating by optimum value, and it quantitatively measures the reliability and robustness of the algorithm. As shown in Table 2, the average value of MSCSO is the closest to the optimum value, indicating that the MSCSO algorithm can stably approach the optimal solution within relatively few iterations, with minimal fluctuations in the best solutions found during the search process and a high consistency in the solutions obtained. This demonstrates that the MSCSO algorithm possesses not only powerful global search capability but also exhibits excellent robustness. In contrast, the average value and optimum value differences are larger for the other algorithms.

Standard deviation is an important metric for measuring the stability and reliability of an algorithm. When comparing different algorithms, a lower standard deviation usually indicates that the algorithm possesses stronger robustness and stability in complex optimization problems. As shown in Table 2, the standard deviation value for MSCSO is the lowest, indicating that the solutions obtained by the algorithm are highly stable and can consistently yield relatively uniform and near-optimal results across multiple iterations. In contrast, the other algorithms exhibit larger standard deviations, reflecting greater fluctuations in their solutions and lower stability.

Similarly, by comparing the optimum value and average value in Table 3, it is evident that MSCSO continues to demonstrate superior performance on the f₂(x) function. It is important to note that although SSA’s standard deviation value is relatively low, this does not indicate high stability. On the contrary, this phenomenon results from SSA repeatedly becoming trapped in the same local optimum, making effective global exploration difficult.

Based on the above analysis of the figures and tables, the MSCSO algorithm exhibits significant advantages in solving complex optimization problems, particularly in terms of convergence speed, solution accuracy, stability, and robustness. Therefore, MSCSO is well-suited to the subsequent modeling steps, where it will be responsible for optimizing the key parameters of the forecasting model and identifying the optimal parameter set.

2.2.5. Ablation Study of MSCSO Algorithm

To further investigate the individual contributions of each strategy within the proposed MSCSO algorithm, we designed and conducted a set of ablation experiments. In these experiments, we systematically removed or disabled key strategies within the algorithm to evaluate their specific impact on overall optimization performance. Figure 8 presents the performance of various strategy combinations on the Schwefel’s 2.26 function and the Shekel function, while

Table 4. Statistical performance metrics of MSCSO ablation combinations on the f₁(x) function.

	MSCSO	SCSO	SCSO+ UTCM	SCSO+ Sensitivity	SCSO+ UTCM+ Sensitivity	SCSO+ Levy	SCSO+ Levy+ UTCM	SCSO+ Levy+ Sensitivity
Optimum value	−12,569.4866	−12,569.4817	−12,569.4863	−12,569.4848	−12,569.4821	−12,569.4863	−12,569.4863	−12,569.4865
Average value	−12,511.7415	−11,751.6299	−11,951.6153	−12,019.1106	−12,120.0159	−12,227.7709	−12,368.0221	−12,428.8010
Standard deviation	673.4711	1410.7477	1240.7430	1219.5118	1146.9482	1210.6691	982.5113	989.9060

and

Table 5. Statistical performance metrics of MSCSO ablation combinations on the f₂(x) function.

	MSCSO	SCSO	SCSO+ UTCM	SCSO+ Sensitivity	SCSO+ UTCM+ Sensitivity	SCSO+ Levy	SCSO+ Levy+ UTCM	SCSO+ Levy+ Sensitivity
Optimum value	−10.5364	−10.5364	−10.5364	−10.5364	−10.5364	−10.5364	−10.5364	−10.5364
Average value	−10.4978	−10.2461	−10.3250	−10.3630	−10.3821	−10.4182	−10.4615	−10.4821
Standard deviation	0.5752	1.3372	1.1576	1.1349	0.8817	0.8262	0.6691	0.6258

list the best value, mean, and standard deviation of the results for each combination.

Due to the complex structure and large number of local optima in the Schwefel’s 2.26 function, the influence of each strategy on the optimization process is more pronounced. As shown clearly in Figure 8a, combining different improvement strategies with the baseline SCSO algorithm leads to notable differences in optimization performance. As initialization methods and search strategies are gradually introduced, the performance of the baseline SCSO improves consistently.

Specifically, both SCSO + UTCM and SCSO + Sensitivity combinations enhance the search capabilities of the baseline algorithm to a certain extent. UTCM improves the uniformity of the initial population distribution, providing better starting points for subsequent search, while Sensitivity Optimization directly modifies the algorithm’s search behavior. Though their mechanisms differ, they show comparable performance improvements in the figure. The combination of SCSO + UTCM + Sensitivity integrates the advantages of both strategies, improving accuracy while maintaining search stability.

Among all the improvements, Lévy flight contributes the most significant enhancement. Owing to its strong jump behavior and powerful global search capability, it effectively helps the algorithm escape local optima. When Lévy flight is combined with the UTCM initialization strategy and the Sensitivity adjustment mechanism, optimization performance is further boosted, ultimately forming the complete MSCSO algorithm.

Notably, as shown in Table 4, the standard deviation of SCSO + Lévy + UTCM is smaller than that of SCSO + Lévy + Sensitivity. This is because UTCM produces a more evenly distributed initial population, enabling higher-quality solutions in the early stages and thus improving solution stability. Although its best and mean values are slightly lower than those of SCSO + Lévy + Sensitivity, its reduced volatility indicates better convergence consistency.

The Shekel function features multiple local optima and a relatively concentrated solution space, which leads to more similar convergence curves among different combinations. Figure 8b and Table 5 display the optimization performance of various MSCSO module combinations on this function. The results also confirm that with the incremental introduction of strategies, both convergence precision and result stability improve consistently.

In summary, the ablation study results clearly demonstrate the independent contributions of each strategy in enhancing the optimization performance of MSCSO. UTCM effectively improves population diversity and uniformity, offering a superior starting point for the search process. Sensitivity Improvement enhances the algorithm’s adaptability in fine-grained local searches. The Lévy flight mechanism, with its long-jump distribution, significantly increases the algorithm’s ability to escape local optima and strengthens global exploration. These strategies act synergistically at different levels, significantly improving the convergence speed, solution accuracy, and stability of SCSO, ultimately resulting in an MSCSO framework with superior overall performance.

2.3. TCN

The Temporal Convolutional Network (TCN) is a newly improved and optimized network structure based on traditional convolutional neural networks and recurrent neural networks [23]. Addressing the complexity and long time span characteristics of power load time series, TCN combines causal convolution and dilated convolution to achieve deep capture of historical load data and strict unidirectional temporal information propagation. As shown in Figure 9, the core structure of TCN includes causal convolution layers, dilated convolution layers, and residual connections. This design not only enables accurate modeling of long-term load variation patterns but also achieves efficient parallel computation. Compared with RNN family models (such as LSTM, GRU, etc.), TCN effectively avoids the vanishing gradient problem in power load forecasting and demonstrates higher computational efficiency and numerical stability.

The receptive field of TCN is jointly determined by the kernel size, dilation factor, and network depth. Its convolution operation can be expressed as Equation (29):

$$F(t)=(x\ast df)(t)={\displaystyle \sum _{i=0}^{u-1}f(i)\cdot x_{t-p\cdot i}}$$

(29)

In Equation (29), $x$ represents the input sequence, $\ast$ denotes the convolution operation, $d$ is the dilation factor, $u$ is the kernel size, $f\left(i\right)$ is the i-th element of the convolution kernel, and $x_{t-p\cdot i}$ is the corresponding input element.

The Residual Block of TCN consists of causal dilated convolution, weight normalization, ReLU activation function, and a dropout regularization layer, as shown in Figure 10.

This structural arrangement utilizes weight normalization to effectively suppress gradient explosion and accelerate convergence. The ReLU activation function and Dropout layer within the residual blocks work together to mitigate overfitting, while the residual branch implements dimension-matching nonlinear mapping through a 1 × 1 convolution.

To address the shortcomings of the above-mentioned TCN, this paper adopts the following two targeted modifications.

2.3.1. SwishPlus Activation Function Replacing the ReLU Activation Function

The standard TCN adopts the ReLU activation function [24] to achieve data nonlinearity. Due to the complexity of power load data, the characteristics of ReLU present certain drawbacks, making the model prone to the problem of neuron paralysis during the training process. Therefore, based on the Swish activation function [25], this paper innovatively proposes the SwishPlus activation function to replace ReLU. Its non-saturating property can effectively address this defect. The specific formulas for the ReLU function, Swish function, and SwishPlus function are as follows:

$$\mathrm{Re}LU=\max \left(0,x\right)$$

(30)

$$Swish=x\ast Sigmoid(x)$$

(31)

$$SwishPlus=x\ast Sigmoid(x)+\delta \times x, \delta =0.15$$

(32)

Figure 11 shows the comparison between the SwishPlus activation function and the ReLU activation function curves. As observed from Figure 11, when x > 0, both the ReLU function and the SwishPlus function output non-zero values, but the SwishPlus activation function exhibits better nonlinearity. When x < 0, the ReLU function outputs zero values, whereas the SwishPlus function outputs non-zero and nonlinear values. Although this sacrifices part of the model’s overfitting suppression capability, it effectively resolves the problem of neuron death.

The SwishPlus function shows a significant improvement in stimulating neurons compared to the Swish function. When the input value is greater than 0, the output values of the Swish function and the ReLU function are similar, whereas there is a considerable difference between their values and those of the SwishPlus function. Using the SwishPlus function enables smoother and more continuous activation in neural networks, which facilitates more efficient gradient propagation. This is mainly because the SwishPlus function retains small activation values even when the input is negative, unlike the ReLU function, which truncates values on the negative half-axis directly to zero. This characteristic of retaining negative activation values helps maintain better information flow and gradient propagation in deep networks. Therefore, in terms of gradient updates and model convergence speed, the SwishPlus function demonstrates superior properties, significantly improving model performance in specific tasks. Figure 12 shows the residual connection unit after replacing the ReLU function with the SwishPlus function.

2.3.2. Self-Attention Mechanism

The Self-Attention mechanism [22] models direct associations between arbitrary time steps in a sequence through an attention weight matrix to capture long-term dependencies in the data. It computes attention weights based on the similarity between the Query and Key, enabling adaptive weight assignment to different time steps. This dynamic weight allocation mechanism can effectively handle sudden changes and abnormal patterns in load data. The detailed formulas of the Self-Attention mechanism are provided below.

Given the input sequence $X$ as

$$X\in R^{N\times d}$$

(33)

$N$ denotes the sequence length, and $d$ denotes the feature dimension, $X={[x_1,x_2,\dots ,x_n]}^T,x_i\in R^d$ Linear projection transformation:

$$Q=X{W}^Q\in R^{N\times dk};K=X{W}^K\in R^{N\times dk};V=X{W}^V\in R^{N\times dv}$$

(34)

$W^Q\in R^{d\times dk}$ is the Query projection matrix, $W^K\in R^{d\times dk}$ is the Key projection matrix, and $W^V\in R^{d\times dv}$ is the Value projection matrix.

Attention weight calculation:

$$Attention(Q,K)=soft\max (S)\in R^{N\times N}$$

(35)

$$S=({\displaystyle \frac{Q{K}^T}{\sqrt{d_K}}})$$

(36)

$$Z=Attention(Q,K)·V$$

(37)

Here, $Attention(Q,K)$ is the attention function, $S$ is the similarity matrix, and $Z$ is the final output representation matrix.

The following are the advantages provided by the Self-Attention mechanism in short-term load forecasting tasks:

• Enhanced local temporal association: In short-term load forecasting, load data exhibit significant intraday fluctuations and interday correlations. The Self-Attention mechanism can adaptively learn the dependencies between arbitrary time points and accurately capture these periodic features.
• Powerful global modeling capability: The Self-Attention mechanism allows each moment in the load sequence to directly associate with all historical moments, effectively extracting similar daily load patterns. This is particularly important for accurately forecasting load variations under abnormal conditions such as holidays or special weather events.
• Improved parallel computing efficiency: Compared to traditional Attention mechanisms, the Self-Attention mechanism derives $Q$, $K$, and $V$ from the same input sequence, making the computation more efficient and suitable for handling high-frequency sampled load data.

This structural design that combines Self-Attention with TCN not only enhances the advantage of TCN in local feature extraction but also strengthens the model’s capability to capture global dependencies in the load sequence through Self-Attention, while achieving significant improvements in computational efficiency.

2.3.3. Establishment of the MSCSO + SA TCN Power Load Forecasting Model

Since the hyperparameters—kernel size, number of filters, and batch size—in the TCN model significantly affect its forecasting performance, the MSCSO algorithm is employed to optimize these parameters and construct the MSCSO + SA TCN load forecasting model. The specific implementation steps are detailed below, and the model construction process is illustrated in Figure 13.

(1)

UMAP is applied to reduce the dimensionality of the historical power load data, and the output data are used as the model input data.

(2)

The input data obtained in step (1) are divided into a testing set and a training set in a ratio of 30% to 70%.

(3)

Identify the important parameters in SA TCN that require optimization (kernel size, number of filters, and batch size) and use MSCSO to optimize the parameter set.

(4)

Assign the optimal parameter set obtained by MSCSO to the SA TCN.

(5)

Train the SA TCN power load forecasting model using the training set.

(6)

Evaluate the forecasting performance of SA TCN using the testing set data.

3. Results

3.1. Data Processing

This paper uses the Panama power load dataset as the research subject, selecting real hourly load data from 1 January 2019 to 27 June 2020. Given that the study focuses on short-term load forecasting, the one-and-a-half-year span covers multiple seasons and typical load fluctuation patterns, which is sufficient for supporting model training and evaluation. The dataset, sourced from public repositories, contains nine load-related feature variables—such as temperature, relative humidity, liquid precipitation, and wind speed—all of which are collected in real time by automated sensors deployed around the power system.

Table 6. Meaning of each parameter name in load dataset.

Column Name	Description	Unit
nat_demand	National electricity load	MWh
T2M_toc	Temperature at 2 m in Tocumen, Panama city	°C
QV2M_toc	Relative humidity at 2 m in Tocumen, Panama city	%
TQL_toc	Liquid precipitation in Tocumen, Panama city	l/m2
W2M_toc	Wind Speed at 2 m in Tocumen, Panama city	m/s
dayOfWeek	Day of the week, starting on Saturdays	[1, 7]
weekend	Weekend binary indicator	1 = weekend, 0 = weekday
holiday	Holiday binary indicator	1 = holiday, 0 = regular day
hourOfDay	Hour of the day	[0, 23]

provides the names and descriptions of these feature variables. The original dataset includes 13,033 samples, each consisting of 9 features, totaling 117,297 data points. To facilitate model training and validation, the dataset is split in a 7:3 ratio, with 82,107 data points used for training and 35,190 for testing. In this section, all experiments were conducted using Python 3.9.

To enhance forecasting performance and ensure data quality, the raw sensor data are preprocessed through denoising, missing value and outlier correction, feature correlation analysis, and variable selection. Specifically, for missing entries and abrupt extreme values (such as sudden spikes or drops), an interpolation strategy based on the mean of adjacent time points is applied. This method replaces the anomalous values with the average of their neighboring observations, thereby maintaining the temporal continuity of the input data. Furthermore, to construct a more compact and informative feature set, the Uniform Manifold Approximation and Projection (UMAP) technique is employed to reduce the dimensionality of selected variables.

Although the scale of this dataset provides a rich informational foundation for modeling, it also presents two significant issues: first, some features may contain redundancy or weak correlations that could interfere with model learning; second, although the data dimensionality is not high, in time series modeling, stacking multiple time steps can significantly increase the complexity of the feature space, thereby increasing the computational cost and affecting forecasting accuracy.

3.1.1. Spearman and UMAP

To address the above issues, this paper introduces Spearman correlation analysis before modeling to filter the original features and identify variables that are highly correlated with the load values. Additionally, the UMAP algorithm is applied to reduce feature dimensionality while preserving the data structure, thereby improving model efficiency and forecasting performance. Spearman correlation is suitable for handling data with non-normal distributions or nonlinear relationships, and its calculation formula is as follows:

$$\rho ={\displaystyle \frac{{\displaystyle \sum _{i=1}^N\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}}{\sqrt{{\displaystyle \sum _{\mathrm{i}=1}^N{\left(x_i-\overline{x}\right)}^2{\displaystyle \sum _{\mathrm{i}=1}^N{\left(y_i-\overline{y}\right)}^2}}}}}$$

(38)

Here, $\rho$ is the computed correlation coefficient, $x_i$ and $y_i$ are any two features selected for the current calculation, and $\overline{x}$ and $\overline{y}$ are the mean values of the respective features.

Figure 14 presents the correlation heatmap of the feature variables based on the Spearman correlation coefficients, where the color gradient from deep blue to deep red represents the transition from negative correlation to positive correlation. The results show a significant positive correlation between the temperature feature and the load (nat_demand), indicating that temperature changes have a strong positive impact on power load and are an important explanatory factor for load fluctuations. The correlation between Hour Of Day and the load is also notable, at 0.21, suggesting that load variations exhibit a certain degree of intraday periodicity. In contrast, Relative Humidity, Wind Speed, and Liquid Precipitation exhibit generally low correlations with the load, with correlation coefficients all below 0.2, indicating that these features have limited explanatory power for electricity load. Therefore, these features are removed or subjected to dimensionality reduction during subsequent feature selection and dimensionality reduction processes to simplify the input space and enhance the model’s generalization performance.

During the data preprocessing stage, this paper adopts the UMAP algorithm, which retains information related to the load contained in the data while effectively reducing dimensionality. Specifically, based on the results of the Spearman correlation analysis, features highly correlated with the load, T2M_toc and Hour of Day, are retained without processing. Six features with lower correlations, including Relative Humidity, Wind Speed, and Liquid Precipitation, are designated for dimensionality reduction. The UMAP algorithm is applied to these variables to extract their structural information from the high-dimensional space and map them into two low-dimensional features. This approach avoids the crude elimination of information, effectively compresses the dimensionality of each sample in the input data, and reduces data volume. The dataset structure used for training and testing the forecasting model includes both the UMAP features and the original high value features.

Figure 15 presents the results of UMAP dimensionality reduction. As shown in the figure, the data points cluster into multiple clearly defined regions within the two-dimensional space. The overall distribution is relatively dispersed, but there is strong density within the clusters, reflecting the presence of complex and significant local structural relationships in the original high-dimensional features. Color mapping is used to represent the magnitude of the load values, with a gradient from deep purple to bright yellow corresponding to changes from low load to high load. Unlike a linear variation trend, Figure 15 shows that the load values vary within each cluster and that there are also noticeable differences in load values between different clusters. This indicates that not only does the data exhibit good clustering performance in the feature space, but also that the distribution of load values in the reduced-dimensional space demonstrates a certain degree of continuity and hierarchical pattern. These observations confirm that UMAP dimensionality reduction not only preserves the structural information of the original features but also effectively reveals the load distribution patterns, aiding subsequent analysis of the main factors influencing load variation and enhancing the interpretability of the model.

3.1.2. Correlation-Based Analysis of Key Influencing Variables

In load forecasting, identifying the driving mechanisms of environmental variables behind load fluctuations is essential for constructing efficient model architectures and enhancing model interpretability. This section conducts the analysis from two perspectives: first, a quantitative evaluation of the influence of each original variable on load variation based on Spearman correlation coefficients; second, a performance comparison under different feature processing strategies to investigate the impact of feature engineering on model prediction outcomes.

Table 7. Meaning of each parameter name in load dataset after UMAP dimensionality reduction.

Column Name	Description
nat_demand	National electricity load
T2M_toc	Temperature at 2 m in Tocumen, Panama city
hourOfDay	Hour of the day
UMAP_1	Low-dimensional feature 1 extracted by UMAP after reducing the dimensionality of other features.
UMAP_2	Low-dimensional feature 2 extracted by UMAP after reducing the dimensionality of other features.

lists all the feature names used for training and testing the forecasting model, along with explanations of the feature names. This includes the two low-dimensional features (UMAP_1 and UMAP_2) generated after UMAP dimensionality reduction. These two features were derived from the dimensionality reduction of six original features that had relatively low correlations with the load. Figure 16 illustrates the differences in correlation between the six original features and the two reduced-dimensional features. As shown in Figure 16, the correlations between UMAP_1 and UMAP_2 and the load variable significantly increased compared to the six features subjected to dimensionality reduction. The experimental results demonstrate that UMAP not only effectively reduced the data dimensionality but also successfully integrated and preserved key information from the original features. The new features resulting from dimensionality reduction surpassed the original features in both expressive power and correlation, providing higher representativeness and modeling value.

The observed improvement is primarily attributed to UMAP’s ability to preserve the spatial structure among samples and capture nonlinear relationships between original features during the dimensionality reduction process, thereby generating more representative features. Compared to traditional linear filtering methods, the embedding variables extracted by UMAP (UMAP_1 and UMAP_2) are not merely compressed outputs; rather, they integrate latent information from multiple weakly correlated features while preserving both local and global structures. As a result, their correlation with load significantly increases.

Figure 17 illustrates the performance differences of three representative time series forecasting models—LSTM, GRU, and TCN—across three feature processing stages: original features, Spearman-based filtering, and UMAP-based dimensionality reduction, in the context of load forecasting tasks.

Experimental results indicate that removing features with low correlation to load variation based on Spearman analysis can moderately enhance model performance in terms of RMSE, MAE, and R², although the magnitude of improvement is relatively limited. To further explore this, we applied the UMAP dimensionality reduction method to six low-correlation environmental features, compressing their high-dimensional structure into two low-dimensional variables. These were then combined with the original high-correlation variables to form the final input feature set for model training and forecasting. The results show that feature combinations incorporating UMAP-processed variables consistently outperformed the other two strategies across all models, with notably reduced prediction errors in RMSE and MAE, thus improving both model accuracy and stability.

Additionally, both the Spearman correlation heatmap and bar chart experiments reveal that the temperature variable T2M_toc and hourOfDay are the two original features most strongly correlated with load variation. In the Spearman analysis, these two features demonstrated significantly higher correlation coefficients compared to other variables, reflecting their dominant influence on load fluctuations. In the bar chart experiment, the strategy of retaining these high-correlation features while applying dimensionality compression to the remaining redundant variables also led to a significant enhancement in overall model prediction performance, further confirming the representativeness of this feature combination in load behavior modeling. This analysis not only provides a quantitative basis for feature selection but also offers empirical support for understanding the underlying mechanisms between environmental variables and load variation.

Accordingly, the use of the UMAP dimensionality reduction method in this study exhibits three significant advantages. First, UMAP effectively preserved the local structure and similarity in the original data, ensuring that the reduced-dimensional features retained good representativeness. Second, by compressing and integrating redundant features, it improved the simplicity and effectiveness of feature expression and reduced the risk of model interference. Third, the data compression achieved through dimensionality reduction significantly reduced both the feature dimensionality and the complexity of model training, providing more efficient input data for subsequent load forecasting modeling. These advantages indicate that UMAP not only enhanced data processing efficiency but also established a solid foundation for building stable and accurate models, addressing previous issues such as increased computational costs due to high data dimensionality and the negative impact of poorly correlated features on forecasting accuracy.

After dimensionality reduction, the original dataset was compressed into a new dataset comprising five key features, meaning that each sample in the transformed dataset contained exactly five features. Following this, the dataset was sequentially divided into a training set and a testing set, with the first 70% of the samples (a total of 45,615) used for model training, and the remaining 30% (a total of 19,550) reserved for testing. The entire dimensionality reduction process is computationally efficient and time-saving, enabling rapid execution even on standard computing devices. This compression of feature dimensionality not only significantly reduced the computational complexity of the model, but also effectively minimized the interference from redundant information during the training process, thereby laying a solid foundation for efficient modeling and enhanced prediction accuracy.

It is worth noting that the entire feature engineering process was completed prior to model training and falls within the scope of unsupervised preprocessing. The Spearman correlation analysis was based solely on statistical relationships between variables and did not involve any label information. Similarly, UMAP, as a nonlinear dimensionality reduction method, derives the embedded features by preserving structural relationships among variables rather than fitting the prediction target. As demonstrated in Figure 17, models trained with UMAP-compressed features consistently exhibited better prediction performance across multiple architectures, without signs of overfitting. These findings further confirm that the proposed feature compression strategy offers strong generalizability and practical applicability while maintaining robust generalization capability and avoiding overfitting risks.

3.2. Forecasting Model Experiments and Analysis

The forecasting model is the most important component for completing the forecasting task. The experimental design in this section progresses from models with simple structures to models with complex structures. This approach allows for step-by-step validation of the forecasting accuracy and reliability of the proposed model, providing readers with a more structured and detailed demonstration of the model’s forecasting accuracy, stability, and other performance aspects.

To evaluate the forecasting performance comprehensively, this paper adopts three commonly used metrics: R-squared (R²), Mean Absolute Error (MAE), and Root Mean Square Error (RMSE). R² indicates the proportion of variance in the actual data explained by the model, with values closer to 1 representing better fit and predictive ability. MAE measures the average absolute deviation between predicted and actual values, while RMSE further penalizes large errors by calculating the square root of the mean squared error. The formulas for these three evaluation metrics are presented below:

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}{{\displaystyle \sum _{i=1}^n{(y_i-\overline{y})}^2}}}$$

(39)

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|}$$

(40)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}$$

(41)

Here, $y_i$ represents the normalized actual value, ${\widehat{y}}_i$ represents the normalized predicted value, $\overline{y}$ represents the mean value, and n denotes the number of samples.

3.2.1. Basic Forecasting Models

Selecting an appropriate forecasting model as the foundation is a crucial factor in constructing a high-accuracy power load forecasting model. To intuitively assess the forecasting capabilities of different models, this paper selected several mainstream forecasting models for a comparative experiment, specifically XGBoost, LSTM, GRU, and TCN. The experimental results are presented in Figure 18 and Figure 19, and

Table 8. Evaluation metrics for the base model experiment.

Model	RMSE	R2	MAE
XGBoost	64.9015	0.8842	50.4837
LSTM	60.2718	0.9008	44.8494
GRU	57.2706	0.9184	43.8068
TCN	50.8312	0.9231	38.4772

.

Figure 18 illustrates the load forecasting results of different base models, providing a clear view for observing and analyzing the performance differences among the models. The horizontal axis in the figure represents time data in hours, while the vertical axis represents the load values in MWh. The coordinates and units of the magnified subfigure are the same as those of the main figure.

As shown in the figure, among all base models, the forecasting results of the TCN model are the closest to the actual load values. The fitting graph reveals the following observations:

• Regardless of whether the load is at a peak or a valley, LSTM and GRU cannot promptly respond to load changes. This is because recurrent neural networks require several time steps to perceive new feature changes in the input sequence when processing time series data. Consequently, LSTM and GRU exhibit weak short-term trend-capturing abilities under rapidly and sharply changing load patterns, resulting in poor responsiveness to load changes and inaccurate forecasts.
• XGBoost relies on the relationships between static features during forecasting and lacks the capability to model the internal continuity and dynamic variations of time series data. As a result, it cannot effectively capture the temporal characteristics of the sequence during rapid load fluctuations, leading to larger forecasting errors.
• The TCN model can respond quickly to rapid load fluctuations, particularly demonstrating higher forecasting accuracy at peaks and valleys. Overall, its forecasting performance surpasses that of the other models. This advantage is attributed to TCN’s use of dilated convolutions to expand the receptive field, effectively capturing rapid variation features in time series data, and its use of residual connections, which enhance the model’s responsiveness to complex load patterns.

Figure 19 presents the evaluation metrics of different models, facilitating intuitive analysis and comparison of the forecasting performance of each model. The horizontal axis in the figure represents the different forecasting models, distinguished by different colors and labeled with the corresponding model names in the legend. The vertical axes correspond to the three evaluation metrics: RMSE, R², and MAE. The height of each bar represents the value of the corresponding metric, allowing for a clear visualization of each model’s performance across different evaluation criteria.

As shown in Figure 19 and Table 8, the TCN model demonstrated a clear advantage across all evaluation metrics. For the RMSE metric, TCN achieved a value of 50.8312, significantly lower than XGBoost, LSTM, and GRU, indicating the smallest forecasting error. For the R² metric, TCN reached 0.9231, markedly outperforming the other models, which reflects its stronger fitting capability. In terms of the MAE metric, TCN also achieved the best result with a value of 38.4772, further confirming its advantage in forecasting accuracy.

In comparison, although LSTM and GRU, as typical recurrent neural networks, possess certain forecasting capabilities, they still lag slightly behind TCN in terms of overall accuracy and stability. The traditional machine learning model XGBoost exhibited relatively weaker performance in this experiment, indicating certain limitations when handling data with complex temporal dependencies. Considering the performance across various metrics, this paper ultimately selects TCN as the base model for subsequent research.

3.2.2. Validation Experiments for the Performance of the SA TCN

To validate the forecasting performance of the proposed SA TCN, the experimental design is as follows: the original TCN; the TCN(S) with the SwishPlus activation function proposed in this paper; the Att TCN with an attention mechanism (using ReLU as the activation function); and the SA TCN proposed in this paper, which incorporates a self-attention mechanism. Note that the SA TCN model used in subsequent experiments is implemented with the SwishPlus activation function by default. For simplicity in figure labeling and performance reporting, it is uniformly referred to as SA TCN without repeated specification.

As shown in Figure 20, with the progressive improvements made to the TCN model, the degree of fit between the forecasting results and the actual load values has significantly increased. Notably, during the rising phase, peak phase, declining phase, and valley phase of the load curve—accompanied by brief fluctuations—the proposed SA TCN model was able to achieve rapid and stable responses, demonstrating sufficient capability to adapt to load variation trends. Compared with other models, the SA TCN generated smoother forecasting trajectories during the load variation process, and the curve did not exhibit severe fluctuations.

The smoothness of the forecasting curve implies the presence of less noise, which benefits the overall stability and reliability of the forecasting results. A stable and coherent forecasting curve is particularly important for applications such as power load dispatching, generation planning, and energy storage system management. Since power systems require high continuity and controllability of load forecasting results, sharp fluctuations in the forecasts can lead to frequent adjustments in dispatching, increased reserve capacity requirements, and reduced economic efficiency and operational safety of the system. Therefore, while maintaining forecasting accuracy, the SA TCN model effectively enhances the feasibility of power system scheduling and the stability of operations through its naturally smooth response characteristics, demonstrating strong potential for practical application.

According to the results in Figure 21 and

Table 9. Evaluation metrics for the SelfAtt SwishPlus-TCN model experiment.

Model	RMSE	R2	MAE
TCN	50.8312	0.9231	38.4772
TCN(S)	48.6484	0.9366	35.9257
Att TCN	44.9509	0.9444	33.3178
SA TCN	38.3137	0.9590	27.7024

, it can be observed that as the activation function of the TCN is improved and different attention mechanisms are added, the forecasting accuracy of the model gradually increases. The introduction of the SwishPlus activation function and the self-attention mechanism has a significant impact on enhancing the performance of the TCN model. The Original TCN model exhibited the worst performance within the group, whereas the TCN(S) model, which incorporates the SwishPlus activation function, showed noticeable improvements across all evaluation metrics. Specifically, RMSE decreased from 50.8312 to 48.6484, R² increased from 0.9231 to 0.9366, and MAE decreased from 38.4772 to 35.9257, indicating that the SwishPlus activation function effectively enhanced the model’s nonlinear modeling capability and training performance.

On this basis, although the Att TCN model brought a certain degree of performance improvement, the overall optimization magnitude was relatively limited and did not significantly surpass the improvement effect brought by the SwishPlus activation function alone. In contrast, the SA TCN model, which integrates both the SwishPlus activation function and the self-attention mechanism, achieved the best performance across all evaluation metrics, with RMSE further reduced to 38.3137, R² increased to 0.9590, and MAE decreased to 27.7024, significantly outperforming the aforementioned models.

The performance improvement is primarily attributed to the fact that, compared to traditional activation functions, the SwishPlus activation function innovatively maintains a certain level of activation output even in the negative value region. This enables the model to more fully utilize feature information during training, thereby enhancing its nonlinear modeling capability. At the same time, the self-attention mechanism assigns weights based on the importance of each time step in the load sequence, strengthening the model’s ability to capture long-term dependencies.

By sequentially introducing these structural components into the original TCN, the experimental comparisons revealed progressive improvements in forecasting performance. Each module demonstrated a positive effect on temporal modeling, and the overall performance consistently improved as structural enhancements were added. The combined use of both components significantly improved forecasting accuracy and stability, empirically validating the effectiveness and necessity of each part within the proposed SA TCN architecture.

3.2.3. Validation Experiments for Optimizing the SA TCN with Different Optimization Algorithms

In the modeling process of the SA TCN, the parameter configuration of the TCN module plays a critical role in the model’s forecasting performance. To enhance model performance, this paper selects three core hyperparameters in the TCN—kernel size, number of filters, and batch size—for optimization. These parameters respectively influence the receptive field range, feature representation capability, and the efficiency and stability of the training process. Specifically, kernel size determines the number of time steps each convolution layer can cover and forms the basis for balancing between capturing local temporal features and modeling global dependencies. Number of filters controls the feature dimension output of the convolution layer; if the dimension is too low, underfitting may occur, while an excessively high dimension may lead to overfitting and unnecessary computational resource consumption. Batch size directly affects the model’s convergence speed and generalization ability, requiring a trade-off between training stability and efficiency.

To achieve efficient and accurate hyperparameter selection, this paper introduces MSCSO to explore optimal configurations within a broader search space, thereby improving the model’s forecasting accuracy and robustness.

In the MSCSO optimization process, MAE is selected as the fitness function. This choice not only aligns with the loss function used during TCN model training, ensuring consistency between the optimization objective and the learning objective, but also provides good stability and interpretability. Compared to error metrics that are more sensitive to outliers, MAE can more stably reflect the model’s average deviation across the overall sample set, avoiding evaluation distortions caused by individual outliers. Therefore, the fitness function is defined as follows:

$$fitness={\displaystyle \frac{{\displaystyle \sum _{i=1}^n\left|{\widehat{y}}_i-y_i\right|}}{n}}$$

(42)

Here, ${\widehat{y}}_i$ represents the predicted values of the TCN test set, $y_i$ represents the actual values of the test set, and $n$ denotes the number of samples in the test set.

In the SA TCN model hyperparameter optimization experiment, Figure 22 shows the changes in fitness values during the iteration process for different optimization algorithms. As illustrated in the figure, all optimization algorithms effectively reduced the fitness values. In comparison, the proposed MSCSO algorithm—optimized using the UTCM-initialized population, cosine evolution adaptive factor, and Lévy flight strategy—demonstrated the best convergence speed and optimization performance during the search process, reaching the lowest fitness value within 20 iterations. Moreover, the final convergence result outperformed the other comparative algorithms. The SCSO algorithm ranked second, also achieving relatively low fitness values within fewer iterations, but overall it was slightly inferior to MSCSO. Both the SSA and SO algorithms exhibited significantly lower convergence speeds and final fitness levels compared to the former two algorithms. These results fully validate the effectiveness and advantages of MSCSO in hyperparameter optimization and provide reliable support for the further improvement of SA TCN model performance.

Figure 23 illustrates the impact of different optimization algorithms on the forecasting performance of the SA TCN model. Based on the results shown in the figure, two main conclusions can be drawn:

First, all optimization algorithms improved the forecasting performance of the SA TCN model to varying degrees, indicating that hyperparameter optimization can effectively enhance the forecasting accuracy of the model. The original SA TCN model already possessed good capability for capturing long-term dependency features, and the introduction of optimization algorithms further improved the model’s forecasting accuracy for load variations.

Second, among all the compared algorithms, the SA TCN model optimized by the proposed MSCSO demonstrated the best fit to the actual load variation curve, exhibiting superior accuracy. In contrast, while other optimization algorithms were able to capture the general trend of load variations, there were still noticeable deviations between the predicted and actual values in regions with sharp fluctuations or turning points.

In summary, the MSCSO–SA TCN model can capture subtle variation features in the load sequence, thereby significantly improving overall forecasting performance.

According to Figure 24 and

Table 10. Evaluation metrics for the MSCSO—SA TCN model experiment.

Model	RMSE	R2	MAE
SA TCN	38.3137	0.9590	27.7024
SSA-SA TCN	34.5021	0.9675	24.8883
SO-SA TCN	31.3159	0.9733	22.3987
SCSO-SA TCN	28.9039	0.9781	21.1206
MSCSO-SA TCN	24.7072	0.9830	17.5225

, the MSCSO–SA TCN model achieved the best results across all evaluation metrics, demonstrating excellent forecasting performance. Compared to the SA TCN, the MSCSO–SA TCN optimized the RMSE, R², and MAE metrics to 24.7072, 0.9830, and 17.5225, respectively, reflecting higher forecasting accuracy and lower forecasting error, and significantly enhancing the model’s ability to accurately capture load variation trends.

From the comparison results of different optimization algorithms, the introduction of SSA, SO, SCSO, and other algorithms improved the forecasting performance of the SA TCN model to varying degrees, validating the effectiveness of parameter optimization in improving the output accuracy of forecasting models during model development. Moreover, the multi-strategy optimized MSCSO algorithm outperformed all comparative methods, leading not only in accuracy metrics but also demonstrating significant advantages in convergence speed and stability. These results indicate that MSCSO achieves an effective balance between global search capability and local convergence accuracy, further unlocking the potential of the SA TCN architecture in complex time series modeling tasks.

In summary, MSCSO not only effectively accelerated the model’s training convergence process but also significantly enhanced the model’s responsiveness to severe load fluctuations and local variations. With its outstanding performance, the MSCSO–SA TCN model was validated as the optimal structure in this study and demonstrated promising application prospects, offering a new solution for power load forecasting and other complex time series forecasting tasks.

3.2.4. Comparative Evaluation with Transformer-Based Models

In recent years, Transformer and its derivative models have demonstrated strong modeling capabilities in deep learning tasks. These models rely on attention mechanisms and possess powerful nonlinear representational abilities. To further validate the performance advantages of the proposed model, we selected Transformer, Informer, FEDformer, and Autoformer as benchmark models and conducted systematic evaluations under a unified experimental setup. Specifically, Informer reduces computational complexity through sparse self-attention; FEDformer enhances modeling of periodic temporal patterns via frequency domain decomposition; and Autoformer improves the characterization of long-term dependencies using a trend-seasonality decomposition structure. A performance comparison of these models on the same task is presented in

Table 11. Accuracy and resource efficiency comparison among proposed and state-of-the-art forecasting models.

Model	RMSE	R2	MAE	Epochs	Time	Memory Usage
Transformer	59.8201	0.9005	44.1672	20	1983.88	1248.48
FEDformer	58.9196	0.9118	43.0436	20	976.42	1477.87
Informer	48.6961	0.9217	36.5812	20	2033.17	2062.33
Autoformer	43.2894	0.9493	31.3736	20	1607.86	1075.69
SA TCN	38.3137	0.9590	27.7024	50	532.2	254.77
MSCSO-SA TCN	24.7072	0.9830	17.5225	50	863.7	271.42

.

In Table 11, time is measured in seconds, and Memory Usage indicates the memory consumption (MB) during model training. The results show that under the same setting of 20 training epochs, all Transformer-based models—except FEDformer—took more than 25 min to train. On the test hardware configured with an Intel i7-9750H processor and 16 GB RAM, memory usage for these models generally exceeded 1 GB. The data in the table clearly highlight two critical limitations of these models:

• Although Transformer-based models exhibit strong modeling capabilities, they still face several challenges in practical applications. These models often require large-scale training data and come with significant computational and memory costs. For example, the original Transformer paper reports training on eight NVIDIA Tesla P100 GPUs, a hardware configuration rarely available outside research institutions.
• Due to the attention mechanism’s need for global computation across all positions in a sequence, Transformer-based models often incur high time costs during training. This can be a limiting factor for large-scale deployment in resource-constrained engineering environments.

In contrast, the proposed MSCSO-SA TCN model achieves high prediction accuracy while demonstrating strong computational efficiency and resource adaptability. Under the same hardware environment, this model exhibited significantly lower runtime and memory usage over 50 training epochs compared to various Transformer-based architectures, making it especially suitable for deployment in resource-limited scenarios. Additionally, we compared this with the SA TCN model without MSCSO optimization. As shown in the table, incorporating the optimization algorithm led to clear improvements across multiple metrics including RMSE, R², and MAE, with only an additional 5–6 min of training time and negligible increase in memory usage. We also tested several other optimization algorithms (SSA, SO, and SCSO) in combination with SA TCN and found that the increase in training time was comparable to that of MSCSO. This indicates that the proposed MSCSO method delivers performance gains without introducing significant additional computational burden, demonstrating high practical applicability.

3.2.5. Statistical Robustness and Variability Analysis

To further evaluate the robustness and performance consistency of the proposed model under different initialization conditions, this section conducts a comparative analysis based on multiple independent experiments. Each model was trained ten times with randomly initialized parameters, and the prediction error in each run was recorded. The results are presented in the form of error bar plots to visualize the mean prediction error and its confidence interval across runs, thereby providing a more intuitive assessment of the model’s statistical stability and predictive reliability.

Figure 25 illustrates the distribution of prediction errors for each model across ten independent experiments, using error bar plots. In the figure, the horizontal axis represents model types, and the vertical axis shows the mean prediction error, which reflects the overall deviation of the model’s forecasts. The “Mean” refers to the average prediction error across all test samples in each individual run, while the error bars indicate the ±95% Confidence Interval (CI) of this mean, which captures the range of model performance variation under different random initialization settings. The 95% CI implies that if predictions deviate from ground truth, 95% of the prediction errors are expected to lie within this interval.

As shown in the figure, the proposed MSCSO-SA TCN model achieves both lower average prediction errors and narrower confidence intervals across all metrics, indicating superior stability and higher accuracy under varying experimental conditions. These results further confirm the model’s reliability and robustness for practical applications.

4. Conclusions

This paper proposes a power load forecasting model based on a multi-strategy improved MSCSO algorithm and a self-attention mechanism TCN to effectively address short-term load forecasting tasks.

In terms of data processing, to further enhance data quality, the multi-source input features used in this study—including key environmental variables such as temperature, humidity, wind speed, and precipitation—were obtained from automated monitoring devices deployed in the operational environment of the power system. These sensors provide high-timeliness, multi-dimensional time-series information, laying a solid data foundation for subsequent model construction and optimization.

To fully extract the effective features embedded in the sensor data, this paper first employs the Spearman correlation analysis method to filter the variables in the original dataset, retaining those most closely related to power load variations. Subsequently, Uniform Manifold Approximation and Projection (UMAP) is applied to perform dimensionality reduction and reconstruction of the high-dimensional historical load data, generating new features with stronger representational capacity and more compact structure. While preserving local structural characteristics, UMAP effectively reduces data redundancy and training complexity, thereby providing more stable and efficient input data for the model.

The improved MSCSO algorithm proposed in this paper utilizes the UTCM initialization mechanism, resulting in a more uniform population distribution and significantly enhancing the diversity of the initial population. Meanwhile, the dynamic sensitivity design effectively addresses the issue of limited exploration range during the optimization process, further enhancing the algorithm’s global search capability in the middle and later stages. In addition, the introduction of the Lévy flight strategy enables the algorithm to perform large-step jumps during the search process, breaking through local area limitations, expanding the search range, significantly improving the ability to escape local optima and the efficiency of the search process, and making it easier for the algorithm to identify the optimal solution.

In terms of model structure design, this paper innovatively proposes replacing ReLU with SwishPlus as the activation function for the TCN. Compared with ReLU, SwishPlus improves gradient update efficiency and model convergence speed, thereby significantly enhancing model performance. The self-attention mechanism effectively strengthens the improved TCN model’s ability to capture long-range dependency information.

Finally, during the experimental phase, the dataset obtained from the feature engineering steps was used as the training and testing data. The MSCSO algorithm optimized the key parameters of the SA TCN, effectively improving the model’s forecasting accuracy in short-term load forecasting tasks. Experimental validation demonstrated that the proposed MSCSO–SA TCN model exhibited the following advantages in short-term power load forecasting:

• The introduction of the SwishPlus activation function enhanced the model’s gradient transmission capability and nonlinear expression ability, giving the model stronger competitiveness in complex feature learning. The addition of the self-attention mechanism enabled the forecasting model to demonstrate a better feature extraction capability and forecasting robustness under complex load variation scenarios, further improving overall forecasting performance.
• The MSCSO algorithm is an innovative enhancement based on the original SCSO. Although SCSO possesses certain optimization capabilities, previous studies showed that population initialization and global search abilities did not reach optimal levels, resulting in deficiencies in exploration capability and convergence speed. To address this issue, this paper proposed the MSCSO algorithm, which systematically strengthens three aspects: population diversity generation strategy, local optimum escape capability, and global optimization efficiency. Rather than limiting improvements to a single strategy, it adopts a holistic optimization framework to comprehensively enhance algorithm performance. In terms of results, MSCSO demonstrated superior optimization accuracy and convergence speed on both multimodal functions and fixed-dimension multimodal functions. Through these improvements, MSCSO exhibited better adaptability and robustness when tackling complex load forecasting tasks, significantly expanding the algorithm’s application boundaries.
• The proposed model achieved the best performance in the experiments, with results of 24.7072, 0.9830, and 17.5225 for RMSE, R², and MAE, respectively. Compared with the second-best model, the performance improved by 4.1979, 0.0049, and 3.5981, respectively.

In consideration of practical deployment needs within real-world power systems, this study further explores the applicability and operational strategy of the proposed model. On one hand, the MSCSO-SA TCN model adopts a fully data-driven modeling approach that does not rely on prior knowledge specific to any particular region, thus offering strong transferability and generalizability. As long as the target region provides similar environmental variables and load observation data, the model can be directly applied to different regional power systems without requiring structural modifications, showing potential for deployment under diverse climatic conditions.

On the other hand, to address runtime efficiency and maintenance strategies during model deployment, this study adopts an “offline training–online inference” approach. The model is trained once using historical data and then deployed for inference, where it performs rapid predictions without requiring retraining. This approach is well-suited to real-world scenarios that demand high prediction accuracy but are constrained by limited training resources. Furthermore, to improve adaptability in dynamic load environments, we introduce an accuracy-threshold-based model retraining mechanism. During operation, the model’s predictive performance is continuously monitored. If the accuracy of consecutive predictions falls below a predefined threshold and remains unsatisfactory over a specified time window, a retraining process is automatically triggered, using the most recent data to update the model. This mechanism ensures stable performance while avoiding unnecessary retraining, thereby improving resource efficiency and enhancing system robustness in practical applications.

5. Future Prospects

Future research will mainly focus on three aspects: First, further optimizing the model’s ability to extract peak load features, in order to enhance its performance in identifying and modeling extreme load fluctuations. Second, investigating strategies that integrate optimization efficiency with lightweight model design, aiming to improve computational performance and applicability in resource-constrained environments. Third, to enhance the model’s generalization and robustness, we plan to incorporate load time series data with longer temporal coverage and expand experiments to include diverse geographic regions and climate types. This will facilitate a more thorough validation of the model under complex and variable data conditions.