Determination of Stiffness Coefficients at the Internal Vertices of the Tree Based on a Finite Set of Eigenvalues of an Asymmetric Second-Order Linear Differential Operator

Abstract

A second-order linear differential operator A is defined on a tree of arbitrary topology. Any internal vertex P of the tree divides the tree into $m_p$ branches. The restrictions $A_i,i=1,\dots ,m_p$ of the operator A on each of these branches, where the vertex P is considered the root of the branch and the Dirichlet boundary condition is specified at the root. These restrictions must be, in a sense, asymmetric (not similar) to each other. Thus, the distinguished class of differential operators A turns out to have only simple eigenvalues. Moreover, the matching conditions at the internal vertices of the graph contain a set of parameters. These parameters are interpreted as stiffness coefficients. This paper proves that a finite set of eigenvalues allows one to uniquely restore the set of stiffness coefficients. The novelty of the work is the fact that it is sufficient to know a finite set of eigenvalues of intermediate Weinstein problems for uniquely restoring the required stiffness coefficients. We not only describe the results of selected studies but also compare them with each other and establish interconnections.

1. Introduction

This paper studies differential operators on tree graphs. Let a fixed number of edges with known lengths be given. How can one connect the given edges together so the following hold:

(i)

A tree graph is formed;

(ii)

The corresponding Sturm–Liouville operator does not have multiple eigenvalues?

In this case, various combinatorial methods for forming trees from the given edges are possible. This paper identifies a special class of trees with a topology that guarantees simplicity of the eigenvalues of the corresponding Sturm–Liouville operator.

In the second part of this paper, we study the recovery of the stiffness coefficients at the internal vertices of the tree from a finite set of eigenvalues. Similar problems in [1] are related to partial inverse spectral problems for differential operators. Such problems consist in recovering the coefficients of a differential expression in some part of the domain (a finite interval or a geometric graph) from spectral characteristics, while the coefficients in the rest of the domain are known a priori. Typically, partial inverse problems require less spectral data than full inverse problems. The first results on partial inverse problems on graphs were obtained by Pivovarchik [2], Yurko [3], and Yang et al. [4,5,6]. However, the results of these papers were limited to uniqueness theorems for the Sturm–Liouville (Schrödinger) operators on graphs of an elementary structure (star-shaped graphs and simple graphs with loops). Later on, Bondarenko developed a constructive method to solve partial inverse problems on graphs of various types. Using this method, a number of new results have been obtained for differential operators and pencils on star-shaped graphs [7,8,9,10], simple graphs with cycles [11,12], tree graphs (graphs without cycles) [13], and even graphs of an arbitrary geometrical structure [14,15]. These results included not only uniqueness theorems but also constructive algorithms for the solution, solvability, and stability of partial inverse problems.

In this paper, we study differential equations defined on a tree graph. We denote the tree graph by $\Gamma =\{V,E\}$. We divide the set of vertices into two disjoint parts $V=V_1\bigcup V_2$. We call the vertices belonging to $V_1$ boundary vertices and number them from 0 to p. We classify the boundary vertices as those vertices that have a degree equal to 1. Moreover, the root of the tree represents the vertex with the number $k=0.$ We also assume that there is only one edge coming out of the root. We denote the vertices that are not boundary vertices by $V_2$ and call them internal vertices of the tree. The internal vertices are numbered with natural numbers from $p+1$ to r. The edges from E are considered oriented. Each edge has a starting and ending vertex. The number of the edge of the graph coincides with the number of the ending vertex of the edge. Such numbering of edges is realizable. On each edge $e_j\in E$, the differential equation is defined as

$$l_j\left(y_j\right)\equiv -y_j^{″}\left(x_j\right)+q_j\left(x_j\right)·y_j\left(x_j\right)=\lambda y_j\left(x_j\right),x_j\in e_j,$$

(1)

where the real potential $q_j(·)\in L_2\left(e_j\right)$. In what follows, each edge $e_j$ is interpreted as an interval $(0,b_j)$. At the boundary vertices $k\in V_1$, the following boundary conditions are specified:

$$\left\{\begin{array}{cc}{y}_k^{\prime }\left(b_k\right)-h_k{y}_k\left(b_k\right)=0,\hfill & \mathrm{if}k\ne 0,\hfill \\ y_{p+1}^{\prime }\left(0\right)+h_{p+1}{y}_{p+1}\left(0\right)=0,\hfill & \mathrm{if}k=0.\hfill \end{array}\right.$$

(2)

where $h_1,h_2,\dots ,h_{p+1}$ are real numbers. At each internal vertex $j\in V_2$, we require the fulfillment of the matching conditions:

$$\left\{\begin{array}{c}{y}_j\left(b_j\right)=y_{s_j\left(1\right)}\left(0\right)=\dots =y_{s_j\left(m_j\right)}\left(0\right),\hfill \\ y_j^{\prime }\left(b_j\right)-k_j{y}_j\left(b_j\right)=y_{s_j\left(1\right)}^{\prime }\left(0\right)+\dots +y_{s_j\left(m_j\right)}^{\prime }\left(0\right),\hfill \end{array}\right.$$

(3)

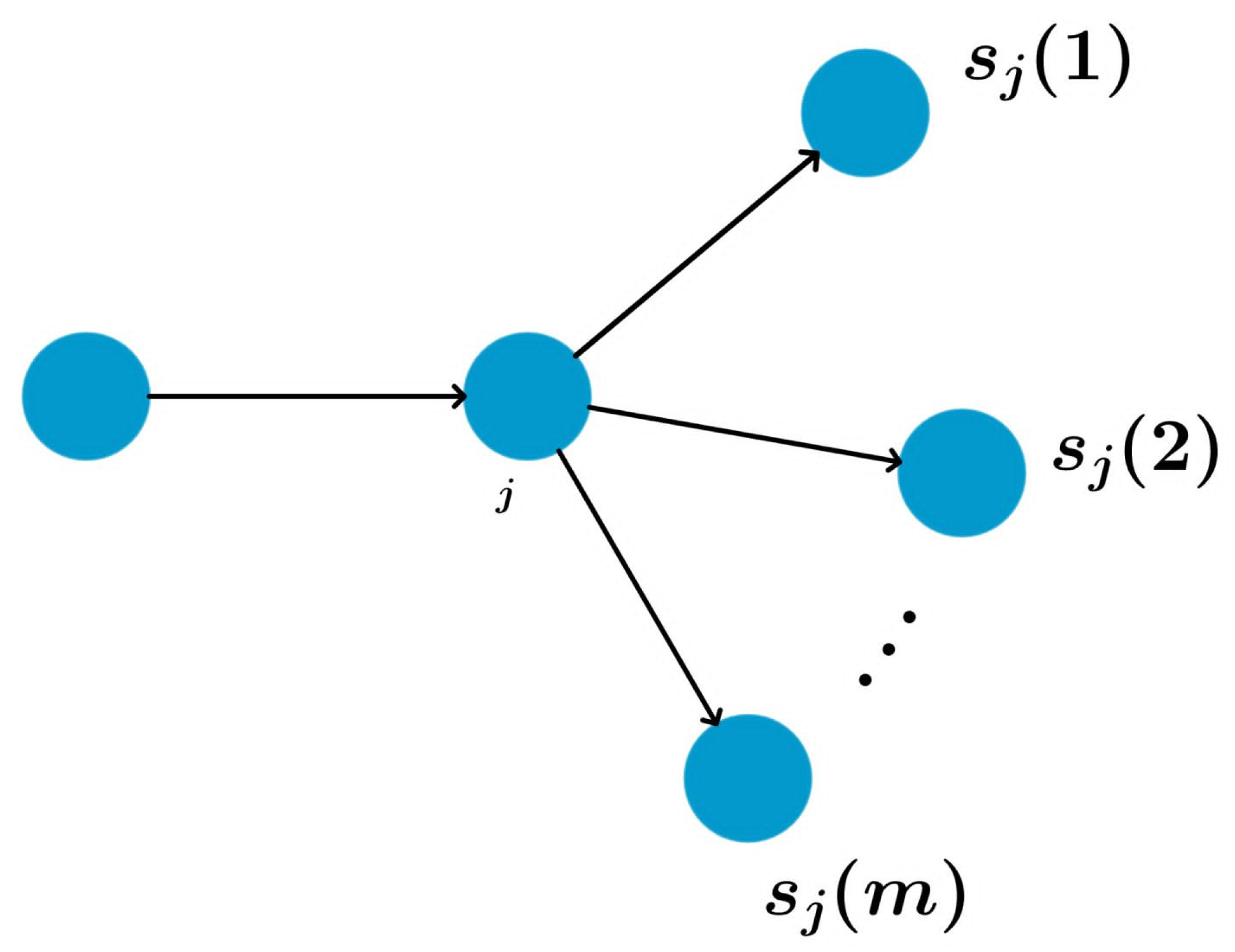
where $s_j\left(1\right),\dots ,s_j\left(m_j\right)$ are the numbers of all edges emanating from vertex j (Figure 1).

Here, the numbers $k_j$ for $j=p+1,\dots ,r$ are considered real. If $k_{p+1}=\dots =k_r=0$, then the conditions (3) turn into the standard Kirchhoff conditions [16]. Note [17] the relation

$$\sum _{d_i\in V}{d}_i=2·r,$$

(4)

where r is the total number of edges in the tree, and $d_i$ is the degree of the i-th vertex of the tree.

In our notation, $d_j=m_j+1$ for $j\in V_2$, and $d_j=1$ for $j\in V_1$. Therefore, the relation (4) takes the form

$$\sum _{j\in V_2}\left(m_j+1\right)+p+1=2·r$$

(5)

The quantity ${\displaystyle \sum _{j\in V_2}}(m_j+1)$ represents the number of matching conditions at the interior vertices, and the quantity $(p+1)$ is the number of boundary conditions at the boundary vertices. The quantity $2r$ represents twice the number of edges in the tree. On each edge, the general solution of a homogeneous linear differential equation of the second order contains two arbitrary constants. Thus, there are only $2r$ arbitrary constants on the tree. To determine them, according to equality (5), exactly $2r$ boundary conditions and matching conditions are specified. Therefore, in a certain sense, the number of conditions (2) and (3) coincides with the number of constants sought.

Thus, the problem (1)–(2)–(3) on a tree graph is a direct eigenvalue problem.

The operator defined by the set of differential expressions $(l_1(·),\dots ,l_r(·))$ on $W_2^2(\Gamma )$ is denoted by ${\Lambda }_{max}$. Let $\Lambda$ denote the restriction of the operator ${\Lambda }_{max}$ to smooth functions satisfying the boundary conditions (2) and the compatibility conditions (3). It is well known [18,19,20] that the operator $\Lambda$ has a purely discrete spectrum consisting of a countable set of eigenvalues. They coincide (counting their multiplicities) with the zeros of the entire function, called the characteristic determinant of $\Delta \left(\lambda \right)$. Recall [21] also that the operator $\Lambda$ is self-adjoint in the space $L_2(\Gamma )$. Consequently, all the eigenvalues of the operator $\Lambda$ are real, and the system of its eigenfunctions forms an orthogonal basis in the space $L_2(\Gamma )$.

Let the graph $\Gamma =\{V,E\}$ have more than one edge. Let j be an arbitrary internal vertex of degree $m_j+1$ (Figure 1). Vertex j splits the tree graph $\Gamma$ into $(m_j+1)$ branches ${\Gamma }_{kj}=\{V_{kj},E_{kj}\}$ for $k=1,\dots ,m_j+1$. By definition, a tree branch is a maximal subtree containing vertex j as the root of the tree. The restriction of operator $\Lambda$ to branch ${\Gamma }_{kj}$ with additional Dirichlet conditions at vertex j is denoted by $\Lambda \left({\Gamma }_{kj}\right)$ for $k=1,\dots ,m_j+1$. Let the numbers $k_{p+1},\dots ,k_r$ be fixed. In what follows, we will assume that the requirement $I(k_{p+1},\dots ,k_r)$ is satisfied.

The lengths of the edges $b_1,\dots ,b_r$ and the numbers $h_1,\dots ,h_{p+1},$ as well as the functions $q_1(·),\dots ,q_r(·)$, are chosen so that for any $j\in V_2$, for all $k,s\in \{0,1,\dots ,m_j+1\}$ and $k\ne s$, the spectra of the operators $\Lambda \left({\Gamma }_{kj}\right)$ and $\Lambda \left({\Gamma }_{sj}\right)$ do not intersect.

Remark 1.

Such a choice is always possible. For example, consider m finite segments with lengths $b_1,\dots ,b_m$. For $i=1,\dots ,m$, consider the real potential $q_i\left(x\right)$ from the space $L_2(0,b_i)$, as well as the real number $h_i$. On the segments $[0,b_i]$ for $i=1,\dots ,m$, introduce the Sturm–Liouville operators

$$F_{i}y\left(x\right)=-y^{″}\left(x\right)+q_i\left(x\right)y\left(x\right),x\in (0,b_i)$$

(6)

with domains

$$D\left(F_i\right)=\{y\in W_2^2[0,b_i]:y\left(0\right)=0,y^{\prime }\left(b_i\right)-h_{i}y\left(b_i\right)=0\}$$

(7)

We choose the numbers $b_1,\dots ,b_m$ so that the spectra of the operators $F_1,\dots ,F_m$ are pairwise disjoint; that is, $\sigma \left(F_i\right)\bigcap \sigma \left(F_j\right)=⌀$ for $i\ne j$. Here, $\sigma \left(F_i\right)$ denotes the spectrum of the operator $F_i$. If $q_1\left(x\right)\equiv q_2\left(x\right)\equiv 0$, then the operators $F_1$ and $F_2$ do not have common eigenvalues for $b_1{h}_1\ne b_2{h}_2$. Thus, positive numbers $b_1,\dots ,b_m$ are chosen so that the operators $F_i$ and $F_j$ have no common eigenvalues for $i\ne j$. Then, the star graph composed of edges of lengths $b_1,\dots ,b_m$ satisfies the requirement $I(k_{p+1},\dots ,k_r)$. By successively connecting the indicated star graphs, we can obtain a tree graph that satisfies the requirement $I(k_{p+1},\dots ,k_r)$.

Let us formulate the main results of the article.

Theorem 1.

Let the requirement $I(k_{p+1},\dots ,k_r)$ be satisfied for fixed $k_{p+1},\dots ,k_r$. Then, the spectrum of the operator Λ consists only of simple real eigenvalues.

Remark 2.

The set of $\{{\phi }_1(x_1,\lambda ),\dots ,{\phi }_r(x_r,\lambda )\}$ unctions from Section 2 are defined in a single way and they form a set of integer functions with respect to λ. The characteristic determinant $\Delta \left(\lambda \right)$ of the operator Λ is written in terms of one of them. More precisely, the characteristic determinant $\Delta \left(\lambda \right)$ is given by the formula $\Delta \left(\lambda \right)={\phi }_{p+1}^{\prime }(0,\lambda )+h_{p+1}{\phi }_{p+1}(0,\lambda )$. Theorem 1 states that the characteristic determinant $\Delta \left(\lambda \right)$ defined in this way can only have simple zeros.

To formulate further results, we introduce the following notation. Let j be one of the numbers $1,\dots ,p$. Choose a path $Pat{h}_j$ connecting the root of the tree with the boundary vertex j. Such a path exists [17], and it is unique.

Let the length of $Pat{h}_j$ be $l\left(j\right)+1$. The path $Pat{h}_j$ represents an ordered sequence of vertices:

$$0\prec {\nu }_{1j}\prec {\nu }_{2j}\prec \dots \prec {\nu }_{l\left(j\right)j}\prec j,$$

where ${\nu }_{1j}=p+1$.

The operator $\Lambda$ for $k_s=0,s={\nu }_{m+1j},{\nu }_{m+2j},\dots ,{\nu }_{l\left(j\right)j}$ is denoted by ${\Lambda }_{mj}$. Let us introduce the characteristic determinants ${\Delta }_{mj}\left(\lambda \right)$ and ${\Delta }_{m+1j}\left(\lambda \right)$, corresponding to the operators ${\Lambda }_{mj}$ and ${\Lambda }_{m+1j}$. In what follows, the requirement $I(k_{p+1},\dots ,k_r)$ for $k_s=0,s={\nu }_{m+1j},{\nu }_{m+2j},\dots ,{\nu }_{l\left(j\right)j}$ will be denoted by $I_{mj}(k_{p+1},\dots ,k_r)$.

Theorem 2.

For $j=1,\dots ,p$ and $m=0,1,\dots ,l\left(j\right)-1$, the zeros of the characteristic determinants ${\Delta }_{mj}\left(\lambda \right)$ and ${\Delta }_{m+1j}\left(\lambda \right)$ are simple and alternate if the requirements $I_{mj}(k_{p+1},\dots ,k_r),I_{m+1,j}(k_{p+1},\dots ,k_r)$ are satisfied.

It follows from Theorem 2 that adding a new spring with stiffness $k_s,s={\nu }_{m+1j}$ shifts all eigenvalues to the left. According to the terminology of monograph [22], the operators ${\Lambda }_{mj}$ and ${\Lambda }_{m-1j}$ correspond to intermediate Weinstein problems. In the case of differential operators on an interval, an analogue of Theorem 2 is proved in the work in [23].

In the final part of the paper, it is proved that the stiffness coefficients $k_{p+1},\dots ,k_r$ are uniquely calculated from a finite set of eigenvalues of the intermediate Weinstein problems. A more general problem of recovering nonlocal matching conditions at an internal vertex of a star graph was solved by N.P. Bondarenko [24]. Moreover, N.P. Bondarenko indicated the necessary and sufficient conditions that an infinite sequence of numbers must satisfy to perform unique recovery. In contrast to the work of N.P. Bondarenko, in the present paper, the unique recovery of the numbers $k_{p+1},\dots ,k_r$ is performed by a finite set of numbers $\{{\lambda }_1,\dots ,{\lambda }_{r-p}\}$. In the case of a differential operator on a segment, the recovery of the boundary coefficients by a finite set of eigenvalues can be found in the work in [25]. The partial inverse problems studied in [1] are often found under different names. Typically, partial inverse problems require less spectral data than full inverse problems. In the literature, partial inverse problems are also called semi-inverse problems, Hochstadt–Lieberman-type problems [26,27], inverse problems with mixed data, and incomplete inverse problems. If we talk about practical applications of such problems, similar problems find application in acoustic diagnostics [28,29]. The object consists of a system of rods and springs; in the process of exploitation the springs can change their elastic characteristics. By the eigenvalues that can be measured by acoustic engineering instruments it is possible to judge the condition of the springs. Several proposals are explored in on the structure of the present paper. In the Section 2, the properties of the eigenvalues of the original problem (1)–(2)–(3) are investigated. In particular, the requirements on the lengths of the tree arcs for which the eigenvalues of the original problem are simple real numbers are found. In the Section 3, the relations between the characteristic determinants of two different problems of the type (1)–(2)–(3) are given. In particular, when adding a new spring at the internal vertex, all eigenvalues shift either to the right or to the left depending on the sign of the added stiffness coefficient. In the Section 4, an algorithm for uniquely restoring all stiffness coefficients from a finite set of eigenvalues of some auxiliary Weinstein problems is proposed.

2. Proof of Theorem 1

Theorem 5.1 of [30] implies the following.

Lemma 1.

For any real $k_{p+1},\dots ,k_r$, the operator Λ is self-adjoint to the space $L_2(\Gamma )$.

Thus, since $\Lambda ={\Lambda }^{\ast }$, the system of eigenfunctions of the operator $\Lambda$ in the space $L_2(\Gamma )$ forms an orthogonal basis. Moreover, all eigenvalues of the operator $\Lambda$ are real numbers.

In order to prove that all eigenvalues of the operator $\Lambda$ are simple, we introduce a set of functions $\{{\phi }_1(x_1,\lambda ),\dots ,{\phi }_r(x_r,\lambda )\}$. First, we define the first p functions ${\phi }_1(x_1,\lambda ),\dots ,{\phi }_p(x_p,\lambda )$ as functions that satisfy Equation (1) and the Cauchy conditions

$${\phi }_j(b_j,\lambda )=1,{\phi }_j^{\prime }(b_j,\lambda )=h_j,j=1,\dots ,p.$$

Such solutions exist and are entire functions in $\lambda$ [31].

Let us define the solutions of Equation (1) at $j=1,\dots ,p$ as follows:

$${\psi }_j(x_j,\lambda )=A_j·{\phi }_j(x_j,\lambda ),$$

where $A_j$ are some quantities that do not depend on $x_j$, but may depend on the parameter $\lambda$. Let us choose an internal vertex of the tree with the maximum height. We denote it by $n\in V_2$, and its height by H. Let the vertex n be connected by edges only with the boundary vertices $s_n\left(1\right),\dots ,s_n\left(m_n\right)$. It is sometimes said [32] that the vertex n is incident with the boundary vertices $s_n\left(1\right),\dots ,s_n\left(m_n\right)$. The number $(m_n+1)$ denotes the degree of the vertex n. Then, in order for the first of the matching conditions (3) to be satisfied at the internal vertex n for the functions $\left\{{\psi }_j(x,\lambda )\right\}$, it is sufficient to choose the constants $A_{s_n\left(1\right)},\dots ,A_{s_n\left(m_n\right)}$ as follows:

$$A_{s_n\left(j\right)}=A_n·\prod _{i=1,i\ne j}^{m_n}{\phi }_{s_n\left(i\right)}(0,\lambda ),$$

(8)

where $A_n$ is some common constant for all $A_{s_n\left(1\right)},\dots ,A_{s_n\left(m_n\right)}$. Note that $A_n$ may depend on the parameter $\lambda$.

As a result, for ${\psi }_n(b_n,\lambda )$ we have the representation

$${\psi }_n(b_n,\lambda )=A_n·\prod _{i=1}^{m_n}{\phi }_{s_n\left(i\right)}(0,\lambda ).$$

(9)

Note that the requirement $I(k_{p+1},\dots ,k_r)$ implies that the inequality ${\phi }_j(0,\lambda )\ne 0,j=1,\dots ,p$ is satisfied.

From the second relation of the form (3) we obtain a representation for ${\psi }_n^{\prime }(b_n,\lambda )$. More precisely, the representation is valid if

$${\psi }_n^{\prime }(b_n,\lambda )=A_n\left(\sum _{j=1}^{m_n}\prod _{i=1,i\ne j}^{m_n}{\phi }_{s_n\left(i\right)}(0,\lambda ){\phi }_{s_n\left(j\right)}^{\prime }(0,\lambda )+k_n\prod _{i=1}^{m_n}{\phi }_{s_n\left(i\right)}(0,\lambda )\right)$$

(10)

Thus, we have found the state of the edge $e_n$ at the end point $x_n=b_n$. This state is determined by the pair of numbers $({\psi }_n(b_n,\lambda ),{\psi }_n^{\prime }(b_n,\lambda ))$. Next, we find the state at an arbitrary point $x_n$ of the edge $e_n$. This state is characterized by the pair of numbers $({\psi }_n(x_n,\lambda ),{\psi }_n^{\prime }(x_n,\lambda ))$. The required pair of numbers is calculated by the formula

$$\left[\begin{array}{c}{\psi }_n(x_n,\lambda )\\ {\psi }_n^{\prime }(x_n,\lambda )\end{array}\right]=\left[\begin{array}{cc}{c}_n(x_n,\lambda )& s_n(x_n,\lambda )\\ c_n^{\prime }(x_n,\lambda )& s_n^{\prime }(x_n,\lambda )\end{array}\right]·\left[\begin{array}{c}{\psi }_n(b_n,\lambda )\\ {\psi }_n^{\prime }(b_n,\lambda )\end{array}\right]$$

(11)

where $c_n(x_n,\lambda )$ and $s_n(x_n,\lambda )$ are solutions of the following Cauchy problem:

$$-y_n^{″}(x_n,\lambda )+q_n\left(x_n\right)y_n(x_n,\lambda )=\lambda y_n(x_n,\lambda ),0<x_n<b_n,$$

$$s_n^{\prime }(b_n,\lambda )=c_n(b_n,\lambda )=1,s_n(b_n,\lambda )=c_n^{\prime }(b_n,\lambda )=0.$$

We denote the function ${\displaystyle \frac{\psi \left(x_n\lambda \right)}{A_n}}$ by ${\phi }_n(x_n,\lambda )$. In particular, for $x_n=0$ we know the state $({\psi }_n(0,\lambda ),{\psi }_n^{\prime }(0,\lambda ))$ at the beginning of the edge $e_n$. Now, we select all internal vertices whose height coincides with the height of vertex $n\in V_2$. Let their numbers be $n_1,\dots ,n_k$. Using the specified algorithm, we calculate their states: $\{({\psi }_{n_1}(0,\lambda ),{\psi }_{n_1}^{\prime }(0,\lambda )),\dots ,({\psi }_{n_k}(0,\lambda ),{\psi }_{n_k}^{\prime }(0,\lambda ))\}$. So, we know the states of all vertices of height H. Knowing the values of $({\psi }_n(0,\lambda ),{\psi }_n^{\prime }(0,\lambda ))$, we can proceed to determining the values of $({\psi }_t(b_t,\lambda ),{\psi }_t^{\prime }(b_t,\lambda ))$, where t is the number of the vertex from which the edge $e_n$ originates. It is clear that the height of vertex t is one less than the height of vertex n. Therefore, we can find the state of $({\psi }_t(b_t,\lambda ),{\psi }_t^{\prime }(b_t,\lambda ))$ using the algorithm we specified above. The height of vertex t is one less than the height of vertex n. Thus, we have managed to decrease the height of the vertices by one. Continuing to decrease the heights of the vertices, we will gradually come to a vertex with a height of zero. That is, we will reach the root of the tree. Thus, we will construct a complete set of functions, ${\phi }_1(x_1,\lambda ),\dots ,{\phi }_r(x_r,\lambda )$. In this case, the requirement $I(k_{p+1},\dots ,k_r)$ implies the fulfillment of the inequalities ${\phi }_j(0,\lambda )\ne 0,j=p+1,\dots ,r$.

As a result, we obtain the following representation:

$${\psi }_{p+1}^{\prime }(0,\lambda )+h_{p+1}{\psi }_{p+1}(0,\lambda )=A_{p+1}\left({\phi }_{p+1}^{\prime }(0,\lambda )+h_{p+1}{\phi }_{p+1}(0,\lambda )\right)$$

where $A_{p+1}$ is some constant. Note that the function ${\phi }_{p+1}(x_{p+1},\lambda )$ is an entire function of $\lambda$.

Lemma 2.

The spectrum of the operator Λ consists of normal eigenvalues that coincide with the zeros of the entire function

$$\Delta \left(\lambda \right)={\phi }_{p+1}^{\prime }(0,\lambda )+h_{p+1}{\phi }_{p+1}(0,\lambda ).$$

The following statement shows the simplicity of the zeros of the entire function $\Delta \left(\lambda \right)$.

Lemma 3.

All eigenvalues of the operator Λ are single-valued.

The proof of Lemma 3 is similar to the proof of Lemma 1 from ref. [23]. Let $\lambda ,\mu$ be arbitrary complex numbers. Consider the difference

$$R={\langle {\Lambda }_{max}\overrightarrow{\Phi }\left(\lambda \right),\overrightarrow{\Phi }\left(\mu \right)\rangle }_{L_2(\Gamma )}-{\langle \Phi \left(\lambda \right),{\Lambda }_{max}\overrightarrow{\Phi }\left(\mu \right)\rangle }_{L_2(\Gamma )},$$

where $\overrightarrow{\Phi }\left(\lambda \right)={[{\phi }_1(x_1,\lambda ),\dots ,{\phi }_r(x_r,\lambda )]}^T$, $\overrightarrow{\Phi }\left(\mu \right)={[{\phi }_1(x_1,\mu ),\dots ,{\phi }_r(x_r,\mu )]}^T$.

In the work in [30], the Lagrange formula is proved for differential operators of the second order on an arbitrary tree. From the Lagrange formula in the work in [30], it follows that

$$R=\sum _{j=1}^p\left[-({\phi }_j^{\prime }(b_j,\lambda )-h_j{\phi }_j(b_j,\lambda ))\overline{{\phi }_j(b_j,\mu )}+{\phi }_j(b_j,\lambda )\overline{({\phi }_j^{\prime }(b_j,\mu )-h_j\phi j(b_j,\mu ))}\right]+$$

$$+({\phi }_{p+1}^{\prime }(0,\lambda )+h_{p+1}{\phi }_{p+1}(0,\lambda )\overline{{\phi }_{p+1}(0,\mu )}-{\phi }_{p+1}(0,\lambda )\overline{({\phi }_{p+1}^{\prime }(0,\mu )+h_{p+1}{\phi }_{p+1}(0,\mu ))}.$$

(12)

Since for $j=1,\dots ,p$ the relations ${\phi }_j^{\prime }(b_j,\lambda )-h_j{\phi }_j(b_j,\lambda )=0$ are true, then from equality of (12) the relation follows

$$R=\Delta \left(\lambda \right)\overline{{\phi }_{p+1}(0,\mu )}-{\phi }_{p+1}(0,\lambda )\overline{\Delta \left(\mu \right)}.$$

(13)

Let $\lambda ={\lambda }_0$ be an arbitrary eigenvalue of the operator $\Lambda$. In equality (13) we pass to the limit as $\mu \to {\lambda }_0$ (for details see the work in [23]). As a result, we have the equality

$$\underset{\mu \to {\lambda }_0}{lim}{\langle \overrightarrow{\Phi }\left({\lambda }_0\right),\overrightarrow{\Phi }\left(\mu \right)\rangle }_{L_2(\Gamma )}=-{\phi }_{p+1}(0,{\lambda }_0){\displaystyle \frac{d}{d\lambda }}\Delta \left(\lambda \right){|}_{\lambda ={\lambda }_0}$$

(14)

Since $\parallel \overrightarrow{\Phi }\left({\lambda }_0\right){\parallel }_{L_2(\Gamma )}^2>0$, then from equality (14) it follows that

$${\displaystyle \frac{d}{d\lambda }}\Delta \left(\lambda \right){|}_{\lambda ={\lambda }_0}\ne 0,{\phi }_{p+1}(0,{\lambda }_0)\ne 0.$$

The first of these inequalities shows that all eigenvalues of the operator $\Lambda$ are prime. Lemma 3 is completely proved. Theorem 1 follows from Lemma 3.

Remark 3.

The meaning of the requirement $I(k_{p+1},\dots ,k_r)$ is that the solutions ${\phi }_1(x_1,\lambda ),{\phi }_2(x_2,\lambda ),\dots ,{\phi }_r(x_r,\lambda )$ that we constructed do not vanish at the internal vertices of the tree.

3. Proof of Theorem 2

Let j be one of the numbers $1,\dots ,p$. Choose a path $Pat{h}_j$ connecting the root of the tree with the boundary vertex j. Such a path exists [2], and it is unique. Let the length of the path $Pat{h}_j$ be $l\left(j\right)+1$. The path $Pat{h}_j$ represents an ordered sequence of vertices:

$$0\prec {\nu }_{1j}\prec {\nu }_{2j}\prec \dots \prec {\nu }_{l\left(j\right)j}\prec j,$$

where ${\nu }_{1j}=p+1$. The operator $\Lambda$ for $k_s=0,s={\nu }_{m+1j},{\nu }_{m+2j},\dots ,{\nu }_{l\left(j\right)j}$ is denoted by ${\Lambda }_{mj}$. In this section, we study the relationship between the characteristic determinants ${\Delta }_{mj}\left(\lambda \right)$ and ${\Delta }_{m-1j}\left(\lambda \right)$ of different operators ${\Lambda }_{mj}$ and ${\Lambda }_{m-1j}$.

Along with the solutions ${\phi }_1(x_1,\lambda ),\dots ,{\phi }_r(x_r,\lambda )$ that were introduced in Section 2, we introduce a set of solutions ${\theta }_{1,mj}(x_1,\lambda ),\dots ,{\theta }_{r,mj}(x_r,\lambda )$ of the system of Equation (1). First, we define the solutions ${\theta }_{k,mj}$ for $k=1,\dots ,j-1,j+1,\dots ,p+1,$ subject to the Cauchy conditions at the boundary vertices:

$$\left\{\begin{array}{c}{\theta }_{k,mj}(b_k,\lambda )=1,{\theta }_{k,mj}^{\prime }(b_k,\lambda )=h_k,1\le k\le p,\hfill \\ {\theta }_{p+1,mj}(0,\lambda )=-1,{\theta }_{p+1,mj}^{\prime }(0,\lambda )=h_{p+1}.\hfill \end{array}\right.$$

Now, we consider the boundary vertex j as the root of the tree, and the vertex with the number 0 as one of the boundary vertices. In this case, the height of each vertex will change, since it is equal to the length of the path connecting the vertex with the root of the tree. The root of the tree has changed, so the height of the vertex will change too.

Further, the solutions ${\theta }_{k,mj}(x_k,\lambda )$ for $r\ge k>p+1$ and $k=j$ are determined in the same way as ${\phi }_{p+1}(x_p,\lambda ),\dots ,{\phi }_r(x_r,\lambda )$ were calculated from the solutions ${\phi }_1(x_1,\lambda ),\dots ,{\phi }_p(x_p,\lambda )$, taking into account the decrease in the heights of the vertices.

Remark 4.

From the requirements $I_{mj}(k_{p+1},\dots ,k_r)$ and $I_{m+1,j}(k_{p+1},\dots ,k_r)$, it follows that the set of functions $[{\theta }_{1,mj}(x_1,\lambda ),\dots ,{\theta }_{r,mj}(x_r,\lambda )]$ does not vanish at the internal vertices of the tree.

Let $\mu =\overline{\lambda }$. Denote this by

$${\overrightarrow{\theta }}_{mj}\left(\mu \right)={[{\theta }_{1,mj}(x_1,\mu ),\dots ,{\theta }_{r,mj}(x_r,\mu )]}^T.$$

Recall that the vector function ${\overrightarrow{\theta }}_{mj}\left(\mu \right)$ corresponds to $k_s=0,$ $s={\nu }_{m+1j},{\nu }_{m+2j},\dots ,{\nu }_{l\left(j\right)j}$, and the numbers $k_s$ for $s={\nu }_{1j},\dots ,{\nu }_{mj}$ can take arbitrary real values. Let us choose another set of parameters $k_{p+1},\dots ,k_r$ according to the following rule: all $k_s$ coincide with $k_s$ for $s\ne {\nu }_{mj}$, and $k_s=0$ for $s={\nu }_{mj}$. Let the solution ${\phi }_1(x_1,\lambda ),\dots ,{\phi }_r(x_r,\lambda )$, constructed in step 2, correspond to the set of parameters $k_{p+1},\dots ,k_r$. For convenience, we denote this set of solutions by ${\phi }_{1m}(x_1,\lambda ),\dots ,{\phi }_{rm}(x_r,\lambda )$. For further purposes, it is convenient to introduce the vector

$${\overrightarrow{\Phi }}_m\left(\lambda \right)={[{\phi }_{1m}(x_1,\lambda ),\dots ,{\phi }_{rm}(x_r,\lambda )]}^T.$$

For the functions ${\overrightarrow{\Phi }}_m\left(\lambda \right)$ and ${\overrightarrow{\theta }}_{mj}\left(\mu \right)$, we consider the difference:

$$R={\langle {\Lambda }_{max}{\overrightarrow{\Phi }}_m\left(\lambda \right),{\overrightarrow{\theta }}_{mj}\left(\mu \right)\rangle }_{L_2(\Gamma )}-{\langle {\overrightarrow{\Phi }}_m\left(\lambda \right),{\Lambda }_{max}{\overrightarrow{\theta }}_{mj}\left(\mu \right)\rangle }_{L_2(\Gamma )}.$$

Applying the Lagrange formula from the work in [30] to calculate the difference R, we obtain the relation

$$0=R=-{\phi }_{j,m}^{\prime }(b_j,\lambda )\overline{{\theta }_{j,mj}(b_j,\mu )}+{\phi }_{j,m}(b_j,\lambda )\overline{{\theta }_{j,mj}^{\prime }(b_j,\mu )}+$$

$$+{\phi }_{p+1,m}^{\prime }(0,\lambda )\overline{{\theta }_{p+1,mj}(0,\mu )}-{\phi }_{p+1,m}(0,\lambda )\overline{{\theta }_{p+1,mj}^{\prime }(0,\mu )}+$$

$$+\left[-{\phi }_{z,m}^{\prime }(b_z,\lambda )\overline{{\theta }_{z,mj}(b_z,\mu )}+{\phi }_{z,m}(b_z,\lambda )\overline{{\theta }_{z,mj}^{\prime }(b_z,\mu )}\right]+$$

$$+\left[{\phi }_{\tau ,m}^{\prime }(0,\lambda )\overline{{\theta }_{\tau ,mj}(0,\mu )}-{\phi }_{\tau ,m}(0,\lambda )\overline{{\theta }_{\tau ,mj}^{\prime }(0,\mu )}\right]+\dots =$$

at $z={\nu }_{mj},\tau ={\nu }_{m+1j}$. Here, the ellipsis … takes into account the contribution of the edges emanating from the vertex m.

Taking into account the boundary conditions (2) and the matching conditions (3), the equality follows from here for $z={\nu }_{mj}$. Note that $\left(\overline{{\theta }_{j,mj}^{\prime }(b_j,\mu )-h_j{\theta }_{j,mj}(b_j,\mu )}\right)$ represents the characteristic determinant of the operator ${\Lambda }_{mj}$. Let us denote this by ${\Delta }_{mj}\left(\lambda \right)=\overline{{\theta }_{j,mj}^{\prime }(b_j,\overline{\lambda })-h_j{\theta }_{j,mj}(b_j,\overline{\lambda })}$.

Lemma 4.

The characteristic determinants of the operators ${\Lambda }_{mj}$ and ${\Lambda }_m$ are related by the relation

$${\Delta }_{mj}\left(\lambda \right)={\Delta }_{m-1,j}\left(\lambda \right)-k_z{\phi }_{z,m}(b_z,\lambda )·\overline{{\theta }_{z,mj}(b_z,\overline{\lambda })}$$

for $z={\nu }_{mj}$.

Similar formulas connecting the characteristic determinants of different operators are given in the work in [23].

Let $\lambda ={\lambda }_n^{\left(mj\right)}$ be an arbitrary eigenvalue of the operator ${\Lambda }_{mj}$. It is easy to see that

$${\phi }_{s,m}(x_s,{\lambda }_n^{\left(mj\right)})={\displaystyle \frac{{\theta }_{s,mj}(x_s,{\lambda }_n^{\left(mj\right)})}{{\theta }_{j,mj}(b_j,{\lambda }_n^{\left(mj\right)})}},x_s\in e_s.$$

(15)

where $e_s$ is an edge from $Pat{h}_j$, and $s\ge {\nu }_{mj}$. That is, the vertex $s\in Pat{h}_j$ is no further to j than the vertex ${\nu }_{mj}$ is to the vertex j. Also note that

$${\theta }_{s,m+1j}(x_s,\lambda )={\theta }_{s,mj}(x_s,\lambda ),x_s\in e_s,\forall \lambda \in C$$

(16)

where $e_s$ is an edge from path $Pat{h}_s$, and $s\le {\nu }_{mj}$. That is, the vertex $s\in Pat{h}_s$ is not further from the root of the tree than the vertex ${\nu }_{mj}$. Let us denote this by

$$W_{m,mj}\left(\lambda \right)={\displaystyle \frac{{\Delta }_{mj}\left(\lambda \right)}{{\Delta }_m\left(\lambda \right)}},$$

which in [22] is called the Weinstein determinant. Then, by the Mittag–Leffler theorem, the meromorphic function $W_{m,mj}\left(\lambda \right)$ is reconstructed from the principal parts of the Laurent expansions in the neighborhood of its poles. Then, from Lemma 3, we obtain a new representation:

$$W_{m,mj}\left(\lambda \right)=1-k_z\sum _{n=1}^{\infty }{\displaystyle \frac{1}{\lambda -{\lambda }_n^{\left(m\right)}}}·\underset{{\lambda }_n^{\left(m\right)}}{res}{\displaystyle \frac{{\phi }_{z,m}(b_z,\lambda )\overline{{\theta }_{z,mj}(b_z,\lambda )}}{{\Delta }_m\left(\lambda \right)}}$$

for $z={\nu }_{mj}$.

Calculate the residue

$$\underset{{\lambda }_n^{\left(m\right)}}{res}{\displaystyle \frac{{\phi }_{z,m}(b_z,\lambda )\overline{{\theta }_{z,mj}(b_z,\lambda )}}{{\Delta }_m\left(\lambda \right)}}=\left[\mathrm{taking}\mathrm{into}\mathrm{account}\left(16\right)\right]=$$

$$={\displaystyle \frac{{\phi }_{z,m}(b_z,{\lambda }_n^{\left(m\right)})\overline{{\theta }_{z,mj}(b_z,{\lambda }_n^{\left(m\right)})}}{\frac{d}{d\lambda }{\Delta }_m\left(\lambda \right){|}_{{\lambda }_n^{\left(m\right)}}}}=$$

$$=\left[\mathrm{taking}\mathrm{into}\mathrm{account}\left(15\right)\right]={\displaystyle \frac{{\theta }_{z,mj}(b_z,{\lambda }_n^{\left(m\right)})\overline{{\theta }_{z,mj}(b_m,{\lambda }_n^{\left(m\right)})}}{{\theta }_{j,mj}(b_z,{\lambda }_n^{\left(m\right)})\frac{d}{d\lambda }\overline{{\Delta }_m\left(\lambda \right)}{|}_{{\lambda }_n^{\left(m\right)}}}}=$$

$$=\left[\mathrm{taking}\mathrm{into}\mathrm{account}\mathrm{the}\mathrm{analogue}\left(14\right)\right]=-{\displaystyle \frac{|{\theta }_{z,mj}(b_z,{\lambda }_n^{\left(m\right)}){|}^2}{\parallel {\overrightarrow{\theta }}_{mj}\left({\lambda }_n^{\left(m\right)}\right){\parallel }^2}}=a_n^{\left(m\right)}\le 0.$$

Then, the Weinstein determinant takes the form

$$W_{m,mj}\left(\lambda \right)=1-k_z\sum _{n=1}^{\infty }{\displaystyle \frac{a_n^{\left(mj\right)}}{\lambda -{\lambda }_n^{\left(m\right)}}},z={\nu }_{mj}.$$

Remark 5.

In fact, the series ${\displaystyle \sum _{n=1}^{\infty }}{\displaystyle \frac{a_n^{\left(mj\right)}}{\lambda -{\lambda }_n^{\left(m\right)}}}$ converges absolutely, since the quantity $\underset{n\ge 1}{sup}\left|a_n^{\left(mj\right)}\right|$ is finite, and the series ${\displaystyle \sum _{n=1}^{\infty }}{\displaystyle \frac{1}{{\lambda }_n^{\left(m\right)}}}$ converges absolutely. The absolute convergence of the series ${\displaystyle \sum _{n=1}^{\infty }}{\displaystyle \frac{1}{{\lambda }_n^{\left(m\right)}}}$ follows from the rough asymptotic formulas for the eigenvalues ${\lambda }_n^{(n-1)}\asymp n^2$. More precise asymptotic formulas for the eigenvalues are given in [13,19]. The boundedness of the quantity $\underset{n}{sup}\left|a_n^{\left(mj\right)}\right|$ follows from the inequalities

$$\left|a_n^{\left(mj\right)}\right|={\displaystyle \frac{|{\theta }_{z,mj}(b_z,{\lambda }_n^{\left(m\right)}){|}^2}{\parallel {\overrightarrow{\theta }}_{mj}\left({\lambda }_n^{\left(m\right)}\right){\parallel }^2}}\le {\displaystyle \frac{|{\theta }_{z,mj}(b_z,{\lambda }_n^{\left(m\right)}){|}^2}{\parallel {\theta }_{z,mj}(·,{\lambda }_n^{\left(m\right)}){\parallel }^2}}\le$$

$$\le {\displaystyle \frac{|{\theta }_{z,mj}(b_z,{\lambda }_n^{\left(m\right)}){|}^2}{\underset{b_z-\delta }{\overset{b_z}{\int }}{\left|{\theta }_{z,mj}(x,{\lambda }_n^{\left(m\right)})\right|}^{2}dx}}\le {\displaystyle \frac{|{\theta }_{z,mj}(b_z,{\lambda }_n^{\left(m\right)}){|}^2}{\delta min\left\{\right|{\theta }_{z,mj}(x,{\lambda }_n^{\left(m\right)}){|}^2:b_{z-\delta }\le x\le b_z\}}}$$

So, it is proven.

Lemma 5.

For all $\lambda \in C$ the following identity holds:

$${\Delta }_{mj}\left(\lambda \right)={\Delta }_m\left(\lambda \right)\left(1-k_z\sum _{n=1}^{\infty }{\displaystyle \frac{a_n^{\left(mj\right)}}{\lambda -{\lambda }_n^{\left(m\right)}}}\right)$$

(17)

where $z={\nu }_{mj}$ and $a_n^{\left(mj\right)}\le 0$.

Identity (17) implies the following statements.

Corollary 1.

If some $a_n^{\left(mj\right)}=0$, then ${\lambda }_n^{\left(m\right)}={\lambda }_n^{\left(mj\right)}$.

Corollary 2.

Let $k_z>0,$ where $z={\nu }_{mj}$. Then, for all $a_n^{\left(mj\right)}<0$ the inequality

$${\lambda }_n^{\left(mj\right)}<{\lambda }_{n+1}^{\left(m\right)}<{\lambda }_{n+1}^{\left(mj\right)}.$$

4. Reconstruction of Stiffness Coefficients from Eigenvalues of Intermediate Weinstein Problems

In this section, we propose a sequential reconstruction of the stiffness coefficients $k_{p+1},\dots ,k_r$ from the eigenvalues of the intermediate Weinstein problems [1]. At the initial stage, we consider the problem of eigenvalues (1)–(3) for $k_{p+1}=\dots =k_r=0$. Let the specified problem (without springs) correspond to the operator ${\Lambda }_0$. In this case, we assume that the functions $q_1(·),\dots ,q_r(·)$ and the numbers $h_1,\dots ,h_{p+1}$ are given. Therefore, the eigenvalues and eigenfunctions of such an unperturbed problem are considered known.

Let j be one of the numbers $1,\dots ,p.$ Then, choose a path $Pat{h}_j$ connecting the root of the tree with the boundary vertex j. Let the length of $Pat{h}_j$ be $l\left(j\right)+1$. The path $Pat{h}_j$ represents an ordered sequence of vertices:

$$0\prec {\nu }_{1j}\prec {\nu }_{2j}\prec \dots \prec {\nu }_{l\left(j\right)j}\prec j,$$

where ${\nu }_{1j}=p+1$. First, let $j=1$. We denote the operator $\Lambda$ by ${\tilde{\Lambda }}_{m1}$ when $k_s=0$, if $s={\nu }_{m+11},{\nu }_{m+21},\dots ,{\nu }_{l\left(1\right)1}$, and also $k_{\tau }=0$ if the vertex $\tau$ does not lie on the path $Pat{h}_1$. Thus, ${\tilde{\Lambda }}_{11}$ corresponds to the problem with one spring. Let ${\lambda }^{\left(11\right)}$ be given as one eigenvalue of the operator ${\tilde{\Lambda }}_{11}$. Compare the characteristic determinants ${\Delta }_0\left(\lambda \right)$ and ${\Delta }_{11}\left(\lambda \right)$, which correspond to the operators ${\Lambda }_0$ and ${\tilde{\Lambda }}_{11}$. Then, equality

$${\Delta }_{11}\left(\lambda \right)={\Delta }_0\left(\lambda \right)-k_{p+1}{\phi }_{p+1,1}(b_{p+1},\lambda )\overline{{\theta }_{p+1,11}(b_{p+1},\lambda )}.$$

(18)

follows from the analogue of Lemma 3. Here, the notation of Lemma 3 is preserved. We substitute the given eigenvalue ${\lambda }^{\left(11\right)}$ of the operator ${\tilde{\Lambda }}_{11}$ into the relation (18). As a result, we have

$${\Delta }_0\left({\lambda }^{\left(11\right)}\right)=k_{p+1}{\phi }_{p+1,1}(b_{p+1},{\lambda }^{\left(11\right)})·\overline{{\theta }_{p+1,11}(b_{p+1},{\lambda }^{\left(11\right)})}.$$

(19)

Note that the quantities ${\Delta }_0\left(\lambda \right),{\phi }_{p+1,1}(b_{p+1},\lambda )$ and ${\theta }_{p+1,11}(b_{p+1},\lambda )$ do not depend on the quantities $k_{p+1},k_{p+2},\dots ,k_r$. Therefore, from equality (19) the number $k_{p+1}$ is uniquely determined if ${\phi }_{p+1,1}(b_{p+1},{\lambda }^{\left(11\right)})·\overline{{\theta }_{p+1,11}(b_{p+1},{\lambda }^{\left(11\right)})}\ne 0.$ It follows from the requirement $I(k_{p+1},\dots ,k_r)$ that the last inequality is satisfied. Thus, for one eigenvalue ${\lambda }^{\left(11\right)}$ of the operator ${\tilde{\Lambda }}_{11}$, it is possible to find only one stiffness coefficient $k_{p+1}$.

Now, consider the operator ${\tilde{\Lambda }}_{21}$, which corresponds to the problem with two springs on the path $Pat{h}_1$. Let ${\lambda }^{\left(21\right)}$ be given as one eigenvalue of the operator ${\tilde{\Lambda }}_{21}$. Let us compare the characteristic determinants ${\Delta }_{11}\left(\lambda \right)$ and ${\Delta }_{21}\left(\lambda \right)$, which correspond to the operators ${\tilde{\Lambda }}_{11}$ and ${\tilde{\Lambda }}_{21}$. Then, the analogue of Lemma 3 implies the equality

$${\Delta }_{21}\left(\lambda \right)={\Delta }_{11}\left(\lambda \right)-k_z{\phi }_{z,2}(b_z,\lambda )\overline{{\theta }_{z,21}(b_z,\lambda )}$$

(20)

where $z={\nu }_{21}$. Here, the notation of Lemma 4 is preserved. We substitute the given eigenvalue ${\lambda }^{\left(21\right)}$ of the operator ${\tilde{\Lambda }}_{21}$ into the relation (20). As a result, we have

$${\tilde{\Delta }}_{11}\left({\lambda }^{\left(21\right)}\right)=k_z{\phi }_{z,2}(b_z,{\lambda }^{\left(21\right)})·\overline{{\theta }_{z,21}(b_z,{\lambda }^{\left(21\right)})},$$

(21)

where $z={\nu }_{21}$.

Note that the quantities ${\tilde{\Delta }}_{11}\left(\lambda \right),{\phi }_{z,2}(b_z,\lambda )$ and ${\theta }_{z,21}(b_z,\lambda )$ are related to the operator ${\tilde{\Lambda }}_{11}$ and do not depend on the quantities $k_{p+2},\dots ,k_r$. Therefore, the eigenvalues and eigenfunctions of the operator ${\tilde{\Lambda }}_{11}$ are considered known, since we have already found $k_{p+1}$. Therefore, from equality (21) the number $k_z$ is uniquely determined if ${\phi }_{z,2}(b_z,{\lambda }^{\left(21\right)})·\overline{{\theta }_{z,21}(b_z,{\lambda }^{\left(21\right)})}\ne 0.$ It follows from the requirement $I(k_{p+1},\dots ,k_r)$ that the last inequality is satisfied.

Thus, using one eigenvalue ${\lambda }^{\left(11\right)}$ of the operator ${\tilde{\Lambda }}_{11}$ and one eigenvalue ${\lambda }^{\left(21\right)}$ of the operator ${\tilde{\Lambda }}_{21}$, it is possible to consistently unambiguously find two stiffness coefficients $k_{p+1},k_z$, where $z={\nu }_{21}$.

The above algorithm allows us to unambiguously calculate the stiffness coefficient $k_{\tau }$ by one eigenvalue of the operator ${\tilde{\Lambda }}_{31}$. Here, $k_{\tau }$ corresponds to the third vertex on the first path $Pat{h}_1$, id est, $\tau ={\nu }_{31}$. In this case, we consider the values $k_{p+1}$ and $k_z$ at $z={\nu }_{21}$ to be known. As a result, the spectral data associated with the operator ${\tilde{\Lambda }}_{21}$ are considered to be precalculated. Continuing our proposed algorithm for calculating the stiffness coefficients $k_{p+1},k_s$, where $s={\nu }_{m1}$ at $m\ge 2$, we find all the spring coefficients of the vertices lying on the first path $Pat{h}_1$. In this case, we assume that the vertex springs on other paths $Pat{h}_j$ for $j>1$ are absent. Then, we move on to the second path, setting $j=2$. We successively determine the coefficients $k_s$ for $s={\nu }_{22},{\nu }_{32},\dots ,{\nu }_{l\left(2\right)2},$ while we assume that the values $k_{p+1},k_{\tau }$ for $\tau ={\nu }_{21},{\nu }_{31},\dots ,{\nu }_{l\left(1\right)1}$ are known. We continue the proposed calculation process for $j=3,\dots ,p$. Thus, all values $k_{p+1},k_{p+2},\dots ,k_r$ will be calculated from a finite set of eigenvalues of the intermediate Weinstein problems.

5. Conclusions

The paper proves that a finite set of eigenvalues allows one to uniquely reconstruct the set of rigidity coefficients of the internal vertices of a tree graph with an arbitrary topology.