Modeling Based on Machine Learning and Synthetic Generated Dataset for the Needs of Multi-Criteria Decision-Making Forensics

Abstract

Information is the primary driver of progress in today’s world, especially given the vast amounts of data available for extracting meaningful knowledge. The motivation for addressing the problem of forensic analysis—specifically the validity of decision making in multi-criteria contexts—stems from its limited coverage in the existing literature. Methodologically, machine learning and ensemble models represent key trends in this domain. Datasets used for such purposes can be either real or synthetic, with synthetic data becoming particularly valuable when real data is unavailable, in line with the growing use of publicly available Internet data. The integration of these two premises forms the central challenge addressed in this paper. The proposed solution is a three-layer ensemble model: the first layer employs multi-criteria decision-making methods; the second layer implements multiple machine learning algorithms through an optimized asymmetric procedure; and the third layer applies a voting mechanism for final decision making. The model is applied and evaluated through a case study analyzing the U.S. Army’s decision to replace the Colt 1911 pistol with the Beretta 92. The results demonstrate superior performance compared to state-of-the-art models, offering a promising approach to forensic decision analysis, especially in data-scarce environments.

1. Introduction

The widespread availability of digital data and information technologies (IT) across all areas of human activity at the beginning of the 21st century has enabled their extensive application for various purposes. One prominent example is the use of machine learning (ML), especially ensemble and hybrid methods, to solve numerous practical classification problems that humans face in daily life, including applications in medicine [1], economics [2], education [3], transportation [4], and beyond. Another important example, when it comes to solving the problem discussed in this paper, is the possibility of using a synthetically generated dataset with suitable artificial intelligence (AI) tools, such as ChatGPT-4, from a large language model (LLM) type.

The authors propose a three-layer ensemble model that uses multi-criteria methods in the first layer, an ensemble of multiple ML algorithms of different types in an optimized asymmetric procedure in the second layer, and a voting method for the final decision in the third layer.

In proposing the model described in this paper, the authors had in mind two fundamental elements that determine the quality of the solution: the dataset used and the methodology applied [5]. Because of that, in the first layer of the model, the well-known Analytic Hierarchy Process (AHP) and Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) multi-criteria methods are used to check the usability of the synthetically generated dataset and further for additional layers of model determination of decision validity in the case of the considered multi-criteria problem having added model layers. In continuation of the proposed model in the second layer, the authors proposed a novel algorithm for determining the most important factors in the considered multi-criteria problem, which determines the best alternative. Namely, it is well known that the type of problem addressed in this paper can be formulated as a binary classification task, defined by two different outcomes of output in the considered problem that can be represented as Yes or No, 1 or 0, etc. The authors opted for a stacking ensemble model, which enhances accuracy and reduces overfitting from a methodological perspective; moreover, it applies to a wide range of predictors and effectively handles potential class imbalances within the dataset, which all distinguish the proposed model from those that we can find in the literature review. By adopting this approach, the authors developed a model that capitalizes on the strengths of two different types of methods included in the ensemble while mitigating their separate weaknesses. Ensemble analysis, regarded as an optimization process for selecting significant subsets from a broader set of influencing factors [6], can be interpreted as a method for determining premises for intelligent decision making [7]. While the literature contains studies that apply various multi-criteria decision-making (MCDM) methods, to assess factor importance in one decision-making knowledge driven process [8], as well as big number of hybrid ML and MCDM methods [9], such known approaches are beyond the scope of this paper because the subject of this paper is proposing an ensemble optimization procedure for forensic validity of the decision made, which uses proposed ensemble advantages of the knowledge-driven MCDM methodology from one side, to check the usability of the generated synthetic dataset and of the data-driven ML methodology, and from another side to optimize the procedure of determining important criteria and making a final decision. The third layer of the proposed model deals with determining the final decision using a voting method.

As we noticed, the main subject of this paper is the forensic validity of the decision made. With this in mind, the authors proposed one model that comprehensively addresses both aspects: dataset selection using the MCDM methodology for validating the usability of the generated synthetic dataset as an input condition and the application of ML as the core methodology for determining the most important criteria through asymmetric optimization and vote-based final decision making. It is well known from the literature that ML methodology is data driven, while MCDM methodology is knowledge driven, so their use together could have benefits since they have complementary advantages but also disadvantages. From four known approaches of common use, the authors implemented, in the proposed model, the second approach, which involves the application of MCDM methods first and then the integration of ML methods [9]. It is also known that each classification problem depends not only on the selected methodology but also on the selected dataset and types of input variables (categorical, numerical, or both types) and the prevalence of some classes. Because of this, the authors considered the possibility of using one type of stacking ensemble of ML as expedient because it is suitable for different classes of criterion types and prevalence and, thus, could be a possible solution to various problems [6]. And, in the end, it is also known that for the decision-making process, besides others and regarding the selection of handguns, various MCDM methods are available, such as AHP, TOPSIS, fuzzy logic [10], and Elimination and Choice Translating Reality (ELECTRE) [11], among others. To assess the impacts of different criteria and, in our considered problem, the handgun-related factors, whether quantitative or qualitative, various methodologies can be employed. These range from classical statistical analysis techniques, such as regression, discriminant, and factor analyses, to more modern MCDM such as large group decision making based on interval rough integrated cloud models [12] and modern ML algorithms that have gained prominence since the early 21st century, including classification algorithms, neural networks, and different ensembles [13].

The proposed ensemble methodology was chosen to solve the problem of handgun selection, applied here through a specific case study analyzing the forensic validity of the decision to adopt a particular type of pistol in the U.S. Army at the end of the 20th century. This analysis may be of practical use to military and police forces worldwide, as they often face similar challenges in real-time decision making regarding the selection of various types of weapons. Moreover, the model proposed in this paper provides a structured approach not only for making such decisions but also for verifying their correctness through data-driven analysis.

Namely, in the armament of various military and police formations, a wide range of weapons is encountered, from so-called light to heavy weapons, but the most commonly used are handguns, i.e., pistols. Determining the influence of various factors on the quality, particularly the shooting accuracy of handguns is important not only for ensuring their most effective use but also for making informed decisions when selecting among the available pistol models on the arms market to equip military or police units. Naturally, the choice of relevant factors may vary depending on the specific type and purpose of the formation. A comprehensive comparative analysis of handguns, both those currently in use and those planned for adoption by the U.S. Army, was provided by Jenkins and Lowrey [14], while an analysis of handgun selection for officers in the Yugoslav Army can be found in [15]. These factors are different types of related conditions [16,17], such as the following:

• Atmospheric variables (temperature, humidity, pressure, wind speed, light, …);
• Physical variables (target distance, trigger pull force, …);
• Biomechanical (grip stability, …);
• Behavioral variables (shooter experience, shooter heart rate, …).

We have addressed some of the most important of them: target distance, wind speed, shooter experience, grip stability, trigger pull force, light, heart rate, ammunition quality, temperature, humidity, and precision.

To assess the impact of the aforementioned handgun-related factors, whether quantitative or qualitative, various methodologies can be employed. These range from usually used modern MCDM as fuzzy and large group decision- making based on interval rough integrated cloud, classical statistical analysis techniques, such as regression, discriminant, and factor analysis, to more modern ML algorithms that have gained prominence since the early 21st century, including classification algorithms, neural networks, and others theirs integrations known as hybrid models [18,19].

The main goal of this paper is to explore the possibility of constructing an ensemble ML model capable of confirming or refuting the correctness of decisions regarding the selection of specific handgun types for use in military or police forces.

To achieve this goal, the authors conducted a study of the following:

• First, we examined a multi-layer model that integrates MCDM and ML methods. MCDM methods are used in beginning layer to provide to the model with necessary suitable dataset, and after that, we used an ensemble methodology integrating two widely used approaches, regression and filter-based feature selection with classification algorithms, into a single ensemble ML model. And on the last and third layer, a voting ensemble is applied for making the final decision. The proposed model is, in this way, practically designed as an asymmetric optimization procedure. The integration aims to leverage the strengths of each method to improve overall performance. Given the complexity of the problem and the wide array of available algorithms and integration strategies for ensemble modeling, the proposed model provides a flexible foundation for future extensions and refinements. According to the authors’ knowledge, a model combining modern ML techniques and MCDM in the proposed configuration for the forensic analysis of handgun selection has not previously been addressed in the existing literature.
• Second, the proposed methodology was evaluated through a case study involving the forensic assessment of the U.S. Army’s 1985 decision to adopt the Beretta 92 handgun in place of the previously used Colt 1911. To enhance the realism of the analysis, the Glock 17, the third most widely used handgun globally, was included in the evaluation [18]. Due to the impracticality of conducting real-world experiments and the lack of publicly available datasets on factors affecting handgun accuracy, the authors utilized synthetic data generated using ChatGPT-4, one of the most prominent AI-based text generation tools, for model evaluation.

The obtained results confirmed the correctness of the historical decision. In support of the research objectives, the authors formulated and addressed two key hypotheses:

• First (conditional) hypothesis: It is possible to use synthetically generated data from the ChatGPT-4 AI tool for this type of forensic analysis.
• Second (final) hypothesis: It is possible to construct a novel ensemble model that solves the problem of handgun type selection in a more effective manner than existing state-of-the-art approaches.

To achieve the stated objective, the remainder of this manuscript is organized into the following sections: After the Introduction presented in the Section 1, the Section 2, ‘Materials and Methods’, describes the methodologies employed in constructing the proposed model. This section includes a comprehensive review of the model in the Section 2.1 and an overview of the data used in the Section 2.2. The Section 3, ‘Proposed Solution’, presents the novel model developed to address the defined problem. The Section 4, ‘Results and Findings’, presents and discusses the results obtained from applying the proposed model to the case study, including an analysis of its performance. Finally, the Section 5, ‘Conclusions’, summarizes the main contributions of the research and outlines directions for future work aimed at developing more efficient and accurate solutions to the problem explored in this study.

2. Materials and Methods

As mentioned in the previous section, the current trend in developing solutions for identifying the influence of individual factors on various processes as well as for supporting intelligent decision making across different domains of human life is increasingly centered around the use of advanced ML, especially ensemble algorithms and hybrid methodologies [19,20], along with the traditionally most frequently used MCDM algorithms, which are also more and more advanced oriented, especially on fuzzy logic and large group decision making with a roughly integrated asymmetric cloud model under multi-granularity linguistic environment. Also, we noticed that the use of synthetically generated data from different AI tools is a trend in the considered type of forensics but also in other analyses when real-world data is hard or impossible to obtain. Namely, the datasets are crucial to evaluating the reproducibility of the proposed methodology, and because of that, when it cannot be generated as real-world data, we use the possibility of creating a synthetic dataset.

These approaches also facilitate the development of ensemble models for intelligent forensic analysis of past decisions [21,22]. Following this trend, the authors of this paper proposed a novel three-layer model for handgun type selection forensics, consisting of the following core components, as illustrated in Figure 1:

• The Input Layer, which handles essential dataset preparation and validation for its suitability in solving the given problem, using MCDM methodology;
• The Base Layer, which integrates two widely adopted approaches—classical regression techniques and modern ML-based feature selection—into a unified ensemble model through an asymmetric optimization procedure;
• The Output Layer, which applies a simple voting mechanism to determine the final decision based on the number of shared significant factors across the different considered handgun type.

To evaluate the proposed model, the authors conducted a case study focused on the forensic analysis of the U.S. Army’s decision, made at the end of the 20th century, to replace the Colt 1911 pistol with the Beretta 92 in 1985. Namely, it is well known that all armies—specifically their educational institutions and units—include a discipline called ‘weapons knowledge with shooting instruction’. One of the key reasons for studying this subject is to evaluate the potential for new tactical and technical requirements for weapons that may be used in the future. This involves considering possibilities from a constructive, technological, or techno-economic perspective. Given that this paper analyzes handguns—which are widely used in terms of quantity—as one of the tools for carrying out state functions, it is of paramount importance to apply all relevant models to support sound decision making regarding innovation or replacement with a new type or model of this technical asset used by the army and police. If the techno-economic analysis of the innovation supports the tactical and technical requirements satisfied by the new (replacement) weapon—derived from a comparison of current usage, the potential of new materials, modern production and maintenance technologies, and projections of future operational environments—then it becomes imperative to proceed with the replacement. Due to the unavailability of real data that informed the original, already mentioned decision and the lack of relevant datasets on prominent open data platforms such as Kaggle, Data.gov, and the UCI Machine Learning Repository, the authors opted to generate synthetic data using the ChatGPT-4 AI tool. This approach was intended to address the data scarcity by producing a dataset that reflects real-world-like scenarios [23,24].

Based on the general functional block diagram of the proposed model, the Methods subsection focuses on the methods used in the Base Layer, where a novel ensemble ML model is introduced for determining the significance of various factors influencing pistol shooting success. This subsection also includes the description of methods used in the Output Layer, which uses a simple voting-based stacking method to make the final decision. Practically, this subsection addresses the methodologies included in the proposed model, which help to examine the second (final) hypothesis stated in the Introduction, which asserts that it is possible to construct a novel ensemble model that effectively solves the problem of handgun type selection forensics. Meanwhile, the Materials subsection provides a description of the synthetic dataset used, along with details on the preprocessing steps necessary to prepare the data for use in the proposed model. This subsection also explains the application of the AHP and TOPSIS methodologies used to evaluate the usability of the preprocessed dataset. Practically, the descriptions of the used synthetic dataset as well as the decision-making methodology in this subsection are necessary to check the first (conditional) hypothesis presented in the Introduction, which states that the use of synthetic data generated by ChatGPT-4 is valid if the outcomes based on this data (i.e., pistol type selection) match the actual decisions made by the U.S. Army.

2.1. Methods

The ML algorithms employed by the authors to address the problem of handgun type selection forensics are designed to induce logical patterns that can later be interpreted and applied by humans to solve various tasks associated with the problem defined by the extracted dataset. The validity of the learned knowledge is assessed by splitting the dataset into a training set and a test set, where the performance of the learning process is measured using predictive accuracy (the proportion of correctly classified instances on previously unseen data).

To address the identified task, the authors propose an ensemble ML model (illustrated in Figure 1) that integrates several types of learners—binary regression, feature selection algorithms, and classification models—into a cohesive framework. This ensemble strategy harnesses the complementary strengths of each component to achieve enhanced performance compared to currently known state-of-the-art models.

In the subsections that follow, the authors briefly present the methodologies incorporated in the proposed ensemble model, as depicted in Figure 1. As previously discussed, this hybrid model combines the MCDM methodology at the first Input Layer with ML methodologies of logistic regression, feature selection, and classification algorithms at the second Base Layer and the voting algorithm at the third Output Layer, with all of them organized within a multi-layered ensemble architecture group.

2.1.1. Logistic (Binary) Regression

In classification, as a widely used ML technique, it is often necessary to develop probabilistic classifiers, models that, in addition to assigning an instance to the most likely class, also provide the probability of belonging to that class. In the binary classification context addressed in this paper (i.e., hit or miss), this involves calculating the probability of each outcome and visualizing the results using separate calibration plots for each class. A probabilistic classifier is considered well calibrated when the predicted probabilities closely match the actual observed frequencies.

This concept of model calibration has been widely adopted by researchers working on problems similar to the one considered in this study. One notable example is univariate calibration using logistic regression in binary classification settings [25].

In general, binary logistic regression models the relationship between categorical dependent variables and one or more independent variables, which can be continuous, binary, or categorical. Among several logistic regression types, the authors employed the Enter method for binary regression in this study. The primary objective of logistic regression is to construct a model that accurately describes the relationship between the outcome variable and the set of predictor variables.

The one more possible form of binary regression is as in (1):

$$\mathrm{o}\mathrm{d}\mathrm{d}\mathrm{s}={\displaystyle \frac{\mathrm{p}}{1-\mathrm{p}}}={\mathrm{e}}^{{\mathrm{b}}_0}·{\mathrm{e}}^{{\mathrm{b}}_1{\mathrm{X}}_1}·{\mathrm{e}}^{{\mathrm{b}}_2{\mathrm{X}}_2}·\dots ·{\mathrm{e}}^{{\mathrm{b}}_{\mathrm{k}}{\mathrm{X}}_{\mathrm{k}}}$$

(1)

From Formula (1), it is evident that when a variable Xi increases by one unit and all other parameters are unchanged, then the odds changes directly proportional by a parameter ${\mathrm{e}}^{\wedge {\mathrm{b}}_{\mathrm{i}}}-1$ (for ${\mathrm{b}}_{\mathrm{i}}>0$ increases; for ${\mathrm{b}}_{\mathrm{i}}<0$ decreases) as it is given in Equation (2).

$${\mathrm{e}}^{{\mathrm{b}}_{\mathrm{i}}(1+{\mathrm{X}}_{\mathrm{i}})}-{\mathrm{e}}^{{\mathrm{b}}_{\mathrm{i}}{\mathrm{X}}_{\mathrm{i}}}={\mathrm{e}}^{{\mathrm{b}}_{\mathrm{i}}{\mathrm{X}}_{\mathrm{i}}}({\mathrm{e}}^{{\mathrm{b}}_{\mathrm{i}}}-1)$$

(2)

So, the calculated factor ${\mathrm{e}}^{{\mathrm{b}}_{\mathrm{i}}}$ is the odds ratio (O.R.) of suitable independent variable ${\mathrm{X}}_{\mathrm{i}}$, which gives the relative amount by which the odds of the outcome decrease ($\mathrm{O}.\mathrm{R}.<1$) or increase ($\mathrm{O}.\mathrm{R}.>1$) when the independent variable increases by one unit.

The authors selected IBM SPSS version 17, one of the most widely used statistical software tools, for conducting the binary regression analysis [26].

2.1.2. Classification Algorithms

Classification methodology is a widely used technique in ML that supports experts across various domains in extracting knowledge from large volumes of data. Classification algorithms belong to the category of supervised ML techniques and are primarily used for predictive modeling. They require labeled instances, where each object is associated with a specific class (attribute), and the goal is to predict the value of this categorical class using the values of other predictor attributes. Some of the most well-known classification methods include decision tree-based algorithms (e.g., ID3, C4.5, and Random Tree), regression-based algorithms (i.e., Linear Regression and logistic regression), Bayesian classifiers (i.e., BayesNet and Naive Bayes), neural networks (i.e., Support Vector Machine and Single/Multi-Layer Perceptron), and association rule-based classifiers (i.e., JRip and PART), among others [27,28,29].

For the problem addressed in this paper, the authors applied a binary classification approach in their proposed ensemble model, classifying data into two categories: positive (true, shooting hit) and negative (false, shooting miss).

The outcomes of the predictions are summarized using a confusion matrix, as shown in

Table 1. The confusion matrix for the two-class classifier.

		Predicted Class
		Positive	Negative
Actual class	Positive	TP (true positive)	FN (false negative)
	Negative	FP (false positive)	TN (true negative)

.

The number of members in the considered set shown in the Table 1 is the sum of positive and negative cases and will be classified with notation N, i.e., $\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}+\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{N}=\mathrm{N}$. All results that are presented in Table 1, for the considered case of a two-class classifier, can be given for most important measures of classification accuracy, precision, recall, and F1 with Formulas (3)–(6), which are described in [28,30,31]:

$$\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}=\left(\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}\right)/\mathrm{N}$$

(3)

$$\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}=\mathrm{T}\mathrm{P}/\left(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}\right)$$

(4)

$$\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}=\mathrm{T}\mathrm{P}/\left(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}\right)$$

(5)

$$\mathrm{F}1 \mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}=2\times (\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\times \mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l})/(\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}+\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l})$$

(6)

The Receiver Operating Characteristic (ROC) curve presents a binary classifier’s performance that is obtained comparing the relationship between sensitivity and specificity for every possible cut-off. The ROC curve is a graph with the x-axis showing 1 − specificity (=false positive fraction = FP/(FP + TN)) and the y-axis showing sensitivity (=true positive fraction = TP/(TP + FN)). The Area Under the Curve ROC (AUCROC) is the most commonly used metric to assess the diagnostic accuracy of a model. AUCROC values greater than 60%mm are considered acceptable, as they indicate a good classification performance. It is important to note that, as established in the literature, when the dataset is imbalanced, the Precision–Recall Curve (PRC) and its corresponding Area Under the Curve PRC (AUCPRC) are preferred over the AUCROC for evaluating model performance [31].

In the proposed model, the authors employed some of the most widely used classification algorithms, each from a different methodological group as categorized in one of the most popular tools for ML, Weka version 3.8.6 [32]. Specifically, they used

• AdaBoost (AB) from the Meta group [33];
• PART from the Rules group [34];
• Random Forest (RF) from the Trees group [35].

2.1.3. Future Selection Techniques

The dimensionality of the dataset used in various ML classification methods has a significant impact on the quality of results. It is well known that dimensionality reduction can lead to improved performance in solving complex problems. Selecting the most significant parameters (factors, criteria, etc.) to form an optimal sub-dataset prior to classification helps achieve better results by reducing noise, minimizing overfitting, and shortening training time [36]. The evaluation process applies various effective measures for eliminating redundant and irrelevant features, such as consistency measures [37] and correlation measures [38].

Feature selection methods are typically categorized into three main groups [39]:

• Filter methods, such as Relief, CorrelationAttributeEval, InfoGain, etc.;
• Wrapper methods, such as Greedy Stepwise, BestFirst, Genetic Search, etc.;
• Embedded methods, which combine the strengths of filters and wrappers, for example, Ridge Regression and decision tree-based algorithms like NBTree.

In the proposed model presented in this paper, the first two groups—filter and wrapper methods—are used. Therefore, a brief description of these two groups is provided in the subsequent paragraphs of this section. Before this short description, it is important to note that while wrapper methods often provide better performance, they are typically more time consuming. Therefore, to balance the strengths and weaknesses of both approaches, the authors chose to use two filter methods and one wrapper method in the proposed asymmetric model.

• Filter methods

For a given dataset, filter methods initiate the search process by defining an initial subset, which may be an empty set, a randomly selected subset, or the full feature set. The algorithm then explores the feature space using a defined search strategy. Each newly generated subset is evaluated using an independent evaluation measure and compared to the previously best-performing subset. If it performs better, it becomes the new best subset. This process continues until a predefined stopping criterion is satisfied. The final outcome of the method is the most recently identified best-performing subset.

Different combinations of search strategies and evaluation measures allow for the development of various algorithms within the filter model framework [40,41,42].

The software tool Weka, which offers built-in functionality for feature selection, was used to reduce the volume of data through the application of multiple algorithms. Because of its flexibility and reliability, Weka was employed to evaluate the proposed model on the selected case study. In practice, the application of these methods enabled the identification of significant factors influencing shooting success (i.e., a hit) across three different pistol types. This process also facilitated the development of a prediction model using the same methodology as described earlier for logistic regression.

For the proposed model, the authors used the following two filter-based feature selection algorithms: Relief and ReliefF algorithm and CorrelationAttributeEval algorithm.

• Wrapper methods

This group of ML feature selection methods relies on suitable modeling algorithms to evaluate subsets of attributes based on how well they support classification or prediction. Such procedures are computationally intensive, primarily because the ML algorithm must be executed repeatedly. Evaluating the model’s performance for each subset becomes increasingly demanding, especially as the number of possible subsets grows exponentially with the number of attributes. To address this complexity, various search strategies are employed, most notably those based on greedy algorithms, for which the general working principle is illustrated in Algorithm 1 [43].

The classification frameworks [44] in which wrapper methods are applied can be categorized based on the attribute search methodology used. They are divided into two groups: randomized methods, which rely on stochastic search approaches, and deterministic wrapper methods.

Algorithm 1: The greedy search technique

1. The solution set with suitable answers is empty at the beginning.  2. In each step, an item is added to the set that represents the solution, continuing until a final solution is reached.  3. The current item is kept only if the solution set is feasible.  4. Else, the item is rejected and is never considered again.

The deterministic methods are further divided into subgroups, one of which employs a complete attribute space search using a sequential strategy. These approaches are time consuming but tend to yield the most accurate results. Due to their reliability, sequential search techniques are among the most commonly used in wrapper algorithms. For this reason, the authors selected the GreedyStepwise algorithm from this subgroup to be included in the proposed model.

2.1.4. Ensemble Methods

It is well established in the literature that ML ensemble methods are based on the principle that combining algorithms of different types can produce better results than any individual algorithm alone, as well as better performance than many existing state-of-the-art models. The most commonly used taxonomy of ensemble methods are as follows:

• Bootstrap (Bagging);
• Boosting;
• Voting;
• Stacking.

Ensemble learning can be described in short, as found in the literature [45]:

• Ensemble learning combines multiple ML and other types of algorithms into a single unified model to improve overall performance. Bagging primarily aims to reduce variance, boosting focuses on minimizing bias, while stacking seeks to enhance classification or prediction accuracy. For these reasons, the authors applied stacking in their proposed model to address the handgun type selection forensics problem, formulating it as a binary classification task.
• Ensemble learning offers several key advantages, including improved accuracy, interpretability, robustness, and model combination.
• It is important to note that in many real-world problems—including the case study presented in this paper—real-time computation is not a strict constraint. Moreover, the continuous advancement of computing technologies enables increasingly faster processing, making the additional computational demands of ensemble models less problematic.

• Voting

Voting is a widely used ensemble learning technique, particularly effective for classification tasks, which is how the authors framed the problem addressed in this paper. However, voting can also be applied to regression problems, as illustrated in Figure 2.

In a voting ensemble, each individual algorithm within the ensemble independently produces a classification or prediction for the input dataset [46]. The final decision is then determined by combining these individual outputs using one of several possible voting schemes:

• Majority Voting: Each model votes for a class label, and the class receiving the majority of votes is selected as the final classification or prediction. This is the approach used by the authors to make the final decision in their model. In the event of a tie (i.e., equal number of votes), a tie-breaking rule is applied, such as selecting the factor with the higher associated probability.
• Weighted Voting: Each model’s vote is assigned a weight based on its individual performance, giving more influence to stronger models.
• Soft Voting: This scheme is used when models provide probability estimates or confidence scores for each class label rather than discrete class predictions.

In the third (output) layer of the proposed model, the authors implemented majority voting to finalize the decision.

They compared the number of significant factors that matched across the three considered types of pistols (or m in the general case). To determine which of the other two (m − 1 in the general case) types should replace a given pistol type, they selected the one with the greatest number of identical significant factors, as previously identified in the second (base) layer of the model (see Figure 2).

• Stacking

The stacking type of the ensemble algorithm, selected by the authors for the second (base) layer of the proposed model—designed to determine the significant factors contributing to successful shooting and to evaluate each of the three selected pistols—involves training multiple ML algorithms and then combining their outputs into a unified predictive or classification model (Figure 3).

This stacking approach typically demonstrates better performance than any of its individual component algorithms, including those considered state of the art for similar problems [47]. Stacking is applicable to both supervised and unsupervised learning tasks; in the presented case study, it is applied in a supervised learning context.

As illustrated in Figure 3, each algorithm within the ensemble is first trained on the available dataset. Subsequently, a meta-learner (combiner algorithm) is trained to make the final classification or prediction based on the outputs of the individual learners. To reduce the risk of overfitting, cross-validation is generally used during the training phase.

Although logistic regression is commonly used as the combiner algorithm in many stacking implementations, the proposed model takes a different approach: it uses classification algorithms as the combiner, while the base learners consist of a binary regression model and several feature selection algorithms. This integration enables more robust identification of critical factors influencing shooting success across multiple pistol types.

2.2. Materials

The determination of the weights of the considered factors influencing pistol shooting accuracy in this study is based on synthetic data generated using ChatGPT-4, an LLM capable of independently analyzing and deriving insights from complex datasets. Recognizing that ChatGPT-4 can only generate data based on patterns learned during its training—and thus may not always reflect real-world distributions or accuracy—the authors designed a real-world use-case scenario comprising a set of expected inputs and outputs to guide the generation of a dataset suitable for the case study [23,24].

The resulting dataset is provided as Supplementary Materials under the following name:

ChatGPTsyntheticGeneratedDatasetHandgunShooting-Colt1911Bereta92Glock17.xls.

To be used with the proposed model (whose functional block diagram is shown in Figure 1), this dataset was processed into three separate datasets, one for each type of pistol, enabling model-specific analysis.

These individual datasets are also included as Supplementary Materials, named as follows:

• ChatGPTsyntheticGeneratedDatasetHandgunShooting-Colt1911.xls;
• ChatGPTsyntheticGeneratedDatasetHandgunShooting-Bereta92.xls;
• ChatGPTsyntheticGeneratedDatasetHandgunShooting-Glock17.xls.

All four Supplementary Files are accessible on the corresponding author’s official website at:

https://it.fdb.edu.rs/wp-content/uploads/2023/06/Current-scientific-work.zip accessed on 1 July 2025.

To evaluate the quality and usability of the synthetically generated dataset for testing the proposed model in solving the considered problem, the authors applied the TOPSIS decision-making method. This was preceded by a critical step: validating whether the decision obtained using the synthetic data matched the historical decision made by the U.S. Army, based on its real-world dataset. This consistency served as the foundation for accepting the dataset’s relevance and suitability for further analysis.

2.2.1. Generation and Preprocessing of the Required Dataset

Considering given the practical unavailability of the original dataset used by the U.S. Army authority to decide on the selection of small arms based on shooting accuracy as one of the core problems that is considered in this paper, the authors opted to use, within their proposed model, synthesized data generated by ChatGPT-4, which belongs to the group of LLMs.

This synthetic dataset refers to artificially generated data that mimics the statistical patterns of real-world data but does not contain actual historical values. Instead, it is produced using algorithmic simulations that replicate realistic distributions and dependencies. Despite lacking real instances, such data can be effectively used for training, testing, and validating ML models, especially in cases like the one in this paper, where real-world data is limited or unavailable [48].

The dataset used to evaluate the novel ensemble model, as presented in this case study, is attached to this paper as Supplementary Materials and is available at:

https://it.fdb.edu.rs/wp-content/uploads/2023/04/ChatGPTsyntheticGeneratedDataset.zip accessed on 1 July 2025.

This dataset was obtained by prompting ChatGPT-4 with the following query:

“I am looking for a database of shooting results using three different types of pistols, depending on 11 factors, with a total of 1000 entries. It must refer to exactly three specific, arbitrarily chosen types of pistols and exactly eleven arbitrarily chosen factors that influence the outcome of the shooting. The table needs to include, in the last column, the success of shooting—i.e., hit or miss.”

The resulting master dataset and its three derived subsets, each corresponding to a specific pistol type, are now ready for preprocessing. This step forms the first phase of the first layer in the proposed three-layer ensemble model (see Figure 1). The data is prepared for the application of binary regression and classification algorithms, which will be used in the second layer of the model.

The following Excel files are included as Supplementary Materials:

• ChatGPTsyntheticGeneratedDatasetHandgunShooing-Colt1911Bereta92Glock17.xls;
• ChatGPTsyntheticGeneratedDatasetHandgunShooting-Colt1911.xls;
• ChatGPTsyntheticGeneratedDatasetHandgunShooting-Bereta92.xls;
• ChatGPTsyntheticGeneratedDatasetHandgunShooting-Glock17.xls.

2.2.2. MCDM Evaluation of the Synthetic Generated Data to Solve the Considered Problem

To evaluate the suitability of the generated dataset for solving the considered problem, the authors used a free online TOPSIS tool [49] to determine the ranking order of the three considered pistol types. The goal was to verify whether the results obtained using the synthetically generated data matched those based on real-world data, specifically, the decision made by the U.S. Army.

As a preparatory step, the authors first applied the AHP method using a freely available AHP tool [50] to assess the relative importance of the individual factors. This assessment was based on the complete (non-reduced) synthesized dataset containing all three pistol types:

ChatGPTsyntheticGeneratedDatasetHandgunShooting-Colt1911Bereta92Glock17.xls.

In addition to the 11 factors originally included in the dataset, the authors incorporated a “price” factor—which was not part of the synthetic data—by using real-world pricing information and expert opinion to estimate its relative importance. This allowed for a more comprehensive analysis.

With the weights of all relevant criteria determined, the authors were able to construct a normalized multi-criteria decision matrix, which served as the input for the TOPSIS tool. This matrix was then used to evaluate the applicability of the synthetic dataset by checking whether it would produce the same decision—i.e., selecting the same optimal pistol type—as was made historically by the U.S. Army.

• AHP

The essence of the AHP method can be summarized as follows: it structures a complex decision-making problem into a hierarchy that may involve multiple criteria, several alternatives, and potentially multiple decision makers (i.e., group decision making), distributed across several hierarchical levels. The method determines the weighting coefficients for both criteria and alternatives at each level, ultimately leading to the formation of a final ranking of alternatives [51].

According to linear algebra theory, any inconsistency or deviation in the values of the decision matrix coefficients leads to corresponding deviations in the matrix’s eigenvalues. Therefore, the objective is to find an eigenvalue that is approximately equal to the trace of the matrix (denoted by n), as this condition indicates minimal judgment errors made by the decision maker. The eigenvalue that satisfies this condition is the largest eigenvalue, and we mark it as ${\lambda }_{\max }$. The consistency index (CI) is a measure of deviation ${\lambda }_{\max }$ from n and is calculated according to Formula (7):

$$CI={\displaystyle \frac{{\lambda }_{\max }-n}{n-1}}$$

(7)

The AHP method considers an inconsistency of less than 10% acceptable, i.e., for a CI value of less than 0.1.

• TOPSIS

The problem of multi-criteria analysis with m alternatives and n criteria can also be represented as a geometric system of m points in an n-dimensional space. Starting from this fact, Hwang and Yoon [52] developed the TOPSIS method, based on the opinion that the optimal alternative, i.e., the point that represents it, should have the smallest distance from the positive-ideal (di+) and the largest distance from the negative-ideal (di−) solutions in the geometric sense. But the problem is that one of these possibilities does not exclude the other. The TOPSIS method overcomes the mentioned problem by defining the proximity index or relative proximity (Ci) to the positive-ideal solution, combining the proximity of the positive-ideal and the distance of the negative-ideal solutions from the observed alternative. The alternative with the highest index of closeness to the positive-ideal solution is chosen as optimal.

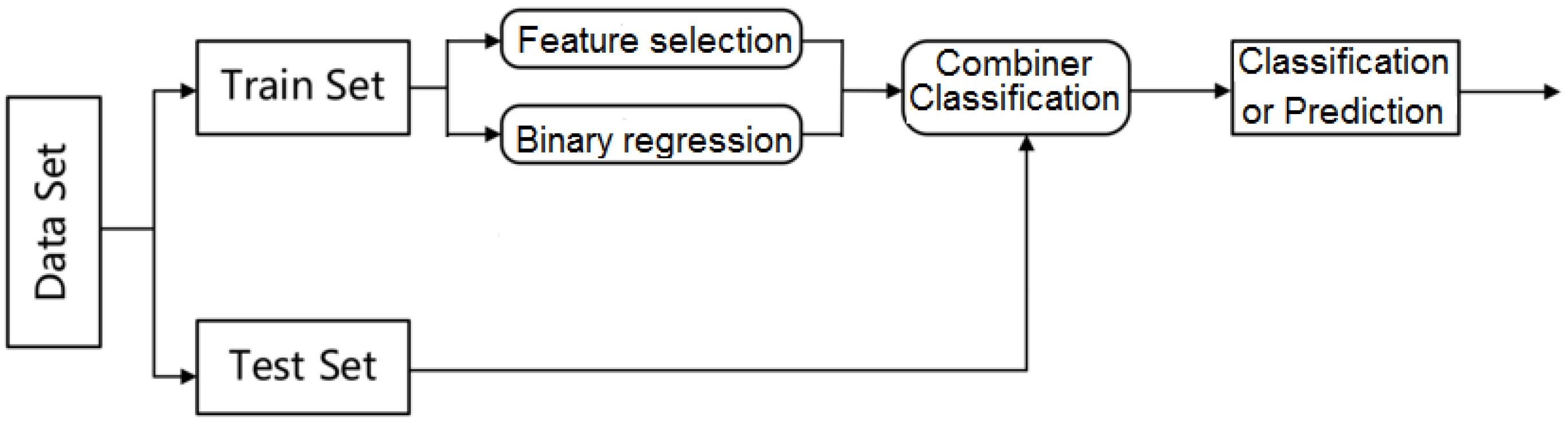
3. Proposed Ensemble Method for Handgun Type Selection Forensics

To address the problem outlined in this paper, following the necessary preprocessing of the synthetically generated dataset—including the evaluation of its applicability as an AI-generated dataset—the authors proceeded according to the block diagram of the proposed model presented in Figure 1, specifically its first part, the Input Layer. Subsequently, the authors introduce a novel ensemble algorithm, described in Algorithm 2 and illustrated through a block diagram in Figure 4, which constitutes the second part, the Base Layer of the proposed model (as shown in Figure 1). This layer is responsible for solving the sub-problem of identifying significant factors that influence shooting accuracy across three (or more, in general m) selected types of pistols.

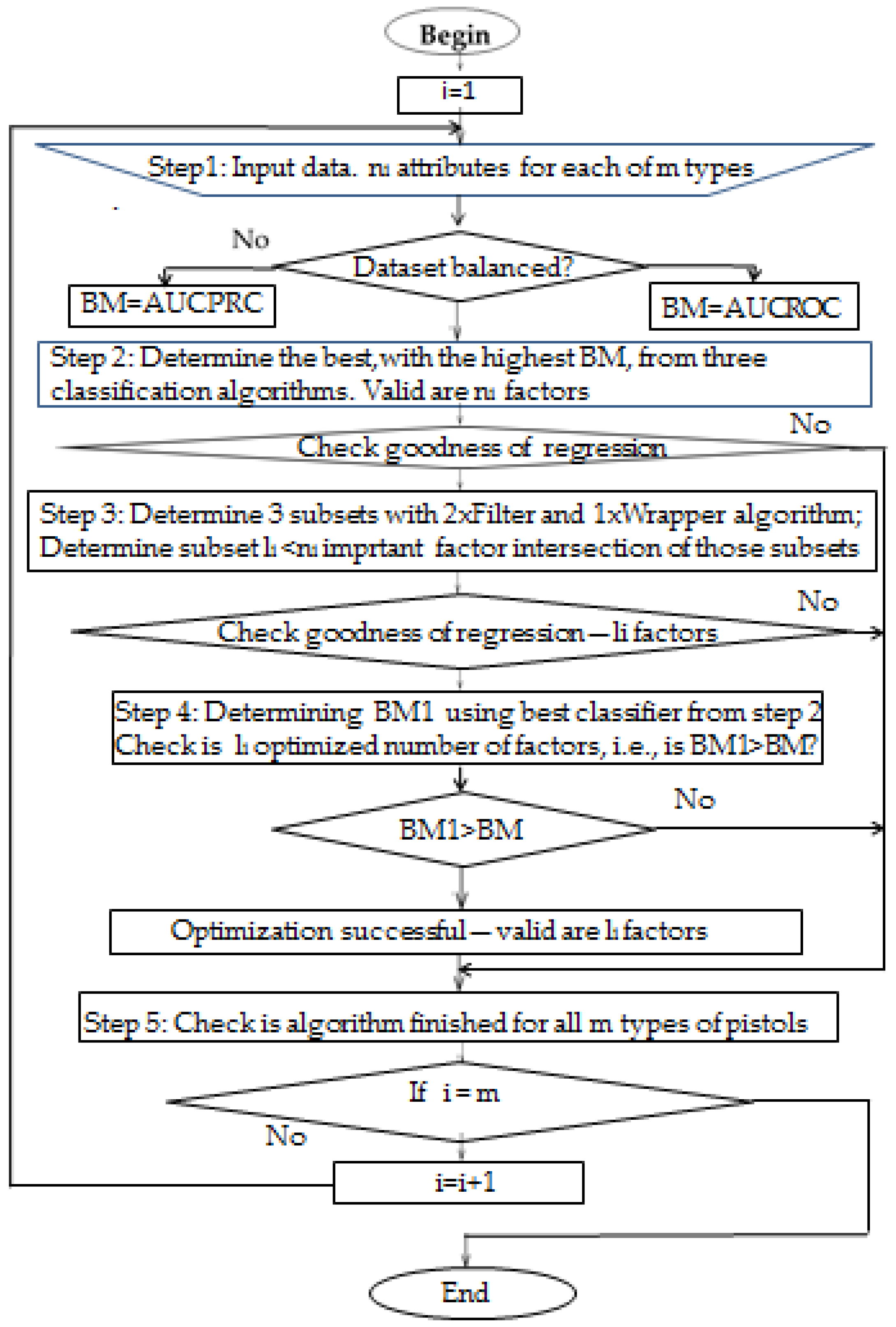
Algorithm 2: Determining biomechanical and atmospheric predictors

Dataset with number of valid $n_i$ attributes; $i=1-m$, m number of types of pistols  * 1. Input preprocessed verified data for one of m types of pistols;  Check balance of uploaded data; IF dataset is balanced BM = AUCROC; GO TO next step  ELSE BM = AUCPRC; GO TO next step  ** 2. Determine best from three classification algorithms AB, PART and RF algorithm which has the highest value of BM.  Perform regression with $n_i$ attributes; check regression goodness;  IF regression OK (Hosmer–Lemeshow), number of attributes is $n_i$;  GO TO next step ELSE GO TO step 5  *** 3. Implement Feature selection with two filter and one wrapper algorithm;  using intersection of obtained results determine $l_i<n_i$ factors;  check regression goodness with $l_i$ factors;  IF regression OK number of attributes is $l_i$; GO TO next step  ELSE number of attributes is $n_i$; GO TO step 5  **** 4. Determine BM1 with best classifier determined in step 2; check $BM1>BM$;  IF Yes number of attributes is $l_i$; GO TO next step  ELSE number of attributes is $n_i$; GO TO step 5  ***** 5. Check is algorithm finished for all types of pistols;  IF $\mathrm{i} < \mathrm{m}$; GO TO step 1 ELSE GO TO end

• * The input consists of already preprocessed and validated data, where for each of the m types of pistols, n_i attributes influencing shooting success are considered. The dataset is then checked for class balance. If the dataset is balanced, the primary performance metric for evaluating the proposed model will be BM = AUC-ROC; otherwise, BM = AUC-PRC will be used.
• ** A binary logistic regression is performed using 11 biomechanical attributes ($n_i$ in the general case) as predictors. The dependent variable represents the binary outcome, either a hit or a miss. If any predictors exhibit unacceptable levels of multicollinearity, they must be excluded from the proposed model. A classification table is used to evaluate the model’s classification accuracy and to compare it against the accuracy expected from random classification. To assess the proportion of variance explained by the model, the Cox–Snell R Square and Nagelkerke R Square statistics are calculated. Finally, the Hosmer and Lemeshow test is applied as the key indicator of the model’s goodness of fit. If the test of goodness is positive, the algorithm continues with the next step, but if opposite, it continues with step 5 without optimization of the number of factors: they remain the same $n_i$ factors. The authors propose that the classification performance of the model be evaluated using the AUC-ROC or AUC-PRC, depending on whether the dataset is balanced, in accordance with standard measures for binary classification problems [30,31]. To determine the best-performing classification algorithm, three algorithms representing distinct classification paradigms—Random Forest (from the Decision Tree group), PART (from the Rule-based group), and AdaBoost (from the Meta-learning group)—as provided in the WEKA tool, are initially tested. The best-performing algorithm among these will be selected for use in Step 4, which involves attribute selection using several feature selection methods to identify the most relevant predictors.
• *** Using three feature selection algorithms—two from the filter group (ReliefF and CorrelationEval) and one from the wrapper group algorithms (GreedyStepwise)—attribute selection is performed. The intersection operation is applied to the three resulting sets obtained from each of these feature selection methods to identify the common attributes. At the end of this step, the quality of the selected attribute subset is evaluated using binary logistic regression, as described in Step 2. The regression model is now constructed with $l_i<n_i$ predictors, where $l_i$ is the number of attributes retained after selection. Model evaluation is performed using a classification table, Cox–Snell R Square, Nagelkerke R Square, and the Hosmer and Lemeshow test, as previously explained. If the evaluation confirms the adequacy of the reduced model, and if the check of goodness of regression is OK, the procedure continues using the optimized subset of $l_i$ attributes. Otherwise, the process terminates with the original $n_i$ attributes retained in the model.
• **** The value of the performance measure BM, defined as in Step 1 and now denoted as BM₁, is determined using the most effective classifier identified in Step 2 of this algorithm. We check if $BM1>BM$ and if yes, an optimized subset of factors is $l_i$, and in the opposite case, the optimized subset is of $n_i$ attributes.
• ***** In the final step of the proposed algorithm, it is checked whether all three datasets (or m datasets in the general case) corresponding to the considered types of pistols have been processed. If this condition is met, the algorithm terminates; otherwise, it returns to Step 1 and continues the procedure.

Figure 4. Proposed stacking ensemble method for determination significant factors in handgun type selection forensics.

Figure 4. Proposed stacking ensemble method for determination significant factors in handgun type selection forensics.

To complete the solution of the problem addressed in this paper, following the successful execution of the first and second parts, the third part—the Output Layer of the proposed model, as shown in Figure 1—is applied. In this final step, a voting approach is used to make the forensic decision regarding pistol type selection. The selected pistol type is determined based on which of the m considered pistol types shares the greatest number of significant factors with the identified optimal set.

4. Results and Findings

The proposed model was evaluated through a case study involving the forensic analysis of the decision made by the U.S. Army in 1985 to adopt the Beretta 92 handgun, replacing the previously used Colt 1911.

To enhance the realism of the analysis, the Glock 17, the third most widely used pistol globally, was also included in the evaluation.

Given the impossibility of conducting real-world experiments and the lack of publicly available datasets on factors influencing handgun shooting accuracy, the authors used synthetically generated data produced by the ChatGPT-4 LLM.

4.1. First Layer of the Proposed Model: Checking the Usability of the Synthetic Generated Dataset

As described in the introduction to Section 2 (Materials and Methods), the advancement of modern IT, particularly machine ML, enables the development of ensemble models for intelligent analysis—including forensic analysis—of previously made decisions, which is the focus of this paper. Leveraging this approach, the authors propose a novel three-layer model for handgun type selection forensics, composed of three fundamental parts—the Input Layer, Base Layer, and Output Layer—as illustrated in Figure 1.

To evaluate the proposed model, the authors conducted a case study focused on the forensic analysis of the U.S. Army’s decision, made in 1985, to replace the Colt 1911 with the Beretta 92 as its standard-issue pistol. As previously explained in Section 2.2 Materials, due to the unavailability of the actual data that informed the original decision as well as the absence of relevant datasets on major open data platforms, the authors opted to generate synthetic data using the ChatGPT-4 AI tool.

This approach was adopted to address the data scarcity in a manner that reflects realistic scenarios.

The data was created in response to the following prompt:

“I am looking for a database of shooting results using three different types of pistols, depending on 11 factors, with a total of 1000 entries. It must refer to exactly three specific, arbitrarily chosen types of pistols and exactly eleven arbitrarily chosen factors that influence the outcome of the shooting. The table needs to include in the last column, success of shooting, i.e., hit or miss”. A synthetic dataset was successfully generated, enabling the implementation and evaluation of the proposed model.

The process began with the execution of the Input Layer, as defined in the first step of the model. The AHP was applied to determine the weights of the 11 factors influencing shooting success for the three considered pistol types.

The results of this analysis are presented in

Table 2. Using AHP for determination of importance of factors in considered problem.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13	Weights
Distance_to_Target/C1	1	1	7/5	7/3	7/3	7/3	7/5	7/5	7	7	7/9	1	7/9	0.107
Wind_Speed/C2		1	7/5	7/3	7/3	7/3	7/5	7/5	7	7	7/9	1	7/9	0.107
Shooter_Experience/C3			1	5/3	5/3	5/3	1	1	5	5	5/9	5/7	5/9	0.076
Grip_Stability/C4				1	1	1	3/5	3/5	3	3	3/9	3/7	3/9	0.046
Trigger_Pull_Force/C5					1	1	3/5	3/5	3	3	3/9	3/7	3/9	0.046
Light_Conditions/C6						1	3/5	3/5	3	3	3/9	3/7	3/9	0.046
Heart_Rate/C7							1	1	5	5	5/9	5/7	5/9	0.076
Ammo_Quality/C8								1	5	5	5/9	5/7	5/9	0.076
Temperature/C9									1	1	1/9	1/7	1/9	0.015
Humidity/C10										1	1/9	1/7	1/9	0.015
Precision/C11											1	9/7	1	0.138
Outcome/C12												1	7/9	0.107
Price/C13													1	0.138

.

By checking the consistency coefficient according to Equation (7), a value of CI = 0 was obtained, confirming the reliability of the conducted AHP analysis. It is important to note that in this first step of the Input Layer of the proposed model, the generated dataset was also divided into separate subsets—one for each of the considered pistol types—in preparation for use in the next Base Layer of the model.

In the second step of this Input Layer, based on the results obtained in the previous step, an evaluation of the usability of the synthetically generated data was conducted. This was achieved by applying the TOPSIS method and performing a multi-criteria analysis to determine the ranking of the three considered pistol types, as presented in

Table 3. The multi-criteria decision matrix for the evaluation of the suitability of the generated data.

	1. Alternative Colt1911	2. Alternative Bereta92	3. Alternative Glock17	Weights
Distance_to_Target	31.09893188	28.89752522	30.10498801	0.10700
Wind_Speed	9.987965214	10.13798654	9.818743842	0.10700
Shooter_Experience	0.67721519	0.662921348	0.716463415	0.07600
Grip_Stability	5.48497407	5.583323259	5.342132363	0.04600
Trigger_Pull_Force	3.523007728	3.482858324	3.48476578	0.04600
Light_Conditions	560.5809053	540.6561038	547.8948968	0.04600
Heart_Rate	117.9697391	117.5425839	119.9949317	0.07600
Ammo_Quality	0.683544304	0.643258427	0.670731707	0.07600
Temperature	15.02015166	14.85945511	15.00268663	0.01500
Humidity	50.66014474	50.28772977	48.44931696	0.01500
Precision	74.45222776	74.78560132	72.75204747	0.13800
Outcome	0.522151899	0.471910112	0.548780488	0.10700
Price	74	111	100	0.13800

.

The results obtained using the TOPSIS method are presented in

Table 4. TOPSIS results applied on a normalized decision matrix for evaluation of the suitability of the generated data.

	1. Alternative Colt1911	2. Alternative Bereta92	3. Alternative Glock17	Weights
Distance_to_Target	0.0643	0.0598	0.0623	0.107
Wind_Speed	0.0622	0.0631	0.0611	0.107
Shooter_Experience	0.0436	0.0427	0.0461	0.076
Grip_Stability	0.0268	0.0272	0.0261	0.046
Trigger_Pull_Force	0.0269	0.0266	0.0266	0.046
Light_Conditions	0.0272	0.0263	0.0266	0.046
Heart_Rate	0.0439	0.0438	0.0447	0.076
Ammo_Quality	0.0453	0.0426	0.0445	0.076
Temperature	0.0087	0.0086	0.0087	0.015
Humidity	0.0088	0.0088	0.0084	0.015
Precision	0.0807	0.0810	0.0788	0.138
Outcome	0.0630	0.0569	0.0662	0.107
Price	0.0616	0.0925	0.0833	0.138
di−	0.21318	0.03101	0.02405
di+	0.03114	0.01131	0.00999
ci	0.213	0.732	0.706

, and they confirm that the decision made by the relevant U.S. Army authority to replace the Colt 1911 with the Beretta 92 was a correct one. The Beretta 92 was identified as the best alternative among the three pistol types considered, as shown in Table 4.

Namely, the results presented in Table 4 clearly show that preference should be given to the Beretta 92 alternative, as it ranks highest according to two out of three key parameters: it is the closest to the positive-ideal solution, it is not the closest to the negative-ideal solution, and most importantly, it has the highest relative closeness index (C_i). In this way, the authors confirmed the usability of the synthetically generated dataset, as it led to the same conclusion as the actual decision made by the U.S. Army authority.

4.2. Second Layer of Proposed Model: Stacking Ensemble for Determining Most Important Factors

Since the results obtained at the end of the Input Layer of the proposed model clearly demonstrated that the synthetically generated dataset is suitable for constructing an effective ensemble ML algorithm, the authors proceeded with the application of the proposed stacking ensemble ML algorithm (Algorithm 2), as outlined in the Base Layer of the model and illustrated in Figure 4.

In the first step of this algorithm, the authors used the three datasets—one for each type of pistol—that had been prepared earlier in Section 4.1: Input Layer of the Proposed Model: Checking the Usability of the Synthetic Dataset. This paper presents detailed results for two of the considered pistol types: Beretta 92, which was chosen to replace the previously used Colt 1911, and Colt 1911 itself, as the correctness of that replacement decision is being evaluated. For the third type, Glock 17, only summary results are provided.

A binary logistic regression procedure was performed using SPSS on the available datasets as part of the first step of Algorithm 2, starting with the dataset for the Beretta 92 pistol. All 11 biomechanical parameters were used as predictor variables, while the binary outcome variable—shooting success (miss = 0, hit = 1)—was used as the dependent variable.

The results of the applied binary regression analysis are presented in

Table 5. Binary regression Bereta 92 dataset with all 11 factors.

Binary Regression: Variables in the Equation
Step 1			B	S.E.	Wald	Df	Sig.	Exp(B)	95% C.I. for EXP(B)
									Lower	Upper
Distance_to_Target			−0.005	0.009	0.285	1	0.594	0.995	0.977	1.013
Wind_Speed			−0.037	0.018	4.232	1	0.040	0.963	0.930	0.998
Shooter_Experience			0.017	0.224	0.006	1	0.939	1.017	0.656	1.577
Grip_Stability			0.096	0.158	0.368	1	0.544	1.101	0.807	1.500
Trigger_Pull_Force			0.188	0.114	2.729	1	0.099	1.206	0.966	1.507
Light_Conditions			0.000	0.000	0.159	1	0.690	1.000	0.999	1.001
Heart_Rate			−0.001	0.003	0.090	1	0.765	0.999	0.992	1.006
Ammo_Quality			0.111	0.226	0.243	1	0.622	1.118	0.718	1.741
Temperature			0.009	0.008	1.341	1	0.247	1.009	0.994	1.024
Humidity			0.005	0.005	0.982	1	0.322	1.005	0.996	1.014
Precision			−0.013	0.017	0.584	1	0.445	0.987	0.954	1.021
Classification Table a,b
	Observed					Predicted				Percentage Correct
						Outcome
						0		1
Step 1	Outcome			0		128		60		68.1
				1		94		74		44.0
	Overall Percentage									56.7
		a. Constant is included in the model. b. The cut-off value is 0.500.
		Model Summary
Step	−2 Log likelihood				Cox–Snell R Square				Nagelkerke R Square
1	483.891 c				0.036				0.027
		c. Estimation terminated at iteration 3 because parameter estimates changed by less than 0.001.
		Hosmer and Lemeshow Test
Step		Chi-square				df			Sig.
1		3.528				8			0.897

.

The obtained results show that the binary regression model, using all 11 considered biomechanical factors, explains 3.6% of the variance according to the Cox & Snell R² and 2.7% according to the Nagelkerke R², indicating a weak association with the data (values greater than 0 but less than 0.4) [53]. The Hosmer and Lemeshow test returned a significance value of 0.897, which is well above 0.05, indicating a good fit between the data and the model [54,55] and confirming that the model is well calibrated [56]. Additionally, none of the 11 factors were excluded due to multicollinearity, suggesting acceptable correlations among the predictors. The accuracy of random classification was calculated as ${\left(168/356\right)}^2+ {\left(188/356\right)}^2= 0.501573$, which corresponds to 50.15%. In contrast, the binary regression model achieved a classification accuracy of 56.7%, which is clearly better than random guessing [57]. Given that the dataset consists of 188 instances labeled as miss and 168 as hit, it can be considered balanced. This balance justifies the use of the AUC-ROC as the primary performance measure for evaluating binary classification models. Since model quality is significantly reflected by the AUC-ROC value [58], this metric is determined in the second step of Algorithm 2, where the analysis continues. The validity of proceeding is supported by the acceptable Hosmer and Lemeshow test result of 0.897.

In this second step, three classification algorithms—each representing a different category as per the WEKA tool’s taxonomy—were applied: Random Forest (Trees group), AdaBoost (Meta group), and PART (Rules group). The model performance was evaluated using the 10-fold cross-validation method [59]. Also, the results obtained in

Table 6. Performance indicators for Bereta92: classification using all 11 factors.

	Precision	Recall	F1 Measure	AUCROC
RandomForest	0.479	0.483	0.479	0.461
Ada Boost	0.441	0.458	0.437	0.433
PART	0.422	0.466	0.409	0.444

show that the proposed asymmetric optimization model using feature selection has better characteristics compared to other considered classifiers taken from the same groups of Weka classifiers, as done in Step 2 of this algorithm, Table 6.

The performance metrics for all three classification algorithms are presented in Table 6, which shows that Random Forest achieved the most accurate prediction results, especially considering the AUCROC as the most important evaluation metric.

In the third step of the proposed Algorithm 2, a feature selection procedure was applied using three algorithms available in the WEKA tool: two filter methods—ReliefF and CorrelationAttributeEval—and one wrapper method, GreedyStepwise. By performing an intersection operation on the sets of selected and non-selected attributes generated by each of the three feature selection algorithms, the authors identified the common attributes deemed important by all methods. As shown in

Table 7. Feature selection algorithms Bereta92: selection of important factors.

	Majority Voting	Relief	CorrelationAttributeEval	GreedyStepwise
Distance_to_Target	●	●		●
Wind_Speed			●
Shooter_Experience	●	●	●
Grip_Stability		●
Trigger_Pull_Force	●	●	●
Light_Conditions	●	●	●
Heart_Rate		●
Ammo_Quality	●	●	●
Temperature	●	●	●
Humidity	●	●	●
Precision	●	●	●

, the following eight biomechanical factors were determined to be significant: target distance, shooter experience, trigger pull force, light, ammunition quality, temperature, humidity, and precision.

In the fourth step of the proposed Algorithm 2, the model checks whether the most important performance measure—AUC-ROC, calculated using the Random Forest classifier (identified in Step 2 as the best-performing algorithm)—improves when using the reduced and optimized set of eight selected factors. If the AUCROC value improves, the model then verifies the goodness of fit of the binary regression model constructed using these reduced factors. If both conditions are met, the procedure proceeds to Step 5, where Algorithm 2 is applied to the next dataset (i.e., for the next pistol type) following the same sequence of steps. Otherwise, the algorithm terminates, as no further optimization through factor reduction is possible.

In our case, the AUC-ROC value improved when using the reduced set of eight factors, as shown in

Table 8. Performance indicators for Bereta92: RandomForest classifier using 8 factors.

	Precision	Recall	F1 Measure	AUCROC
RandomForest—8 factors	0.502	0.506	0.502	o.489
RandomForest—11 factors	0.479	0.483	0.479	0.461
JRip	0.437	0.441	0.438	0.417
Bagging	0.440	0.444	0.441	0.444
REPTree	0.478	0.486	0.476	0.457

, and the binary regression model also demonstrated good calibration, as evidenced by the results in

Table 9. Binary regression using Bereta92 dataset with reduced 8 factors.

Binary Regression: Variables in the Equation
Step 1			B	S.E.	Wald	df	Sig.	Exp(B)	95% C.I. for EXP(B)
									Lower	Upper
Distance_to_Target			−0.009	0.009	0.951	1	0.329	0.991	0.974	1.009
Shooter_Experience			0.001	0.220	0.000	1	0.996	1.001	0.650	1.542
Trigger_Pull_Force			0.118	0.107	1.222	1	0.269	1.125	0.913	1.387
Light_Conditions			0.000	0.000	0.613	1	0.433	1.000	0.999	1.000
Ammo_Quality			0.043	0.222	0.037	1	0.847	1.044	0.675	1.614
Temperature			0.007	0.007	0.935	1	0.334	1.007	0.993	1.022
Humidity			0.003	0.004	0.388	1	0.534	1.003	0.994	1.011
Precision			−0.005	0.004	1.217	1	0.270	0.995	0.987	1.004
Classification Table a,b
	Observed					Predicted				Percentage Correct
						Outcome
						0		1
Step 1	Outcome			0		124		64		66.0
				1		108		60		35.7
	Overall Percentage									51.7
		a. Constant is included in the model. b. The cut-off value is 0.500.
		Model Summary
Step	−2 Log likelihood				Cox–Snell R Square				Nagelkerke R Square
1	489.011 c				0.013				0.017
c. Estimation terminated at iteration 3 because parameter estimates changed by less than 0.001.
		Hosmer and Lemeshow Test
Step		Chi-square				Df				Sig.
1		9.335				8				0.315

. Therefore, we concluded the analysis for the Beretta 92 dataset using the optimized set of eight factors.

Since we have two additional datasets for Colt 1911 and Glock 17 remaining, we repeated Steps 1 through 5 of the proposed Algorithm 2 for these two pistol types, following the same methodology. The obtained results identified the important factors:

• The following eight important factors for the Colt 1911 dataset:

• Target distance, shooter experience, grip stability, trigger pull force, light, temperature, humidity, and precision.

• For the Glock 17 dataset, seven important factors were identified:

• Wind speed, light, heart rate, ammunition quality, temperature, humidity, and precision.

4.3. Third Layer of Proposed Model: Final Decision Making Using Voting

In the third layer of the proposed model, a comparison was made based on the sets of significant factors identified in the previous step—i.e., in the Base Layer of the model—for each of the considered pistol types. By applying a majority voting approach, the model determined which of the pistol types shares the highest number of significant factors with the one being considered for replacement, in this case, the Colt 1911. The results of this comparison are presented in

Table 10. Final decision making: majority voting on which type has most identical significant factors.

	Majority Voting	Colt1911	Bereta92	Glock17
Distance_to_Target	●	●	●
Wind_Speed				●
Shooter_Experience	●	●	●
Grip_Stability		●
Trigger_Pull_Force	●	●	●
Light_Conditions	●	●	●	●
Heart_Rate				●
Ammo_Quality	●		●	●
Temperature	●	●	●	●
Humidity	●	●	●	●
Precision	●	●	●	●

.

From the data presented in Table 10, the following is evident based on the application of majority voting [60]:

• It can be concluded that only three of the considered factors are not important for successful shooting using the three types of pistols considered: Colt 1911, Beretta 92, and Glock 17
• It can be concluded that the Beretta 92 pistol shares seven out of eight significant factors with the Colt 1911, while only one factor is not common. In contrast, the Glock 17 shares only four significant factors with the Colt 1911, while the remaining four are not matched. A logical conclusion follows from this analysis: the decision made by the U.S. Army to replace the Colt 1911 with the Beretta 92 was well founded and justified.

4.4. Discussion of the Obtained Results

Conducting the described case study regarding the U.S. Army’s choice of a standard-issue pistol at the end of the 20th century, based on the results obtained and presented in the first three subsections, in this Section 4 of the paper, the authors have successfully achieved the main goal of this paper:

• The results demonstrated the feasibility of constructing an ensemble ML model capable of forensically evaluating the correctness of a weapon selection decision.
• The results proved the possibility of constructing such a model, which is usable in solving many similar forensics problems in different fields of human life.

Furthermore, the obtained results confirm both hypotheses stated in the Section 1 of this paper:

• The conditional hypothesis, asserting that it is possible to use synthetically generated data—such as that produced by ChatGPT-4 or similar tools—in decision analysis;
• The final hypothesis, stating that it is possible to construct a novel ensemble model that addresses the problem of handgun type selection forensics more effectively than existing state-of-the-art models.

As the authors already mentioned in Section 1, they did not find in the literature a similar or equivalent multi-layered forensic decision model. However, in the middle of the three layers—the Base Layer—a new ensemble algorithm was proposed using an asymmetric optimization procedure that identifies the most important criteria in a multi-criteria decision-making problem, commonly encountered in both the literature and practice. The advantages of the proposed model, particularly the methodology of this layer, are presented in Table 8, and the results confirm the overall benefits of the entire model.

The limitations of the proposed model include the inherent constraints of synthetic datasets and the relatively longer implementation time required for executing the stacking ensemble algorithm used in the Base Layer of the proposed model. However, neither limitation significantly impacts the practical applicability of the model, especially in scenarios involving incomplete or unavailable real-world data and the development of new analytical frameworks.

The 10-fold cross-validation technique is used in this paper as a valuable method for assessing the quality of synthetic data, as it helps determine how well the synthetic data represents real-world conditions [61]. Specifically, by dividing the dataset into subsets used for training and validation, cross-validation offers several advantages:

• Reducing overfitting: It helps identify overfitting issues by evaluating model performance on data that was not seen during training.
• Providing a realistic assessment of performance: By using different subsets for training and validation, it offers a more robust evaluation of how well the model generalizes to new, unseen data.
• Detecting data quality issues: If the synthetic data does not accurately represent real-world data, poor performance on validation sets may reveal underlying quality issues.
• Improving model generalization: By validating models on different data partitions, it ensures the model learns generalizable patterns rather than memorizing training data.

Cross-validation is especially important when working with synthetic data, as it ensures the synthetic dataset is useful. In our case, an alternative validation technique—benchmarking against real data—is not feasible.

By 2025, it is expected that 70% of enterprises will be using synthetic data for AI and analytics, underscoring the critical role synthetic data plays in AI and machine learning development [61]. However, the success of AI models heavily depends on the quality of the training data. Ensuring data realism remains a major challenge.

According to [62], synthetic data is playing an increasingly significant role not only in forensics but also in other domains of human activity. For example, it is projected that by 2030, all training and test data for AI models could be synthetic. Furthermore, some authors already propose the use of synthetic data in digital traffic to address various security issues in digital communication [63].

The authors plan the following directions for future research:

In a methodological context:

• To explore the possibility of using new synthetic multi-criteria decision analysis approaches, such as fuzzy methods and group decision-making techniques, to enhance the characteristics of the proposed model [64]. Of particular interest for the first layer of the model are approaches related to large-group decision making, such as the rough integrated asymmetric cloud model under a multi-granularity linguistic environment [65].
• To include a broader set of classification and feature selection algorithms in order to introduce n-modular redundancy into the second layer of the proposed ensemble algorithm [66]. This enhancement aims to improve prediction performance in similar problem domains across various fields.
• To incorporate an ablation study within the ensemble of machine learning (ML) and multi-criteria decision-making (MCDM) components. Such a study would systematically remove or disable components of the ensemble model to evaluate their individual contributions, thereby identifying which components are most impactful and guiding further performance improvements.

In the application context:

• Given that the model is structurally organized for forensic decision analysis, it is worthwhile to explore its application in other domains beyond the choice of weapons. Potential application areas include transportation and traffic [67], biology [68], medicine [69], economics [70], and the public sector [71].

5. Conclusions

The authors addressed two basic tasks in this paper besides the main task, which was checking the possibility of constructing one model for handgun type selection forensics. These tasks are directly related to testing the two hypotheses formulated to solve the problem described in the study. The results of the conducted research, obtained using the proposed ensemble model that incorporates AHP and TOPSIS multi-criteria decision-making methods, confirmed the first (conditional) hypothesis and its associated research question: it is possible to use synthetically generated data—such as that produced by ChatGPT-4 or similar tools—when the ranking of considered alternatives based on this synthetic data aligns with real-world decisions made using actual data.

The authors also addressed the second (final) hypothesis, demonstrating that it is possible to construct a hybrid model that solves the problem of handgun type selection forensics more effectively than existing state-of-the-art models. This was achieved by aggregating MCDM methods of AHP and TOPSIS with the ML ensemble of three specific classification methods and a binary regression algorithm into a single stacking ensemble ML model, which incorporates three distinct feature selection algorithms as part of its combiner strategy and a voting method at the end. Such an obtained and proposed model leads to superior performance compared to the individual application of each method or previously known models.

Both hypotheses were validated using a case study analyzing the U.S. Army’s decision at the end of the twentieth century to replace the Colt 1911 pistol with the Beretta 92. The analysis also included a third widely used pistol—the Glock 17—and was based on synthetic data generated via ChatGPT-4, an LLM. The obtained results using the proposed model, based on one asymmetric optimization procedure, confirmed the possibility of constructing one model for handgun type selection forensics. The evaluation of results was conducted using 10-fold cross-validation in WEKA software for each applied ML algorithm and the Hosmer–Lemeshow test, along with the Cox & Snell and Nagelkerke R² tests, in SPSS software to assess the goodness of fit of the applied binary regression model.

The authors concluded that the proposed model demonstrated no significant limitations, apart from the fact that synthetic datasets are not directly derived from real-world data. However, this limitation is mitigated by the practical value of such synthetic data in evaluating newly proposed models for problems where real data is scarce or unavailable.

For future work, the authors are going to consider the possibility of using the new synthetic multi-criteria decision analysis approach and explore the inclusion of a broader set of classification and feature selection algorithms, thereby introducing n-modular redundancy into the construction of the proposed ensemble algorithm. The authors also plan to explore the possibility of using new synthetic multi-criteria decision analysis approaches, particularly fuzzy methods and group decision-making techniques, to enhance the characteristics of the proposed model.