A Priori Sample Size Determination for Estimating a Location Parameter Under a Unified Skew-Normal Distribution
Abstract
1. Introduction
2. Properties of the SUN Distribution
- (1)
- The MGF of Y is
- (2)
- The mean of Y is
- (i)
- The ’s are independently and identically SUN-distributed, and
- (ii)
- is SUN-distributed, and
2.1. The APP for Estimating the Location Parameter in One Sample
2.2. The APP to Estimate the Difference in Locations for Two Independent Samples
2.3. The APP on Estimating the Difference in Locations for Matched Pairs
- Note that
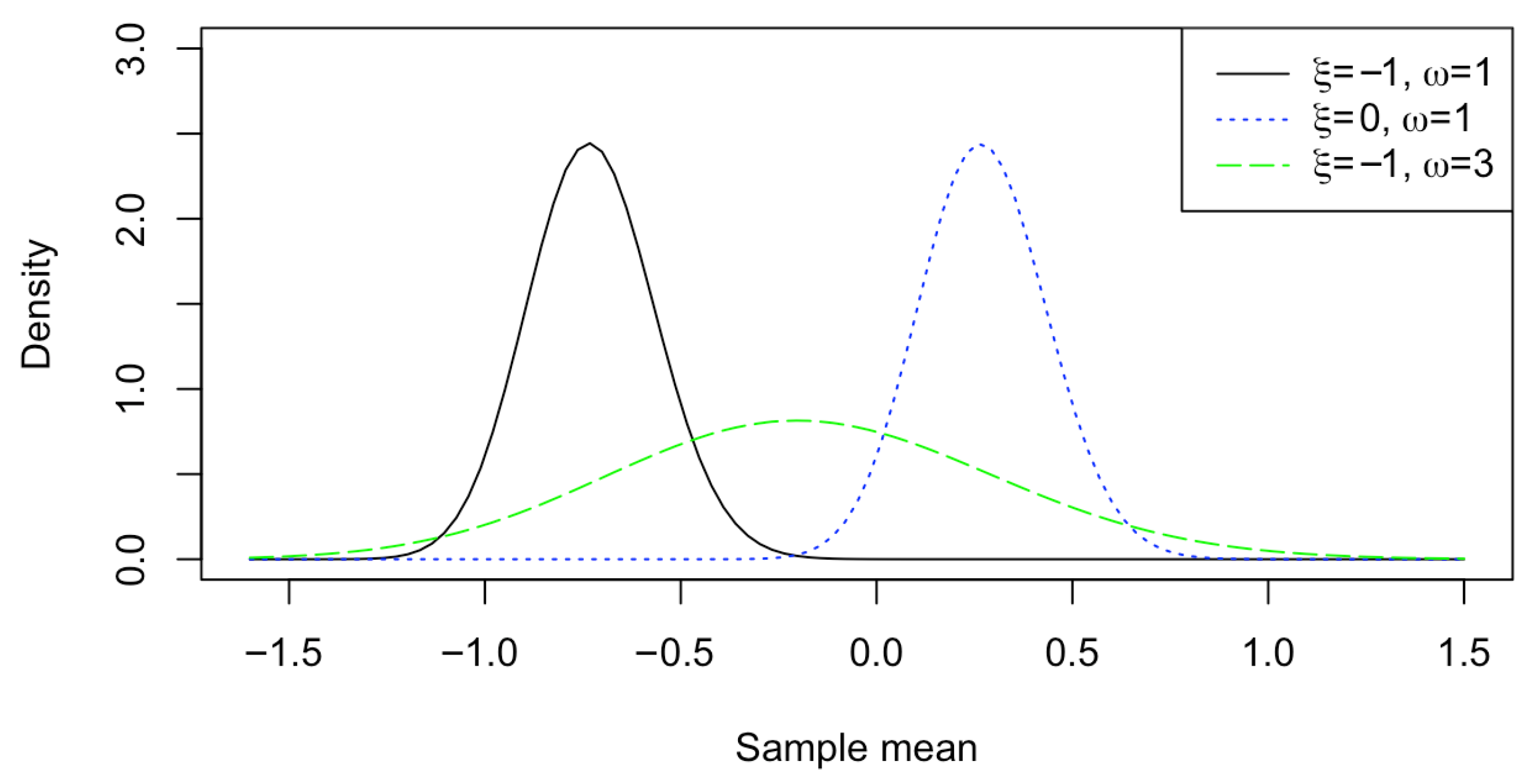
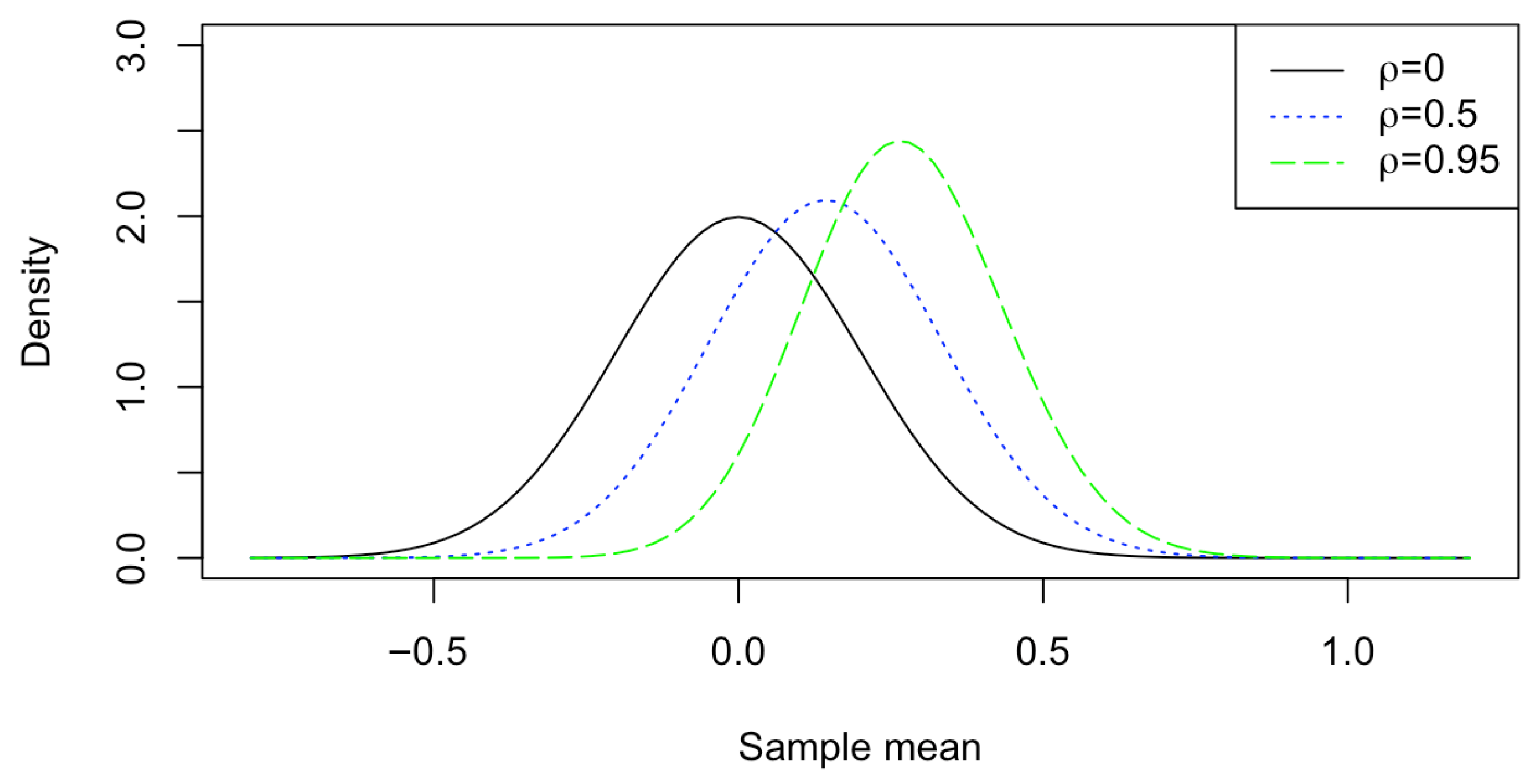
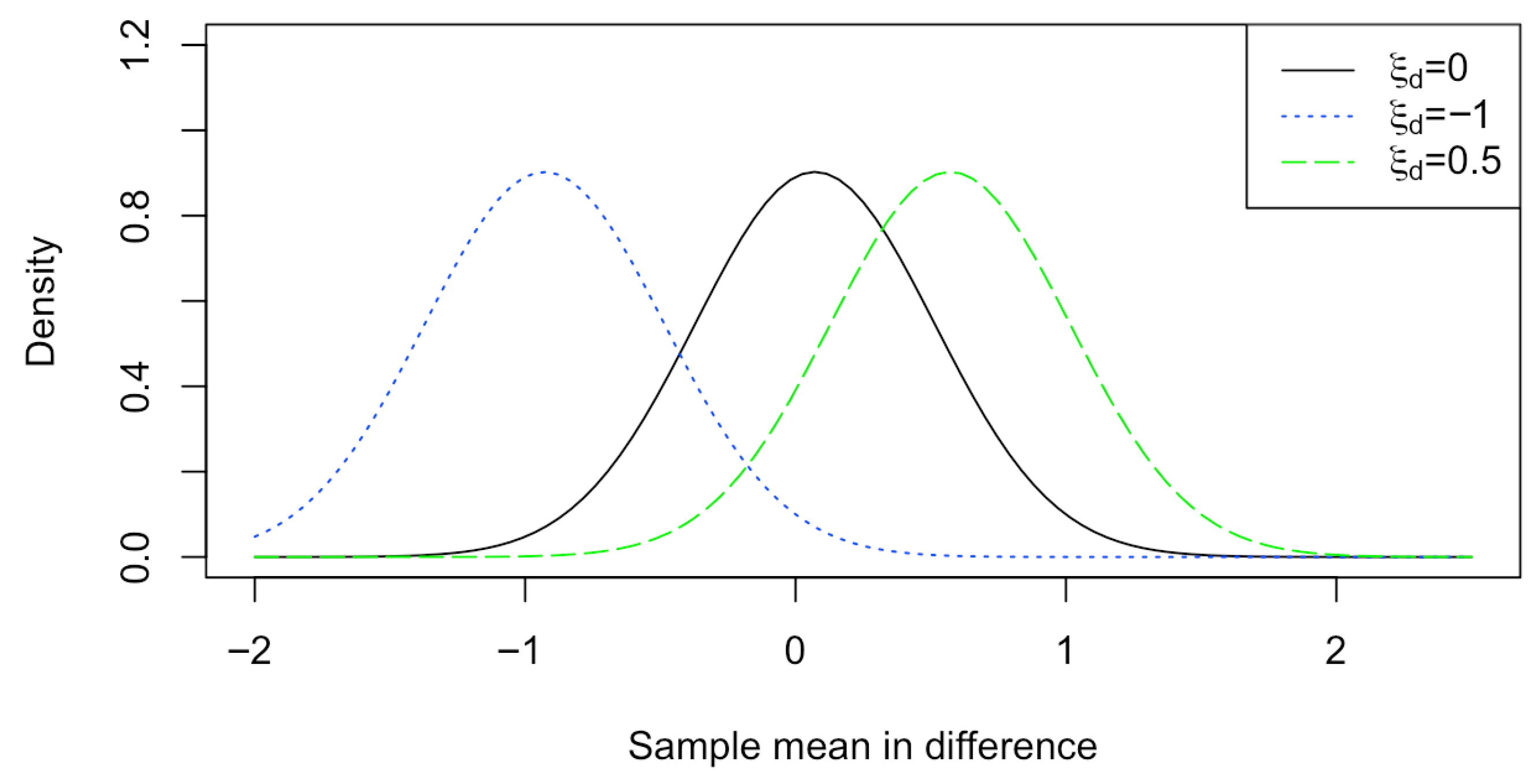
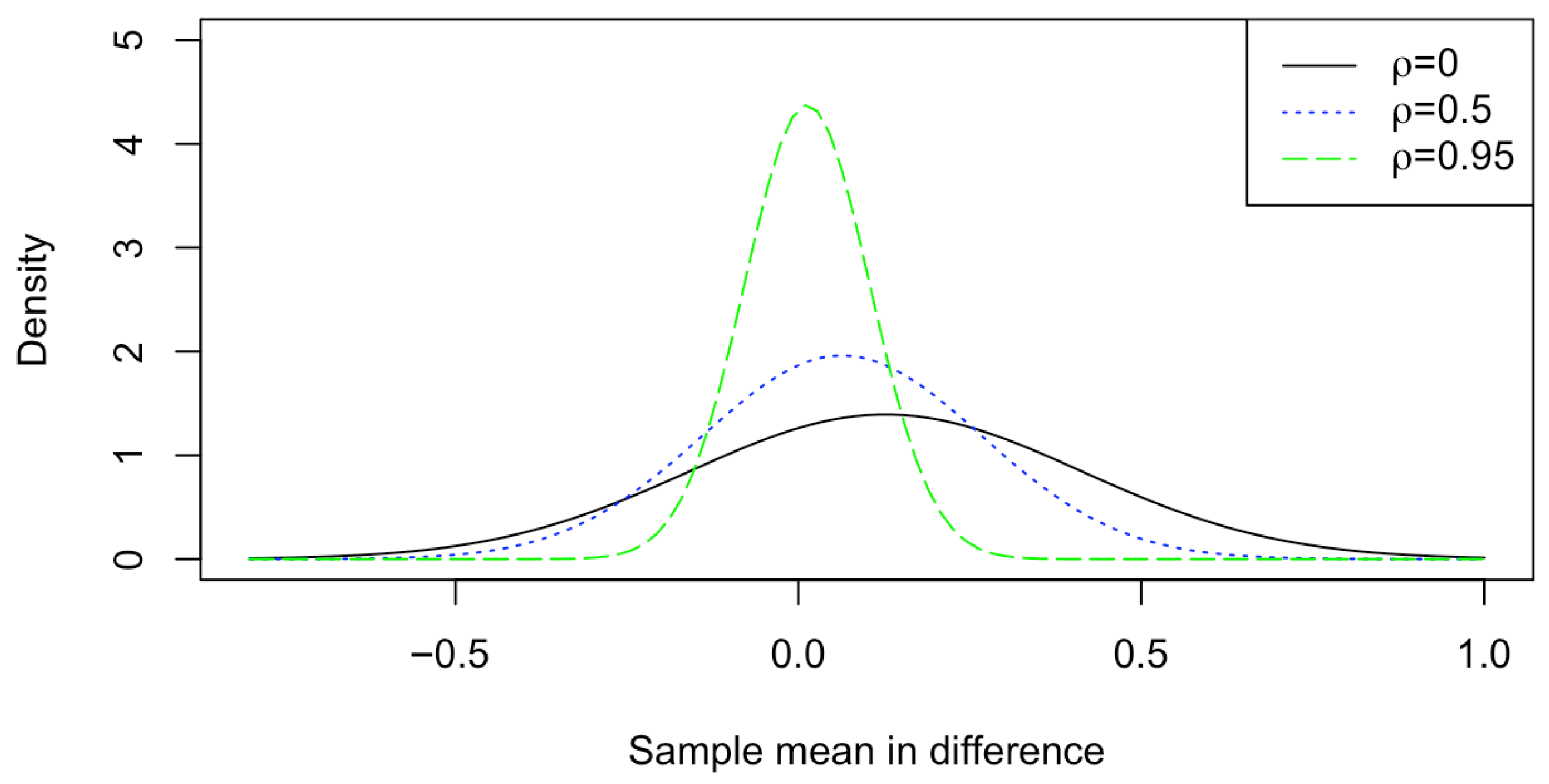
3. Simulation Studies
- Case 1: (One sample) Set up .
- Case 2: (Dependent samples) Set up , , and .
3.1. Sample Sizes and Bounds
3.2. Coverage Probability and Average Length
4. Applications
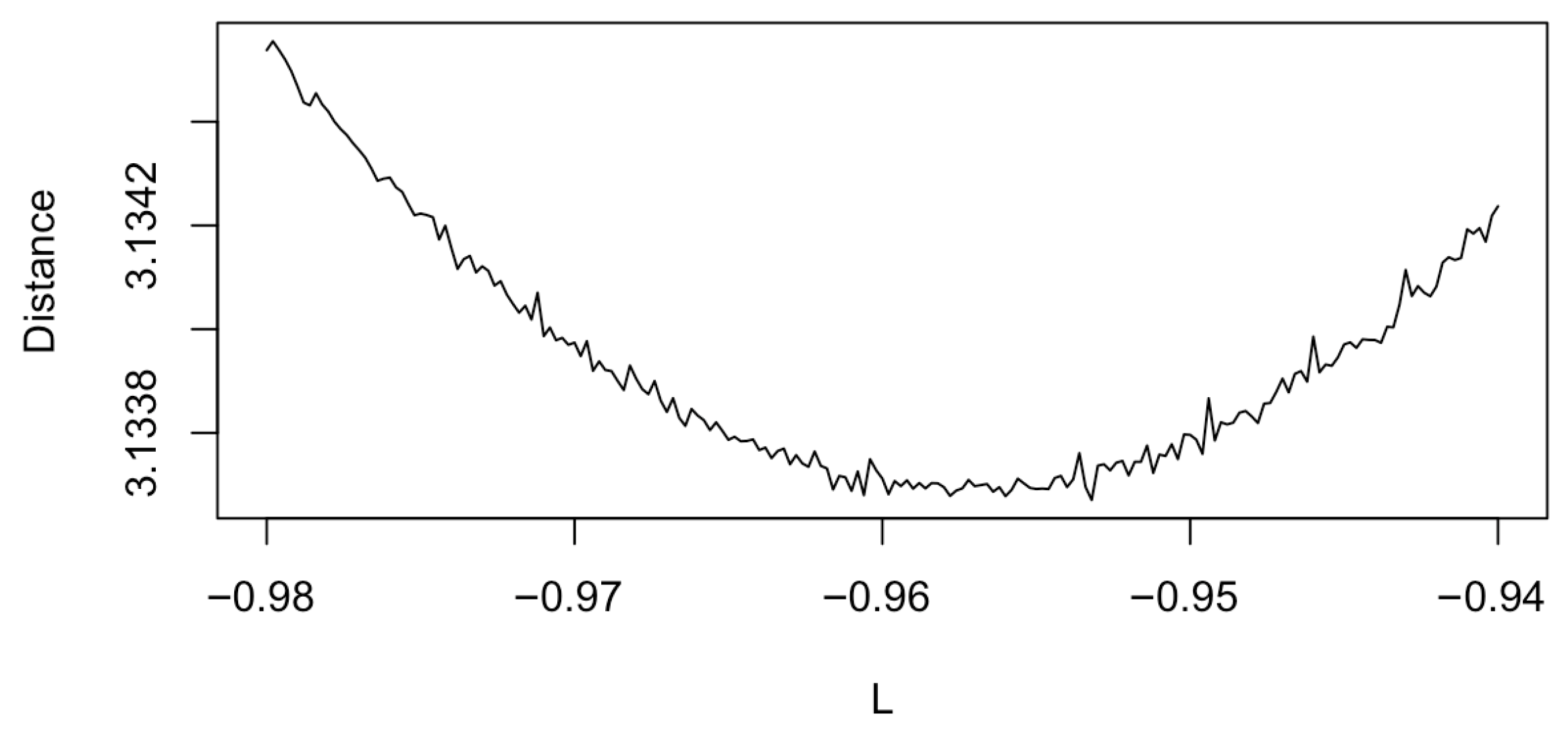
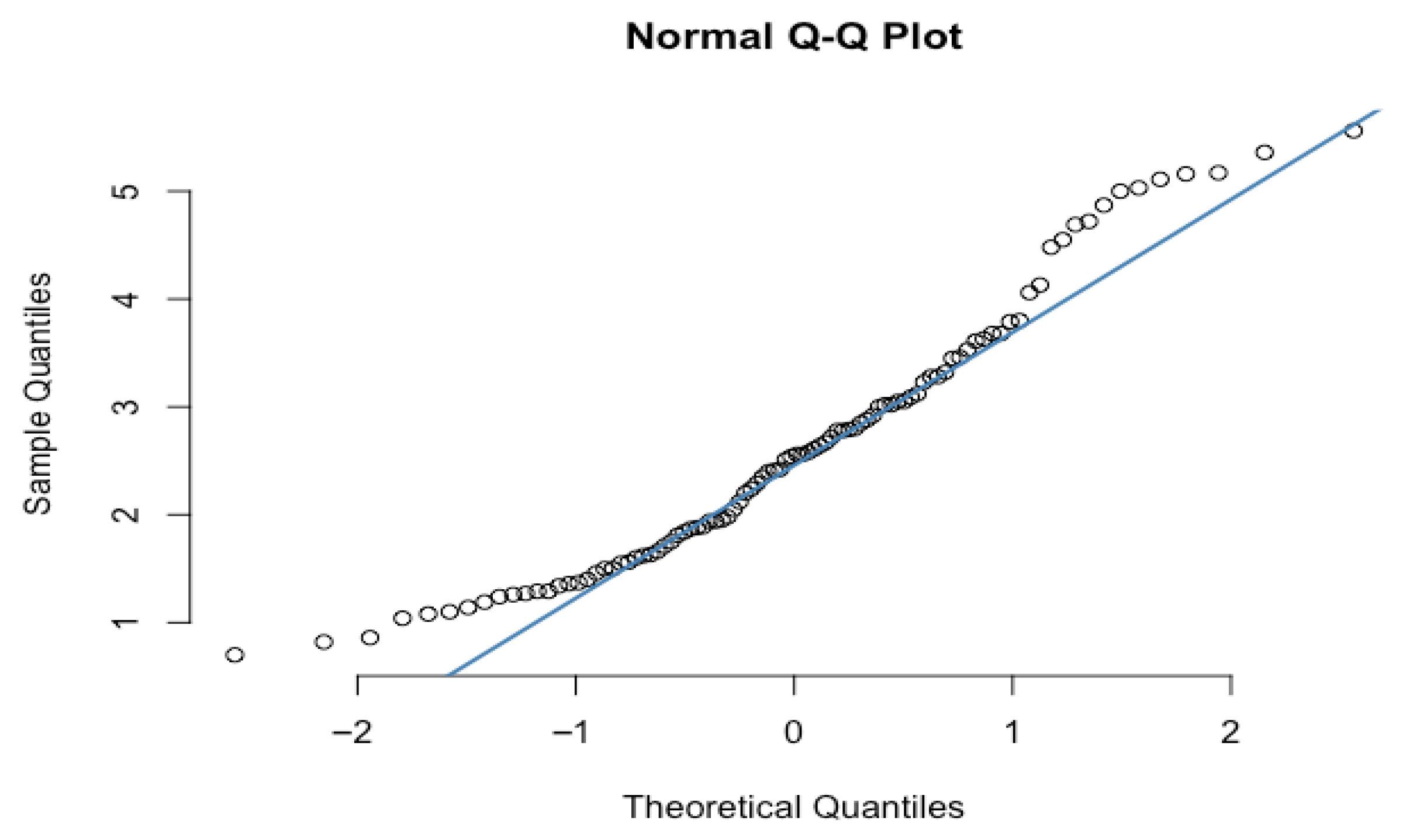
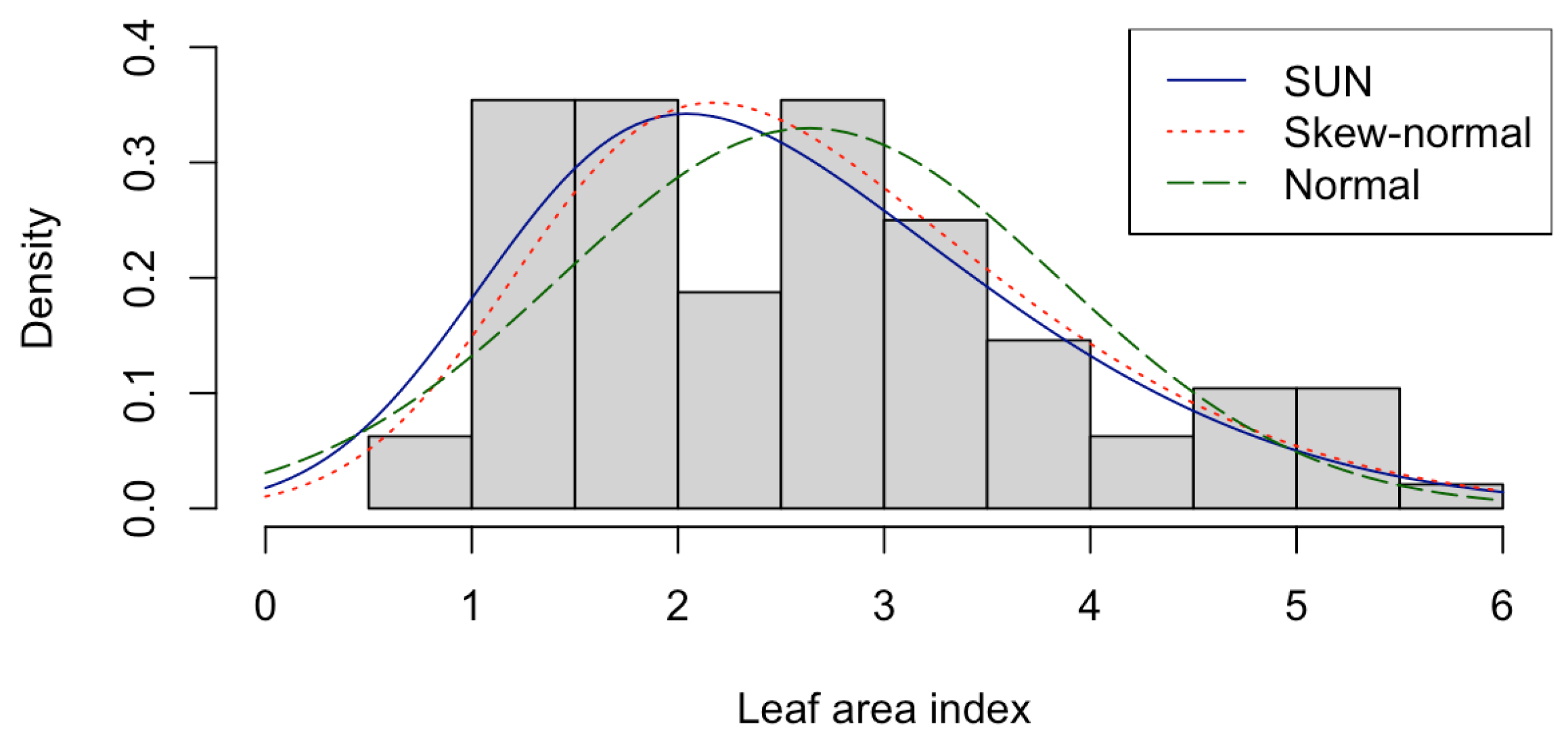
4.1. Leaf Area Index
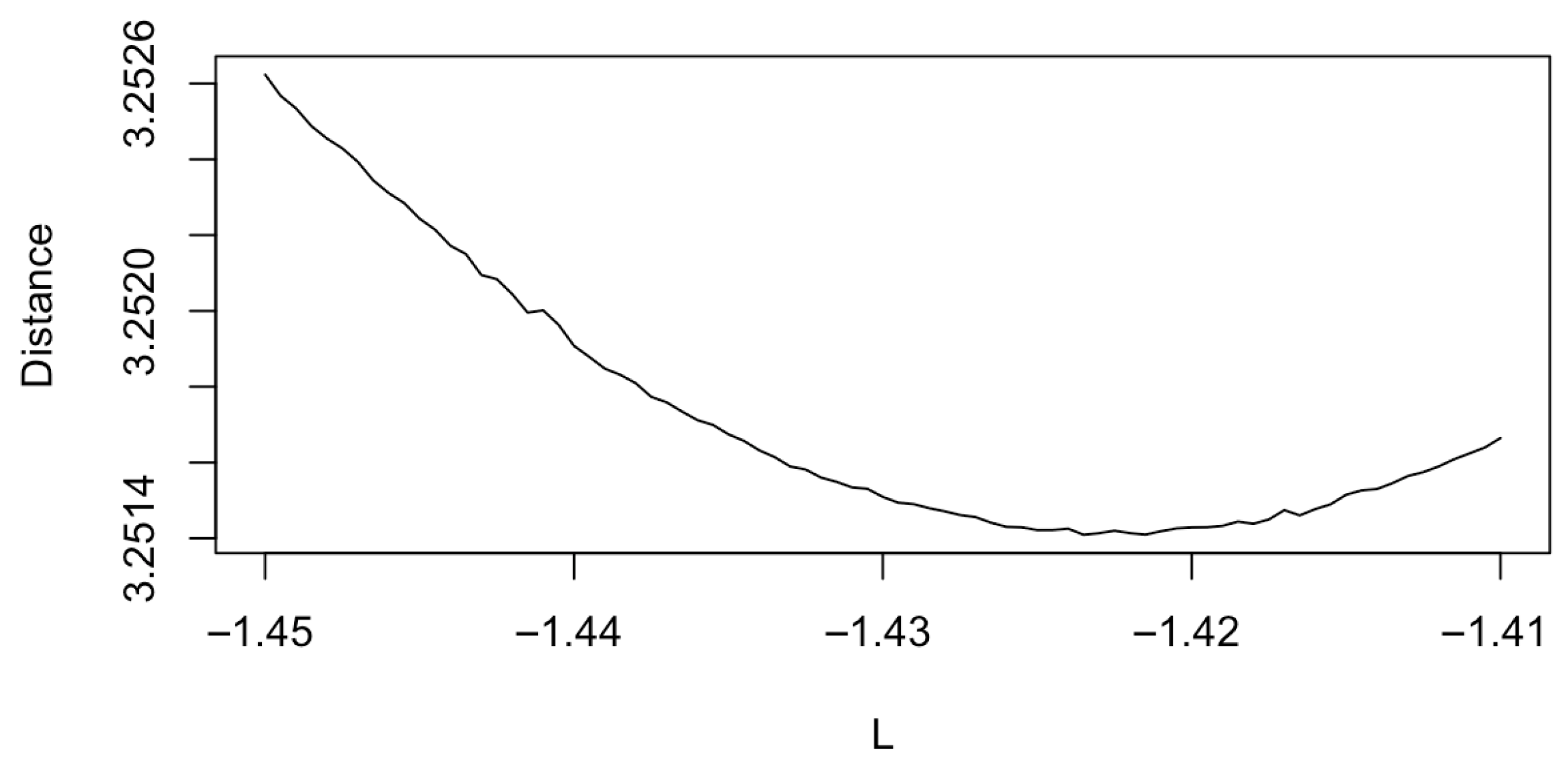
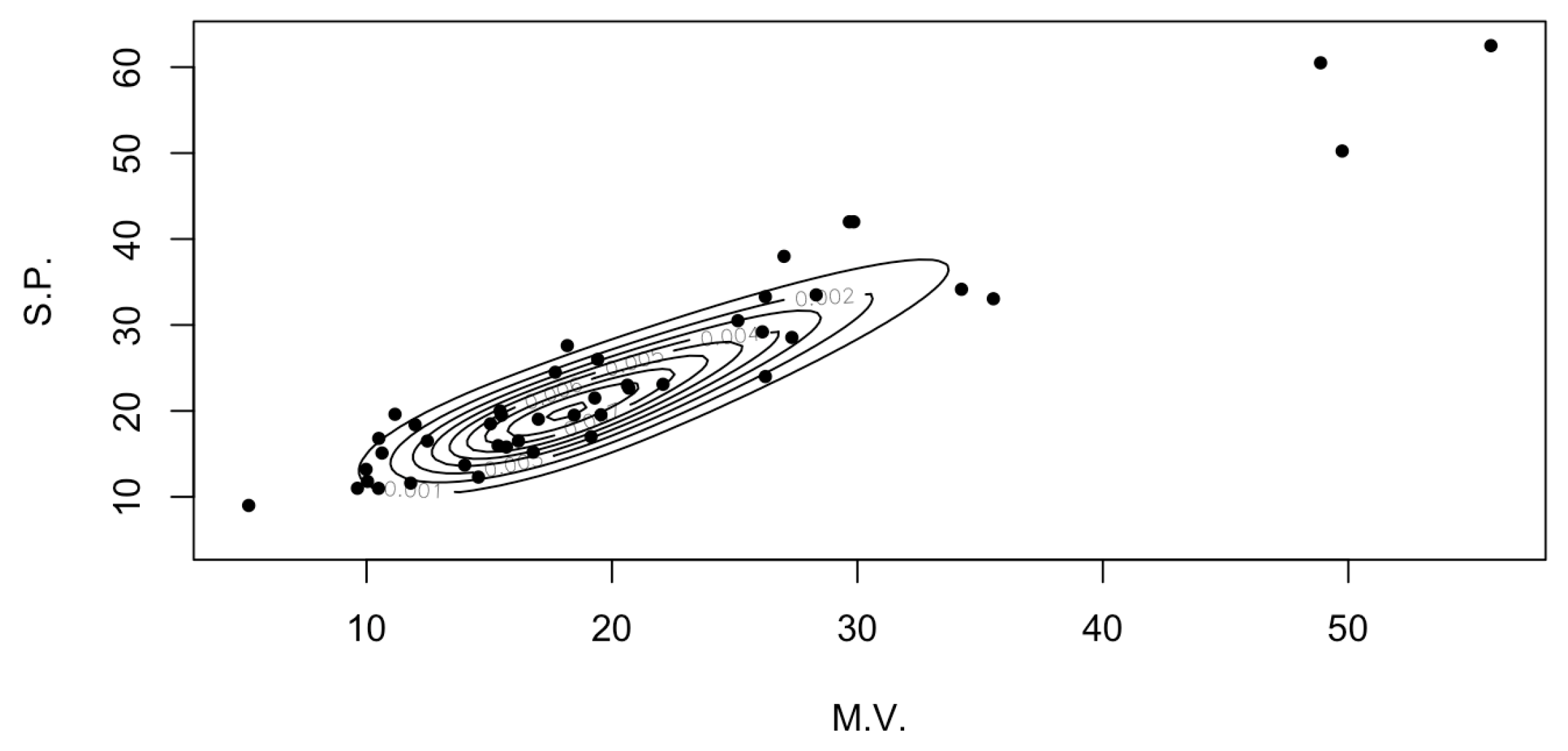
4.2. Sale Price Market Values
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Listing 1. R code for requried sample size. |
 |
 |
References
- Trafimow, D. Using the coefficient of confidence to make the philosophical switch from a posteriori to a priori inferential statistics. Educ. Psychol. Meas. 2017, 77, 831–854. [Google Scholar] [CrossRef] [PubMed]
- Trafimow, D.; MacDonald, J.A. Performing inferential statistics prior to data collection. Educ. Psychol. Meas. 2017, 77, 204–219. [Google Scholar] [CrossRef] [PubMed]
- Trafimow, D.; Wang, T.; Wang, C. From a sampling precision perspective, skewness is a friend and not an enemy. Educ. Psychol. Meas. 2019, 79, 129–150. [Google Scholar] [CrossRef] [PubMed]
- Azzalini, A.; Dalla Valle, A. The multivariate skew-normal distribution. Biometrica 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Wang, C.; Wang, T.; Trafimow, D.; Chen, J. Extending a priori procedure to two independent samples under skew normal settings. Asian J. Econ. Bank. 2019, 3, 29–40. [Google Scholar]
- Wang, C.; Wang, T.; Trafimow, D.; Myüz, H.A. Necessary sample sizes for specified closeness and confidence of matched data under the skew normal setting. Commun.-Stat.-Simul. Comput. 2022, 51, 2083–2094. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, T.; Choy, S.T.B.; Wei, Z.; Zhu, X. Extending the A Priori Procedure for Estimating Location Parameter Under Multivariate Skew Normal Settings. In Optimal Transport Statistics for Economics and Related Topics; Studies in Systems, Decision and Control; Ngoc Thach, N., Kreinovich, V., Ha, D.T., Trung, N.D., Eds.; Springer: Cham, Switzerland, 2024; Volume 483. [Google Scholar] [CrossRef]
- Tong, T.; Trafimow, D.; Wang, T.; Wang, C.; Hu, L.; Chen, X. The a priori procedure (APP) for estimating regression coefficients in linear models. Methodology 2022, 18, 203–220. [Google Scholar] [CrossRef]
- Cao, L.; Wang, C.; Wang, T.; Trafimow, D. The APP for estimating population proportion based on skew normal approximations and the Beta-Bernoulli process. Commun.-Stat.-Simul. Comput. 2024, 53, 167–177. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Azzalini, A. On the unification of families of skew-normal distributions. Scand. J. Stat. 2006, 33, 561–574. [Google Scholar] [CrossRef]
- Gupta, A.K.; Aziz, M.A.; Ning, W. On some properties of the unified skew normal distribution. J. Stat. Theory Pract. 2013, 7, 480–495. [Google Scholar] [CrossRef]
- Amiri, M.; Jamalizadeh, A.; Towhidi, M. Some multivariate singular unified skew-normal distributions and their application. Commun. -Stat.-Theory Methods 2016, 45, 2159–2171. [Google Scholar] [CrossRef]
- Durante, D. Conjugate Bayes for probit regression via unified skew-normal distributions. Biometrika 2019, 106, 765–779. [Google Scholar] [CrossRef]
- Minozzo, M.; Bagnato, L. A unified skew-normal geostatistical factor model. Environmetrics 2021, 32, e2672. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Azzalini, A. Some properties of the unified skew-normal distribution. Stat. Pap. 2022, 63, 461–487. [Google Scholar] [CrossRef]
- Anceschi, N.; Fasano, A.; Durante, D.; Zanella, G. Bayesian conjugacy in probit, tobit, multinomial probit and extensions: A review and new results. J. Am. Stat. Assoc. 2023, 118, 1451–1469. [Google Scholar] [CrossRef]
- Ye, R.D.; Wang, T.H. Inferences in linear mixed models with skew-normal random effects. Acta Math. Sin. Engl. Ser. 2015, 31, 576–594. [Google Scholar] [CrossRef]
- Sahu, S.K.; Dey, D.K.; Branco, M.D. A new class of multivariate skew distributions with applications to Bayesian regression models. Can. J. Stat. 2003, 31, 129–150. [Google Scholar] [CrossRef]
- Gupta, A.K.; Aziz, M.A. Estimation of Parameters of the Unified Skew Normal Distribution Using the Method of Weighted Moments. J. Stat. Theory Pract. 2012, 6, 402–416. [Google Scholar] [CrossRef]
- Wang, S.-H.; Bai, R.; Huang, H.-H. Two-step mixed-type multivariate Bayesian sparse variable selection with shrinkage priors. Electron. J. Statist. 2025, 19, 397–457. [Google Scholar] [CrossRef]
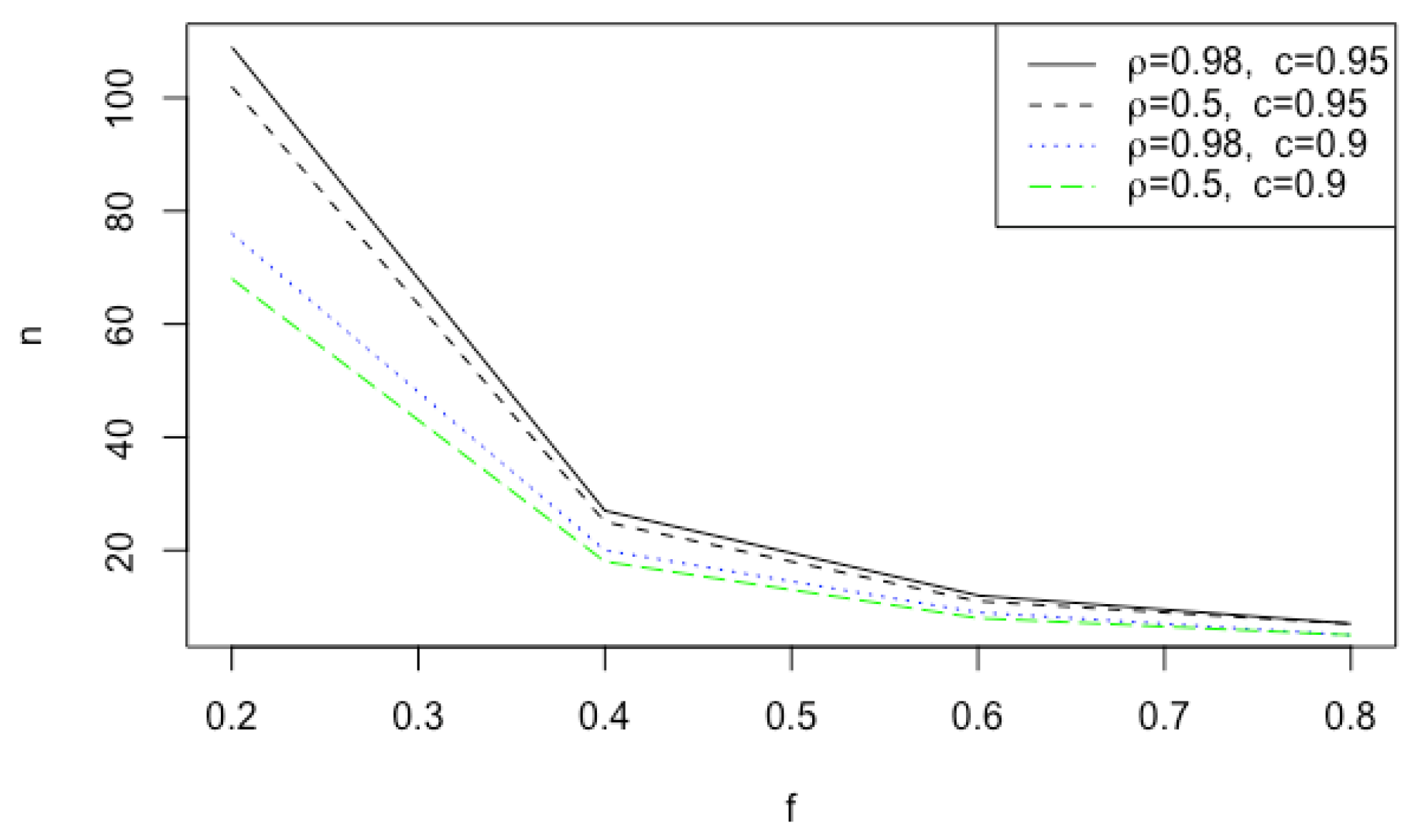
| = 0.5 | = 0.98 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.95 | 102 | 0.455 | 3.259 | −0.198 | 0.200 | 109 | 1.298 | 4.553 | −0.196 | 0.192 |
| 0.9 | 68 | −0.385 | 2.757 | −0.199 | 0.200 | 76 | 1.091 | 3.818 | −0.195 | 0.194 | |
| 0.4 | 0.95 | 25 | −1.149 | 2.585 | −0.392 | 0.392 | 27 | −0.152 | 3.103 | −0.388 | 0.393 |
| 0.9 | 18 | −0.954 | 2.176 | −0.387 | 0.388 | 20 | −0.109 | 2.618 | −0.382 | 0.378 | |
| 0.6 | 0.95 | 11 | −1.387 | 2.347 | −0.590 | 0.592 | 12 | −0.652 | 2.603 | −0.586 | 0.585 |
| 0.9 | 8 | −1.161 | 1.972 | −0.582 | 0.581 | 9 | −0.509 | 2.218 | −0.563 | 0.570 | |
| 0.8 | 0.95 | 7 | −1.484 | 2.250 | −0.740 | 0.742 | 7 | −0.852 | 2.403 | −0.752 | 0.780 |
| 0.9 | 5 | −1.233 | 1.901 | −0.730 | 0.742 | 5 | −0.709 | 2.018 | −0.746 | 0.773 | |
| = 0.5 | = 0.98 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.95 | 96 | −1.232 | 2.641 | −0.199 | 0.200 | 96 | −1.818 | 2.100 | −0.199 | 0.196 |
| 0.9 | 68 | −1.037 | 2.223 | −0.200 | 0.200 | 68 | −1.530 | 1.767 | −0.194 | 0.191 | |
| 0.4 | 0.95 | 24 | −1.585 | 2.289 | −0.396 | 0.393 | 24 | −1.888 | 2.029 | −0.391 | 0.388 |
| 0.9 | 17 | −1.334 | 1.927 | −0.389 | 0.385 | 17 | −1.589 | 1.708 | −0.393 | 0.391 | |
| 0.6 | 0.95 | 11 | −1.728 | 2.205 | −0.591 | 0.589 | 11 | −1.941 | 2.037 | −0.589 | 0.587 |
| 0.9 | 8 | −1.424 | 1.815 | −0.587 | 0.585 | 8 | −1.656 | 1.737 | −0.576 | 0.579 | |
| 0.8 | 0.95 | 6 | −1.761 | 2.113 | −0.772 | 0.776 | 6 | −1.924 | 1.994 | −0.781 | 0.779 |
| 0.9 | 4 | −1.438 | 1.725 | −0.783 | 0.781 | 4 | −1.571 | 1.628 | −0.781 | 0.782 | |
| f | c | n | CP (AL) | CP (AL) | CP (AL) | CP (AL) |
|---|---|---|---|---|---|---|
| 0.2 | 0.95 | 102 | 0.952 (0.3810) | 0.947 (1.1431) | 0.951 (1.1431) | 0.949 (1.1431) |
| 0.9 | 68 | 0.899 (0.3810) | 0.893 (1.1431) | 0.901 (1.1431) | 0.904 (1.1431) | |
| 0.4 | 0.95 | 25 | 0.952 (0.7465) | 0.947 (2.2395) | 0.950 (2.2395) | 0.953 (2.2395) |
| 0.9 | 18 | 0.902 (0.7386) | 0.897 (2.2159) | 0.903 (2.2159) | 0.901 (2.2159) | |
| 0.6 | 0.95 | 11 | 0.951 (1.1255) | 0.954 (3.3765) | 0.949 (3.3765) | 0.947 (3.3765) |
| 0.9 | 8 | 0.896 (1.1079) | 0.901 (3.3238) | 0.905 (3.3238) | 0.902 (3.3238) | |
| 0.8 | 0.95 | 7 | 0.952 (1.4113) | 0.954 (4.2339) | 0.949 (4.2339) | 0.947 (4.2339) |
| 0.9 | 5 | 0.902 (1.4015) | 0.899 (4.2044) | 0.897 (4.2044) | 0.901 (4.2044) |
| f | c | n | CP (AL) | CP (AL) | CP (AL) | CP (AL) |
|---|---|---|---|---|---|---|
| 0.2 | 0.95 | 96 | 0.951 (0.3953) | 0.951 (0.3953) | 0.949 (0.3953) | 0.950 (0.3953) |
| 0.9 | 68 | 0.902 (0.3953) | 0.899 (0.3953) | 0.901 (0.3953) | 0.898 (0.3953) | |
| 0.4 | 0.95 | 24 | 0.950 (0.7907) | 0.949 (0.7907) | 0.951 (0.7907) | 0.953 (0.7907) |
| 0.9 | 17 | 0.901 (0.7906) | 0.904 (0.7906) | 0.899 (0.7906) | 0.896 (0.7906) | |
| 0.6 | 0.95 | 11 | 0.947 (1.1860) | 0.949 (1.1860) | 0.955 (1.1860) | 0.946 (1.1860) |
| 0.9 | 8 | 0.902 (1.1454) | 0.896 (1.1454) | 0.899 (1.1454) | 0.897 (1.1454) | |
| 0.8 | 0.95 | 6 | 0.952 (1.5814) | 0.947 (1.5814) | 0.948 (1.5814) | 0.946 (1.5814) |
| 0.9 | 4 | 0.901 (1.5813) | 0.898 (1.5813) | 0.895 (1.5813) | 0.896 (1.5813) |
| Normal | Skew-Normal | SUN | |
|---|---|---|---|
| 2.6358 | 1.2729 | 1.2729 | |
| 1.2099 | 1.8224 | 1.8224 | |
| - | 2.6888 | - | |
| - | - | 0.9373 | |
| - | - | 1 | |
| - | - | 1 | |
| - | - | 0.1 | |
| AIC | 595.862 | 567.2963 | 547.1149 |
| BIC | 600.9907 | 574.9893 | 554.808 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Tian, W.; Yang, J. A Priori Sample Size Determination for Estimating a Location Parameter Under a Unified Skew-Normal Distribution. Symmetry 2025, 17, 1228. https://doi.org/10.3390/sym17081228
Wang C, Tian W, Yang J. A Priori Sample Size Determination for Estimating a Location Parameter Under a Unified Skew-Normal Distribution. Symmetry. 2025; 17(8):1228. https://doi.org/10.3390/sym17081228
Chicago/Turabian StyleWang, Cong, Weizhong Tian, and Jingjing Yang. 2025. "A Priori Sample Size Determination for Estimating a Location Parameter Under a Unified Skew-Normal Distribution" Symmetry 17, no. 8: 1228. https://doi.org/10.3390/sym17081228
APA StyleWang, C., Tian, W., & Yang, J. (2025). A Priori Sample Size Determination for Estimating a Location Parameter Under a Unified Skew-Normal Distribution. Symmetry, 17(8), 1228. https://doi.org/10.3390/sym17081228








