Hydraulic Flow Patterns in an On-Site Wastewater Treatment Unit Under Various Operating Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Governing Equations of CFD Simulation
2.1.1. 3D Flow with Turbulence Closure
2.1.2. Residence Time Distribution Analysis
2.1.3. Mixing and Mixedness
2.2. Study Site
2.3. Operational Scenarios
2.4. Mesh Quality and Independence Analysis
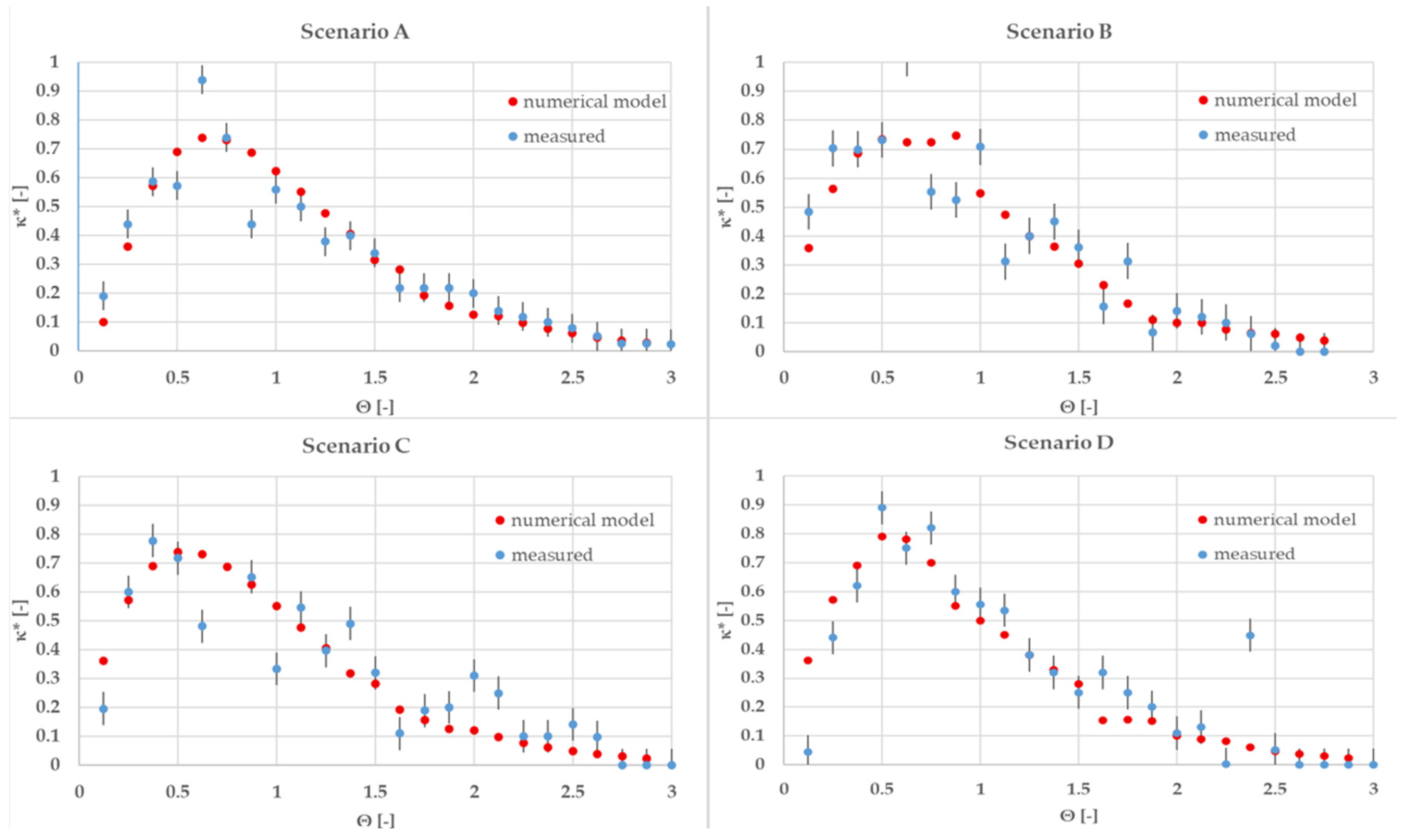
3. Residence Time Analysis—Model Verification
4. Results and Discussion
4.1. Mixing Pattern Analysis
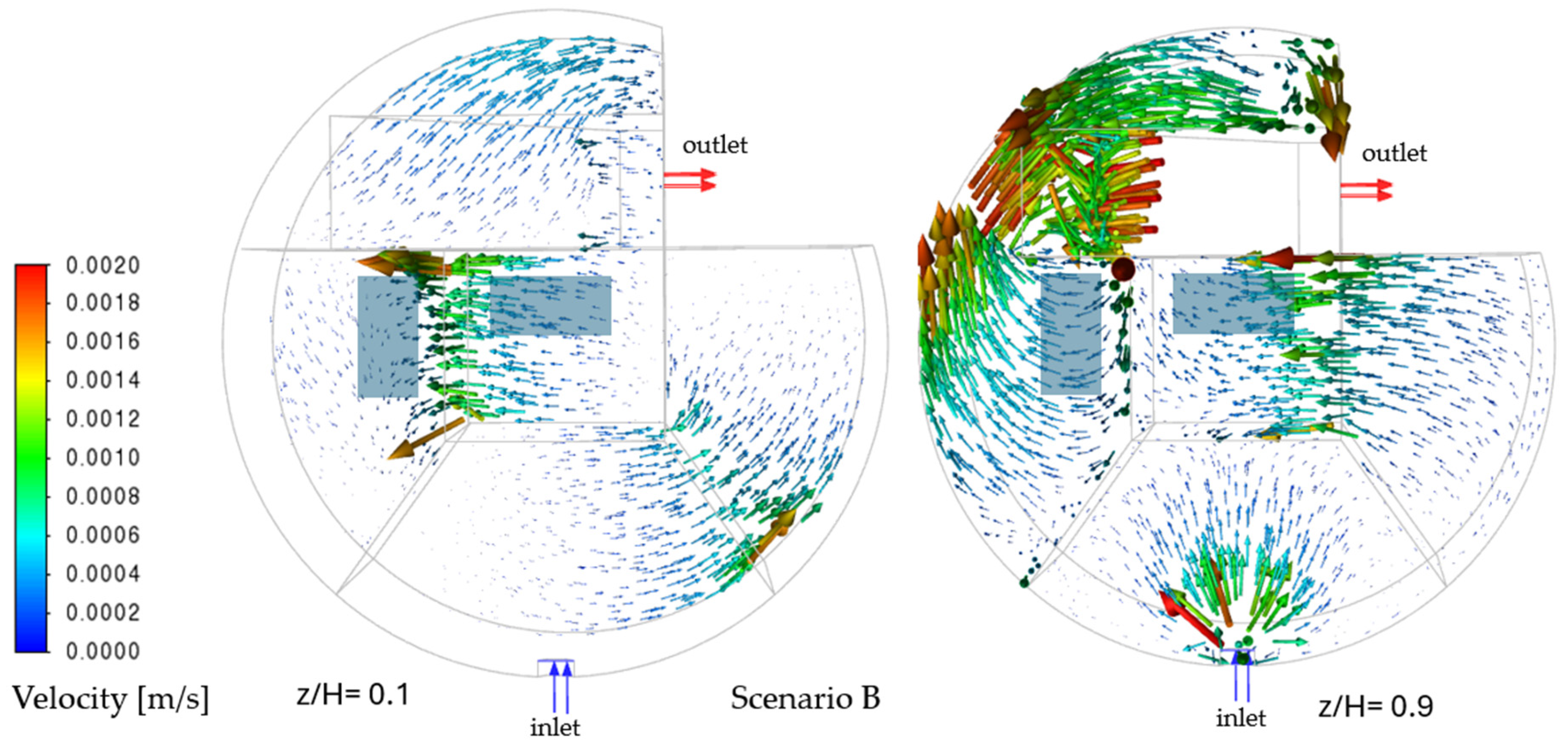
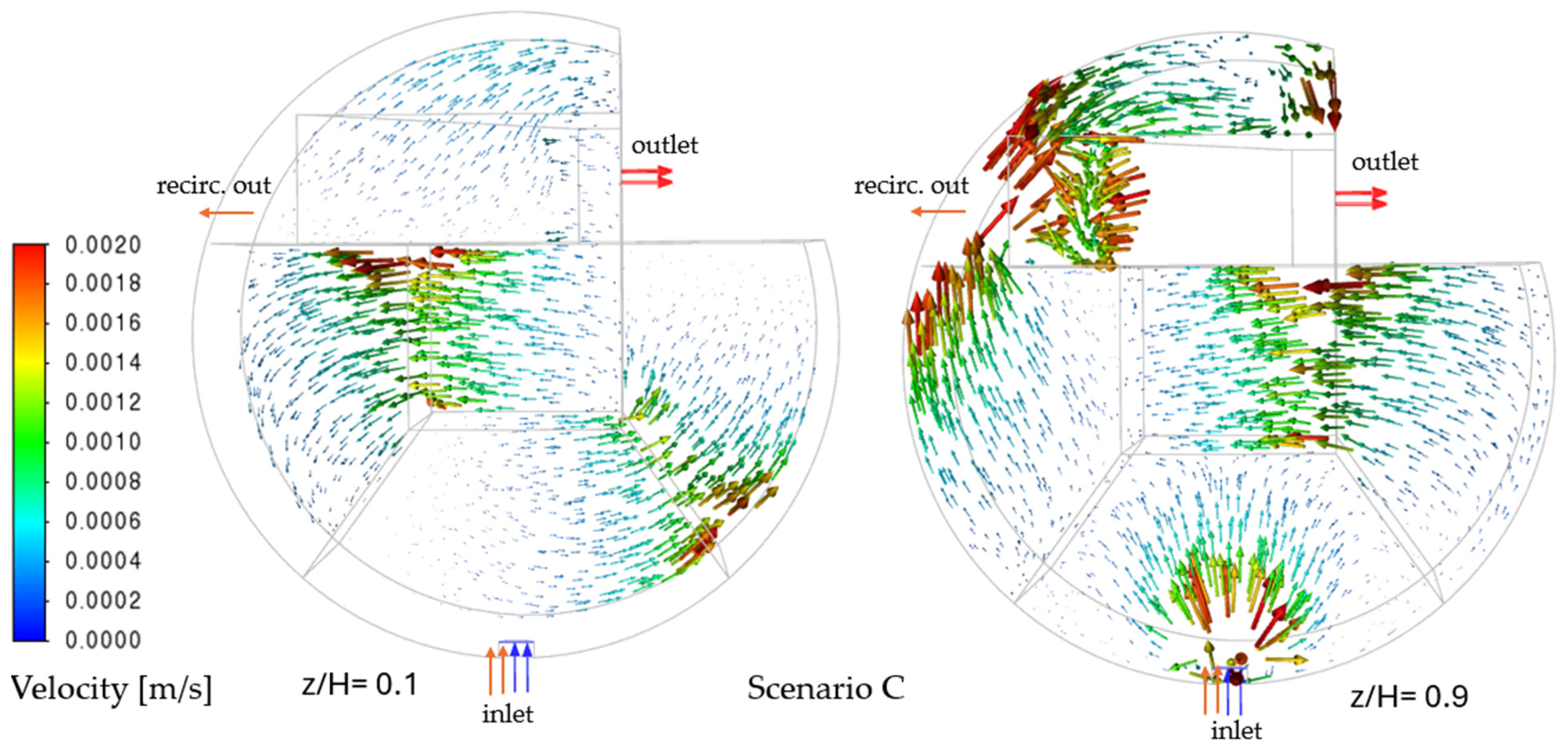
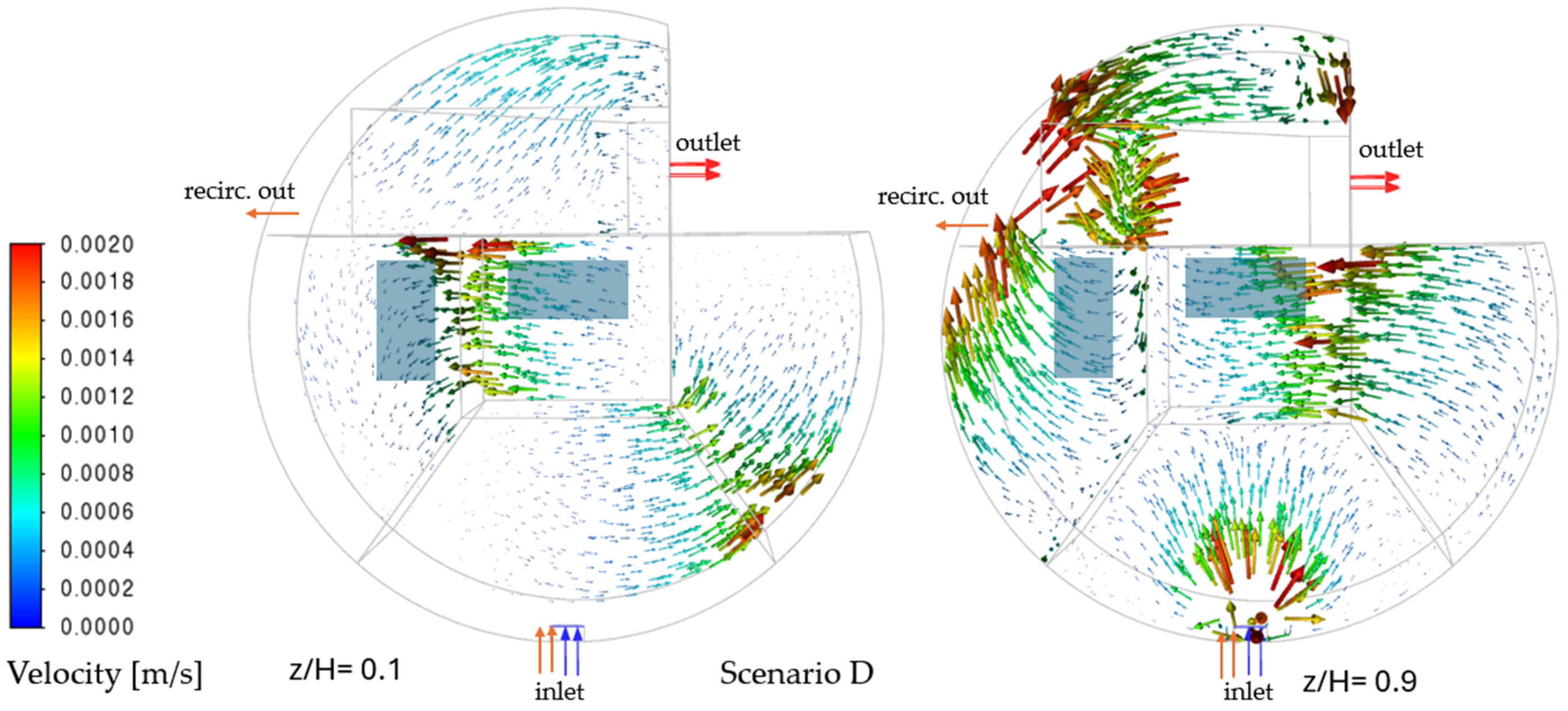
4.2. Flow Field Analysis Across the Scenarios
5. Conclusions
- The numerical model accurately predicted residence time distributions and mixing indices, with model–measurement deviations ranging from ±2% (inflow only) to ±10% (combined mechanisms), validating the CFD approach for design and diagnostics.
- Mixing index analysis revealed that Zone 6 consistently underperformed (index ≤ 0.69), confirming literature reports that geometric dead zones persist despite operational adjustments and require structural redesign for mitigation.
- The study confirms that inflow is essential for maintaining system-wide momentum and preventing the lack of momentum, as the scenarios without inflow (Scenario E) saw the mean mixing indices drop to 0.52 and dead zones expand beyond 10% of the volume.
- These results support the application of CFD-based optimization and targeted design modifications—such as extending aeration, adjusting recirculation rates, and reconfiguring outlets—to improve the efficiency and resilience of small-capacity wastewater treatment units.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ricciardo Calderaro, M.; Fusco, A.; Amitrano, C.C. The European Union Regulation 2020/741: From the Management of Water Resources to the EU Legislation for Its Reuse. In Water Reuse and Unconventional Water Resources: A Multidisciplinary Perspective; Springer Nature: Cham, Switzerland, 2024; pp. 395–412. [Google Scholar]
- Derco, J.; Guľašová, P.; Legan, M.; Zakhar, R.; Žgajnar Gotvajn, A. Sustainability Strategies in Municipal Wastewater Treatment. Sustainability 2024, 16, 9038. [Google Scholar] [CrossRef]
- Massoud, M.A.; Tarhini, A.; Nasr, J.A. Decentralized approaches to wastewater treatment and management: Applicability in developing countries. J. Environ. Manag. 2009, 90, 652–659. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Li, P.; Li, H.; Zhang, B.; He, Y. To centralize or to decentralize? A systematic framework for optimizing rural wastewater treatment planning. J. Environ. Manag. 2021, 300, 113673. [Google Scholar] [CrossRef] [PubMed]
- Jakubaszek, A.; Stadnik, A. Technical and technological analysis of individual wastewater treatment systems. Civ. Environ. Eng. Rep. 2018, 28, 87–99. [Google Scholar] [CrossRef]
- Mirra, R.; Ribarov, C.; Valchev, D.; Ribarova, I. Towards Energy Efficient Onsite Wastewater Treatment. Civ. Eng. J. 2020, 6, 1218–1226. [Google Scholar] [CrossRef]
- Rosso, D.; Stenstrom, M.K.; Garrido-Baserba, M. Aeration and mixing. In Biological Wastewater Treatment: Principles, Modeling and Design, 2nd ed.; Chen, G., Ekama, G.A., van Loosdrecht, M.C.M., Brdjanovic, D., Eds.; IWA Publishing: London, UK, 2023. [Google Scholar]
- Nguyen, N.T.; Vo, T.S.; Tran-Nguyen, P.L.; Nguyen, M.N.; Pham, V.H.; Matsuhashi, R.; Vo, T.T.B.C. A comprehensive review of aeration and wastewater treatment. Aquaculture 2024, 591, 741113. [Google Scholar] [CrossRef]
- Wu, Z.L.; Zhang, Q.; Xia, Z.Y.; Gou, M.; Sun, Z.Y.; Tang, Y.Q. The responses of mesophilic and thermophilic anaerobic digestion of municipal sludge to periodic fluctuation disturbance of organic loading rate. Environ. Res. 2023, 218, 114783. [Google Scholar] [CrossRef]
- Diaz-Elsayed, N.; Xu, X.; Balaguer-Barbosa, M.; Zhang, Q. An evaluation of the sustainability of onsite wastewater treatment systems for nutrient management. Water Res. 2017, 121, 186–196. [Google Scholar] [CrossRef]
- Dubois, V.; Boutin, C. Comparison of the design criteria of 141 onsite wastewater treatment systems available on the French market. J. Environ. Manag. 2018, 216, 299–304. [Google Scholar] [CrossRef]
- Sarathai, Y.; Koottatep, T.; Morel, A. Hydraulic characteristics of an anaerobic baffled reactor as onsite wastewater treatment system. J. Environ. Sci. 2010, 22, 1319–1326. [Google Scholar] [CrossRef]
- Connelly, K.N.; Wenger, S.J.; Gaur, N.; McDonald, J.M.B.; Occhipinti, M.; Capps, K.A. Assessing relationships between onsite wastewater treatment system maintenance patterns and system-level variables. Sci. Total Environ. 2023, 870, 161851. [Google Scholar] [CrossRef] [PubMed]
- Laurent, J.; Samstag, R.; Wicks, J.; Nopens, I. (Eds.) CFD Modelling for Wastewater Treatment Processes: IWA Working Group on Computational Fluid Dynamics; IWA Publishing: London, UK, 2022. [Google Scholar]
- Zapata Rivera, A.M.; Ducoste, J.; Peña, M.R.; Portapila, M. Computational Fluid Dynamics Simulation of Suspended Solids Transport in a Secondary Facultative Lagoon Used for Wastewater Treatment. Water 2021, 13, 2356. [Google Scholar] [CrossRef]
- Engstler, E.; Kerschbaumer, D.J.; Langergraber, G. Evaluating the performance of small wastewater treatment plants. Front. Environ. Sci. 2022, 10, 948366. [Google Scholar] [CrossRef]
- Chowaniec, K.; Fryźlewicz-Kozak, B. The influence of mixing process on wastewater treatment. Tech. Trans. 2014, 2014, 3–10. [Google Scholar]
- Hellsten, A. Some improvements in Menter’s k-omega SST turbulence model. In Proceedings of the 29th AIAA Fluid Dynamics Conference, Albuquerque, NM, USA, 15–18 June 1998; p. 2554. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Cham, Switzerland, 2001; ISBN 978-3-540-42074-3. [Google Scholar]
- Pouraria, H.; Park, K.-H.; Seo, Y. Numerical Modelling of Dispersed Water in Oil Flows Using Eulerian-Eulerian Approach and Population Balance Model. Processes 2021, 9, 1345. [Google Scholar] [CrossRef]
- Rodrigues, A.E. Residence time distribution (RTD) revisited. Chem. Eng. Sci. 2021, 230, 116188. [Google Scholar] [CrossRef]
- Manenti, S.; Todeschini, S.; Collivignarelli, M.C.; Abbà, A. Integrated RTD−CFD hydrodynamic analysis for performance assessment of activated sludge reactors. Environ. Process. 2018, 5, 23–42. [Google Scholar] [CrossRef]
- Karches, T.; Buzás, K. Methodology to determine residence time distribution and small scale phenomena in settling tanks. WIT Trans. Eng. Sci. 2011, 70, 117–125. [Google Scholar] [CrossRef]
- Bérard, A.; Blais, B.; Patience, G.S. Experimental methods in chemical engineering: Residence time distribution—RTD. Can. J. Chem. Eng. 2020, 98, 848–867. [Google Scholar] [CrossRef]
- Cao, Z.; Deng, J.; Yuan, W.; Chen, Z. Integration of CFD and RTD analysis in flow pattern and mixing behavior of rotary pressure exchanger with extended angle. Desalin. Water Treat. 2016, 57, 15265–15275. [Google Scholar] [CrossRef]
- Lima Neto, I.E.; Zhu, D.Z.; Rajaratnam, N. Effect of tank size and geometry on the flow induced by circular bubble plumes and water jets. J. Hydraul. Eng. 2008, 134, 833–842. [Google Scholar] [CrossRef]
- Oliveira, E.P.; Souza, T.S.; Okada, D.Y.; Damasceno, L.H.S.; Moura, R.B. Effect of air flow, intermittent aeration time and recirculation ratio in the hydrodynamic behavior of a structured bed reactor. Chem. Eng. J. 2020, 394, 124988. [Google Scholar] [CrossRef]
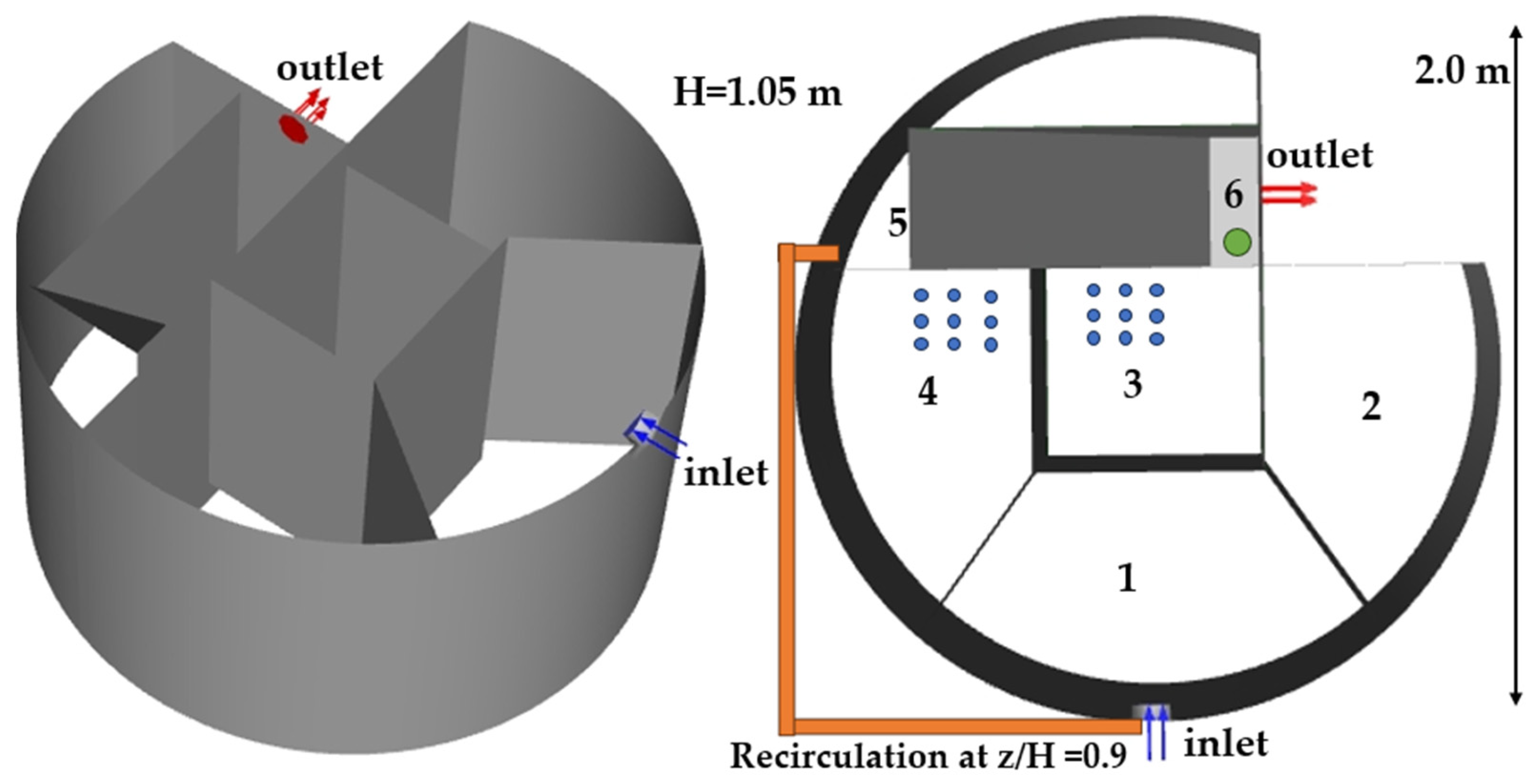



| Zone No. | Volume [m3] | Aerated | Recirculation | Role |
|---|---|---|---|---|
| 1 | 0.76 | No | From zone 5 | Balancing |
| 2 | 0.59 | No | - | Anaerobic |
| 3 | 0.42 | Yes | - | Aerobic |
| 4 | 0.59 | Yes | - | Aerobic |
| 5 | 0.54 | No | To zone 1 | Aerobic |
| 6 | 0.26 | No | - | Settling |
| Scenario | Inflow | Aeration | Recirculation |
|---|---|---|---|
| A | ON | OFF | OFF |
| B | ON | ON | OFF |
| C | ON | OFF | ON |
| D | ON | ON | ON |
| E | OFF | ON | ON |
| Mesh Density | No. of Elements | Volume-Averaged Mixing Index | Turbulent Kinetic Energy (TKE) | Turbulent Dissipation Rate (ε) |
|---|---|---|---|---|
| Coarse | 401,480 | 0.612 | 0.283 | 0.375 |
| Practical | 722,664 | 0.597 | 0.269 | 0.333 |
| Fine | 1,003,700 | 0.596 | 0.267 | 0.332 |
| Zone | Scenario A | Scenario B | Scenario C | Scenario D | Scenario E |
|---|---|---|---|---|---|
| 1 | 0.62 ± 0.08 | 0.65 ± 0.06 | 0.89 ± 0.03 | 0.93 ± 0.02 | 0.78 ± 0.07 |
| 2 | 0.58 ± 0.09 | 0.67 ± 0.07 | 0.71 ± 0.05 | 0.86 ± 0.04 | 0.49 ± 0.11 |
| 3 | 0.53 ± 0.11 | 0.85 ± 0.04 | 0.63 ± 0.08 | 0.91 ± 0.03 | 0.69 ± 0.09 |
| 4 | 0.49 ± 0.12 | 0.88 ± 0.03 | 0.59 ± 0.09 | 0.94 ± 0.02 | 0.72 ± 0.08 |
| 5 | 0.47 ± 0.13 | 0.87 ± 0.04 | 0.83 ± 0.05 | 0.95 ± 0.01 | 0.81 ± 0.06 |
| 6 | 0.41 ± 0.15 | 0.52 ± 0.10 | 0.48 ± 0.11 | 0.69 ± 0.07 | 0.22 ± 0.017 |
| Scenario | Operation | Mean Residence Time, τ (h) | Mean Mixing Index (Full Reactor) | Zone 6 Mixing Index | Max Velocity (m/s, Main Zones) |
|---|---|---|---|---|---|
| A | Inflow only | 13.16 | 0.52 (±0.08) | 0.41 (±0.15) | 0.0016 |
| B | Inflow + aeration | 12.3 | 0.62 (±0.07) | 0.67 (±0.13) | 0.0018 |
| C | Inflow + recirculation (5 → 1) | 11.3 | 0.67 (±0.06) | 0.53 (±0.12) | 0.0018 |
| D | Inflow + aeration + recirculation | 9.4 | 0.88 (±0.04) | 0.69 (±0.07) | 0.0018 |
| E | Aeration + recirculation, no inflow | — * | 0.52 (±0.10) | 0.22 (±0.17) | 0.0012 (local) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karches, T.; Papp, T. Hydraulic Flow Patterns in an On-Site Wastewater Treatment Unit Under Various Operating Conditions. Symmetry 2025, 17, 1190. https://doi.org/10.3390/sym17081190
Karches T, Papp T. Hydraulic Flow Patterns in an On-Site Wastewater Treatment Unit Under Various Operating Conditions. Symmetry. 2025; 17(8):1190. https://doi.org/10.3390/sym17081190
Chicago/Turabian StyleKarches, Tamás, and Tamás Papp. 2025. "Hydraulic Flow Patterns in an On-Site Wastewater Treatment Unit Under Various Operating Conditions" Symmetry 17, no. 8: 1190. https://doi.org/10.3390/sym17081190
APA StyleKarches, T., & Papp, T. (2025). Hydraulic Flow Patterns in an On-Site Wastewater Treatment Unit Under Various Operating Conditions. Symmetry, 17(8), 1190. https://doi.org/10.3390/sym17081190







