Abstract
Effective fault feature extraction and classification methods serve as the foundation for achieving the efficient fault diagnosis of planetary gearboxes. Considering the vibration signals of planetary gearboxes that contain both symmetrical and asymmetrical components, this paper proposes a novel feature extraction method integrating an adaptive multi-bandpass filter (AMBPF) and refined composite multi-scale fuzzy entropy (RCMFE). And a dream optimization algorithm (DOA)–least squares support vector machine (LSSVM) is also proposed for fault classification. Firstly, the AMBPF is proposed, which can effectively and adaptively separate the meshing frequencies, harmonic frequencies, and their sideband frequency information of the planetary gearbox, and is combined with RCMFE for fault feature extraction. Secondly, the DOA is employed to optimize the parameters of the LSSVM, aiming to enhance its classification efficiency. Finally, the fault diagnosis of the planetary gearbox is achieved by the AMBPF, RCMFE, and DOA-LSSVM. The experimental results demonstrate that the proposed method achieves significantly higher diagnostic efficiency and exhibits superior noise immunity in planetary gearbox fault diagnosis.
1. Introduction
Planetary gearboxes are widely employed in the transmission components of large-scale equipment such as wind turbines, helicopters, and ships, owing to their high load-carrying capacity, stable transmission performance, and high efficiency [1,2]. Due to the harsh operational environments, gears are highly susceptible to failures such as wear, cracks, and tooth breakage [3]. Failing to detect such faults in a timely manner may exacerbate the damage, thereby causing more substantial losses. Therefore, the research on fault diagnosis of planetary gearboxes holds crucial academic and engineering significance.
The vibration signals of planetary gearboxes contain rich information and are widely used in fault diagnosis [4,5,6]. The structure of planetary gearboxes is typically symmetric, and their vibration signals should exhibit symmetry. However, when collecting vibration signals, complex transmission paths and environmental noise can disrupt such symmetry, leading to characteristics such as weak fault features, strong nonlinearity, low signal-to-noise ratio, and modulation [7,8]. At present, fault diagnosis methods for planetary gearboxes based on vibration signals can be divided into two categories: feature extraction-based classification methods and deep learning-based methods [1,9]. While deep learning-based fault diagnosis methods can achieve effective fault diagnosis, their widespread application is constrained by the requirement for massive data samples and substantial computational time [10]. Moreover, the “black-box” nature of deep learning models renders their feature mapping processes difficult to interpret, precluding effective analysis of fault mechanisms. In contrast, feature extraction-based classification methods not only enable accurate classification but also reveal the intrinsic relationships between signals and faults, thereby facilitating in-depth research on fault mechanisms [11]. However, extracting effective fault features from complex vibration signals containing both symmetrical and asymmetrical components has become a critical challenge in the fault diagnosis of planetary gearboxes.
Many signal processing methods have been proposed to extract fault feature information embedded in vibration signals [11]. Time domain analysis methods can intuitively detect faults by analyzing information such as the peak value, kurtosis, and variance of time domain waveforms [12,13]. These methods offer strong real-time performance but are insensitive to early-stage weak faults [10]. Frequency domain analysis methods transform time domain signals into the frequency domain and identify faults by analyzing changes in fault characteristic frequencies, such as rotational frequency, meshing frequency, and sideband frequency [14,15]. Although these methods have clear physical meanings, they cannot effectively describe the time domain variation characteristics of signals [16]. Time–frequency analysis methods, which can well describe how signal frequency components change over time [17], are widely used in vibration signal analysis, such as wavelet transform (WT) [18], empirical mode decomposition (EMD) [19], and variational mode decomposition (VMD) [20]. WT requires reasonable customization of wavelet-basis thresholds during decomposition to distinguish close frequency components [21], while EMD and VMD may suffer from mode mixing [22,23]. These limitations may render time–frequency analysis methods ineffective at distinguishing the features of the rotational frequency, meshing frequency, harmonics, and sideband frequencies of planetary gearboxes. Several studies have also indicated that the incorporation of denoising methods in signal processing can effectively enhance the accuracy of fault diagnosis [24,25].
Entropy is a crucial characteristic parameter that reflects the complexity, irregularity, and uncertainty of time series [26]. Many entropy methods have been proposed and applied to vibration signal analysis for fault diagnosis, such as sample entropy (SE) [27], permutation entropy (PE) [28], dispersion entropy (DE) [29], and fuzzy entropy (FE) [30]. Compared with other entropy methods, FE exhibits stronger robustness to noise and sample data length, better capability in descripting the nonlinear relationships of signals, and lower sensitivity to parameter selection [31]. To describe the complexity of signals at multiple time scales, multi-scale fuzzy entropy (MFE) was proposed based on multi-scale coarse-grained signals [32]. However, as the time scale expands, the coarse-grained sequence becomes substantially shorter, resulting in insufficient data for precise entropy estimation [33]. This ultimately compromises the stability and reliability of entropy calculations. The refined composite multi-scale fuzzy entropy (RCMFE) method enhances entropy calculation accuracy and reliability by employing a window translation approach to compute weighted averages across multiple coarse-grained sequences [34].
Another critical issue in fault diagnosis lies in establishing the correspondence between fault features and fault types. Machine learning-based classification methods offer an effective approach to solving this problem and have been widely applied. Backpropagation (BP) neural networks exhibit relatively low training efficiency and lack interpretability in their feature classification outcomes [35]. While the K-nearest neighbors (KNN) method requires no explicit training phase and offers strong interpretability for feature classification, it suffers from low prediction efficiency [36]. Support vector machines (SVMs) demonstrate robust capabilities in handling nonlinear relationships and achieve high prediction efficiency [37]. However, their training efficiency degrades significantly with large-scale datasets due to the computational burden of solving the quadratic programming (QP) problem inherent in their training processes [38]. Least squares support vector machines (LSSVMs) address this limitation by transforming the QP problem into a system of solving linear equations [39]. This modification substantially enhances training efficiency and provides a degree of interpretability regarding the classification of feature samples. Despite their numerous advantages, the performance of LSSVMs is heavily dependent on the selection of their hyperparameters [40]. Consequently, various optimization algorithms, including the genetic algorithm (GA) [41], the sparrow search algorithm (SSA) [42], particle swarm optimization (PSO) [43], and the gray wolf optimizer (GWO) [44,45], have been employed to optimize the parameters of LSSVMs. However, searching for more efficient optimization methods to optimize LSSVMs has always been a research hotspot among scholars.
In this paper, an adaptive multi-bandpass filter (AMBPF) is proposed and combined with RCMFE for fault feature extraction in planetary gearboxes. The AMBPF employs a combination of multiple bandpass filters to individually isolate each characteristic frequency and its associated sidebands. Crucially, the bandwidth of each filter is adaptively determined based on the trace ratio of fuzzy entropy for different signal classes. Feature vectors for fault diagnosis are constructed by computing the RCMFE of the multiple signal components extracted by the AMBPF system. Furthermore, the dream optimization algorithm (DOA) [46] is employed to optimize the parameters of the LSSVM, aiming to enhance its classification efficiency. Overall, this paper proposes a novel fault diagnosis method for planetary gearboxes, integrating the AMBPF, RCMFE, and DOA-LSSVM. The experimental results demonstrate that the proposed method achieves significantly higher diagnostic efficiency and exhibits superior noise immunity in planetary gearbox fault diagnosis.
The organization of this paper is as follows: the methods used in this paper are introduced in Section 2, including the RCMFE, AMBPF, and DOA-LSSVM. Section 3 presents the framework diagram of the proposed fault diagnosis method. In Section 4, the proposed feature extraction method and fault diagnosis method are applied to a planetary gearbox in experimental studies. Finally, the conclusion and main contributions are drawn in Section 5.
2. Methods
2.1. RCMFE
RCMFE is a nonlinear dynamic signal analysis method. It employs a moving average approach to compute the multi-scale fuzzy entropy, offering advantages such as enhanced computational stability and reduced estimation errors [33]. The primary computational steps of RCMFE for a given time series are as follows [47]:
For a given scale factor, τ, the original time series is subjected to a coarse-graining procedure, as follows:
where denotes the coarse-grained time series, and τ denotes the distinct sequences derived from the original signal as .
The coarse-grained time series is mapped to a high-dimensional reconstruction space as follows:
where m denotes the embedding dimension.
The similarity distance between adjacent state vectors in the reconstruction space is computed using the Chebyshev distance metric, as follows:
where is the similarity distance between and .
The fuzzy similarity distance between adjacent state vectors is subsequently transformed through an exponential fuzzy membership function, as follows:
where n and r are the gradient steepness and bandwidth of the fuzzy membership function.
The similarity between high-dimensional sequences is calculated as follows:
RCMFE is calculated as follows:
2.2. Adaptive Multi-Bandpass Filter
Vibration signals in planetary gearboxes are predominantly characterized by harmonic components resulting from gear meshing dynamics. These components typically manifest as the fundamental gear meshing frequency and its harmonics. During operational fault development, characteristic sideband components frequently emerge surrounding these primary meshing frequencies [48], as depicted in Figure 1. Both the meshing frequencies and their corresponding sidebands which have symmetry represent essential diagnostic signatures for fault identification.
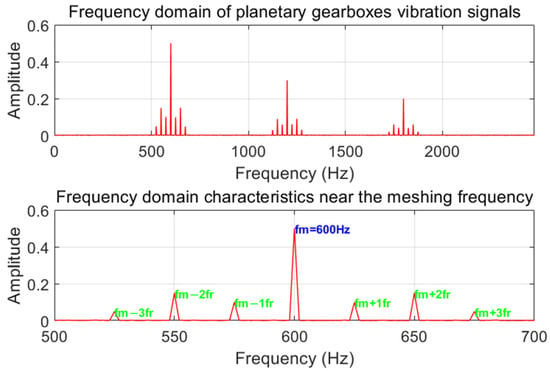
Figure 1.
Schematic diagram of spectral characteristics in a planetary gearbox.
Due to the complex kinematic structure of planetary gearboxes, their vibration signals exhibit numerous meshing frequency harmonics and intricate sideband patterns [5]. To effectively extract diagnostic information embedded within these meshing frequency components and associated sidebands, an adaptive multi-bandpass filter (AMBPF) is proposed for signal separation in this paper. This approach isolates individual meshing frequency constituents and their corresponding sideband structures for independent feature extraction. The schematic diagram of the proposed AMBPF is illustrated in Figure 2.
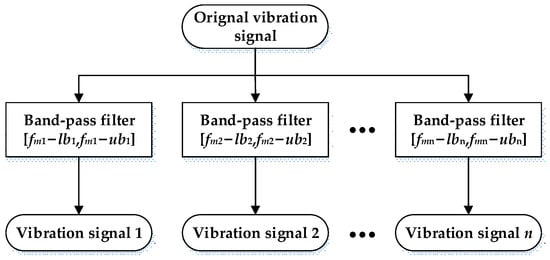
Figure 2.
Schematic diagram of the AMBPF.
Where fmi (i = 1, 2, …, n) represent the dominant meshing frequencies and their harmonics. The detail values can be obtained from gearbox parameters and operational conditions. [fmi − lbi, fmi − ubi] represent the lower and upper bounds of the bandpass filter which require careful selection to ensure the transmission of both primary meshing frequencies and their fault-indicative sideband components. To address this, we propose an adaptive boundary determination method based on multi-scale fuzzy entropy and trace ratio optimization. The implementation procedure comprises the following steps:
Step 1: Planetary gearbox vibration samples are filtered through the bandpass filter with passband [fmi − lbi, fmi − ubi]. Then, the multi-scale fuzzy entropy is computed for each filtered signal with scale factor τ. Consider C to be distinct operational states represented in the dataset. The sample count of the i-th class is . The multi-scale fuzzy entropy value and its mean value vector of the i-th class are (j = 1, 2, …, ) and , respectively. The mean value vector of MFE across all samples is .
Step 2: The within-class scatter matrix and the between-class scatter matrix are calculated as follows [49]:
where and have the dimensions τ × τ. A smaller intra-class scatter indicates greater compactness within each category, thereby enhancing discriminability during classification. Conversely, a larger inter-class scatter signifies greater separation between class centroids, which facilitates class separation.
Step 3: The trace ratio of the inter-class scatter matrix to the intra-class scatter matrix is calculated as follows:
where represents the trace of a matrix. Maximizing the trace ratio achieves optimal inter-sample separability, thus adaptively determining the optimal bandpass filter parameters through the following optimization:
2.3. LSSVM Parameter Optimization by DOA
2.3.1. LSSVM
An LSSVM is an enhanced variant of an SVM; it demonstrates promising performance in data classification [38]. The fundamental principle is formalized as follows:
For a given d-dimensional input sample U = {Ui | i = 1, 2, …, Ns}, the output is T = {Ti | i = 1, 2, …, Ns}, and the LSSVM decision function is formulated as:
where denotes the weight vector, b represents the bias, and constitutes the nonlinear mapping function.
The optimization objective of an LSSVM with equality constraints admits the following formulation:
where is the regularization parameter and represents the i-th slack variable.
By introducing Lagrange multipliers and selecting an appropriate kernel function, the LSSVM model is derived as
where is the Lagrange coefficient and K(·) is the kernel function.
As evidenced by Equations (11) and (12), both the regularization parameter and the kernel function parameters directly govern the classification accuracy of the LSSVM. So, the hyperparameter optimization can enhance model performance.
2.3.2. DOA
The dream optimization algorithm (DOA) proposed by Lang et al. (2025) [46], is a dream-inspired metaheuristic algorithm that integrates memory retention, forgetting replenishment, and dream sharing strategies. This synthesis endows DOA with exceptional computational stability, potent exploration capacity, and robust local optima evasion capabilities.
Consider an optimization problem of dimensionality D. The decision variables are bounded within the lower and upper limits, denoted as BL and BU, respectively. The objective is to minimize the fitness value Fitnessmin and identify the corresponding optimal solution . The DOA is primarily divided into three phases—the initialization phase, the exploration phase, and the exploitation phase—as follows:
- (1)
- Initialization phase
The initial parameters are defined as follows: population size Np, maximum iteration count Tmax, demarcation iteration Td, and exploitation forgetting dimension coefficient kr. The initial positions of individuals within the population are initialized according to the following equation:
where represents the value of the j-th dimension of the i-th individual in the population. rand represents a random number between 0 and 1. and represent the low boundary and upper boundary of the j-th dimension.
- (2)
- Exploration phase
During the exploration phase (iteration count from 0 to Td), individuals are partitioned into q groups based on differing memory capacities. Within each group, individuals update their positions by inheriting the positions of the best-performing individual from each group in the previous iteration through a memory-based strategy, as follows:
where denotes the initial position of the i-th individual (belonging to e-th group) at (t + 1)-th iteration, and represents the position of the optimal individual in the e-th group at the t-th iteration.
During iteration, individuals undergo a dual mechanism of dimension forgetting and replenishment. This strategy entails forgetting position information in selected dimensions while acquiring updated positional data for these dimensions through replenishment, thereby balancing the global and local search capabilities of the DOA.
Owing to heterogeneous memory capacities across groups, the number of forgetting dimensions of each group is different and is denoted as k1, k2, …, kq. Within the e-th group, ke is randomly selected from the D-dimensional space of each individual; the dimension index set is , and their positions are updated as follows:
where denotes the position of the j-th dimension of the i-th individual at the (t + 1)-th iteration. represents the position of the j-th dimension of the optimal individual in the e-th group at the t-th iteration.
To enhance the local optimum escape capability of the DOA, a dream sharing strategy is incorporated during the exploration phase. This strategy operates concurrently with the dimension forgetting and replenishment mechanism, allowing individuals to randomly adopt positional information from other individuals in the forgetting dimensions to update their positions as follows:
where m is a random integer ranging from 1 to Np.
- (3)
- Exploitation phase
During the exploitation phase (iteration count from Td to Tmax), the population is no longer divided into groups, and all individuals undergo iterative updates collectively. During this phase, the memory strategy is still employed to inherit the positions of the optimal individuals from the previous iteration, as follows:
where denotes the position of the globally optimal individual after the t-th iteration, and denotes the initial position of the i-th individual at the (t + 1)-th iteration.
Since all individuals in the population share the same forgetting dimension kr, kr dimensions are randomly selected from the D-dimensional space, and the position update is performed using the forgetting supplementation strategy as follows:
where denotes the position of the j-th dimension of the i-th individual at the (t + 1)-th iteration. denotes the position of the j-th dimension of the optimal individual in the population after the t-th iteration.
Through iterative optimization in the initialization, exploration, and development phases, the algorithm can efficiently search for the global optimal solution in the search space and avoid falling into local optima.
2.3.3. DOA-LSSVM
The DOA is employed to optimize the parameters and , aiming to enhance its classification efficiency. Meanwhile, 10-fold cross-validation is applied to the sample data as the objective function for parameter optimization to improve the generalization ability of LSSVM classification. The specific process is illustrated in Figure 3.
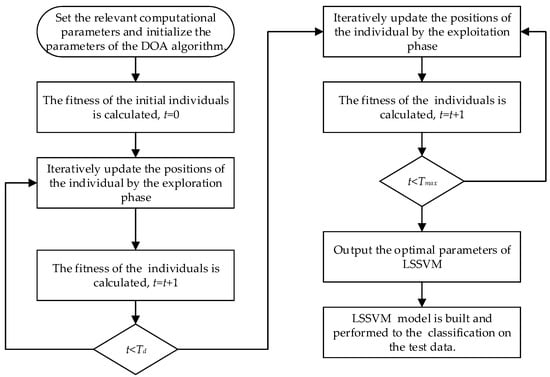
Figure 3.
The Flowchart of DOA-LSSVM.
3. The Proposed Fault Diagnosis Method
In this paper, a feature extraction method based on AMBPF and RCMFE is proposed and the DOA-LSSVM is also proposed to enhance classification efficiency. The framework diagram of the planetary gearbox fault diagnosis method proposed in this paper is illustrated in Figure 4.
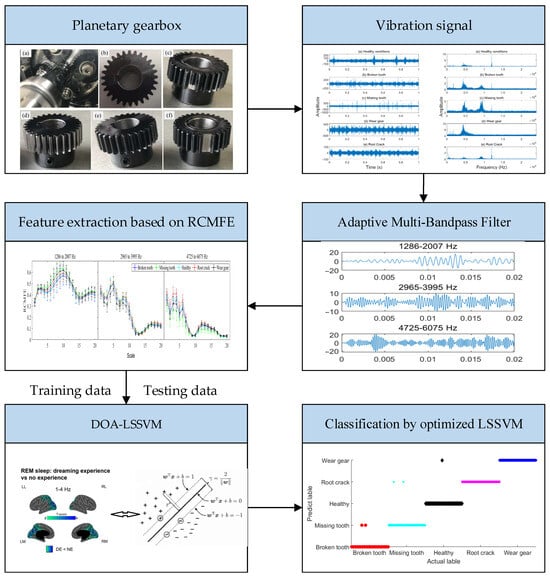
Figure 4.
The framework diagram of the proposed fault diagnosis method.
The specific steps of the proposed fault diagnosis method are as follows:
Step 1: The vibration signals of the planetary gearbox are acquired, and the proposed AMBPF method is used to obtain signals at different bandpass frequencies. These signals can better reflect the characteristics of the main meshing frequencies and their sideband frequencies.
Step 2: For signals passed through different bandpass filters, RCMFE is employed to extract the embedded feature information and construct feature vectors.
Step 3: The DOA is adopted to optimize the hyperparameters of the LSSVM, thereby enhancing the classification efficiency of the LSSVM.
Step 4: The vibration signal data of the planetary gearbox under different operating conditions are utilized to train and validate the proposed fault diagnosis model.
4. Experiment Studies
4.1. Experiments and Data Description
The publicly accessible dataset named ‘WT-Planetary gearbox dataset’, which is provided by Liu et al. [1], was utilized to validate the proposed fault diagnosis method in this paper. The vibration dataset can be obtained at the following link: https://github.com/Liudd-BJUT/WT-planetary-gearbox-dataset (accessed on 5 November 2024). The vibration signals of this dataset were collected from a planetary gearbox with a single-row planetary gear structure using an experimental test setup. The experimental setup is composed of a drive motor, a planetary gearbox, a fixed-shaft gearbox, a load, and a vibration signal measurement and acquisition device, whose structure is shown in Figure 5 [1]. The intrinsic parameters of the planetary gearbox, operating parameters, and parameters of the sampling device are listed in Table 1.

Figure 5.
Diagram of the experimental setup.

Table 1.
The parameters of the planetary gearbox and the sampling device.
The experimental setup was used to acquire vibration data of the planetary gearbox under five different operating conditions of the sun gear (healthy, broken tooth, missing tooth, wear gear, and root crack) at varying rotational speeds, and the vibration signal of planetary gearbox was collected by the vibration signal measurement and acquisition device. Since the initial parameters of the AMBPF proposed in this paper require estimating the main frequencies and their harmonics of the planetary gearbox based on the sun gear’s rotational frequency, the effectiveness of the proposed feature extraction and fault diagnosis method at a sun gear rotational frequency of 20 Hz are given in Section 4.2 and Section 4.3. The generalization ability of the proposed method under different sun gear rotational frequencies is validated in Section 4.4. The time domain and frequency domain waveforms of the original vibration signals collected under different operating conditions at a rotational frequency of 20 Hz are shown in Figure 6. To verify the fault diagnosis capability of the proposed method in noisy environments, white noise with a signal-to-noise ratio (SNR) of 3 dB was added to the original vibration signals, and their time domain and frequency domain waveforms are shown in Figure 7.
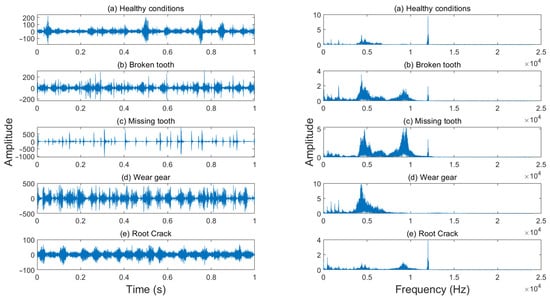
Figure 6.
Original time and frequency domain waveforms of vibration signals (fr = 20 Hz).
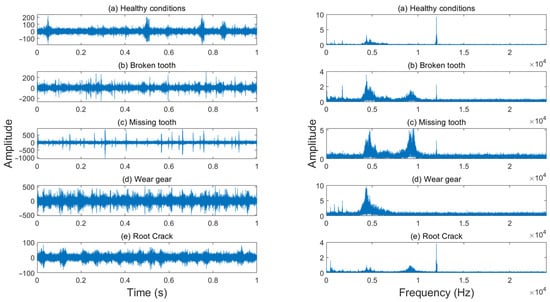
Figure 7.
Time and frequency domain waveforms of vibration signals with additional white noise SNR = 3 dB (fr = 20 Hz).
The original dataset needs to be divided into several sample sets under different operating conditions to verify the effectiveness of the proposed fault diagnosis method. Since the public sample set has a large amount of data for each condition, the vibration data collected for each operating condition in this paper are equally divided into 400 groups. In total, 1024 consecutive data points were randomly selected from each group as sample data. A total of 80% of the samples in each group were used as training samples, and 20% were used as test samples.
4.2. Comparison of Feature Extraction
To verify the effectiveness of the proposed feature extraction method, AMBPF-RCMFE was employed to extract features from the sample data. As shown in Table 1, the dominant meshing frequencies of the planetary gearbox are 437.5 Hz and 1750 Hz at a sun gear rotational frequency of 20 Hz. Through the spectral analysis of the planetary gearbox, it was found that the maximum dominant frequency was close to 12,000 Hz. Therefore, the center frequencies of the filters used in this paper were set as {437.5, 1750, 3500, 5250, 7000, 8750, 10,500, and 12,250} Hz. Through the optimization of the filtering parameters of the multi-channel filter using the proposed AMBPF in this paper, the bandwidths of the multi-channel bandpass filters were obtained as {[179, 667], [1286, 2007], [2965, 3995], [4725, 6075], [6735, 7875], [8310, 9625], [10,001, 11,063], and [11,716, 12,670]} Hz. The filtered signals were processed by RCMFE to obtain the sample features. The features extracted from several channels of AMBPF-RCMFE were compared with those directly extracted by refined composite multi-scale sample entropy (RCMSE), refined composite multi-scale dispersion entropy (RCMDE), and RCMFE to the vibration signals. The software for RCMSE, RCMDE, and RCMFE can be obtained from https://github.com/HamedAzami/NLDyn/blob/main/Final_V10p.rar (accessed on 24 December 2024). The mean and SD values of the different entropy feature extraction methods across 400 group samples for each five operating states are shown in Figure 8 and Figure 9.
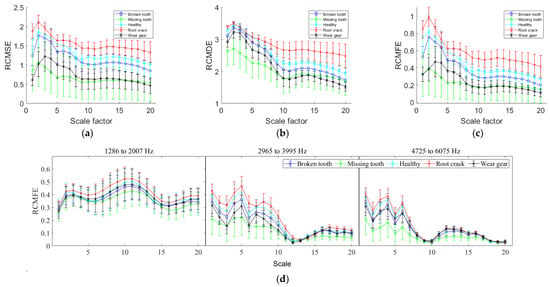
Figure 8.
Feature extraction by different methods with original vibration data. (a) RCMSE; (b) RCMDE; (c) RCMFE; and (d) AMBPF-RCMFE (some of BPF).
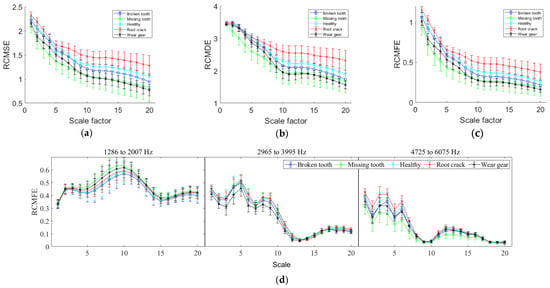
Figure 9.
Feature extraction by different methods with additional white noise SNR = 3 dB. (a) RCMSE; (b) RCMDE; (c) RCMFE; and (d) AMBPF-RCMFE (some of BPF).
It can be observed from Figure 8 and Figure 9 that the multi-scale entropy-based features can distinguish different states in some scales, indicating that multi-scale entropy can serve as a fault diagnosis feature for planetary gearboxes. Additionally, the discriminability of features without additional noise is significantly better than that with added noise, indicating that noise has an adverse effect on fault feature extraction.
Since multi-scale entropy requires the joint comparison of differences across multiple scales to distinguish different states, it is difficult to intuitively observe the advantages and disadvantages of each fault feature extraction method. To address this problem, supervised t-stochastic neighbor embedding (S-t-SNE) [50] is utilized for visual dimensionality reduction in this paper. The results after S-t-SNE dimensionality reduction are shown in Figure 10 and Figure 11.

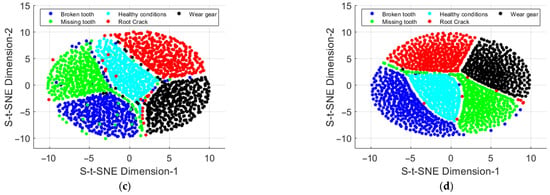
Figure 10.
Feature extraction by different methods with original vibration data. (a) RCMSE; (b) RCMDE; (c) RCMFE; and (d) AMBPF-RCMFE.
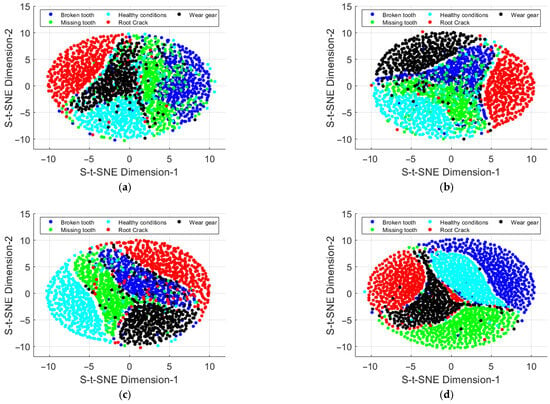
Figure 11.
Feature extraction by different methods with additional white noise SNR = 3 dB. (a) RCMSE; (b) RCMDE; (c) RCMFE; and (d) AMBPF-RCMFE.
It can be observed from Figure 10 and Figure 11 that features based on RCMSE exhibit blurred boundaries across different operating states. RCMDE-based features show distinct discrimination boundaries without additional noise, though some samples fail to cluster effectively. The discriminative boundaries of RCMDE features become blurred in the presence of added noise. While RCMFE-based features demonstrate relatively clear boundaries across operating states, a significant number of samples are misclassified, a phenomenon exacerbated by additional noise. In contrast, the AMBPF-RCMFE feature extraction method effectively discriminates all operating states both with and without added noise, confirming its robust feature extraction capability and noise suppression performance.
The proposed AMF-RCMFE combined with DOA-LSSVM was employed for the fault diagnosis of the planetary gearbox. The software of the DOA and LSSVM can be obtained via the following links: https://ww2.mathworks.cn/matlabcentral/fileexchange/178419-dream-optimization-algorithm-doa (accessed on 6 May 2025) and http://www.esat.kuleuven.be/sista/lssvmlab (accessed on 16 December 2024), respectively. Comparative analyses were conducted with feature extraction based on RCMSE, RCMDE, and RCMFE. A total of 1600 samples (80% of the dataset) were used for training, while the remaining 400 samples (20%) were applied for validation. The fault diagnosis results by different feature extraction methods are shown in Figure 12.
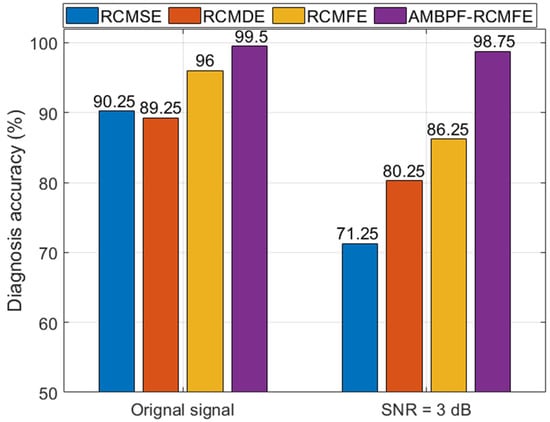
Figure 12.
Fault diagnosis results by different feature extraction methods.
It can be seen from Figure 12 that without adding additional noise, the fault diagnosis accuracy rates based on RCMSE and RCMDE are 90.25% and 89.25%, respectively. However, when the noise level increases, the fault diagnosis accuracy rates drop significantly. The fault diagnosis accuracy rate based on RCMFE performs satisfactorily without additional noise, reaching 96%, but only 86% under the condition of 3 dB of additional noise. The AMBPF-RCMFE feature extraction method proposed in this paper shows good fault diagnosis performance in both cases, with the fault diagnosis accuracy rates reaching 99.5% and 98.75%, respectively. The above results show that the proposed feature extraction method can effectively extract the operational characteristics of the planetary gearbox and has strong noise suppression capability.
The confusion matrix for the diagnosis results of the proposed fault diagnosis method is presented in Figure 13.
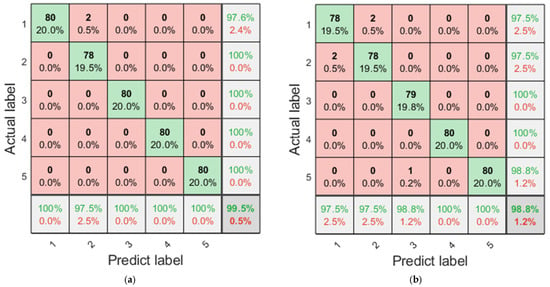
Figure 13.
The confusion matrix for the diagnosis results of the proposed fault diagnosis method. (a) Original signal; (b) SNR = 3 dB. (The meanings of the labels: 1—broken tooth, 2—missing tooth, 3—healthy, 4—root crack, and 5—wear gear.)
As can be seen from Figure 13, under the condition of no additional noise, two samples of the “missing tooth” state were misdiagnosed as the “broken tooth” state, with all other diagnoses being correct. In the presence of additional noise, misdiagnoses still tend to occur between the “missing tooth” and “broken tooth” states. Nevertheless, the overall diagnostic accuracy remained favorable in both scenarios.
4.3. Comparison of the Proposed Fault Diagnosis Method
In this section, verification research is conducted on the DOA-LSSVM proposed in this paper. Firstly, to demonstrate the superiority of the DOA, it was compared with PSO and GWO in optimizing LSSVM. The parameters of different optimization algorithms are listed in Table 2. Figure 14 shows the convergence curves of the average misdiagnosis rate for the LSSVM models optimized by different algorithms over 10 runs.

Table 2.
The parameters of different optimization algorithms.
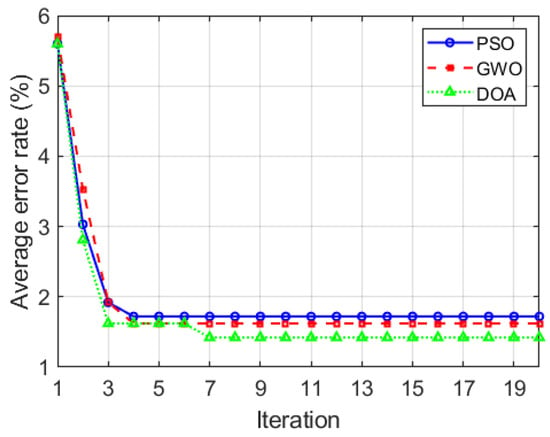
Figure 14.
Comparison of average convergence curves for different optimization algorithms (10 runs).
It can be observed from Figure 14 that the DOA outperforms both PSO and GWO in terms of convergence speed and optimal value search capability, demonstrating that the DOA has a strong global exploration ability and the capacity to escape local optima. The decrease in the objective function during the optimization process indicates that the optimization of LSSVM hyperparameters can effectively improve fault classification efficiency.
Then, the proposed DOA-LSSVM was compared to a BP neural network, SVM, and LSSVM for classification performance based on different features (based on the signal with additional white noise SNR = 3 dB). The fault diagnosis results are shown in Figure 15.
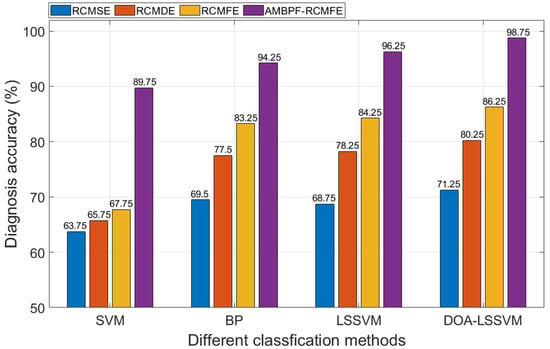
Figure 15.
Fault diagnosis results of different classification methods with different features extraction methods.
It can be observed from Figure 15 that, regardless of the classification method, the fault feature extraction method proposed in this paper outperforms the feature extraction methods of RCMSE, RCMDE, and RCMFE. Under the same feature extraction method, the performance of the proposed DOA-LSSVM is superior to that of the BP neural network, SVM, and LSSVM. The above results indicate that the proposed DOA-LSSVM fault diagnosis method possesses an excellent classification capability.
4.4. Fault Diagnosis for Different Rotating Frequencies
To verify the generalization ability of the proposed fault diagnosis method under different sun gear rotational speeds, vibration signals under different operating conditions at sun gear rotational frequencies of 20 Hz, 30 Hz, 40 Hz, and 50 Hz were used for fault diagnosis. The fault diagnosis results are shown in Figure 16.
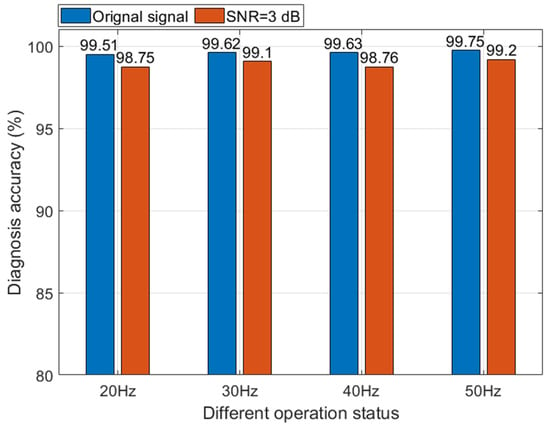
Figure 16.
The fault diagnosis accuracy of the proposed method under different rotating frequencies.
The results show that the proposed method exhibits high fault diagnosis efficiency for different rotational speeds and under background noise conditions. In the absence of additional noise, the fault diagnosis accuracy rate exceeds 99.51%. When subjected to 3 dB of additional noise, the fault diagnosis accuracy rate still exceeds 98.75%. The results indicate that the proposed method has good generalization ability.
In addition, the simulation study of the method proposed in this paper was conducted on a computer (Lenovo made in China) equipped with an Intel i7-8700 CPU in Suqian, China. The method was programmed and implemented using MATLAB 2022b. Under single-thread operation, the average diagnostic time for each sample is 1.204 s, and the diagnostic speed can meet the requirements of some real engineering application scenarios.
5. Conclusions
Effective fault feature extraction and classification methods are crucial for efficient fault diagnosis in planetary gearboxes. In this paper, an AMBPF-RCMFE fault feature extraction method is proposed which can fully reflect the variations in meshing frequencies and their sideband frequencies during changes in the operational state of a planetary gearbox. Additionally, a DOA-LSSVM fault classification method is proposed to enhance fault diagnosis efficiency. The following conclusions are drawn from the experimental studies:
- (1)
- Through visual dimensionality reduction in features extracted by different methods, it is evident that the features extracted by the proposed AMBPF-RCMFE exhibit strong boundary discrimination between samples of different states and an excellent clustering effect among samples of the same state, both with and without additional noise. The classifiability of the proposed method is significantly superior to that extracted by RCMSE, RCMDE, and RCMFE.
- (2)
- The DOA optimization algorithm demonstrates a faster convergence speed and stronger optimal value search capability than PSO and GWO. After optimizing the hyperparameters of the LSSVM, it effectively improves the fault diagnosis classification efficiency of the model.
- (3)
- The proposed method exhibits strong noise suppression capability. The fault diagnosis accuracy rates reach 98.75% with an additional 3 dB of noise. Meanwhile, it achieves high diagnostic efficiency under different operating conditions and rotational speeds; the accuracy rate of fault diagnosis exceeds 99.51% and 98.75% in the absence of additional noise and in the presence of additional noise, respectively.
Author Contributions
Methodology, X.X.; software, A.W.; formal analysis, X.X.; data curation, H.S. and X.X.; writing—original draft, X.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Jiangsu Engineering Research Center of Key Technology for Intelligent Manufacturing Equipment and the Suqian Key laboratory of Intelligent Manufacturing (Grant No. M202108).
Data Availability Statement
The data that support the findings of this study are available upon request from the authors. The data are not publicly available due to [The dataset is large in size, and there is no suitable server for making the data publicly available].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, D.; Cui, L.; Cheng, W. A review on deep learning in planetary gearbox health state recognition: Methods, applications, and dataset publication. Meas. Sci. Technol. 2023, 35, 012002. [Google Scholar] [CrossRef]
- Chen, R.; Huang, X.; Yang, L.; Xu, X.; Zhang, X.; Zhang, Y. Intelligent fault diagnosis method of planetary gearboxes based on convolution neural network and discrete wavelet transform. Comput. Ind. 2019, 106, 48–59. [Google Scholar] [CrossRef]
- Hilbert, M.; Smith, W.A.; Randall, R.B. The effect of signal propagation delay on the measured vibration in planetary gearboxes. J. Dyn. Monit. Diagn. 2022, 1, 9–18. [Google Scholar] [CrossRef]
- Feng, Z.; Zuo, M.J. Vibration signal models for fault diagnosis of planetary gearboxes. J. Sound Vib. 2012, 331, 4919–4939. [Google Scholar] [CrossRef]
- Nie, Y.; Li, F.; Wang, L.; Li, J.; Wang, M.; Sun, M.; Li, Y. Phenomenological vibration models of planetary gearboxes for gear local fault diagnosis. Mech. Mach. Theory 2022, 170, 104698. [Google Scholar] [CrossRef]
- Nie, Y.; Wang, L.; Li, F.; Li, J.; Cui, P.; Hu, J.; Li, G.; Li, Y. A novel mathematical model of transmission path effect for the research of vibration characteristics of planetary gearboxes. Mech. Mach. Theory 2022, 176, 105022. [Google Scholar] [CrossRef]
- Lei, Y.; Han, D.; Lin, J.; He, Z. Planetary gearbox fault diagnosis using an adaptive stochastic resonance method. Mech. Syst. Signal Process. 2013, 38, 113–124. [Google Scholar] [CrossRef]
- Mo, S.; Liu, Y.; Huang, X.; Zhang, W. Nonlinear vibration and superharmonic resonance analysis of wind power planetary gear system. Nonlinear Dyn. 2024, 112, 4085–4115. [Google Scholar] [CrossRef]
- Sharma, V. A Review on Vibration-Based Fault Diagnosis Techniques for Wind Turbine Gearboxes Operating Under Nonstationary Conditions. J. Inst. Eng. (India) Ser. C 2021, 102, 507–523. [Google Scholar] [CrossRef]
- Ma, S.; Chu, F.; Han, Q. Deep residual learning with demodulated time-frequency features for fault diagnosis of planetary gearbox under nonstationary running conditions. Mech. Syst. Signal Process. 2019, 127, 190–201. [Google Scholar] [CrossRef]
- Zhang, C.; Mousavi, A.A.; Masri, S.F.; Gholipour, G.; Yan, K.; Li, X. Vibration feature extraction using signal processing techniques for structural health monitoring: A review. Mech. Syst. Signal Process. 2022, 177, 109175. [Google Scholar] [CrossRef]
- Zimroz, R.; Bartkowiak, A. Two simple multivariate procedures for monitoring planetary gearboxes in non-stationary operating conditions. Mech. Syst. Signal Process. 2013, 38, 237–247. [Google Scholar] [CrossRef]
- Feng, Z.; Zuo, M.J. Fault diagnosis of planetary gearboxes via torsional vibration signal analysis. Mech. Syst. Signal Process. 2013, 36, 401–421. [Google Scholar] [CrossRef]
- Sawalhi, N. Vibration sideband modulations and harmonics separation of a planetary helicopter gearbox with two different configurations. Adv. Acoust. Vib. 2016, 1, 9820768. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, K.; Wei, D.; Zuo, M.J. Amplitudes of characteristic frequencies for fault diagnosis of planetary gearbox. J. Sound Vib. 2018, 432, 119–132. [Google Scholar] [CrossRef]
- He, G.; Ding, K.; Li, W.; Li, Y. Frequency response model and mechanism for wind turbine planetary gear train vibration analysis. IET Renew. Power Gener. 2017, 11, 425–432. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M. Fault diagnosis of wind turbine planetary gearbox under nonstationary conditions via adaptive optimal kernel time–frequency analysis. Renew. Energy 2014, 66, 468–477. [Google Scholar] [CrossRef]
- Khazaee, M.; Ahmadi, H.; Omid, M.; Banakar, A.; Moosavian, A. Feature-level fusion based on wavelet transform and artificial neural network for fault diagnosis of planetary gearbox using acoustic and vibration signals. Insight-Non-Destr. Test. Cond. Monit. 2013, 55, 323–330. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.; Yang, X.; Dong, C. A Fault Feature Extraction Method for Motor Bearing and Transmission Analysis. Symmetry 2017, 9, 60. [Google Scholar] [CrossRef]
- Liu, C.; Cheng, G.; Chen, X.; Pang, Y. Planetary gears feature extraction and fault diagnosis method based on VMD and CNN. Sensors 2018, 18, 1523. [Google Scholar] [CrossRef]
- Teng, W.; Ding, X.; Cheng, H.; Han, C.; Liu, Y.; Mu, H. Compound faults diagnosis and analysis for a wind turbine gearbox via a novel vibration model and empirical wavelet transform. Renew. Energy 2019, 136, 393–402. [Google Scholar] [CrossRef]
- Cheng, G.; Chen, X.; Li, H.; Li, P.; Liu, H. Study on planetary gear fault diagnosis based on entropy feature fusion of ensemble empirical mode decomposition. Measurement 2016, 91, 140–154. [Google Scholar] [CrossRef]
- Wei, S.; Wang, D.; Peng, Z.; Feng, Z. Variational nonlinear component decomposition for fault diagnosis of planetary gearboxes under variable speed conditions. Mech. Syst. Signal Process. 2022, 162, 108016. [Google Scholar] [CrossRef]
- Han, D.; Qi, H.; Wang, S.; Hou, D.; Kong, J.; Wang, C. Adaptive maximum generalized Gaussian cyclostationarity blind deconvolution for the early fault diagnosis of high-speed train bearings under non-Gaussian noise. Adv. Eng. Inform. 2024, 62, 102731. [Google Scholar] [CrossRef]
- Han, D.; Qi, H.; Hou, D.; Wang, S.; Kong, J.; Xu, X.; Wang, C. Dynamic detection mechanism model of acoustic emission for high-speed train axle box bearings with local defects. Mech. Syst. Signal Process. 2025, 235, 112943. [Google Scholar] [CrossRef]
- Aguayo-Tapia, S.; Avalos-Almazan, G.; Rangel-Magdaleno, J.D.J. Entropy-based methods for motor fault detection: A review. Entropy 2024, 26, 299. [Google Scholar] [CrossRef]
- Li, Y.; Feng, K.; Liang, X.; Zuo, M.J. A fault diagnosis method for planetary gearboxes under non-stationary working conditions using improved Vold-Kalman filter and multi-scale sample entropy. J. Sound Vib. 2019, 439, 271–286. [Google Scholar] [CrossRef]
- Kuai, M.; Cheng, G.; Pang, Y.; Li, Y. Research of Planetary Gear Fault Diagnosis Based on Permutation Entropy of CEEMDAN and ANFIS. Sensors 2018, 18, 782. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.C.; Ni, Q. A novel adaptive bandwidth selection method for Vold–Kalman filtering and its application in wind turbine planetary gearbox diagnostics. Struct. Health Monit. 2023, 22, 1027–1048. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy. Mech. Mach. Theory 2013, 70, 441–453. [Google Scholar] [CrossRef]
- Luukka, P. Feature selection using fuzzy entropy measures with similarity classifier. Expert Syst. Appl. 2011, 38, 4600–4607. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wang, R.; Huang, W. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. J. Sound Vib. 2016, 360, 277–299. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Tong, J.; Liu, Q. Generalized refined composite multiscale fuzzy entropy and multi-cluster feature selection based intelligent fault diagnosis of rolling bearing. ISA Trans. 2022, 123, 136–151. [Google Scholar] [CrossRef] [PubMed]
- Minhas, A.S.; Singh, G.; Singh, J.; Kankar, P.K.; Singh, S. A novel method to classify bearing faults by integrating standard deviation to refined composite multi-scale fuzzy entropy. Measurement 2020, 154, 107441. [Google Scholar] [CrossRef]
- Strączkiewicz, M.; Barszcz, T. Application of artificial neural network for damage detection in planetary gearbox of wind turbine. Shock. Vib. 2016, 1, 4086324. [Google Scholar] [CrossRef]
- Gbashi, S.M.; Adedeji, P.A.; Olatunji, O.O.; Madushele, N. Optimal feature selection for a weighted k-nearest neighbors for compound fault classification in wind turbine gearbox. Results Eng. 2025, 25, 103791. [Google Scholar] [CrossRef]
- Lihui, C.; Yang, L.; Donghua, Z. Fault diagnosis of the planetary gearbox based on ssDAG-SVM. IFAC-PapersOnLine 2018, 51, 263–267. [Google Scholar] [CrossRef]
- Heidari, M.; Homaei, H.; Golestanian, H.; Heidari, A. Fault diagnosis of gearboxes using wavelet support vector machine, least square support vector machine and wavelet packet transform. J. Vibroengineering 2016, 18, 860–875. [Google Scholar] [CrossRef]
- Suykens, J.A.; De Brabanter, J.; Lukas, L.; Vandewalle, J. Weighted least squares support vector machines: Robustness and sparse approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, J. A novel carbon price prediction model based on optimized least square support vector machine combining characteristic-scale decomposition and phase space reconstruction. Energy 2022, 253, 124167. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Q.; Huang, R.; Wang, S.; Liu, X. A prediction method for deck-motion based on online least square support vector machine and genetic algorithm. J. Mar. Sci. Technol. 2019, 24, 382–397. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Y.; Zhang, Y.; He, Z.; Yuan, W.; Yang, Y.; Qiu, W.; Li, L. A combined model based on SSA, neural networks, and LSSVM for short-term electric load and price forecasting. Neural Comput. Appl. 2021, 33, 773–788. [Google Scholar] [CrossRef]
- Deng, W.; Yao, R.; Zhao, H.; Yang, X.; Li, G. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 2019, 23, 2445–2462. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Z.; Qian, X. Rolling bearing fault diagnosis based on generalized multiscale mean permutation entropy and GWO-LSSVM. IET Sci. Meas. Technol. 2023, 17, 243–256. [Google Scholar] [CrossRef]
- Xia, X.; Wang, X. Fault Diagnosis of Planetary Gearbox Based on Hierarchical Refined Composite Multiscale Fuzzy Entropy and Optimized LSSVM. Entropy 2025, 27, 512. [Google Scholar] [CrossRef]
- Lang, Y.; Gao, Y. Dream Optimization Algorithm (DOA): A novel metaheuristic optimization algorithm inspired by human dreams and its applications to real-world engineering problems. Comput. Methods Appl. Mech. Eng. 2025, 436, 117718. [Google Scholar] [CrossRef]
- Li, Y.; Miao, B.; Zhang, W.; Chen, P.; Liu, J.; Jiang, X. Refined composite multiscale fuzzy entropy: Localized defect detection of rolling element bearing. J. Mech. Sci. Technol. 2019, 33, 109–120. [Google Scholar] [CrossRef]
- Luo, S.; Wang, Y.; Dai, H.; Long, X.; Peng, Z. Theoretical and experimental investigation on gearbox vibration signal separation of planetary gear set. Mech. Mach. Theory 2024, 200, 105723. [Google Scholar] [CrossRef]
- Yu, H.; Ni, J.; Xu, S.; Qin, B.; Jv, H. Estimating harmfulness of class imbalance by scatter matrix based class separability measure. Intell. Data Anal. 2014, 18, 203–216. [Google Scholar] [CrossRef]
- Hajderanj, L.; Weheliye, I.; Chen, D. A new supervised t-SNE with dissimilarity measure for effective data visualization and classification. In Proceedings of the 8th International Conference on Software and Information Engineering, Cairo, Egypt, 9–12 April 2019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).