Abstract
Preserving quantum entanglement in multipartite systems under environmental decoherence is a critical challenge for quantum information processing. In this work, we investigate the dynamics of W-type entanglement in a system of three photons, focusing on the effects of Markovian and non-Markovian decoherence regimes. Using the lower bound of concurrence (LBC) as a measure of entanglement, we analyze the time evolution of the LBC for photons initially prepared in a W state under the influence of dephasing noise. We explore the dependence of entanglement dynamics on system parameters such as the dephasing angle and refractive-index difference, alongside environmental spectral properties. Our results, obtained within experimentally feasible parameter ranges, reveal how the enhancement of entanglement preservation can be achieved in Markovian and non-Markovian regimes according to the system parameters. These findings provide valuable insights into the robustness of W-state entanglement in tripartite photonic systems and offer practical guidance for optimizing quantum protocols in noisy environments.
Keywords:
three-photon system; pure dephasing; W-type entanglement; LBC measure; symmetric and asymmetric interactions; experimental ranges PACS:
03.67.Mn; 03.65.Yz; 42.50.-p; 71.55.Jv
1. Introduction
Quantum entanglement, a cornerstone of quantum mechanics, plays a pivotal role in quantum information processing, enabling applications such as quantum computing, cryptography, and teleportation [1]. The W states hold a unique position among the various types of multipartite entangled states due to their robustness against particle loss and utility in quantum communication protocols [2]. However, the practical implementation of such states is often hindered due to environmental decoherence, which can rapidly degrade the entanglement [3]. Therefore, understanding the dynamics of entanglement in the presence of decoherence is essential for developing robust quantum technologies. Quantum networks [4,5] are envisioned to connect quantum devices across distant locations, enabling novel applications in distributed quantum computing [6,7], key distribution [8], and network sensing [9,10]. While bipartite entanglement, such as Bell states, is commonly used for networking, many advanced applications require the distribution of multipartite entanglement among multiple nodes. However, multipartite entanglement transmission, as its bipartite counterpart, is severely limited by channel losses, imposing a fundamental trade-off between the distance of distribution and the rate [11]. Multi-particle entanglement, such as the W-type entanglement explored in this study, lies at the heart of quantum networks, enabling advanced quantum communication protocols and distributed quantum computing. The establishment of scalable quantum networks relies on quantum repeaters, which leverage multi-particle entangled states to extend entanglement over long distances [12,13]. These networks have far-reaching applications, including secure conference key agreement, where multi-particle entanglement facilitates the distribution of cryptographic keys among multiple parties [14,15]. However, environmental decoherence poses a significant challenge to preserving such entanglement, necessitating robust characterization and mitigation strategies.
To overcome these limitations, single-photon path entanglement, a superposition of zero- and one-photon states, has emerged as a promising approach. Heralded entanglement distribution using single-photon interference detection has been shown to mitigate the rate-loss trade-off for bipartite systems [16,17], and this concept has recently been extended to multipartite entanglement distribution [18,19,20]. Despite its advantages in loss tolerance, the experimental characterization of single-photon path entanglement remains challenging due to its nonclassical nature as a superposition of different photon-number states. A common method for evaluating this entanglement involves combining the two modes via a beam splitter, transforming the entanglement of the path into a single-photon state and a vacuum [11,16,17,21,22,23]. Although this technique simplifies state evaluation, it is incompatible with real-world quantum networks, where measurements are restricted to local operations. For practical quantum networks, local measurement schemes are essential. Recent advances have demonstrated the evaluation of bipartite entanglement using weak local oscillators [11,16,21,24], paving the way for the verification of scalable entanglement in distributed systems. Extending these methods to multipartite entanglement, particularly in the W-states’ context, remains an open challenge with significant implications for quantum networking.
In this work, we focus on the dynamics of W-type entanglement in a system of three photons, a paradigmatic example of a tripartite entangled system. Specifically, we investigate the effects of Markovian and Non-Markovian decoherence on entanglement preservation, using the lower bound of concurrence (LBC) as a quantifier [25]. The LBC provides a computationally tractable measure of entanglement for mixed states and is particularly useful for analyzing entanglement evolution in open quantum systems [26]. We study the time evolution of the LBC for photons initially prepared in a W-state, subject to dephasing noise characterized by a dephasing angle. By varying this angle, we explore how different environmental conditions influence the dynamics of entanglement. Our analysis spans both Markovian and non-Markovian regimes, highlighting the role of environmental memory effects in preserving entanglement. The results are obtained within experimentally feasible parameter ranges, ensuring their relevance for practical quantum systems [27]. This investigation advances our understanding of entanglement dynamics in tripartite systems and provides practical insights into optimizing quantum protocols in noisy environments. The findings underscore the importance of tailoring environmental interactions to enhance entanglement preservation, particularly in non-Markovian regimes. To investigate the non-Markovian dynamics of three-photon polarization systems, we propose a model based on two Fabry–Perot cavities, which generate a two-peaked Gaussian spectral profile [28,29,30,31]. This setup is particularly effective for studying the interplay between photonic coherence and environmental memory effects, as it allows for precise control over the spectral properties of the environment. To quantify the entanglement dynamics in these systems, we employ the lower bound of concurrence (LBC) as a measure of W-type entanglement in tripartite photonic systems. The LBC is a computationally efficient and experimentally accessible metric, which makes it well suited to characterizing entanglement in mixed states under non-Markovian conditions. We examine the LBC in a selected initial state of interest that aligns with experimentally feasible parameter ranges. This method enables a thorough comprehension of how environmental memory effects impact the preservation and degradation of entanglement in three-photon polarization systems. Our results provide important insights into the durability of W-type entanglement within realistic quantum networks, where non-Markovian effects are crucial.
The structure of this paper is as follows. Section 1 delves into the non-Markovian dynamics governing polarization states in a single-photon system, which is treated as an open quantum system. The frequency dependencies are characterized by a dual-peaked Gaussian distribution. Within this framework, we establish the density matrix formalism for the degree of freedom of polarization. Building on this foundation, we generalize our analysis to a three-photon scenario, deriving the full reduced-density matrix for a pair of nonidentical qubit systems. This systematic progression enables a comprehensive exploration of non-Markovian phenomena across experimentally accessible parameter regimes. In Section 2, we explore the application of the lower bound of concurrence (LBC) as a metric for quantifying non-classical correlations within a tripartite quantum system. The LBC serves as a key indicator of the degree of quantum correlations present in the proposed system. Our investigation is confined to particular initial configurations of photon-polarization states, specifically those described by the W-state while maintaining maximally mixed marginal states. In Section 3, we highlight the principal results of our investigation, obtained by applying various analytical measures to examine the proposed system in a carefully chosen initial state. Through a detailed evaluation, we demonstrate the effectiveness of these measures in capturing the system’s behavior, providing a thorough insight into its dynamics. Additionally, we investigate the influence of identical and nonidentical dephasing rates on the individual qubits, a critical aspect that shapes the coherence and correlation characteristics of the system. By contrasting cases with uniform and non-uniform dephasing rates, we seek to clarify their impact on non-Markovian dynamics and their role in steering the system’s evolution. Our analysis is conducted within experimentally realistic parameter ranges to ensure applicability. This evaluation highlights the capabilities and constraints of the measures employed in characterizing non-Markovian behavior and their responsiveness to variations in experimental conditions. Finally, Section 4 concludes the paper with comments and a summary of the results.
2. Non-Markovian Framework for Photonic Systems
In this section, we go through the non-Markovian framework, beginning with an analysis of a single-photon system and subsequently extending our investigation to a three-photon scenario. This systematic approach allows us to explore how non-Markovian effects emerge in systems with varying numbers of photons, providing valuable insights that can be generalized to more complex multi-photon systems.
2.1. Model for a Single Photon
This investigation focuses on an open quantum system, where the polarization state of a photon acts as the primary system, while its frequency serves as the environmental degree of freedom. To simulate the non-Markovian dynamics of the photon, we employ an experimental setup comprising a tunable Fabry-Pérot (FP) cavity, an interference filter, and a quartz plate [28,29,30,31,32]. The FP cavity generates a frequency comb for the photon, which is then filtered to produce two distinct peaks using an interference filter. The resulting frequency distribution, denoted as , represents the probability density of the photon occupying a frequency mode, . This distribution is modeled as a superposition of two Gaussian profiles [33]:
where and are the central frequencies of the two peaks, is their common width, and the distribution is normalized, such that . The parameter , defined within the interval , controls the relative weights of the two peaks. By adjusting the tilt angle of the FP cavity, this parameter can be precisely tuned to achieve the desired frequency distribution.
After filtering, the photon’s polarization undergoes non-Markovian dephasing due to its interaction with the frequency modes in the quartz plate. This interaction is described by the Hamiltonian [34], with :
where and are the refractive indices for horizontal and vertical polarizations, respectively. This interaction induces a frequency-dependent phase shift, leading to non-Markovian dynamics in the photon’s polarization.
The initial state of the system is given by , where with represents the polarization state of the photon, and the environmental state is as follows:
with .
The time-evolved polarization state of the photon at time t is obtained by tracing out the environmental degrees of freedom:
where is the quantum map, and is the time evolution operator for the system–environment interaction.
The density matrix for the degree of freedom of polarization is given by [35]:
where
represents the dephasing function, with .
Using the frequency distribution from Equation (1), can be expressed as follows:
2.2. Dynamics of a Tripartite System
We now analyze a composite system composed of three independent subsystems, labeled A, B, and C. Each subsystem consists of a qubit () that interacts locally with its own environment () and the associated decoherence function is determined by the spectral characteristics of that environment, encoded in the frequency distribution function . Initially, the qubits and their respective environments are assumed to be uncorrelated (see Figure 1).
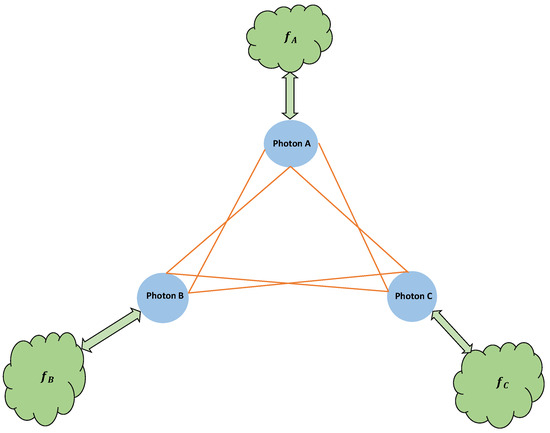
Figure 1.
Schematic representation of the three-photon W-type entangled state subjected to independent decoherence channels. The triangle connecting the photons symbolizes the symmetric sharing of entanglement among subsystems A, B, and C. The connecting lines are not intended to represent spatial or temporal ordering.
In this study, we assume that the three photons do not interact directly with one another. The dynamics of entanglement are, therefore, solely governed by their individual interactions with local environments, as described by the decoherence models applied to each subsystem.
The time evolution of the reduced density matrix for each qubit () is governed by the Kraus operators [36], which describe the interaction between the qubit and its environment. The reduced density matrix for each qubit can be expressed as
For the composite system , the total time evolution operator can be decomposed into the tensor product of the individual evolution operators . Consequently, the reduced density matrix for the three-qubit system in the Kraus representation is given as follows:
This formulation highlights the independent evolution of each qubit–environment pair while capturing the collective dynamics of the tripartite system.
2.3. Basis Representation and Matrix Elements
We adopt the polarization basis states for each qubit. By inserting the identity operator between the Kraus operators and the density matrices in Equation (8), the dynamics of each qubit can be rewritten as follows:
where
The tensor encodes the decoherence-induced transformation of the elements of the density matrix of the S subsystem, providing a compact representation of the reduced dynamics in the Kraus formalism [36].
Extending this to the three-qubit system, the dynamics of can be expressed as follows:
where the indices .
2.4. Reduced Density Matrix for the Tripartite System
Using the reduced density matrix formalism for polarization degrees of freedom Equation (5) [35], we construct the full reduced density matrix for the three-qubit system. We define the basis states as follows:
The off-diagonal elements are given as follows:
Here, represents the decoherence function for the subsystem , and ensures the sensitivity of . Equations (13) and (14) provide a complete description of the evolution of the three-qubit density matrix for any initial state.
This framework allows us to investigate the effects of non-Markovian dynamics in a tripartite system, offering insights into the interplay between coherence and environmental interactions.
3. Entanglement Measures for Three Photons
Suppose that, initially, the three photons are prepared in the state with all coefficients being nonzero; such a configuration corresponds to genuine tripartite entanglement, as the state cannot be factorized into any bipartite form [2,37,38,39,40,41,42]. This entanglement is quantified by the three-qubit concurrence . For a general three-qubit pure state,
with the normalization condition , the concurrence is defined as follows [40]:
The concurrence for any mixed three-qubit state is given by the convex roof [38,40]:
where represents all possible pure states that form the decomposition with probabilities and . Due to the difficulty of solving this minimization problem, we approximate it using the lower bound of concurrence (LBC):
Here, the bipartite concurrences are defined as follows:
where are the eigenvalues of the matrix , with representing the six generators of SO(4) and being the Pauli-y matrix.
4. Results and Discussion
This section focuses on the temporal evolution of entanglement in a system of three qubits. To achieve this, it is essential to employ a suitable and mathematically rigorous entanglement measure.
We consider the W-state , which is a key resource in quantum information processing due to its entanglement properties and robustness; i.e, if one qubit is lost, the remaining two qubits retain some entanglement, making W-states useful in noisy quantum systems. It can be prepared using a sequence of quantum gates, and its preparation is a standard task in quantum computing experiments [1,43,44,45,46,47,48,49]. In addition, W-states are used in quantum protocols such as quantum secret sharing, quantum error correction, and quantum networks. Furthermore, the W-state is symmetric under the permutation of the qubits, which makes it easier to analyze and manipulate in certain quantum algorithms.
The initial density matrix is defined as the outer product of the state vector with itself
Using the three-qubit basis, the density matrix will be an matrix with nonzero entries only in the block corresponding to the , , and subspaces. The rest of the matrix will be zero.
The density matrix on the full basis of 3 qubits is
This matrix represents the initial state in the full 3-qubit Hilbert space.
The functions , , and represent the time-dependent decoherence of each qubit, which arises from interactions with an environment or intrinsic dynamics.
Making use of the definition of the lower bound of concurrence, we can obtain
Specifically, in the case of symmetric interactions where , the result is derived as follows:
In our analysis, we explore the dynamics of quantum entanglement in photon-polarization states under experimentally attainable conditions. We adopt the following parameters: the difference in refractive indices, ; the spectral width of the frequency distribution, Hz; the central frequencies of two Gaussian peaks, Hz (approximately 704.5 nm wavelength) and Hz (approximately 700.3 nm wavelength); and the driving time, ps, where Hz is the frequency separation. These values are selected to align with experimentally feasible ranges, as supported by recent studies [29], providing a realistic basis for analyzing entanglement dynamics under dephasing noise. Importantly, our framework is designed to accommodate other parameter values within experimental limits. For instance, variations in , , or can be explored to assess their impact on quantum entanglement. This adaptability allows the model to be applied to a variety of experimental setups, enhancing our understanding of how environmental factors influence quantum entanglement. This, in turn, aids in determining conditions that preserve entanglement in photon polarization states, minimizing the decoherence effect and enabling robust quantum technology applications.
Figure 2 depicts the time evolution of LBC for a tripartite photonic system initially prepared in a W state, under the influence of dephasing noise characterized by varying and environmental spectral widths, , with the fixed parameters , , and . Under symmetric Markovian interactions (), the system experiences LBC decay due to memoryless environmental coupling, which disrupts the quantum entanglement dynamics. This effect is pronounced with a narrower spectral width ( THz), intensifying the decoherence through a concentrated frequency distribution, while a broader THz marginally slows the loss of entanglement by diluting environmental interactions. Non-Markovian symmetric interactions () exploit environmental memory to significantly affect the decay of entanglement in the presence of sudden death and sudden birth phenomena of entanglement, with the broader enhancing this resilience, and the narrower still conferring some protection. In asymmetric configurations, the robustness of the entanglement varies. Asymmetric case 1 () also exhibits the sudden death and sudden birth phenomena as two photons benefit from non-Markovian dynamics while the Markovian photon introduces a decoherence pathway. Compared to the configuration with two non-Markovian photons, the asymmetric case 2 () exhibits a moderate decay in LBC, resulting in a better preservation of entanglement with a more stable LBC over time. These findings emphasize the pivotal role of non-Markovian dynamics and environmental spectral widths in shaping entanglement robustness in tripartite photonic systems under pure dephasing effects. They provide critical insights for designing multipartite quantum systems, suggesting that controlling non-Markovian interactions, particularly with larger spectral widths, is key to achieving resilient quantum entanglement in the presence of noise.
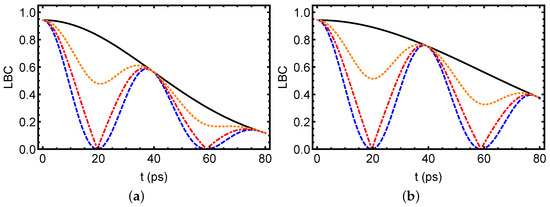
Figure 2.
Time evolution of the LBC as a function of time t for photons initially prepared in the W-state for the different angle values under both Markovian and non-Markovian dynamics. The system parameters are set as , PHz (approximately 704.5 nm), and PHz (approximately 700.3 nm) [29]. Subfigures (a,b) are for THz and THz, respectively. The color coding follows: the solid black line corresponds to the fully Markovian case (symmetric) (); the dashed blue line corresponds to a case (three photons in non-Markovian environments) (); the dot-dashed red line corresponds to case 1 (two photons in non-Markovian environments) (); and the dotted brown line corresponds to case 2 (one photon in a non-Markovian environment) . The used units are as follows: petahertz Hz, terahertz Hz.
On the other hand, the near-identical initial values of the LBC in Figure 2 reflect the intrinsic symmetry of the initial W-type entangled state and the consistent choice of initial parameters, which ensures similar degrees of bipartite entanglement, regardless of the specific phase configuration. In addition, the observed similarity in the LBC dynamics for the cases and can be attributed to the partial symmetry in the phase configuration, which results in a more balanced entanglement distribution. In contrast, the asymmetric configuration disrupts this balance, leading to a distinct decay behavior of the entanglement.
In Figure 3, we illustrate the dynamics of LBC within a tripartite photonic system initialized in a W-state with identical dephasing configurations and frequencies, considering . We can observe that the refractive index difference emerges as a pivotal parameter influencing the preservation of quantum entanglement. With reduced to 0.003, compared to 0.01 in Figure 2, the photonic system exhibits a marked improvement in the robustness of the entanglement, evidenced by the slower decay of the LBC over time. This reduction in minimizes the frequency-dependent phase shifts that drive dephasing, effectively decreasing the system’s susceptibility to decoherence. In subfigure (a), where the spectral width is 1.8 THz, the smaller results in a noticeably slower decrease in LBC compared to the larger scenarios , indicating improved entanglement stability. This effect becomes even more pronounced in subfigure (b), with a narrower of 1.2 THz, where the interplay between the reduced and the constrained spectral width, leading to the superior preservation of entanglement, contrary to typical expectations under broader spectra. The decreased curtails phase variations across frequencies, allowing environmental effects to maintain entanglement more effectively, particularly when paired with a narrower . Consequently, minimizing not only universally bolsters the photonic system’s resilience against dephasing noise but also optimizes the exploitation of Markovian and non-Markovian dynamics, underscoring its critical role in designing quantum systems for robust entanglement maintenance.
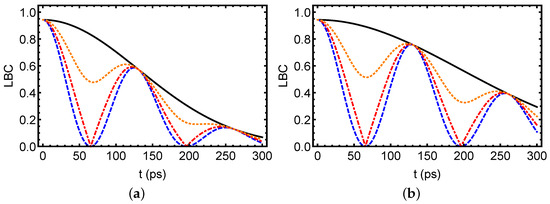
Figure 3.
Time evolution of the LBC as a function of time t for photons initially prepared in the W-state for different angle values under both Markovian and non-Markovian dynamics. The system parameters are set to , PHz (approximately 704.5 nm) and PHz (approximately 700.3 nm). Subfigures (a,b) correspond to THz and THz, respectively. The color coding follows: the solid line represents ; the dashed line corresponds to ; the dot-dashed line indicates ; and the dotted line corresponds to .
On the other hand, the phase parameter originates from the structure of the environmental frequency distribution , modeled as a superposition of two Gaussian profiles with tunable relative weights. The values and correspond to specific configurations of this distribution, namely a single-peak profile and a balanced two-peak profile, which can be achieved by adjusting the tilt angle of the Fabry–Pérot cavity [33]. These cases were chosen to illustrate the contrasting effects of spectral asymmetry on the entanglement dynamics in a physically meaningful and experimentally relevant manner.
The comparative analysis of the dynamics of entanglement in Figure 2 and Figure 3 elucidates the critical differences in decoherence behavior under distinct system and environmental conditions, bearing significant consequences for applications of quantum information such as quantum teleportation and quantum cryptography. These findings, corroborated in recent references [31,35,50,51,52], emphasize that tailoring environmental and system parameters can substantially bolster entanglement stability, providing actionable strategies for designing quantum systems resilient to noise. Specifically, the prolonged entanglement observed aligns with the requirements of quantum cryptography, enhancing the secure key distribution while also supporting the fidelity of the teleportation. This dual-figure analysis not only deepens the theoretical understanding of decoherence dynamics but also paves the way for practical advancements in quantum information processing, guiding the development of robust multipartite quantum networks. These recent advances highlight the critical role of tailoring environmental parameters to optimize entanglement, providing a robust foundation for mitigating decoherence in practical quantum information protocols. Thus, not only do our results deepen the theoretical understanding of entanglement dynamics but they also offer actionable strategies for designing resilient quantum systems in real-world applications. Although we do not introduce a quantitative measure of non-Markovianity, the comparative behavior of LBC under different environmental configurations demonstrates that non-Markovian effects can mitigate the degradation of entanglement, as evidenced by slower decay rates and the presence of entanglement stabilization in certain asymmetric cases.
5. Conclusions
In this work, we have addressed the critical challenge of preserving quantum entanglement in multipartite systems under environmental decoherence, with a specific focus on W-type entanglement in a tripartite photonic system. By employing the LBC as a measure, we systematically analyzed the time evolution of entanglement for three photons initially prepared in a W state, subjected to dephasing noise in both Markovian and non-Markovian decoherence regimes. Our investigation explored the influence of key system parameters, namely the dephasing angle, the refractive index difference, and the environmental spectral properties, on the dynamics of entanglement. The results demonstrated that the preservation of the entanglement can be significantly improved by carefully tuning these parameters. Specifically, in the Markovian regime, we observed that entanglement undergoes a steady decay, which can be mitigated by optimizing the spectral width and refractive-index difference to reduce the rate of decoherence. However, the non-Markovian regime revealed richer dynamics, including entanglement sudden death and revival, driven by environmental memory effects that can be harnessed to maintain entanglement over longer periods, particularly with broader spectral widths and smaller refractive-index differences. These findings are grounded in experimentally feasible parameter ranges, ensuring their practical relevance for current quantum photonic technologies. By identifying optimal configurations, such as a reduced refractive-index difference and tailored spectral widths, this study provided actionable strategies for experimentalists to enhance the robustness of W-state entanglement against dephasing noise.
The insights obtained in this study not only enhance the theoretical understanding of the dynamics of entanglement in open quantum systems but also provide a meaningful direction to optimize quantum information protocols in the presence of noise. Although the work is primarily theoretical, its relevance extends to practical scenarios, particularly in the design of entangled photonic systems for use in quantum technologies. The interplay observed between Markovian and non-Markovian decoherence highlights the critical role of environmental control and engineering in the development of resilient quantum architectures. In general, this work contributes to the bridge between theoretical models and experimental viability, advancing the pursuit of robust quantum systems capable of operating reliably under realistic conditions.
Author Contributions
Writing—original draft preparation, K.B. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2503).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Dür, W.; Vidal, G.; Cirac, J.I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 2000, 62, 062314. [Google Scholar] [CrossRef]
- Aolita, L.; de Melo, F.; Davidovich, L. Open-system dynamics of entanglement: A key issues review. Rep. Prog. Phys. 2015, 78, 042001. [Google Scholar] [CrossRef] [PubMed]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Wehner, S.; Elkouss, D.; Hanson, R. Quantum internet: A vision for the road ahead. Science 2018, 362, eaam9288. [Google Scholar] [CrossRef]
- Lo, H.K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photonics 2014, 8, 595–604. [Google Scholar] [CrossRef]
- Fitzsimons, J.F. Quantum information density scaling and qubit operation time constraints of CMOS silicon-based quantum computer architectures. Npj Quantum Inf. 2017, 3, 23. [Google Scholar] [CrossRef]
- Epping, M.; Kampermann, H.; macchiavello, C.; Bruß, D. Multi-partite entanglement can speed up quantum key distribution in networks. New J. Phys. 2017, 19, 093012. [Google Scholar] [CrossRef]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photonics 2020, 12, 1012–1236. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhuang, Q. Distributed quantum sensing. Quantum Sci. Technol. 2021, 6, 043001. [Google Scholar] [CrossRef]
- Ottaviani, C.; Lupo, C.; Laurenza, R.; Pirandola, S. Modular network for high-rate quantum conferencing. Commun. Phys. 2017, 2, 712–722. [Google Scholar] [CrossRef]
- Li, C.L.; Yin, H.L.; Chen, Z.B. Asynchronous quantum repeater using multiple quantum memory. Rep. Prog. Phys. 2024, 87, 127901. [Google Scholar] [CrossRef]
- Azuma, K.; Economou, S.E.; Elkouss, D.; Hilaire, P.; Jiang, L.; Lo, H.K.; Tzitrin, I. Quantum repeaters: From quantum networks to the quantum internet. Rev. Mod. Phys. 2023, 95, 045006. [Google Scholar] [CrossRef]
- Fu, Y.; Yin, H.L.; Chen, T.Y.; Chen, Z.B. Long-distance measurement-device-independent multiparty quantum communication. Phys. Rev. Lett. 2015, 114, 090501. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.M.; Lu, Y.S.; Fu, Y.; Yin, H.L.; Chen, Z.B. Multi-field quantum conferencing overcomes the network capacity limit. Commun. Phys. 2024, 7, 410. [Google Scholar] [CrossRef]
- Azuma, K.; Tamaki, K.; Lo, H.K. All-photonic quantum repeaters. Nat. Commun. 2015, 6, 6787. [Google Scholar] [CrossRef]
- Luong, D.; Jiang, L.; Kim, H.; Lütkenhaus, N. Role of syndrome information on a one-way quantum repeater using teleportation-based error correction. Phys. Rev. A 2016, 94, 052304. [Google Scholar] [CrossRef]
- Ribeiro, J.; Murta, G.; Wehner, S. Reply to “Comment on ‘Fully device-independent conference key agreement”. Phys. Rev. A 2019, 100, 026302. [Google Scholar] [CrossRef]
- Patil, A.; Pant, M.; Englund, D.; Towsley, D.; Guha, S. Entanglement generation in a quantum network at distance-independent rate. Npj Quantum Inf. 2022, 8, 041051. [Google Scholar] [CrossRef]
- Goodenough, K.; Elkouss, D.; Wehner, S. Optimizing repeater schemes for the quantum internet. Phys. Rev. A 2021, 103, 032610. [Google Scholar] [CrossRef]
- Takeoka, M.; Guha, S.; Wilde, M.M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nat. Commun. 2014, 5, 5235. [Google Scholar] [CrossRef]
- Tahira, R.; Ikram, M.; Bougouffa, S.; Zubairy, M.S. Entanglement dynamics of high-dimensional bipartite field states inside the cavities in dissipative environments. J. Phys. At. Mol. Opt. Phys. 2010, 43, 035502. [Google Scholar] [CrossRef]
- Bougouffa, S.; Ficek, Z. Effect of retardation in the atom–field interaction on entanglement in a double Jaynes–Cummings system. J. Phys. At. Mol. Opt. Phys. 2013, 46, 224006. [Google Scholar] [CrossRef]
- Jin, R.B.; Shimizu, R.; Morohashi, I.; Wakui, K.; Takeoka, M.; Izumi, S.; Sakamoto, T.; Fujiwara, M.; Yamashita, T.; Miki, S.; et al. Efficient Generation of Twin Photons at Telecom Wavelengths with 10 GHz Repetition-Rate-Tunable Comb Laser. Osa Tech. Dig. 2015. [Google Scholar] [CrossRef]
- Mintert, F.; Carvalho, A.R.R.; Kuś, M.; Buchleitner, A. Measures and dynamics of entangled states. Phys. Rep. 2005, 415, 207–259, Erratum in Phys. Rep. 2005, 419, 143. [Google Scholar] [CrossRef]
- Jaeger, G.; Sergienko, A.V.; Saleh, B.E.A.; Teich, M.C. Entanglement, mixedness, and spin-flip symmetry in multiple-qubit systems. Phys. Rev. A 2003, 68, 022318. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. Open Quantum Electrodynamics; Oxford University Press: Oxford, UK, 2007; pp. 568–618. [Google Scholar] [CrossRef]
- Xu, J.S.; Li, C.F.; Gong, M.; Zou, X.B.; Shi, C.H.; Chen, G.; Guo, G.C. Experimental Demonstration of Photonic Entanglement Collapse and Revival. Phys. Rev. Lett. 2010, 104, 100502. [Google Scholar] [CrossRef]
- Liu, B.H.; Li, L.; Huang, Y.F.; Li, C.F.; Guo, G.C.; Laine, E.M.; Breuer, H.P.; Piilo, J. Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 2011, 7, 931–934. [Google Scholar] [CrossRef]
- Li, C.F.; Guo, G.C.; Piilo, J. Non-Markovian quantum dynamics: What does it mean? EPL Europhys. Lett. 2012, 127, 50001. [Google Scholar] [CrossRef]
- Gu, W.; Li, T.; Tian, Y.; Yi, Z.; Li, G.x. Two-photon dynamics in non-Markovian waveguide QED with a giant atom. Phys. Rev. A 2024, 110, 033707. [Google Scholar] [CrossRef]
- Deffner, S.; Lutz, E. Quantum Speed Limit for Non-Markovian Dynamics. Phys. Rev. Lett. 2013, 111, 010402. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Laine, E.M.; Breuer, H.P.; Piilo, J.; Li, C.F.; Guo, G.C. Nonlocal Memory Effects in the Dynamics of Open Quantum Systems. Phys. Rev. Lett. 2013, 108, 210402, Erratum in Phys. Rev. Lett. 2013, 111, 229901. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.S.; Sun, K.; Li, C.F.; Xu, X.Y.; Guo, G.C.; Andersson, E.; Franco, R.L.; Compagno, G. Experimental recovery of quantum correlations in absence of system-environment back-action. Nat. Commun. 2013, 4, 2851. [Google Scholar] [CrossRef] [PubMed]
- Kraus, K. States, Effects, and Operations: Fundamental Notions of Quantum Theory; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Tokyo, Japan, 1983. [Google Scholar]
- Acin, A.; Andrianov, A.; Jané, E.; Tarrach, R. Quantum-information processing with ferroelectrically coupled quantum dots. Phys. Rev. A 2001, 64, 052306. [Google Scholar] [CrossRef]
- Gao, X.H.; Fei, S.M.; Wu, K. Lower bounds of concurrence for tripartite quantum systems. Phys. Rev. A 2006, 74, 050303. [Google Scholar] [CrossRef][Green Version]
- Gühne, O.; Tóth, G. Entanglement detection. Phys. Rep. 2009, 474, 1–75. [Google Scholar] [CrossRef]
- Li, M.; Fei, S.M.; Wang, Z.X. A lower bound of concurrence for multipartite quantum states. J. Phys. Math. Theor. 2009, 42, 145303. [Google Scholar] [CrossRef]
- An, N.B.; Kim, J.; Kim, K. Nonperturbative analysis of entanglement dynamics and control for three qubits in a common lossy cavity. Phys. Rev. A 2010, 82, 032316. [Google Scholar] [CrossRef]
- An, N.B.; Kim, J.; Kim, K. Entanglement dynamics of three interacting two-level atoms within a common structured environment. Phys. Rev. A 2011, 84, 022329. [Google Scholar] [CrossRef]
- Vidal, G.; Dür, W.; Cirac, J.I. Reversible Combination of Inequivalent Kinds of Multipartite Entanglement. Phys. Rev. Lett. 2000, 85, 062314. [Google Scholar] [CrossRef]
- Acin, A.; Andrianov, A.; Jané, E.; Tarrach, R. Three-qubit pure-state canonical forms. J. Phys. Math. Gen. 2001, 64, 6725–6739. [Google Scholar] [CrossRef]
- Wunderlich, C.; Hannemann, T.; Körber, T.; Häffner, H.; Roos, C.; Hänsel, W.; Blatt, R.; Schmidt-Kaler, F. Robust state preparation of a single trapped ion by adiabatic passage. J. Mod. Opt. 2007, 54, 1541–1549. [Google Scholar] [CrossRef]
- Pati, A.K.; Agrawal, P. Special issue on quantum information theory. Quantum Inf. Process. 2012, 11, 637–638. [Google Scholar] [CrossRef]
- Sangouard, N.; Simon, C.; de Riedmatten, H.; Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 2011, 83, 33–80. [Google Scholar] [CrossRef]
- Eibl, M.; Kiesel, N.; Bourennane, M.; Kurtsiefer, C.; Weinfurter, H. Experimental Realization of a Three-Qubit Entangled W State. Phys. Rev. Lett. 2004, 92, 077901. [Google Scholar] [CrossRef]
- Grassl, M.; Rötteler, M. Nonadditive quantum codes. In Quantum Error Correction; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhu, K.D. Detecting large extra dimensions with optomechanical levitated sensors. Eur. Phys. J. 2019, 79, 1. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).