Probabilistic Load-Shedding Strategy for Frequency Regulation in Microgrids Under Uncertainties

Abstract

This paper proposes a novel integer-mixed probabilistic optimal power flow (IM-POPF) strategy for frequency regulation in islanded microgrids under uncertain operating conditions. Existing load-shedding approaches face critical limitations: continuous frameworks fail to reflect the discrete nature of actual load disconnections, while deterministic models inadequately capture the stochastic behavior of renewable generation and load variations. The proposed approach formulates load shedding as an integer optimization problem where variables are categorized as integer (load disconnection decisions at specific nodes) and continuous (voltages, power generation, and steady-state frequency), better reflecting practical power system operations. The key innovation combines integer load-shedding optimization with efficient uncertainty propagation through Unscented Transformation, eliminating the computational burden of Monte Carlo simulations while maintaining accuracy. Load and renewable uncertainties are modeled as normally distributed variables, and probabilistic constraints ensure operational limits compliance with predefined confidence levels. The methodology integrates Differential Evolution metaheuristics with Unscented Transformation for uncertainty propagation, requiring only 137 deterministic evaluations compared to 5000 for Monte Carlo methods. Validation on an IEEE 33-bus radial distribution system configured as an islanded microgrid demonstrates significant advantages over conventional approaches. Results show 36.5-fold computational efficiency improvement while achieving 95.28% confidence level compliance for frequency limits, compared to only 50% for deterministic methods. The integer formulation requires minimal additional load shedding (21.265%) compared to continuous approaches (20.682%), while better aligning with the discrete nature of real-world operational decisions. The proposed IM-POPF framework successfully minimizes total load shedding while maintaining frequency stability under uncertain conditions, providing a computationally efficient solution for real-time microgrid operation.

1. Introduction

1.1. Background and Context

Microgrids (MGs) represent a promising solution for integrating distributed energy resources and enhancing power system resilience, particularly in remote areas where connection to the main grid is challenging or uneconomical. When operating in islanded mode, these systems face significant challenges in maintaining frequency stability due to the absence of support from the main grid.

Unlike conventional power systems with large synchronous generators that provide natural inertia, microgrids often rely on power electronic interfaces that lack this stabilizing characteristic, making frequency control more challenging compared to traditional systems without distributed energy resources [1]. In addition, the limited power reserve and generation capacity in MGs make them more vulnerable to load and generation imbalances compared to grid-connected operations.

Frequency regulation in islanded microgrids is critical as even small imbalances between generation and load can lead to significant frequency deviations, potentially triggering cascading failures and system collapse. Under-frequency load-shedding schemes are particularly important where only one grid-forming resource may be available for frequency regulation [2].

A comprehensive review of load-shedding strategies for microgrids in islanded operation can be found in [3], emphasizing energy management strategies to maintain the reliability of energy flow between load and supply when disconnected from the main grid.

Traditional load-shedding approaches typically involve fixed frequency thresholds and predetermined load-shedding quantities. Under-frequency load shedding has been a common approach to manage frequency stability in microgrids by detecting power deficits and shedding selected loads based on predefined priorities [4]. However, these approaches face several limitations: (i) they often do not account for the stochastic nature of renewable generation; (ii) they may shed more or less load than necessary; (iii) they do not consider load types and priorities effectively, and (iv) they do not adapt to changing system conditions.

Multi-scenario approaches have been developed to address the probabilistic nature of renewable generation in microgrids, with [5] proposing a genetic algorithm-based method that determines optimal load shedding for underfrequency relays considering multiple scenarios with probabilities defined from historical meteorological data and Markov models, demonstrating effectiveness in microgrids with gas turbines, wind generators, and solar photovoltaic systems.

Recent research has shifted toward more sophisticated and adaptive approaches. Adaptive load-shedding schemes have been developed to regulate grid frequency by measuring system parameters like voltage and frequency signals and implementing stepwise load shedding at locations experiencing the highest voltage drop and frequency variation [6]. These approaches adjust the load-shedding step based on factors such as shedding speed, location, value, and rate of frequency change.

Intelligent control strategies have emerged as promising solutions for improving load-shedding performance, with [7] developing an online-trained Petri probabilistic wavelet fuzzy neural network controller to replace traditional proportional–integral controllers in battery energy storage systems, achieving fast load shedding and improved power sharing in islanded microgrids with droop control.

Two-stage under-frequency load-shedding strategies have been proposed, dividing the process into a fast load-shedding stage and a risk avoidance stage. The first stage addresses rapid frequency decreases, while the second stage accounts for risk loss caused by load uncertainty [8]. These approaches demonstrate improved performance by considering both immediate stability needs and longer-term risk mitigation. Additionally, ref. [9] introduced an innovative load-shedding model for island microgrids that combines the improved Analytic Hierarchy Process (AHP) algorithm for load ranking with the Power Stability Index (PSI) to minimize customer impact while ensuring frequency returns to acceptable ranges and maintaining voltage quality and stability.

Coordinated load-shedding strategies have been proposed to address both voltage and frequency stability simultaneously, with [10] presenting a four-dimensional voltage–frequency load-shedding strategy that uses piecewise linear curves to determine proper load-shedding locations and amounts, achieving more than 20% optimization in load rejection compared to conventional methods.

On the other hand, ref. [11] addresses frequency stability through a coordinated operation strategy focusing on rapid energy storage power adjustment and hierarchical under-frequency load shedding. The approach categorizes energy storage systems based on support time characteristics and implements control strategies that integrate energy storage power allocation with load-shedding decisions.

Optimization-based approaches have gained significant attention. Optimization models have been developed for secondary control of islanded microgrids, considering the action of primary control and references from tertiary control, solved using linear approximations of frequency-dependent power flow equations [12]. These models aim to restore frequency and voltages to nominal values while respecting the capacity limits of renewable sources and energy storage devices.

In ref. [13], a dynamic load-shedding strategy for islanded microgrids with limited generation resources was developed, formulating the problem as a stochastic optimization based on the Markov decision process to maximize economic performance while managing uncertainties from intermittent energy sources and load variations.

Computing approaches, such as genetic algorithms and artificial neural networks, have been used to control microgrid frequency by automatically adjusting and optimizing controller coefficients [14]. These approaches can handle the nonlinearities and complexities of microgrid systems better than conventional controllers. Conversely, ref. [15] uses Knowledge-Aggregation-based Proximal Policy Optimization to balance exploration and exploitation in frequency control strategies, incorporating active power symmetry and equilibrium considerations. This work shows how reinforcement learning approaches can enhance frequency regulation performance under renewable energy uncertainties. Furthermore, recent advances in deep reinforcement learning have shown promising results for adaptive frequency control of islanded microgrids, with [16] proposing a Learning-Driven Load Frequency Control (LD-LFC) method using graph-network-based deep reinforcement learning to address the complex and nonlinear control challenges introduced by high renewable energy penetration and random load disturbances.

Novel approaches to address low inertia include virtual inertia emulation and demand response. Virtual synchronous generators created through appropriate control mechanisms can provide virtual inertia to improve system stability, while plug-in electric vehicles can be used for power charging/discharging to support frequency regulation [17]. These approaches increase the natural inertia in MGs.

Although advances have been made in frequency regulation for islanded microgrids, current approaches face limitations that compromise their effectiveness under real-world conditions. Most existing load-shedding strategies use either continuous frameworks that fail to reflect the integer nature of actual load disconnections or rely on deterministic models that inadequately capture the stochastic behavior of renewable generation and load variations. The lack of integrated frameworks that combine integer load-shedding decisions with uncertainty propagation through probabilistic methods represents a gap in the current literature.

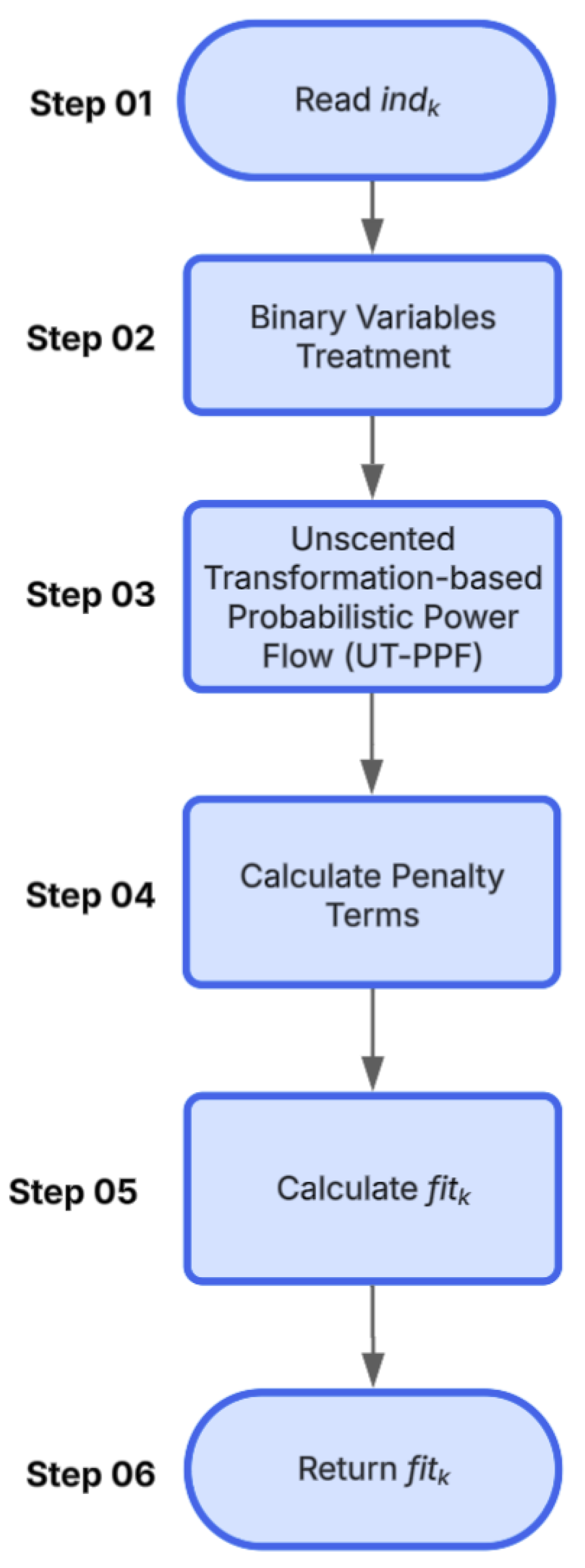
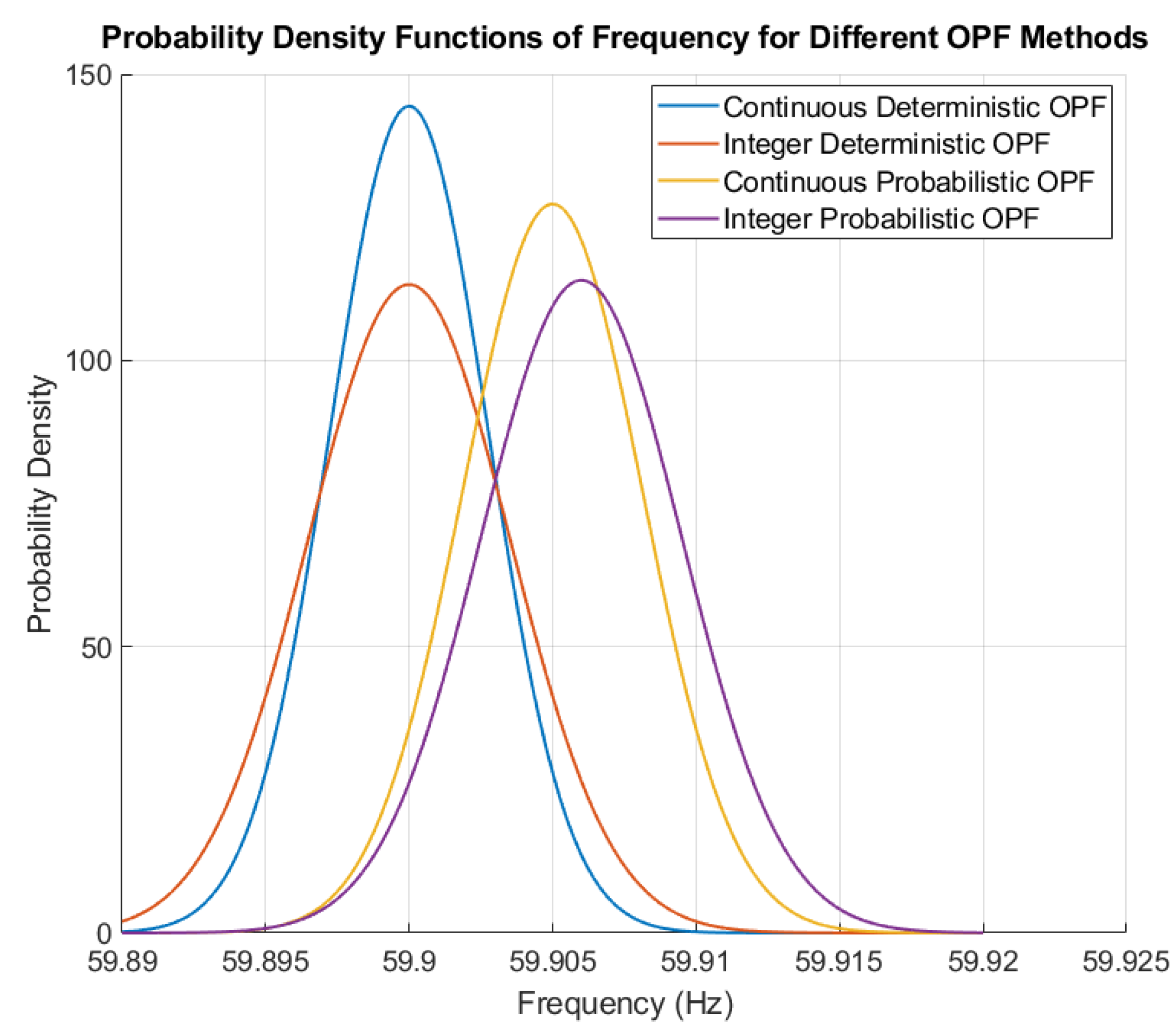
In this context, this paper addresses these limitations by proposing a novel integer-mixed probabilistic optimal power flow (IM-POPF) framework that integrates discrete load-shedding decisions with uncertainty modeling. Existing approaches fall into three categories: continuous probabilistic methods that allow unrealistic partial load disconnections, deterministic integer methods that ignore uncertainty, and deterministic continuous methods that suffer from both limitations. Unlike these approaches, the proposed IM-POPF method categorizes variables as integer (load shedding at specific nodes) and continuous (voltages, power generation, and frequency), accurately reflecting real-world power system operations where loads can only be completely disconnected or maintained, not partially adjusted.

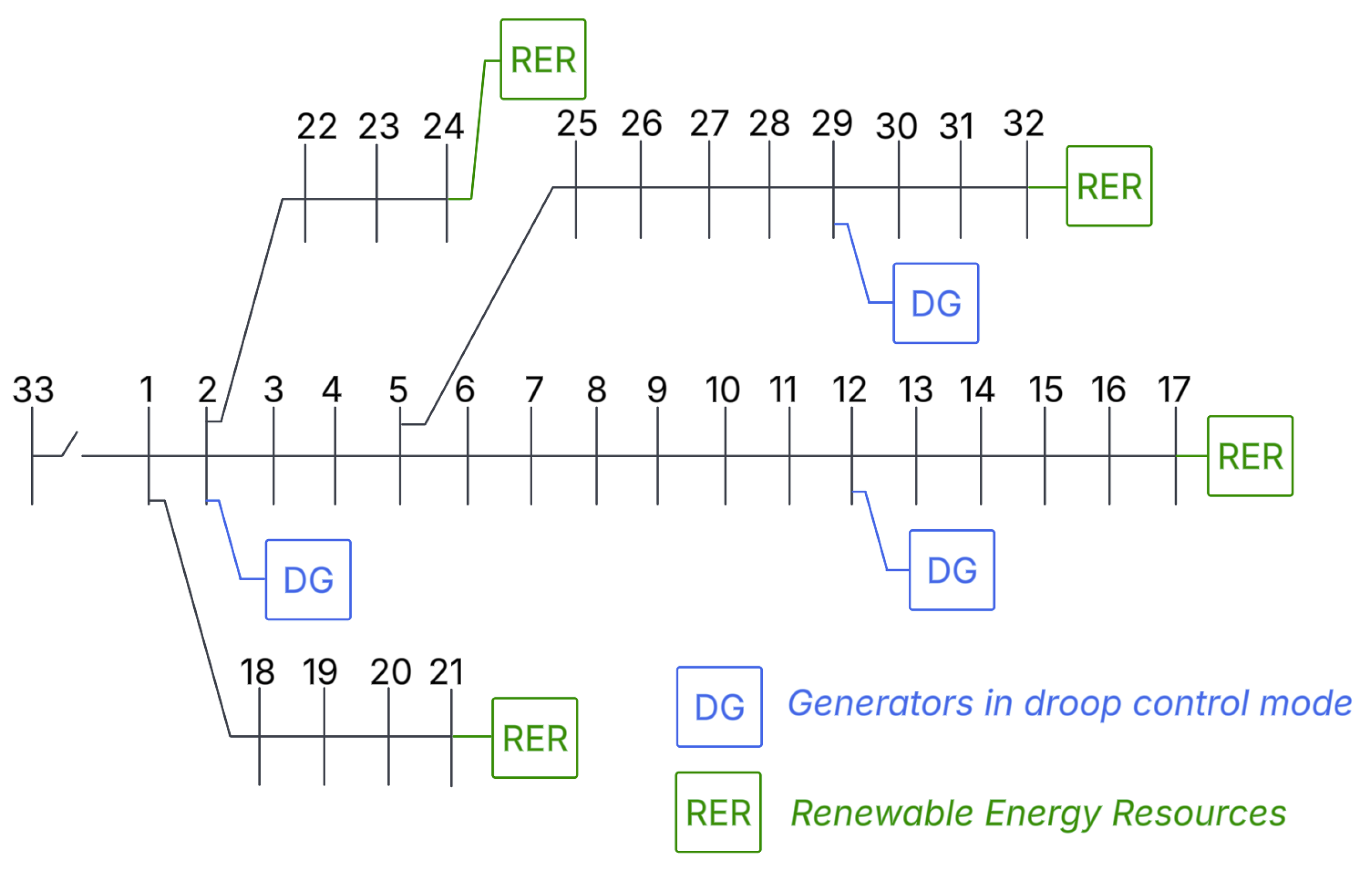
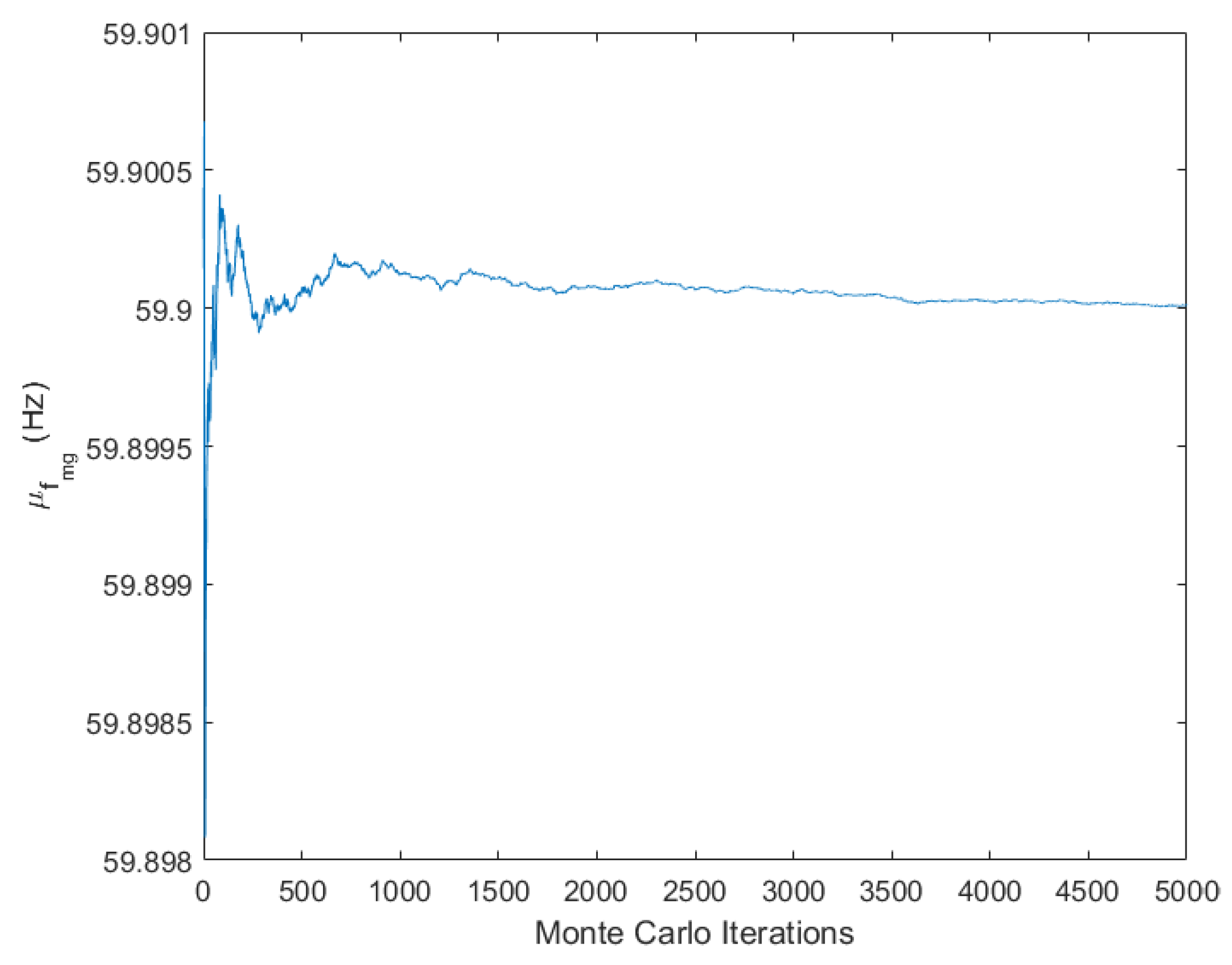
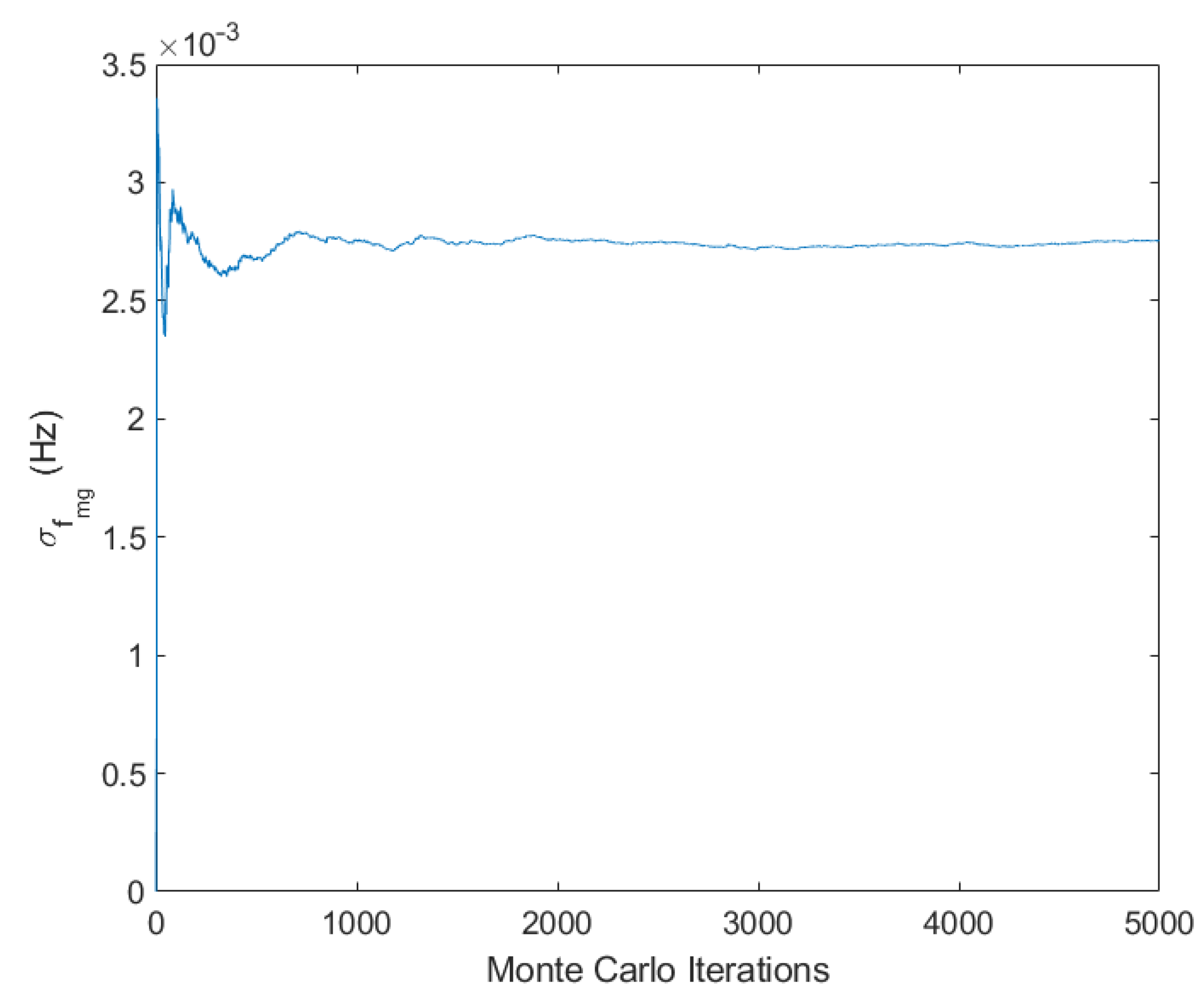
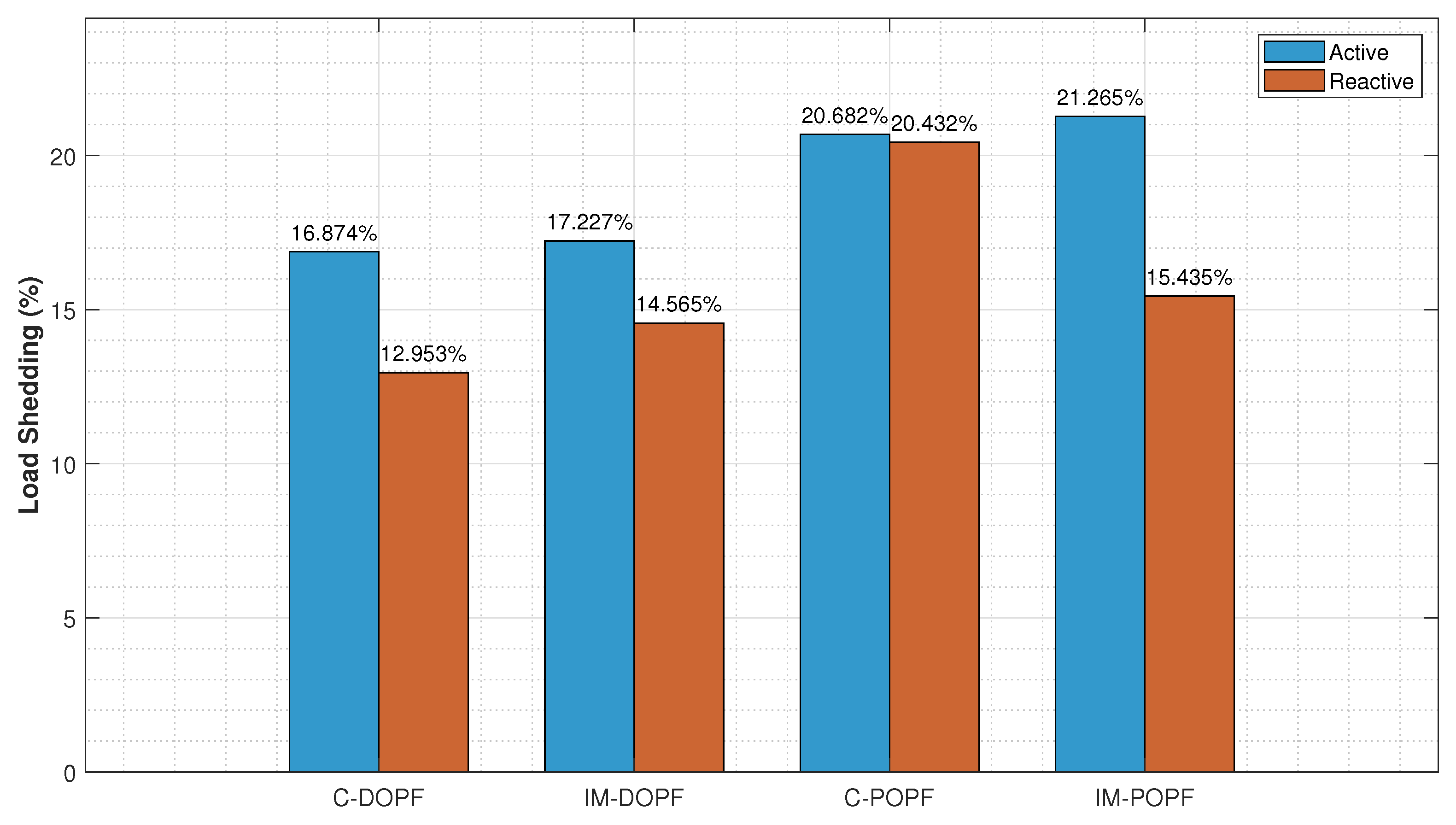
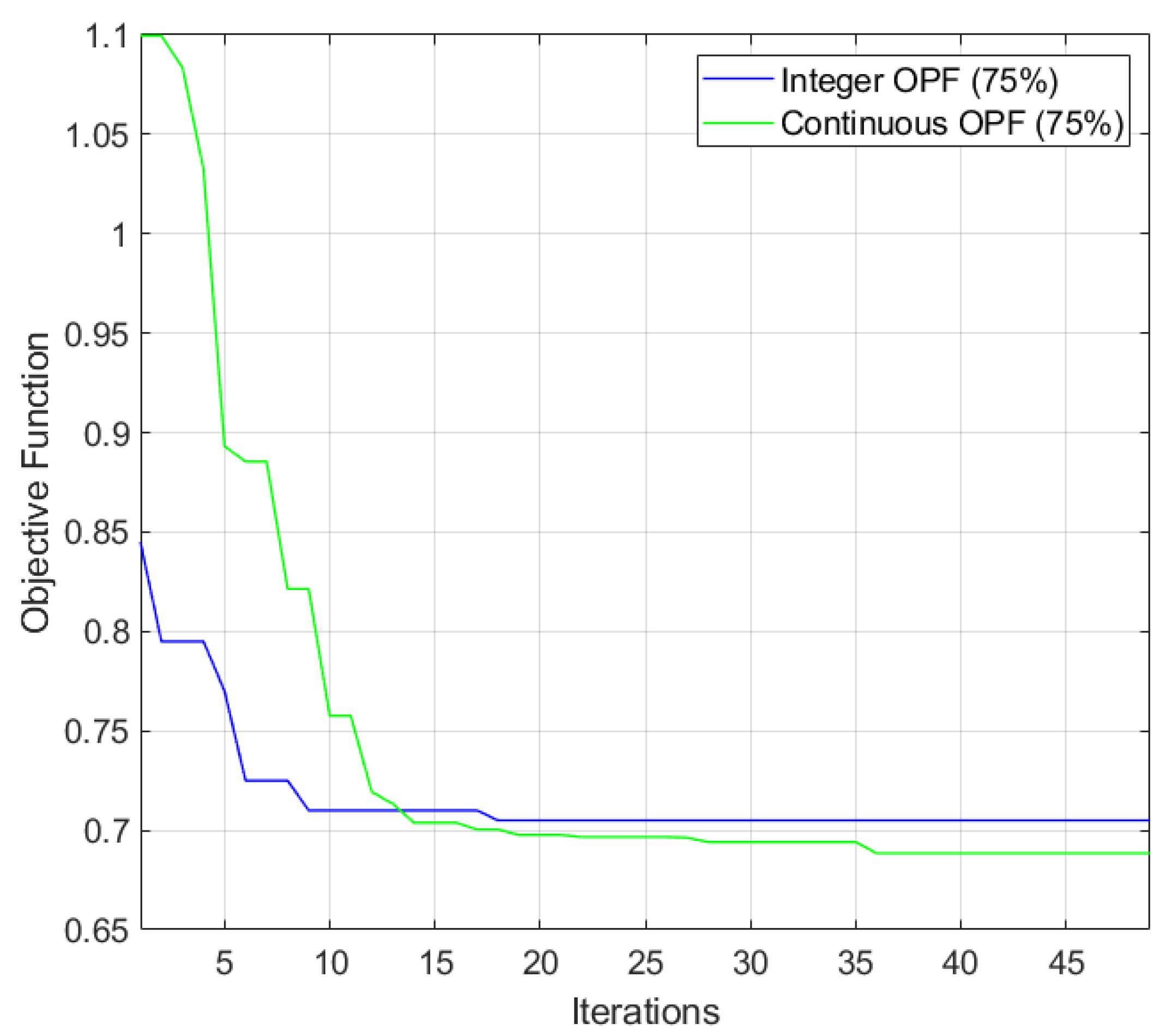
The key innovation lies in the first-time integration of discrete load-shedding optimization with efficient probabilistic uncertainty propagation, combining Differential Evolution (DE) metaheuristics with the Unscented Transformation (UT) technique. This approach enables uncertainty propagation without the computational burden associated with Monte Carlo simulations (MCSs), requiring only 137 samples versus 5000 for MCSs while maintaining equivalent accuracy. The practical relevance of the integer formulation is crucial, as actual microgrid switching devices can only perform complete load disconnections, making continuous optimization solutions impractical for direct implementation. Validation on an IEEE 33-bus microgrid system demonstrates that this integrated approach achieves 95.28% confidence level compliance compared to 50% for deterministic methods, while requiring only 0.58% additional load shedding compared to continuous formulations, confirming the practical superiority of the IM-POPF framework in minimizing total load shedding while maintaining frequency stability under uncertain conditions.

1.2. Key Contributions of This Work

This paper’s contributions include the following:

• Development of IM-POPF that combines discrete load-shedding decisions with uncertainty modeling, unlike existing continuous or deterministic approaches.
• Integration of Unscented Transformation with integer optimization, achieving 36.5-fold reduction in evaluations compared to Monte Carlo while maintaining accuracy.
• Sigmoid function treatment of binary variables enables discrete load disconnection modeling within probabilistic optimization.
• Simultaneous enforcement of probabilistic constraints for all operational limits (frequency, voltage, power generation) with 95% confidence level.
• Demonstration on IEEE 33-bus microgrid system showing 95.28% confidence compliance vs. 50% for deterministic methods with minimal additional load shedding.

1.3. Paper Organization

The remainder of this paper is organized as follows: Section 2 provides the background necessary to understand the proposed approach, including deterministic and probabilistic power flow formulations for islanded microgrids, the Unscented Transform method, confidence levels, and deterministic optimal power flow. Section 3 presents the proposed approach, detailing the mathematical formulation of the integer-mixed probabilistic optimal power flow problem, the treatment of binary variables, individuals’ structure for the metaheuristic algorithms, fitness function calculation, and the complete framework for solving the proposed problem. Section 4 reports the simulation results, beginning with system description and data, followed by a detailed analysis of the IEEE 33-bus islanded microgrid test case under various scenarios (base case, deterministic OPF, and probabilistic OPF), along with general comments, additional analyses, and a discussion of the limitations of the proposed methodology. Finally, Section 5 concludes the paper by summarizing the main findings and suggesting directions for future research.

2. Background

2.1. Deterministic Power Flow for Islanded Microgrids

Islanded microgrids require generators to operate under droop control for frequency regulation [18], and this characteristic must be considered in computational tools used for planning and operation [19]. The most common tool is power flow analysis, which, for AC islanded microgrids, follows the formulation presented in (1)–(5). In this case, a deterministic approach is adopted, without uncertainties considered, and the vectors of the input variables (x) and output (y) are defined in (6) and (7).

Equations (1) and (2) represent the active and reactive power balance at each system node. Equations (3) and (4) model the droop control behavior of generators involved in frequency regulation. The droop characteristics are illustrated in Figure 1. Finally, Equation (5) establishes the angular reference.

$$P_{gk}+P_{gk}^{RER}-P_{dk}-P_k=0,k\in {\mathsf{\Omega }}_B$$

(1)

$$\begin{array}{cc}\hfill & Q_{gk}-Q_{dk}-Q_k=0,k\in {\mathsf{\Omega }}_B\end{array}$$

(2)

$$\begin{array}{cc}\hfill & P_{gk}-{\displaystyle \frac{1}{s_{pk}}}\left(f_k^{*}-f_{mg}\right)=0,k\in {\mathsf{\Omega }}_G\end{array}$$

(3)

$$\begin{array}{cc}\hfill & Q_{gk}-{\displaystyle \frac{1}{s_{qk}}}\left(V_k^{*}-V_k\right)=0,k\in {\mathsf{\Omega }}_G\end{array}$$

(4)

$$\begin{array}{cc}\hfill & {\theta }_k^{ref}=0\end{array}$$

(5)

where the following apply:

• $P_{gk}$ and $Q_{gk}$ represent the active and reactive power generated at bus k. If no generator is connected to the bus k, then $P_{gk}=Q_{gk}=0$.
• $P_{dk}$ and $Q_{dk}$ represent the active and reactive power loads at bus k.
• $P_{gk}^{\mathrm{RER}}$ represents the active power generated by the renewable energy resource (RER) connected to bus k. This power is assumed to be known. If no RER is connected, then $P_{gk}^{\mathrm{RER}}=0$.
• $P_k$ and $Q_k$ are the active and reactive power injections at node k, calculated as functions of the system topology (admittance matrix) and the complex nodal voltages [20].
• $s_{pk}$ and $s_{qk}$ are the frequency and voltage droop coefficients of dispatchable generator k (see Figure 1). These parameters are assumed to be known.
• $f_k^{*}$ and $V_k^{*}$ are the frequency and voltage setpoints of dispatchable generator k (see Figure 1). These parameters are assumed to be known.
• $f_{mg}$ represents the steady-state microgrid frequency.
• ${\theta }_k^{\mathrm{ref}}$ indicates that node k is selected as the reference bus.
• ${\mathsf{\Omega }}_B$ is the set of system nodes (with $n_b$ elements).
• ${\mathsf{\Omega }}_G$ is the set of dispatchable generators (with $n_g$ elements).

$$\begin{array}{cc}\hfill & x=\left[\left[P_{d1}\dots P_{dnb}\right],\left[Q_{d1}\dots Q_{dnb}\right],\left[P_{g1}^{RER}\dots P_{gnrer}^{RER}\right]\right]\end{array}$$

(6)

$$\begin{array}{cc}\hfill & y=\left[\left[V_1\dots V_{nb}\right],\left[{\theta }_1\dots {\theta }_{nb}\right],\left[P_{g1}\dots P_{gng}\right],\left[Q_{g1}\dots Q_{gng}\right],\left[f_{mg}\right]\right]\end{array}$$

(7)

The deterministic power flow for islanded microgrids, formulated in (1)–(5), uses the Newton–Raphson method to compute the output variables y defined in (7), given the input variables x in (6) [21,22].

2.2. Probabilistic Power Flow

In practice, uncertainties are present in the loads and in the power generated by RER units, which are part of the input variables in (6). These uncertainties can be modeled using a normal distribution [23], with mean ${\mu }_{x_k}$ and standard deviation ${\sigma }_{x_k}$, as defined in (8). Equation (9) defines the input mean vector ($x_m$) and the input variance matrix ($P_x$).

$$\begin{array}{cc}\hfill & f\left(x_k\right)={\displaystyle \frac{1}{{\sigma }_{x_k}\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{{\left(x_k-{\mu }_{x_k}\right)}^2}{2{\sigma }_{x_k}^2}}}\end{array}$$

(8)

$$\begin{array}{c}{x}_m=\left[\begin{array}{c}{\mu }_{P_{dk}}\\ {\mu }_{Q_{dk}}\\ {\mu }_{P_{gi}^{RER}}\end{array}\right]\\ P_x=\left[\begin{array}{ccc}{\sigma }_{P_{dk}}^2& 0& 0\\ 0& {\sigma }_{Q_{dk}}^2& 0\\ 0& 0& {\sigma }_{P_{gi}^{RER}}^2\end{array}\right]\end{array}$$

(9)

where

• $k=1,\dots ,nb$ and $i=1,\dots ,nrer$;
• ${\mu }_{P_{dk}}$, ${\mu }_{Q_{dk}}$, and ${\mu }_{P_{gk}^{RER}}$ represent the mean values of loads and renewable energy generation at a node k;
• ${\sigma }_{P_{dk}}$, ${\sigma }_{Q_{dk}}$, and ${\sigma }_{P_{gk}^{RER}}$ represent the standard deviations of loads and renewable energy at a node k.

Probabilistic power flow (PPF) can be represented as a nonlinear function $g\left(x\right)$ in (10), which estimates the probabilistic characteristics of the outputs—namely, the mean ${\mu }_y$ and standard deviation ${\sigma }_y$—given the probabilistic characteristics of the inputs, i.e., the mean ${\mu }_x$ and standard deviation ${\sigma }_x$ [21,23,24].

$$\mathit{y}=g\left(\mathit{x}\right)$$

(10)

In general, the methods for solving the PPF are based on sampling the input variables with a deterministic power flow solved for each sample. For clarity, Figure 2 presents a sample matrix for a system with three load nodes and two nodes equipped with RER units.

2.3. Probabilistic Power Flow for Islanded Microgrids Using the Monte Carlo Simulation

Figure 3 shows the procedure for solving (10) using the Monte Carlo simulation [25]. In Step 1, the required number of samples is defined and the microgrid data is imported. In Step 2, a sample—vector $x_i$, whose structure is defined in (6)—is generated according to Equations (8) and (9), as illustrated in Figure 2.

In Step 3, the deterministic power flow described in Section 2.1 is solved to compute the corresponding output vector $y_i$ (as defined in (7)), which is then stored in Step 4. In Step 5, it is verified whether the desired number of samples has been reached. If so, Step 6 computes the mean and standard deviation, and the process is concluded in Step 7. Otherwise, the procedure returns to Step 2 to generate a new sample.

2.4. Probabilistic Power Flow for Islanded Microgrids Using the Unscented Transform

The Unscented Transformation method employs a reduced set of deterministically calculated samples, significantly lowering the computational burden compared to Monte Carlo simulation. Each sample is referred to as a Sigma Point ${\chi }_{\mathbf{i}}$, with the same structure illustrated in Figure 2. Figure 4 presents the steps for solving (10) (probabilistic power flow) using the Unscented Transformation. Step 1 and Steps 4 and 5 correspond to Step 1 and Steps 3 and 4 of Figure 3, respectively.

Firstly, the vector of means $x_m$ and the matrix with variances $P_x$ are defined according to Equation (9) in Step 1. Taking into account $nb$ load nodes and $nrer$ nodes with RER generators, the dimensions of $x_m$ and $P_x$ are ($(2nb+nrer)\times 1$) and ($(2nb+nrer)\times (2nb+nrer)$), respectively.

Being n uncertain variables (in this paper $n=2nb+nrer$), in Step 2, $2n+1$ Sigma Points are calculated. Each Sigma Point ${\chi }_i$ is a column vector representing a sample whose structure follows the one shown in Figure 2. Unlike Monte Carlo simulation, Sigma Points are deterministically calculated according to Equations (11)–(13).

$${\chi }_1=x_m$$

(11)

$${\chi }_{i+1}=x_m+u_i,i=1,\dots ,n$$

(12)

$${\chi }_{i+1}=x_m-u_i,i=1,\dots ,n$$

(13)

where $u_i$ is a row vector of the matrix U, calculated using Cholesky decomposition, as presented in Equations (14) [26].

$$U^{T}U=(n+\kappa )P_x$$

(14)

In (14), $\kappa$ is a parameter empirically tuned so that the results (means and variances of output variables) are close to those provided by the Monte Carlo simulation [21,27]. In this paper, $\kappa =2$ is considered.

For each Sigma Point, a deterministic power flow is performed (Section 2.1) in Step 4 of Figure 4 to obtain $f_{m{g}_i}$, where i denotes the i^th Sigma Point. In this step, all output variables are computed (see (7)), with frequency selected for illustration purposes.

Once all Sigma Points are evaluated, the means (${\mu }_{f_{mg}}$) and standard deviations (${\sigma }_{f_{mg}}$) of output variables are estimated in Step 7 by (15) and (16). For this purpose, weight factors $W_i$ are required.

$${\mu }_{f_{mg}}=\sum _{i=1}^{2n+1}{W}_i·f_{m{g}_i}$$

(15)

$${\sigma }_{f_{mg}}=\sqrt{\sum _{i=1}^{2n+1}{W}_i·{\left({\mu }_{f_{mg}}-f_{m{g}_i}\right)}^2}$$

(16)

The weight factors $W_i$ are obtained by (17)–(19). It is important to say that the sum of all weights must be equal to unity (see (20)).

$$W_1={\displaystyle \frac{\kappa }{n+\kappa }}$$

(17)

$$W_{i+1}={\left(2(n+\kappa )\right)}^{-1},i=1,\dots ,n$$

(18)

$$W_{i+n+1}={\left(2(n+\kappa )\right)}^{-1},i=1,\dots ,n$$

(19)

$$\sum _{i=1}^{2n+1}{W}_i=1$$

(20)

2.5. Confidence Levels

In the context of deterministic optimization problems, constraints are modeled according to Equation (21). However, when uncertainties are present, the concept of confidence levels is employed [28], where the probability of satisfying the constraints $P_r\left\{y_i^{min}\le y_i\le y_i^{max}\right\}$ must be greater than or equal to a specified confidence level ${\gamma }_{y_i}$, as expressed in Equation (22).

$$\begin{array}{cc}\hfill & y_i^{min}\le y_i\le y_i^{max}\end{array}$$

(21)

$$\begin{array}{cc}\hfill & P_r\left\{y_i^{min}\le y_i\le y_i^{max}\right\}\ge {\gamma }_{y_i}\end{array}$$

(22)

2.6. Deterministic Optimal Power Flow for Islanded Microgrids

Load shedding is a strategy to maintain frequency within acceptable limits. In ref. [29], a continuous deterministic optimal power flow (C-DOPF) is proposed to minimize load shedding in islanded microgrids. However, a more practical strategy consists of allowing only full load shedding, modeled through an integer-mixed deterministic optimal power flow (IM-DOPF). Equations (23)–(33) present the general formulation of the deterministic optimal power flow for load shedding.

The objective function is given in (23), where ${\alpha }_k$ represents the load-shedding factor: if ${\alpha }_k=0$, the full load on bus k is preserved; if ${\alpha }_k=1$, the load is entirely curtailed (i.e., 100% load shedding). Equations (24)–(28) are similar to those of the deterministic power flow, with the difference being the inclusion of the load-shedding factor. It is important to note that load shedding is performed while maintaining a constant power factor.

Equations (29)–(32) define the constraints on continuous variables, including steady-state microgrid frequency, voltage magnitudes, and active and reactive power generation. Equation (33) defines the bounds for the load-shedding factors.

In the C-DOPF case, partial load shedding is permitted ($0\le {\alpha }_k\le 1$), and the problem is solved using the Interior Point Method [30]. In contrast, in the IM-DOPF formulation, only full load shedding is allowed (${\alpha }_k\in \{0,1\}$), and the problem is solved using the Differential Evolution method [31], following a framework similar to the one proposed in the next section. Note that this work does not allow simultaneous application of continuous and integer load shedding. Therefore, only one of the constraints in (33) is considered.

$$\begin{array}{ccc}min\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill & & F_{\left(\mathit{z}\right)}={\sum }_{k\in {\mathsf{\Omega }}_B}{\alpha }_k{P}_{dk}\end{array}$$

(23)

$$\begin{array}{cc}\hfill & P_{gk}+P_{gk}^{RER}-(1-{\alpha }_k)P_{dk}-P_k=0,k\in {\mathsf{\Omega }}_B\end{array}$$

(24)

$$\begin{array}{cc}\hfill & Q_{gk}-(1-{\alpha }_k)Q_{dk}-Q_k=0,k\in {\mathsf{\Omega }}_B\end{array}$$

(25)

$$\begin{array}{cc}\hfill & P_{gk}-{\displaystyle \frac{1}{s_{pk}}}\left(f_k^{*}-f_{mg}\right)=0,k\in {\mathsf{\Omega }}_G\end{array}$$

(26)

$$\begin{array}{cc}\hfill & Q_{gk}-{\displaystyle \frac{1}{s_{qk}}}\left(V_k^{*}-V_k\right)=0,k\in {\mathsf{\Omega }}_G\end{array}$$

(27)

$$\begin{array}{cc}\hfill & {\theta }_k^{ref}=0\end{array}$$

(28)

$$\begin{array}{ccc}\mathrm{st}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill & & f_{mg}^{min}\le f_{mg}\le f_{mg}^{max}\end{array}$$

(29)

$$\begin{array}{cc}\hfill & V_k^{min}\le V_k\le V_k^{max},k\in {\mathsf{\Omega }}_B\end{array}$$

(30)

$$\begin{array}{cc}\hfill & P_{gk}^{min}\le P_{gk}\le P_{gk}^{max},k\in {\mathsf{\Omega }}_G\end{array}$$

(31)

$$\begin{array}{cc}\hfill & Q_{gk}^{min}\le Q_{gk}\le Q_{gk}^{max},k\in {\mathsf{\Omega }}_G\end{array}$$

(32)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}0\le {\alpha }_k\le 1,\hfill & \mathrm{if}\mathrm{partial}\mathrm{load}\mathrm{shedding}\mathrm{is}\mathrm{allowed}\hfill \\ {\alpha }_k\in \{0,1\},\hfill & \mathrm{if}\mathrm{only}\mathrm{full}\mathrm{load}\mathrm{shedding}\mathrm{is}\mathrm{allowed}\hfill \end{array}\right.,k\in {\mathsf{\Omega }}_B\end{array}$$

(33)

3. Proposed Approach

3.1. Mathematical Formulation

This paper proposes a probabilistic optimal power flow formulation for load shedding in islanded microgrids, in which the decision variables $\mathit{w}$ are defined in (34). These variables comprise the load-shedding factors $\mathit{z}$, as given in (35), and the power flow variables $\mathit{y}$, as defined in (36).

$$\begin{array}{cc}\hfill & w=\left[\left[z\right],\left[y\right]\right]\end{array}$$

(34)

$$\begin{array}{cc}\hfill & z=\left[{\alpha }_1\dots {\alpha }_k\dots {\alpha }_{nb}\right]\end{array}$$

(35)

$$\begin{array}{cc}\hfill & y=\left[\left[V_1\dots V_{nb}\right],\left[{\theta }_1\dots {\theta }_{nb}\right],\left[P_{g1}\dots P_{gng}\right],\left[Q_{g1}\dots Q_{gng}\right],\left[f_{mg}\right]\right]\end{array}$$

(36)

The general formulation of the proposed approach is presented in Equations (37)–(47). The objective function, given in (37), aims to minimize the total load to be shed. The power balance equations, droop control characteristics, and angular reference are described in (38)–(42).

In this approach, the droop parameters ($s_{pk}$, $s_{qk}$, $f_k^{*}$, and $V_k^{*}$) are assumed to be known. Moreover, the loads and RER generation are modeled as normally distributed random variables, as discussed in Section 2.2. Consequently, the output variables ($V_k$, ${\theta }_k$, $P_{gk}$, $Q_{gk}$, and $f_{mg}$) become uncertain, and Equations (43)–(46) express the probability constraints associated with their operating limits.

Finally, the proposed formulation considers that load shedding—whose factors are bounded by (47)—may be continuous ($0\le {\alpha }_k\le 1$) or integer (${\alpha }_k\in \{0,1\}$). It is important to note that, in this work, simultaneous application of continuous and integer load shedding is not allowed; thus, only one of these constraint types is considered per optimization scenario.

$$\begin{array}{ccc}min\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill & & F_{\left(\mathit{z}\right)}={\sum }_{k\in {\mathsf{\Omega }}_B}{\alpha }_k{P}_{dk}\end{array}$$

(37)

$$\begin{array}{cc}\hfill & P_{gk}+P_{gk}^{RER}-(1-{\alpha }_k)P_{dk}-P_k=0,k\in {\mathsf{\Omega }}_B\end{array}$$

(38)

$$\begin{array}{cc}\hfill & Q_{gk}-(1-{\alpha }_k)Q_{dk}-Q_k=0,k\in {\mathsf{\Omega }}_B\end{array}$$

(39)

$$\begin{array}{cc}\hfill & P_{gk}-{\displaystyle \frac{1}{s_{pk}}}\left(f_k^{*}-f_{mg}\right)=0,k\in {\mathsf{\Omega }}_G\end{array}$$

(40)

$$\begin{array}{cc}\hfill & Q_{gk}-{\displaystyle \frac{1}{s_{qk}}}\left(V_k^{*}-V_k\right)=0,k\in {\mathsf{\Omega }}_G\end{array}$$

(41)

$$\begin{array}{cc}\hfill & {\theta }_k^{ref}=0\end{array}$$

(42)

$$\begin{array}{ccc}\mathrm{st}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill & & P_r\left\{f_{mg}^{min}\le f_{mg}\le f_{mg}^{max}\right\}\ge {\gamma }_{f_{mg}}\end{array}$$

(43)

$$\begin{array}{cc}\hfill & P_r\left\{V_k^{min}\le V_k\le V_k^{max}\right\}\ge {\gamma }_{V_k},k\in {\mathsf{\Omega }}_B\end{array}$$

(44)

$$\begin{array}{cc}\hfill & P_r\left\{P_{gk}^{min}\le P_{gk}\le P_{gk}^{max}\right\}\ge {\gamma }_{P_{gk}},k\in {\mathsf{\Omega }}_G\end{array}$$

(45)

$$\begin{array}{cc}\hfill & P_r\left\{Q_{gk}^{min}\le Q_{gk}\le Q_{gk}^{max}\right\}\ge {\gamma }_{Q_{gk}},k\in {\mathsf{\Omega }}_G\end{array}$$

(46)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}0\le {\alpha }_k\le 1,\hfill & \mathrm{if}\mathrm{partial}\mathrm{load}\mathrm{shedding}\mathrm{is}\mathrm{allowed}\hfill \\ {\alpha }_k\in \{0,1\},\hfill & \mathrm{if}\mathrm{only}\mathrm{full}\mathrm{load}\mathrm{shedding}\mathrm{is}\mathrm{allowed}\hfill \end{array}\right.,k\in {\mathsf{\Omega }}_B\end{array}$$

(47)

3.2. Binary Variable Treatment

The proposed approach can assume a continuous formulation when partial load shedding is allowed. In this case, the constraint ${\alpha }_k\in \{0,1\}$ is not included in (47). However, when only full load shedding is permitted, the constraint ${\alpha }_k\in \{0,1\}$ becomes active, and the problem is characterized as a Mixed-Integer Nonlinear Programming (MINLP) problem.

The integer variables $\mathit{z}$ in Equation (35) are handled using the sigmoid function defined in Equation (48), as introduced in [32]. This strategy enables the use of continuous optimization techniques to solve the probabilistic optimal power flow problem described in Section 3.1.

Figure 5 illustrates the sigmoid function: given a continuous optimization variable $z_k$, the corresponding sigmoid value $\mathrm{sig}\left(z_k\right)$ is computed. Based on the condition defined in Equation (49), it becomes possible to model the binary nature of the variable ${\alpha }_k$. Finally, Equation (50) imposes bounds on the continuous variable $z_k$.

$$sig\left(z_k\right)={\displaystyle \frac{1}{1+e^{-10\left(z_k-0.5\right)}}}$$

(48)

$${\alpha }_k=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}sig\left(z_k\right)\ge 0.5\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(49)

$$\begin{array}{cc}\hfill & 0\le z_k\le 1\hfill \end{array}$$

(50)

3.3. Individual Structure

The approach proposed in Section 3.1 is solved using a framework based on Differential Evolution [31] and the Unscented Transformation-based probabilistic power flow described in Section 2.4. Individuals of Differential Evolution follow the structure defined in Equation (51).

$${ind}_k=\left[\begin{array}{ccccccc}{z}_1\hfill & z_2\hfill & \cdots \hfill & z_p\hfill & \cdots \hfill & z_{nb-1}\hfill & z_{nb}\hfill \end{array}\right]$$

(51)

where $nb$ is the number of nodes in the microgrid; ${ind}_k$ denotes the $k^{th}$ individual; $z_p$ denotes the load-shedding factor of node $p^{th}$. It is important to note that during the optimization process, individuals must satisfy the bounds defined in (50).

3.4. Fitness Function Calculation

For each individual $in{d}_k$ in Equation (51), a fitness function $fi{t}_k$ is calculated following the procedure depicted in Figure 6. In Step 01, the continuous individual’s values in Equation (51) are read. Step 02 applies the sigmoid function as discussed in Section 3.2, for the integer load shedding. If continuous load shedding is allowed, no binary treatment is performed.

Once the load-shedding factors are determined, in Step 03, the loads are adjusted (shed), and the Unscented Transformation-based probabilistic power flow (UT-PPF), as described in Section 2.4, is executed to compute the mean and standard deviation of the output variables. In addition, the probabilities of meeting operational limits are also evaluated. It is important to note that the application of UT-PPF within a probabilistic load-shedding framework for islanded microgrids constitutes a contribution of this paper. Since the Unscented Transformation relies on a reduced set of deterministically selected samples, it provides a significant computational performance advantage compared to the Monte Carlo simulation approach.

In Step 04, the set of penalty terms is calculated according to Equations (54)–(62). These terms are nonzero when the probabilities of satisfying the operational limits fall below the required confidence levels, or when the probabilistic power flow fails to converge.

In Step 05, the fitness function is computed according to Equations (52)–(53), with empirically selected weights: ${\beta }_1={\beta }_6=1$, and ${\beta }_2=\dots ={\beta }_5=10$. Finally, Step 06 returns the fitness value $fi{t}_k$.

$$fi{t}_k=\sum _{i=1}^6{\beta }_i{F}_i$$

(52)

$$F_1=\sum _{k\in {\mathsf{\Omega }}_B}{\alpha }_k{P}_{dk}$$

(53)

$$F_2=\Delta P_{r{f}_{mg}}$$

(54)

$$\Delta P_{r{f}_{mg}}=\left\{\begin{array}{cc}\left|P_r\left\{f_{mg}^{min}\le f_{mg}\le f_{mg}^{max}\right\}-{\gamma }_{f_{mg}}\right|,\hfill & \mathrm{if}{P}_r\left\{f_{mg}^{min}\le f_{mg}\le f_{mg}^{max}\right\}<{\gamma }_{f_{mg}}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(55)

$$F_3=\sum _{k=1}^{nb}\Delta P_{r{V}_k}$$

(56)

$$\Delta P_{r{V}_k}=\left\{\begin{array}{cc}\left|P_r\left\{V_k^{min}\le V_k\le V_k^{max}\right\}-{\gamma }_{V_k}\right|,\hfill & \mathrm{if}{P}_r\left\{V_k^{min}\le V_k\le V_k^{max}\right\}<{\gamma }_{V_k}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(57)

$$F_4=\sum _{k=1}^{ng}\Delta P_{r{P}_{gk}}$$

(58)

$$\Delta P_{r{P}_{gk}}=\left\{\begin{array}{cc}\left|P_r\left\{P_{gk}^{min}\le P_{gk}\le P_{gk}^{max}\right\}-{\gamma }_{P_{gk}}\right|,\hfill & \mathrm{if}{P}_r\left\{P_{gk}^{min}\le P_{gk}\le P_{gk}^{max}\right\}<{\gamma }_{P_{gk}}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(59)

$$F_5=\sum _{k=1}^{ng}\Delta P_{r{Q}_{gk}}$$

(60)

$$\Delta P_{r{Q}_{gk}}=\left\{\begin{array}{cc}\left|P_r\left\{Q_{gk}^{min}\le Q_{gk}\le Q_{gk}^{max}\right\}-{\gamma }_{Q_{gk}}\right|,\hfill & \mathrm{if}{P}_r\left\{Q_{gk}^{min}\le Q_{gk}\le Q_{gk}^{max}\right\}<{\gamma }_{Q_{gk}}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(61)

$$F_6=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}\mathrm{the}\mathrm{UT}\mathrm{PPF}\mathrm{converged}\hfill \\ {10}^{10},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(62)

3.5. Proposed Framework for Solving the Proposed Problem

The proposed approach is solved by the Differential Evolution algorithm [31]. It is a population-based metaheuristic that iteratively improves a specific solution to an optimization problem using an evolutionary process. Figure 7 shows the DE algorithm. In Step 01, parameters such as population size, mutation scaling factor, and crossover rate are defined according to [33]. In Step 02, feasible solutions are generated. Step 03 evaluates each solution (individual) as discussed in Section 3.4 and depicted in Figure 6. If the maximum number of generations (iterations) is reached in Step 04, the results are returned in Step 05. Otherwise, evolutionary operators (mutation, crossover, and selection) are applied in Steps 06, 07, and 08. For further information on evolutionary operators, the reader is referred to [31,33].

4. Results

This section presents the validation and performance analysis of the proposed IM-POPF methodology for load shedding in islanded microgrids. The approach is evaluated on an IEEE 33-bus radial distribution system configured as an islanded microgrid under various uncertainty scenarios.

All simulations were implemented in MATLAB R2010a, with power flow calculations using the Newton–Raphson method. Optimization was performed via a custom Differential Evolution implementation with parameter specifications: population size of 50, 30 generations, mutation factor of 0.5, and crossover rate of 0.9. The analysis compares deterministic and probabilistic formulations for both continuous and integer load-shedding strategies, demonstrating the computational efficiency of the Unscented Transformation approach versus Monte Carlo simulation. Performance metrics include load-shedding requirements, confidence level compliance, computational efficiency, and system reliability under varying uncertainty levels.

4.1. System Description and Data

This work analyzes the IEEE 33-bus microgrid, illustrated in Figure 8 [34,35,36]. Islanding is assumed to occur due to the disconnection between nodes 33 (substation) and 1. At the nominal operating point, considered the base case in this study, the total power demands are 3.715 MW and 2.3 MVAr, as detailed in

Table 1. Power loads of the IEEE 33-bus microgrid. Adapted from [34].

Node	${\mathit{P}}_{\mathit{dk}}^{\mathit{nom}}$ (kW)	${\mathit{Q}}_{\mathit{dk}}^{\mathit{nom}}$ (kVAr)
1	100	60
2	90	40
3	120	80
4	60	30
5	60	20
6	200	100
7	200	100
8	60	20
9	60	20
10	45	30
11	60	35
12	60	35
13	120	80
14	60	10
15	60	20
16	60	20
17	90	40
18	90	40
19	90	40
20	90	40
21	90	40
22	90	50
23	420	200
24	420	200
25	60	25
26	60	25
27	60	20
28	120	70
29	200	600
30	150	70
31	210	100
32	60	40
Total	3.715 MW	2.300 MVAr

. Branch data is available in [34]. The power, voltage, and frequency bases are 1 MVA, 12.66 kV, and 60 Hz, respectively. Bus 1 is adopted as the angular reference.

Three distributed generation units operating in droop control mode are assigned on buses 2, 12, and 29. Their operational limits and droop curve parameters (setpoints) are presented in

Table 2. Limits of variables.

Variable	Lower Bound	Upper Bound
$P_{gk}$ (MW)	0	1.5
$Q_{gk}$ (MVAr)	−2.0	2.0
$V_k$ (pu)	0.9	1.1
$f_{mg}$ (Hz)	59.9	60.1

and

Table 3. Droop curve parameter.

Variable	Value
$f_k^{*}$ (Hz)	60
$V_k^{*}$ (pu)	1.01
$s_{pk}$ (pu)	0.002
$s_{qk}$ (pu)	0.002

. Sensitivity analysis on these parameters was not performed, as it is outside the scope of this study. Furthermore, the microgrid includes four renewable energy resource (RER)-based generators, each with a nominal power of 150 kW, as indicated in

Table 4. Power of each renewable energy resource.

Variable	${\mathit{P}}_{\mathit{gk}}^{\mathit{rer}}$ (kW)
IEEE 33-bus	150

.

4.2. IEEE 33-Bus Islanded Microgrid

4.2.1. Base Case

The deterministic power flow described in Section 2.1 is performed for the base case, with results summarized in

Table 5. Deterministic power flow solution.

Variable	Bus 02	Bus 12	Bus 29
$P_{gk}$ (MW)	1.0511	1.0511	1.0511
$Q_{gk}$ (MVAr)	1.7261	−0.1339	0.7360
$f_{mg}$ = 59.8739 Hz

. As observed, the microgrid frequency ($f_{mg}=59.8739$ Hz) falls outside the acceptable range ($59.9\le f_{mg}\le 60.1$ Hz). Under these conditions, a load-shedding strategy must be applied.

4.2.2. Deterministic OPF

The deterministic optimal power flow, presented in Section 2.6, has been performed, and the results are summarized in

Table 6. Load shedding using the Deterministic OPF.

Node	${\mathit{P}}_{\mathit{dk}}^{\mathit{nom}}$	${\mathit{\alpha }}_{\mathit{k}}^{\mathit{continuous}}$ (%)	${\mathit{\alpha }}_{\mathit{k}}^{\mathit{integer}}$ (%)
1	100	2.67	100
2	90	1.65	100
3	120	1.40	0
4	60	2.58	100
5	60	1.65	100
6	200	0.46	0
7	200	0.33	0
8	60	0.59	0
9	60	0.40	0
10	45	0.52	0
11	60	0.35	0
12	60	0.23	100
13	120	0.12	0
14	60	0.24	0
15	60	0.24	0
16	60	0.25	0
17	90	0.16	0
18	90	3.61	0
19	90	27.23	0
20	90	35.88	0
21	90	11.08	100
22	90	2.80	0
23	420	57.44	0
24	420	70.53	0
25	60	1.64	0
26	60	1.50	0
27	60	1.00	0
28	120	0.40	100
29	200	0.20	0
30	150	0.35	0
31	210	0.27	0
32	60	0.96	100

. The first analysis focuses on the frequency of the microgrid. The continuous OPF solution enables load shedding such that the frequency reaches 59.9 Hz—the lower bound of the acceptable range—as shown in

Table 7. Continuous deterministic optimal power flow solution.

Variable	Bus 02	Bus 12	Bus 29
$P_{gk}$ (MW)	0.83332	0.83332	0.83332
$Q_{gk}$ (MVAr)	0.97118	0.10028	0.9396
$f_{mg}$ = 59.9 Hz

. To achieve this, 16.874% of the active power load is shed, as reported in

Table 8. Continuous deterministic OPF—load-shedding results.

	Active	Reactive
Nominal	3.715 MW	2.3 MVAr
Load Preserved	3.0881 MW	2.0021 MVAr
Load Shedding	0.6269 MW	0.2979 MVAr
Percentual	16.874%	12.953%

. It is important to note that the load shedding is performed while maintaining a constant power factor; therefore, the percentage of reactive power shedding differs from that of active power. In contrast, the integer load-shedding approach requires a slightly higher increase: 17.227% of the nominal active power load is cut, as shown in

Table 9. Integer deterministic OPF—load-shedding results.

	Active	Reactive
Nominal	3.715 MW	2.3 MVAr
Load Preserved	3.075 MW	1.965 MVAr
Load Shedding	0.645 MW	0.335 MVAr
Percentual	17.227%	14.565%

. Additional results, including active and reactive power generation values, are available in Table 7 and

Table 10. Integer deterministic optimal power flow solution.

Variable	Bus 02	Bus 12	Bus 29
$P_{gk}$ (MW)	0.83331	0.83331	0.83331
$Q_{gk}$ (MVAr)	1.3655	−0.022305	0.6405
$f_{mg}$ = 59.9 Hz

.

As discussed in Section 2.2, both the load demands and the power outputs of RER-based generators are subject to uncertainty, which requires a probabilistic analysis to assess the likelihood that the output variables remain within their operational limits. Considering 32 buses and 4 RER-based generators, a total of 68 uncertain input variables are evaluated: 32 active and 32 reactive power loads, in addition to 4 generation values.

First, uncertain input variables are modeled using a normal distribution with a mean equal to the nominal value and a standard deviation equal to 10% of the respective nominal value. The Monte Carlo simulation was carried out considering 5000 samples, as discussed in Section 2.3, to validate the results obtained by the deterministic optimal power flow in Section 4.2.2.

In addition, the UT-based probabilistic power flow, discussed in Section 2.4, has also been performed. In this case, according to the Unscented Transformation flowchart in Figure 4, and considering the number of uncertain input variables as 68 ($n=32+32+4=68$), the total number of UT samples is 137 ($2n+1$). Therefore, the maximum number of samples used in the probabilistic power flow analysis is 5000 for MCS and 137 for UT.

An interesting point is the number of samples in the UT. According to Table 6, the integer deterministic OPF disconnects 8 nodes; therefore, 24 nodes remain, reducing the number of uncertain input variables to $n=24+24+4=52$. As a result, the number of UT samples becomes 105 ($2n+1$).

Table 11. Probabilistic validation of continuous deterministic OPF solution.

	UT	MCS
Samples	137	5000
${\mu }_{f_{mg}}$ (Hz)	59.9	59.9
${\sigma }_{f_{mg}}$ (Hz)	0.0027623	0.0027207
$P_r\left\{f_{mg}^{min}\le f_{mg}\le f_{mg}^{max}\right\}(\%)$	50.008	50.683

and

Table 12. Probabilistic validation of integer deterministic OPF solution.

	UT	MCS
Samples	105	5000
${\mu }_{f_{mg}}$ (Hz)	59.9	59.9
${\sigma }_{f_{mg}}$ (Hz)	0.0035226	0.0034839
$P_r\left\{f_{mg}^{min}\le f_{mg}\le f_{mg}^{max}\right\}(\%)$	49.917	49.336

present the results for the validation of continuous and integer deterministic OPF, respectively. It can be seen that the mean and standard deviation of the frequency, the selected output variable for analysis, are very similar in both cases. Regarding the standard deviation, the estimation errors of the Unscented Transformation relative to the MCS are small: $4.16\times {10}^{-5}$ for the continuous case (Table 11) and $3.87\times {10}^{-5}$ for the integer case (Table 12).

As a result of the probabilistic power flow, the probabilities of satisfying the limits of the output variable can be computed. The goal is to assess whether the confidence levels defined in Section 2.5—95% in this study, as adopted in [37,38]—are met. It can be seen that the probabilities of meeting the frequency limits are close to 50%, significantly below the target confidence level. This highlights the importance of using a probabilistic OPF approach, such as those proposed in this paper (continuous and integer approaches).

It is important to note that the number of samples required for MCS depends on the characteristics of the problem being addressed. In this study, a total of 5000 samples were adopted according to recommendations from the literature on power flow analysis [21,23,25]. To assess the adequacy of this sample size, the convergence of MCS was evaluated during the validation of the continuous deterministic optimal power flow solution (Table 11).

The trajectories of the mean and standard deviation of the frequency are shown in Figure 9 and Figure 10, respectively. It can be observed that both metrics stabilize after approximately 1500 to 2000 iterations. This value is significantly higher than the number of samples required by the Unscented Transformation (137), which reinforces the computational advantage of adopting the UT-based approach in the proposed methodology.

4.2.3. Probabilistic OPF

The probabilistic optimal power flow proposed in Section 3 is applied to determine the minimum load shedding required to ensure that the probability that the output variables remain within their limits is greater than or equal to the confidence level of 95%. All output variables are considered, with the microgrid frequency used for illustration purposes.

The Differential Evolution algorithm, illustrated in Figure 7, is executed with 30 generations and a population of 50 individuals. Input uncertainties are modeled with a standard deviation of 10% of their nominal values. Considering the Unscented Transformation, a total of 50 individuals × 30 generations × 137 samples = 205,500 deterministic power flow evaluations (as defined in Section 2.1) are performed.

If the Monte Carlo simulation were used instead, the total would reach $50\times 30\times 5000$ evaluations. This corresponds to approximately 36.5 times more executions than required by the Unscented Transformation. This result highlights the computational efficiency of the proposed UT-based approach, which significantly reduces the number of samples needed for probabilistic analysis while maintaining accuracy.

Table 13. Load shedding using the Probabilistic OPF.

Node	${\mathit{P}}_{\mathit{dk}}^{\mathit{nom}}$	${\mathit{\alpha }}_{\mathit{k}}^{\mathit{continuous}}$ (%)	${\mathit{\alpha }}_{\mathit{k}}^{\mathit{integer}}$ (%)
1	100	16.76	100
2	90	53.84	0
3	120	1.43	0
4	60	34.68	0
5	60	66.04	100
6	200	15.48	0
7	200	1.98	0
8	60	14.70	100
9	60	0.95	0
10	45	25.92	0
11	60	26.74	100
12	60	19.48	0
13	120	6.06	0
14	60	11.74	0
15	60	94.80	100
16	60	30.35	100
17	90	12.62	0
18	90	30.68	0
19	90	76.11	0
20	90	0.078	0
21	90	37.57	100
22	90	29.76	100
23	420	1.24	0
24	420	30.54	0
25	60	24.64	0
26	60	42.68	0
27	60	1.41	100
28	120	16.51	0
29	200	23.29	0
30	150	7.95	100
31	210	20.93	0
32	60	4.54	0

presents the load-shedding factors obtained for the continuous and integer formulations. A detailed breakdown of the solutions is provided in

Table 14. Continuous probabilistic OPF—load-shedding results.

	Active	Reactive
Nominal	3.715 MW	2.3 MVAr
Load Preserved	2.9467 MW	1.8301 MVAr
Load Shedding	0.7683 MW	0.46995 MVAr
Percentual	20.682%	20.432%

and

Table 15. Integer probabilistic OPF—load-shedding results.

	Active	Reactive
Nominal	3.715 MW	2.3 MVAr
Load Preserved	2.925 MW	1.945 MVAr
Load Shedding	0.79 MW	0.355 MVAr
Percentual	21.265%	15.435%

, where it can be seen that the integer formulation requires slightly higher load shedding.

Regarding the probabilistic indices,

Table 16. Probabilistic validation of continuous probabilistic OPF solution.

	UT	MCS
Samples	137	5000
${\mu }_{f_{mg}}$ (Hz)	59.905	59.905
${\sigma }_{f_{mg}}$ (Hz)	0.0031336	0.0031042
$P_r\left\{f_{mg}^{min}\le f_{mg}\le f_{mg}^{max}\right\}(\%)$	95.282	95.467

and

Table 17. Probabilistic validation of integer probabilistic OPF solution.

	UT	MCS
Samples	97	5000
${\mu }_{f_{mg}}$ (Hz)	59.906	59.906
${\sigma }_{f_{mg}}$ (Hz)	0.0034991	0.0034572
$P_r\left\{f_{mg}^{min}\le f_{mg}\le f_{mg}^{max}\right\}(\%)$	95.251	95.465

confirm once again that the results obtained with Monte Carlo simulation and Unscented Transformation are very similar.

In contrast to the deterministic OPF, the probabilistic OPF ensures that the probabilities of meeting the frequency limits now satisfy the required confidence level of 95%. A quantitative comparison of the load-shedding amounts will be presented in the following section.

4.2.4. General Comments

Figure 11 presents the frequency probability density functions for four Optimal Power Flow solutions. These figures were obtained using the results of Table 11, Table 12, Table 16 and Table 17.

The blue and orange curves represent the deterministic OPFs validation—continuous and integer, respectively—and both concentrate the mean exactly at the lower frequency limit of 59.90 Hz, since the load was adjusted to operate at the boundary. In contrast, the yellow and purple curves, corresponding to the continuous and integer probabilistic OPFs, shift the mean slightly to the right (around 59.905–59.906 Hz). Although these curves exhibit greater dispersion, the standard deviation remains around 0.003 Hz. This slight shift toward higher frequencies, combined with controlled variability, increases the probability of satisfying the operational limits.

Another important comparison involves the amount of load shedding required by the four approaches: (i) C-DOPF, (ii) IM-DOPF, (iii) C-POPF, and (iv) IM-POPF. The results are shown in Figure 12. As expected, continuous formulations result in lower load shedding as a result of their ability to finely adjust load values. In contrast, the integer formulations require higher load shedding since they operate under fixed shedding steps (0 or 100%). Furthermore, when uncertainties are considered, probabilistic OPF approaches require greater load shedding to ensure compliance with the prescribed confidence level. The impact of the confidence level on the solution will be discussed in the next subsection.

The results demonstrate that the proposed IM-POPF methodology provides a practical solution for real-time microgrid operation, addressing challenges faced by system operators. The computational efficiency achieved through Unscented Transformation (97.3% reduction in evaluations) makes the approach feasible for online implementation, where rapid decision-making is crucial during frequency disturbances. The integer formulation’s discrete load-shedding capability aligns with actual switching device limitations, where loads cannot be partially disconnected but must be fully shed or maintained. This practical constraint is often overlooked in continuous optimization approaches, yet it significantly impacts real-world implementation. Furthermore, the probabilistic framework’s ability to maintain 95% confidence levels provides operators with reliability guarantees that deterministic methods cannot offer, particularly important for important loads and regulatory compliance in islanded operations.

4.2.5. Additional Analysis

The proposed approach has been applied considering a standard deviation of 10% for the input variables (loads and power from RER-based generators). As shown in Table 16 and Table 17, the continuous POPF satisfies the frequency limits with a probability of 95.28%, while the integer-mixed POPF achieves a probability of 95.25%.

To evaluate the impact of different standard deviation values, the probabilistic OPF solution previously obtained in Table 13 is validated using the Unscented Transformation-based power flow method presented in Section 2.4. The results are summarized in

Table 18. Probability of frequency staying within limits for different uncertainty levels (%).

Uncertainty (%)	C-POPF	IM-POPF
2.5	100.00	100.00
5.0	99.96	99.96
10.0	95.28	95.25
12.5	90.94	90.90
15.0	86.71	86.66

. As expected, the greater the uncertainty (measured by the standard deviation), the lower the probability of satisfying the frequency constraints. These findings reinforce the importance of accurate forecasting tools to reduce uncertainty in loads and RER-based generation (such as wind and solar sources).

The impact of the pre-specified confidence level is another important aspect of the analysis. To this end, the probabilistic OPF was performed considering a reduced confidence level of 75%. Continuous and integer formulations were applied, and the results are presented in Figure 13, comparing the two levels: 95% (previously considered) and 75%.

The first observation confirms previous findings: the integer formulation requires greater load shedding. The second observation is that the lower the confidence level, the smaller the amount of load that needs to be shed.

Finally, Figure 14 illustrates the convergence of the objective function (associated with the percentage of load shed) for both continuous and integer OPF under a 75% confidence level. Initially, the integer OPF presents a lower objective value due to its coarser search space, while the continuous OPF exhibits a faster improvement in the early iterations. After approximately 15 generations, both approaches converge, with the continuous OPF achieving a slightly lower final value, demonstrating its superior ability to fine-tune load adjustments. These results confirm the robustness and computational efficiency of the proposed optimization framework.

4.3. Limitations of the Proposed Methodology

When compared to existing load-shedding strategies in the literature, our approach bridges the gap between theoretical optimization and practical implementation constraints. Traditional under-frequency load-shedding schemes typically use fixed thresholds and predetermined sequences, which may result in excessive or insufficient load removal. Our probabilistic approach dynamically adjusts shedding amounts based on uncertainty levels, providing more precise control. The slight increase in load shedding required by the integer formulation (0.58% additional) is a reasonable trade-off for practical implementability, especially considering the substantial improvement in confidence level compliance. The methodology’s scalability to different microgrid configurations and uncertainty scenarios positions it as a valuable tool for the growing deployment of renewable-based islanded systems, where uncertainty management becomes increasingly critical for reliable operation.

Despite promising results, the proposed approach presents some limitations. One of them is its restricted applicability to balanced islanded microgrids. However, the framework can be extended to other types and configurations of microgrids by adapting the deterministic power flow model used within the Unscented Transformation evaluations. The proposed method is more suitable for operation planning rather than real-time applications, given the computational cost—despite the reduced number of samples required by the Unscented Transformation. This limitation could be mitigated through parallel computing or by exploring alternative probabilistic methods with lower computational demands.

An alternative solution would be to apply machine learning techniques to estimate the mean and standard deviation of the output variables, thereby avoiding the need to solve multiple deterministic power flows. Additionally, the integer formulation currently leads to total or null load shedding at each node. Adopting a step-based shedding strategy, when permitted by operational procedures, would offer greater flexibility and could be incorporated into the proposed framework with appropriate adjustments.

5. Conclusions

This paper proposed a novel integer-mixed probabilistic optimal power flow (IM-POPF) formulation to minimize load shedding in islanded AC microgrids under uncertainty while ensuring frequency stability. The approach integrates an innovative combination of discrete load-shedding decisions with probabilistic uncertainty modeling through Unscented Transformation and Differential Evolution optimization.

The key quantitative achievements demonstrate significant improvements over existing methods. The Unscented Transformation approach reduces computational evaluations by 97.3%, requiring only 205,500 deterministic power flow calculations compared to 7,500,000 for the Monte Carlo simulation while maintaining equivalent accuracy. The probabilistic formulation ensures 95.28% confidence level compliance for frequency limits, compared to only 50% achieved by deterministic methods. The integer load-shedding formulation requires minimal additional load shedding (21.265%) compared to continuous approaches (20.682%), representing only 0.58% difference while providing practical discrete operational capability.

Validation on the IEEE 33-bus microgrid confirms robust performance across varying uncertainty levels from 2.5% to 15% standard deviation, with consistent confidence level maintenance. The results demonstrate that higher confidence levels require proportionally increased load shedding, while lower uncertainty levels improve system performance, emphasizing the importance of accurate forecasting for renewable generation and load demands.

The proposed IM-POPF framework addresses the gap between theoretical continuous optimization and real-world discrete operational requirements in islanded microgrids. The methodology provides power system operators with a computationally efficient tool for frequency regulation under uncertainty that reflects practical switching constraints while ensuring probabilistic reliability guarantees.

Future work will extend the methodology to unbalanced microgrids, investigate alternative uncertainty propagation methods, and explore machine learning techniques to further reduce computational requirements while maintaining solution quality. The framework can also be adapted for other microgrid optimization objectives and operational scenarios.