Stratified Median Estimation Using Auxiliary Transformations: A Robust and Efficient Approach in Asymmetric Populations
Abstract
1. Introduction
2. Motivation and Research Gap
- Methodological contribution: A new class of transformation-based ratio product estimators is proposed for the stratified estimation of the population median using robust and nontraditional auxiliary variables.
- Improved stability across strata: Through the use of transformation techniques within each stratum, the estimator maintains consistent performance and minimizes the effect of internal variation.
- Theoretical contribution: Bias and mean-squared error (MSE) expressions are derived using first-order approximations, and mathematical conditions for superior performance are established.
- Empirical contribution: The proposed estimators are evaluated through comprehensive simulation studies using five asymmetric distributions and validated using three real-world datasets, with performance assessed via percent relative efficiency (PRE).
- Effective with small sample sizes: It delivers accurate median estimates even when sample sizes within strata are limited, making it practical for studies with restricted data availability.
- Resistant to outliers: Its design naturally reduces the impact of extreme values, ensuring more dependable and stable median estimates.
- Effective in applied fields: The estimator is particularly useful in fields such as health, education, and economics, where data often show departures from normality and are grouped into strata.
3. Concepts and Existing Estimators
4. Suggested Class of Estimators
- whereNote: The pairings of robust statistics in Table 2 (e.g., with , with etc.) were selected based on heuristic reasoning, aiming to combine measures that reflect complementary aspects of the auxiliary variable, such as central tendency and dispersion. These combinations are not empirically optimized but are grounded in the statistical properties of the paired measures.
5. Mathematical Comparison
- (i):
- (ii):
- (iii):
- (iv):
- (v):
- (vi):
- (vii):
- (viii):
6. Results and Discussion
6.1. Simulation Study
- Simulated data 1: The modest skewness and dispersion in the distribution of X is represented by the Gamma distribution, which is described as Gamma with
- Simulated data 2: The slight skew distribution of X is represented by the log-normal distribution, which is described as Log-Normal with
- Simulated data 3: The heavy-tailed distribution of X is represented by the Cauchy distribution, which is described as Cauchy with
- Simulated data 4: The baseline distribution of X is represented by a uniform distribution, which is described as uniform with
- Simulated data 5: The high skew distribution of X is represented by the exponential distribution, which is described as exponential with
- Based on the above-described distribution, generate a dataset of observations for the variables X and Y.
- To evaluate the precision of estimators, compute the necessary statistical measures, including the largest and smallest values. In addition, the optimal values of the existing estimators are obtained.
- Samples of size for each stratum can be chosen using SRSWOR from each population .
- The percent relative efficiency values for all estimators discussed in this study are calculated across different sample sizes. This phase ensures that the PREs of each estimator are analyzed for a collection of samples.
- Following 6000 repetitions of steps 3 and 4, use the formulas below to compute the percent relative efficiency values:
6.2. Real-Life Application
- : This variable represents the total quantity of fish harvested from all sources during the year 1995, including both commercial and recreational fishing activities;
- This variable refers to the number of fish caught in 1994 by individuals participating in recreational marine fishing, excluding any form of commercial harvesting;
- : This variable denotes the overall count of fish collected in 1995, serving as a measure of that year’s total harvest;
- This variable represents the number of fish captured by recreational marine fishermen in 1994, reflecting the impact of non-commercial fishing on the total catch.
- Employment level by division and district in 2010;
- Number of registered factories by division and district in 2010;
- Employment level by division and district in 2012;
- Number of registered factories by division and district in 2012.
- Represents the aggregate count of students who registered during the academic session 2012–2013;
- Denotes the overall number of government-operated primary schools for both male and female students in the same academic year;
- Refers to the total enrollment of students recorded for the 2012–2013 school year;
- Refers to the complete number of government-managed middle schools catering to both boys and girls during the 2012–2013 academic period.
6.3. Discussion
- The results from both simulated and real datasets, as presented in Table 3 and Table 4, indicate that the PRE values of all newly introduced estimators exceed those of the previously established ones discussed in Section 3. This highlights the enhanced effectiveness of the suggested estimators in relation to existing techniques.
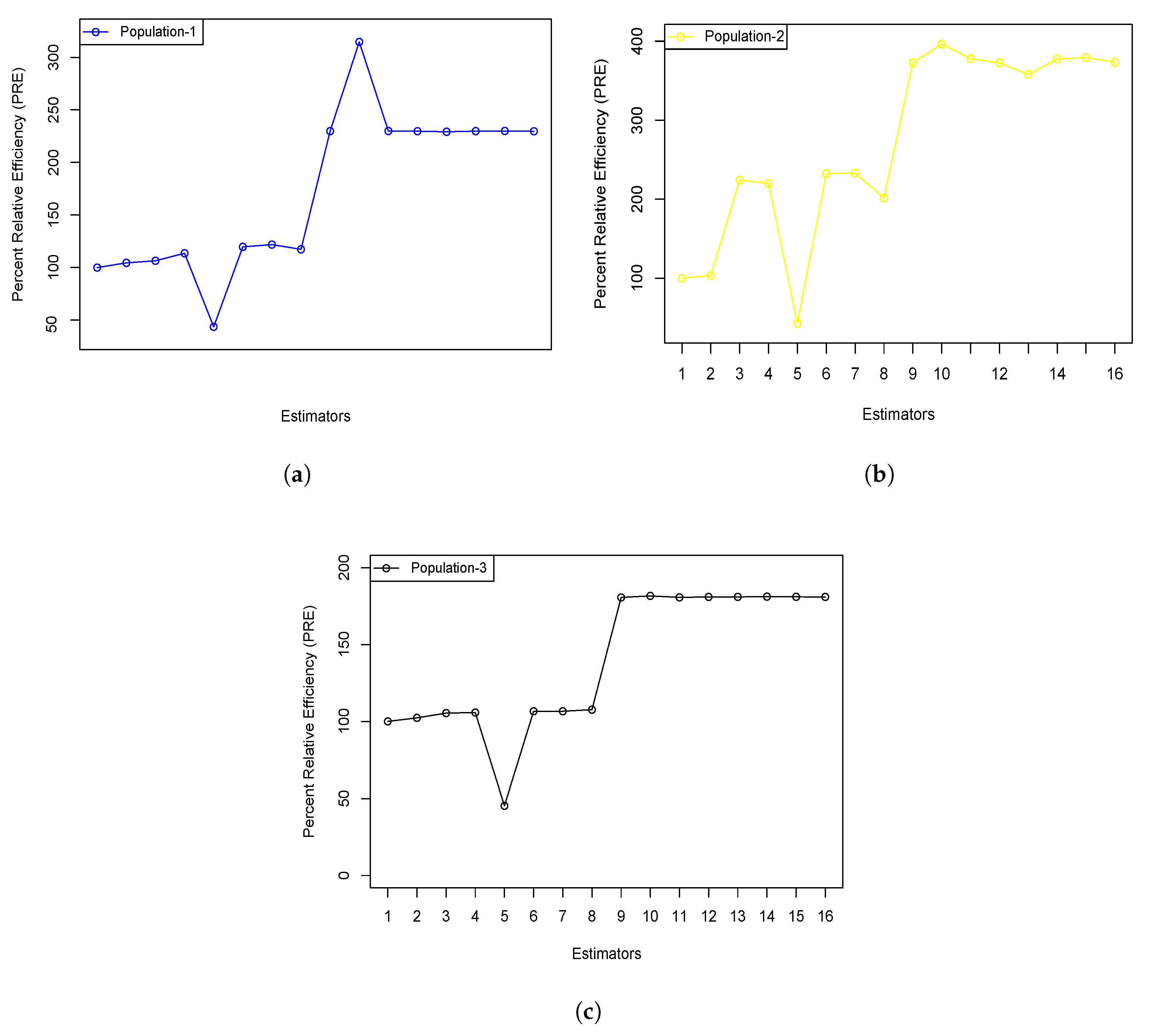
- Additionally, the upward trend in the graphical representations shown in Figure 1 and Figure 2, based on various distributions and actual datasets, further confirms that the new estimators consistently achieve higher PRE values than the conventional estimators. The inverse correlation between the PRE values of the new and traditional estimators strengthens the idea that the newly introduced estimators offer a more efficient estimation method.
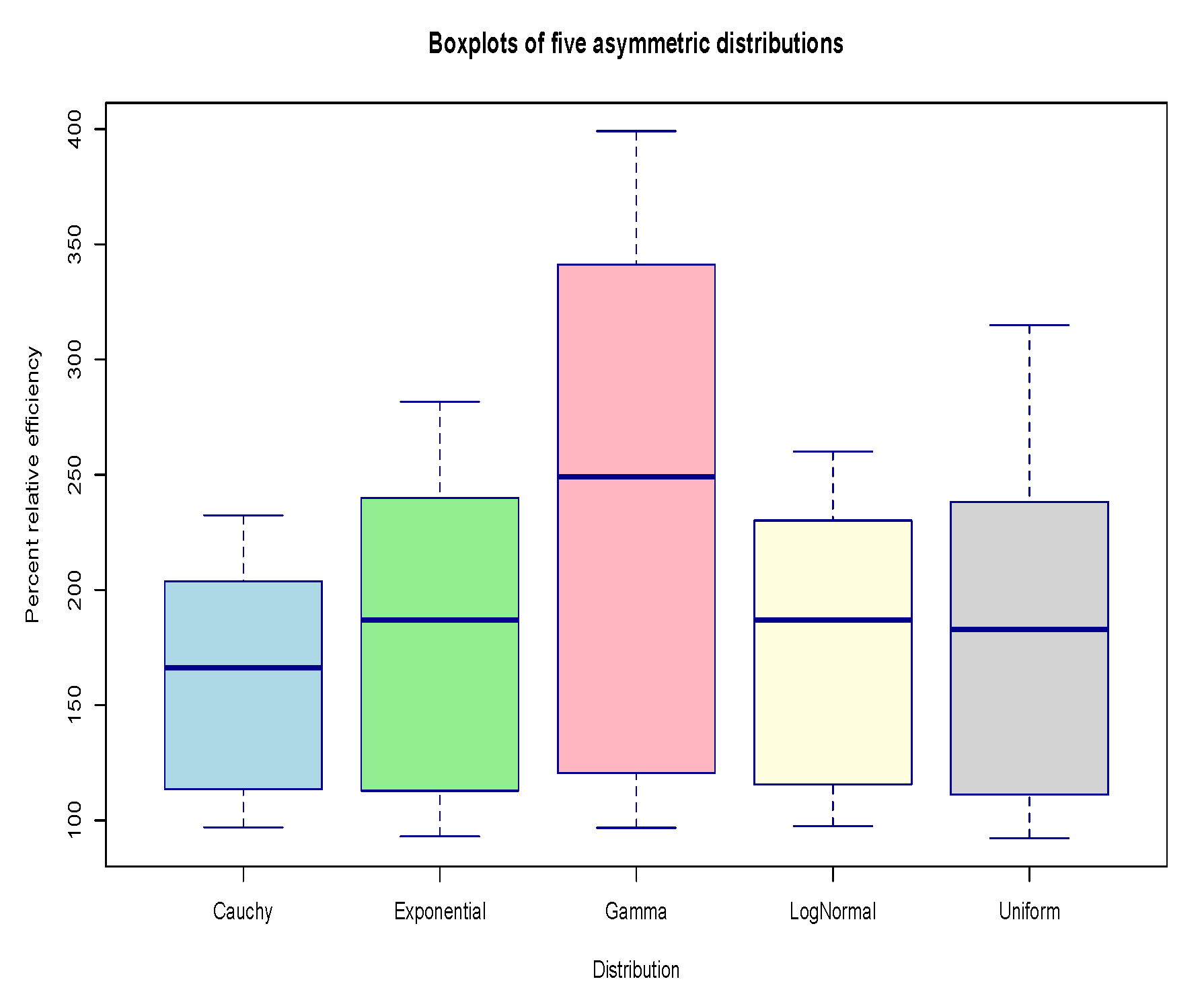
- Furthermore, the box-plots presented in Figure 3 and Figure 4 visually highlight the superior performance of the proposed estimators. These plots display the distribution of percent relative efficiency (PRE) values across both simulated and real datasets, highlighting the consistently higher central tendency and narrower spread of the proposed estimators compared to traditional methods. The compact interquartile ranges and elevated median lines observed in the proposed estimator boxplots signify both robustness and efficiency, particularly under asymmetric and skewed distributions.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gross, S. Median estimation in sample surveys. In Proceedings of the Section on Survey Research Methods; American Statistical Association Ithaca, Alexandria, VA, USA; 1980. [Google Scholar]
- Sedransk, J.; Meyer, J. Confidence intervals for the quantiles of a finite population: Simple random and stratified simple random sampling. J. R. Stat. Soc. Ser. B (Methodol.) 1978, 40, 239–252. [Google Scholar] [CrossRef]
- Philip, S.; Sedransk, J. Lower bounds for confidence coefficients for confidence intervals for finite population quantiles. Commun. Stat.-Theory Methods 1983, 12, 1329–1344. [Google Scholar] [CrossRef]
- Kuk, Y.C.A.; Mak, T.K. Median estimation in the presence of auxiliary information. J. R. Stat. Soc. Ser. B 1989, 51, 261–269. [Google Scholar] [CrossRef]
- Zaman, T.; Bulut, H. An efficient family of robust-type estimators for the population variance in simple and stratified random sampling. Commun. Stat.-Theory Methods 2023, 52, 2610–2624. [Google Scholar] [CrossRef]
- Daraz, U.; Alomair, M.A.; Albalawi, O.; Al Naim, A.S. New techniques for estimating finite population variance using ranks of auxiliary variable in two-stage sampling. Mathematics 2024, 12, 2741. [Google Scholar] [CrossRef]
- Alghamdi, A.S.; Alrweili, H. A comparative study of new ratio-type family of estimators under stratified two-phase sampling. Mathematics 2025, 13, 327. [Google Scholar] [CrossRef]
- Alomair, M.A.; Daraz, U. Dual transformation of auxiliary variables by using outliers in stratified random sampling. Mathematics 2024, 12, 2839. [Google Scholar] [CrossRef]
- Alghamdi, A.S.; Almulhim, F.A. Optimizing finite population mean estimation using simulation and empirical data. Mathematics 2025, 13, 1635. [Google Scholar] [CrossRef]
- Rao, T.J. On certail methods of improving ration and regression estimators. Commun. -Stat.-Theory Methods 1991, 20, 3325–3340. [Google Scholar] [CrossRef]
- Khoshnevisan, M.; Singh, H.P.; Singh, S.; Smarandache, F. A General Class of Estimators of Population Median Using Two Auxiliary Variables in Double Sampling; VirginiaPolytechnic Institute and State University: Blacksburg, VA, USA,, 2002. [Google Scholar]
- Singh, S.; Joarder, A.H.; Tracy, D.S. Median estimation using double sampling. Aust. N. Z. J. Stat. 2001, 43, 33–46. [Google Scholar] [CrossRef]
- Singh, S. Advanced Sampling Theory With Applications: How Michael Selected Amy; Springer Science & Business Media: Berlin, Germany, 2003; Volume 2. [Google Scholar]
- Gupta, S.; Shabbir, J.; Ahmad, S. Estimation of median in two-phase sampling using two auxiliary variables. Commun. Stat.-Theory Methods 2008, 37, 1815–1822. [Google Scholar] [CrossRef]
- Aladag, S.; Cingi, H. Improvement in estimating the population median in simple random sampling and stratified random sampling using auxiliary information. Commun. Stat.-Theory Methods 2015, 44, 1013–1032. [Google Scholar] [CrossRef]
- Solanki, R.S.; Singh, H.P. Some classes of estimators for median estimation in survey sampling. Commun. Stat.-Theory Methods 2015, 44, 1450–1465. [Google Scholar] [CrossRef]
- Daraz, U.; Wu, J.; Albalawi, O. Double exponential ratio estimator of a finite population variance under extreme values in simple random sampling. Mathematics 2024, 12, 1737. [Google Scholar] [CrossRef]
- Daraz, U.; Wu, J.; Alomair, M.A.; Aldoghan, L.A. New classes of difference cum-ratio-type exponential estimators for a finite population variance in stratified random sampling. Heliyon 2024, 10, e33402. [Google Scholar] [CrossRef]
- Daraz, U.; Alomair, M.A.; Albalawi, O. Variance estimation under some transformation for both symmetric and asymmetric data. Symmetry 2024, 16, 957. [Google Scholar] [CrossRef]
- Almulhim, F.A.; Alghamdi, A.S. Simulation-based evaluation of robust transformation techniques for median estimation under simple random sampling. Axioms 2025, 14, 301. [Google Scholar] [CrossRef]
- Daraz, U.; Almulhim, F.A.; Alomair, M.A.; Alomair, A.M. Population median estimation using auxiliary variables: A simulation study with real data across sample sizes and parameters. Mathematics 2025, 13, 1660. [Google Scholar] [CrossRef]
- Hussain, M.A.; Javed, M.; Zohaib, M.; Shongwe, S.C.; Awais, M.; Zaagan, A.A.; Irfan, M. Estimation of population median using bivariate auxiliary information in simple random sampling. Heliyon 2024, 10, e28891. [Google Scholar] [CrossRef]
- Shabbir, J.; Gupta, S. A generalized class of difference type estimators for population median in survey sampling. Hacet. J. Math. Stat. 2017, 46, 1015–1028. [Google Scholar] [CrossRef]
- Irfan, M.; Maria, J.; Shongwe, S.C.; Zohaib, M.; Bhatti, S.H. Estimation of population median under robust measures of an auxiliary variable. Math. Probl. Eng. 2021, 2021, 4839077. [Google Scholar] [CrossRef]
- Shabbir, J.; Gupta, S.; Narjis, G. On improved class of difference type estimators for population median in survey sampling. Commun. Stat.-Theory Methods 2022, 51, 3334–3354. [Google Scholar] [CrossRef]
- Subzar, M.; Lone, S.A.; Ekpenyong, E.J.; Salam, A.; Aslam, M.; Raja, T.A.; Almutlak, S.A. Efficient class of ratio cum median estimators for estimating the population median. PLoS ONE 2023, 18, e0274690. [Google Scholar] [CrossRef] [PubMed]
- Iseh, M.J. Model formulation on efficiency for median estimation under a fixed cost in survey sampling. Model Assist. Stat. Appl. 2023, 18, 373–385. [Google Scholar] [CrossRef]
- Shahzad, U.; Ahmad, I.; Alshahrani, F.; Almanjahie, I.M.; Iftikhar, S. Calibration-based mean estimators under stratified median ranked set sampling. Mathematics 2023, 11, 1825. [Google Scholar] [CrossRef]
- Bhushan, S.; Kumar, A.; Lone, S.A.; Anwar, S.; Gunaime, N.M. An efficient class of estimators in stratified random sampling with an application to real data. Axioms 2023, 12, 576. [Google Scholar] [CrossRef]
- Alghamdi, A.S.; Alrweili, H. New class of estimators for finite population mean under stratified double phase sampling with simulation and real-life application. Mathematics 2025, 13, 329. [Google Scholar] [CrossRef]
- Bahl, S.; Tuteja, R. Ratio and product type exponential estimators. J. Inf. Optim. Sci. 1991, 12, 159–164. [Google Scholar] [CrossRef]
- Daraz, U.; Shabbir, J.; Khan, H. Estimation of finite population mean by using minimum and maximum values in stratified random sampling. J. Mod. Appl. Stat. Methods 2018, 17, 20. [Google Scholar] [CrossRef]
- Daraz, U.; Khan, M. Estimation of variance of the difference-cum-ratio-type exponential estimator in simple random sampling. Res. Math. Stat. 2021, 8, 1899402. [Google Scholar] [CrossRef]
- Daraz, U.; Agustiana, D.; Wu, J.; Emam, W. Twofold auxiliary information under two-phase sampling: An improved family of double-transformed variance estimators. Axioms 2025, 14, 64. [Google Scholar] [CrossRef]
- Daraz, U.; Wu, J.; Agustiana, D.; Emam, W. Finite population variance estimation using Monte Carlo simulation and real life application. Symmetry 2025, 17, 84. [Google Scholar] [CrossRef]
- Bureau of Statistics. Punjab Development Statistics Government of the Punjab, Lahore, Pakistan; Bureau of Statistics: Islamabad, Pakistan, 2013. [Google Scholar]
- Bureau of Statistics. Punjab Development Statistics Government of the Punjab, Lahore, Pakistan; Bureau of Statistics: Islamabad, Pakistan, 2014. [Google Scholar]


| Symbol | Description | Symbol | Description |
|---|---|---|---|
| N | Population size | L | Number of strata |
| Units in hth stratum | Sample size in hth stratum | ||
| Y | Study variable | X | Auxiliary variable |
| Y for ith unit in hth stratum | X for ith unit in hth stratum | ||
| Pop. median of Y in hth stratum | Pop. median of X in hth stratum | ||
| Sample median of Y | Sample median of X | ||
| Weight of hth stratum | Correction factor, hth stratum | ||
| Correlation of medians in hth stratum | Joint probability of medians | ||
| Relative error for Y | Relative error for X | ||
| Interquartile range | Quartile deviation | ||
| Midrange | Quartile average | ||
| Trimean | Decile mean | ||
| Minimum of X | Maximum of X |
| Sub-Classes of the Recommended Estimator | ||
|---|---|---|
| Estimator | |||||
|---|---|---|---|---|---|
| 100.000 | 100.000 | 100.000 | 100.000 | 100.000 | |
| 114.927 | 110.097 | 108.239 | 108.479 | 109.554 | |
| 118.571 | 112.727 | 111.143 | 108.182 | 110.696 | |
| 122.352 | 118.571 | 116.000 | 113.802 | 115.000 | |
| 96.756 | 97.483 | 96.966 | 92.333 | 93.061 | |
| 177.500 | 153.636 | 143.854 | 152.500 | 149.091 | |
| 226.842 | 176.206 | 151.536 | 175.729 | 165.000 | |
| 135.161 | 125.000 | 133.182 | 120.000 | 124.638 | |
| 311.428 | 215.000 | 193.225 | 226.364 | 223.345 | |
| 300.000 | 216.000 | 186.875 | 206.667 | 208.750 | |
| 271.250 | 197.692 | 180.909 | 190.000 | 208.750 | |
| 336.154 | 235.454 | 200.000 | 250.000 | 240.000 | |
| 365.000 | 247.142 | 215.000 | 278.889 | 259.230 | |
| 346.134 | 224.782 | 207.241 | 226.364 | 240.000 | |
| 399.090 | 260.000 | 232.369 | 315.000 | 281.666 | |
| 375.000 | 247.142 | 223.333 | 278.888 | 259.237 |
| Estimator | Population-I | Population-II | Population-III |
|---|---|---|---|
| 100 | 100 | 100 | |
| 104.483 | 103.490 | 102.309 | |
| 106.462 | 224.1987 | 105.401 | |
| 113.592 | 220.089 | 105.773 | |
| 43.616 | 42.76373 | 45.312 | |
| 119.703 | 232.478 | 106.597 | |
| 121.855 | 233.110 | 106.611 | |
| 117.347 | 201.569 | 107.622 | |
| 229.832 | 372.780 | 180.626 | |
| 314.652 | 393.385 | 181.625 | |
| 229.912 | 378.001 | 180.668 | |
| 229.732 | 372.7041 | 180.952 | |
| 229.183 | 357.866 | 180.970 | |
| 229.813 | 377.564 | 181.150 | |
| 229.972 | 379.312 | 181.031 | |
| 229.648 | 373.538 | 180.954 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, A.S.; Almulhim, F.A. Stratified Median Estimation Using Auxiliary Transformations: A Robust and Efficient Approach in Asymmetric Populations. Symmetry 2025, 17, 1127. https://doi.org/10.3390/sym17071127
Alghamdi AS, Almulhim FA. Stratified Median Estimation Using Auxiliary Transformations: A Robust and Efficient Approach in Asymmetric Populations. Symmetry. 2025; 17(7):1127. https://doi.org/10.3390/sym17071127
Chicago/Turabian StyleAlghamdi, Abdulaziz S., and Fatimah A. Almulhim. 2025. "Stratified Median Estimation Using Auxiliary Transformations: A Robust and Efficient Approach in Asymmetric Populations" Symmetry 17, no. 7: 1127. https://doi.org/10.3390/sym17071127
APA StyleAlghamdi, A. S., & Almulhim, F. A. (2025). Stratified Median Estimation Using Auxiliary Transformations: A Robust and Efficient Approach in Asymmetric Populations. Symmetry, 17(7), 1127. https://doi.org/10.3390/sym17071127





