A Monte Carlo Simulation Framework for Evaluating the Robustness and Applicability of Settlement Prediction Models in High-Speed Railway Soft Foundations
Abstract
1. Introduction
2. Methods
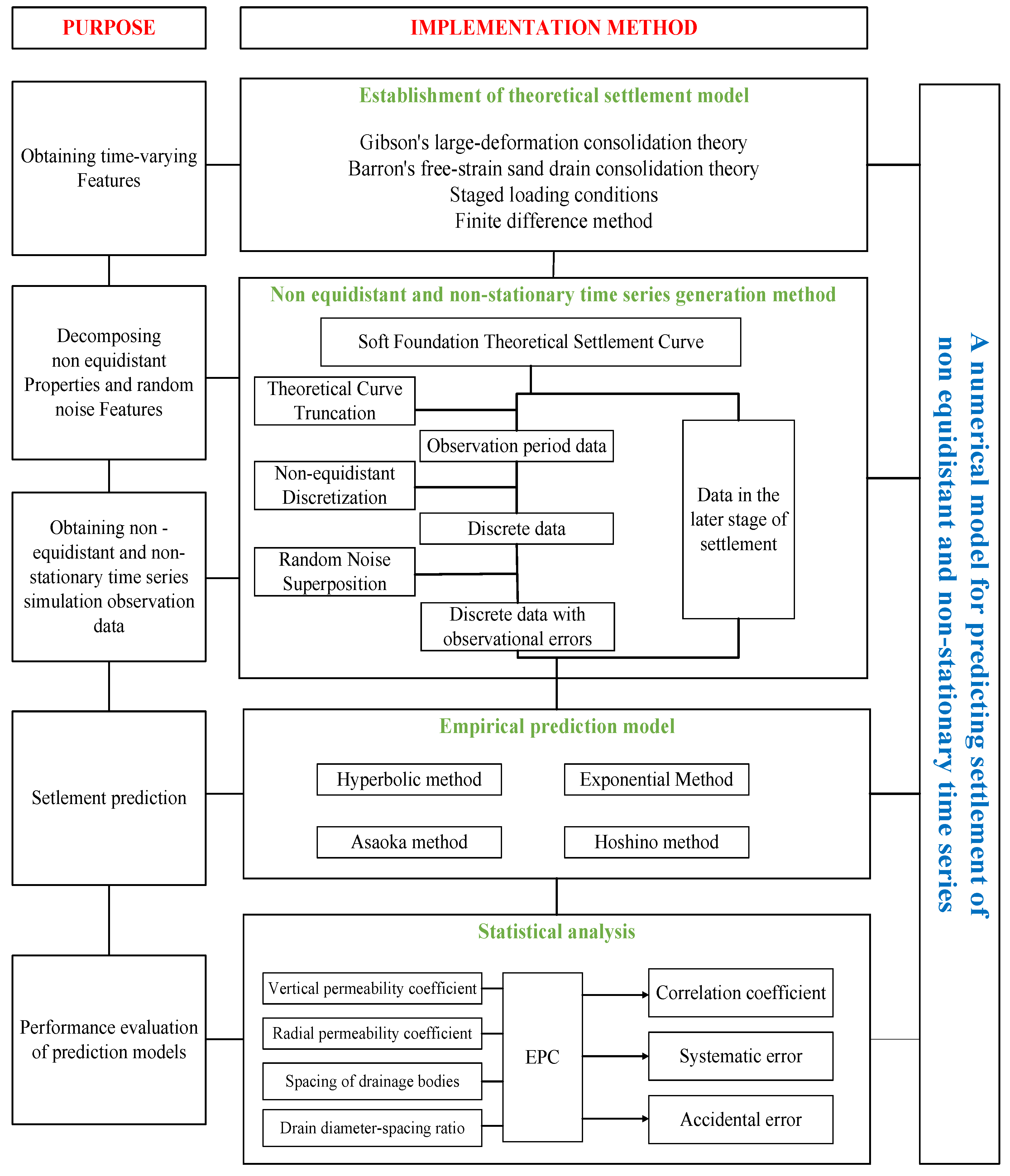
2.1. Establishment of the Prediction Numerical Analysis Model
2.1.1. Establishment of Settlement Theoretical Model
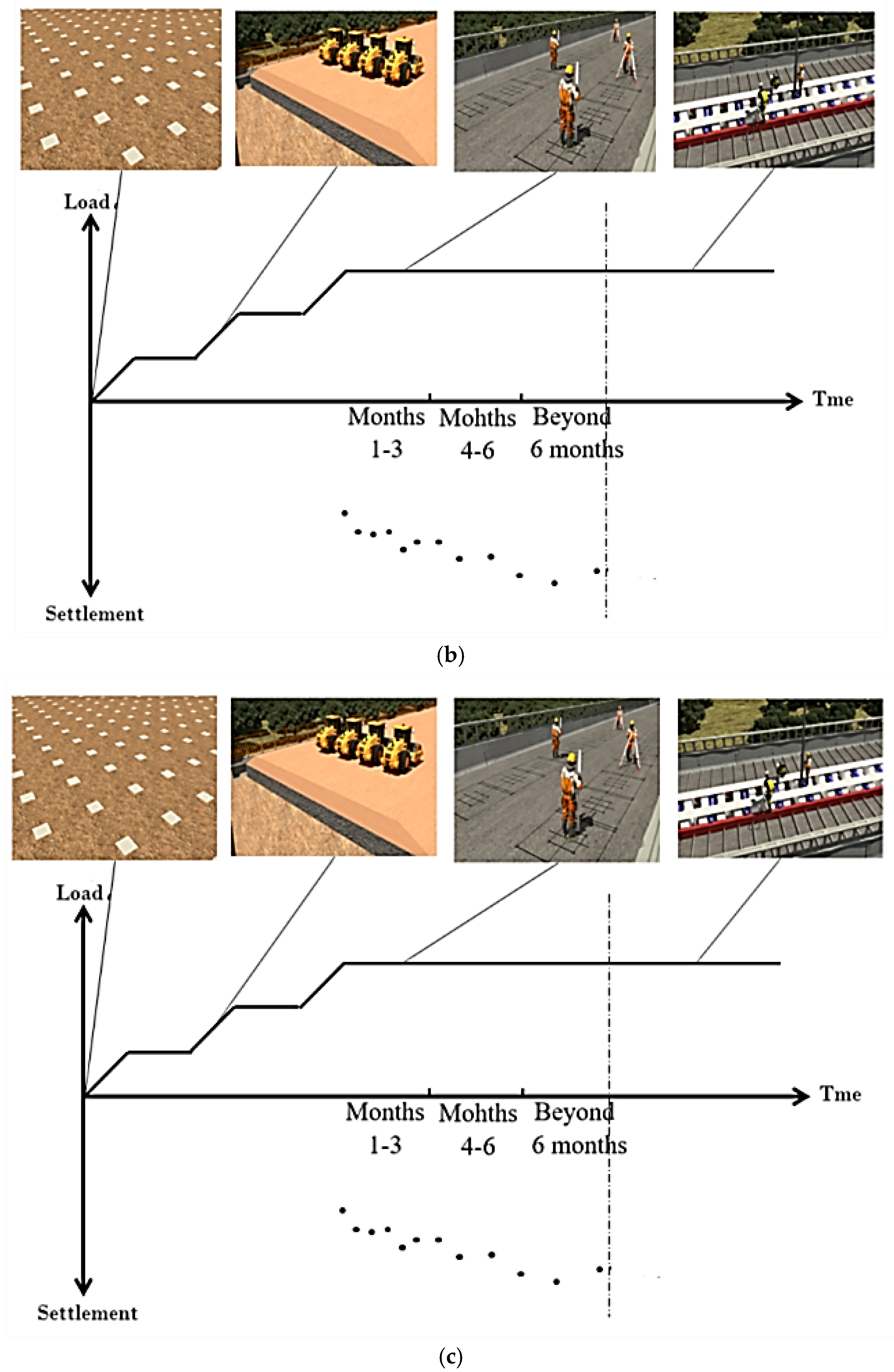
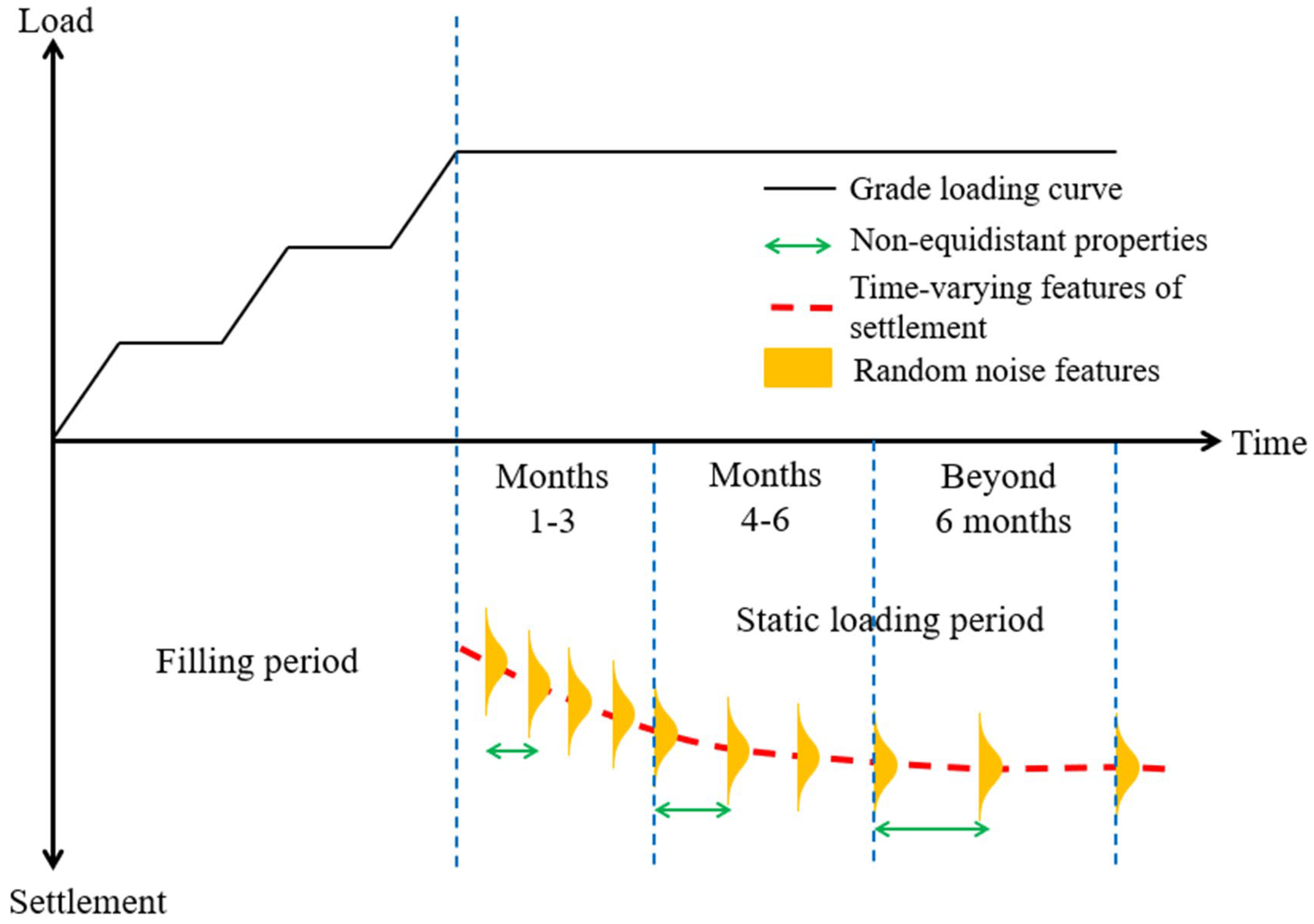
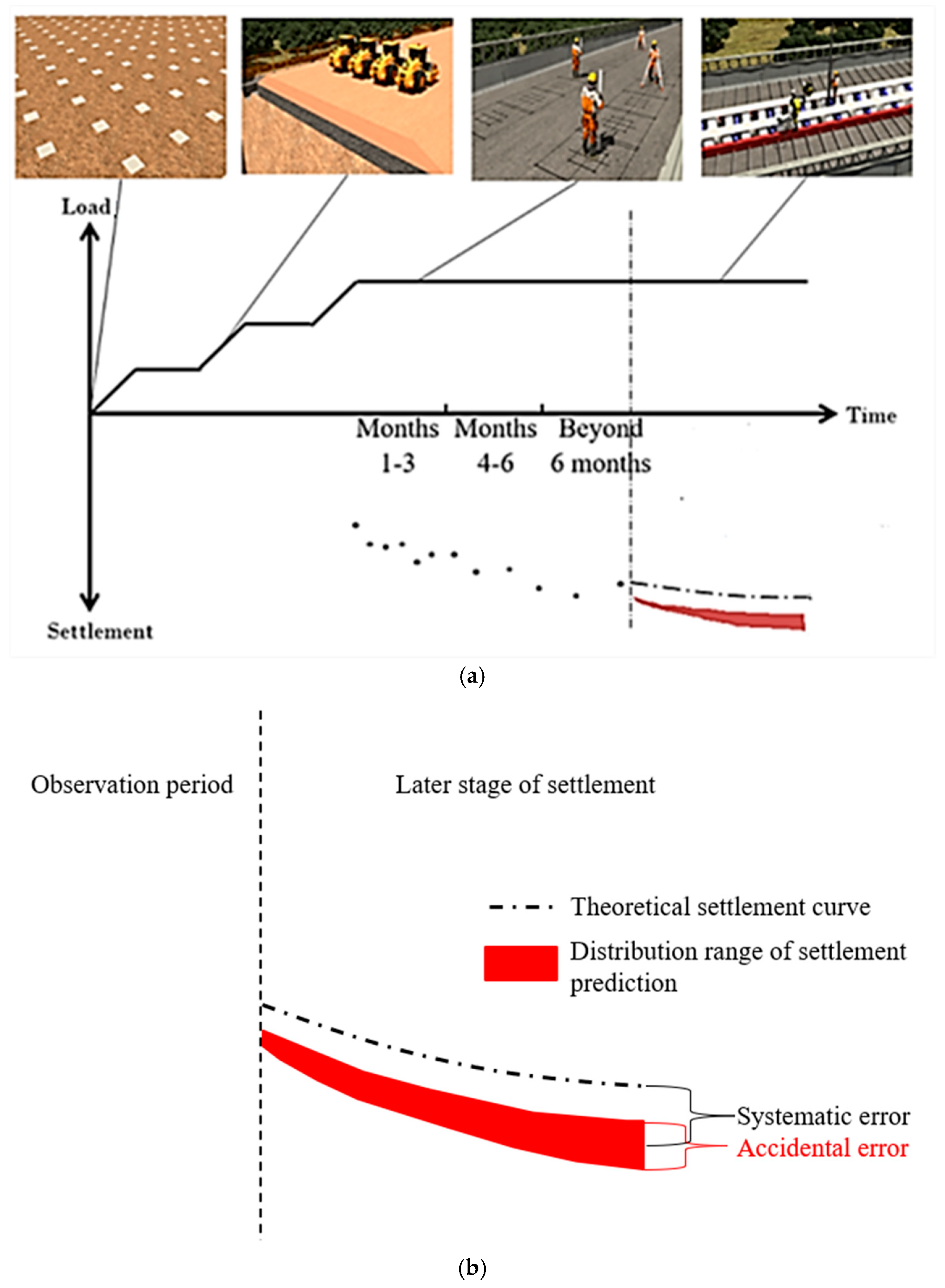
2.1.2. Method for Generating NENSTS
2.1.3. Solution Strategy and Result Statistical Methods
Objective Function of Prediction Models
Normalization of Permeability for Surcharge-Preloaded Soft Foundations
Statistical Analysis of Prediction Results
2.2. Verification of the Predictive Numerical Analysis Model
2.2.1. Reliability Verification of the Settlement Theoretical Model
2.2.2. Convergence Testing of Monte Carlo Simulation
- (1)
- Settlement Prediction Mean Convergence
- (2)
- Settlement Prediction Standard Deviation Convergence
2.3. Parameterization of the Predictive Numerical Analysis Model
2.3.1. Parameter Selection for the Settlement Theoretical Model
- (1)
- Soil Property Parameters
- (2)
- Loading Conditions
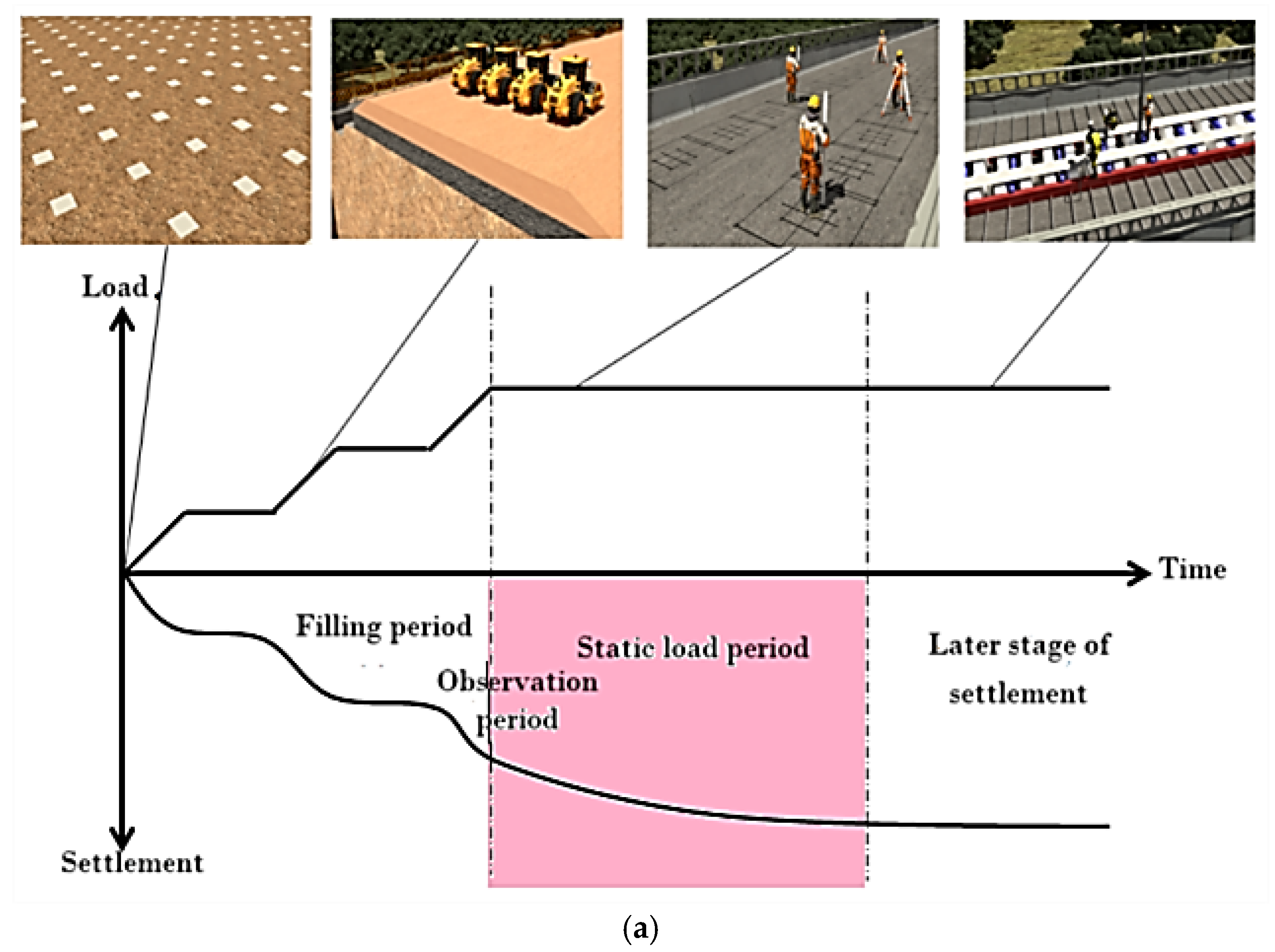
2.3.2. Observational Condition Parameters
- (1)
- Measurement Accuracy
- (2)
- Observation Frequency and Duration
3. Results and Discussion
3.1. Variation Patterns of Evaluation Index for Empirical Prediction Models
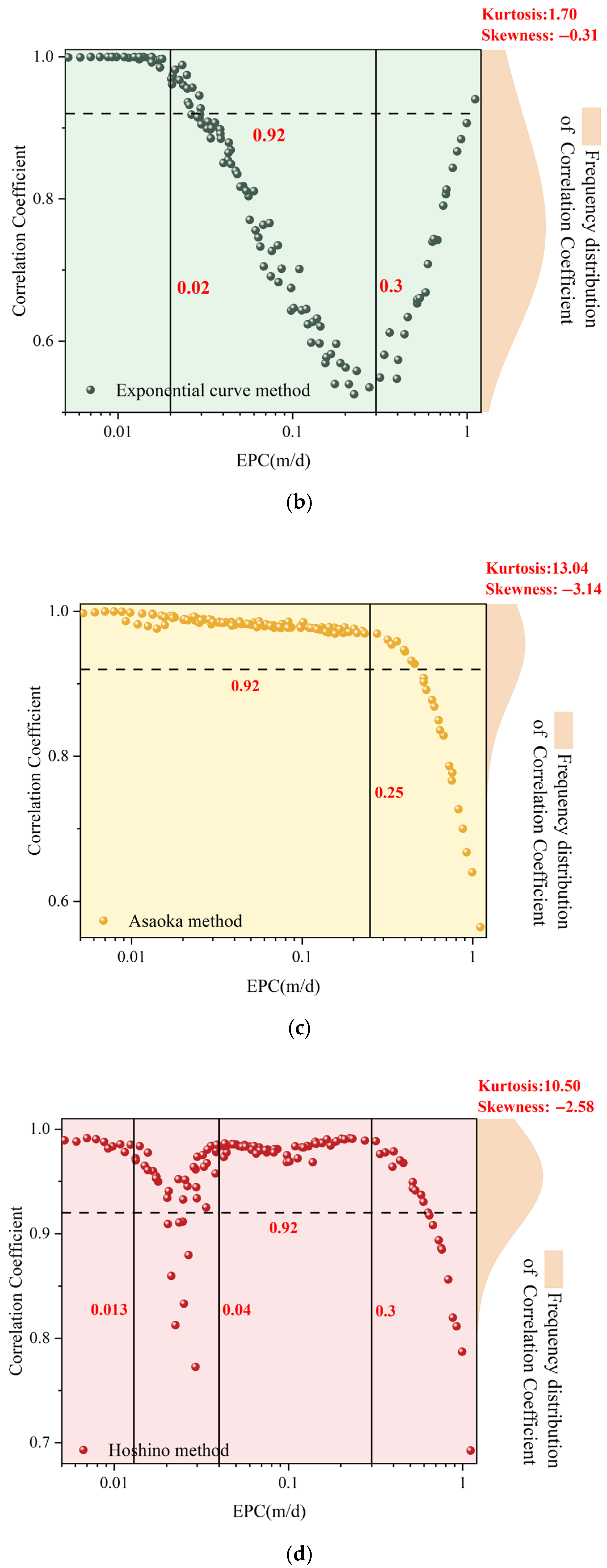
3.1.1. Correlation Coefficient Variation Patterns
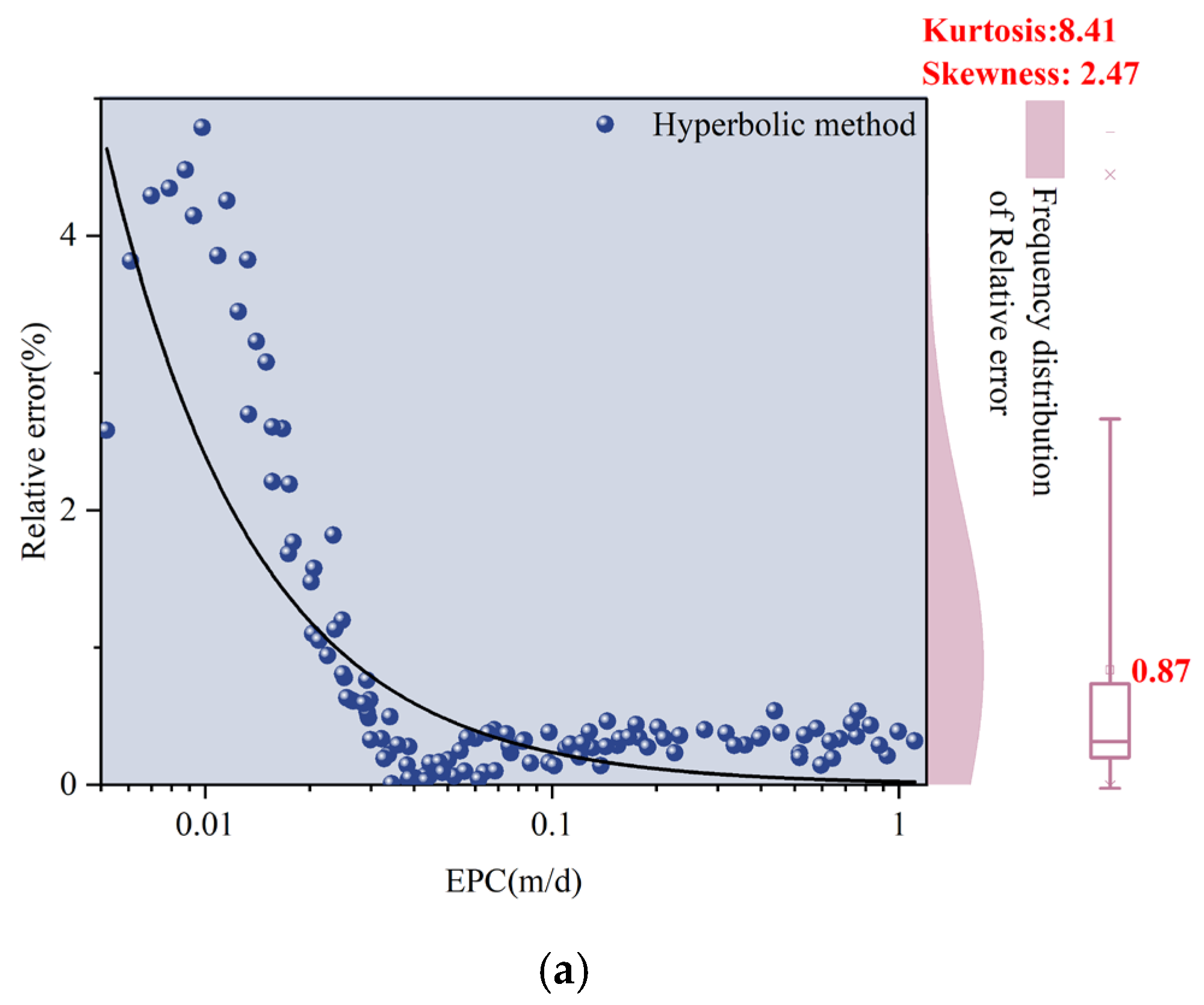
3.1.2. Systematic Error Variation Patterns
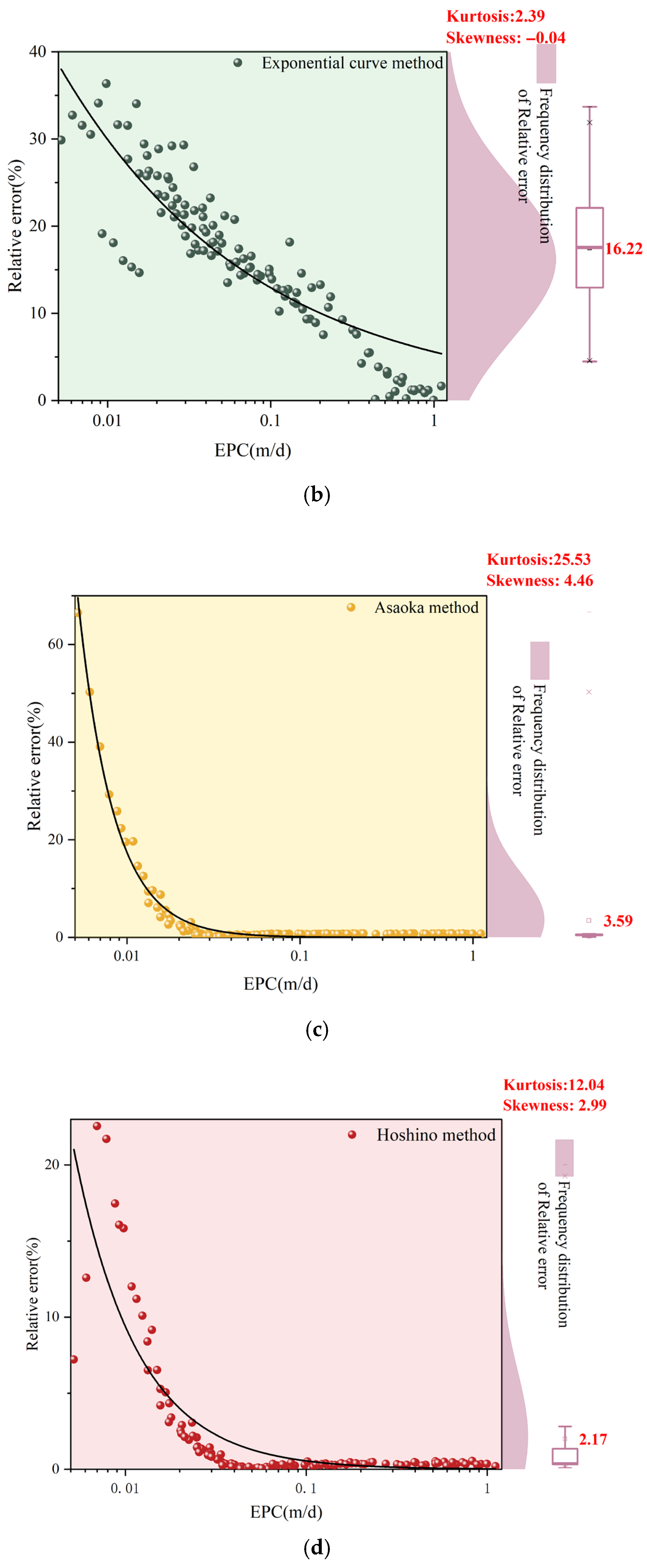
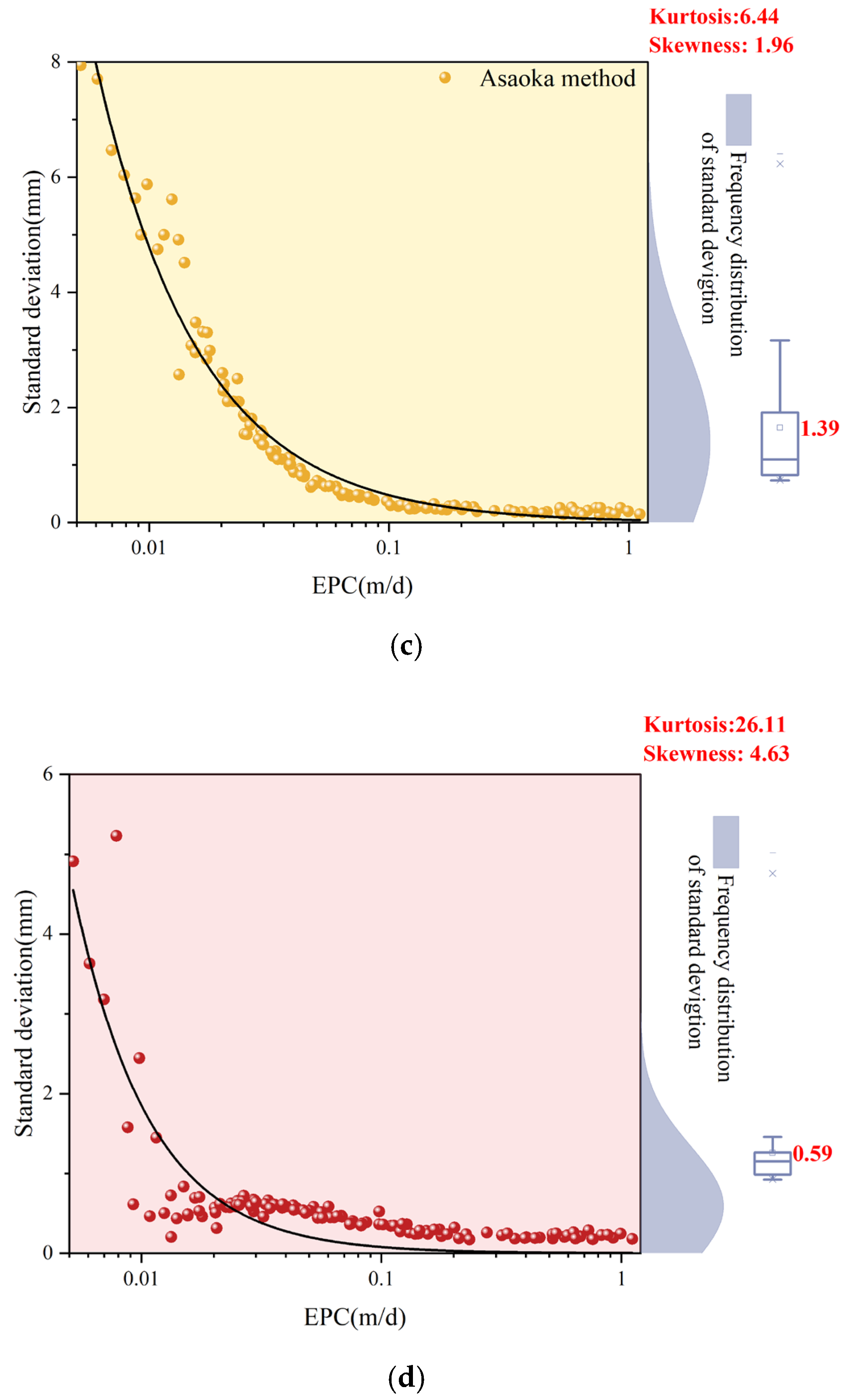
3.1.3. Random Error Variation Patterns
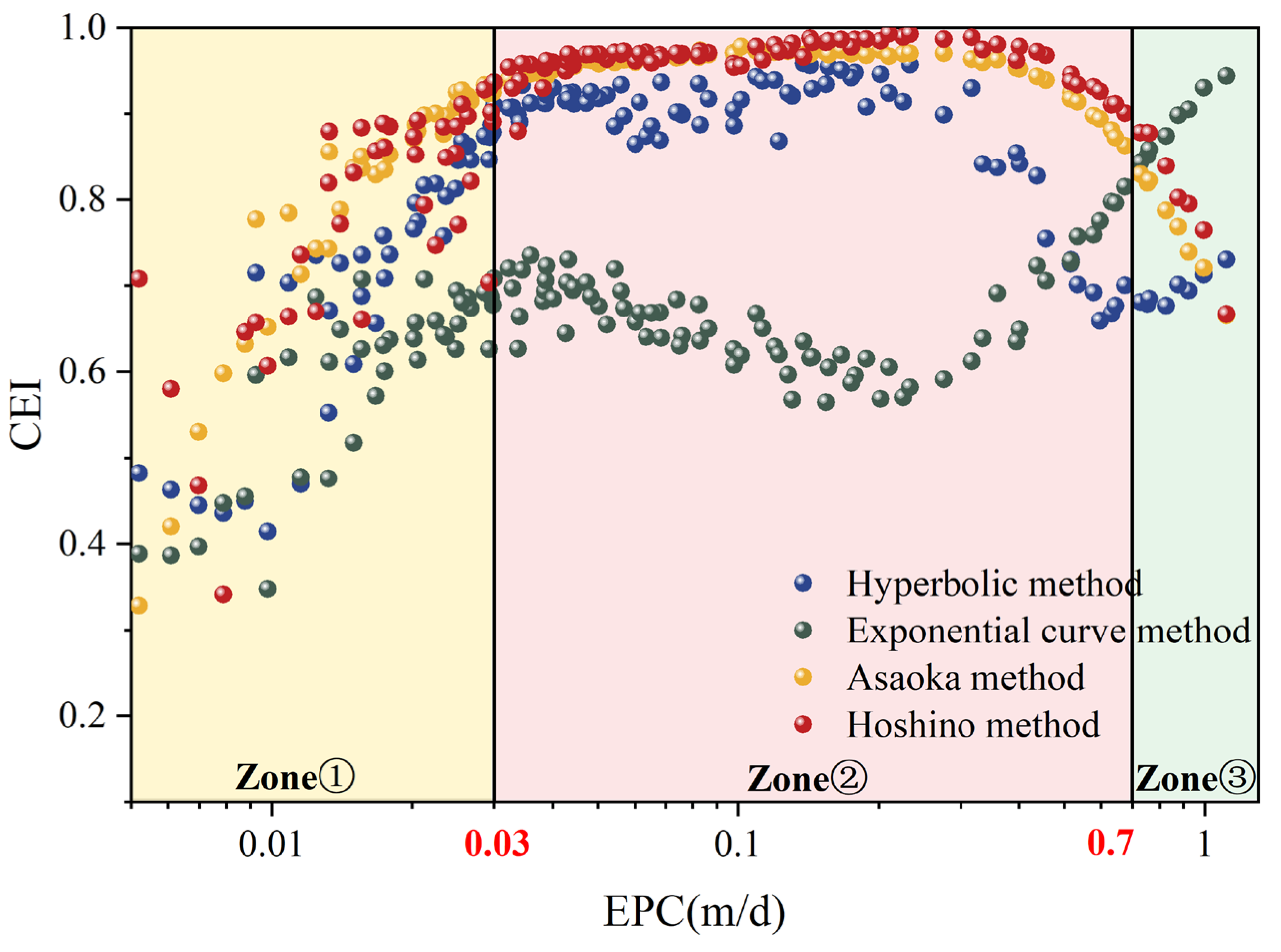
3.2. Optimal Application Range Maps of Empirical Models
3.2.1. Determination of Comprehensive Evaluation Index (CEI)
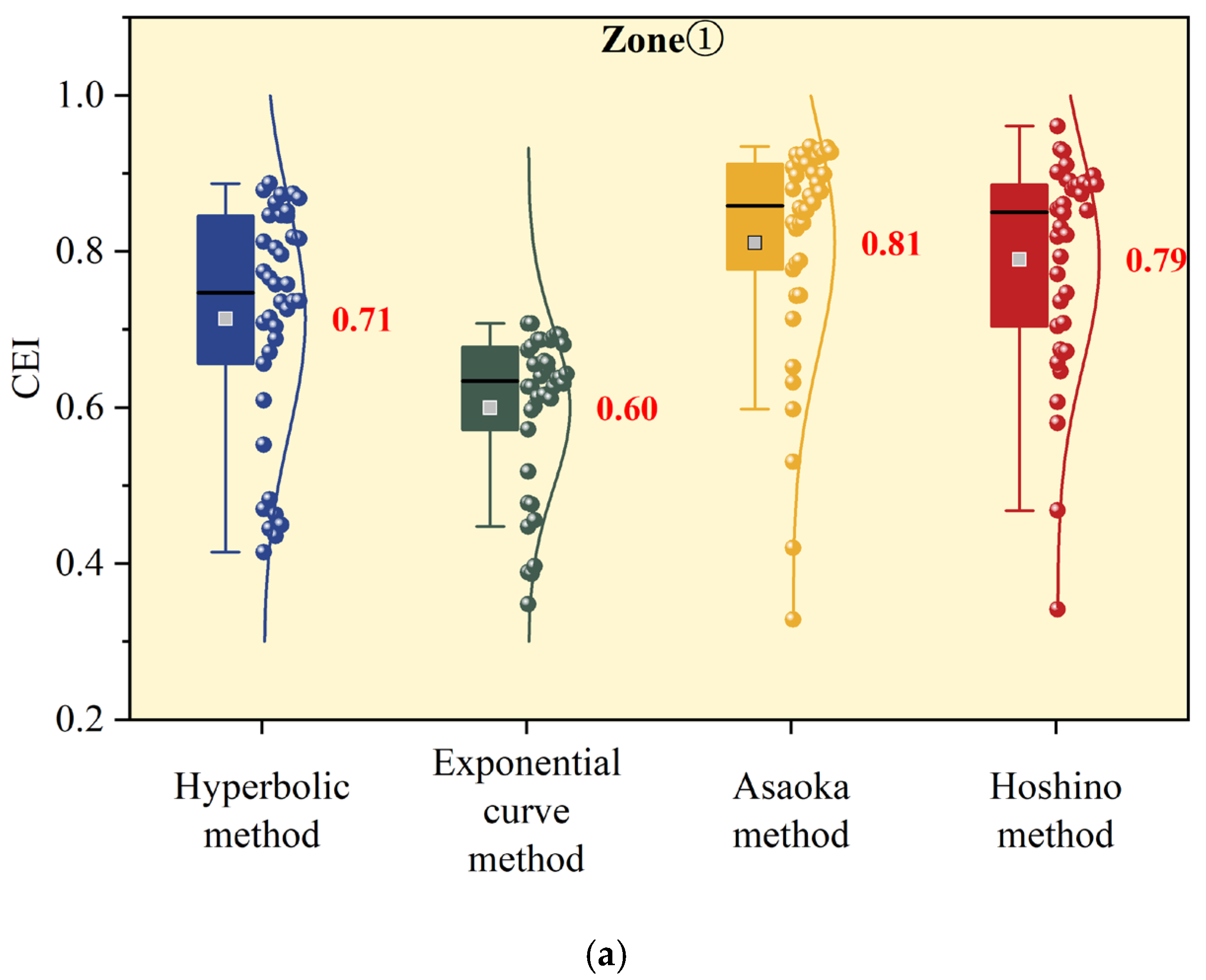
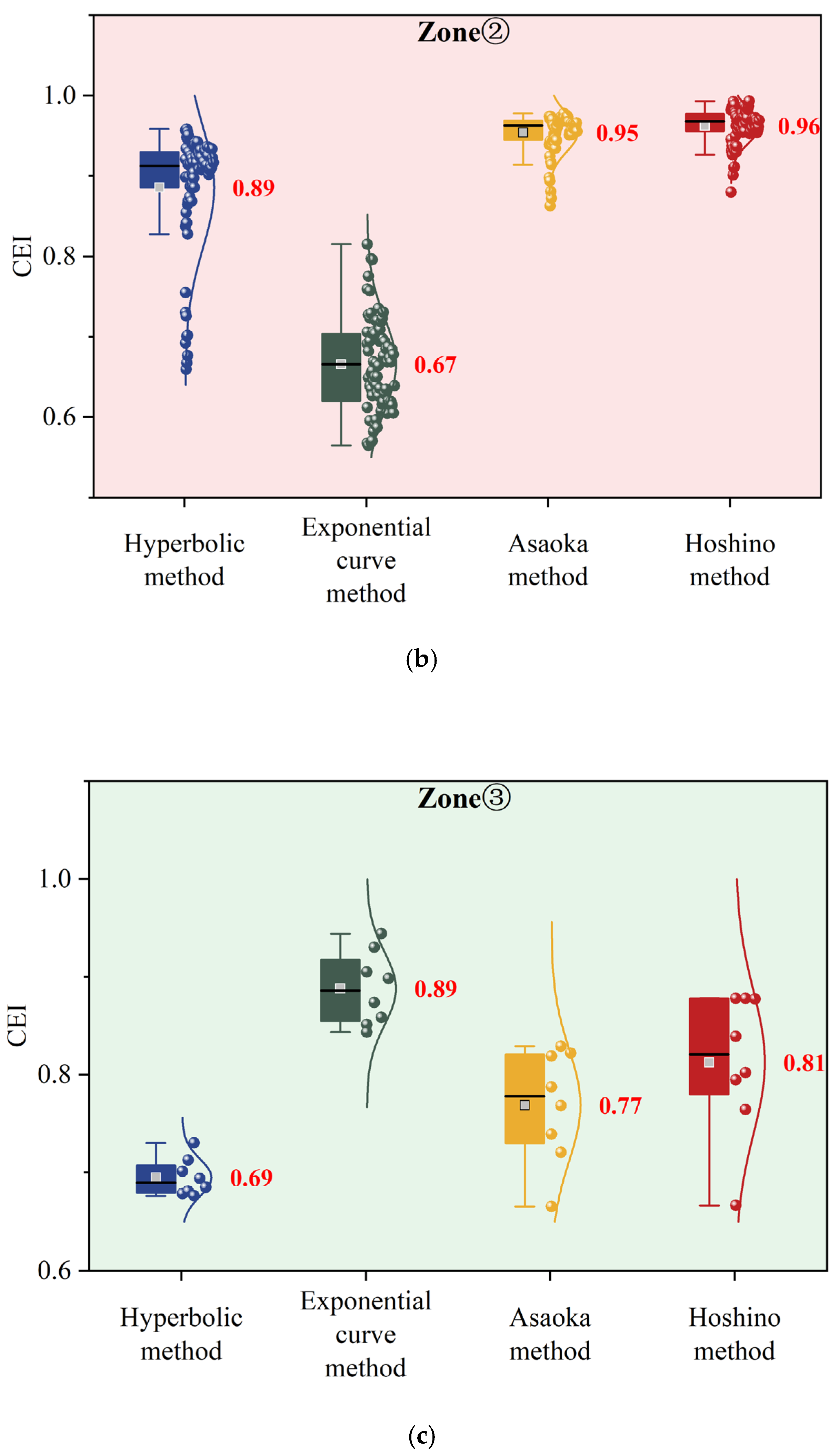
3.2.2. Determination of Optimal Application Scope
4. Case Study Validation
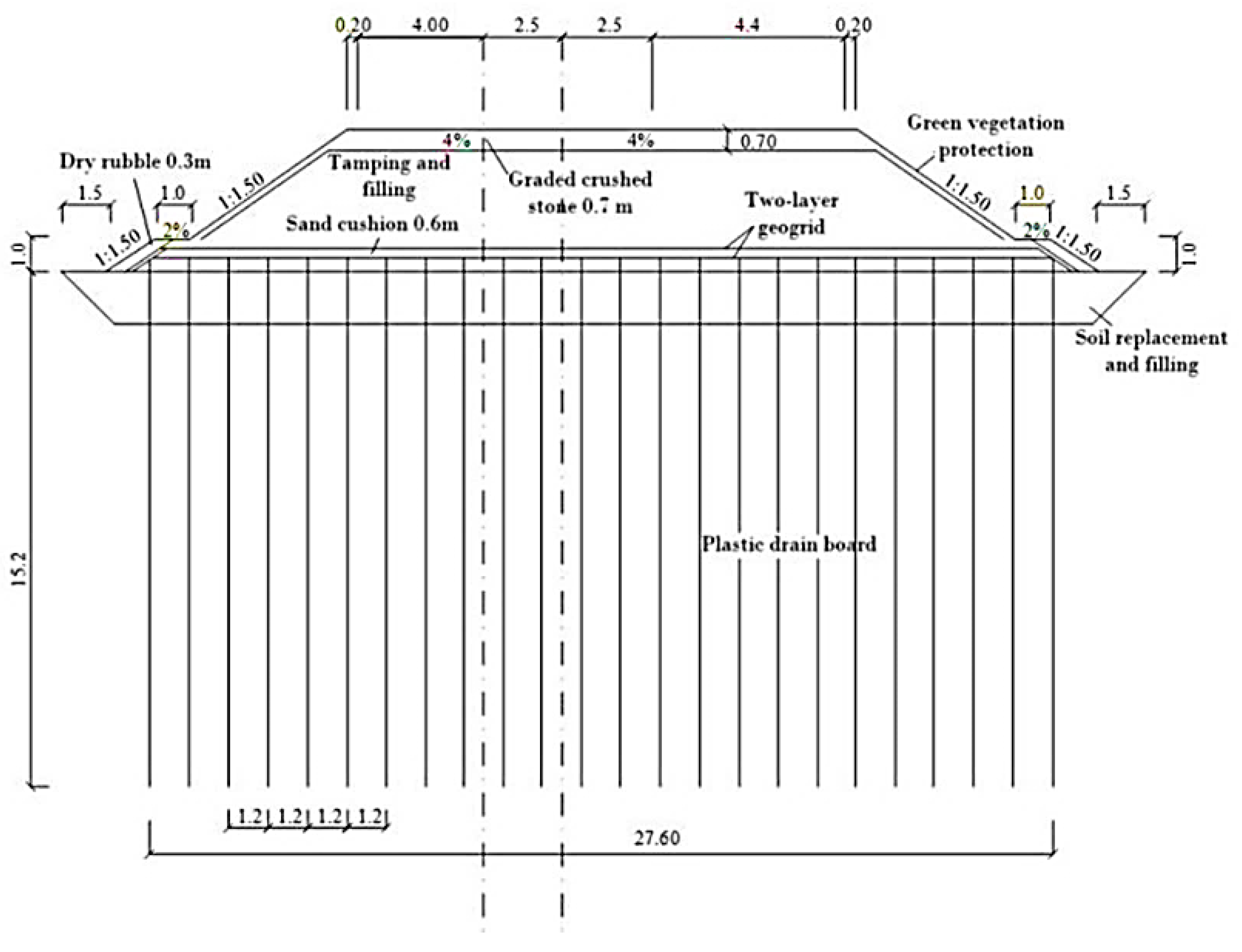
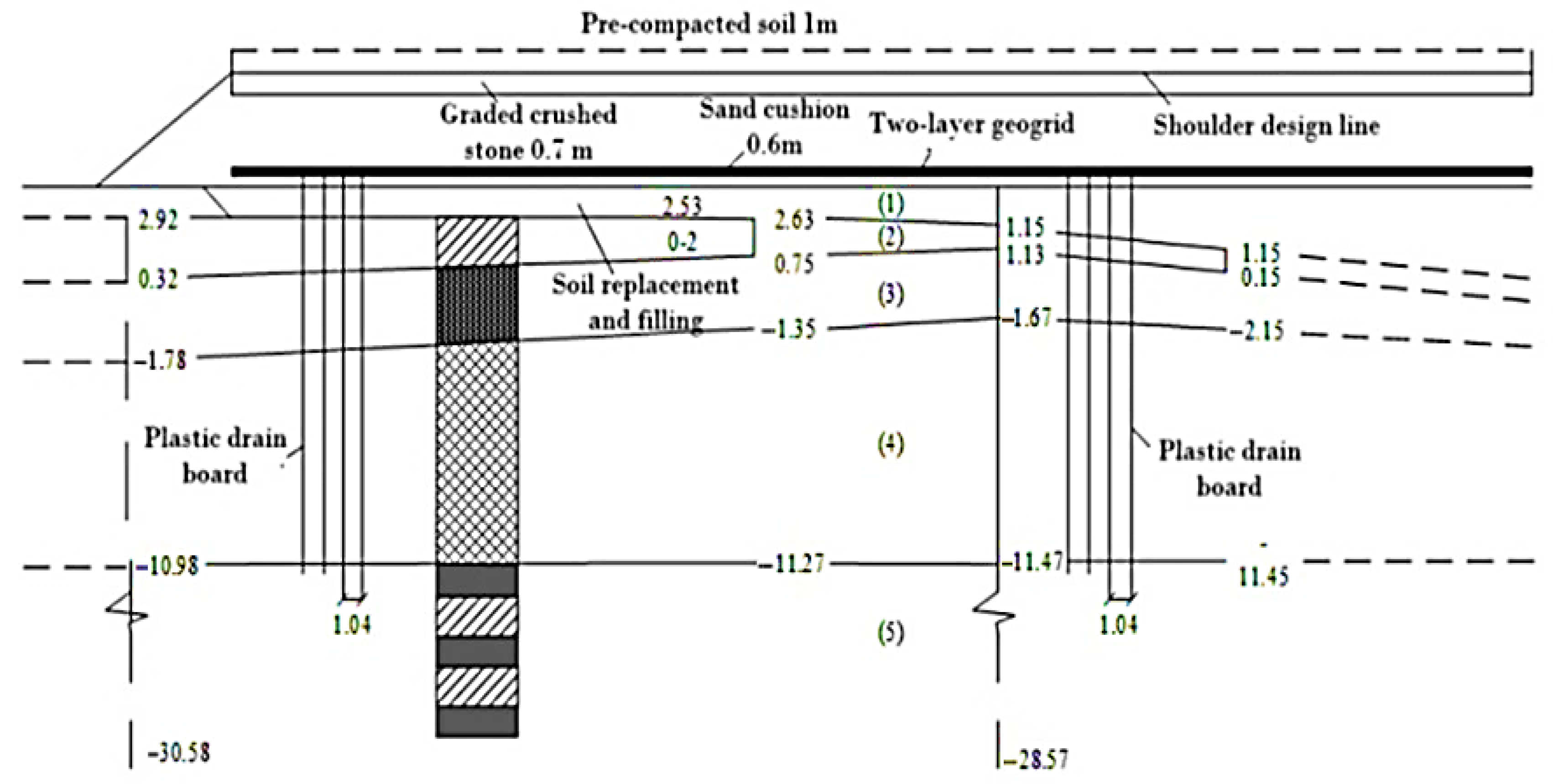
4.1. Instance Overview
- (1)
- Design Key Parameters
- (2)
- Soft Foundation Geotechnical Parameters
- (3)
- Deformation Monitoring Conditions and Data
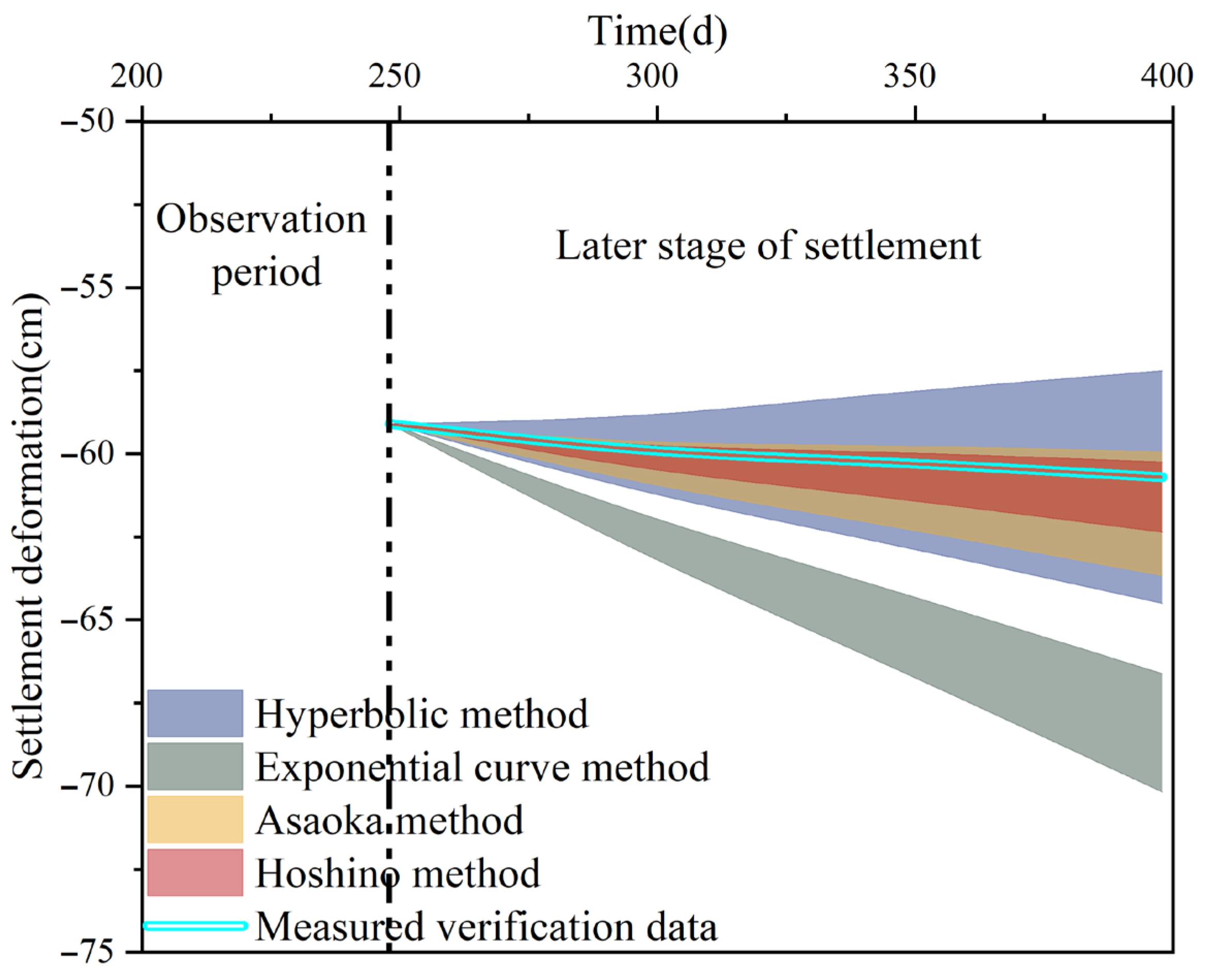
4.2. Selection of Settlement Prediction Model
4.3. Validation of Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Formulation of Settlement Theoretical Model
- (1)
- The soil is fully saturated, and both soil particles and pore water are incompressible.
- (2)
- The soil layer experiences radial–vertical drainage. Both radial and vertical seepage follow non-Darcian flow relationships characterized by a non-Newtonian exponent. In this study, the condition is simplified by assuming that permeability coefficients remain constant (independent of void ratio changes).
- (3)
- Free strain conditions are met, and the lateral deformation of the soil layer is neglected (i.e., there is no displacement at the radial inner and outer boundaries).
- (4)
- External loading conforms to staged loading conditions.
- (5)
- The top boundary is fully permeable, while the bottom boundary and the radial outer boundary are impermeable. Additionally, well resistance and smear effects are ignored.
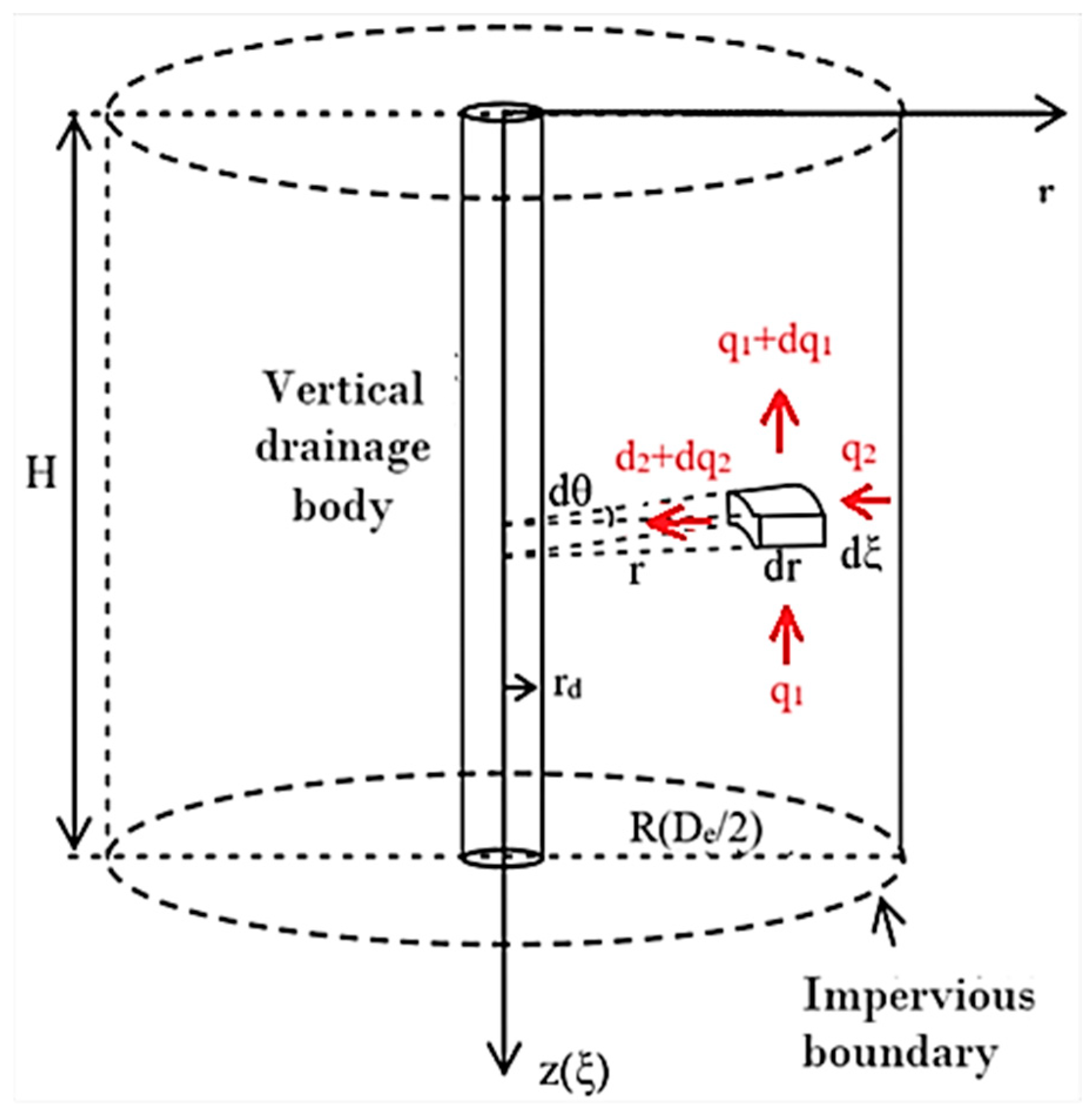
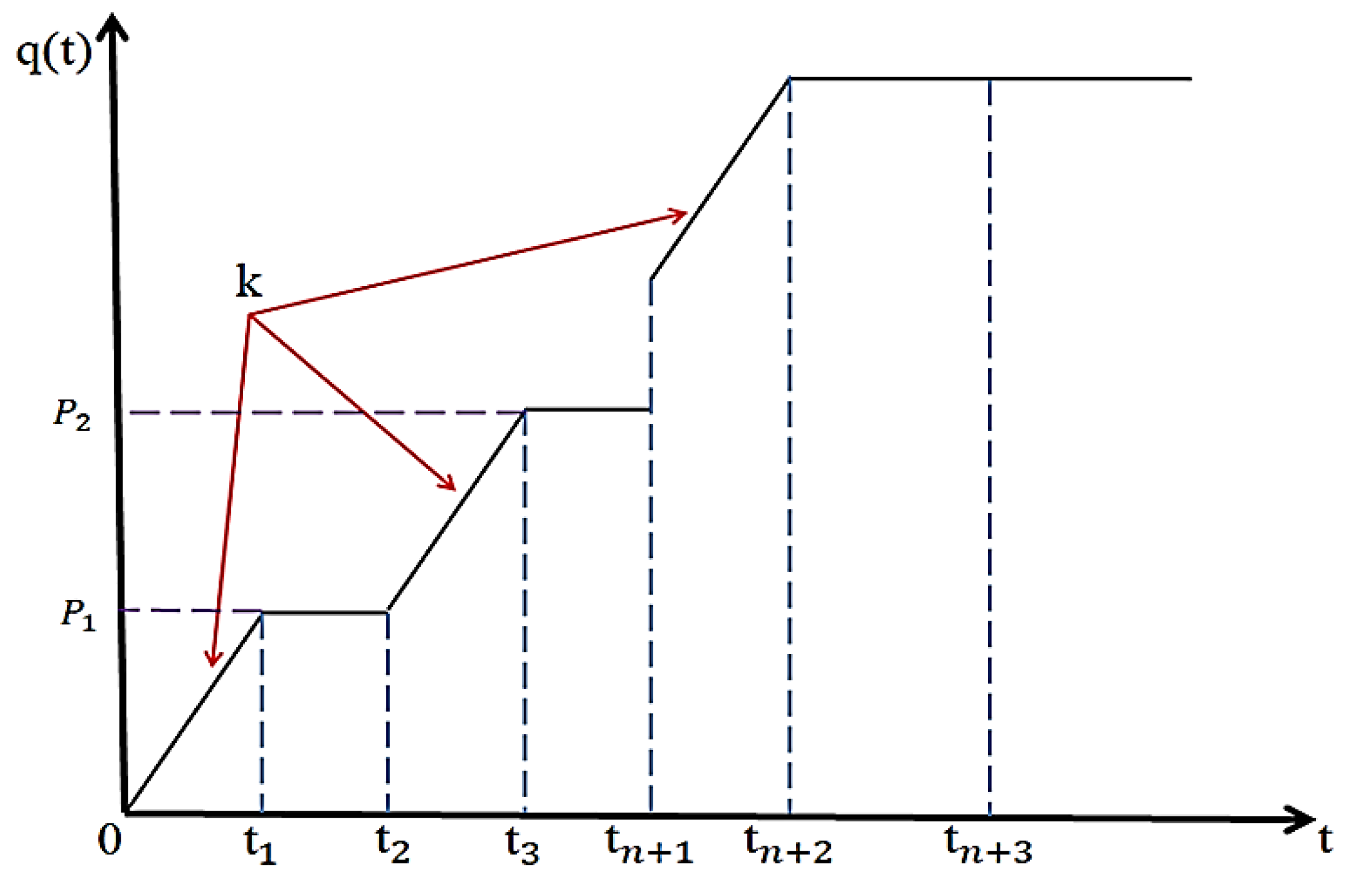
Appendix B. Schematic Diagram of Generating Simulated Observational Data for NENSTS

References
- Skempton, A.W.; Bjerrum, L. A Contribution to the settlement analysis of foundations on clay. Géotechnique 1957, 7, 168–178. [Google Scholar] [CrossRef]
- Zhai, J. Machine-learning-based road soft soil foundation treatment and settlement prediction method. Sci. Program. 2022, 2022, 3463413. [Google Scholar] [CrossRef]
- Indraratna, B.; Rujikiatkamjorn, C.; Ameratunga, J.; Boyle, P. Performance and prediction of vacuum combined surcharge consolidation at port of brisbane. J. Geotech. Geoenviron. Eng. 2011, 137, 1009–1018. [Google Scholar] [CrossRef]
- Indraratna, B.; Rujikiatkamjorn, C.; Balasubramaniam, A.S.; McIntosh, G. Soft ground improvement via vertical drains and vacuum assisted preloading. Geotext. Geomembr. 2012, 30, 16–23. [Google Scholar] [CrossRef]
- Ministry of Railways of the People’s Republic of China. Technical Guidelines for the Evaluation of Ballastless Track Laying Conditions for Passenger Dedicated Line Lines Tie Jianshe [2006]; No. 158; China Railway Publishing House: Beijing, China, 2006. [Google Scholar]
- Q/CR 9230-2016; Technical Specification for Observation and Evaluation of Settlement Deformation of Railway Engineering. China State Railway Group Co., Ltd., China Railway Publishing House: Beijing, China, 2017.
- Cheng, C.Q.; Sa-Ngasoongsong, A.; Beyca, O.; Le, T.; Yang, H.; Kong, Z.Y.; Bukkapatnam, S.T.S. Time series forecasting for nonlinear and non-stationary processes: A review and comparative study. IIE Trans. 2015, 47, 1053–1071. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, H.X.; Wang, J.M.; Long, M.S. Non-stationary transformers: Exploring the stationarity in time series forecasting. In Proceedings of the Advances in Neural Information Processing Systems 35 (NeurIPS 2022), New Orleans, LA, USA, 28 November–9 December 2022; pp. 9881–9893. [Google Scholar]
- Juang, C.H.; Wang, L. Reliability-based robust geotechnical design of spread foundations using multi-objective genetic algorithm. Comput. Geotech. 2013, 48, 96–106. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.L.; Cao, Y.; Ahmed, B. Application of time series analysis and PSO–SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China. Eng. Geol. 2016, 204, 108–120. [Google Scholar] [CrossRef]
- Wang, L.Y.; Li, T.F.; Wang, P.C.; Liu, Z.; Zhang, Q. BiLSTM for predicting post-construction subsoil settlement under embankment: Advancing sustainable infrastructure. Sustainability 2023, 15, 14708. [Google Scholar] [CrossRef]
- Suebsombut, P.; Sekhari, A.; Sureephong, P.; Belhi, A.; Bouras, A. Field data forecasting using LSTM and Bi-LSTM approaches. Appl. Sci. 2021, 11, 11820. [Google Scholar] [CrossRef]
- Raubitzek, S.; Neubauer, T. A fractal interpolation approach to improve neural network predictions for difficult time series data. Expert Syst. Appl. 2021, 169, 114474. [Google Scholar] [CrossRef]
- Yen, N.Y.; Chang, J.W.; Liao, J.Y.; Yong, Y.M. Analysis of interpolation algorithms for the missing values in IoT time series: A case of air quality in Taiwan. J. Supercomput. 2020, 76, 6475–6500. [Google Scholar] [CrossRef]
- Tan, Q.L.; Wei, J.; Hu, J. Applications of wavelet neural network model to building settlement prediction: A case study. Sens. Transducers 2014, 169, 1–8. [Google Scholar]
- Zhang, R.J. Application of wavelet neural network in building settlement prediction. E3S Web Conf. 2020, 198, 03014. [Google Scholar] [CrossRef]
- Zhou, T.; Jie, Y.X.; Wei, Y.J.; Zhang, Y.Y.; Chen, H. A real-time prediction interval correction method with an unscented Kalman filter for settlement monitoring of a power station dam. Sci. Rep. 2023, 13, 4055. [Google Scholar] [CrossRef]
- Tao, Y.Q.; Sun, H.L.; Cai, Y.Q. Predicting soil settlement with quantified uncertainties by using ensemble Kalman filtering. Eng. Geol. 2020, 276, 105753. [Google Scholar] [CrossRef]
- Luo, X.L.; Gan, W.J.; Wang, L.X.; Chen, Y.; Meng, X. A prediction model of structural settlement based on EMD-SVR-WNN. Adv. Civ. Eng. 2020, 2020, 8831965. [Google Scholar] [CrossRef]
- Kliesch, K.; Johmann, S.; El-Mossallamy, Y.; Neidhart, T. Zur setzungsprognose bei erdbauwerken mit fester fahrbahn-erfahrungen an 43 km neubaustrecke. In Proceedings of the Entwicklungen in der Bodenmechanik, Bodendynamik und Geotechnik; Springer: Berlin/Heidelberg, Germany, 2002; pp. 333–346. [Google Scholar]
- Liu, J.F.; Zhao, G.T. Selection of prediction models in railway subgrade settlement assessment. Railway Eng. 2010, 11, 64–68. [Google Scholar] [CrossRef]
- Li, C.L. A simplified method for prediction of embankment settlement in clays. J. Rock Mech. Geotech. Eng. 2014, 6, 61–66. [Google Scholar] [CrossRef]
- Park, H.; Lee, S.; Hwang, D. Parameter evaluation and performance comparison of MSW settlement prediction models in various landfill types. J. Environ. Eng. 2007, 133, 64–72. [Google Scholar] [CrossRef]
- Sivakugan, N.; Johnson, K. Settlement predictions in granular soils: A probabilistic approach. Geotechnique 2004, 54, 499–502. [Google Scholar] [CrossRef]
- Chen, P.Y.; Yu, H.M. Foundation settlement prediction based on a Novel NGM Model. Math. Probl. Eng. 2014, 2014, 242809. [Google Scholar] [CrossRef]
- Kanayama, M.; Rohe, A.; van Paassen, L.A. Using and improving neural network models for ground settlement prediction. Geotech. Geol. Eng. 2014, 32, 687–697. [Google Scholar] [CrossRef]
- Sridharan, A.; Murthy, N.S.; Prakash, K. Rectangular hyperbola method of consolidation analysis. Géotechnique 1987, 37, 355–368. [Google Scholar] [CrossRef]
- Zeng, G.X.; Yang, X.L. Analysis of foundation subsidence of sand wells. J. Zhejiang Univ. 1959, 34–72. [Google Scholar]
- Asaoka, A. Observational procedure of settlement prediction. Soils Found. 1978, 18, 87–101. [Google Scholar] [CrossRef]
- Kong, J.; Kim, H.; Chun, B. Settlement analysis for improvement effect of soft ground method in incheon cheongna site. J. Korean GEO-Environ. Soc. 2012, 13, 19–26. [Google Scholar]
- Menke, W. Review of the generalized least squares method. Surv. Geophys. 2015, 36, 1–25. [Google Scholar] [CrossRef]
- Chai, J.C.; Shen, S.L.; Miura, N.; Bergado Dennes, T. Simple method of modeling PVD-improved subsoil. J. Geotech. Geoenviron. Eng. 2001, 127, 965–972. [Google Scholar] [CrossRef]
- Li, Q.F.; Wang, Z.; Yu, Y. Optimization of area replacement ratio of stone column based on robustness principle. J. Jilin Univ. Earth Sci. Ed. 2022, 52, 171–180. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Zhou, W.H.; Cai, Y.Q. Large-strain elastic viscoplastic consolidation analysis of very soft clay layers with vertical drains under preloading. Can. Geotech. J. 2014, 51, 144–157. [Google Scholar] [CrossRef]
- Editorial Board of Engineering Geology Handbook. Handbook of Engineering Geology, 5th ed.; China Architecture & Building Press: Beijing, China, 2018; pp. 538–539. [Google Scholar]
- Leroueil, S.; Bouclin, G.; Tavenas, F.; Bergeron, L.; Rochelle, P.L. Permeability anisotropy of natural clays as a function of strain. Can. Geotech. J. 1990, 27, 568–579. [Google Scholar] [CrossRef]
- Adams, A.; Nordquist, T.; Germaine, J.; Flemings, P. Permeability anisotropy and resistivity anisotropy of mechanically compressed mudrocks. Can. Geotech. J. 2016, 53, 1474–1482. [Google Scholar] [CrossRef]
- Basak, P. Soil structure and its effects on hydraulic conductivity. Soil Sci. 1972, 114, 417–422. [Google Scholar] [CrossRef]
- Gao, Y.B.; Bao, W.P.; Lou, K.M. Laboratory studies on the sensitivity of layer No.4 soft clay in Shanghai. J. Tongji Univ. Nat. Sci 2015, 43, 140–145. [Google Scholar] [CrossRef]
- Liu, X.J.; Song, B.K.; Sun, Z.Q.; Jiao, W.X. Critical filling height of embankment over soft soil: A three-dimensional upper-bound limit analysis. Buildings 2025, 15, 395. [Google Scholar] [CrossRef]
- TB 10101-2018; Railroad Engineering Survey Specification. National Railway Administration of People’s Republic, China Railway Publishing House: Beijing, China, 2018.
- TB10001-2016; Code for the Design of Railway Subgrades. National Railway Administration of People’s Republic, China Railway Publishing House: Beijing, China, 2017.
- Xie, K.; Chen, X.B.; Li, T.F.; Deng, Z.-X.; Yao, J.-K.; Tang, L.-B. A framework for determining the optimal moisture content of high-speed railway-graded aggregate materials based on the lab vibration compaction method. Constr. Build. Mater. 2023, 392, 131764. [Google Scholar] [CrossRef]
- Zhu, Y.X.; Tian, D.Z.; Yan, F. Effectiveness of entropy weight method in decision-making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Yang, Y.H. Elements of information theory. J. Am. Stat. Assoc. 2008, 103, 429. [Google Scholar] [CrossRef]
- Pearson, E.S. A further development of tests for normality. Biometrika 1930, 22, 239–249. [Google Scholar] [CrossRef]
- Pearson, E.S.I. Note on Tests for Normality. Biometrika 1931, 22, 423–424. [Google Scholar] [CrossRef]
- Li, G.X.; Zhang, B.Y.; Yu, Y.Z. Soil Mechanics, 3rd ed.; Tsinghua University Press: Beijing, China, 2022. [Google Scholar]
- Liu, Z.Y.; Cui, P.L.; Zhang, J.C.; Xia, Y. Consoidation analysis of ideal sand-drained ground with fractional-derivative merchant model and non-darcian flow described by non-newtonian index. Math. Probl. Eng. 2019, 2019, 5359076. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Zhang, J.C.; Duan, S.Q.; Xia, Y.; Cui, P. A consolidation modelling algorithm based on the unified hardening constitutive relation and Hansbo’s flow rule. Comput. Geotech. 2020, 117, 103233. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Xia, Y.Y.; Shi, M.S.; Zhang, J.C.; Zhu, X.M. Numerical simulation and experiment study on the characteristics of non-darcian flow and rheological consolidation of saturated clay. Water 2019, 11, 1385. [Google Scholar] [CrossRef]
- Nguyen, B.P.; Do, T.H.; Kim, Y.-T. Large-strain analysis of vertical drain-improved soft deposit consolidation considering smear zone, well resistance, and creep effects. Comput. Geotech. 2020, 123, 103602. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, W.; Liu, Q.X.; Zhao, Y.M. Consolidation behaviors of double-layered vertical drains ground considering power function permeability and compressibility variation. Rock Soil Mech. 2013, 34, 3117–3126. [Google Scholar] [CrossRef]
- Cao, Y.P.; Sun, Z.J.; Ding, J.W.; Ji, F. Axisymmetric large-strain consolidation model for dredged clay with high water content. Chin. J. Geotech. Eng. 2016, 38, 1904–1910. [Google Scholar] [CrossRef]
- Yao, Y.P.; Kong, L.M.; Hu, J. An elastic-viscous-plastic model for overconsolidated clays. Sci. China Technol. Sci. 2012, 56, 441–457. [Google Scholar] [CrossRef]
- Swartzendruber, D. Modification of darcy’s law for the flow of water in soils. Soil Sci. 1962, 93, 22–29. [Google Scholar] [CrossRef]
- Cai, Y.Q.; Geng, X.Y. Consolidation analysis of a semi-infinite transversely isotropic saturated soil under general time-varying loadings. Comput. Geotech. 2009, 36, 484–492. [Google Scholar] [CrossRef]
- Nash, D.; Ryde, S. Modeling consolidation accelerated by vertical drains in soils subject to creep. Geotechnique 2001, 51, 257–273. [Google Scholar] [CrossRef]
- Liu, Z.L.; Song, P.; Li, J.S.; Li, J.; Zhang, X.-B. An optimized implicit finite-difference scheme for the two-dimensional Helmholtz equation. Geophys. J. Int 2015, 202, 1805–1826. [Google Scholar] [CrossRef][Green Version]


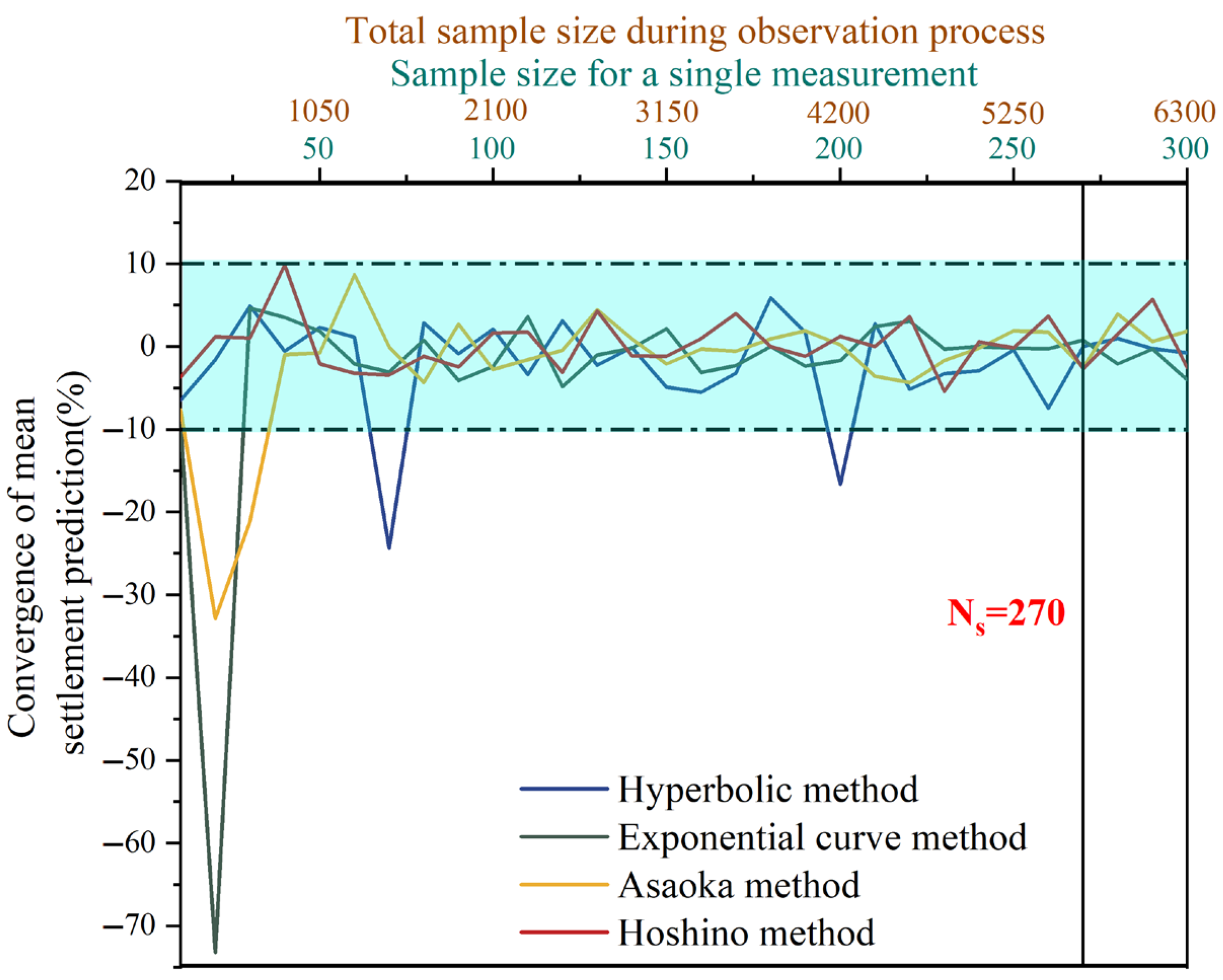
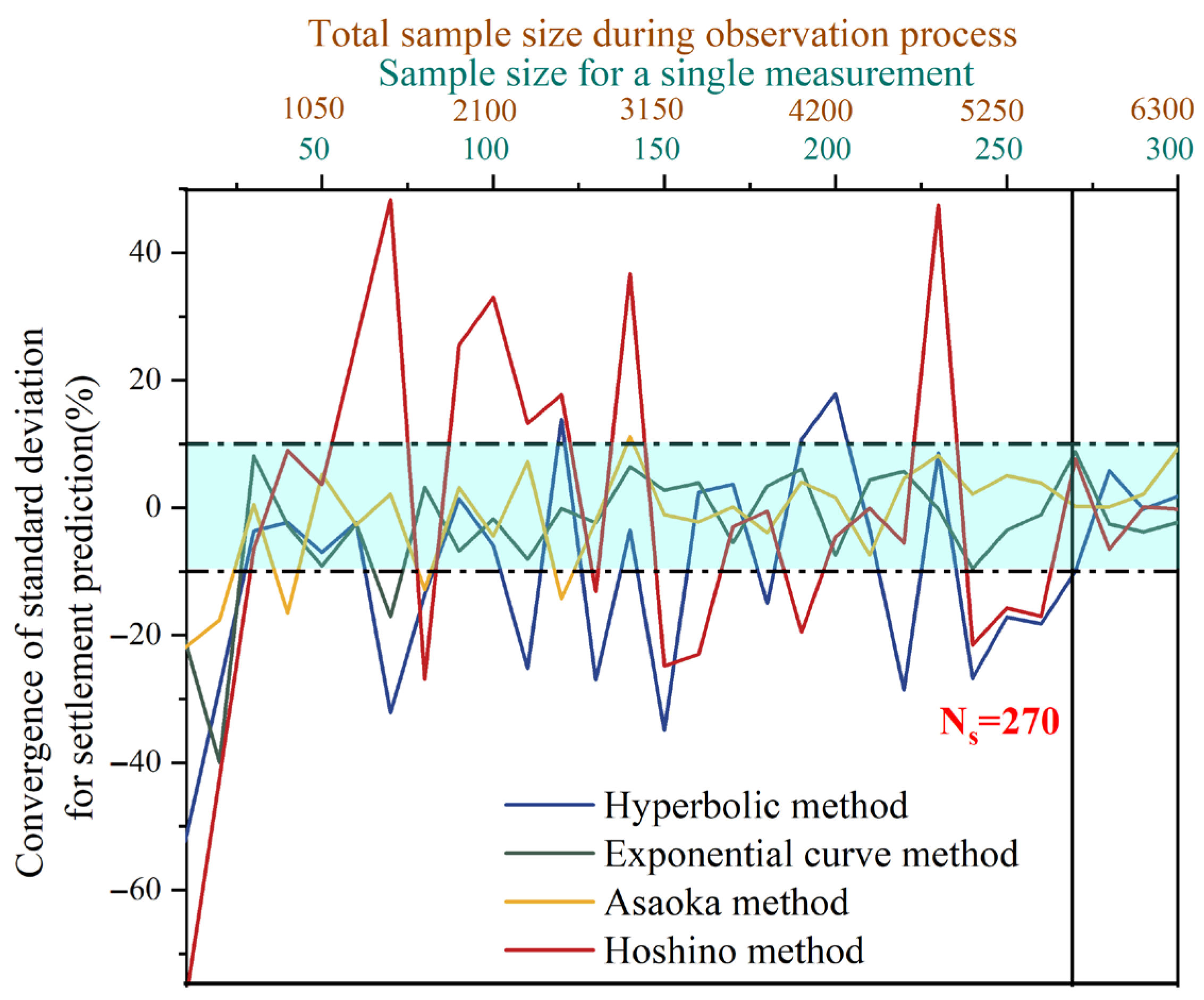
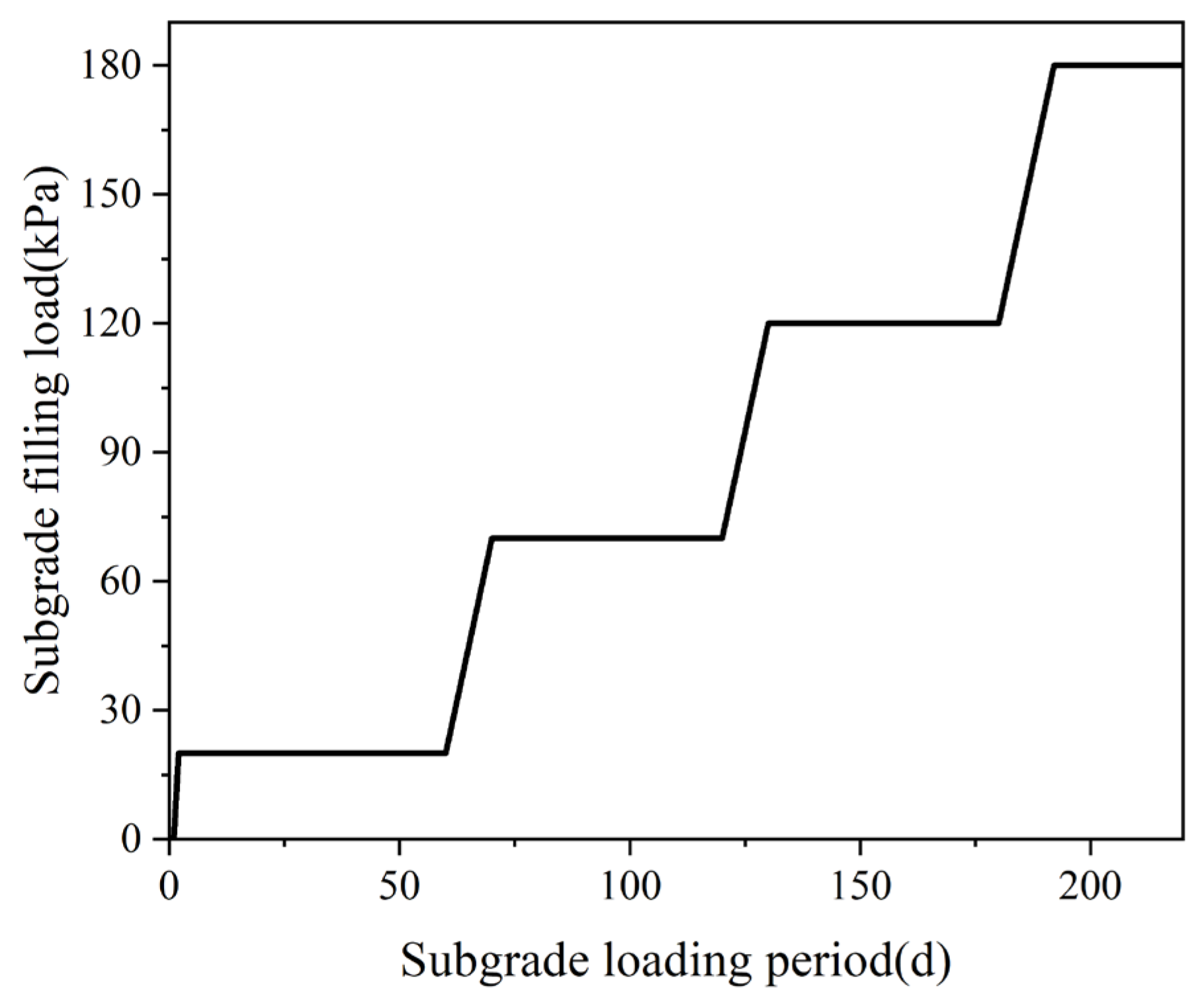
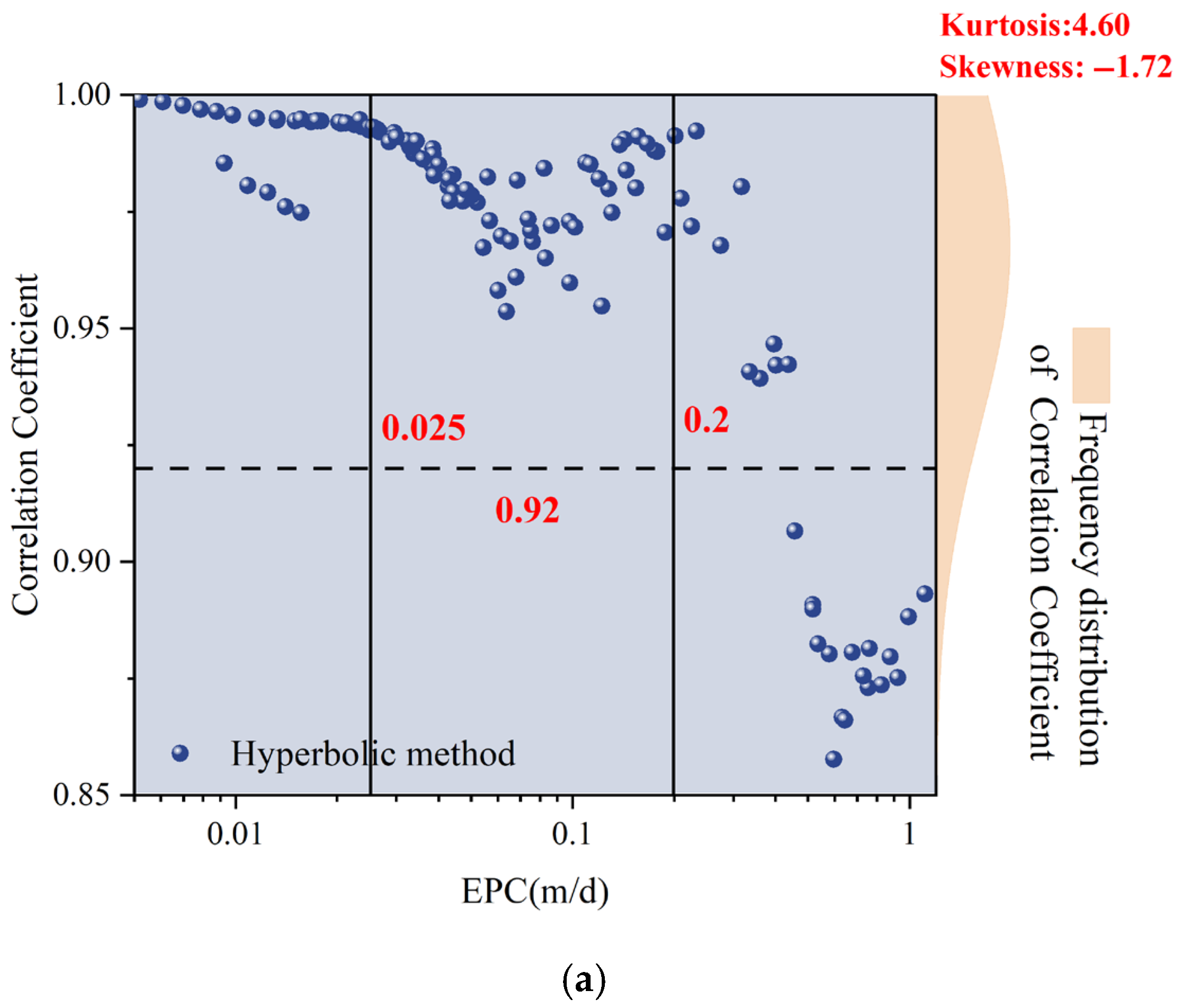

| Sand drain radius, (m) | Void ratio, | Soft soil thickness, (m) | Swelling index, | Radial permeability coefficient, (m/d) |
| 0.033 | 2.359 | 6 | 0.0436 | 2.73 × 10−4 |
| Effective radius of sand drain, (m) | Water content, (%) | Soft soil density, (g/cm3) | Compression index, | Vertical permeability coefficient, (m/d) |
| 0.525 | 88 | 1.5 | 0.741 | 0.94 × 10−4 |
| Soft Soil Density, (g/cm3) | Compression Index, | Vertical Permeability Coefficient, (10−4 m/d) | Effective Radius of Sand Drain, (m) | Soil Soft Thickness, (m) |
| 1.9 | 0.5 | 2.76/4.92/7.08/9.24/11.3/13.6 | 0.5/1.0/1.5/2.0 | 10 |
| Void ratio, | Swelling index, | Anisotropy ratio, | Vane shear strength, (kPa) | Drainage type |
| 1.67 | 0.05 | 1.1/1.3/1.5/1.7/1.9 | 30 [39] | Single-sided drainage |
| Deformation Measurement Grade | Elevation Error (mm) |
|---|---|
| Class I | ±0.3 |
| Class II | ±0.5 |
| Class III | ±1.0 |
| Class IV | ±2.0 |
| Observation Phase (Static Period) | Frequency |
|---|---|
| Months 1–3 | 1 time/week |
| Months 4–6 | 1 time/2 weeks |
| Beyond 6 months | 1 time/month |
| Stratum | Soil Layer Thickness, (m) | Water Content, (%) | Soil Density, (g/cm3) | Specific Gravity, | Void Ratio, | Plasticity Index, (%) | Coefficient of Compressibility, (MPa−1) | Coefficient of Consolidation, (10−4 cm2/s) |
|---|---|---|---|---|---|---|---|---|
| Miscellaneous Fill (QmL) | 0~1.55 | — | — | — | — | — | — | — |
| Soft Clay (Q4mL) | 0.9~2.9 | 34.7 | 1.85 | 2.74 | 0.99 | 16.5 | 0.19 | 3.063 |
| Sandy Soil (Q4mL) | 0.6~3.0 | 35.1 | 1.84 | 2.71 | 0.99 | 10.6 | 0.36 | 6.391 |
| Mucky Clay with Silt (Q4mL) | 8.8~10.1 | 47.4 | 1.73 | 2.74 | 1.33 | 17.3 | 0.58 | 2.533 |
| Silty Sand with Clay (Q4mL) | 4.6~10.5 | 27.8 | 1.91 | 2.71 | 0.81 | 6.8 | 0.15 | 8.698 |
| Correlation Coefficient | Systematic Error (%) | Random Error (mm) | CEI | |
|---|---|---|---|---|
| Hyperbolic | 0.97 | 0. 5 | 1.75 | 0.87 |
| Exponential | 0.7 | 12.74 | 0.89 | 0.64 |
| Asaoka | 0.98 | 1.73 | 0.93 | 0.94 |
| Hoshino | 0.98 | 0.92 | 0.53 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wang, L.; Li, T.; Guo, H.; Chen, F.; Zhao, Y.; Zhang, Q.; Wang, T. A Monte Carlo Simulation Framework for Evaluating the Robustness and Applicability of Settlement Prediction Models in High-Speed Railway Soft Foundations. Symmetry 2025, 17, 1113. https://doi.org/10.3390/sym17071113
Liu Z, Wang L, Li T, Guo H, Chen F, Zhao Y, Zhang Q, Wang T. A Monte Carlo Simulation Framework for Evaluating the Robustness and Applicability of Settlement Prediction Models in High-Speed Railway Soft Foundations. Symmetry. 2025; 17(7):1113. https://doi.org/10.3390/sym17071113
Chicago/Turabian StyleLiu, Zhenyu, Liyang Wang, Taifeng Li, Huiqin Guo, Feng Chen, Youming Zhao, Qianli Zhang, and Tengfei Wang. 2025. "A Monte Carlo Simulation Framework for Evaluating the Robustness and Applicability of Settlement Prediction Models in High-Speed Railway Soft Foundations" Symmetry 17, no. 7: 1113. https://doi.org/10.3390/sym17071113
APA StyleLiu, Z., Wang, L., Li, T., Guo, H., Chen, F., Zhao, Y., Zhang, Q., & Wang, T. (2025). A Monte Carlo Simulation Framework for Evaluating the Robustness and Applicability of Settlement Prediction Models in High-Speed Railway Soft Foundations. Symmetry, 17(7), 1113. https://doi.org/10.3390/sym17071113








