A Multi-Objective Method for Enhancing the Seismic Resilience of Urban Water Distribution Networks
Abstract
1. Introduction
2. Related Works
- (1)
- Prevailing research on enhancing seismic resilience of WDNs predominantly focuses on specific earthquake damage scenarios, failing to systematically account for uncertainties inherent in seismic inputs, system responses, and recovery processes during resilience assessment. These uncertainties cascade and accumulate across phases, significantly compromising the accuracy of seismic resilience evaluations.
- (2)
- Current research predominantly focuses on theoretical methodologies for resilience enhancement, yet fails to develop integrated software platforms. This gap significantly impedes the provision of technical decision-support tools for urban WDN administrators to implement resilience enhancement strategies.
3. Methodology
3.1. Seismic Hazard Analysis
3.2. Seismic Vulnerability Analysis of Water Supply Pipelines
3.3. Hydraulic Analysis of the WDN
3.4. Resilience Evaluation Model
3.5. The Multi-Objective Approach to Enhance the Resilience of WDNs
3.6. Monte Carlo Simulation
3.7. Software Development
- (1)
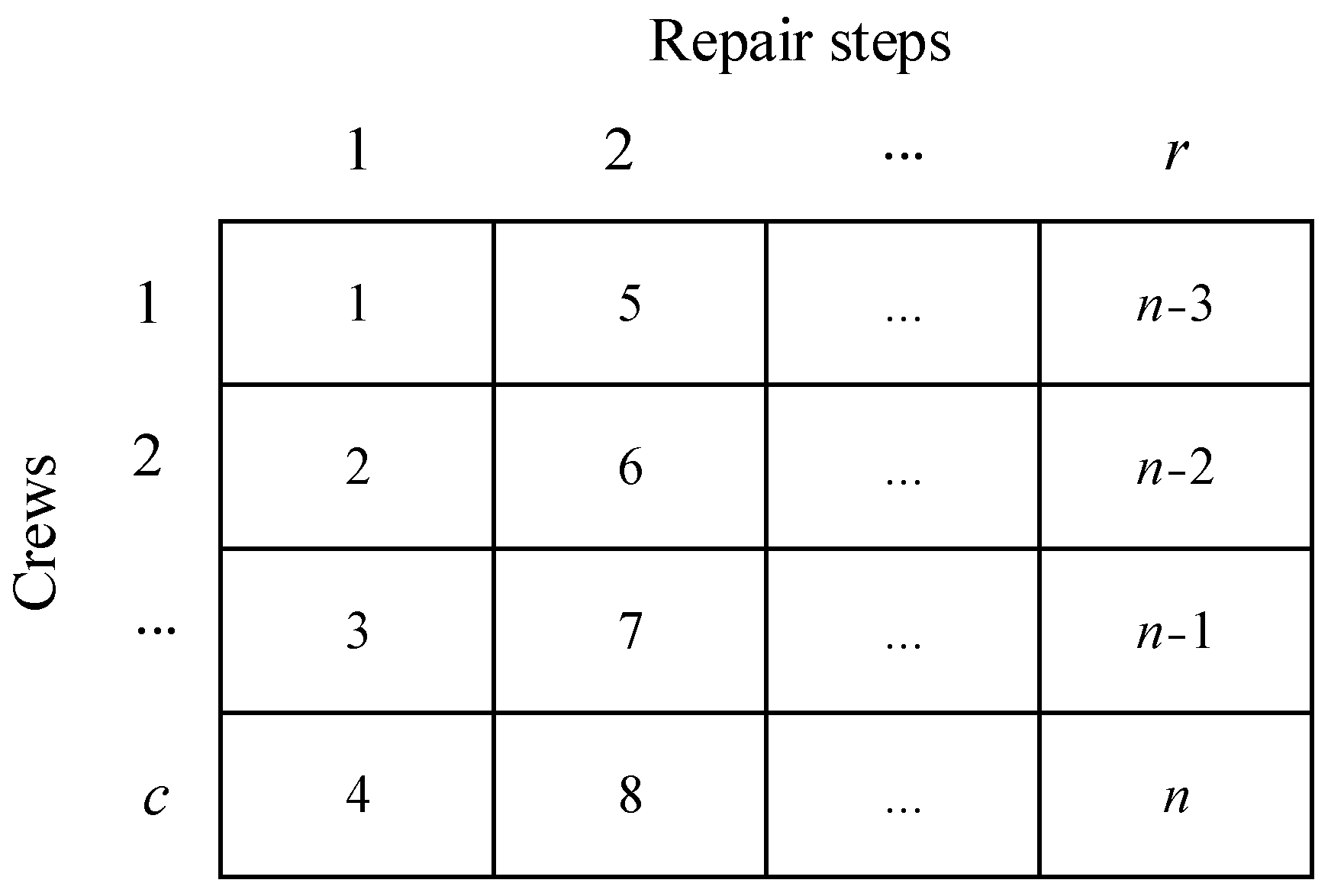
- Input the fundamental data of the WDN, encompassing its topology, physical structure, and hydraulic parameters; additionally, specify the analysis parameters for the genetic algorithm and the number of Monte Carlo simulations, denoted as N.
- (2)
- Set the ground motion parameters and calculate the ground motion intensity for each pipeline segment across the WDN, utilizing the seismic hazard analysis model outlined in Section 3.1.
- (3)
- Utilizing the ground motion intensity in conjunction with the seismic vulnerability analysis model for water supply pipelines as outlined in Section 3.2, determine the probability of each pipeline being in a state of basic intactness, moderate damage, or severe damage.
- (4)
- The Monte Carlo simulation method is employed to generate a random number within the range of 0 to 1, which is then compared to the pipeline damage probability to determine whether the pipeline is in a state of intactness, leakage, or bursting, thereby determining the damage scenario of the WDN following the earthquake.
- (5)
- Utilizing the hydraulic analysis model outlined in Section 3.3, determine the post-earthquake hydraulic head for each node within the earthquake-damaged pipe network, and subsequently evaluate the seismic performance of the WDN.
- (6)
- By configuring the number of repair crews and repair costs, randomly generating pipeline repair times, and leveraging the optimization model in Section 3.5, the genetic algorithm is applied to derive the optimal repair sequences for repair time, repair cost, hydraulic recovery index, and multi-objective optimization for all damaged pipelines.
- (7)
- Based on the four repair sequences, the corresponding seismic performance recovery process curves of the WDN is plotted, and the seismic resilience, repair time, and cost are calculated.
- (8)
- Steps (4)–(7) are repeated N times to obtain the average values of seismic resilience, repair time, and cost for the WDN.
4. Case Study
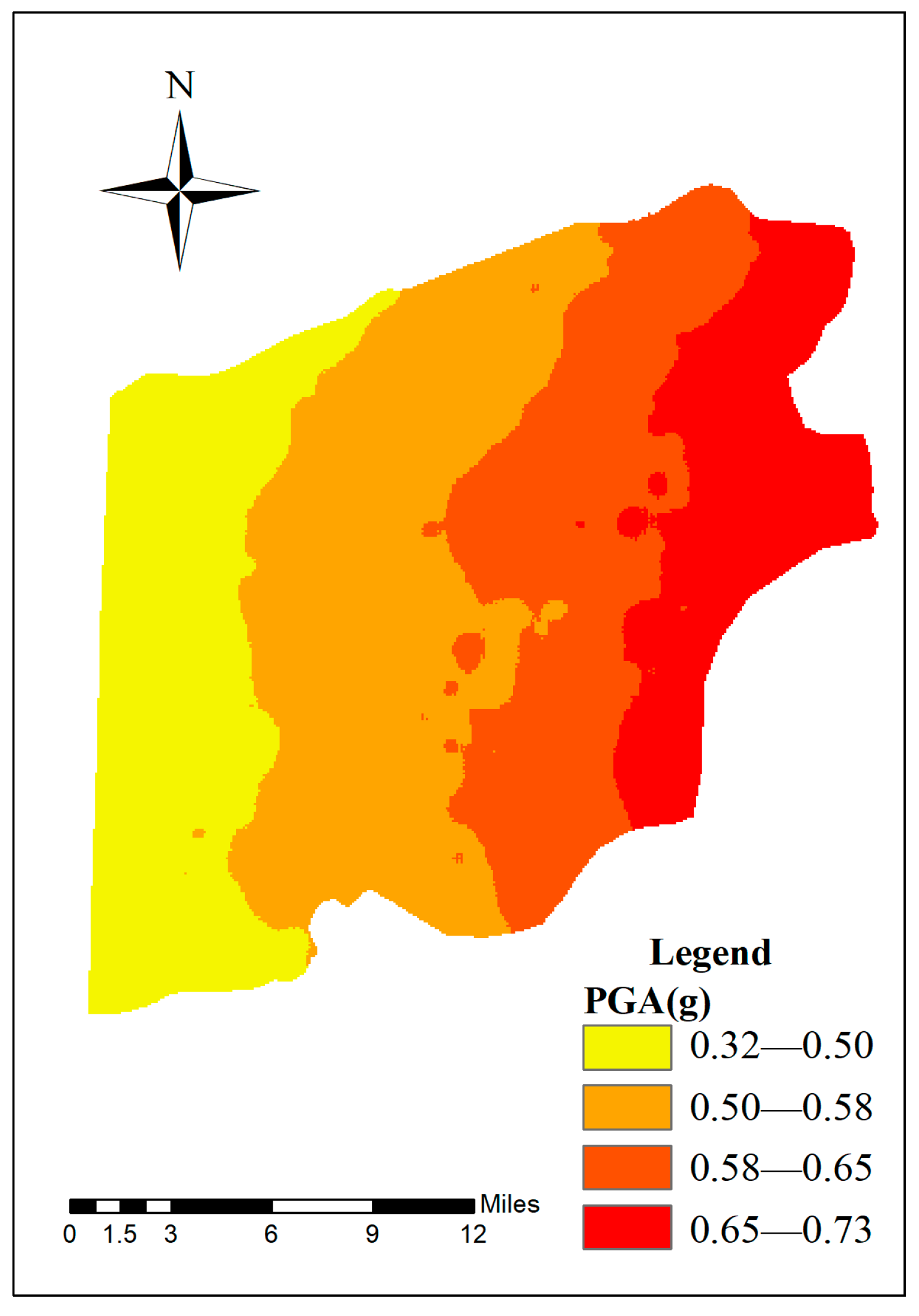
4.1. Seismic Hazard
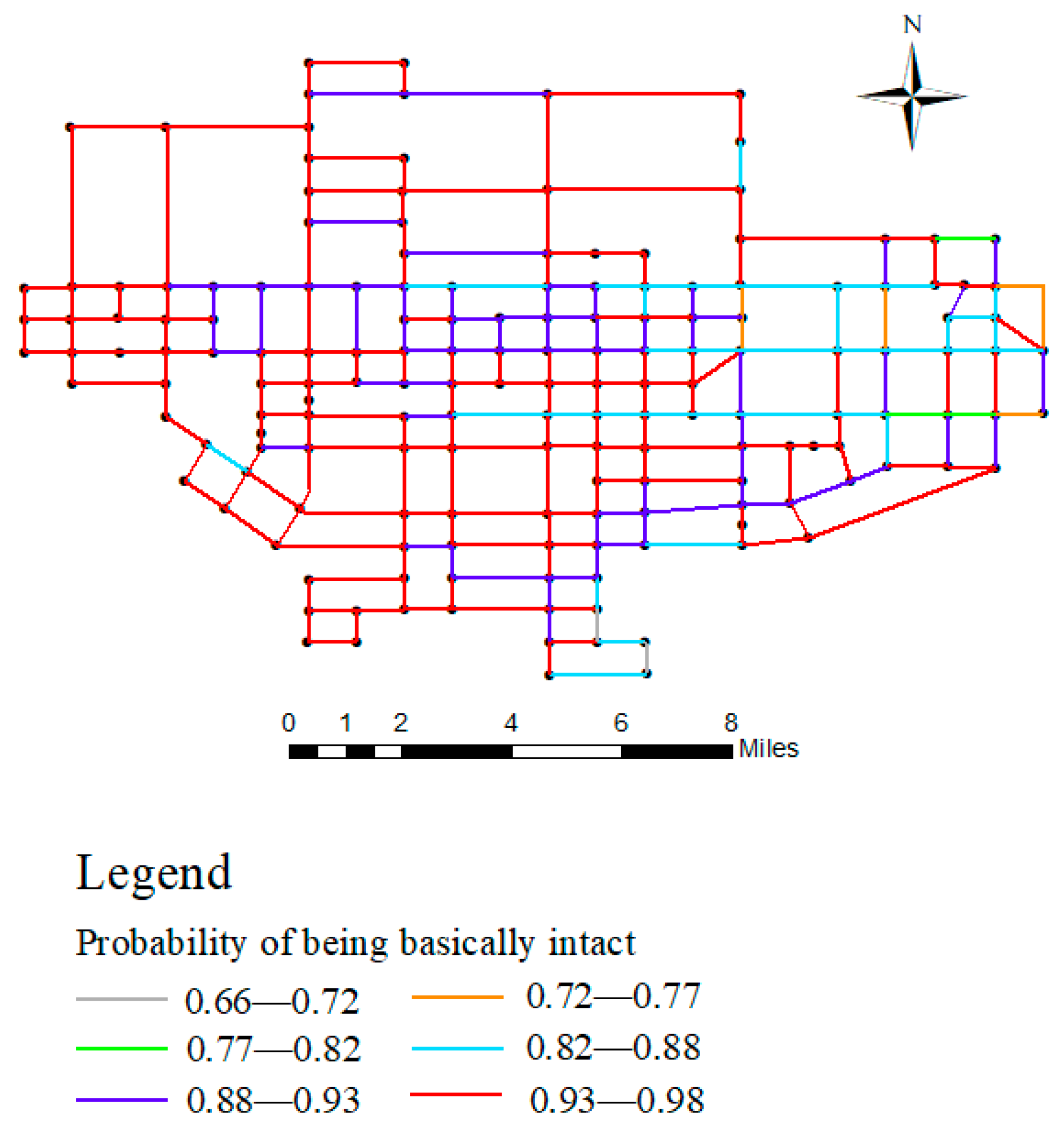
4.2. Pipeline Failure Probability
4.3. Seismic Resilience Improvement Strategy
5. Discussion
5.1. Discussion of Uncertainty
5.2. Discussion of Resilience Enhancement Effects
6. Conclusions
- (1)
- The seismic resilience of the WDN varies significantly across different pipe network failure scenarios. This study employs a random simulation method to account for various uncertainties, including the number of damaged pipelines, types of damage, maintenance time, and repair sequences. In contrast to traditional deterministic methods, the results of this analysis are more accurate and comprehensive.
- (2)
- Given that the water supply pipeline materials in Xi’an City primarily consist of steel pipes, polyethylene pipes, and ductile iron pipes, each of which has good seismic performance, the number of pipeline damages is minimal under the earthquake scenarios defined in this study. The seismic resilience of the WDN exceeds 0.88 across all four repair strategies, indicating a generally favorable overall resilience.
- (3)
- The seismic resilience improvement method that utilizes the hydraulic recovery index attains the highest average seismic resilience for the WDN. In contrast, while the multi-objective seismic resilience improvement method results in a 0.2% decrease in the average seismic resilience effect of the WDN, it simultaneously reduces the average maintenance time by 10.7 h and saves maintenance costs amounting to CNY 7375.8. Furthermore, in comparison to the conventional random repair approach for damaged pipelines, the multi-objective-based repair method proposed in this study demonstrates superior performance in enhancing seismic resilience, improving hydraulic recovery index, reducing repair costs, and minimizing repair time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Klise, K.A.; Bynum, M.; Moriarty, D.; Murray, R. A software framework for assessing the resilience of drinking water systems to disasters with an example earthquake case study. Environ. Model. Softw. 2017, 95, 420–431. [Google Scholar] [CrossRef] [PubMed]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Framework for analytical quantification of disaster resilience. Eng. Struct. 2010, 32, 3639–3649. [Google Scholar] [CrossRef]
- Ouyang, M.; Dueñas-Osorio, L.; Min, X. A three-stage resilience analysis framework for urban infrastructure systems. Struct. Saf. 2012, 36, 23–31. [Google Scholar] [CrossRef]
- Reed, D.A.; Kapur, K.C.; Christie, R.D. Methodology for assessing the resilience of networked infrastructure. IEEE Syst. J. 2009, 3, 174–180. [Google Scholar] [CrossRef]
- Zobel, C.W. Quantitatively representing nonlinear disaster recovery. Decis. Sci. 2014, 45, 1053–1082. [Google Scholar] [CrossRef]
- Ayyub, B.M. Systems resilience for multihazard environments: Definition, metrics, and valuation for decision making. Risk Anal. 2014, 34, 340–355. [Google Scholar] [CrossRef]
- Munoz, A.; Dunbar, M. On the quantification of operational supply chain resilience. Int. J. Prod. Res. 2015, 53, 6736–6751. [Google Scholar] [CrossRef]
- Nan, C.; Sansavini, G. A quantitative method for assessing resilience of interdependent infrastructures. Reliab. Eng. Syst. Saf. 2017, 157, 35–53. [Google Scholar] [CrossRef]
- Tran, H.T.; Balchanos, M.; Domercant, J.C.; Mavris, D.N. A framework for the quantitative assessment of performance-based system resilience. Reliab. Eng. Syst. Saf. 2017, 158, 73–84. [Google Scholar] [CrossRef]
- Qi, Q.; Shao, C.; Yang, H.; Cui, H.; Chen, Z.; Gong, W. Axial-flexure-shear model for seismic analysis of RC thin-walled hollow piers. Soil Dyn. Earthq. Eng. 2025, 195, 109375. [Google Scholar] [CrossRef]
- Esposito, S.; Giovinazzi, S.; Elefante, L.; Iervolino, I. Performance of the L’Aquila (central Italy) gas distribution network in the 2009 (Mw 6.3) earthquake. Bull. Earthq. Eng. 2013, 11, 2447–2466. [Google Scholar] [CrossRef]
- Kircher, C.A.; Whitman, R.V.; Holmes, W.T. HAZUS earthquake loss estimation methods. Nat. Hazards Rev. 2006, 7, 45–59. [Google Scholar] [CrossRef]
- Yazdani, A.; Otoo, R.A.; Jeffrey, P. Resilience enhancing expansion strategies for water distribution systems: A network theory approach. Environ. Model. Softw. 2011, 26, 1574–1582. [Google Scholar] [CrossRef]
- Ouyang, M.; Yu, M.H.; Huang, X.Z.; Luan, E.J. Emergency response to disaster-struck scale-free network with redundant systems. Phys. A Stat. Mech. Its Appl. 2008, 387, 4683–4691. [Google Scholar] [CrossRef]
- Pahwa, S.; Hodges, A.; Scoglio, C.; Wood, S. Topological analysis of the power grid and mitigation strategies against cascading failures. In Proceedings of the 2010 IEEE International Systems Conference, San Diego, CA, USA, 5 April 2010; pp. 272–276. [Google Scholar]
- Lorenz, I.S.; Pelz, P.F. Optimal resilience enhancement of water distribution systems. Water 2020, 12, 2602. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, Z.; Gong, H. Effects comparison of different resilience enhancing strategies for municipal water distribution network: A multidimensional approach. Math. Probl. Eng. 2015, 2015, 438063. [Google Scholar] [CrossRef][Green Version]
- Shi, P. Seismic Response Modeling of Water Supply Systems. Ph.D. Dissertation, Cornell University, Ithaca, NY, USA, 2006. [Google Scholar]
- Li, W.; Mazumder, R.K.; Li, Y. Topology-based resilience metrics for seismic performance evaluation and recovery analysis of water distribution systems. J. Pipeline Syst. Eng. Pract. 2023, 14, 04022070. [Google Scholar] [CrossRef]
- Long, L.; Yang, H.; Zheng, S.; Cai, Y. Seismic Resilience Evaluation of Urban Multi-Age Water Distribution Systems Considering Soil Corrosive Environments. Sustainability 2024, 16, 5126. [Google Scholar] [CrossRef]
- Han, Z.; Ma, D.; Hou, B.; Wang, W. Seismic resilience enhancement of urban water distribution system using restoration priority of pipeline damages. Sustainability 2020, 12, 914. [Google Scholar] [CrossRef]
- Afandizadeh, S.; Jahangiri, A.; Kalantari, N. Determination of the optimal network configuration for emergency evacuation by simulated annealing algorithm. Nat. Hazards 2013, 69, 1315–1335. [Google Scholar] [CrossRef]
- Liu, W.; Song, Z.; Ouyang, M.; Li, J. Recovery-based seismic resilience enhancement strategies of water distribution networks. Reliab. Eng. Syst. Saf. 2020, 203, 107088. [Google Scholar] [CrossRef]
- Song, Z.; Liu, W.; Shu, S. Resilience-based post-earthquake recovery optimization of water distribution networks. Int. J. Disaster Risk Reduct. 2022, 74, 102934. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Q.X. Seismic resilience analysis of water distribution networks with multi-components and resilience improvement strategies. J. Seismol. Res. 2023, 46, 271–279. [Google Scholar]
- Mazumder, R.K.; Salman, A.M.; Li, Y. Post-disaster sequential recovery planning for water distribution systems using topological and hydraulic metrics. Struct. Infrastruct. Eng. 2022, 18, 728–743. [Google Scholar] [CrossRef]
- Alfonso, L.; Jonoski, A.; Solomatine, D. Multiobjective optimization of operational responses for contaminant flushing in water distribution networks. J. Water Resour. Plan. Manag. 2010, 136, 48–58. [Google Scholar] [CrossRef]
- Osman, H.; Ammar, M.; El-Said, M. Optimal scheduling of water network repair crews considering multiple objectives. J. Civ. Eng. Manag. 2017, 23, 28–36. [Google Scholar] [CrossRef]
- Assad, A.; Moselhi, O.; Zayed, T. Resilience-driven multiobjective restoration planning for water distribution networks. J. Perform. Constr. Facil. 2020, 34, 04020072. [Google Scholar] [CrossRef]
- Long, L.; Zheng, S.S.; Yang, Y.; Zhou, Y. Research on the recovery strategy of the urban water supply networks after an earthquake. J. Seismol. Res. 2022, 45, 352–361. [Google Scholar]
- Haghighi, M.; Delnavaz, A.; Safehian, M.; Delnavaz, M. Strategic Management and Seismic Resilience Enhancement of Water Distribution Network Using Artificial Neural Network Model. J. Pipeline Syst. Eng. Pract. 2025, 16, 04024053. [Google Scholar] [CrossRef]
- Pudasaini, B.; Shahandashti, S.M. Seismic resilience enhancement of water pipe networks using hybrid metaheuristic optimization. In Planning and Design, Proceedings of Lifelines 2020 Conference, San Antonio, Texas, 9–12 August 2020; Pulido, J.F., Poppe, M., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2020; pp. 428–436. [Google Scholar]
- Zong, C.; Ji, K.; Wen, R.; Bi, X.; Ren, Y.; Zhang, X. Seismic resilient three-stage enhancement for gas distribution network using computational optimization algorithms. Soil Dyn. Earthq. Eng. 2022, 152, 107057. [Google Scholar] [CrossRef]
- Fan, X.; Yu, X. Resilience of Water Distribution Network: Enhanced Recovery Assisted by Artificial Intelligence (AI) Considering Dynamic Water Demand Change. In 1971 San Fernando Earthquake and Lifeline Infrastructure, Proceedings of Lifelines 2022 Conference, Online, 31 January—11 February 2022; Davis, C.A., Yu, K., Taciroglu, E., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2022; pp. 880–891. [Google Scholar]
- Fan, X.; Zhang, X.; Yu, X. A graph convolution network-deep reinforcement learning model for resilient water distribution network repair decisions. Comput.-Aided Civ. Infrastruct. Eng. 2022, 37, 1547–1565. [Google Scholar] [CrossRef]
- Xie, L.L.; Ma, Y.H.; Zhai, C.H. Performance-Based Seismic Design and Design Ground Motion; Science Publishing Institute: Beijing, China, 2009. [Google Scholar]
- Panza, G.F.; Vaccari, F.; Cazzaro, R. Deterministic seismic hazard assessment. In Proceedings of the Vrancea Earthquakes: Tectonics, Hazard and Risk Mitigation: Contributions from the First International Workshop on Vrancea Earthquakes, Bucharest, Romania, 1–4 November 1997; Springer: Dordrecht, The Netherlands, 1999; pp. 269–286. [Google Scholar]
- Dai, K.; Bi, K.; Song, G.; Jiang, Z.; Yu, X. Evaluating the Seismic Risk of FRP Retrofitting Schemes for Corroded RC Frame Structures Based on Benefit-Cost Assessment. Earthq. Eng. Resil. 2025, 4, 97–115. [Google Scholar] [CrossRef]
- Cornell, C.A. Engineering seismic risk analysis. Bull. Seismol. Soc. Am. 1968, 58, 1583–1606. [Google Scholar] [CrossRef]
- Fan, W.; Du, W.; Wang, X.; Shao, H.; Wen, Y. Seismic motion attenuation relations in Shaanxi areas. Earthq. Eng. Eng. Dyn. 2011, 31, 47–54. [Google Scholar]
- Kassem, M.M.; Nazri, F.M.; Farsangi, E.N. The seismic vulnerability assessment methodologies: A state-of-the-art review. Ain Shams Eng. J. 2020, 11, 849–864. [Google Scholar] [CrossRef]
- Dai, K.Y.; Yu, X.H.; Lu, D.G.; Qian, K. Fragility functions for corroded reinforced concrete columns. J. Build. Eng. 2024, 82, 108124. [Google Scholar] [CrossRef]
- Isoyama, R.; Ishida, E.; Yune, K.; Shirozu, T. Seismic damage estimation procedure for water supply pipelines. Water Supply 2000, 18, 63–68. [Google Scholar]
- Chen, L.L.; Li, J. Aseismatic serviceability analysis of water supply network. Eng. Mech. 2004, 21, 45–50. [Google Scholar]
- Choi, J.; Kang, D. Improved hydraulic simulation of valve layout effects on post-earthquake restoration of a water distribution network. Sustainability 2020, 12, 3492. [Google Scholar] [CrossRef]
- Gupta, R.; Bhave, P.R. Comparison of methods for predicting deficient-network performance. J. Water Resour. Plan. Manag. 1996, 122, 214–217. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic algorithm. Evolutionary algorithms and neural networks. In Theory and Applications; Springer Nature: Berlin/Heidelberg, Germany, 2019; pp. 43–55. [Google Scholar]
- Mahadevan, S. Monte carlo simulation. In Mechanical Engineering; Marcel Dekker: New York, NY, USA; Basel, Switzerland, 1997; pp. 123–146. [Google Scholar]
- Surhone, L.M.; Timpledon, M.T.; Marseken, S.F. SharpDevelop; Betascript Publishing: Beau Bassin, Mauritius, 2010. [Google Scholar]
- Lam, H.; Thai, T.L. NET Framework Essentials, 3rd ed.; O’Reilly: Sebastopol, CA, USA, 2003. [Google Scholar]
- Pacurari, D.I. The Use of Oracle Spatial and ArcSDE for Geodatabase Access; West Virginia University Libraries: Morgantown, WV, USA, 2002. [Google Scholar]
- Chen, F.G. Research on Site Effect Based on Multiple Factors and Its Application. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2020. [Google Scholar]
- GB 18306-2015; Seismic Ground Motion Parameters Zonation Map of China. China Standard Press: Beijing, China, 2015.
- FEMA. Multi-Hazard Loss Estimation Methodology, Earthquake Model (HAZUS-MHMR4). Washington, D.C. 2003. Available online: https://www.fema.gov/sites/default/files/2020-09/fema_hazus_flood-model_technical-manual_2.1.pdf (accessed on 4 January 2025).
- GB/T 18208.4-2011; Post-Earthquake Field Works-Part 4: Assessment of Direct Loss. Seismological Press: Beijing, China, 2011.





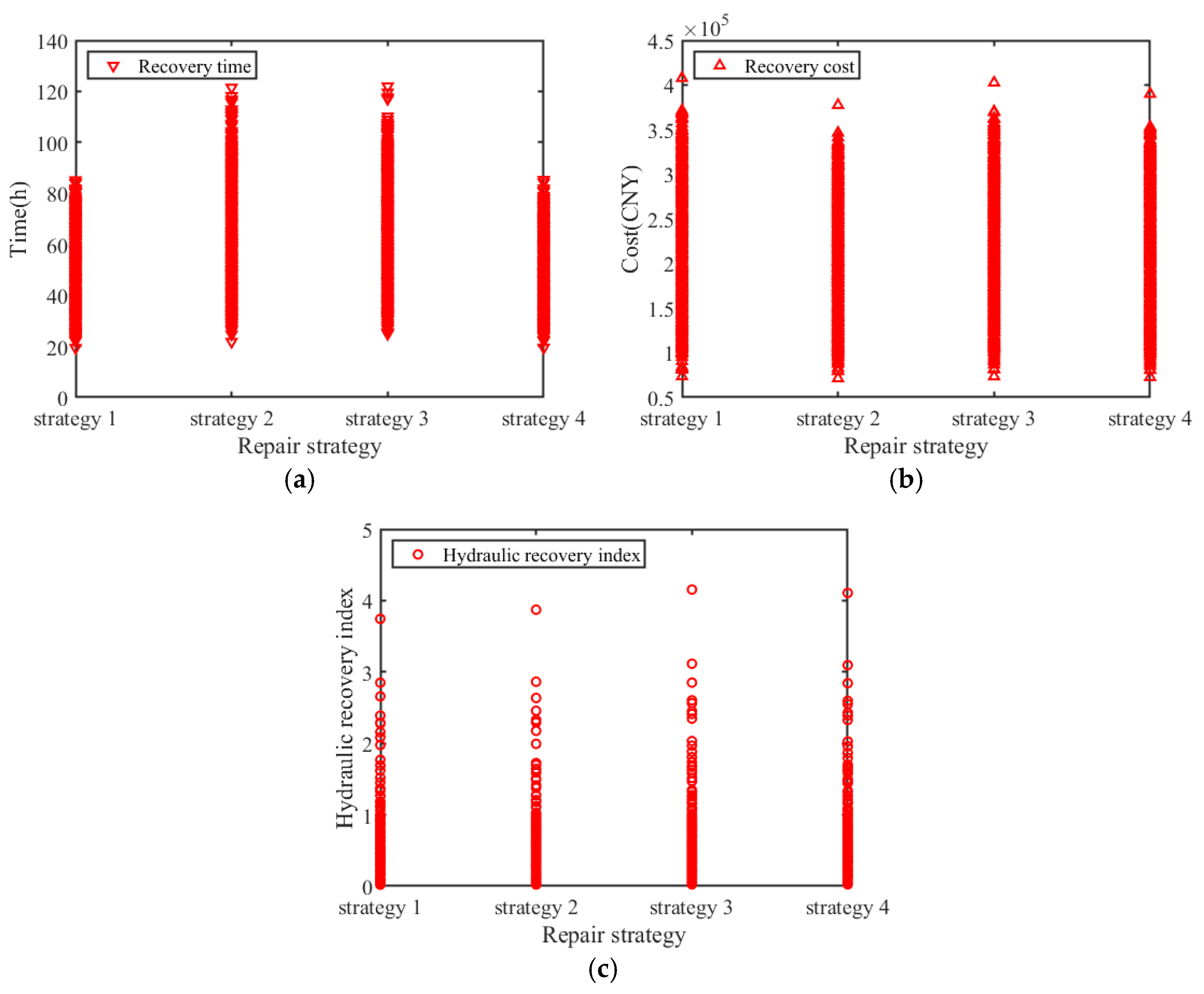



| Methods | Strategy 1 | Strategy 2 | Strategy 3 | Strategy 4 | |
|---|---|---|---|---|---|
| Indicators | |||||
| Time/h | 48.8492 | 61.3650 | 59.7332 | 49.0257 | |
| Cost/CNY | 215,526.53 | 201,418.49 | 214,637.07 | 207,261.23 | |
| Hydraulic recovery index | 0.3599 | 0.3624 | 0.3973 | 0.3950 |
| Optimization Methods | Repair Crews | Pipelines Repair Sequence |
|---|---|---|
| Strategy 1 | 1 | Pipe 58➔99➔43➔67➔260➔171 |
| 2 | Pipe 256➔228➔92➔204➔17➔181 | |
| 3 | Pipe 167➔169➔189➔30➔182➔274 | |
| 4 | Pipe 192➔36➔49➔235➔53➔10 | |
| Strategy 2 | 1 | Pipe 274➔36➔204➔53➔30➔260 |
| 2 | Pipe 10➔43➔49➔99➔58➔235 | |
| 3 | Pipe 182➔181➔167➔169➔92➔67 | |
| 4 | Pipe 228➔189➔192➔256➔17➔171 | |
| Strategy 3 | 1 | Pipe 92➔17➔10➔235➔67➔169 |
| 2 | Pipe 189➔256➔49➔182➔171➔99 | |
| 3 | Pipe 192➔167➔30➔43➔204➔53 | |
| 4 | Pipe 228➔181➔36➔58➔274➔260 | |
| Strategy 4 | 1 | Pipe 17➔10➔228➔256➔58➔204 |
| 2 | Pipe 67➔189➔49➔171➔36➔53 | |
| 3 | Pipe 192➔182➔274➔43➔260➔99 | |
| 4 | Pipe 92➔181➔235➔167➔30➔169 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, L.; Pan, Z.; Yang, H.; Yang, Y.; Liu, F. A Multi-Objective Method for Enhancing the Seismic Resilience of Urban Water Distribution Networks. Symmetry 2025, 17, 1105. https://doi.org/10.3390/sym17071105
Long L, Pan Z, Yang H, Yang Y, Liu F. A Multi-Objective Method for Enhancing the Seismic Resilience of Urban Water Distribution Networks. Symmetry. 2025; 17(7):1105. https://doi.org/10.3390/sym17071105
Chicago/Turabian StyleLong, Li, Ziang Pan, Huaping Yang, Yong Yang, and Feiyu Liu. 2025. "A Multi-Objective Method for Enhancing the Seismic Resilience of Urban Water Distribution Networks" Symmetry 17, no. 7: 1105. https://doi.org/10.3390/sym17071105
APA StyleLong, L., Pan, Z., Yang, H., Yang, Y., & Liu, F. (2025). A Multi-Objective Method for Enhancing the Seismic Resilience of Urban Water Distribution Networks. Symmetry, 17(7), 1105. https://doi.org/10.3390/sym17071105






