Structured Stability of Hybrid Stochastic Differential Equations with Superlinear Coefficients and Infinite Memory
Abstract
1. Introduction
- This work systematically examines stability impacts induced by distinct system structures under different Markovian modes, employing phase space theory for analytical characterization. The M-matrix approach developed in this paper provides a comprehensive demonstration of how such symmetric switching rules influence the stability of variable-structure systems.
- The final case study uncovers a profound phenomenon: even when a highly nonlinear subsystem exhibits inherent instability, properly designed Markovian switching can induce global stability in the overall hybrid system. This stabilization arises from Markovian switching’s transition probabilities and subsystem dynamics synergistically averaging out unstable modes via ergodicity. This finding significantly enriches the stability theory of nonlinear stochastic systems.
- In this study, we adopt the phase space as our analytical framework, departing from the conventional space commonly employed in stability analysis. This deliberate choice of phase space introduces several technical challenges that demand more sophisticated analytical treatment. Specifically, the space requires the development of new estimation techniques to handle memory-dependent functions, as well as careful consideration of the fading memory properties in stability proofs.
2. Preliminaries
- (i)
- Fix and let δ be the Dirac measure at (for the definition of the Dirac measure, see [21], p. 9). Then, for any and ,which means that .
- (ii)
- Let . Then, and, for any ,which also means that for .
3. Main Result
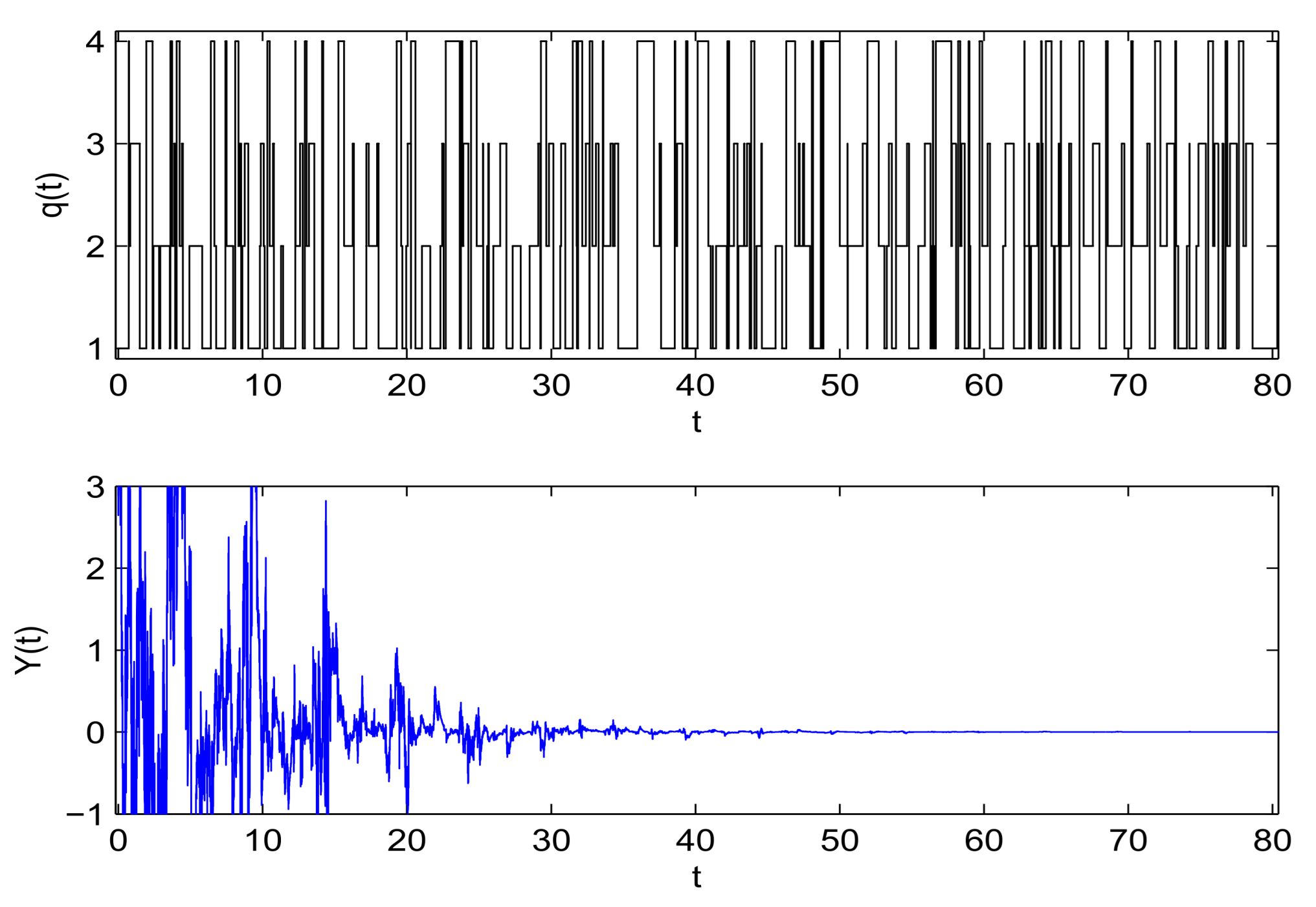
4. Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guedda, L.; Raynaud de Fitte, P. Existence and dependence results for semilinear functional stochastic differential equations with infinite delay in a Hilbert space. Mediterr. J. Math. 2016, 13, 4153–4174. [Google Scholar] [CrossRef]
- Shi, B.; Mao, X.; Wu, F. Stabilisation with general decay rate by delay feedback control for nonlinear neutral stochastic functional differential equations with infinite delay. Syst. Control Lett. 2023, 172, 105435. [Google Scholar] [CrossRef]
- Wang, L.; Li, J. Asymptotic Bismut formula for Lions derivative of McKean-Vlasov neutral stochastic differential equations with infinite memory. Commun. Pure Appl. Anal. 2025, 24, 1118–1139. [Google Scholar] [CrossRef]
- Yao, X.; You, S.; Mao, W.; Mao, X. On the decay rate for a stochastic delay differential equation with an unbounded delay. Appl. Math. Lett. 2025, 166, 109541. [Google Scholar] [CrossRef]
- Lu, C. Dynamics of a stochastic Markovian switching predator–prey model with infinite memory and general Lévy jumps. Math. Comput. Simul. 2021, 181, 316–332. [Google Scholar] [CrossRef]
- Lu, B.; Zhu, Q.; He, P. Exponential stability of highly nonlinear hybrid differently structured neutral stochastic differential equations with unbounded delays. Fractal Fract. 2022, 6, 385. [Google Scholar] [CrossRef]
- Zhao, S.f. On β-extinction and stability of a stochastic Lotka-Volterra system with infinite delay. Acta Math. Appl. Sin. 2024, 40, 1045–1059. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Tian, Y.; Wei, D.; Huang, Z. Sliding mode control for stochastic SIR models with telegraph and Lévy noise: Theory and applications. Symmetry 2025, 17, 963. [Google Scholar] [CrossRef]
- Hu, L.; Mao, X.; Zhang, L. Robust stability and boundedness of nonlinear hybrid stochastic differential delay equations. IEEE Trans. Autom. Control 2013, 58, 2319–2332. [Google Scholar] [CrossRef]
- Fei, W.; Hu, L.; Mao, X.; Shen, M. Structured robust stability and boundedness of nonlinear hybrid delay systems. SIAM J. Control Optim. 2018, 56, 2662–2689. [Google Scholar] [CrossRef]
- Shen, M.; Mei, C.; Deng, S. Analysis on structured stability of highly nonlinear pantograph stochastic differential equations. Syst. Sci. Control Eng. 2019, 7, 54–64. [Google Scholar] [CrossRef]
- Lu, B.; Song, R.; Zhu, Q. Exponential stability of highly nonlinear hybrid NSDEs with multiple time-Dependent delays and different structures and the Euler-Maruyama method. J. Frankl. Inst. 2022, 359, 2283–2316. [Google Scholar] [CrossRef]
- Xu, H.; Mao, X. Structured stabilisation of superlinear delay systems by bounded discrete-time state feedback control. Automatica 2024, 159, 111409. [Google Scholar] [CrossRef]
- Shi, B.; Mao, X.; Wu, F. Stabilisation of hybrid system with different structures by feedback control based on discrete-time state observations. Nonlinear Anal. Hybrid Syst. 2022, 45, 101198. [Google Scholar] [CrossRef]
- Hino, Y.; Murakami, S.; Naito, T. Functional Differential Equations with Infinite Delay; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Mei, C.; Fei, C.; Fei, W.; Mao, X. Exponential stabilization by delay feedback control for highly nonlinear hybrid stochastic functional differential equations with infinite delay. Nonlinear Anal. Hybrid Syst. 2021, 40, 101026. [Google Scholar] [CrossRef]
- Li, G.; Li, X.; Mao, X.; Song, G. Hybrid stochastic functional differential equations with infinite delay: Approximations and numerics. J. Differ. Equ. 2023, 374, 154–190. [Google Scholar] [CrossRef]
- Zhao, L.; Fan, Q. Delay feedback control based on discrete-time state observations for highly nonlinear hybrid stochastic functional differential equations with infinite delay. Int. J. Control. Autom. Syst. 2024, 22, 560–570. [Google Scholar] [CrossRef]
- Wu, F.; Yin, G.; Mei, H. Stochastic functional differential equations with infinite delay: Existence and uniqueness of solutions, solution maps, Markov properties, and ergodicity. J. Differ. Equ. 2017, 262, 1226–1252. [Google Scholar] [CrossRef]
- Zhen, Y.; Xi, F. Numerical solutions of regime-switching functional diffusions with infinite delay. Stoch. Model. 2024, 40, 617–633. [Google Scholar] [CrossRef]
- Kallenberg, O. Foundations of Modern Probability; Springer: New York, NY, USA, 2006. [Google Scholar]
- Hu, Y.; Wu, F.; Huang, C. Robustness of exponential stability of a class of stochastic functional differential equations with infinite delay. Automatica 2009, 45, 2577–2584. [Google Scholar] [CrossRef]
- Mao, X.; Yuan, C. Stochastic Differential Equations with Markovian Switching; Imperial College Press: London, UK, 2006. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Applications, 2nd ed.; Horwood Publishing: Chichester, UK, 2007. [Google Scholar]
- Zhang, M.; Zhu, Q.; Tian, J. Convergence rates of partial truncated numerical algorithm for stochastic age-dependent cooperative Lotka–Volterra system. Symmetry 2024, 16, 1659. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, C.; Shen, M. Structured Stability of Hybrid Stochastic Differential Equations with Superlinear Coefficients and Infinite Memory. Symmetry 2025, 17, 1077. https://doi.org/10.3390/sym17071077
Mei C, Shen M. Structured Stability of Hybrid Stochastic Differential Equations with Superlinear Coefficients and Infinite Memory. Symmetry. 2025; 17(7):1077. https://doi.org/10.3390/sym17071077
Chicago/Turabian StyleMei, Chunhui, and Mingxuan Shen. 2025. "Structured Stability of Hybrid Stochastic Differential Equations with Superlinear Coefficients and Infinite Memory" Symmetry 17, no. 7: 1077. https://doi.org/10.3390/sym17071077
APA StyleMei, C., & Shen, M. (2025). Structured Stability of Hybrid Stochastic Differential Equations with Superlinear Coefficients and Infinite Memory. Symmetry, 17(7), 1077. https://doi.org/10.3390/sym17071077





