Abstract
This research developed a complex physical and mathematical model of the flat rolling theory problem. This model takes into account the influence of many parameters affecting the roll’s gripping capacity and the overall stability of the entire rolling process. It is important to emphasize that the method of the argument of functions of a complex variable does not rely on simplifying assumptions commonly associated with: the linearized theory of plasticity; or the decoupled solution of stress and strain fields. Furthermore, it does not utilize the rigid-plastic material model. Within this method, solutions are developed based on the complete formulation of the system of equations in terms of stresses and strains, incorporating constitutive relations, thermal effects, and boundary conditions that define a well-posed problem in the theory of plasticity. The presented applied problem is closed in nature, yet it accounts for the effects of mechanical loading and satisfies the system of equation. For this purpose, such factors as roll geometry, physical and mechanical properties of the rolled metal (including its fluidity, hardness, plasticity, and structure heterogeneity), rolling speed, metal temperature, roll lubrication, and many other parameters that can influence the process have been taken into account. Based on the developed mathematical model, a new, previously undescribed force factor significantly affecting the capture of metal by rolls and the stability of the rolling process was identified and investigated in detail. This factor is associated with force stretching of metal in the lagging zone—the area behind the rolls, where the metal has already left the deformation zone, but continues to experience residual stress. It was shown that this stretching, depending on the process parameters, can both contribute to the rolling stability and, on the contrary, destabilize it, causing oscillations and non-uniformity of deformation. The qualitative indicators of transient regime stability have been determined for various values of the parameter α. Specifically, for α = 0.077, the ratio f/α ranges from 1.10 to 1.95; for α = 0.129, the ratio f/α ranges from 1.19 to 1.95; and for α = 0.168, the ratio f/α ranges from 1.28 to 1.95.
1. Introduction
An analysis of the findings presented in [1] indicates that the gripping ability of the rolls significantly influences the manifestation of the limiting deformation zone effect during plastic forming, the associated process parameters, and the stability conditions of the established rolling process. The complex nature of this effect is attributed to its multiparametric character and the non-uniform loading of different regions within the deformation zone.
The core premise of this study lies in a mathematical model that accounts for the varying force conditions across different subzones within the deformation region, particularly where counter-directional metal flows interact [1,2]. These interactions result in fundamentally different stress distributions. The mutual penetration of these force zones within a unified deformation field alters the stress state of the material within the plastic flow region. This interaction has been corroborated by experimental investigations of contact stresses reported in the literature [3,4]. Figure 6, published in [1], illustrates the combined influence of factors such as the coefficient of friction, gripping angle, and the geometric shape factor of the deformation zone. The diagram reveals distinct profiles of normal contact stresses in the lagging and leading zones. The stress curve is predominantly concave in the lagging zone, whereas it becomes convex in the leading zone. Tangential stresses, shown in the right-hand graph, intersect the zero axis, indicating the presence of a forward slip zone and, consequently, the occurrence of metal gripping by the rolls. At minimal friction coefficients, the standard stress curve remains concave across the deformation region, reflecting the presence of longitudinal tensile stresses. Since these stresses do not exceed the material’s yield strength, plastic deformation is absent, signifying a loss of rolling process stability. Under these conditions, the tangential stress line also fails to intersect the zero axis, confirming the absence of forward slip and the resulting instability.
This analysis suggests the necessity of evaluating the gripping ability of the rolls and process stability using a dual-parameter approach. Specifically, these factors include: (1) the ratio between the normal (ejecting) force and the frictional (gripping) force in the lagging zone, and (2) the magnitude of the tensile force generated in the same region. The tensile stresses result from the opposing actions of the normal pressure and the retractive frictional force at the entry point of the deformation zone.
This tensile force, arising from the lagging zone, shortens the length of the forward slip zone and reduces contact pressure in the reverse-flow region. The interaction between these opposing forces is particularly pronounced during the initial stages of deformation, which substantially influences the stress profile.
Thus, the deformation zone is subjected to both vertical compressive forces from the normal and frictional components, as well as longitudinal tensile forces originating in the lagging region. The longitudinal tension and the ratio of normal to retractive forces collectively determine the rolling process’s stability and the rolls’ metal gripping effectiveness.
It is important to emphasize that metal capture by rolls is, fundamentally, a process of forming a stressed and deformed material state within a constrained space under prescribed process parameters. Stress distributions are analyzed across the entire length of the deformation site. To better visualize the behavior during gripping. The limiting deformation zone is the region where rolling instability becomes apparent. In contrast, the attainability zone refers to the area affected by tensile stresses from the lagging region that influence both force and kinematic process parameters.
As shown in Figure 6 [1], under conditions of a small gripping angle (0.129 radians) and low friction coefficient (0.05), rolling instability occurs due to the failure of metal capture. This is illustrated by the tangential stress profile that does not intersect the zero axis. In the absence of plastic deformation and effective gripping, this visualization of the process stress state is made possible through the developed mathematical model of a unified deformation zone, incorporating the interaction of counter-flowing metal streams under asymmetric loading [5,6,7,8,9,10].
This work is a continuation and development of the method of argument of functions of a complex variable, a method for solving continuum mechanics problems, applied to applied problems. It is a fundamental development that covers a range of solid mechanics areas in different states and areas of practical tasks. The first attempts to formulate particular provisions of the method were published in [11,12]. Then, the main development of the method was in the works [5,6,7,8,9,10,13] and others, where no particular questions of the theory were formulated, but general approaches that make it possible to use the invariance of differential relations in continuum mechanics. Based on the invariance of transformations, articles have been published on problems in the theory of plasticity [1,2,9], theory of elasticity [5,6,7,8], and problems of dynamic processes [5]. At the fundamental level, practical issues of geomechanics [6,10], the mechanics of loading beams, with complex boundary conditions, and in different reference frames [8], the wave theory of the dynamic problem [5], with applications to rotational vibrations in the main line of a rolling mill, were considered.
The accelerating pace of technological progress is radically changing the conditions of applied problems. We no longer deal with simple boundaries and conditions; they are becoming increasingly complex and interconnected. This complexity requires a change in our approach to modeling [14,15].
The mathematical theory of plasticity is based on specific ideas, covering its range of applied problems; it allows the generalization of these solutions by approaches inaccessible to other schemes [16]. The problem is the non-linearity of the problems of plasticity theory, including boundary conditions, the complexity of their analytical solution, and generalization.
The most significant difficulty in solving problems of the theory of plasticity belongs to spatial problems [17], especially if a closed problem is considered in the formulation and solution. It is very difficult to reconcile the result obtained in terms of stresses and deformations (strain rates). Experience shows that decisions lose their relevance due to neglecting lost schemes and adopting unreasonable simplifications.
In [18], the loading of metal during deformation is investigated. However, loadings can be considered somewhat more broadly, for example, asymmetric and symmetrical, which increases the range of issues being addressed.
When setting problems in mechanics, systems of equations that can be attributed to the equations of mathematical physics are considered [19]. First of all, these are hyperbolic, elliptic, and parabolic partial differential equations. The greatest degree of generalization of solutions is considered precisely in mathematical physics. These include methods of separation of variables, characteristics, Riemann, Fourier, Dalamber, integral transformations, etc.
In many solutions of the theory of plasticity and elasticity, the method of stress functions is used [20,21], which shows a reliable result (it can be effectively used, with certain simplifications, as a test of the theory of the argument of functions of a complex variable).
The scientific literature presented in studies [22,23,24,25,26] is devoted to the investigation of the stress–strain state of plastic media, addressing a range of fundamental challenges and proposing novel approaches to their resolution. In particular, the work in [22] identifies significant discrepancies between theoretical models and experimental data in the description of plastic deformation. These inconsistencies arise due to the mismatch between stress and strain fields within the material. The authors of [22] propose an original explanation of these contradictions based on the effect of twisting of conjugated slip planes. This finding offers a fundamentally new perspective on the process of plastic shape change, opening up new possibilities for modeling and predicting material behavior.
Special attention is given to the interpretation of processes involving multidirectional metal flow, such as rolling, where the proposed approach ensures not only qualitative but also quantitative agreement between theoretical predictions and experimental observations. Furthermore, this method may lead to the development of advanced metal processing technologies that improve both efficiency and the quality of the final product. At a detailed level, the analysis incorporates complex microstructural interactions, taking into account the influence of crystalline structure and lattice defects on the macroscopic behavior of the material.
Study [23] makes a significant contribution to the methodology of solving plastic deformation problems. The authors employ the method of additional variables, which is analogous to the introduction of argument functions in differential equations. This approach enables the linkage between different types of differential equations, thereby considerably expanding the mathematical toolkit available for analyzing stress–strain states. Despite its notable effectiveness, the application of this method remains limited at present.
Cyclic loading is shown in the case of a simple shear, which finds a corresponding response of internal stresses [24]. The basic trigonometric function is introduced into consideration. Its possibilities are shown when boundary conditions change, but it does not match with other basic functions.
Article [25] shows an example of applying the argument of a function using a coordinate reference system, which significantly expands the possibilities of the solution. A distinctive feature of this approach to solving a closed problem lies in the presence of identical functional variables within the stress, strain, and temperature fields, appearing in specific combinations. Another important aspect of the solution methodology is the introduction of two function arguments, which represent trigonometric and fundamental substitutions. These substitutions ultimately serve to close the formulation, ensuring a complete and self-consistent solution to the problem.
They can be used as closing functions for solving the problem in the future. In [26], the loading at the base of a certain discontinuity was studied. The heterogeneity of the stress state was characterized by trigonometric and exponential expressions. The proposed combination of functions makes it possible to expand the scope of their application through simplifications of boundary conditions.
The present study examines a solution approach based on the method of fundamental substitution, as described in detail in [27]. However, a review of the literature reveals substantial differences in the application of this method. In particular, study [28] proposes the use of an exponential function as the argument, which unfortunately limits the applicability of the method to the current problem. The narrow specialization of this approach prevents its adaptation to more general cases.
An alternative methodology is presented in [29], where the use of the R-function method is explored. This approach could potentially serve as a theoretical foundation for the application of argument functions, offering a more flexible and universal analytical framework. However, further analysis indicates that the R-function method is primarily employed in a broader range of problems, including variational principles in mechanics. As such, its application to the current problem may be excessive and not conducive to achieving an optimal solution. Moreover, the direct use of R-function in this context is not straightforward and would require additional investigation.
Another approach, discussed in [30], is based on the use of differential relations to transition from one variable to another. While this method is effective in certain specific cases, it is not well-suited for generalizations involving argument functions. Its limitations stem from the fact that the differential relations used in [30] lack the necessary flexibility to address more complex, nonlinear scenarios that often arise when argument functions are employed.
Study [31] addresses the mathematical justification of boundary conditions using the collocation method. This is a particularly important aspect, as the accurate formulation of boundary conditions remains one of the main challenges in continuum mechanics.
In conclusion, it should be emphasized that the trends in improving the theoretical and technical issues of continuum mechanics are determined by areas that are based on generalizations and combinations of approaches of different schemes, methods, technologies, and development prospects. In engineering, the most promising solutions take place at the junction of directions [14], in the theory of solved problems, obtaining not the solutions themselves, but the conditions of their existence [30]. Achieving such a fundamental result is justified by the fact that the reliability of the data obtained and the possibility of obtaining justifiable solutions in general are enhanced.
In this regard, a complex technological problem arises related to the development of rolling schemes that occur during the formation of an exciting friction force and a buoyant force of normal pressure.
This possibility is achievable when the process modes are related to the stability parameters of the rolling process.
The purpose of this study is to develop a comprehensive theoretical and practical framework for understanding the mechanics of metal capture by rolls, the conditions ensuring minimal process stability, and the dominant influence of stress-reducing factors. This is achieved through the resolution of a closed planar problem within the theory of plasticity, taking into account the complex interplay of multiparametric factors that govern the plastic deformation process.
2. Materials and Research Method
The object of the study is the stress state of the metal under conditions of deformation, force, and geometric impact on the gripping ability of rolls and the stability of the rolling process.
The hypothesis of the study is a new model of the gripping ability of rolls and the stability of the process under the influence of tensile stresses from the lagging zone, combining a visual assessment of the result from the tangential and normal stresses.
The assumptions of the study are to consider a new process of minimal rolling stability and the process of suppressing the effects of increasing stresses on the parameters of plastic forming.
The present work is based on a novel method for solving problems in continuum mechanics—namely, the method of argument functions of a complex variable. A key feature of this method is its unified approach to solving a wide range of both theoretical and applied problems. These include problems in elasticity theory, plasticity, and the theory of dynamic processes. The method can be considered a fundamental direction in the ongoing development of continuum mechanics.
3. Development of a Physical and Mathematical Model of the Planar Rolling Theory Problem Under Conditions of Multiparametric Factors Affecting the Capture and Stability of the Process
The work [1] shows the effect of asymmetry of deformation, as a controlling factor, on the parameters of plastic forming. The effect is revealed, which manifests itself in a decrease in the force load with an increase in the deformation effect. It determines the zone of achievability of the limiting deformation focus, in conditions of manifestation of the effect through loss of stability or the process of metal slipping in the rolls. The analysis showed that the capture of metal by rolls is a determining factor in the implementation of this phenomenon. In this regard, there is a need to study the influence of the multicomponent rolling process on the conditions and parameters of the formation of the gripping capacity of the rolls, and the possibility of realizing the stability of the process. For the sake of completeness of this problem, the entire focus of deformation is considered, and not a part of a limited space.
The following approaches to solving the applied problem are considered. Fundamental and trigonometric substitution is used. The statement system of equations has the form [9]:
where —the normal stress; —the tangential stress; k—the resistance to plastic shear (variable); and —the linear and shear rates of deformation; T—the temperature of the metal at a given point.
The conditions at the boundary are set in stresses and through the rate of deformation:
where —the shear strain rate characterizing the boundary condition; —the shear stress characterizing the boundary condition.
Solving the system of Equation (1) and boundary conditions (2) allows us to obtain a general result in terms of stresses and strain rates, which consists of the fact that the deformation and force fields contain the same sets of functions that allow us to obtain a mathematical model of the plastic medium, or simply close the problem in terms of stress fields and strain rates. In this formulation, the stress solution is supported by the solution of the deformation problem, which increases the reliability of the result and meets the energy conditions of interaction in the deformation site [9].
The previously obtained result from [9] is used to obtain the result of an applied asymmetric problem of the theory of plasticity, with a limited force component of the process. In this case, the formulation is simplified, and the task is completed by the power characteristics of the process.
Taking into account (1) and (2), we have the following simplified formulation of the stress problem:
Differential equations of equilibrium:
The Huber-Mises plasticity equation:
Differential equation of continuity of stress deformations:
boundary conditions:
where —the average normal stress; —a constant value determined by the problem condition.
The deformation component of the process, the equation of continuity of deformation entered the force part through the average normal stress.
Expression (6), for boundary conditions, relates the components of the stress tensor to the tangential contact stress. This representation of the contact tangential stress (6) introduces great uncertainties into the process of obtaining the result. To linearize the boundary conditions and the solution itself, the following record of the boundary conditions is taken:
where —the intensity of tangential stresses; —an unknown coordinate function or the first argument function; —the angle of inclination of the site. Comparing formulas (6) and (7), it can be shown that the tangential stresses for boundary conditions (6) and the difference for normal stresses are related by the following expressions:
In [32], the well-known differential equation for determining tangential stresses is expressed in terms of the intensity of tangential stresses :
From (8) and (9), it becomes clear that the transformations are determined by expression (7). The trigonometric substitution of the relation under the radical has been performed, which made it possible to linearize the right side of expression (9) and linearize the boundary conditions. This approach is of interest because, for linear partial differential equations, a fundamental substitution is allowed [33], accompanied by some special features. These features are that the exponent is an unknown function. Hence, we have:
where —an unknown function or the second argument is a function. Taking into account substitutions, expressions (8) and (10) can be written as:
Taking into account the transitions (8), (10), (11), the statement of the problem is specified: what mathematical relations should satisfy the argument of function (8) and (10) to close the solution of the problem, turning the hyperbolic Equation (9) into an identity. Generalized fundamental approaches to solving problems in the theory of plasticity using a function of a complex variable are of interest [34]. Then, substituting expressions (8) and (10) in (11), we express the tangential stress in terms of a function of a complex variable, obtaining:
Using dependence (12) and Equation (9), we express the differential equation in terms of a complex variable:
Equation (13) has a number of features. In the process of transformations, the same brackets and appeared for different operators, and the conditions for the existence of the variable Hσ were determined for this equation. For the purpose of simplification, we can proceed to the Cauchy–Riemann relations and Laplace equations, taking the above brackets equal to zero, we have:
The next feature of Equation (13) is the variable Hσ, which can have the following function:
where C0 and C1—constants that determine the stresses at the entrance and exit from the deformation site; l—the length of the deformation site.
Variable (15) identifies the process of asymmetry along the deformation source, which allows you to set different boundary conditions at the entrance and exit from the deformation source.
To solve this problem, it becomes necessary to develop a theory and mathematical model of the process that takes into account the influence of multicomponent factors on the gripping ability of rolls.
Substituting the Cauchy–Riemann relations (14) into the differential (13), we make sure that it turns into an identity, and this allows us to determine the magnitude of the tangential stress.
The basic expression (11) and the conditions for the existence of the solution (14) define the tangential stress function in the following form:
One more feature of the solution should be emphasized. In Equation (13), the derivatives of the variable Hσ in coordinates were determined by dependence on the Cauchy–Riemann relations. This made it possible to exclude them from further consideration and simplify the task.
From the equilibrium equations (1), with a known functional dependence (16), it is possible to determine the normal components of the stress tensor. After separating the variables of the equilibrium equations, we have:
Integrating, using the equation of continuity of deformations (5), we have, [1]:
by
Solution (17) satisfies the equilibrium equations, differential Equation (9) or (13), and the equation of continuity of deformations (5). To what extent is the Huber–Mises plasticity condition satisfied? Substituting expressions (17) into Equation (4), taking into account we obtain:
If the Huber–Mises plasticity condition is fulfilled, we have an identical satisfaction of the plasticity condition for the following planar problem, (1):
Result (17) completely satisfies the system of Equations (3)–(5) in an analytical form. Thus, on the basis of solving a closed problem of the theory of plasticity, a particular solution of problem (17) is presented in a closed form.
Based on the solution of the closed problem of the theory of plasticity (17), using defining boundary conditions, there is a need to develop and develop a mathematical model for a stress-state analysis under conditions of multicomponent influence on the gripping ability of rolls and the stability of the rolling process.
The need to study the effect of multicomponent rolling is associated with an additional study of the effect of plastic forming, in conditions of reduced force exposure by increasing strain loading.
There are certain limitations of the process associated with a single-zone focus of deformation with the stability of the process implementation on the one hand, and the implementation of the effect of plastic forming on the other.
The main issue of the problem is to identify the conditions for the existence of a single-zone deformation center during a stable rolling process.
Let us use solution (17) and expression (15):
by
To determine the integration constants, we use the boundary and obvious conditions in the deformation focus. The origin is placed in the middle of the deformation focus, and the axis of the abscissa is shown in the direction of rolling. By
where and , and , and , and and —the values of the functions and at the edges of the hearth; shear strain resistance; coefficients that take into account the effects of support and tension during rolling at the entrance and exit from the hearth of deformation. When substituting boundary conditions (19) into (18), we have:
Comparing expressions (18)–(20), we conclude that the data obtained allow us to consider the asymmetry along the length of the deformation site and take into account the change in the stress state.
For further analysis of the stress state under asymmetric loading (18), it is necessary to determine the argument of the functions and . The mathematical model provides such an opportunity. Solving the Laplace equations and matching the result with the Cauchy–Riemann conditions, we have the first argument function for the trigonometric dependence:
where —the angle of inclination of the contact site; —the position of the neutral segment relative to the origin; and and —constants that determine the values of trigonometric functions along the edges of the deformation site, taking into account the influence of the kinematics of the process on the force characteristics of the deformation site.
Let us review and comment on the use of boundary conditions that determine the reliability of qualitative and quantitative indicators of the problem being solved. Let us look at this in more detail.
Coordinates of the point at the exit from the deformation site ; the angle of inclination of the platform at the exit from the deformation center ; the kinematic component in the complex of parameters at the exit from the deformation site ; friction index and grip angle and ; coordinates of the point at the entrance to the deformation site ; the angle of inclination of the site at the entrance to the deformation site ; and the kinematic component in the complex of parameters at the entrance to the deformation site . Substituting the boundary conditions in expression (21), we obtain the following:
Through constant integrations (22), the nature of the stress distribution in the hearth and the kinematic rolling conditions are influenced, which are indicated to a certain extent by a neutral angle. This adds to the multicomponent nature of the process to assess the stress state, including the asymmetry of the distribution along the deformation site.
As the analysis shows, expressions (22), to some extent, characterize the interaction of lagging and advancing zones. Taking into account the Cauchy–Riemann relations and the Laplace equations (17), the function is determined as follows:
Taking into account (21) and the boundary conditions, a neutral angle is determined as follows, indicating the position of the neutral section in the deformation focus:
where —the kinematic component; —relative compression.
In the kinematic component (24), the friction index, taking into account the obvious conditions of the deformation site, can be represented by:
where a and b—constants characterizing the coefficient of friction at the entrance and exit from the deformation site; —coefficient of friction.
When solving kinematic problems, it becomes necessary to solve the kinematics of the process when the advance zone is zero. In this case, we have the following relationship between the coefficient of friction and the angle of capture:
We determine the coefficient of friction to be as follows:
For , we have as follows:
Using expression (23), taking into account the boundary conditions, the constant integrations of and are determined as follows:
Substituting expressions for , taking into account expressions (20), the working formulas are obtained for calculating the stress state of the strip during rolling, including c for a single-zone deformation focus (with limited gripping capacity of the rolls):
The relative contact-specific pressures were calculated using formulas (28). Figure 1 shows the stress distribution along the length of the deformation site depending on the shape factor l/h, [1], which is awaiting its physical and theoretical substantiation.
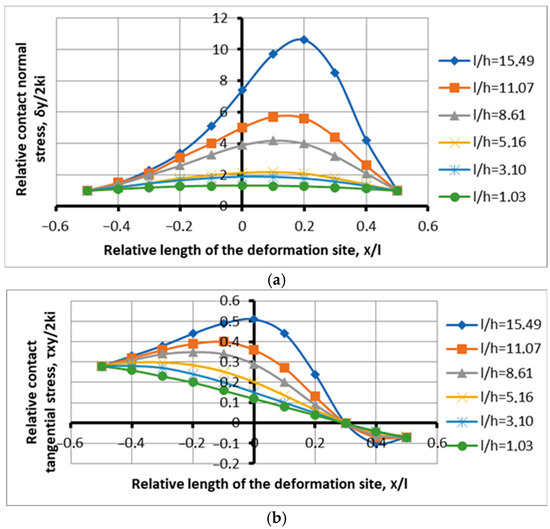
Figure 1.
Distribution of contact stresses along the length of the deformation site depending on the shape factor at l/h = 1.03–15.49; α = 0.077; and f = 0.3: (a) distribution of normal stresses; (b) distribution of tangential stresses.
There is a change in the stress state in the treatment area depending on the factor of the deformation focus shape. The concavity and convexity of the contact stress diagram are indicated, the position of the maximum normal stresses along the length of the deformation focus is changed, and the magnitude of the contact stresses is changed. On the side of tangential stresses, the stability of the rolling process is fixed by the presence of an advanced zone.
Based on the analysis of the data, in particular the approach, the equivalence of the states of influence of the shape factor and stretching from the lag zone is established, which determines the kinematics of the process and the force characteristics of the compression focus. With this formulation of the question, this statement must be substantiated and proved. Prove by identifying the process features through the gripping ability of the rolls and the stability of the rolling process.
4. Investigation of the Process of Minimal Stability and the Process of Partial Suppression of Zeroing Stress Factors Under Conditions of Multiparametric Influence
In this regard, based on the work in [1] confirming similar approaches to the effects of plastic forming, the possibilities of defining the process through the factor of multicomponent and the features of the gripping ability of the rolls are considered.
In the proposed work, the processes of metal capture by rolls, the conditions for the implementation of a stable rolling process are investigated, depending on a number of determining factors: contact friction (through the coefficient of friction); compression; and shape factor. Obviously, these factors will also have an impact not only on the gripping ability of the rolls, but also on the realization of the achievability of the effect of the limiting deformation focus.
The need to review the conditions for realizing the gripping ability of rolls, the conditions for the loss of stability of the process, is explained by the fact that existing developments for capturing metal with rolls [35] are insufficient, not explaining many theoretical and practical provisions of the process. These include the following: the concavity of the normal stress plots in the lag zone and along the entire length of the deformation site, the absence of plastic deformation when the rolls slip, an explanation of the mechanics of negative advance [36], the absence of a lead zone when realizing the gripping ability of the rolls, the phenomenon of tightening the roll height before entering the deformation site [37], etc.
In this regard, the consideration of these issues is carried out in greater detail. It is known that the initial capture of metal by rolls occurs under conditions when the pulling forces of contact friction are not less than the normal pushing forces from the rolls [35]. At the same time, the capture of metal by rolls during a steady process can be greater than the initial angle of up to two values of the primary capture. It follows from this that, having overcome the capture at the initial moment of time, it is possible to double the capture angle without losing the stability of the process. In [1], it was proposed, based on the solution of the planar problem of the theory of plasticity, to characterize the trapping ability not only by the contact plots of tangents, but also by normal stresses. Following the work in [1], it was shown that the loss of stability is determined not by one, but by two factors—the capture and the degree of stretching of the lag zone in the treatment area.
In this assessment, the influence of these two parameters on the stability of the process must be guided by tangential and normal stresses reacting to the stretching of the strip in the lag zone.
Tangential stresses vary along the length of the deformation source with a transition in the neutral section through the zero line. If there is no transition through zero, then, there is no advance zone, and a loss of stability should occur, i.e., a slip. Normal stresses organize another criterion for assessing the stability of the rolling process—this is rolling under conditions of back tension of the strip from the lag zone, which affects the stability, shape of the plots of normal contact stresses, and the magnitude and kinematics of processing. The concavity of the plot is a qualitative and quantitative assessment of the tensile effect in the lag zone or along the entire length of the deformation focus. Such approaches are known in the literature, but the stretching of the strip was not linked to the stability of the process, with the gripping ability of the rolls. Attention should be paid to the fact that a decrease in contact stresses below the permissible limits, i.e., the concavity of the relative stress diagram of less than unity or stresses less than the yield point, indicates the absence of plastic deformation. Then the rolling process, as such, does not exist, there is no capture, there is no stability process.
This connection of strip stretching with plastic processing, stability of the process, and the gripping ability of the rolls is a defining and indicative reason for the emergence of a new process quality, additional force, and kinematic effects on the plastic forming zone.
It follows from this that the processes contributing to the presence of deformation accompany the processes of metal capture by rolls. The presence of plastic deformation is obviously determined by the multicomponent effect on the compression zone.
There are examples of the influence of factors ensuring the presence of a roll forming at the time of metal capture by rolls. It was shown in [36,37] that at the entrance to the deformation site, there is a strip tightening along the height of the rolled product. This indicates the presence of tensile stresses in the lag zone along its entire length, and the greater the magnitude, the thinner the strip. Thus, in the lag zone, the strip is stretched in height, which corresponds to the physical model of operation [1]. The following is an example of plastic deformation, which has increased the capture of metal by rolls. This is the impact plastic impact of the workpiece on the contact surface of the rolls. When the workpiece comes into local contact with the rolls at the entrance to the deformation site, local plastic deformation occurs, which ensures that the metal is captured by the rolls [38].
Figure 2 presents experimental data on the plastic flow of metal during the periodic rolling of truck axles under conditions involving a gradual transition from metal capture by the rolls to the subsequent stage—periodic rolling along the length of the deformation zone. The data were obtained using high-speed video recording of the periodic rolling process [39]. Rolling is carried out using rolls with a variable radius, resulting in a gradual increase and decrease in reduction along the deformation zone. The process is captured at the moment when the maximum radii of the upper and lower rolls are aligned along a straight line. At this point, the reduction at the inflection zone reaches its peak, significantly influencing the metal flow behavior. The material spreads from the inflection zone in opposite directions, as evidenced by the distortion of the coordinate grid. From the standpoint of the rolls’ gripping capacity, a gradual transition is observed—from the initial metal capture by the rolls to the stage of intensive plastic deformation—while maintaining a stable rolling process. It is clearly shown here that the transition from initial capture to the implementation of a stable process occurs due to increasing plastic compression.
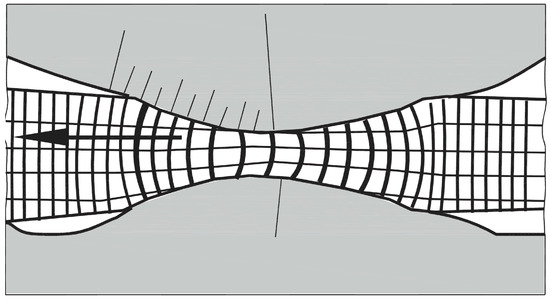
Figure 2.
Periodic rolling. Plastic zone from primary capture to maximum compression with a gradual transition along the length of the deformation site.
The next argument in favor of the deformation component during capture is rolling with a negative advance [36]. These studies have shown that stable rolling occurs not only in the absence of an advance zone, but also under process conditions when the circumferential speed of the rolls is greater than the speed of the strip exit from the deformation zone. Thus, plastic deformation of the strip is allowed beyond the known limits of initial metal capture by rolls. In this case, the fact of such a phenomenon is important. Finally, it should be noted that the factors contributing to the presence of plastic deformation at the moment of capture are the parameters of the reinforcement process. It must be taken into account when assessing the impact on the gripping ability of the rolls and the loss of rolling stability.
Based on the proposed physical model of the trapping ability of rolls, and the method of solving problems of continuum mechanics, the argument of functions, the theoretical part, and the mathematical model on the verge of stability of the process were worked out. There was an opportunity to look at where the roll slip partially appears. In this state, which represents the stage of interaction of the multidirectional forces of the deformation site, signs of additional impact on the deformation site can be detected. They manifest themselves in the zones of achievability of the limiting deformation focus, with the parameters of the process realization.
It is possible to visually assess the stress state of the strip during excessive metal capture by rolls. At the same time, it should be borne in mind that the loss of stability of the rolling process is the slipping of metal in the rolls; the maximum capture of metal by rolls is the capture when the stability of the process is lost; and the extreme capture of metal by rolls is the capture of metal by rolls beyond the limits of the stability of the process. Although the extreme grip involves roll slipping, however, the working option is stress distribution during roll slipping, if the mathematical model of the process allows it.
Figure 3 shows diagrams of the extreme capture of metal by rolls at different values of the shape factor, and a coefficient of friction of 0.015, less than the angle of capture of 0.077. Their ratio is significantly less than 1, equal to 0.195. If this ratio is equal to one, the gripping capacity of the rolls is fixed under stable rolling conditions. Since the process is prohibitive, there is no capture of metal by rolls, which is confirmed by the diagrams of tangential and normal stresses, Figure 3.
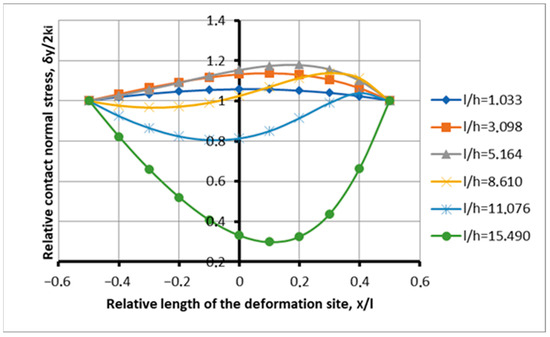
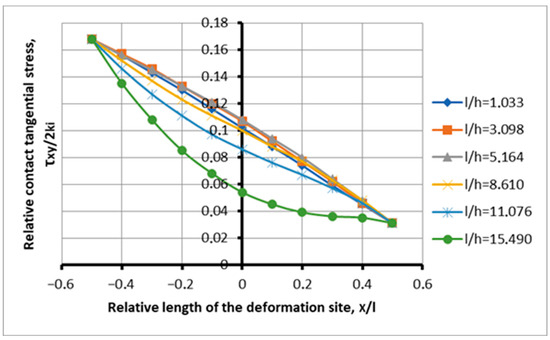
Figure 3.
Distribution of contact stresses along the length of the deformation site under conditions of excessive metal capture by rolls at l/h = 1.033–15.49; f = 0.015; and α = 0.077.
Deflections of the normal and tangential stress plots are observed, which indicate the presence of tensile stresses from the lag zone. The relative tangential stresses have a maximum value at the entrance to the deformation zone (0.168) and a minimum value at the exit from the lag zone (0.031), without reaching the zero line, therefore, without crossing it. The deflections of the plots occur for the same values of tangential stresses as normal ones. At the same time, for plots 1.033–5.164, the limits of variation of deflections of tangential stresses remained unchanged because there are no changes in friction, conditions of metal capture by rolls.
From the analysis of the exorbitant process, it follows that high strips react poorly to the effect of tensile stresses from the lag zone, and in the case of metal capture by rolls, the deflections of the diagrams showing the effects of this stretching will be minimal or will be absent altogether.
The reaction of high strips to stretching, in an exorbitant process, to some extent reflects the mechanics of the negative advance process, which allows for the absence of an advance zone when metal is captured by rolls and the presence of capture with negative metal flow kinematics. This is confirmed by experimental studies in [35,40]. Consequently, there are processes in which a steady rolling process takes place not only with an advance of zero, but also in processes in which the circumferential speed of the rolls is higher than the speed of the strip at the outlet of the deformation zone. Thus, the conventional criterion for the rolls’ gripping ability—defined by the ratio between the normal expelling force and the frictional gripping force—does not fully capture the complexity of the process. To adequately explain the aforementioned characteristics, an additional factor must be considered, the presence of a tensile force acting from the lagging zone.
The influence of process kinematics under conditions of extreme (limit) gripping is considered, taking into account the boundary conditions and the leading zone through the neutral angle of bite. The multidirectional effect of forces on the deformation source creates a back tension on the deformable strip. The back tension affects not only the force, but also the kinematic parameters of the process [41]. Thus, two factors are formed related to the loss of stability of the process—this is capture, and the process is determined by the action of tensile forces from the lag zone. Eventually, a process is formed with the concavity or convexity of the normal stress plots. The modes presented above have the same physical basis and model, they may not coincide in terms of interaction conditions, they may counteract each other, or coincide. The stretching factor forms the process of the limiting focus of deformation, which is a fundamental indicator of the effect of plastic forming. It should be added that the proposed approach does not pretend to make fundamental changes in the theory of the gripping ability of rolls at small gripping angles and friction coefficients. However, it captures the appearance of a new quality in the extreme capture, which to a certain extent characterizes the process of plastic forming in conditions of negative advance or advance tending to zero.
As for the stability of the process, the diagram of the loss of stability from tangential stresses repeats to a certain extent the diagram of the loss of stability of normal stresses. The partial or complete concavity of the normal stress plots relative to unity (Figure 3) is repeated partially or completely by the concavity of the tangential stress plots.
Figure 4 shows the rolling process with a minimum gripping angle of 0.077, but with an increased coefficient of friction of 0.085, which ensures primary gripping in the absence of an advance zone. Such a process turned out to be possible after the second factor of influence or, the factor of the action of stretching on the parameters of the stress state in the deformation site, was introduced into consideration. From the preliminary analysis, there is no capture for tangential stresses, and for normal stresses, capture is ensured by the presence of plastic deformation in the lag zone (there is no deflection of the plot below the limit line, the ordinate of which is equal to unity). The ratio of the coefficient of friction and the angle of capture, which forms the primary capture, is 1.10. Consequently, the capture of metal by rolls is ensured in the absence of an advanced zone. It follows from this that the advance zone is not a criterion for the gripping ability of the rolls.
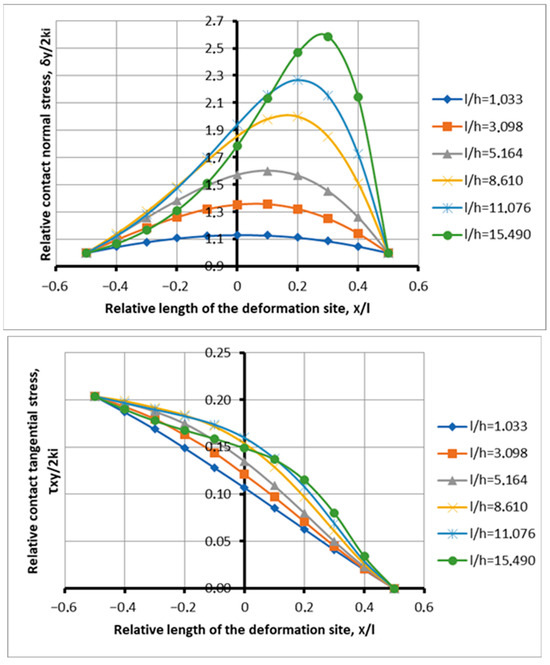
Figure 4.
Distribution of contact stresses along the length of the deformation focus when metal is captured by rolls under transient conditions at l/h = 1.033–15.49; f = 0.085; and α = 0.077.
It follows from the analysis that with an increase in the shape factor from the values of 1.033 to 5.614, the contact maximum normal stresses increase within the range of 1.132–1.602. Subsequently, there is an increase in stress to 1.998, for a factor of 8.61, and a further increase to 2.586 for a factor of form 15.49. At the same time, there is a decrease in the load in the lag area. For a shape factor of 15.49, up to three curves down, including a shape factor of 3.098 (Figure 4).
This confirms, for the most part, the effect of plastic forming of the deformation site, i.e., a decrease in the force load with an increase in the deformation component (the deformation component of the process, the shape factor of the deformation site).
In comparison, with the process indicated in Figure 4, the main factors of influence that determine the ambiguity of the metal capture process by rolls are confirmed and strengthened. On the one hand, the coefficient of friction is greater than the angle of capture, which characterizes the stability of the process. On the other hand, the absence of an advanced zone characterizes the loss of rolling stability. At first glance, this contradiction can be explained by introducing the lag zone stretching factor, which characterizes the stability of the rolling process. The first three thicknesses (shape factor 1.033; 3.098; and 5.164), Figure 3 and Figure 4, show that with small gripping angles and small values of the coefficient of friction, the stretching factor does not work. When rolling medium and thin strips, the effect of the tensile stress in the lag zone increases, and contact stress diagrams fail, resulting in thinner strips. Maximum stresses steadily respond to an increase in the coefficient of friction (1.132; 1.353; 1.602; 1.998; 2.269; and 2.586), and the stresses in the lag zone steadily respond to an increase in the tensile stresses of the opposing forces (the abscissa axis is 0.2 at 1.107; 1.261; 1.383; 1.485; 1.474; and 1.31). The plots of the curves, which, for normal stresses, show the zones of achievability of the limiting deformation focus, but do not exceed the permissible lines of stability of the process.
Of interest is the combination of the zero advance zone and the capture of metal by rolls (Figure 4). In accordance with the physical capture model, with the corresponding ratio of the coefficient of friction to the angle of capture greater than unity (1.10), the capture of metal by rolls is ensured. At the same time, there must be a zone of advance. The question arises why, with an increase in the coefficient of friction, the tensile force increases, and not the advance zone, which is mutually opposite. The tensile force arises from the action of two opposing friction forces and normal pressure in the lag zone. There is a posterior tension from the side of the entrance to the deformation site. With an increase in the gripping force, the stress state within the deformation zone is restructured; the tensile force originating from the lagging zone is neutralized, and the leading zone expands. The transverse metal flow is not considered in this analysis. However, taking into account the kinematics of the metal flow, the back tension at the entrance to the deformation zone reduces the advance zone. In addition, with a steady process, based on the law of action and counteraction, the oppositely directed force of normal pressure increases, increasing the tensile force. With a low coefficient of friction and an increased tensile force, it becomes sufficient to eliminate the advance zone. It can be assumed that with a significant increase in the coefficient of friction, the trapping ability of the friction force increases and becomes sufficient to neutralize the tensile force.
The peculiarity of this analysis is that such a process can exist in principle. Due to the increased tensile load in the lag zone, with an increase in the gripping coefficient of friction, conditions arise for gripping in the absence of an advance zone. Indeed, the rear tension changes the kinematics of the deformation focusing on the direction of reducing the advance zone (exit from the rolls). Thus, when the tensile force is introduced into consideration, it becomes possible to evaluate additional effects with the adjustment of the capture process under the action of tensile stresses. Therefore, the process under consideration, with a zero advance zone, can be characterized as a transitional one, since it contains elements of a process with loss of stability and elements of a stable rolling process. Obviously, the concept of the rolling transition process should be expanded, linking it to the effect of the limiting deformation focus.
The next feature is the implementation, within the limits of this process, of the zone of attainability of the limiting deformation focus. This is clearly confirmed by the plots of the curves in Figure 5, even with the minimum value of the capture angle. Such a transitional process is a kind of guideline in the design of a rolling force circuit using the effect of plastic forming. As a result, a transitional process with minimal stability is shown, or a regime on the verge of stability of the process.
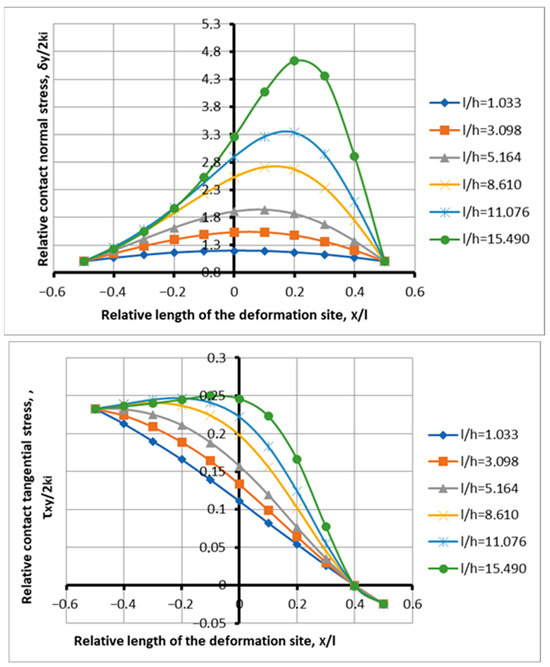
Figure 5.
Distribution of contact stresses along the depth of the deformation center during the capture of metal by rolls under the conditions of the determining process at l/h = 1.033–15.49; f = 0.15; and α = 0.077.
Figure 5 shows the distribution of contact stresses depending on the shape factor with a minimum capture angle of 0.077 radians, with the presence of a full-fledged advance zone, determined by the coefficient of friction equal to 0.15.
This is significantly higher than the previous figures for friction (Figure 5). The ratio of the coefficient of friction to the angle of capture in this case is 1.95. This is twice the specified ratio for the transition process. There are no signs of loss of stability, both tangentially and under normal stresses.
The need for such consideration is related to the comparison of a process in which, due to an increase in the coefficient of friction, the influence of the zone of attainability of the limiting deformation focus is minimal. The manifestation of the reachability zones is clearly shown when comparing Figure 4 and Figure 5.
Let us look at the issue in more detail. With an increase in the shape factor, a steady increase in maximum contact stresses was formed along the processing zone 1.195; 1.534; 1.940; 2.707; 3.334; and 4.637. In the lag zone, there was no decrease in the plots below the previous numbers of shape factors, as was the case for the transitional deformation focus. However, there is an overlap of the concavity of the plots in the lag zone at different sections of the hearth length. According to the tangential stresses, a stable bulge of the tangential stress plots appeared along the length of the processing zone. The change in tangential stresses is in the range of 0.025–0.233, which indicates the advance zone. To estimate the convexity of the plots, within the zero abscissa of the relative values of the tangential stresses, we have 0.111; 0.133; 0.157; 0.198; 0.222; and 0.246. As can be seen, the convexity of the tangential stress plots increases with increasing shape factor. In the advanced zone, the shape of the tangential stress plots has a concave shape, which is associated with a change in sign. The advanced zone has been identified against the background of an increase in the tangential stress trapping ability of the rolls. For this rolling process, there are practically no factors influencing tensile stresses, i.e., the reach zone of the ultimate deformation focus. Tension stresses are suppressed almost along the entire length of the deformation site. In contrast to the process in Figure 6, a new quality appears when the increased tensile force from an increase in the coefficient of friction is suppressed by the increasing ability of metal to be captured by rolls (Figure 6). The exception is the last curve corresponding to the shape factor of 15.49, the thinnest strip. Indeed, if we analyze the result, we can detect a slight decrease in specific pressures in the lag zone for this curve.
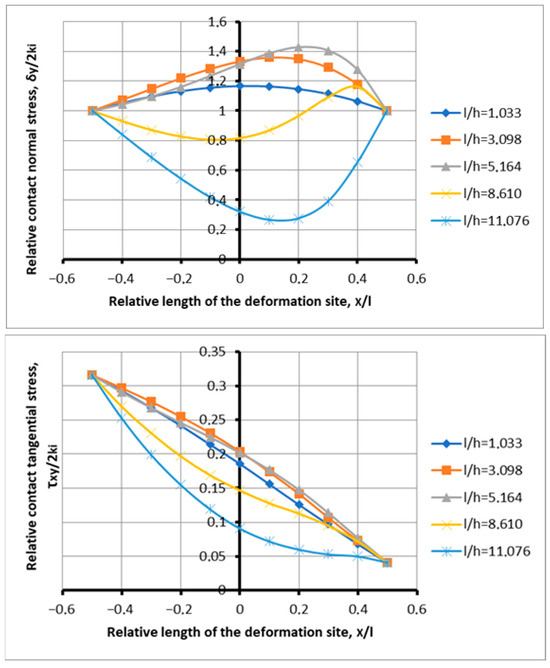
Figure 6.
Distribution of contact stresses along the length of the deformation site under conditions of excessive metal capture by rolls at l/h = 1.033–11.07; f = 0.05; and α = 0.129.
At the beginning of the lag zone, a known dependence of stress on the shape factor still appears, with the abscissa at 0.1. As the shape factor increases, the contact stresses rise within the range of 1.185 to 2.529. At abscissas of −0.2 to −0.5, and for a shape factor of 15.49 at the end of the lag zone, a slight decrease in normal stresses is observed. Although this is a minor segment in the overall dataset, the decrease can be attributed to a small, yet present, influence of tensile stresses in the lag zone for thin strips.
A special feature of this process, with a minimum capture angle of 0.077 radians, under conditions of two-factor gripping ability of the rolls, is the implementation of a process with an overwhelming effect on tensile stresses in the lag zone.
Figure 6 shows diagrams of the extreme process of metal capture by rolls at different values of the shape factor, a minimum coefficient of friction of 0.05, and an increased angle of capture of 0.129. The ratio of the coefficient of friction to the angle of capture is less than one, and is equal to 0.388. With the increasing concavity of the curves, this is almost twice as much as the same ratio for Figure 3, but the process is also prohibitive.
You should pay attention to the number of analyzed curves. The curve for the shape factor 15.49 is not shown here. Already in Figure 3, it was clear from the concavity of the curve that its process implementation capabilities were below critical. At the same time, with high coefficients of friction, the implementation of this process took place at the highest achievable zones of the maximum deformation focus, i.e., reducing the load relative to the lower strain load.
The tangential and normal stress diagrams confirm the extreme capture of metal by rolls (Figure 6), with the difference that instead of a capture angle of 0.077 radians, a capture angle of 0.129 radians is used, which makes its own changes to the process parameters.
Relative tangential stresses, in comparison with the capture angle of 0.077 radians (0.168–0.031), have increased, and have a maximum value at the entrance to the deformation center (0.316) and a minimum value at the exit from the lag zone (0.041), without reaching the zero line, therefore, without crossing it. There is no advanced zone. From this, it can be seen that there was an increase in tangential stresses as a reaction to an increase in the angle of capture. Normal stresses also respond to an increase in the angle of capture. If the processes in Figure 3 show a decrease in the process load on curves 8.61 (partial loss); 11.07; and 15.49, then in Figure 7, the deflections of the normal stress plots have a place with shape factors of 8.61; 11.07; and 15.49 (thin stripes). Curve 5.164 moved down to the previous number 3.098 in the lag zone (Figure 6). At the same time, curve 15.49 fell into the achievability zone already in the processes of Figure 5. There is no loss of stability in the process of only two plots (1.033; 3.098), instead of three (Figure 3). Deflections occur for the same curves in the tangential stress diagrams.
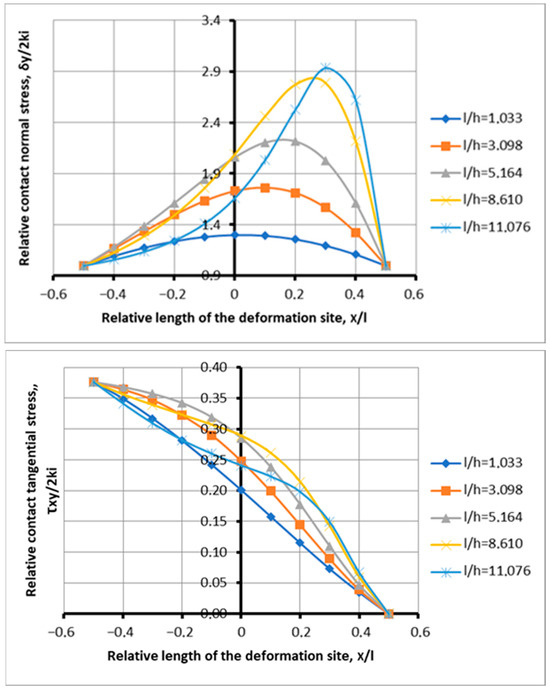
Figure 7.
Distribution of contact stresses along the depth of the deformation focus when metal is captured by rolls under conditions of a transient process roll capacity at l/h = 1.033–11.07; f = 0.153; and α = 0.129.
It is of interest to analyze the stress plots between the abscissas (0.2 and 0.2), the distribution of which is different (Figure 7).
Indeed, with a shape factor of 5.164, the normal stresses increase along the deformation source towards the outlet. An increase in stress is observed towards the output, and for the factor 3.098 up to and including the abscissa 0.1. When comparing curves 5.164 and 3.098 in the range of 0.2–0.1, as expected, the values with the shape factor in ascending order correspond to large values. However, in the lag zone, the stress state has changed to the opposite, starting from an abscissa of 0.0. To stresses with a form factor of 3.098, in the lag zone. Values of a larger value correspond. Thus, the curve in the extreme grip with the number 5.164 is the fourth stress curve, which reacted to an increase in the angle of capture by reducing the load in the lag zone.
A special feature of this process is the strengthening of the tensile force by increasing the angle of capture and its effect on the excessive capture of metal by rolls. With an increase in the angle of capture, there is an increase in the effect on the normal force in the direction of entry into the deformation site. According to the law of action and reaction, there is an increase in the trapping friction force, which is marked by an increase in the values of tangential stresses. The strength and tension of stretching increase, or the force of back tension from the lag zone. It should be noted that in previous processes, there was also an increase in the tensile force, but under the influence of an increase in the coefficient of friction, rather than the angle of capture. Under the influence of increased back tension, the possibilities of the gripping ability of the rolls decrease. In the extreme state, the conditions for the implementation of the process deteriorate even more, which is confirmed by the increased number of diagrams with a concave shape of contact stresses (Figure 6).
Figure 7 shows the contact stress diagrams of the transient deformation focus, with a capture angle of 0.129, and shape factors of 1.033–11.07.
The rolling process is shown with a gripping angle of 0.129, but with a coefficient of friction that allows for the primary capture of metal by rolls of 0.153, in the absence of an advance zone. The ratio of the coefficient of friction to the angle of capture is 1.19. This is more than with a capture angle of 0.077 radians. There is a similar pattern to the existence of a process with a zero advance zone, as with a capture angle of 0.077 radians. There is also a transitional process for the angle of capture of 0.129, with a slight increase in the ratio of the coefficient of friction to the angle of capture. The increase in the ratio was 0.09. The capabilities of the physical and mathematical model made it possible to determine the coefficient of friction, at which there is no advance zone, and the possibility of implementing the process at an angle of 0.129 radians, in a stable rolling mode.
The trends indicated in the extreme deformation focus (Figure 8) are confirmed in the transition process (Figure 7).
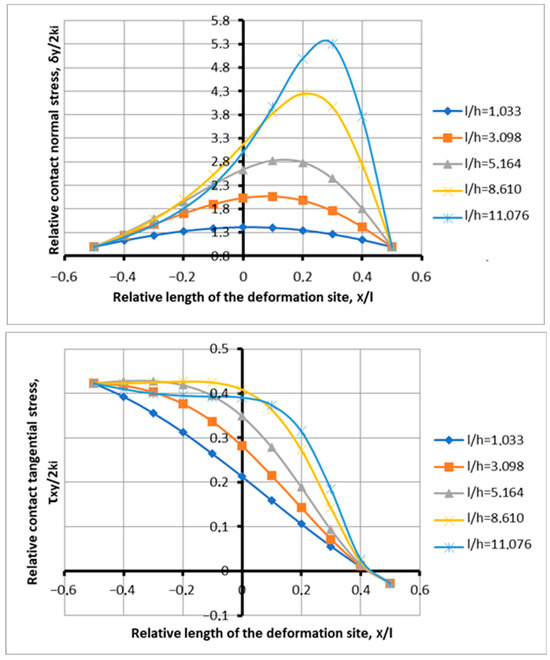
Figure 8.
Distribution of contact stresses along the length of the deformation focus when metal is captured by rolls under the conditions of the determining process at l/h = 1.033–11.07; f = 0.251; and α = 0.129.
Let us consider the features of the transition process with a change in the loading of the hearth. With an increase in the angle of capture, there was an increase in the maximum normal contact stresses for all shape factors in comparison with the transient process (Figure 6). An increase in the shape factor contributed to an increase in the maximum contact stresses, respectively, 1.293; 1.761; 2.215; 2.791; and 2.936. At the same time, for the same plots in the zone of lag in abscess 0.2, the following distribution was obtained 1.239; 1.495; 1.614; 1.496; and 1.247. There was a decrease in contact stresses in the lag zone for large values of shape factors. According to Figure 8, the curve for the plot (8.61) moved lower by two positions, the curve (11.07) moved lower by three positions (Figure 9), which confirms the effect of plastic forming. These movements of the curves indicate the presence of zones of attainability of the limiting deformation focus.
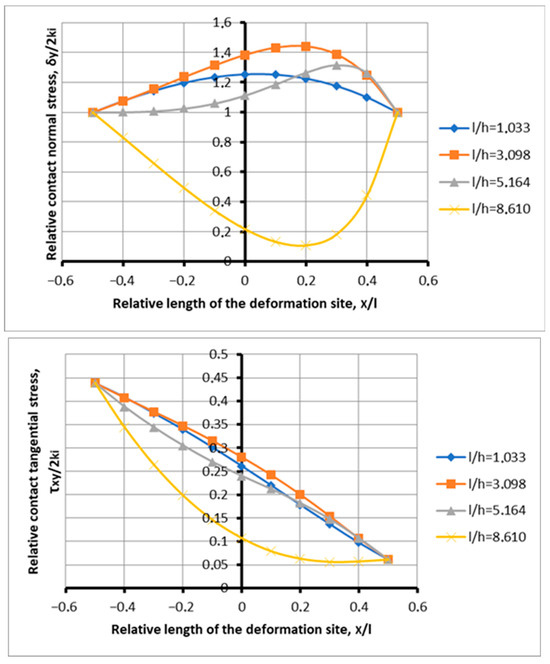
Figure 9.
Distribution of contact stresses along the length of the deformation site under conditions of excessive metal capture by rolls at l/h = 1.033–8.61; f = 0.05; and α = 0.168.
The tangential stresses changed their magnitude relative to the transient process with a capture angle of 0.077 radians. The limits of change in tangential stresses (Figure 8) are 0.0–0.376, and the tangential stresses (Figure 6) are 0.0–0.204. With an increase in the angle of capture, tangential stresses reacted with their growth. The convexity of the tangential stress diagram with an increase in the shape factor, for the zero abscissa, within 0.201; 0.248; 0.285; 0.289; and 0.241, increased relative to the capture angle of 0.077 radians within 0.107; 0.121; 0.135; 0.154; 0.160; and 0.149. Changes in tangential stresses characterize the processes of self-regulation of counter-directional friction forces and normal pressure in the lag zone.
When rolling strips of high height, i.e., for the first three values of the curves of the shape factor, with an increase in the angle of capture, there is no decrease in contact stresses in the lag zone, and there are no zones of achievability of the limiting deformation focus. Indeed, the maximum values of normal stresses for the three lower curves have an increasing tendency up to 2.215. At the same time, in the lag zone for the same curves, there is also an increase from 1.239 to 1.614, rather than a decrease, within the horizontal axis 0.2. In the same row, but when rolling thin strips with a factor of 8.61 and 11.07, a decrease in specific pressures in the range of 1.496–1.247 is recorded in the lag zone, which indicates the presence of tensile stresses. The presented model of the stress state change indicates the possibility of a transient process with an increase in the capture angle of 0.129 radians. There are zones of achievability of the limiting deformation focus for thin strips, i.e., the effect is confirmed with an increase in the angle of capture.
The next feature of the considered transient deformation focus is an increase in tensile stress with an increase in the angle of capture. This increase is indicated by the magnitude of the decrease in normal contact stresses in the lag zone when the other indicators of the compared processes are equal. The indicators of the transition process shown in Figure 5 and Figure 8 are compared. The lag zone for thin stripes is selected with the same value of the abscissa axis equal to −0.2, with the same shape factor of 8.61 and 11.07. For Figure 5, on one horizontal axis −0.2, we have stresses for the shape factor of 8.61 and 11.07, respectively, 1.485 and 1.474. For Figure 8, on one horizontal axis 0.2, there are stresses for the shape factor of 8.61 and 11.07, respectively, 1.496 and 1.247. The difference within the same figure gives a stress drop between the plots of adjacent values of the shape factor, which must be compared. Indeed, we have the following:
1.496 − 1.247 = 0.249; 1.485 − 1.474 = 0.011.
The first difference refers to Figure 7, with a large angle of capture, and the second to Figure 4, with a smaller angle of capture. The deflections are different from 0.249 and 0.011. The deflections are larger where the gripping angles are large, therefore, where the tensile stresses are greater.
It should be noted that the tensile stresses increase with an increase in the coefficient of friction and with an increase in the angle of capture, but in different ways. If we give a general formulation, it should be borne in mind of, “if the forces involved in the formation of the back tension change their magnitude, then the tensile stresses from their interaction increase in accordance with the processes accompanied by this reinforcement, the capture of friction forces or the reverse flow of metal from the normal pushing pressure.” As a result, when implementing a process with an increased gripping angle to 0.129 radians, it is shown that with a given ratio of gripping angle and the coefficient of friction, a transitional process is possible that combines elements of an exorbitant process and elements of a stable rolling process. The effects of tensile stresses on the rolling processes of high strips are limited. Tensile stresses have a decisive effect on the rolling processes of thin and medium strips, which manifests itself in the areas of achievability of the maximum deformation focus or the effect of reducing the force load.
Figure 8 shows the contact stress diagrams with a gripping angle of 0.129 radians and a coefficient of friction of 0.251, which corresponds to the ratio of the coefficient of friction to the gripping angle of 1.95, in the presence of a full-fledged advance zone.
There is a steady increase in maximum normal stresses with an increase in the shape factor of the deformation site within 1.409; 2.067; 2.824; 4.249; and 5.308.
The limits of change of tangential stresses for all shape factors are the same, in the range of −0.028–0.423, which are greater than tangential stresses, with a capture angle of 0.077 (−0.025–0.233), which determines the presence of an advance zone. There are significant differences in the curves determined by the convexity of the tangential stress plots in the lag zone. Moreover, the parameters characterizing their magnitude mainly depend on the shape factor and are, for the zero value of the abscissa, within 0.213; 0.282; 0.349; 0.409; and 0.391. In this list, the last value belongs to a curve that has fallen below the previous one with a shape factor of 8.61 (Figure 8), which is explained by the increasing effect of the tensile force in the lag zone.
A feature of this process is the reaction of the force characteristics of the hearth to an increase in the angle of capture to a value of 0.129, which was reflected in an increase in the concavity of the normal stress plots during rolling of thin-walled strips.
At the same time, all rolling processes, represented by the ratio of the coefficient of friction to the angle of capture of 1.95, correspond to the realization of stable metal capture by rolls and the process itself.
This information boils down to one thing, the reinforcing factor is the combined effect of the angle of capture and the coefficient of friction.
With an increase in the angle of capture (compression), contact stresses increase, and the coefficient of friction acts in the same direction (Figure 6) [1].
The stresses at the outlet of the deformation source for both capture angles are characterized by high stresses at the entrance to the deformation source. At the same time, before the abscissa 0.1, stresses with large compression correspond to large stresses, after the abscissa 0.1, the stress state changes to the opposite.
An increase in the angle of capture leads to a redistribution of the stress state of the metal along the length of the deformation site.
When comparing the results of the studies of the processes shown in Figure 6 and Figure 9, it can be seen that there is a stable rolling process, with different coefficients of friction (from 0.150 to 0.251), for different angles of capture. There was no decrease in the concavity of the plots below the minimum value (less than one). Plastic deformation was present in the lag zone, and a two-zone deformation site was formed. With this ratio of technological parameters of the process, partial suppression of the zeroing stretching factors in the lag zone is manifested. On the one hand, there was a departure from the process of minimal stability, due to an increase in the coefficient of friction. On the other hand, there were zones of achievability of the maximum deformation focus, due to an increase in the angle of capture.
But with all this, the suppression of tensile stresses in the compression zone is different. With a minimum gripping angle of 0.077 and a coefficient of friction of 0.150, tensile stresses practically did not manifest themselves. In the following case, there was an increase in the grip angle (0.129) and the coefficient of friction (0.251). At the same time, the effect of the coefficient of friction on the suppression of tensile stresses in the lag zone was insufficient to achieve a zero advance zone, as it was present at a capture angle of 0.077 radians. The influence of the gripping angle, but not the coefficient of friction, on the stress state parameters in this case was decisive, since the interaction of factors considered led to the appearance of a load reduction effect with an increase in strain loading.
With the combined action of the coefficient of friction and the angle of capture, their influence was the predominant indicator for contact stresses along the length of the deformation site. For the lag zone, smaller angles and the coefficient of friction correspond to higher values of contact stresses, and larger angles and the coefficient of friction correspond to lower values of contact stresses. As a result, returning to Figure 5 and Figure 8, there is a transition from the process of almost complete suppression of stretching in the lag zone to the process of significantly increasing the influence of tensile stresses, with a characteristic manifestation of the effect of reducing the load with increasing strain.
Figure 9 shows diagrams of the extreme process of metal capture by rolls at different values of the shape factor; the minimum coefficient of friction is 0.05 and the maximum, within the limits of this study, the angle of capture is 0.168. The ratio of the coefficient of friction to the angle of capture is less than unity and is equal to 0.298. This is more than the same ratio for the capture angle of 0.077, equal to 0.195, and less for the capture angle of 0.129, equal to 0.388. Thus, we have another transcendental process of metal capture by rolls, confirmed by the new transcendental curves of Figure 9.
There was a decrease in the number of curves compared to the prohibitive processes shown in Figure 3 and Figure 6. The absence of prohibitive curves with a shape factor of 15.49; 11.07, and the addition of a curve with a shape factor of 8.61, confirms that the prohibitive capture mode is characterized by even less stability in the critical state of the new process.
The trends of additional regulatory influences from the lag zone are increasing due to the emergence of new zones of achievability of the limiting deformation focus. For the thinnest strip, when considered with a shape factor of 5.164, the deflection of the plot is noted below the strip with a shape factor of 1.033, which may indicate that the maximum stability values for all types of loading have been reached. The process, with a minimum coefficient of friction and a maximum grip angle, can be explained by the action of back tension from the lag zone. With an increase in the angle of capture, there is an increased effect of the buoyant force from the deformation site. According to the law of action and counteraction, the value of the trapping friction force increases, which is confirmed by an increase in tangential stresses in the lag zone. Under the influence of increased counter-directional forces, the tensile force in the deformation site increases. The effect of back tension promotes the reverse flow of metal from the deformation site, which eliminates the causes of the appearance of the advanced zone, exacerbating the process of excessive capture. The normal contact stresses in the lag zone decrease, which is recorded by the contact stress diagrams (Figure 9). Another deflection appears on the tangential stress plot. You should pay attention. In Figure 4, an increase in the tensile force is characterized by an increase in the gripping friction force, and in this case, there is an increase in the tensile force due to an increase in the pushing force of normal pressure. The contact pressure plots of the high strips, shape factor 1.033; 3.098; and 5.164, also reacted to the increase in the angle of capture by their realignment. The curves with a factor of the form 5.164 and 3.098 are reversed. The lower one (3.098) went up, and the upper one (5.164) went down. At the same time, in the lag zone, the last curve dropped below the 1.033 curve. Similar changes in the stress state occurred for tangential stresses at a capture angle of 0.168 radians. The complex restructuring of the stress state towards a deterioration in the gripping ability of the rolls during excessive gripping is confirmed by the two-component grip and the appearance of new regulatory factors in the deformation focus.
Figure 10 shows the rolling process with a gripping angle of 0.168 radians, but with a coefficient of friction that allows for the primary gripping of metal with rolls of 0.215, in the absence of an advance zone.
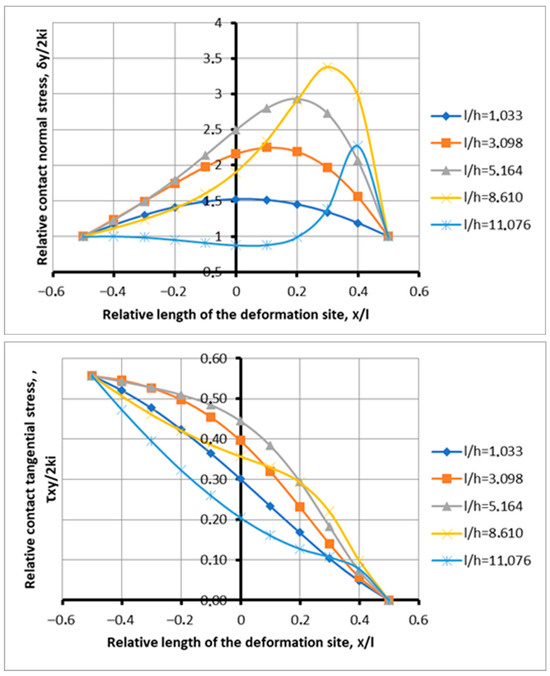
Figure 10.
Distribution of contact stresses along the length of the deformation focus when metal is captured by rolls under transient conditions at l/h = 1.033–11.07; f = 0.215; and α = 0.168.
The ratio of the coefficient of friction to the angle of capture is 1.28, which is higher than the similar ratio of 1.19 with a capture angle of 0.129 radians. This process is defined as a transitional one, since the development allows for the presence of a zero zone of advance and capture of metal by rolls. The process of loss of stability of the thinnest strip with a deformation focus shape factor of 11.07 is considered. In the lag zone, with a complete set of data on the capture of metal by rolls, there was an increased effect of the zeroing factor, i.e., stretching of the strip from the lag zone. It can be seen from the figure that the normal contact stress diagram has an unacceptable concavity, less than one. This indicates that the stresses in the deformation site are less than the yield point, and there is no plastic deformation in this area of the deformation site. The transition process is realized on the verge of loss of stability, and is characterized by a maximum reduction in force. Let us analyze this process in more detail. With an increase in the shape factor, the maximum normal stresses increased to the number 8.61 in the following sequence: 1.522; 2.248; 2.932; and 3.383. This is determined by an increase in the coefficient of friction to a value of 0.215, compared with the coefficient of friction of 0.153, of the previous transient (Figure 7). Tangential stresses also increase in comparison with the transient (Figure 9), respectively, from 0.0–0.376 to 0.0–0.557. This increase in tangential stresses is explained by the interaction of oppositely directed gripping forces and normal pressures. With an increase in the capture of metal by rolls, the pushing effect of the normal force from the deformation site increases. According to the law of action and counteraction, the force of metal capture by rolls increases, which is confirmed by an increase in tangential stresses. As a result of the interaction, the tensile force in the lag zone increases to the maximum values. The tensile force suppresses the friction stress, and the stress state is rebuilt. Table 1 shows the process data characterizing the limiting deformation focus at a maximum capture angle of 0.168 radians.

Table 1.
The values of the normal stresses of the transient process under the conditions of the limiting deformation.
As can be seen from Table 1, the loading of the deformation site leads to a gradual shift in load reduction towards the lag zone for all shape factors.
The earlier conclusion is confirmed that, first of all, it concerns thin and especially thin stripes. Comparing the limits of stress variation with a shape factor of 1.033 and 11.07, we have the following data, respectively, 1.16.1.522 and 0.880.2.373. The entire lag zone has variation limits of 0.880–0.991. The stresses are outside the plastic deformation zone. The stresses with the number 11.07 sank below the plot with the shape factor of 8.61 and are comparable to the plot with the number 5.164. In addition, the stresses in the lag zone for the shape factor 8.61 dropped below the 1.033 plot, which indicates the presence of a significant zone of achievability of the limiting deformation focus of the next curve.
It is possible to quantify the subsidence zone or the increase in tensile stresses in the lag zone, as this was performed in relation to the capture angle of 0.129 radians. For the same parameters of the shape factor and the abscissa axis, −0.2, a sample was made for a capture angle of 0.168 radians, respectively, 1.394 and 0.956. Then, the difference between these values will be 0.438, which is significantly greater than for the same parameters, only with a capture angle of 0.129 radians equal to 0.249. The values of tensile stresses have increased many times. Consequently, such an increase in tensile stresses contributes to the fastest achievement of a process with a limiting focus of deformation, i.e., loss of stability, slip of the strip in the rolls.
The curves of the plots of the factors of the form 1.033–5.164 (large- and medium-thick strips) did not respond to the accessibility zone.
As a result, we have a transitional rolling process, with zeroing of the stress state, due to an increase in stretching in the lag zone. This is a vivid example of confirmation of the effect of plastic forming, an obvious decrease in rolling force at maximum strain load, despite the fact that there is no advance zone in this process. It follows from this analysis that the presented transition process meets all the requirements that the process of the ultimate deformation focus, or the process of loss of stability with a single-zone deformation focus, must meet [1].
In the studies above, it is shown that the implementation of the process with a single-zone deformation focus is on the verge of its stability. We have a process within which the effect of plastic forming is determined. For the possibility of its optimization, the inverse problem is of interest, i.e., the suppression of the force regulating effect from the lag zone, in conditions of increasing the exciting forces of the deformation focus. Figure 5 and Figure 8 show the minimal impact of tensile stresses on the parameters of the compression zone for the defining modes. The question arises about the effect of tensile stresses on the process parameters at the maximum angle of capture.
Figure 11 shows the capture of metal by rolls with the following parameters of the determining process: a capture angle of 0.168 radians; a coefficient of friction of 0.327, in the presence of an advance zone; and the ratio of the coefficient of friction to the angle of capture is 1.95, which is similar to the same ratio with a capture angle of 0.129 radians.
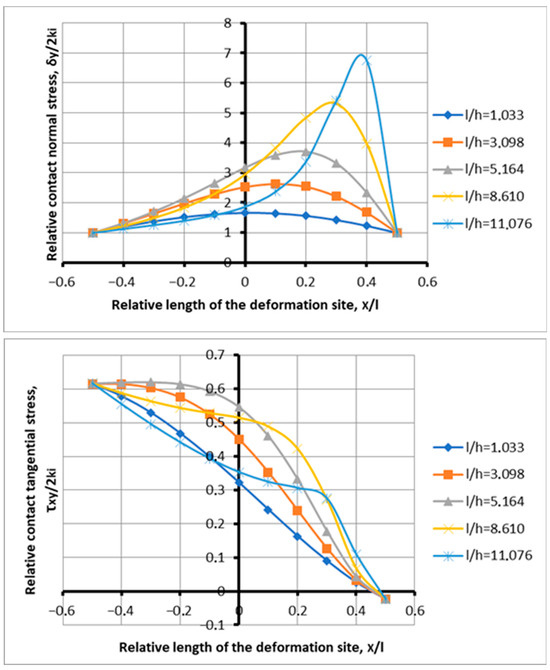
Figure 11.
Distribution of contact stresses along the length of the deformation focus when metal is captured by rolls under the conditions of the determining process at l/h = 1.033-11.07; f = 0.327; and α = 0.168.
It is known that as the shape factor increases, the contact stresses also increase. This pattern is followed by the first three processes with numbers 1.033; 3.098; and 5.164 (large- and medium-height strips) and the maximum stresses of the strips with shape factors 8.61; 11.07 (thin strips). There is no loss of stability of the process. However, the last two curves at maximum specific pressures have dips in the contact stress diagrams in the lag zone. This leads to a sharp decrease in the rolling force, relative to the plots with a smaller shape factor. There is an influence on the deformation site of tensile stresses from the lag zone. As can be seen from the figure, with an increase in the coefficient of friction, this factor did not disappear, but the deflections of the plots smaller than one disappeared, which indicates the presence of plastic deformation in the lag zone. There is a partial suppression of tensile stresses in the lag zone, and the process of stable rolling is realized.
The maximum value of the tangential stress at the entrance to the deformation source of 0.616 is determined by the amount of compression. This is confirmed by the distribution of stresses depending on the angle of capture in the determining processes with the presence of an advanced zone (Figure 6, Figure 9 and Figure 11); we have 0.077–0.233; 0.129–0.423; and 0.168–0.616.
The change in normal stresses is more complex. Table 2 shows the values of the normal contact stresses of the determining process, with partial suppression of tensile stresses in the lag zone.

Table 2.
Values of contact normal stresses under conditions of partial suppression of the force regulating effect.
All parameters in Table 2 are greater than the values in Table 1. This is due to the influence of a higher coefficient of friction of 0.327 and a grip angle of 0.168 radians. There is no sagging of the maximum contact stress diagrams in comparison with Table 1. There is a general pattern of reducing the force load on the hearth, starting with a factor of form 8.61, in relation to the lag zone.
At the same time, there is no data on relative normal stresses of less than unity, especially for thin bands with a shape factor of 11.07. For this shape factor, the following loading parameters occur along the length of the hearth: 1.0; 6.751; 5.401; 3.374; 2.374; 1.874; 1.591; 1.404; 1.260; 1.131; and 1.0. Consequently, unlike Table 1, plastic deformation is carried out at all points of the deformation site, i.e., the rolling process is stable. This is a feature of this defining process, as for the processes in Figure 6 and Figure 9. In this case, the direction of avoiding rolling with the maximum deformation focus, which was indicated in Figure 10 and Table 1, was determined in the direction of increasing the stability of the plastic forming regime.
When considering normal stresses as a whole, they exhibit a complex and non-linear pattern of variation. An increase in stress levels is observed at relative lengths of 0.4 and 0.3, with the following values: 1.232; 1.679; 2.340; 3.981; 6.751 and 1.423; 2.217; 3.313; 5.320; 5.401, respectively, according to the data from Figure 1. For abscissas 0.2 and 0.1, a decrease in stress is recorded, corresponding to a reduction in the deformation zone thickness and a transition of the 11.07 and 8.61 curves toward the limit deformation zone. The transition is more effective for the stress distribution with a shape factor of 11.07 compared to that of 8.61. This is confirmed by the curves in the lag zone and the stress distributions in Figure 11.
Unlike the transitional process shown in Figure 10, the processes involving a leading zone exhibit no signs of instability. However, the influence of tensile stress remains a determining factor. At the maximum bite angle, when the roll’s gripping capacity is at its lowest, as illustrated in Figure 10, partial suppression of tensile forces is observed, and the deformation zone transitions from a single-zone to a dual-zone structure. No concavities in the stress profiles associated with the absence of plastic deformation are present. This is attributed to the enhanced contact friction forces, which effectively neutralize the tensile forces.
As a result, signs of stabilization begin to emerge in the defining processes illustrated in Figure 5 and Figure 8. Process stability and the rolls’ gripping capability are restored. This is particularly evident in the consistent increase of maximum normal stresses across all shape factors. Accordingly, tensile effects are reduced, creating conditions conducive to plastic deformation in the lag zone. Excessive dips in the stress profiles within the deformation zone are eliminated.
However, with all this, there is a decrease in stresses relative to processes with a lower shape factor, i.e., there remain areas of achievability of the ultimate deformation focus. And these reachability zones, at a given angle of capture, are very significant. The reachability zones do not completely disappear with an increase in the coefficients of friction. Therefore, an increase in the coefficients of friction is necessary for further compensation. Hence, the relevant question is to what extent the process of increasing frictional stresses should be carried out, taking into account the achievability of the ultimate deformation focus.
The peculiarities of this process, from the point of view of optimizing the achievement of the effect of plastic forming, are the conditions for the implementation of rolling on the verge of loss of stability of the process. This introduces a lot of uncertainty in solving this problem. To solve this problem, it is necessary to know what is the certainty or stability of a process, or a process without slipping rolls. In this case, against the background of the maximum angle of capture, the process is destabilized from the point of view of metal capture by rolls. There is a process of suppressing the tensile effect on the plastic focus of deformation. The last example shows that the process exists, and there are parameters of this process that indicate the limits of enhanced metal capture by rolls, i.e., stabilization of the process.
In Ref. [1], the literature review outlines key issues related to the effect of plastic deformation, which may manifest at the threshold of rolling process stability, particularly during the rolling of thin strips. Implementing the process near the stability limit necessitates justification of concepts such as process instability and clarification of the conditions for material capture, which, although addressed in the literature, are not yet generalized for specific problem settings. For instance, Ref. [41] demonstrates that metal slippage within the rolls leads to a transformation of the stress distribution from a convex to a concave profile. This concavity indicates the absence of plastic deformation, i.e., a loss of process stability. A similar conclusion is drawn in Ref. [42], where the rolling process in continuous mills is analyzed. The influence of back tension is associated with a shift in the shape of the contact stress profile in the lagging zone toward concavity, resulting in reduced contact stresses both in that zone and within the deformation region as a whole.
5. The Results of a Study of the Stress State of a Metal Under the Influence of Multiparametric Factors
The presented research is characterized as the development of a method for solving problems of continuum mechanics, the method of argument of functions of a complex variable. Based on the solution of the closed problem of plasticity theory, the practical problem of rolling theory is considered related to the identification of the features and effects of plastic forming in conditions of multidirectional plastic flow of metal and asymmetric loading of the deformation site. The result shown in [1] is a decrease in the force loading of the deformation site with increased strain exposure. This process corresponds to certain implementation conditions related to the gripping ability of the rolls and the stability of the rolling process.
The defining idea of this study is the factor of stretching the lag zone, and its effect on the force and kinematic parameters of the process. All this is supported by modern experimental studies on the exciting ability of rolls, including negative advance in the plastic forming zone.
The use of the stretching factor makes it possible to adjust the boundary conditions, the kinematics of the process, and take into account the interaction of multidirectional metal flow zones with loading asymmetry, which expands the possibilities of implementing a force loading mode on a plastic deformation site. For example, consider the capture of metal by rolls with a zero advance zone. Or the implementation of capture, when the rate of metal exit from the deformation site is less than the circumferential speed of the rolls. This is a negative metal advance factor. With this formulation of the question, there is a need for additional research on the capture of metal by rolls, the stability of rolling, and the features that accompany these processes.
The developed physical model of the effect on the deformation site formed the basis of a mathematical model of the process, which manifests itself through metal capture and the stability of the rolling process. The assessment of the effect of the back tension force was determined by the concavity of the contact stress diagrams in the hearth, which gives the process clarity and obvious reliability of the result. Since the mathematical model of the process makes it possible to analyze the process based on contact stress diagrams, it becomes possible to visually evaluate the capture process and stability under the influence of tensile force. At the same time, the factors influencing the processes were different combinations of several parameters, the angle of capture, the coefficient of friction, and the geometry of the deformation site. Three modes of interaction are considered: a process with excessive metal capture by rolls, a transitional single-zone focus, and a defining process with a two-zone focus of deformation.
A visual analysis of the gripping ability of an exorbitant deformation focus has shown that the well-known method for determining the capture of metal by rolls, by establishing the relationship between the retracting forces of friction and the pushing forces of normal pressure, does not characterize the capture process sufficiently. Some features of the process are not explained. It is proposed to supplement the capture model with another factor—the stretching effect from the side of the lag zone of interacting forces. As the angle of capture increases, the tensile effect of the lag zone on the extreme capture increases, with an increase in the number of curves with unacceptable deflections along the entire length of the deformation site. The deflections of the plots are the effect of stretching forces.
Another process has been investigated, which is characterized not by reaching the maximum deformation focus, but on the contrary, by increasing the gripping ability of the rolls and the stability of the rolling process. The zeroing effect of gravity forces decreases, but does not disappear. It is not single-zone, has an advanced zone, and is characterized by a counter-directional flow of metal. In this case, there is no strengthening of tensile stresses. On the contrary, their effect is partially suppressed. This process is realized by the increasing action of contact friction forces. The suppressive effect of stretching is determined by the appearance of an advanced zone, the absence of zeroing plots of normal stresses, and, therefore, the presence of plastic deformation in the lag zone, an increase in tangential stresses, i.e., an increase in the gripping ability of the rolls, etc. The presented mode stabilizes rolling, but departs from the process of minimal stability, despite the presence of zones of achievability of the ultimate deformation site, determined by large angles of capture.
Blanks of the minimum value of the shape factor 1–5 practically do not react to the action of tensile stresses from the lag zone. In this case, there is no effect of the achievability of the ultimate deformation site.
As a result, the presence of a tensile force, confirmed by theoretical and experimental studies by various authors, in the processes of capture and stability leads to the effect of plastic forming, determined by the zones of achievability of the maximum deformation focus or the effect of reducing the load with increasing strain.
To realize the effect of plastic deformation, it is first necessary to define the process of the limiting deformation zone, the implementation of which enables an approach to the threshold of process instability. Under these conditions, the effect of plastic deformation is activated. Such a process should be unstable, i.e., implemented on the verge of loss of stability, in the zones of attainability of the ultimate deformation focus. This is a transitional process that has access to the implementation of the zero advance zone. For the zero zone, the coefficient of friction can be determined if the angle of capture is known, taking the numerator of the fraction equal to zero in expression (24). A special case of solving this problem is expression (27):
This allows you to calculate a process with a zero advance zone.
For further analysis, it is necessary to know the limits of the stability of the process at given capture angles; by ratio indicator f/ = 1.10–1.95; ratio indicator f/ = 1.19–1.95; and ratio indicator f/ = 1.28–1.95.
6. Conclusions
- The concept of roll gripping capacity and rolling process stability has been revised using a physical model with more determinative force characteristics, including the interaction of oppositely directed force schemes, particularly the tensile force acting from the lagging zone.
- Based on the developed mathematical model, a new force factor influencing the gripping mechanism and process stability has been identified and studied—the tensile force originating from the lagging zone.
- A novel single-zone deformation mode has been revealed, characterized by minimal process stability, and quantified deformation parameters across various zones of the deformation region (1.132; 1.353; 1.602; 1.998; 2.269; and 2.586) and (1.107; 1.261; 1.383; 1.485; 1.474; and 1.310). The process has been investigated under varying geometric, deformation, and force conditions.
- The regime of partial suppressive action of stress-neutralizing factors in the metal has been examined under variable geometric, deformation, and force influences affecting both the roll gripping capacity and process stability.
- Stability indicators of transitional rolling modes have been determined for the following conditions: α = 0.077, the ratio f/α ranges from 1.10 to 1.95; α = 0.129, f/α = 1.19–1.95; and α = 0.168, f/α = 1.28–1.95.
Author Contributions
Conceptualization, V.C. and I.V.; methodology, I.V. and V.C.; investigation, A.N. and S.L.; data curation, S.K.; writing—original draft preparation, V.C. and I.V.; writing—review and editing, I.V., A.N. and S.L.; supervision, V.C. and S.L.; project administration, V.C.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant no. AP 19678682).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chigirinsky, V.; Naizabekov, A.; Lezhnev, S.; Naumenko, O.; Kuzmin, S. Determining the patterns of asymmetric interaction of plastic medium with counter-directional metal flow. East. Eur. J. Enterp. Technol. 2024, 1, 66–82. [Google Scholar] [CrossRef]
- Chigirinsky, V.; Naizabekov, A.; Lezhnev, S.; Kuzmin, S.; Panin, E.; Tolkushkin, A.; Volokitina, I.; Yordanova, R.; Knapinski, M. Effect of the limiting deformation zone under conditions of asymmetric loading during rolling of medium thickness strips. J. Chem. Technol. Metall. 2024, 59, 993–1002. [Google Scholar] [CrossRef]
- Chekmarev, A.P.; Klimenko, P.L. Specific Pressure and Rolling Moment Arm; DMeti: Dnipro, Ukraine, 1965; pp. 210–237. [Google Scholar]
- Klimenko, P.L. Contact Stresses in Rolling; Porogi: Dnepropetrovsk, Ukraine, 2007; 285p. [Google Scholar]
- Chigirinsky, V.; Putnoki, A. Development of a dynamic model of transients in mechanical systems using argument-functions. East.-Eur. J. Enterp. Technol. 2017, 3, 11–22. [Google Scholar] [CrossRef][Green Version]
- Rusnák, J.; Malega, P.; Svetlík, J.; Rudy, V.; Šmajda, N. The Research of the Rolling Speed Influence on the Mechanism of Strip Breaks in the Steel Rolling Process. Materials 2020, 13, 3509. [Google Scholar] [CrossRef]
- Sonmez, M.S.; Denissova, A.; Gelmanova, Z. Obtaining Symmetrical Gradient Structure in Copper Wire by Combined Processing. Symmetry 2024, 16, 1515. [Google Scholar] [CrossRef]
- Chigirinsky, V.; Naumenko, O. Advancing a generalized method for solving problems of continuum mechanics as applied to the Cartesian coordinate system. East. Eur. J. Enterp. Technol. 2021, 5, 14–24. [Google Scholar] [CrossRef]
- Gao, Z.J.; Li, J.Y.; Feng, Z.H. Influence of hot rolling on the microstructure of lean duplex stainless steel 2101. Int. J. Miner. Metall. Mater. 2019, 26, 1266–1273. [Google Scholar] [CrossRef]
- Panin, E.; Fedorova, T.; Lawrinuk, D.; Kolesnikov, A.; Yerzhanov, A.; Gelmanova, Z.; Liseitsev, Y. Improvement of strength and performance properties of copper wire during severe plastic deformation and drawing process. Case Stud. Constr. Mater. 2023, 19, e02609. [Google Scholar] [CrossRef]
- Chigirinsky, V.V. Determination of the Stress State of a Plastic Body under Plane Strain Conditions. Izv. Vuzov. Ferr. Metall. 1990, 7, 32–33. [Google Scholar]
- Shevchenko, I.V.; Kovalchuk, O.M. Enhancing the durability of mechanical equipment in the balancing system of rolling mill rolls. Bull. Lutsk Natl. Tech. Univ. 2023, 6, 75–80. [Google Scholar]
- Huang, J.; Zang, Y.; Gao, Z.; Zeng, L. Influence of asymmetric structure parameters on rolling mill stability. J. Vibroengineering 2017, 19, 4840–4853. [Google Scholar] [CrossRef]
- Minaev, A.A. Combined Metallurgical Processes; UNITEKH: Donetsk, Ukraine, 2008; 549p. [Google Scholar]
- Drahobetskyi, V.V.; Shapoval, O.O.; Shchepetov, V.V.; Zahirniak, M.V.; Lotous, V.V.; Lehotkin, H.I.; Sliepinin, O.H.; Kresanov, Y.S. Controlled Effects of Plastic Deformation of Billets for Metallurgy and Transport; Madrid Printing House: Kharkiv, Russia, 2017; 243p. [Google Scholar]
- Zubchaninov, V.G. Mathematical Theory of Plasticity; Tver State Technical University: Tver, Russia, 2002; 300p. [Google Scholar]
- Radeev, Y.N. Spatial Problems in the Mathematical Theory of Plasticity; Samara University Publishing: Samara, Russia, 2007; 448p. [Google Scholar]
- Bondar, V.S.; Danshin, V.V. Plasticity: Proportional and Non-Proportional Loading; Fizmatlit: Moscow, Russia, 2008; 176p. [Google Scholar]
- Koshlyakov, N.S.; Gliner, E.B.; Smirnov, M.M. Partial Differential Equations of Mathematical Physics; Higher School: Moscow, Russia, 1970; 710p. [Google Scholar]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity; Nauka: Moscow, Russia, 1979; 560p. [Google Scholar]
- Nadai, A. Plasticity and Fracture of Solids; Foreign Literature Publishing House: Moscow, Russia, 1954; 647p. [Google Scholar]
- Dorofeyev, O.A.; Kovtun, V.V. Estimation of the Stress-Strain State of a Discrete Medium by a Plastic Flow Model. Probl. Tribol. 2019, 93, 29–38. [Google Scholar] [CrossRef]
- Stampouloglou, I.H.; Theotokoglou, E.E. Additional separated-variable solutions of the biharmonic equation in polar coordinates. J. Appl. Mech. 2010, 77, 2. [Google Scholar] [CrossRef]
- El-Naaman, A.; Nielsen, K.L.; Niordson, C.F. An investigation of back stress formulations under cyclic loading. Mech. Mater. 2019, 130, 76–87. [Google Scholar] [CrossRef]
- Lopez-Crespo, P.; Camas, D.; Antunes, F.V.; Yates, J.R. A study of the evolution of crack tip plasticity along a crack front. Theor. Appl. Fract. Mech. 2018, 98, 59–66. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.-P.; Li, C.-W. Elastic-plastic stress-strain calculation at notch root under monotonic, uniaxial and multiaxial loadings. Theor. Appl. Fract. Mech. 2017, 92, 33–46. [Google Scholar] [CrossRef]
- Pathak, H. Three-dimensional quasi-static fatigue crack growth analysis in functionally graded materials (FGMs) using coupled FE-XEFG approach. Theor. Appl. Fract. Mech. 2017, 92, 59–75. [Google Scholar] [CrossRef]
- Correia, J.D.O.; Huffman, P.J.; De Jesus, A.M.P.; Cicero, S.; Fernandez-Canteli, A.; Berto, F.; Glinka, G. Unified two-stage fatigue methodology based on structural details. Theor. Appl. Fract. Mech. 2017, 92, 252–265. [Google Scholar] [CrossRef]
- Synekop, N.S.; Lobanova, L.S.; Parkhomenko, L.A. The R-Function Method in Dynamic Problems of Elasticity Theory; KhGUPT: Kharkiv, Russia, 2015; 95p. [Google Scholar]
- Sneddon, I.N.; Berry, D.S. Classical Theory of Elasticity; Grigolyuk, E.I., Ed.; Smirnov, A.I., Translator; State Publishing House for Physical and Mathematical Literature: Moscow, Russia, 1961; 219p. [Google Scholar]
- Hussein, N.S. Solution of a Problem Linear Plane Elasticity with Mixed Boundary Conditions by the Method of Boundary Integrals. Math. Probl. Eng. 2014, 2014, 11. [Google Scholar] [CrossRef]
- Arkulis, G.E.; Dorogobid, V.G. Theory of Plasticity; Metallurgy: Moscow, Russia, 1987; 251p. [Google Scholar]
- Tikhonov, A.N.; Samarskii, A.A. Equations of Mathematical Physics; Moscow State University Publishing: Moscow, Russia, 1999; 799p. [Google Scholar]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Nauka: Moscow, Russia, 1966; 709p. [Google Scholar]
- Chekmarev, A.P.; Nefedov, A.A.; Nikolaev, V.A. Theory of Longitudinal Rolling; Kharkiv State University Publishing: Kharkiv, Ukraine, 1965; 158p. [Google Scholar]
- Grudev, A.P. Roll Bite Capability of Rolling Mills; SP Intermet Engineering: Moscow, Russia, 1998; 283p. [Google Scholar]
- Smirnov, V.S. Theory of Rolling; Metallurgy: Moscow, Russia, 1967; 460p. [Google Scholar]
- Chekmarev, A.P.; Mashkovtsev, R.A.; Nosenko, O.P. Production of Tube Billets; Metallurgy: Moscow, Russia, 1970; 304p. [Google Scholar]
- Chekmarev, A.P.; Smolyaninov, A.F. Experimental Study of Longitudinal Periodic Rolling. In Production and Application of Economical Rolled Profiles; Collection of Scientific Papers: Dnepropetrovsk, Ukraine, 1961; pp. 135–150. [Google Scholar]
- Maksimenko, O.P.; Romanyuk, R.Y. Analysis of Longitudinal Stability in Rolling Processes Considering Internal Forces and Strip Tension Regime. Izv. Vuzov. Ferr. Metall. 2009, 10, 32–34. [Google Scholar]
- Tselikov, A.I. Theory of Calculation of Forces in Rolling Mills; Metallurgy: Moscow, Russia, 1962; 495p. [Google Scholar]
- Chekmarev, A.P.; Grechko, V.P.; Getmanets, V.V.; Khovrin, B.V. Rolling on Small-Section Mills; Metallurgy: Moscow, Russia, 1967; 363p. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).