Decentralized-Output Feedback Sampled-Data Disturbance Rejection Control for Dual-Drive H-Gantry System

Abstract

In this paper, we tackle the decentralized-output feedback sampled-data disturbance rejection control for a dual-drive H-Gantry (DDHG) system with a symmetrical structure. For the DDHG system with disturbances, only the position information of the system at the sampling points can be utilized, such that the traditional control methods based on full state information of the DDHG system could not be used. To this end, a linear discrete-time generalized-proportional-integral observer (GPIO) based on the position information and reference trajectory of DDHG at the sampling points is constructed first, such that unmeasured states and disturbance can be estimated simultaneously. Then, a GPIO-based decentralized-output feedback sampled-data control (GPIO-DOFC) method is proposed by utilizing the estimations of the unmeasured states and disturbance. A strict theoretical analysis of the closed-loop system is carried out, which demonstrates that the desired trajectory could be tracked under the proposed GPIO-DOFC method. Finally, comparative studies are carried out between the proposed GPIO-DOFC method and the extended-state observer-based decentralized-output feedback sampled-data control (ESO-DOFC) method. These confirm the efficacy and feasibility of the proposed control scheme.

1. Introduction

The dual-drive H-Gantry (DDHG) is universally preferred in some high-speed, high-precision equipment, such as circuit assembly, water jet cutting machines, laser cutting machines, medical instruments, precision processing equipment, and so on [1,2,3,4,5,6]. The DDHG model can be described as a class of second-order uncertain systems, which are both uncertain and nonlinear, i.e., the output of the DDHG system is not proportional to the input, and the system has uncertain parameters and disturbance caused by other factors. Due to the high-performance control of the gantry system demands, the gantry stage is driven coordinately by two motors in practice. Therefore, it is imperative to design an effective controller for the DDHG system such that the coordinated motion between the two servo motors can be realized.

In recent years, the synchronous control problem of the DDHG system has attracted increased attention from the control community. Based on the establishment of an accurate multiple-input and multiple-output (MIMO) mathematical model of a dual-driven gantry, using an adaptive robust control algorithm, a synchronization control method is proposed that directly considers the additive rotation dynamics under uncertain parameters and uncertain nonlinear conditions [1]. To restrain the coupling of the system, a cross-coupled optimal synchronizing controller [2] is designed by the evaluation of an optimal cross-coupled compensator and reduces the synchronous error considerably. It is well known that almost all practical systems inevitably suffer from unknown external disturbances, unmodeled dynamics, and nonlinear uncertainties. To improve the control performance of practical control systems against uncertainties and disturbance, some significant control schemes have been established, such as adaptive control, sliding mode control (SMC), and other traditional control methods, as well as improved control schemes such as data-driven control, event-triggered control, and integral synovial output control [7,8,9]. In [3], an adaptive fractional order sliding mode controller is constructed for the DDHG system. In addition, the merit of the adaptive fractional order SMC algorithm is verified by the results. Two robust synchronization control strategies [4] are proposed for the DDHG system based on internal model control (IMC) and SMC separately. It is shown that both the synchronization accuracy and the tracking accuracy of the DDHG system can be improved significantly under the proposed two control strategies. Refs. [5,6] proposed different adaptive robust controllers for the DDHG system, which could improve the estimation accuracy of system parameters and the adaptive ability against uncertain parameters. For complicated systems, which are composed of multiple interconnected subsystems, the control purposes of these systems are usually excessive due to the information processing and experimental requirements. Compared with a centralized control scheme, a decentralized control scheme demonstrates more advantages, such as reducing the computing burden of the system and enhancing the robustness and reliability against interacting operation failures, and so on [10]. For MIMO flexure-linked DDHG systems, several decentralized control approaches are proposed in [11,12,13,14,15,16]. It should be pointed out that all the aforementioned results for the DDHG system are based on continuous-time control design.

Compared with the existing linear or continuous-time results, the discrete-time approximation of the nonlinear systems is a more challenging and attractive problem. In particular, the sampled-data control design problem for nonlinear systems has gained wide attention. Discrete-time controller designs based on the discrete-time approximation of the nonlinear system are studied in [17,18]. These can only guarantee semi-global stabilization. In [19], a sampled-data control law is constructed for a class of nonlinear systems such that the global-output feedback stabilization (GOFS) can be realized. With the aforementioned control scheme, the GOFS problem of a class of upper triangular systems with input delay via sampled data is solved in [20]. Ref. [21] extended the results of [19] and proposed a linear hybrid stabilizer using dual-rate sampled-data state feedback for an active suspension system of electric vehicles. Inspired by [19], the problem of GOFS by sampled data for a class of nonlinear systems with uncertain output function is discussed in [22], and the maximum allowable sampling period for the constructed linear sampled-data output feedback controller can be obtained by an explicit formula. Based on the sampled-data control technology, the problem of GOFS for a class of feedforward nonlinear systems is investigated in [23], and the method of how to choose the scaling gain and the sampling period is given at the same time. Ref. [24] considers the problem of sampled-data stabilization for a class of nonlinear descriptor systems, and a systematic sampled-data output feedback controller design procedure is proposed using partial state information of the system. In addition, sampled-data control has been applied to a networked environment by some scholars. An event-based sampled-data disturbance rejection controller is proposed in [25], which uses disturbance/uncertainty estimation and an attenuation technique. This methodology is applicable to the disturbed system in a networked environment when only using measurable outputs. Moreover, theories and methods of disturbance estimation and compensation have been proposed and applied to different systems. A new cascaded extended-state observer-based SMC method and a cascaded finite-time sliding mode observer were proposed and applied to a flexible joint robot in [26,27], which can effectively estimate the states and disturbances. Furthermore, a reduced-order extended-state observer and a novel finite-time generalized-proportional-integral observer based on sliding mode control were proposed and applied to two Brunovsky systems. The former can compensate not only lumped interference but also the estimation error of concentrated interference [28]. The latter can quickly estimate and compensate error estimates of states and disturbances in a limited time [29].

As far as we know, the problem of decentralized-output feedback disturbance rejection control for the DDHG system via sampled data has never been investigated in the literature. The major obstacle is the lack of theoretical support and systematic guidelines; therefore, the problem of how to design a decentralized-output feedback disturbance rejection controller in a sampled-data manner remains open. Another difficulty is how to design an observer based on the output information at the sampling points such that both the unmeasured states and disturbance can be recovered. To remedy such an issue, this paper will concentrate on the decentralized-output feedback sampled-data disturbance rejection controller design problem for the DDHG system. The contributions of this paper can be summarized as follows.

1.

This paper is the first work to address the decentralized-output feedback sampled-data disturbance rejection control problem for the DDHG system.

2.

Due to the limited system output information (i.e., the system output information can be used at the sampling points) and the presence of disturbance, the existing control approaches for the DDHG system cannot be used. Inspired by [19,24,28], a high-gain linear discrete-time generalized-proportional-integral observer (GPIO) is constructed based on the position information and reference trajectory of DDHG at the sampling points such that unmeasured states and disturbance could be estimated simultaneously.

3.

Based on the output feedback domination approach [19,24] and estimation of disturbance, a decentralized-output feedback sampled-data disturbance rejection controller with simple form is proposed for the DDHG system. A rigorous theoretical analysis based on Lyapunov theory is conducted for the closed-loop system, which demonstrates that the desired trajectory could be tracked by choosing the appropriate scaling gain and sampling period.

The rest of this paper is organized as follows. In Section 2, the problem formulation and preliminaries are introduced. The design of the decentralized-output feedback sampled-data disturbance rejection controller is given in Section 3. Simulation results are shown in Section 4. Section 5 comprises the conclusion of the paper.

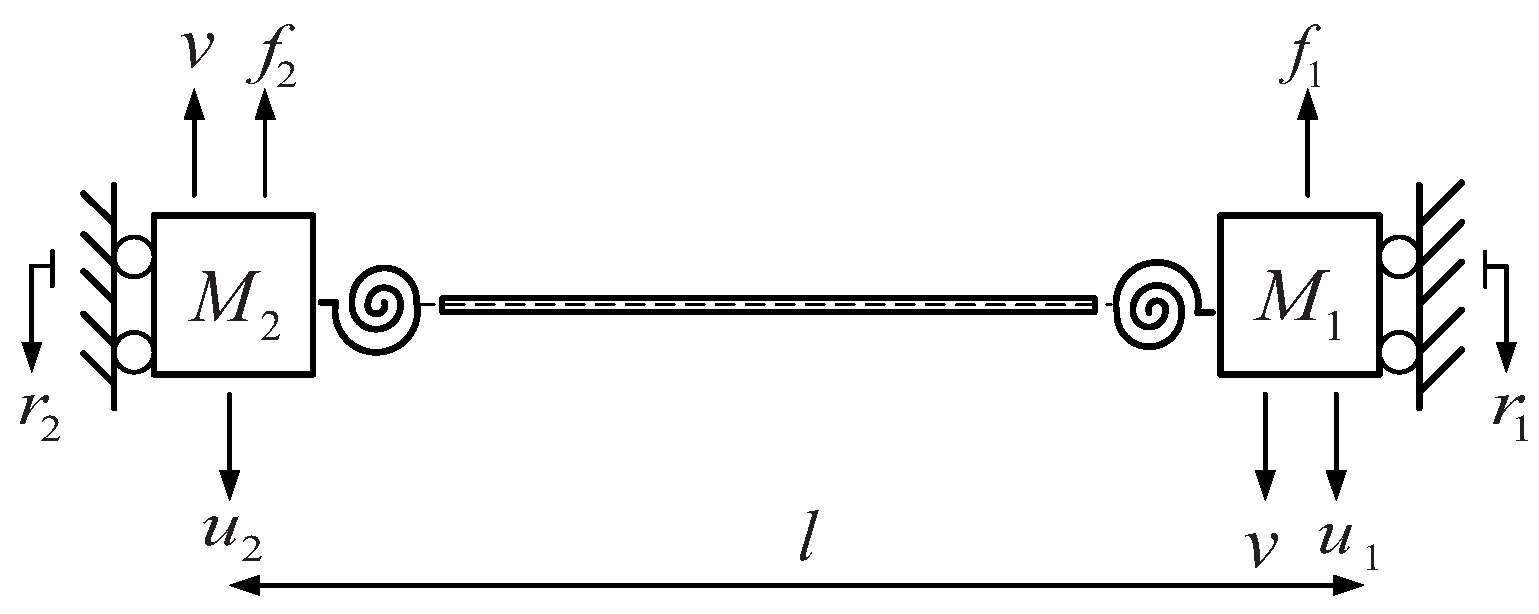
2. Model Description

In the common structure of DDHG, the two parallel carriages of the gantry stage are usually driven by linear actuators, which move the cross-arms in series. For the DDHG system, the cross-arms carry the payload. The whole system is mainly composed of two parallel carriages connected to one cross-arm and use the end-effector to guide the third bracket. The carriages are moved by a linear motor which is driven by a Copley accelerator. Figure 1 demonstrates the schematic diagram of DDHG. By simplifying the model, the system is converted to the parameter model in Figure 2.

Considering that the mass of the two carriages is often known in practice, the DDHG is modeled as a coupled linear system with parametric uncertainties in [13]

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{M}_1{\ddot{r}}_1=K_f{u}_1-\Gamma {\dot{r}}_1+v-f_1{b}_1\left(t\right)\hfill \\ M_2{\ddot{r}}_2=K_f{u}_2-\Gamma {\dot{r}}_2-v-f_2{b}_2\left(t\right)\hfill \end{array}\right.\end{array}$$

(1)

where $v=K_v(r_2-r_1), M_i={\displaystyle \frac{m_e+m_c}{2}}+m_i, b_i\left(t\right)(i=1,2)$ is a unit step function. The parameter symbols referred to in the model are shown in

Table 1. Nomenclature used in DDHG.

Name	Description	Unit
$K_f$	Force constant	N/A
$m_i$	Mass of carriage i	kg
$m_e$	Mass of end-effector	kg
$m_c$	Mass of cross-arm	kg
$r_i$	Position of carriage i	m
$u_i$	Control current of carriage i	A
$f_i$	Coulomb friction in carriage i	N
$K_v$	Stiffness of flexure	N/m
$\Gamma$	Damping coefficient in each carriage	Ns/m

.

The practical system is inevitably affected by modeling errors and internal and external factors, which may be summarized as disturbance. To improve the control performance of the generalized DDHG system, an advanced control strategy is needed to remove the influence of disturbance. By defining the new state variable $\tilde{x}={[{\tilde{x}}_{11},{\tilde{x}}_{12},{\tilde{x}}_{21},{\tilde{x}}_{22}]}^{\mathrm{T}}={[r_1,{\dot{r}}_1,r_2,{\dot{r}}_2]}^{\mathrm{T}}$, ${[{\tilde{x}}_{11},{\tilde{x}}_{21}]}^{\mathrm{T}}={[y_1,y_2]}^{\mathrm{T}}$, the generalized DDHG System Equation (1) can be written as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\tilde{x}}}_{i1}={\tilde{x}}_{i2}\hfill \\ {\dot{\tilde{x}}}_{i2}={\tilde{u}}_i\left(t\right)+w_i\left(t\right)+{\pounds }_i\left(t,\tilde{x}\left(t\right)\right),i=1,2\hfill \\ y_i={\tilde{x}}_{i1}\hfill \end{array}\right.\end{array}$$

(2)

where $w_i\left(t\right)=-{\displaystyle \frac{f_i{b}_i\left(t\right)}{M_i}}$, ${\pounds }_i(t,\tilde{x}\left(t\right))={\displaystyle \frac{-1}{M_i}}(K_v{\tilde{x}}_{11}+\Gamma {\tilde{x}}_{i2}-K_v{\tilde{x}}_{21})$, and ${\tilde{u}}_i\left(t\right)={\displaystyle \frac{K_f{u}_i}{M_i}}$ is the control input of the system, and $y_i\left(t\right)\in R$ is the control output that can be measured.

According to the expression of ${\pounds }_i(t,\tilde{x}\left(t\right))$, the following assumption is made.

Assumption 1.

For $i=1,2$, there exists a constant $c_0$ such that

$$\begin{array}{c}\hfill \left|{\pounds }_i\left(t,\tilde{x}\left(t\right)\right)\right|\le c_0\left(\left|{\tilde{x}}_{11}\right|+\left|{\tilde{x}}_{12}\right|+\left|{\tilde{x}}_{21}\right|+\left|{\tilde{x}}_{22}\right|\right)\end{array}$$

(3)

In this paper, our aim is to design a dynamic decentralized-output feedback sampled-data disturbance rejection controller based on the sampled output information of System Equation (2), such that the specified trajectory $s\left(t\right)$ can be tracked asymptotically. Considering the tracking characteristics of the two carriages of the DDHG in practice, it is supposed that the desired trajectories of the two subsystems are the same. For the control objective, the following assumption is needed.

Assumption 2.

$s\left(t\right)$ is known and satisfies the following conditions: (i) $s\left(t\right)$ is continuous and bounded; (ii) For any $t(t\ge 0)$, there exists the continuous and bounded derivative $\left(\dot{s},\ddot{s},\dots ,s^{(p+2)}\right)$ with order $p+2$.

Let $x_{i1}={\tilde{x}}_{i1}-s\left(t\right)$; System Equation (2) can be transformed into the following system

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_{i1}=x_{i2}\hfill \\ {\dot{x}}_{i2}={\tilde{u}}_i\left(t\right)+{\pounds }_i\left(t,x\left(t\right)\right)+d_i\left(t\right)\hfill \\ y_i=x_{i1}\hfill \end{array}\right.i=1,2\end{array}$$

(4)

where $d_i\left(t\right)=w_i\left(t\right)-{\displaystyle \frac{\Gamma }{M_i}}\dot{s}\left(t\right)-\ddot{s}\left(t\right),$ represents the lumped disturbance.

Assumption 3.

The disturbance $d_i\left(t\right),(i=1,2)$ satisfies the following two conditions: (i) $d_i\left(t\right)\in C^p$, and (ii) there exists a positive constant ${\eta }_i$ such that $|d_i^{\left(p\right)}(t)|\le {\eta }_i$, $i=1,2$.

To address the decentralized-output feedback control of System Equation (4), System Equation (4) is rewritten as

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{\dot{x}}_i\left(t\right)={\tilde{M}}_i{x}_i\left(t\right)+{\tilde{N}}_i({\tilde{u}}_i\left(t\right)+d_i\left(t\right))\hfill \\ +{\tilde{F}}_i(t,x\left(t\right))\hfill \\ y_i\left(t\right)={\tilde{C}}_i{x}_i\left(t\right),\hfill \end{array}\right.i=1,2\hfill \end{array}$$

(5)

where $x_i\left(t\right)={\left[x_{i1}\left(t\right),x_{i2}\left(t\right)\right]}^{\mathrm{T}}$, ${\tilde{N}}_i={\left[\begin{array}{cc}0& 1\end{array}\right]}^{\mathrm{T}}$,

$$\begin{array}{c}\hfill {\tilde{C}}_i=\left[\begin{array}{cc}1& 0\end{array}\right],{\tilde{M}}_i=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right],{\tilde{F}}_i(t,x\left(t\right))=\left[\begin{array}{c}0\\ {\pounds }_i(t,x\left(t\right))\end{array}\right].\end{array}$$

In order to improve the accuracy of the estimation, we define the following set of auxiliary variables

$$x_{i3}\left(t\right)=d_i\left(t\right),x_{i4}\left(t\right)={\dot{d}}_i\left(t\right),\dots ,x_{i,p+2}\left(t\right)={d_i}^{(p-1)}\left(t\right).$$

Then, the nonlinear System Equation (5) is extended to the system described by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\Phi }}_i\left(t\right)=M_i{\Phi }_i\left(t\right)+N_i{\tilde{u}}_i\left(t\right)\hfill \\ +F_i(t,x\left(t\right),d_i^{\left(p\right)}\left(t\right))\hfill \\ y_i\left(t\right)=C_i{\Phi }_i\left(t\right)\hfill \end{array}\right.i=1,2\end{array}$$

(6)

where ${\Phi }_i\left(t\right)={\left[x_{i1}\left(t\right),x_{i2}\left(t\right),\dots ,x_{i,m+2}\left(t\right)\right]}^{\mathrm{T}}$,

$$M_i=\left[\begin{array}{cc}{O}_{(p+1)\times 1}& I_{(p+1)\times (p+1)}\\ O_{1\times 1}& O_{1\times (p+1)}\end{array}\right],$$

$$N_i=\left[\begin{array}{c}{\tilde{N}}_i\\ O_{p\times 1}\end{array}\right],C_i={\left[\begin{array}{c}{\tilde{C}}_i^{\mathrm{T}}\\ O_{p\times 1}\end{array}\right]}^{\mathrm{T}},$$

$F_i(t,x\left(t\right),d^{\left(p\right)}\left(t\right))={\left[\begin{array}{ccc}{\tilde{F}}_i(t,x\left(t\right))& O_{(p-1)\times 1}& d^{\left(p\right)}\left(t\right)\end{array}\right]}^{\mathrm{T}}$.

Consider the following coordinate transformation:

$$\begin{array}{c}\hfill {\delta }_{i,l}={\displaystyle \frac{x_{i,l}}{L^{l-1}}},l=1,\dots ,p+2,v_i\left(t\right)={\displaystyle \frac{{\tilde{u}}_i\left(t\right)}{L^2}},\end{array}$$

(7)

where $L\ge 1$ is a scaling gain waiting to be determined.

In view of Equation (7), System Equation (6) is transformed into the following form

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\delta }}_i\left(t\right)=L{M}_i{\delta }_i\left(t\right)+L{N}_i{v}_i\left(t\right)\hfill \\ +{\psi }_i(t,\delta \left(t\right),{d_i}^{\left(p\right)}\left(t\right))\hfill \\ y_i\left(t\right)=C_i{\delta }_i\left(t\right)\hfill \end{array}\right.i=1,2\end{array}$$

(8)

where

$$\begin{array}{cc}\hfill & {\psi }_i(t,\delta \left(t\right),{d_i}^{\left(p\right)}\left(t\right))\hfill \\ \hfill & ={\left[{\tilde{F}}_i(t,x\left(t\right))/L,O_{1\times (p-1)},{d_i}^{\left(p\right)}\left(t\right)/L^{(p+1)}\right]}^{\mathrm{T}}\hfill \\ \hfill & ={\left[0,{\pounds }_i(t,\delta \left(t\right))/L,O_{1\times (p-1)},{d_i}^{\left(p\right)}\left(t\right)/L^{(p+1)}\right]}^{\mathrm{T}}.\hfill \end{array}$$

In the next step, we will design a discrete-time observer in linear form based on sampled output, i.e., $y\left(t\right)=y\left(t_k\right)$($t\in [t_k,t_{k+1}), t_k=kT, T$ is the sampling period), to estimate the unmeasured states and disturbance of System Equation (8), and then construct a simple linear sampled-data output feedback controller based on the estimated value of the observer and output feedback dominant approach, such that the system output can track the desired trajectory.

Remark 1.

The purpose of the coordinate transformation is to introduce the high-gain L to dominate the nonlinear term.

3. Main Results

3.1. Design of Sampled-Data Disturbance Observer

Inspired by the continuous-time high-gain observer design methods in [30,31], we design the following sampled-data disturbance observer with ${\delta }_i\left(t_k\right)$ for the extended nonlinear System Equation (8)

$$\begin{array}{cc}\hfill {\dot{\widehat{\delta }}}_i\left(t\right)=& L{M}_i{\widehat{\delta }}_i\left(t\right)+L{N}_i{v}_i\left(t\right)\hfill \\ \hfill & +L{H}_i{\delta }_{i1}\left(t_k\right),\forall t\in \left[t_k,t_{k+1}\right)\hfill \end{array}$$

(9)

where ${\widehat{\delta }}_i\left(t\right)={\left[{\widehat{\delta }}_{i1}\left(t\right),{\widehat{\delta }}_{i2}\left(t\right),\dots ,{\widehat{\delta }}_{i,p+2}\left(t\right)\right]}^{\mathrm{T}}$, $H_i={\left[a_{i1},a_{i2},\dots ,a_{i,p+2}\right]}^{\mathrm{T}}$ and $a_{ij},j=1,\dots ,n$ are the coefficients of the Hurwitz polynomial $p_1\left(h\right)=h^{p+2}+a_{i1}{h}^{p+1}+\dots +a_{i,p+1}h+a_{i,p+2}.$

3.2. Construction of Decentralized-Output Feedback Sampled-Data Controller

According to the designed sampled-data disturbance observer, the decentralized-output feedback sampled-data controller is constructed in the form

$$\begin{array}{cc}\hfill v_i\left(t\right)& =v_i\left(t_k\right)=-k_{i1}{\widehat{\delta }}_{i1}\left(t_k\right)-k_{i2}{\widehat{\delta }}_{i2}\left(t_k\right)-{\widehat{\delta }}_{i3}\left(t\right)\hfill \\ \hfill & =-K_i{\widehat{\delta }}_i\left(t_k\right),\forall t\in \left[t_k,t_{k+1}\right)\hfill \end{array}$$

(10)

where $K_i=\left[k_{i1},k_{i2},1,0,\dots ,0\right],k_{ij}>0$ are the coefficients of the Hurwitz polynomial $p_2\left(h\right)=h^{p+2}+k_{i,p+2}{h}^{p+1}+\dots +k_{i2}h+k_{i1}.$

Theorem 1.

Consider uncertain nonlinear System Equation (1); if Assumptions 1–3 hold, the states of the closed-loop system consisting of System Equation (1), sampled-data disturbance observer Equation (9), and decentralized-output feedback sampled-data disturbance rejection controller Equation (10) will globally asymptotically converge to the following bounded region:

$$\begin{array}{c}\hfill \mathfrak{B}=\left\{{Z|\parallel Z\parallel }^2\le {\displaystyle \frac{{\lambda }_M\left(P\right)(1-ϵ\left(t\right)){\eta }^2\parallel P\parallel }{\Phi \left(ϵ\right(t),P,L,𝒱)}}\right\}\end{array}$$

where $\Phi (ϵ\left(t\right),P,L,𝒱)=(1-ϵ\left(t\right))(L{\lambda }_m\left(P\right)-c_2{\lambda }_M\left(P\right))-2L{\lambda }_M\left(P\right)ϵ\left(t\right)\parallel P\parallel 𝒱$, $c_2=2c_1+\parallel P\parallel$, $\eta =$ max{${\eta }_1$, ${\eta }_2$}, $𝒱=(\parallel H_1\parallel +\parallel H_2\parallel )+\sqrt{2}(\parallel K_1\parallel +\parallel K_2\parallel )$, $ϵ\left(t\right)$ is mentioned in Lemma 1, $P=$ diag{$P_1,P_2$}, ${\lambda }_M\left(P\right)$, and ${\lambda }_m\left(P\right)$ represent the maximum eigenvalue and minimum eigenvalue of the matrix P, respectively.

Proof. 

Based on System Equation (8), Observer Equation (9) and Controller Equation (10), we have

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{\dot{\delta }}_i\left(t\right)\\ {\dot{\widehat{\delta }}}_i\left(t\right)\end{array}\right]=& L\left[\begin{array}{cc}{M}_i& O\\ O& {\widehat{A}}_i\end{array}\right]\left[\begin{array}{c}{\delta }_i\left(t\right)\\ {\widehat{\delta }}_i\left(t\right)\end{array}\right]\hfill \\ \hfill & -L\left[\begin{array}{c}{N}_i\\ N_i\end{array}\right]K_i{\widehat{\delta }}_i\left(t_k\right)+L\left[\begin{array}{c}O\\ H_i\end{array}\right]{\delta }_1\left(t_k\right)\hfill \\ \hfill & +\left[\begin{array}{c}{\psi }_i(t,\delta \left(t\right),{d_i}^{\left(p\right)}\left(t\right))\\ O\end{array}\right],\hfill \\ \hfill & \forall t\in \left[t_k,t_{k+1}\right).\hfill \end{array}$$

(11)

Due to the fact that ${\delta }_{i1}\left(t_k\right)=C_i{\delta }_i\left(t_k\right)=C_i{\delta }_i\left(t\right)+C_i\left[{\delta }_i\left(t_k\right)-{\delta }_i\left(t\right)\right], {\widehat{\delta }}_i\left(t_k\right)={\widehat{\delta }}_i\left(t\right)+{\widehat{\delta }}_i\left(t_k\right)-{\widehat{\delta }}_i\left(t\right),$ it follows from System Equation (11) that

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{\dot{\delta }}_i\left(t\right)\\ {\dot{\widehat{\delta }}}_i\left(t\right)\end{array}\right]= & L\left[\begin{array}{cc}{M}_i& -N_i{K}_i\\ H_i{C}_i& {\widehat{A}}_i-N_i{K}_i\end{array}\right]\left[\begin{array}{c}{\delta }_i\left(t\right)\\ {\widehat{\delta }}_i\left(t\right)\end{array}\right]\hfill \\ \hfill & + \left[\begin{array}{c}{\psi }_i(t,\delta \left(t\right),{d_i}^{\left(p\right)}\left(t\right))\\ O\end{array}\right]\hfill \\ \hfill & - L\left[\begin{array}{c}{N}_i\\ N_i\end{array}\right]K_i\left[{\widehat{\delta }}_i\left(t_k\right)-{\widehat{\delta }}_i\left(t\right)\right]\hfill \\ \hfill & + L\left[\begin{array}{c}O\\ H\end{array}\right]C_i\left[{\delta }_i\left(t_k\right)-{\delta }_i\left(t\right)\right],\hfill \\ \hfill & \forall t\in \left[t_k,t_{k+1}\right).\hfill \end{array}$$

(12)

Denote

$$\begin{array}{cc}\hfill {\mathcal{A}}_i& =\left[\begin{array}{cc}{M}_i& -N_i{K}_i\\ H_i{C}_i& {\widehat{A}}_i-N_i{K}_i\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}{M}_i& -N_i{K}_i\\ H_i{C}_i& M_i-H_i{C}_i-N_i{K}_i\end{array}\right].\hfill \end{array}$$

Note that ${\widehat{A}}_i=M_i-H_i{C}_i$ and $M_i-N_i{K}_i$ are Hurwitz matrices. In fact,

$$\begin{array}{cc}\hfill & {\mathcal{A}}_i=\left[\begin{array}{cc}{M}_i& -N_i{K}_i\\ H_i{C}_i& M_i-H_i{C}_i-N_i{K}_i\end{array}\right]\hfill \\ \hfill & ={\left[\begin{array}{cc}I& O\\ -I& I\end{array}\right]}^{-1}\left[\begin{array}{cc}{M}_i-N_i{K}_i& -N_i{K}_i\\ O& {\widehat{A}}_i\end{array}\right]\left[\begin{array}{cc}I& O\\ -I& I\end{array}\right],\hfill \end{array}$$

implies that ${\mathcal{A}}_i$ is a Hurwitz matrix as well. Hence, there is a positive definite matrix $P_i={P_i}^{\mathrm{T}}\in {\mathbb{R}}^{(2p+4)\times (2p+4)}$ such that ${\mathcal{A}}_i^{\mathrm{T}}{P}_i+P_i{\mathcal{A}}_i=-I.$

For System Equation (11), we define

$$\begin{array}{c}\hfill Z\left(t\right)=\left[\begin{array}{c}{Z}_1\left(t\right)\\ Z_2\left(t\right)\end{array}\right],Z_i\left(t\right)=\left[\begin{array}{c}{\delta }_i\left(t\right)\\ {\widehat{\delta }}_i\left(t\right)\end{array}\right],\end{array}$$

and construct the following Lyapunov function for the i-th subsystem of the closed-loop system:

$$\begin{array}{c}\hfill V_i\left(Z_i\right)={Z_i}^{\mathrm{T}}\left(t\right)P_i{Z}_i\left(t\right).\end{array}$$

Taking the derivative of $V_i\left(Z_i\right)$ along the trajectory of the $i$th subsystem of the closed-loop System Equation (12) yields

$$\begin{array}{cc}\hfill & {\dot{V}}_i\left(Z_i\left(t\right)\right)\hfill \\ \hfill & = -L\Vert Z_i\left(t\right){\Vert }^2\hfill \\ \hfill & + 2{Z_i}^{\mathrm{T}}\left(t\right)P_i\left[\begin{array}{c}{\phi }_i(t,\delta \left(t\right),{d_i}^{\left(p\right)}\left(t\right))\\ O\end{array}\right]\hfill \\ \hfill & + 2L{Z_i}^{\mathrm{T}}\left(t\right)P_i\left[\begin{array}{c}{N}_i\\ N_i\end{array}\right]K_i\left[{\widehat{\delta }}_i\left(t_k\right)-{\widehat{\delta }}_i\left(t\right)\right]\hfill \\ \hfill & + 2L{Z_i}^{\mathrm{T}}\left(t\right)P_i\left[\begin{array}{c}O\\ H_i\end{array}\right]\left[{\delta }_{i1}\left(t_k\right)-{\delta }_{i1}\left(t\right)\right].\hfill \end{array}$$

Let $V\left(Z\left(t\right)\right)=V_1\left(Z_1\left(t\right)\right)+V_2\left(Z_2\left(t\right)\right)$. Then, one has

$$\begin{array}{cc}\hfill \dot{V}\left(Z\left(t\right)\right)& = -L(\parallel Z_1\left(t\right){\parallel }^2+\parallel Z_2\left(t\right){\parallel }^2)\hfill \\ \hfill & + 2Z_1^{\mathrm{T}}\left(t\right)P_1\left[\begin{array}{c}{\psi }_1(t,\delta \left(t\right),{d_1}^{\left(p\right)}\left(t\right))\\ O\end{array}\right]\hfill \\ \hfill & + 2Z_2^{\mathrm{T}}\left(t\right)P_2\left[\begin{array}{c}{\psi }_2(t,\delta \left(t\right),{d_2}^{\left(p\right)}\left(t\right))\\ O\end{array}\right]\hfill \\ \hfill & + 2L{Z_1}^{\mathrm{T}}\left(t\right)P_1\left[\begin{array}{c}O\\ H_1\end{array}\right]\left[{\delta }_{11}\left(t_k\right)-{\delta }_{11}\left(t\right)\right]\hfill \\ \hfill & + 2L{Z_2}^{\mathrm{T}}\left(t\right)P_2\left[\begin{array}{c}O\\ H_2\end{array}\right]\left[{\delta }_{21}\left(t_k\right)-{\delta }_{21}\left(t\right)\right]\hfill \\ \hfill & + 2L{Z_1}^{\mathrm{T}}\left(t\right)P_1\left[\begin{array}{c}{N}_1\\ N_1\end{array}\right]K_1\left[{\widehat{\delta }}_1\left(t_k\right)-{\widehat{\delta }}_1\left(t\right)\right]\hfill \\ \hfill & + 2L{Z_2}^{\mathrm{T}}\left(t\right)P_2\left[\begin{array}{c}{N}_2\\ N_2\end{array}\right]K_2\left[{\widehat{\delta }}_2\left(t_k\right)-{\widehat{\delta }}_2\left(t\right)\right].\hfill \end{array}$$

(13)

In what follows, we will give estimations for some terms on the right-hand side of Equation (13). First, according to Assumptions 1 and Equation (4), there exists a constant $c_1$ such that $∥{\psi }_i(t,\delta \left(t\right),{d_i}^{\left(p\right)}\left(t\right))∥\le c_1∥Z∥+\eta .$

Therefore, we can observe that

$$\begin{array}{cc}\hfill & ∥2{Z_i}^T\left(t\right)P_i\left[\begin{array}{c}{\psi }_i(t,\delta \left(t\right),{d_i}^{\left(p\right)}\left(t\right))\\ O\end{array}\right]∥\hfill \\ \hfill & \le 2\parallel Z_i\parallel \parallel P_i\parallel (c_1\parallel Z_i\parallel +\eta )\hfill \\ \hfill & =2c_1\parallel Z_i{\parallel }^2\parallel P_i\parallel +2\eta \parallel P_i\parallel \parallel Z_i\parallel \hfill \\ \hfill & \le 2c_1\parallel Z_i{\parallel }^2\parallel P_i\parallel +\parallel P_i\parallel {\eta }^2+\parallel P_i\parallel \parallel Z_i{\parallel }^2\hfill \\ \hfill & =(2c_1+\parallel P_i\parallel )\parallel Z_i{\parallel }^2+\parallel P_i\parallel {\eta }^2\hfill \end{array}$$

(14)

The following lemma is needed, which is beneficial to estimate the last two terms.

Lemma 1.

There exists a function $ϵ\left(t\right)>0$, such that the following inequality holds

$$\begin{array}{c}\hfill \parallel Z\left(t\right)-Z\left(t_k\right)\parallel \le {\displaystyle \frac{ϵ\left(t\right)}{(1-ϵ(t\left)\right)}}\parallel Z\left(t\right)\parallel ,\forall t\in [t_k,t_{k+1}]\end{array}$$

(15)

The proof of Lemma 1 is included in [8].

With the help of Equation (15), the following estimates can be obtained:

$$\begin{array}{cc}\hfill & ∥2L{Z}_i^{\mathrm{T}}\left(t\right)P_i\left[\begin{array}{c}O\\ H_i\end{array}\right]\left[{\delta }_{i1}\left(t_k\right)-{\delta }_{i1}\left(t\right)\right]∥\hfill \\ \hfill & \le 2L{\displaystyle \frac{ϵ\left(t\right)}{(1-ϵ(t\left)\right)}}\parallel P_i\parallel \parallel H_i\parallel \parallel Z_i{\parallel }^2\hfill \end{array}$$

(16)

and

$$\begin{array}{cc}\hfill & ∥2L{Z_i}^{\mathrm{T}}\left(t\right)P_i\left[\begin{array}{c}{N}_i\\ N_i\end{array}\right]K_i\left[{\widehat{\delta }}_i\left(t_k\right)-{\widehat{\delta }}_i\left(t\right)\right]∥\hfill \\ \hfill & \le 2\sqrt{2}L{\displaystyle \frac{ϵ\left(t\right)}{(1-ϵ(t\left)\right)}}\parallel P_i\parallel \parallel K_i\parallel \parallel Z_i{\parallel }^2\hfill \end{array}$$

(17)

Inserting Equations (14), (16), and (17) into Equation (13), we have

$$\begin{array}{cc}\hfill & \dot{V}\left(Z\left(t\right)\right)\hfill \\ \hfill & \le -{L\parallel Z\parallel }^2+2(2c_1+{\parallel P\parallel )\parallel Z\parallel }^2+\parallel P\parallel {\eta }^2\hfill \\ \hfill & +2L{\displaystyle \frac{ϵ\left(t\right)}{(1-ϵ(t\left)\right)}}\parallel P\parallel (\parallel H_1\parallel +\parallel H_2{\parallel )\parallel Z\parallel }^2\hfill \\ \hfill & +2\sqrt{2}L{\displaystyle \frac{ϵ\left(t\right)}{(1-ϵ(t\left)\right)}}\parallel P\parallel (\parallel K_1\parallel +\parallel K_2{\parallel )\parallel Z\parallel }^2\hfill \\ \hfill & \le \left({\displaystyle \frac{-L}{{\lambda }_M\left(P\right)}}+{\displaystyle \frac{c_2}{{\lambda }_m\left(P\right)}}+{\displaystyle \frac{2Lϵ\left(t\right)\parallel P\parallel 𝒱}{(1-ϵ\left(t\right)){\lambda }_m\left(P\right)}}\right)V\left(Z\left(t\right)\right)\hfill \\ \hfill & +\parallel P\parallel {\eta }^2\hfill \end{array}$$

(18)

To ensure the convergence of the closed-loop system, the coefficient before $V\left(Z\right(t\left)\right)$ should be negative. We choose an appropriate constant L such that

$$\begin{array}{c}\hfill L>max\left\{{\displaystyle \frac{{\lambda }_M\left(P\right)(2c_1+\parallel P\parallel )(1-ϵ\left(t\right))}{{\lambda }_m\left(P\right)(1-ϵ\left(t\right))-2{\lambda }_M\left(P\right)ϵ\left(t\right)\parallel P\parallel 𝒱}},1\right\}\end{array}$$

(19)

From Equation (18), we have

$$\begin{array}{cc}\hfill & V\left(Z\right(t\left)\right)\hfill \\ \hfill & \le {\displaystyle \frac{{\lambda }_m\left(P\right){\lambda }_M\left(P\right)(1-ϵ\left(t\right)){\eta }^2\parallel P\parallel }{\Phi \left(ϵ\right(t),P,L,𝒱)}}\hfill \\ \hfill & + e^{-{\displaystyle \frac{\Phi \left(ϵ\right(t),P,L,𝒱)}{{\lambda }_m\left(P\right){\lambda }_M\left(P\right)(1-ϵ\left(t\right))}}t}\hfill \\ \hfill & \times \left[V\left(0\right)-{\displaystyle \frac{{\lambda }_m\left(P\right){\lambda }_M\left(P\right)(1-ϵ\left(t\right)){\eta }^2\parallel P\parallel }{\Phi \left(ϵ\right(t),P,L,𝒱)}}\right]\hfill \end{array}$$

When the scaling gain L meets the condition Equation (19), then the states of closed-loop System Equation (11) can globally asymptotically converge to the bounded region $\mathfrak{B}$. □

Remark 2.

In fact, it can be proved that the conclusion of Theorem 1 still holds for the piecewise smooth trajectories $s\left(t\right)$.

Remark 3.

According to the proposed control strategy, the disturbances are compensated for by the estimations of the $\mathit{GPIO}$, while the uncertainty from another part of the system can be suppressed by the high gain, which is beneficial to the $\mathit{DDHG}$ system.

4. Parameters Selection

The following is the procedure of parameter selection.

Step 1: Choose the appropriate p to extend the system.

Step 2: A suitable $L>1$ satisfying Equation (19) is selected to make the closed-loop system stable, and coordinate transformation is carried out according to Equation (7).

Step 3: Select the appropriate observer gain $a_{i1},a_{i2},\dots ,a_{i,p+2}$ to satisfy the Hurwitz polynomial.

Step 4: Select the appropriate controller gain $k_{i1},k_{i2},\dots ,k_{i,p+2}$ to satisfy the Hurwitz polynomial.

Step 5: Choose the appropriate sampling period T.

5. Simulation Examples

In this part, we will show the effectiveness of the proposed control scheme for the DDHG system through two sets of simulation experiments. Due to the symmetrical nature of the system’s structure, the same trajectories are given for both subsystems. Although the estimation effect will be better with the increase of the observer order p, the increase of the order will increase the gain of the observer, so $p=2$ is chosen in the experiment. At the same time, the generalized-proportional-integral observer (GPIO) will be reduced to an extended-state observer (ESO) at $p=1$, which is employed to compare with the GPIO in terms of the estimation for both the tracking error and lumped disturbance. We can have the comparative controller, which consists of the decentralized-output feedback sampled-data controller Equation (10) with the ESO (ESO-DOFSC), while the control scheme presented in this paper is denoted as GPIO-DOFSC. The integral of the time-multiplied absolute value of error (ITAE) and the root mean square error (RMSE) are used as the performance indices [32].

Table 2. The values of experimental parameters.

Name	Description	Value
$K_f$	Force constant	62.8 N/A
$M_1$	Mass of carriage 1	16.5 kg
$M_2$	Mass of carriage 2	18.4 kg
$K_v$	Stiffness of flexure	4887.3 N/m
$\Gamma$	Damping coefficient	172.7 Ns/m

lists the system parameter values.

Case I: Continuous and smooth tracking trajectory

Consider the sinusoidal tracking trajectory curve, which is continuous and smooth in Figure 3.

The control parameters for GPIO-DOFSC are set as follows: $L=8, k_{11}=k_{12}=k_{21}=k_{22}=4, h_{11}=h_{21}=16, h_{12}=h_{22}=96, h_{13}=h_{23}=256, h_{14}=h_{24}=256$, and the sampling period $T=0.005$. To have a fair comparison, the same bandwidths of controller and observer are still selected as the ESO-DOFSC control scheme. $h_{11}=h_{21}=12, h_{12}=h_{22}=48, h_{13}=h_{23}=64$ in the ESO-DOFSC control scheme.

The external disturbance is taken as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}di{s}_1\left(t\right)=0.3sin2t+0.5sint+0.5\hfill \\ di{s}_2\left(t\right)=0.4cos2t+0.2sin2t+0.3\hfill \end{array}\right.\end{array}$$

Figure 4 displays the simulation results of the GPIO-DOFSC and ESO-DOFSC methods.

The actual and expected positions of the subsystem of the two methods are shown in Figure 4a, which shows that the decentralized-output feedback sampled-data disturbance controller can render system outputs to the expected positions in a short time. It can be seen from Figure 4a,b that the system under the action of GPIO-DOFSC scheme is always around the zero-tracking error. Comparatively, the system under the action of ESO-DOFSC has poor tracking features. This indicates that the control scheme presented in this paper is reasonable and effective. Figure 4c shows the estimations of the lumped disturbance of the two observers in each subsystem, which indicates that the proposed control scheme can effectively compensate and estimate the disturbance. The response curves of the control signal under the two observers are illustrated in Figure 4d. The simulation results show that the system with the GPIO-DOFSC scheme has better performance for the continuous smooth trajectory, and the purpose of disturbance rejection can be achieved. The values of ITAE and RMSE also demonstrate the effectiveness of the proposed scheme. The specific results are shown in

Table 3. Performance index comparisons for two different control approaches.

Test Type	Control Approach	ITAE	RMSE
Case I	GPIO-DOFSC	0.1068	0.0021
	ESO-DOFSC	1.9825	0.0116
Case II	GPIO-DOFSC	0.0202	0.0009
	ESO-DOFSC	0.2041	0.0021

.

In order to verify the effectiveness of the control scheme for piecewise smooth trajectories, the tracking trajectories in [4] are employed in Case II.

Case II: Continuous and piecewise smooth tracking trajectory

Consider the point-to-point curve, which is continuous and piecewise smooth in Figure 5.

The control parameters are set as follows: $L = 10, k_{11} = 9, k_{12} = 6, k_{21} = 9,$$k_{22} = 6$, $h_{11} = h_{21} = 24, h_{12} = h_{22} = 216, h_{13} = h_{23} = 828, h_{14} = h_{24} = 1296$, and $T = 0.002$. The same bandwidth of controller and observer are still selected as the ESO-DOFSC control scheme. Therefore, $h_{11} = h_{21} = 18, h_{12} = h_{22} = 108, h_{13} = h_{23} = 216$ in the ESO-DOFSC control scheme. External interference is the same as Case I. Figure 6 displays the simulation results.

Figure 6a demonstrates that the decentralized-output feedback sampled-data disturbance rejection controller can also put the output track in the desired position for piecewise smooth trajectories in a short time. Comparatively, the tracking effect of the GPIO-DOFSC scheme is significantly more satisfactory than that of the ESO-DOFSC scheme. Moreover, Table 3 shows the quantitative comparison of the two methods under the ITAE and RMSE, i.e., two performance indicators. The index value of the control scheme proposed in the paper is significantly smaller, indicating that the GPIO-DOFSC scheme is still better in the case of a piecewise smooth trajectory.

6. Conclusions

The problem of decentralized-output feedback sampled-data disturbance rejection control for the DDHG system has been studied in this paper. By designing a simple sampled-data output feedback controller with tunable scaling gain and sampling period, the closed-loop system can achieve global stability under the conditions of linear growth and information of the output at discrete points. The simulation results show that the proposed control scheme could be used to deal with both the smooth and piecewise smooth trajectory-tracking problems effectively. Compared to the ESO-DOFSC scheme, the proposed GPIO-DOFSC control scheme made the ITAE and RMSE reduce by 90% and 57%, respectively.

7. Future Work

The obtained results are based on fixed-period sampling control. Designing a decentralized event-triggered output feedback disturbance rejection controller for the DDHG system is one of our future research endeavors.