A Novel Approach to Ruled Surfaces Using Adjoint Curve

Abstract

In this study, ruled surfaces are examined where the direction vectors are unit vectors derived from Smarandache curves, and the base curve is taken as an adjoint curve constructed using the integral curve of a Smarandache-type curve generated from the first and second Bishop normal vectors. The newly generated ruled surfaces will be referred to as Bishop adjoint ruled surfaces. Explicit expressions for the Gaussian and mean curvatures of these surfaces have been obtained, and their fundamental geometric properties have been analyzed in detail. Additionally, the conditions for developability, minimality, and singularities have been investigated. The asymptotic and geodesic behaviors of parametric curves have been examined, and the necessary and sufficient conditions for their characterization have been derived. Furthermore, the geometric properties of the surface generated by the Bishop adjoint curve and its relationship with the choice of the original curve have been established. The constructed ruled surfaces exhibit a notable degree of geometric regularity and symmetry, which naturally arise from the structural behavior of the associated adjoint curves and direction fields. This underlying symmetry plays a central role in their formulation and classification within the broader context of differential geometry. Finally, the obtained surfaces are illustrated with figures.

1. Introduction

The study of curves and surfaces in differential geometry plays a significant role in understanding the geometric and topological properties of space. Among the various analytical tools in this field, the Bishop frame offers a flexible alternative to the classical Frenet–Serret frame. While the Frenet frame may become undefined at points where the curvature vanishes, the Bishop frame remains well-defined along the entire curve. This property makes it particularly useful for analyzing curves with zero torsion or polynomial structure. Due to these advantages, the Bishop frame has become an indispensable tool in geometric modeling, computer-aided design (CAD), and kinematics. Bishop provided a detailed study of the advantages of the parallel transport frame and its comparison with the Frenet frame in three-dimensional Euclidean space [1].

One of the most extensively studied topics in differential geometry is the theory of ruled surfaces, which has garnered significant interest among researchers. A ruled surface is defined as a surface formed by the continuous motion of a straight line along a given curve in three-dimensional space. These surfaces are characterized by a family of lines (called rulings) that determine their structure [2]. Due to their unique structural properties, ruled surfaces are widely used in geometric modeling and architectural design [3,4]. Two fundamental geometric properties of ruled surfaces are developability and minimality. Developable surfaces are those that can be unrolled onto a flat plane without distortion and have zero Gaussian curvature. These surfaces are commonly used in sheet metal forming, shipbuilding, and textile design, as they allow materials to be bent and cut with minimal deformation, thereby simplifying manufacturing processes. On the other hand, minimal surfaces are those that locally minimize their surface area and have zero mean curvature. Such surfaces naturally appear in soap films, membrane structures, and material science, where energy minimization plays a critical role. Numerous studies on developable and minimal surfaces can be found in the literature (see [5,6,7,8]).

In addition to their theoretical contributions, ruled surfaces are indispensable in many real-world engineering problems. They are especially important in areas such as kinematics, computer-aided design (CAD), and geometric modeling. These applications often require continuous and smooth transitions between different positions or states. The flexibility of the Bishop frame allows for stable and smooth surface constructions without encountering singularities. This is a significant advantage in fields like robot motion planning, surface optimization, and CNC tool path design. As a result, there is a growing need for new types of ruled surfaces that are not only mathematically elegant but also computationally feasible and structurally advantageous. In this regard, the design of new ruled surfaces in Euclidean and Lorentzian spaces using different moving frames has recently become a noteworthy and important research topic. Some of the recent studies in this field can be found in references [6,9,10,11,12,13,14,15,16].

An interesting class of curves in differential geometry is Smarandache curves, which were first introduced in Minkowski space [17]. These curves are defined such that their position vectors consist of the Frenet–Serret frame vectors of another regular curve. In recent years, these curves have also been studied in Euclidean space, finding applications in various areas such as kinematics, robotics, and theoretical physics [18]. Many studies on this subject are available in the literature [19,20,21,22]. Introducing new curves and surfaces in differential geometry is crucial for expanding its application areas. In this study, a new family of ruled surfaces is constructed using the adjoint curves of Smarandache curves, which possess wide application potential. The base curve is defined as the adjoint curve obtained from the integral of a Smarandache-type curve derived from the first and second Bishop normal vectors of a given curve $\alpha$. The direction vectors are composed of unit vectors obtained through transformations of Smarandache curves. As a result, seven distinct surfaces, denoted by ${\Phi }_1(s,v)$ through ${\Phi }_7(s,v)$ are generated and referred to as Bishop adjoint ruled surfaces. For each surface, the Gaussian and mean curvatures are calculated, and the conditions for developability, minimality, and singularities are examined in detail. Additionally, the asymptotic and geodesic behaviors of the parametric curves on these surfaces are investigated, and the necessary and sufficient conditions for these properties are established. Furthermore, the relationship between the geometric properties of the surface and the originally selected curve is analyzed. Finally, graphical illustrations of the constructed surfaces are provided to highlight their geometric features.

Although various approaches exist for constructing ruled surfaces many based on classical Frenet formulations or direct parametrizations the method proposed in this study offers significant advantages. The ruled surfaces constructed using adjoint curves derived from Bishop-type Smarandache curves inherently avoid the singularities that arise in classical methods, particularly in regions where curvature or torsion vanishes. This alternative frame enables smoother and more stable surface generation and is highly beneficial for applications requiring geometric regularity and structural coherence. Comparisons with previous techniques demonstrate the computational feasibility and geometric consistency achieved through the proposed method. Additionally, the constructed ruled surfaces exhibit an intrinsic symmetry pattern that naturally emerges from the adjoint curve mechanism and directional transformations. This symmetry makes a notable contribution to the classification and structural integrity of the surfaces within the frame of differential geometry.

2. Preliminaries

This section introduces some fundamental concepts required for the subsequent developments. Let $\alpha =\alpha \left(s\right)$ be a differentiable unit speed curve in ${\mathbb{E}}^3$, with Frenet apparatus $\{\mathbf{t},\mathbf{n},\mathbf{b},\kappa ,\tau \}$. When $\alpha$ is a unit speed curve, its unit tangent vector is $\mathbf{t}\left(s\right)={\alpha }^{\prime }\left(s\right)$ and its curvature is $\kappa =\parallel {\alpha }^{″}\left(s\right)\parallel$. The relation ${\alpha }^{″}\left(s\right)=\kappa \left(s\right)\mathbf{n}\left(s\right)$ and $\mathbf{b}\left(s\right)=\mathbf{t}\left(s\right)\times \mathbf{n}\left(s\right)$ gives the principal normal vector and the unit binormal vector of $\alpha$, respectively.

Next, the well-known Frenet formula is expressed as:

$$\left[\begin{array}{c}{\mathbf{t}}^{\prime }\\ {\mathbf{n}}^{\prime }\\ {\mathbf{b}}^{\prime }\end{array}\right]=\left[\begin{array}{ccc}0& \kappa & 0\\ -\kappa & 0& \tau \\ 0& -\tau & 0\end{array}\right]\left[\begin{array}{c}\mathbf{t}\\ \mathbf{n}\\ \mathbf{b}\end{array}\right]$$

where $\tau \left(s\right)=⟨{\mathbf{n}}^{\prime }\left(s\right),\mathbf{b}\left(s\right)⟩$ is the torsion of $\alpha$.

The derivative formula of the Bishop frame is given as:

$$\left[\begin{array}{c}{\mathbf{t}}^{\prime }\\ {\mathit{\zeta }}_1^{\prime }\\ {\mathit{\zeta }}_2^{\prime }\end{array}\right]=\left[\begin{array}{ccc}0& k_1& k_2\\ -k_1& 0& 0\\ -k_2& 0& 0\end{array}\right]\left[\begin{array}{c}\mathbf{t}\\ {\mathit{\zeta }}_1\\ {\mathit{\zeta }}_2\end{array}\right]$$

The set $\{\mathbf{t},{\mathit{\zeta }}_1,{\mathit{\zeta }}_2\}$ is referred to as the Bishop trihedron. The curvatures $k_1$ and $k_2$ are called Bishop curvatures.

The relation matrix can be expressed as:

$$\left[\begin{array}{c}\mathbf{t}\\ \mathbf{n}\\ \mathbf{b}\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\theta \left(s\right)& sin\theta \left(s\right)\\ 0& -sin\theta \left(s\right)& cos\theta \left(s\right)\end{array}\right]\left[\begin{array}{c}\mathbf{t}\\ {\mathit{\zeta }}_1\\ {\mathit{\zeta }}_2\end{array}\right]$$

where $\theta \left(s\right)=arctan\left({\displaystyle \frac{k_2\left(s\right)}{k_1\left(s\right)}}\right)$, $k_1\left(s\right)\ne 0$, $\tau \left(s\right)=-{\displaystyle \frac{d\theta \left(s\right)}{ds}}$ and $\kappa \left(s\right)=\sqrt{k_1^2\left(s\right)+k_2^2\left(s\right)}$. Thus, $k_1$ and $k_2$ effectively correspond to Cartesian coordinates for the polar coordinates $(\kappa ,\theta )$ with $\theta \left(s\right)=-\int \tau \left(s\right)ds+{\theta }_0$. The Bishop curvatures are given by:

$$k_1\left(s\right)=\kappa \left(s\right)cos\theta \left(s\right),k_2\left(s\right)=\kappa \left(s\right)sin\theta \left(s\right).$$

Definition 1 

([23]). Let α be an s-arc length parameterized regular curve with nonvanishing torsion and $\{{\mathbf{t}}_{\alpha },{\mathbf{n}}_{\alpha },{\mathbf{b}}_{\alpha }\}$ be the Frenet frame of α. The adjoint curve of α is defined by:

$$\beta \left(s\right)={\int }_{s_0}^s{\mathbf{b}}_{\alpha }\left(u\right)du.$$

Definition 2 

([19]). Let α be an s-arc length parameterized regular curve with nonvanishing torsion and $\{{\mathbf{t}}_{\alpha },{\mathbf{n}}_{\alpha },{\mathbf{b}}_{\alpha }\}$ be the Frenet frame of α. Smarandache TN, NB, and TNB curves are defined respectively by:

$$\beta ={\displaystyle \frac{1}{\sqrt{2}}}({\mathbf{t}}_{\alpha }+{\mathbf{n}}_{\alpha }),\gamma ={\displaystyle \frac{1}{\sqrt{2}}}({\mathbf{n}}_{\alpha }+{\mathbf{b}}_{\alpha }),\mu ={\displaystyle \frac{1}{\sqrt{3}}}({\mathbf{t}}_{\alpha }+{\mathbf{n}}_{\alpha }+{\mathbf{b}}_{\alpha }).$$

To assist the reader in following the derivations throughout the paper, Table 1 summarizes frequently used notations related to the Bishop frame, adjoint curves, and the construction of ruled surfaces. In particular, the definitions of each ruled surface ${\Phi }_i(s,v)$ are included to clarify their generating vector fields.

Table 1. Summary of frequently used notations and ruled surface definitions.

Symbol	Meaning
$\alpha (s)$	Unit speed curve in Euclidean 3-space
${\mathbf{t}}_{\alpha }$	Tangent vector of $\alpha (s)$
${\mathit{\zeta }}_1^{\alpha }$, ${\mathit{\zeta }}_2^{\alpha }$	Bishop frame vectors orthogonal to ${\mathbf{t}}_{\alpha }$
$k_1^{\alpha }$, $k_2^{\alpha }$	Bishop curvatures of $\alpha (s)$
$\beta (s)$	Bishop adjoint curve derived from $\alpha (s)$
${\mathbf{t}}_{\beta }$	Tangent vector of $\beta (s)$
${\mathit{\zeta }}_1^{\beta }$, ${\mathit{\zeta }}_2^{\beta }$	Bishop frame vectors for $\beta (s)$
$k_1^{\beta }$, $k_2^{\beta }$	Bishop curvatures of $\beta (s)$
${\Phi }_1(s,v)$	Ruled surface generated by ${\mathbf{t}}_{\beta }(s)$
${\Phi }_2(s,v)$	Ruled surface generated by ${\mathit{\zeta }}_1^{\beta }(s)$
${\Phi }_3(s,v)$	Ruled surface generated by ${\mathit{\zeta }}_2^{\beta }(s)$
${\Phi }_4(s,v)$	Ruled surface generated by ${\displaystyle \frac{1}{\sqrt{2}}}({\mathbf{t}}_{\beta }+{\mathit{\zeta }}_1^{\beta })$
${\Phi }_5(s,v)$	Ruled surface generated by ${\displaystyle \frac{1}{\sqrt{2}}}({\mathbf{t}}_{\beta }+{\mathit{\zeta }}_2^{\beta })$
${\Phi }_6(s,v)$	Ruled surface generated by ${\displaystyle \frac{1}{\sqrt{2}}}({\mathit{\zeta }}_1^{\beta }+{\mathit{\zeta }}_2^{\beta })$
${\Phi }_7(s,v)$	Ruled surface generated by ${\displaystyle \frac{1}{\sqrt{3}}}({\mathbf{t}}_{\beta }+{\mathit{\zeta }}_1^{\beta }+{\mathit{\zeta }}_2^{\beta })$

Definition 3 

([24]).  Let α be an s-arc length parameterized regular curve with Bishop apparatus $\{{\mathbf{t}}_{\alpha },{\mathit{\zeta }}_1^{\alpha },{\mathit{\zeta }}_2^{\alpha },k_1^{\alpha },k_2^{\alpha }\}$, where ${\mathbf{t}}_{\alpha }$ denotes the unit tangent vector of α, ${\mathit{\zeta }}_1^{\alpha }$ and ${\mathit{\zeta }}_2^{\alpha }$ are the first and second Bishop normal vectors, respectively, and $k_1^{\alpha }$, $k_2^{\alpha }$ are the corresponding Bishop curvatures. The ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve associated with α is defined by:

$$\beta \left(s^{*}\left(s\right)\right)={\displaystyle \frac{1}{\sqrt{2}}}\int ({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right))ds.$$

Theorem 1 

([24]). Let α be an s-arc length parameterized regular curve in ${\mathbb{E}}^3$ with Bishop apparatus $\{{\mathbf{t}}_{\alpha },{\mathit{\zeta }}_1^{\alpha },{\mathit{\zeta }}_2^{\alpha },k_1^{\alpha },k_2^{\alpha }\}$, and let β be the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve of α. The Frenet vector fields, curvature, and torsion of β are given by:

$${\mathbf{t}}_{\beta }={\displaystyle \frac{1}{\sqrt{2}}}({\mathit{\zeta }}_1^{\alpha }+{\mathit{\zeta }}^{\alpha }),{\mathbf{n}}_{\beta }=-{\mathbf{t}}_{\alpha },{\mathbf{b}}_{\beta }={\displaystyle \frac{1}{\sqrt{2}}}({\mathit{\zeta }}_1^{\alpha }-{\mathit{\zeta }}_2^{\alpha }),$$

$${\kappa }_{\beta }={\displaystyle \frac{1}{\sqrt{2}}}{k}_2^{\alpha }(1+h),$$

(1)

$${\tau }_{\beta }=0,$$

(2)

where $h={\displaystyle \frac{k_1^{\alpha }}{k_2^{\alpha }}}$.

Theorem 2 

([24]). Let α be an s-arc length parameterized regular curve, and β its adjoint curve in ${\mathbb{E}}^3$, with the Bishop apparatus of these curves given, respectively, as:

$$\{{\mathbf{t}}_{\alpha },{\mathit{\zeta }}_1^{\alpha },{\mathit{\zeta }}_2^{\alpha },k_1^{\alpha },k_2^{\alpha }\}\mathrm{and}\{{\mathbf{t}}_{\beta },{\mathit{\zeta }}_1^{\beta },{\mathit{\zeta }}_2^{\beta },k_1^{\beta },k_2^{\beta }\}.$$

Then, the Bishop vector fields and curvatures of β are given by:

$${\mathit{\zeta }}_1^{\beta }=-cos{\theta }_{\beta }{\mathbf{t}}_{\alpha }+{\displaystyle \frac{1}{\sqrt{2}}}sin{\theta }_{\beta }{\mathit{\zeta }}_1^{\alpha }-{\displaystyle \frac{1}{\sqrt{2}}}sin{\theta }_{\beta }{\mathit{\zeta }}_2^{\alpha },$$

$${\mathit{\zeta }}_2^{\beta }=-sin{\theta }_{\beta }{\mathbf{t}}_{\alpha }-{\displaystyle \frac{1}{\sqrt{2}}}cos{\theta }_{\beta }{\mathit{\zeta }}_1^{\alpha }+{\displaystyle \frac{1}{\sqrt{2}}}cos{\theta }_{\beta }{\mathit{\zeta }}_2^{\alpha },$$

$$\begin{array}{cc}\hfill k_1^{\beta }& ={\displaystyle \frac{1}{\sqrt{2}}}{k}_2^{\alpha }(1+h)cos{\theta }_{\beta },\hfill \\ \hfill k_2^{\beta }& ={\displaystyle \frac{1}{\sqrt{2}}}{k}_2^{\alpha }(1+h)sin{\theta }_{\beta },\hfill \end{array}$$

(3)

where ${\theta }_{\beta }=-\int {\tau }_{\beta }\left(s\right)ds$ and $h={\displaystyle \frac{k_1^{\alpha }}{k_2^{\alpha }}}$.

Theorem 3 

([25]). Let the unit speed curve $\alpha :I\to {\mathbb{E}}^3$ be a slant helix with non-zero natural Bishop curvatures. Then α is a slant helix if and only if ${\displaystyle \frac{k_1}{k_2}}$ is constant.

A ruled surface is a type of surface generated by the motion of a straight line depending on the parameter of a curve. The parametric equation of such a surface is given by:

$$\Phi (s,v)=\alpha \left(s\right)+vx\left(s\right)$$

where $\alpha \left(s\right)$ is referred to as the base curve, $x\left(s\right)$ is the director curve, which determines the orientation of the ruling lines, and v is a constant representing displacement along the ruling direction.

The normal vector field $U_{\Phi }$, the Gaussian curvature $K_{\Phi }$, and the mean curvature $H_{\Phi }$ of the surface $\Phi (s,v)$ are given by the following expressions:

$$U_{\Phi }={\displaystyle \frac{{\Phi }_s\times {\Phi }_v}{\parallel {\Phi }_s\times {\Phi }_v\parallel }}$$

(4)

$$K_{\Phi }={\displaystyle \frac{eg-f^2}{EG-F^2}}$$

(5)

$$H_{\Phi }={\displaystyle \frac{Eg-2fF+eG}{2(EG-F^2)}}$$

(6)

where the first and second fundamental form coefficients are defined as:

$$E=⟨{\Phi }_s,{\Phi }_s⟩,F=⟨{\Phi }_s,{\Phi }_v⟩,G=⟨{\Phi }_v,{\Phi }_v⟩,$$

$$e=⟨{\Phi }_{ss},U_{\Phi }⟩,f=⟨{\Phi }_{sv},U_{\Phi }⟩,g=⟨{\Phi }_{vv},U_{\Phi }⟩.$$

Proposition 1 

([26]). A ruled surface is developable if and only if its Gaussian curvature vanishes.

Proposition 2 

([26]). A regular surface is minimal if and only if its mean curvature vanishes.

3. Ruled Surfaces Obtained from the Adjoint Curve of the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$ Smarandache Curve According to the Bishop Frame

The ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$ Bishop adjoint curve used in this section was previously defined in Definition 3. Based on this definition, the analysis of the corresponding ruled surfaces is carried out here.

3.1. Adjoint Ruled Surfaces with Director Vector ${\mathbf{t}}_{\beta }$

Definition 4. 

Let β be the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve of α in ${\mathbb{E}}^3$, with the associated Bishop apparatus of β denoted as $\{{\mathbf{t}}_{\beta },{\mathit{\zeta }}_1^{\beta },{\mathit{\zeta }}_2^{\beta },k_1^{\beta },k_2^{\beta }\}$. Consider β as the base curve, and ${\mathbf{t}}_{\beta }$ the generator vector. We define the ${\Phi }_1(s,v)$-Bishop adjoint ruled surface as follows:

$${\Phi }_1(s,v)={\displaystyle \frac{1}{\sqrt{2}}}\int ({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right))ds+v{\mathbf{t}}_{\beta }\left(s\right).$$

Theorem 4. 

The Gauss and mean curvatures of the ${\Phi }_1(s,v)$-Bishop adjoint ruled surface are given by:

$$K_{{\Phi }_1}=0,$$

(7)

$$H_{{\Phi }_1}={\displaystyle \frac{{\left({\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}\right)}^{\prime }{\left(k_2^{\beta }\right)}^2}{2v{\left({\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)}^2}}.$$

(8)

Proof. 

The partial derivatives of the ruled surface ${\Phi }_1(s,v)=\beta \left(s\right)+v{\mathbf{t}}_{\beta }\left(s\right)$ are computed using the Bishop frame as follows:

$${\Phi }_{1s}(s,v)={\mathbf{t}}_{\beta }+v{k}_1^{\beta }{\mathit{\zeta }}_1^{\beta }+v{k}_2^{\beta }{\mathit{\zeta }}_2^{\beta },$$

$${\Phi }_{1ss}(s,v)=-v\left({(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right){\mathbf{t}}_{\beta }+\left(k_1^{\beta }+v{(k_1^{\beta })}^{\prime }\right){\mathit{\zeta }}_1^{\beta }+\left(k_2^{\beta }+v{(k_2^{\beta })}^{\prime }\right){\mathit{\zeta }}_2^{\beta },$$

$${\Phi }_{1v}(s,v)={\mathbf{t}}_{\beta },{\Phi }_{1sv}(s,v)=k_1^{\beta }{\mathit{\zeta }}_1^{\beta }+k_2^{\beta }{\mathit{\zeta }}_2^{\beta },{\Phi }_{1vv}(s,v)=0.$$

The unit normal vector field from Equation (4) is:

$$U_{{\Phi }_1}={\displaystyle \frac{{\Phi }_{1s}\times {\Phi }_{1v}}{\parallel {\Phi }_{1s}\times {\Phi }_{1v}\parallel }}={\displaystyle \frac{k_2^{\beta }}{\sqrt{{(k_1^{\beta })}^2+{(k_2^{\beta })}^2}}}{\mathit{\zeta }}_1^{\beta }-{\displaystyle \frac{k_1^{\beta }}{\sqrt{{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2}}}{\mathit{\zeta }}_2^{\beta }.$$

The first fundamental form coefficients are:

$$E_{{\Phi }_1}=⟨{\Phi }_{1s},{\Phi }_{1s}⟩=1+v^2\left({(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right),F_{{\Phi }_1}=⟨{\Phi }_{1s},{\Phi }_{1v}⟩=1,G_{{\Phi }_1}=⟨{\Phi }_{1v},{\Phi }_{1v}⟩=1.$$

The second fundamental form coefficients are:

$$e_{{\Phi }_1}=⟨{\Phi }_{1ss},U_{{\Phi }_1}⟩={\displaystyle \frac{v\left(k_2^{\beta }{(k_1^{\beta })}^{\prime }-k_1^{\beta }{(k_2^{\beta })}^{\prime }\right)}{\sqrt{{(k_1^{\beta })}^2+{(k_2^{\beta })}^2}}},f_{{\Phi }_1}=⟨{\Phi }_{1sv},U_{{\Phi }_1}⟩=0,g_{{\Phi }_1}=⟨{\Phi }_{1vv},U_{{\Phi }_1}⟩=0.$$

Finally, by substituting these into Equations (5) and (6), we obtain Equations (7) and (8). □

Corollary 1. 

The ${\Phi }_1(s,v)$-Bishop adjoint ruled surface is a developable surface.

Proof. 

From Equation (7) and Proposition 1, the surface ${\Phi }_1(s,v)$ is a developable surface. □

Corollary 2 

([24]). If the curve α is an s-arc length parameterized regular curve in ${\mathbb{E}}^3$ with a Bishop frame, then the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve of α is a slant helix.

Corollary 3. 

The ${\Phi }_1(s,v)$-Bishop adjoint ruled surface is a minimal surface.

Proof. 

From Equation (8), it follows that the surface ${\Phi }_1(s,v)$ is minimal if and only if its mean curvature satisfies $H_{{\Phi }_1}=0$. Since the curve $\beta$ is a slant helix, the ratio of its curvature functions remains constant, which gives:

$${\left({\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}\right)}^{\prime }=0.$$

Thus, $H_{{\Phi }_1}=0$, confirming that ${\Phi }_1(s,v)$ is a minimal surface. □

Remark 1. 

Geometrically, this condition ensures the vanishing of the mean curvature, indicating that the surface locally minimizes its area—a fundamental trait of minimal surfaces.

Theorem 5. 

The ${\Phi }_1(s,v)$-Bishop adjoint ruled surface is regular at every point and contains no singular point.

Proof. 

According to the definition given by Do Carmo [2], the surface ${\Phi }_1(s,v)$ possesses a singular point at $(s_{\theta },v_{\theta })$ if and only if

$$\parallel {\Phi }_{1s}\times {\Phi }_{1v}\parallel (s_{\theta },v_{\theta })=0.$$

Thus, we have:

$$\parallel {\Phi }_{1s}\times {\Phi }_{1v}\parallel (s_{\theta },v_{\theta })=\sqrt{{(k_1^{\beta })}^2+{(k_2^{\beta })}^2}=0.$$

However, since the curve $\beta$ is a slant helix, we know that $k_1^{\beta }\ne 0$, $k_2^{\beta }\ne 0$. As a result, $\sqrt{{(k_1^{\beta })}^2+{(k_2^{\beta })}^2}\ne 0$. This contradiction implies that the surface ${\Phi }_1(s,v)$ has no singular points, proving that it is regular at every point. □

Remark 2. 

Geometrically, the regularity of the surface ${\Phi }_1(s,v)$ indicates that its parametric derivatives ${\Phi }_{1s}$ and ${\Phi }_{1v}$ remain linearly independent for all $(s,v)$. This ensures that the surface does not locally degenerate into a curve or point. In the context of Bishop adjoint ruled surfaces, this regularity reflects the continuous and well-defined behavior of the generating slant helix and its associated direction vectors.

Theorem 6. 

Let ${\Phi }_1={\Phi }_1(s,v)$ be a Bishop adjoint ruled surface. Then the s- and v-parameter curves of ${\Phi }_1$ are always asymptotic.

Proof. 

On a surface, s-parametric curves are asymptotic if and only if the coefficient $e_{{\Phi }_1}$ equals zero [2]. That is,

$$e_{{\Phi }_1}={\displaystyle \frac{v(k_2^{\beta }{(k_1^{\beta })}^{\prime }-k_1^{\beta }{(k_2^{\beta })}^{\prime })}{\sqrt{{(k_1^{\beta })}^2+{(k_2^{\beta })}^2}}}=0.$$

Since the curve $\beta$ is a slant helix, the ratio of its curvature functions remains constant, which gives:

$$k_2^{\beta }{\left(k_1^{\beta }\right)}^{\prime }-k_1^{\beta }{\left(k_2^{\beta }\right)}^{\prime }=0.$$

Thus, we conclude that $e_{{\Phi }_1}=0$.

Conversely, v-parametric curves are asymptotic if and only if the coefficient g is zero [2]. Since this condition holds for $g_{{\Phi }_1}$, v-parametric curves on ${\Phi }_1(s,v)$ are always asymptotic. □

Theorem 7. 

Let ${\Phi }_1={\Phi }_1(s,v)$ be a Bishop adjoint ruled surface. Then the s-parameter curves of ${\Phi }_1$ are not geodesic, but the v-parameter curves are always geodesic.

Proof. 

For the s-parametric curves to be geodesic on the ${\Phi }_1(s,v)$-Bishop adjoint ruled surface, the following condition must be satisfied [2]:

$$U_{{\Phi }_1}\times {\Phi }_{1ss}=0.$$

Expanding this equation:

$${\displaystyle \frac{\left[({(k_1^{\beta })}^2+{(k_2^{\beta })}^2+v(k_1^{\beta }{(k_1^{\beta })}^{\prime }+k_2^{\beta }{(k_2^{\beta })}^{\prime })){\mathbf{t}}_{\beta }+v{k}_1^{\beta }({(k_1^{\beta })}^2+{(k_2^{\beta })}^2){\mathit{\zeta }}_1^{\beta }+v{k}_2^{\beta }({(k_1^{\beta })}^2+{(k_2^{\beta })}^2){\mathit{\zeta }}_2^{\beta }\right]}{\sqrt{{(k_1^{\beta })}^2+{(k_2^{\beta })}^2}}}=0.$$

Rearranging and simplifying, we obtain the following equations:

$${(k_1^{\beta })}^2+{(k_2^{\beta })}^2+v(k_1^{\beta }{(k_1^{\beta })}^{\prime }+k_2^{\beta }{(k_2^{\beta })}^{\prime })=0,$$

$$k_1^{\beta }v({(k_1^{\beta })}^2+{(k_2^{\beta })}^2)=0,$$

$$k_2^{\beta }v({(k_1^{\beta })}^2+{(k_2^{\beta })}^2)=0.$$

For these equations to hold, it is necessary that $v=0$, $k_1^{\beta }=0$, and $k_2^{\beta }=0$. However, since the curve $\beta$ is a slant helix, we have $k_1^{\beta }\ne 0$, $k_2^{\beta }\ne 0$, and $v\ne 0$. Under these conditions, the second and third equations cannot be satisfied simultaneously, leading to a contradiction. Therefore, s-parametric curves on the ${\Phi }_1(s,v)$-Bishop adjoint ruled surface are not geodesic.

In addition, since $U_{{\Phi }_1}\times {\Phi }_{1vv}=0$, the v-parameter curves are always geodesic on the ${\Phi }_1(s,v)$-Bishop adjoint ruled surface. □

3.2. Adjoint Ruled Surfaces with Director Vector ${\mathit{\zeta }}_1^{\beta }$

Definition 5. 

Let β be the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve of α in ${\mathbb{E}}^3$, with the associated Bishop apparatus of β denoted as $\{{\mathbf{t}}_{\beta },{\mathit{\zeta }}_1^{\beta },{\mathit{\zeta }}_2^{\beta },k_1^{\beta },k_2^{\beta }\}$. Consider β as the base curve, and ${\mathit{\zeta }}_1^{\beta }$ the generator vector. We define the ${\Phi }_2(s,v)$-Bishop adjoint ruled surface as follows:

$${\Phi }_2(s,v)={\displaystyle \frac{1}{\sqrt{2}}}\int \left({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right)\right)ds+v{\mathit{\zeta }}_1^{\beta }\left(s\right)$$

Theorem 8. 

The Gauss and mean curvatures of the ${\Phi }_2(s,v)$-Bishop adjoint ruled surface are given by:

$$K_{{\Phi }_2}=0$$

(9)

$$H_{{\Phi }_2}={\displaystyle \frac{k_2^{\beta }}{2(1-v{k}_1^{\beta })}}$$

(10)

Proof. 

The partial derivatives of ${\Phi }_2(s,v)$ concerning s and v are expressed as follows:

$${\Phi }_2(s,v)=\beta (s)+v{\mathit{\zeta }}_1^{\beta }$$

$${\Phi }_{2s}(s,v)=(1-v{k}_1^{\beta }){\mathbf{t}}_{\beta },{\Phi }_{2v}(s,v)={\mathit{\zeta }}_1^{\beta }$$

$${\Phi }_{2ss}(s,v)=-v{(k_1^{\beta })}^{\prime }{\mathbf{t}}_{\beta }+(1-v{k}_1^{\beta })k_1^{\beta }{\mathit{\zeta }}_1^{\beta }+(1-v{k}_1^{\beta })k_2^{\beta }{\mathit{\zeta }}_2^{\beta }$$

$${\Phi }_{2sv}(s,v)=-k_1^{\beta }{\mathbf{t}}_{\beta },{\Phi }_{2vv}(s,v)=0$$

The definition of the unit normal vector field of the ${\Phi }_2(s,v)$-Bishop adjoint ruled surface is given as follows using Equation (4):

$$U_{{\Phi }_2}={\displaystyle \frac{{\Phi }_{2s}\times {\Phi }_{2v}}{\parallel {\Phi }_{2s}\times {\Phi }_{2v}\parallel }}={\mathit{\zeta }}_2^{\beta }$$

The first fundamental form coefficients $E_{{\Phi }_2},F_{{\Phi }_2},G_{{\Phi }_2}$ and the second fundamental form coefficients $e_{{\Phi }_2},f_{{\Phi }_2},g_{{\Phi }_2}$ of the ${\Phi }_2(s,v)$-Bishop adjoint ruled surface are calculated as follows:

$$E_{{\Phi }_2}=⟨{\Phi }_{2s},{\Phi }_{2s}⟩={(1-v{k}_1^{\beta })}^2,F_{{\Phi }_2}=⟨{\Phi }_{2s},{\Phi }_{2v}⟩=0,G_{{\Phi }_2}=⟨{\Phi }_{2v},{\Phi }_{2v}⟩=1$$

$$e_{{\Phi }_2}=⟨{\Phi }_{2ss},U_{{\Phi }_2}⟩=(1-v{k}_1^{\beta })k_2^{\beta },f_{{\Phi }_2}=⟨{\Phi }_{2sv},U_{{\Phi }_2}⟩=0,g_{{\Phi }_2}=⟨{\Phi }_{2vv},U_{{\Phi }_2}⟩=0$$

Finally, by substituting these relations into Equations (5) and (6), we obtain Equations (9) and (10). □

Corollary 4. 

The ${\Phi }_2(s,v)$-Bishop adjoint ruled surface is a developable surface.

Corollary 5. 

The ${\Phi }_2(s,v)$-Bishop adjoint ruled surface is a non-minimal surface.

Proof. 

Since the curve $\beta$ is a slant helix, its second curvature $k_2^{\beta }$ is nonzero. From Equation (10), it follows that the mean curvature $H_{{\Phi }_2}$ is not identically zero. Therefore, the surface ${\Phi }_2(s,v)$ is not minimal. □

Theorem 9. 

A necessary and sufficient condition for the ${\Phi }_2(s,v)$-Bishop adjoint ruled surface to exhibit a singularity at the point $(s_{\theta },v_{\theta })$ is given by:

$$k_1^{\beta }={\displaystyle \frac{1}{v_{\theta }}}.$$

Proof. 

According to the definition given by Do Carmo [2], the surface ${\Phi }_2(s,v)$ has a singular point at $(s_{\theta },v_{\theta })$ if and only if the cross product of its partial derivatives vanishes at that point, that is,

$$\parallel {\Phi }_{2s}\times {\Phi }_{2v}\parallel (s_{\theta },v_{\theta })=0.$$

Using the known expressions, this condition becomes

$$1-v_{\theta }{k}_1^{\beta }=0,$$

which gives

$$k_1^{\beta }={\displaystyle \frac{1}{v_{\theta }}}.$$

Thus, the proof is complete. □

Theorem 10. 

Let ${\Phi }_2={\Phi }_2(s,v)$ be a Bishop adjoint ruled surface. Then the s-parameter curves of ${\Phi }_2$ are not asymptotic, but the v-parameter curves are always asymptotic.

Proof. 

On a surface, s-parametric curves are asymptotic if and only if the coefficient $e_{{\Phi }_2}$ equals zero [2]. That is,

$$e_{{\Phi }_2}=(1-v{k}_1^{\beta })k_2^{\beta }=0.$$

Thus, we obtain either

$$k_2^{\beta }=0\mathrm{or}{k}_1^{\beta }={\displaystyle \frac{1}{v}}.$$

Nevertheless, the point that satisfies the above condition for $k_1^{\beta }$ is singular, and $k_2^{\beta }\ne 0$. Therefore, the s-parametric curves are not asymptotic. Conversely, v-parametric curves are asymptotic if and only if the coefficient g is zero [2]. Since this condition holds for $g_{{\Phi }_2}$, v-parametric curves on ${\Phi }_2(s,v)$ are always asymptotic. □

Theorem 11. 

Let ${\Phi }_2={\Phi }_2(s,v)$ be a Bishop adjoint ruled surface. Then the s-parameter curves of ${\Phi }_2$ are not geodesic, but the v-parameter curves are always geodesic.

Proof. 

For the s-parametric curves to be geodesic on the ${\Phi }_2(s,v)$-Bishop adjoint ruled surface, the following condition must be satisfied [2]:

$$U_{{\Phi }_2}\times {\Phi }_{2ss}=-v{(k_1^{\beta })}^{\prime }{\mathit{\zeta }}_1^{\beta }-(1-v{k}_1^{\beta })k_1^{\beta }{\mathbf{t}}_{\beta }=0.$$

This leads to the following system of differential equations:

$$\begin{array}{cc}\hfill -v{(k_1^{\beta })}^{\prime }& =0,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill (1-v{k}_1^{\beta })k_1^{\beta }& =0.\hfill \end{array}$$

(12)

Since $v\ne 0$, Equation (11) implies that ${(k_1^{\beta })}^{\prime }=0$, which means that $k_1^{\beta }$ is constant. From Equation (12), given that $k_1^{\beta }\ne 0$, it follows that

$$k_1^{\beta }={\displaystyle \frac{1}{v}}.$$

However, the point satisfying this condition for $k_1^{\beta }$ is singular. Therefore, the s-parametric curve is not geodesic. In addition, since $U_{{\Phi }_2}\times {\Phi }_{2vv}=0$, the v-parameter curves are always geodesic on the ${\Phi }_2(s,v)$-Bishop adjoint ruled surface. □

3.3. Adjoint Ruled Surfaces with Director Vector ${\mathit{\zeta }}_2^{\beta }$

Definition 6. 

Let β be the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve of α in ${\mathbb{E}}^3$, with the associated Bishop apparatus of β denoted as $\{{\mathbf{t}}_{\beta },{\mathit{\zeta }}_1^{\beta },{\mathit{\zeta }}_2^{\beta },k_1^{\beta },k_2^{\beta }\}$. Consider β as the base curve, and ${\mathit{\zeta }}_2^{\beta }$ the generator vector. We define the ${\Phi }_3(s,v)$-Bishop adjoint ruled surface as follows:

$${\Phi }_3(s,v)={\displaystyle \frac{1}{\sqrt{2}}}\int \left({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right)\right)ds+v{\mathit{\zeta }}_2^{\beta }\left(s\right)$$

Theorem 12. 

The Gauss and mean curvatures of the ${\Phi }_3(s,v)$-Bishop adjoint ruled surface are given by:

$$K_{{\Phi }_3}=0$$

(13)

$$H_{{\Phi }_3}={\displaystyle \frac{-k_1^{\beta }}{2(1-v{k}_2^{\beta })}}$$

(14)

Proof. 

The partial derivatives of ${\Phi }_3(s,v)$ concerning s and v are expressed as follows:

$${\Phi }_3(s,v)=\beta (s)+v{\mathit{\zeta }}_2^{\beta }$$

$${\Phi }_{3s}(s,v)=(1-v{k}_2^{\beta }){\mathbf{t}}_{\beta },{\Phi }_{3v}(s,v)={\mathit{\zeta }}_2^{\beta }$$

$${\Phi }_{3ss}(s,v)=-v{(k_2^{\beta })}^{\prime }{\mathbf{t}}_{\beta }+(1-v{k}_2^{\beta })k_1^{\beta }{\mathit{\zeta }}_1^{\beta }+(1-v{k}_2^{\beta })k_2^{\beta }{\mathit{\zeta }}_2^{\beta }$$

$${\Phi }_{3sv}(s,v)=-k_2^{\beta }{\mathbf{t}}_{\beta },{\Phi }_{3vv}(s,v)=0$$

The definition of the unit normal vector field of the ${\Phi }_3(s,v)$-Bishop adjoint ruled surface is given as follows using Equation (4):

$${\mathbf{U}}_{{\Phi }_3}={\displaystyle \frac{{\Phi }_{3s}\times {\Phi }_{3v}}{\parallel {\Phi }_{3s}\times {\Phi }_{3v}\parallel }}=-{\mathit{\zeta }}_1^{\beta }$$

The first fundamental form coefficients $E_{{\Phi }_3},F_{{\Phi }_3},G_{{\Phi }_3}$ and the second fundamental form coefficients $e_{{\Phi }_3},f_{{\Phi }_3},g_{{\Phi }_3}$ of the ${\Phi }_3(s,v)$-Bishop adjoint ruled surface are calculated as follows:

$$E_{{\Phi }_3}=⟨{\Phi }_{3s},{\Phi }_{3s}⟩={(1-v{k}_2^{\beta })}^2$$

$$F_{{\Phi }_3}=⟨{\Phi }_{3s},{\Phi }_{3v}⟩=0,G_{{\Phi }_3}=⟨{\Phi }_{3v},{\Phi }_{3v}⟩=1$$

$$e_{{\Phi }_3}=⟨{\Phi }_{3ss},U_{{\Phi }_3}⟩=-(1-v{k}_2^{\beta })k_1^{\beta }$$

$$f_{{\Phi }_3}=⟨{\Phi }_{3sv},U_{{\Phi }_3}⟩=0,g_{{\Phi }_3}=⟨{\Phi }_{3vv},U_{{\Phi }_3}⟩=0$$

Finally, by substituting these relations into Equations (5) and (6), we obtain Equations (13) and (14). □

Corollary 6. 

The ${\Phi }_3(s,v)$-Bishop adjoint ruled surface is a developable surface.

Corollary 7. 

The ${\Phi }_3(s,v)$-Bishop adjoint ruled surface is a non-minimal surface.

Proof. 

From Equation (14), the surface is minimal if and only if $k_1^{\beta }=0$. However, since $k_1^{\beta }\ne 0$, the surface ${\Phi }_3(s,v)$ is not minimal. □

Corollary 8. 

Every parametric curve on the ${\Phi }_3(s,v)$-Bishop adjoint ruled surface is a line of curvature.

Proof. 

According to the definition given by Do Carmo [2], a parametric curve on a ruled surface is a line of curvature if and only if $F=f=0$. Since this condition holds for the surface ${\Phi }_3(s,v)$, it follows that every parametric curve on the Bishop adjoint ruled surface is a line of curvature. □

Theorem 13. 

A necessary and sufficient condition for the ${\Phi }_3(s,v)$-Bishop adjoint ruled surface to exhibit a singularity at the point $(s_{\theta },v_{\theta })$ is given by:

$$k_2^{\beta }={\displaystyle \frac{1}{v_{\theta }}}.$$

Proof. 

According to the definition given by Do Carmo [2], the surface ${\Phi }_3(s,v)$ has a singular point at $(s_{\theta },v_{\theta })$ if and only if the cross product of its partial derivatives vanishes at that point, that is,

$$\parallel {\Phi }_{3s}\times {\Phi }_{3v}\parallel (s_{\theta },v_{\theta })=0.$$

Using the known expressions, this condition becomes

$$1-v_{\theta }{k}_2^{\beta }=0,$$

which gives

$$k_2^{\beta }={\displaystyle \frac{1}{v_{\theta }}}.$$

Thus, the proof is complete. □

Theorem 14. 

Let ${\Phi }_3={\Phi }_3(s,v)$ be a Bishop adjoint ruled surface. Then the s-parameter curves of ${\Phi }_3$ are not asymptotic, but the v-parameter curves are always asymptotic.

Proof. 

On a surface, s-parametric curves are asymptotic if and only if the coefficient $e_{{\Phi }_3}$ equals zero [2]. That is,

$$e_{{\Phi }_3}=-(1-v{k}_2^{\beta })k_1^{\beta }=0.$$

Thus, we obtain either

$$k_1^{\beta }=0\mathrm{or}{k}_2^{\beta }={\displaystyle \frac{1}{v}}.$$

Nevertheless, the point that satisfies the above condition for $k_2^{\beta }$ is singular, and $k_1^{\beta }\ne 0$. Therefore, the s-parametric curves are not asymptotic. Conversely, v-parametric curves are asymptotic if and only if the coefficient g is zero [2]. Since this condition holds for $g_{{\Phi }_3}$, v-parametric curves on ${\Phi }_3(s,v)$ are always asymptotic. □

Theorem 15. 

Let ${\Phi }_3={\Phi }_3(s,v)$ be a Bishop adjoint ruled surface. Then the s-parameter curves of ${\Phi }_3$ are not geodesic, but the v-parameter curves are always geodesic.

Proof. 

For the s-parametric curves to be geodesic on the ${\Phi }_3(s,v)$-Bishop adjoint ruled surface, the following condition must be satisfied [2]:

$$U_{{\Phi }_3}\times {\Phi }_{3ss}=-v{(k_2^{\beta })}^{\prime }{\mathit{\zeta }}_1^{\beta }-(1-v{k}_2^{\beta })k_2^{\beta }{\mathbf{t}}_{\beta }=0.$$

This leads to the following system of differential equations:

$$\begin{array}{cc}\hfill -v{(k_2^{\beta })}^{\prime }& =0,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill (1-v{k}_2^{\beta })k_2^{\beta }& =0.\hfill \end{array}$$

(16)

Since $v\ne 0$, Equation (15) implies that ${(k_2^{\beta })}^{\prime }=0$, which means that $k_2^{\beta }$ is constant. From Equation (16), given that $k_2^{\beta }\ne 0$, it follows that

$$k_2^{\beta }={\displaystyle \frac{1}{v}}.$$

However, the point satisfying this condition for $k_2^{\beta }$ is singular. Therefore, the s-parametric curve is not geodesic. In addition, since $U_{{\Phi }_3}\times {\Phi }_{3vv}=0$, the v-parameter curves are always geodesic on the ${\Phi }_3(s,v)$-Bishop adjoint ruled surface. □

3.4. Adjoint Ruled Surfaces with Director Vector ${\mathit{t}}_{\beta }{\mathit{\zeta }}_1^{\beta }$

Definition 7. 

Let β be the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve of α in ${\mathbb{E}}^3$, with the associated Bishop apparatus of β denoted as $\{{\mathbf{t}}_{\beta },{\mathit{\zeta }}_1^{\beta },{\mathit{\zeta }}_2^{\beta },k_1^{\beta },k_2^{\beta }\}$. Consider β as the base curve, and $\frac{1}{\sqrt{2}}\left({\mathbf{t}}_{\beta }{\left(s\right)}_{+}{\mathit{\zeta }}_1^{\beta }\left(s\right)\right)$ the generator vector. We define the ${\Phi }_4(s,v)$-Bishop adjoint ruled surface as follows:

$${\Phi }_4(s,v)={\displaystyle \frac{1}{\sqrt{2}}}\int \left({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right)\right)ds+{\displaystyle \frac{1}{\sqrt{2}}}\left(t_{\beta }\left(s\right)+{\mathit{\zeta }}_1^{\beta }\left(s\right)\right)$$

Theorem 16. 

The Gauss and mean curvatures of the ${\Phi }_4(s,v)$-Bishop adjoint ruled surface are given by:

$$K_{{\Phi }_4}=-{\displaystyle \frac{{(k_2^{\beta })}^2}{\left({(\sqrt{2}-v{k}_1^{\beta })}^2+v^2\left({(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right)-1\right)\left(v^2{(k_2^{\beta })}^2+{(1-\sqrt{2}v{k}_1^{\beta })}^2\right)}}$$

(17)

$$H_{{\Phi }_4}={\displaystyle \frac{v^2{k}_2^{\beta }\left(2\left({\left(\frac{k_1^{\beta }}{k_2^{\beta }}\right)}^{\prime }·k_2^{\beta }+2{(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right)\right)-\sqrt{2}v\left(2k_1^{\beta }{k}_2^{\beta }-{(k_2^{\beta })}^{\prime }\right)}{2\sqrt{v^2{(k_2^{\beta })}^2+{(1-\sqrt{2}v{k}_1^{\beta })}^2}\left({(\sqrt{2}-v{k}_1^{\beta })}^2+v^2\left({(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right)-1\right)}}$$

(18)

Proof. 

The partial derivatives of ${\Phi }_4(s,v)$ concerning s and v are expressed as follows:

$$\begin{array}{c}{\Phi }_4(s,v)=\beta (s)+{\displaystyle \frac{v}{\sqrt{2}}}\left({\mathbf{t}}_{\beta }+{\mathit{\zeta }}_1^{\beta }\right)\\ {\Phi }_{4s}(s,v)=\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_1^{\beta }\right){\mathbf{t}}_{\beta }+{\displaystyle \frac{v}{\sqrt{2}}}{k}_1^{\beta }{\mathit{\zeta }}_1^{\beta }+{\displaystyle \frac{v}{\sqrt{2}}}{k}_2^{\beta }{\mathit{\zeta }}_2^{\beta }\\ {\Phi }_{4ss}(s,v)=-{\displaystyle \frac{v}{\sqrt{2}}}\left({(k_1^{\beta })}^{\prime }+{(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right)t_{\beta }\\ +\left(\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_1^{\beta }\right)k_1^{\beta }+{\displaystyle \frac{v}{\sqrt{2}}}{(k_1^{\beta })}^{\prime }\right){\mathit{\zeta }}_1^{\beta }\\ +\left(\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_1^{\beta }\right)k_2^{\beta }+{\displaystyle \frac{v}{\sqrt{2}}}{(k_2^{\beta })}^{\prime }\right){\mathit{\zeta }}_2^{\beta }\\ {\Phi }_{4v}(s,v)={\displaystyle \frac{1}{\sqrt{2}}}{t}_{\beta }+{\displaystyle \frac{1}{\sqrt{2}}}{\mathit{\zeta }}_1^{\beta },{\Phi }_{4sv}(s,v)=-{\displaystyle \frac{k_1^{\beta }}{\sqrt{2}}}{t}_{\beta }+{\displaystyle \frac{k_1^{\beta }}{\sqrt{2}}}{\mathit{\zeta }}_1^{\beta }+{\displaystyle \frac{k_2^{\beta }}{\sqrt{2}}}{\mathit{\zeta }}_2^{\beta },{\Phi }_{4vv}(s,v)=0\end{array}$$

The definition of the unit normal vector field of the ${\Phi }_4(s,v)$-Bishop adjoint ruled surface is given as follows using Equation (4):

$$U_{{\Phi }_4}={\displaystyle \frac{{\Phi }_{4s}\times {\Phi }_{4v}}{∥{\Phi }_{4s}\times {\Phi }_{4v}∥}}={\displaystyle \frac{(-\sqrt{2}v{k}_2^{\beta }){\mathbf{t}}_{\beta }+(\sqrt{2}v{k}_2^{\beta }){\mathit{\zeta }}_1^{\beta }+(1-\sqrt{2}v{k}_1^{\beta }){\mathit{\zeta }}_2^{\beta }}{2\sqrt{v^2{(k_2^{\beta })}^2+{(1-\sqrt{2}v{k}_1^{\beta })}^2}}}$$

The first fundamental form coefficients $E_{{\Phi }_4},F_{{\Phi }_4},G_{{\Phi }_4}$ and the second fundamental form coefficients $e_{{\Phi }_4},f_{{\Phi }_4},g_{{\Phi }_4}$ of the ${\Phi }_4(s,v)$-Bishop adjoint ruled surface are calculated as follows:

$$E_{{\Phi }_4}=⟨{\Phi }_{4s},{\Phi }_{4s}⟩={(1-v{k}_2^{\beta })}^2$$

$$F_{{\Phi }_4}=⟨{\Phi }_{4s},{\Phi }_{4v}⟩=0,G_{{\Phi }_4}=⟨{\Phi }_{4v},{\Phi }_{4v}⟩=1$$

$$e_{{\Phi }_4}=⟨{\Phi }_{4ss},U_{{\Phi }_4}⟩=-(1-v{k}_2^{\beta })k_1^{\beta }$$

$$f_{{\Phi }_4}=⟨{\Phi }_{4sv},U_{{\Phi }_4}⟩=0,g_{{\Phi }_4}=⟨{\Phi }_{4vv},U_{{\Phi }_4}⟩=0$$

Finally, by substituting these relations into Equations (5) and (6), we obtain Equations (17) and (18). □

Corollary 9. 

The ${\Phi }_4(s,v)$-Bishop adjoint ruled surface is a non-developable surface.

Proof. 

Since the second curvature $k_2^{\beta }\ne 0$, the Bishop adjoint ruled surface ${\Phi }_4(s,v)$ is non-developable. □

Corollary 10. 

For the Bishop adjoint ruled surface ${\Phi }_4(s,v)$ to be minimal, the following relation must hold between the curvature functions:

$$k_1^{\beta }=\pm \sqrt{{\displaystyle \frac{-2\left({(k_2^{\beta })}^3+\sqrt{2}{k}_2^{\beta }-\sqrt{2}{(k_2^{\beta })}^{\prime }\right)}{v{k}_2^{\beta }}}}.$$

From Equation (18), the Bishop adjoint ruled surface ${\Phi }_4(s,v)$ is minimal if and only if

$$v^2{k}_2^{\beta }\left(2\left({\left({\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}\right)}^{\prime }{k}_2^{\beta }+2{(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right)\right)-\sqrt{2}v\left(2k_1^{\beta }{k}_2^{\beta }-{(k_2^{\beta })}^{\prime }\right)=0.$$

Since the curve $\beta$ is a slant helix, it satisfies the condition ${\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}=c$, where c is a constant. Thus, its derivative vanishes:

$${\left({\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}\right)}^{\prime }=0.$$

Substituting this into the equation above yields the desired relation.

Theorem 17. 

The Bishop adjoint ruled surface ${\Phi }_4(s,v)$ is regular at every point and contains no singularities.

Proof. 

According to the definition given by Do Carmo [2], the surface ${\Phi }_4(s,v)$ possesses a singular point at $(s_{\theta },v_{\theta })$ if and only if

$$∥{\Phi }_{4s}\times {\Phi }_{4v}∥(s_{\theta },v_{\theta })=v_{\theta }^2{(k_2^{\beta })}^2+{\left(1-\sqrt{2}{v}_{\theta }{k}_1^{\beta }\right)}^2=0.$$

However, since the curve $\beta$ is a slant helix, we know that $k_1^{\beta }\ne 0$ and $k_2^{\beta }\ne 0$. As a result,

$$v_{\theta }^2{(k_2^{\beta })}^2+{\left(1-\sqrt{2}{v}_{\theta }{k}_1^{\beta }\right)}^2\ne 0.$$

This contradiction implies that the surface ${\Phi }_4(s,v)$ does not admit any singular point, and hence it is regular at every point. □

Theorem 18. 

For the Bishop adjoint ruled surface ${\Phi }_4(s,v)$, the s-parametric curves are asymptotic if and only if

$$k_1^{\beta }=\pm \sqrt{{\displaystyle \frac{-\left(v^2{(k_2^{\beta })}^3+\sqrt{2}v{(k_2^{\beta })}^{\prime }+k_2^{\beta }\right)}{v{k}_2^{\beta }}}},$$

while the v-parametric curves are always asymptotic.

Proof. 

On a surface, the s-parametric curves are asymptotic if and only if $e=0$ [2]. Therefore, the condition

$$v^2{k}_2^{\beta }\left(2\left({\left({\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}\right)}^{\prime }{k}_2^{\beta }+2{(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right)\right)-\sqrt{2}v\left(2k_1^{\beta }{k}_2^{\beta }-{(k_2^{\beta })}^{\prime }\right)+2k_2^{\beta }=0$$

must be satisfied. Since the curve $\beta$ is a slant helix, it satisfies ${\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}=c$, where c is a constant. Hence, its derivative vanishes:

$${\left({\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}\right)}^{\prime }=0.$$

Substituting this into the above equation yields the desired relation. □

Theorem 19. 

Let ${\Phi }_4={\Phi }_4(s,v)$ be a Bishop adjoint ruled surface. Then the s-parameter curves of ${\Phi }_4$ are not geodesic, but the v-parameter curves are always geodesic.

Proof. 

For the s-parametric curves to be geodesics on the Bishop adjoint ruled surface ${\Phi }_4(s,v)$, the following condition must be satisfied:

$$U_{{\Phi }_4}\times {\Phi }_{4ss}=X_1{\mathbf{t}}_{\beta }+Y_1{\mathit{\zeta }}_1^{\beta }+Z_1{\mathit{\zeta }}_2^{\beta }=0,$$

where the coefficients $X_1$, $Y_1$, and $Z_1$ are given by:

$$X_1={\displaystyle \frac{\sqrt{2}v{k}_2^{\beta }\left(1-\frac{v}{\sqrt{2}}{k}_1^{\beta }\right)k_2^{\beta }-2(1-\sqrt{2}v{k}_1^{\beta })\left(\left(1-\frac{v}{\sqrt{2}}{k}_1^{\beta }\right)k_1^{\beta }+\frac{v}{\sqrt{2}}{\left(k_1^{\beta }\right)}^{\prime }\right)+v^2{k}_2^{\beta }{\left(k_2^{\beta }\right)}^{\prime }}{2\sqrt{v^2{\left(k_2^{\beta }\right)}^2+{(1-\sqrt{2}v{k}_1^{\beta })}^2}}},$$

$$Y_1={\displaystyle \frac{\sqrt{2}v{k}_2^{\beta }\left(1-\frac{v}{\sqrt{2}}{k}_1^{\beta }\right)k_2^{\beta }+v^2{k}_2^{\beta }{\left(k_1^{\beta }\right)}^{\prime }-\sqrt{2}v(1-\sqrt{2}v{k}_1^{\beta })\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)}{2\sqrt{v^2{\left(k_2^{\beta }\right)}^2+{(1-\sqrt{2}v{k}_1^{\beta })}^2}}},$$

$$Z_1={\displaystyle \frac{v{k}_2^{\beta }\left[-\sqrt{2}\left(1-\frac{v}{\sqrt{2}}{k}_1^{\beta }\right)k_1^{\beta }+v{k}_2^{\beta }\left(v{\left(k_1^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)-v{k}_2^{\beta }{\left(k_1^{\beta }\right)}^{\prime }\right]}{2\sqrt{v^2{\left(k_2^{\beta }\right)}^2+{(1-\sqrt{2}v{k}_1^{\beta })}^2}}}.$$

In order for the curves to be geodesic, all three of the following equations must hold:

$$\sqrt{2}v{k}_2^{\beta }\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_1^{\beta }\right)k_2^{\beta }-2(1-\sqrt{2}v{k}_1^{\beta })\left(\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_1^{\beta }\right)k_1^{\beta }+{\displaystyle \frac{v}{\sqrt{2}}}{\left(k_1^{\beta }\right)}^{\prime }\right)+v^2{k}_2^{\beta }{\left(k_2^{\beta }\right)}^{\prime }=0,$$

$$\sqrt{2}v{k}_2^{\beta }\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_1^{\beta }\right)k_2^{\beta }+v^2{k}_2^{\beta }{\left(k_1^{\beta }\right)}^{\prime }-\sqrt{2}v(1-\sqrt{2}v{k}_1^{\beta })\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)=0,$$

$$v{k}_2^{\beta }\left[-\sqrt{2}\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_1^{\beta }\right)k_1^{\beta }+v{k}_2^{\beta }\left(v{\left(k_1^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)-v{k}_2^{\beta }{\left(k_1^{\beta }\right)}^{\prime }\right]=0.$$

However, given that the curve $\beta$ is a slant helix and satisfies the relation $k_1^{\beta }=c{k}_2^{\beta }$ with $k_1^{\beta }\ne 0$, $k_2^{\beta }\ne 0$, there is no common solution that satisfies all three equations simultaneously. Therefore, the s-parametric curves on ${\Phi }_4(s,v)$ are not geodesics. In addition, since $U_{{\Phi }_4}\times {\Phi }_{4vv}=0$, the v-parameter curves are always geodesic on the ${\Phi }_4(s,v)$-Bishop adjoint ruled surface. □

3.5. Adjoint Ruled Surfaces with Director Vector ${\mathit{t}}_{\beta }{\mathit{\zeta }}_2^{\beta }$

Definition 8. 

Let β be the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve of α in ${\mathbb{E}}^3$, with the associated Bishop apparatus of β denoted as $\{{\mathbf{t}}_{\beta },{\mathit{\zeta }}_1^{\beta },{\mathit{\zeta }}_2^{\beta },k_1^{\beta },k_2^{\beta }\}$. Consider β as the base curve, and $\frac{1}{\sqrt{2}}({\mathbf{t}}_{\beta }+{\mathit{\zeta }}_2^{\beta }\left(s\right))$ the generator vector. We define the ${\Phi }_5(s,v)$-Bishop adjoint ruled surface as follows:

$${\Phi }_5(s,v)={\displaystyle \frac{1}{\sqrt{2}}}\int \left({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right)\right)ds+{\displaystyle \frac{1}{\sqrt{2}}}\left({\mathbf{t}}_{\beta }+{\mathit{\zeta }}_2^{\beta }\left(s\right)\right)$$

Theorem 20. 

The Gauss and mean curvatures of the ${\Phi }_5(s,v)$-Bishop adjoint ruled surface are given by:

$$K_{{\Phi }_5}=-{\displaystyle \frac{{(k_1^{\beta })}^2}{\left({(\sqrt{2}-v{k}_2^{\beta })}^2+v^2\left({(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right)-1\right)\left(v^2{(k_1^{\beta })}^2+{(1-\sqrt{2}v{k}_2^{\beta })}^2\right)}}$$

(19)

$$H_{{\Phi }_5}={\displaystyle \frac{-v^2{k}_1^{\beta }\left(2\left({\left(\frac{k_2^{\beta }}{k_1^{\beta }}\right)}^{\prime }{k}_1^{\beta }+2{(k_2^{\beta })}^2+{(k_1^{\beta })}^2\right)\right)+\sqrt{2}v\left(2k_1^{\beta }{k}_2^{\beta }-{(k_1^{\beta })}^{\prime }\right)}{2\sqrt{v^2{(k_1^{\beta })}^2+{(1-\sqrt{2}v{k}_2^{\beta })}^2}\left({(\sqrt{2}-v{k}_2^{\beta })}^2+v^2\left({(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right)-1\right)}}$$

(20)

Proof. 

The Bishop adjoint ruled surface ${\Phi }_5(s,v)$ is given by:

$${\Phi }_5(s,v)=\beta (s)+{\displaystyle \frac{v}{\sqrt{2}}}\left({\mathbf{t}}_{\beta }+{\mathit{\zeta }}_2^{\beta }\right).$$

The partial derivatives of ${\Phi }_5(s,v)$ are computed as:

$${\Phi }_{5s}(s,v)=\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_2^{\beta }\right){\mathbf{t}}_{\beta }+{\displaystyle \frac{v}{\sqrt{2}}}{k}_1^{\beta }{\mathit{\zeta }}_1^{\beta }+{\displaystyle \frac{v}{\sqrt{2}}}{k}_2^{\beta }{\mathit{\zeta }}_2^{\beta },$$

$$\begin{array}{cc}\hfill {\Phi }_{5ss}(s,v)=& -{\displaystyle \frac{v}{\sqrt{2}}}\left({(k_2^{\beta })}^{\prime }+{(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right)t_{\beta }\hfill \\ \hfill & +\left(\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_2^{\beta }\right)k_1^{\beta }+{\displaystyle \frac{v}{\sqrt{2}}}{(k_1^{\beta })}^{\prime }\right){\mathit{\zeta }}_1^{\beta }\hfill \\ \hfill & +\left(\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_2^{\beta }\right)k_2^{\beta }+{\displaystyle \frac{v}{\sqrt{2}}}{(k_2^{\beta })}^{\prime }\right){\mathit{\zeta }}_2^{\beta }\hfill \end{array}$$

$${\Phi }_{5v}(s,v)={\displaystyle \frac{1}{\sqrt{2}}}{\mathbf{t}}_{\beta }+{\displaystyle \frac{1}{\sqrt{2}}}{\mathit{\zeta }}_2^{\beta },{\Phi }_{5sv}(s,v)=-{\displaystyle \frac{k_2^{\beta }}{\sqrt{2}}}{t}_{\beta }+{\displaystyle \frac{k_1^{\beta }}{\sqrt{2}}}{\mathit{\zeta }}_1^{\beta }+{\displaystyle \frac{k_2^{\beta }}{\sqrt{2}}}{\mathit{\zeta }}_2^{\beta },{\Phi }_{5vv}(s,v)=0.$$

The unit normal vector field of ${\Phi }_5(s,v)$ is given by:

$$\begin{array}{cc}\hfill U_{{\Phi }_5}=& {\displaystyle \frac{\sqrt{2}v{k}_1^{\beta }}{2\sqrt{v^2{(k_1^{\beta })}^2+{(1-\sqrt{2}v{k}_2^{\beta })}^2}}}{\mathbf{t}}_{\beta }\hfill \\ \hfill & -{\displaystyle \frac{1-\sqrt{2}v{k}_2^{\beta }}{\sqrt{v^2{(k_1^{\beta })}^2+{(1-\sqrt{2}v{k}_2^{\beta })}^2}}}{\mathit{\zeta }}_1^{\beta }\hfill \\ \hfill & -{\displaystyle \frac{\sqrt{2}v{k}_1^{\beta }}{2\sqrt{v^2{(k_1^{\beta })}^2+{(1-\sqrt{2}v{k}_2^{\beta })}^2}}}{\mathit{\zeta }}_2^{\beta }\hfill \end{array}$$

The coefficients of the first fundamental form are:

$$E_{{\Phi }_5}=⟨{\Phi }_{5s},{\Phi }_{5s}⟩={\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_2^{\beta }\right)}^2+{\displaystyle \frac{v^2}{2}}\left({(k_1^{\beta })}^2+{(k_2^{\beta })}^2\right),$$

$$F_{{\Phi }_5}=⟨{\Phi }_{5s},{\Phi }_{5v}⟩={\displaystyle \frac{1}{\sqrt{2}}},G_{{\Phi }_5}=⟨{\Phi }_{5v},{\Phi }_{5v}⟩=1.$$

The coefficients of the second fundamental form are

$$e_{{\Phi }_5}=⟨{\Phi }_{5ss},U_{{\Phi }_5}⟩={\displaystyle \frac{-v^2{k}_1^{\beta }\left(2\left({\left(\frac{k_2^{\beta }}{k_1^{\beta }}\right)}^{\prime }{k}_1^{\beta }+2{(k_2^{\beta })}^2+{(k_1^{\beta })}^2\right)\right)+\sqrt{2}v\left(2k_1^{\beta }{k}_2^{\beta }-{(k_1^{\beta })}^{\prime }\right)-2k_1^{\beta }}{2\sqrt{v^2{(k_1^{\beta })}^2+{(1-\sqrt{2}v{k}_2^{\beta })}^2}}},$$

$$f_{{\Phi }_5}=⟨{\Phi }_{5sv},U_{{\Phi }_5}⟩=-{\displaystyle \frac{\sqrt{2}{k}_1^{\beta }}{2\sqrt{v^2{(k_1^{\beta })}^2+{(1-\sqrt{2}v{k}_2^{\beta })}^2}}},g_{{\Phi }_5}=⟨{\Phi }_{5vv},U_{{\Phi }_5}⟩=0.$$

Finally, by substituting these expressions into Equations (5) and (6), we obtain the Gaussian curvature $K_{{\Phi }_5}$ and mean curvature $H_{{\Phi }_5}$ as given in Equations (19) and (20). □

Corollary 11. 

The ${\Phi }_5(s,v)$-Bishop adjoint ruled surface is a non-developable surface.

Proof. 

Since the first curvature $k_1^{\beta }\ne 0$, the Bishop adjoint ruled surface ${\Phi }_5(s,v)$ is non-developable. □

Corollary 12. 

For the Bishop adjoint ruled surface ${\Phi }_5(s,v)$ to be minimal, the following relation must hold between the curvature functions:

$$k_1^{\beta }=\pm \sqrt{{\displaystyle \frac{-\left(2v{\left(k_2^{\beta }\right)}^3+2\sqrt{2}{\left(k_2^{\beta }\right)}^2-\sqrt{2}{\left(k_2^{\beta }\right)}^{\prime }\right)}{v{k}_2^{\beta }}}}$$

Proof. 

From Equation (20), the Bishop adjoint ruled surface ${\Phi }_5(s,v)$ is minimal if and only if

$$-v^2{k}_1^{\beta }\left(2\left({\left({\displaystyle \frac{k_2^{\beta }}{k_1^{\beta }}}\right)}^{\prime }{k}_1^{\beta }+2{\left(k_2^{\beta }\right)}^2+{\left(k_1^{\beta }\right)}^2\right)\right)+\sqrt{2}v\left(2k_1^{\beta }{k}_2^{\beta }-{\left(k_1^{\beta }\right)}^{\prime }\right)=0.$$

Since the curve $\beta$ is a slant helix, it satisfies the condition ${\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}=c$, where c is a constant. Therefore, the derivative of this ratio vanishes:

$${\left({\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}\right)}^{\prime }=0.$$

Substituting this into the above equation yields the desired relation. □

Theorem 21. 

The Bishop adjoint ruled surface ${\Phi }_5(s,v)$ is regular at every point and contains no singularities.

Proof. 

According to the definition given by Do Carmo [2], the surface ${\Phi }_5(s,v)$ possesses a singular point at $(s_{\theta },v_{\theta })$ if and only if

$$∥{\Phi }_{5s}\times {\Phi }_{5v}∥(s_{\theta },v_{\theta })={\displaystyle \frac{1}{2}}\left(v_{\theta }^2{\left(k_2^{\beta }\right)}^2+{\left(1-\sqrt{2}{v}_{\theta }{k}_1^{\beta }\right)}^2\right)=0.$$

However, since the curve $\beta$ is a slant helix, we know that $k_1^{\beta }\ne 0$ and $k_2^{\beta }\ne 0$. Therefore,

$$v_{\theta }^2{\left(k_2^{\beta }\right)}^2+{\left(1-\sqrt{2}{v}_{\theta }{k}_1^{\beta }\right)}^2\ne 0.$$

This contradiction implies that the surface ${\Phi }_5(s,v)$ does not admit any singular points, and hence it is regular at every point. □

Theorem 22. 

For the Bishop adjoint ruled surface ${\Phi }_5(s,v)$, the s-parametric curves are asymptotic if and only if

$$k_1^{\beta }=\pm \sqrt{{\displaystyle \frac{-\left(v^2{\left(k_2^{\beta }\right)}^3+\sqrt{2}v{\left(k_2^{\beta }\right)}^{\prime }+k_2^{\beta }\right)}{v{k}_2^{\beta }}}},$$

while the v-parametric curves are always asymptotic.

Proof. 

The s-parametric curves on the surface ${\Phi }_5(s,v)$ are asymptotic if and only if the following condition is satisfied:

$$-v^2{k}_1^{\beta }\left(2\left({\left({\displaystyle \frac{k_2^{\beta }}{k_1^{\beta }}}\right)}^{\prime }{k}_1^{\beta }+2{\left(k_2^{\beta }\right)}^2+{\left(k_1^{\beta }\right)}^2\right)\right)+\sqrt{2}v\left(2k_1^{\beta }{k}_2^{\beta }-{\left(k_1^{\beta }\right)}^{\prime }\right)-2k_1^{\beta }=0.$$

Since the curve $\beta$ is a slant helix, it satisfies the condition ${\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}=c$, where c is a constant. Therefore, the derivative vanishes:

$${\left({\displaystyle \frac{k_1^{\beta }}{k_2^{\beta }}}\right)}^{\prime }=0.$$

Substituting this into the equation yields the desired relation. □

Theorem 23. 

Let ${\Phi }_5={\Phi }_5(s,v)$ be a Bishop adjoint ruled surface. Then the s-parameter curves of ${\Phi }_5$ are not geodesic, but the v-parameter curves are always geodesic.

Proof. 

In order for the s-parametric curves to be geodesics on the Bishop adjoint ruled surface ${\Phi }_5(s,v)$, the following condition must be satisfied:

$$U_{{\Phi }_5}\times {\Phi }_{5ss}=X_1{\mathbf{t}}_{\beta }+Y_1{\mathit{\zeta }}_1^{\beta }+Z_1{\mathit{\zeta }}_2^{\beta }=0,$$

where the coefficients $X_1$, $Y_1$, and $Z_1$ are given by:

$$X_1={\displaystyle \frac{\sqrt{2}v{k}_1^{\beta }\left(1-\frac{v}{\sqrt{2}}{k}_2^{\beta }\right)k_1^{\beta }-2(1-\sqrt{2}v{k}_2^{\beta })\left(\left(1-\frac{v}{\sqrt{2}}{k}_2^{\beta }\right)k_2^{\beta }+\frac{v}{\sqrt{2}}{\left(k_2^{\beta }\right)}^{\prime }\right)+v^2{k}_1^{\beta }{\left(k_1^{\beta }\right)}^{\prime }}{2\sqrt{v^2{\left(k_1^{\beta }\right)}^2+{\left(1-\sqrt{2}v{k}_2^{\beta }\right)}^2}}},$$

$$Y_1={\displaystyle \frac{-\sqrt{2}v{k}_1^{\beta }\left(1-\frac{v}{\sqrt{2}}{k}_2^{\beta }\right)k_2^{\beta }-v^2{k}_1^{\beta }{\left(k_2^{\beta }\right)}^{\prime }+v^2{k}_1^{\beta }\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)}{2\sqrt{v^2{\left(k_1^{\beta }\right)}^2+{\left(1-\sqrt{2}v{k}_2^{\beta }\right)}^2}}},$$

$$Z_1={\displaystyle \frac{\sqrt{2}v{k}_1^{\beta }\left(1-\frac{v}{\sqrt{2}}{k}_2^{\beta }\right)k_1^{\beta }+v^2{k}_1^{\beta }{\left(k_1^{\beta }\right)}^{\prime }+\sqrt{2}v(1-\sqrt{2}v{k}_2^{\beta })\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)}{2\sqrt{v^2{\left(k_1^{\beta }\right)}^2+{\left(1-\sqrt{2}v{k}_2^{\beta }\right)}^2}}}.$$

Thus, for the s-parametric curves to be geodesics, the following three equations must simultaneously hold:

$$\sqrt{2}v{k}_1^{\beta }\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_2^{\beta }\right)k_1^{\beta }-2(1-\sqrt{2}v{k}_2^{\beta })\left(\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_2^{\beta }\right)k_2^{\beta }+{\displaystyle \frac{v}{\sqrt{2}}}{\left(k_2^{\beta }\right)}^{\prime }\right)+v^2{k}_1^{\beta }{\left(k_1^{\beta }\right)}^{\prime }=0,$$

$$-\sqrt{2}v{k}_1^{\beta }\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_2^{\beta }\right)k_2^{\beta }-v^2{k}_1^{\beta }{\left(k_2^{\beta }\right)}^{\prime }+v^2{k}_1^{\beta }\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)=0,$$

$$\sqrt{2}v{k}_1^{\beta }\left(1-{\displaystyle \frac{v}{\sqrt{2}}}{k}_2^{\beta }\right)k_1^{\beta }+v^2{k}_1^{\beta }{\left(k_1^{\beta }\right)}^{\prime }+\sqrt{2}v(1-\sqrt{2}v{k}_2^{\beta })\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)=0.$$

However, given that the curve $\beta$ is a slant helix and satisfies the relation $k_1^{\beta }=c{k}_2^{\beta }$ with $k_1^{\beta }\ne 0$, $k_2^{\beta }\ne 0$, there exists no common solution that satisfies all three equations simultaneously. Therefore, the s-parametric curves on ${\Phi }_5(s,v)$ are not geodesics. □

3.6. Adjoint Ruled Surfaces with Director Vector ${\mathit{\zeta }}_1^{\beta }{\mathit{\zeta }}_2^{\beta }$

Definition 9. 

Let β be the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve of α in ${\mathbb{E}}^3$, with the associated Bishop apparatus of β denoted as $\{{\mathbf{t}}_{\beta },{\mathit{\zeta }}_1^{\beta },{\mathit{\zeta }}_2^{\beta },k_1^{\beta },k_2^{\beta }\}$. Consider β as the base curve, and $\frac{1}{\sqrt{2}}({\mathit{\zeta }}_1^{\beta }\left(s\right)+{\mathit{\zeta }}_2^{\beta }\left(s\right))$ the generator vector. We define the ${\Phi }_6(s,v)$-Bishop adjoint ruled surface as follows:

$${\Phi }_6(s,v)={\displaystyle \frac{1}{\sqrt{2}}}\int \left({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right)\right)ds+{\displaystyle \frac{1}{\sqrt{2}}}\left({\mathit{\zeta }}_1^{\beta }\left(s\right)+{\mathit{\zeta }}_2^{\beta }\left(s\right)\right)$$

Theorem 24. 

The Gauss and mean curvatures of the ${\Phi }_6(s,v)$-Bishop adjoint ruled surface are given by:

$$K_{{\Phi }_6}=0$$

(21)

$$H_{{\Phi }_6}={\displaystyle \frac{k_2^{\beta }-k_1^{\beta }}{2\sqrt{2}-2v(k_1^{\beta }+k_2^{\beta })}}$$

(22)

Proof. 

The partial derivatives of the Bishop adjoint ruled surface ${\Phi }_6(s,v)$ with respect to s and v are expressed as follows:

$${\Phi }_6(s,v)=\beta \left(s\right)+{\displaystyle \frac{v}{\sqrt{2}}}\left({\mathit{\zeta }}_1^{\beta }+{\mathit{\zeta }}_2^{\beta }\right),$$

$${\Phi }_{6s}(s,v)=\left(1-{\displaystyle \frac{v}{\sqrt{2}}}(k_1^{\beta }+k_2^{\beta })\right){\mathbf{t}}_{\beta },$$

$${\Phi }_{6ss}(s,v)=-{\displaystyle \frac{v}{\sqrt{2}}}\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_2^{\beta }\right)}^{\prime }\right){\mathbf{t}}_{\beta }+\left(1-{\displaystyle \frac{v}{\sqrt{2}}}(k_1^{\beta }+k_2^{\beta })\right)k_1^{\beta }{\mathit{\zeta }}_1^{\beta }+\left(1-{\displaystyle \frac{v}{\sqrt{2}}}(k_1^{\beta }+k_2^{\beta })\right)k_2^{\beta }{\mathit{\zeta }}_2^{\beta },$$

$${\Phi }_{6v}(s,v)={\displaystyle \frac{1}{\sqrt{2}}}{\mathit{\zeta }}_1^{\beta }+{\displaystyle \frac{1}{\sqrt{2}}}{\mathit{\zeta }}_2^{\beta },{\Phi }_{6sv}(s,v)=-{\displaystyle \frac{1}{\sqrt{2}}}(k_1^{\beta }+k_2^{\beta })t_{\beta },{\Phi }_{6vv}(s,v)=0.$$

The unit normal vector field of the surface ${\Phi }_6(s,v)$ is given by:

$$U_{{\Phi }_6}={\displaystyle \frac{{\Phi }_{6s}\times {\Phi }_{6v}}{\parallel {\Phi }_{6s}\times {\Phi }_{6v}\parallel }}=-{\displaystyle \frac{1}{\sqrt{2}}}{\mathit{\zeta }}_1^{\beta }+{\displaystyle \frac{1}{\sqrt{2}}}{\mathit{\zeta }}_2^{\beta }.$$

The coefficients of the first fundamental form are computed as:

$$E=⟨{\Phi }_{6s},{\Phi }_{6s}⟩={\left(1-{\displaystyle \frac{v}{\sqrt{2}}}(k_1^{\beta }+k_2^{\beta })\right)}^2,F=⟨{\Phi }_{6s},{\Phi }_{6v}⟩=0,G=⟨{\Phi }_{6v},{\Phi }_{6v}⟩=1.$$

The coefficients of the second fundamental form are:

$$e=⟨{\Phi }_{6ss},U_{{\Phi }_6}⟩=(k_2^{\beta }-k_1^{\beta })\left({\displaystyle \frac{1}{\sqrt{2}}}-{\displaystyle \frac{v}{2}}(k_1^{\beta }+k_2^{\beta })\right),f=⟨{\Phi }_{6sv},U_{{\Phi }_6}⟩=0,g=⟨{\Phi }_{6vv},U_{{\Phi }_6}⟩=0.$$

Finally, by substituting these expressions into Equations (5) and (6), we obtain the Gaussian curvature $K_{{\Phi }_6}=0$ and the mean curvature

$$H_{{\Phi }_6}={\displaystyle \frac{k_2^{\beta }-k_1^{\beta }}{2\sqrt{2}-2v(k_1^{\beta }+k_2^{\beta })}},$$

as given in Equations (21) and (22). □

Corollary 13. 

The ${\Phi }_6(s,v)$-Bishop adjoint ruled surface is a developable surface.

Corollary 14. 

The Bishop adjoint ruled surface ${\Phi }_6(s,v)$ is a minimal surface if and only if $k_2^{\beta }=k_1^{\beta }$.

Proof. 

Assume that the surface ${\Phi }_6(s,v)$ is minimal. Then, from Equation (22), the mean curvature satisfies:

$$H_{{\Phi }_6}={\displaystyle \frac{k_2^{\beta }-k_1^{\beta }}{2\sqrt{2}-2v(k_1^{\beta }+k_2^{\beta })}}=0.$$

Solving this equation yields the condition:

$$k_2^{\beta }=k_1^{\beta }.$$

Hence, the surface is minimal if and only if this equality holds. □

Corollary 15. 

If the Bishop adjoint ruled surface ${\Phi }_6(s,v)$ is minimal, then the angle ${\theta }_{\beta }$ satisfies:

$${\theta }_{\beta }={\displaystyle \frac{\pi }{4}}+k\pi ,k\in \mathbb{Z}.$$

Proof. 

The result follows directly from Equation (3). □

Theorem 25. 

A necessary and sufficient condition for the Bishop adjoint ruled surface ${\Phi }_6(s,v)$ to exhibit a singularity at the point $(s_{\theta },v_{\theta })$ is given by:

$$k_1^{\beta }+k_2^{\beta }={\displaystyle \frac{\sqrt{2}}{v_{\theta }}}.$$

Proof. 

According to the definition given by Do Carmo [2], the surface ${\Phi }_6(s,v)$ has a singular point at $(s_{\theta },v_{\theta })$ if and only if

$$∥{\Phi }_{6s}\times {\Phi }_{6v}∥(s_{\theta },v_{\theta })=1-{\displaystyle \frac{v_{\theta }}{\sqrt{2}}}(k_1^{\beta }+k_2^{\beta })=0.$$

Solving this equation yields the condition:

$$k_1^{\beta }+k_2^{\beta }={\displaystyle \frac{\sqrt{2}}{v_{\theta }}}.$$

This completes the proof. □

Theorem 26. 

For the Bishop adjoint ruled surface ${\Phi }_6(s,v)$, the s-parametric curves are asymptotic if and only if $k_1^{\beta }=k_2^{\beta }$, while the v-parametric curves are always asymptotic.

Proof. 

On a surface, s-parametric curves are asymptotic if and only if $e=0$ [2]. For the surface ${\Phi }_6(s,v)$, the second fundamental form coefficient e is given by:

$$e=(k_2^{\beta }-k_1^{\beta })\left({\displaystyle \frac{1}{\sqrt{2}}}-{\displaystyle \frac{v}{2}}(k_1^{\beta }+k_2^{\beta })\right)=0.$$

This equation holds if and only if either

$$k_2^{\beta }=k_1^{\beta }\mathrm{or}{k}_1^{\beta }+k_2^{\beta }={\displaystyle \frac{\sqrt{2}}{v}}.$$

However, the second condition corresponds to a singular point on the surface, as shown in Theorem 25. Therefore, the only valid condition for the s-parametric curves to be asymptotic is

$$k_1^{\beta }=k_2^{\beta }.$$

This completes the proof. □

Theorem 27. 

Let ${\Phi }_6={\Phi }_6(s,v)$ be a Bishop adjoint ruled surface. Then the s-parameter curves of ${\Phi }_6$ are not geodesic, but the v-parameter curves are always geodesic.

Proof. 

For the s-parametric curves to be geodesics on the Bishop adjoint ruled surface ${\Phi }_6(s,v)$, the following condition must be satisfied:

$$U_{{\Phi }_6}\times {\Phi }_{6ss}={\displaystyle \frac{1}{2}}\left[(2\sqrt{2}+v(k_1^{\beta }+k_2^{\beta })){\mathbf{t}}_{\beta }-v\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_2^{\beta }\right)}^{\prime }\right){\mathit{\zeta }}_1^{\beta }-v\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_2^{\beta }\right)}^{\prime }\right){\mathit{\zeta }}_2^{\beta }\right]=0.$$

From this expression, the following system is obtained:

$$2\sqrt{2}+v(k_1^{\beta }+k_2^{\beta })=0,{\left(k_1^{\beta }\right)}^{\prime }+{\left(k_2^{\beta }\right)}^{\prime }=0.$$

Solving the system yields:

$$k_1^{\beta }+k_2^{\beta }=-{\displaystyle \frac{2\sqrt{2}}{v}},k_1^{\beta }=k_2^{\beta }+c,c\in \mathbb{R}.$$

However, as previously established in Theorem 25, the condition $k_1^{\beta }+k_2^{\beta }={\displaystyle \frac{\sqrt{2}}{v}}$ defines a singular point on the surface.

Therefore, the points satisfying the above conditions are singular, and the s-parametric curves cannot be geodesics on ${\Phi }_6(s,v)$. □

3.7. Adjoint Ruled Surfaces with Director Vector ${\mathit{t}}_{\beta }{\mathit{\zeta }}_1^{\beta }{\mathit{\zeta }}_2^{\beta }$

Definition 10. 

Let β be the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve of α in ${\mathbb{E}}^3$, with the associated Bishop apparatus of β denoted as $\{{\mathbf{t}}_{\beta },{\mathit{\zeta }}_1^{\beta },{\mathit{\zeta }}_2^{\beta },k_1^{\beta },k_2^{\beta }\}$. Consider β as the base curve, and $\frac{1}{\sqrt{3}}({\mathbf{t}}_{\beta }+{\mathit{\zeta }}_1^{\beta }\left(s\right)+{\mathit{\zeta }}_2^{\beta }\left(s\right))$ the generator vector. We define the ${\Phi }_7(s,v)$-Bishop adjoint ruled surface as follows:

$${\Phi }_7(s,v)={\displaystyle \frac{1}{\sqrt{2}}}\int \left({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right)\right)ds+{\displaystyle \frac{1}{\sqrt{3}}}\left({\mathit{t}}_{\beta }+{\mathit{\zeta }}_1^{\beta }\left(s\right)+{\mathit{\zeta }}_2^{\beta }\left(s\right)\right)$$

Theorem 28. 

The Gauss and mean curvatures of the ${\Phi }_7(s,v)$-Bishop adjoint ruled surface are given by:

$$K_{{\Phi }_7}={\displaystyle \frac{{(k_2^{\beta }-k_1^{\beta })}^2}{3\left(1-3{\left(1-\frac{v}{\sqrt{3}}(k_1^{\beta }+k_2^{\beta })\right)}^2+v^2\left({\left(k_2^{\beta }\right)}^2+{\left(k_1^{\beta }\right)}^2\right)\right)}}$$

(23)

$$\begin{array}{cc}\hfill H_{{\Phi }_7}={\displaystyle \frac{1}{6\sqrt{3}\left({\left(1-\frac{v}{\sqrt{2}}(k_1^{\beta }+k_2^{\beta })\right)}^2-\frac{2}{\sqrt{3}}\right)}}& \left[v^2\right(\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_2^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)(k_2^{\beta }-k_1^{\beta })\hfill \\ \hfill & -(k_1^{\beta }+k_2^{\beta })k_1^{\beta }(k_1^{\beta }+2k_2^{\beta })+{\left(k_1^{\beta }\right)}^{\prime }(k_1^{\beta }+2k_2^{\beta })\hfill \\ \hfill & +(k_1^{\beta }+k_2^{\beta })k_2^{\beta }(k_2^{\beta }+2k_1^{\beta })-{\left(k_2^{\beta }\right)}^{\prime }(k_2^{\beta }+2k_1^{\beta }))\hfill \\ \hfill & +\sqrt{3}v\left(2(k_1^{\beta }-k_2^{\beta })+{\left(k_2^{\beta }\right)}^{\prime }-{\left(k_1^{\beta }\right)}^{\prime }\right)+(k_2^{\beta }-k_1^{\beta })]\hfill \end{array}$$

(24)

Proof. 

The partial derivatives of the Bishop adjoint ruled surface ${\Phi }_7(s,v)$ with respect to s and v are expressed as follows:

$$\begin{array}{cc}\hfill {\Phi }_7(s,v)& =\beta \left(s\right)+{\displaystyle \frac{v}{\sqrt{3}}}\left({\mathbf{t}}_{\beta }+{\mathit{\zeta }}_1^{\beta }+{\mathit{\zeta }}_2^{\beta }\right),\hfill \\ \hfill {\Phi }_{7s}(s,v)& =\left(1-{\displaystyle \frac{v}{\sqrt{3}}}(k_1^{\beta }+k_2^{\beta })\right){\mathbf{t}}_{\beta }+{\displaystyle \frac{v{k}_1^{\beta }}{\sqrt{3}}}{\mathit{\zeta }}_1^{\beta }+{\displaystyle \frac{v{k}_2^{\beta }}{\sqrt{3}}}{\mathit{\zeta }}_2^{\beta },\hfill \\ \hfill {\Phi }_{7ss}(s,v)& =-{\displaystyle \frac{v}{\sqrt{3}}}\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_2^{\beta }\right)}^{\prime }\right){\mathbf{t}}_{\beta }\hfill \\ \hfill & +\left(\left(1-{\displaystyle \frac{v}{\sqrt{3}}}(k_1^{\beta }+k_2^{\beta })\right)k_1^{\beta }+{\displaystyle \frac{v}{\sqrt{3}}}{\left(k_1^{\beta }\right)}^{\prime }\right){\mathit{\zeta }}_1^{\beta }\hfill \\ \hfill & +\left(\left(1-{\displaystyle \frac{v}{\sqrt{3}}}(k_1^{\beta }+k_2^{\beta })\right)k_2^{\beta }+{\displaystyle \frac{v}{\sqrt{3}}}{\left(k_2^{\beta }\right)}^{\prime }\right){\mathit{\zeta }}_2^{\beta },\hfill \\ \hfill {\Phi }_{7v}(s,v)& ={\displaystyle \frac{1}{\sqrt{3}}}\left({\mathbf{t}}_{\beta }+{\mathit{\zeta }}_1^{\beta }+{\mathit{\zeta }}_2^{\beta }\right),\hfill \\ \hfill {\Phi }_{7sv}(s,v)& =-{\displaystyle \frac{1}{\sqrt{3}}}(k_1^{\beta }+k_2^{\beta }){\mathbf{t}}_{\beta }+{\displaystyle \frac{k_1^{\beta }}{\sqrt{3}}}{\mathit{\zeta }}_1^{\beta }+{\displaystyle \frac{k_2^{\beta }}{\sqrt{3}}}{\mathit{\zeta }}_2^{\beta },\hfill \\ \hfill {\Phi }_{7vv}(s,v)& =0.\hfill \end{array}$$

The unit normal vector field of ${\Phi }_7(s,v)$ is given by:

$$U_{{\Phi }_7}={\displaystyle \frac{v(k_1^{\beta }-k_2^{\beta }){\mathbf{t}}_{\beta }+(-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })){\mathit{\zeta }}_1^{\beta }+(\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })){\mathit{\zeta }}_2^{\beta }}{\sqrt{v^2{(k_1^{\beta }-k_2^{\beta })}^2+{\left(-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })\right)}^2+{\left(\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })\right)}^2}}}.$$

The coefficients of the first fundamental form are:

$$E_{{\Phi }_7}={\left(1-{\displaystyle \frac{v}{\sqrt{3}}}(k_1^{\beta }+k_2^{\beta })\right)}^2+{\displaystyle \frac{v^2}{3}}\left({\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right),F_{{\Phi }_7}={\displaystyle \frac{1}{\sqrt{3}}},G_{{\Phi }_7}=1.$$

The coefficients of the second fundamental form are:

$$\begin{array}{cc}\hfill e_{{\Phi }_7}& ={\displaystyle \frac{\begin{array}{cc}\hfill & -\sqrt{3}{v}^2\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_2^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)(k_1^{\beta }-k_2^{\beta })\hfill \\ \hfill & +\left(\sqrt{3}-v(k_1^{\beta }+k_2^{\beta })\right)k_1^{\beta }+v{\left(k_1^{\beta }\right)}^{\prime }\left(-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })\right)\hfill \\ \hfill & +\left(\sqrt{3}-v(k_1^{\beta }+k_2^{\beta })\right)k_2^{\beta }+v{\left(k_2^{\beta }\right)}^{\prime }\left(\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })\right)\hfill \end{array}}{\begin{array}{cc}\hfill & v^2{(k_1^{\beta }-k_2^{\beta })}^2+{\left(-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })\right)}^2+{\left(\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })\right)}^2\hfill \end{array}}},\hfill \\ \hfill f_{{\Phi }_7}& ={\displaystyle \frac{k_2^{\beta }-k_1^{\beta }}{3}},g_{{\Phi }_7}=0.\hfill \end{array}$$

Finally, by substituting these expressions into Equations (5) and (6), we obtain the Gaussian and mean curvature formulas given in Equations (23) and (24). □

Corollary 16. 

The Bishop adjoint ruled surface ${\Phi }_7(s,v)$ is a developable surface if and only if $k_1^{\beta }=k_2^{\beta }$.

Corollary 17. 

If $k_1^{\beta }=k_2^{\beta }$, then the Bishop adjoint ruled surface ${\Phi }_7(s,v)$ is a minimal surface.

Theorem 29. 

A necessary and sufficient condition for the Bishop adjoint ruled surface  ${\Phi }_7(s,v)$ to exhibit a singularity at the point $(s_{\theta },v_{\theta })$ is that

$$k_1^{\beta }=k_2^{\beta }={\displaystyle \frac{\sqrt{3}}{3v_{\theta }}}.$$

Proof. 

According to the definition given by Do Carmo [2], the surface ${\Phi }_7(s,v)$ possesses a singular point at $(s_{\theta },v_{\theta })$ if and only if

$$∥{\Phi }_{7s}\times {\Phi }_{7v}∥(s_{\theta },v_{\theta })={\displaystyle \frac{1}{3}}\sqrt{v_{\theta }^2{(k_1^{\beta }-k_2^{\beta })}^2+{\left(-\sqrt{3}+v_{\theta }(k_1^{\beta }+2k_2^{\beta })\right)}^2+{\left(\sqrt{3}-v_{\theta }(k_2^{\beta }+2k_1^{\beta })\right)}^2}.$$

This expression equals zero if and only if the following system holds:

$$v_{\theta }(k_1^{\beta }-k_2^{\beta })=0,-\sqrt{3}+v_{\theta }(k_1^{\beta }+2k_2^{\beta })=0,\sqrt{3}-v_{\theta }(k_2^{\beta }+2k_1^{\beta })=0.$$

Solving this system yields:

$$k_1^{\beta }=k_2^{\beta }={\displaystyle \frac{\sqrt{3}}{3v_{\theta }}}.$$

Thus, the proof is complete. □

Theorem 30. 

For the Bishop adjoint ruled surface ${\Phi }_7(s,v)$, the s-parametric curves are not asymptotic, whereas the v-parametric curves are always asymptotic.

Proof. 

On a surface, the s-parametric curves are asymptotic if and only if $e=0$ [2]. For the surface ${\Phi }_7(s,v)$, the second fundamental form coefficient e is computed as follows:

$$e=⟨{\Phi }_{7ss},U_{{\Phi }_7}⟩={\displaystyle \frac{\begin{array}{cc}& -\sqrt{3}{v}^2\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_2^{\beta }\right)}^{\prime }+{\left(k_1^{\beta }\right)}^2+{\left(k_2^{\beta }\right)}^2\right)(k_1^{\beta }-k_2^{\beta })\hfill \\ & +\left(\sqrt{3}-v(k_1^{\beta }+k_2^{\beta })\right)k_1^{\beta }+v{\left(k_1^{\beta }\right)}^{\prime }\left(-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })\right)\hfill \\ & +\left(\sqrt{3}-v(k_1^{\beta }+k_2^{\beta })\right)k_2^{\beta }+v{\left(k_2^{\beta }\right)}^{\prime }\left(\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })\right)\hfill \end{array}}{v^2{(k_1^{\beta }-k_2^{\beta })}^2+{\left(-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })\right)}^2+{\left(\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })\right)}^2}}=0.$$

This expression vanishes if and only if the following system holds:

$$v(k_1^{\beta }-k_2^{\beta })=0,-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })=0,\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })=0.$$

Solving this system gives:

$$k_1^{\beta }=k_2^{\beta }={\displaystyle \frac{\sqrt{3}}{3v}}.$$

However, this condition characterizes a singular point on the surface (as shown previously). Therefore, the s-parametric curves on ${\Phi }_7(s,v)$ cannot be asymptotic. □

Theorem 31. 

Let ${\Phi }_7={\Phi }_7(s,v)$ be a Bishop adjoint ruled surface. Then the s-parameter curves of ${\Phi }_7$ are not geodesic, but the v-parameter curves are always geodesic.

Proof. 

In order for the s-parametric curves to be geodesics on the Bishop adjoint ruled surface ${\Phi }_7(s,v)$, the following condition must be satisfied:

$$U_{{\Phi }_7}\times {\Phi }_{7ss}=X_1{\mathbf{t}}_{\beta }+Y_1{\mathit{\zeta }}_1^{\beta }+Z_1{\mathit{\zeta }}_2^{\beta }=0,$$

where the coefficients $X_1,Y_1,Z_1$ are given by:

$$\begin{array}{cc}\hfill X_1& ={\displaystyle \frac{\begin{array}{cc}\hfill & (-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta }))\left(\left(1-\frac{v}{\sqrt{3}}(k_1^{\beta }+k_2^{\beta })\right)k_2^{\beta }+\frac{v}{\sqrt{3}}{\left(k_2^{\beta }\right)}^{\prime }\right)\hfill \\ \hfill & +(-\sqrt{3}+v(k_2^{\beta }+2k_1^{\beta }))\left(\left(1-\frac{v}{\sqrt{3}}(k_1^{\beta }+k_2^{\beta })\right)k_1^{\beta }+\frac{v}{\sqrt{3}}{\left(k_1^{\beta }\right)}^{\prime }\right)\hfill \end{array}}{\sqrt{\begin{array}{cc}\hfill & v^2{(k_1^{\beta }-k_2^{\beta })}^2+{\left(-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })\right)}^2\hfill \\ \hfill & +{\left(\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })\right)}^2\hfill \end{array}}}},\hfill \\ \hfill Y_1& ={\displaystyle \frac{\begin{array}{cc}\hfill & -v(k_1^{\beta }-k_2^{\beta })\left(\left(1-\frac{v}{\sqrt{3}}(k_1^{\beta }+k_2^{\beta })\right)k_2^{\beta }+\frac{v}{\sqrt{3}}{\left(k_2^{\beta }\right)}^{\prime }\right)\hfill \\ \hfill & -\frac{v}{\sqrt{3}}\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_2^{\beta }\right)}^{\prime }\right)\left(\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })\right)\hfill \end{array}}{\sqrt{\begin{array}{cc}\hfill & v^2{(k_1^{\beta }-k_2^{\beta })}^2+{\left(-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })\right)}^2\hfill \\ \hfill & +{\left(\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })\right)}^2\hfill \end{array}}}},\hfill \\ \hfill Z_1& ={\displaystyle \frac{\begin{array}{cc}\hfill & v(k_1^{\beta }-k_2^{\beta })\left(\left(1-\frac{v}{\sqrt{3}}(k_1^{\beta }+k_2^{\beta })\right)k_1^{\beta }+\frac{v}{\sqrt{3}}{\left(k_1^{\beta }\right)}^{\prime }\right)\hfill \\ \hfill & +\frac{v}{\sqrt{3}}\left({\left(k_1^{\beta }\right)}^{\prime }+{\left(k_2^{\beta }\right)}^{\prime }\right)\left(-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })\right)\hfill \end{array}}{\sqrt{\begin{array}{cc}\hfill & v^2{(k_1^{\beta }-k_2^{\beta })}^2+{\left(-\sqrt{3}+v(k_1^{\beta }+2k_2^{\beta })\right)}^2\hfill \\ \hfill & +{\left(\sqrt{3}-v(k_2^{\beta }+2k_1^{\beta })\right)}^2\hfill \end{array}}}}.\hfill \end{array}$$

Solving the system $X_1=0,Y_1=0,Z_1=0$ yields:

$$k_1^{\beta }=k_2^{\beta }={\displaystyle \frac{\sqrt{3}}{3v}}.$$

However, this condition defines a singular point on the surface ${\Phi }_7(s,v)$ (as previously shown). Therefore, the s-parametric curves cannot be geodesics on the surface. □

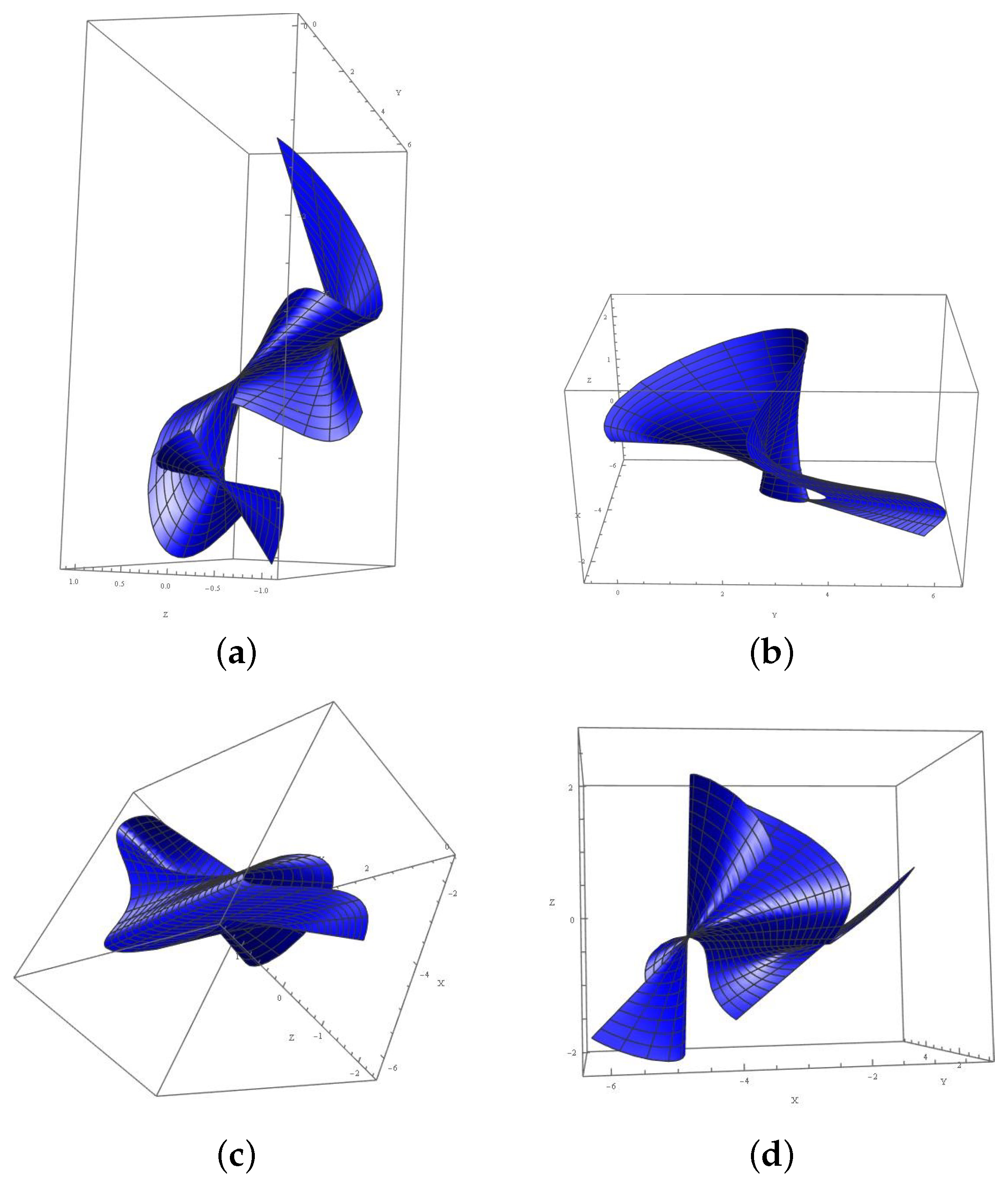
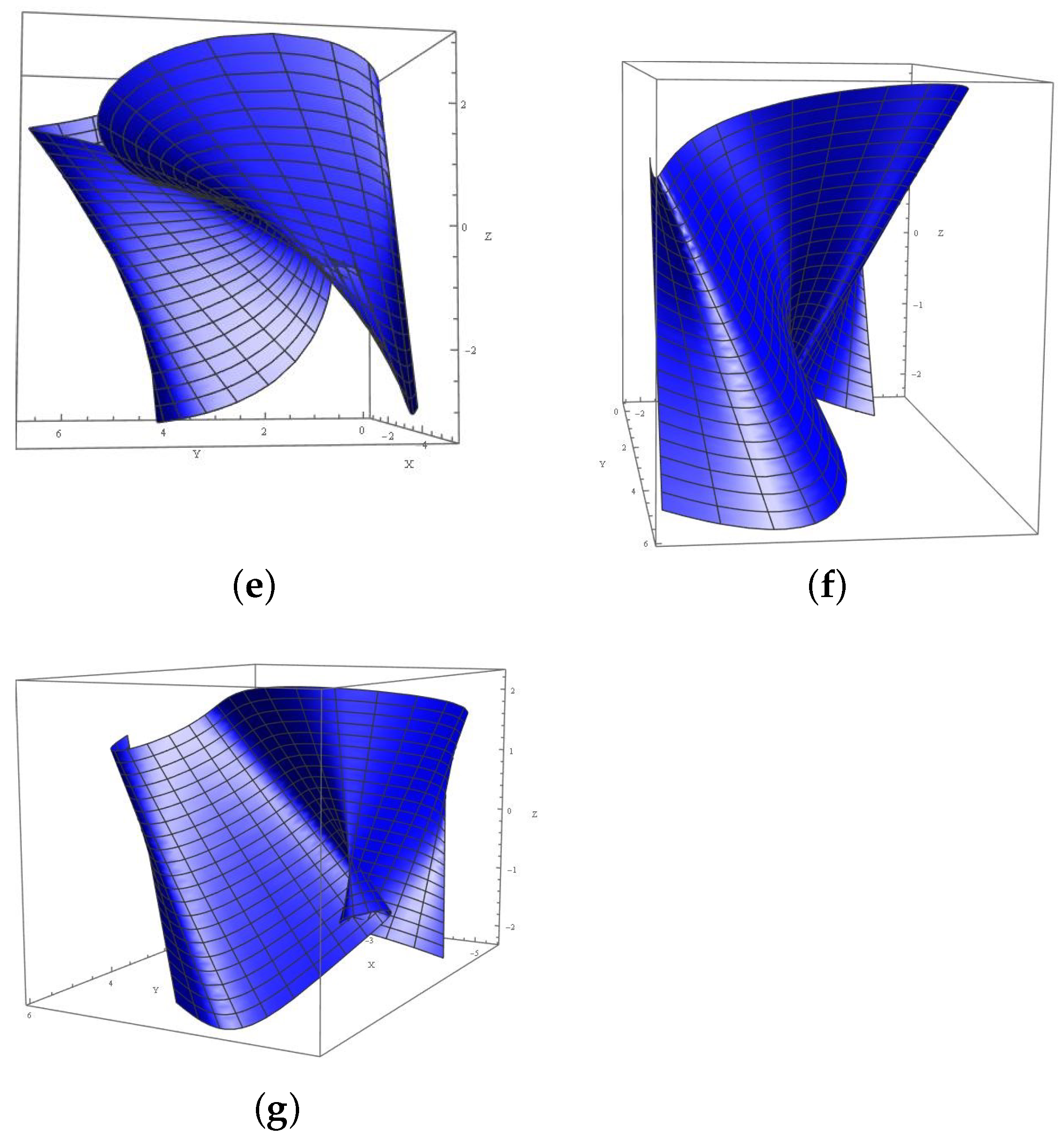
Example 1. 

Consider the unit speed curve α in ${\mathbb{E}}^3$, given by

$$\alpha \left(s\right)=\left({\displaystyle \frac{1}{2}}coss,{\displaystyle \frac{1}{2}}sins,{\displaystyle \frac{\sqrt{3}}{2}}s\right).$$

The Bishop trihedron of α, as well as the ${\mathit{\zeta }}_1^{\alpha }{\mathit{\zeta }}_2^{\alpha }$-Bishop adjoint curve, were previously obtained in [24]. In this section, we explicitly compute the Bishop adjoint ruled surfaces ${\Phi }_1(s,v)$ through ${\Phi }_7(s,v)$ associated with the curve α.

$$\begin{array}{cc}\hfill {\Phi }_1(s,v)& ={\displaystyle \frac{1}{\sqrt{2}}}\int \left({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right)\right)ds+v{\mathbf{t}}_{\beta }\left(s\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{c}3\sqrt{3}cos\left(s\right)sin\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)-{\displaystyle \frac{11}{2}}sin\left(s\right)cos\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)\\ -3\sqrt{3}cos\left(s\right)cos\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)-{\displaystyle \frac{11}{2}}sin\left(s\right)sin\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)\\ 3\sqrt{3}sin\left(s\right)sin\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)+4cos\left(s\right)cos\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)+7cos\left(s\right)sin\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)\\ -3\sqrt{3}sin\left(s\right)cos\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)\\ {\displaystyle \frac{1}{2}}sin\left(s\right)+{\displaystyle \frac{1}{2}}cos\left(s\right)\end{array}\right)\hfill \\ \hfill & +{\displaystyle \frac{v}{\sqrt{2}}}\left(\begin{array}{c}-cos\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)cos\left(s\right)-{\displaystyle \frac{\sqrt{3}}{4}}sin\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)sin\left(s\right)\\ -sin\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)cos\left(s\right)+{\displaystyle \frac{\sqrt{3}}{4}}cos\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)sin\left(s\right)\\ -cos\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)sin\left(s\right)+{\displaystyle \frac{\sqrt{3}}{4}}sin\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)cos\left(s\right)\\ -sin\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)sin\left(s\right)-{\displaystyle \frac{\sqrt{3}}{4}}cos\left({\displaystyle \frac{\sqrt{3}}{2}}s\right)cos\left(s\right)\\ -{\displaystyle \frac{1}{2}}sin\left(s\right)+{\displaystyle \frac{1}{2}}cos\left(s\right)\end{array}\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\Phi }_2(s,v)& ={\displaystyle \frac{1}{\sqrt{2}}}\int \left({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right)\right)ds+v{\mathit{\zeta }}_1^{\beta }\left(s\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{c}3\sqrt{3}cosssin\left(\frac{\sqrt{3}}{2}s\right)-\frac{11}{2}sinscos\left(\frac{\sqrt{3}}{2}s\right)\\ -3\sqrt{3}cosscos\left(\frac{\sqrt{3}}{2}s\right)-\frac{11}{2}sinssin\left(\frac{\sqrt{3}}{2}s\right)\\ 3\sqrt{3}sinssin\left(\frac{\sqrt{3}}{2}s\right)+4cosscos\left(\frac{\sqrt{3}}{2}s\right)\\ +7cosssin\left(\frac{\sqrt{3}}{2}s\right)-3\sqrt{3}sinscos\left(\frac{\sqrt{3}}{2}s\right)\\ \frac{1}{2}sins+\frac{1}{2}coss\end{array}\right)\hfill \\ \hfill & +v\left(\begin{array}{c}{\displaystyle \frac{cos\theta }{2}}sins+{\displaystyle \frac{sin\theta }{\sqrt{2}}}\left(-cos\left(\frac{\sqrt{3}}{2}s\right)coss-\frac{\sqrt{3}}{4}sin\left(\frac{\sqrt{3}}{2}s\right)sins\right.\\ \left.+sin\left(\frac{\sqrt{3}}{2}s\right)coss-\frac{\sqrt{3}}{4}cos\left(\frac{\sqrt{3}}{2}s\right)sins\right)\\ -{\displaystyle \frac{cos\theta }{2}}coss+{\displaystyle \frac{sin\theta }{\sqrt{2}}}\left(-cos\left(\frac{\sqrt{3}}{2}s\right)sins+\frac{\sqrt{3}}{4}sin\left(\frac{\sqrt{3}}{2}s\right)coss\right.\\ \left.+sin\left(\frac{\sqrt{3}}{2}s\right)sins+\frac{\sqrt{3}}{4}cos\left(\frac{\sqrt{3}}{2}s\right)coss\right)\\ -{\displaystyle \frac{cos\theta \sqrt{3}}{2}}-{\displaystyle \frac{sin\theta }{2\sqrt{2}}}(sins+coss)\end{array}\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\Phi }_3(s,v)& ={\displaystyle \frac{1}{\sqrt{2}}}\int \left({\mathit{\zeta }}_1^{\alpha }\left(s\right)+{\mathit{\zeta }}_2^{\alpha }\left(s\right)\right)ds+v{\mathit{\zeta }}_2^{\alpha }\left(s\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{c}3\sqrt{3}cosssin\left(\frac{\sqrt{3}}{2}s\right)-\frac{11}{2}sinscos\left(\frac{\sqrt{3}}{2}s\right)\\ -3\sqrt{3}cosscos\left(\frac{\sqrt{3}}{2}s\right)-\frac{11}{2}sinssin\left(\frac{\sqrt{3}}{2}s\right)\\ 3\sqrt{3}sinssin\left(\frac{\sqrt{3}}{2}s\right)+4cosscos\left(\frac{\sqrt{3}}{2}s\right)\\ +7cosssin\left(\frac{\sqrt{3}}{2}s\right)-3\sqrt{3}sinscos\left(\frac{\sqrt{3}}{2}s\right)\\ \frac{1}{2}sins+\frac{1}{2}coss\end{array}\right)\hfill \\ \hfill & +v\left(\begin{array}{c}{\displaystyle \frac{sin\theta }{2}}sins-{\displaystyle \frac{cos\theta }{\sqrt{2}}}\left(-cos\left(\frac{\sqrt{3}}{2}s\right)coss-\frac{\sqrt{3}}{4}sin\left(\frac{\sqrt{3}}{2}s\right)sins\right.\\ \left.+sin\left(\frac{\sqrt{3}}{2}s\right)coss-\frac{\sqrt{3}}{4}cos\left(\frac{\sqrt{3}}{2}s\right)sins\right)\\ -{\displaystyle \frac{sin\theta }{2}}coss-{\displaystyle \frac{cos\theta }{\sqrt{2}}}\left(-cos\left(\frac{\sqrt{3}}{2}s\right)sins+\frac{\sqrt{3}}{4}sin\left(\frac{\sqrt{3}}{2}s\right)coss\right.\\ \left.+sin\left(\frac{\sqrt{3}}{2}s\right)sins+\frac{\sqrt{3}}{4}cos\left(\frac{\sqrt{3}}{2}s\right)coss\right)\\ -{\displaystyle \frac{sin\theta \sqrt{3}}{2}}+{\displaystyle \frac{1}{2\sqrt{2}}}cos\theta (sins+coss)\end{array}\right)\hfill \end{array}$$

Similar computations can also be carried out for the surfaces ${\Phi }_4$–${\Phi }_7$, and the graphs of all Bishop adjoint ruled surfaces ${\Phi }_1(s,v)$–${\Phi }_7(s,v)$ are presented in Figure 1a–g.

Figure 1. (a) The ${\Phi }_1(s,v)$ Bishop adjoint developable minimal ruled surface; (b) The ${\Phi }_2(s,v)$ Bishop adjoint developable non-minimal ruled surface; (c) The ${\Phi }_3(s,v)$ Bishop adjoint developable non-minimal ruled surface; (d) The ${\Phi }_4(s,v)$ Bishop adjoint non-developable ruled surface; (e) The ${\Phi }_5(s,v)$ Bishop adjoint non-developable ruled surface; (f) The ${\Phi }_6(s,v)$ Bishop adjoint developable minimal ruled surface; (g) The ${\Phi }_7(s,v)$ Bishop adjoint developable minimal ruled surface.

Although the algebraic structure of each ${\Phi }_i(s,v)$ surface is defined by a specific direction vector, the visual differences observed in the plotted surfaces provide important geometric intuition. For example, the surface ${\Phi }_1(s,v)$, constructed using the tangent vector $t_{\beta }$, exhibits a helicoidal behavior with vanishing curvature conditions. This structure arises from the consistent twist generated by the tangent direction, while still satisfying the criteria for developability and minimality. In contrast, the surfaces ${\Phi }_2(s,v)$ and ${\Phi }_3(s,v)$, generated respectively by ${\mathit{\zeta }}_1^{\beta }$ and ${\mathit{\zeta }}_2^{\beta }$, appear more open and flared, reflecting the influence of curvature components orthogonal to the tangent. The mixed constructions in ${\Phi }_4(s,v)$, ${\Phi }_5(s,v)$, and ${\Phi }_6(s,v)$ result in more complex twisting and expanding behaviors due to the combination of multiple direction vectors. Finally, the surface ${\Phi }_7(s,v)$, involving the sum ${\mathbf{t}}_{\beta }+{\mathit{\zeta }}_1^{\beta }+{\mathit{\zeta }}_2^{\beta }$, displays the most spatially expansive form, capturing the compounded geometric influence of all three directions. These visual characteristics align well with the analytically derived curvature and singularity results, offering an intuitive validation of the theoretical findings.

4. Discussion

This study highlights the role of Smarandache curves, ruled surfaces, and the Bishop frame in the construction of different geometric structures. Known for their unique structure and transformation properties, Smarandache curves play a crucial role in differential geometry and geometric modeling. Integrating these curves with the Bishop frame has provided an alternative to the classical Frenet-Serret frame, enabling the construction of new ruled surfaces. Consequently, a new class of surfaces has been introduced to theoretical geometry and applied mathematics. Furthermore, the findings of this study demonstrate that Bishop adjoint ruled surfaces possess significant geometric properties in terms of developability, minimality, and singularity conditions. These results contribute to the expansion of ruled surface theory and offer new perspectives on curve-surface relationships. Additionally, by analyzing the asymptotic and geodesic properties of parametric curves on these surfaces, potential applications in kinematics, differential geometry, and mechanical modeling have been highlighted. The findings of this study are expected to shed light on future research exploring adjoint ruled surfaces in higher dimensions, particularly in fields such as Lorentz geometry and relativity physics. One of the main theoretical challenges in such generalizations is the adaptation of the Bishop frame to indefinite metrics, as orthonormality conditions and curvature relations differ significantly in these settings. Furthermore, especially when dealing with null (lightlike) curves or time-like singularities, symbolic or numerical integration in pseudo-Riemannian manifolds can lead to substantial computational difficulties.

5. Conclusions

In this study, a new class of ruled surfaces was introduced using adjoint curves derived from Smarandache-type vectors. The base curve was taken as the Bishop adjoint curve defined by the linear combination ${\mathit{\zeta }}_1^{\alpha }+{\mathit{\zeta }}_2^{\alpha }$, with the direction vectors constructed accordingly. Seven distinct ruled surfaces were generated, for which explicit expressions of Gaussian and mean curvatures were derived. Furthermore, their geometric characteristics including developability, minimality, and singularity conditions were thoroughly examined. To provide a comprehensive comparison, the geodesic and asymptotic behaviors of the parameter curves, along with the aforementioned surface properties, are summarized in Table 2, Table 3 and Table 4.

Table 2. Developability and minimality of the ruled surfaces ${\Phi }_i(s,v)$.

Surface	Developability	Minimality
${\Phi }_1(s,v)$	Developable	Minimal
${\Phi }_2(s,v)$	Developable	Not minimal
${\Phi }_3(s,v)$	Developable	Not minimal
${\Phi }_4(s,v)$	Not developable	Conditionally minimal
${\Phi }_5(s,v)$	Not developable	Conditionally minimal
${\Phi }_6(s,v)$	Developable	Minimal under curvature ratio condition
${\Phi }_7(s,v)$	Developable under curvature ratio condition	Minimal under curvature ratio condition

Table 3. Singularity conditions of the ruled surfaces ${\Phi }_i(s,v)$.

Surface	Singularity Condition
${\Phi }_1(s,v)$	No singularities (regular everywhere)
${\Phi }_2(s,v)$	Singularity at $(s_{\theta },v_{\theta })$ if $k_1^{\beta }={\displaystyle \frac{1}{v_{\theta }}}$
${\Phi }_3(s,v)$	Singularity at $(s_{\theta },v_{\theta })$ if $k_2^{\beta }={\displaystyle \frac{1}{v_{\theta }}}$
${\Phi }_4(s,v)$	No singularities (regular everywhere)
${\Phi }_5(s,v)$	No singularities (regular everywhere)
${\Phi }_6(s,v)$	Singularity at $(s_{\theta },v_{\theta })$ if $k_1^{\beta }+k_2^{\beta }={\displaystyle \frac{\sqrt{2}}{v_{\theta }}}$
${\Phi }_7(s,v)$	Singularity at $(s_{\theta },v_{\theta })$ if $k_1^{\beta }=k_2^{\beta }={\displaystyle \frac{\sqrt{3}}{3v_{\theta }}}$

Table 4. Geodesic and asymptotic nature of parameter curves on ${\Phi }_i(s,v)$.

Surface	s-Parameter Curve	v-Parameter Curve
${\Phi }_1(s,v)$	Asymptotic, not geodesic	Geodesic and asymptotic
${\Phi }_2(s,v)$	Not asymptotic, not geodesic	Geodesic and asymptotic
${\Phi }_3(s,v)$	Not asymptotic, not geodesic	Geodesic and asymptotic
${\Phi }_4(s,v)$	Conditionally asymptotic, not geodesic	Geodesic and asymptotic
${\Phi }_5(s,v)$	Conditionally asymptotic, not geodesic	Geodesic and asymptotic
${\Phi }_6(s,v)$	Conditionally asymptotic, not geodesic	Geodesic and asymptotic
${\Phi }_7(s,v)$	Not asymptotic, not geodesic	Geodesic and asymptotic

The proposed method offers a smoother and more stable construction than classical approaches, particularly in regions where curvature vanishes. By combining the flexibility of the Bishop frame with the structural richness of adjoint curves, this framework introduces a novel class of ruled surfaces into the literature, contributing both theoretical insights and practical applications in kinematics, mechanical modeling, and differential geometry.

Finally, graphical visualizations were provided to illustrate the geometric features of the constructed surfaces.