Novel Methods for Multi-Switch Generalized Projective Anti-Synchronization of Fractional Chaotic System Under Caputo–Fabrizio Derivative via Lyapunov Stability Theorem and Adaptive Control
Abstract
1. Introduction
2. Preliminaries
3. Problem Description
4. MSGPAS of Fractional Chaotic System
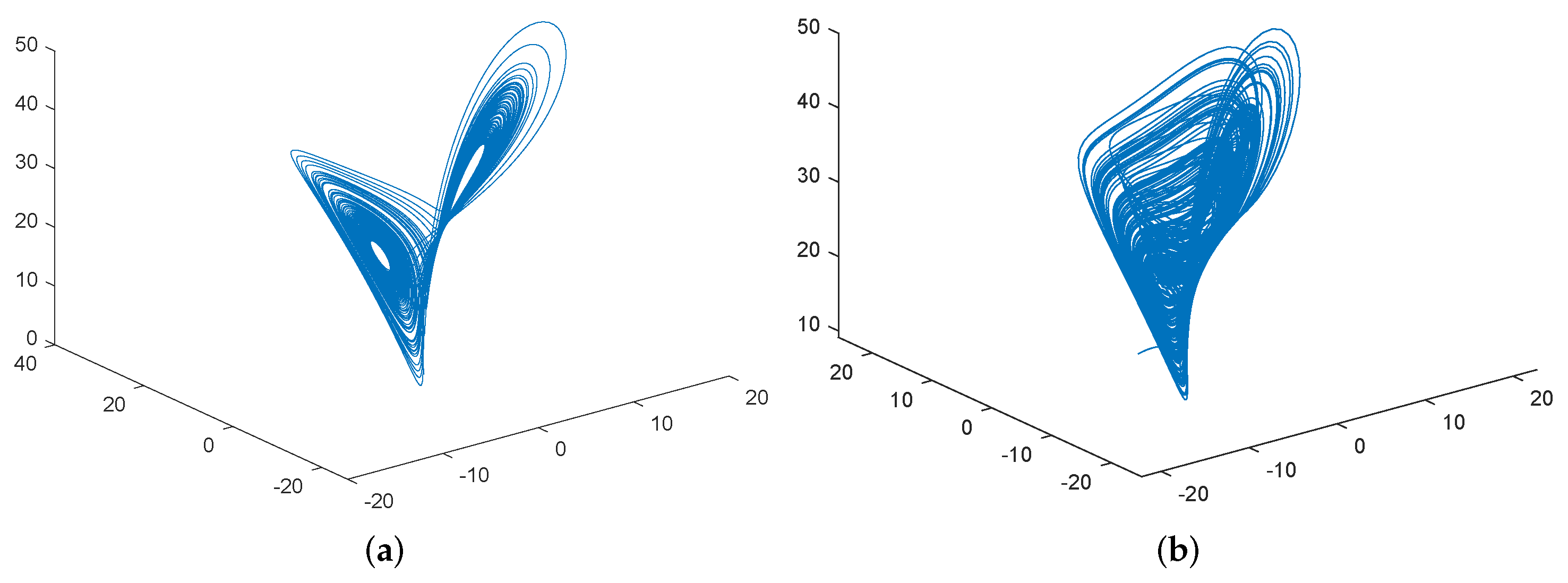
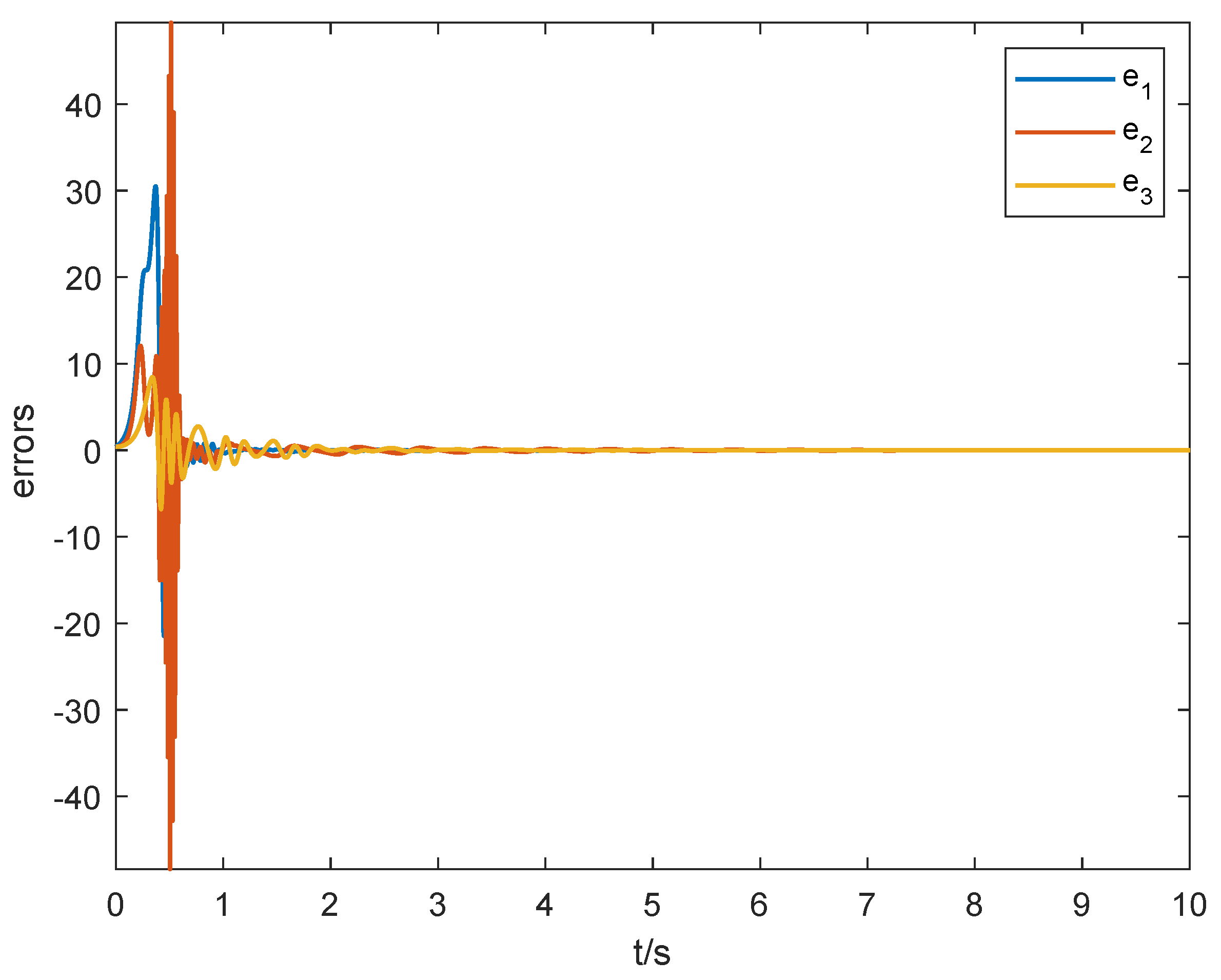
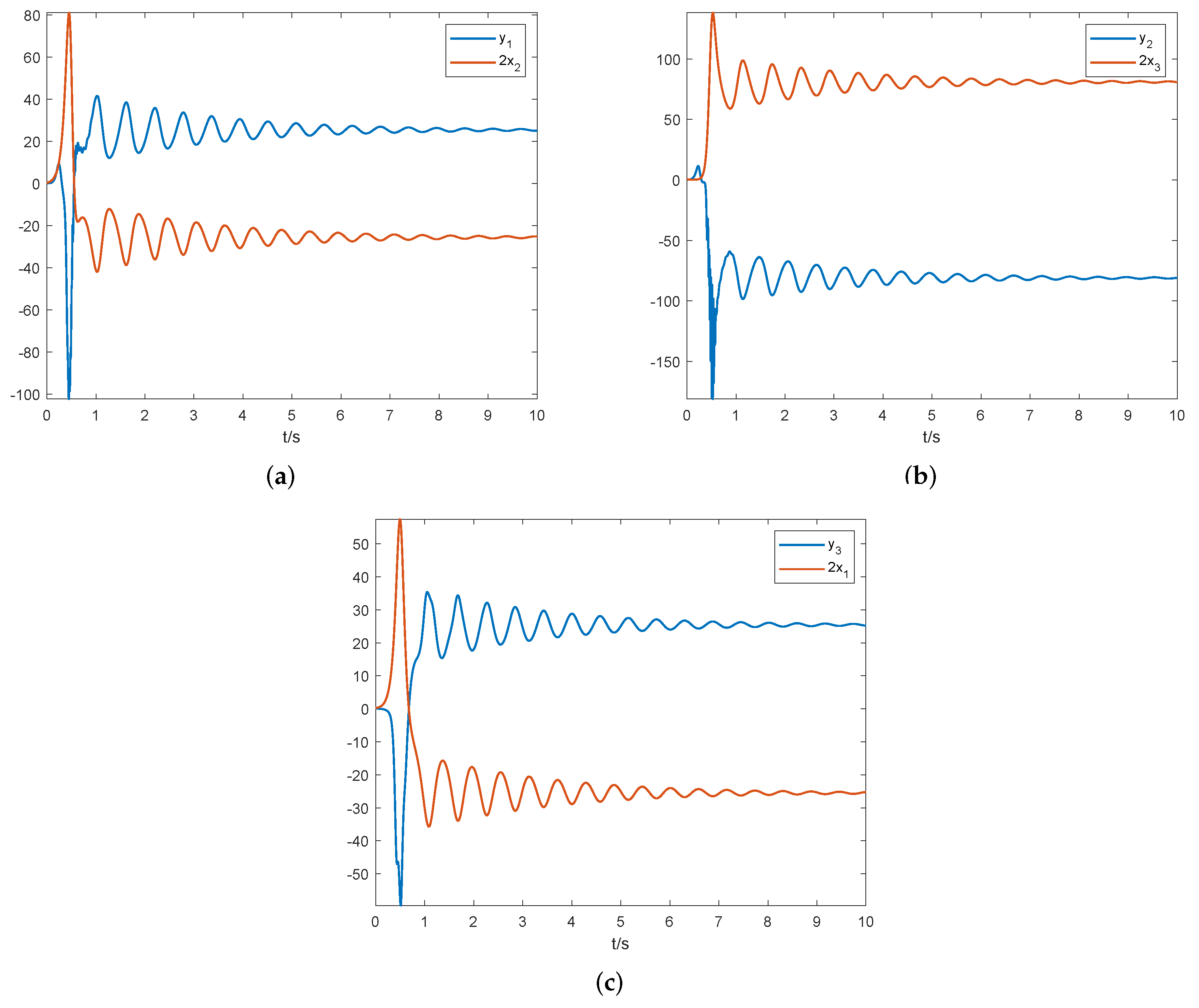
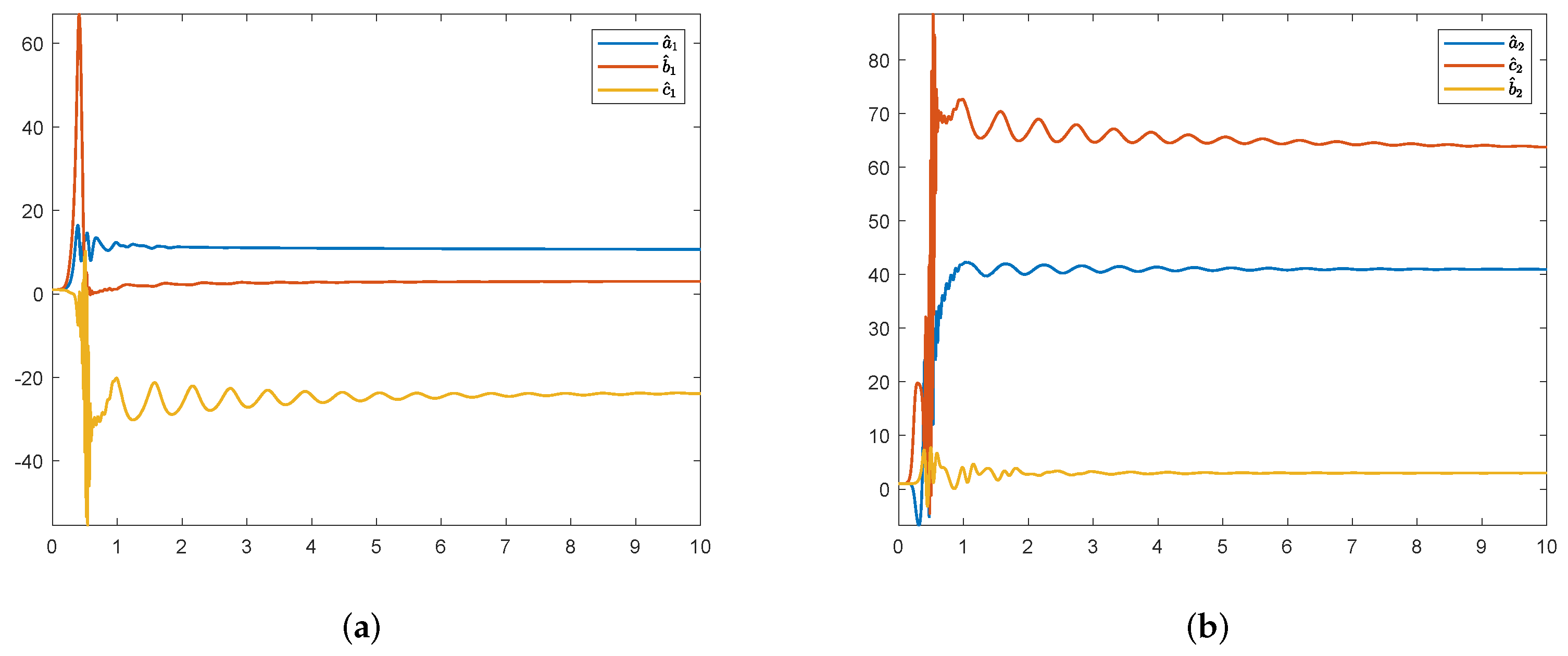
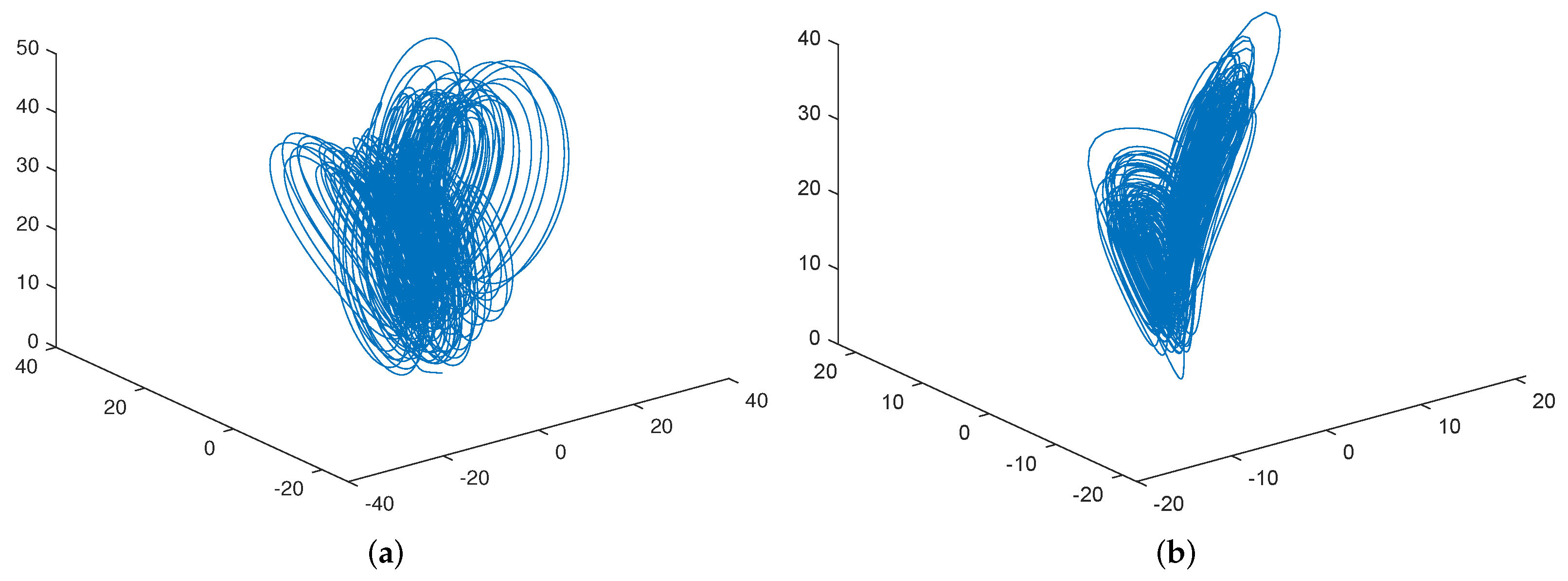
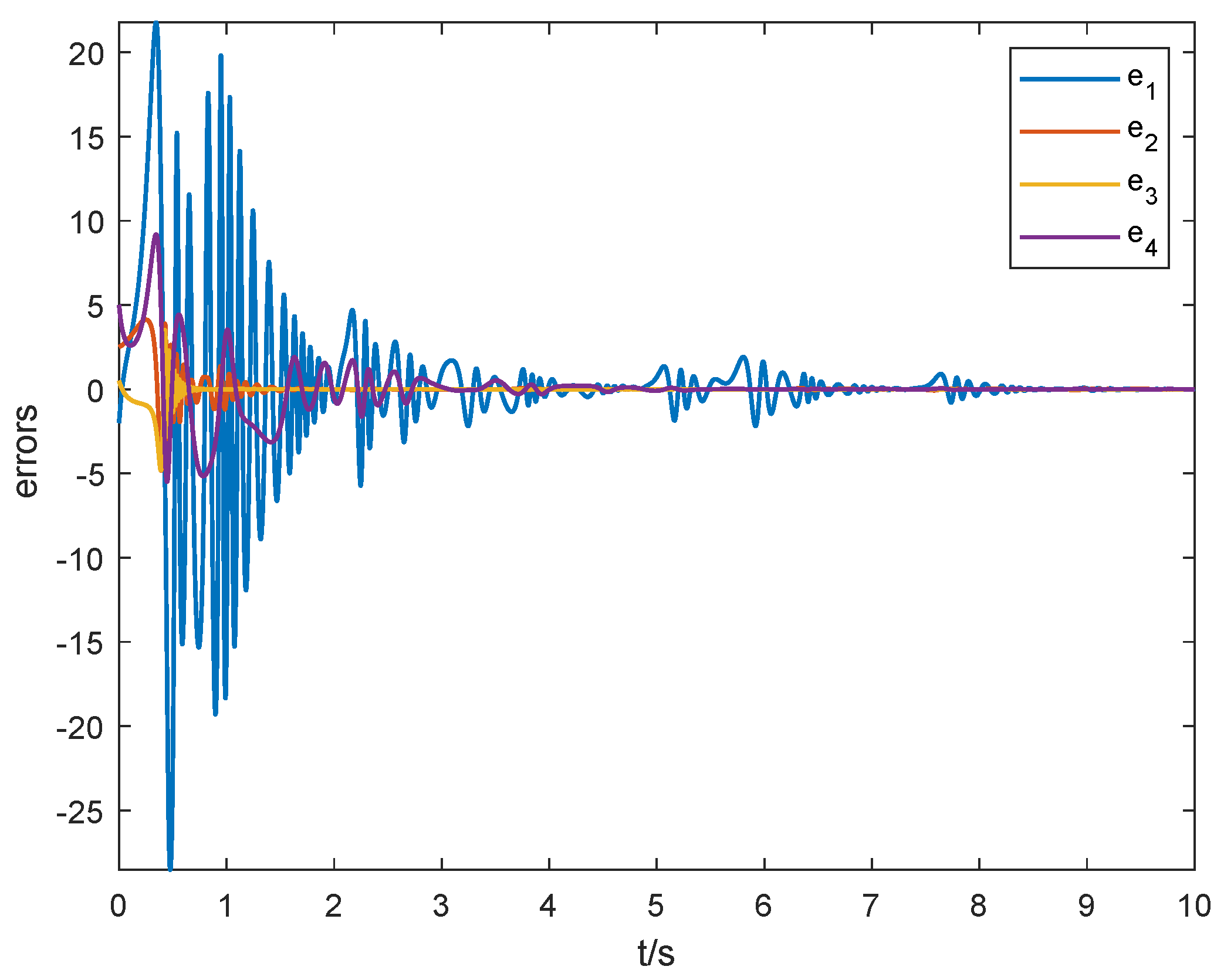
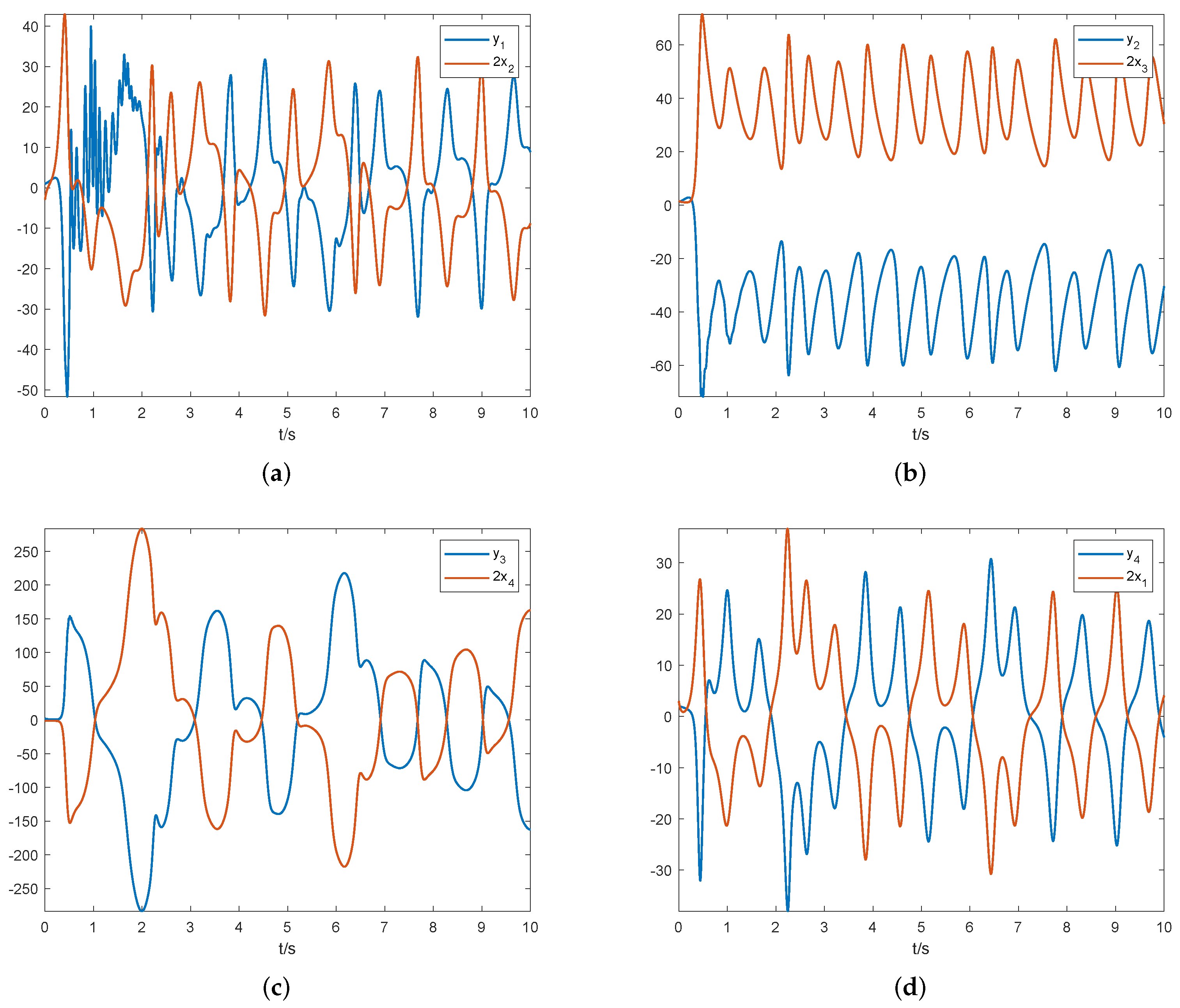
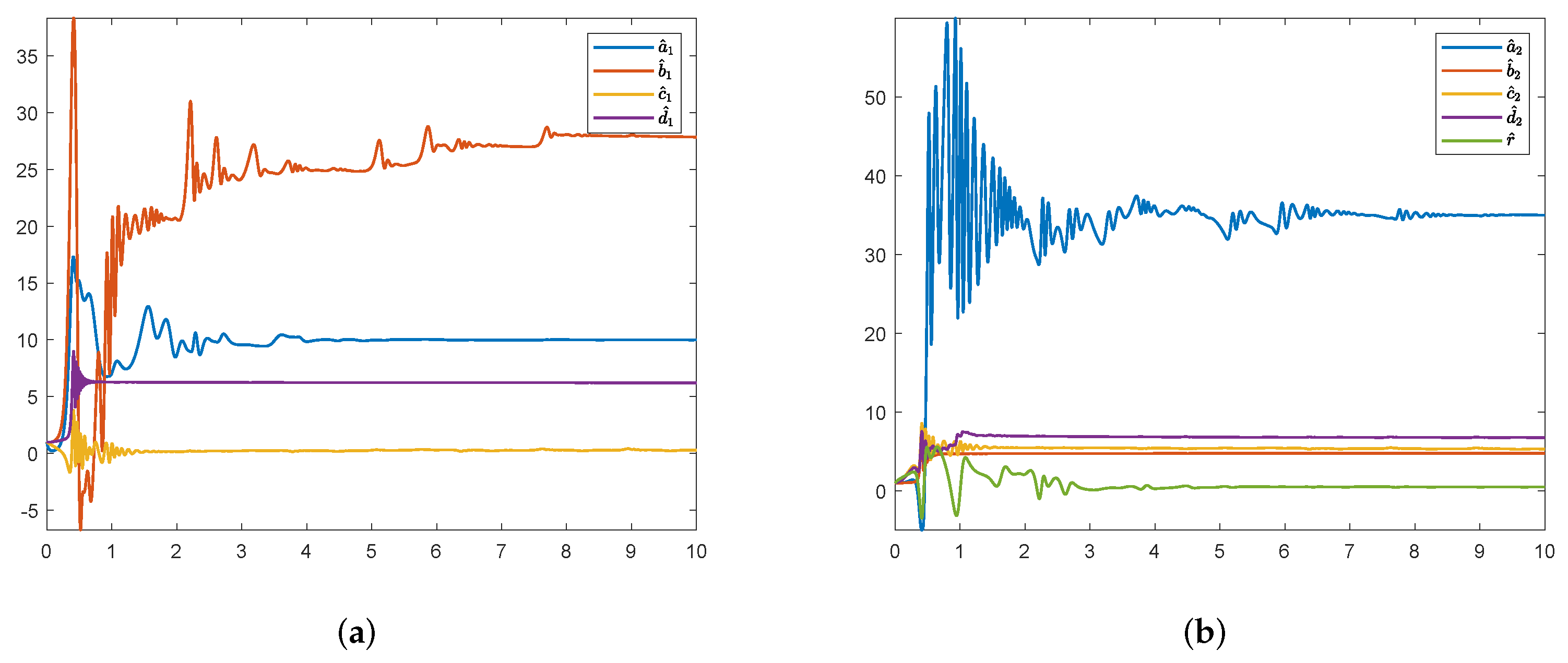
5. Numerical Simulation
5.1. MSGPAS of Fractional Chaotic System
5.2. MSGPAS of Fractional Hyperchaotic System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Butzer, P.L.; Westphal, U. An introduction to fractional calculus. In Applications of Fractional Calculus in Physics; World Scientific Publishing: Singapore, 2000; pp. 1–85. [Google Scholar]
- Chen, L.P.; Liu, C.; Lopes, A.M.; Lin, Y.; Liu, Y.X.; Chen, Y.Q. LMI synchronization conditions for variable fractional-order one-sided Lipschitz chaotic systems with gain fluctuations. Chaos Solitons Fractals 2024, 189, 115695. [Google Scholar] [CrossRef]
- Eshaghi, S.; Kadkhoda, N.; Inc, M. Chaos control and synchronization of a new fractional laser chaotic system. Qual. Theory Dyn. Syst. 2024, 23, 241. [Google Scholar] [CrossRef]
- Han, T.; Zhang, K.; Jiang, Y.; Rezazadeh, H. Chaotic Pattern and Solitary Solutions for the (21)-Dimensional Beta-Fractional Double-Chain DNA System. Fractal Fract. 2024, 8, 415. [Google Scholar] [CrossRef]
- Mo, W.; Bao, H. Mean-square bounded synchronization of fractional-order chaotic Lure systems under deception attack. Phys. A Stat. Mech. Appl. 2024, 641, 129726. [Google Scholar] [CrossRef]
- Puente-Cordova, J.G.; Rentera-Baltirrez, F.Y.; Lopez-Walle, B.; LOpez-Walle, B.; Aguilar-Garib, J.A. Dielectric and Viscoelastic Behavior of Polyvinyl Butyral Films. Polymers 2023, 15, 4725. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef] [PubMed]
- Ojo, K.S.; Ogunjo, S.T.; Fuwape, I.A. Modified hybrid combination synchronization of chaotic fractional order systems. Soft Comput. 2022, 26, 11865–11872. [Google Scholar] [CrossRef]
- Yadav, V.K.; Kumar, R.; Leung, A.Y.T.; Das, S. Dual phase and dual anti-phase synchronization of fractional order chaotic systems in real and complex variables with uncertainties. Chin. J. Phys. 2019, 57, 282–308. [Google Scholar] [CrossRef]
- Hamoudi, A.; Djeghali, N.; Bettayeb, M. High-order sliding mode-based synchronisation of fractional-order chaotic systems subject to output delay and unknown disturbance. Int. J. Syst. Sci. 2022, 53, 2876–2900. [Google Scholar] [CrossRef]
- Wang, F.; Zheng, Z. Quasi-projective synchronization of fractional order chaotic systems under input saturation. Phys. A Stat. Mech. Appl. 2019, 534, 122132. [Google Scholar] [CrossRef]
- Li, B.; Zhou, X.; Wang, Y. Combination Synchronization of Three Different Fractional-Order Delayed Chaotic Systems. Complexity 2019, 2019, 5184032. [Google Scholar] [CrossRef]
- Talebi, S.P.; Godsill, S.J.; Mandic, D.P. Filtering structures for α-stable systems. IEEE Control. Syst. Lett. 2022, 7, 553–558. [Google Scholar] [CrossRef]
- Bendoukha, S.; Abdelmalek, S. The fractional chua chaotic system: Dynamics, synchronization, and application to secure communications. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 77–88. [Google Scholar] [CrossRef]
- Mansouri, D.; Bendoukha, S.; Abdelmalek, S.; Youkana, A. On the complete synchronization of a time-fractional reactionCdiffusion system with the NewtonCLeipnik nonlinearity. Appl. Anal. 2021, 100, 675–694. [Google Scholar] [CrossRef]
- Gupta, S.; Varshney, P.; Srivastava, S. Whale optimization based synchronization and control of two identical fractional order financial chaotic systems. J. Intell. Fuzzy Syst. 2022, 42, 929–942. [Google Scholar] [CrossRef]
- Almuzaini, M.; Alzahrani, A. Control and synchronization of a novel realizable nonlinear chaotic system. Fractal Fract. 2023, 7, 253. [Google Scholar] [CrossRef]
- Echenausa-Monroy, J.L.; Rodrguez-Martne, C.A.; Alvarez, J.; Ramirez, J.P. Synchronization in Dynamically Coupled Fractional-Order Chaotic Systems: Studying the Effects of Fractional Derivatives. Complexity 2021, 2021, 7242253. [Google Scholar] [CrossRef]
- Shao, K.; Guo, H.; Han, F. Finite-time projective synchronization of fractional-order chaotic systems via soft variable structure control. J. Mech. Sci. Technol. 2020, 34, 369–376. [Google Scholar] [CrossRef]
- Meng, X.; Wu, Z.; Gao, C.; Jiang, B.; Karimi, H.R. Finite-time projective synchronization control of variable-order fractional chaotic systems via sliding mode approach. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2503–2507. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Zehrour, O.; Bendoukha, S.; Grassi, G.; Pham, V.T. Synchronisation of integer-order and fractional-order discrete-time chaotic systems. Pramana 2019, 92, 52. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Y.; Yang, S. Adaptive synchronization of fractional-order complex chaotic system with unknown complex parameters. Entropy 2019, 21, 207. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Feng, S.; Yang, S. Complex Modified Projective Synchronization of Fractional-order Complex-Variable Chaotic System with Unknown Complex Parameters. Entropy 2019, 21, 407. [Google Scholar] [CrossRef]
- Almatroud, A.O. Synchronisation of two different uncertain fractional-order chaotic systems with unknown parameters using a modified adaptive sliding-mode controller. Adv. Differ. Equ. 2020, 2020, 78. [Google Scholar] [CrossRef]
- Liu, D.; Li, T.; Wang, Y. Adaptive dual synchronization of fractional-order chaotic system with uncertain parameters. Mathematics 2022, 10, 470. [Google Scholar] [CrossRef]
- Sabaghian, A.; Balochian, S.; Yaghoobi, M. Synchronisation of 6D hyper-chaotic system with unknown parameters in the presence of disturbance and parametric uncertainty with unknown bounds. Connect. Sci. 2020, 32, 362–383. [Google Scholar] [CrossRef]
- Pan, W.; Li, T.; Sajid, M.; Pu, L. Parameter identification and the finite-time combinationCcombination synchronization of fractional-order chaotic systems with different structures under multiple stochastic disturbances. Mathematics 2022, 10, 712. [Google Scholar] [CrossRef]
- Hailong, Z.; Ding, Z.; Wang, L. Predefined-time multi-switch combination-combination synchronization of fractional-order chaotic systems with time delays. Phys. Scr. 2024, 99, 105223. [Google Scholar] [CrossRef]
- Li, B.; Wang, Y.; Zhou, X. Multi-switching combination synchronization of three fractional-order delayed Systems. Appl. Sci. 2019, 9, 4348. [Google Scholar] [CrossRef]
- Shahzad, M. Exploring the Different Order of Switches During Multi-switching Synchronization. Iran. J. Sci. 2024, 48, 965–977. [Google Scholar] [CrossRef]
- Sayed, W.S.; Radwan, A.G. Generalized switched synchronization and dependent image encryption using dynamically rotating fractional-order chaotic systems. AEU-Int. J. Electron. Commun. 2020, 123, 153268. [Google Scholar] [CrossRef]
- Sabzalian, M.H.; Mohammadzadeh, A.; Zhang, W.; Jermsittiparsert, K. General type-2 fuzzy multi-switching synchronization of fractional-order chaotic systems. Eng. Appl. Artif. Intell. 2021, 100, 104163. [Google Scholar] [CrossRef]
- Pan, W.; Li, T.; Wang, Y. The multi-switching sliding mode combination synchronization of fractional order non-identical chaotic system with stochastic disturbances and unknown parameters. Fractal Fract. 2022, 6, 102. [Google Scholar] [CrossRef]
- Liu, D.; Li, T.; He, X. Fixed-Time Multi-Switch Combined-Combined Synchronization of Fractional-Order Chaotic Systems with Uncertainties and External Disturbances. Fractal Fract. 2023, 7, 281. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Salahshour, S.; Ahmadian, A.; Salimi, M.; Pansera, B.A.; Ferrara, M. A new Lyapunov stability analysis of fractional-order systems with nonsingular kernel derivative. Alex. Eng. J. 2020, 59, 2985–2990. [Google Scholar] [CrossRef]
- Toh, Y.T.; Phang, C.; Loh, J.R. New predictor-corrector scheme for solving nonlinear differential equations with Caputo-Fabrizio operator. Math. Methods Appl. Sci. 2019, 42, 175–185. [Google Scholar] [CrossRef]
- Petrás, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Li, T.; Wang, Y.; Kang, R. Novel Methods for Multi-Switch Generalized Projective Anti-Synchronization of Fractional Chaotic System Under Caputo–Fabrizio Derivative via Lyapunov Stability Theorem and Adaptive Control. Symmetry 2025, 17, 957. https://doi.org/10.3390/sym17060957
Zhao Y, Li T, Wang Y, Kang R. Novel Methods for Multi-Switch Generalized Projective Anti-Synchronization of Fractional Chaotic System Under Caputo–Fabrizio Derivative via Lyapunov Stability Theorem and Adaptive Control. Symmetry. 2025; 17(6):957. https://doi.org/10.3390/sym17060957
Chicago/Turabian StyleZhao, Yu, Tianzeng Li, Yu Wang, and Rong Kang. 2025. "Novel Methods for Multi-Switch Generalized Projective Anti-Synchronization of Fractional Chaotic System Under Caputo–Fabrizio Derivative via Lyapunov Stability Theorem and Adaptive Control" Symmetry 17, no. 6: 957. https://doi.org/10.3390/sym17060957
APA StyleZhao, Y., Li, T., Wang, Y., & Kang, R. (2025). Novel Methods for Multi-Switch Generalized Projective Anti-Synchronization of Fractional Chaotic System Under Caputo–Fabrizio Derivative via Lyapunov Stability Theorem and Adaptive Control. Symmetry, 17(6), 957. https://doi.org/10.3390/sym17060957






