Symmetry-Aware CVAE-ACGAN-Based Feature Generation Model and Its Application in Fault Diagnosis
Abstract
1. Introduction
- A method is introduced to address the challenges of acquiring failure data in mechanical equipment, particularly data monotonicity and uncontrollability, which impede diagnostic accuracy. The proposed model incorporates the categorical attributes of fault data, enhancing controllability and reducing monotonicity, thereby enabling the generation of effective class-conditional features.
- A thorough comparison of feature generation models is conducted using four performance metrics: accuracy, precision, recall, and average results. The proposed features are evaluated through diagnostic outcomes, confusion matrices, and t-SNE visualizations. The experimental results demonstrate that the proposed model outperforms existing approaches in terms of accuracy, precision, stability, and convergence speed.
- In addition to conventional classification metrics, this work introduces root mean square error (RMSE) and mean absolute error (MAE) to quantitatively assess the similarity between generated features and real vibration data. By supplementing the evaluation system with these error-based metrics, the effectiveness and fidelity of feature generation are validated more comprehensively, which further demonstrates the model’s robustness and generalization capability across benchmark datasets.
2. Conditional Variational Autoencoder
3. Auxiliary Classifier GAN
4. Fault Diagnosis Based on CVAE-ACGAN
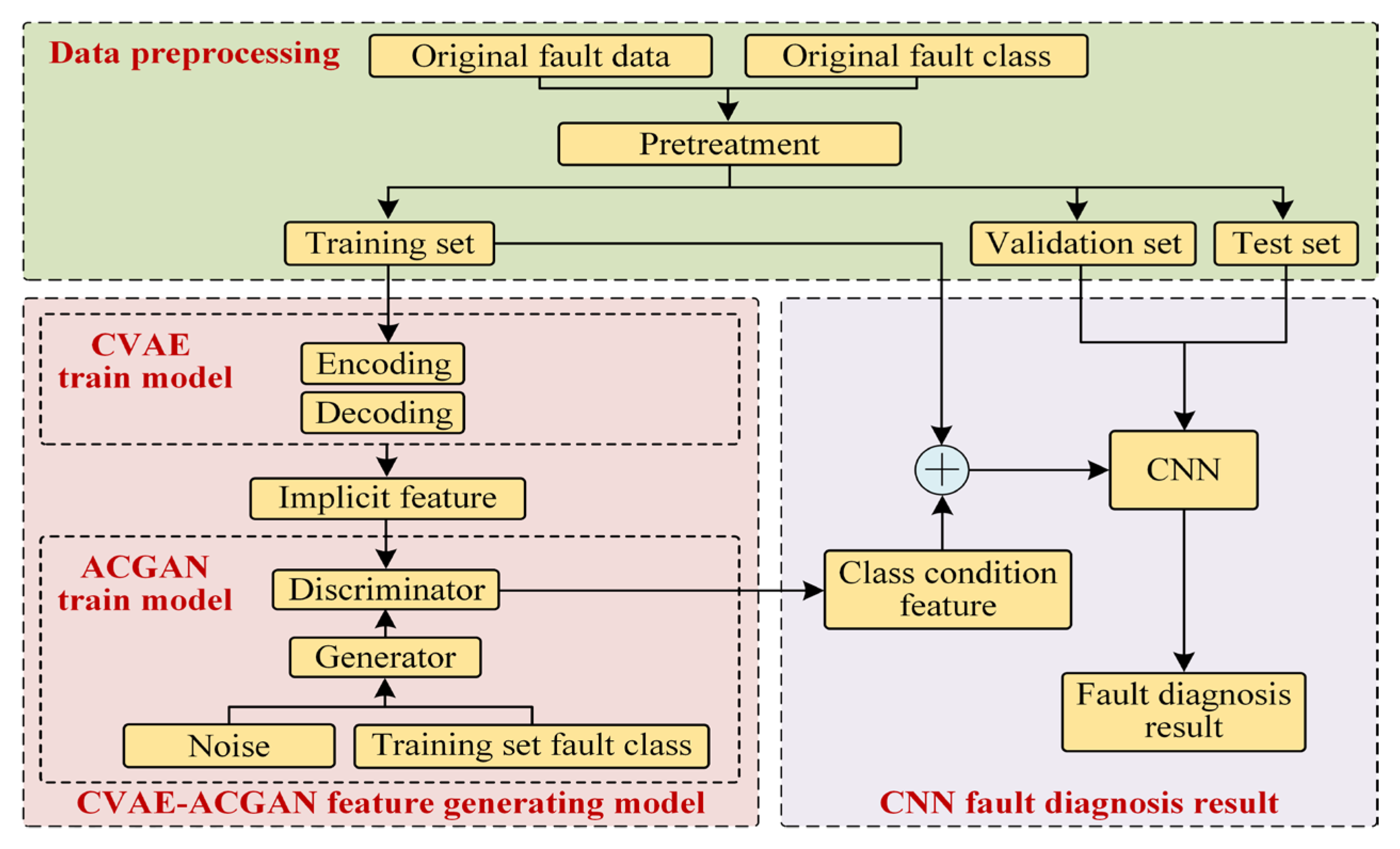
4.1. Model Building
- Step 1: The bearing vibration signal is used as the original fault dataset, and original fault class attributes are defined accordingly. After preprocessing, including data cleaning and segmentation, the dataset is divided into a training set, validation set, and test set.
- Step 2: The training set is input into the CVAE network, where implicit features conditioned on the fault class are extracted through an encoding–decoding training process.
- Step 3: The implicit features extracted by the CVAE serve as real data inputs for the discriminator, and the adversarial training between the generator and discriminator is iteratively optimized to produce effective class-condition features.
- Step 4: The class-condition features generated by the ACGAN are combined with the original training set to form an augmented dataset, which is then used to train a CNN-based fault diagnosis model. Supervised learning is performed with a Softmax classifier, and gradient descent is applied to minimize the loss function, enhancing the CNN model’s performance.
- Step 5: The test set and validation set are input into the CNN fault diagnosis model to ensure that the predicted classes align as closely as possible with the actual classes. The classification performance of the model is then verified, and the fault diagnosis results are output for comparative analysis.
4.2. Structural Parameters of CVAE-ACGAN
- Batch size: 64;
- Epochs: 50;
- Learning rates: An initial learning rate of 0.001 was set for the CVAE network and an initial learning rate of 0.0002 for the ACGAN;
- Optimizer: Adam optimization algorithm with momentum parameters set as and .
4.3. Theoretical Discussion on Symmetry-Preserving Mechanisms
5. Experimental Validation
5.1. Evaluation Index
5.2. CWRU Bearing Dataset
5.3. PADERBORN Bearing Dataset
5.4. Diagnostic Performance and Validation
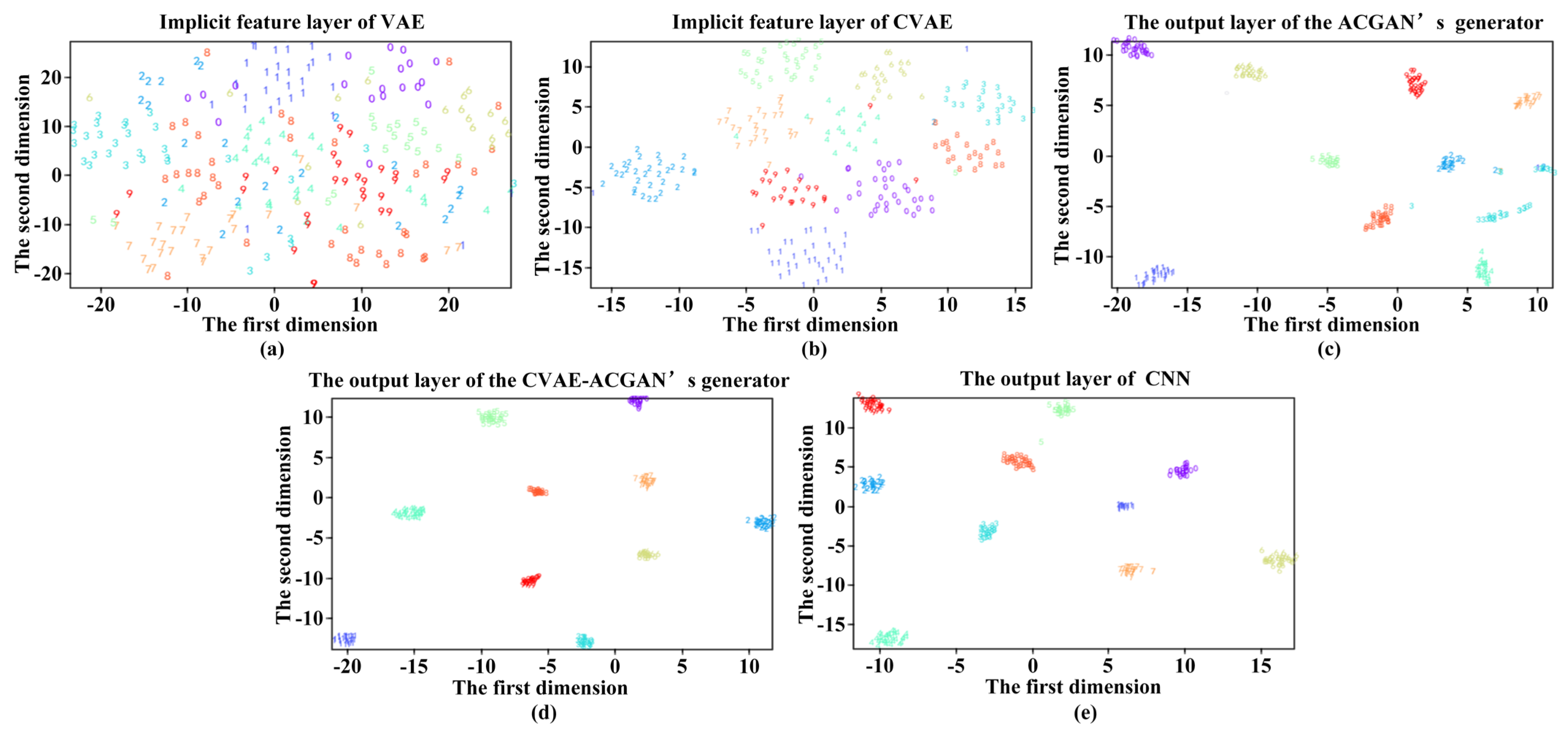
5.4.1. CVAE-ACGAN Model Effect Verification
5.4.2. Comparison with Other Generative Models
5.4.3. Discussion on Model Robustness and Practical Applicability
- Class imbalance: The class-conditional feature generation capability of the CVAE-ACGAN enables targeted data augmentation, effectively compensating for minority fault types and mitigating imbalance issues often encountered in industrial datasets.
- Non-synthetic noise: The adversarial learning framework is designed to learn from both clean and noisy samples. This property enables the model to remain resilient when exposed to diverse noise distributions, as supported by its consistently strong performance on the PADERBORN dataset, which features higher levels of environmental and operational noise than the CWRU dataset.
- Partial or missing labels: The generative nature of the model offers natural compatibility with semi-supervised or weakly supervised learning settings, allowing for effective feature learning even in cases where label information is incomplete or uncertain—a frequent issue in large-scale industrial monitoring systems.
5.5. Computational Complexity and Resource Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ojaghi, M.; Yazdandoost, N. Oil-whirl fault modeling, simulation, and detection in sleeve bearings of squirrel cage induction motors. IEEE Trans. Energy Convers. 2015, 30, 1537–1545. [Google Scholar] [CrossRef]
- Liang, K.; Zhao, M.; Lin, J.; Ding, C.; Jiao, J.; Zhang, Z. A novel indicator to improve fast kurtogram for the health monitoring of rolling bearing. IEEE Sens. J. 2020, 20, 12252–12261. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing. Neurocomputing 2018, 30, 47–64. [Google Scholar] [CrossRef]
- Mao, W.; Feng, W.; Liu, Y.; Zhang, D.; Liang, X. A new deep auto-encoder method with fusing discriminant information for bearing fault diagnosis. Mech. Syst. Signal Process. 2021, 150, 107233. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, L.; Zhao, W.; Fan, Y.; Ding, X.; Yuan, X. Zero-shot learning for compound fault diagnosis of bearings. Expert Syst. Appl. 2022, 190, 116197. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, W.; Liao, Y.; Song, Z.; Shi, J.; Jiang, X.; Shen, C.; Zhu, Z. Bearing fault diagnosis via generalized logarithm sparse regularization. Mech. Syst. Signal Process. 2022, 167, 108576. [Google Scholar] [CrossRef]
- She, B.; Tian, F.; Liang, W. Fault diagnosis method based on deep convolution variational self-encoding network. J. Instrum. 2018, 39, 27–35. [Google Scholar] [CrossRef]
- Dong, S.; Pei, X.; Wu, W.; Tang, B.; Zhao, X. Rolling bearing fault diagnosis method based on multi-layer noise reduction technology and improved convolutional neural network. Chin. J. Mech. Eng. 2021, 57, 148–156. [Google Scholar] [CrossRef]
- Ali, J.B.; Fnaiech, N.; Saidi, L.; Chebel-Morello, B.; Fnaiech, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar] [CrossRef]
- Zhang, G.; Tian, F.; Liang, W.; Bo, S. Health factor construction method based on multi-scale AlexNet network. Syst. Eng. Electron. Technol. 2020, 42, 245–252. [Google Scholar] [CrossRef]
- Das, R.; Christopher, A.F. Prediction of failed sensor data using deep learning techniques for space applications. Wirel. Pers. Commun. 2023, 128, 1941–1962. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.; Zhou, B. Intelligent fault diagnosis of rolling bearing using hierarchical convolutional network based health state classification. Adv. Eng. Inform. 2017, 32, 139–151. [Google Scholar] [CrossRef]
- Xiong, X.; Jiao, H.; Li, X.; Niu, M. A Wasserstein gradient-penalty generative adversarial network with deep auto-encoder for bearing intelligent fault diagnosis. Meas. Sci. Technol. 2020, 31, 045006. [Google Scholar] [CrossRef]
- Shao, L.; Lu, N.; Jiang, B.; Simani, S.; Song, L.; Liu, Z. Generative adversarial networks for data augmentation in machine fault diagnosis. IEEE Sens. J. 2023, 23, 15176–15187. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, C.; Jiang, X. Imbalanced fault diagnosis of rolling bearing using improved MsR-GAN and feature enhancement-driven CapsNet. Mech. Syst. Signal Process. 2022, 168, 108664. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, H.; Wu, Z.; Li, X. Rolling bearing fault diagnosis using variational autoencoding generative adversarial networks with deep regret analysis. Measurement 2021, 168, 108371. [Google Scholar] [CrossRef]
- Liang, P.; Deng, C.; Wu, J.; Yang, Z. Intelligent fault diagnosis of rotating machinery via wavelet transform, generative adversarial nets and convolutional neural network. Measurement 2020, 159, 107768. [Google Scholar] [CrossRef]
- Gao, X.; Ji, W.; Zhao, B.; Jia, X.; Huang, Z.; Ren, B. Multi-classification method of smart meter fault based on CVAE-CNN model under unbalanced data set. Power Syst. Technol. 2021, 45, 3052–3060. [Google Scholar] [CrossRef]
- Dai, J.; Wang, J.; Zhu, Z.; Huang, W.; Huang, W. Mechanical system anomaly detection based on generative confrontation network and automatic encoder. Chin. J. Sci. Instrum. 2019, 40, 16–26. [Google Scholar] [CrossRef]
- Guo, Q.; Li, Y.; Song, Y.; Wang, D.; Chen, W. Intelligent fault diagnosis method based on full 1-D convolutional generative adversarial network. IEEE Trans. Ind. Informat. 2020, 16, 2044–2053. [Google Scholar] [CrossRef]
- Sohn, K.; Yan, X.; Lee, H. Learning structured output representation using deep conditional generative models. In Proceedings of the 29th Annual Conference on Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Kuo, P.; Huang, C.J. A high-precision artificial neural networks model for short-term energy load forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef]
- Kingma, D.P.; Mohamed, S.; Rezende, D.J.; Welling, M. Semi-supervised learning with deep generative models. In Proceedings of the 28th Annual Conference on Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Saito, K.; Watanabe, K.; Ushiku, Y.; Harada, T. Maximum classifier discrepancy for unsupervised domain adaptation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Wang, Y.; Si, P.; Lei, Z.; Yang, Y. Topic-enhanced controllable CVAE for dialogue generation (Student Abstract). In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Li, Y.; Cao, P.; Shi, Y.; Zhang, Y. VAACGAN many-to-many speech conversion based on fusion sentence embedding. J. Beijing Univ. Aeronaut. Astronaut. 2019, 47, 500–508. [Google Scholar] [CrossRef]
- Sun, C.; Wang, Y.; Xia, Y. Fault diagnosis of helicopter planetary gear cracks based on SCAE-ACGAN. J. Vib. Test. Diagn. 2021, 41, 495–502. [Google Scholar] [CrossRef]
- Odena, A.; Olah, C.; Shlens, J. Conditional image synthesis with auxiliary classifier GANs. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 28th Annual Conference on Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Han, G.; Zhang, X.; Wang, H.; Mao, C. Curiosity-driven variational autoencoder for deep Q network. In Proceedings of the 24th Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD), Singapore, 11–14 May 2020. [Google Scholar]
- Waheed, A.; Goyal, M.; Gupta, D.; Khanna, A.; Al-Turjman, F.; Pinheiro, P. CovidGAN: Data augmentation using auxiliary classifier GAN for improved COVID-19 detection. IEEE Access 2020, 8, 91916–91923. [Google Scholar] [CrossRef]
- Bronstein, M.M.; Bruna, J.; Cohen, T.; Velikovi, P. Geometric Deep Learning Grids, Groups, Graphs, Geodesics, and Gauges. arXiv 2021, arXiv:2104.13478. [Google Scholar] [CrossRef]
- Zaheer, M.; Kottur, S.; Ravanbakhsh, S.; Poczos, B.; Salakhutdinov, R.R.; Smola, A.J. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017.
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Cohen, T.; Welling, M. Group equivariant convolutional networks. In Proceedings of the 33rd International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Smith, W.A.; Randall, R.B. Rolling-element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Zuo, L.; Xu, F.; Zhang, C.; Xiahou, T.; Liu, Y. A multi-layer spiking neural network-based approach to bearing fault diagnosis. Reliab. Eng. Syst. Saf. 2022, 225, 108561. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, S.; Gu, D.; Sun, X.; Wang, L.; Wei, Y.; Zhang, H. Enhanced data-driven fault diagnosis for machines with small and unbalanced data based on variational auto-encoder. Meas. Sci. Technol. 2022, 31, 035004. [Google Scholar] [CrossRef]
- Wang, Y.R.; Sun, G.D.; Jin, Q. Imbalanced sample fault diagnosis of rotating machinery using conditional variational auto-encoder generative adversarial network. Appl. Soft Comput. 2020, 92, 106333. [Google Scholar] [CrossRef]
- Li, W.; Zhong, X.; Shao, H.; Cai, B.; Yang, X. Multi-mode data augmentation and fault diagnosis of rotating machinery using modified ACGAN designed with new framework. Adv. Eng. Inform. 2022, 52, 101552. [Google Scholar] [CrossRef]






| Network Layer | Number of Channels | Nuclear Size | Stride | |
|---|---|---|---|---|
| CVAE | Convolutional layer 1 | 16 | 66 × 1 | 2 |
| Pooling layer 1 | - | - | 2 × 1 | |
| Convolutional layer 2 | 32 | 4 × 1 | 2 | |
| Pooling layer 2 | - | - | 2 × 1 | |
| Dense | 200 | - | - | |
| Unpooling layer 2 | - | - | 2 × 1 | |
| Deconvolution layer 2 | 32 | 4 × 1 | 2 | |
| Unpooling layer 1 | - | - | 2 × 1 | |
| Deconvolution layer 1 | 16 | 66 × 1 | 2 | |
| ACGAN generator | Dense 1 | 1024 | - | - |
| Dense 2 | 12,800 | - | - | |
| Deconvolution layer 1 | 64 | 4 × 1 | 2 | |
| Deconvolution layer 2 | 1 | 4 × 1 | 2 | |
| ACGAN discriminator | Convolutional layer 1 | 64 | 4 × 1 | 2 |
| Convolutional layer 2 | 256 | 4 × 1 | 2 | |
| Dense 1 | 12,800 | - | - | |
| Dense 2 | 1024 | - | - |
| Fault Data/Class | Training Set | Test Set | Validation Set |
|---|---|---|---|
| X_data | (7160, 1024) | (2053, 1024) | (1027, 1024) |
| Y_class | (7160, 10) | (2053, 10) | (1027, 10) |
| Number | Fault Location | Damage Degree | Man-Made Damage |
|---|---|---|---|
| K001 | Health | Health | Health |
| KA01 | Outer ring | 1 | EDM |
| KA05 | Outer ring | 1 | Manual electric engraving |
| KI01 | Inner ring | 1 | EDM |
| KI05 | Inner ring | 1 | Manual electric engraving |
| Network Layer | Number of Channels | Nuclear Size | Stride |
|---|---|---|---|
| Convolutional layer 1 | 16 | 3 × 1 | 1 |
| Convolutional layer 2 | 32 | 4 × 1 | 1 |
| Convolutional layer 3 | 64 | 4 × 1 | 2 |
| Pooling layer 1 | - | - | 2 × 1 |
| Pooling layer 2 | - | - | 2 × 1 |
| Pooling layer 3 | - | - | 2 × 1 |
| CNN | CVAE_ACGAN_CNN | ||
|---|---|---|---|
| Mean ± std, % | 97.89% ± 0.32% | 99.21% ± 0.11% | |
| 95% CI (%) | [97.68, 98.10] | [99.13, 99.29] | |
| Mean ± std, % | 95.84% ± 0.27% | 97.81% ± 0.09% | |
| 95% CI (%) | [95.67, 96.01] | [97.73, 97.89] | |
| Mean ± std, % | 96.63% ± 0.31% | 98.24% ± 0.13% | |
| 95% CI (%) | [96.43, 96.83] | [98.15, 98.33] | |
| Mean ± std, % | 95.25% ± 0.29% | 97.78% ± 0.12% | |
| 95% CI (%) | [95.07, 95.43] | [97.69, 97.87] | |
| RMSE | Mean ± std | 0.108 ± 0.007 | 0.081 ± 0.003 |
| 95% CI | [0.103, 0.113] | [0.079, 0.083] | |
| MAE | Mean ± std | 0.087 ± 0.004 | 0.060 ± 0.002 |
| 95% CI | [0.084, 0.090] | [0.059, 0.061] | |
| GAN_CNN | VAE_CNN | ACGAN_CNN | CVAE_CNN | CVAE_ACGAN_CNN | ||
|---|---|---|---|---|---|---|
| Mean ± std, % | 97.98% ± 0.23% | 86.26% ± 0.25% | 98.17% ± 0.21% | 87.68% ± 0.22% | 99.21% ± 0.11% | |
| 95% CI (%) | [97.83, 98.13] | [86.10, 86.42] | [98.03, 98.31] | [87.53, 87.83] | [99.13, 99.29] | |
| Mean ± std, % | 86.47% ± 0.35% | 84.98% ± 0.28% | 97.02% ± 0.15% | 86.38% ± 0.24% | 97.81% ± 0.09% | |
| 95% CI (%) | [86.25, 86.69] | [84.80, 85.16] | [96.92, 97.12] | [86.22, 86.54] | [97.75, 97.87] | |
| Mean ± std, % | 97.33% ± 0.19% | 83.83% ± 0.26% | 97.82% ± 0.16% | 84.94% ± 0.21% | 98.24% ± 0.13% | |
| 95% CI (%) | [97.20, 97.46] | [83.67, 83.99] | [97.71, 97.93] | [84.80, 85.08] | [98.15, 98.33] | |
| Mean ± std, % | 91.05% ± 0.31% | 84.18% ± 0.27% | 96.98% ± 0.17% | 85.61% ± 0.23% | 98.49% ± 0.10% | |
| 95% CI (%) | [90.85, 91.25] | [84.01, 84.35] | [96.86, 97.10] | [85.46, 85.76] | [98.41, 98.57] | |
| RMSE | Mean ± std | 0.107 ± 0.006 | 0.158 ± 0.009 | 0.099 ± 0.005 | 0.151 ± 0.008 | 0.081 ± 0.003 |
| 95% CI | [0.102, 0.112] | [0.153, 0.163] | [0.096, 0.104] | [0.146, 0.156] | [0.079, 0.083] | |
| MAE | Mean ± std | 0.086 ± 0.004 | 0.137 ± 0.007 | 0.079 ± 0.003 | 0.127 ± 0.006 | 0.060 ± 0.002 |
| 95% CI | [0.083, 0.089] | [0.132, 0.142] | [0.077, 0.081] | [0.123, 0.131] | [0.059, 0.061] | |
| GAN_CNN | VAE_CNN | ACGAN_CNN | CVAE_CNN | CVAE_ACGAN_CNN | ||
|---|---|---|---|---|---|---|
| Mean ± std, % | 95.07% ± 0.29% | 82.67% ± 0.30% | 97.74% ± 0.22% | 83.49% ± 0.25% | 99.36% ± 0.12% | |
| 95% CI (%) | [94.88, 95.26] | [82.48, 82.86] | [97.60, 97.88] | [83.33, 83.65] | [99.27, 99.45] | |
| Mean ± std, % | 85.42% ± 0.32% | 83.62% ± 0.27% | 96.84% ± 0.17% | 85.68% ± 0.23% | 98.71% ± 0.10% | |
| 95% CI (%) | [85.23, 85.61] | [83.45, 83.79] | [96.73, 96.95] | [85.54, 85.82] | [98.64, 98.78] | |
| Mean ± std, % | 96.26% ± 0.27% | 82.86% ± 0.29% | 96.98% ± 0.16% | 84.03% ± 0.24% | 98.18% ± 0.11% | |
| 95% CI (%) | [96.09, 96.43] | [82.68, 83.04] | [96.87, 97.09] | [83.87, 84.19] | [98.10, 98.26] | |
| Mean ± std, % | 89.92% ± 0.30% | 83.85% ± 0.31% | 96.82% ± 0.18% | 85.04% ± 0.26% | 98.44% ± 0.10% | |
| 95% CI (%) | [89.73, 90.11] | [83.66, 84.04] | [96.70, 96.94] | [84.87, 85.21] | [98.36, 98.52] | |
| RMSE | Mean ± std | 0.121 ± 0.007 | 0.169 ± 0.009 | 0.103 ± 0.005 | 0.158 ± 0.008 | 0.080 ± 0.003 |
| 95% CI | [0.116, 0.126] | [0.164, 0.174] | [0.100, 0.108] | [0.153, 0.163] | [0.078, 0.082] | |
| MAE | Mean ± std | 0.100 ± 0.005 | 0.144 ± 0.007 | 0.086 ± 0.004 | 0.134 ± 0.006 | 0.059 ± 0.002 |
| 95% CI | [0.095, 0.105] | [0.139, 0.149] | [0.083, 0.089] | [0.130, 0.138] | [0.058, 0.060] | |
| Model | Param Count (M) | Layers | FLOPs (G) | Train Time/Epoch (s) | Infer Time (s) | Peak GPU (MB) | Acc (%) |
|---|---|---|---|---|---|---|---|
| VAE | 0.81 | 12 | 0.42 | 14.2 | 0.54 | 1230 | 86.26 |
| CVAE | 0.83 | 14 | 0.47 | 16.1 | 0.56 | 1340 | 87.68 |
| GAN | 0.78 | 10 | 0.40 | 15.4 | 0.52 | 1280 | 97.98 |
| ACGAN | 0.96 | 16 | 0.52 | 18.8 | 0.59 | 1570 | 98.17 |
| CVAE-ACGAN | 1.35 | 22 | 0.69 | 26.3 | 0.75 | 2050 | 99.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Liu, Y.; Zhang, Y.; Chu, M. Symmetry-Aware CVAE-ACGAN-Based Feature Generation Model and Its Application in Fault Diagnosis. Symmetry 2025, 17, 947. https://doi.org/10.3390/sym17060947
Ma L, Liu Y, Zhang Y, Chu M. Symmetry-Aware CVAE-ACGAN-Based Feature Generation Model and Its Application in Fault Diagnosis. Symmetry. 2025; 17(6):947. https://doi.org/10.3390/sym17060947
Chicago/Turabian StyleMa, Long, Yingjie Liu, Yue Zhang, and Ming Chu. 2025. "Symmetry-Aware CVAE-ACGAN-Based Feature Generation Model and Its Application in Fault Diagnosis" Symmetry 17, no. 6: 947. https://doi.org/10.3390/sym17060947
APA StyleMa, L., Liu, Y., Zhang, Y., & Chu, M. (2025). Symmetry-Aware CVAE-ACGAN-Based Feature Generation Model and Its Application in Fault Diagnosis. Symmetry, 17(6), 947. https://doi.org/10.3390/sym17060947




