Ultra-Low Bitrate Predictive Portrait Video Compression with Diffusion Models
Abstract
1. Introduction
- We propose a predictive portrait video compression framework that encodes only keyframes and leverages the predicted results as reconstructed frames, thereby enabling high-quality compression at ultra-low bitrates.
- We design a video frame prediction model based on conditional latent diffusion, termed the temporal diffusion prediction model. By integrating the 3D causal convolution with temporal attention mechanism, the model fully exploits the temporal correlations in video data, thereby enabling high-quality video prediction.
- An adaptive coding strategy is developed. This strategy ensures predicted frames meet the current quality threshold for reconstruction while dynamically controlling the sequence length of keyframes, thereby effectively reducing transmission costs.
2. Related Work
2.1. Traditional and Hybrid Video Compression
2.2. End-to-End Video Compression
2.3. Diffusion Model Based Image and Video Compression
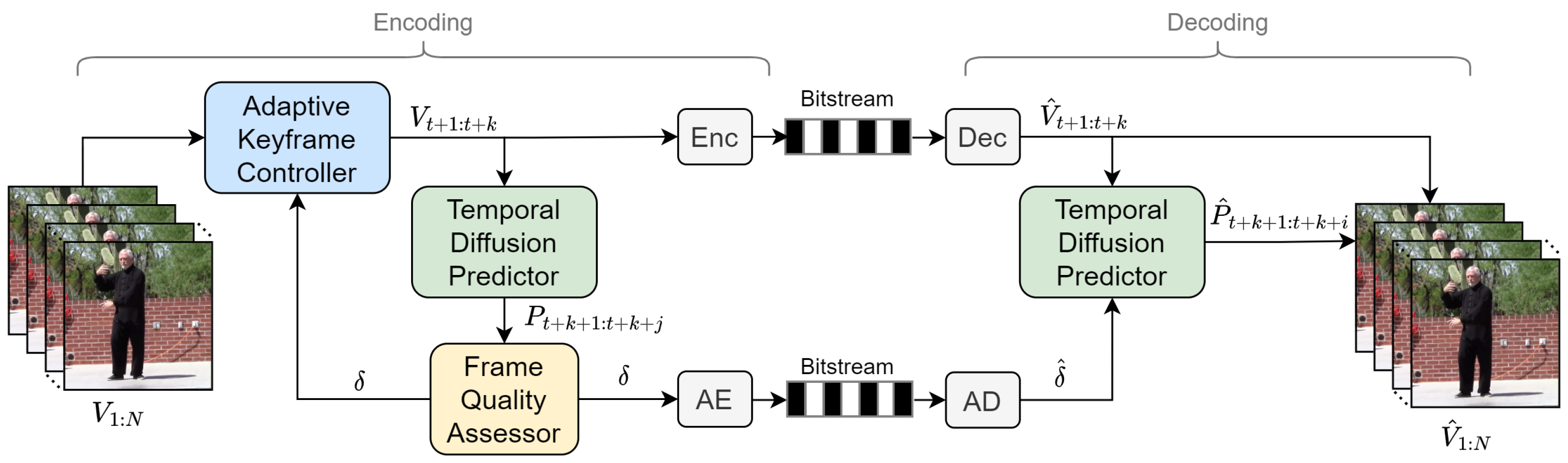
3. Methodology
3.1. Overview
3.2. Temporal Diffusion Prediction Model
3.3. Adaptive Coding Strategy
| Algorithm 1 Adaptive coding strategy |
|
4. Experimental Results
4.1. Datasets and Evaluation Metrics
4.1.1. Datasets
- Penn Action [49] is a human action dataset that contains 2326 RGB video sequences of 15 different actions. Following [50], we employ eight kinds of actions. We evenly divide the standard dataset into two subsets for training and evaluation and crop and resize them to a resolution of based on the bounding boxes of the bodies.
- TaiChiHD [51] is a dataset of TaiChi performance videos of 84 individuals. It contains 2884 training videos and 285 test videos and we resize the resolution of .
- Fashion [52] is a dataset of a single model dressed in diverse textured clothing. It contains 500 training videos and 100 test videos and we resize the resolution of .
4.1.2. Evaluation Metrics
4.2. Implementation Details
4.3. Compression Performance Comparison
4.3.1. Baselines
4.3.2. Quantitative Results
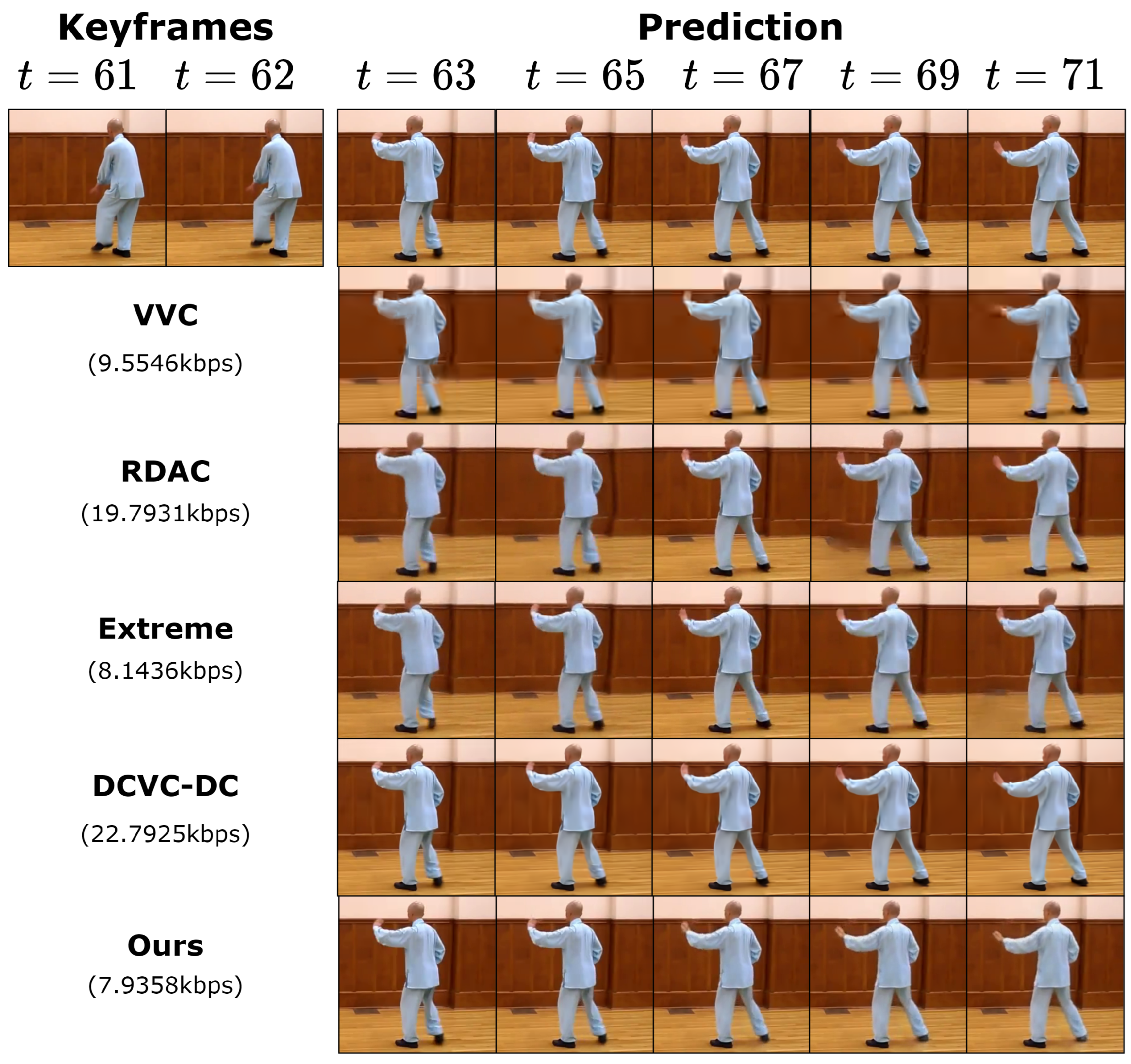
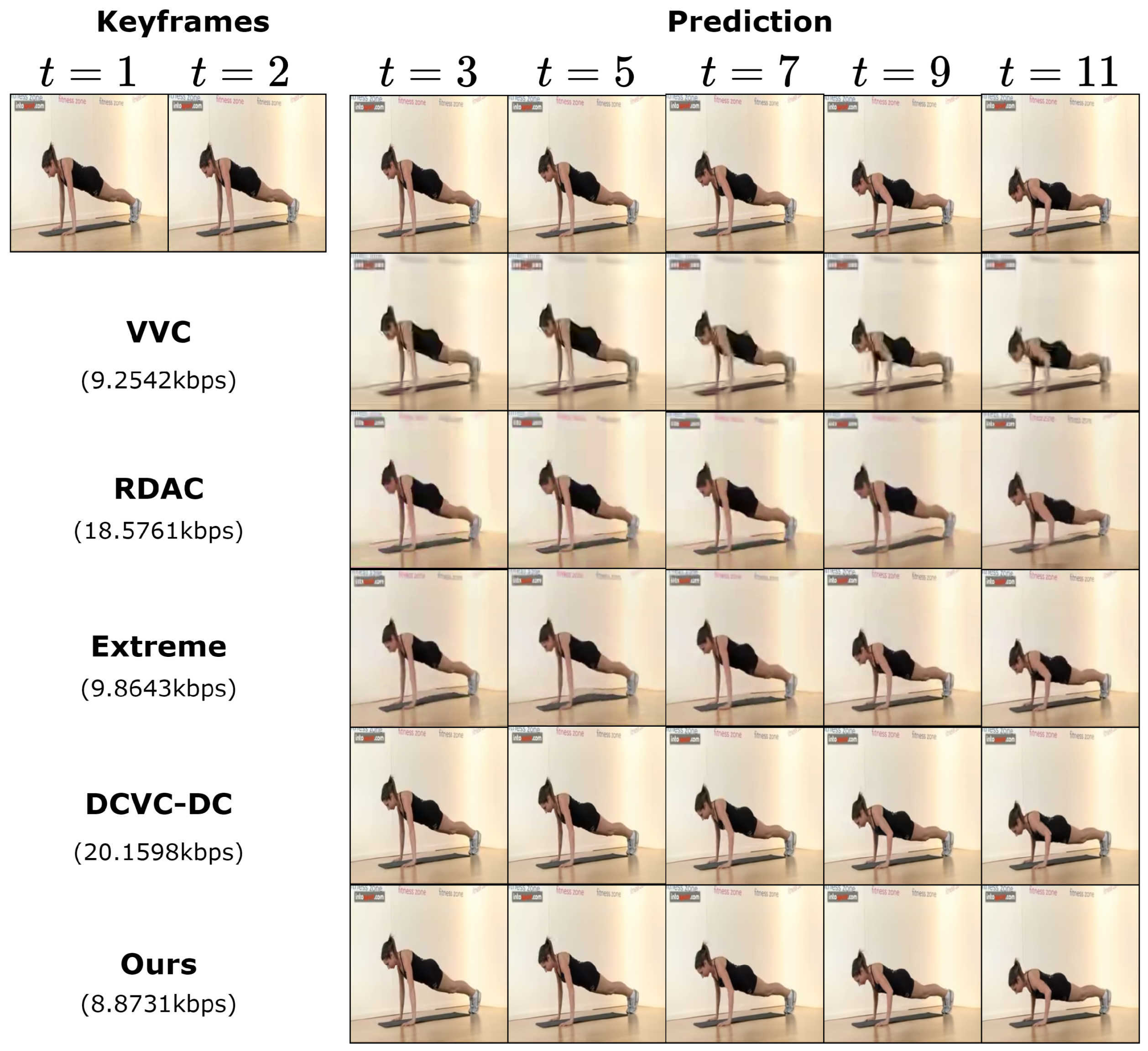
4.3.3. Qualitative Results
4.3.4. Complexity
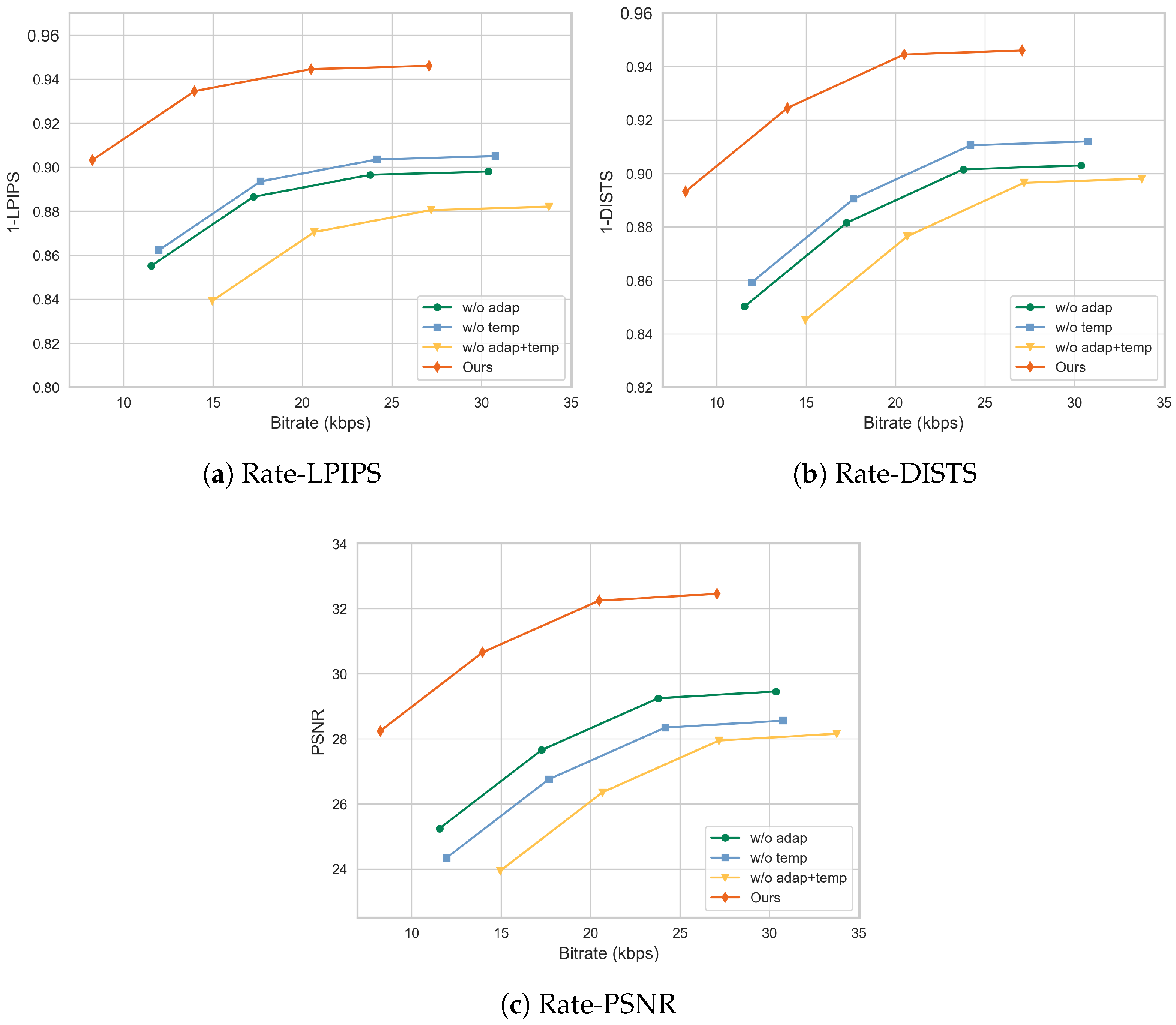
4.4. Ablation Study
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wiegand, T.; Sullivan, G.J.; Bjontegaard, G.; Luthra, A. Overview of the H. 264/AVC video coding standard. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 560–576. [Google Scholar] [CrossRef]
- Sullivan, G.J.; Ohm, J.R.; Han, W.J.; Wiegand, T. Overview of the high efficiency video coding (HEVC) standard. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1649–1668. [Google Scholar] [CrossRef]
- Bross, B.; Wang, Y.K.; Ye, Y.; Liu, S.; Chen, J.; Sullivan, G.J.; Ohm, J.R. Overview of the versatile video coding (VVC) standard and its applications. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 3736–3764. [Google Scholar] [CrossRef]
- Hoang, T.M.; Zhou, J. Recent trending on learning based video compression: A survey. Cogn. Robot. 2021, 1, 145–158. [Google Scholar] [CrossRef]
- Lu, G.; Ouyang, W.; Xu, D.; Zhang, X.; Cai, C.; Gao, Z. Dvc: An end-to-end deep video compression framework. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11006–11015. [Google Scholar]
- Li, J.; Li, B.; Lu, Y. Deep contextual video compression. Adv. Neural Inf. Process. Syst. 2021, 34, 18114–18125. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Voleti, V.; Jolicoeur-Martineau, A.; Pal, C. Mcvd-masked conditional video diffusion for prediction, generation, and interpolation. Adv. Neural Inf. Process. Syst. 2022, 35, 23371–23385. [Google Scholar]
- Yang, R.; Srivastava, P.; Mandt, S. Diffusion probabilistic modeling for video generation. Entropy 2023, 25, 1469. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, J.; Cheng, W.; Paudel, D.; Yang, J. Extdm: Distribution extrapolation diffusion model for video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 19310–19320. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Pan, Z.; Zhou, X.; Tian, H. Extreme generative image compression by learning text embedding from diffusion models. arXiv 2022, arXiv:2211.07793. [Google Scholar]
- Yang, R.; Mandt, S. Lossy image compression with conditional diffusion models. Adv. Neural Inf. Process. Syst. 2023, 36, 64971–64995. [Google Scholar]
- Chen, L.; Li, Z.; Lin, B.; Zhu, B.; Wang, Q.; Yuan, S.; Zhou, X.; Cheng, X.; Yuan, L. Od-vae: An omni-dimensional video compressor for improving latent video diffusion model. arXiv 2024, arXiv:2409.01199. [Google Scholar]
- Ma, W.; Chen, Z. Diffusion-based perceptual neural video compression with temporal diffusion information reuse. arXiv 2025, arXiv:2501.13528. [Google Scholar]
- Li, B.; Liu, Y.; Niu, X.; Bait, B.; Han, W.; Deng, L.; Gunduz, D. Extreme Video Compression with Prediction Using Pre-trained Diffusion Models. In Proceedings of the 2024 16th International Conference on Wireless Communications and Signal Processing (WCSP), Hefei, China, 24–26 October 2024; pp. 1449–1455. [Google Scholar]
- Yu, L.; Lezama, J.; Gundavarapu, N.B.; Versari, L.; Sohn, K.; Minnen, D.; Cheng, Y.; Birodkar, V.; Gupta, A.; Gu, X.; et al. Language Model Beats Diffusion–Tokenizer is Key to Visual Generation. arXiv 2023, arXiv:2310.05737. [Google Scholar]
- Li, Z.; Wang, W.; Li, H.; Xie, E.; Sima, C.; Lu, T.; Yu, Q.; Dai, J. Bevformer: Learning bird’s-eye-view representation from lidar-camera via spatiotemporal transformers. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 47, 2020–2036. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, D.; Bankoski, J.; Grange, A.; Han, J.; Koleszar, J.; Wilkins, P.; Xu, Y.; Bultje, R. The latest open-source video codec VP9-an overview and preliminary results. In Proceedings of the 2013 Picture Coding Symposium (PCS), San Jose, CA, USA, 8–11 December 2013; pp. 390–393. [Google Scholar]
- Chen, Y.; Murherjee, D.; Han, J.; Grange, A.; Xu, Y.; Liu, Z.; Parker, S.; Chen, C.; Su, H.; Joshi, U.; et al. An overview of core coding tools in the AV1 video codec. In Proceedings of the 2018 Picture Coding Symposium (PCS), San Francisco, CA, USA, 24–27 June 2018; pp. 41–45. [Google Scholar]
- Zhang, J.; Jia, C.; Lei, M.; Wang, S.; Ma, S.; Gao, W. Recent development of AVS video coding standard: AVS3. In Proceedings of the 2019 Picture Coding Symposium (PCS), Ningbo, China, 11–15 November 2019; pp. 1–5. [Google Scholar]
- Wieckowski, A.; Brandenburg, J.; Hinz, T.; Bartnik, C.; George, V.; Hege, G.; Helmrich, C.; Henkel, A.; Lehmann, C.; Stoffers, C.; et al. VVenC: An open and optimized VVC encoder implementation. In Proceedings of the 2021 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Shenzhen, China, 5–9 July 2021; pp. 1–2. [Google Scholar]
- Akbulut, O.; Konyar, M.Z. Improved intra-subpartition coding mode for versatile video coding. Signal Image Video Process 2022, 16, 1363–1368. [Google Scholar] [CrossRef]
- Amna, M.; Imen, W.; Soulef, B.; Fatma Ezahra, S. Machine Learning-Based approaches to reduce HEVC intra coding unit partition decision complexity. Multimed. Tools Appl. 2022, 81, 2777–2802. [Google Scholar] [CrossRef]
- Yang, R.; Liu, H.; Zhu, S.; Zheng, X.; Zeng, B. DFCE: Decoder-friendly chrominance enhancement for HEVC intra coding. IEEE Trans. Circuits Syst. Video Technol. 2022, 33, 1481–1486. [Google Scholar] [CrossRef]
- Zhao, T.; Huang, Y.; Feng, W.; Xu, Y.; Kwong, S. Efficient VVC intra prediction based on deep feature fusion and probability estimation. IEEE Trans. Multimed. 2022, 25, 6411–6421. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, X.; Xiong, R.; Zhao, D.; Gao, W. Neural network-based enhancement to inter prediction for video coding. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 826–838. [Google Scholar] [CrossRef]
- Shang, X.; Li, G.; Zhao, X.; Zuo, Y. Low complexity inter coding scheme for Versatile Video Coding (VVC). J. Vis. Commun. Image Represent. 2023, 90, 103683. [Google Scholar] [CrossRef]
- Ma, C.; Liu, D.; Peng, X.; Li, L.; Wu, F. Convolutional neural network-based arithmetic coding for HEVC intra-predicted residues. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 1901–1916. [Google Scholar] [CrossRef]
- Meng, X.; Jia, C.; Zhang, X.; Wang, S.; Ma, S. Deformable Wiener Filter for Future Video Coding. IEEE Trans. Image Process. 2022, 31, 7222–7236. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Zhang, Y.; Li, N.; Wu, W.; Wang, S.; Kwong, S. Neural Network Based Multi-Level In-Loop Filtering for Versatile Video Coding. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 12092–12096. [Google Scholar] [CrossRef]
- Hu, Z.; Lu, G.; Xu, D. FVC: A New Framework towards Deep Video Compression in Feature Space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1502–1511. [Google Scholar]
- Guo, H.; Kwong, S.; Jia, C.; Wang, S. Enhanced motion compensation for deep video compression. IEEE Signal Process. Lett. 2023, 30, 673–677. [Google Scholar] [CrossRef]
- Hu, Y.; Jung, C.; Qin, Q.; Han, J.; Liu, Y.; Li, M. HDVC: Deep video compression with hyperprior-based entropy coding. IEEE Access 2024, 12, 17541–17551. [Google Scholar] [CrossRef]
- Li, J.; Li, B.; Lu, Y. Hybrid spatial-temporal entropy modelling for neural video compression. In Proceedings of the 30th ACM International Conference on Multimedia, Lisbon, Portugal, 10–14 October 2022; pp. 1503–1511. [Google Scholar]
- Li, J.; Li, B.; Lu, Y. Neural video compression with diverse contexts. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 22616–22626. [Google Scholar]
- Sheng, X.; Li, L.; Liu, D.; Li, H. Vnvc: A versatile neural video coding framework for efficient human-machine vision. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4579–4596. [Google Scholar] [CrossRef]
- Li, J.; Li, B.; Lu, Y. Neural video compression with feature modulation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 26099–26108. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 139–144. [Google Scholar]
- Konuko, G.; Valenzise, G.; Lathuilière, S. Ultra-low bitrate video conferencing using deep image animation. In Proceedings of the ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 4210–4214. [Google Scholar]
- Konuko, G.; Lathuilière, S.; Valenzise, G. A hybrid deep animation codec for low-bitrate video conferencing. In Proceedings of the 2022 IEEE International Conference on Image Processing (ICIP), Bordeaux, France, 16–19 October 2022; pp. 1–5. [Google Scholar]
- Konuko, G.; Lathuilière, S.; Valenzise, G. Predictive coding for animation-based video compression. In Proceedings of the 2023 IEEE International Conference on Image Processing (ICIP), Kuala Lumpur, Malaysia, 8–11 October 2023; pp. 2810–2814. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014; p. 14. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]
- Witten, I.H.; Neal, R.M.; Cleary, J.G. Arithmetic coding for data compression. Commun. ACM 1987, 30, 520–540. [Google Scholar] [CrossRef]
- Chen, X.; Lei, W.; Zhang, W.; Meng, H.; Guo, H. Model-based portrait video compression with spatial constraint and adaptive pose processing. Multimed. Syst. 2024, 30, 311. [Google Scholar] [CrossRef]
- Gu, X.; Wen, C.; Ye, W.; Song, J.; Gao, Y. Seer: Language instructed video prediction with latent diffusion models. arXiv 2023, arXiv:2303.14897. [Google Scholar]
- Blattmann, A.; Rombach, R.; Ling, H.; Dockhorn, T.; Kim, S.W.; Fidler, S.; Kreis, K. Align your latents: High-resolution video synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 22563–22575. [Google Scholar]
- Zhang, W.; Zhu, M.; Derpanis, K.G. From actemes to action: A strongly-supervised representation for detailed action understanding. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2248–2255. [Google Scholar]
- Zhao, L.; Peng, X.; Tian, Y.; Kapadia, M.; Metaxas, D. Learning to forecast and refine residual motion for image-to-video generation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 387–403. [Google Scholar]
- Siarohin, A.; Lathuilière, S.; Tulyakov, S.; Ricci, E.; Sebe, N. First order motion model for image animation. Adv. Neural Inf. Process. Syst. 2019, 32, 7137–7147. [Google Scholar]
- Zablotskaia, P.; Siarohin, A.; Zhao, B.; Sigal, L. Dwnet: Dense warp-based network for pose-guided human video generation. arXiv 2019, arXiv:1910.09139. [Google Scholar]
- Ding, K.; Ma, K.; Wang, S.; Simoncelli, E.P. Image quality assessment: Unifying structure and texture similarity. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2567–2581. [Google Scholar] [CrossRef]
- Song, J.; Meng, C.; Ermon, S. Denoising diffusion implicit models. arXiv 2020, arXiv:2010.02502. [Google Scholar]



| Datasets | Metrics | VVC [3] | RDAC [42] | Extreme [16] | DCVC-DC [36] | Proposed |
|---|---|---|---|---|---|---|
| Penn Action | Bitrate (kbps) | 7.8992 | 19.3188 | 8.2875 | 21.5244 | 7.7517 |
| PSNR (↑) | 29.0025 | 23.8252 | 22.4154 | 36.5420 | 28.6248 | |
| LPIPS (↓) | 0.2420 | 0.2251 | 0.1223 | 0.0936 | 0.1007 | |
| DISTS (↓) | 0.2635 | 0.2134 | 0.1050 | 0.1032 | 0.0886 | |
| TaiChiHD | Bitrate (kbps) | 8.9744 | 16.9623 | 8.9214 | 20.8461 | 8.5186 |
| PSNR (↑) | 28.0949 | 24.1158 | 24.8417 | 35.2847 | 27.4569 | |
| LPIPS (↓) | 0.2140 | 0.1662 | 0.1525 | 0.0681 | 0.0614 | |
| DISTS (↓) | 0.2319 | 0.2040 | 0.1396 | 0.1185 | 0.0945 | |
| Fashion | Bitrate (kbps) | 8.9421 | 14.3497 | 9.4523 | 19.4912 | 8.2478 |
| PSNR (↑) | 29.0217 | 26.1536 | 26.4863 | 32.1523 | 28.3516 | |
| LPIPS (↓) | 0.1627 | 0.1752 | 0.1219 | 0.0702 | 0.0621 | |
| DISTS (↓) | 0.2012 | 0.1514 | 0.1021 | 0.0986 | 0.1032 |
| Encoding Time | Decoding Time | All | |
|---|---|---|---|
| VVC [22] | 326.861 s | 0.142 s | 327.003 s |
| Proposed | 65.352 s | 43.811 s | 109.163 s |
| Datasets | Metrics | w/o Temp | w/o Adap | w/o Temp + Adap | Full Model |
|---|---|---|---|---|---|
| Penn Action | Bitrate (kbps) | 10.5221 | 9.6541 | 13.1585 | 7.7517 |
| PSNR (↑) | 25.5422 | 26.7845 | 23.8561 | 28.6248 | |
| LPIPS (↓) | 0.1254 | 0.1342 | 0.1473 | 0.1007 | |
| DISTS (↓) | 0.1128 | 0.1231 | 0.1385 | 0.0886 | |
| TaiChiHD | Bitrate (kbps) | 12.2441 | 11.8795 | 15.2528 | 8.5186 |
| PSNR (↑) | 23.5247 | 24.4163 | 23.1254 | 27.4569 | |
| LPIPS (↓) | 0.1025 | 0.1094 | 0.1254 | 0.0614 | |
| DISTS (↓) | 0.1284 | 0.1732 | 0.1424 | 0.0945 | |
| Fashion | Bitrate (kbps) | 10.0125 | 10.5569 | 11.5814 | 8.2478 |
| PSNR (↑) | 26.8458 | 27.5967 | 24.5568 | 28.3516 | |
| LPIPS (↓) | 0.1158 | 0.1088 | 0.1205 | 0.0621 | |
| DISTS (↓) | 0.1246 | 0.1147 | 0.1384 | 0.1032 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Lei, W.; Zhang, W.; Wang, Y.; Liu, M. Ultra-Low Bitrate Predictive Portrait Video Compression with Diffusion Models. Symmetry 2025, 17, 913. https://doi.org/10.3390/sym17060913
Chen X, Lei W, Zhang W, Wang Y, Liu M. Ultra-Low Bitrate Predictive Portrait Video Compression with Diffusion Models. Symmetry. 2025; 17(6):913. https://doi.org/10.3390/sym17060913
Chicago/Turabian StyleChen, Xinyi, Weimin Lei, Wei Zhang, Yanwen Wang, and Mingxin Liu. 2025. "Ultra-Low Bitrate Predictive Portrait Video Compression with Diffusion Models" Symmetry 17, no. 6: 913. https://doi.org/10.3390/sym17060913
APA StyleChen, X., Lei, W., Zhang, W., Wang, Y., & Liu, M. (2025). Ultra-Low Bitrate Predictive Portrait Video Compression with Diffusion Models. Symmetry, 17(6), 913. https://doi.org/10.3390/sym17060913







