Reliability Evaluation of Two-Stage Uncertain Multi-State Weighted k-Out-of-n Systems

Abstract

A class of complex systems can be structurally decomposed into several typical multi-state weighted k/n systems. In view of this, this paper proposes a reliability model to evaluate the reliability of such systems. The system reliability evaluation process is divided into two critical stages: (1) Primary stage: Structural reliability analysis (system-level) and (2) Secondary stage: Subsystem reliability verification (component-level). In practical applications, when there is a lack of operational data, expert experience is needed to evaluate the states and availability weights of components, which is a typical application scenario for uncertainty theory. Under the framework of uncertainty theory, two-stage reliability measures and importance measures are defined, and corresponding calculation formulas are derived. To improve computational efficiency, a binary search algorithm is proposed. Finally, an application case of SDN was proposed to demonstrate the effectiveness of the theory and method. This study provides an idea for the reliability modeling of complex systems (multiple pipeline transmissions, power systems, distributed computing, etc.) in the absence of operational data.

1. Introduction

In modern engineering practice, k-out-of-n (k/n) weighted systems have become fundamental to reliability engineering, with critical applications spanning redundant system design, sensor networks, and quality control. Originally proposed by Wu and Chen [1] as a generalized reliability decision model, the k/n weighted system architecture integrates $n$ components with differentiated weights, requiring the weighted contribution sum to meet a predetermined threshold $k$ for normal operation. Recent advancements in this domain have demonstrated remarkable progress through three key research trajectories: (1) Algorithmic Innovations: Building upon the foundational model, Wu and Chen [1] pioneered a recursive decomposition algorithm with state space compression, achieving significant computational efficiency gains. This was followed by Chang et al.’s [2] development of a fast reliability algorithm for circular continuous weighted k/n systems, later optimized by Higashiyama [3] through dimensional reduction techniques. (2) Model Generalization: Zhang [4] revolutionized traditional frameworks by introducing stochastic component weights governed by probability distributions, enhancing real-world applicability. Hamdan et al. [5] extended this paradigm to heterogeneous component systems, establishing survival signature theory for multi-type weighted k/n systems. Li and Zuo [6] evaluated the reliability of a multi-state weighted k/n system using a binary search algorithm, recursive algorithm, and generalized generating function. (3) Architectural Evolution: Chen and Yang [7] broke new ground with their two-stage k/n system model incorporating shared components, while Chaube and Singh [8] integrated fuzzy set theory to address epistemic uncertainty in two-level systems. These developments have propelled k/n system theory toward greater structural complexity and practical relevance.

In addition to the above achievements, significant progress has been made in the reliability research of weighted k-out-of-n systems at both theoretical and practical levels in recent years. Zhang [4] was the first to systematically study systems with random weights and heterogeneous components, comparing the performance of different component selection strategies through random orders (such as regular random orders or increasing convex/concave orders), and proposing the optimal grouping strategy, laying a theoretical foundation for subsequent research. Bisht and Singh [9] further extended the model to dynamic scenarios and proposed a weighted (k₁, k₂)-out-of-n repairable system model, which combines Lz transformation and queuing theory to analyze time-varying reliability indicators (such as availability and expected profit), providing a new method for dynamic maintenance scenarios such as solar power generation systems.

Eryilmaz [10] filled the research gap in discrete life weighted systems by optimizing the number of spare parts through an average loss capacity model, supporting maintenance decisions for digital control equipment. Li et al. [11] proposed a Copula-based dependency modeling method for multi failure mode systems, and combined it with a case study of a fighter turbocharging subsystem to verify the critical impact of component correlation on reliability. Bian et al. [12] studied a system where degradation and shock interact together, established closed reliability functions under extreme and cumulative shock models, and revealed the coupling mechanism of multi-component failures in microelectromechanical systems.

Despite these achievements, traditional reliability paradigms remain constrained by their dependence on historical failure data—a critical limitation when analyzing emerging complex systems (e.g., deep-sea exploration equipment or space stations), where empirical data scarcity invalidates conventional large-number assumptions. This methodological impasse prompted Liu’s [13] uncertainty theory, which established a rigorous mathematical framework for quantifying subjective uncertainty through axiomatic measures and distribution functions. Diverging from probability theory’s randomness focus and fuzzy set theory’s ambiguity handling, uncertainty theory specifically addresses expert judgment quantification, enabling reliability analyses under severe data paucity.

Subsequent developments have significantly expanded the applications of uncertainty theory: Hu et al. [14] formulated uncertain programming models for redundant systems optimization, and applied uncertain parameters to discrete-series parallel systems [15], and extended them to general systems [16]; Shi et al. [17,18,19] developed competing failure models incorporating dual uncertainty dependencies; Gao and Yao [20] pioneered uncertainty-based importance measures for system diagnostics; Gao et al. [21] achieved a theoretical breakthrough with the first two-state k/n weighted system model, later extended by Sheng and Ke [22] to multi-state scenarios with an uncertain weight. Gao and Zhang [23,24] applied multi-state k/n systems in environments where uncertainty and randomness coexist.

Current research exhibits three critical limitations: (1) An over-reliance on simplistic topological assumptions (linear/circular structures with independent failures) that are incongruent with real-world systems’ hierarchical architectures. (2) Static weight models are inadequate for capturing dynamic importance variations. (3) Deterministic correlation assumptions fail to address uncertainty coupling effects in complex systems. Empirical analyses of aerospace systems, smart grids, and industrial automation networks reveal that these oversimplifications create substantial gaps between theoretical models and engineering realities.

To bridge these gaps, this study proposes a groundbreaking two-stage uncertain multi-state weighted k/n system (UMW-k/n) reliability model, featuring three theoretical innovations: (1) Hierarchical evaluation framework: Implementing macro–micro analysis through a system-level architecture reliability assessment (considering subsystem topology and interactions) followed by a component-level reliability characterization within subsystems. (2) Uncertainty integration: A unified representation of system states and weight parameters via uncertain variables effectively addresses cognitive uncertainty in data-scarce environments. (3) Decoupling algorithm: Novel reliability evaluation methodology resolving the coupled effects of state-weight uncertainties through independent uncertainty.

The subsequent sections are organized as follows: Section 2 outlines uncertainty theory fundamentals. Section 3 constructs the UMW-k/n reliability analysis framework. Section 4 develops the two-stage evaluation methodology. Section 5 establishes importance measurement theory. The concluding section discusses implications and future research directions.

2. Preliminary

This section will introduce some theories used in the article.

Definition 1. 

(Liu [13]). Suppose $\mathcal{L}$ is an $\sigma \text{-}$algebra on a nonempty set $\Gamma$, and the set function $M$ on it is an uncertain measure that satisfies the following:

(1) $M\left\{\Gamma \right\}=1$.

(2) $M\left\{A\right\} + M\left\{A^c\right\}=1$ for any event $A\in \mathcal{L}$.

(3) For any countable sequence of events $A_1,A{}_2,\dots ,$ we have

$$M\left\{\underset{i=1}{\overset{\infty }{{\displaystyle \cup }}}{A}_i\right\}\le {\displaystyle \sum _{i=1}^{\infty }M\left\{A_i\right\}}.$$

(4) For any countable sequence of events $A_1,A{}_2,\dots ,$ we have

$$M\left\{{\displaystyle \prod _{i=1}^{\infty }{\Lambda }_i}\right\}\le \underset{i=1}{\overset{\infty }{{\displaystyle \Lambda }}}M\left\{{\Lambda }_i\right\}$$

Then, the triplet $\left(\Gamma ,\mathcal{L},\mathcal{M}\right)$ is called an uncertain space.

Theorem 1. 

(Liu [13]). Let ${\xi }_1, {\xi }_2, \dots , {\xi }_n$ be a set of independent uncertain variables, and if $f\left(x_1, x_2, \dots , x_n\right)$ is a strictly increasing multivariate function, then

$$M\left\{f\left({\xi }_1, {\xi }_2, \dots , {\xi }_n\right)\ge x\right\}=\underset{f\left(x_1, x_2, \dots , x_n\right)\ge x}{\sup }\underset{1\le i\le n}{\min }\left\{{\xi }_i\ge x_i\right\}.$$

For example, assuming that ${\xi }_1, {\xi }_2$ are positive uncertain variables, according to Theorem 1, $M\left\{{\xi }_1+{\xi }_2\ge x\right\}=\underset{x_1+x_2\ge x}{\sup }\underset{1\le i\le 2}{\min }\left\{{\xi }_i\ge x_i\right\}$.

Theorem 2. 

(Liu [25]). Assuming a system is composed of $n$ uncertain components ${\xi }_1, {\xi }_2, \dots , {\xi }_n$ with the structural function $f\left(x_1, x_2, \dots , x_n\right)$, and the reliability measures of each component ${\xi }_1, {\xi }_2, \dots , {\xi }_n$ are ${\alpha }_1, {\alpha }_2, \dots , {\alpha }_n$, then the reliability measure of the system is

$$R=\left\{\begin{array}{l}\underset{f\left(x_1, x_2, \dots , x_n\right)=1}{\sup }\underset{1\le i\le n}{\min }{\nu }_i(x_i),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\underset{f\left(x_1, x_2, \dots , x_n\right)=1}{\sup }\underset{1\le i\le n}{\min }{\nu }_i(x_i)<0.5\\ 1-\underset{f\left(x_1, x_2, \dots , x_n\right)=0}{\sup }\underset{1\le i\le n}{\min }{\nu }_i(x_i),\hspace{0.33em}\hspace{0.33em}if\underset{f\left(x_1, x_2, \dots , x_n\right)=1}{\sup }\underset{1\le i\le n}{\min }{\nu }_i(x_i)\ge 0.5\end{array}\right.,$$

where $x_i$ takes values of either 0 or 1, and $v_i$ is defined by

$$v_i(x_i)=\left\{\begin{array}{l} {\alpha }_i, if x_i=1\\ 1-{\alpha }_i, if x_i=0\end{array}\right.$$

for $i=1,2,\dots ,n$, respectively.

3. Reliability Analysis of UMW-k/n System

The UMW-k/n system is a multi-state weighted k-out-of-n system, where the state is an uncertain variable. Consider an uncertain multistate weighted k-out-of-n (UMW-k/n) system comprising $n$ components. Each component $i$ possesses $N+1$ distinct operational states denoted by $x_i\in \left\{0,1,\dots ,N\right\}$, where $x_i=0$ indicates complete failure and $x_i=N$ represents perfect symmetrical function. The state value demonstrates monotonic improvements in operational performance, with higher values corresponding to superior working conditions. The performance metric associated with state $i$ is quantified by $u_i(x_i)$, where $u_i(x_i)$:$\{0,1,\dots ,N\}\to R^{+}$ is a predefined non-decreasing function.

In practical engineering applications, a precise determination of the component states $x_i$ proves infeasible due to system complexity and environmental uncertainties. To address this epistemic uncertainty, expert assessments are incorporated through uncertainty theory. Specifically, each component state $x_i$ is modeled as an uncertain variable, formally establishing the UMW-k/n system framework.

Definition 2 (Component Reliability Measure). 

The reliability measure for component $i$ maintaining at least state $j$ is given by

$${\nu }_i(j)=M\{x_i\ge j\},\hspace{0.33em}i=0,1,\dots ,n.$$

(1)

Definition 3 (System Reliability Measure). 

The system-level reliability measure is defined as

$$R(k)=M\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)\ge k}\right\},$$

(2)

where $k$ denotes a predetermined threshold that may exceed $n$, accommodating scenarios requiring super-additive performance accumulation.

This formulation enables a rigorous reliability evaluation under uncertainty by systematically integrating component-state dependencies and performance weighting.

Example 1. 

A UMW-k/n system has three components whose states $x_i,i=1,2,\dots ,n$ are independent and uncertain variables. The performance values and reliability measures corresponding to each component state are shown in

Table 1. The state $x_i$ and performance $u_i(x_i)$ of the component.

${\mathit{x}}_{\mathit{i}}$	0	1	2	3
$u_1(x_i)$	0	0.4	0.7	1
$u_2(x_i)$	0	0.5	0.6	1
$u_3(x_i)$	0	0.3	0.8	1

and

Table 2. The state $x_i$ and reliability ${\nu }_i(j)$ of the component.

	State	0	1	2	3
Component
1		1	0.9	0.7	0.2
2		1	0.8	0.5	0.4
3		1	0.7	0.3	0.1

, respectively. Therefore, the reliability measure of the system is

$$R(1.6)=M\left\{{\displaystyle \sum _{i=1}^3{u}_i(x_i)\ge 1.6}\right\}=0.4.$$

(3)

As defined by system reliability measurement,

$$R(1.6)=M\left\{{\displaystyle \sum _{i=1}^3{u}_i(x_i)\ge k}\right\}=M\left\{u_1(x_1)+u_2(x_2)+u_3(x_3)\ge 1.6\right\}.$$

(4)

On the one hand,

$$\left\{u_1(x_1)+u_2(x_2)+u_3(x_3)\ge 1.6\right\}\supset \left\{x_1\ge 1,x_2\ge 3,x_3\ge 1\right\},$$

so

$$\begin{array}{l}R(1.6)=M\left\{u_1(x_1)+u_2(x_2)+u_3(x_3)\ge 1.6\right\}\ge M\left\{x_1\ge 1,x_2\ge 3,x_3\ge 1\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=M\left\{x_1\ge 1\right\}\wedge M\left\{x_2\ge 3\right\}\wedge M\left\{x_3\ge 1\right\}=0.4\end{array}.$$

(5)

On the other hand, we have

$$\left\{u_1(x_1)+u_2(x_2)+u_3(x_3)<1.6\right\}\supset \left\{x_1<3,x_2<3,x_3<2\right\},$$

so

$$\begin{array}{l}R(1.6)=1-M\left\{u_1(x_1)+u_2(x_2)+u_3(x_3)\le 1.6\right\}\le 1-M\left\{x_1<3,x_2<3,x_3<2\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=1-\left\{1-M\left\{x_1\ge 3\right\}\right\}\wedge \left\{1-M\left\{x_2\ge 3\right\}\right\}\wedge \left\{1-M\left\{x_3\ge 2\right\}\right\}=0.4\end{array}.$$

(6)

Combining Equations (5) and (6), there is Equation (3) that holds.

Theorem 3. 

The states of the components in the UMW-k/n system are independent uncertain variables $x_i(i=1,2,\dots ,n)$, and the corresponding performance values are $u_i(x_i)$. Therefore, the reliability measure of the UMW-k/n system is

$$R(k)\hspace{0.33em}=\underset{u_1(c_1)+u_2(c_2)+\dots +u_n(c_n)\ge k}{\sup }\underset{1\le i\le n}{\min }\left\{M\{x_i\ge c_i\}\right\}.$$

(7)

Proof of Theorem 3. 

Assuming the multivariate function is

$$w(c_1,c_2,\dots ,c_n)={\displaystyle \sum _{i=1}^n{u}_i(c_i)},$$

Then, according to Theorem 1, the reliability measure of the UMW-k/n system is

$$\begin{array}{l}R(k)=M\left\{f(x_1,x_2,\dots ,x_n)\ge k\right\}=\underset{w(c_1,c_2,\dots ,c_n)\ge k}{\sup }\underset{1\le i\le n}{\min }\left\{M\{x_i\ge c_i\}\right\}\\ =\underset{u_1(c_1)+u_2(c_2)+\dots +u_n(c_n)\ge k}{\sup }\underset{1\le i\le n}{\min }\left\{M\{x_i\ge c_i\}\right\}\end{array}.$$

(8)

□

Example 2. 

Considering the UMW-k/n system in Example 1, there is a total of 30 state combinations that satisfy ${\displaystyle \sum _{i=1}^3{u}_i(x_i)\ge 1.6}$. Among them, the combination (1,3,1) is the best, and the reliability measure of the system is

$$R(1.6)=\underset{u_1(c_1)+u_2(c_2)+\dots +u_n(c_n)\ge 1.6}{\sup }\underset{1\le i\le n}{\min }\left\{M\{x_i\ge c_i\}\right\}=M\left\{x_1\ge 1\right\}\wedge M\left\{x_2\ge 3\right\}\wedge M\left\{x_3\ge 1\right\}=0.4.$$

(9)

Theorem 4. 

The states of the components in the UMW-k/n system are independent uncertain variables $x_i(i=1,2,\dots ,n)$, and the corresponding performance values are $u_i(x_i)$. Therefore, the reliability measure of the UMW-k/n system is

$$R(k)=\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{i=1}^n{u}_i(1_i(\nu )}\right.)\ge k\right\},$$

(10)

where

$$1_i(\nu )=\left\{\begin{array}{l}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\nu }_i(1)<\nu \le 1\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}1\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\nu }_i(2)<\nu \le {\nu }_i(1)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}⋮\\ N-1,\hspace{0.33em}\hspace{0.33em}{\nu }_i(N)<\nu \le {\nu }_i(N-1)\\ \hspace{0.33em}\hspace{0.33em}N,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0<\nu \le {\nu }_i(N)\end{array}\right.i=1,2,\dots ,n.$$

is a real-valued step function.

Proof of Theorem 4. 

Denote

$${\nu }_0=\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{i=1}^n{u}_i(1_i(\nu ))}\right.\ge k\right\},$$

(11)

Firstly, for any ${\nu }_l<{\nu }_0$ when the reliability measures ${\nu }_1,{\nu }_2,\dots ,{\nu }_n$ of the components are all greater than ${\nu }_l$, then

$$\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\ge k\right\}\supset \left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\ge {\displaystyle \sum _{i=1}^n{u}_i(1_i(\nu ))}\right\}\hspace{0.33em}\supset \underset{i=1}{\overset{n}{\cap }}\left\{x_i\ge 1_i({\nu }_l)\right\},$$

then

$${\displaystyle \sum _{i=1}^n{u}_i(1_i({\nu }_l)})\ge k.$$

This is because

$$\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\ge k\right\}\supset \left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\ge {\displaystyle \sum _{i=1}^n{u}_i(1_i(\nu ))}\right\}\hspace{0.33em}\supset \underset{i=1}{\overset{n}{\cap }}\left\{x_i\ge 1_i({\nu }_l)\right\},$$

According to the independence and monotonicity of uncertain variables, there is

$$M\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\ge k\right\}\ge M\left\{\underset{i=1}{\overset{n}{\cap }}\left\{x_i\ge 1_i({\nu }_l)\right\}\right\}\hspace{0.33em}\hspace{0.33em}=\underset{1\le i\le n}{\min }M\left\{x_i\ge 1_i({\nu }_l)\right\}\ge {\nu }_l.$$

The inequality above holds for any ${\nu }_l<{\nu }_0$, so

$$M\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\ge k\right\}\ge \underset{{\alpha }_l\le {\alpha }_0}{\sup }{\nu }_l\hspace{0.33em}=\hspace{0.33em}{\nu }_0.$$

(12)

In addition, for any ${\nu }_{\mathrm{u}}>{\nu }_0$, where the reliability measures ${\nu }_1,{\nu }_2,\dots ,{\nu }_n$ of the components are all less than ${\nu }_u$, then

$${\displaystyle \sum _{i=1}^n{u}_i(1_i({\nu }_u)})<k.$$

Therefore,

$$\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}<k\right\}\supset \left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\le {\displaystyle \sum _{i=1}^n{u}_i}(1_i({\nu }_u))\right\}\hspace{0.33em}\supset \underset{i=1}{\overset{n}{\cap }}\left\{x_i\le 1_i({\nu }_u)\right\}.$$

and

$$\begin{array}{l}M\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}<k\right\}\ge M\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\le {\displaystyle \sum _{i=1}^n{u}_i}(1_i({\nu }_u))\right\}\hspace{0.33em}=\underset{1\le i\le n}{\min }M\left\{x_i\le 1_i({\nu }_u)\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\underset{1\le i\le n}{\min }\left\{1-M\left\{x_i\ge 1_i({\nu }_u)+1\right\}\right\}\ge 1-{\nu }_u\end{array},$$

Thus,

$$M\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\ge k\right\}\le {\nu }_u.$$

(13)

The inequality (13) above holds for any ${\nu }_0<{\nu }_u$, so

$$M\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\ge k\right\}\le \underset{{\alpha }_0<{\alpha }_u}{\inf }{\nu }_u=\hspace{0.33em}{\nu }_0,$$

(14)

Combining Equations (12) and (14), there is

$$M\left\{{\displaystyle \sum _{i=1}^n{u}_i(x_i)}\ge k\right\}\hspace{0.33em}=\hspace{0.33em}{\nu }_0.$$

(15)

Theorem 3.2 is proven. □

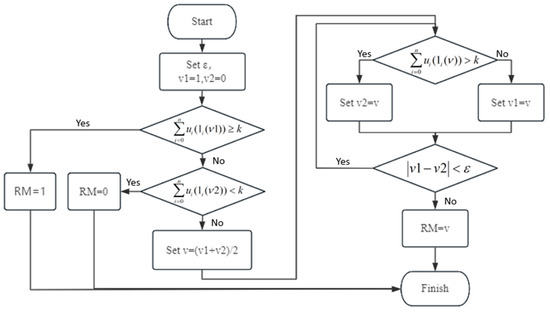
According to Theorem 4, we designed a binary search algorithm to calculate the reliability measure of UMW-k/n system. The steps are as follows, and the flowchart is shown in Figure 1.

Algorithm 1. Binary Search Algorithm for Calculating the Reliability Measure $RM$ of System

Step 1 Set solution accuracy $\epsilon$.

Step 2 Set ${\nu }_1=1$, if ${\displaystyle \sum _{i=1}^n{u}_i(1_i({\nu }_1)})\ge k$, then $RM=1$ and end the program.

Step 3 Set ${\nu }_2=0$, if ${\displaystyle \sum _{i=1}^n{u}_i(1_i({\nu }_1)})<k$, then $RM=0$ and end the program.

Step 4 Set $\nu =({\nu }_1+{\nu }_2)/2$, if ${\displaystyle \sum _{i=1}^n{u}_i(1_i(\nu )})>k$, then ${\nu }_2=\nu$, or otherwise ${\nu }_1=\nu$.

Step 5 Determine $\left|{\nu }_1-{\nu }_2\right|<\epsilon$, then $RM=\nu$ and end the program, or otherwise return to Step 4 to continue.

Example 3. 

Considering the UMW-k/n system in Example 1, and according to Algorithm 1, the reliability measure of the system at $k=1.6$ is calculated using MATLAB R2018b.

$$R(1.6)=0.3995.$$

This example mutually confirms the feasibility of the theory and algorithm with examples 1 and 2.

4. Two Stage UMW-k/n System

Structurally, a two-stage UMW-k/n system is composed of $m$ subsystems that follow a certain structure, which is called a one-stage structure and is characterized by a structural function $G(x)$. The subsystem is a UMW-k/n system, which is called a two-stage structure. The working state of the $j\mathrm{th}$ component in the $i\mathrm{th}$ subsystem is denoted as $x_{ij}\in \left\{0,1,\dots ,N\right\}$. At the time $x_{ij}=0$, the $j\mathrm{th}$ component failed to work, and the larger the value of state $x_{ij}$, the better the working state of the component. When $x_{ij}=N$ occurs, the $j\mathrm{th}$ component works perfectly symmetrically and the two-stage UMW-k/n system works normally, then

$$G(s_1,s_2,\dots ,s_m)=1,$$

(16)

where $s_i$ represents the working states of the $i\mathrm{th}$ subsystem, and

$$s_i=\left\{\begin{array}{l}1,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\displaystyle \sum _{i=1}^n{u}_i(x_i)\ge k_i}\\ 0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\displaystyle \sum _{i=1}^n{u}_i(x_i)<k_i}\end{array}\right..$$

A typical two-stage UMW-k/n system includes a series UMW-k/n system and a parallel UMW-k/n system. The structural function of the series system of UMW-k/n is

$$G(s_1,s_2,\dots ,s_m)=\min \left\{s_1,s_2,\dots ,s_m\right\},$$

(17)

and the structural function of the parallel system of UMW-k/n is

$$G(s_1,s_2,\dots ,s_m)=\max \left\{s_1,s_2,\dots ,s_m\right\}.$$

(18)

The second stage of the two-stage UMW-k/n system consists of $m$ subsystems, each of which is a system of UMW-k/n with $n$ components. $k_i$ is the weight threshold of the system of the $i\mathrm{th}$ UMW-k/n, and the $m$ UMW-k/n subsystems form a threshold vector $K={\left[k_1,k_i,\dots ,k_m\right]}^T$. Therefore,

$$\begin{array}{l}Subsystem 1:u_{11}(x_1)+u_{12}(x_2)+\dots +u_{1n}(x_n)\ge k_1\\ Subsystem 2:u_{21}(x_1)+u_{22}(x_2)+\dots +u_{2n}(x_n)\ge k_2\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}⋮\\ Subsystem m:u_{m1}(x_1)+u_{m2}(x_2)+\dots +u_{mn}(x_n)\ge k_m\end{array},$$

where $u_{ij}(\cdot )$ is the performance weight of the $j\mathrm{th}$ component of the $i\mathrm{th}$ subsystem.

For a two-stage series connected system with UMW-k/n, all $m$ systems with UMW-k/ns in the second layer must work, meaning that all $m$ equations above must hold for the system to function properly; for a two-stage parallel system with UMW-k/n, at least one of the $m$ systems with UMW-k/n in the second layer is working, that is, at least one of the $m$ equations above holds, and the system is working normally. When $m=1$, the two-stage system with UMW-k/n degenerates into an UMW-k/n system.

Definition 4. 

Assuming that the first stage structural function of the two-stage UMW-k/n system is $G(s_1,s_2,\dots ,s_m)$, there are $m$ UMW-k/n subsystems $s_1,s_2,\dots ,s_m$ in the second stage. Then, the system’s reliability measure is

$$RM=M\left\{G(s_1,s_2,\dots ,s_m)=1\right\}$$

(19)

Theorem 5. 

Assuming that the two-stage UMW-k/n system has $m$ subsystems $s_1,s_2,\dots ,s_m$ and structural functions $G(s_1,s_2,\dots ,s_m)$, and the subsystems $s_1,s_2,\dots ,s_m$ are independent of each other with reliability measures of ${\nu }_1,{\nu }_2,\dots ,{\nu }_m$, respectively, then the system’s reliability measure is

$$RM=\left\{\begin{array}{l}\underset{G(s_1,s_2,\dots ,s_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(s_i),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\underset{G(s_1,s_2,\dots ,s_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(s_i)<0.5\\ 1-\underset{G(s_1,s_2,\dots ,s_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(s_i),\hspace{0.33em}\hspace{0.33em}if\underset{G(s_1,s_2,\dots ,s_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(s_i)\ge 0.5\end{array}\right.$$

(20)

where $s_i$ is taken as 0 or 1, and the $i\mathrm{th}$subsystem reliability measure is

$${\nu }_i(s_i)=\left\{\begin{array}{l}{\nu }_i,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{s}_i=1\\ 1-{\nu }_i,\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{s}_i=0\end{array}\right.\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}i=1,2\dots m$$

Proof of Theorem 5. 

According to Definition 4 for reliability measurement for two-stage UMW-k/n systems, then

$$RM=⋮\left\{G(s_1,s_2,\dots ,s_m)=1\right\}$$

(21)

According to Theorem 2, Equation (20) holds and Theorem 5 is proven. □

Example 4. 

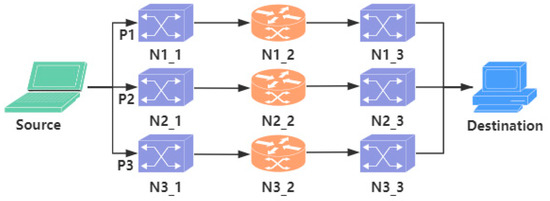
The 5G core network controlled by a software-defined network (SDN) utilizes multi-path fault-tolerant technology to create a nearly “zero defect” communication environment for remote surgery, autonomous driving, industrial automation, and other applications. This innovative architecture deeply integrates the centralized control advantages of SDN with the ultra-low latency characteristics of 5G networks, and achieves lossless transmission of medical data in complex network environments through intelligent path dynamic optimization mechanisms.

Figure 2 shows how the 5G core network controlled by a software-defined network (SDN) utilizes multi-path fault-tolerant technology to build a highly reliable communication environment to support critical applications such as remote surgery. The “Source” on the left side of the image represents the surgical terminal (such as the surgeon’s console or medical imaging equipment), while the “Destination” on the right side represents the remote surgical robot or medical data center. The data transmission between the two is carried out through three independent paths (P1, P2, and P3), with each path consisting of three network nodes (Nx_1, Nx_2, and Nx_3), ensuring that even if one path fails, the data can still be stably transmitted through the backup path. The SDN controller monitors the transmission quality of each path in real-time (such as latency, packet loss rate, and jitters) and dynamically adjusts the data flow. For example, when the N1_2 node of the P1 path experiences an increase in latency due to network congestion, the SDN can immediately switch critical data (such as surgical instructions) to the P2 or P3 path. The nodes of each path adopt a dual switch architecture, responsible for data forwarding and redundant backup, further reducing the risk of a single point failure.

To ensure the transmission of critical data for remote surgery, in Figure 2, it is required that at least two out of three paths work simultaneously, with each path having two states. When the total performance weight of path i is greater than $k_i$, $P_i=1$, meaning that the working state of path i is completely normal. Otherwise, when $P_i=0$, the working state of path i fails, and

$$P_i=\left\{\begin{array}{l}1,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\displaystyle \sum _{i=1}^n{u}_i(x_i)\ge k_i}\\ 0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\displaystyle \sum _{i=1}^n{u}_i(x_i)<k_i}\end{array}\right.,i=1,2,\dots$$

There are currently three paths (P1–P3), each consisting of three core nodes connected in a series (ingress router → backbone router → egress router), as shown in Figure 2. Each node has its own multi-state reliability model, which means each node has four states, as shown in

Table 3. Node state descriptions.

States	Description	Typical Scenario
3	Perfect performance mode	Load < 60%, no faults
2	Degraded mode	Load > 80% or slight congestion
1	Semi performance mode	Load > 90% or severe congestion
0	Failure mode	Hardware malfunction/link interruption

. The performance values corresponding to different states of nodes are shown in

Table 4. States and performance values $u_i(x_i)$ of components.

	States	0	1	2	3
Components
N1-1		0	0.5	0.9	1
N1-2		0	0.4	0.8	1
N1-3		0	0.3	0.7	1
N2-1		0	0.2	0.6	1
N2-2		0	0.5	0.8	1
N2-3		0	0.4	0.8	1
N3-1		0	0.3	0.7	1
N3-2		0	0.2	0.6	1
N3-3		0	0.3	0.7	1

, and the reliability measures corresponding to different states of nodes are shown in

Table 5. States and reliability measurement ${\nu }_i(j)$ of Components.

	States	0	1	2	3
Components
N1-1		1	0.95	0.80	0.70
N1-2		1	0.83	0.85	0.75
N1-3		1	0.98	0.87	0.70
N2-1		1	0.90	0.70	0.20
N2-2		1	0.80	0.60	0.40
N2-3		1	0.70	0.30	0.10
N3-1		1	0.90	0.80	0.50
N3-2		1	0.80	0.75	0.40
N3-3		1	0.70	0.80	0.60

.

For each path to function properly, the performance weight must not be lower than 1.6. Therefore, paths P1–P3 are three typical UMW-k/n systems, and the reliability measure is calculated according to Algorithm 1,

$${\nu }_1(P_1)=M\left\{P_1=1\right\}=M\left\{{\displaystyle \sum _{i=1}^3{u}_i(x_i)\ge 1.6}\right\}=0.8502$$

$${\nu }_2(P_2)=M\left\{P_2=1\right\}=M\left\{{\displaystyle \sum _{i=1}^3{u}_i(x_i)\ge 1.6}\right\}=0.5995$$

$${\nu }_3(P_3)=M\left\{P_3=1\right\}=M\left\{{\displaystyle \sum _{i=1}^3{u}_i(x_i)\ge 1.6}\right\}=0.7498$$

These three paths are integrated into a network through structural functions, with the specific structural function being

$$G(P_1,P_2,P_3)=(P_1\wedge P_2)\vee (P_2\wedge P_3)\vee (P_1\wedge P_3)$$

(22)

There are eight possible combinations of $(P_1,P_2,P_3)$, as shown in

Table 6. The combinations of $(P_1,P_2,P_3)$.

Status of Subsystem	$\mathit{G}({\mathit{P}}_1,{\mathit{P}}_2,{\mathit{P}}_3)=1$	$\underset{1\le \mathit{i}\le 3}{\mathbf{min}}{\mathit{\nu }}_{\mathit{i}}({\mathit{P}}_{\mathit{i}})$
(0,0,0)	No	0.1498
(0,0,1)	No	0.1498
(0,1,0)	No	0.1498
(0,1,1)	Yes	0.1498
(1,0,0)	No	0.3502
(1,0,1)	Yes	0.4005
(1,1,0)	Yes	0.3502
(1,1,1)	Yes	0.5995

.

According to Table 6, it can be calculated that

$$\underset{G(P_1,P_2,P_3)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(P_i)=0.5995>0.5$$

According to Theorem 5, the reliability measure of a computing system is

$$R(1.6)=1-\underset{G(P_1,P_2,P_3)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(P_i)=1-0.3502=0.6498$$

(23)

5. Importance Measurement of Two-Stage UMW-k/n System

Importance measurement is an important indicator of system reliability, describing the impact of a component’s operation on system reliability. Gao and Yao [20] introduced importance measurements in uncertain reliability systems, which have attracted the attention of many scholars. The idea of importance comes from Birnbaum importance, which extends to the application of multi-state components in the framework of uncertainty theory.

For the uncertain two-stage UMW-k/n system, the importance measurement is also divided into two stages. The first stage is the importance measurement of the UMW-k/n system, which refers to the impact of the system’s operation on its reliability; the second stage is the measurement of component importance, which refers to the impact of component operation on system reliability.

Definition 5. 

If there are $m$ UMW-k/n subsystems in a two-stage UMW-k/n system, $s_i(i=1,2,\dots ,m)$, representing the working state of the $i\mathrm{th}$ UMW-k/n subsystems, then the importance measure of $i\mathrm{th}$ UMW-k/n subsystems is

$$I{M}_i=M\left\{G(s_1,\dots ,s_{i-1},1,s_{i+1},\dots ,s_m)=1\right\}-M\left\{G(s_1,\dots ,s_{i-1},0,s_{i+1},\dots ,s_m)=1\right\}.$$

(24)

Definition 6. 

Assuming a two-stage UMW-k/n system has $m$ UMW-k/n subsystems, $s_i(i=1,2,\dots ,m)$ represents the working state of the $i\mathrm{th}$ UMW-k/n subsystem, where each UMW-k/n subsystem has $n$ components and their states are represented as $x_{i,1},x_{i,2},\dots ,x_{i,n},i=1,2,\dots ,m$. Therefore, the importance measure of $z_{i,j}$is

$$I{M}_{i,j}(k)=M\left\{w(x_{i,1},\dots ,x_{i,j-1},N,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}-M\left\{w(x_{i,1},\dots ,x_{i,j-1},0,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}$$

(25)

where $z_{i,j}$ is the $j\mathrm{th}$ component of the $i\mathrm{th}$ UMW-k/n subsystem, $w$ is the state weight function, and $N$ is the optimal state.

Definition 7. 

Assuming that the first stage structural function of a two-stage UMW-k/n system is $G(s_1,s_2,\dots ,s_m)$, there are $m$ UMW-k/n subsystems $s_1,s_2,\dots ,s_m$ in the second stage, and the $i\mathrm{th}$ subsystem works if $s_i=1$, otherwise if $s_i=0$, then the importance measure of $z_{i,j}$ to the two-stage UMW-k/n system is

$$I{M}_i^j=M\left\{G(s_1,s_2,\dots ,s_i,\dots ,s_m)=1\right\}-M\left\{G(s_1,s_2,\dots ,{s^{\prime }}_i,\dots ,s_m)=1\right\}$$

(26)

where ${s^{\prime }}_i$ is the subsystem state where the $j\mathrm{th}$ component of $i\mathrm{th}$UMW-k/n subsystem fails.

Theorem 6. 

If the uncertain variables $x_{i,1},x_{i,2},\dots ,x_{i,n}$ are the states of the components of the$i\mathrm{th}$ UMW-k/n subsystem and are independent of each other, then the importance measure of $z_{i,j}$ is

$$I{M}_{i,j}(k)\hspace{0.33em}\hspace{0.33em}=\underset{u_1(c_1)+\dots +u_j(N)+\dots +u_n(c_n)\ge k}{\sup }\underset{\begin{array}{l}1\le q\le n\\ \hspace{0.33em}q\ne j\end{array}}{\min }\{M\{x_{i,q}\ge c_q\}\}-\underset{u_1(c_1)+\dots +u_j(0)+\dots +u_n(c_n)\ge k}{\sup }\underset{\begin{array}{l}1\le q\le n\\ \hspace{0.33em}q\ne j\end{array}}{\min }\{M\{x_{i,q}\ge c_q\}\}\hspace{0.33em}$$

(27)

where $c_q$ takes $0,1,\dots ,N$.

Proof of Theorem 6. 

According to Definition 6 and Theorem 1, then

$$\begin{array}{l}I{M}_{i,j}(k)=M\left\{w(x_{i,1},\dots ,x_{i,j-1},N,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}-M\left\{w(x_{i,1},\dots ,x_{i,j-1},0,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\underset{u_1(c_1)+\dots +u_j(N)+\dots +u_n(c_n)\ge k}{\sup }\underset{\begin{array}{l}1\le q\le n\\ \hspace{0.33em}q\ne j\end{array}}{\min }\{M\{x_{i,q}\ge c_q\}\}\hspace{0.33em}-\underset{u_1(c_1)+\dots +u_j(0)+\dots +u_n(c_n)\ge k}{\sup }\underset{\begin{array}{l}1\le q\le n\\ \hspace{0.33em}q\ne j\end{array}}{\min }\{M\{x_{i,q}\ge c_q\}\}\end{array}$$

□

Theorem 7. 

The two-stage UMW-k/n system consists of $m$ UMW-k/n systems, and the importance measure of $z_{i,j}$ is

$$I{M}_{i,j}(k)=\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{q=0.q\ne j}^n{u}_{i,q}(1_{i,q}(\nu )}\right.)+u_{i,j}(N)\ge k\right\}\hspace{0.33em}-\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{q=0,q\ne j}^n{u}_{i,q}(1_{i,q}(\nu ))}\right.\ge k\right\}$$

(28)

where $1_{i,j}(\nu )=\left\{\begin{array}{l}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\nu }_{i,j}(1)<\nu \le 1\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}1,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\nu }_{i,j}(2)<\nu \le {\nu }_{i,j}(1)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}⋮\\ N-1,\hspace{0.33em}\hspace{0.33em}{\nu }_{i,j}(N)<\nu \le {\nu }_{i,j}(N-1)\\ \hspace{0.33em}\hspace{0.33em}N,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0<\nu \le {\nu }_{i,j}(N)\end{array}\right., i=1,2,\dots ,n$ is real step function, and $u_{i,j}$ is the performance value of the $j\mathrm{th}$ component for the $i\mathrm{th}$ subsystem.

Proof of Theorem 7. 

According to Theorem 4, the reliability measure of $z_{i,j}$ operating perfectly is

$$\begin{array}{l}R(k)=\hspace{0.33em}M\left\{f(x_{i,1},\dots ,x_{i,j-1},N,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}\hspace{0.33em}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=M\left\{{\displaystyle \sum _{q=1,q\ne j}^n{u}_{i,q}(x_{i,q})}\ge k,x_{i,j}=N\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{q=1,q\ne j}^n{u}_{i,q}(1_{i,q}(\nu )}\right.)+u_{i,j}(N)\ge k\right\}\end{array}$$

The reliability measure of $z_{i,j}$ failure is

$$\begin{array}{l}R(k)=\hspace{0.33em}M\left\{f(x_{i,1},\dots ,x_{i,j-1},0,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}\hspace{0.33em}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=M\left\{{\displaystyle \sum _{q=1,q\ne j}^n{u}_{i,q}(x_{i,q})}\ge k,x_{i,j}=0\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{q=1,q\ne j}^n{u}_{i,q}(1_{i,q}(\nu )}\right.)\ge k\right\}\end{array}$$

According to Definition 6 for the importance measure, Theorem 7 holds and is proven. □

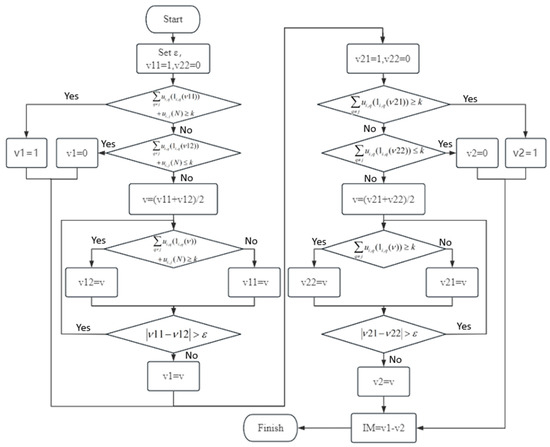
According to the above Theorem, the importance measurement algorithm for the UMW-k/n system is as follows, and the flowchart is shown in Figure 3.

Algorithm 2. Binary Search Algorithm for Calculating Importance Measure of UMW-k/n System

Step 1 Set solution accuracy $\epsilon$.

Step 2 Let ${\nu }_{11}=1$. If ${\displaystyle \sum _{q\ne j}{u}_{i,q}}{1}_{i,q}({\nu }_{11})+u_{i,j}(N)\ge k$, then ${\nu }_1=1$. Jump to Step 6.

Step 3 Let ${\nu }_{12}=0$. If ${\displaystyle \sum _{q\ne j}{u}_{i,q}(1_{i,q}({\nu }_{12}))+u_{i,j}(N)}\le k$, then ${\nu }_1=0$. Jump to Step 6.

Step 4 Calculate $\nu ={\nu }_{11}+{\nu }_{12}/2$. If ${\displaystyle \sum _{q\ne j}{u}_{i,q}(1_{i,q}(\nu ))+u_{i,j}(N)}\ge k$, then ${\nu }_{12}=\nu$, and otherwise ${\nu }_{11}=v$.

Step 5 If $\left|{\nu }_{11}-{\nu }_{12}\right|>\epsilon$, return to Step 4 to continue. Otherwise, ${\nu }_1={\displaystyle \frac{{\nu }_{11}+{\nu }_{12}}{2}}$. Jump to Step 6.

Step 6 Let ${\nu }_{21}=1$. If ${\displaystyle \sum _{q\ne j}{u}_{i,q}(1_{i,q}({\nu }_{21}))}\ge k$, then ${\nu }_2=1$. Jump to Step 10.

Step 7 Let ${\nu }_{22}=0$. If ${\displaystyle \sum _{q\ne j}{u}_{i,q}(1_{i,q}({\nu }_{21}))}\le k$, then ${\nu }_2=0$. Jump to Step 10.

Step 8 Calculate $\nu =({\nu }_{21}+{\nu }_{22})/2$. If ${\displaystyle \sum _{q\ne j}{u}_{i,q}(1_{i,q}(\nu ))}\ge k$, then ${\nu }_{22}=\nu$. Otherwise, ${\nu }_{21}=v$.

Step 9 If $\left|{\nu }_{21}-{\nu }_{22}\right|>\epsilon$, return to Step 8 to continue. Otherwise, ${\nu }_2=({\nu }_{21}+{\nu }_{22})/2$. Jump to Step 10.

Step 10 The importance measure of the $j\mathrm{th}$ component of the subsystem is $IM={\nu }_1-{\nu }_2$.

Example 5. 

Considering the system in Example 2, when the working state of component 1 is 3, according to Theorem 3, there are 13 combinations of states that satisfy the condition $u_1(x_1)+u_2(x_2)+u_3(x_3)\ge 1.6$, among which the best combination is (3,1,1), and the calculated reliability measure is 0.7. When the working state of component 1 is 0, there are 3 combinations of states that satisfy the condition, among which the best combination is (0,3,2), and the calculated reliability measure is 0.3. According to Definition 6, the system importance measure of component 1 is calculated as

$$I{M}_1=0.7-0.3=0.4$$

Example 6. 

Considering the system in Example 4, according to Algorithm 1, the system reliability measure for the perfect operation of component N1-1 in path 1 is calculated as follows:

$$R(1.6)=M\left\{P_1=1\right\}=M\left\{u_1(3)+u_2(x_2)+u_3(x_3)\ge 1.6\right\}=0.9302$$

According to Algorithm 1, the system reliability measure for the failure of component N1-1 in path 1 is calculated as follows:

• $R(1.6)=M\left\{{P^{\prime }}_1=1\right\}=M\left\{u_1(0)+u_2(x_2)+u_3(x_3)\ge 1.6\right\}=0.7385$.

According to Algorithm 2, the subsystem importance measure of component N1-1 in path 1 is calculated as

$${IM}_{1,1}(1.6)=0.9302-0.7385=0.1917.$$

The importance measurement of component N1-1 relative to the overall system in path 1, as defined in Definition 7, is

$${IM}_1^1=M\left\{G\right(P_1,P_2,P_3)=1\}-M\left\{G\right({P_1}^{\prime },P_2,P_3)=1\}=0.7498-0.7385=0.0113.$$

Theorem 8. 

The two-stage UMW-k/n system consists of $m$ UMW-k/n subsystems, with the structural function $G(s_1,s_2,\dots ,s_m)$, and the states of the subsystem $s_1,s_2,\dots ,s_m$ are independent of each other. If the reliability measures of the $m$ UMW-k/n subsystems are $v_1,v_2,\dots ,v_m$, then the importance measure of $z_{i,j}$ relative to the overall system is

$$I{M}_i^j=\left\{\begin{array}{l}\underset{G(s_1,\dots ,s_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)-\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\underset{G(s_1,\dots ,s_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)<0.5,\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)<0.5\\ 1-\underset{G(s_1,\dots ,s_i,\dots ,s_m)=0}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)-\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l),\hspace{0.33em}\hspace{0.33em}if\underset{G(s_1,\dots ,s_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)\ge 0.5,\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)<0.5\\ \underset{G(s_1,\dots ,s_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)+\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=0}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)-1,\hspace{0.33em}\hspace{0.33em}if\underset{G(s_1,\dots ,s_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)<0.5,\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)\ge 0.5\\ \underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=0}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)\hspace{0.33em}-\underset{G(s_1,\dots ,s_i,\dots ,s_m)=0}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\underset{G(s_1,\dots ,s_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)\ge 0.5,\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(s_l)\ge 0.5\end{array}\right.$$

(29)

where $s_l\in \left\{0,1\right\},l=1,2\dots m$ and ${\nu }_l(s_l)=\left\{\begin{array}{l}{\nu }_l,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{s}_l=1\\ 1-{\nu }_l,\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{s}_l=0\end{array}\right.\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}l=1,2\dots m$. When l = i, ${\nu }_i$ is the reliability measure of the $j\mathrm{th}$ component of the $i\mathrm{th}$ UMW-k/n system working perfectly in the system, the reliability measurement of subsystem is

$${\nu }_i({s^{\prime }}_i)=\left\{\begin{array}{l}{{\nu }^{\prime }}_i,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{s^{\prime }}_i=1\\ 1-{{\nu }^{\prime }}_i,\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{s^{\prime }}_i=0\end{array}\right., \hspace{0.33em}i=1,2\dots m$$

${{\nu }^{\prime }}_i$ is the reliability measure for the complete failure of the $j\mathrm{th}$ component for the $i\mathrm{th}$ subsystem, and ${s^{\prime }}_i$ is the subsystem’s operational state.

Proof of Theorem 8. 

According to Definition 7,

$$I{M}_i^j=M\left\{G(s_1,\dots ,s_i,\dots ,s_m)=1\right\}-M\left\{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1\right\}$$

(30)

According to the Theorem 2,

$$M\left\{G(s_1,\dots ,s_i,\dots ,s_m)=1\right\}=\left\{\begin{array}{l}\underset{G(s_1,\dots ,s_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le m}{\min }{\nu }_l(s_l),if\underset{G(s_1,\dots ,s_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le m}{\min }{\nu }_l(s_l)<0.5\\ 1-\underset{G(s_1,\dots ,s_i,\dots ,s_m)=0}{\sup }\underset{1\le l\le m}{\min }{\nu }_l(s_l),\hspace{0.33em}if\underset{G(s_1,\dots ,s_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le m}{\min }{\nu }_l(s_l)\ge 0.5\end{array}\right.,$$

(31)

$$M\left\{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1\right\}=\left\{\begin{array}{l}\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le m}{\min }{\nu }_l(s_l),\hspace{0.33em}if\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le m}{\min }{\nu }_l(s_l)<0.5\\ 1-\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=0}{\sup }\underset{1\le l\le m}{\min }{\nu }_l(s_l),\hspace{0.33em}if\underset{G(s_1,\dots ,{s^{\prime }}_i,\dots ,s_m)=1}{\sup }\underset{1\le l\le m}{\min }{\nu }_l(s_l)\ge 0.5\end{array}\right..$$

(32)

Substitute (31) and (32) into Equation (30) to prove Theorem 8. □

Example 7. 

Considering the system in Example 6, there are four combinations that meet the conditions $G(P_1,P_2,P_3)=1$, and the optimal combination is (1,1,1). It can be calculated that

$$\underset{G(P_1,P_2,P_3)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(P_l)=\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(P_l)=0.5995>0.5$$

Similarly, there are four combinations that meet the conditions $G({P^{\prime }}_1,P_2,P_3)=1$, and the optimal combination is (1,1,1). It can be calculated that

$$\underset{G({P^{\prime }}_1,P_2,P_3)=1}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(P_l)=\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(P_l)=0.5995>0.5$$

According to Theorem 8, the importance measure of component N1-1 of path 1 relative to the overall system is

$$I{M}_1^1=\underset{G({P^{\prime }}_1,P_2,P_3)=0}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(P_l)-\underset{G(P_1,P_2,P_3)=0}{\sup }\underset{1\le l\le \mathrm{m}}{\min }{\nu }_l(P_l)=0.2615-0.2502=0.0113$$

Examples 6 and 7 mutually confirm the feasibility of the theory and algorithm.

6. Conclusions and Future Research

This study presents a novel mathematical model for the reliability assessment of two-stage uncertain multi-state weighted k-out-of-n (UMW-k/n) systems, addressing critical challenges in evaluating complex systems with inherent uncertainties. The proposed framework employs a two-phase analytical approach: (1) The first phase focuses on analyzing system-level reliability through a comprehensive consideration of topological relationships and interactions among subsystems; (2) While the second phase conducts detailed local reliability assessments at the subsystem level, we rigorously define reliability metrics for two-stage UMW-k/n systems and establish corresponding calculation formulas. To optimize computational performance, we develop an efficient numerical algorithm based on binary search optimization, achieving an optimal balance between computational accuracy and processing efficiency. Furthermore, we introduce specialized component importance measures for two-stage UMW-k/n systems, complete with derivation formulas, rigorous mathematical proofs, and proposed numerical algorithms for solving indicators. Case studies validate the model’s practical effectiveness, particularly in scenarios involving interdependent component failures and multi-state performance degradation. While demonstrating significant advances, we acknowledge the current limitations in modeling continuous-state systems and multi-layered structural complexities. These limitations suggest valuable directions for future research, including the following: extension to continuous-state systems, development of multi-stage reliability models, and incorporation of adaptive learning mechanisms for dynamic system analysis.