Importance Measures Analysis of Two-Stage Uncertain Weighted k-out-of-n Systems

Abstract

This paper proposes a two-stage weighted k-out-of-n (W-k/n) system reliability model based on uncertainty theory to address the problem of traditional W-k/n system theory being difficult to apply to the reliability evaluation of complex systems with two-layer structures. This model effectively solves the evaluation problem in the case of insufficient data by decomposing the reliability assessment of complex systems into two stages: system structure reliability and subsystem reliability. In the model, the system state and weights are described by uncertain variables that follow a certain distribution. Under the framework of uncertainty theory, two-stage reliability measures and importance measures are defined, and corresponding calculation formulas are derived. In order to reduce computational complexity, a corresponding numerical solution method including traverse search algorithm and binary search algorithm is proposed. The effectiveness of the method is also demonstrated through a project management case of electronic consumer goods. This study provides new theoretical ideas and methodological support for reliability modeling of complex systems under data loss conditions.

1. Introduction

The k-out-of-n (k/n) system was first proposed by Barlow and Proschan [1] in 1965 and operates when at least $k$ of its $n$ components function normally. Subsequently, many scholars conducted researched on it [2,3,4], this concept has become fundamental in reliability theory and engineering, with extensive applications in solar power generating systems [5], unmanned aerial reconnaissance systems [6], and wind farms (system) [7]. Bian et al. [8] considered the G system with k/n among multiple components in the dependent competition failure model and calculated the reliability of the system. Ivanova [9] proposed a numerical research method for sensitivity analysis of repairable k/n models.

Subsequent research by Wu and Chen [10] introduced the weighted k/n (W-k/n) system, where component contributions are characterized by weight values. Significant efforts have been devoted to developing reliability calculation methods for W-k/n systems. Zhang [11] developed a reliability calculation method for random W-k/n systems with heterogeneous components, where weights are treated as random variables rather than constants. Hamdan et al. [7] established a reliability model for W-k/n systems with multiple components, deriving system survival signatures and reliability functions under various assumptions. Li et al. [12] calculated the importance of each component and the correlation between components in a W-k/n system based on copula functions. Eryilmaz [13] believes that the lifetime distribution of components is a discrete distribution, and analyzes the impact of component weights on component failures and the redundancy optimization problem of optimal component number in a W-k/n system.

Following Zadeh’s introduction of fuzzy set theory in 1965, Cai [14] established a reliability theory framework based on fuzzy sets in 1996. Lin et al. [15] investigated fuzzy reliability evaluation for systems with multiple correlated degradation processes. Yu and Tang [16] studied reliability evaluation of systems subject to competitive degradation and stochastic shocks using fuzzy theory. Utkin [17] developed a recursive algorithm for calculating fuzzy reliability of various repairable systems, accounting for component uncertainties through fuzzy theory. Cheng [18] applied fuzzy theory to continuous k/n systems, while Wu [19] employed fuzzy Bayesian methods to evaluate reliability of systems with uncertainty, particularly for linear and circular continuous k/n systems with complex nonlinear dependencies. Guan and Wu [20] examined repairable continuous k/n systems with fuzzy states, incorporating multiple maintenance resources.

Beyond probability and fuzzy theories, Liu [21] pioneered uncertainty theory for reliability analysis, examining four typical systems. Zhang et al. [22] applied uncertainty theory to reliability and studied systems where uncertainty and randomness coexist, known as belief reliability. Liu et al. applied uncertainty theory to software reliability [23] and degradation models [24]. Hu et al. [25] applied uncertainty theory to redundant system optimization. Shi et al. [26] proposed a reliability model with uncertain failure thresholds, applying it to composite insulator failure processes. Shi et al. [27] further developed a reliability model for bi-uncertain dependent competitive failure systems. Gao and Yao [28] introduced importance measures into uncertain reliability theory. Gao et al. [29] and Sheng and Ke [30], respectively, proposed reliability models for uncertain two-state and multi-state W-k/n systems, analyzing their reliability functions and importance measures, with symmetry extensions by Gao and Yang [31].

While these studies have advanced reliability theory, they primarily focus on single-structure k/n systems, which often inadequately represent complex systems. To address this limitation, we propose a two-stage uncertain binary W-k/n (UBW-k/n) system model that divides reliability evaluation into system structural reliability (first stage), representing overall system reliability, and subsystem reliability (second stage), characterizing local reliability. The model describes system states and weights as distinct uncertain variables, providing deterministic reliability functions, solution methods, and numerical computation methods. This approach offers theoretical foundations and practical methods for complex system reliability modeling.

Our model differs from traditional k/n models in that: (1) We use uncertainty theory to evaluate the reliability of the system, and our method is more suitable for situations where data are lacking; (2) The model we propose is an extension of traditional models and is more suitable for reliability assessment of complex system structures in practical engineering applications. (3) The two-stage k/n model with uncertain weights divides the system structure into two stages, namely, the overall system structure and the k/n subsystem structure with uncertain weights. The system structure refers to the overall structure of W-k/n subsystems being interconnected, and the W-k/n model is just a subsystem of our proposed model.

The remainder of this paper is organized as follows: Section 2 introduces uncertainty theory fundamentals; Section 3 presents reliability analysis of UBW-k/n systems; Section 4 develops reliability analysis for two-stage UBW-k/n systems; Section 5 examines importance measures for two-stage systems; Section 6 concludes with research summary and future directions.

2. Preliminary

To help readers understand the theories used, the following will introduce relevant content.

Definition 1 

(Liu [32]). Suppose $\mathcal{L}$ be an $\sigma$-algebra on a nonempty set $\Gamma$, and the set function $\text{ℳ}$ on it is an uncertain measure that satisfies:

(1) 

$\text{ℳ}\left\{\Gamma \right\}=1$.

(2) 

$\text{ℳ}\left\{\mathcal{A}\right\}+\text{ℳ}\left\{{\mathcal{A}}^c\right\}=1$ for any event $\mathcal{A}\in \mathcal{L}$.

(3) 

For any countable sequence of events ${\mathcal{A}}_1,{\mathcal{A}}_2\dots$, we have $\text{ℳ}\left\{\underset{i=1}{\overset{\infty }{{\displaystyle \cup }}}{\mathcal{A}}_i\right\}\le {\displaystyle \sum _{i=1}^{\infty }\text{ℳ}\left\{{\mathcal{A}}_i\right\}}$.

Then the triplet  $\left(\Gamma ,\mathcal{L},\text{ℳ}\right)$  is called an uncertain space.

Theorem 1 

(Liu [32]). Let ${\xi }_1, {\xi }_2, \dots , {\xi }_n$ are a set of independent uncertain variables, and if $f\left(x_1, x_2, \dots , x_n\right)$ is a strictly increasing multivariate function, then

$$\text{ℳ}\left\{f\left({\xi }_1, {\xi }_2, \dots , {\xi }_n\right)\ge x\right\}=\underset{f\left(x_1, x_2, \dots , x_n\right)\ge x}{\sup }\underset{1\le i\le n}{\min }\left\{{\xi }_i\ge x_i\right\}.$$

For example, assuming that ${\xi }_1,{\xi }_2$ are positive uncertain variables, according to Theorem 1,

$$\text{ℳ}\left\{{\xi }_1+{\xi }_2\ge x\right\}=\underset{x_1+x_2\ge x}{\sup }\underset{1\le i\le 2}{\min }\left\{{\xi }_i\ge x_i\right\}.$$

Theorem 2 

(Liu [21]). Assuming a system is composed of $n$ uncertain components ${\xi }_1, {\xi }_2, \dots , {\xi }_n$, and the reliability measures of each component ${\xi }_1, {\xi }_2, \dots , {\xi }_n$ are ${\nu }_1, {\nu }_2, \dots , {\nu }_n$, with the structural function $f\left(x_1, x_2, \dots , x_n\right)$ strictly increasing, then the reliability measure of the system is

$$RM=\left\{\begin{array}{l}\underset{f\left(x_1, x_2, \dots , x_n\right)=1}{\sup }\underset{1\le i\le n}{\min }{\nu }_i(x_i),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\underset{f\left(x_1, x_2, \dots , x_n\right)=1}{\sup }\underset{1\le i\le n}{\min }{\nu }_i(x_i)\le 0.5\\ 1-\underset{f\left(x_1, x_2, \dots , x_n\right)=0}{\sup }\underset{1\le i\le n}{\min }{\nu }_i(x_i),\hspace{0.33em}\hspace{0.33em}if\underset{f\left(x_1, x_2, \dots , x_n\right)=1}{\sup }\underset{1\le i\le n}{\min }{\nu }_i(x_i)\ge 0.5\end{array}\right.,$$

where $x_i$ take values either 0 or 1, and $v_i$ are defined by

$$v_i(x_i)=\left\{\begin{array}{l} {\alpha }_i, if x_i=1\\ 1-{\alpha }_i,if x_i=0\end{array}\right.$$

for $i=1,2,\dots ,n$, respectively.

3. Reliability Analysis of UBW-k/n System

The UBW-k/n system has $n$ components with states of $x_i(i=1,2,\dots ,n)$. At that time $x_i=1$, the components were working normally, symmetrically at that time $x_i=0$, they are completely failed. The weight of the $i\mathrm{th}$ component of the system is ${\omega }_i\ge 0$. When the sum of the systems of the product of weights and states is at least $k$, the system works, and $k$ may be greater than $n$, in which $k$ is a given value.

In engineering applications, different components contribute differently to the reliability of the system. The same type of component contributes differently to the system under different structures, and the same component contributes differently to the system at different times, therefore, different weights are assigned to the components. Similarly, the states of a component vary at different times and environments. And in the absence of running data, the state $x_i$ or weight ${\omega }_i$ of components cannot be accurately obtained, it is necessary to invite experts to estimate based on experience. To address this subjective factor, we introduce uncertainty theory in the process of analyzing system reliability, where the system state $x_i$ and weight ${\omega }_i$ are characterized by different uncertain variables; uncertainty distribution is often obtained in practical applications by conducting research on multiple experts and considering the importance of different experts.

Assuming that (1) the states of the various components of the system are independent of each other; (2) the weights of each component in the system are mutually independent; (3) the component state and weight are independent of each other; (4) the system threshold $k$ is independent of both the system state and weight.

The reliability measure of the $i\mathrm{th}$ component’s operation is defined as

$${\nu }_i=\text{ℳ}\{x_i=1\},i=1,2,\dots ,n,$$

and the reliability measure of system operation is defined as

$$RM=\text{ℳ}\left\{{\displaystyle \sum _{i=1}^n{\omega }_i\cdot x_i\ge k}\right\}.$$

Example 1. 

A UBW-k/n system has three components, whose weights ${\omega }_i$ and states $x_i$ are independent uncertain variables, as shown in

Table 1. Weight of components.

Components	1	2	3
Weights	$\mathcal{N}(1,2)$	$\mathcal{N}(2,3)$	$\mathcal{N}(2,4)$

and

Table 2. States and reliability measurement of components.

	States	0	1
Components
1		0.5	0.5
2		0.4	0.6
3		0.7	0.7

. Then the reliability measure of the system $k=2$ is

$$RM=\text{ℳ}\left\{{\displaystyle \sum _{i=1}^3{\omega }_i\cdot x_i\ge 2}\right\}=0.6.$$

Defined by the system reliability measurement

$$RM=\text{ℳ}\left\{{\displaystyle \sum _{i=1}^3{\omega }_i\cdot x_i\ge k}\right\}=\text{ℳ}\left\{{\omega }_1\cdot x_1+{\omega }_2\cdot x_2+{\omega }_3\cdot x_3\ge 2\right\}.$$

Next, we will calculate this measure.

On the one hand,

$$\left\{{\omega }_1\cdot x_1+{\omega }_2\cdot x_2+{\omega }_3\cdot x_3\ge 2\right\}\supset \left\{x_1\ge 0,x_2\ge 1,x_3\ge 1\right\},$$

we have

$$\begin{array}{l}RM=\text{ℳ}\left\{{\omega }_1\cdot x_1+{\omega }_2\cdot x_2+{\omega }_3\cdot x_3\ge 2\right\}\ge \text{ℳ}\left\{x_1\ge 0,x_2\ge 1,x_3\ge 1\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\text{ℳ}\left\{x_1\ge 0\right\}\wedge \text{ℳ}\left\{x_2\ge 1\right\}\wedge \text{ℳ}\left\{x_3\ge 1\right\}=0.6.\end{array}$$

On the other hand,

$$\left\{{\omega }_1\cdot x_1+{\omega }_2\cdot x_2+{\omega }_3\cdot x_3<2\right\}\supset \left\{x_1=0,x_2=1,x_3\le 1\right\},$$

we have

$$\begin{array}{l}RM=1-\text{ℳ}\left\{{\omega }_1\cdot x_1+{\omega }_2\cdot x_2+{\omega }_3\cdot x_3\le 2\right\}\le 1-\text{ℳ}\left\{x_1=0,x_2=1,x_3\le 1\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=1-\left\{1-\text{ℳ}\left\{x_1\ge 1\right\}\right\}\wedge \left\{1-\text{ℳ}\left\{x_2\ge 1\right\}\right\}\wedge \left\{1-\text{ℳ}\left\{x_3\ge 2\right\}\right\}=0.6.\end{array}$$

Based on the conclusions drawn from the above two aspects, then $RM=0.6$.

Theorem 3. 

In the UBW-k/n system, the weights ${\omega }_i(i=1,2,\dots ,n)$ and states $x_i(i=1,2,\dots ,n)$ of the components are independent uncertain variables, so the reliability measure of UBW-k/n system is

$$RM\hspace{0.33em}=\underset{w_1{j}_1+w_2{j}_2+\dots +w_n{j}_n\ge k}{\sup }\underset{1\le i\le n}{\min }\min \left\{\text{ℳ}\{{\omega }_i\ge w_i\},\text{ℳ}\{x_i\ge j_i\}\right\}.$$

Proof of Theorem 3. 

Assuming a multivariate function

$$f(w_1,w_2,\dots ,w_n,j_1,j_2,\dots ,j_n)={\displaystyle \sum _{i=1}^n{w}_i{j}_i},$$

then the reliability measure of the UBW-k/n system is

$$RM=\text{ℳ}\left\{f({\omega }_1,{\omega }_2,\dots ,{\omega }_n,x_1,x_2,\dots ,x_n)\ge k\right\}.$$

According to Theorem 1, we have

$$\begin{array}{l}RM=\underset{f(w_1,w_2,\dots ,w_n,j_1,j_2,\dots ,j_n)\ge k}{\sup }\underset{1\le i\le n}{\min }\min \left\{\text{ℳ}\{{\omega }_i\ge w_i\},\text{ℳ}\{x_i\ge j_i\}\right\}\\ =\underset{w_1{j}_1+w_2{j}_2+\dots +w_n{j}_n\ge k}{\sup }\underset{1\le i\le n}{\min }\min \left\{\text{ℳ}\{{\omega }_i\ge w_i\},\text{ℳ}\{x_i\ge j_i\}\right\}.\end{array}$$

□

Theorem 4. 

In the UBW-k/n system, the weights ${\omega }_i$ and states $x_i(i=1,2,\dots ,n)$ of the components are independent uncertain variables, the reliability measure of UBW-k/n system is

$$RM=\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}}\right.(1-\nu )1_i(\nu )\ge k\right\},$$

where ${\varphi }_i$ is the uncertainty distribution function of ${\omega }_i$, and $1_i(\nu )=\left\{\begin{array}{l}0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\nu \le {\nu }_i\\ 1,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\nu >v_i\end{array}\right.$ is a real number step function, $i=1,2,\dots ,n$.

Proof of Theorem 4. 

Define

$${\nu }_0=\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}}\right.(1-\nu )1_i(\nu )\ge k\right\}.$$

First, for any ${\nu }_l<{\nu }_0$, and the reliability ${\nu }_1,{\nu }_2,\dots ,{\nu }_n$ of the components are all greater than ${\nu }_l$, then

$${\displaystyle \sum _{i=0}^n{\varphi }_i^{-1}}(1-{\nu }_l)1_i({\nu }_l)\ge k.$$

Because

$$\begin{array}{l}\left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}\ge k\right\}\supset \left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}\ge {\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}(1-{\nu }_l)}{1}_i({\nu }_l)\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \supset \underset{i=1}{\overset{n}{\cap }}\left\{{\omega }_i>{\varphi }_i^{-1}(1-{\nu }_l)\cap \left(x_i\ge 1_i({\nu }_l)\right)\right\}\end{array},$$

based on independence and monotonicity of uncertain variables, there are

$$\begin{array}{l}M\left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}\ge k\right\}\ge M\left\{\underset{i=1}{\overset{n}{\cap }}\left\{({\omega }_i>{\varphi }_i^{-1}(1-{\nu }_l))\cap \left(x_i\ge 1_i({\nu }_l)\right)\right\}\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\underset{1\le i\le n}{\min }\min \left\{M\left\{{\omega }_i>{\varphi }_i^{-1}(1-{\nu }_l)\right\},M\left\{x_i\ge 1_i({\nu }_l)\right\}\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\min \left\{{\nu }_l,1\right\}={\nu }_l\end{array}.$$

The inequality above holds for any ${\nu }_l<{\nu }_0$, so

$$M\left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}\ge k\right\}\ge \underset{{\nu }_l<{\nu }_0}{\sup }{\nu }_l\hspace{0.33em}=\hspace{0.33em}{\nu }_0.$$

In addition, for any ${\nu }_{\mathrm{u}}>{\nu }_0$ symmetrically, the reliability measures ${\nu }_1,{\nu }_2,\dots ,{\nu }_n$ of the components are all less than ${\nu }_u$, then

$${\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}}(1-{\nu }_u)1_i({\nu }_u)<k,$$

thus

$$\begin{array}{l}\left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}<k\right\}\supset \left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}\le {\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}(1-{\nu }_u)}{1}_i({\nu }_u)\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} \supset \underset{i=1}{\overset{n}{\cap }}\left\{({\omega }_i\le {\varphi }_i^{-1}(1-{\nu }_u))\cap \left(x_i\le 1_i({\nu }_u)\right)\right\}.\end{array}$$

Based on uncertain independence and monotonicity of uncertain variables, there are

$$\begin{array}{l}M\left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}<k\right\}\ge M\left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}\le {\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}(1-{\nu }_u)}{1}_i({\nu }_u)\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\underset{1\le i\le n}{\min }\min \left\{M\left\{{\omega }_i\le {\varphi }_i^{-1}(1-{\nu }_u)\right\},M\left\{x_i\le 1_i({\nu }_u)\right\}\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\min \left\{1-{\nu }_u,\underset{1\le i\le n}{\min }\left\{1-M\left\{x_i\ge 1_i({\nu }_u)\right\}\right\}\right\}=1-{\nu }_u\end{array},$$

Thus

$$M\left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}\ge k\right\}\le {\nu }_u.$$

The inequality above holds for any ${\nu }_0<{\nu }_u$, then

$$M\left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}\ge k\right\}\le \underset{{\alpha }_0<{\alpha }_u}{\inf }{\nu }_u=\hspace{0.33em}{v}_0,$$

so

$$M\left\{{\displaystyle \sum _{i=1}^n{\omega }_i{x}_i}\ge k\right\}\hspace{0.33em}=\hspace{0.33em}{\nu }_0.$$

Theorem 4 is proven. □

According to Theorem 4, a traverse search algorithm was designed to calculate the reliability measure of the UBW-k/n system, with the following steps.

Example 2. 

If the UBW-k/n system contains 10 components, i.e., $n=10$, the weights ${\omega }_i$ and states $x_i(i=1,2,\dots ,n)$ of the $ith$ component are independent uncertain variables, the state and reliability measures of each component are shown in Table 3, and the weights are shown in Table 4. Calculate the following equations according to Algorithm 1 using MATLAB R2018b.

$${\displaystyle \sum _{i=0}^n{\varphi }_i^{-1}}(1-\alpha )1_i(\alpha ){|}_{\alpha =0.9}=8.3<24,{\displaystyle \sum _{i=0}^n{\varphi }_i^{-1}}(1-\alpha )1_i(\alpha ){|}_{\alpha =0.8}=15.4<24,$$

$${\displaystyle \sum _{i=0}^n{\varphi }_i^{-1}}(1-\alpha )1_i(\alpha ){|}_{\alpha =0.7}=21.64<24,{\displaystyle \sum _{i=0}^n{\varphi }_i^{-1}}(1-\alpha )1_i(\alpha ){|}_{\alpha =0.6}=24.72\ge 24.$$

Then the reliability measure of the system ( $k=24$) is

$$RM=0.6$$

Algorithm 1. Traverse search algorithm for calculating the system reliability measurement $RM$

Step 1 Set solution accuracy $\epsilon$.

Step 2 Let $\nu =1$, if ${\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}}(1-\nu )1_i(\nu )\ge k$, then $RM=1$ and exit the program.

Step 3 Let $\nu =\nu -\hspace{0.33em}\epsilon$

Step 4 If ${\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}}(1-\nu )1_i(\nu )<k$, then return to Step 3, else $RM=\nu$ and exit the program.

Table 3. States and reliability of components.

	Component	1	2	3	4	5	6	7	8	9	10
States
0		0.5	0.4	0.3	0.5	0.1	0.1	0.2	0.1	0.3	0.2
1		0.5	0.6	0.7	0.5	0.9	0.9	0.8	0.9	0.7	0.8

Table 3. States and reliability of components.

	Component	1	2	3	4	5	6	7	8	9	10
States
0		0.5	0.4	0.3	0.5	0.1	0.1	0.2	0.1	0.3	0.2
1		0.5	0.6	0.7	0.5	0.9	0.9	0.8	0.9	0.7	0.8

Table 4. Weights of components.

Component	1	2	3	4	5	6	7	8	9	10
Weights	$\mathcal{L}(1,2.2)$	$\mathcal{L}(2,2.5)$	$\mathcal{L}(2,2.8)$	$\mathcal{L}(2,3)$	$\mathcal{L}(2,3.4)$	$\mathcal{L}(3,3.6)$	$\mathcal{L}(3,4)$	$\mathcal{L}(3,4)$	$\mathcal{L}(3,4)$	$\mathcal{L}(3,4.6)$

Table 4. Weights of components.

Component	1	2	3	4	5	6	7	8	9	10
Weights	$\mathcal{L}(1,2.2)$	$\mathcal{L}(2,2.5)$	$\mathcal{L}(2,2.8)$	$\mathcal{L}(2,3)$	$\mathcal{L}(2,3.4)$	$\mathcal{L}(3,3.6)$	$\mathcal{L}(3,4)$	$\mathcal{L}(3,4)$	$\mathcal{L}(3,4)$	$\mathcal{L}(3,4.6)$

The computational complexity of Algorithm 1 increases significantly. In order to further improve the computational speed, another binary search algorithm was designed to calculate the reliability measure of the UBW-k/n system. The steps are as follows:

Example 3. 

Considering the system shown in Example 2, and according to Algorithm 2, the reliability measure of the system is calculated using MATLAB R2018b programming

$$RM=0.5977.$$

Algorithm 2. Binary search algorithm for calculating the system reliability measurement $RM$

Step 1 Set solution accuracy $\epsilon$.

Step 2 Let ${\nu }_1=1$, if ${\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}}(1-{\nu }_1)1_i({\nu }_1)\ge k$, then $RM=1$ and exit the program.

Step 3 Let ${\nu }_2=0$, if ${\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}}(1-{\nu }_2)1_i({\nu }_2)<k$, then $RM=0$ and exit the program.

Step 4 If ${\displaystyle \sum _{i=1}^n{\varphi }_i^{-1}}(1-{\displaystyle \frac{{\nu }_1+{\nu }_2}{2}})1_i({\displaystyle \frac{{\nu }_1+{\nu }_2}{2}})>k$, then ${\nu }_2={\displaystyle \frac{{\nu }_1+{\nu }_2}{2}}$, else if ${\nu }_1={\displaystyle \frac{{\nu }_1+{\nu }_2}{2}}$.

Step 5 If $\left|{\nu }_1-{\nu }_2\right|>\epsilon$, then return to Step 4 to continue, else if $RM={\displaystyle \frac{{\nu }_1+{\nu }_2}{2}}$ and exit the program.

The computational complexity of Algorithm 1 is $\left(1/\epsilon \right)\cdot O\left(n\right)$, which requires $\left(1/\epsilon \right)\cdot O\left(n\right)$ multiplications to complete. Therefore, for doubling of computational accuracy, the computational complexity also doubles. The computational complexity of Algorithm 2 is $\left(-\log \epsilon \right)\cdot O\left(n\right)$, which requires $\left(-\log \epsilon \right)\cdot O\left(n\right)$ multiplications to complete. When the computational accuracy is the same, the computational complexity is much lower than that of Algorithm 1.

Table 5. Time consumption comparison of two algorithms at different accuracies.

	Accuracy $\mathit{\epsilon }$	10−2	10−3	10−5
Algorithm
Algorithm 1		0.014 s	0.108 s	9.824 s
Algorithm 2		0.005 s	0.005 s	0.006 s

shows a comparison of the computation time between the two algorithms in Example 3. As the computational accuracy increases, the computational complexity of Algorithm 1 is much more sensitive than that of Algorithm 2.

4. Two-Stage UBW-k/n System

Structurally, a two-stage system of UBW-k/n is composed of $m$ subsystems that follow a certain structure. This structure is called a one-stage structure and is characterized by structural functions $\varphi (x)$. Each subsystem is a UBW-k/n system, which is called a two-stage structure. The working state of component $j$ in the subsystem $i$ is denoted as $x_{ij}$. At that time $x_{ij}=1$, the component $j$ was working normally, symmetrically at that time $x_{ij}=0$, component $j$ failed. If a two-stage system with UBW-k/n is working properly, then

$$\varphi (y_1,y_2,\dots ,y_m)=1,$$

where $y_i$ represents the working states of $i\mathrm{th}$ subsystem and

$$y_i=\left\{\begin{array}{l}1,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\displaystyle \sum _{j=1}^n{\omega }_{ij}\cdot x_{ij}>k_i}\\ 0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\displaystyle \sum _{j=1}^n{\omega }_{ij}\cdot x_{ij}<k_i}\end{array}\right.,i=1,2,\dots ,m.$$

A typical two-stage UBW-k/n system includes a series UBW-k/n system and a parallel UBW-k/n system. The structural function of the series system of UBW-k/n is

$$\varphi (y_1,y_2,\dots ,y_m)=y_1\wedge y_2\wedge \dots \wedge y_m,$$

and the structural function of the parallel system of UBW-k/n is

$$\varphi (y_1,y_2,\dots ,y_m)=y_1\vee y_2\vee \dots \vee y_m.$$

The second stage of the two-stage UBW-k/n system consists of $m$ subsystems, each of which is a system of UBW-k/n with $n$ components. $k_i$ is the weight threshold of the system of UBW-k/n, and $m$ UBW-k/n subsystems form a threshold vector $K={\left[k_1,k_i,\dots ,k_m\right]}^T$. Therefore

$$\begin{array}{l}Subsystem 1:{\omega }_{11}{x}_1+{\omega }_{12}{x}_2+\dots +{\omega }_{1n}{x}_n\ge k_1\\ Subsystem 2:{\omega }_{21}{x}_1+{\omega }_{22}{x}_2+\dots +{\omega }_{2n}{x}_n\ge k_2\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}⋮\\ Subsystem m:{\omega }_{m1}{x}_1+{\omega }_{m2}{x}_2+\dots +{\omega }_{mn}{x}_n\ge k_m\end{array}$$

where ${\omega }_{ij}$ is the weight of the $j\mathrm{th}$ component of the $i\mathrm{th}$ subsystem.

For a two-stage series system with UBW-k/n, all $m$ systems with UBW-k/ns in the second layer must work, meaning that all $m$ equations above must hold for the system to function properly; for a two-stage parallel system with UBW-k/n, at least one of the $m$ systems with UBW-k/ns in the second layer is working, that is, at least one of the $m$ equations above holds, and the system is working normally. When $m=1$, the two-stage system with UBW-k/n degenerates into a UBW-k/n system.

Definition 2. 

Assuming that the first-stage structural function of the two-stage UBW-k/n system is $\varphi (y_1,y_2,\dots ,y_m)$, there are $m$ UBW-k/n subsystems $y_1,y_2,\dots ,y_m$ in the second stage, and the $ith$ UBW-k/n subsystem works $y_i=1$, otherwise $y_i=0$. Then the system’s reliability measure is

$$RM=\text{ℳ}\left\{\varphi (y_1,y_2,\dots ,y_m)=1\right\}.$$

Theorem 5. 

Assuming that the two-stage UBW-k/n system has $m$ subsystems $y_1,y_2,\dots ,y_m$ and structural functions $\varphi (y_1,y_2,\dots ,y_m)$, and the subsystems $y_1,y_2,\dots ,y_m$ are independent of each other with reliability measures of ${\nu }_1,{\nu }_2,\dots ,{\nu }_m$, respectively, then the system’s reliability measure is

$$RM=\left\{\begin{array}{l}\underset{\varphi (y_1,y_2,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\underset{\varphi (y_1,y_2,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)<0.5\\ 1-\underset{\varphi (y_1,y_2,\dots ,y_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i),\hspace{0.33em}\hspace{0.33em}if\underset{\varphi (y_1,y_2,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)>0.5\end{array}\right.,$$

where $y_i$ is taken as 0 or 1, and the $ith$ subsystem reliability measure is

$${\nu }_i(y_i)=\left\{\begin{array}{l}\hspace{0.33em}\hspace{0.33em}{\nu }_i,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{y}_i=1\\ 1-{\nu }_i,\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{y}_i=0\end{array}\right.\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}i=1,2\dots m.$$

Proof of Theorem 5. 

According to the Definition 2 of reliability measurement for two-stage UBW-k/n systems, then

$$RM=\text{ℳ}\left\{\varphi (y_1,y_2,\dots ,y_m)=1\right\}.$$

According to Theorem 2,

$$RM=\left\{\begin{array}{l}\underset{\varphi (y_1,y_2,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\underset{\varphi (y_1,y_2,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)<0.5\\ 1-\underset{\varphi (y_1,y_2,\dots ,y_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i),\hspace{0.33em}\hspace{0.33em}if\underset{\varphi (y_1,y_2,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)>0.5\end{array}\right..$$

□

Example 4. 

F products, as precision-assembled products in the high-end consumer electronics field, are currently in a rapidly growing and fiercely competitive market environment. This category has a high global annual growth rate, but the product lifecycle is short, and market competition is showing a white-hot trend. In this context, time is the core competitiveness. If a new product launch is delayed, it will directly lose market share during the initial launch window and lead to a decline in profit margins.

This product feature places extremely high demands on supply chain management and production collaboration. As a complex product composed of multiple precision modules, the production of F products involves a global supply chain network and multi-node manufacturing processes, and any delay in any link will have a chain reaction. To ensure the timely delivery of products, it is necessary to establish a refined time coordination mechanism and implement strict control over key nodes in the supply chain and production process. Meanwhile, in response to uncertain factors such as fluctuations in raw material supply and equipment failures, it is necessary to establish a risk assessment system to reduce potential delivery risks.

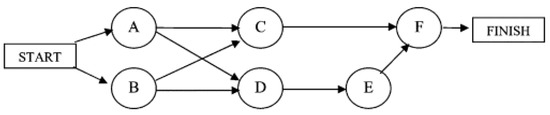
Figure 1 shows the project management process of product F. Product F is assembled from products C and D. The entire production process consists of the following six nodes, as shown in Figure 1. The uncertainty measure for each node’s normal operation is $v$, as shown in

Table 6. Product assembly activity table.

Node	Precursor	The Reliability of Nodes ($\mathit{v}$)	Duration (Days)	Delay (Days)
A (Training workers)	None	0.99	6	${\omega }_1~L\left(1,2\right)$
B (Purchase raw materials)	None	0.99	9	${\omega }_2~L\left(3,4\right)$
C (Product 1)	A, B	0.99	16	${\omega }_3~L\left(3,4\right)$
D (Product 2)	A, B	0.96	7	${\omega }_4~L\left(2,3\right)$
E (Test Product 2)	D	0.98	10	${\omega }_5~L\left(2,3\right)$
F (Assemble products 1 and 2)	C, E	0.95	12	${\omega }_6~L\left(4,5\right)$

. Use $x_i,i=1,2,\dots ,6$ to represent the delay state of node A, B, …, F, with a delay of $x_i=1$ and no delay of $x_i=0$.

From the network diagram, the entire project has four paths.

(1)

START—A—C—F—FINISH (No delay required for 34 days),

(2)

START—B—C—F—FINISH (No delay required for 37 days),

(3)

START—A—D—E—F—FINISH (No delay required for 35 days),

(4)

START—B—D—E—F—FINISH (No delay required for 38 days).

From this, it can be inferred that completing the assembly of the entire product F without delay takes at least 38 days. If the longest assembly period for the product F is 40 days, the longest delays for each path are 7, 4, 6, and 3, respectively, then

$$\begin{array}{l}\mathrm{S}ubsystem\hspace{0.33em}{y}_1:\hspace{0.33em}{\omega }_1\cdot x_1+0\cdot x_2+{\omega }_3\cdot x_3+0\cdot x_4+0\cdot x_5+{\omega }_6\cdot x_6\ge 7\\ \mathrm{S}ubsystem\hspace{0.33em}{y}_2:\hspace{0.33em}0\cdot x_1+{\omega }_2\cdot x_2+{\omega }_3\cdot x_3+0\cdot x_4+0\cdot x_5+{\omega }_6\cdot x_6\ge 4\\ \mathrm{S}ubsystem\hspace{0.33em}{y}_3:\hspace{0.33em}{\omega }_1\cdot x_1+0\cdot x_2+0\cdot x_3+{\omega }_4\cdot x_4+{\omega }_5\cdot x_5+{\omega }_6\cdot x_6\ge 6\\ \mathrm{S}ubsystem\hspace{0.33em}{y}_4:\hspace{0.33em}0\cdot x_1+{\omega }_2\cdot x_2+0\cdot x_3+{\omega }_4\cdot x_4+{\omega }_5\cdot x_5+{\omega }_6\cdot x_6\ge 3\end{array}$$

As long as one of the above inequalities is satisfied, the assembly of product F cannot be completed on time, and the system fails. Therefore, this is a series UBW-k/n system, where the first-layer structure function $\varphi (y_1,y_2,y_3,y_4)=y_1\wedge y_2\wedge y_3\wedge y_4$, $y_i(i=1,\dots 4)$ represents the working state of the $i\mathrm{th}$ subsystem. The second layer consists of four UBW-k/n subsystems with weights of 7, 4, 6, and 3, respectively. Using Algorithm 2, the reliability measures are calculated for each subsystem

$${\nu }_1=0.9497, {\nu }_2=0.9604,\hspace{0.33em}{\nu }_3=0.9497, {\nu }_4=0.9897.$$

According to Theorem 5, the reliability measure of the system is calculated as

$$\underset{\varphi (y_1,y_2,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)={\nu }_1\wedge {\nu }_2\wedge {\nu }_3\wedge {\nu }_4=0.9497>0.5,$$

so

$$\begin{array}{l}RM=\text{ℳ}\left\{\varphi (y_1,y_2,y_3,y_4)=1\right\}=1-\underset{\varphi (y_1,y_2,\dots ,y_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=1-(1-{\nu }_1)\vee (1-{\nu }_2)\vee (1-{\nu }_3)\vee (1-{\nu }_4)=0.9497.\end{array}$$

5. Importance Measurement of Two-Stage UBW-k/n System

The importance measure describes the impact of a component’s operation on the overall reliability of the system. The larger the importance measure, the more important the component is. Importance analysis helps identify the weakest links in the system, providing a basis for resource allocation, maintenance strategy formulation, and system optimization. In the process of system reliability design, it is important to avoid the occurrence of components with excessive importance measurement. In the context of limited maintenance costs, the importance measurement of each component in the system should be balanced as much as possible.

Introduced by Gao and Yao [28] in 2016, uncertain reliability systems have attracted the attention of many scholars. For uncertain two-stage UBW-k/n systems, the importance measurement is also divided into two stages. The first stage is the importance measurement of the UBW-k/n system, which refers to the impact of UBW-k/n subsystem operation on system reliability; the second stage is the measurement of component importance, which is to quantify the contribution of component operation to system reliability.

Definition 3. 

If there are $m$ UBW-k/n subsystems in a two-stage UBW-k/n system, $y_i(i=1,2,\dots ,m)$ representing the working state of $ith$ UBW-k/n subsystems, then the importance measure of $ith$ UBW-k/n subsystems is

$$I{\text{ℳ}}_i=\text{ℳ}\left\{\varphi (y_1,\dots ,y_{i-1},1,y_{i+1},\dots ,y_m)=1\right\}-\text{ℳ}\left\{\varphi (y_1,\dots ,y_{i-1},0,y_{i+1},\dots ,y_m)=1\right\}.$$

Definition 4. 

Assuming a two-stage UBW-k/n system has $m$ UBW-k/n subsystems, $y_i(i=1,2,\dots ,m)$ represents the working state of the $i\mathrm{th}$ UBW-k/n subsystem, where each UBW-k/n subsystem has $n$ components and their states are represented as $x_{i,1},x_{i,2},\dots ,x_{i,n},i=1,2,\dots ,m$. Therefore, the importance measure of $s_{i,j}$ is

$$I{\text{ℳ}}_{i,j}=\text{ℳ}\left\{f(x_{i,1},\dots ,x_{i,j-1},1,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}-\text{ℳ}\left\{f(x_{i,1},\dots ,x_{i,j-1},0,x_{i,j+1},\dots ,x_{i,n})\ge k\right\},$$

denoting $s_{i,j}$ as the $jth$ component of the $ith$ UBW-k/n subsystem, and $f(\cdot )$ is the state weight function.

Definition 5. 

Assuming that the first-stage structural function of a two-stage UBW-k/n system is $\varphi (y_1,y_2,\dots ,y_m)$, there are $m$ UBW-k/n subsystems $y_1,y_2,\dots ,y_m$ in the second stage, and the $i\mathrm{th}$ subsystem works $y_i=1$, otherwise $y_i=0$, then the importance measure of $s_{i,j}$ to the two-stage UBW-k/n system is

$$I{\text{ℳ}}_i^j=\text{ℳ}\left\{\varphi (y_1,y_2,\dots ,y_i,\dots ,y_m)=1\right\}-\text{ℳ}\left\{\varphi (y_1,y_2,\dots ,{y^{\prime }}_i,\dots ,y_m)=1\right\},$$

where $y_i^{\prime }$ is the subsystem state where the $jth$ component of $ith$ UBW-k/n subsystem fails.

Theorem 6. 

If the uncertain variables $x_{i,1},{\omega }_{i,1},x_{i,2},{\omega }_{i,2},\dots ,x_{i,n},{\omega }_{i,n}$ are the states and weights of the various components of the $ith$ UBW-k/n subsystem and are independent of each other, then the importance measure of $s_{i,j}$ is

$$\begin{array}{l}I{\text{ℳ}}_{i,j}\hspace{0.33em}\hspace{0.33em}=\underset{w_1{j}_1+w_2{j}_2+\dots +w_n{j}_n\ge k}{\sup }\underset{\begin{array}{l}1\le q\le n\\ \hspace{0.33em}q\ne j\end{array}}{\min }\min \{\text{ℳ}\{{\omega }_{i,q}\ge w_q\},\text{ℳ}\{{\omega }_{i,j}\ge w_j\},\text{ℳ}\{x_{i,q}\ge j_q\},\text{ℳ}\{{\omega }_{i,j}\ge 1\}\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}-\underset{w_1{j}_1+w_2{j}_2+\dots +w_n{j}_n\ge k}{\sup }\underset{\begin{array}{l}1\le q\le n\\ \hspace{0.33em}q\ne j\end{array}}{\min }\min \{\text{ℳ}\{{\omega }_{i,q}\ge w_q\},\text{ℳ}\{x_{i,q}\ge j_q\}\}\end{array},$$

where $w_q$ is a nonnegative real number, and $j_q$ takes as 0 or 1.

Proof of Theorem 6. 

According to the Definition 3 and Theorem 1, then

$$\begin{array}{l}I{\text{ℳ}}_{i,j}=\text{ℳ}\left\{f(x_{i,1},\dots ,x_{i,j-1},1,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}-\text{ℳ}\left\{f(x_{i,1},\dots ,x_{i,j-1},0,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\underset{w_1{j}_1+w_2{j}_2+\dots +w_n{j}_n\ge k}{\sup }\underset{\begin{array}{l}1\le q\le n\\ \hspace{0.33em}q\ne j\end{array}}{\min }\min \{\text{ℳ}\{{\omega }_{i,q}\ge w_q\},\text{ℳ}\{{\omega }_{i,j}\ge w_j\},\text{ℳ}\{x_{i,q}\ge j_q\},\text{ℳ}\{{\omega }_{i,j}\ge 1\}\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}-\underset{w_1{j}_1+w_2{j}_2+\dots +w_n{j}_n\ge k}{\sup }\underset{\begin{array}{l}1\le q\le n\\ \hspace{0.33em}q\ne j\end{array}}{\min }\min \{\text{ℳ}\{{\omega }_{i,q}\ge w_q\},\text{ℳ}\{x_{i,q}\ge j_q\}\}\end{array}.$$

□

Theorem 7. 

If the uncertain variables $x_{i,1},{\omega }_{i,1},x_{i,2},{\omega }_{i,2},\dots ,x_{i,n},{\omega }_{i,n},$ are the states and weights of the various components of the ith UBW-k/n subsystem, which are independent of each other, and the inverse distributions of the uncertain weights ${\omega }_{i,1},{\omega }_{i,2},\dots ,{\omega }_{i,n}$ are ${\varphi }_{i,1}^{-1},{\varphi }_{i,2}^{-1},\dots ,{\varphi }_{i,n}^{-1}$, then the importance measure of $s_{i,j}$ to the two-stage UBW-k/n system is

$$\begin{array}{l}I{\text{ℳ}}_{i,j}=\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{q\ne j}{\varphi }_{i,q}^{-1}(1-\nu )}{1}_{i,q}(\nu )+{\varphi }_{i,j}^{-1}(1-\nu )\ge k\right.\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}-\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{q\ne j}{\varphi }_{i,q}^{-1}(1-\nu )}{1}_{i,q}(\nu )\ge k\right.\right\}\end{array},$$

where $1_{i,j}(\nu )=\left\{\begin{array}{l}0,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\nu \le {\nu }_{i,j}\\ 1,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\nu >{\nu }_{i,j}\end{array}\right.$ is real step function, and ${\nu }_{i,j}$ is the reliability measure of the $jth$ component for the $ith$ subsystem.

Proof of Theorem 7. 

According to Theorem 3, the reliability measure of $s_{i,j}$ operating normally is

$$\begin{array}{l}RM=\hspace{0.33em}\text{ℳ}\left\{f(x_{i,1},\dots ,x_{i,j-1},1,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}\hspace{0.33em}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\text{ℳ}\left\{{\displaystyle \sum _{q=1}^n{w}_{i,q}{x}_{i,q}}\ge k,x_{i,j}=1\right\}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{q\ne j}{\varphi }_{i,q}^{-1}(1-\nu )}{1}_{i,q}(\nu )+{\varphi }_{i,j}^{-1}(1-\nu )\ge k\right.\right\}\end{array}.$$

The reliability measure of the $s_{i,j}$ failure is

$$\begin{array}{l}R=\hspace{0.33em}\text{ℳ}\left\{f(x_{i,1},\dots ,x_{i,j-1},0,x_{i,j+1},\dots ,x_{i,n})\ge k\right\}\hspace{0.33em}\\ \hspace{0.33em}\hspace{0.33em}=\text{ℳ}\left\{{\displaystyle \sum _{q=1}^n{w}_{i,q}{x}_{i,q}}\ge k,x_{i,j}=0\right\}\\ \hspace{0.33em}\hspace{0.33em}=\sup \left\{\nu \in [0,1]\left|{\displaystyle \sum _{q\ne j}{\varphi }_{i,q}^{-1}(1-\nu )}{1}_{i,q}(\nu )\ge k\right.\right\}\end{array}.$$

According to Definition 4 of importance measure, Theorem 7 holds and is proven. □

According to the above Theorem 7, the importance measurement algorithm for the UBW-k/n system is as follows.

Example 5. 

Considering the system in Example 2, according to Algorithm 3, the subsystem importance measure of component 4 is calculated as follows

$$I{\text{ℳ}}_4=0.6914-0.5977=0.0937.$$

Algorithm 3. Binary search algorithm for calculating the importance measure of UBW-k/n system

Step 1 Set solution accuracy $\epsilon$.

Step 2 Let ${\nu }_{11}=1$, if ${\displaystyle \sum _{q\ne j}{\varphi }_q^{-i}(1-{\nu }_{11})}{1}_q({\nu }_{11})+{\varphi }_j^{-i}(1-{\nu }_{11})\ge k$, then ${\nu }_1=1$ and go to Step 6.

Step 3 Let ${\nu }_{12}=0$, if ${\displaystyle \sum _{q\ne j}{\varphi }_q^{-i}(1-{\nu }_{12})}{1}_q({\nu }_{12})+{\varphi }_j^{-i}(1-{\nu }_{12})\le k$, then ${\nu }_1=0$ and go to Step 6.

Step 4 If ${\displaystyle \sum _{q\ne j}{\varphi }_q^{-i}(1-\frac{{\nu }_{11}+{\nu }_{12}}{2})}{1}_q({\displaystyle \frac{{\nu }_{11}+{\nu }_{12}}{2}})+{\varphi }_j^{-i}(1-{\displaystyle \frac{{\nu }_{11}+{\nu }_{12}}{2}})\ge k$, then ${\nu }_{12}={\displaystyle \frac{{\nu }_{11}+{\nu }_{12}}{2}}$, else ${\nu }_{11}={\displaystyle \frac{{\nu }_{11}+{\nu }_{12}}{2}}$.

Step 5 If $\left|{\nu }_{11}-{\nu }_{12}\right|>\epsilon$, then return to Step 4 to continue, else ${\nu }_1={\displaystyle \frac{{\nu }_{11}+{\nu }_{12}}{2}}$ and go to Step 6.

Step 6 Let ${\nu }_{21}=1$, if ${\displaystyle \sum _{q\ne j}{\varphi }_q^{-i}(1-{\nu }_{21})}{1}_q({\nu }_{21})\ge k$, then ${\nu }_2=1$ and go to Step 10.

Step 7 Let ${\nu }_{22}=0$, if ${\displaystyle \sum _{q\ne j}{\varphi }_q^{-i}(1-{\nu }_{22})}{1}_q({\nu }_{22})\le k$, then ${\nu }_2=0$ and go to Step 10.

Step 8 If ${\displaystyle \sum _{q\ne j}{\varphi }_q^{-i}(1-\frac{{\nu }_{21}+{\nu }_{22}}{2})1_q(\frac{{\nu }_{21}+{\nu }_{22}}{2})\ge k}$, then ${\nu }_{22}={\displaystyle \frac{{\nu }_{21}+{\nu }_{22}}{2}}$, else ${\nu }_{21}={\displaystyle \frac{{\nu }_{21}+{\nu }_{22}}{2}}$.

Step 9 If $\left|{\nu }_{21}-{\nu }_{22}\right|>\epsilon$, then return to Step 8 to continue, else ${\nu }_2={\displaystyle \frac{{\nu }_{21}+{\nu }_{22}}{2}}$ and go to Step 10.

Step 10 The importance measure of the $j\mathrm{th}$ component of the subsystem is $I\text{ℳ}={\nu }_1-{\nu }_2$.

Example 6. 

Considering the system in Example 4, the system reliability measure for the operation of component 3 of UBW-k/n subsystem 1 is calculated according to Algorithm 2

$$RM=\text{ℳ}\left\{{\omega }_1\cdot x_1+0\cdot x_2+{\omega }_3\cdot 1+0\cdot x_4+0\cdot x_5+{\omega }_6\cdot x_6\ge 7\right\}=0.9502.$$

According to Algorithm 2, the system reliability measure for the failure of component 3 in UBW-k/n subsystem 1 is calculated as follows

$$RM=\text{ℳ}\left\{{\omega }_1\cdot x_1+0\cdot x_2+{\omega }_3\cdot 0+0\cdot x_4+0\cdot x_5+{\omega }_6\cdot x_6\ge 7\right\}=0.$$

According to Definition 4, the subsystem importance measure of component 3 in UBW-k/n subsystem 1 is calculated as

$$I{\text{ℳ}}_{1,3}\hspace{0.33em}=0.9502-0=0.9502.$$

The importance measure of the third component of UBW-k/n subsystem 1 relative to the overall system, as defined in Definition 5, is

$$I{\text{ℳ}}_1^3=\text{ℳ}\left\{\varphi (y_1,y_2,y_3,y_4)=1\right\}-\text{ℳ}\left\{\varphi ({y^{\prime }}_1,y_2,y_3,y_4)=1\right\}=0.9497-0=0.9497.$$

Theorem 8. 

The two-stage UBW-k/n system consists of $m$ UBW-k/n subsystems, with structural function $\varphi (y_1,y_2,\dots ,y_m)$ and states of the subsystem $y_1,y_2,\dots ,y_m$ are independent of each other. The reliability measures of the $m$ UBW-k/n subsystems are ${\nu }_1,{\nu }_2,\dots ,{\nu }_m$, then the importance measure of the $jth$ component for the $ith$ subsystem relative to the overall system is

$$I{\text{ℳ}}_i^j=\left\{\begin{array}{l}\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)-\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)<0.5,\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)<0.5.\\ 1-\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)-\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i),\hspace{0.33em}\hspace{0.33em}if\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)\ge 0.5,\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)<0.5.\\ \underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)+\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)-1,\hspace{0.33em}\hspace{0.33em}if\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)<0.5,\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)\ge 0.5.\\ \underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)-\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}if\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)\ge 0.5,\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)\ge 0.5.\end{array}\right.$$

where $y_i$ takes 0 or 1, and the reliability measurement of subsystem

$${\nu }_i(y_i)=\left\{\begin{array}{l}\hspace{0.33em}\hspace{0.33em}{\nu }_i,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{y}_i=1\\ 1-{\nu }_i,\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{y}_i=0\end{array}\right.,{\nu }_i(y_i^{\prime })=\left\{\begin{array}{l}\hspace{0.33em}\hspace{0.33em}{\nu }_i^{\prime },\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{y^{\prime }}_i=1\\ 1-{\nu }_i^{\prime },\hspace{0.33em}\hspace{0.33em}if\hspace{0.33em}{y^{\prime }}_i=0\end{array}\right.,\hspace{0.33em}i=1,2\dots m.$$

${{\nu }^{\prime }}_i$ is the reliability measure for the complete failure of the $jth$ component for the $ith$ subsystem, $y_i^{\prime }$ is the subsystem’s operational state.

Proof of Theorem 8. 

According to the Definition 5,

$$I{\text{ℳ}}_i^j=\text{ℳ}\left\{\varphi (y_1,y_2,\dots ,y_i,\dots ,y_m)=1\right\}-\text{ℳ}\left\{\varphi (y_1,y_2,\dots ,{y^{\prime }}_i,\dots ,y_m)=1\right\}$$

(1)

According to Theorem 2,

$$\text{ℳ}\left\{\varphi (y_1,y_2,\dots ,y_i,\dots ,y_m)=1\right\}=\left\{\begin{array}{l}\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i),\hspace{0.33em}\hspace{0.33em}if\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)<0.5\\ 1-\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i),\hspace{0.33em}if\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)\ge 0.5\end{array}\right.,$$

(2)

$$\text{ℳ}\left\{\varphi (y_1,y_2,\dots ,{y^{\prime }}_i,\dots ,y_m)=1\right\}=\left\{\begin{array}{l}\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i),\hspace{0.33em}\hspace{0.33em}if\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)<0.5\\ 1-\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i),\hspace{0.33em} if\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)\ge 0.5\end{array}\right..$$

(3)

Substitute (2) and (3) into Equation (1) to prove Theorem 8. □

Example 7. 

Considering the system in Example 6, the importance measure of the third component for the first subsystem relative to the overall system is obtained from Theorem 8,

$$\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)=\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)={\nu }_1\wedge {\nu }_2\wedge {\nu }_3\wedge {\nu }_4=0.9497\ge 0.5,$$

$$\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)=\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)={{\nu }^{\prime }}_1\wedge {\nu }_2\wedge {\nu }_3\wedge {\nu }_4=0<0.5,$$

so

$$\begin{array}{l}\hspace{0.33em}I{\text{ℳ}}_1^3=1-\underset{\varphi (y_1,\dots ,y_i,\dots ,y_m)=0}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)-\underset{\varphi (y_1,\dots ,{y^{\prime }}_i,\dots ,y_m)=1}{\sup }\underset{1\le i\le \mathrm{m}}{\min }{\nu }_i(y_i)\\ =1-(1-{\nu }_1)\vee (1-{\nu }_2)\vee (1-{\nu }_3)\vee (1-{\nu }_4)-0=0.9497.\end{array}$$

6. Conclusions and Future Research

Reliability evaluation of complex systems represents a significant practical challenge. This paper proposes a mathematical model for two-stage UBW-k/n systems within the framework of uncertainty theory. The model decomposes system reliability evaluation into two distinct stages: system structural reliability, which characterizes the overall reliability of interconnected subsystems, and subsystem reliability, representing local system reliability. The study formally defines a reliability measure for assessing two-stage UBW-k/n systems under uncertainty conditions, accompanied by a corresponding solution method. To address computational complexity challenges, we propose an efficient binary search algorithm for numerical computation of system reliability measures under uncertainty.

In addition, this paper also explores the importance measure of two-stage UBW-k/n systems and provides corresponding definitions, calculation formulas for using distributions, and inverse distribution. Finally, the effectiveness of the model is verified through specific examples. The research results show that the model can effectively evaluate the reliability and importance measures of two-stage UBW-k/n systems in uncertain environments. However, this article still has certain limitations as it does not cover situations such as multiple states, continuous states, and multiple stages. To improve the practical scope of the model, further research can be conducted on the models in these situations.