BHE+ALBERT-Mixplus: A Distributed Symmetric Approximate Homomorphic Encryption Model for Secure Short-Text Sentiment Classification in Teaching Evaluations
Abstract
1. Introduction
- We propose a BHE distributed symmetric approximate homomorphic encryption algorithm. To address the challenge of homomorphic encryption for non-polynomial functions in the BERT model, the BHE algorithm provides a distributed, approximate workflow. By using a “computation simplification” method to approximate non-polynomial functions such as GELU, Softmax, and LayerNorm within the hybrid model, this approach enables the fusion model to support inference under a fully homomorphic encryption (FHE) environment.
- We develop a BHE-compatible ALBERT-Mixplus (a mixing plus enhancements variant of ALBERT) text sentiment classification fusion model. When data are encrypted under the CKKS homomorphic encryption scheme, ALBERT-Mixplus can still effectively extract deep semantic features of sentiment. Experimental results demonstrate that with only a modest increase in training overhead, ALBERT-Mixplus outperforms mainstream classification models on multiple performance metrics.
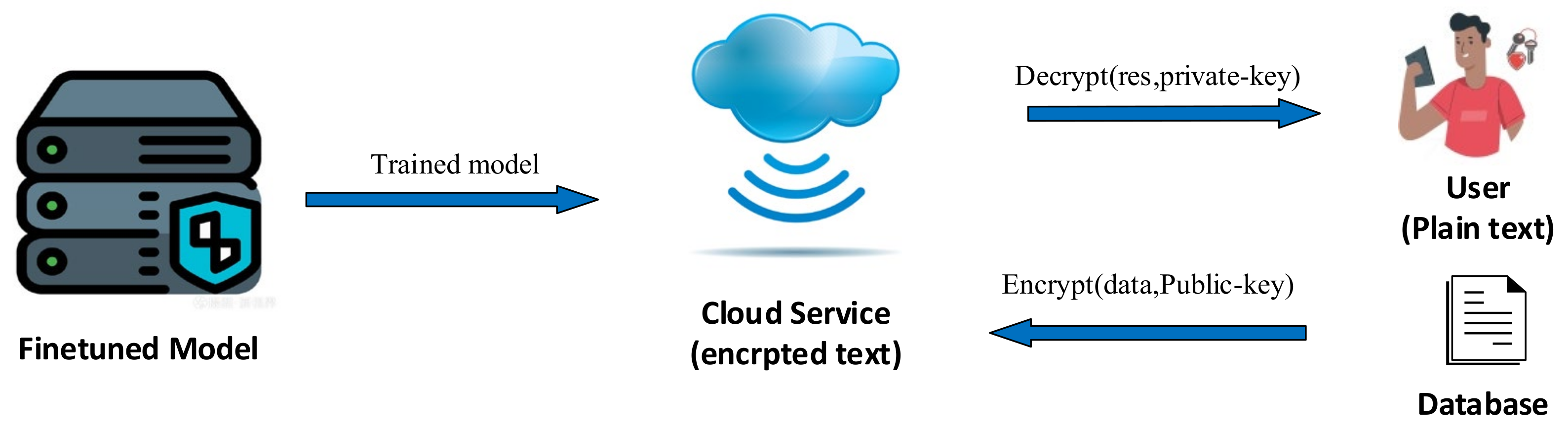
- We design a cloud–user distributed symmetric deployment paradigm to overcome homomorphic encryption limitations. Content that cannot be computed under CKKS encryption on the cloud is returned to the user side for local processing. As shown in Figure 1, this workflow architecture offers a practical solution for AI + business distributed application scenarios in higher education, leveraging local data storage, cloud-based computation, and secure, efficient communication.
2. Related Works
2.1. Current Research Status on Sentiment Classification of Teaching Evaluation Short Texts
2.2. HE in Privacy-Preserving Sentiment Analysis
3. BHE+ALBERT-Mixplus
3.1. Preliminaries
3.1.1. Fully Homorphic Encryption (FHE)Algorithm
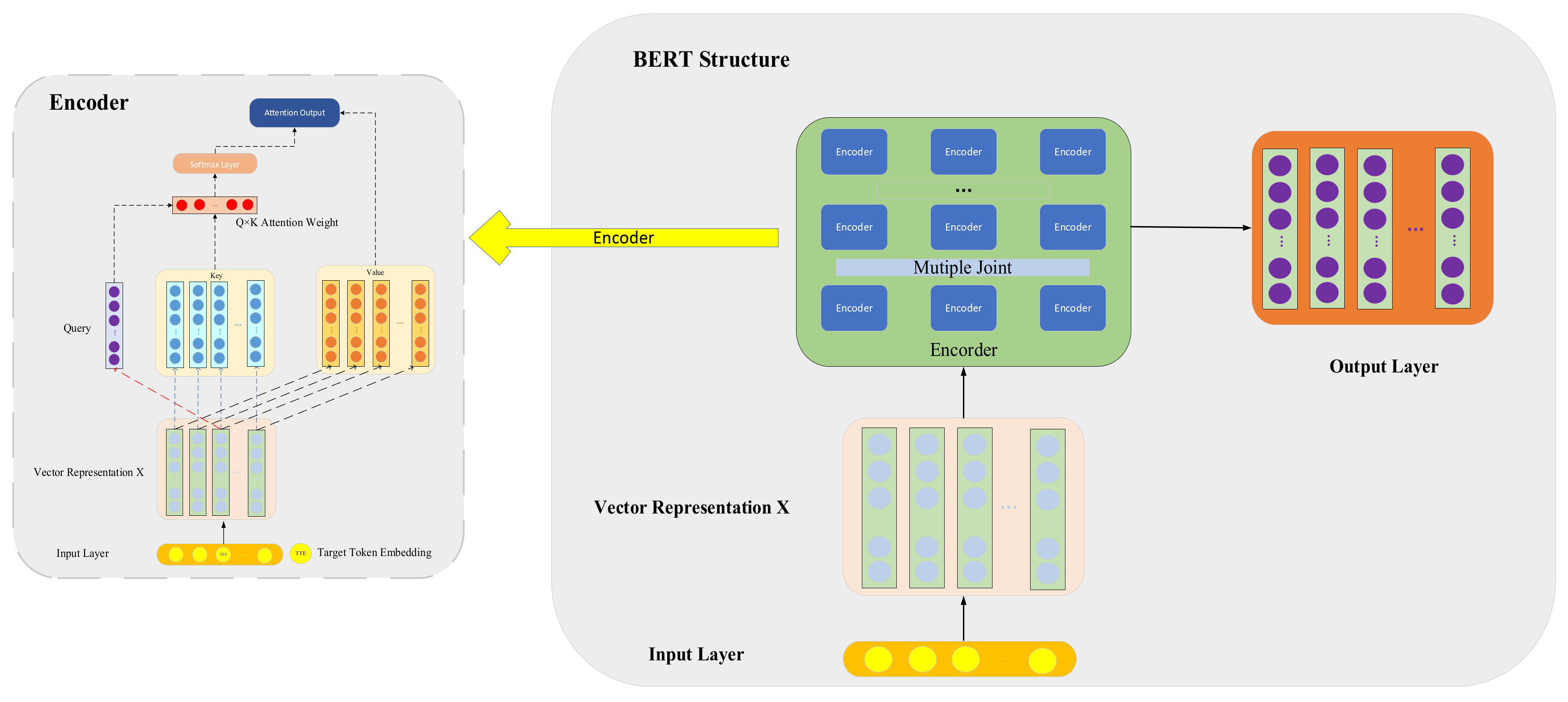
3.1.2. Pre-Trained BERT Model
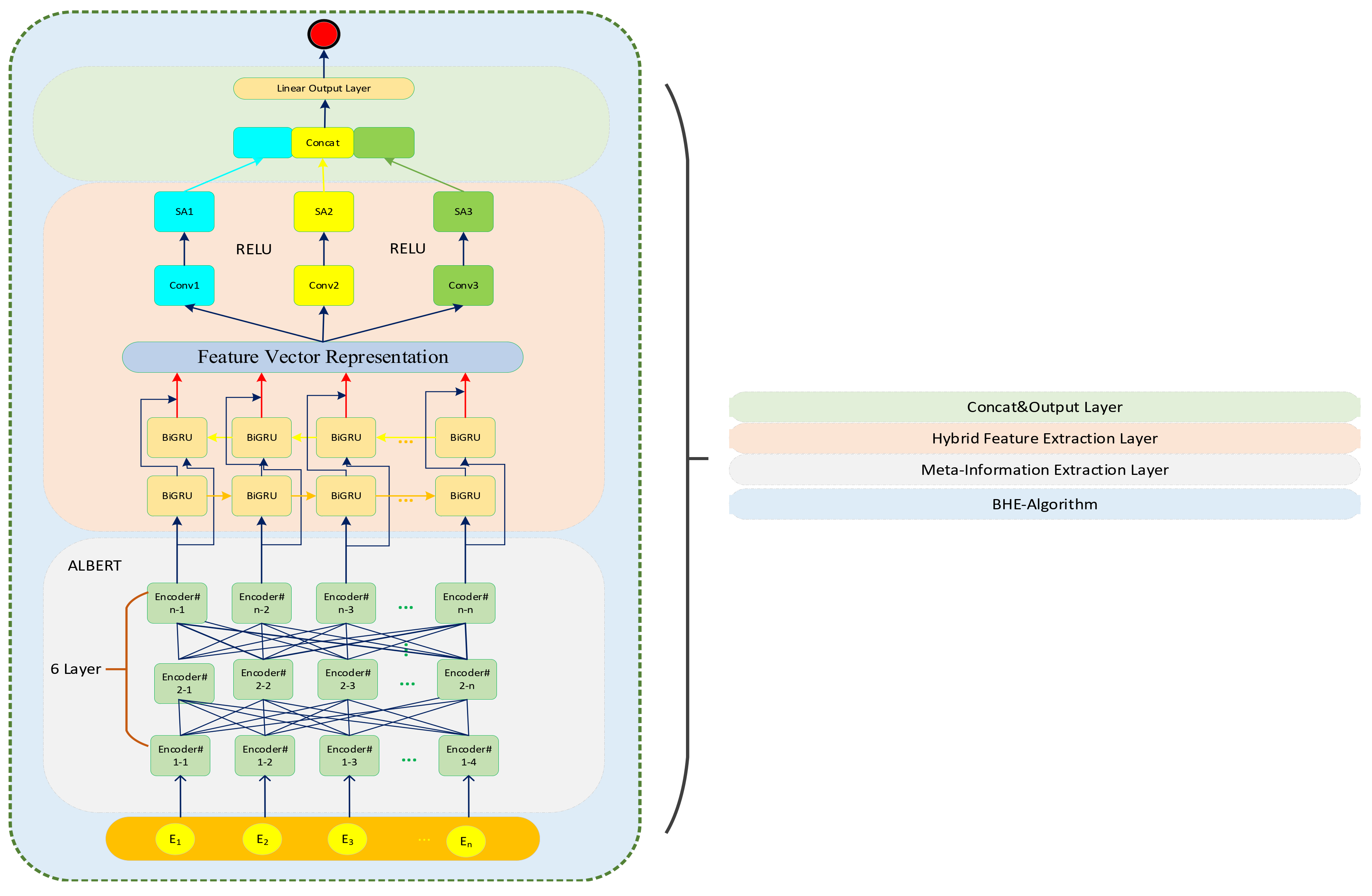
3.2. Overview of BHE+ALBERT-Mixplus
3.3. Meta-Information Extraction Layer
- The query, key, and value matrices are mapped through different linear transformations.
- The Appo-Softmax classifier, approximated using the BHE algorithm, computes the different attention representations according to Equation (2).
- Concatenating the different attention feature representations , can be denoted as . In this model, we set the depth of self-attention to 8.
- The concatenated matrix is multiplied by a weight matrix , resulting in the final representation , which incorporates information from all self-attention heads. This representation is then fed into the position-wise feed-forward network (FFN).
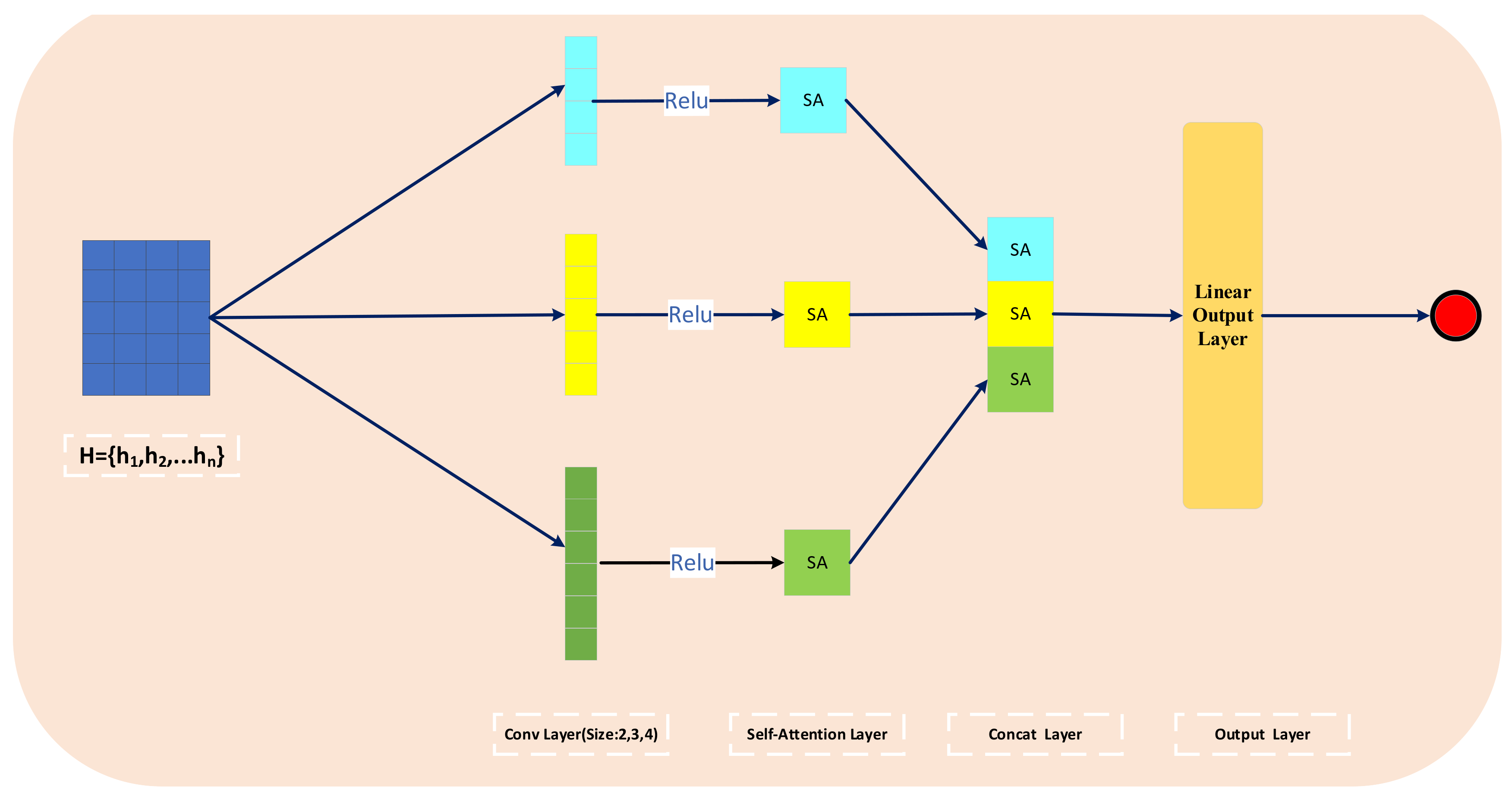
3.4. Hybrid Feature Extraction Layer
3.5. BHE Approximate Homomorphic Encryption Algorithm
- Integration of User Devices for FHE Predictions: Traditional FHE-based encryption algorithms typically rely entirely on cloud servers. The BHE algorithm incorporates user-side devices to address the issue of non-polynomial operations in FHE encryption within the model. This approach helps improve inference efficiency and enhances the privacy protection capabilities of sentiment classification models.
- Simplification of Computation for Approximating Non-Polynomial Functions: The BHE algorithm employs a “simplified computation” concept to approximate non-polynomial functions in the ALBERT model, such as GELU, Softmax, and LayerNorm. Since these functions cannot be directly computed under homomorphic encryption, BHE uses approximation techniques to enable homomorphic encryption support.
- Establishment of a Staged Approximation Workflow: The BHE algorithm divides the approximation workflow for the ALBERT model into two phases: initially replacing GELU and Softmax functions, followed by incorporating LayerNorm approximation after standard fine-tuning. This staged approach ultimately transforms the model into one that fully supports homomorphic encryption operations.
3.5.1. Symmetrical Approximation Workflow
| Algorithm 1: BHE Symmetrical Approximation Workflow |
| Data: labeled course-appraisal data . Input: Pre-trained ALBERT-Mixplus model , Appro-Softmax model . 1. .//Replace Tanh GELU and Softmax 2. While not done do 3. Sample batches(xi,yi)from . 4. let(xi,yi)optimise with . End 5. //add Appro-LN 6. While not done do Sample batches(xi,yi)from . Freeze the parameters of except . . ). Update with loss . End .//drop the origin layernorm (LN) Return |
3.5.2. Gaussion Error Linear Units (GELU)
| Algorithm 2: ReLU HE Workflow |
| 1. Split ReLU Computation //U represent user device. 2. . 3. //use private-key to Decrypt data from user side. 4. // represent the plain-txet outcome of the Max operation. 5. //C represent cloud device. |
3.5.3. Softmax
3.5.4. LayerNorm
- Approximation of Mean and Variance: To compute the mean and variance, BHE utilizes an estimation method based on addition and multiplication.
- Piecewise Polynomial Fitting: BHE approximates the LN operation using a set of precomputed piecewise polynomials. These polynomials are derived through fitting and optimization on extensive training data, providing high approximation accuracy across different input ranges.
- Iterative Optimization: By training on a large number of samples, the model learns the optimal polynomial parameters, achieving high-precision approximation of LN.
3.5.5. The Workflow of BHE-Based Text Sentiment Classification Task
| Algorithm 3: BHE-based Text Sentiment Classification Workflow |
| Input: Plain-text Query , Private-key , , encrypted BHE-based model . 1. Client construct word-embedding . 2. Client encrypts: . 3. Cloud proceeds the BHE-based model: . 4. Client disposes activation fuction: . 5. Cloud gets the result and continues: . 6. Client decrypts classification results: |
4. Experiments
4.1. Experimental Data and Performance Metrics
4.2. Experimental Environment and Parameter Settings
4.3. Analysis of Experimental Results
- (A)
- CNN [7]: Utilizing convolutional kernels and pooling to extract textual features, CNNs are an early classic model for text sentiment classification.
- (B)
- BiLSTM [8]: BiLSTM can process both forward and backward word vectors simultaneously and concatenate the final hidden states as global features, effectively capturing contextual semantic dependencies.
- (C)
- Transformer [9]: Composed of multiple encoders and decoders, the transformer model is based on a self-attention mechanism. It can process sequence data in parallel, significantly enhancing training speed and efficiency.
- (D)
- BERT [10]: A pre-trained language model based on the transformer architecture, which retains only the Encoder component of the transformer, can understand text context bidirectionally. By pre-training on a large-scale corpus and then fine-tuning on specific tasks, it significantly improves the accuracy of tasks such as question answering, text classification, and named entity recognition.
- (E)
- BERT-GRU-ATT [15]: A hybrid model that combines BERT, GRU, and attention provides context-aware word representations and captures bidirectional textual information. The GRU processes sequential data to capture temporal dependencies, while attention dynamically focuses on important parts of the sequence, thereby enhancing the model’s ability to capture key information.
- (F)
- BG-TCA (bidirectional gated temporal convolutional attention) [16]: BG-TCA consists of three models: BERT, GRU, and TCA. It introduces a temporal contextual attention (TCA) mechanism, which enhances the model’s accuracy in handling sentences with complex semantic relationships. This approach is commonly used in various downstream tasks in natural language processing.
- (G)
- EK-INIT-CNN (Embedding Knowledge Initialization Convolutional Neural Network) [17]: EK-INIT-CNN is specifically designed for sentiment classification tasks involving Weibo (Chinese) text. This model combines embedding knowledge initialization with a CNN-based hybrid approach. At the start of model training, prior knowledge is used to initialize the model, thereby enhancing its learning capability and stability.
- (H)
- TextGCN (Text Graph Convolutional Network) [18]: TextGCN represents textual data as a graph, where documents or words are treated as nodes, and their relationships (such as co-occurrence or semantic similarity) are treated as edges. Graph convolution operations are used to learn node representations, thereby capturing the complex semantic and structural information in the text data.
- (I)
- Bert-GCN [19]: Building on TextGCN, the features of graph nodes are initialized using pre-trained BERT, and joint training is employed to obtain feature representations.
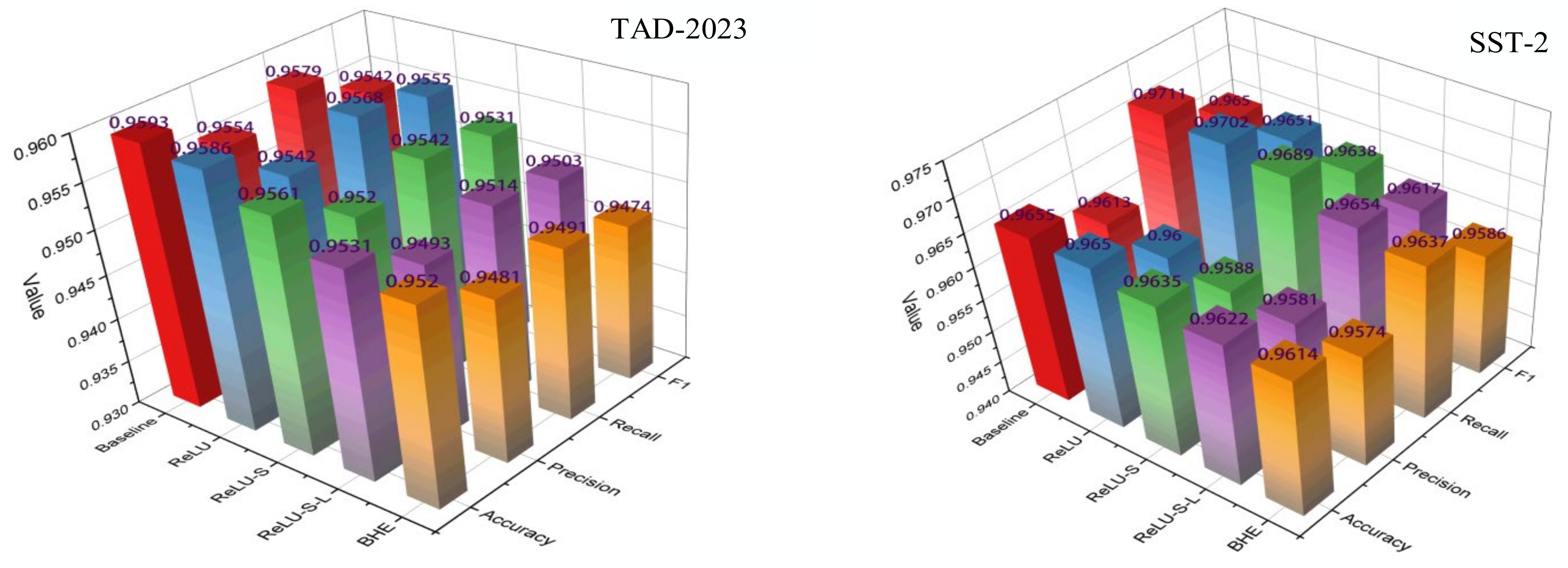
4.3.1. The Impact of the BHE on ALBERT-Mixplus Model
- (A)
- Baseline: The hybrid model is used without any replacements or approximations, and the original training dataset is employed for fine-tuning the pre-trained model.
- (B)
- ReLU: The GELU activation function in the hybrid model is replaced with ReLU.
- (C)
- ReLU-S: In addition to replacing GELU with ReLU, the Softmax function is substituted with the approximate Softmax model, referred to as Appro-Softmax.
- (D)
- ReLU-S-L: Building on the ReLU-S model, all approximations, including Appro-LN, are applied.
- (E)
- BHE: The approximate fine-tuned hybrid model is encrypted using the SEAL algorithm library and applied to the sentiment classification task.
4.3.2. The Impact of Each Component in the Hybrid Feature Extraction Layer on the ALBERT-Mixplus Model
- (A)
- Baseline: ALBERT-Mixplus: Only approximate homomorphic operations are performed, with no additional modifications made to the hybrid feature extraction layer.
- (B)
- w/o BiGRU: Removal of the BiGRU component from the hybrid feature extraction layer, while retaining the MCNN-MCO and MCNN-SA models.
- (C)
- w/o MCNN-SA: Removal of the MCNN-SA component from the hybrid feature extraction layer, while retaining the BiGRU and MCNN-MCO components.
- (D)
- w/o MCNN-MCO: Removal of the multi-scale convolution operations from the MCNN component in the hybrid feature extraction layer, while retaining the BiGRU and MCNN-SA components.
- (E)
- w/o BiGRU and MCNN-SA: Removal of both the BiGRU and MCNN-SA components from the hybrid feature extraction layer, while retaining the MCNN-MCO component, i.e., ALBERT + MCO.
- (F)
- w/o BiGRU and MCNN-MCO: Removal of both the BiGRU and MCNN-MCO components from the hybrid feature extraction layer, i.e., ALBERT + MCNN-SA.
- (G)
- w/o MCNN-MCO and MCNN-SA: Removal of both the MCNN-MCO and MCNN-SA components from the hybrid feature extraction layer, i.e., ALBERT + BiGRU.
- (H)
- ALBERT: Removal of the entire hybrid feature extraction layer, retaining only the ALBERT model.
4.3.3. The Impact of ALBERT on the Performance of the Hybrid Model in Standard Fine-Tuning
- (A)
- Baseline: This refers to the proposed BHE+ALBERT-Mixplus model. The meta-information extraction layer utilizes the ALBERT-Base version, with approximate homomorphic fine-tuning training conducted as described in Section 3.5.1.
- (B)
- BERT-Base: The meta-information extraction layer employs the BERT-Base model, while the hybrid feature extraction layer remains unchanged. The BERT-Base model has the same hidden layer and attention head configurations as the ALBERT-Base model but has approximately nine times the number of parameters.
- (C)
- BERT-Large: The meta-information extraction layer uses the BERT-Large model, with the hybrid feature extraction layer unchanged. The BERT-Large model includes 24 hidden layers and 16 attention heads, making it suitable for handling larger datasets and more complex tasks. It has approximately three times the number of parameters of the BERT-Base model.
- (D)
- ALBERT-Base: The meta-information extraction layer utilizes the ALBERT-Base model, with the hybrid feature extraction layer remaining unchanged. ALBERT-Base leverages cross-layer parameter sharing, which significantly reduces the total number of parameters while maintaining performance.
4.3.4. The Effect of Weight Decay
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, K.; Feng, Y.; Zhang, L.; Wang, R.; Wang, W.; Yuan, X.; Cui, X.; Li, X.; Li, H. An effective personality-based model for short text sentiment classification using BiLSTM and self-attention. Electronics 2023, 12, 3274. [Google Scholar] [CrossRef]
- Islam, M.S.; Kabir, M.N.; Ghani, N.A.; Zamli, K.Z.; Zulkifli, N.S.A.; Rahman, M.M. Challenges and future in deep learning for sentiment analysis: A comprehensive review and a proposed novel hybrid approach. Artif. Intell. Rev. 2024, 57, 62. [Google Scholar] [CrossRef]
- Sivakumar, S.; Rajalakshmi, R. Context-aware sentiment analysis with attention-enhanced features from bidirectional transformers. Soc. Netw. Anal. Min. 2022, 12, 104. [Google Scholar] [CrossRef]
- Xu, W.; Chen, J.; Ding, Z.; Wang, J. Text sentiment analysis and classification based on bidirectional gated recurrent units (grus) model. arXiv 2024, arXiv:2404.17123. [Google Scholar] [CrossRef]
- Esuli, A.; Sebastiani, F. Sentiwordnet: A publicly available lexical resource for opinion mining. In Proceedings of the Proceedings of the Fifth International Conference on Language Resources and Evaluation (LREC’06), Genoa, Italy, 22–28 May 2006; Volume 6, pp. 417–422. [Google Scholar]
- Pang, B.; Lee, L. Opinion mining and sentiment analysis. Found. Trends® Inf. Retr. 2008, 2, 1–135. [Google Scholar] [CrossRef]
- Kim, Y. Convolutional Neural Networks for Sentence Classification. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP 2014), Doha, Qatar, 25–29 October 2014; pp. 1746–1751. [Google Scholar]
- Xiao, Z.; Liang, P.J. Chinese sentiment analysis using bidirectional LSTM with word embedding. In Proceedings of the Cloud Computing and Security: Second International Conference, ICCCS 2016, Nanjing, China, 29–31 July 2016; Revised Selected Papers, Part II 2. pp. 601–610. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the North American Chapter of the Association for Computational Linguistics (NAACL): Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Liu, Z.; Lin, W.; Shi, Y.; Zhao, J. A robustly optimized BERT pre-training approach with post-training. In Proceedings of the 20th China National Conference on Chinese Computational Linguistics, Huhhot, China, 13–15 August 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 471–484. [Google Scholar]
- Lan, Z.; Chen, M.; Goodman, S.; Gimpel, K.; Sharma, P.; Soricut, R. Albert: A lite bert for self-supervised learning of language representations. arXiv 2019, arXiv:1909.11942. [Google Scholar]
- Zhao, J.; Zhang, Z.; Chen, K. A Unified Framework for Multimodal Sentiment Analysis Using BERT and DINOv2. arXiv 2025, arXiv:2503.07943. [Google Scholar]
- Ananthi, D.; Prakash, A. An Attention-Enhanced Bidirectional Long Short-Term Memory with Contextual Semantic Knowledge for Enhancing Sentiment Analysis. Int. J. Intell. Eng. Syst. 2025, 18, 947–962. [Google Scholar]
- Zhao, D.; Huang, D.; Meng, J.; Dong, Y.; Zhang, P. Chinese Entity Relations Classification Based on BERT-GRU-ATT. Comput. Sci. 2022, 49, 319–325. [Google Scholar]
- Guo, X.; Lai, H.; Yu, Z.; Gao, S.; Xiang, Y. Emotion classification of case-related microblog comments integrating emotional knowledge. Chin. J. Comput. 2021, 44, 564–578. [Google Scholar]
- Ren, J.; Wu, W.; Liu, G.; Chen, Z.; Wang, R. Bidirectional gated temporal convolution with attention for text classification. Neurocomputing 2021, 455, 265–273. [Google Scholar] [CrossRef]
- Yao, L.; Mao, C.; Luo, Y. Graph convolutional networks for text classification. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 7370–7377. [Google Scholar]
- Li, Y.; Zuo, X.; Zuo, W.; Liang, S.; Zhu, Y.; Zhu, Y. Causality extraction based on BERT-GCN. J. Jilin Univ. Sci. Ed. 2023, 61, 325–330. [Google Scholar]
- Subramaniyaswamy, V.; Jagadeeswari, V.; Indragandhi, V.; Jhaveri, R.H.; Vijayakumar, V.; Kotecha, K.; Ravi, L. Somewhat homomorphic encryption: Ring learning with error algorithm for faster encryption of IoT sensor signal-based edge devices. Secur. Commun. Netw. 2022, 2022, 2793998. [Google Scholar] [CrossRef]
- Serengil, S.; Ozpinar, A. Encrypted Vector Similarity Computations Using Partially Homomorphic Encryption: Applications and Performance Analysis. arXiv 2025, arXiv:2503.05850. [Google Scholar]
- Pan, Y.; Chao, Z.; He, W.; Jing, Y.; Hongjia, L.; Liming, W. FedSHE: Privacy preserving and efficient federated learning with adaptive segmented CKKS homomorphic encryption. Cybersecurity 2024, 7, 40. [Google Scholar] [CrossRef]
- Panzade, P.; Takabi, D.; Cai, Z. MedBlindTuner: Towards Privacy-Preserving Fine-Tuning on Biomedical Images with Transformers and Fully Homomorphic Encryption. In AI for Health Equity and Fairness: Leveraging AI to Address Social Determinants of Health; Springer Nature Switzerland: Cham, Switzerland, 2024; pp. 197–208. [Google Scholar]
- Hamza, R.; Hassan, A.; Ali, A.; Bashir, M.B.; Alqhtani, S.M.; Tawfeeg, T.M.; Yousif, A. Towards secure big data analysis via fully homomorphic encryption algorithms. Entropy 2022, 24, 519. [Google Scholar] [CrossRef]
- Jia, H.; Cai, D.; Yang, J.; Qian, W.; Wang, C.; Li, X.; Yang, S. Efficient and privacy-preserving image classification using homomorphic encryption and chunk-based convolutional neural network. J. Cloud Comput. 2023, 12, 175. [Google Scholar] [CrossRef]
- Rovida, L.; Leporati, A. Encrypted image classification with low memory footprint using fully homomorphic encryption. Int. J. Neural Syst. 2024. [Google Scholar] [CrossRef]
- Kim, M.; Song, Y.; Xia, Y.; Zhan, J. PrivFT: Private and Fast Text Classification with Homomorphic Encryption. arXiv 2021, arXiv:2101.12345. [Google Scholar]
- Zhang, T.; He, Z.; Lee, R.B. Privacy-preserving machine learning through data obfuscation. arXiv 2018, arXiv:1807.01860. [Google Scholar]
- Florencio, M.; Alencar, L.; Lima, B. An End-to-End Homomorphically Encrypted Neural Network. arXiv 2025, arXiv:2502.16176. [Google Scholar]
- Song, T.; Li, Y.; Meng, F.; Xie, P.; Xu, D. A novel deep learning model by Bigru with attention mechanism for tropical cyclone track prediction in the Northwest Pacific. J. Appl. Meteorol. Climatol. 2022, 61, 3–12. [Google Scholar] [CrossRef]
- Cui, Z.; Chen, W.; Chen, Y. Multi-scale convolutional neural networks for time series classification. arXiv 2016, arXiv:1603.06995. [Google Scholar]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic encryption for arithmetic of approximate numbers. In Proceedings of the Advances in Cryptology—ASIACRYPT 2017: 23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Part I 23. pp. 409–437. [Google Scholar]
- Lu, J.; Yao, J.; Zhang, J.; Zhu, X.; Xu, H.; Gao, W.; Xu, C.; Xiang, T.; Zhang, L. Soft: Softmax-free transformer with linear complexity. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Online, 6–14 December 2021; Volume 34, pp. 21297–21309. [Google Scholar]
- Liu, L.; Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Han, J. On the variance of the adaptive learning rate and beyond. arXiv 2019, arXiv:1908.03265. [Google Scholar]
- Ting, T.T.; Lim, E.T.S.; Lee, J.; Wong, J.S.; Tan, J.H.; Tam, R.C.M.; Chaw, J.K.; Aitizaz, A.; Teoh, C.K. Educational big data mining: Mediation of academic performance in crime among digital age young adults. Online J. Commun. Media Technol. 2024, 14, e202403. [Google Scholar] [CrossRef]






| Model Parameters | Values |
|---|---|
| Operating System | Ubuntu 20.04 |
| Graphics Card | NVIDIA RTX 2080 Super |
| GPU Memory | 12 GB |
| Deep Learning Framework | PyTorch 1.10.0 |
| Python Version | 3.9 |
| SEAL-Py | SEAL-Py 4.1 |
| Model Parameters | Values |
|---|---|
| ALBERT-Hidden Layer Dimension | 768 |
| Number of ALBERT-Hidden Layer | 12 |
| Number of ALBERT-Attention Head | 12 |
| Learning Rate | 2 × 10−5 |
| BiGRU-Hidden Layer Dimension | 256 |
| BiGRU-Layer | 2 |
| Convolutional Kernel Size | (2,3,4) |
| CNN-Feature Map | 128 |
| Self-Attention Dimension | 512 |
| Maximum Sequence Length | 128 |
| Batch_size | 32 |
| Epochs | 8 |
| Dropout | 0.5 |
| Optimizer | RAdam [34] |
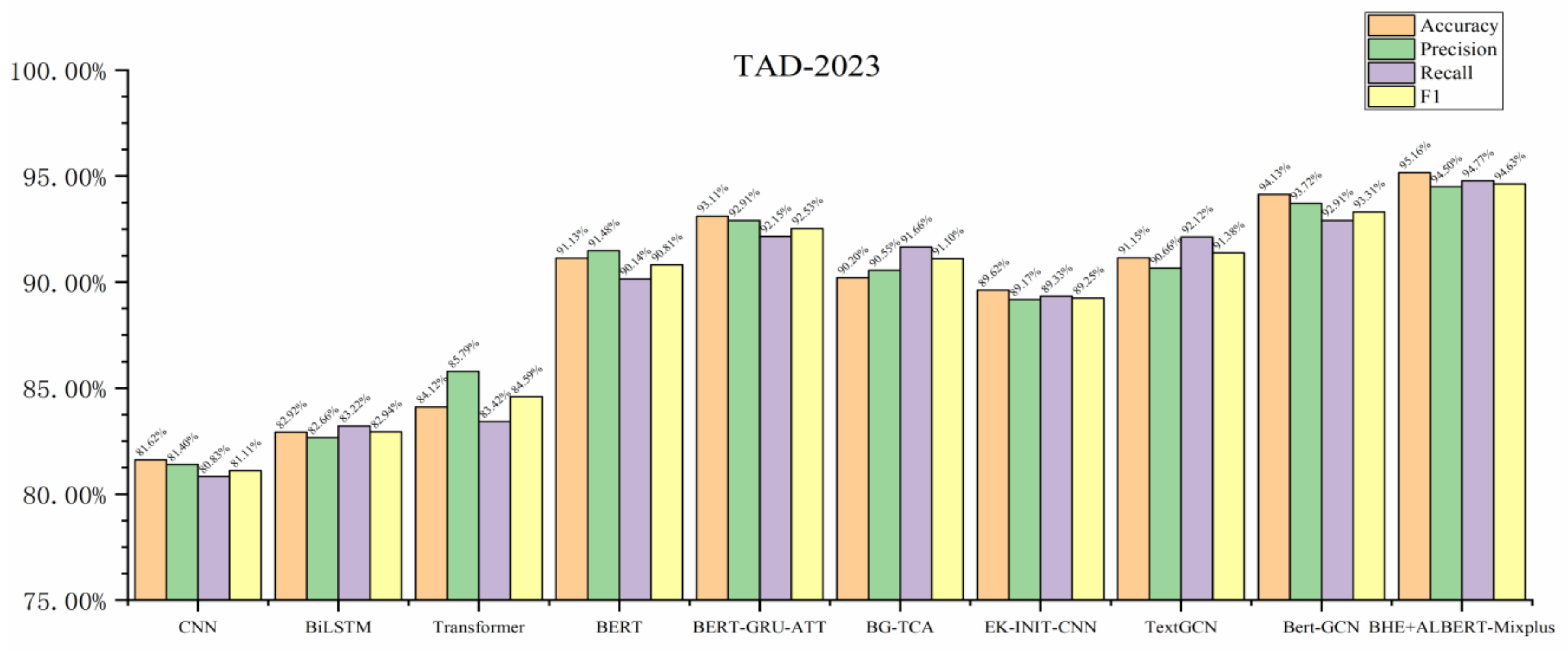
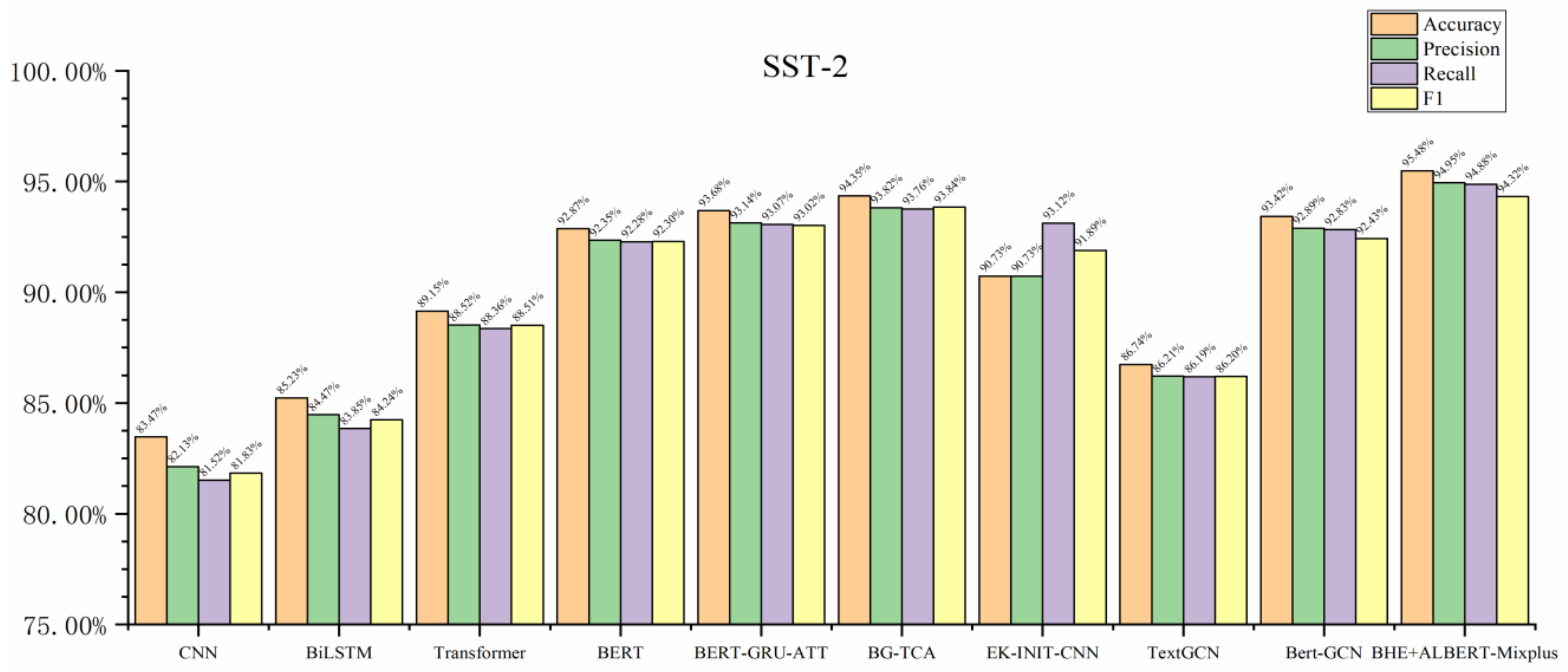
| Model | TAD-2023 | SST-2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1 | Accuracy | Precision | Recall | F1 | |
| CNN | 81.62% | 81.40% | 80.83% | 81.11% | 83.47% | 82.13% | 81.52% | 81.83% |
| BiLSTM | 82.92% | 82.66% | 83.22% | 82.94% | 85.23% | 84.47% | 83.85% | 84.24% |
| Transformer | 84.12% | 85.79% | 83.42% | 84.59% | 89.15% | 88.52% | 88.36% | 88.51% |
| BERT | 91.13% | 91.48% | 90.14% | 90.81% | 92.87% | 92.35% | 92.28% | 92.30% |
| BERT-GRU-ATT | 93.11% | 92.91% | 92.15% | 92.53% | 93.68% | 93.14% | 93.07% | 93.02% |
| BG-TCA | 90.20% | 90.55% | 91.66% | 91.10% | 94.35% | 93.82% | 93.76% | 93.84% |
| EK-INIT-CNN | 89.62% | 89.17% | 89.33% | 89.25% | 90.73% | 90.73% | 93.12% | 91.89% |
| TextGCN | 91.15% | 90.66% | 92.12% | 91.38% | 86.74% | 86.21% | 86.19% | 86.20% |
| Bert-GCN | 94.13% | 93.72% | 92.91% | 93.31% | 93.42% | 92.89% | 92.83% | 92.43% |
| BHE+ALBERT-Mixplus | 95.16% | 94.50% | 94.77% | 94.63% | 95.48% | 94.95% | 94.88% | 94.32% |
| Model | TAD-2023 | SST-2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | F1 | Accuracy | Precision | Recall | F1 | |
| Baseline | 95.93% | 95.54% | 95.79% | 95.42% | 96.55% | 96.13% | 97.11% | 96.50% |
| ReLU | 95.86% | 95.42% | 95.68% | 95.55% | 96.46% | 96.00% | 97.02% | 96.51% |
| ReLU-S | 95.61% | 95.20% | 95.42% | 95.31% | 96.37% | 95.88% | 96.89% | 96.38% |
| ReLU-S-L | 95.31% | 94.93% | 95.14% | 95.03% | 96.22% | 95.81% | 96.54% | 96.17% |
| BHE | 95.20% | 94.81% | 94.91% | 94.74% | 96.14% | 95.74% | 96.37% | 95.86% |
| Perf↓ | 0.73% | 0.73% | 0.88% | 0.68% | 0.41% | 0.39% | 0.74% | 0.64% |
| Model Parameters | ALBERT-Base | BERT-Base | BERT-Large |
|---|---|---|---|
| Hidden Layer Dimension | 768 | 768 | 768 |
| Number of Hidden Layer | 12 | 12 | 24 |
| Number of Attention Head | 12 | 12 | 16 |
| Maximum Sequence Length | 128 | 128 | 128 |
| Total Parameters | 12 M | 108 M | 340 M |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Sarah Maidin, S.; Dewi, D.A. BHE+ALBERT-Mixplus: A Distributed Symmetric Approximate Homomorphic Encryption Model for Secure Short-Text Sentiment Classification in Teaching Evaluations. Symmetry 2025, 17, 903. https://doi.org/10.3390/sym17060903
Zhang J, Sarah Maidin S, Dewi DA. BHE+ALBERT-Mixplus: A Distributed Symmetric Approximate Homomorphic Encryption Model for Secure Short-Text Sentiment Classification in Teaching Evaluations. Symmetry. 2025; 17(6):903. https://doi.org/10.3390/sym17060903
Chicago/Turabian StyleZhang, Jingren, Siti Sarah Maidin, and Deshinta Arrova Dewi. 2025. "BHE+ALBERT-Mixplus: A Distributed Symmetric Approximate Homomorphic Encryption Model for Secure Short-Text Sentiment Classification in Teaching Evaluations" Symmetry 17, no. 6: 903. https://doi.org/10.3390/sym17060903
APA StyleZhang, J., Sarah Maidin, S., & Dewi, D. A. (2025). BHE+ALBERT-Mixplus: A Distributed Symmetric Approximate Homomorphic Encryption Model for Secure Short-Text Sentiment Classification in Teaching Evaluations. Symmetry, 17(6), 903. https://doi.org/10.3390/sym17060903






