New Bayesian Estimation Method Based on Symmetric Projection Space and Particle Flow Velocity
Abstract
1. Introduction
2. Bayesian Estimation Model
3. Bayesian Filter Estimator Design-Based Projection Flow Velocity
3.1. Solving the Prior Probability for State Updates
3.2. Using Particle Flow Velocity for Measurement Update
4. Illustrative Simulation Examples and Analysis
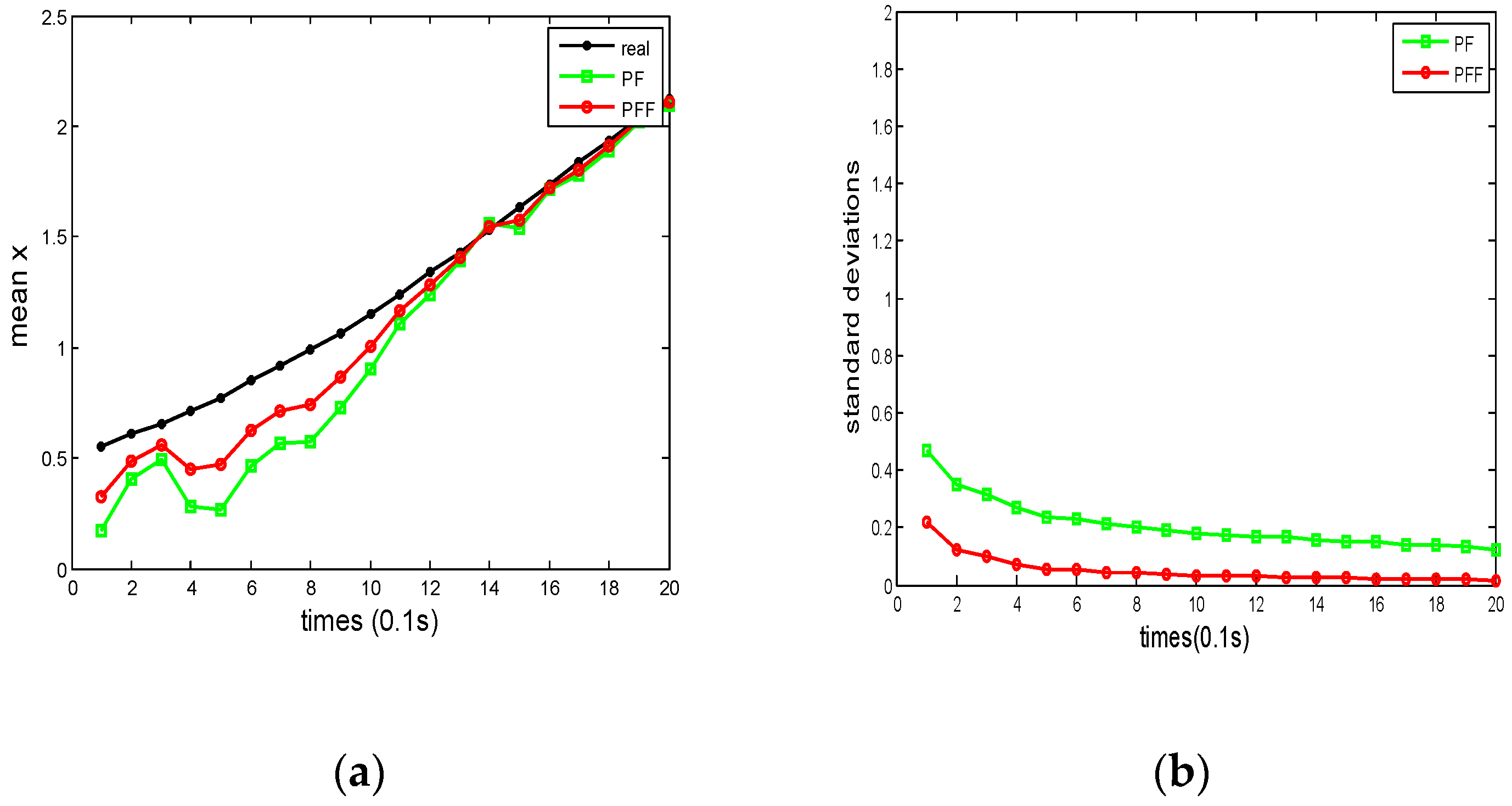
4.1. Example 1 and Analysis
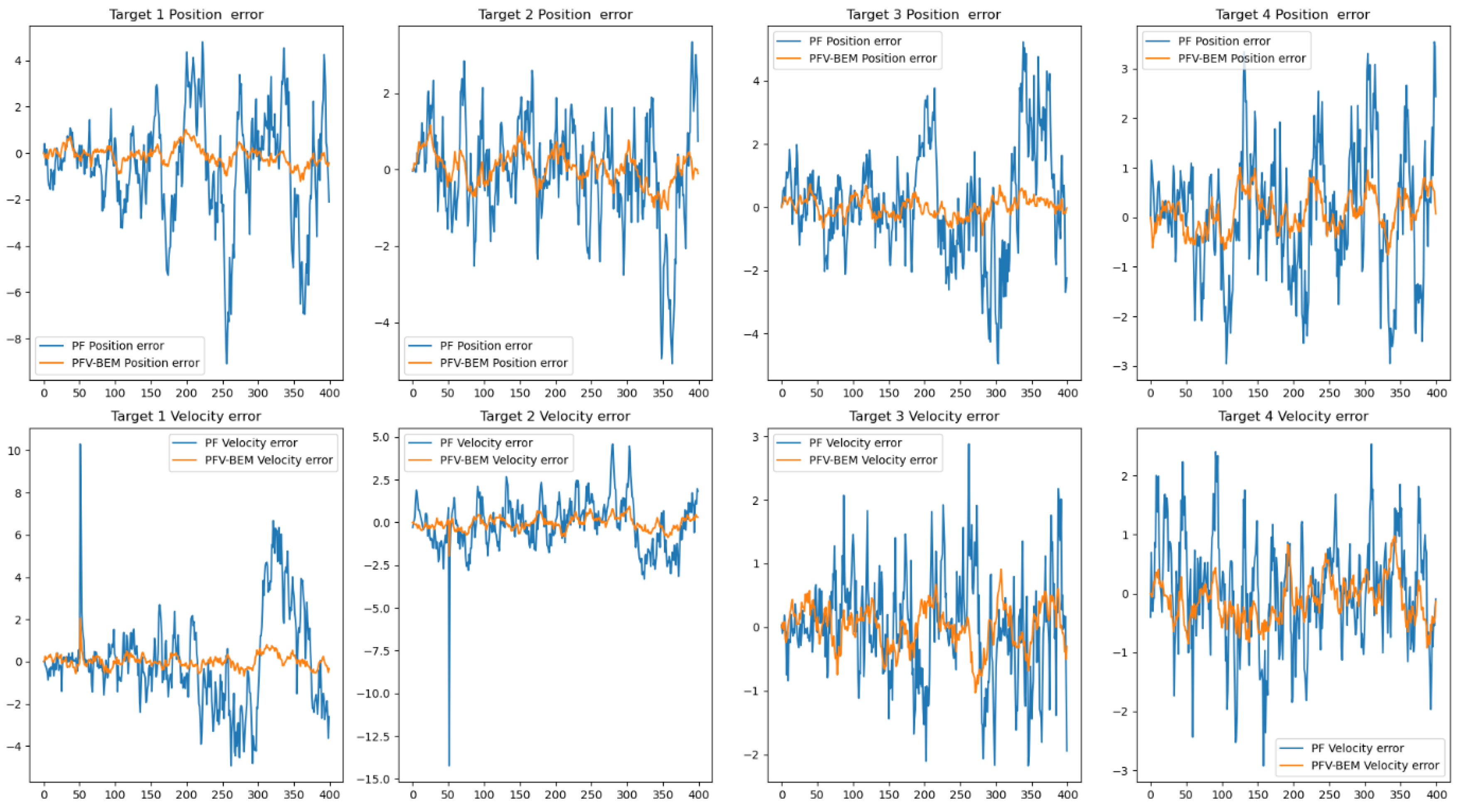
4.2. Example 2 and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shang, J.; Chen, T. Optimal stealthy integrity attacks on remote state estimation: The maximum utilization of historical data. Automatic 2021, 128, 109555. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, L.; Ma, Y. An FEM-based State Estimation Approach to Nonlinear Hybrid Positioning Systems. Math. Probl. Eng. 2013, 2013, 165–195. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. Trans. ASME J. Basic Eng. 1960, 82, 34–35. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Markley, F.L.; Cheng, Y. Survey of Nonlinear Attitude Estimation Methods. J. Guid. Control Dyn. 2007, 30, 12–28. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Zhang, N.; Wang, J.; Jiao, Z.; Zhong, Y. Research on the Algorithm of Combined GNSS/SINS Navigation System based on Adaptive UKF. In Proceedings of the 2023 IEEE 6th International Conference on Electronic Information and Communication Technology (ICEICT), Qingdao, China, 21–24 July 2023; pp. 535–540. [Google Scholar]
- Javanfar, E.; Rahmani, M. Optimal Lp filtering for discrete-time non-Gaussian dynamic systems. IET Control Theory Appl. 2021, 15, 2111–2127. [Google Scholar] [CrossRef]
- Elliott, R.J.; Krishnamurthy, V. Finite dimensional filters for ML estimation of discrete-time Gauss-Markov models. In Proceedings of the 36th IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; Volume 2, pp. 1637–1642. [Google Scholar]
- Wang, R.; Wang, X. A novel constrained skew-Gaussian filter and its application to maneuverable reentry vehicle tracking. Aerosp. Sci. Technol. 2024, 155, 109666. [Google Scholar] [CrossRef]
- Meng, H.; Li, X.R.; Jilkov, V.P. Discrete-time linear skew-Gaussian system and its recursive fixed-dimensional exact density filtering. Automatica 2024, 159, 111314. [Google Scholar] [CrossRef]
- Ann, C.B.; William, E.S. Bayesian Estimation of Multivariate Location Parameters. Handb. Stat. 2005, 25, 221–244. [Google Scholar]
- Nidhan, C.; Subhashis, G.; Anindy, R.; William, E.S. Bayesian Methods for Function Estimation. In Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 2005; Volume 25, pp. 373–414. [Google Scholar]
- Sachin, C.P.; Shankar, N.; Prakash, J.; Gopaluni, B.; Shah, S.L. Nonlinear Bayesian state estimation: A review of recent developments. Control Eng. Pract. 2012, 20, 933–953. [Google Scholar]
- Xu, H.; Wen, X.; Yuan, H.; Duan, K.; Liu, W.; Wang, Y. Fixed-point iteration gaussian sum filtering estimator whith unknown time varying non gaussian measurement noise. Signal Process. 2018, 153, 132–142. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Z.; Li, N.; Chambers, J. A novel adaptive kalman filter with inaccurate process and measurement noise covariance matrices. IEEE Trans. Autom. Control 2018, 63, 594–601. [Google Scholar]
- Park, S.; Hwang, P.J.; Kim, E.; Kang, H.J. A new evolutionary particle filter for the prevention of sample impoverishment. IEEE Trans. Evol. Comput. 2009, 13, 801–809. [Google Scholar] [CrossRef]
- Dong, X.; Chisci, L.; Cai, Y. An adaptive variational Bayesian filter for nonlinear multi-sensor systems with unknown noise statistics. Signal Process. 2021, 179, 107837. [Google Scholar] [CrossRef]
- Javanfar, E.; Rahmani, M. Data-Based Filters for Non-Gaussian Dynamic Systems with Unknown Output Noise Covariance. IEEE/CAA J. Autom. Sin. 2024, 11, 866–877. [Google Scholar] [CrossRef]
- Qian, Y.; Shi, X.L.; Zeng, H.W.; Ahmad, M. Direct tracking of noncircular sources for multiple arrays via improved unscented particle filter method. Etri J. 2023, 45, 394–403. [Google Scholar] [CrossRef]
- Kotecha, J.H.; Djuric, P.M. Gaussian particle filtering. IEEE Trans. Signal Process. 2003, 51, 2592–2601. [Google Scholar] [CrossRef]
- Doucet, A.; de Freitas, O. Rao-Blackwellised particle filtering for dynamic bayesian networks. In Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence, San Francisco, CA, USA, 30 June–3 July 2000; pp. 176–183. [Google Scholar]
- Beard, R.; Kenney, J.; Gunther, J.; Lawton, J.; Stirling, W. Nonlinear Projection filter based Guidance, Control and Nonlinear on galerkin approximation. J. Guid. Control Dyn. 1999, 22, 258–266. [Google Scholar] [CrossRef]
- Hosseiny, A.; Jaberipur, G. Complex exponential functions: A high-precision hardware realization. Integration 2020, 73, 18–29. [Google Scholar] [CrossRef]
- Hatamzadeh-Varmazyar, S.; Masouri, Z.; Babolian, E. Numerical method for solving arbitrary linear differential equations using a set of orthogonal basis functions and operational matrix. Appl. Math. Model. 2016, 40, 233–253. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Z.; Zhang, Y.; Xiong, X.; Fan, F.; Ma, S. Research on Projection Filtering Method Based on Projection Symmetric Interval and Its Application in Underwater Navigation. Symmetry 2021, 13, 1715. [Google Scholar] [CrossRef]
- Gardiner, C. The Fokker–Planck Equation. In Elements of Stochastic Methods; AIP Publishing LLC: Melville, NY, USA, 2021; pp. 8-1–8-12. [Google Scholar]
- Benes, V.E. Exact finite-dimensional filters for certain diffusions with nonlinear drift. Stochastics 1981, 5, 65–92. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, J.; Wu, Z.; Chen, L. New Bayesian Estimation Method Based on Symmetric Projection Space and Particle Flow Velocity. Symmetry 2025, 17, 899. https://doi.org/10.3390/sym17060899
Tan J, Wu Z, Chen L. New Bayesian Estimation Method Based on Symmetric Projection Space and Particle Flow Velocity. Symmetry. 2025; 17(6):899. https://doi.org/10.3390/sym17060899
Chicago/Turabian StyleTan, Juan, Zijun Wu, and Lijuan Chen. 2025. "New Bayesian Estimation Method Based on Symmetric Projection Space and Particle Flow Velocity" Symmetry 17, no. 6: 899. https://doi.org/10.3390/sym17060899
APA StyleTan, J., Wu, Z., & Chen, L. (2025). New Bayesian Estimation Method Based on Symmetric Projection Space and Particle Flow Velocity. Symmetry, 17(6), 899. https://doi.org/10.3390/sym17060899




