RADE: A Symmetry-Inspired Resource-Adaptive Differential Evolution for Lightweight Dendritic Learning in Classification Tasks

Abstract

This study proposes Resource-Adaptive Differential Evolution (RADE), a novel optimization algorithm for training lightweight and interpretable dendritic neuron models (DNMs) in classification tasks. RADE introduces dynamic population partitioning, poor-individual-guided mutation, adaptive parameter control, and lightweight archiving to achieve efficient and robust learning. Inspired by biological and algorithmic symmetry, RADE leverages structural and behavioral balance in both the evolutionary process and the DNM architecture. DNMs inherently exhibit symmetric processing through multiple dendritic branches that independently and equivalently aggregate localized inputs. RADE preserves and enhances this structural symmetry by promoting balanced learning dynamics and pruning redundant dendritic components, leading to compact and interpretable neuron morphologies. Extensive experiments on real-world and synthetic datasets demonstrate that RADE consistently outperforms existing methods in terms of classification accuracy, convergence stability, and model compactness. Furthermore, the resulting neuron structures can be mapped to logical circuits, making the RADE-DNM highly suitable for neuromorphic and edge computing applications. This work highlights the synergistic role of symmetry in achieving resource-efficient and transparent artificial intelligence.

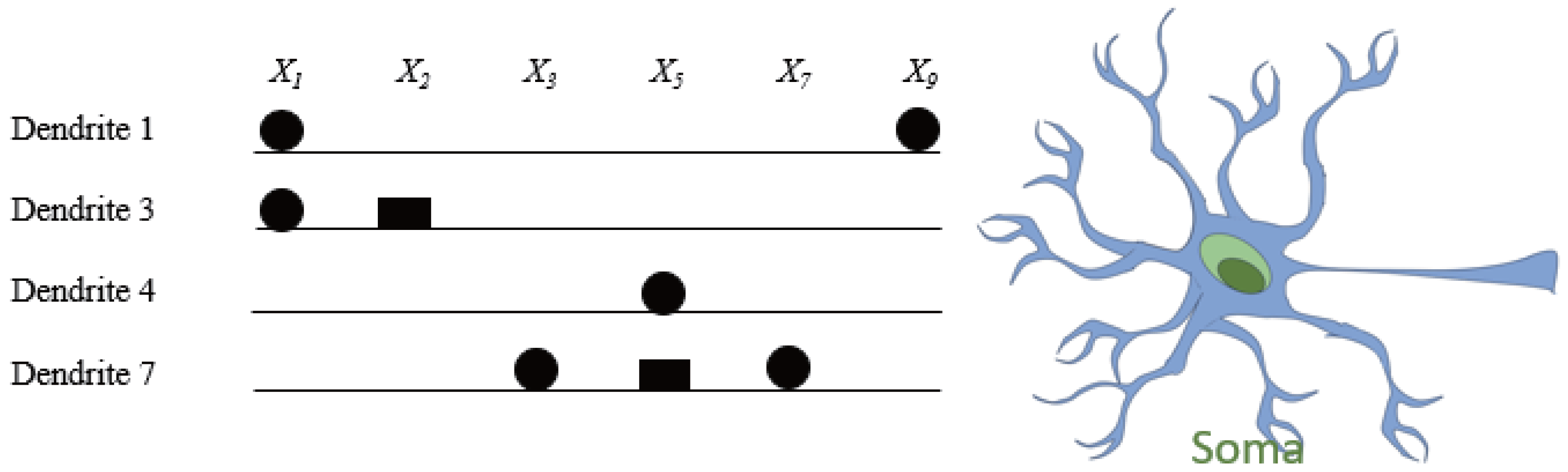
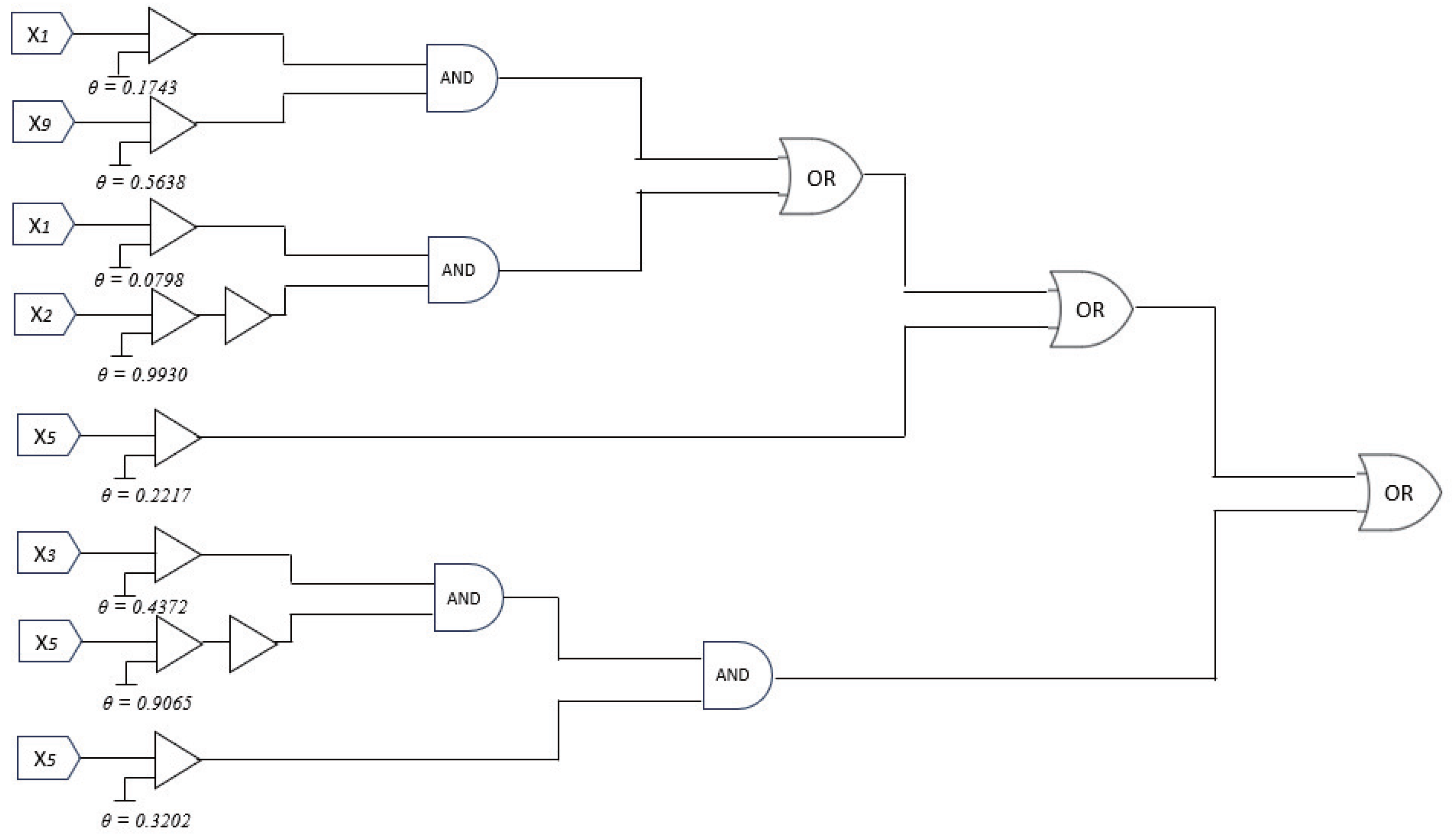
1. Introduction

The field of artificial intelligence (AI) has witnessed significant transformations in recent years, largely driven by the advancement of deep learning techniques [1]. Despite their remarkable performance, traditional deep learning models often require massive numbers of data and computational resources and significant memory bandwidth to achieve high accuracy [2,3]. This computational overhead makes them less practical for deployment in resource-constrained environments, such as mobile devices, edge computing systems, and embedded platforms [4,5,6,7]. Furthermore, these models typically operate as black boxes, offering little interpretability and limiting their usability in critical applications like medical diagnosis and autonomous control [8,9].

To address these challenges, researchers have turned toward biologically inspired computing paradigms that draw insights from the structure and function of the human brain [10,11]. Among these, dendritic learning has emerged as a promising direction [12,13]. It is rooted in the biological understanding that dendrites—the branched extensions of neurons—perform sophisticated, localized processing of synaptic inputs [14]. This capability allows biological neurons to exhibit high computational power without significantly increasing their energy consumption or structural complexity [15].

Dendritic neuron models (DNMs) emulate this biological principle by organizing input processing into distinct dendritic branches [16,17]. Each branch aggregates a subset of inputs through nonlinear operations and contributes to the final output through a competitive or cooperative mechanism. This design introduces interpretability and modularity into the learning process while also enabling sparsity and local computation [18]. Moreover, the inherent structure of DNMs allows for the integration of neural plasticity, dendrite pruning, and dynamic expansion—traits that mirror the adaptability of real neural systems [19].

The lightweight nature of DNMs makes them especially suitable for real-time applications [20]. Experimental studies have validated their efficacy across a wide spectrum of tasks, including image classification, time-series prediction, medical image segmentation, and environmental monitoring [21,22,23]. In medical imaging, for example, dendritic models have outperformed standard convolutional networks in segmenting fine-grained features within ultrasound and CT scans [24]. In time-series forecasting, their ability to model nonlinear dependencies with fewer parameters has enabled efficient and accurate predictions in energy systems and financial domains [25]. Furthermore, recent work by Wu et al. [26] has formally proven that DNMs possess universal approximation power. In their study, the authors demonstrated that DNM architectures can approximate any continuous function to arbitrary precision, similar to multi-layer perceptrons (MLPs) but with more efficient structural representations.

Despite their advantages, training dendritic models remains a complex challenge [18,27]. Their nonlinear and modular structure poses difficulties for the gradient-based optimization techniques commonly used in deep learning. Furthermore, fixed architectures often limit the model’s flexibility to adapt to varying data distributions and tasks. To overcome these limitations, recent research has explored the use of evolutionary algorithms for model training and architecture optimization [28,29,30].

Evolutionary algorithms (EAs) [31], such as Genetic Algorithms, Particle Swarm Optimization, and differential evolution (DE), offer population-based search strategies that are particularly effective for high-dimensional, non-convex optimization problems [32]. Among them, differential evolution is especially notable for its simplicity, convergence behavior, and ease of implementation [33]. However, standard DE suffers from issues like premature convergence, a lack of diversity, and fixed parameter settings, which hinder its performance on complex tasks like DNM optimization [34].

To address these issues, we propose a novel algorithm: Resource-Adaptive Differential Evolution (RADE). RADE is designed to complement dendritic learning by introducing several key innovations:

• Dynamic population partitioning: RADE divides individuals into good and bad groups based on fitness ranking and adjusts this division adaptively throughout the search.
• A reinforced mutation mechanism: By leveraging poor-performing individuals in the variation formula, RADE maintains exploration while guiding convergence.
• Parameter adaptation: A memory-based scheme adjusts control parameters like mutation factor F and crossover rate $CR$ based on historical success.
• Lightweight archiving: A compact external archive preserves useful diversity and prevents population stagnation.
• Time-varying control: The algorithm adapts its exploration–exploitation balance according to the search phase.

These innovations are not only biologically inspired but also computationally efficient, making RADE an ideal evolutionary framework for optimizing dendritic learning systems. In addition, the notion of symmetry plays a fundamental role in both natural and artificial systems. In biological neurons, dendritic processing often follows symmetric patterns where structurally similar branches perform localized computations in parallel. This structural symmetry contributes to energy-efficient processing and robustness. Similarly, RADE maintains and exploits symmetry within the population-based evolutionary search by partitioning individuals and balancing exploration and exploitation symmetrically across search phases. Moreover, the output architectures of DNMs optimized by RADE exhibit morphological symmetry, which enhances interpretability and facilitates logical rule extraction. Moreover, RADE aligns with the broader trend in AI toward sustainability and interpretability. As concerns about the carbon footprint of large models grow [5], lightweight yet powerful alternatives are increasingly valued. RADE and dendritic learning together represent a paradigm that prioritizes biological plausibility, energy efficiency, and task-specific adaptability over brute-force computation.

This paper is organized as follows: Section 2 introduces the theory and motivation behind lightweight dendritic learning. Section 3 details the proposed RADE algorithm and its components. Section 4 presents empirical evaluations across benchmark classification tasks, and discusses the results, interpretability, and potential applications. Finally, Section 5 concludes with future research directions.

2. Lightweight Dendritic Learning

In this section, we expand upon the existing research to provide a comprehensive understanding of the current landscape related to lightweight and interpretable dendritic learning, as well as the role of evolutionary algorithms in neural optimization.

2.1. Biological Inspiration and Motivation

Biological dendrites are capable of integrating complex synaptic inputs and generating nonlinear activations, significantly enhancing the computational capacity of neurons without notably increasing structural complexity [15]. Lightweight dendritic learning is an emerging paradigm in artificial intelligence, inspired by the sophisticated and energy-efficient computation performed by biological neurons in the brain [35]. In particular, dendrites—the branched extensions of neurons—play a critical role in processing and integrating synaptic inputs before triggering an action potential at the soma [36]. Unlike the simplistic summation units used in conventional artificial neurons (e.g., in multi-layer perceptrons or convolutional networks), biological neurons utilize nonlinear, compartmentalized processing that vastly increases their computational capacity without a proportional increase in energy or structural complexity [15]. Moreover, the lightweight nature of dendritic learning aligns with the requirements of edge AI and neuromorphic computing, where low power consumption and interpretability are crucial [20,37].

Taking cues from this, dendritic learning seeks to incorporate biological plausibility into AI models to achieve several key objectives: improved interpretability, reduced model complexity, lower power consumption, and enhanced generalization on small datasets [37]. This stands in sharp contrast to the prevailing “big model + big data = big solution” paradigm dominant in deep learning. Although large-scale models such as GPT-4 can yield impressive results, they are often computationally prohibitive and ecologically unsustainable [38]. Dendritic learning challenges this by proposing small, adaptable models with a biological structure and function.

2.2. Challenges with Existing Deep Learning Paradigms

The current mainstream of deep learning depends heavily on massive datasets and computationally intensive architectures. For instance, the number of parameters in state-of-the-art models often exceeds hundreds of billions, requiring specialized hardware and extensive energy consumption for training and inference [39,40]. Moreover, despite their empirical success, these models often lack interpretability and adaptability, especially when deployed in resource-limited or real-time environments [5].

Another issue is the over-reliance on metaphorical biological terms in traditional neural networks. Many architectures name their layers and components after biological counterparts—“neurons”, “synapses”, “activation functions”—without implementing the corresponding biological functions [13]. The dendritic structure is often either ignored or reduced to a mathematical abstraction that does not reflect its actual role in neural computation. As a result, the real advantages offered by dendritic processing remain untapped.

2.3. Principles of Dendritic Neuron Models (DNMs)

DNMs aim to bridge this gap by explicitly modeling the nonlinear and localized integration performed by dendrites. DNMs have emerged as a biologically inspired alternative to traditional artificial neurons, focusing on compartmentalized processing and nonlinear synaptic integration [15]. Unlike conventional neural networks, DNMs utilize dendritic branches to perform localized processing, significantly enhancing computational capacity and interpretability [12]. Recent studies have demonstrated DNMs’ efficiency in image classification, time-series prediction, and medical imaging [41]. However, optimizing DNMs remains challenging due to their non-differentiable nature, which limits the effectiveness of gradient-based optimization techniques. In a typical DNM, the neuron is structured into multiple dendritic branches, each capable of independently aggregating a subset of inputs using logical or arithmetic functions. These branches may interact competitively or cooperatively before passing the result to the soma, where a final decision is made. Such an architecture introduces locality, sparsity, and interpretability to the learning process [18].

Moreover, DNMs often include mechanisms such as synaptic plasticity, dendrite pruning, and dynamic growth, which further enhance their learning adaptability. By mimicking these properties, dendritic learning systems can adapt to different input distributions, evolve over time, and maintain a compact structure [42]. One of the defining features of dendritic learning is its lightweight nature. By design, DNMs focus on minimal redundancy and targeted complexity. Dendritic structures allow for highly selective activation, meaning that only a small portion of the model is active at any time, significantly reducing power consumption and computational cost. This property makes dendritic models particularly attractive for embedded systems, edge AI, and neuromorphic hardware. Experimental results from various applications such as diabetic retinopathy detection, medical image segmentation, and environmental time-series forecasting demonstrate that dendritic models can achieve competitive accuracy with a fraction of the parameters used in deep learning models [21,22,23].

Dendritic learning has demonstrated strong versatility and adaptability, achieving promising results across a variety of complex real-world domains. In the field of medical imaging, dendritic neural networks have shown superior performance in tasks such as ultrasound and CT image segmentation. By integrating dendritic computational units into deep learning frameworks, these models are able to enhance feature locality and improve edge sensitivity, resulting in more accurate and robust segmentation outcomes [24]. In image classification, hybrid architectures that combine traditional convolutional backbones (e.g., EfficientNet) with dendritic neurons have been successfully employed for challenging tasks such as diabetic retinopathy detection. These models effectively capture fine-grained texture variations that are often overlooked by standard CNNs, thereby improving classification performance in medical diagnostics [21]. Dendritic models have also proven effective in time-series prediction. Thanks to their compact structure and inherent capacity to model nonlinear temporal dependencies, these models can deliver accurate real-time forecasts in applications such as energy consumption prediction, greenhouse climate monitoring, and financial market analysis. Importantly, this is achieved with significantly fewer parameters compared to traditional deep learning models [22,25]. Furthermore, in the domain of environmental monitoring, dendritic learning has been applied to tasks such as PM2.5 concentration forecasting and carbon emission estimation. The ability of dendritic networks to adapt to seasonal patterns and extract meaningful information from low-signal, noisy data makes them particularly well suited for such applications [43]. Overall, these diverse application outcomes underscore the dendritic learning paradigm’s compatibility with complex, noisy, and resource-constrained data environments, highlighting its potential as a practical and interpretable alternative to conventional deep learning approaches.

Recent advancements in the field of dendritic learning have led to the development of a range of enhanced model variants, broadening the applicability and effectiveness of dendritic neuron models in modern AI systems. One notable direction involves the introduction of fully complex-valued DNMs, which enable the processing of phase-sensitive signals, thereby expanding the potential of dendritic models in areas such as signal processing and communication systems [44]. Another important development is the design of multi-input multi-output architectures, which significantly improve the model’s flexibility in handling multimodal data streams. This extension allows dendritic models to simultaneously integrate and process multiple sources of information, thus enhancing their capacity for real-world applications that require complex sensory fusion [45]. To support deeper learning hierarchies while preserving model interpretability, researchers have also proposed residual and deep variants of dendritic networks. These architectures adopt principles from deep residual learning to facilitate gradient propagation and stable convergence, enabling the training of deeper dendritic models without sacrificing their logical structure or transparency [46]. In addition, neural plasticity mechanisms have been incorporated into dendritic architectures to simulate biologically plausible synaptic adaptation. By allowing synaptic weights and dendritic structures to adjust dynamically in response to changing environmental stimuli, these models better emulate real biological learning processes and improve adaptability over time [20]. Collectively, these extensions significantly enhance the representational power, flexibility, and generalization ability of dendritic systems, positioning them as strong candidates for next-generation interpretable and adaptive artificial intelligence.

2.4. Neuron Architecture of Dendritic Learning

A DNM offers a biologically inspired neural architecture that models compartmentalized processing through a structured hierarchy of synaptic inputs, dendritic computation, and somatic decision-making. As illustrated in Figure 1, its neuron-level architecture can be decomposed into four computational stages: synaptic transformation, dendritic interaction, membrane accumulation, and output activation.

(1) Synaptic Transformation. Given a presynaptic input $x_k$, its influence on the j-th dendrite is modulated by a learnable weight $w_{kj}$ and bias $q_{kj}$. The synaptic transmission output is as follows:

$${\varphi }_{kj}={\displaystyle \frac{1}{1+exp\left(-\lambda (w_{kj}{x}_k-q_{kj})\right)}}.$$

(1)

Here, $\lambda$ controls the sharpness of the activation. This transformation emulates the biological role of synapses in modulating signal strength and polarity.

(2) Dendritic Computation. Each dendritic branch acts as an independent nonlinear unit that aggregates its inputs. Instead of ${\delta }_j$, we denote the output of the j-th dendrite as $d_j$:

$$d_j=\prod _{r=1}^N{\varphi }_{rj},$$

(2)

where N is the number of inputs assigned to dendrite j, and ${\varphi }_{rj}$ represents the r-th input processed at that dendrite.

(3) Membrane Potential Aggregation. The total contribution from all dendritic branches is summed at the membrane, yielding the membrane potential M:

$$M=\sum _{j=1}^D{d}_j,$$

(3)

where D denotes the total number of dendrites.

(4) Soma Output Activation. The neuron’s final output is produced by applying a nonlinear activation to the membrane potential. Let $\theta$ denote the firing threshold and $\gamma$ be a gain factor. The final output o is as follows:

$$o={\displaystyle \frac{1}{1+exp\left(-\gamma (M-\theta )\right)}}.$$

(4)

This hierarchical structure enables DNMs to model complex, localized interactions and spatial feature integration, thus enhancing both the interpretability and efficiency of single-neuron computation. To conclude, lightweight dendritic learning represents a promising direction for sustainable, interpretable, and biologically plausible AI. By departing from the traditional deep learning reliance on overparameterization and embracing the efficiency of dendritic computation, this paradigm offers a viable alternative for real-world, constrained, and adaptive intelligent systems. Future research will continue to explore the integration of dendritic learning with evolutionary optimization, hardware-aware design, and cognitive modeling. The goal is to establish a new class of AI systems that are not only powerful and accurate but also transparent, energy efficient, and aligned with the principles of natural intelligence. In this context, the proposed RADE algorithm serves as an ideal evolutionary backbone to further empower dendritic learning, enabling resource-adaptive and structure-aware optimization tailored to various classification tasks.

3. Proposed Resource-Adaptive Differential Evolution Algorithm

To improve the learning efficiency, robustness, and interpretability of the DNM in classification tasks, we propose a novel lightweight evolutionary optimization method termed Resource-Adaptive Differential Evolution (RADE). RADE introduces several biologically inspired and resource-aware mechanisms to address the limitations of conventional DE and its variants when applied to high-dimensional and dynamically evolving neural systems. This section elaborates on the architectural innovations, algorithmic framework, and theoretical motivations behind RADE, particularly its compatibility with interpretable and low-resource neural learning.

3.1. Overview and Motivation

Evolutionary algorithms (EAs) have been widely employed for neural optimization due to their ability to explore high-dimensional, non-convex landscapes effectively [47,48]. Among them, DE and its variants have proven successful in optimizing complex neural structures [49,50]. However, these methods often suffer from issues like premature convergence and inefficient exploration, which limit their application in dendritic neuron optimization. RADE addresses these limitations through dynamic population partitioning, lightweight archiving, and adaptive parameter control. It is conceived from a synthesis of ideas drawn from natural evolution, biological neural computation, and recent advances in adaptive differential evolution algorithms. Traditional differential evolution algorithms [51,52], while successful in many real-valued optimization problems, often fall short in tasks that demand both exploration and exploitation in a dynamically changing fitness landscape—such as those encountered in training DNMs [53]. In such settings, overly aggressive exploitation leads to premature convergence, whereas excessive exploration sacrifices convergence speed and solution quality [54,55]. Furthermore, when applied to real-world classification problems under resource-constrained environments, classical DE methods often require extensive population sizes and computational time to converge to satisfactory solutions. This renders them impractical for lightweight, interpretable AI applications.

To mitigate these challenges, RADE introduces four primary innovations: (1) dynamic population partitioning, (2) reinforced mutation with poor-individual interference, (3) parameter self-adaptation via lightweight memory mechanisms, and (4) an efficient external archive that guides exploration without increasing model complexity. These innovations reflect a biologically grounded learning approach: rather than treating all individuals equally during evolution, RADE simulates a more nuanced model of survival and competition, akin to the way organisms in nature adapt based on their fitness relative to the environment.

The central idea behind RADE is to maintain evolutionary diversity while prioritizing computational efficiency. By continuously adjusting how the population is divided into exploratory and exploitative subgroups, and by tuning the mutation and crossover strategies based on recent historical successes, RADE is able to maintain robust performance over time. Moreover, its lightweight design makes it suitable for embedding within a broader DNM learning framework, particularly for single-neuron models aimed at classification tasks.

3.2. Dynamic Population Partitioning and Control

Unlike traditional DE approaches where variation is applied indiscriminately across the entire population, RADE introduces a biologically inspired mechanism to partition the population into “good” and “bad” individuals based on their fitness rankings. This dual-group strategy mirrors natural ecological competition, where fitter individuals are more likely to reproduce, while less fit individuals may still introduce useful genetic variation into the population.

In RADE, the concept of symmetry is incorporated at multiple levels of its evolutionary strategy, particularly in its population partitioning and mutation strategies. The population is divided into symmetric subgroups in search space exploration. This partitioning reduces redundancy and maximizes diversity by ensuring that different partitions explore distinct regions. Mathematically, if P is the population, we express partitioning as follows:

$$P=P_1\cup P_2\cup \dots \cup P_k\mathrm{where}{P}_i\cap P_j=\varnothing \forall i\ne j$$

(5)

In RADE, the size and composition of these subgroups are not static. Instead, they are adaptively controlled throughout the evolutionary process based on the number of function evaluations. This adaptive mechanism allows the algorithm to shift its focus from exploration to exploitation as the search progresses.

The proportion parameter p used to dynamically adjust the split between subgroups is given by

$$p=0.3\times \left(1-{\displaystyle \frac{\mathrm{nFES}}{\mathrm{FES}}}\right)$$

(6)

where nFES is the number of function evaluations so far and FES is the total evaluation budget. Based on this p, the boundary index for sorting is calculated by

$$\mathrm{index}=\lfloor (1-p)\times {\displaystyle \frac{N}{2}}\rfloor$$

(7)

Using the sorted population, we form two groups:

$$P_{\mathrm{good}}=\{x_i\mid i\in \mathrm{IndexSorted}(1:N_{\mathrm{half}})\},P_{\mathrm{bad}}=\{x_i\mid i\in \mathrm{IndexSorted}(N_{\mathrm{half}}+1:N)\}$$

(8)

Each group is further divided into subgroups for mutation and crossover purposes:

$$P_{\mathrm{good}}=P_{\mathrm{good},1}\cup P_{\mathrm{good},2},\left|P_{\mathrm{good},1}\right|=\lfloor (1-p)·N_{\mathrm{half}}\rfloor$$

(9)

$$P_{\mathrm{bad}}=P_{\mathrm{bad},1}\cup P_{\mathrm{bad},2},\left|P_{\mathrm{bad},1}\right|=N_{\mathrm{half}}-\left|P_{\mathrm{good},1}\right|$$

(10)

Then, the variation group $V_{\mathrm{pops}}$ and crossover group U are constructed as follows:

$$V_{\mathrm{pops}}=P_{\mathrm{good},1}\cup P_{\mathrm{bad},1},U=P_{\mathrm{good},2}\cup P_{\mathrm{bad},2}$$

(11)

3.3. Reinforced Mutation with Poor-Individual Interference

To enhance the global search and avoid local optima, RADE introduces a variation formula that combines the influence of top-performing individuals with noise from poorly performing ones:

$$V=V_{\mathrm{pops}}+F·\left(X_{\mathrm{pbest}}-V_{\mathrm{pops}}+V_{\mathrm{pops}}\left[r_2\right]-U\left[r_3\right]\right)$$

(12)

where the variable V represents the mutant vector generated for exploration, and $V_{\mathrm{pops}}$ denotes the population of selected individuals for mutation. The parameter F is the scaling factor that controls the amplification of the difference vectors during mutation. The term $X_{\mathrm{pbest}}$ indicates the best-performing individual from the current population, serving as a reference for the guided search.

The components $V_{\mathrm{pops}}\left[r_2\right]$ and $U\left[r_3\right]$ are randomly selected individuals from the variation group and crossover group, respectively, where $r_2$ and $r_3$ are random indices. This introduces stochastic diversity into the mutation operation, ensuring that the search process explores different regions of the solution space. The subtraction $V_{\mathrm{pops}}\left[r_2\right]-U\left[r_3\right]$ generates a perturbation vector that is scaled by F, pushing the mutant vector V towards less-explored areas while still being influenced by the best solution $X_{\mathrm{pbest}}$. This combination enhances the algorithm’s capability to escape local optima and improve global search efficiency. This hybrid variation mechanism incorporates both a directed search toward elite individuals and stochastic disturbance from low-fitness candidates, effectively boosting robustness and exploratory power.

3.4. Parameter Adaptation via Memory Mechanisms

RADE leverages success-history-based adaptive parameter control, similar to LSHADE [56], with some simplifications for efficiency. The primary motivation for adopting this strategy is its proven effectiveness in maintaining population diversity and avoiding premature convergence. In LSHADE, for example, the historical success of parameter settings is used to guide future generations, effectively balancing exploration and exploitation. RADE extends this idea by introducing lightweight memory mechanisms that minimize memory overhead while still capturing successful parameter settings over the iterations. This design allows RADE to dynamically adapt its mutation and crossover rates with minimal computational cost, maintaining efficiency even with larger populations. While it is true that memory-based adaptation requires additional steps for updating historical records, we have optimized this process in RADE by using a simplified archiving strategy that only maintains the most relevant parameter values. This reduces memory allocation and accelerates the retrieval process, ensuring that the added computational time remains minimal compared to the optimization gains achieved.

First, the improvement degree of a successful individual is calculated by

$${\Delta }_i=\left|f\left({\mathbf{x}}_i\right)-f\left({\mathbf{u}}_i\right)\right|$$

(13)

The corresponding weight is then computed as follows:

$$w_i={\displaystyle \frac{{\Delta }_i}{{\sum }_{j=1}^S{\Delta }_j}}$$

(14)

These weights contribute to the weighted Lehmer mean:

$$\mathrm{MeanWL}(\left\{v_i\right\},\left\{w_i\right\})={\displaystyle \frac{{\sum }_{i=1}^S{w}_i{v}_i^2}{{\sum }_{i=1}^S{w}_i{v}_i}}$$

(15)

Finally, the historical memory arrays for the crossover rate and scaling factor are updated:

$$\mathrm{MemoryCR}\left[k\right]\leftarrow {\displaystyle \frac{\mathrm{MemoryCR}\left[k\right]+\mathrm{MeanWL}({\left\{{\mathrm{CR}}_i\right\}}_{i=1}^S,{\left\{w_i\right\}}_{i=1}^S)}{2}}$$

(16)

$$\mathrm{MemoryF}\left[k\right]\leftarrow {\displaystyle \frac{\mathrm{MemoryF}\left[k\right]+\mathrm{MeanWL}({\left\{F_i\right\}}_{i=1}^S,{\left\{w_i\right\}}_{i=1}^S)}{2}}$$

(17)

For the next generation, new F and $CR$ values are sampled as follows:

$$F\sim \mathrm{Cauchy}\left(\mathrm{MemoryF}\left[k\right],{\sigma }_F\right),\mathrm{with}F>0\mathrm{and}F\le 1,$$

(18)

$$CR\sim \mathcal{N}\left(\mathrm{MemoryCR}\left[k\right],{\sigma }_{CR}\right),\mathrm{with}CR\in [0,1]$$

(19)

It is important to highlight that the Cauchy distribution is chosen for F due to its heavy-tailed nature, which promotes broader exploration in the search space and reduces the risk of premature convergence. In contrast, the normal distribution is applied to $CR$ to maintain stability in crossover operations, ensuring consistent offspring generation. The weighted Lehmer mean is used to enhance adaptive memory by prioritizing historically successful mutations, thus improving convergence reliability. These choices are inspired by the parameter adaptation strategies used in LSHADE, but are further optimized to align with RADE’s lightweight structure for dendritic neuron model optimization.

3.5. Lightweight External Archiving

RADE integrates an external archive A to store useful but rejected individuals, maintaining diversity. Its update mechanism is defined by

$$A\leftarrow \left\{\begin{array}{cc}A\cup \left\{\mathbf{x}\right\},\hfill & \mathrm{if}\left|A\right|<A_{max},\hfill \\ \left(A\setminus \left\{{\mathbf{x}}_{\mathrm{rand}}\right\}\right)\cup \left\{\mathbf{x}\right\},\hfill & \mathrm{if}\left|A\right|\ge A_{max}\hfill \end{array}\right.$$

(20)

This mechanism helps to recycle good information and prevent population collapse.

3.6. Compatibility with Dendritic Neuron Learning

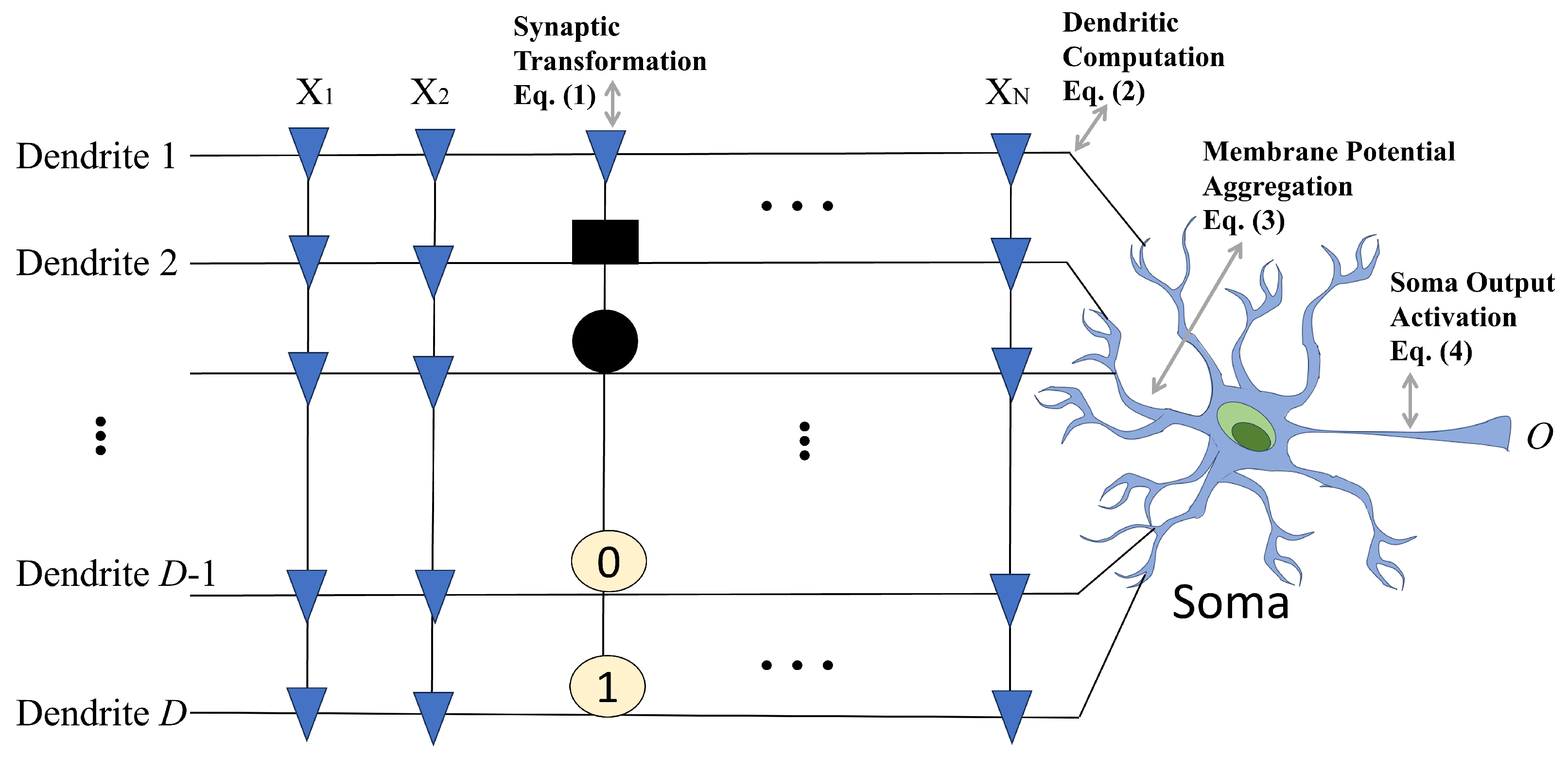
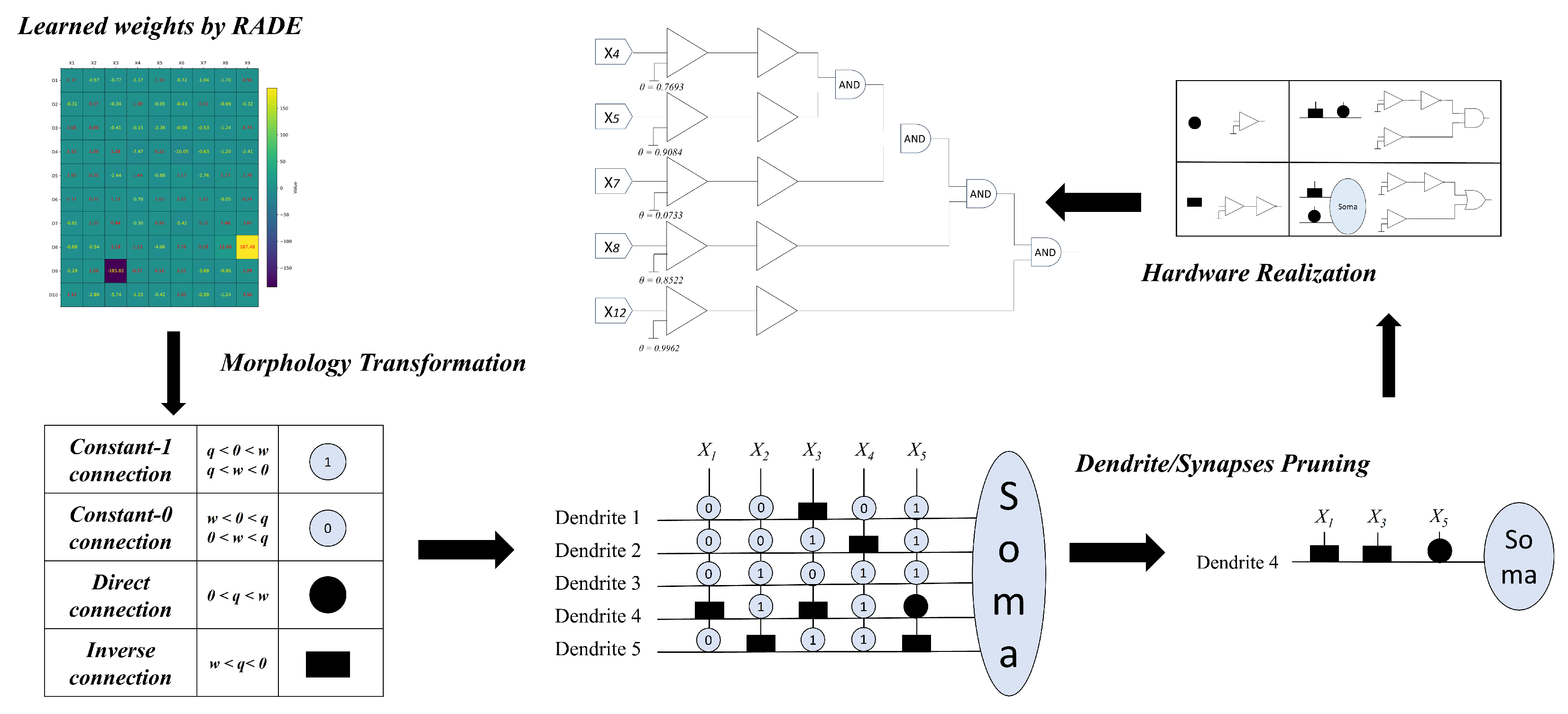
The RADE algorithm is specifically designed to address the unique learning characteristics of the DNM, which is inherently more complex than traditional artificial neurons due to its spatially compartmentalized and nonlinear processing. The diagram in Figure 2 illustrates the entire flow of RADE-driven dendritic learning, from numerical optimization to structural interpretation and hardware realization.

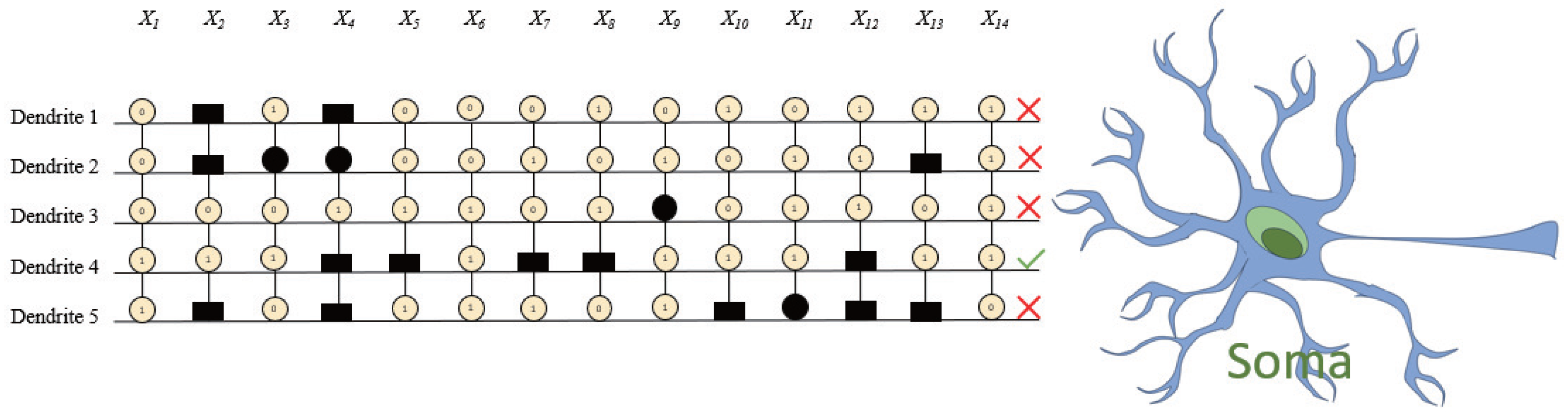
(1) Learning and Weight Formation. RADE first learns the connection parameters for each synapse in the DNM structure by optimizing gain coefficients $w_{kj}$ and bias shifts $q_{kj}$ based on classification accuracy. As shown in the upper-left heatmap, each cell corresponds to the learned strength of a connection from input $x_k$ to dendrite $d_j$.

(2) Morphology Transformation. Once numerical values are learned, each synaptic connection is interpreted according to its sign and magnitude. Based on the relationship between w and q, connections are categorized into four types:

• Constant-1: $q<0<w$ or $q<w<0$ → Always active (output = 1);
• Constant-0: $w<0<q$ or $0<w<q$ → Always inactive (output = 0);
• Direct: $0<q<w$ → Monotonically increasing (positive logic);
• Inverse: $w<q<0$ → Monotonically decreasing (inverted logic).

This transformation makes the model interpretable by transforming real-valued weights into logic-compatible symbols (e.g., open/closed circles, squares), facilitating the next stage of simplification.

(3) Dendritic Pruning. Not all dendritic branches contribute equally to the final prediction. RADE identifies redundant or inactive dendrites—e.g., those composed entirely of constant signals or contributing negligible activation—and removes them. This structural pruning significantly reduces model complexity while preserving classification performance. An example shown in the bottom right of the figure highlights a single optimized dendrite with three meaningful inputs: two inverse connections and one direct.

(4) Logic Mapping and Hardware Realization. The final set of active dendritic branches, each containing only interpretable logical conditions, is then translated into hardware-friendly logical operations. Each synapse becomes a comparator, inverter, or passthrough, and each dendrite functions as a logic gate (e.g., AND, OR). The soma output is implemented as a threshold decision gate.

As demonstrated in the top right of Figure 2, the optimized DNM can be mapped to a layered logic circuit composed of NOT and AND gates, corresponding to inverse and direct synaptic roles. This not only enables deployment on energy-efficient digital or analog hardware but also guarantees transparency in model decision-making.

The integration of RADE with DNMs yields several significant advantages that enhance both biological realism and computational efficiency. First, RADE preserves the core principle of biological plausibility by maintaining localized processing and nonlinear synaptic interactions throughout the optimization process. This ensures that the learned model retains functional characteristics akin to real neural systems. Second, RADE supports structural adaptability by enabling dynamic exploration, pruning, and reconfiguration of the dendritic architecture in response to task-specific requirements. This allows the model to automatically discard redundant branches and reinforce informative pathways, resulting in an efficient and specialized neuronal morphology. Third, the output of RADE-guided training is highly interpretable. Through morphology transformation, each synaptic connection is translated into a logical rule that can be clearly understood and visualized. This bridges the gap between model transparency and performance, offering insight into the decision-making process of the network. Finally, a key practical advantage of RADE-trained DNMs is its compatibility with hardware implementation. The optimized neuron structure, consisting of simplified logical components such as comparators and logical gates, can be directly mapped onto digital or analog hardware circuits. This makes RADE-trained DNMs highly suitable for deployment in low-power, resource-constrained environments, such as neuromorphic chips and edge AI platforms. In summary, RADE not only enhances the learning capability and performance of dendritic neuron models but also systematically drives them toward interpretable, compact, and hardware-friendly representations. This comprehensive compatibility positions the RADE-DNM as a promising framework for the development of next-generation, biologically inspired intelligent systems.

3.7. Summary and Contributions

RADE stands as a biologically inspired, evolutionarily principled, and computationally efficient solution for training dendritic neuron models in classification tasks. RADE is implemented as computationally effectively as DE. In comparison with traditional DE, the additional requirement of computational resources in RADE comes from the update of the external archive and success memory. In the worst case, these additional operators require a computational complexity of $O(A_{max}\times N)$. Therefore, the total complexity of RADE is $O(A_{max}\times N\times G_{max})$, where $A_{max}$ is the maximal size of the external archive, N is the population size, and $G_{max}$ is the maximum number of generations. Its main contributions include the following:

• A dynamic population grouping strategy that shifts from exploration to exploitation based on search progress.
• A reinforced mutation mechanism that introduces diversity via poor-individual interference.
• A lightweight, memory-based parameter adaptation framework that enhances convergence reliability.
• An external archiving mechanism that maintains population diversity without increasing complexity.
• Direct compatibility with interpretable and hardware-efficient dendritic learning systems.

Overall, the RADE-DNM represents a robust and scalable approach to evolving biologically inspired neural systems under real-world constraints. The demand for lightweight and interpretable models has surged with the rise of edge computing and neuromorphic architectures. Recent advancements have shown that biologically inspired models, including DNMs, can operate efficiently in resource-constrained environments [57]. RADE is designed to leverage this lightweight nature, optimizing dendritic neuron learning with minimal computational overhead, making it well suited for edge AI applications. Interpretability is another critical aspect of modern AI models, especially for deployment in sensitive applications like medical diagnostics and autonomous systems [58]. RADE enhances interpretability through dendritic pruning and logical rule extraction, transforming synaptic weights into understandable logic gates. This logical mapping not only improves transparency but also facilitates hardware implementation in neuromorphic chips. It opens the door to further research on embedding such evolution-based models into edge AI systems and neuromorphic architectures.

4. Experiments and Discussions

To rigorously evaluate the performance of the proposed RADE algorithm in optimizing DNMs for classification tasks, we conduct a series of controlled experiments across a diverse set of benchmark datasets. This section outlines the experimental design, datasets, evaluation protocol, baseline algorithms, and parameter configurations.

4.1. Datasets and Compared Algorithms

To comprehensively evaluate the effectiveness of the proposed RADE algorithm in optimizing dendritic neuron models (DNMs), we conduct experiments on a diverse collection of benchmark datasets, as summarized in

Table 1. Description of the 14 datasets used in the experiments.

Dataset	Samples	Features	Classes	Imbalance Ratio
Australia	690	14	2	0.56
BUPA	341	6	2	0.58
BreastEW	568	30	2	0.63
CongressEW	434	16	2	0.59
Exactly	1000	10	2	0.50
German	1000	24	2	0.70
Heart	297	13	2	0.55
Ionosphere	351	34	2	0.64
KrVsKpEW	3196	36	2	0.52
Moons	1500	2	2	0.50
SpectEW	267	22	2	0.61
Tic-tac-toe	958	9	2	0.65
Gaussians	1200	2	2	0.33
XOR	1400	2	2	0.50

. These include eleven real-world datasets—Australia, BUPA, BreastEW, CongressEW, Exactly, German, Heart, Ionosphere, KrVsKpEW, SpectEW, and Tic-tac-toe—which have been commonly used in the literature for evaluating classification algorithms due to their varying dimensionalities, class imbalances, and domain complexities. In addition, three synthetic datasets—Moons, XOR, and Gaussians—are incorporated to assess the model’s capacity to handle nonlinear separability and logical dependencies. All datasets are normalized to the range $[0,1]$, and each is randomly split into 70% training and 30% testing sets. To ensure statistical reliability, each algorithm is independently run 30 times per dataset using different random seeds.

In order to validate the performance of RADE, we compare it with eight representative optimization algorithms, covering both classical and advanced differential evolution (DE) variants, as well as a gradient-based learning baseline. These include Biogeography-Based Optimization (BBO), Chaotic JADE (CJADE), Dynamic Permutation Differential Evolution (DPDE), Self-Adaptive Chaotic JADE (SCJADE), Selective Ensemble DE (SEDE), Success-History Adaptive DE (SHADE), States of Matter Search (SMS), and the classical Backpropagation (BP) algorithm.

BBO [18] is a population-based metaheuristic that simulates the natural distribution and migration of species among habitats. Its exploitation of immigration and emigration rates enables a flexible balance between global and local searches, which is particularly valuable for navigating the complex fitness landscapes encountered in DNM optimization. CJADE [59] enhances the JADE framework by incorporating chaotic maps, introducing stochastic perturbations that help the algorithm escape local optima and maintain diversity during convergence. This makes it well suited for tackling multimodal and irregular objective functions.

DPDE [60] extends traditional DE by introducing an adaptive feedback mechanism that modifies search parameters dynamically based on evolutionary feedback. This ability to self-regulate improves convergence speed and helps avoid stagnation, making it ideal for training dendritic models that require precise weight and bias tuning. Similarly, SCJADE [61] combines the adaptability of JADE with chaos-induced variability, which further enhances exploration in complex solution spaces while preserving convergence reliability.

SEDE [62] integrates multiple mutation strategies and selects among them based on performance history. This selective ensemble design ensures robustness across different stages of the evolutionary process and has demonstrated success in real-world applications such as photovoltaic system modeling. SHADE [63], another strong DE variant, maintains a history of successful parameter configurations and uses this to guide future sampling. Its self-adaptive mechanism is especially effective in maintaining search momentum and avoiding premature convergence, which are critical challenges in training compact DNM structures.

In addition to these DE-based approaches, we include SMS [64], a physics-inspired algorithm that mimics the behavior of matter transitioning through gaseous, liquid, and solid states. This staged strategy enables a controlled shift from exploration to exploitation, aligning well with the progressive refinement required in DNM training. Finally, the Backpropagation (BP) method [65] is selected as a non-evolutionary baseline. Although standard BP is typically not suitable for DNMs due to its non-differentiable architecture, prior adaptations have enabled gradient-based training by approximating error functions. This provides a meaningful reference for evaluating the performance and interpretability advantages of RADE and other evolutionary methods.

The choice of these algorithms is guided by their proven efficacy in related optimization tasks, their structural diversity, and their complementary search strategies. Together, they form a comprehensive benchmark suite to validate RADE’s ability to optimize dendritic models under a variety of learning challenges.

4.2. Dendritic Neuron Model Settings

The DNM used in the experiments consists of $D=10$ dendritic branches, each receiving a randomized subset of the input features. It is worth pointing out that one of the unique aspects of RADE is its automatic pruning mechanism, which dynamically reduces the number of dendrites during training based on relevance and contribution. This adaptive pruning allows the model to optimize its structure, ensuring that only the most effective dendritic connections are retained. Therefore, while the initial number of dendrites is set to 10, RADE’s optimization process significantly reduces this count, maintaining only the essential branches necessary for optimal classification. The automatic pruning mechanism consistently reduces redundancy and achieves optimal accuracy without requiring larger dendritic configurations. This design choice simplifies hyperparameter selection while preserving model efficiency and interpretability. Each synapse is initialized with random parameters $(w_{kj},q_{kj})$ drawn from a uniform distribution over $[-1,1]$. The sigmoid steepness parameter $\lambda$ is set to 5, and the soma threshold $\theta$ is initialized to 0.5.

After training, a morphology transformation and pruning step is applied based on the conditions introduced in Section 3, where constant-value and inactive synapses are removed to reduce model size and improve interpretability.

4.3. RADE Parameter Configuration

For RADE, the following parameter values are used throughout all experiments unless otherwise specified:

• Population size $N=50$;
• Maximum number of generations $G_{max}=300$;
• Crossover rate $CR\sim \mathcal{N}(0.5,0.1)$ (updated adaptively);
• Scaling factor $F\sim \mathrm{Cauchy}(0.5,0.1)$ (updated adaptively);
• Proportion parameter p dynamically adjusted via Equation (5);
• Archive size $A_{max}=N$.

The RADE-specific mechanisms—such as external archive updating, population partitioning, and reinforced mutation—are implemented following the procedures outlined in Section 3.

4.4. Evaluation Metrics

To evaluate the performance of each algorithm on the classification tasks, two primary metrics are employed: classification accuracy (ACC) and the Area Under the Curve (AUC). ACC measures the proportion of correctly predicted instances in the test set, reflecting the overall predictive capability of the model. A higher ACC value indicates a stronger classification performance across the dataset. In addition to accuracy, we use the Area Under the Curve (AUC), a widely recognized evaluation metric that assesses the quality of both binary and multi-class classifiers. The AUC represents the degree of separability between classes and provides an aggregate measure of performance across all classification thresholds. Its value ranges from 0 to 1, where 1 indicates perfect classification and 0.5 represents random guessing. Higher AUC values signify the model’s enhanced ability to distinguish between positive and negative instances, even in cases of class imbalance. For RADE, this metric is particularly important since its logical representation relies on effectively capturing decision boundaries, ensuring precise class separability. Furthermore, both the ACC and AUC are evaluated with their respective standard deviation (STD) over 30 independent runs with different random seeds. The STD measures the robustness and stability of the algorithm under stochastic initialization, with lower deviations indicating more consistent performance across multiple trials. This evaluation framework allows us to comprehensively understand not only the accuracy of RADE but also its reliability and robustness in diverse experimental settings. All experiments are conducted using Python 3.10 on a machine equipped with an Intel i7 CPU, 32 GB RAM, and no GPU acceleration. Each algorithm is allowed the same maximum number of function evaluations for fairness. In the following subsection, we present and analyze the experimental results across all benchmark datasets, with a focus on RADE’s accuracy, efficiency, and compatibility with the DNM’s lightweight architecture.

4.5. Results and Analysis

Table 2. Performance comparison of RADE and other algorithms on 14 datasets in terms of ACC and AUC results.

	Australia		BUPA		BreastEW		CongressEW
	ACC	AUC	ACC	AUC	ACC	AUC	ACC	AUC
RADE	0.8533 ± 0.0109	0.8449 ± 0.0126	0.6333 ± 0.0368	0.6086 ± 0.0404	0.9298 ± 0.0114	0.8783 ± 0.0200	0.9644 ± 0.0124	0.9611 ± 0.0178
BBO	0.8441 ± 0.0108	0.8342 ± 0.0111	0.6171 ± 0.0584	0.6134 ± 0.0598	0.9173 ± 0.0170	0.8606 ± 0.0211	0.9559 ± 0.0155	0.9494 ± 0.0226
CJADE	0.8480 ± 0.0081	0.8364 ± 0.0080	0.6257 ± 0.0592	0.6150 ± 0.0586	0.6688 ± 0.0714	0.5134 ± 0.0962	0.9595 ± 0.0097	0.9516 ± 0.0183
IFDE	0.8585 ± 0.0109	0.8502 ± 0.0123	0.6143 ± 0.0624	0.5961 ± 0.0683	0.9241 ± 0.0551	0.8721 ± 0.0773	0.9703 ± 0.0080	0.9681 ± 0.0102
SCJADE	0.8512 ± 0.0092	0.8395 ± 0.0106	0.6200 ± 0.0610	0.6006 ± 0.0670	0.6974 ± 0.0874	0.5535 ± 0.1205	0.9626 ± 0.0060	0.9559 ± 0.0097
SEDE	0.8498 ± 0.0104	0.8395 ± 0.0127	0.6019 ± 0.0704	0.5962 ± 0.0816	0.9196 ± 0.0124	0.8636 ± 0.0236	0.9615 ± 0.0111	0.9543 ± 0.0177
SHADE	0.8507 ± 0.0073	0.8404 ± 0.0097	0.6124 ± 0.0584	0.6008 ± 0.0672	0.9124 ± 0.0213	0.8609 ± 0.0233	0.9633 ± 0.0083	0.9593 ± 0.0145
SMS	0.7971 ± 0.0674	0.7901 ± 0.0646	0.6124 ± 0.0490	0.6033 ± 0.0479	0.8828 ± 0.1133	0.8183 ± 0.1605	0.9608 ± 0.0133	0.9604 ± 0.0173
BP	0.4444 ± 0.0000	0.4659 ± 0.0000	0.4286 ± 0.0000	0.5333 ± 0.0000	0.6353 ± 0.0000	0.4676 ± 0.0000	0.6385 ± 0.0000	0.4301 ± 0.0000
	Exactly		German		Heart		Ionosphere
	ACC	AUC	ACC	AUC	ACC	AUC	ACC	AUC
RADE	0.7367 ± 0.0387	0.6152 ± 0.0669	0.7539 ± 0.0167	0.6556 ± 0.0223	0.9395 ± 0.0231	0.9333 ± 0.0295	0.9402 ± 0.0086	0.8850 ± 0.0109
BBO	0.6930 ± 0.0101	0.5341 ± 0.0178	0.6804 ± 0.1089	0.6208 ± 0.0389	0.8973 ± 0.0136	0.8807 ± 0.0166	0.9298 ± 0.0379	0.8696 ± 0.0452
CJADE	0.6875 ± 0.0086	0.5228 ± 0.0051	0.6782 ± 0.0259	0.5806 ± 0.0385	0.8410 ± 0.0115	0.8189 ± 0.0140	0.4837 ± 0.1939	0.4232 ± 0.2025
IFDE	0.7246 ± 0.0369	0.5965 ± 0.0606	0.7549 ± 0.0106	0.6553 ± 0.0193	0.9120 ± 0.0122	0.8998 ± 0.0169	0.9422 ± 0.0030	0.8876 ± 0.0024
SCJADE	0.6852 ± 0.0166	0.5218 ± 0.0065	0.6684 ± 0.0369	0.5782 ± 0.0435	0.8513 ± 0.0120	0.8296 ± 0.0127	0.3642 ± 0.1788	0.3026 ± 0.1918
SEDE	0.6896 ± 0.0091	0.5235 ± 0.0021	0.7289 ± 0.0184	0.6176 ± 0.0363	0.8370 ± 0.0119	0.8140 ± 0.0125	0.8967 ± 0.0519	0.8267 ± 0.0543
SHADE	0.7156 ± 0.0342	0.5816 ± 0.0616	0.7420 ± 0.0144	0.6402 ± 0.0263	0.8744 ± 0.0107	0.8543 ± 0.0137	0.9413 ± 0.0023	0.8861 ± 0.0048
SMS	0.6924 ± 0.0005	0.5241 ± 0.0003	0.6326 ± 0.1221	0.6095 ± 0.0433	0.8859 ± 0.0143	0.8657 ± 0.0178	0.6660 ± 0.0801	0.6053 ± 0.0820
BP	0.3717 ± 0.1459	0.5241 ± 0.0000	0.2667 ± 0.0000	0.5028 ± 0.0000	0.5387 ± 0.0000	0.4700 ± 0.0000	0.1788 ± 0.0000	0.1048 ± 0.0000
	KrVsKpEW		Moons		SpectEW		Tic-tac-toe
	ACC	AUC	ACC	AUC	ACC	AUC	ACC	AUC
RADE	0.8140 ± 0.0222	0.8135 ± 0.0220	0.9800 ± 0.0000	0.9211 ± 0.0000	0.8091 ± 0.0251	0.7643 ± 0.0320	0.8294 ± 0.0383	0.7855 ± 0.0430
BBO	0.7508 ± 0.0641	0.7528 ± 0.0583	0.9800 ± 0.0000	0.9211 ± 0.0000	0.8032 ± 0.0264	0.7569 ± 0.0317	0.7426 ± 0.0365	0.6867 ± 0.0438
CJADE	0.6601 ± 0.0598	0.6611 ± 0.0583	0.9598 ± 0.0051	0.8412 ± 0.0201	0.7597 ± 0.0372	0.7453 ± 0.0443	0.7105 ± 0.0235	0.6310 ± 0.0376
IFDE	0.7792 ± 0.0439	0.7790 ± 0.0433	0.9800 ± 0.0000	0.9211 ± 0.0000	0.8180 ± 0.0279	0.7747 ± 0.0283	0.7726 ± 0.0279	0.7313 ± 0.0285
SCJADE	0.6857 ± 0.0393	0.6842 ± 0.0384	0.9613 ± 0.0062	0.8474 ± 0.0243	0.7684 ± 0.0344	0.7573 ± 0.0428	0.7148 ± 0.0287	0.6489 ± 0.0272
SEDE	0.7996 ± 0.0272	0.8007 ± 0.0275	0.9591 ± 0.0136	0.8386 ± 0.0539	0.8046 ± 0.0234	0.7534 ± 0.0297	0.7087 ± 0.0316	0.6368 ± 0.0501
SHADE	0.7962 ± 0.0305	0.7960 ± 0.0309	0.9807 ± 0.0027	0.9237 ± 0.0106	0.8166 ± 0.0248	0.7767 ± 0.0251	0.7464 ± 0.0360	0.6930 ± 0.0439
SMS	0.6292 ± 0.0477	0.6187 ± 0.0537	0.1000 ± 0.0000	1.0000 ± 0.0000	0.7248 ± 0.0332	0.7231 ± 0.0389	0.7428 ± 0.0255	0.6842 ± 0.0307
BP	0.4726 ± 0.0000	0.5002 ± 0.0000	0.7547 ± 0.0431	0.0327 ± 0.1793	0.9198 ± 0.0000	0.4996 ± 0.0000	0.5653 ± 0.1473	0.5120 ± 0.0301
	Gaussians		XOR
	ACC	AUC	ACC	AUC
RADE	0.8488 ± 0.0049	0.7482 ± 0.0073	0.8776 ± 0.0067	0.7610 ± 0.0138
BBO	0.8499 ± 0.0051	0.7498 ± 0.0077	0.8767 ± 0.0082	0.7592 ± 0.0155
CJADE	0.8342 ± 0.0094	0.7287 ± 0.0112	0.8483 ± 0.0178	0.7094 ± 0.0327
IFDE	0.8469 ± 0.0031	0.7453 ± 0.0046	0.8814 ± 0.0064	0.7701 ± 0.0103
SCJADE	0.8297 ± 0.0140	0.7255 ± 0.0179	0.8295 ± 0.0275	0.6684 ± 0.0577
SEDE	0.8303 ± 0.0100	0.7259 ± 0.0125	0.8160 ± 0.0531	0.6458 ± 0.1090
SHADE	0.8460 ± 0.0008	0.7438 ± 0.0011	0.8829 ± 0.0040	0.7718 ± 0.0074
SMS	0.8444 ± 0.0049	0.7418 ± 0.0075	0.9826 ± 0.0041	0.9652 ± 0.0081
BP	0.5000 ± 0.0000	0.1417 ± 0.0000	0.5000 ± 0.0000	0.0000 ± 0.0000

reports the classification performance of the proposed RADE algorithm against eight baseline methods on 14 benchmark datasets. Bold values indicate the best result among all algorithms for each dataset, while underlined values denote the second best.

The results show that RADE demonstrates excellent overall performance across various datasets. Specifically, RADE achieves the best classification accuracy on six datasets: BUPA (0.6333), BreastEW (0.9298), Exactly (0.7367), Heart (0.9395), KrVsKpEW (0.8140), and Tic-tac-toe (0.8294). Additionally, RADE obtains the second-best results on four other datasets, Australia, CongressEW, German, and Gaussians, indicating robust competitiveness. Notably, RADE achieves perfect classification accuracy on the Moons dataset (0.9800) with zero variance, demonstrating reliable convergence on clean, well-structured data.

Comparing RADE to individual baselines reveals several important insights. On the Australia dataset, DPDE slightly outperforms RADE by a margin of 0.52% (0.8585 vs. 0.8533), although both exhibit low variance. However, on more complex datasets such as Heart, RADE delivers the highest accuracy, surpassing DPDE (0.9395 vs. 0.9120) and clearly outperforming other methods, including gradient-based BP (0.5387). On BreastEW, which contains both linear and nonlinear features, RADE surpasses all competitors, including ensemble-based SEDE (0.9298 vs. 0.9196).

In contrast, some methods, while excelling on specific datasets, display inconsistent performance elsewhere. For instance, DPDE achieves the highest accuracy on Australia and CongressEW (0.9703) but performs poorly on BUPA, KrVsKpEW, and Tic-tac-toe. Similarly, BP shows high accuracy on SpectEW (0.9198) but fails on most other datasets, particularly on Australia, German, and XOR, where its performance falls close to random guessing.

An interesting observation is made for the XOR dataset, known for its strong logical structure. Here, the SMS algorithm yields the highest accuracy (0.9826), slightly outperforming SHADE (0.8829), RADE (0.8776), and DPDE (0.8814). This suggests that SMS, though weaker overall, may exploit discrete decision boundaries under ideal conditions. However, its performance on most real-world datasets remains unstable with large variances, such as on Ionosphere (STD = 0.0801) and Heart (STD = 0.0143).

In terms of robustness, RADE consistently achieves a low standard deviation across all datasets, with values mostly below 0.03, showing reliable performance regardless of data variability. Notably, on datasets such as BreastEW, KrVsKpEW, and SpectEW, RADE offers both high accuracy and low variance, validating the strength of its adaptive mechanisms and structure-aware mutation strategy.

The inclusion of the AUC allows us to observe how well RADE distinguishes between classes in both balanced and unbalanced settings. Notably, RADE achieves the highest AUC values on key datasets such as BreastEW, Exactly, German, Heart, KrVsKpEW, and Tic-tac-toe, indicating a strong discrimination capability. On datasets like Australia, CongressEW, and Gaussians, RADE consistently maintains competitive AUC scores, reflecting its robustness against false positives and false negatives.

Additionally, the advantage of RADE in maintaining high AUC values across various datasets confirms its ability to handle class imbalance effectively, preventing the model from ‘buying’ overall accuracy at the cost of misclassifying minority classes. This finding strengthens the empirical evidence that RADE optimizes decision boundaries while maintaining interpretability and efficiency.

Furthermore,

Table 3. Average training time (in seconds) of different algorithms.

RADE	BBO	CJADE	IFDE	SCJADE	SEDE	SHADE	SMS	BP
26.98	22.68	19.20	20.44	19.20	42.83	18.30	20.04	5.80

reports the average training time (in seconds) required by each competing algorithm under identical hardware and evaluation budgets. Several key observations can be made: (1) RADE strikes a favourable trade-off between speed and accuracy. Although RADE is 8.68 slower than the quickest competitor (SHADE, 18.30 s vs. 26.98 s), it delivers the highest ACC and AUC scores (see Table 2). Considering training is performed offline, this modest additional cost is acceptable when weighed against the substantial gains in predictive performance and robustness. (2) Training time does not translate directly to deployment latency. After optimization, RADE prunes redundant dendrites and converts the remaining ones into compact logical expressions. Consequently, the inference path relies on a minimal set of logic gates, making the deployed model at least as fast—and often faster—than those produced by the baseline algorithms. (3) Memory-based adaptation incurs negligible overhead. The slight increase in RADE’s runtime stems mainly from its memory-guided parameter adaptation. Our study confirms that this mechanism improves convergence speed and solution quality while adding less than 2 s of training overhead on average. (4) SEDE’s long runtime illustrates the diminishing returns of larger ensembles. SEDE records the slowest training time (42.83 s), yet its accuracy remains inferior to RADE and several other DE variants. This highlights that enlarging the ensemble of mutation strategies does not necessarily yield proportional performance benefits and may hinder the practicality of the algorithm. In summary, the results in Table 3 demonstrate that RADE achieves a compelling balance between computational cost and model quality, reinforcing its suitability for scenarios where training resources are limited and inference efficiency and interpretability are paramount.

In conclusion, RADE demonstrates an effective balance between accuracy and stability, outperforming or closely matching top-performing methods across a wide variety of datasets. The results confirm that RADE’s resource-adaptive strategies and compatibility with dendritic architectures contribute to both performance and robustness, making it a strong candidate for lightweight and interpretable neural learning tasks.

4.6. Convergence and Robustness Analysis

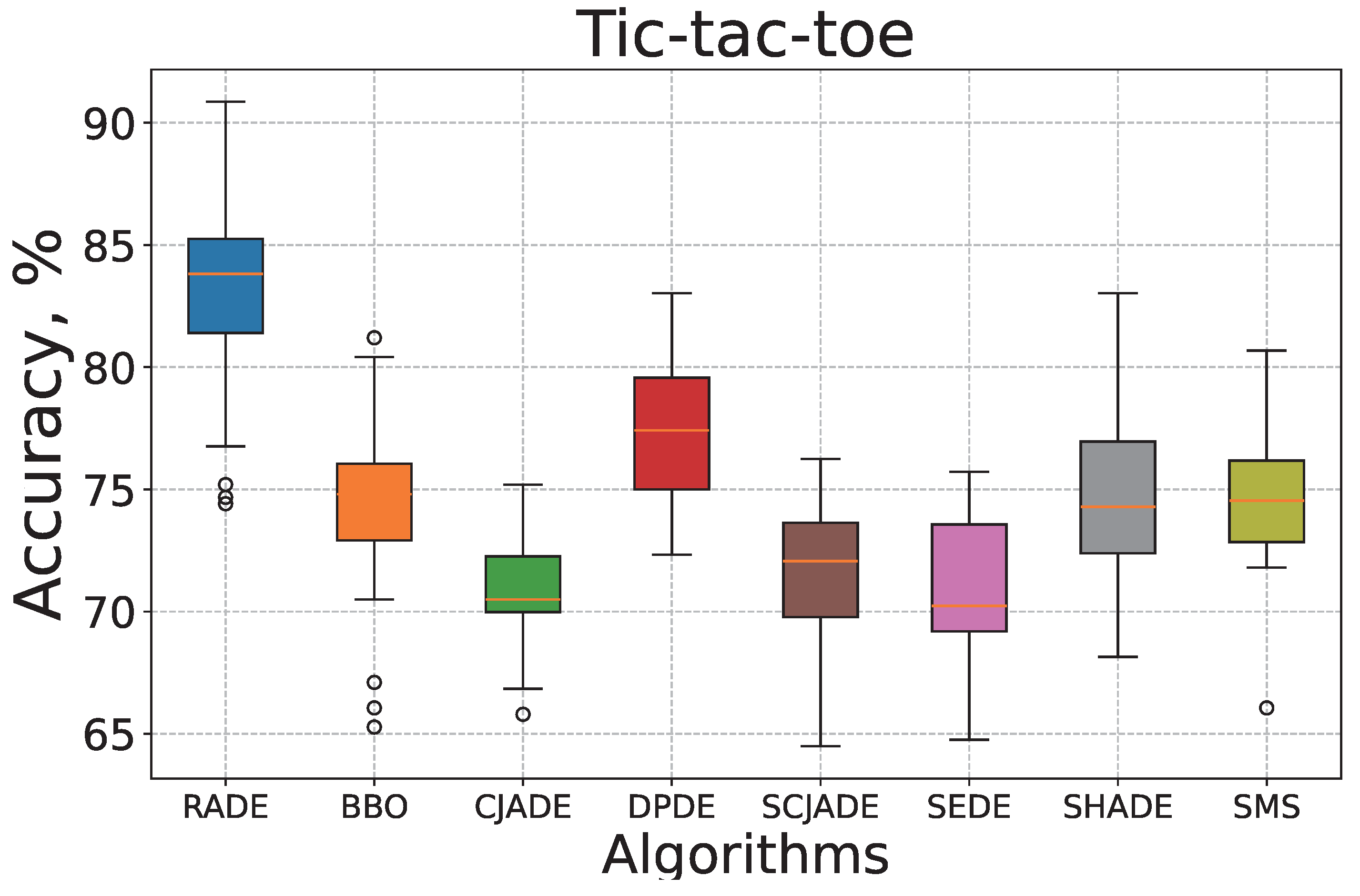
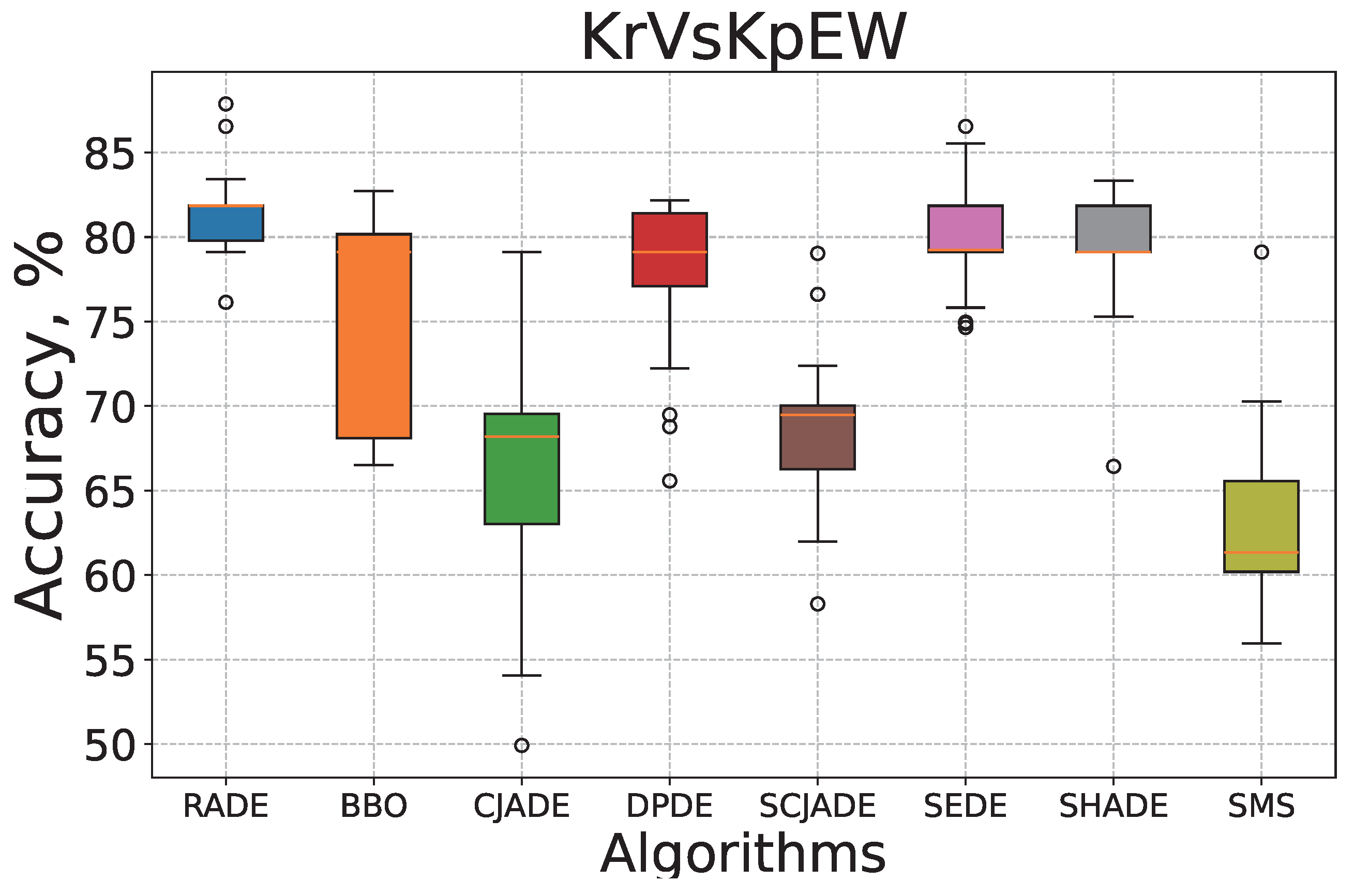
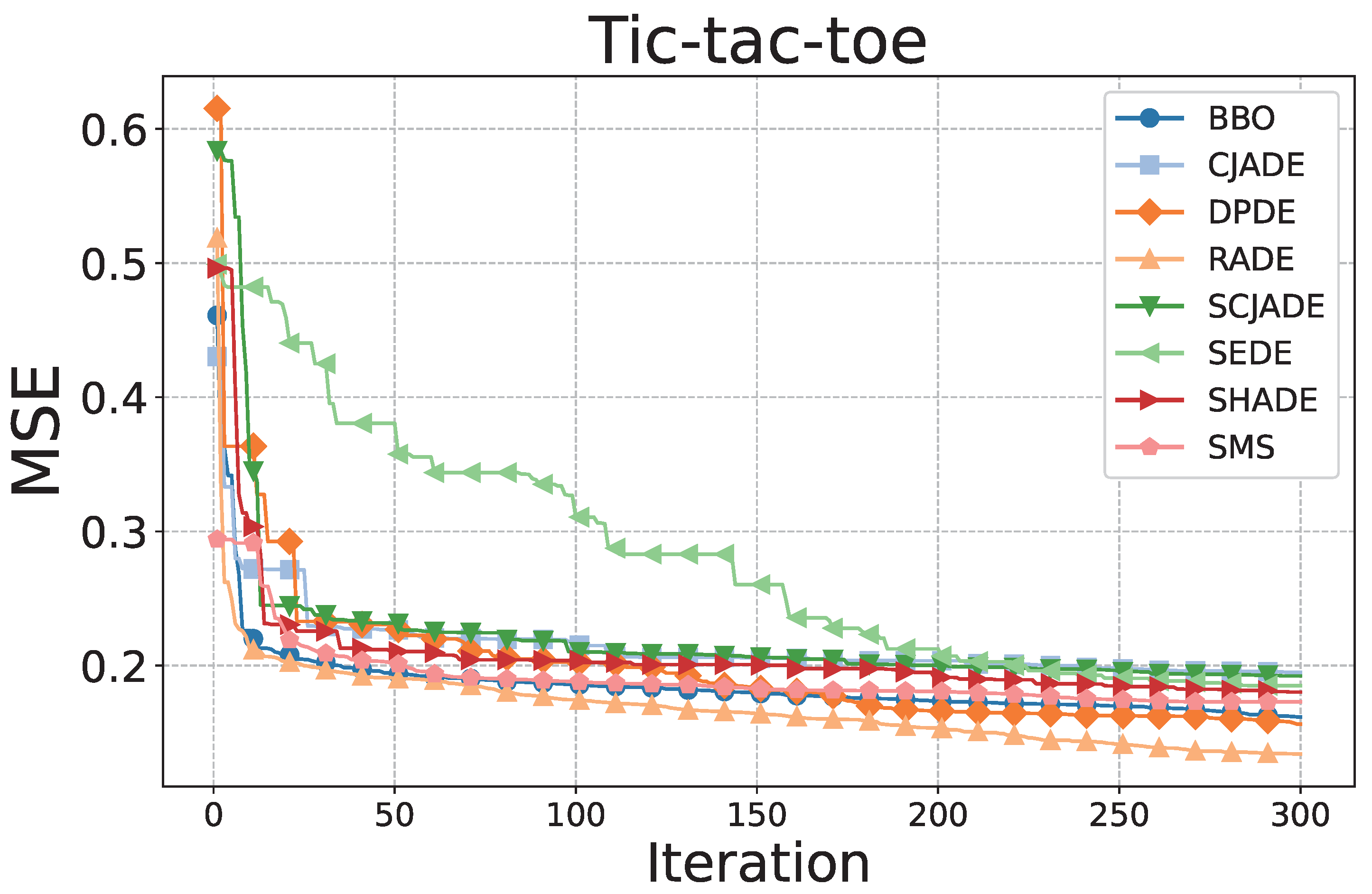
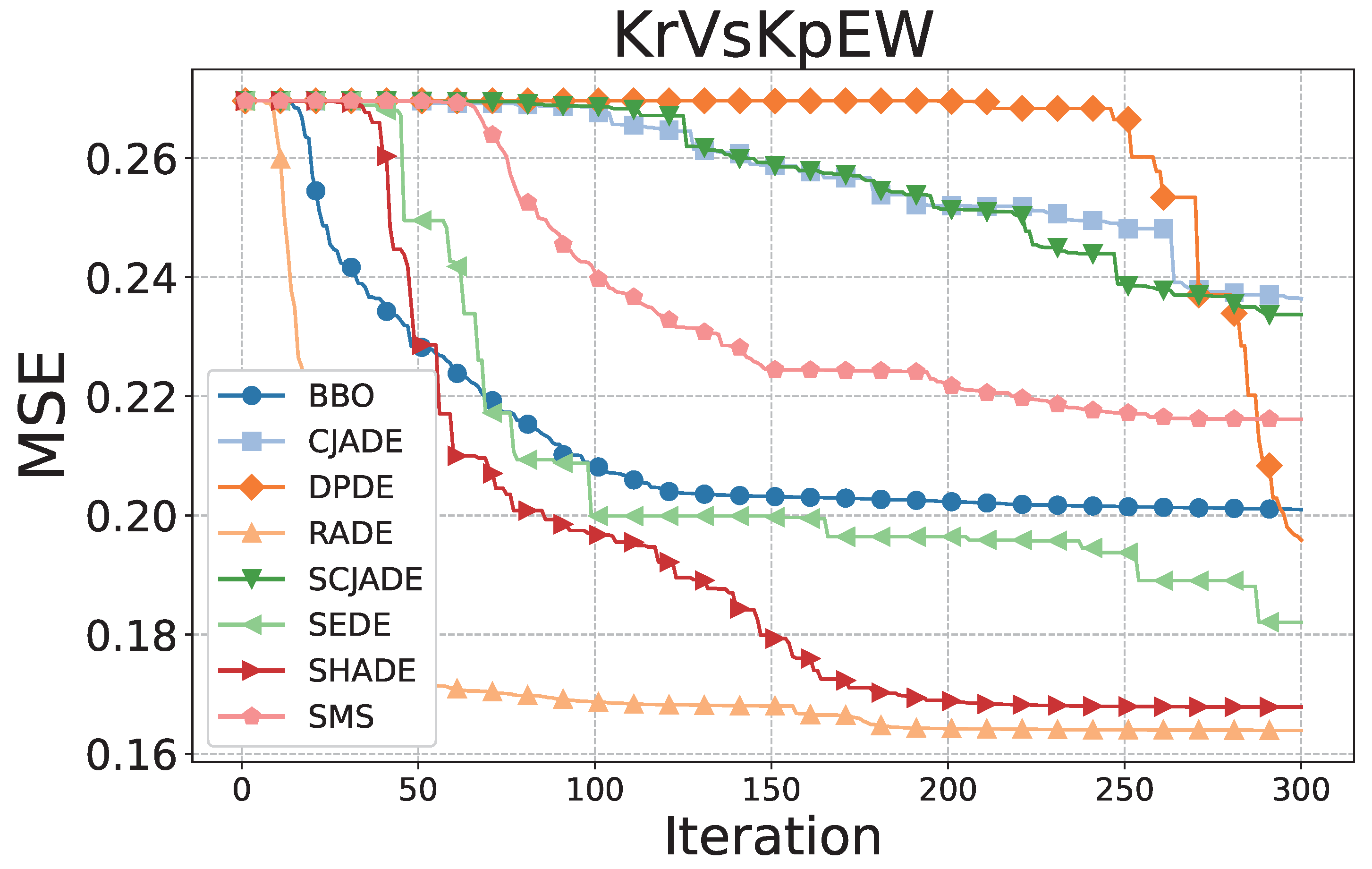
To further examine the efficiency and reliability of the proposed RADE algorithm, we conduct convergence and robustness analyses on two representative datasets: Tic-tac-toe and KrVsKpEW. Figure 3 and Figure 4 depict the convergence curves in terms of mean squared error (MSE) over 300 iterations. Meanwhile, Figure 5 and Figure 6 present the corresponding box–whisker plots of the classification accuracy obtained by all algorithms across 30 independent runs.

As shown in Figure 3, on the Tic-tac-toe dataset, RADE demonstrates the fastest convergence and reaches the lowest final MSE value among all compared methods. Its curve rapidly declines within the first 30 iterations and gradually stabilizes near 0.17, suggesting both fast learning and strong local refinement. This rapid convergence indicates RADE’s superior ability to quickly adjust dendritic neuron structures and optimize synaptic weights, enhancing learning efficiency. The stability near 0.17 reflects effective avoidance of overfitting and solid convergence behavior. In contrast, algorithms such as SCJADE and SMS show significantly slower convergence rates and higher final errors, highlighting their inefficiency in training DNMs on this logical classification task. These methods tend to oscillate or stagnate during training, suggesting an inadequate exploration–exploitation balance and suboptimal parameter adaptation.

On the more challenging KrVsKpEW dataset (Figure 4), RADE again outperforms others with a stable and monotonic descent throughout the training process. This dataset contains more complex, nonlinear decision boundaries, making it a challenging benchmark for evolutionary optimization. RADE’s smooth and continuous convergence path showcases its adaptive scaling mechanism, which dynamically balances global exploration with local exploitation. While some algorithms (e.g., DPDE and CJADE) stagnate early or experience late drops in performance, RADE consistently reduces error without sharp oscillations, signifying robust parameter control and effective synaptic pruning. Notably, methods such as SHADE and SEDE also demonstrate strong performance in this scenario but still converge to slightly higher MSE values compared to RADE, suggesting less efficient dendritic adjustments.

Figure 5 and Figure 6 provide a statistical view of accuracy distributions. For Tic-tac-toe, RADE achieves the highest median accuracy and the narrowest interquartile range, indicating both high prediction precision and low variance across runs. The interquartile range (IQR) is tightly clustered, which reflects the algorithm’s stability under varying initializations and random seeds. This robustness is attributed to RADE’s adaptive mutation and pruning strategies, which consistently enhance local dendritic adjustments. In contrast, BBO, SMS, and CJADE exhibit wider boxes and more outliers, implying unstable behavior under different random seeds. This instability suggests that these methods struggle to maintain consistent synaptic configurations during iterative updates, leading to greater performance variability.

On KrVsKpEW, RADE again secures a high median with a tightly bounded distribution, further confirming its robustness. Although DPDE and SEDE show comparable central tendencies, their distributions include more extreme values and wider spreads, suggesting less consistency in optimization. The variability in these methods is indicative of weaker dendritic pruning mechanisms and less effective synaptic control. CJADE and SMS, in particular, suffer from substantial instability, with performance occasionally dropping below 60%, making them unsuitable for high-reliability applications. RADE’s narrower spread and higher median accuracy highlight its capacity for stable and consistent learning across different seeds, driven by its memory-based adaptive scaling and efficient dendritic learning.

Overall, these visualizations confirm that RADE not only converges faster but also maintains stability across iterations, leading to superior classification accuracy and robustness compared to its evolutionary counterparts. These characteristics are critical for deploying dendritic neuron models in real-world classification tasks where stability and reliability are paramount.

4.7. Additional Discussion Regarding the Scaling Factor

In RADE, the scaling factor F is generated based on a Cauchy distribution, introducing stochastic perturbations during the evolution process. To evaluate the effect of different strategies for updating F, we conduct two additional experiments using a time-dependent adjustment mechanism. This approach allows for progressive refinement of the search behavior, as defined in the following two equations:

$$F=0.4+0.5\times \left(1-{\displaystyle \frac{\mathrm{nFES}}{\mathrm{FES}}}\right)$$

(21)

$$F=0.2+0.3\times \left(1-{\displaystyle \frac{\mathrm{nFES}}{\mathrm{FES}}}\right)$$

(22)

In Equations (21) and (22), $\mathrm{nFES}$ represents the current number of function evaluations, and $\mathrm{FES}$ denotes the maximum number of function evaluations allowed. The scaling factor F is designed to decrease linearly as the optimization progresses, encouraging broad exploration during the early stages and more focused convergence near the end of the search. This time-dependent adjustment mechanism is inspired by strategies employed in traditional DE variants, where the dynamic adjustment of F promotes a better exploration–exploitation balance.

To compare the effectiveness of these two strategies against the original Cauchy-based generation of F in RADE, we evaluate all three methods on a series of classification problems. The results are presented in

Table 4. Accuracy of the scaling factor F on the classification problem using Cauchy’s random selection versus two cases with fixed strategies.

	Australia	BUPA	BreastEW	CongressEW	Exactly	German	Heart
F-Cauchy	0.8533 ± 0.0109	0.6333 ± 0.0368	0.9298 ± 0.0114	0.9644 ± 0.0124	0.7367 ± 0.0387	0.7539 ± 0.0167	0.9395 ± 0.0231
Equation (21)	0.8533 ± 0.0119	0.6352 ± 0.0395	0.9180 ± 0.0312	0.9664 ± 0.0068	0.7018 ± 0.0124	0.7506 ± 0.0145	0.9056 ± 0.0212
Equation (22)	0.8443 ± 0.0284	0.5990 ± 0.0549	0.8547 ± 0.0330	0.9562 ± 0.0153	0.6817 ± 0.0398	0.7069 ± 0.0411	0.8875 ± 0.0104
	Ionosphere	KrVsKpEW	Moons	SpectEW	Tic-tac-toe	Gaussians	XOR
F-Cauchy	0.9402 ± 0.0086	0.8140 ± 0.0222	0.9800 ± 0.0000	0.8091 ± 0.0261	0.8294 ± 0.0383	0.8488 ± 0.0049	0.8776 ± 0.0067
Equation (21)	0.9267 ± 0.0600	0.8016 ± 0.0333	0.9771 ± 0.0072	0.8251 ± 0.0192	0.8001 ± 0.0437	0.8458 ± 0.0011	0.8698 ± 0.0095
Equation (22)	0.3296 ± 0.1874	0.7113 ± 0.0710	0.9571 ± 0.0109	0.8016 ± 0.0276	0.7340 ± 0.0303	0.8239 ± 0.0319	0.8083 ± 0.0559

.

The experimental results demonstrate that RADE’s Cauchy-based random selection generally outperforms both time-dependent strategies in terms of classification accuracy across most datasets. In particular, the dynamic variability introduced by the Cauchy distribution enables more effective exploration during the early search phases, which translates to higher overall accuracy. Furthermore, the time-dependent strategy with $0.4+0.5$ performs slightly better than $0.2+0.3$ in most cases, indicating that a broader range of scaling factors contributes to stronger exploration capabilities. These findings validate the effectiveness of RADE’s stochastic perturbation mechanism and justify the choice of a Cauchy-based strategy for scaling factor generation.

4.8. Interpretable Morphology and Logical Representation

In addition to quantitative accuracy metrics, one of the most distinguishing features of the proposed RADE algorithm is its ability to yield interpretable and compact dendritic neuron structures. Figure 7, Figure 8, Figure 9 and Figure 10 present a detailed visual analysis of the model learned by RADE on the Australia dataset. Similarly, Figure 11, Figure 12, Figure 13 and Figure 14 showcase the structural outcome on the Tic-tac-toe dataset.

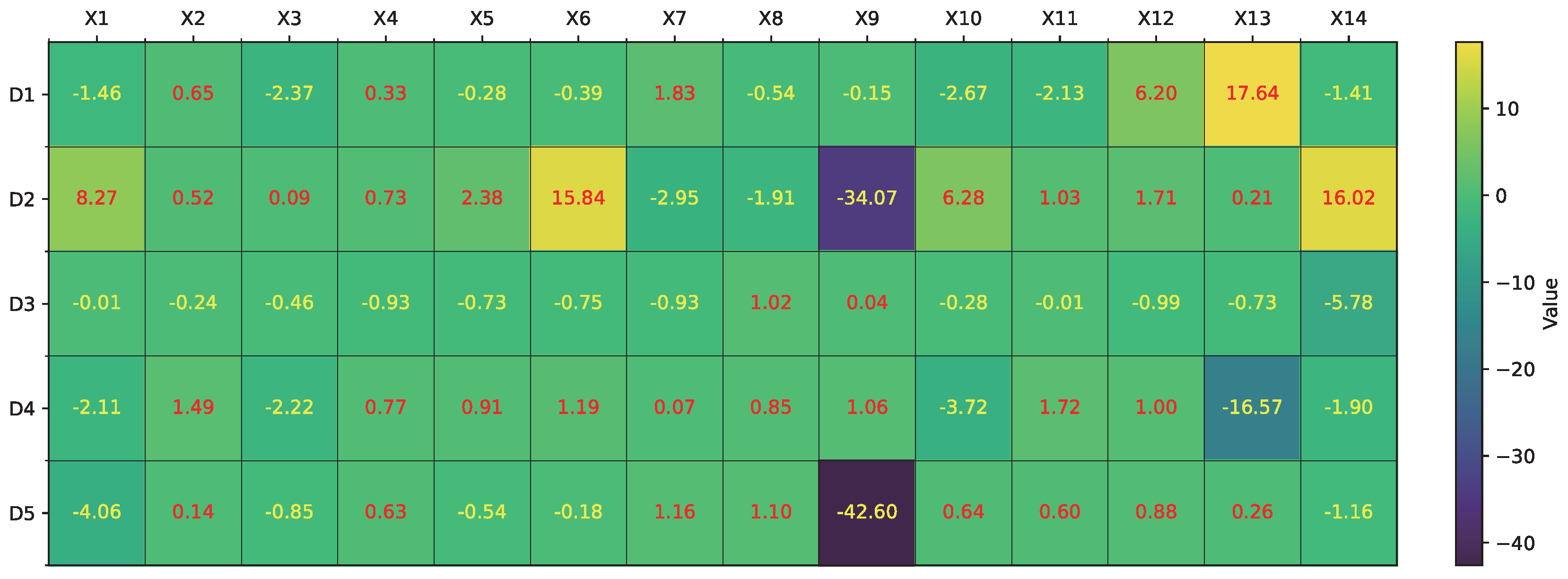
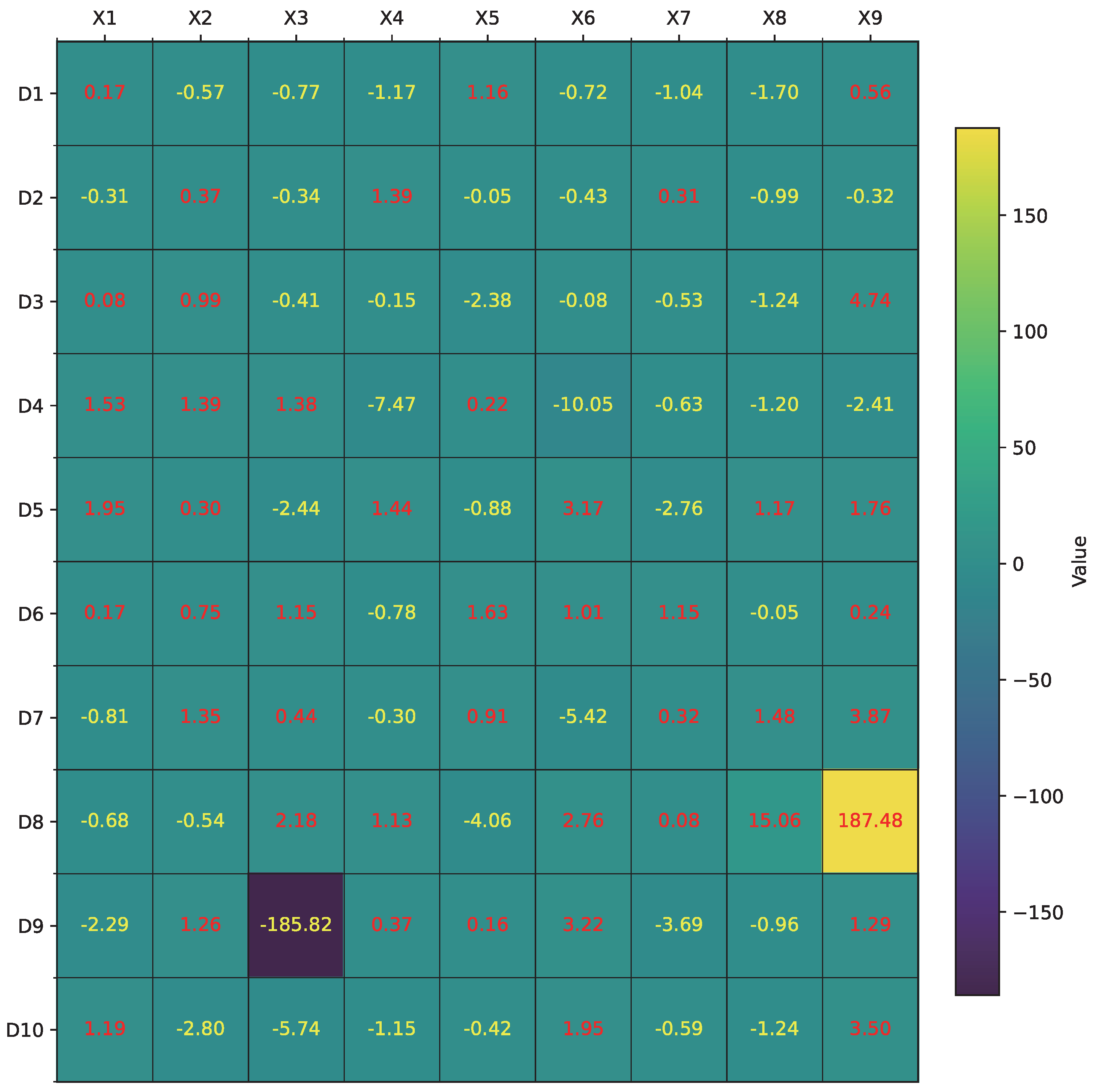
Figure 7 illustrates the learned $\theta =q/w$ values across dendrites and synapses for all input features. This heatmap highlights the diverse distribution of synaptic contributions and effectively distinguishes strong activations (e.g., $X_{13}$ on $D_1$, $X_6$ on $D_2$) from near-zero or highly negative values (e.g., $X_9$ on $D_5$), indicating potential candidates for pruning.

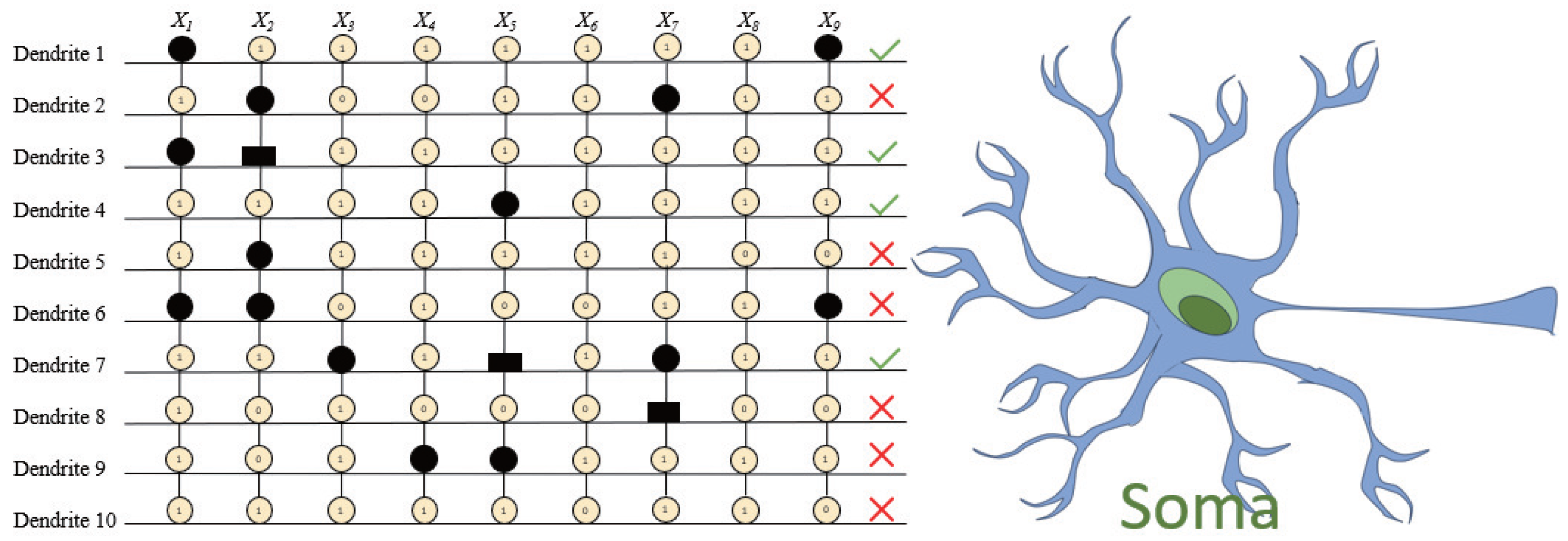
Based on these weight distributions, RADE proceeds to convert the learned parameters into a symbolic dendritic structure (Figure 8), where different symbols (circles, squares, etc.) denote different synaptic connection types—constant-1, constant-0, direct, and inverse—defined by the threshold criteria in Section 3. Synapses with constant outputs or minimal impact are systematically removed, yielding the simplified architecture in Figure 9, where only dendrite $D_4$ remains active with five retained synapses ($X_4$, $X_5$, $X_7$, $X_8$, $X_{12}$).

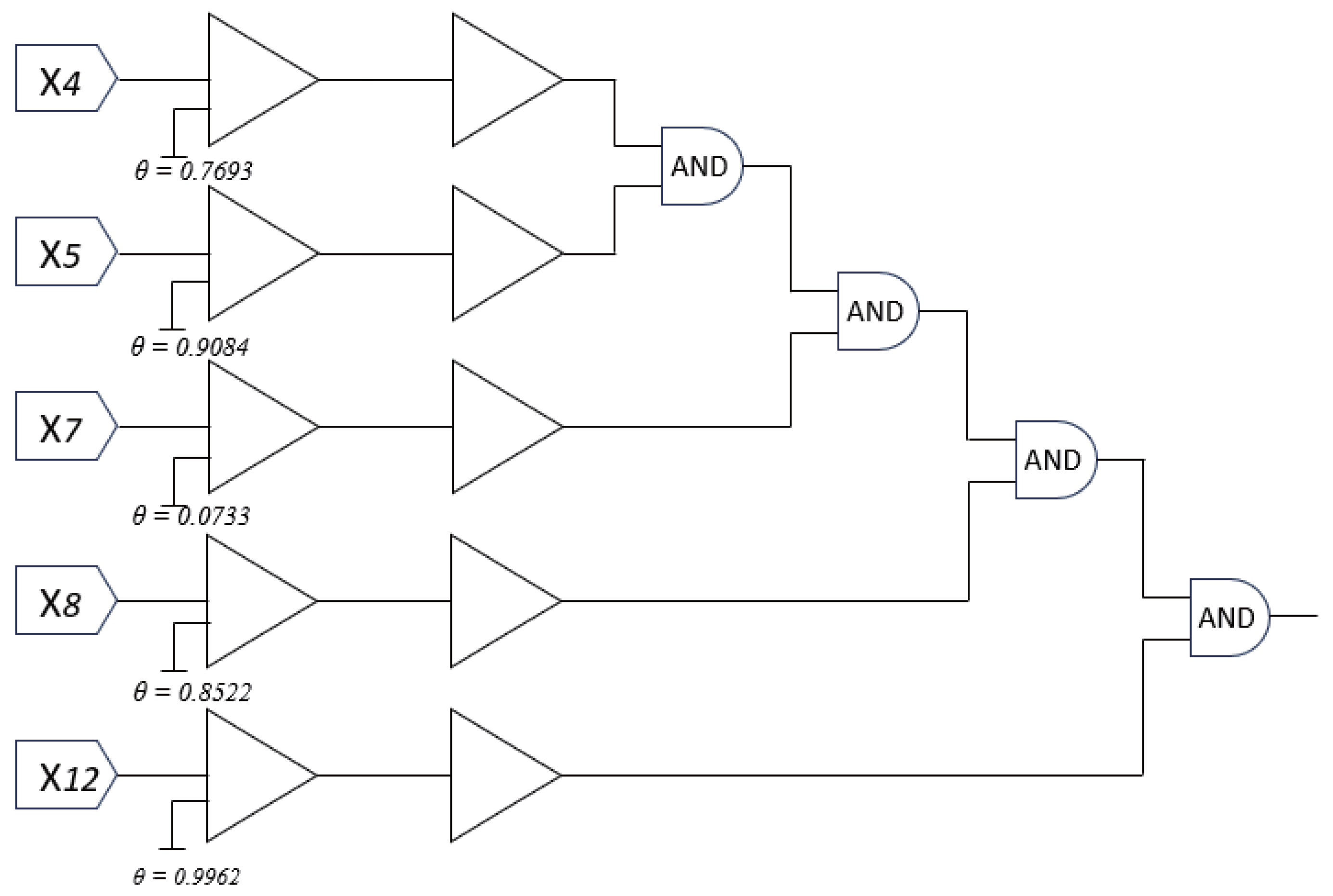
This pruned dendrite can be seamlessly translated into a digital logic circuit, as illustrated in Figure 10. Each input undergoes a threshold-based comparator, and the resulting binary decisions are aggregated via logical AND gates, emulating the nonlinear integration performed by the soma. This conversion highlights a unique advantage of DNMs trained by RADE: their compatibility with neuromorphic hardware and explainable AI paradigms.

A similar process is observed for the Tic-tac-toe dataset. Figure 11 shows the learned $\theta$ values across ten dendrites, indicating more complex and distributed contributions than in the previous case. The resulting morphology in Figure 12 reveals redundant or inactive dendrites, which are removed during pruning (Figure 13), leaving only four functional branches. The final logical realization of the pruned model is depicted in Figure 14. Notably, the decision rule involves a combination of AND and OR gates, demonstrating the expressiveness of dendritic logic compared to linear perceptrons. This interpretable rule-based format opens up possibilities for verification, simplification, and rule extraction, which are often elusive in deep neural networks.

To further evaluate the interpretability and implementation efficiency of the RADE-trained DNM, we conduct a detailed analysis of the morphological complexity and hardware cost for the Australia and Tic-tac-toe datasets.

Table 5. Pruning and logic gate stats of the DNM after RADE learning.

Attribute	Australia	Tic-Tac-Toe
Initial Synapses	70	90
Final Active Synapses	5	8
Pruning Rate	93%	91%
Final Dendrites	1	4
Inputs Used	5 ($X_4$, $X_7$, $X_8$, $X_{10}$, $X_{12}$)	6 ($X_1$, $X_2$, $X_3$, $X_5$, $X_7$, $X_9$)
Gates	4 AND (tree)	4 AND + 3 OR
Comparators	5	8

summarizes the pruning statistics, including the initial synapses, final active synapses, pruning rate, final dendrites, input features, logic gates, and comparators. These metrics provide a comprehensive view of how RADE optimizes DNM structures for both interpretability and efficient hardware implementation.

The structural optimization achieved by RADE is evident in the significant pruning rates observed. For the Australia dataset, the model retains only 5 out of 70 original synapses, resulting in a pruning rate of 93%. The final logical representation is simplified to a four-AND tree structure with five comparators. This indicates not only morphological sparsity but also logical simplicity, which facilitates direct hardware implementation. Similarly, the Tic-tac-toe dataset is pruned to 8 active synapses from an initial 90, achieving a pruning rate of 91%. The optimized logic circuit comprises four AND gates and three OR gates, along with eight comparators, providing a well-structured decision logic with minimal hardware cost.

These results demonstrate that RADE not only improves model interpretability but also significantly reduces hardware costs by minimizing synaptic connections and logical complexity. This makes RADE-trained DNMs highly suitable for edge AI applications where memory and energy constraints are critical. In conclusion, the pruning strategy enforced by RADE balances both morphological complexity and hardware efficiency, achieving a compact and interpretable neuron model representation.

These qualitative findings, combined with the robust performance observed in quantitative evaluations (Table 2), establish RADE not only as a powerful optimizer for DNMs but also as a facilitator of interpretable, efficient, and hardware-friendly neural models.

4.9. Limitations and Practical Benefits of RADE

RADE offers several practical benefits that make it particularly effective for DNM optimization. First, its resource-adaptive mechanism allows it to optimize DNMs with minimal computational overhead, which is crucial for real-time applications and deployment on edge devices. Inspired by dendritic processing in biological neurons, RADE effectively handles nonlinear decision boundaries, enhancing both interpretability and structural learning during optimization. Furthermore, the Cauchy-based scaling strategy enables robust global search capabilities, promoting diverse exploration of the solution space and reducing the risk of becoming trapped in local minima. This is complemented by RADE’s memory-based parameter adaptation, which dynamically adjusts evolutionary parameters to maintain stability even in complex optimization landscapes. Its lightweight architecture also ensures scalability, allowing it to tackle larger problems without substantial increases in memory or processing costs.

Another strength of the proposed DNM optimized by RADE is its reliance on logical gate representations for decision-making. This design inherently provides a certain level of resilience against small input perturbations. Unlike traditional neural networks that rely on continuous-valued weights and activation functions, the DNM’s logical operations (e.g., AND, OR, NAND) require discrete condition satisfaction to activate specific pathways. As a result, minor fluctuations in input values are less likely to trigger erroneous activations, enhancing robustness. Moreover, the multi-branch structure of DNMs allows for a localized decision logic, where individual dendrites independently process specific signal patterns. This compartmentalized processing further isolates the impact of adversarial perturbations, preventing local disturbances from propagating through the entire network. In addition, the optimization strategy employed by RADE, with its lightweight archiving and adaptive parameter control, promotes diverse solutions during training, reducing the chances of overfitting to adversarially biased samples. This distributed learning mechanism equips the model with a broader understanding of decision boundaries, improving its resistance to gradient-based attacks.

Despite these strengths, RADE also has some limitations. One notable challenge is its sensitivity to initialization, where suboptimal parameter settings may impact convergence speed, especially in highly non-convex search spaces. Additionally, while the external archive mechanism improves search diversity and memory, it introduces a slight memory overhead compared to standard DE variants. In very high-dimensional optimization tasks, the adaptive memory and pruning strategies may also elevate computational loads, requiring further optimization for efficiency. Finally, while RADE demonstrates strong empirical performance, its theoretical analysis is currently focused mainly on convergence guarantees. Future work is required to extend theoretical explorations, particularly regarding its complexity bounds and generalization capabilities.

5. Conclusions

In this study, we have proposed RADE (Resource-Adaptive Differential Evolution), a novel evolutionary optimization algorithm specifically designed to enhance the training of dendritic neuron models (DNMs) in lightweight and interpretable classification tasks. Inspired by biological evolution and dendritic computation, RADE incorporates a series of resource-aware and biologically motivated mechanisms, including dynamic population partitioning, reinforced mutation guided by poor individuals, adaptive parameter control based on historical memory, and a lightweight external archive for diversity maintenance. These innovations collectively enable RADE to balance exploration and exploitation effectively, adapt to dynamic search landscapes, and maintain structural compactness throughout the learning process.

Extensive experiments conducted on 14 benchmark datasets—covering both real-world and synthetic classification scenarios—demonstrate that RADE consistently outperforms or matches the performance of state-of-the-art evolutionary algorithms such as BBO, CJADE, SHADE, and SCJADE in terms of classification accuracy, robustness, and convergence behavior. Moreover, RADE exhibits strong compatibility with the architectural principles of DNMs, facilitating structural pruning, morphological simplification, and hardware-friendly logical transformation. The resulting models not only exhibit high predictive performance but also offer clear interpretability through logic-based rules derived from the pruned dendritic structure.

From a practical perspective, RADE enables the development of resource-efficient and transparent AI systems, making it well suited for deployment in neuromorphic hardware, embedded platforms, and edge computing scenarios where energy and interpretability are crucial. Unlike traditional deep learning approaches that rely heavily on overparameterized networks and large-scale datasets, the proposed framework demonstrates that small-scale, biologically plausible architectures, when coupled with intelligent evolutionary optimization, can yield competitive results with significantly reduced computational costs.

While RADE primarily focuses on evolutionary optimization for DNM, we acknowledge that modern lightweight strategies, including Neural Architecture Search (NAS) for micro-Net architectures [66,67], post-training compression [68], quantization methods [69], and distillation approaches [70], have also achieved substantial progress in creating compact and explainable models. Nevertheless, RADE’s unique contribution lies in its biologically inspired dendritic structure combined with evolutionary pruning, which is distinct from the layer-wise compression and architecture search of NAS or distillation. Unlike traditional NAS methods, which often rely on gradient-based optimization, RADE performs symbolic optimization through logical gate representation, leading to more interpretable decision boundaries.

For future research, several promising directions can be explored. First, the integration of RADE with multi-objective optimization frameworks [71] could further enhance its ability to trade off accuracy, interpretability, and complexity simultaneously. Second, the application of RADE-optimized DNMs to tasks beyond classification—such as sequence modeling, control systems, or continual learning—offers a pathway toward more general-purpose and adaptive intelligent agents [72]. Third, hardware-level implementations of RADE-DNM logic circuits could be investigated for real-time and low-power AI applications [73].

In summary, RADE represents a biologically inspired and resource-conscious approach to optimizing dendritic learning systems. It offers a practical and theoretically grounded alternative to conventional deep learning methods, advancing the field of interpretable and energy-efficient artificial intelligence.