Graphical Approach: 2-Complete Decompositions of Groups

Abstract

Let G be a group and let $A_1,A_2$ be nonempty subsets of G. We say that $[A_1,A_2]$ is a 2-complete decomposition of G if $G=A_1{A}_2$ and $A_1,A_2$ are disjoint. In this paper, we define a factor graph of a group and determine the symmetrical relationship between factor graphs and 2-complete decompositions. We then characterize groups that have a complete decomposition $[A_1,A_2]$ where one of the sets, $A_1,A_2$, is of size two, or of size three and contains the identity.

1. Introduction

Let G be a group and let $A_1,A_2,\dots ,A_k$ be nonempty subsets of G. The product of $A_1,A_2,\dots ,A_k$ is defined to be the set

$$A_1{A}_2\dots A_k=\{a_1{a}_2\dots a_k:a_i\in A_i\mathrm{for}i=1,2,\dots ,k\}.$$

The sequence $A_1,A_2\dots ,A_k$ is said to form a factorization of G if each element in G can be uniquely expressed as a product of $a_1,a_2,\dots ,a_k$ with $a_i\in A_i$ for each $i=1,2,\dots ,k$. Hajós [1] introduced the concept of factoring a group into its subsets to reformulate a geometry problem by Minkowski [2]. The reformulated problem was solved in [3] and the result is now known as Hajós’s Theorem.

Let G be a group and let $A,B$ be subsets of G with some given properties. A problem of interest is to determine the structure of G when $G=AB$. For example, Itô [4] proved that a group which is a product of two abelian subgroups must be metabelian. The reader may refer to the survey by Amberg and Kazarin [5] for results on the structure of a group which is a product of two subgroups, each with properties different from one another.

A related problem is to determine the structure of a group G when G can be factorized as a product of two sets with some given properties. A nonempty subset A of an abelian group G is said to be periodic if there exists a nonidentity element, $g\in G$, such that $Ag=A$. An abelian group G is said to have the Hajós property if, in each factorization $G=AB$, one of the sets $A,B$ is periodic. Hajós [6] initiated the program of classifying finite abelian groups with the Hajós property. A complete list of these groups was given by Sands [7]. In a related work, Levy and Maróti [8] showed that a group G can be factorized as a product of two normal subsets, say X and Y, if and only if G is a central product of $\langle X\rangle$ and $\langle Y\rangle$, and the subgroup $\langle X\rangle \cap \langle Y\rangle$ satisfies certain conditions. A study on finite groups that can be factorized as a product of normal subsets can also be found in [9].

We define a complete decomposition of a group as follows:

Definition 1.

Let G be a group and let $A_1,A_2,\dots ,A_k(k>1)$ be nonempty subsets of G. The sequence $[A_1,A_2,\dots ,A_k]$ is a complete decomposition of G if

(i) 

$G=A_1{A}_2\dots A_k$, and

(ii) 

$A_i\cap A_j=⌀$ for all $i,j=1,2,\dots ,k$ with $i\ne j$.

The sets $A_1,A_2,\dots ,A_k$ are called the factors of the complete decomposition. If G is finite, then the sum ${\sum }_{i=1}^k|A_i|$ is called the size of the complete decomposition.

The product representation in a complete decomposition is not necessarily unique, distinguishing it from a group factorization, where uniqueness is required. For a subset $A\subseteq G$ of an additive group G, the difference set of A is defined as $A-A=\{a_1-a_2:a_1,a_2\in A\}$, which captures all elements expressible as differences of elements in A. For subsets $A,B$ of G, $A,B$ is a factorization of G if and only if $G=A+B$ and $(A-A)\cap (B-B)=\left\{0\right\}$. In contrast, a complete decomposition $[A,B]$ of a group G (typically considered in multiplicative context in this paper) requires $A\cap B=\varnothing$ and $G=AB$, focusing on the product of two disjoint subsets that cover the entire group without requiring unique representation.

Chin and Chen [10] proved that every cyclic group of order at least six has a complete decomposition. Chin, Wang, and Wong [11] extended this result by showing that every abelian group with at least six elements has a complete decomposition. In [12], Chin, Wang, and Wong determined the minimum size of complete decompositions of finite cyclic groups. Chin, Wang, and Wong [13] characterized all finite abelian groups that have a complete decomposition that is also a group factorization. Notice that the authors of [10,11,12,13] study the problem of complete decompositions in an abelian framework.

Given a complete decomposition $[A_1,A_2,\dots ,A_k]$ of a nonabelian group, G, permuting the sets $A_1,A_2,\dots ,A_k$ does not necessarily form a complete decomposition of G. Sin, Chen, and Wong [14] used multisets to construct complete decompositions of dihedral groups. As an application in cryptography, Sin and Chen [15,16] provided a key exchange protocol based on the complete decomposition search problem by using dihedral groups and generalized quaternion groups as the platform groups.

There are several types of graphs that can be associated with a group, such as Cayley graph, the commuting graph, the generating graph, and the power graph. Comparisons among these graphs can be found in [17]. Graphical methods are often used to classify or characterize groups. For example, Ghouchan and Azimi [18] introduced the notion of factorization graph to characterize finite groups with connected factorization graphs and classify finite groups with connected bipartite factorization graphs.

In this paper, we focus on complete decompositions with two factors, and we call such a complete decomposition a 2-complete decomposition. We investigate 2-complete decompositions using a graphical approach. The notion of a factor graph is defined and used to determine the criteria for each of the sets $\{x,y\}$ and $\{1,x,y\}$ to be a factor of some 2-complete decomposition, where x and y are group elements. As a consequence, we determine the structure of groups that have a 2-complete decomposition such that one of the factors is of size two, or of size three and contains the identity. We then use these results to prove that every group of size at least six has a complete decomposition.

2. Main Problems

For a nonempty subset A of a group G, we define $A^{-1}=\{a^{-1}:a\in A\}$ and $A^n=\{g_1{g}_2\dots g_n:g_i\in A\mathrm{for}i=1,2,\dots ,n\}$ for each positive integer n.

Lemma 1.

If a group G has a complete decomposition $[A,B]$, then the sequences $[B^{-1},A^{-1}]$, $[G\setminus B,B]$ and $[A,G\setminus A]$ are also complete decompositions of G.

Proof. 

Suppose that $A^{-1}\cap B^{-1}\ne ⌀$. Then, $a^{-1}=b^{-1}$ for some $a\in A$ and $b\in B$. It follows that $a=b\in A\cap B=⌀$; this is a contradiction. Hence, $A^{-1}\cap B^{-1}=⌀$. Let $g\in G$. Then, $g^{-1}=ab$ for some $a\in A$ and $b\in B$. This implies that $g=b^{-1}{a}^{-1}\in B^{-1}{A}^{-1}$. Thus, $G=B^{-1}{A}^{-1}$ and we conclude that $[B^{-1},A^{-1}]$ is a complete decomposition of G.

Now, $A\cap B=⌀$ implies that $A\subseteq G\setminus B$. Therefore, $G=AB\subseteq (G\setminus B)B\subseteq G$; hence, we get $G=(G\setminus B)B$. Since $(G\setminus B)\cap B=⌀$, we conclude that $[G\setminus B,B]$ is a complete decomposition of G. Similarly, $[A,G\setminus A]$ is also a complete decomposition of G. □

Corollary 1.

If a group G has a 2-complete decomposition, then G has a complete decomposition $[A,B]$, such that $1\in A$.

Proof. 

Let $[A,B]$ be a complete decomposition of G. If $1\in B$, then by Lemma 1, $[B^{-1},A^{-1}]$ is a complete decomposition of G, such that $1\in B^{-1}$. Suppose that $1\notin B$. By Lemma 1, $[G\setminus B,B]$ is a complete decomposition of G, such that $1\in G\setminus B$. Therefore, the corollary follows. □

Let G be a group that has a 2-complete decomposition, say $[A,B]$. If $|B|=1$, then $G=AB=A$; hence, $B=G\cap B=A\cap B=⌀$; this is a contradiction. Hence, $|B|\ge 2$. Based on this observation, one of the questions that arises is how small can $|B|$ be.

As in the case for $|B|$, we must have $|A|\ge 2$. By Corollary 1, we may assume that $1\in A$. Suppose that $|A|=2$, say $A=\{1,x\}$. Since $x\in G=AB$, it follows that $x=ab$ for some $a\in A$ and $b\in B$. If $a=1$, then $x=b\in B$; this contradicts the fact that $A\cap B=⌀$. If $a=x$, then $1=b\in B$; again, this is a contradiction. Thus, $|A|\ge 3$. A similar question that arises is how small can $|A|$ be.

We state the following problems that will be considered in Section 4:

Problem 1.

Let G be a group that has a 2-complete decomposition. What is the smallest size of a subset Y of G can there be so that there exists a subset X of G, such that $[X,Y]$ is a complete decomposition of G? If such a complete decomposition exists, what can be said about the structure of G?

Problem 2.

Let G be a group that has a 2-complete decomposition. What is the smallest size of a subset X of G with $1\in X$ so that there exists a subset Y of G, such that $[X,Y]$ is a complete decomposition of G? If such a complete decomposition exists, what can be said about the structure of G?

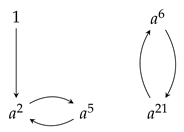
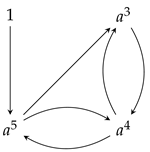
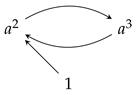
3. Factor Graph

In this section, we introduce the notion of factor graph which will be used to study 2-complete decompositions.

Definition 2.

Let G be a group and let $A,S$ be subsets of G. The directed graph $\mathcal{G}(A,S)$ is defined to be the graph with vertex set A and for any two vertices $x,y\in A$, there is a directed edge $(x,y)$ in the edge set if and only if $y^{-1}x\in S$. The graph $\mathcal{G}(A,S)$ is called a factor graph if

(1) 

$1\in A$;

(2) 

$A\cap S=⌀$;

(3) 

For each $a\in A$, there exists $a^{\prime }\in A$, such that $(a,a^{\prime })$ is an edge.

By conditions (1) and (2), it follows that $1\notin S$. Therefore, $(a,a)$ is not an edge for any $a\in A$, i.e., a factor graph cannot have any loops. Note that, by condition (3), for each $a\in A$, there exists $s\in S$, such that $a{s}^{-1}\in A$.

Lemma 2.

Let G be a group and let $A,S$ be subsets of G. If $\mathcal{G}(A,S)$ is a factor graph, then $(a,1)$ is not an edge for all $a\in A$.

Proof. 

Let $a\in A$. If $(a,1)$ is an edge, then $1^{-1}a=s$ for some $s\in S$. This implies that $a=s\in A\cap S=⌀$; this is a contradiction. □

As a consequence, from Lemma 2, it follows that $|A|\ge 3$ for any factor graph $\mathcal{G}(A,S)$. The following proposition discusses the connectedness of a factor graph.

Proposition 1.

Let G be a group and let $A,S$ be subsets of G, such that the factor graph $\mathcal{G}(A,S)$ is defined. If $|A|=3$ or 4, then $\mathcal{G}(A,S)$ is weakly connected.

Proof. 

By condition $\left(3\right)$ of Definition 2, there exist $a,a^{\prime }\in A$, such that $(1,a)$ and $(a,a^{\prime })$ are edges. Note that $1,a,a^{\prime }$ must be all distinct.

If $|A|=3$, then it follows that $A=\{1,a,a^{\prime }\}$. In this case, ignoring the direction of the edges, $\mathcal{G}(A,S)$ is a connected graph.

If $|A|=4$, we write $A=\{1,a,a^{\prime },a^{″}\}$. By condition $\left(3\right)$ of Definition 2 and Lemma 2, $(a^{″},a)$ or $(a^{″},a^{\prime })$ must be an edge. Now, ignoring the direction of the edge, $\mathcal{G}(A,S)$ is a connected graph.

In summary, $\mathcal{G}(A,S)$ is a weakly connected graph. □

Remark 1.

Let G be a group with a factor graph $\mathcal{G}(A,S)$. For $|A|\ge 5$, $\mathcal{G}(A,S)$ may not be weakly connected. Take the cyclic group $\langle a\rangle$ of order 25 as an example. Consider the sets $A=\{1,a^2,a^5,a^6,a^{21}\}$ and $S=\{a^3,a^{10},a^{15},a^{22},a^{23}\}$. The factor graph $\mathcal{G}(A,S)$ is:We can see that the factor graph is not weakly connected.

Let G be a group with a factor graph $\mathcal{G}(A,S)$. Consider a nonidentity element x of A. Since $(x,1)$ and $(x,x)$ are not edges, the out-degree of x is at most $|A|-2$. This bound can be attained by considering the following example: Consider the cyclic group $\langle a\rangle$ of order $2n+1$ where $n\ge 3$. Take $A=\{1,a^{2n-3},a^{2n-2},a^{2n-1}\}$ and $S=\{a,a^2,a^{2n}\}$. It is not hard to see that the out-degree of $a^{2n-2}$ is $|A|-2=2$. The factor graph $\mathcal{G}(A,S)$ with $n=3$ is given below.

The maximum in-degree of x is at most $|A|-1$. This bound can be attained by considering the following example: Consider the cyclic group $\langle a\rangle$ of order $2n$ where $n\ge 3$. Take $A=\{1,a^{2n-4},a^{2n-3}\}$ and $S=\{a,a^4,a^{2n-1}\}$. Clearly, the in-degree of $a^2$ is $|A|-1=2$. The factor graph $\mathcal{G}(A,S)$ with $n=3$ is given below:

For the identity element 1, its out-degree is the number of elements in A whose inverse belongs to S, and its in-degree is obviously 0. Indeed, the maximum out-degree of 1 is at most $|A|-1$.

Lemma 3.

Let G be a finite group and let $A,S$ be subsets of G, such that the factor graph $\mathcal{G}(A,S)$ is defined.

(i) 

If the out-degree of 1 is $|A|-1$, then $|A|\le ⌊{\displaystyle \frac{|G|+1}{2}}⌋$.

(ii) 

If the in-degree of a vertex $x\in A\setminus \left\{1\right\}$ is $|A|-1$, then $|A|\le ⌊{\displaystyle \frac{|G|+1}{2}}⌋$.

Proof. 

Since the out-degree of 1 is the number of elements in A whose inverse belongs to S, we have

$$|G|\ge |A|+|S|\ge |A|+|A|-1=2|A|-1,$$

(1)

which implies that $|A|\le ⌊{\displaystyle \frac{|G|+1}{2}}⌋$. Hence (i) holds.

Since the in-degree of x is $|A|-1$, we have $x^{-1}a\in S$ for each $a\in A\setminus \left\{x\right\}$. This implies that $|S|\ge |A|-1$. Therefore, (1) holds and it follows that (ii) holds. □

Let G be a group and let $A,S$ be subsets of G, such that the factor graph $\mathcal{G}(A,S)$ is defined. Then, $\mathcal{G}(A,G\setminus A)$ is also a factor graph and $\mathcal{G}(A,S)$ is a subgraph of $\mathcal{G}(A,G\setminus A)$. Motivated by Lemma 3, we introduce the following definition.

Definition 3.

Let G be a group and let $A,S$ be subsets of G, such that the factor graph $\mathcal{G}(A,S)$ is defined. Then, $\mathcal{G}(A,S)$ is said to be of maximal max-out-degree if the out-degree of 1 is $|A|-1$, $|A|=⌊{\displaystyle \frac{|G|+1}{2}}⌋$, and $S=G\setminus A$.

Similar to the notion of maximal max-in-degree, Lemma 3 leads to the notion of maximal max-in-degree, as follows:

Definition 4.

Let G be a group and let $A,S$ be subsets of G, such that the factor graph $\mathcal{G}(A,S)$ is defined. Then, $\mathcal{G}(A,S)$ is said to be of maximal max-in-degree if the in-degree of a vertex $x\in A\setminus \left\{1\right\}$ is $|A|-1$, $|A|=⌊{\displaystyle \frac{|G|+1}{2}}⌋$ and $S=G\setminus A$.

A factor graph $\mathcal{G}(A,S)$ models relationships in A via S, with edges showing ratios in S. A maximal max-out-degree factor graph has the identity with maximum outgoing edges ($|A|-1$) and balanced sets ($|A|=\lfloor {\displaystyle \frac{|G|+1}{2}}\rfloor$, $S=G\setminus A$). A maximal max-in-degree factor graph has a nonidentity vertex with maximum incoming edges, with similar size constraints. These maximize connectivity and aid in constructing complete decompositions.

For a group G with a factor graph $\mathcal{G}(A,S)$ that is maximal max-out-degree, it is not hard to see that if $|G|$ is odd, then $|G|=2|A|-1$, whereas if $|G|$ is even, then $|G|=2|A|$.

Lemma 4.

Let G be a direct product of finite groups $G_1$ and $G_2$. Let $\mathcal{G}(A_1,S_1)$ and $\mathcal{G}(A_2,S_2)$ be maximal max-out-degree factor graphs of $G_1$ and $G_2$, respectively. Let

$$\begin{array}{cc}\hfill A_3& =A_2{A}_1\cup S_2(A_1\setminus \left\{1\right\});\hfill \\ \hfill S_3& =S_2\cup (A_2\cup S_2)S_1.\hfill \end{array}$$

If $|G_1|$ is odd, then $\mathcal{G}(A_3,S_3)$ is a maximal max-out-degree factor graph of G.

Proof. 

Clearly, $1\in A_3$ and $A_3\cap S_3=⌀$. Since $|G_1|$ is odd, $|A_1|={\displaystyle \frac{|G_1|+1}{2}}$. Now,

$$|A_3|=|A_2\cup S_2||A_1|-|S_2|={\displaystyle \frac{|G_1||G_2|+|G_2|}{2}}-|S_2|.$$

If $|G_2|$ is even, then $|S_2|={\displaystyle \frac{|G_2|}{2}}$, so, $|A_3|={\displaystyle \frac{|G_1||G_2|}{2}}$. If $|G_2|$ is odd, then $|S_2|={\displaystyle \frac{|G_2|-1}{2}}$, so, $|A_3|={\displaystyle \frac{|G_1||G_2|+1}{2}}$. In either case, $|A_3|=⌊{\displaystyle \frac{|G|+1}{2}}⌋$.

Let $y\in A_3\setminus \left\{1\right\}$. We consider the following cases:

Case 1: $y\in A_2{A}_1$. Then, $y=a{b}_1$ for some $a\in A_2$ and $b_1\in A_1$. Then, $y^{-1}=a^{-1}{b}_1^{-1}$. If $b_1=1$, then $y^{-1}=a^{-1}\in S_2\subseteq S_3$, for $a\ne 1$. If $b_1\ne 1$, then $b_1^{-1}\in S_1$ and $y^{-1}=a^{-1}{b}_1^{-1}\in S_2{S}_1\subseteq S_3$.

Case 2: $y\in S_2(A_1\setminus \left\{1\right\})$. Then, $y=a{b}_2$ for some $a\in S_2$ and $b_2\in A_1\setminus \left\{1\right\}$. Then, $y^{-1}=a^{-1}{b}_2^{-1}$ and $b_2^{-1}\in S_1$. This means $y^{-1}=a^{-1}{b}_2^{-1}\in A_2{S}_1\subseteq S_3$. Hence, the out-degree of 1 is $|A_3|-1$.

It is left to show that, for each $y_1\in A_3\setminus \left\{1\right\}$, there is a $y_2\in A_3\setminus \left\{1\right\}$, such that $(y_1,y_2)$ is an edge, i.e., $y_2^{-1}{y}_1\in S_3$.

Case 1: $y_1\in A_2{A}_1$. Then, $y_1=a{b}_1$ for some $a\in A_2$ and $b_1\in A_1$. Since $\mathcal{G}(A_1,S_1)$ is a factor graph, there is a $b_2\in A_1$, such that $b_2^{-1}{b}_1\in S_1$. Setting $y_2=a{b}_2$, we see that $y_2^{-1}{y}_1\in A_2{S}_1\subseteq S_3$.

Case 2: $y_1\in S_2(A_1\setminus \left\{1\right\})$. Then, $y_1=a{b}_3$ for some $a\in S_2$ and $b_3\in A_1\setminus \left\{1\right\}$. As before, there is a $b_4\in A_1$, such that $b_4^{-1}{b}_3\in S_1$. Setting $y_2=a{b}_3$, we see that $y_2^{-1}{y}_1\in A_2{S}_1\subseteq S_3$.

This completes the proof of the lemma. □

Lemma 5.

Let $G=\langle a\rangle$ be a cyclic group of order $2n+1$ and $n\ge 4$. Let

$$\begin{array}{cc}\hfill A& =\left\{a^i:i=0,1,\dots ,n-1,n+1\right\};\hfill \\ \hfill S& =\left\{a^i:i=n,n+2,n+3,\dots ,2n\right\}.\hfill \end{array}$$

Then, $\mathcal{G}(A,S)$ is a maximal max-out-degree factor graph of G.

Proof. 

Clearly, for each $y\in A\setminus \left\{1\right\}$, $y^{-1}\in S$. So, the out-degree of 1 is $|A|-1$. Now, $|A|=n+1={\displaystyle \frac{|G|+1}{2}}$, $(a^i,a^{n-1})$ is an edge for all $i=1,2,\dots ,n-2$, $(a^{n-1},a^{n+1})$ is an edge, and $(a^{n+1},a)$ is an edge. Hence, $\mathcal{G}(A,S)$ is a maximal max-out-degree factor graph of G. □

Lemma 6.

Let $G=\langle a\rangle$ be a cyclic group of order $2n$ and $n\ge 5$. Let

$$\begin{array}{cc}\hfill A& =\left\{a^i:i=0,1,\dots ,n-2,n+1\right\};\hfill \\ \hfill S& =\left\{a^i:i=n-1,n,n+2,n+3,\dots ,2n-1\right\}.\hfill \end{array}$$

Then, $\mathcal{G}(A,S)$ is a maximal max-out-degree factor graph of G.

Proof. 

Clearly, for each $y\in A\setminus \left\{1\right\}$, $y^{-1}\in S$. So, the out-degree of 1 is $|A|-1$. Now, $|A|=n={\displaystyle \frac{|G|}{2}}$, $(a^i,a^{n-2})$ is an edge for all $i=1,2,\dots ,n-3$, $(a^{n-2},a^{n+1})$ is an edge, and $(a^{n+1},a)$ is an edge. Hence, $\mathcal{G}(A,S)$ is a maximal max-out-degree factor graph of G. □

Theorem 1.

Let G be a direct product of cyclic groups where at most one of the cyclic factors is of even order. If each of the cyclic factors is of order at least 9, then G has a maximal max-out-degree factor graph.

Proof. 

Let $G=G_1\times G_2\times \cdots \times G_m$, where each $G_i$ is a cyclic group of order at least 9 and each $G_i$ ($i\ge 2$) is a cyclic group of odd order, except $G_1$ may possibly be of even order. If $m=1$, then the theorem follows from Lemmas 5 and 6.

Assume that the theorem holds for $m-1$, where $m\ge 2$. Let $H=G_2\times \cdots \times G_m$. Then, H has a maximal max-out-degree factor graph $\mathcal{G}(A^{\prime },S^{\prime })$. By Lemma 5 or 6, $G_1$ has a maximal max-out-degree factor graph $\mathcal{G}(A_1,S_1)$. The theorem then follows from Lemma 4. □

The following theorem shows the existence of a maximal max-in-degree factor graph of a cyclic group of even order.

Theorem 2.

Let $G=\langle a\rangle$ be a cyclic group of order $2n$ and $n\ge 3$. Let

$$\begin{array}{cc}\hfill A& =\left\{a^i:i=0,1,3,5,\dots ,2n-3\right\};\hfill \\ \hfill S& =\left\{a^i:i=2,4,6,\dots ,2n-2,2n-1\right\}.\hfill \end{array}$$

Then, $\mathcal{G}(A,S)$ is a maximal max-in-degree factor graph of G.

Proof. 

Clearly, the in-degree of a is $|A|-1$. Now, $|A|=n={\displaystyle \frac{|G|}{2}}$, $(a^i,a)$ is an edge for all $i=3,5,\dots ,2n-3$, and $(a,a^3)$ is an edge. Hence, $\mathcal{G}(A,S)$ is a maximal max-in-degree factor graph of G. □

The following results show the symmetrical relationships between a factor graph and a 2-complete decomposition.

Lemma 7.

Let G be a group and let $A,B$ be subsets of G.

(i) 

If $[A,B]$ is a complete decomposition of G with $1\in A$, then $\mathcal{G}(A,B)$ is a factor graph.

(ii) 

If $\mathcal{G}(A,B)$ is a factor graph, then $[A,G\setminus A]$ is a complete decomposition of G.

(iii) 

If $\mathcal{G}(G\setminus B,B)$ is a factor graph, then $[G\setminus B,B]$ is a complete decomposition of G.

Proof. 

(i)

Suppose that $[A,B]$ is a complete decomposition of G with $1\in A$. By the assumption, we have $A\cap B=⌀$. It is left to show, that for all $a\in A$, there exists $a^{\prime }\in A$, such that $(a,a^{\prime })$ is an edge in $\mathcal{G}(A,B)$. Let $a\in A$. Since $G=AB$, we have $a=a_1{b}_1$ for some $a_1\in A$ and $b_1\in B$. So, $a_1^{-1}a=b_1\in B$ and $(a,a_1)$ is an edge. Hence, $\mathcal{G}(A,B)$ is a factor graph.

(ii)

Suppose that $\mathcal{G}(A,B)$ is a factor graph. Clearly, $A\cap (G\setminus A)=⌀$. From $A\cap B=⌀$, we have $B\subseteq G\setminus A$. Let $g\in G$. If $g\in G\setminus A$, then $g=1g\in A(G\setminus A)$. If $g\in A$, then there exists $a\in A$, such that $(g,a)$ is an edge in $\mathcal{G}(A,B)$. So, $a^{-1}g=b$ for some $b\in B$, i.e., $g=ab\in AB\subseteq A(G\setminus A)$. Hence, $G\subseteq A(G\setminus A)\subseteq G$ and we get $G=A(G\setminus A)$. We conclude that $[A,G\setminus A]$ is a complete decomposition of G.

(iii)

Suppose that $\mathcal{G}(G\setminus B,B)$ is a factor graph. By (ii), it follows that $[G\setminus B,B]=[G\setminus B,G\setminus (G\setminus B\left)\right]$ is a complete decomposition of G.

□

Corollary 2.

A group G has a 2-complete decomposition if and only if there exist subsets $A,B$ of G, such that $\mathcal{G}(A,B)$ is a factor graph.

Proof. 

Suppose G has a 2-complete decomposition. By Corollary 1, G has a complete decomposition $[A,B]$, such that $1\in A$. We conclude that $\mathcal{G}(A,B)$ is a factor graph by Lemma 7(i).

Conversely, suppose that $\mathcal{G}(A,B)$ is a factor graph for some subsets $A,B$ of G. By Lemma 7(ii), we conclude that $[A,G\setminus A]$ is a complete decomposition of G. □

Let G be a group and let $A,S$ be subsets of G, such that the factor graph $\mathcal{G}(A,S)$ is defined. For each positive integer n, a directed path of length n in the factor graph $\mathcal{G}(A,S)$ is defined to be a sequence

$$\begin{array}{c}\hfill P=(a_1,a_2,\dots ,a_n,a_{n+1})\end{array}$$

such that $a_1,a_2,\dots ,a_n,a_{n+1}\in A$ and $(a_i,a_{i+1})$ is an edge for $1\le i\le n$. The vertices $a_1$ and $a_{n+1}$ are called the initial point and terminal point of P, respectively. For $1\le i\le n$, $(a_i,a_{i+1})$ is an edge implies that $a_i\ne a_{i+1}$. Let P be a path of length at least two. If $a_i\ne a_j$ for $1\le i<j\le n$ and $a_{n+1}=a_1$, then P is called a cycle of length n. The path P is called an extended cycle if $a_i\ne a_j$ for $1\le i<j\le n$ and $a_{n+1}=a_t$ for some $1\le t\le n-1$. Clearly, a cycle is an extended cycle. A vertex $a\in A$ is said to be contained in the extended cycle P if $a=a_i$ for some $1\le i\le n+1$.

Theorem 3.

Let G be a group and let $A,B$ be disjoint subsets of G with $2\le |A|<\infty$, such that $1\in A$. Then, $\mathcal{G}(A,B)$ is a factor graph if and only if every vertex in A is contained in an extended cycle in $\mathcal{G}(A,B)$.

Proof. 

Suppose that $\mathcal{G}(A,B)$ is a factor graph. Let $a_1\in A$. Then, $(a_1,a_2)$ is an edge for some $a_2\in A\setminus \left\{a_1\right\}$. Now, $(a_2,a_3)$ is an edge for some $a_3\in A\setminus \left\{a_2\right\}$. If $a_3=a_1$, then $a_1$ is contained in the extended cycle

$$\begin{array}{c}\hfill (a_1,a_2,a_3).\end{array}$$

Suppose that $a_3\ne a_1$. Then, $(a_3,a_4)$ is an edge for some $a_4\in A\setminus \left\{a_3\right\}$. If $a_4=a_1$ or $a_4=a_2$, then $a_1$ is contained in the extended cycle

$$\begin{array}{c}\hfill (a_1,a_2,a_3,a_4).\end{array}$$

Suppose that we have found distinct elements $a_1,a_2,\dots ,a_n$ in A, such that $(a_i,a_{i+1})$ is an edge for all $1\le i\le n-1$. Now, $(a_n,a_{n+1})$ is an edge for some $a_{n+1}\in A\setminus \left\{a_n\right\}$. If $a_{n+1}=a_t$ for some $1\le t\le n-1$, then $a_1$ is contained in the extended cycle

$$\begin{array}{c}\hfill (a_1,a_2,\dots ,a_n,a_{n+1}).\end{array}$$

If $a_{n+1}\ne a_t$ for all $1\le t\le n-1$, then $a_1,a_2,\dots ,a_n,a_{n+1}$ are distinct elements of A. Since A is finite, this process cannot go on indefinitely. So, there must exist an integer $m\ge 2$, such that

$$\begin{array}{c}\hfill (a_1,a_2,\dots ,a_m,a_{m+1})\end{array}$$

is an extended cycle.

Conversely, suppose that every vertex in A is contained in an extended cycle in $\mathcal{G}(A,B)$. Let $a\in A$. Then, a is contained in an extended cycle

$$\begin{array}{c}\hfill (a_1,a_2,\dots ,a_n,a_{n+1})\end{array}$$

with $n\ge 2$. This means that $a=a_{i_0}$ for some $1\le i_0\le n+1$. If $i_0=n+1$, then since $a_{n+1}=a_j$ for some $1\le j\le n-1$, we may relabel $i_0=j$. So, we may assume that $1\le i_0\le n$. Now, $(a,a_{i_0+1})=(a_{i_0},a_{i_0+1})$ is an edge. By the assumptions, we have $1\in A$ and $A\cap B=⌀$. Hence, we conclude that $\mathcal{G}(A,B)$ is a factor graph. □

A proof of the following corollary was discussed earlier (just after the proof of Corollary 1). Here, we give another proof by using Theorem 3.

Corollary 3.

If a group G has a complete decomposition $[A,B]$, such that A is a finite set containing 1, then $|A|\ge 3$ and $|B|\ge 2$.

Proof. 

By Lemma 7(i), $\mathcal{G}(A,B)$ is a factor graph. Since $1\in A$, by Theorem 3, the vertex 1 is contained in an extended cycle, say

$$\begin{array}{c}\hfill (x_1,x_2,\dots ,x_n,x_{n+1})\end{array}$$

with $n\ge 2$. By Lemma 2, $(a,1)$ is not an edge for all $a\in A$. Therefore, $x_1=1$ and $x_i\ne 1$ for all $2\le i\le n+1$. If $n=2$, then $x_3=x_1=1$ and $(x_2,x_3)=(x_2,1)$ is an edge; this is a contradiction. Hence, $n\ge 3$ and we conclude that $|A|\ge n\ge 3$. Now, suppose that $|B|=1$, say $B=\left\{b\right\}$. Note that $(x_1,x_2)$ is an edge implies that $x_2=x_1{b}^{-1}=b^{-1}$. Therefore, we have $x_3=b^{-2},\dots ,x_{n+1}=b^{-n}$. Next, $x_{n+1}=x_j$ for some $2\le j\le n-1$ implies that $b^{-n}=b^{-j+1}$. So, $x_{n-j+2}=b^{-n+j-1}=1$. This is possible only if $n-j+2=1$, i.e., $j=n+1$; this is a contradiction. We conclude that $|B|\ge 2$. □

4. Existence of Complete Decompositions

In this section, we determine some criteria for a two-element subset of a group to be a factor of a 2-complete decomposition. In other words, we shall address Problem 1.

Lemma 8.

Let G be a group and let $A=\{x,y\}$ be a two-element subset of G. Then, A is a factor of a 2-complete decomposition of G if and only if $x^2\ne y^2$ and $xy\ne yx$.

Proof. 

Suppose that A is a factor of a 2-complete decomposition of G. Then, either $[A,B]$ or $[B,A]$ is a complete decomposition of G for some subset B of G.

Case 1: $[B,A]$ is a complete decomposition of G. Suppose that $1\in A$. By Lemma 1, $[A^{-1},B^{-1}]$ is also a complete decomposition of G. By Corollary 3, $|A|=|A^{-1}|\ge 3$; this is a contradiction. Thus, $1\notin A$. By Lemma 1, $[G\setminus A,A]$ is a complete decomposition of G with $1\in G\setminus A$. Therefore, $\mathcal{G}(G\setminus A,A)$ is a factor graph by Lemma 7(i).

Since $1\notin A$, we have $xy\notin A$. So, $xy\in G\setminus A$ and there exists $a\in A$, such that $(xy,xy{a}^{-1})$ is an edge. Note that $xy{a}^{-1}\in G\setminus A$. If $a=y$, then $x=xy{a}^{-1}\notin A$; this is a contradiction. Thus, $a=x$ and $xy{x}^{-1}\notin A$. In particular, $xy{x}^{-1}\ne y$, i.e., $xy\ne yx$.

If $x^2\in A$, then $x^2=x$ or $x^2=y$. If the former holds, then $x=1\notin A$; this is a contradiction. If the latter holds, then $xy=yx$; again, this is a contradiction. So, $x^2\in G\setminus A$ and there exists $a\in A$, such that $(x^2,x^2{a}^{-1})$ is an edge. Note that $x^2{a}^{-1}\in G\setminus A$. If $a=x$, then $x=x^2{a}^{-1}\notin A$; this is a contradiction. Thus, $a=y$ and $x^2{y}^{-1}\notin A$. In particular, $x^2{y}^{-1}\ne y$, i.e., $x^2\ne y^2$.

Case 2: $[A,B]$ is a complete decomposition of G. Suppose that $1\in A$. By Corollary 3, $|A|\ge 3$; this is a contradiction. Thus, $1\notin A$. By Lemma 1, $[B^{-1},A^{-1}]$ is a complete decomposition of G where $A^{-1}=\{x^{-1},y^{-1}\}$. Since $1\notin A$, we have $1\notin A^{-1}$. By arguments similar to that in Case 1, it follows that $x^{-1}{y}^{-1}\ne y^{-1}{x}^{-1}$ and ${\left(x^{-1}\right)}^2\ne {\left(y^{-1}\right)}^2$, which imply $xy\ne yx$ and $x^2\ne y^2$.

Conversely, suppose that $x^2\ne y^2$ and $xy\ne yx$. Then, $1\notin A$. We aim to show that $[G\setminus A,A]$ is a complete decomposition of G. By Lemma 7(iii), it is sufficient to show that $\mathcal{G}(G\setminus A,A)$ is a factor graph. Since $1\in G\setminus A$ and $(G\setminus A)\cap A=⌀$, it is left to show that for all $b\in G\setminus A$, there exists $b^{\prime }\in G\setminus A$, such that $(b,b^{\prime })$ is an edge in $\mathcal{G}(G\setminus A,A)$.

From $1\notin A$, $x\ne y$, $x^2\ne y^2$ and $xy\ne yx$, it follows that $xy,y^2,xy{x}^{-1},y^2{x}^{-1}$ are contained in $G\setminus A$. Therefore, $(xy,xy{x}^{-1})$ and $(y^2,y^2{x}^{-1})$ are edges. Let $b\in G\setminus A$, such that $b\ne xy$ and $b\ne y^2$. Then, $b{y}^{-1}\ne x$ and $b{y}^{-1}\ne y$. So, $b{y}^{-1}\in G\setminus A$; hence, $(b,b{y}^{-1})$ is an edge. We conclude that $\mathcal{G}(G\setminus A,A)$ is a factor graph and the result follows. □

Berkovich, Freiman, and Praeger [19] defined a group G to have the small squaring property on k-sets if $|K^2|<k^2$ for all k-element subsets K of G. For two group elements, $x,y$, note that ${\{x,y\}}^2=\{x^2,y^2,xy,yx\}$. By Lemma 8, a group G does not have a complete decomposition $[A,B]$, such that $|A|=2$ or $|B|=2$ if and only if $x^2=y^2$ or $xy=yx$ for all $x,y\in G$, or, equivalently, G has the small squaring property on 2-sets since ${|\{x,y\}}^2|<2^2=4$ for all $x,y\in G$.

Dedekind [20] proved that a nonabelian group for which all subgroups are normal must be a direct product of the form $Q_8\times E\times D$, where $Q_8$ is the quaternion group of order eight, E is an elementary abelian 2-group, and D is a torsion abelian group with all elements of odd order. By using Dedekind’s structure theorem, Freiman [21] proved that a nonabelian group that has the small squaring property on 2-sets must be a direct product of $Q_8$ and an elementary abelian 2-group. Hence, we can deduce that, if a group G does not have a complete decomposition $[A,B]$, such that $|A|=2$ or $|B|=2$, then G is abelian or G is a direct product of $Q_8$ and an elementary abelian 2-group. In what follows, we prove this result without using Dedekind’s structure theorem and we show that the converse of the result also holds.

Theorem 4.

A group G has a complete decomposition $[A,B]$, such that $|A|=2$ or $|B|=2$ if and only if G is nonabelian and G is not isomorphic to a direct product of $Q_8$ and an elementary abelian 2-group.

Proof. 

Suppose that G has a complete decomposition $[A,B]$, such that $|A|=2$ or $|B|=2$. By Lemma 8, there exist $x,y\in G$, such that $x^2\ne y^2$ and $xy\ne yx$. Therefore, G is nonabelian. Suppose to the contrary that $G=Q_8\times E$ where $Q_8$ is the quaternion group generated by quaternions $i,j$ and E is an elementary abelian 2-group. Note that $Z\left(G\right)=\{\pm 1\}\times E$ and $G\setminus Z\left(G\right)=(Q_8\setminus \{\pm 1\})\times E$. Hence, all elements of order four lie in $G\setminus Z\left(G\right)$ and all elements of order two lie in $Z\left(G\right)$. Furthermore, note that $G^2=\left\{(\pm 1,1)\right\}$. Since $x,y\in G\setminus Z\left(G\right)$, both $x,y$ must have order four. Therefore, $x^2=y^2=(-1,1)$; this is a contradiction.

Conversely, suppose that G does not have any complete decomposition $[A,B]$, such that $|A|=2$ or $|B|=2$. We aim to show that G is abelian or G is isomorphic to a direct product of $Q_8$ and an elementary abelian 2-group. By Lemma 8, either $xy=yx$ or $x^2=y^2$ for all $x,y\in G$.

Now, we claim that, for all $x,y\in G$, either $x^{-1}yx=y$ or $x^{-1}yx=y^{-1}$. Let $a,b\in G$. Then, either $ab=ba$ or $a^2=b^2$. If $ab=ba$, then $a^{-1}ba=b$. Suppose that $ab\ne ba$. Now, a and $ab$ do not commute, for otherwise, $a\left(ab\right)=\left(ab\right)a$, i.e., $ab=ba$. Therefore, we must have $a^2={\left(ab\right)}^2=abab$, i.e., $a^{-1}ba=b^{-1}$. Hence, either $x^{-1}yx=y$ or $x^{-1}yx=y^{-1}$ for all $x,y\in G$. Using this fact, we see that every subgroup of G is normal.

If $xy=yx$ for all $x,y\in G$, then G must be abelian. Suppose that there exist $h,g\in G$, such that $hg\ne gh$, i.e., $h^{-1}gh\ne g$. So, $h^2=g^2$ and $h^{-1}gh=g^{-1}$. This implies that

$$g^{-2}={\left(h^{-1}gh\right)}^2=h^{-1}{g}^{2}h=h^{-1}{h}^{2}h=h^2=g^2$$

and thus $g^4=1$. If $g^2=1$, then $h^{-1}gh=g^{-1}=g$; this is a contradiction. Hence, g is of order four and the group generated by $g,h$, say H, is the quaternion group $Q_8$. In fact,

$$H=〈g,h:g^4=1,g^2=h^2,h^{-1}gh=g^{-1}〉\cong Q_8.$$

For any $x\in G$, we will prove that $x\in H{C}_G\left(H\right)$ by discussing four distinct cases below.

Case 1: $[x,g]=1$ and $[x,h]=1$. We have $x\in C_G\left(H\right)\subseteq H{C}_G\left(H\right)$.

Case 2: $[x,g]\ne 1$ and $[x,h]=1$. Then, $x^{-1}gx=g^{-1}$. From $h^{-1}gh=g^{-1}$, we get $hg=g^{-1}h$. Therefore, $x^{-1}xhg=hg=g^{-1}h=x^{-1}gxh.$ By canceling $x^{-1}$, we get $xhg=gxh$, that is, $[xh,g]=1$. Since $[x,h]=1$, it follows that $[xh,h]=1$, so $xh\in C_G\left(H\right)$. We conclude that $x=\left(xh\right)h^{-1}\in H{C}_G\left(H\right)$.

Case 3: $[x,g]=1$ and $[x,h]\ne 1$. Then, $x^{-1}hx=h^{-1}$. From $h^{-1}gh=g^{-1}$ and $g^2=h^2$, we get $gh=h{g}^{-1}=h^{-1}g$. Next, $x^{-1}xgh=gh=h^{-1}g=x^{-1}hxg$. By canceling $x^{-1}$, we get $xgh=hxg$, that is, $[xg,h]=1$. Since $[x,g]=1$, it follows that $[xg,g]=1$, so $xg\in C_G\left(H\right)$. We conclude that $x=\left(xg\right)g^{-1}\in H{C}_G\left(H\right)$.

Case 4: $[x,g]\ne 1$ and $[x,h]\ne 1$. By case 2, we have $[xh,g]=1$ and hence $[xhg,g]=1$. If $[xh,h]=1$, then $xh\in C_G\left(H\right)$ and $x=\left(xh\right)h^{-1}\in H{C}_G\left(H\right)$. If $[xh,h]\ne 1$, by case 3, we have $[xhg,h]=1$, so $xhg\in C_G\left(H\right)$, it follows that $x=\left(xhg\right)\left(g^{-1}{h}^{-1}\right)\in H{C}_G\left(H\right)$.

In summary, we conclude that $G=H{C}_G\left(H\right)$.

Let $c\in C_G\left(H\right)$. Since $cg$ and h do not commute, we get ${\left(cg\right)}^2=h^2$ and hence, $c^2=g^{-2}{h}^2=1$. This implies that $C_G\left(H\right)$ is of exponent two. Thus, $C_G\left(H\right)$ is an elementary abelian 2-group. Regard $C_G\left(H\right)$ as a vector space over ${\mathbb{Z}}_2$. Since $g^2\ne 1$ and $g^2\in C_G\left(H\right)$, the set $\left\{g^2\right\}$ can be extended to a basis for $C_G\left(H\right)$, say $\mathcal{B}$. Let $E={\prod }_{x\in \mathcal{B}\setminus \left\{g^2\right\}}\langle x\rangle$. We have $C_G\left(H\right)=E\times \langle g^2\rangle$ and E does not contain $g^2$. Then, it follows that $C_G\left(H\right)=E\cup g^{2}E$ and $H\cap E=\left\{1\right\}$. Next, we see that $G=H{C}_G\left(H\right)=H(E\cup g^{2}E)=HE$. We conclude that $G=H\times E\cong Q_8\times E$. □

Next, we shall address Problem 2. From ([11] Theorem 3.3), an abelian group G has a complete decomposition of order two if and only if $|G|\ge 6$ and G is not an elementary abelian 2-group. The proof of ([11] Theorem 3.3) relies on ([11] Lemma 3.2). Surprisingly, the conditions given in ([11] Lemma 3.2) are necessary and sufficient for the existence of a complete decomposition $[A,B]$ of a nonabelian group with $1\in A$ and $|A|=3$ as well (see the next lemma).

Lemma 9.

Let G be a group and let $A=\{1,x,y\}$ be a subset of G. Then, A is a factor of a 2-complete decomposition of G if and only if all the following conditions are satisfied:

(i) 

$x\ne y^2$;

(ii) 

$y\ne x^2$;

(iii) 

$xy\ne 1$;

(iv) 

$x^2\ne 1$ or $y^2\ne 1$.

Proof. 

Suppose that A is a factor of a 2-complete decomposition of G. Then, either $[A,B]$ or $[B,A]$ is a complete decomposition of G. We first assume that $[A,B]$ is a complete decomposition of G. By Lemma 7(i), $\mathcal{G}(A,B)$ is a factor graph. By Theorem 3, the vertex 1 is contained in an extended cycle in $\mathcal{G}(A,B)$. By Lemma 2, $(a,1)$ is not an edge for all $a\in A$. So, the only possible extended cycles in $\mathcal{G}(A,B)$ are

$$\begin{array}{c}\hfill P_1=(1,x,y,x),\\ \hfill P_2=(1,y,x,y).\end{array}$$

Without loss of generality, suppose that $\mathcal{G}(A,B)$ contains the extended cycle $P_1$. Then, there exist $u,v,w\in B$, such that $x=1u^{-1}$, $y=x{v}^{-1}$ and $x=y{w}^{-1}$. Since $x^{-1}=u\notin A$, it follows that $x^2\ne 1$ and $xy\ne 1$. From $y^{-1}x=v\notin A$, we get $x\ne y^2$. Finally, from $x^{-1}y=w\notin A$, we obtain $y\ne x^2$. Hence, conditions (i)–(iv) hold.

Now, suppose that $[B,A]$ is a complete decomposition of G. By Lemma 1, $[A^{-1},B^{-1}]$ is a complete decomposition of G where $A^{-1}=\{1,x^{-1},y^{-1}\}$. By the previous arguments, the analogue of conditions (i)–(iv) for $x^{-1}$ and $y^{-1}$ hold. It is straightforward to see then that the elements $x,y$ also satisfy conditions (i)–(iv).

Conversely, suppose that the set A satisfies all the conditions (i)–(iv). For condition (iv), we shall assume that $x^2\ne 1$. We aim to show that $[A,G\setminus A]$ is a complete decomposition of G. By Lemma 7(ii), it is sufficient to show that $\mathcal{G}(A,G\setminus A)$ is a factor graph. Since $1\in A$ and $A\cap (G\setminus A)=⌀$, it is left to show that for all $a\in A$, there exists $a^{\prime }\in A$, such that $(a,a^{\prime })$ is an edge in $\mathcal{G}(A,G\setminus A)$. From $x^2\ne 1$ and $xy\ne 1$, we see that $x^{-1}\notin A$. So, $x^{-1}\in G\setminus A$ and $(1,x)$ is an edge since $x=1{\left(x^{-1}\right)}^{-1}$. From $x\ne y^2$ and $y\ne 1$, we see that $y^{-1}x\notin A$. So, $y^{-1}x\in G\setminus A$ and $(x,y)$ is an edge since $y=x{\left(y^{-1}x\right)}^{-1}$. Finally, from $y\ne x^2$ and $x\ne 1$, we see that $x^{-1}y\notin A$. So, $x^{-1}y\in G\setminus A$ and $(y,x)$ is an edge since $x=y{\left(x^{-1}y\right)}^{-1}$. Hence, $\mathcal{G}(A,G\setminus A)$ is a factor graph and we conclude that the result follows. □

Theorem 5.

A group G has a complete decomposition $[A,B]$, such that $1\in A$ and $|A|=3$ if and only if $|G|\ge 6$ and G is not an elementary abelian 2-group.

Proof. 

Suppose that G has a complete decomposition $[A,B]$ with $A=\{1,x,y\}$. By Lemma 9, we may assume that $x\ne y^2$, $y\ne x^2$, $xy\ne 1$ and $x^2\ne 1$. So, G is not an elementary abelian 2-group. Note that $1,x,y,xy,x^2$ are distinct elements. Therefore, $|G|\ge 5$. If $|G|=5$, then $G=\langle x\rangle$ is a cyclic group of order five. Note that $y\ne 1,x,x^2$. If $y=x^3$, then $y^2=x^6=x$; this is a contradiction. If $y=x^4$, then $xy=x^5=1$; again, this is a contradiction. We conclude that $|G|\ge 6$.

Conversely, suppose that $|G|\ge 6$ and G is not an elementary abelian 2-group. It is sufficient to find two elements $x,y$ in G, such that conditions (i)–(iv) in Lemma 9 are satisfied. If G has an element a of order at least six, then we take $x=a$ and $y=a^3$. Suppose that every element in G is of order less than six. Since G is not an elementary abelian 2-group, there exists $c\in G$, such that $c^2\ne 1$. Since $|G|\ge 6>|c|$, it follows that $\langle c\rangle \ne G$; hence, there exists $d\in G$, such that $d\notin \langle c\rangle$. This implies that $\langle d\rangle \cap \langle c\rangle ⊊\langle d\rangle$. If $\langle d\rangle \cap \langle c\rangle =\left\{1\right\}$, then we take $x=c$ and $y=d$. Suppose that $\langle d\rangle \cap \langle c\rangle \ne \left\{1\right\}$. Since $\langle d\rangle$ has a nontrivial proper subgroup $\langle d\rangle \cap \langle c\rangle$ and $|d|\le 5$, by Lagrange’s Theorem, the only possibility is $|d|=4$ and $\langle d\rangle \cap \langle c\rangle =\langle d^2\rangle$. Since two divides $|c|$ and $c^2\ne 1$, it follows that $|c|=4$. In this case, we take $x=c$ and $y=d$. It is straightforward to verify that in each case, x and y satisfy conditions (i)–(iv) in Lemma 9; hence, G has a complete decomposition $[A,B]$ where $A=\{1,x,y\}$. □

Corollary 4.

Every nonabelian group has a complete decomposition $[A,B]$, such that $|A|=3$ or $|B|=3$.

Proof. 

This follows from Theorem 5 and the fact that every nonabelian group is of size at least six and cannot be an elementary abelian 2-group. □

Corollary 5.

Let G be a group. The following statements are equivalent:

(i) 

G has a complete decomposition $[A,B]$, such that $1\in A$ and $|A|=3$.

(ii) 

G has a complete decomposition $[A,B]$, such that $|A|=3$ or $|B|=3$.

(iii) 

G has a 2-complete decomposition.

(iv) 

$|G|\ge 6$ and G is not an elementary abelian 2-group.

Proof. 

(i) ⇒ (ii) ⇒ (iii) is obvious. If G is abelian, then the implication (iii) ⇒ (iv) follows from ([11] Theorem 3.3). If G is nonabelian, then the implication (iii) ⇒ (iv) is trivial. Lastly, the implication (iv) ⇒ (i) follows from Theorem 5. □

Remark 2.

Let G be a group that has a 2-complete decomposition. By Corollary 4, $|G|\ge 6$ and G is not an elementary abelian 2-group. If G is nonabelian and G is not isomorphic to a direct product of $Q_8$ and an elementary abelian 2-group, then Theorem 4 tells us that the smallest size of a subset Y of G so that there exists a subset X of G for $[X,Y]$ to be a complete decomposition of G is two. If G is abelian or G is not isomorphic to a direct product of $Q_8$ and an elementary abelian 2-group, then Theorems 4 and 5 tell us that the smallest size of Y is three. This gives an answer for Problem 1.

Remark 3.

Theorem 5 tells us that the smallest size of a subset X of the group G with $1\in X$ so that there exists a subset Y of G for $[X,Y]$ to be a complete decomposition of G is three. If such a complete decomposition exists, then $|G|\ge 6$ and G is not an elementary abelian 2-group. This gives an answer for Problem 2.

Corollary 6.

A group G has a complete decomposition if and only if $|G|\ge 6$.

Proof. 

If G is abelian, then the corollary follows from ([11] Theorem 3.4). If G is nonabelian, then $|G|\ge 6$ and by Corollary 5, G has a complete decomposition. □

5. Conclusions and Future Work

In this paper, we have explored the concept of complete decompositions of groups through a novel graphical approach, introducing the notion of factor graphs to study 2-complete decompositions. Our main results provide significant insights into the structure of groups admitting such decompositions. Specifically, Theorem 3 establishes a crucial connection between factor graphs and complete decompositions, showing that a factor graph $\mathcal{G}(A,B)$ exists if and only if every vertex in A is contained in an extended cycle. Theorem 4 characterizes groups with complete decompositions where one factor has size two, demonstrating that such groups are nonabelian and not isomorphic to a direct product of the quaternion group $Q_8$ and an elementary abelian 2-group. Theorem 5 further determines that a group has a complete decomposition with a factor of size three containing the identity if and only if the group has at least six elements and is not an elementary abelian 2-group. Finally, Corollary 6 generalizes these findings, concluding that every group of order at least six admits a complete decomposition.

These results extend the understanding of group factorizations, particularly through the lens of factor graphs, and provide a framework for analyzing the structural properties of groups based on their decompositions. The graphical approach not only offers a new perspective on complete decompositions but also facilitates the study of group properties through combinatorial and graph-theoretic methods.

Looking ahead, several promising directions for future research emerge from this work:

• Hypergraphs for higher-order decompositions: The current study focuses on complete decompositions of order two using factor graphs. Extending this framework to hypergraphs could provide insights into complete decompositions with more than two factors, potentially revealing new structural properties of groups through higher-dimensional graphical representations.
• Nonabelian group classes: While our results cover general groups, further investigation into specific classes of nonabelian groups, such as symmetric groups or simple groups, could yield more refined characterizations of complete decompositions and their associated factor graphs.
• Cryptographic applications: The application of complete decompositions in cryptography, as explored in [15,16], suggests potential for developing new cryptographic protocols. Future work could focus on leveraging factor graphs to design secure key exchange protocols or other cryptographic primitives based on the complete decomposition search problem.
• Factor graph properties: The properties of factor graphs, such as connectivity, degree constraints, and cycle structures, warrant further exploration. Investigating these properties could lead to new graph-theoretic tools for classifying groups or understanding the constraints on complete decompositions.

These directions aim to deepen the understanding of group decompositions and their applications, building on the graphical framework established in this paper. By addressing these challenges, future research can further bridge group theory, graph theory, and applied mathematics, opening new avenues for theoretical and practical advancements.