ChainImputer: A Neural Network-Based Iterative Imputation Method Using Cumulative Features

Abstract

The goal of missing value imputation is to replace the missing values in the dataset with specific values. In particular, this preprocessing step plays a crucial role in knowledge discovery and data mining, as most data analysis methods assume complete data and cannot be applied directly to datasets with missing entries. Among various approaches, the neural network-based missing value imputation method has recently gained significant attention due to its superior prediction accuracy based on its excellent capability to fit the given training dataset. Specifically, these approaches conventionally begin by applying a naïve missing value imputation to fill all missing entries in the dataset and then train the network on the completed data. Thus, the performance of missing value imputation can be limited because the neural network is trained on an unreliable dataset filled with roughly guessed values. Instead, we may consider an alternative strategy to use only the features without missing values or carefully imputed features obtained during the imputation process, which can be regarded as an asymmetric process because it progressively adds the newly imputed features into the training dataset. In this study, we propose an effective neural network-based imputation method that incrementally constructs a cumulative feature set during training. The experimental results on 25 publicly available datasets showed that the proposed method outperforms conventional methods significantly.

1. Introduction

Missing values frequently occur in data analysis due to various factors such as incomplete manual data entry, measurement errors, or sensor malfunctions [1]. These unobserved values cannot be directly used in analyzing the characteristics of the data, potentially degrading model performance or even preventing the application of subsequent procedures [2,3]. As a result, most studies considered missing value imputation (MVI) before conducting their analysis, indicating that an accurate imputation is essential for reliable analysis and modeling [4]. Although a variety of naïve MVI methods, such as mean imputation [5], have been widely applied, these methods refer to simple approaches that fill in missing values based solely on the statistical properties of observed data and often fail to capture complex feature interactions [6]. In contrast, neural network (NN)-based approaches have recently attracted significant attention due to their ability to effectively infer missing values from incompletely observed inputs, resulting in high imputation accuracy [7].

The strategy to impute the missing values can be divided into chain and non-chain approaches. Among them, the chain approach can be regarded as an asymmetric process because the chain approach iteratively imputes feature values and progressively adds the newly imputed features into the training dataset. As a result, the input feature space grows step by step—similar to a natural number sequence (1, 2, 3, 4, 5, …), which introduces an asymmetric structure. In contrast, non-chain approaches can be regarded as symmetric approaches due to maintaining a fixed number of features throughout the process, resulting in a geometrically symmetric training dataset. For example, if we plot the number of features used in each iteration, the chain-based approach forms a right triangle as the feature set grows progressively over time. In this regard, non-chain imputers maintain a constant number of features across iterations, resulting in a rectangular shape. The advantage of the asymmetric chain approach is that it is more focused and detailed since each iteration only tries to impute one feature while using other already imputed features. This can lead to more accurate results at each step. In contrast, the symmetric non-chain approach looks at the whole dataset at once, so it might struggle to predict accurate values because it includes noisy or irrelevant features in the input.

In conventional NN-based MVI methods, the missing values are replaced with the outputs of the NN [8]. To train the NN for missing value prediction, all the features except the target feature are used as a training dataset. Because the training dataset might also contain missing values, a naïve MVI method, such as mean imputation, is typically applied before the training process since conventional NN-based methods cannot handle missing values directly. However, such an approach can lead to inaccurate predictions, as the model is trained on a dataset containing roughly estimated values. This issue becomes more severe when the original dataset contains a large number of missing values, as the NN fits into a significantly distorted dataset.

Ideally, all the distorted features should be excluded from the training dataset to avoid an inaccurate NN model, which can be achieved by considering only features without missing values. However, in practice, there is no guarantee that there will always be a sufficient number of features without missing values, especially when the original dataset contains a large amount of missing data. As an alternative, feature imputation can be performed as an iterative process, where features carefully imputed by the neural network in previous iterations are included in the training dataset to impute the values of the next feature. This approach helps to minimize distortion while ensuring a sufficient quality of features. Despite the widespread use of advanced data generation mechanisms in NN-based MVI methods, such as autoencoders [9,10,11,12], generative adversarial networks (GANs) [13,14,15,16], and attention mechanisms [17,18,19], the aforementioned chain approach, although widely used in multilabel learning (e.g., classifier chains), has been rarely explored in NN-based MVI studies.

In this study, we focus on an effective MVI method following asymmetric strategy. Specifically, the proposed method first identifies the features without missing values from the original dataset. Then, the employed NN is trained on the selected features, considering the next feature with missing values as a target. After the target feature is imputed, it is added to the input of the subsequent imputation steps. The experimental results and statistical tests on 25 publicly available datasets showed that the proposed method significantly outperforms the conventional methods regarding missing value prediction accuracy. The implementation is accessible via GitHub at https://github.com/KhrTim/ChainImputer, accessed on 18 May 2025, supporting reproducibility and further research.

The remainder of this paper is organized as follows. Section 2 reviews existing approaches to missing value imputation, including classical, neural, attention-based, and diffusion-based methods. Furthermore, we describe our proposed solution and provide the mathematical foundation and time complexity analysis in Section 3. Section 4 contains an experimental evaluation of our method in comparison with counterparts. Finally, in Section 5, we provide additional experimental results comparing variations of the proposed method.

2. Related Work

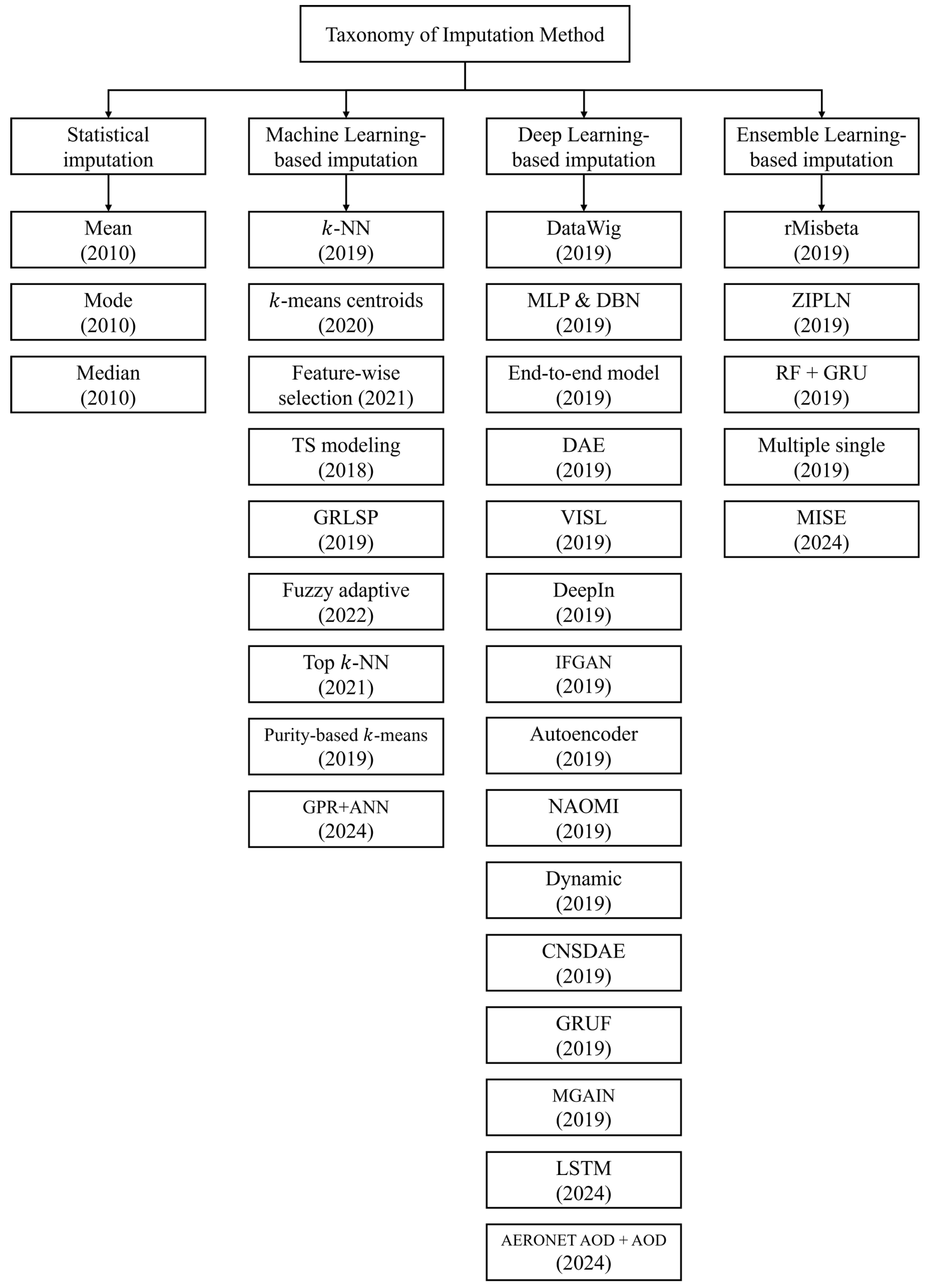
As MVI is a steady topic in machine learning, statistical imputation methods are widely used for handling missing data. Figure 1 shows a taxonomy of the imputation methods. For example, in the work of [20], statistical methods are chosen for their simplicity. Mean, mode, and median imputations are simple techniques that fill in missing values by computing the corresponding statistic from the observed values within each feature. Statistical imputation methods offer the advantage of being fast and straightforward in imputing missing values. However, the drawback is that they tend to underestimate variance and ignore relationships with other variables, making it challenging to impute accurate values [5].

Machine learning-based imputation involves constructing predictive models to estimate missing values in a dataset [21]. One of the advantages of machine learning-based imputation is its significantly greater flexibility compared to statistical methods, enabling better predictions by capturing higher-order interactions within the data [5]. The k-nearest neighbor (k-NN) imputation is one type of machine learning-based imputation methods [22]. k-NN imputation replaces missing values using information from the k-nearest neighboring data points. This enhances the completeness of the dataset while maintaining the valuable information for further analysis. However, inaccuracies may occur if the missing feature patterns are complex or unique. Additionally, locating neighbors for imputation can be challenging if the data distribution is highly imbalanced.

There are many ongoing studies related to machine learning-based imputation [23]. The experimental studies demonstrate the validity of various machine learning-based MVI methods [21]. While the chain approach has been widely applied in various domains, such as classifier chains in multilabel learning [24], the first imputation method based on this approach was proposed by Van Buuren and Groothuis-Oudshoorn [25], introducing the widely used Multiple Imputation by Chained Equations (MICE). Conventionally, Tsai C. et al. [26] conducted a comparative performance experiment among five widely used supervised learning methods: k-nearest neighbors (k-NN), classification and regression trees (CART), multi-layer perceptron neural networks (MLP), Naive Bayes, and support vector machines (SVMs). In their study, Yadav et al. [27] compared the experimental results of missing value imputation using visualization and imputation of missing values (VIM), MICE, nonparametric missing value imputation using random forest (MissForest), and Harrell miscellaneous (HMISC) methods. Wang et al. [28] performed a comparative analysis using two renowned imputation methods—autoregressive integrated moving average (ARIMA) and linear interpolation (LI) models—as well as three machine learning approaches: k-NN, multi-layer perceptron (MLP), and support vector regression (SVR) (a Support Vector Machine (SVM) regression used for missing value imputation). Palanivinayagam et al. [29] analysed the performance of five machine learning models: Naive Bayes, SVM, k-nearest neighbours, random forest, and linear regression. The experimental results showed that the SVM classifier achieves the highest accuracy, highlighting its importance in diabetes research and addressing missing data. Li et al. [30] tested six machine learning algorithms to predict hospital readmissions within 30 days for elderly patients (aged 65 and above). Experiments were conducted using RandomForest, LogisticRegression, XGBoost, LGBM, MLP, and Random + XGBoost and the results indicated that the RF + XGBoost algorithm exhibited superior overall performance in terms of Area Under the Curve (AUC) for prediction.

Raja et al. [31] introduced a novel imputation method based on rough k-means centroids that utilizes unsupervised machine learning methods to handle missing values. Another clustering-based method performs the imputation using a similarity-based spectral clustering approach, top k-nearest neighbor approach, and clustering [32]. Alternatively, the data-driven missing value imputation technique incorporates feature-wise selection to perform accurate imputations [33]. The Takagi–Sugeno (TS) modeling method is a promising approach for incomplete datasets, utilizing Bayesian networks for missing value imputation [34]. The GRLSR method precisely imputes missing values in incomplete data by combining sample self-representation and local data structure [35]. Meanwhile, the fuzzy adaptive imputation approach (FAIA) is a fuzzy-based information decomposition method to address missing value problems in imbalanced data streams [36]. Another novel imputation approach is a query selection method that considers the imputation uncertainty in active learning with missing values [37]. In addition, the purity-based k-NN imputation method considers data purity and improves results by estimating high-purity instances as candidates [38]. Yet another K-NN method extension named Focalize K-NN leverages correlated features and temporal lags to improve the performance of the traditional K-NN imputer [39].

Deep learning-based imputation involves feeding data into the input layer of a neural network and computing the predicted output. The difference between each predicted value and its corresponding ground truth is then calculated [4]. In other words, training through multiple layers enables the model to discover complex relationships embedded within the data structure and improve imputation performance through fine-tuning [40]. Missing values can be imputed using traditional deep learning techniques such as long-short-term memory (LSTM) networks and Convolutional Neural Networks (CNN) [35]. A more recent type of deep learning-based imputation is DataWig [8]. DataWig (DW) creates a model for each feature to perform imputation. It aims to estimate the probabilities of possible values for a target feature using information from other features, including those with missing values. Accurately capturing the full range of data characteristics can be challenging in datasets with many missing values. As a result, the model may struggle to understand and handle missing values fully. Lin et al. [41] evaluated the performance of two supervised methods—Multi-layer perceptron (MLP) and deep belief networks (DBN). Morales-Alvarez et al. [42] introduced VISL—a novel scalable structure learning approach that simultaneously infers the structure between variable groups and imputes missing values using deep learning in the context of missing data. Another approach, DeepIn, is a missing value imputation solution for continuous missing patterns found in Internet-of-Things devices in smart spaces [43]. Alternatively, dynamic imputation is a method to enhance the training of neural networks in the presence of missing values [44]. Yet another DNN model imputes missing values in the hourly aerosol optical depth product by combining AERONET with a numerical model [45]. Furthermore, Bidirectional Recurrent Imputation for Time Series (BRITS) [46] treats missing values as trainable variables within a bidirectional recurrent neural network, allowing end-to-end optimization over time-series data.

The autoencoder introduces a new way to model the characteristics of a given dataset [47]. For example, an autoencoder can leverage information from neighboring data points to perform data imputation [9]. Expanding the applications of autoencoders, a different method was developed by modifying a denoising autoencoder (DAE) into a cluster-based imputation framework [10]. Gjorshoska et al. [11] utilized the autoencoder imputation method for resolving missing values in the food composition database (FCDB). A completely modified denoising stacking autoencoder (CMSDAE) is used for missing value imputation, particularly to enhance the quality of the MTL version [12]. Psychogyios et al. [48] proposed a method based on DAE with kNN for the pre-imputation task for the missing value imputation in the electronic health records.

An alternative solution comes from using the GAN, as was done by Zhang et al. [13], who applied the end-to-end GAN for multivariate time series, addressing the problem of imputed values being significantly different from actual values. Generative adversarial imputation networks (GAIN) [49] introduced a framework in which a generator imputes missing values conditioned on observed data, while a discriminator learns to distinguish imputed from real values using a hint mechanism, achieving state-of-the-art results. Another GAN-based solution named IFGAN is a missing value imputation algorithm based on feature-specific GAN [14]. Furthermore, multiple generative adversarial imputation networks (MGAIN) is an imputation method that simplifies the network structure of GAIN and reduces the demand for data [15]. Non-autoregressive multi-resolution imputation (NAOMI) is a new deep generative model for imputing long-range sequences [16].

More recent studies explore the attention mechanism [50] capabilities in the MVI area tasks. One method of attention application was demonstrated by Koswar et al. [17], who proposed a framework that leverages between-feature or between-sample attentions. Another approach, named SAITS, operates with a weighted combination of two diagonally masked self-attention blocks, which explicitly capture temporal dependencies and feature correlations between time steps [18]. ImputeFormer combines strengths of low-rank and deep learning models, introducing a low rankness-induced transformer to balance strong inductive bias and high expressivity [19].

Another recent branch of MVI studies employs diffusion models for missing values generation. For example, Chen et al. apply a schrödinger bridge problem to probabilistic time series imputation by generating missing values conditioned on observed data [51]. Alternatively, in the work of Wang et al. [52], the evidence lower bound (ELBO) was re-derived in the scenario of multivariate time series imputation to take into account the correlations between observed and missing values. In the proposed multivariate imputation diffusion model (MIDM), the newly derived ELBO was enhanced with noise sampling and denoising mechanisms for multivariate time series imputation. Biloš et al. propose yet another method that adapts the noise generation and denoising mechanisms for time-series oriented scenario with irregularly sampled observations [53]. To overcome difficulties occurring in temporal electronic health records analysis, Dai et al. [54] proposed a Similarity-Aware Diffusion Model-Based Imputation (SADI), an imputation method that utilizes information across dependent variables. Following the diffusion ideas, Yang et al. [55] utilized a high-frequency filter to boost the residual term imputation, supplemented by a dominant-frequency filter for the trend and seasonal imputation in their proposed solution named multivariate time series imputation (FGTI). Lastly, to achieve an imputation consistency in terms of intra-consistency between observed and imputed values, and inter-consistency between adjacent windows, Zhou et al. [56] employed a contrastive complementary mask in Multivariate Time Series Consistent Imputation (MTSCI) to generate dual views during the forward noising process.

Ensemble-based imputation uses a combination of machine learning-based imputation and deep learning-based imputation. One type of ensemble-based imputation is stacked ensemble (SE) [57]. After filling the NaN values with the k-NN imputer, stacked ensemble (SE) creates a stacked ensemble classifier using models such as Extreme Gradient Boosting (XGB), random forest (RF), and Extra Tree Classifier (ETC). It is crucial to be aware that the predictions from each alternative imputation method are combined to make the final prediction. However, this approach can lead to a degradation in the performance of the final prediction if each model is overfitting.

Currently, there are many ongoing studies related to ensemble-based imputation. rMisbeta utilizes robust estimators based on the minimum beta divergence method. Experimental results show that data matrices imputed by rMisbeta outperform other statistical tools such as Zero, k-NN, SVD, EM, and RF. Furthermore, rMisbeta is an accurate, simple, and fast tool for missing value imputation [58]. Meanwhile, zero-inflated Poisson log-normal (ZIPLN) model is a feasible imputation method that uses a mixture distribution [59]. In particular, the missing data imputation method based on random forest proposes a multi-step prediction for imputation and an ensemble model combining attention-based GRU models [60]. In addition, the multiple single imputation method based on ensemble learning applies missing value prediction using bootstrap sampling in the ensemble method, assigns weights to these predictions, aggregates them, and generates the final prediction [61]. Rao et al. proposed a multimodal imputation-based stacked ensemble (MISE) model to classify and predict air quality [62]. It has demonstrated superior performance through experimental validation. Jung et al. [63] utilized a bagging ensemble of multi-layer perceptrons, known as a Softmax ensemble network, to determine the ensemble weights for each MLP. Samad et al. [64] demonstrated that the linear regressor of MICE, replaced by ensemble learning and deep neural networks, improves both the imputation accuracy of MICE and the classification accuracy of imputed data.

As missing value imputation methods continue to evolve, increasing emphasis is being placed on their applicability to real-world scenarios, where data may be irregular, incomplete, and collected under complex conditions. For instance, GRUF captures the past states of time series data collected from devices and appropriately fills in missing values using both historical sensor readings and temporally aligned data from neighboring nodes via edge computing [65]. A recent study by Jiang and Zhang [66] proposed an interpretable diffusion-based imputation framework tailored for industrial soft sensing, incorporating resampling strategies and Fourier-based components to enhance both accuracy and model transparency.

3. Proposed Method

Table 1. Notations used for describing the proposed method.

Symbol	Name	Description
F	Dataset	Entire dataset
x	Input	Input features or independent variables
y	Output	Output or dependent variable
f	Number of features	Total number of features
$F_{missing}$	Dataset with missing values	Dataset containing missing values
$F_{imputed}$	Dataset by imputing missing values	Datasets without missing values
M	Imputation model	Model used for imputation

summarizes the notations used to describe the proposed method. F denotes a set of datasets, comprising an input vector $x_i$ and a corresponding label $y_i$, represented as $F={(x_i,y_i)}_{i=1}^f$. Here, f denotes a feature, while each observation in the dataset consists of multiple such features. MVI aims to fill in missing values within the dataset ($F_{missing}$). It selects input features based on the provided list of features (train_col) and trains an imputation model denoted as M to predict missing values using the selected input features. After filling in missing values with the model M, denoted as $F_{imputed}$, the dataset is updated.

The procedure of conventional NN-based MVI methods is as follows [8]. Suppose we have an original feature set F where its features may contain missing values. Then, the algorithm chooses a target feature f containing missing values from F. Next, all the other features $F\setminus f$ are chosen to form the training dataset for NN. After that, a naïve MVI, such as mean imputation, is performed on each feature in $F\setminus f$ if it contains missing values. Thus, $F\setminus f$ can be filled with many roughly guessed values, resulting in an inaccurate prediction model. Lastly, $\widehat{f}$, which is an imputed version of f by trained NN, replaces f from F, and then these steps are repeated until there are no features with missing values in F. We argue that the advantage of employing NN, which is expected to yield accurate predictions on the missing value based on its strong fitting capability, can be nullified because NN will learn the roughly guessed values for its prediction at all repetitions. Instead, we may consider a natural imputation strategy as follows. Starting from F, the algorithm chooses $f_1$ with missing values and tries to train an NN using features $F\setminus f_1$. Because the training process cannot proceed if there are missing values in $F\setminus f_1$, the algorithm chooses $f_2$, which is the second target feature of imputation, and then tries to train an NN using features $F\setminus \{f_1,f_2\}$. At the end of this recursive procedure, a set of features will remain that contains no missing values. Hence, a new feature, a carefully imputed version of the original feature, can be obtained after the employed NN is trained and imputation is performed. Next, in the backward stage of the recursive procedure, these features are inherently involved in the training of NN for the current recursion. When the recursion process is completed, all the missing values in F are imputed.

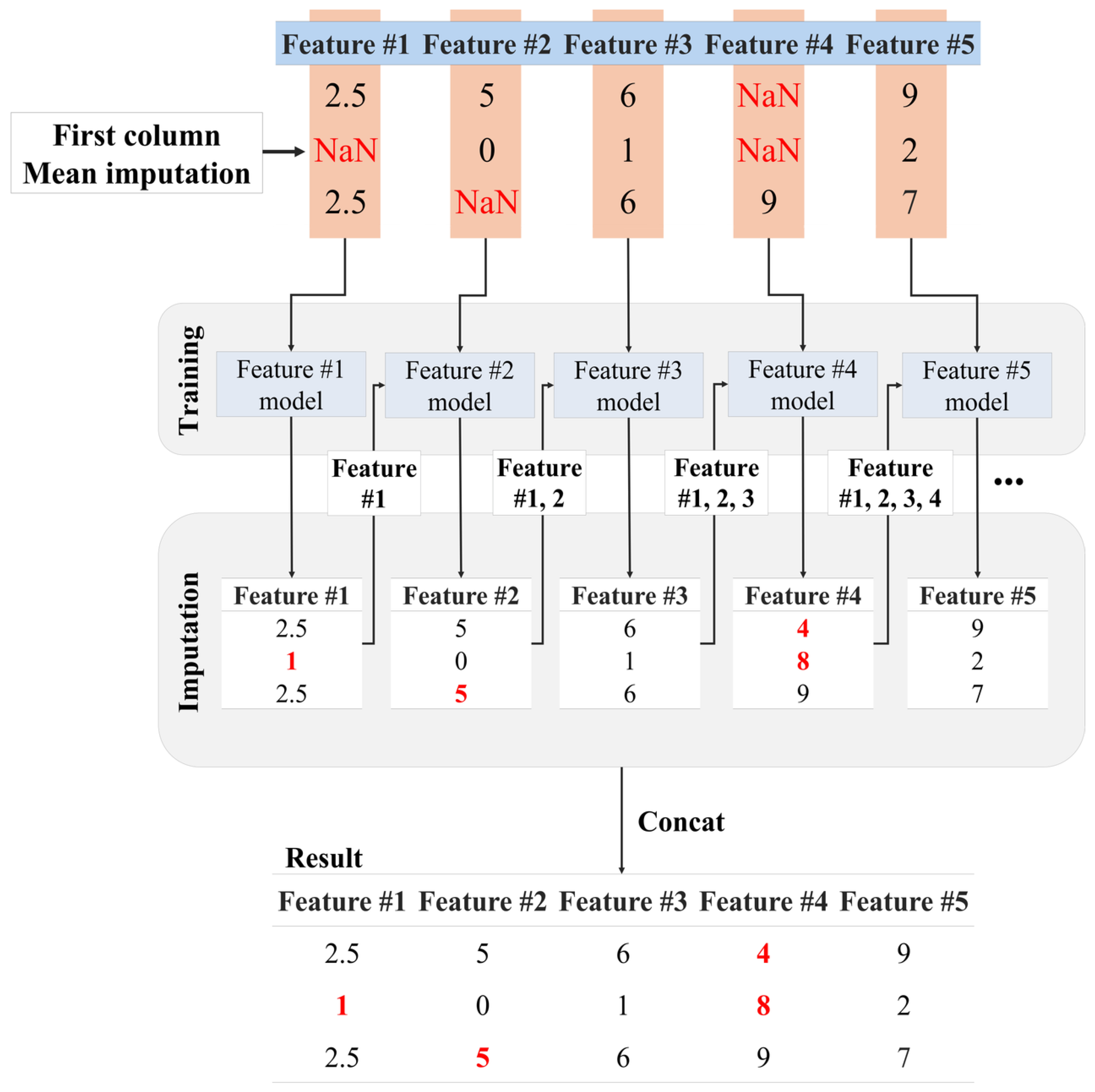
In Figure 2, the proposed method models for each feature using the available data. When missing values are encountered in the first feature, a common approach consists of replacing them with the mean of the existing values within the feature because there are no trainable features without missing values. If there are features without missing values, an NN can be used to train on those features and then impute the missing value of the first feature. Next, the missing values in the second feature are imputed based on the NN trained on the first feature. This iterative process continues sequentially for each feature. It allows for the gradual refinement of the models and incorporates more complex relationships between features. We argue that this iterative approach helps reduce the impact of missing values and adjusts the imputation process according to the characteristics and dependencies present in each dataset feature.

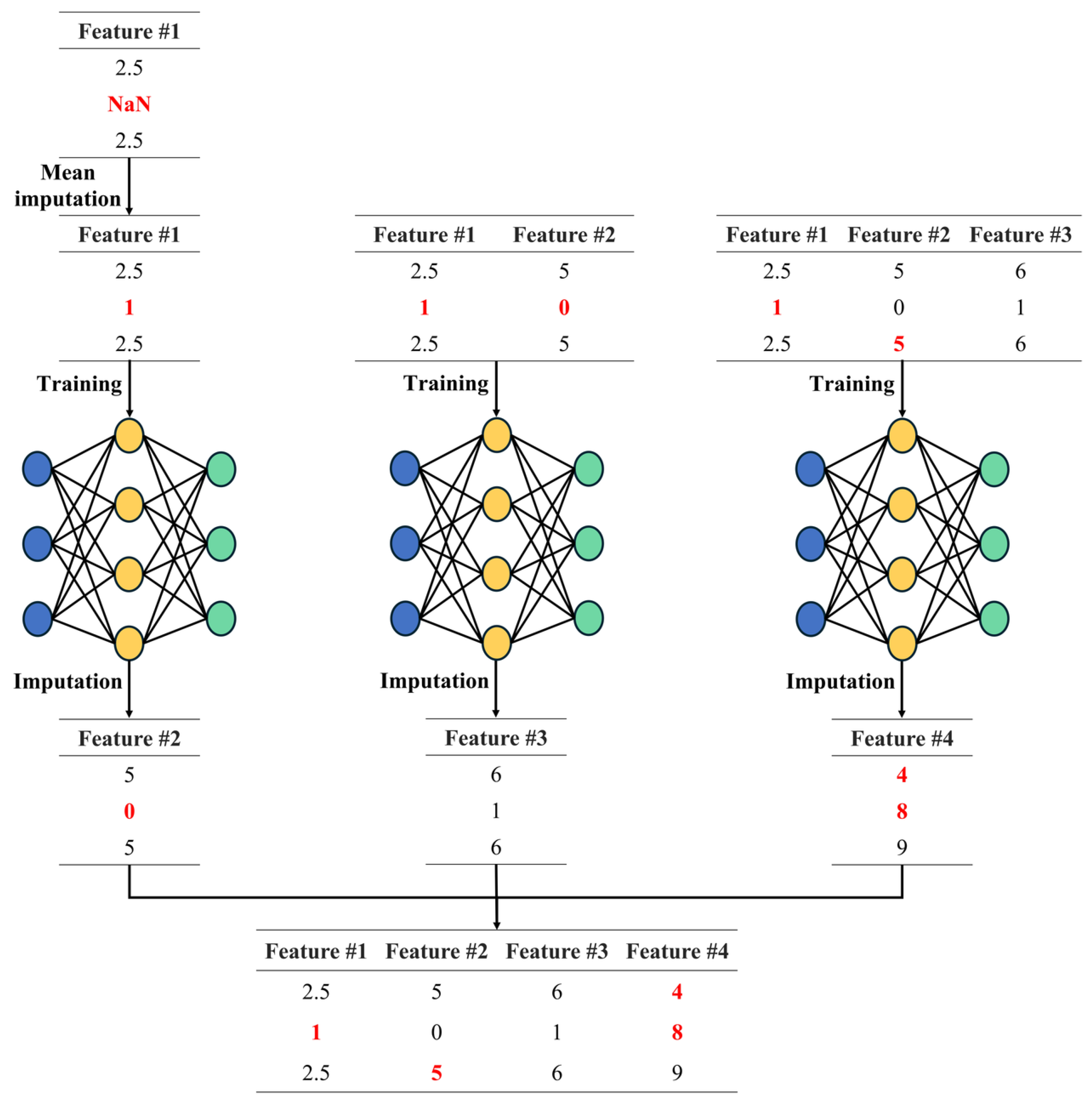
In Figure 3, the proposed method iteratively trains models to handle missing values, utilizing previously imputed missing values to train each new model and replacing all missing values in the dataset. The proposed method trains a model using the current input features and leverages it to replace missing values, ensuring a robust and reliable data analysis process. The training process of the proposed method involves constructing independent models for each feature and using the imputed results from the preceding feature to predict missing values sequentially. This process can be expressed as follows. First, the training for the first feature is conducted as

$$M_1=M(F_{impute{d}_1},F_{impute{d}_1}^{\left(1\right)}),$$

(1)

where $F_{impute{d}_1}$ represents the dataset after filling in the missing values for the first feature. Subsequently, the training for the second feature is carried out as

$$M_2=M(F_{impute{d}_{1,2}},F_{impute{d}_{1,2}}^{\left(2\right)}),$$

(2)

where $F_{impute{d}_{1,2}}$ denotes the dataset after filling in missing values for both the first and second features, and $F_{impute{d}_{1,2}}^{\left(2\right)}$ represents the dataset used to train the model for the second feature. This iterative process continues for each subsequent feature. Specifically, the model $M_i$ for the i-th feature is trained using the imputed results from features 1 through i. This can be written as

$$M_i=M(F_{impute{d}_{1,\dots ,i}},F_{impute{d}_{1,\dots ,i}}^{\left(i\right)}),$$

(3)

where $F_{impute{d}_{1,\dots ,i}}$ represents the dataset after filling in missing values for features 1 through i, and $F_{impute{d}_{1,\dots ,i}}^{\left(i\right)}$ represents the dataset used to train the model for the i-th feature. This process ensures that each feature-wise model is trained using the imputed results from previous features, facilitating accurate imputation of missing values across the dataset.

It is worth noting that, unlike traditional chain-based methods such as MICE, the proposed method introduces two key differences. First, the feature ordering for imputation is not determined randomly, but is predefined based on the ascending order of missingness ratios. Second, the proposed method adopts an asymmetric structure by incrementally constructing a cumulative feature set. Each newly imputed feature is incorporated into the input of the subsequent imputation step, enabling more informed training and progressive refinement of the neural models. This progressive structure helps reduce the distortion caused by unreliable inputs in the early stages of the imputation process.

Algorithm 1 presents a method for imputing missing values in a dataset. The proposed method, called ChainImputer, employs a chain approach, leveraging initially complete features or mean imputation, followed by model-based imputation using MXNet. First, the original feature set F is initialized (Line 2), and S, which will contain features without missing values, is set to an empty set (Line 3). The algorithm iterates over each feature f in the feature set F (Line 4). For each feature, it checks if there are missing values (Line 5). If a feature f has no missing values, it is added to the set S (Line 6.) If, after processing all features, the set S is empty, indicating that all features in F have missing values, the algorithm selects a random feature f from the feature set F (Line 10). It then uses a mean imputation method to fill in the missing values of f to create the initial feature (Line 11). The imputed feature $f^{\prime }$ is then added to the set S and removed from F (Lines 12–13). For each remaining feature f in the feature set F, the algorithm uses an MXNet model trained on the features in S to impute the missing values in f (Line 16). Next, the original feature f is removed from the feature set F, and the imputed feature $f^{\prime }$ is then added to the set S (Lines 17–18). This process is repeated until all the features in F are considered.

Algorithm 1 Procedures of proposed imputation method

1: procedure ChainImputer(F)                                   ▹ Proposed missing value imputer 2:     Initialize F to the original feature set; 3:     $S\leftarrow \varnothing$; 4:     for each feature $f\in F$ do 5:         if f has no missing values then 6:            $S\leftarrow S\cup f$; 7:         end if 8:     end for 9:     if $S=\varnothing$ then                                   ▹ When there is no features for training MXNet 10:         Choose a random feature $f\in F$; 11:         $f^{\prime }\leftarrow meanImputer\left(f\right)$; 12:         $F\leftarrow F\setminus f$; 13:         $S\leftarrow S\cup f$; 14:     end if 15:     for each feature $f\in F$ do 16:         $f^{\prime }\leftarrow mxNet(S,f)$;                           ▹ complete f using MXNet trained based on S 17:         $F=F\setminus f$; 18:         $S\leftarrow S\cup f^{\prime }$; 19:     end for 20: end procedure

An imputed entry is an estimate and may deviate from the true value. If that entry is repeatedly reused as an input during later stages of the chain, its estimation error can propagate and accumulate, potentially degrading subsequent predictions. Therefore, an imputation schedule that minimizes the number of times previously imputed entries are reused provides a principled way to limit cumulative noise. We now show that the ascending-missingness order achieves this minimum.

Let $n_1^m\le n_2^m\le \dots \le n_{\left|F\right|}^m$ denote the missing-value counts sorted in ascending order. If the feature with $n_i^m$ missing entries is imputed at position i, its column will be reused in exactly $\left|F\right|-i$ subsequent models. The total number of imputed entries reused for an ordering $\pi$ is therefore formalized as follows:

Proposition 1

(Re-use cost). For any permutation π of $\{1,\dots ,|F\left|\right\}$, the cumulative count of imputed entries that are reused during the chain is

$$T\left(\pi \right)=\sum _{i=1}^{\left|F\right|}{n}_{\pi \left(i\right)}^m\left(\left|F\right|-i\right).$$

(4)

Lemma 1.

Consider two positions, $i<j$ with $n_i^m<n_j^m$, placed in reverse order inside π. Swapping their positions decreases $T\left(\pi \right)$.

Proof. 

Let $d_i=\left|F\right|-i$ and $d_j=\left|F\right|-j$ so that $d_i>d_j$. Before the swap, the contribution of these two features to (4) is $n_j^m{d}_i+n_i^m{d}_j$. After swapping, it becomes $n_i^m{d}_i+n_j^m{d}_j$. Their difference satisfies

$$\left(n_j^m-n_i^m\right)\left(d_i-d_j\right)>0,$$

(5)

so the swap strictly reduces $T\left(\pi \right)$. □

Theorem 1

(Optimality of ascending order). The ascending-missingness schedule $n_1^m,n_2^m,\dots ,n_{\left|F\right|}^m$ minimizes $T\left(\pi \right)$ in (4) over all permutations π.

Proof. 

Starting from any permutation, repeatedly apply the swap described in Lemma 1 to every inverted pair. Each swap lowers $T\left(\pi \right)$ and strictly reduces the inversion count. The process terminates only when no inversions remain, i.e., when the list is in ascending order, which therefore attains the global minimum. □

By Theorem 1, the ascending-missingness order minimizes $T\left(\pi \right)$; hence, it reuses the fewest imputed entries and introduces the least cumulative distortion in subsequent training steps.

Based on Algorithm 1, we analyze the time complexity of the proposed ChainImputer and compare it with the neural network-based baseline DW for a balanced perspective. Let n denote the number of instances, $d=\left|F\right|$ the number of features, a the overall missing rate, T the number of training epochs, $g(n,a)$ the cost of applying a simple filler to one column (for example, mean imputation so that $g(n,a)=\mathcal{O}\left(n\right)$); and $h\left(n\right)$ the cost of one network epoch over the entire data set. DW first imputes the complete table once and then trains for T epochs [8], which leads to

$$\mathcal{O}\left(g(n,a)+Th\left(n\right)\right).$$

(6)

ChainImputer processes the d columns in sequence: for each feature it produces predicted values for that column and then trains the network for T epochs, resulting in

$$\mathcal{O}\left(dg(n,a)+dTh\left(n\right)\right).$$

(7)

Although this worst-case big-$\mathcal{O}$ bound is larger, ChainImputer begins with a single input feature, and the effective $h\left(n\right)$ increases gradually as the model incorporates more columns during the imputation process. Consequently, for data sets with substantial sparsity or moderate feature counts, its observed running time can be comparable to, or even less than, that of DW in practice, despite the higher asymptotic bound.

4. Experimental Results

This section presents experimental comparisons between the proposed model and existing approaches to validate its performance. We describe the experimental design to support this evaluation, covering the dataset, baseline imputation models, performance metrics, and statistical testing procedures.

4.1. Experimental Settings

The UCI machine learning repository dataset is used for the benchmark. The datasets represent various domains: health, social, biology, business, etc.

Table 2. Summary of datasets used in the experimental evaluation of the imputation methods. Each dataset is characterized by its domain, number of instances (rows), number of attributes (columns), total number of missing values, and data types (categorical, integer, or real-valued). These datasets span various fields including biology, medicine, business, and social science, ensuring the generalizability and robustness of the proposed method. Dataset references are provided for reproducibility.

Dataset	Domain	Instances	Attributes	Missing Values	Type	Reference
Abalone	Biology	4176	9	7517	Categorical	[67]
Adult	Social	32,560	15	97,680	Categorical	[68]
Ai4i	Computer Science	10,000	6	12,000	Real	[69]
Bank-marketing	Business	4521	17	15,371	Categorical	[70]
Blood	Business	748	5	748	Real	[71]
Breast	Health, Medicine	285	10	570	Categorical	[23]
Contraceptive	Health, Medicine	1473	10	2946	Categorical, Integer	[72]
Credit	Business	689	16	2205	Integer, Real	[73]
Echocardiogram	Health, Medicine	129	12	310	Integer, Real	[74]
Forty	Social	320	10	640	Integer, Real	[75]
Haberman	Health, Medicine	305	4	244	Integer	[76]
Heart	Health, Medicine	302	14	846	Categorical	[23]
Hepatitis	Health, Medicine	154	20	616	Integer, Real	[77]
Iris	Biology	149	5	149	Real	[78]
Liver	Health, Medicine	344	7	482	Categorical	[79]
Lymph	Health, Medicine	148	19	562	Categorical	[67]
Magic	Physics, Chemistry	19,019	11	41,842	Real	[80]
Maternal	Health, Medicine	1014	7	1420	Real	[81]
Monk	Social	415	7	581	Categorical	[82]
National-health	Health, Medicine	2278	9	4101	Real	[83]
Obesity	Health, Medicine	2111	17	7191	Integer	[84]
Rice	Biology	3809	8	6094	Real	[85]
Wholesale	Business	440	7	616	Integer	[86]
Wine	Social	177	14	496	Integer, Real	[34]
Yeast	Biology	1484	9	2671	Real	[87]

provides descriptions of the datasets used in the experiments. The datasets employed contain attributes and instances across a diverse range. The number of classes remains consistent for binary classification. A detailed description of employed datasets can be found in Appendix A. These datasets, each with their unique characteristics, serve as valuable resources for evaluating the effectiveness of the proposed imputation method across diverse domains and data types. Each dataset was randomly corrupted with missing values at a rate of 20% of the original data for the experiment; therefore, each prepared dataset falls under the Missing Completely At Random (MCAR) category. This preprocessing step was conducted before the experiments to compare the performance of missing value imputation methods. A 30-fold random split was applied to datasets, with each split following an 8:2 ratio for training and testing.

The proposed model compared three models using $RMSE$. The parameters for the three comparison models were set according to the values recommended in their respective studies. The description of the three comparative experimental models is as follows:

• DataWig (DW): DW creates a model for each feature to perform imputation. It aims to estimate the probability of all potential values for a feature given an imputation model and information from other features, especially those containing NaN values [8].
• k-Nearest Neighbor (k-NN) imputation: k-NN imputation replaces missing values by using the nearest neighbor observation value k for data points with missing values. This enhances the completeness of the dataset and allows for valuable information for analysis [22].
• Stacked Ensemble (SE): After filling the NaN value with the k-NN imputer, it predicts a stacked ensemble classifier with Extreme Gradient Boosting (XGB), random forest (RF), and Extra Tree Classifier (ETC) models [57].

Specifically, DW was chosen because it has been shown to outperform GAIN, a GAN-based method, and DAE in its original study [8]. SE integrates a variety of traditional machine learning algorithms, including tree-based models, and has demonstrated superior performance over other conventional imputation techniques. Therefore, DW and SE offer strong baseline comparisons from both deep learning and traditional machine learning perspectives.

Table 3. Hyperparameter settings used in our experiments.

Method	Batch Size	Epochs	Loss Function	Optimizer	Learning Rate
Proposed	8	10	Regression	$ReLU$	$4\times {10}^{-3}$
DW	32	50	Cross-entropy	$Adam$	$1\times {10}^{-3}$
k-NN	32	50	Cross-entropy	$Adam$	1 $\times {10}^{-3}$
SE	32	50	Cross-entropy	$Adam$	$1\times {10}^{-3}$

shows the hyperparameter settings of each method where that of the comparison models were referenced from [44]. In contrast, the hyperparameters for the proposed method were determined based on its rapid convergence in preliminary experiments. In particular, we employed a regression loss with ReLU activation to better suit the continuous nature of the imputation task, and used $RMSE$ as the evaluation metric, which is standard for assessing numerical reconstruction accuracy. A neural network with one hidden layer was constructed using a TensorFlow-based framework. The use of a single hidden layer is motivated by the incremental nature of the chain imputation process, where the number of input features is initially small and increases gradually. In such settings, deeper architectures may lead to overfitting, especially during the early stages of training. Similarly, the proposed method utilized an MXNET-based framework to create a neural network with one hidden layer, consistent with the comparison experimental model [8]. Specifically, MXNET was chosen for its lightweight symbolic–imperative hybrid engine, which enabled rapid prototyping with lower GPU memory consumption. $RMSE$ is employed as the evaluation measure. The metric is the most commonly used metric to estimate the performance of the missing value imputation methods [88]. It measures the difference between imputed values and actual values. After averaging the squared errors between predicted and actual values, the square root of this value is taken to calculate $RMSE=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n{(y-\widehat{y})}^2}{n}}}$, where y and $\widehat{y}$ represent the original value, but hidden to the MVI methods, and the imputed data, respectively. A lower value indicates higher performance.

Lastly, statistical tests are performed to validate the superiority among imputation models. The Friedman test is a non-parametric equivalent that assesses repeatedly measured outcomes by separating the dataset by the algorithm and assigning ranks to measure them [89], written as

$$R_j={\displaystyle \frac{1}{N}}\sum _{i=1}^N{r}_i^j.$$

The rank of the j-th method for the i-th dataset, derived from the experimental results, can be denoted as $r_i^j$ when employing N datasets and k methods. Assuming equality of $R_j$, ${\chi }_F^2$ is calculated as

$${\chi }_F^2={\displaystyle \frac{12N}{k(k+1)}}\left(\sum _j{R}_j^2-{\displaystyle \frac{k{(k+1)}^2}{4}}\right).$$

Then, Friedman statistics $F_F$ are distributed according to the $F_F$-distribution, with $k-1$ and $(k-1)(N-1)$ degrees of freedom, that can be calculated as

$$F_F={\displaystyle \frac{(N-1){\chi }_F^2}{N(k-1)-{\chi }_F^2}}.$$

If there is a statistically significant difference ($p<0.05$), a post hoc test is conducted in the Friedman test. The Bonferroni–Dunn test was chosen as the post hoc test because there was a statistically significant difference between this and the Friedman tests. The Critical Difference ($CD$) is used to compare the differences between the average ranks of algorithms, written as

$$CD=q_{\alpha }\sqrt{{\displaystyle \frac{k(k+1)}{6N}}}.$$

4.2. Comparison Results and Analysis

Table 4. Root Mean Square Error ($RMSE$) comparison across datasets for the proposed imputation method and three baselines: DW (Datawig), k-NN (K-nearest neighbors), and SE (Stacked Ensemble). The bottom row shows the average rank of each method across all datasets, where a lower rank indicates better overall performance. The proposed method achieves the lowest average rank (1.24), demonstrating superior imputation accuracy across diverse datasets.

Dataset	Proposed	DW	k-NN	SE
Abalone	0.2007 ± 0.0599	0.5095 ± 0.0100	0.5531 ± 0.0103	0.6562 ± 0.0025
Adult	0.1894 ± 0.0946	0.2146 ± 0.0011	0.2582 ± 0.0006	0.5803 ± 0.0010
Ai4i	0.1658 ± 0.0401	0.1724 ± 0.0009	0.2448 ± 0.0037	0.3185 ± 0.0016
Bank-marketing	0.2209 ± 0.1340	0.2621 ± 0.0013	0.3186 ± 0.0014	0.3842 ± 0.0030
Blood	0.1573 ± 0.0648	0.2227 ± 0.0492	0.2670 ± 0.0486	0.5643 ± 0.0268
Breast	0.3897 ± 0.1880	0.5641 ± 0.0153	0.7109 ± 0.0168	0.6371 ± 0.0122
Contraceptive	0.2815 ± 0.0736	0.2884 ± 0.0017	0.3589 ± 0.0026	0.6943 ± 0.0042
Credit	0.2836 ± 0.1344	0.3368 ± 0.0321	0.3905 ± 0.0308	0.7025 ± 0.0205
Echocardiogram	0.3054 ± 0.1292	0.3853 ± 0.0461	0.4030 ± 0.0525	0.5213 ± 0.0716
Forty	0.2238 ± 0.0686	0.2602 ± 0.0280	0.3151 ± 0.0271	1.2588 ± 0.0478
Haberman	0.1892 ± 0.0689	0.2222 ± 0.0288	0.3045 ± 0.0543	1.2584 ± 0.0584
Heart	0.3094 ± 0.1359	0.3699 ± 0.0043	0.4442 ± 0.0083	0.7026 ± 0.0098
Hepatitis	0.3547 ± 0.1433	0.4654 ± 0.0380	0.4182 ± 0.0334	0.9933 ± 0.0612
Iris	0.3267 ± 0.0619	0.5403 ± 0.0206	0.7072 ± 0.0363	0.6469 ± 0.0207
liver	0.1793 ± 0.1038	0.2610 ± 0.0047	0.3243 ± 0.0082	0.2460 ± 0.0115
Lymph	0.4645 ± 0.2037	0.4574 ± 0.0137	0.4302 ± 0.0112	0.7228 ± 0.0127
Magic	0.1316 ± 0.0631	0.1475 ± 0.0005	0.1693 ± 0.0009	0.6622 ± 0.0010
Maternal	0.3013 ± 0.1888	0.2543 ± 0.0125	0.2397 ± 0.0117	0.6346 ± 0.0059
Monk	0.3885 ± 0.0494	0.3885 ± 0.0122	0.5307 ± 0.0295	0.6863 ± 0.0358
National-health	0.1784 ± 0.1242	0.2783 ± 0.0103	0.3055 ± 0.0086	0.4986 ± 0.0026
Obesity	0.2380 ± 0.0769	0.2698 ± 0.0021	0.2819 ± 0.0024	0.4786 ± 0.0033
Rice	0.1755 ± 0.0315	0.1748 ± 0.0014	0.1883 ± 0.0019	0.7074 ± 0.0033
Wholesale	0.0722 ± 0.0111	0.1613 ± 0.0420	0.1726 ± 0.0448	1.2148 ± 0.0446
Wine	0.2339 ± 0.0673	0.2786 ± 0.0045	0.2589 ± 0.0072	0.6830 ± 0.0116
Yeast	0.1228 ± 0.0396	0.1641 ± 0.0236	0.1637 ± 0.0039	0.6207 ± 0.0031
Avg.Rank	1.24	2.08	2.84	3.84

presents experimental results for employed datasets, showing the performance of the proposed method alongside three comparison models, focusing on the $RMSE$ values. These results indicate the robustness and efficacy of our proposed method in accurately imputing missing values. The experimental results, represented in average $RMSE$ and standard deviation, underscore the superiority of the proposed method over the comparison models. The proposed method achieves superior results on 22 out of the 25 datasets compared to existing methods. Notably, on the Abalone dataset, the proposed method achieved a performance score of 0.2007, clearly outperforming the comparison models. Similarly, the proposed method demonstrated superior performance in the Adult dataset with a mean $RMSE$ of 0.1894 compared to the other models. In addition, the experimental results indicate that the proposed method exhibits remarkable consistency and effectiveness across various datasets. For instance, it consistently outperforms the comparison models in datasets such as Blood, Contraceptive, and Magic, as evidenced by its significantly lower $RMSE$ values. With an average rank of 1.24, the method consistently proved its effectiveness.

As shown in

Table 5. Summary of the Friedman statistic $F_F$($k=4$, $N=25$) and Critical Value in terms of $RMSE$ measure between the proposed method and comparison models.

Evaluation Measure	Friedman Statistic	Critical Values ($\mathit{\alpha }$ = 0.05)
$RMSE$	55.867	2.276

, the Friedman test, conducted with a 95% confidence interval, confirmed statistically significant differences between the groups, with a Chi-squared statistic of 55.867 and a p-value of 2.276. Subsequently, the Bonferroni–Dunn test followed as a post hoc test, revealing clear distinctions between the comparison models and the proposed method as shown in Figure 4. The proposed method consistently outperformed the comparison models, with a notable margin beyond $CD=0.8742$. Experimental results showed the superior performance of the proposed method across 22 datasets, as evidenced by its significantly lower $RMSE$ values. Statistical tests further support the effectiveness of the proposed method, confirming its efficacy in accurately imputing missing values.

The proposed method uses a chain imputer, which sequentially constructs models for each feature while stacking them for training. Figure 5 illustrates the percentage change in $RMSE$ resulting from iterative feature refinement across different training iterations for two datasets: Breast and Yeast. For each dataset, a set of selected features is shown along the x-axis, while the y-axis indicates the relative change in $RMSE$ (%). The lines in each plot correspond to specific training iterations—namely, epochs 1, 20, 40, and 60—allowing observation of how the influence of individual features evolves as training progresses. The black dashed line at 0% serves as a baseline, denoting no change in RMSE. In the context of missing value imputation, a positive percent change implies that the permuted feature is important for accurate imputation—its disruption leads to increased reconstruction error. Conversely, a negative percent change suggests that the feature may be noisy or uninformative, as its permutation leads to a reduction in RMSE. Features near 0% are likely neutral, contributing minimally to the imputation process. From the plots, it can be observed that certain features, such as age and menopause in the Breast dataset and erl in the Yeast dataset, exhibit increasing positive influence on imputation accuracy across training iterations, indicating that the model increasingly relies on them. In contrast, features like inv-nodes and gvh show persistent negative impacts, possibly due to inconsistent or misleading patterns in the data. This analysis highlights how feature relevance for imputation evolves during training and can be used to assess feature robustness and model dependency in the presence of missing values.

5. Discussion

In this section we discuss the results of additional experiments that affect our proposed solution performance. As shown in

Table 6. $RMSE$ comparison of the ChainImputer method under three different feature ordering schemes: ascending (ChainImputer), random shuffle, and descending order. The average rank across all datasets is presented in the final row, with a lower value indicating better overall performance. The default ordering scheme of ChainImputer consistently outperforms the other ordering strategies with the lowest average rank (1.64), suggesting that the ascending feature order provides more effective imputation performance than randomized or descending arrangements.

Dataset	ChainImputer	Random Shuffle	Descending
Abalone	0.2007 ± 0.0599	0.2028 ± 0.0614	0.2043 ± 0.0632
Adult	0.1894 ± 0.0946	0.1991 ± 0.0730	0.2096 ± 0.0186
Ai4i	0.1658 ± 0.0401	0.1771 ± 0.0075	0.1635 ± 0.0408
Bank-marketing	0.2209 ± 0.1340	0.2089 ± 0.1069	0.2193 ± 0.1352
Blood	0.1573 ± 0.0648	0.1591 ± 0.0645	0.1502 ± 0.0568
Breast	0.3897 ± 0.1880	0.3950 ± 0.1841	0.3925 ± 0.1789
Contraceptive	0.2815 ± 0.0736	0.2468 ± 0.0677	0.2658 ± 0.0632
Credit	0.2836 ± 0.1344	0.2840 ± 0.1342	0.2848 ± 0.1342
Echocardiogram	0.3054 ± 0.1292	0.3060 ± 0.1296	0.3057 ± 0.1297
Forty	0.2238 ± 0.0686	0.2431 ± 0.0379	0.1974 ± 0.0810
Haberman	0.1892 ± 0.0689	0.1800 ± 0.0731	0.2050 ± 0.0595
Heart	0.3094 ± 0.1359	0.3119 ± 0.1333	0.3121 ± 0.1325
Hepatitis	0.3547 ± 0.1433	0.3664 ± 0.1377	0.3869 ± 0.1290
Iris	0.3267 ± 0.0619	0.3330 ± 0.0624	0.3431 ± 0.0647
liver	0.1793 ± 0.1038	0.1990 ± 0.0595	0.1814 ± 0.1131
Lymph	0.4645 ± 0.2037	0.4673 ± 0.1977	0.4819 ± 0.2057
Magic	0.1316 ± 0.0631	0.1406 ± 0.0525	0.1484 ± 0.0157
Maternal	0.3013 ± 0.1888	0.3276 ± 0.1680	0.3111 ± 0.1804
Monk	0.3885± 0.0494	0.3893 ± 0.0502	0.3875 ± 0.0455
National-health	0.1784 ± 0.1242	0.1775 ± 0.2076	0.1958 ± 0.1155
Obesity	0.2380 ± 0.0769	0.2312 ± 0.0747	0.2453 ± 0.0751
Rice	0.1755 ± 0.0315	0.1584 ± 0.0380	0.1538 ± 0.0330
Wholesale	0.0722 ± 0.0111	0.0698 ± 0.0116	0.0705 ± 0.0115
Wine	0.2339 ± 0.0673	0.2348 ± 0.0674	0.2345 ± 0.0673
Yeast	0.1228 ± 0.0396	0.1224 ± 0.0390	0.1228 ± 0.0387
Avg.Rank	1.64	2.24	2.08

, our experiments have shown that the order in which features are selected for imputation significantly affects the overall accuracy of the value imputation process. Following the options of IterativeImputer class from the scikit-learn library, we conducted the experiments with three ordering schemes: ascending, descending, and random [90]. The ascending scheme is used in the default implementation of our method and, in this approach, the next column is selected if it contains the least amount of missing values among the unprocessed columns. For the descending iteration scheme, the next feature is chosen based on the maximal amount of missing values among unprocessed columns. Finally, in the random shuffle scheme, the next feature is chosen randomly. In this experimental setup, each feature was individually corrupted with missing values ranging from 1% to 22%. This approach enables a clearer comparison of performance differences between ordering schemes, as opposed to scenarios where all features are corrupted at the same rate. Following our previous methodology, we conducted the experiments using 30-fold cross-validation. The results confirm that the default ordering scheme of the ChainImputer—ascending imputation—achieves the best performance. Processing features with fewer missing values first helps mitigate error propagation in subsequent features, leading to more accurate overall imputations.

ChainImputer can be extend to time-series or spatial domains by ordering features along temporal or spatial proximity, so early steps exploit the most reliable neighborhood while later steps refine heavily corrupted segments. In addition, even under severe missingness ($>50\%$), the proposed method retains all n instances at every step, whereas chained-equation baselines lose training rows as soon as a target column contains gaps. Because each iteration adds a full column of n newly imputed values, the effective sample size grows monotonically, supporting stable performance in high-dimensional settings with extreme data loss.

6. Conclusions

In this paper, the proposed chain imputer method not only demonstrates a systematic approach to handling missing values but also significantly enhances imputation accuracy. The results show the superiority of the proposed method in imputing missing values across diverse datasets. The proposed method proves to be both robust and effective, outperforming the comparison models by yielding lower $RMSE$ values in 22 out of 25 datasets. Its high performance in datasets such as Abalone and Adult is particularly notable, suggesting that it can provide a reliable solution for imputing missing values across various fields. The Friedman and Bonferroni–Dunn post hoc tests further validate the superiority of the proposed method. The significant differences observed between the groups confirm that the proposed method consistently outperforms the comparison models. The Bonferroni–Dunn test highlights the clear superiority of the proposed method. Such statistical validation contributes to establishing the proposed method as a practical solution for MVI tasks and enhances confidence in the experimental results. In conclusion, the experimental results and in-depth analysis presented in this study suggest that by combining chain strategy and neural network modeling, a robust and adaptable methodology can ensure the reliability and performance of the data analysis process.

Despite its effectiveness, the proposed method has some limitations. First, the current implementation is tightly coupled with the MXNet framework, which may restrict portability and optimization opportunities in other environments. Future work will explore alternative architectures and platforms to improve scalability. Second, the imputation order, which is currently determined in a heuristic manner, can impact performance. A more principled approach based on entropy-driven feature informativeness will be investigated to derive an optimal imputation sequence. Third, the hyperparameters for each comparison method, including the proposed model, were not independently optimized but were adopted from previously published experimental settings. Although this ensures consistency and reproducibility, it may affect the comparative performance. As a future direction, systematic tuning procedures such as grid search or Bayesian optimization could be applied to each method to ensure a fair and balanced evaluation. These limitations point to important directions for future research that can further improve the robustness and generalizability of the proposed method.

Furthermore, valuable insights and outcomes are anticipated from applying the proposed method in various fields, potentially leading to advancements in research, industry, and decision-making practices. Enhancing imputation performance leads to more reliable results in various tasks such as predictive modeling, classification, and clustering. Imputation of missing values helps minimize the risk of distorted data and unreliable insights in data-driven analyses. Additionally, the advantage of utilizing the proposed method is its applicability to datasets with missing values across various fields. Extending this approach to larger and more diverse datasets, including real-world applications, is expected to produce reliable results.