Abstract
Compilers play a crucial role in software development, as most software must be compiled into binaries before release. Analyzing the compiler version from binary files is of great importance in software reverse engineering, maintenance, traceability, and information security. In this work, we propose a novel framework for compiler version identification. Firstly, we generated 1000 C language source codes using CSmith and subsequently compiled them into 16,000 binary files using 16 distinct versions of compilers. The symmetric distribution of the dataset among different compiler versions may ensure unbiased model training. Then, IDA Pro was used to decompile the binary files into assembly instruction sequences. From these sequences, we extracted frequency-based features via the Bag-of-Words (BOW) model and sequence-based features derived from the grey-level co-occurrence matrix (GLCM). Finally, we introduced a divide-and-conquer framework (DIANA-SVM) to effectively classify compiler versions. The experimental results demonstrate that traditional Support Vector Machine (SVM) models struggle to accurately identify compiler versions using compiled executable files. In contrast, DIANA-SVM’s symmetric data separation approach enhances performance, achieving an accuracy of 94% (±0.375%). This framework enables precise identification of high-risk compiler versions, offering a reliable tool for software supply chain security. Theoretically, our GLCM-based sequence modeling and divide-and-conquer framework advance feature extraction methodologies for binary files, offering a scalable solution for similar classification tasks beyond compiler identification.
1. Introduction
The compiler serves as a vital tool for converting high-level programming languages (e.g., C, C++) into executable machine code [1,2]. When distinct compiler versions compile identical source files, subtle differences will manifest in the resulting binaries. Conversely, these variances in the compilation results can be harnessed to differentiate among the compiler versions.
This reverse analysis carries substantial theoretical and practical implications. Firstly, the study of the compiler version identification problem holds great theoretical significance within the fields of software reverse engineering and machine learning algorithm research. It facilitates a profound comprehension of the operational mechanisms of compilers across diverse versions and compilation options. Extracting features from such fine-grained binary files and leveraging these features for version identification enables the exploration of novel feature extraction methodologies and pattern recognition algorithms, offering references for pattern recognition issues in other related domains.
Furthermore, the identification of compiler versions is of substantial practical importance in software maintenance, traceability, and information security [3]. Variations in compiler versions can influence the software’s susceptibility to security vulnerabilities. Certain security vulnerabilities might emerge exclusively under particular compiler versions. Through the identification of the compiler version, security professionals can perform more focused vulnerability scanning and remediation, thereby bolstering the security of the software system.
The identification of compiler versions also plays a vital role in malware detection. The compiler can serve as one of the channels through which malware is injected, and this particular mode of injection is notoriously difficult to detect [4,5]. A notable example is the 2015 XcodeGhost incident, where hackers infected an unofficial version of Apple’s Xcode compiler, distributing 2500 infected iOS apps to 128 million users. The malware enabled data theft and remote control. To detect unofficial software distributions or tampered compilers, compiler version validation is critical.
Nevertheless, reverse analysis of compiler versions from binary files presents certain challenges, given that binary files derived from the same source file exhibit a high degree of similarity. However, even when using the same compiler, the compilation results of different source codes can vary significantly. Specifically, when the same source file is compiled using different compilers, the inter-class distance of the resulting binary files is small. Conversely, when different source files are compiled with the same compiler, the intra-class distance of the generated binary files is relatively large. This situation renders the reverse analysis of the compiler version from binary files an extremely challenging task.
Most existing studies center on analyzing the compilation outcomes of identical source code under diverse compilation parameters. Consequently, the issue of a large intra-class distance does not arise. We replicated the algorithms in certain previous works and discovered that their classification performance with respect to the dataset employed in this paper was less than satisfactory: traditional SVM [6] achieved only 23% accuracy, while NeuralCI [7] reached merely 35%.
In this paper, we propose a novel and comprehensive feature extraction framework tailored for binary files. This framework is devised to extract the time domain and frequency domain features encapsulated within binary files and carry out feature dimensionality reduction. To tackle the challenge of large intra-class distances within binary files, we introduce a feature extraction approach based on instruction frequency, designed to be insensitive to such intra-class variations. Concerning the problem of small inter-class distances, we put forward a classifier designated as DIANA_SVM. This classifier is formulated by integrating the divide-and-conquer strategy with SVM (Support Vector Machine) and Divisive Analysis. Experiments show that DIANA-SVM achieves 94% accuracy on 16 compiler versions, outperforming traditional methods by over 70%. Overall, this research offers novel methodological approaches for the feature extraction and classification of binary files.
The paper is organized as follows: In Section 2, we introduce the works related to this paper. In Section 3.1, we introduce the experimental environments and the datasets. In Section 3.2, we introduce the method to extract frequency and sequence features from the texts decompiled by IDA Pro and discrimination functions. In Section 4, we present the experimental results while explaining the rationale for dimensionality reduction and the motivation behind DIANA-SVM’s development. We further extend our framework’s evaluation by comparing classification performances across DIANA-SVM, DIANA-KNN, and DIANA-RF. Section 5 discusses the theoretical and practical significance of this study. Section 6 summarizes our works and examines why the DIANA-SVM framework achieves superior results. Additionally, we discuss its limitations and outline promising directions for future research. The main structure of our work is as follows in Figure 1. Different colors in the Figure 1 represent different categories of results.
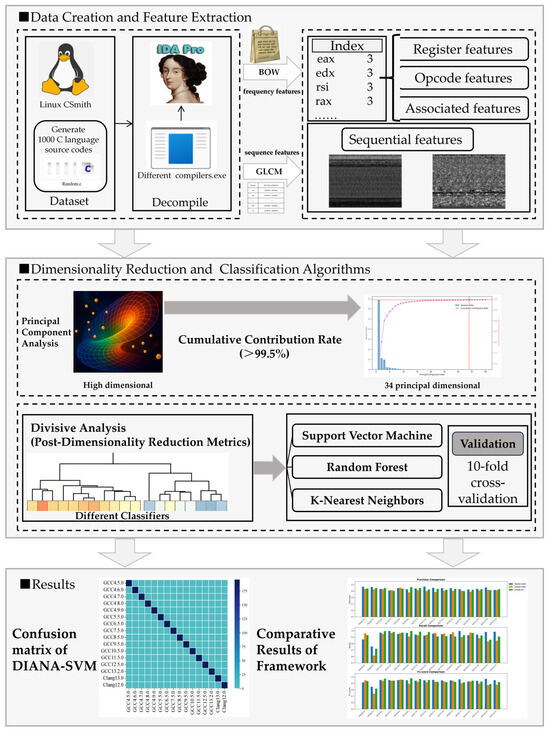
Figure 1.
This article’s flowchart.
2. Related Works
During source code compilation, various intermediate files are generated, enabling compiler identification by security analysts. The compiling flow of compilers is shown in Figure 2. These files include .i files, .s files, .o files, and .exe files [6]. Most of the related research is focused on finding the best strategies for analyzing binary files due to limited access to intermediate files.

Figure 2.
The compiling flow of compilers.
Compiler identification can generally be divided into two approaches: traditional machine learning frameworks and deep learning frameworks [8]. The difference between them is that works employing traditional machine learning frameworks place more emphasis on designing and extracting discriminative features, as well as innovating classification models. These works often use decompilation tools such as IDA Pro [9] and PEiD [10] to decompile binary files into machine instructions and then extract effective features from them. N-grams [11], N-perms [12], hash [13], and Word2Vec [13] are common features used in this group.
In contrast, works using deep learning frameworks typically feed binary files directly into neural networks, enabling the neural networks to automatically extract features. Such works usually attach greater importance to the design and innovation of network architectures.
2.1. Related Works Using Traditional Machine Learning Frameworks
In 2010, Rosenblum used non-executable fields in the gaps between functions from binary files as features representing different compilers and leveraged machine learning methods for classification [14]. They extended the work in 2011 by proposing the use of Origin tools to further identify similar compilers within the same family [15]. They extracted features of graphs such as the instruction frequency of instructions, subgraphs of control flow graphs, and specific function layout. This tool identifies compiler families, versions, and optimization levels at the function level.
Toderici traced malicious code to specific compilers during detection in 2013 [16]. However, the focus of this paper is mainly on detecting malicious code after transformation, rather than the recognition of the compilers.
Rahimian proposed the BinComp system for recognizing compilers in 2015 [17]. Rahimian decompiled binary files into disassembly files, and extracted syntax and semantic features such as compiler flag information and attribute control flow diagrams of compiler-related functions as features. Rahimian aimed to capture both the surface patterns and the deep behavioral characteristics of compilers.
Tian, Z. proposed NeuralCI, a novel framework leveraging sequence-oriented neural networks for fine-grained compiler identification at the function level in 2021 [7]. Their approach introduced a lightweight abstraction strategy to normalize assembly instructions, preserving compiler-specific patterns (e.g., opcode-register combinations) while masking function-specific noise (e.g., memory offsets). By training CNN and BiGRU-based models augmented with attention mechanisms (scaled dot-product, additive, and query-based), NeuralCI achieved advanced accuracy in detecting compiler families, optimization levels, and major versions.
Li, L. represented binary files in hexadecimal format and then converted them into grayscale images in 2022 [18]. Li extracted image features using a convolutional neural network (CNN). Additionally, they disassembled the binary files into assembly files and extracted the opcodes from the entire dataset. The 184 most frequently occurring opcodes were selected as the features. These two sets of features were then combined to serve as the basis for identifying malicious code. Li proposed a cross-modal learning framework that synergistically combines spatial patterns from hexadecimal visualization with semantic features from disassembled opcodes.
Tang introduced a method for malware detection and classification in 2023 [19]. Tang combined block byte features with hexadecimal N-gram features. Meanwhile, Zhang Y explored a visual-based approach by converting binary files into grayscale images [20]. Zhang extracted five texture features from these images and employed three machine learning algorithms, i.e., K-Nearest Neighbor (KNN), Naive Bayes (NB), and Random Forest (RF), for classification. Their experimental results demonstrated that the Random Forest (RF) algorithm achieved the highest classification accuracy of 95%. Tang proposed a hybrid detection framework that synergistically integrates block byte features with hexadecimal n-gram analysis.
Similarly, Conti, M. extracted two types of texture features from grayscale images [21]: statistical features based on pixel points and eight features derived from the gray-level co-occurrence matrix (GLCM). By calculating the mean and standard deviation of these eight features across four directions, they conducted classification experiments with the ensemble method, achieving an accuracy of 98%. Binary-to-image conversion has advanced compiler analysis methodologies.
Yao categorized binary files into decompilable and non-decompilable categories in 2023 [6]. Yao adopted different strategies for the two types of binary files. For decompilable files, Yao converted them into assembly language and then extracted frequency-based characteristics of registers and opcodes. Finally, these features were fed into a model that integrates Support Vector Machine (SVM), Decision Tree (DT), Light Gradient Boosting Machine (LightGBM), and Extreme Gradient Boosting (XGBoost). The final identification result was determined through voting. For non-decompilable files, Yao converted the binary files into grayscale images and extracted texture features including GLCM features, byte histogram features, and byte entropy histogram features. These features were then fed into the above models for analysis. Yao’s methodology is notably thorough, incorporating considerations for whether the binary files are packed or unpacked.
2.2. Related Works Using Deep Learning Frameworks
Raff E used the raw bytes of three library files in the PE header file as input for the neural network, achieving an accuracy of 90% [22]. It has been proven that neural networks can construct valid features without manual feature engineering. However, binaries often exceed the input size limits of sequence models (e.g., millions of bytes), requiring specialized preprocessing. To address this, Wen, Q. extracted binary fragments of a specific length from binary files, mixed the obtained binary fragments to form a data corpus, and fed the small fragments into a CNN network for training, achieving good experimental results [23].
Pizzolotto directly fed raw bytecode into long short-term memory (LSTM) networks and convolutional neural networks (CNNs), respectively, learning intrinsic byte-level features and performing classification in 2020 [24]. They selected a suitable deep learning model based on recognition accuracy and ultimately chose the CNN with an accuracy of up to 98%.
Falana converted binary files into RGB images in 2022 [25]. Falana applied convolutional neural networks (CNNs) and generative adversarial networks (GANs) for classification. This method showed promising classification results with an accuracy of up to 99%.
Jiang extracted the control flow graphs of functions from disassembled files as features, including the adjacency matrix and basic blocks [26]. These features were then input to a graph convolutional network long-short term memory (GCN-LSTM) model. However, this method is based on function-level feature extraction. In the subsequent experiments, they found that the control flow graphs of compiler-related functions from different optimization levels were almost identical.
Current research on compiler identification encounters several limitations. For instance, most existing studies concentrate on differentiating merely 2–3 compiler versions, with a major focus on discerning different optimization levels. Moreover, the features employed are usually simplistic, and there is scant exploration of model fusion. Thus, in this work, we propose a novel approach for compiler version identification. We emphasize constructing a comprehensive dataset that better reflects real-world conditions and employ an advanced machine learning model capable of learning version-specific similarities and differences as latent features, thereby achieving more precise compiler version recognition.
3. Materials and Methods
3.1. Materials
This study employs a signature-matching-based method, which entails decompiling binary files and comparing specific signatures or patterns within a constructed dataset to identify compilers. Compilers from different families vary significantly in development environments and other aspects. Thus, identifying compilers within the same family poses a greater challenge. Additionally, since the default compilation optimization level is widely used by developers, focusing on version differences aligns more closely with real-world scenarios. Accordingly, this article focuses on the recognition of different versions of compilers. Our study includes 14 representative GCC versions spanning annual major releases, along with two versions from the Clang compiler family. As of the writing of this study, the latest GCC version has been updated to 13.2.0. We aim to maximize the quantity and representativeness of versions within a single compiler family. The strategies and concepts presented in this paper can also provide insights for recognizing minor versions under different major versions. The setup and environment are illustrated in Table 1.

Table 1.
Experimental setup and environment.
Accurate compiler recognition requires a comprehensive dataset that authentically reflects the behavior of various compiler versions. The ability to distinguish between versions is determined by source code diversity in the dataset. Existing research mainly focuses on improving identification methods based on open-source code sets for testing. However, these datasets may lack representativeness, failing to accurately reflect the real behavior of compilers [27]. Such behavioral information reveals compilation strategy preferences across different compiler versions. This article utilizes CSmith [28], a compiler testing tool, to create 1000 diverse C source codes. Each program varies significantly in content and structure, maximizing the diversity of compiler behavior in binary files. This method makes our conclusions more robust. We compiled source codes with different compiler versions, creating the dataset for our study. The detailed information of the dataset is shown in Table 2. In the classification experiment, we utilized the train_test_split tool from the scikit-learn toolkit to divide the dataset into two parts: the training set and the test set. The proportion of the test set was set to 20%. The random_state parameter was fixed at 42 to facilitate the reproduction of the results.

Table 2.
The construction results of the datasets.
3.2. Methods
3.2.1. Feature Extraction
The dataset constructed for this study consists of binary files compiled using 16 compiler versions. The binary files are machine code generated by different compilers, which directly corresponds to assembly language. Converting binary files into assembly code significantly improves readability and interpretability, facilitating analysis by security researchers. Therefore, this article employs the IDA Pro tool to decompile machine code into assembly language for subsequent processing.
There is a well-known dispute regarding the authorship of the last forty chapters of “Dream of the Red Chamber”. The question is whether they were written by Cao Xueqin or Gao E. Through analyzing high-frequency words, erotic discourse patterns, and dialectal expressions, Jilong Pan demonstrated that Cao Xueqin was the more likely author [29,30]. Drawing inspiration from this approach, we treat assembly code as machine-readable “text” that can be classified using similar frequency-based features [31].
Different compilers processing the same codes can be viewed as authors producing distinct “versions” of the same core content. Once we identify the language styles of different “authors”, the identification of the compilers can be addressed. Language style encompasses two key aspects: the frequency of common words and the sequence of speech. In the context of assembly language, these aspects directly parallel the usage frequency of assembly instructions (such as registers and opcodes) and the order in which these instructions are arranged. By analyzing these elements, we can discern distinct language styles for different compilers. These styles are characterized by two main features: frequency-based (opcode counts) and sequence-based (instruction order) patterns.
By recording the linguistic style and preferences of the compiler in assembly language, distinctive features can be formulated. These features enable us to accurately identify the compilers. As illustrated in Figure 3, the compilation results show text of varying lengths. This variation indicates that different compilers employ distinct specific instructions, instruction combinations, and instruction orders when compiling the same code. As established, the primary subjects of specific instructions, instruction combinations, and instruction sequences are registers and opcodes in assembly language [32]. In summary, for the analysis of disassembly files, two different aspects of features can be extracted: frequency-based features and sequence-based features of registers and opcodes [10]. Frequency-based features are obtained by recording the occurrence of registers and opcodes in the decompiled files, while sequence-based features capture the arrangement of these registers and opcodes.
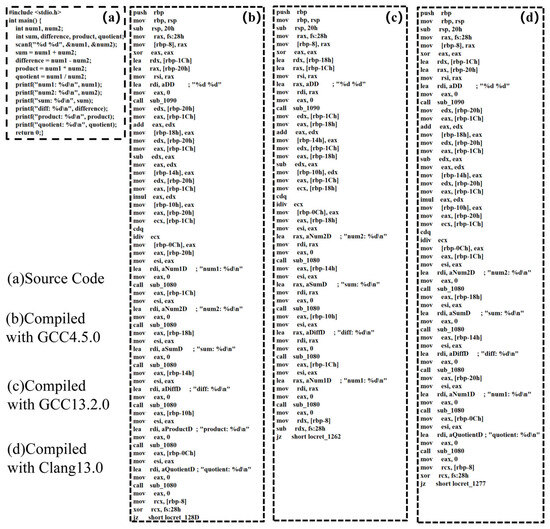
Figure 3.
Comparison of decompilation results.
Frequency-based features: For extracting frequency-based features, this study uses Bag-of-Words (BoW) to record the global usage frequencies of 42 common registers (eax, ebx, cs, ds, ss, etc.) and 92 common opcodes (add, bt, call, cdq, cld, etc.) [6] in each file as a global discriminative feature for different versions of the compiler. While global frequencies provide overall trends, they may miss finer-grained local features. This study extracted N-gram features based on statistical feature sequences [33], with the value of N set to 2 and 3. Specifically, the study identified the 98 most frequently occurring combinations of opcodes, registers, and certain specific parameters (such as mov + rax, mov + eax, lea + rcx, mov + ecx + edx, etc.) across all files. These combinations are used as local discriminative features to distinguish between compilers. The process is illustrated in Figure 4.
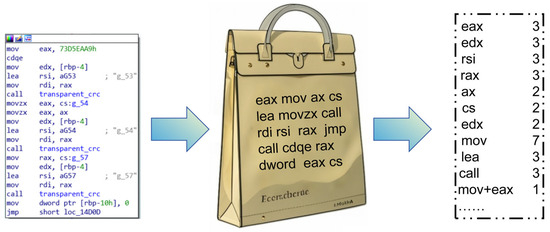
Figure 4.
Extraction process of frequency-based features.
Figure 5 shows the average frequency features of registers and opcodes. It exhibits both similar and distinct usage frequencies of compilers for certain instructions. For instance, the instruction of “mov” has an average usage frequency exceeding 4800 times of each version, whereas instructions like “esp” and “dh” have much lower frequencies, averaging between 0 and 1. Meanwhile, different versions of compilers have varying degrees of frequency in the use of registers and opcodes. Specifically, the average usage frequency of “rax” is significantly higher in GCC 11.5.0 than in other versions, while it is significantly lower in GCC 5.5.0 compared to other versions. The variances in the utilization frequencies of machine code within binary files generated by compilers of diverse versions suggest that frequency-based features can act as pivotal attributes for compiler version identification.
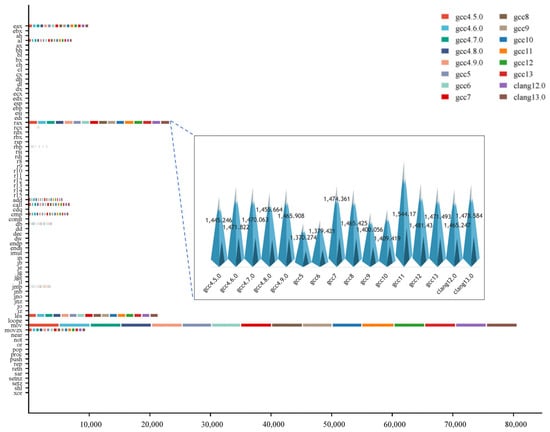
Figure 5.
Average frequency features of each version.
Sequence-based features: For sequence-based features, the study focuses on extracting the arrangement of registers and opcodes. Specifically, we examine each line of the decompiled files to identify the presence of registers or opcodes. This process generates a binary representation, where the presence of a feature is marked as 1 and its absence as 0. This binary encoding provides a clear and concise way to capture the sequence of events within the assembly code. The occurrences of registers and opcodes from the same version are then stored in the same table. The rough extraction result of each file is shown on the left of Figure 6. It is important to note that the sequence-based features and frequency-based features are not in the same dimension and cannot be directly used to establish a discrimination function. Moreover, due to the diverse source codes and compilation strategies of different compiler versions, the sequential features vary in the number of lines.
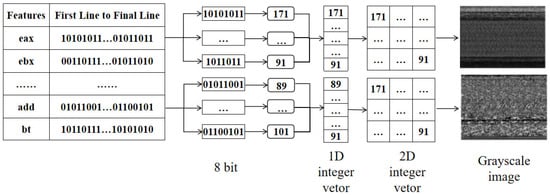
Figure 6.
Process of converting sequential features into grayscale images.
In order to analyze the sequence-based features and frequency-based features in the same dimension, and to create sequence-based features of the same size from different data, this study utilizes the Binary-to-Matrix (B2M) algorithm. This algorithm processes each register and opcode sequence from decompiled files, converting them into grayscale image representations. From these images, we extract gray-level co-occurrence matrix (GLCM) features [34], which serve to normalize the feature space. This approach provides two key advantages: it maximally preserves the sequential characteristics of instruction ordering while enabling dimensional compatibility with frequency features. By quantifying the co-occurrence statistics of instruction patterns, we maintain the essential sequential information while creating a unified representation space.
The technical implementation proceeds through several precise steps. Firstly, each tuple of the initial features is read every 8 bits as an integer constant from 0 to 255, converting sequence-based features into 134 (which is the sum of registers and opcodes) one-dimensional vectors. Following Nataraj’s optimization methodology [35], the one-dimensional vectors of each register and opcode sequence in the same file are transformed into two-dimensional matrices according to the optimal image width of different compiled file sizes. Each matrix element corresponds to a pixel value in the range 0–255, where 0 represents pure black and 255 represents pure white. This transformation yields 134 grayscale images per analyzed file, providing a visual representation of the sequential patterns while maintaining mathematical rigor for subsequent analysis.
The computational complexity of the gray-level co-occurrence matrix is determined by the gray level and size of the image. For an image G with L gray levels and dimensions R × C, the complexity scales as O( × R × C). Additionally, given that there are 10,000 × 134 images, the computational cost becomes prohibitively high. To address this challenge, we strategically reduce the maximum grayscale level from 256 to 8, significantly lowering the computational burden while maintaining the texture feature integrity. Although this reduction produces visually subdued images, empirical testing confirms it minimally affects texture feature extraction accuracy.
Subsequently, we constructed four gray-level co-occurrence matrices from four distinct directions (0, , , and ) with a unit step size (d = 1), as illustrated in Figure 7 and Figure 8. This directional selection serves two critical purposes: (1) it comprehensively captures fundamental angular relationships between pixels and (2) preserves the sequential ordering information of instructions across different code lines. The unit step size ensures maximal preservation of local spatial relationships, maintaining fine-grained detail in the feature representation. The four-directional approach forms the foundation for GLCM’s effectiveness in retaining the essential sequential patterns identified in our earlier extraction process.
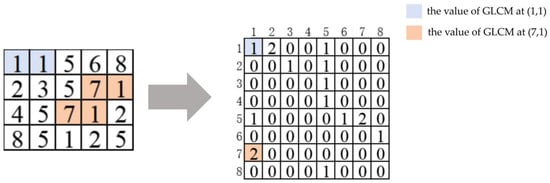
Figure 7.
Process of converting grayscale images into GLCMs.
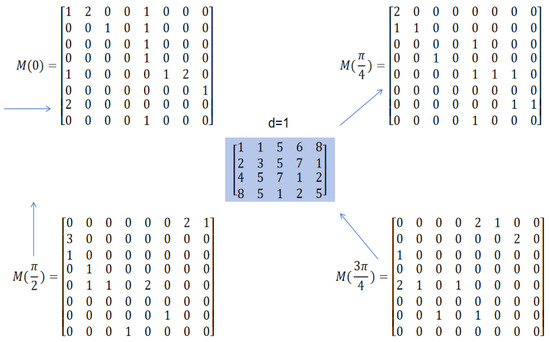
Figure 8.
Gray-level symbiosis in four directions.
The GLCM approach enables extraction of five key statistical features that characterize assembly code patterns: Angular Second Moment (ASM), contrast (CON), Inverse Difference Moment (IDM), Entropy (ENT), and correlation (COR). These metrics provide quantitative measures of texture properties critical for comparing compiler-generated code structures.
Angular Second Moment (ASM) quantifies image uniformity and texture coarseness by calculating the squared sum of GLCM elements. It yields higher values when matrix elements concentrate along the diagonal (indicating uniform grayscale) and lower values for evenly distributed elements (characteristic of noisy images). The formula of ASM is shown in Formula (1).
where represents each element of the gray-level co-occurrence matrix.
Contrast (CON) directly reflects the contrast in brightness between a pixel value and its corresponding neighboring pixel values, indicating the clarity of the image and the depth of texture grooves. The deeper the texture groove, the greater the contrast. Additionally, the more pixel pairs with high contrast, the higher this value will be. In other words, the larger the values of elements far from the diagonal in the GLCM, the larger the CON will be. The formula of CON is shown in Formula (2).
Inverse Difference Moment (IDM) reflects the homogeneity of the image texture and measures the amounts of local changes in image texture. A large IDM value indicates a lack of variation among different regions of the image texture, suggesting a very uniform local area. If the diagonal elements of the GLCM have larger values, IDM will take larger values. Therefore, continuous grayscale images will have larger IDM values. The formula of IDM is shown in Formula (3).
Entropy (ENT) is a measure of the texture information of an image. It measures the randomness that represents the degree of non-uniformity or complexity of the texture in the image. A uniform distribution of GLCM values indicates that the image is almost random or has a lot of noise, and ENT will have a large value. The formula of ENT is shown in Formula (4).
Correlation reflects the consistency of image texture. It measures the similarity of elements in the spatial gray-level co-occurrence matrix in the row or column direction, and the magnitude of the correlation value reflects the local gray-level correlation in the image. When the values of matrix elements are uniformly equal, the correlation value is large; on the contrary, if the pixel values of the matrix differ greatly, the correlation value is small. The formula of is shown in Formula (5).
where is the mean of the GLCM rows, is the standard deviation of the GLCM rows; is the mean of the GLCM columns, and is the standard deviation of the GLCM columns.
This process converts two-dimensional sequential features into a one-dimensional representation comprising 134 × 4 × 5 features (134 registers and opcodes × 4 directions × 5 statistical features). This comprehensive set of features allows for a detailed analysis of the compiler-generated assembly code patterns, providing insights into the texture and structure of the code at a granular level.
This comprehensive approach successfully resolves the dimensional incompatibility between sequential and frequency features while preserving the discriminative power of instruction sequence patterns. The resulting unified feature representation enables robust compiler version identification through combined analysis of sequential and frequency characteristics [36].
3.2.2. Feature Dimensionality Reduction
High-dimensional features risk impairing the model’s generalization capabilities. It is not conducive to the promotion of future classification work. Dimensionality reduction addresses this issue while improving the clustering of similar data points and the separation of dissimilar ones, ultimately enhancing classification accuracy. Therefore, it is necessary to reduce the dimensionality of the data here.
This article employs Principal Component Analysis (PCA) [37], a dimensionality reduction technique aimed at identifying an orthogonal transformation that captures the maximum variance within the data. PCA seeks to project the original data onto a new set of uncorrelated variables, known as principal components, that retain as much of the original information as possible, with the largest covariance.
The calculation method for the new covariance matrix is shown in Formula (6).
If both and ′ are centralized data, the covariance matrix can be simplified into Formula (7).
The original objective is converted into finding a transformation, A, that maximizes C’. If the unit vector in the new coordinates works, then the equation to be calculated is transformed into Formula (8).
where 1. The final result is the eigenvector of the covariance matrix C of the original data, with the eigenvalues of C and their corresponding eigenvectors. Among them, a new indicator variable is calculated as Formula (9).
Finally, by calculating the cumulative contribution rate of each principal component, we can select the number of principal components that best represent the original data. The cumulative contribution rate is shown in Formula (10).
PCA can reduce dimensionality while retaining the most significant information from the dataset. The cumulative contribution rate quantifies the proportion of total variance explained by selected principal components. By selecting the principal components that cumulatively explain a substantial portion of the variance, the original data can be effectively explained in a lower-dimensional space. This effort not only preserves the essence of the data but also simplifies the model, enhancing generalization capability and robustness for classification tasks.
3.2.3. Identification Function
The Divisive Analysis (DIANA) algorithm is a divisive hierarchical clustering method [38] which first initializes all objects into a cluster and then classifies the cluster based on the average linkage of . The calculation of is shown in Formula (11).
Until the specified number of clusters is reached or the distance of two clusters exceeds a certain threshold, this algorithm is particularly useful for its ability to create clusters that are distinct from one another based on the maximum average distance, which helps in forming the most similar groups. The basic process is shown in Table 3 [38].

Table 3.
The process of DIANA algorithm.
Support Vector Machine (SVM) is a powerful classifier that performs well in binary classification on data using supervised learning [39]. It aims to find a hyperplane that can separate different categories. Any hyperplane can be described by the following linear Formula (12):
An optimization problem is established by following Formula (13).
In the formula: is the normal vector; is a constant term; is the penalty factor; and is a relaxation variable.
By finding the solution of the optimal normal vector ω and constant term b, the optimal classification surface can be obtained. To transform the above equation into a quadratic programming problem, the corresponding Lagrange function is introduced, and the classification problem becomes the following Formula (14).
The decision boundary of SVM is based on the maximal margin hyperplane for separating the learning sample. SVM is known for its effectiveness in high-dimensional spaces and its ability to handle non-linear relationships through the use of kernel functions.
Traditional SVM performs well in classifying significantly different versions but faces challenges with highly similar versions due to poor data separability. The fundamental limitation stems from SVM’s approach of comparing all versions simultaneously, regardless of their similarity levels. While kernel functions map data into higher-dimensional spaces to find separating hyperplanes, this transformation often fails to adequately distinguish nearly identical versions, resulting in classification inaccuracies. Consequently, the SVM’s reliance on the kernel function for class separation can be less effective when the data points are closely related, highlighting the need for enhanced methods to address the classification of highly similar versions. This limitation suggests that SVM may achieve better performance when specifically applied to version pairs with high similarity, as the reduced variance within such subsets allows for more precise separation boundaries.
Our experimental observations reveal that the false positives of various genuine versions tend to cluster around certain versions, such as GCC4.50, GCC11.5.0, GCC12.5.0, and GCC13.2.0, which exhibiting poor discrimination within each other. Other versions also exhibit similar results. This may be attributed to the similarity in compilation strategies for the same cluster. Based on the signature-matching-based methods, versions in the same cluster show “similar differences” compared with other clusters. Given these findings, our model needs further refinement based on the experimental data to accurately identify compiler versions.
Some versions exhibit significant differences, which make them easily distinguishable, while others show subtle differences, which makes them difficult to distinguish. Therefore, this article adopts a strategy that regards differences and similarities among different compilers as implicit features and employs a divide-and-conquer approach. Our solution, DIANA-SVM, combines the complementary strengths of DIANA clustering and SVM classification through a two-phase approach:
First, DIANA’s hierarchical clustering organizes compiler versions into broad categories, naturally grouping similar versions while separating distinct ones. This preprocessing step effectively reduces the classification complexity by creating pairwise groupings. Then we select the appropriate K based on the clustering situation so that each cluster contains at most two categories.
Second, the model applies SVM’s robust binary classification capability to precisely separate version pairs within each two-category cluster. Single-category clusters are directly output as classification results. As illustrated in Figure 9, this hybrid architecture specifically addresses the natural clustering tendency observed among versions with similar compilation strategies.
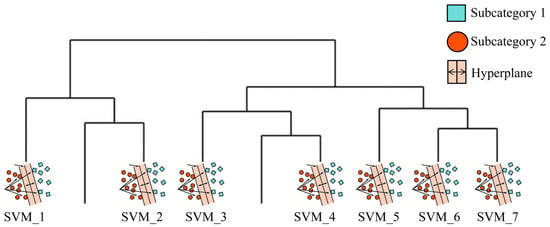
Figure 9.
Schematic diagram of DIANA-SVM.
We aim to adopt a method of divide and conquer to avoid multiple classifications in a single model. This is because the more categories there are, the higher the misclassification rate and the probability of overfitting will be [40].
Our two-stage DIANA-SVM framework effectively addresses the challenge of recognizing versions among numerous variants. SVM is adept at finding the hyperplane that maximally separates two classes, even in cases where the data are not linearly separable. To enhance the precision of SVM classifications, it is essential for DIANA to effectively distinguish between similarities and differences among the versions. This rough separation allows SVM to operate more accurately on the subsets of data that have been pre-classified by DIANA. By treating version similarities and differences as implicit features, our method overcomes the shortcomings of rough identification and insufficient expression in signature-matching-based methods. When the model finds the optimal hyperplane that separates different versions in each cluster, it will achieve a symmetrical balance of the data points in each cluster.
4. Experiments and Results
In the experimental stage, frequency-based and sequence-based features were first extracted, followed by necessary preprocessing steps, including standardization and normalization. To mitigate the influence of varying file sizes, frequency-based features underwent line-wise standardization. Sequential features exhibited discrepancies in units and scales and were therefore subjected to column-wise standardization.
After preprocessing, each sample comprised 2912 features, of which 232 were frequency-based features (134 + 98 dimensions) and 2680 were sequence-based features. To address the risk of overfitting associated with high-dimensional data, the PCA algorithm was applied to reduce the dimensions and preserve the most information. Given that frequency features and sequence features are derived from distinct operations, it is essential to apply separate processes to each before conducting PCA.
The results of the PCA ablation experiment are shown in Table 4. A traditional SVM classifier was used to evaluate the performance of PCA. From Table 4, it can be observed that the accuracy of the test set is relatively low when PCA dimensionality reduction is not utilized. We attribute this to the fact that the high dimensionality of the original features makes the data sparse in the high-dimensional space. As a result, the training set struggles to fully cover the regions within the high dimensional space. Additionally, when the dimensionality is high, the model has a higher degree of freedom, which more easily leads to overfitting. Table 4 also illustrates the accuracies of the training set and test set associated with 95%, 99%, and 99.5% cumulative explained variance. When merely 95% cumulative explained variance is maintained, the test set accuracy persists at its original level, whereas the training set accuracy diminishes. This can potentially be attributed to the substantial loss of features during the dimensionality reduction procedure. When the cumulative explained variance is 99% or 99.5%, the accuracies of both the training and test sets surpass those obtained without PCA. Specifically, the optimal performance is attained at 99.5% cumulative explained variance. The confusion matrix for the SVM classifier after dimensionality reduction is presented in Figure 10.

Table 4.
Identification results of different scales of dimension reduction.
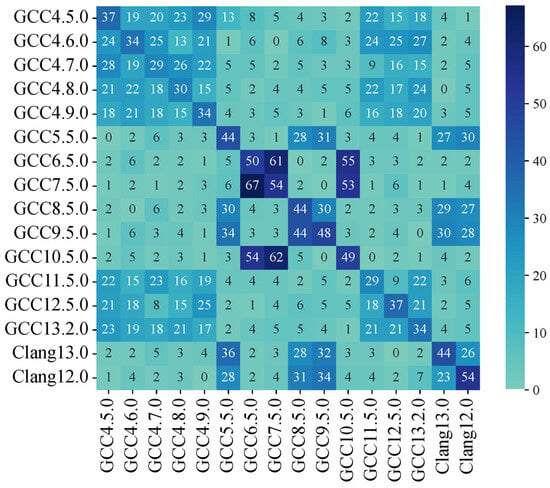
Figure 10.
Confusion matrix of SVM after dimensionality reduction.
As shown in Figure 11, the first 34 principal components were retained, accounting for 99.5% of the total variance. Subsequently, the feature dimensionality was reduced to 34, yielding a new feature set.
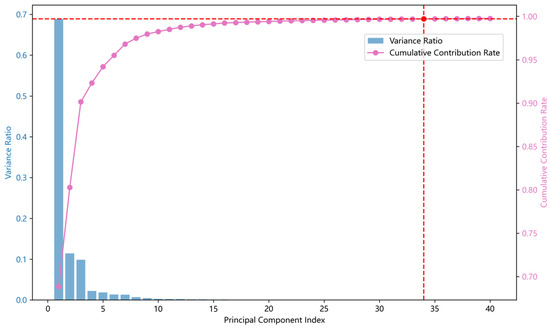
Figure 11.
Cumulative contribution rate of principal components.
Table 4 indicates that the overall accuracy remained relatively low. As shown in Figure 10, the confusion matrix revealed that the false-positive rates of genuine compiler versions tend to cluster around certain versions, such as GCC4.5.0, GCC4.6.0, GCC4.7.0, GCC4.8.0, GCC4.9.0, GCC11.5.0, GCC12.5.0, and GCC13.2.0, indicating poor discriminability among them. This may be attributed to the similarity in compilation strategies among the listed versions. They exhibited “similar differences” compared with other versions based on the signature-matching-based methods. Therefore, the model should be further refined based on experimental results to achieve accurate identification of compiler versions.
By analyzing frequency-based and sequence-based features, it becomes evident that some versions exhibit significant differences, which make them easily distinguishable, while others show subtle differences, which makes them difficult distinguish. To capture these implicit similarities and differences, a divide-and-conquer framework was adopted. DIANA, a divisive hierarchical clustering method, was utilized to progressively isolate clusters with significant differences through iterative separations, aligning with this approach. Initially, this article first uses DIANA to roughly categorize various compiler versions, dividing them into pairs. Given that SVM excels at binary separation via optimal hyperplanes, we use SVM models to achieve a further separation with version pairs of high similarity. This two-stage approach addresses coarse feature granularity and insufficient expression in traditional methods by utilizing the similarities and differences of different compilers and leveraging the advantages of SVM to improve the accuracy and efficiency of compiler recognition.
The optimal parameters for both DIANA and SVM are summarized in Table 5. For the SVM component, we performed parameter optimization using 10-fold cross-validation to ensure robust model performance. The model achieved 94.1% (±0.0375%) test accuracy with minimal standard error, indicating excellent reliability. Statistical analysis of the training–testing accuracy difference (p < 0.01, computed via Formula 15)) confirmed the model’s robustness and generalization capability.

Table 5.
Parameters and results of DIANA-SVM.
These results collectively indicate that the optimized SVM configuration achieves both high precision and generalizability in the DIANA framework.
In the initial DIANA split, the 10 versions were broadly categorized into three distinct clusters with significant differences: Cluster 1 (GCC4.5.0, GCC4.6.0, GCC4.7.0, GCC4.8.0, GCC4.9.0, GCC13.2.0, GCC11.5.0, GCC12.5.0), Cluster 2 (GCC5.5.0, GCC8.5.0, GCC9.5.0, Clang13.0,Clang12.0), and Cluster 3 (GCC10.5.0, GCC6.5.0, GCC7.5.0). Apart from a few isolated points, the clustering results are consistent with the versions that are difficult to separate in a single SVM model. The first split result is shown in Figure 12. Subsequent iterations of DIANA—the second, third, and fourth—further separated the versions with substantial differences within each cluster until they were divided into pairs. The results reveal that adjacent versions exhibited the highest similarity and were eventually clustered into pairs generally. The final clustering reflected the sequential nature of compiler development—adjacent versions, which differ only by incremental strategy adjustments, consistently formed pairs—underscoring the method’s alignment with real-world release timelines.
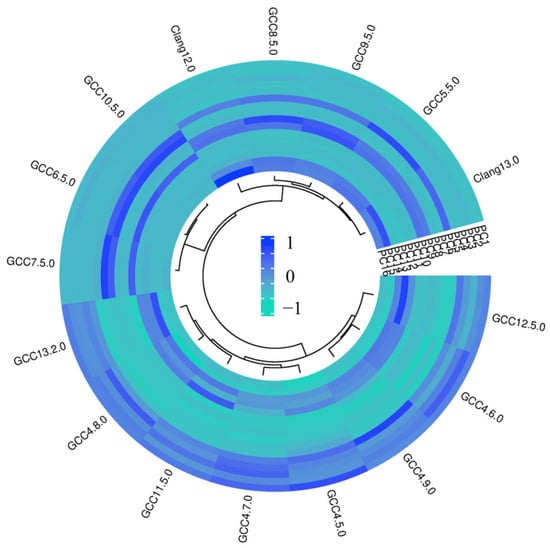
Figure 12.
Split result of DIANA-SVM.
By leveraging the binary classification capabilities of SVM, we can identify a hyperplane that effectively distinguishes between two highly similar versions. This approach addresses the limitations of traditional methods, such as rough identification and insufficient expression. The results demonstrate that, when accounting for both similarities and differences between versions, the accuracy is significantly higher than when using the SVM model alone. Specifically, the recognition accuracy on the test set reaches 94%, with the majority of versions achieving good recognition. The confusion matrix is shown in Figure 13.
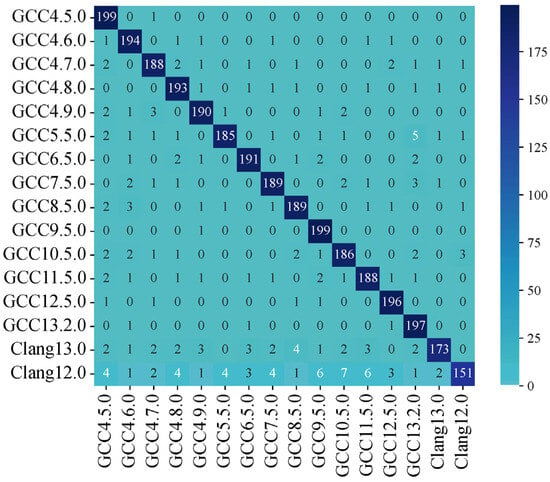
Figure 13.
Confusion matrix of DIANA-SVM.
By comparing Figure 13 with Figure 10, it can be observed that after combining with DIANA, the discriminative ability of SVM has been significantly enhanced. In the confusion matrix of Figure 13, the majority of the values are located on the diagonal, indicating that the recognition effect for each version is quite good. When compared to the basic Support Vector Machine (SVM), the performance of the fusion model integrated with Divisive Analysis has been markedly enhanced. Without the application of PCA dimensionality reduction, the SVM’s performance on the test set stands at merely 16%. Once PCA dimensionality reduction is implemented, the SVM’s performance ascends to 23%. Nevertheless, upon incorporating Diverse Analysis, the recognition capability surges directly to 94%. We ascribe this enhancement to the fact that Divisive Analysis, functioning as a clustering algorithm, can initially perform a clustering analysis on the data, thereby uncovering the internal structure and hierarchical relationships therein. It divides the dataset into distinct clusters, ensuring that data points within the same cluster display a high degree of similarity, while those in different clusters exhibit substantial differences. This clustering outcome can aid the SVM in more comprehensively comprehending the data distribution, offering valuable prior information for subsequent classification tasks.
Moreover, subsequent to the application of Divisive Analysis for clustering, the initially intricate data distribution is streamlined into multiple relatively uncomplicated intra-cluster distributions. Data points within each cluster exhibit greater concentration and similarity. This empowers the SVM to more readily discern appropriate classification boundaries when processing data within each cluster, thereby alleviating the classification difficulty. In essence, training an individual SVM model for each cluster is tantamount to implementing a divide-and-conquer approach. When contrasted with directly training a solitary SVM model on the entirety of the dataset, the quantity of data within each cluster is comparatively small, and the complexity that the model must learn is proportionally decreased. Consequently, the SVM model is enabled to fit the data within each cluster more effectively, mitigating the risk of overfitting and augmenting the model’s generalization capabilities.
To expand our work, we also compare the recognition results of DIANA combined with K-Nearest Neighbors (KNN) and Random Forest (RF) and calculate the precision, recall, and F1 scores on the training and testing sets. The comparison is shown in Table 6 and Table 7. The results indicate that under the divide-and-conquer approach, all classifiers have shown good performance, further demonstrating that our research is actually a framework and SVM can be replaced with better classifiers.

Table 6.
Comparison in accuracy of different classifiers within the framework.

Table 7.
Comparison in details of different classifiers within the framework.
5. Theoretical and Practical Implication
Theoretically, this study introduces a novel compiler behavior analysis framework by decompiling binaries into assembly sequences and fusing Bag-of-Words (BOW) with gray-level co-occurrence matrix (GLCM) features. The GLCM converts instruction patterns into measurable texture statistics, overcoming traditional limitations of isolated-frequency or semantic analysis. It provides a novel methodological reference for sequence pattern mining in binary files. The DIANA-SVM framework synergizes hierarchical clustering and classification: DIANA groups structurally similar samples, while SVM executes localized binary decisions. This “divide-and-conquer” strategy provides a universal solution for similar classification tasks beyond compiler identification.
Practically, this framework provides a robust tool for enhancing software supply chain security. Its precise compiler version identification enables security analysts to detect vulnerabilities associated with specific compiler releases, including those exploited in high-profile attacks like XcodeGhost. Developers can validate compiler compatibility during development, reducing version mismatch risks. With 94% accuracy and scalable performance, the solution supports malware detection and forensic investigations requiring precise compiler origin tracing. Its divide-and-conquer architecture combines hierarchical clustering with SVM classification, outperforming standalone models in handling subtle feature differences. This hybrid approach sets a benchmark for fine-grained classification tasks across IoT security and forensic analysis.
6. Conclusions
In this work, a novel approach for compiler identification has been developed. A dataset consisting of 1000 source codes and 16,000 binary files compiled by 16 different versions of the GCC compiler was presented. During the feature-extraction stage, the binary files were decompiled into assembly instructions, and then frequency-based and sequence-based features were extracted from the decompiled documents. To integrate these heterogeneous features into a unified representation, the B2M algorithm was applied to convert sequential tuples of register and opcode patterns into grayscale images and to extract GLCM features. In the classification stage, we developed a divide-and-conquer framework that boosts recognition accuracy by combining DIANA with SVM. Experimental findings suggest that the integration of clustering and classification algorithms can substantially improve the classification performance of fine-grained samples. In this paper, through the incorporation of the DIANA and SVM algorithms, we attained a training accuracy of 97% and a test set accuracy of 94% on the compiler classification dataset employed in this research.
The DIANA-SVM framework adopts a divide-and-conquer strategy. In the first stage, DIANA groups similar versions and separates dissimilar ones, eliminating unnecessary comparisons. Additionally, binary classification tasks have the simplest decision boundaries; more complex boundaries increase the training difficulty and cost. As a result, in the second stage, SVM achieves significantly higher accuracy than when used alone.
Although the compiler version identification method proposed in this paper has achieved remarkable progress, several challenges remain. First, the work presented here is founded on an experimental dataset, rather than real-world binary files. Second, with the continuous advancement of technology, compiler versions are in a state of constant iteration. Consequently, adaptive learning will be a pivotal direction for future related research. This approach can assist in identifying compilers not present in the offline training set, thereby enhancing the generalization ability of the identification method.
Furthermore, the incorporation of certain new technologies should be considered. For instance, neural networks equipped with attention mechanisms are capable of better capturing the key features of compilers [41,42], and byte-embedding technology can represent compiler information more precisely [43]. By integrating these novel technologies, we have the potential to boost the performance and accuracy of compiler version identification.
Author Contributions
Conceptualization, P.W. and P.Z.; methodology, C.L.; software, Y.Z.; validation, C.L., P.W. and P.Z.; formal analysis, C.L.; investigation, P.W.; data curation, C.L.; writing—original draft preparation, C.L.; visualization, C.L.; supervision, P.W. and P.Z.; project administration, P.W. and P.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, M.; Liu, Y.; Liu, X.; Sun, Q.; You, X.; Yang, H.; Luan, Z.; Gan, L.; Yang, G.; Qian, D.P. The Deep Learning Compiler: A Comprehensive Survey. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 708–727. [Google Scholar] [CrossRef]
- Wei, M.; Li, J.; Han, L.; Gao, W.; Zhao, R.; Wang, H. Support and Optimization of Multi-Granularity Quantization Framework for Deep Learning Compiler. Comput. Eng. 2025, 51, 62–72. [Google Scholar]
- Wang, J.; Jiang, W.; Zhang, C. Research on Risk Analysis of Open Source Software Supply Chain Security. Chin. Acad. Cyberspace Stud. 2024, 10, 862–869. [Google Scholar]
- Vinayakumar, R.; Alazab, M.; Soman, K.P.; Poornachandran, P.; Venkatraman, S. Robust Intelligent Malware Detection Using Deep Learning. IEEE Access. 2019, 7, 46717–46738. [Google Scholar] [CrossRef]
- Liu, R. Research on Security Protection Technology Based on Clang Compiler in Linux System. Master’s Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2019. [Google Scholar]
- Yao, Y. Feature Extraction and Recognition of C Language Compiler Based on Binary Files. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2023. [Google Scholar]
- Tian, Z.; Huang, Y.; Xie, B.; Chen, Y.; Chen, L.; Wu, D. Fine-grained compiler identification with sequence-oriented neural modeling. IEEE Access 2021, 9, 49160–49175. [Google Scholar] [CrossRef]
- Li, Q.; Peng, H.; Li, J.; Xia, C.; Yang, R.; Sun, L.; Yu, P.S.; He, L. A Survey on Text Classification: From Traditional to Deep Learning. ACM Trans. Intell. Syst. Technol. 2022, 13, 1–41. [Google Scholar] [CrossRef]
- Rohleder, R. Hands-on ghidra-a tutorial about the software reverse engineering framework. In Proceedings of the 3rd ACM Workshop on Software Protection, London, UK, 15 November 2019; pp. 77–78. [Google Scholar]
- Zhang, J.; Qin, Z.; Yin, H.; Ou, L.; Zhang, K. A feature-hybrid malware variants detection using CNN based opcode embedding and BPNN based API embedding. Comput. Secur. 2019, 84, 376–392. [Google Scholar] [CrossRef]
- Raff, E.; Zak, R.; Cox, R.; Sylvester, J.; Yacci, P.; Ward, R.; Tracy, A.; McLean, M.; Nicholas, C. An investigation of byte n-gram features for malware classification. J. Comput. Virol. Hacking Tech. 2021, 14, 1–20. [Google Scholar] [CrossRef]
- Karim, M.E.; Walenstein, A.; Lakhotia, A.; Parida, L. Malware phylogeny generation using permutations of code. J. Comput. Virol. 2019, 1, 13–23. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, F.; Jia, L. Malicious code detection method based on perceptual hash algorithm and feature fusion. Comput. Appl. 2021, 41, 780. [Google Scholar]
- Rosenblum, N.E.; Miller, B.P.; Zhu, X. Extracting compiler provenance from program binaries. In Proceedings of the 9th ACM SIGPLAN-SIGSOFT Workshop on Program Analysis for Software Tools and Engineering, Toronto, ON, Canada, 5–6 June 2010; pp. 21–28. [Google Scholar]
- Rosenblum, N.; Miller, B.P.; Zhu, X. Recovering the toolchain provenance of binary code. In Proceedings of the 2011 International Symposium on Software Testing and Analysis, Toronto, ON, Canada, 17–21 July 2011; pp. 100–110. [Google Scholar]
- Toderici, A.H.; Stamp, M. Chi-squared distance and metamorphic virus detection. J. Comput. Virol. Hacking Tech. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Rahimian, A.; Shirani, P.; Alrbaee, S.; Wang, L.; Debbabi, M. Bincomp: A stratified approach to compiler provenance attribution. Digit. Investig. 2015, 14, S146–S155. [Google Scholar] [CrossRef]
- Li, L.; Ding, Y.; Li, B.; Qiao, M.; Ye, B. Malware classification based on double byte feature encoding. Alex. Eng. J. 2022, 61, 91–99. [Google Scholar] [CrossRef]
- Tang, Y.; Qi, X.; Jing, J.; Liu, C.; Dong, W. BHMDC: A byte and hex n-gram based malware detection and classification method. Comput. Secur. 2023, 128, 103118. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, W.; Zhu, T.; Ren, Y. SaaS: A situational awareness and analysis system for massive android malware detection. Future Gener. Comput. Syst. 2019, 95, 548–559. [Google Scholar] [CrossRef]
- Conti, M.; Khandhar, S.; Vinod, P. A few-shot malware classification approach for unknown family recognition using malware feature visualization. Comput. Secur. 2022, 122, 102887. [Google Scholar] [CrossRef]
- Raff, E.; Sylvester, J.; Nicholas, C. Learning the pe header, malware detection with minimal domain knowledge. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, Dallas, TX, USA, 3 November 2017; pp. 121–132. [Google Scholar]
- Wen, Q.; Chow, K.P. CNN based zero-day malware detection using small binary segments. Forensic Sci. Int. Digit. Investig. 2021, 38, 301128. [Google Scholar] [CrossRef]
- Pizzolotto, D.; Inoue, K. Identifying compiler and optimization options from binary code using deep learning approaches. In Proceedings of the 2020 IEEE International Conference on Software Maintenance and Evolution (ICSME), Adelaide, SA, Australia, 28 September–2 October 2020; pp. 232–242. [Google Scholar]
- Falana, O.J.; Sodiya, A.S.; Onashoga, S.A.; Badmus, B.S. Mal-Detect: An intelligent visualization approach for malware detection. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 1968–1983. [Google Scholar] [CrossRef]
- Jiang, S.; Hong, Y.; Fu, C.; Qian, Y.; Han, L. Function-level obfuscation detection method based on Graph Convolutional Networks. J. Inf. Secur. Appl. 2021, 61, 102953. [Google Scholar] [CrossRef]
- Liu, C.; Saul, R.; Sun, Y.; Raff, E.; Fuchs, M.; Southard Pantano, T.; Holt, J.; Micinski, K. Assemblage: Automatic Binary Dataset Construction for Machine Learning. arXiv 2024, arXiv:2405.03991. [Google Scholar]
- Yang, X.; Chen, Y.; Eide, E.; Regehr, J. Finding and understanding bugs in C compilers. In Proceedings of the 32nd ACM SIGPLAN Conference on Programming Language Design and Implementation, San Jose, CA, USA, 4–8 June 2011; pp. 283–294. [Google Scholar]
- Pan, J. Exploring the Author Controversy in the Last Forty Chapters of ”Dream of the Red Chamber” from the Perspective of Word Frequency and Word Frequency: A Comparative Study Based on Mathematical Statistics Software. In Proceedings of the International Academic Forum on Cultural and Artistic Innovation (III), Beijing, China, 15–17 July 2022. [Google Scholar]
- Li, H.; Liu, Y. Plagiarism Judgment Based on Language Model and Feature Classification. Comput. Eng. 2013, 39, 230–234. [Google Scholar]
- Feuerriegel, S.; Maarouf, A.; Bär, D.; Geissler, D.; Schweisthal, J.; Pröllochs, N.; Robertson, C.E.; Rathje, S.; Hartmann, J.; Mohammad, S.M.; et al. Using Natural Language Processing to Analyse Text Data in Behavioural Science. Nat. Rev. Psychol. 2025, 4, 96–111. [Google Scholar] [CrossRef]
- Stone, M. The Role of Assembly Language in Modern Compiler Design. J. Comput. Sci. Technol. 2020, 35, 210–225. [Google Scholar]
- Tian, X.; Huang, Y. Analysis of Malicious Application Detection Method Based on N-gram Algorithm. Comput. Simul. 2023, 40, 470–474. [Google Scholar]
- Alibabaei, S.; Rahmani, M.; Tahmasbi, M.; Tahmasebi Birgani, M.J.; Razmjoo, S. Evaluating the Gray Level Co-Occurrence Matrix-Based Texture Features of Magnetic Resonance Images for Glioblastoma Multiform Patients’ Treatment Response Assessment. J. Med. Signals Sens. 2023, 13, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Nataraj, L.; Karthikeyan, S.; Jacob, G.; Manjunath, B.S. Malware images: Visualization and automatic classification. In Proceedings of the 8th International Symposium on Visualization for Cyber Security, Pittsburgh, PA, USA, 20 July 2011; pp. 1–7. [Google Scholar]
- Şahin, D.Ö.; Kural, O.E.; Akleylek, S.; Kılıç, E. Permission-based Android malware analysis by using dimension reduction with PCA and LDA. J. Inf. Secur. Appl. 2021, 63, 102995. [Google Scholar] [CrossRef]
- Vichi, M.; Cavicchia, C.; Groenen, P.J.F. Hierarchical means clustering. J. Classif. 2022, 39, 553–577. [Google Scholar] [CrossRef]
- Cohen-Addad, V.; Kanade, V.; Mallmann-Trenn, F.; Mathieu, C. Hierarchical Clustering: Objective Functions and Algorithms. J. ACM. 2019, 66, 1–42. [Google Scholar] [CrossRef]
- Yao, L.; Wan, Y.; Ni, H.; Xu, B. Action unit classification for facial expression recognition using active learning and SVM. Multimed. Tools Appl. 2021, 80, 24287–24301. [Google Scholar] [CrossRef]
- Cerrada, M.; Aguilar, J.; Altamiranda, J.; Sánchez, R.-V. A Hybrid Heuristic Algorithm for Evolving Models in Simultaneous Scenarios of Classification and Clustering. Knowl. Inf. Syst. 2019, 61, 755–798. [Google Scholar]
- Barut, O.; Luo, Y.; Li, P.; Zhang, T. R1DIT: Privacy-Preserving Malware Traffic Classification With Attention-Based Neural Networks. IEEE Trans. Netw. Serv. Manag. 2023, 20, 2071–2085. [Google Scholar] [CrossRef]
- Ravi, V.; Alazab, M. Attention-Based Convolutional Neural Network Deep Learning Approach for Robust Malware Classification. Comput. Intell. 2023, 39, 145–168. [Google Scholar] [CrossRef]
- Yuan, B.; Wang, J.; Liu, D.; Guo, W.; Wu, P.; Bao, X. Byte-Level Malware Classification Based on Markov Images and Deep Learning. Comput. Secur. 2020, 92, 101740. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).