CTIFERK: A Thermal Infrared Facial Expression Recognition Model with Kolmogorov–Arnold Networks for Smart Classrooms

Abstract

Accurate recognition of student emotions in smart classrooms is vital for understanding learning states. Visible light-based facial expression recognition is often affected by illumination changes, making thermal infrared imaging a promising alternative due to its robust temperature distribution symmetry. This paper proposes CTIFERK, a thermal infrared facial expression recognition model integrating Kolmogorov–Arnold Networks (KANs). By incorporating multiple KAN layers, CTIFERK enhances feature extraction and fitting capabilities. It also balances pooling layer information from the MobileViT backbone to preserve symmetrical facial features, improving recognition accuracy. Experiments on the Tufts Face Database, the IRIS Database, and the self-constructed GUET thermalface dataset show that CTIFERK achieves accuracies of 81.82%, 82.19%, and 65.22%, respectively, outperforming baseline models. These results validate CTIFERK’s effectiveness and superiority for thermal infrared expression recognition in smart classrooms, enabling reliable emotion monitoring.

1. Introduction

Current research on classroom facial expression recognition primarily focuses on the application of visible light images. For instance, Shou et al. [1] proposed a Residual Channel Attention Transformer Masking Network (RCTMasking-Net) for facial expression recognition in classrooms, while Yuan et al. [2] used MTCNN for face detection and image segmentation in classroom images and introduced a visual motion analysis method that integrates global and local features for classroom expression recognition. However, these studies fail to consider the impact of environmental light changes on visible light images. For example, Beveridge et al. [3] demonstrate that illumination variations, such as side lighting or extreme lighting conditions can degrade face recognition performance by introducing strong shadows and asymmetry, potentially reducing the accuracy of visible-light-based models for subtle expressions like confusion or boredom by up to 20–30%.

Unlike prior studies that predominantly rely on visible light images, this research pioneers the application of thermal infrared facial expression recognition in smart classrooms, offering a novel solution tailored to educational environments. Compared to visible light, thermal infrared facial images capture the distribution of facial temperature features and are uniquely unaffected by illumination, making them highly valuable for expression recognition in low-light scenarios [4,5,6]. To date, no researchers have applied thermal infrared expressions to classroom settings. Traditional facial expression recognition models are based on Multilayer Perceptrons (MLPs), which, according to the universal approximation theorem, can approximate any continuous function. However, MLPs require more neurons or deeper networks to achieve the same approximation effect and their approximation process lacks the efficient mathematical structure of KANs. MLPs also often face issues such as overfitting, vanishing or exploding gradients, and scalability problems [7]. In contrast, the Kolmogorov–Arnold Network (KAN) provides a mathematically efficient structure that mitigates these problems, offering improved interpretability and fitting capabilities [8]. This raises the possibility of leveraging a KAN to enhance thermal infrared facial expression recognition in educational contexts.

Ethical considerations for this study, particularly regarding the recording of students in classrooms for the GUET thermalface dataset, include anonymizing thermal images using mosaicing techniques to obscure identifiable features and obtaining informed consent from participants, ensuring compliance with privacy regulations.

1.1. Research Questions

This study aims to address the gaps in current research by exploring the application of thermal infrared facial expression recognition in smart classrooms. Specifically, it seeks to answer the following research questions (RQs):

• RQ1: How can thermal infrared facial images be effectively utilized to recognize student expressions in smart classroom environments, overcoming the limitations of visible-light-based methods under varying illumination conditions?
• RQ2: To what extent does the integration of a Kolmogorov–Arnold Network (KAN) into a thermal infrared facial expression recognition model improve accuracy and robustness compared to traditional MLP-based approaches?
• RQ3: What are the practical challenges and performance differences when applying a thermal infrared recognition model to a real-world classroom dataset compared to controlled public datasets?

1.2. Contribution

This paper proposes CTIFERK, a novel thermal infrared facial expression recognition model combining MobileViT and Kolmogorov–Arnold Networks (KANs) for smart classrooms. The main contributions are as follows:

• We introduce CTIFERK, which integrates multiple KAN layers to process pooled feature vectors from the MobileViT backbone, enhancing feature extraction and fitting capabilities compared to traditional MLP-based models. Unlike prior works such as IRFacExNet [9] and MobileNetv3 with the Binary Dragonfly Algorithm [10], which rely on convolutional neural networks (CNNs) or MLPs, CTIFERK leverages the KAN’s mathematically efficient structure to mitigate overfitting and improve interpretability, achieving superior accuracy (e.g., 81.82% on Tufts Face Database vs. 76.36% for IRFacExNet and MobileNetv3).
• We constructed the GUET thermalface dataset, tailored for smart classroom settings, capturing 1852 thermal infrared images across six expression categories. Unlike the controlled settings of public datasets like the Tufts Face Database and IRIS Thermal/Visible Face Database, GUET thermalface addresses real-world classroom challenges, such as varying resolutions and head poses. Experiments on GUET thermalface and public datasets demonstrate CTIFERK’s robustness, with accuracies of 65.22%, 81.82%, and 82.19%, respectively, outperforming baselines like IRFacExNet [9] and MobileNetv3 [10].

These contributions advance thermal infrared facial expression recognition by addressing the limitations in existing methods, particularly for dynamic educational environments, offering a scalable solution for smart education.

The remainder of this paper is organized as follows: Section 2 introduces related work. Section 3 outlines the datasets used in the experiments and introduces the proposed model, model evaluation metrics, and experimental environment. Section 4 analyzes the experimental results to evaluate the performance of the proposed algorithm. Section 5 provides a discussion of the experimental results. Finally, Section 6 concludes the paper and provides future research directions.

2. Related Work

In the field of thermal infrared facial expression recognition, Nguyen et al. [11] developed a facial expression computing system based on thermal infrared images, effectively overcoming the limitations of visible light images. Ilikci et al. [12] improved the YOLO algorithm to achieve facial expression detection in thermal infrared images and systematically compared the detection performance of YOLO, ResNet, and DenseNet. Nguyen et al. [13] integrated visible light and thermal infrared images and used wavelet transform and Principal Component Analysis (PCA) for expression recognition. Kamath et al. [14] employed features extracted from the VGG-Face CNN model for expression recognition in thermal infrared images. Rooj et al. [15] generated a set of optimal local region-specific filters using convolutional sparse coding for feature extraction and proposed a supervised dimensionality reduction algorithm to improve the accuracy of thermal infrared image expression recognition. Filippini et al. [16] introduced an automatic facial expression recognition model using a feedforward neural network as the deep learning algorithm. Assiri et al. [17] divided the entire facial image into four parts and proposed a ten-fold cross-validation method to improve recognition accuracy using Convolutional Neural Networks (CNNs). Bhattacharyya et al. [9] proposed a deep learning network called IRFacExNet for facial expression recognition from thermal infrared images, which consists of transformation units and residual units and employs a cosine annealing learning rate scheduler and snapshot ensembling method. Prasad et al. [10] introduced a new MobileNetv3 deep learning technique for classifying facial expressions in thermal infrared images, which normalizes the images and uses the Binary Dragonfly Algorithm (BDA) to extract facial features, followed by expression recognition using MobileNetv3. A summary of the related work on thermal infrared expression recognition is shown in

Table 1. Summary of related work on thermal infrared expression recognition.

Researcher/Reference	Method/Model	Key Techniques or Approaches	Main Features or Contributions
Nguyen et al. [11]	Thermal Infrared Emotion Computing System	Emotion estimation based on thermal infrared images	Overcomes limitations of visible light images with thermal-region-based recognition
Ilikci et al. [12]	Improved YOLO Algorithm	Systematic comparison of YOLO, ResNet, and DenseNet	Achieves facial expression detection in thermal images with performance comparison
Nguyen et al. [13]	Visible and Thermal Infrared Fusion	Wavelet transform, Principal Component Analysis (PCA)	Integrates visible and thermal infrared sequences to enhance recognition accuracy
Kamath et al. [14]	VGG-Face CNN Feature Extraction	Convolutional Neural Network (CNN)	Uses pre-trained VGG-Face model to extract features for thermal expression recognition
Rooj et al. [15]	Convolutional Sparse Coding with Supervised Dimensionality Reduction	Local region-specific filters, sparse coding	Generates optimal filters and proposes supervised dimensionality reduction for improved accuracy
Filippini et al. [16]	Automatic Expression Recognition Model	Feedforward Neural Network (Deep Learning)	Automates thermal infrared expression recognition based on bio-signal analysis
Assiri et al. [17]	CNN with Ten-Fold Cross-Validation	Divides facial image into four parts, machine learning	Enhances accuracy by partitioning and cross-validating thermal facial images
Bhattacharyya et al. [9]	IRFacExNet	Transformation units, residual units, cosine annealing learning rate, snapshot ensembling	Proposes a deep learning network designed for thermal facial expression recognition with high performance
Prasad et al. [10]	MobileNetv3 with Binary Dragonfly Algorithm (BDA)	Image normalization, BDA feature extraction, MobileNetv3 classification	Introduces a novel MobileNetv3 technique for thermal expression classification with optimized feature extraction

.

Currently, there have been many attempts to utilize and improve KANs that have mainly falling into two categories: modifying the basis functions of the KAN and integrating KANs with commonly used neural network models. For example, Aghaei [18] replaced the B-spline curves in a KAN with rational functions, while Abueidda et al. [19] used Gaussian radial basis functions to enhance the computational speed and approximation capability of the original KAN. In terms of integration, Drokin [20] replaced the fixed activation functions and linear transformations in CNNs with KANs, while Wang et al. [21] incorporated a KAN into physics-informed neural networks to enable the model to solve partial differential equations efficiently and accurately.

3. Materials and Methods

3.1. Dataset

This paper used the public thermal infrared facial datasets Tufts Face Database and IRIS Thermal/Visible Face Database for experiments. The Tufts Face Database is currently the most comprehensive large-scale facial dataset, containing over 10,000 images of 74 females and 38 males from more than 10 countries, with ages ranging from 4 to 70 years. This database includes six types of images: visible light, near-infrared, thermal infrared, computer-generated sketch images, recorded videos, and 3D images. For this experiment, we used the thermal infrared images with expression labels, which consist of 558 thermal infrared facial images of 112 individuals, labeled as (1) neutral, (2) smile, (3) sleepy, (4) shocked, and (5) wearing sunglasses. The IRIS Thermal/Visible Face Database is a collection of the OTCBVS benchmark dataset. It contains thermal and visible light facial images under various illumination conditions, positions, and facial expressions. The dataset includes 320 × 240 pixel thermal and visible light images of 30 individuals, covering different lighting conditions. For this experiment, we used the thermal infrared images in the Expression folder of the IRIS Thermal/Visible Face Database, which consist of 737 thermal infrared facial images of 30 individuals, labeled as (1) surprised, (2) laughing, and (3) angry. To study student thermal infrared facial expressions in a classroom setting, the most important foundational work is to construct a student classroom thermal infrared facial expression dataset. Therefore, this paper introduces the GUET thermalface dataset for smart classrooms, which comprises 1852 images of six expression categories (“happy”, “focused”, “confused”, “tired”, “distracted”, and “bored”) captured from students attending a particular course in 2023.The GUET thermalface dataset was captured using the YOSEEN X thermal imager produced by the YOSEEN INFRARED company (Wuhan, China, resolution: 640 × 480, thermal sensitivity: <50 mK@25 °C, frame rate: 30 Hz, with a camera installed on the podium during students’ classes. The details are shown in

Table 2. Distribution of the datasets.

Dataset	Distribution
Tufts Face Database	neutral	smile	sleepy	shocked	sunglasses
	111	112	112	111	112
IRIS Database	surprised	laughing	angry
	255	254	228
GUET thermalface	happy	focused	confused	tired	distracted	bored
	157	424	397	332	406	136

.

A single train–test split was used instead of cross-validation due to differences in the collection methods and scenarios of the three datasets, with the dataset split into 80% for the training and 20% for the validation.

3.2. The Classroom Thermal Infrared Facial Expression Recognition Model with KAN (CTIFERK)

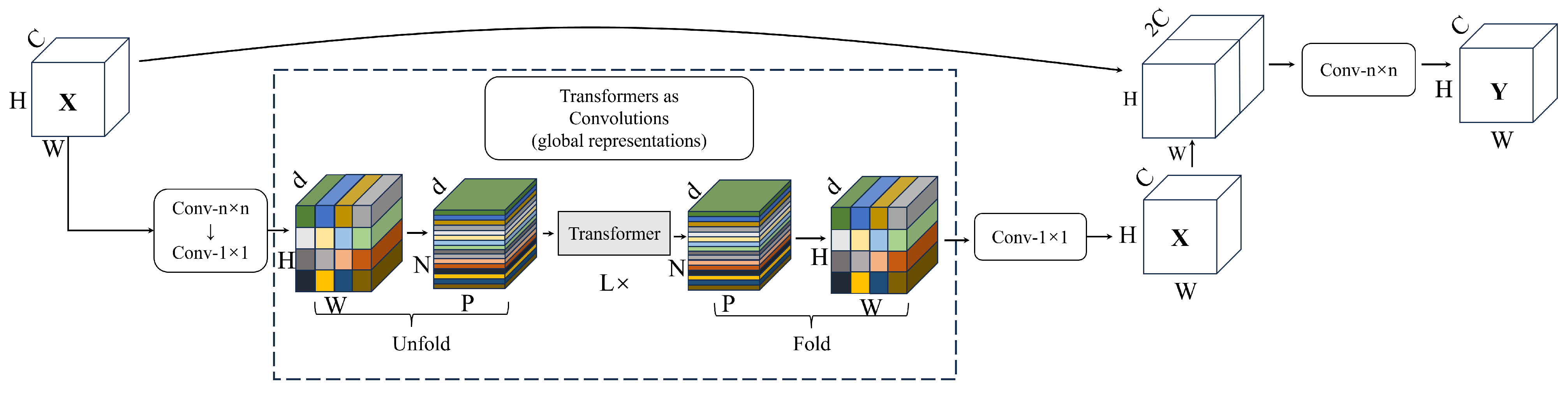
This section introduces the structure of the CTIFERK model. The overall structure of the model is shown in Figure 1. The model consists of MV2 modules, MViT modules, and KAN modules; MobileViT was chosen as the backbone due to its lightweight architecture and its ability to balance parameter efficiency with high accuracy, outperforming heavier models like IRFacExNet in resource-constrained settings while achieving competitive accuracy for thermal infrared images [9]. KAN enhances this by replacing MLPs with a mathematically efficient structure, improving fitting and reducing overfitting. The convolutional layers of the MobileViT model are used to extract low-level and mid-level features from the thermal infrared facial images, while the Transformer modules are used to extract high-level semantic features from the input images. In the MobileViT model, the input to the Transformer module is the feature map extracted by the convolutional layers. Each position’s feature vector represents the semantic information of the pixel at that position in the feature space. The Transformer module encodes these feature vectors using the self-attention mechanism, retaining local features while preserving global information. The feature vectors are then transformed nonlinearly by the feedforward network. The combined action of the self-attention mechanism and the feedforward network enhances the model’s predictive accuracy. Finally, the output of the backbone network is pooled by a global pooling layer, and the resulting feature vectors are input into the multi-layer KAN network for feature processing and prediction.

3.2.1. MViT Structure

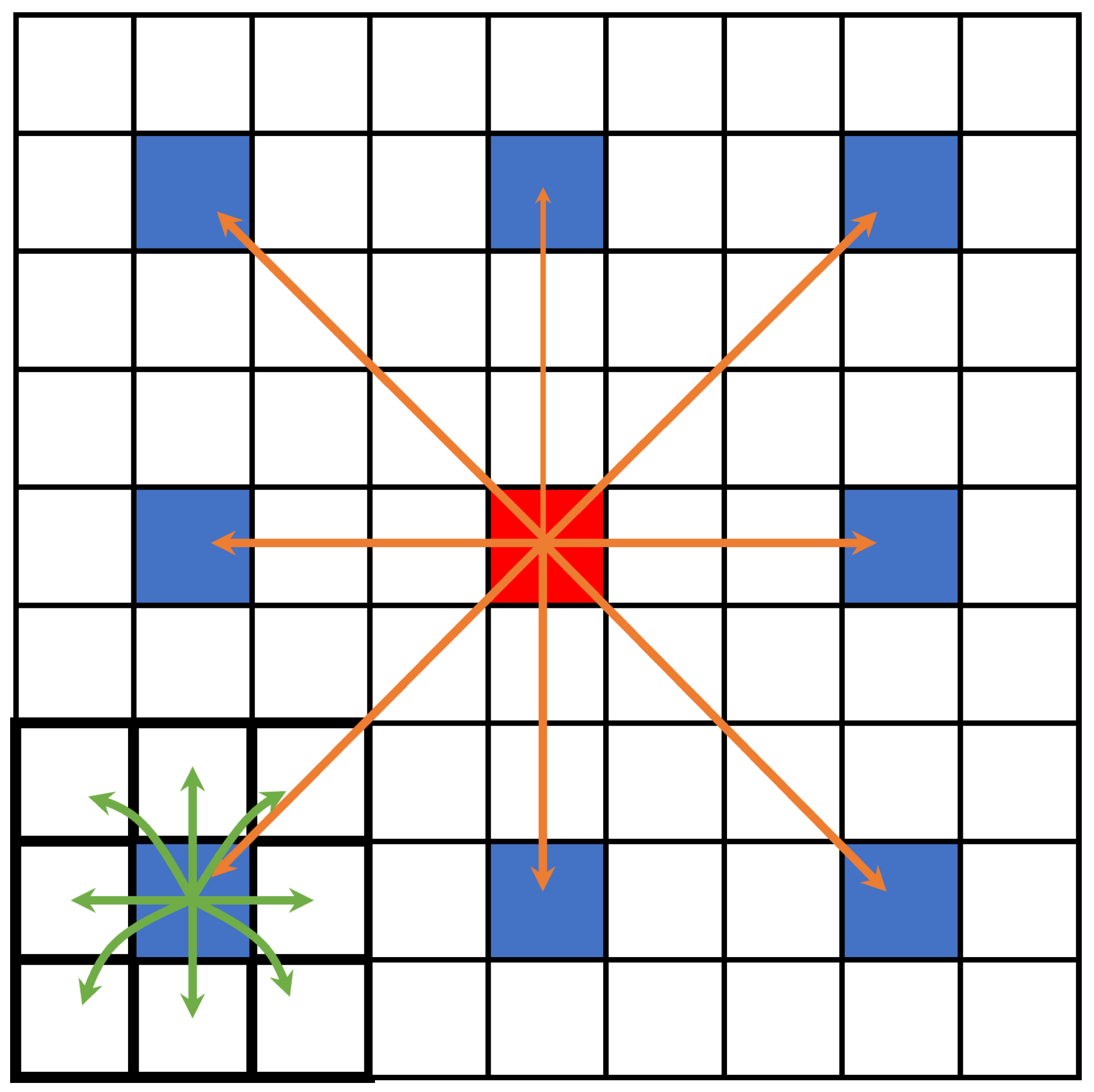
The internal structure of MViT is shown in Figure 2. It has the characteristic of modeling local and global information in the input tensor with relatively fewer parameters. When input tensor $X\in {\mathbb{R}}^{H\times W\times C}$, since the $n\times n$ convolutional layer can project the input tensor into a higher-dimensional space (dimension d, $d>C$), the tensor $X\in {\mathbb{R}}^{H\times W\times C}$ is transformed into tensor ${\mathrm{X}}_L\in {\mathbb{R}}^{H\times W\times d}$ through an $n\times n$ standard convolutional layer and a pointwise convolutional layer.

Unfold ${\mathrm{X}}_L$ into N non-overlapping flat patches $X_U\in {\mathbb{R}}^{P\times N\times d}$. Here, $P=w\times h$, $N={\displaystyle \frac{H\times W}{P}}$ is the number of patches, and $h\le n$ and $w\le n$ are the height and width of each patch. For each patch $p\in \left\{1,\dots ,P\right\}$, the transformer encodes the patch to obtain $X_G\in {\mathbb{R}}^{P\times N\times d}$, as given by the following formula:

$$X_G\left(p\right)=Transformer\left(X_U\left(p\right)\right),1\le p\le P$$

(1)

where $X_G\left(p\right)$ is the global feature representation for patch p, $X_U\left(p\right)$ is the unfolded patch input, $Transformer(\ast )$ denotes the Transformer encoding function, and P is the total number of patches.

$X_U\left(p\right)$ uses convolution to encode the local information within $n\times n$ regions, while $X_G\left(p\right)$ encodes the global information of patches at the p-th position. Therefore, each pixel in $X_G$ can encode information from all pixels in X. As shown in Figure 3, in the MobileViT pixel attention map, the red pixel uses the Transformer to apply attention mechanisms to the blue pixels, while the blue pixels use convolution to encode information from neighboring pixels. This is equivalent to the red pixel encoding information from all pixels in the image.

After folding $X_G\in {\mathbb{R}}^{P\times N\times d}$, we obtain ${\mathrm{X}}_F\in {\mathbb{R}}^{H\times W\times d}$; ${\mathrm{X}}_F$ is projected into a C-dimensional space via pointwise convolution, then concatenated with the input tensor X. Finally, an $n\times n$ convolutional layer is used to fuse these concatenated features.

3.2.2. KAN Structure

The Kolmogorov–Arnold Network (KAN) is a network structure established based on the Kolmogorov–Arnold Representation Theorem (KAR) and B-spline curves. It employs univariate functions as the network’s weights and activation functions, which are adjusted during model training. The formula for the Kolmogorov–Arnold Representation Theorem (KAR) is as follows:

$$f(x_1,\dots ,x_n)=\sum _{q=1}^{2n+1}{\Phi }_q\left(\sum _{p=1}^n{\varphi }_{q,p}\left(x_p\right)\right)$$

(2)

In Equation (2), $f(x_1,\dots ,x_n)$ is a multivariate function, ${\varphi }_{q,p}\left(x_p\right)$ are univariate functions. The upper limit of the outer summation is 2n + 1, which is related to the input dimension n. ${\Phi }_q$ is the q-th function in the outer summation, ${\varphi }_{q,p}\left(x_p\right)$ is the function combining the q-th and p-th terms, and $x_p$ is the p-th component of the input vector.

The activation function of KAN is the sum of the basis function and the spline function. Therefore, the activation function $\varphi \left(x\right)$ is given by the sum of the basis function b(x) and the spline function, with the calculation formula as follows:

$$\varphi \left(x\right)=b\left(x\right)+spline\left(x\right)$$

(3)

$$b\left(x\right)=silu\left(x\right)={\displaystyle \frac{x}{1+e^{-x}}}$$

(4)

$$spline\left(x\right)=\sum _i{c}_i{B}_i\left(x\right)$$

(5)

In Equation (5), $c_i$ are trainable parameters used to adjust the weights of each spline function and $B_i\left(x\right)$ are the B-spline functions used to form the spline combinations.

In the Kolmogorov–Arnold Representation (KAR) theorem, the inner functions form one KAN layer and the outer functions form another KAN layer. The theorem in Equation (5) essentially represents a combination of two KAN layers. By stacking multiple KAN layers, the KAN structure can be extended to arbitrary widths and depths. This allows the construction of a transfer matrix between the input and output, with the calculation formula as follows:

$$x_{l+1}=\underset{{\Phi }_l}{\underbrace{\left[\begin{array}{cccc}{\varphi }_{l,1,1}(·)& {\varphi }_{l,1,2}(·)& \dots & {\varphi }_{l,1,n_l}(·)\\ {\varphi }_{l,2,1}(·)& {\varphi }_{l,2,2}(·)& \dots & {\varphi }_{l,2,n_l}(·)\\ \dots & \dots & \dots & \dots \\ {\varphi }_{l,n_{l+1},1}(·)& {\varphi }_{l,n_{l+1},2}(·)& \dots & {\varphi }_{l,n_{l+1},n_l}(·)\end{array}\right]x_l}}$$

(6)

In Equation (6), $x_{l+1}$ is the output of the ($l+1$)-th layer, ${\varphi }_{l,i,j}(·)$ is the activation function for each edge, and $x_l$ is the input to the l-th layer. By expressing the multi-layer function cascade relationship in matrix form, the formula for calculating the output of the KAN model is as follows:

$$KAN\left(x\right)=({\Phi }_{l-1}\odot {\Phi }_{l-2}\odot \dots \odot {\Phi }_1\odot {\Phi }_0)x$$

(7)

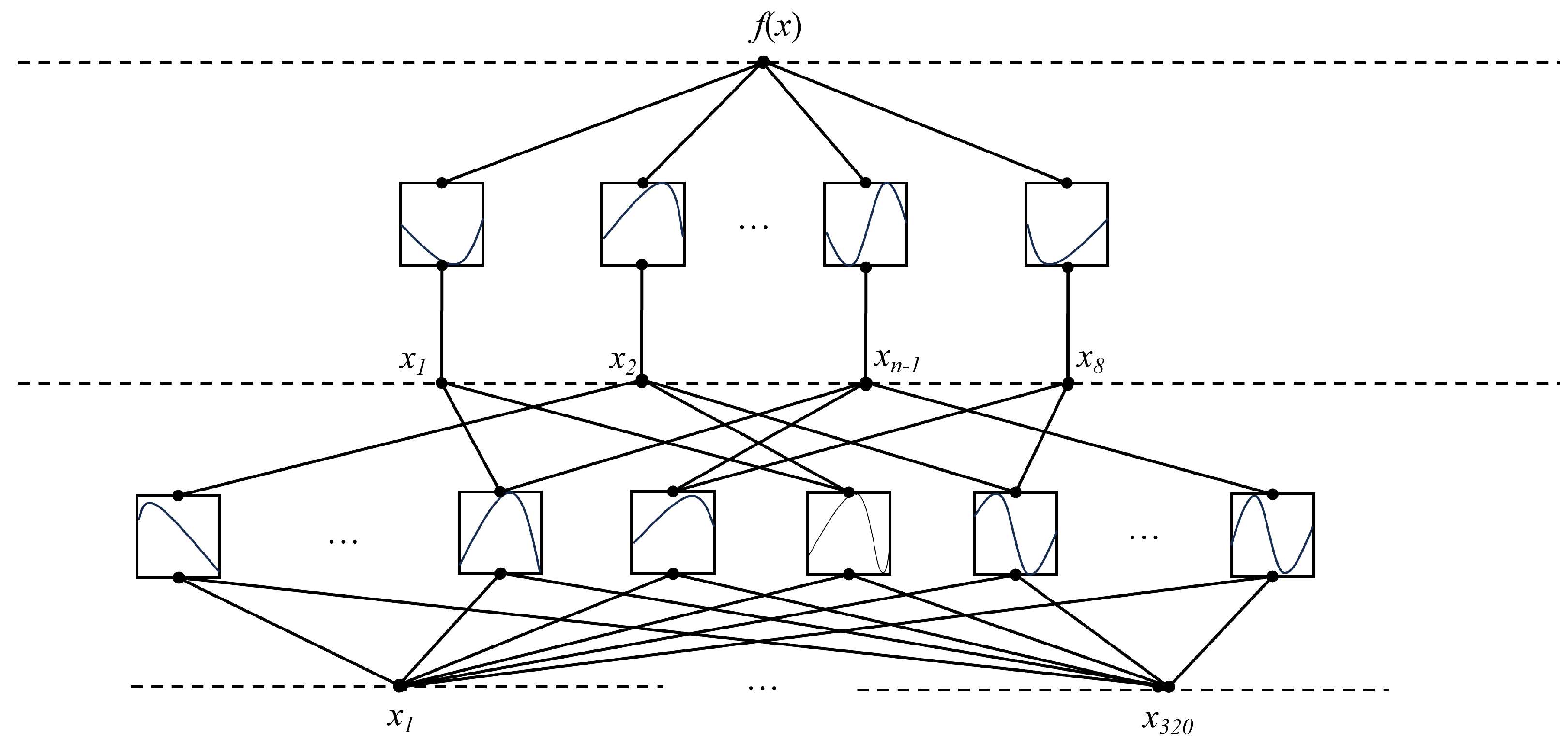
In Equation (7), KAN(x) represents the output of the KAN network, ${\Phi }_l$ is the function matrix corresponding to the l-th KAN layer, and x is the input sensor. The KAN model established in this paper consists of two layers, and the structure of the three-layer KAN is shown in Figure 4.

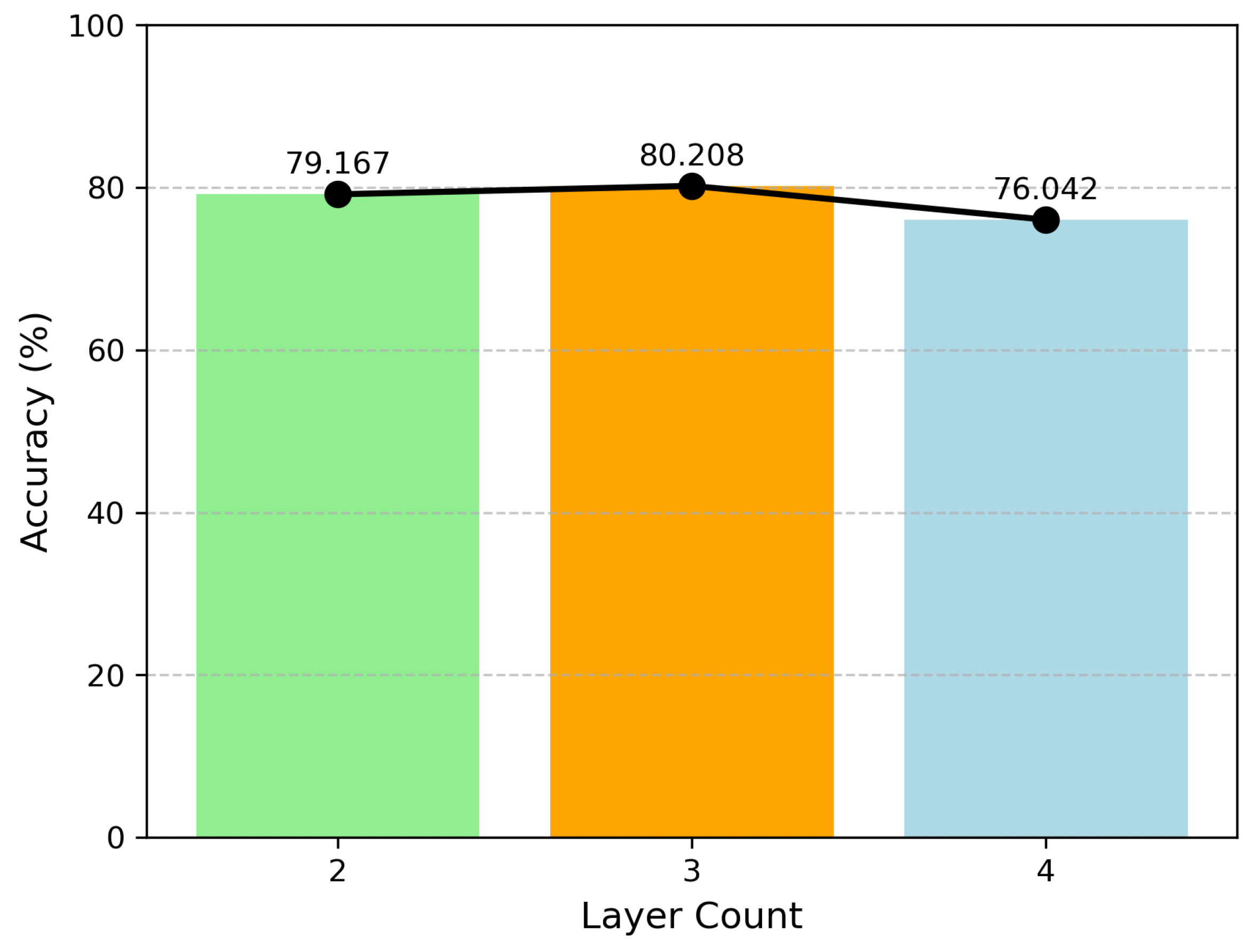
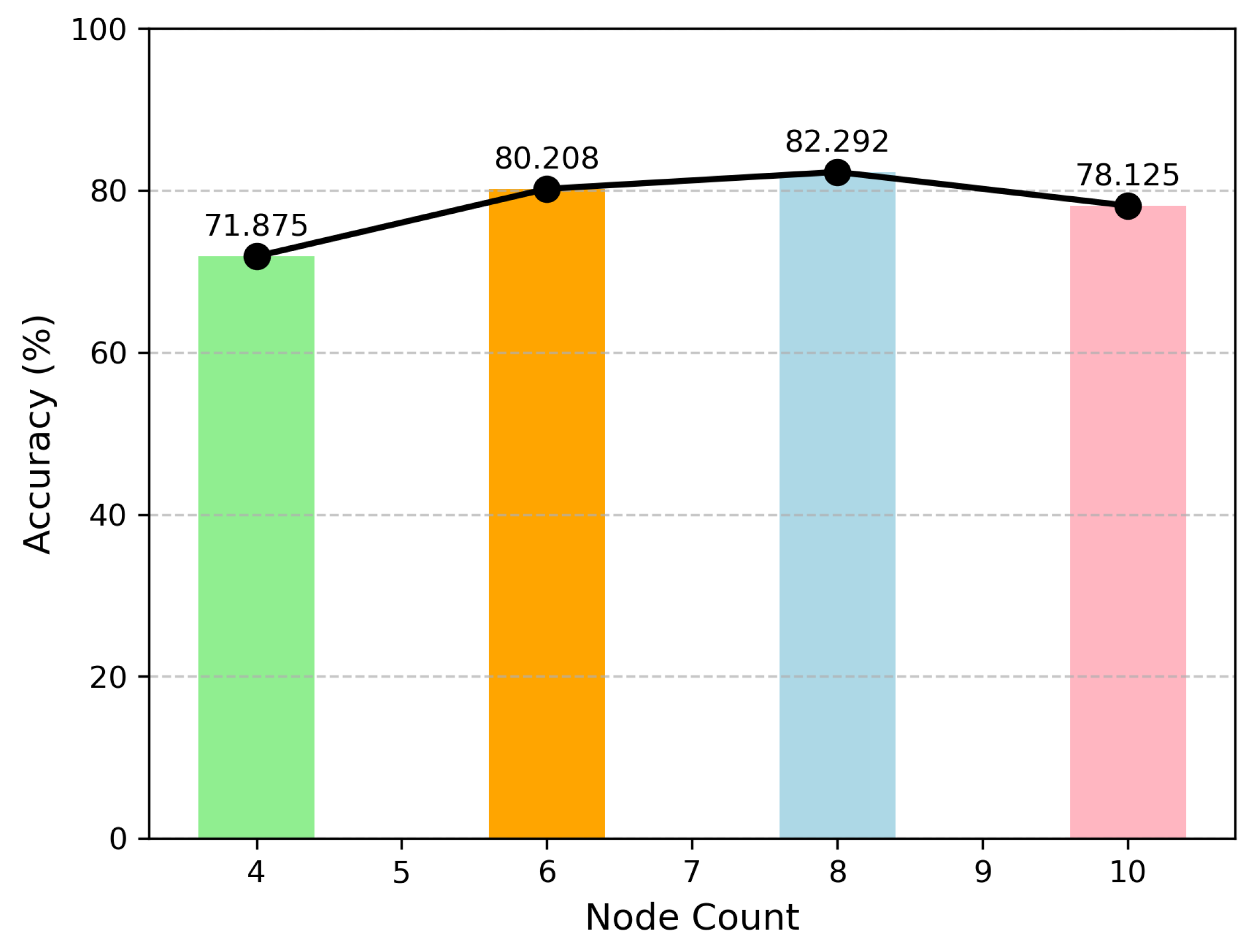
The first layer is a KAN layer with dimensions [320, 8]. It takes a tensor with 320 channels output from the pooling layer as input, and each node represents the sum of 320 learned activation functions. The second layer is a KAN layer with dimensions [8, n], which further trains the 8 nodes output from the first layer and sums the resulting activation functions. f(x) represents the output of the KAN model, with a total of n output variables corresponding to the categories in the dataset.

3.3. Metrics

Model performance was evaluated using accuracy (Acc, proportion of correct predictions), precision (positive predictive value), recall (sensitivity), F1 score (harmonic mean of precision and recall), and ROC curves with AUC (area under the curve) to assess the classification robustness across thresholds.

3.3.1. Acc

Accuracy is the proportion of correct predictions made by a model out of all predictions. It measures how often the model is right, regardless of the class (positive or negative).

$$Acc={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(8)

TP (True Positives): Number of positive cases correctly predicted.

TN (True Negatives): Number of negative cases correctly predicted.

FP (False Positives): Number of negative cases incorrectly predicted as positive.

FN (False Negatives): Number of positive cases incorrectly predicted as negative.

3.3.2. Precision

Precision measures the proportion of true positive predictions out of all positive predictions made by the model.

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(9)

3.3.3. Recall

Recall measures the proportion of actual positive cases that the model correctly identifies.

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(10)

3.3.4. F1 Score

The F1 score is the harmonic mean of precision and recall. It provides a single metric that balances the trade-off between precision and recall and is especially useful when the dataset is imbalanced.

$$F1Score=2\times {\displaystyle \frac{Precision\times Recall}{Precision+Recall}}$$

(11)

3.3.5. ROC Curve and AUC

A ROC curve (Receiver Operating Characteristic curve) is a graphical plot that shows the trade-off between the True Positive Rate (TPR) and the False Positive Rate (FPR) at various classification thresholds. AUC stands for Area Under the Curve, specifically the area under the Receiver Operating Characteristic (ROC) curve.

$$TPR={\displaystyle \frac{TP}{TP+FN}}$$

(12)

$$FPR={\displaystyle \frac{FP}{FP+TN}}$$

(13)

$$AUC={\int }_0^{1}TPR\left(FPR\right)d\left(FPR\right)$$

(14)

3.3.6. Cohen’s Kappa

Cohen’s Kappa is a statistical measure designed to evaluate the agreement between two raters or classifiers while correcting for agreement that could occur by chance. In the context of multi-class classification, Cohen’s Kappa extends naturally from its binary form to handle multiple categories. It is widely used in machine learning, psychology, and other fields to assess inter-rater reliability or classification consistency across more than two classes.

$$\kappa ={\displaystyle \frac{p_0-p_e}{1-p_e}}$$

(15)

$p_0$ is the proportion of samples where the predicted and true labels match. For a multi-class confusion matrix, this is the sum of the diagonal elements divided by the total number of samples:

$$p_0={\displaystyle \frac{{\sum }_{i=1}^k{c}_{ii}}{N}}$$

(16)

where $c_{ii}$ is the number of samples correctly classified for category i, k is the number of classes, and N is the total number of samples. $p_e$ is the proportion of agreement expected by chance, calculated as the sum of the products of the marginal probabilities for each class:

$$p_e=\sum _{i=1}^{k}P\left(true\right(i\left)\right)\times P\left(predicted\left(i\right)\right)$$

(17)

where $P\left(true\left(i\right)\right)={\displaystyle \frac{{\sum }_j{c}_{ij}}{N}}$ is the row sum for class (i) and $P\left(predicted\left(i\right)\right)={\displaystyle \frac{{\sum }_j{c}_{ji}}{N}}$ is the column sum for class (i).

3.3.7. MCC

The Matthews Correlation Coefficient (MCC) was originally developed for binary classification but can be adapted for multi-class problems. In its binary form, MCC measures the correlation between predicted and actual labels using all four elements of a confusion matrix. For multi-class classification, MCC is typically computed by applying the One-vs.-Rest (OvR) approach for each class and then averaging the results.

$$MCC={\displaystyle \frac{TP\times TN-FP\times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}}$$

(18)

3.3.8. Cohen’s d

Cohen’s d is a statistical measure used to quantify the effect size, representing the standardized difference between the means of two groups relative to their pooled standard deviation. It is widely applied in machine learning, psychology, and social sciences to assess the magnitude of differences, such as model performance in classification accuracy.

$$d={\displaystyle \frac{M_1-M_2}{s}}$$

(19)

$M_1$ and $M_2$ are the means of the two groups, and s is the pooled standard deviation, calculated as

$$s=\sqrt{{\displaystyle \frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}}$$

(20)

where $s_1$ and $s_2$ are the standard deviations, $n_1$ and $n_2$ are sample sizes, and $s_1^2$ and $s_2^2$ are variances. Common thresholds are $\left|d\right|=0.2$ (small), $0.5$ (medium), and $0.8$ (large).

3.4. Experimental Design

The experimental environment is shown in

Table 3. Experimental environment.

Experimental Environment	Environment Configuration
Operating systems	Win10
CPU	Intel Xeon W-2145 (8 cores, 3.7 GHz)
Video Cards	GeForce RTX 2080ti (11 GB VRAM)
RAM	64GB DDR4
ROM	2T SSD
Programming Languages	Python 3.6
Framework	Pytorch 1.10.2
Additional Libraries	NumPy 1.19.2, OpenCV 3.4.1.15, scikit-learn 0.24.2

.

The CTIFERK model was trained using the cross-entropy loss function, which is widely used in classification tasks due to its effectiveness in handling multi-class problems like thermal infrared expression recognition. Compared to other loss functions, such as focal loss (which is often used to address class imbalance) or triplet loss (commonly employed in face recognition studies), cross-entropy loss demonstrated stable convergence and superior generalization across diverse expression classes in our datasets. These advantages led us to choose cross-entropy loss as the primary loss function for our model.

Key hyperparameters, such as the learning rate, batch size, and epoch count, were selected based on a grid search over ranges (learning rate: [1 $\times {10}^{-4}$, 1 $\times {10}^{-3}$, 1 $\times {10}^{-2}$]; batch size: [16, 32, 64]; epochs: [100, 150, 200]) to maximize validation accuracy on the database. After experimentation, it was ultimately decided to use the Adam optimizer for gradient descent optimization, with the learning rate of the backbone network set to 1 $\times {10}^{-3}$. In the training process, the learning rate is reduced to 0.1 of its original value every 30 epochs. The input image size was set to $224\times 224$, as this resolution balances computational efficiency with sufficient detail for thermal infrared data, which typically has lower spatial cues than visible light images. The thermal images in our datasets (e.g., GUET thermalface at 640 × 480) retain critical temperature distribution patterns even after resizing to $224\times 224$. This resolution aligns with MobileViT’s architecture, optimized for $224\times 224$ inputs, ensuring efficient processing on classroom hardware. The batch size was set to 32, and the total number of training epochs was 150.

4. Experimental Results and Analysis

4.1. Model Experiments

To verify the advantages and effectiveness of the proposed KAN integration, the CTIFERK model was compared with five baseline models, including IRFacExNet and MobileNetV3, on two public datasets (Tufts Face Database and IRIS Thermal/Visible Face Database) and one classroom dataset (GUET thermalface). The validation accuracy and ROC curves were used as evaluation metrics. The validation accuracy curves for the models on the three datasets are shown in Figure 5.

From Figure 5, it can be observed that, for all three datasets, the proposed CTIFERK model outperformed the other baseline models after the 30th epoch and converged rapidly. This indicates that the proposed model’s design and training strategy have significant advantages, enabling the model to learn effective expression features in a short time and exhibit good generalization performance.

The ROC curves for the models on the three datasets are shown in Figure 6.

From Figure 6, it can be seen that, for all three datasets, the AUC values of the proposed CTIFERK model are superior to those of the baseline models, indicating better classification performance.

The performance metrics of the CTIFERK model and other baseline models on the three datasets are shown in

Table 4. Performance metrics of algorithms on datasets. Bold indicates best results per metric. The brackets indicate the standard deviation of the ten training results.

Dataset	Model	Acc (%)	AUC	Mean Precision	Mean Recall	Mean F1 Score	GFLOPs	Params (M)	Inference Time (ms)
The Tufts Face Database	ResNet50	70.91	0.89	72.67	70.91	71.33	4.12	23.52	25.6
	IRFacExNet [9]	76.36	0.90	77.00	76.36	76.60	1.86	1.97	15.2
	SEResNet50	75.45	0.93	75.39	75.45	75.28	4.13	26.06	26.1
	MobileNetv3 [10]	76.36	0.93	79.56	76.36	77.26	0.06	1.52	8.5
	MobileViT	80.91	0.93	82.14	80.91	81.30	0.26	0.95	11.8
	CTIFERK	81.82 (0.42)	0.96	84.11 (0.61)	81.82 (0.45)	82.44 (0.39)	0.26	0.98	12.3
IRIS Database	ResNet50	60.96	0.77	65.73	60.15	59.58	4.12	23.52	25.6
	IRFacExNet [9]	75.34	0.87	76.64	75.11	75.47	1.86	1.97	15.2
	SEResNet50	73.97	0.88	79.10	73.76	74.59	4.13	26.06	26.1
	MobileNetv3 [10]	75.34	0.92	75.65	75.32	75.44	0.06	1.52	8.5
	MobileViT	81.51	0.90	82.87	81.29	81.67	0.26	0.95	11.8
	CTIFERK	82.19 (0.28)	0.93	83.51 (0.37)	82.03 (0.29)	82.42 (0.34)	0.26	0.98	12.3
GUET thermalface	ResNet50	60.87	0.84	61.95	56.17	57.83	4.12	23.52	25.6
	IRFacExNet [9]	64.03	0.86	62.49	61.23	61.75	1.86	1.97	15.2
	SEResNet50	59.51	0.85	58.29	53.89	54.65	4.13	26.06	26.1
	MobileNetv3 [10]	60.87	0.86	58.76	57.17	57.73	0.06	1.52	8.5
	MobileViT	58.42	0.84	54.83	53.58	54.05	0.26	0.95	11.8
	CTIFERK	65.22 (0.89)	0.87	64.22 (0.97)	60.95 (0.86)	62.01 (0.67)	0.26	0.98	12.3

.

Table 4 presents the performance metrics of CTIFERK and baseline models (ResNet50, IRFacExNet [9], SEResNet50, MobileNetv3 [10], and MobileViT) across the three datasets. CTIFERK achieves the highest accuracy on all datasets, 81.82% on Tufts, 82.19% on IRIS, and 65.22% on GUET thermalface, with AUC values of 0.96, 0.93, and 0.87, respectively, indicating robust classification performance. The standard deviations of accuracy (0.42, 0.28, and 0.89) from ten training runs confirm CTIFERK’s consistent superiority over baselines, with Cohen’s d values (1.076, 0.626, and 3.799) reflecting significant improvements, particularly on the challenging GUET dataset (

Table 5. Cohen’s Kappa, MCC, and Cohen’s d of CTIFERK on the three datasets.

Dataset	Cohen’s Kappa	MCC						Cohen’s d
Tufts Face Database	0.773	neutral	smile	sleepy	shocked	sunglasses		1.076
		0.578	0.659	0.854	0.823	1.000
IRIS Database	0.721	surprised	laughing	angry				0.626
		0.771	0.653	0.759
GUET thermalface	0.533	happy	focused	confused	tired	distracted	bored	3.799
		0.495	0.668	0.589	0.541	0.606	0.297

). Compared to MobileNetv3’s lightweight design (0.06 GFLOPs), CTIFERK’s 0.26 GFLOPs and 12.3 ms inference time (vs. 8.5 ms for MobileNetv3) remain practical for real-time classroom applications, balancing accuracy and efficiency.

4.2. KAN Hyperparameter Experiments

To optimize the performance of the CTIFERK model, we conducted hyperparameter experiments on the Kolmogorov–Arnold Network (KAN) layers integrated into the architecture, focusing on the number of KAN layers and the number of nodes in the intermediate hidden layer. These experiments were performed on the Tufts Face Database, consistent with the settings in Table 4.

First, we varied the number of KAN layers (2, 3, and 4). The results, shown in Figure 7, indicate accuracies of 79.167%, 80.208%, and 76.042%, respectively. The three-layer configuration achieved the highest accuracy, suggesting an optimal balance between model capacity and generalization. Increasing to four layers led to a performance drop, likely due to overfitting caused by excessive model complexity. Subsequently, we fixed the number of layers at three and tested the number of nodes in the intermediate hidden layer (4, 6, 8, and 10). As depicted in Figure 8, the accuracies were 71.875%, 80.208%, 82.292%, and 78.125%, respectively. The eight-node configuration yielded the highest accuracy of 82.292%, closely aligning with CTIFERK’s performance in Table 4 (81.82%). Fewer nodes (4) limited expressive power, while more nodes (10) introduced overfitting risks.

These results highlight that a three-layer KAN with eight nodes optimizes CTIFERK’s performance, balancing accuracy and computational efficiency, making it suitable for practical deployment in facial expression recognition tasks.

4.3. Ablation Experiments

The proposed CTIFERK model was compared with MobileViT on the Tufts Face Database, IRIS Thermal/Visible Face Database, and GUET thermalface datasets. The confusion matrices are shown in Figure 9, where the horizontal axis represents the predicted labels and the vertical axis represents the true labels. The Cohen’s Kappa, MCC, and Cohen’s d of each category of CTIFERK on the three datasets are shown in Table 5.

As shown in the confusion matrices in Figure 9, on the Tufts Face Database, CTIFERK achieves the highest accuracy for the “sunglasses” class (100%) due to its distinct thermal signature, characterized by cooler regions around the eyes. Although the “sunglasses” class is pedagogically irrelevant for classroom emotion recognition, it is included in the analysis to serve as a technical benchmark, highlighting CTIFERK’s ability to distinguish unique thermal patterns, which strengthens its robustness for other expression classes. The “smile” class has the lowest accuracy because “Smile” and “Neutral” have more similar head postures, making “Smile” more likely to be misidentified as “Neutral”. On the IRIS Database, “Surprise” has the lowest accuracy because its thermal signature is similar to “Laughing” and “Anger” and is not easy to distinguish. In GUET thermalface, “focus” has the highest accuracy, “happy” and “boredom” have low accuracy because the amount of data obtained in the classroom is less than that for the other expressions, and “tiredness” is easily misidentified as “spacing out” because their head postures are similar. The overall recognition accuracy of the CTIFERK model is improved across all three datasets; this indicates that the integration of a KAN has enhanced the model’s accuracy. Additionally, the recognition performance for each category has been improved, demonstrating that KAN has certain advantages over MLP in the context of thermal infrared facial expression recognition.

As can be seen from Table 5, in the Tufts Face Database, the Kappa value is close to 0.8, indicating that the classifier performs very well on this dataset. The MCC ranges from 0.578 to 1.000, indicating consistent and strong performance overall, with the sunglasses category’s perfect performance driving up the mean. The Cohen’s d of 1.076 suggests a large effect size, confirming CTIFERK’s significant accuracy improvement over MobileViT. In the IRIS Database, the Kappa value is slightly lower than that of the Tufts Face Database but still exceeds 0.7, demonstrating high classification consistency and good performance. The MCC ranges from 0.653 to 0.771, indicating that CTIFERK performs well on this dataset, while the Cohen’s d of 0.626 reflects a medium effect size, indicating a moderate improvement over MobileViT. In the GUET thermalface dataset, the Kappa value is 0.533 and the performance is weaker, affected by category imbalance or sparse intervals. The MCC ranges from 0.297 to 0.668, indicating weak overall performance, with the low MCC of the bored class significantly lowering the average due to insufficient data. However, the Cohen’s d of 3.799 demonstrates a very large effect size, highlighting CTIFERK’s substantial accuracy advantage over MobileViT, likely driven by the large performance gap in this challenging dataset.

However, in the GUET thermalface dataset, the overall recognition performance is lower compared to the first two datasets. This is due to the setup distance and resolution limitations of the equipment in the classroom, which result in insufficient detail in the captured thermal infrared facial images of the students. As a consequence, the model is unable to capture detailed information from the images. In contrast, the first two datasets were captured with the equipment facing the subjects directly, and each image contained only one person. Therefore, the recognition accuracy in the GUET thermalface dataset is relatively lower than that of the first two datasets.

Moreover, certain categories in the GUET thermalface dataset have similar head poses. For example, the head poses for “happy”, “focused”, and “confused” are similar, and the head poses for “tired”, “distracted”, and “bored” are also similar. As a result, the model tends to misclassify “happy” as “focused” or “confused”, and it may also confuse “tired” with “distracted”.

4.4. Visualization Analysis

To further understand the performance of the CTIFERK model, we randomly selected nine thermal images of faces with different emotional expressions from each expression in the three datasets and used GradCAM visualization technology to generate attention heat maps to reveal the attention areas during the recognition process, as shown in Figure 10. The (a)–(i) rows correspond to nine representative expressions: neutral, shocked, sleepy, smiling, surprised, laughing, angry, happy, and focused. The (I) column is the original thermal image, the (II) column is the attention visualization result obtained by the MobileViT model, and the (III) column is the attention visualization result of the proposed CTIFERK model.

Based on the analysis of Figure 10, the attention heatmaps of CTIFERK (column III) demonstrate more precise focus on key regions compared to MobileViT (column II) across various expressions. Specifically, for (a) neutral and (b) shocked expressions, CTIFERK predominantly focuses on the entire facial area; in (c) sleepy, it significantly concentrates on the eye region; in (d) smiling, its attention is primarily directed to the mouth area; for (e) surprised, (f) laughing, and (g) angry expressions, CTIFERK emphasizes the combination of the mouth and facial regions; and in (h) happy and (i) focus expressions, CTIFERK exhibits a more centralized focus on the face’s central region compared to MobileViT. These results indicate that CTIFERK achieves higher precision and specificity in capturing expression-related key features.

4.5. Practical Effectiveness

To assess CTIFERK’s practical utility, we analyzed its performance in real-world classroom settings using the GUET thermalface dataset. Despite lower accuracy (65.22%) compared to controlled datasets (81.82–82.19%), CTIFERK outperforms baselines by 1–7%, demonstrating resilience to challenges like low resolution and varying head poses. Confusion matrices (Figure 9) reveal that misclassifications, such as “happy” confused with “focused” or “tired” with “distracted”, stem from similar head poses and limited data for certain classes (e.g., “bored” with 136 images). These issues highlight the need for enhanced imaging hardware and pose normalization techniques. CTIFERK’s attention heatmaps (Figure 10) show precise focus on key facial regions (e.g., mouth for “smiling”, eyes for “sleepy”), improving over MobileViT’s broader attention, which enhances its ability to capture the subtle expression cues critical for classroom emotion monitoring.

4.6. Real-World Implications

CTIFERK’s ability to operate under varying illumination conditions makes it ideal for dynamic classroom environments, enabling real-time emotion tracking to support personalized learning. For instance, detecting “confused” or “bored” expressions can prompt teacher interventions, enhancing student engagement. Its lightweight architecture (0.98 M parameters) supports deployment on standard hardware, with an inference time of 12.3 ms suitable for real-time applications. However, the GUET dataset’s lower performance underscores hardware limitations (e.g., YOSEEN X imager’s 640 × 480 resolution), suggesting that higher-resolution thermal cameras could further boost accuracy. These findings position CTIFERK as a scalable solution for smart education with the potential to transform pedagogical strategies through affective computing.

5. Discussion

This study aimed to tackle the challenge of accurately recognizing student facial expressions in smart classroom environments, especially under varying illumination conditions where traditional visible-light-based methods struggle. By leveraging thermal infrared imaging and integrating the Kolmogorov–Arnold Network (KAN) into the CTIFERK model, we developed a novel approach tailored to educational settings. Below, we discuss the findings in relation to the research questions outlined in Section 1.1.

RQ1: How can thermal infrared facial images be effectively utilized to recognize student expressions in smart classroom environments, overcoming the limitations of visible-light-based methods under varying illumination conditions?

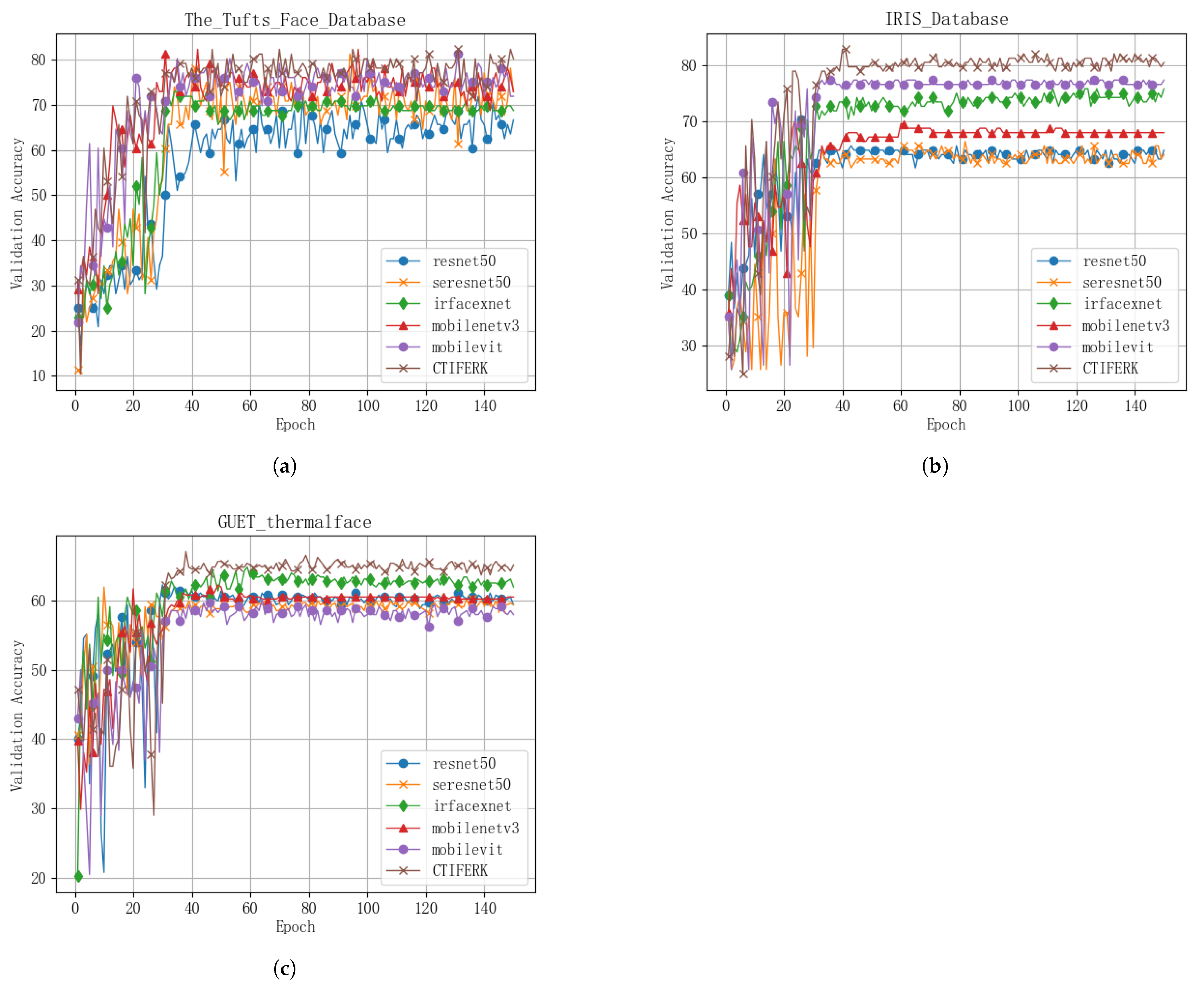
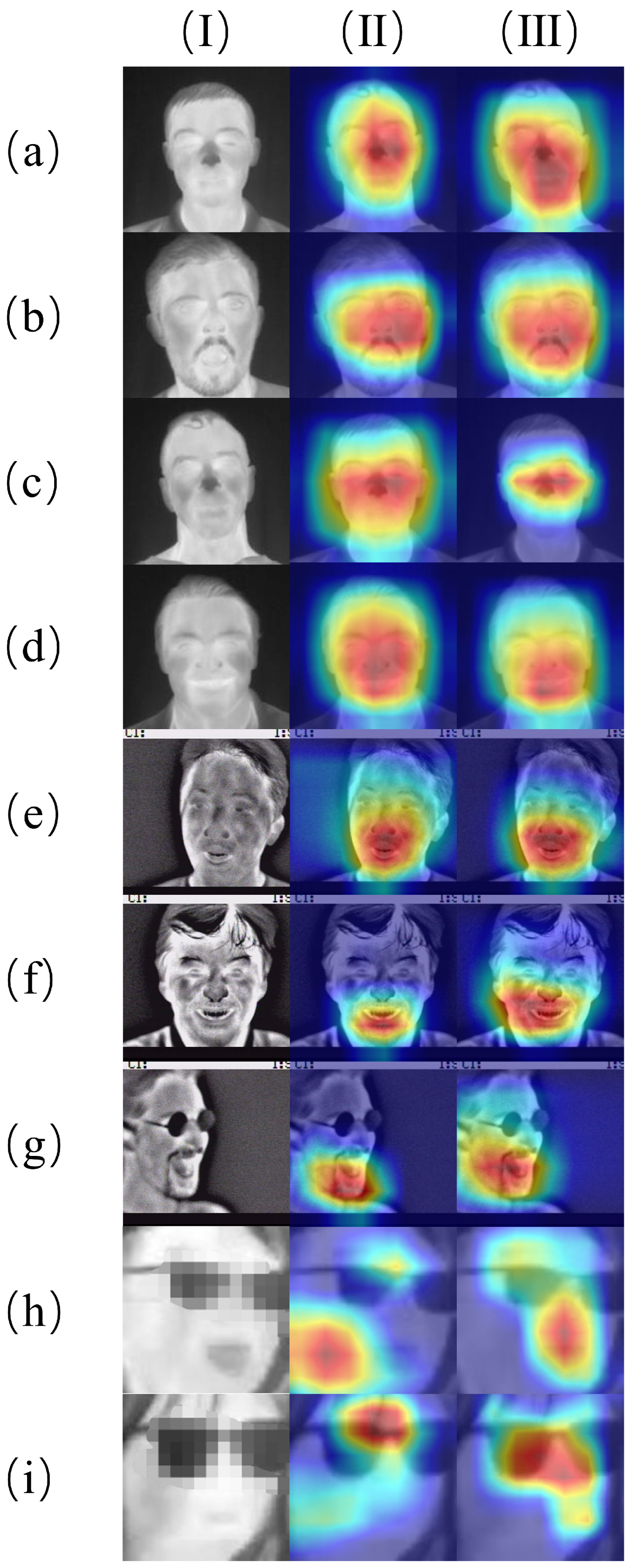
The experimental results show that thermal infrared facial images, which capture temperature distribution symmetry unaffected by lighting changes, offer a robust alternative to visible-light-based methods. The CTIFERK model achieved accuracies of 81.82% on the Tufts Face Database and 82.19% on the IRIS Thermal/Visible Face Database, significantly outperforming baseline models like ResNet50 and MobileNetv3 under controlled conditions. Even on the real-world GUET thermalface dataset where accuracy dropped to 65.22%, CTIFERK maintained superiority over baselines, indicating its ability to address illumination-related limitations. This success stems from KAN’s multi-layer structure, which preserves symmetrical facial features during learning, enhancing feature extraction in low-light or variable-light scenarios. However, challenges such as lower resolution in classroom settings suggest that improved imaging hardware is needed to fully unlock this potential.

RQ2: To what extent does the integration of Kolmogorov–Arnold Networks (KANs) into a thermal infrared facial expression recognition model improve accuracy and robustness compared to traditional MLP-based approaches?

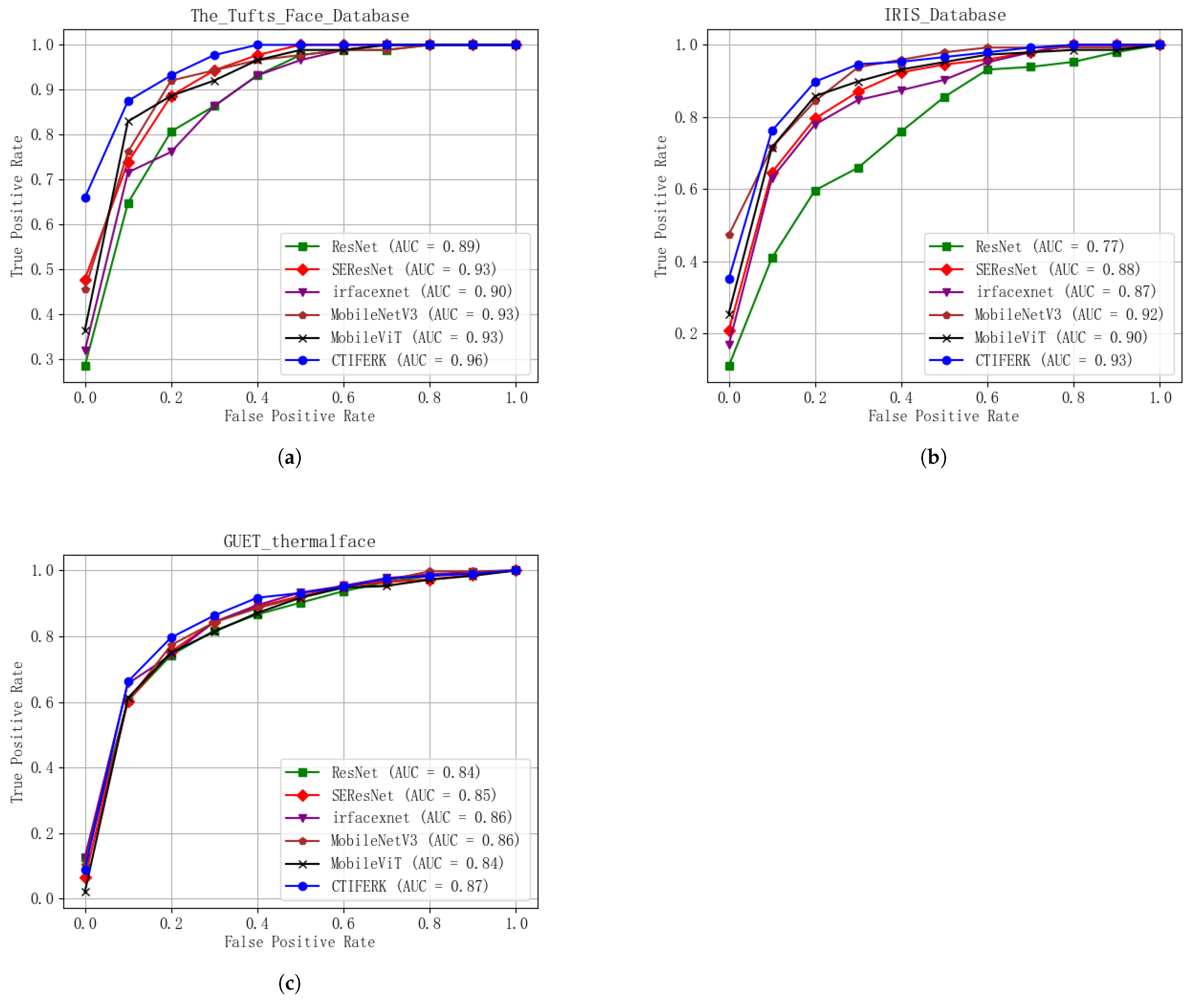
Integrating a KAN into CTIFERK markedly improves accuracy and robustness over traditional MLP-based models. Ablation experiments (Figure 9) and performance metrics (Table 4) reveal that CTIFERK consistently surpasses MobileViT alone, with accuracy gains of 1–7% across datasets. Higher AUC values in ROC curves (Figure 9) further confirm enhanced classification robustness. Table 5 underscores the KAN’s impact, with Cohen’s Kappa values and MCC ranges reflecting strong, consistent performance. Unlike MLPs, which are prone to overfitting and scalability issues, KAN’s mathematical efficiency mitigates these risks, as shown by rapid convergence after the 30th epoch (Figure 5), validating its advantage in thermal infrared facial expression recognition.

RQ3: What are the practical challenges and performance differences when applying a thermal infrared recognition model to a real-world classroom dataset compared to controlled public datasets?

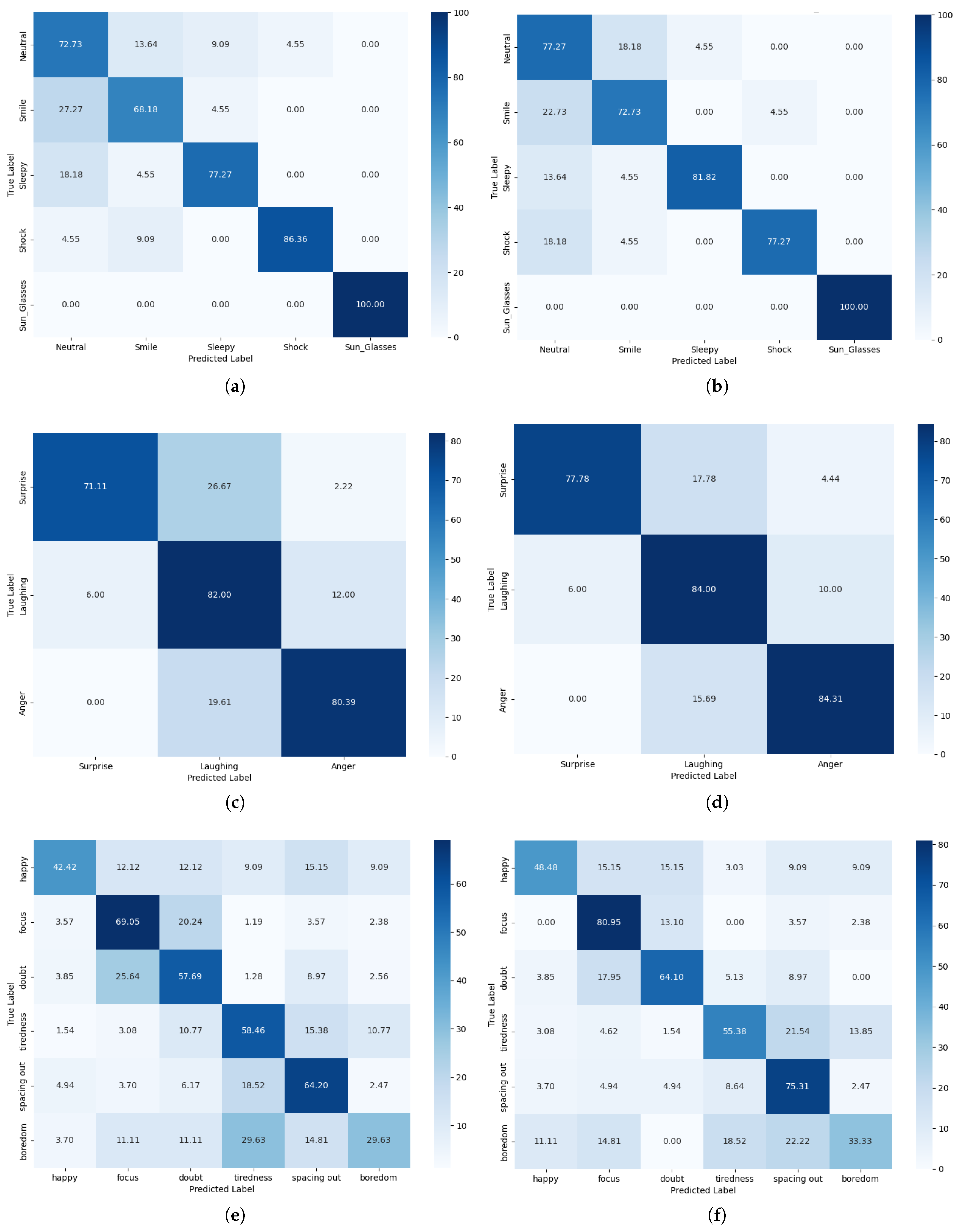
The GUET thermalface dataset’s lower accuracy (65.22%) compared to Tufts (81.82%) and IRIS (82.19%) highlights the practical challenges in real-world classroom settings. Key issues include the YOSEEN X imager’s lower resolution and greater capture distance, which hinder fine-grained feature extraction. Confusion matrices (Figure 9) reveal that overlapping head poses—e.g., between “happy”, “focused”, and “confused” or “tired”, “distracted”, and “bored”—cause misclassifications, a problem less evident in controlled datasets with single-subject, high-resolution images. The Kappa value of 0.533 and MCC range of 0.297–0.668 on GUET thermalface (Table 5) indicate weaker performance due to data imbalance and sparse intervals. While CTIFERK excels in controlled environments, its real-world application demands hardware upgrades and techniques like pose normalization to address these challenges.

From a practical perspective, the CTIFERK model’s ability to monitor student emotions in real-time, regardless of lighting conditions, holds significant promise for smart classrooms. By leveraging thermal infrared imaging, CTIFERK enables personalized learning and teacher interventions through reliable engagement tracking with minimal computational complexity (0.98 M vs. 0.95 M parameters for MobileViT), making it feasible for standard hardware. Ablation experiments (Figure 9) reinforce the value of integrating Kolmogorov–Arnold Networks (KANs), showing consistent accuracy gains of 1–7% over MobileViT and improved per-category performance, aligning with prior work highlighting KAN’s superiority over MLPs in interpretability and fitting efficiency.

This study confirms that thermal infrared facial expression recognition, powered by CTIFERK, offers a viable alternative to visible-light-based methods. As shown in Table 4, CTIFERK achieved accuracies of 81.82% on the Tufts Face Database and 82.19% on the IRIS Thermal/Visible Face Database, significantly outperforming baselines. However, its performance on the real-world GUET thermalface dataset (65.22%) is lower, with a Cohen’s Kappa of 0.533 and MCC range of 0.297–0.668 (Table 5), reflecting the practical challenges in classroom settings.

Several limitations hinder CTIFERK’s real-world application. First, hardware constraints pose significant barriers. The YOSEEN X thermal imager, costing approximately USD 7000, limits adoption in resource-constrained educational settings. Its low resolution and greater capture distance further restrict fine-grained feature extraction, contributing to misclassifications, as seen in GUET thermalface’s confusion matrices (Figure 9). Additionally, CTIFERK requires controlled conditions, such as fixed camera positions and minimal occlusions, which are often infeasible in dynamic classrooms. Second, algorithmic challenges arise from the KAN architecture and MobileViT. While mathematically efficient, KAN’s reliance on B-spline computations is computationally intensive for high-dimensional inputs, potentially limiting scalability on low-power devices. MobileViT, despite its lightweight design, struggles with subtle expression variations in low-resolution thermal images, exacerbating GUET’s lower accuracy. Third, data-related issues compound these challenges. The GUET thermalface dataset’s category imbalances and sparse intervals, particularly for the “bored” class, lead to misclassifications due to overlapping head poses (e.g., “happy” vs. “focused” or “tired” vs. “distracted”). Manual annotation of 1852 images across six expression categories, cross-referenced with visible light images, required approximately 100 h of expert labeling, highlighting the resource-intensive nature of thermal image annotation. Finally, a potential confounding factor is elevated skin temperature due to fever, which may alter facial thermal patterns, mimicking emotions like “angry” or “surprised”. CTIFERK mitigates this through intensity normalization during preprocessing, but residual effects persist.

Future work will address these limitations to enhance CTIFERK’s scalability and robustness. Upgrading imaging hardware to support higher resolution will improve feature extraction and reduce misclassifications in dynamic settings. Noise-robust preprocessing and pose normalization techniques can mitigate head pose overlaps and environmental constraints, enabling deployment in uncontrolled classrooms. Incorporating multi-modal data, such as facial temperature, and physiological baselines, like body temperature measurements, will filter fever-related artifacts, ensuring accurate emotion mapping. To address annotation costs, semi-supervised or active learning could prioritize high-impact samples, potentially reducing labeling time by 30–50% while maintaining performance. Optimizing KAN’s computational efficiency and enhancing MobileViT’s handling of subtle expressions will further improve scalability on low-power devices, advancing CTIFERK’s applicability in educational analytics.

Despite these challenges, CTIFERK’s robust performance and real-time capabilities underscore its potential to transform smart classrooms by facilitating data-driven, personalized education. Continued advancements in hardware, algorithms, and data processing will unlock its full potential, contributing to the broader goal of enhancing educational outcomes through affective computing.

6. Conclusions

Aiming at the problem of thermal infrared facial expression recognition in classroom learning scenarios, we propose a thermal infrared facial expression recognition model based on MobileViT and KAN (CTIFERK). By integrating the Kolmogorov–Arnold Network (KAN) into the image classification network to process image features, the overall fitting capability of the model is enhanced, thereby further improving the model’s accuracy and outperforming existing thermal infrared facial expression recognition models. Experimental results demonstrate CTIFERK’s superior performance, achieving 81.82% accuracy on the Tufts Face Database, 82.19% on the IRIS Database, and 65.22% on GUET thermalface, outperforming baselines in smart classroom scenarios. Beyond its superior performance, CTIFERK has significant implications for smart education, enabling real-time emotion monitoring to support personalized learning and teacher interventions. Its robustness to lighting conditions broadens its applicability to diverse classroom settings, potentially transforming educational analytics and student engagement strategies.

For future research, we plan to enhance CTIFERK’s ability to handle high-dimensional datasets by integrating multi-modal data, such as combining thermal infrared images with physiological signals (e.g., heart rate or skin conductance) to capture richer emotional cues. Preliminary experiments will involve collecting synchronized thermal and physiological data from a small cohort of students in a controlled classroom setting to evaluate feature fusion techniques, such as attention-based multi-modal transformers. Additionally, we aim to employ data augmentation techniques, including generative adversarial networks (GANs), to increase the diversity of thermal infrared facial images, addressing the limitations of low-resolution and sparse datasets like GUET thermalface. Upgrading to high-resolution thermal imaging hardware (e.g., FLIR T-series with 1280 × 960 resolution) will also be explored to capture finer facial details, with initial tests planned on a subset of the GUET thermalface dataset to quantify improvements in feature extraction and recognition accuracy.