Comprehensive Evaluation on Traffic Safety of Mixed Traffic Flow in a Freeway Merging Area Based on a Cloud Model: From the Perspective of Traffic Conflict
Abstract
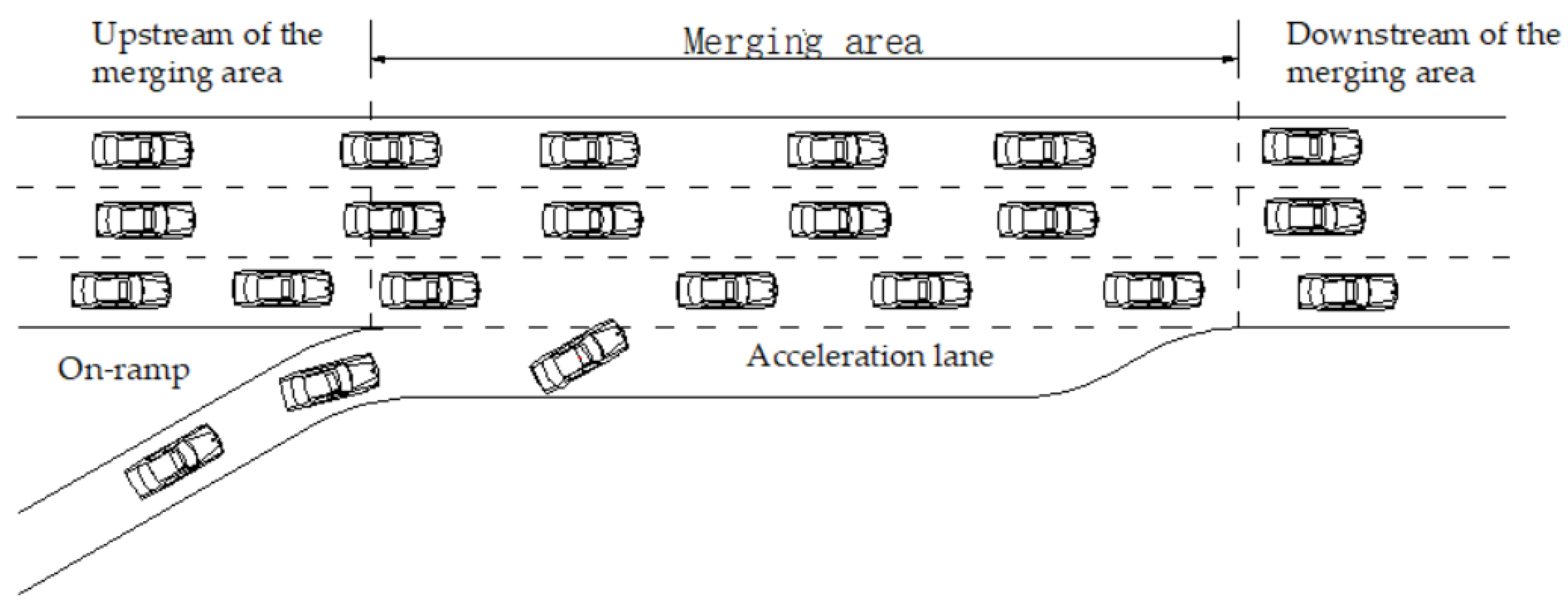
1. Background
2. Literature Review
2.1. Simulation Model of Mixed Traffic Flow
2.2. Safety Evaluation of Mixed Traffic in Merging Areas
2.3. Application of SSMs
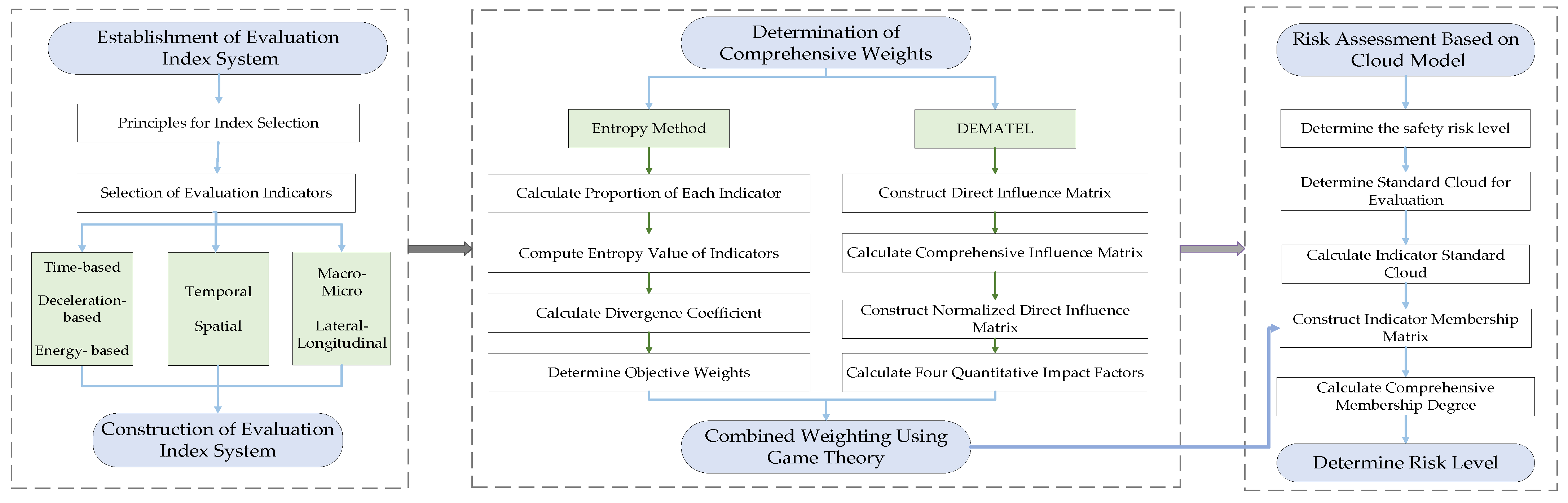
3. Methodology
3.1. Framework of the Evaluation System
3.2. Establishment of Evaluation Index System
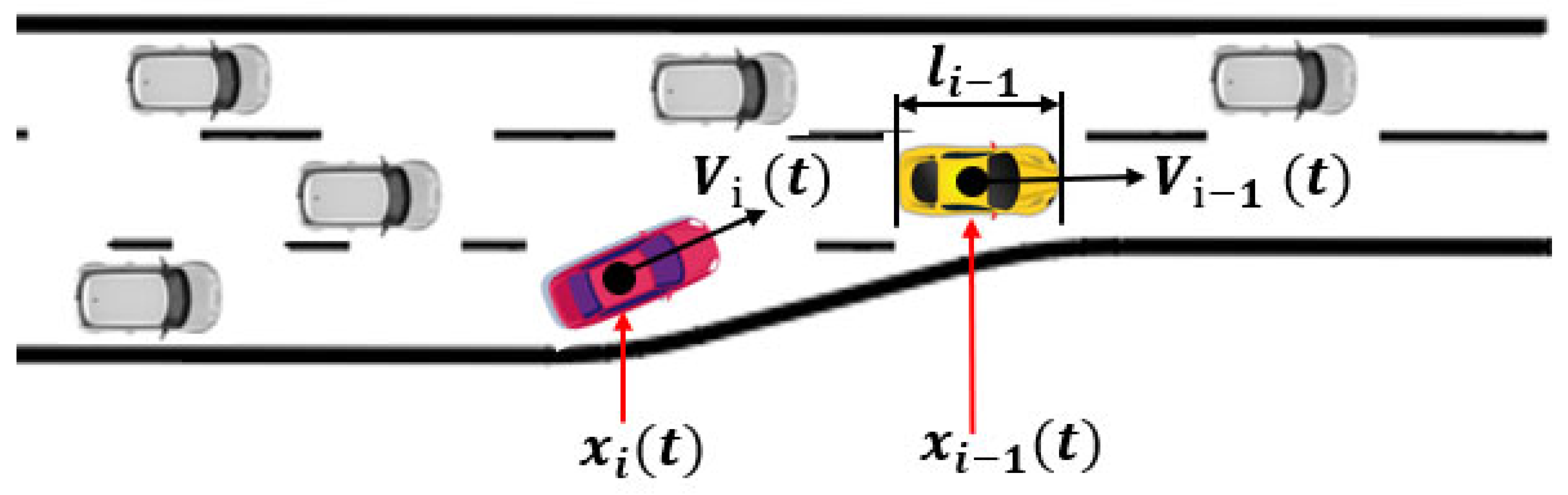
- Modified Time to Collision (MTTC)
- 2.
- Lane Change Time to Collision (LCTTC)
- 3.
- Deceleration Rate to Avoid a Crash (DRAC)
- 4.
- Time Headway
- 5.
- Speed Standard Deviation (SD)
- 6.
- Emergency-Lane-change Risk Frequency (ELCRF)
3.3. Determination of Weight of Index
3.3.1. Calculating Objective Weights by Entropy Method
3.3.2. Calculating Subjective Weights by the DEMATEL Method
3.3.3. Calculating Final Weights Using Game Theory
3.4. Comprehensive Evaluation of Cloud Model Based on Fuzzy Clustering
3.4.1. Cloud Model Theory
3.4.2. Modified Cloud Model
- Initialization: Construct the initial membership matrix ensuring
- Calculate the cluster center
- 3.
- Update membership matrix
- 4.
- Iteration: Repeat Steps 2–3 until convergence; i.e., when the change in objective function satisfies , where .
- 5.
- Output result: The final cluster centers are taken as the expected values of the cloud model. Then, the entropy and hyper-entropy are calculated as:where denotes the expected value of cluster ; is constant and taken as 0.1.
4. Case Study
4.1. Simulation Design
4.2. Simulation Result Analysis
4.2.1. Temporal Dimension
4.2.2. Spatial Dimension
4.3. Comprehensive Evaluation Result
4.3.1. Weights of Indicators
4.3.2. Safety Evaluation Based on Cloud Model
- (1)
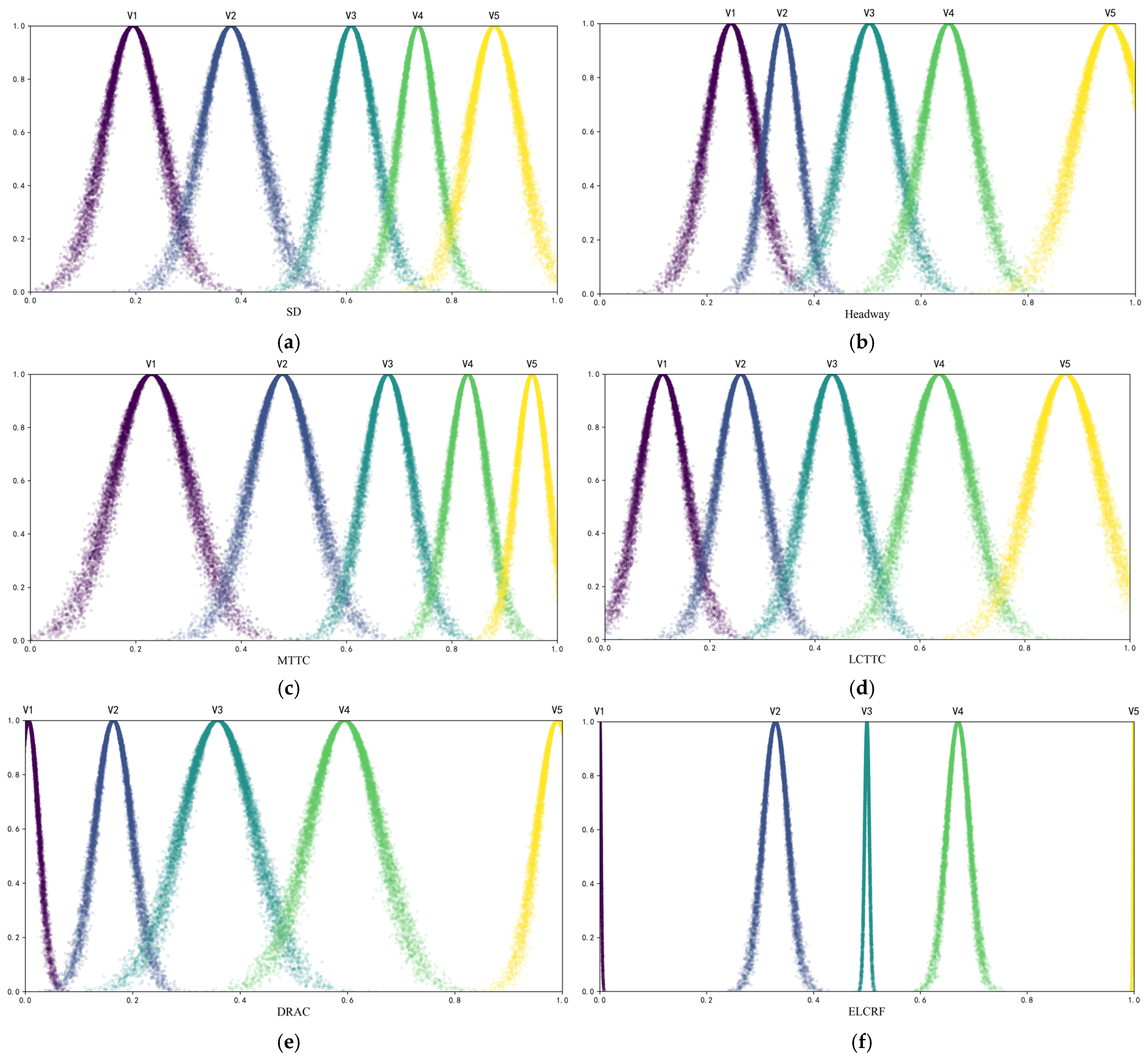
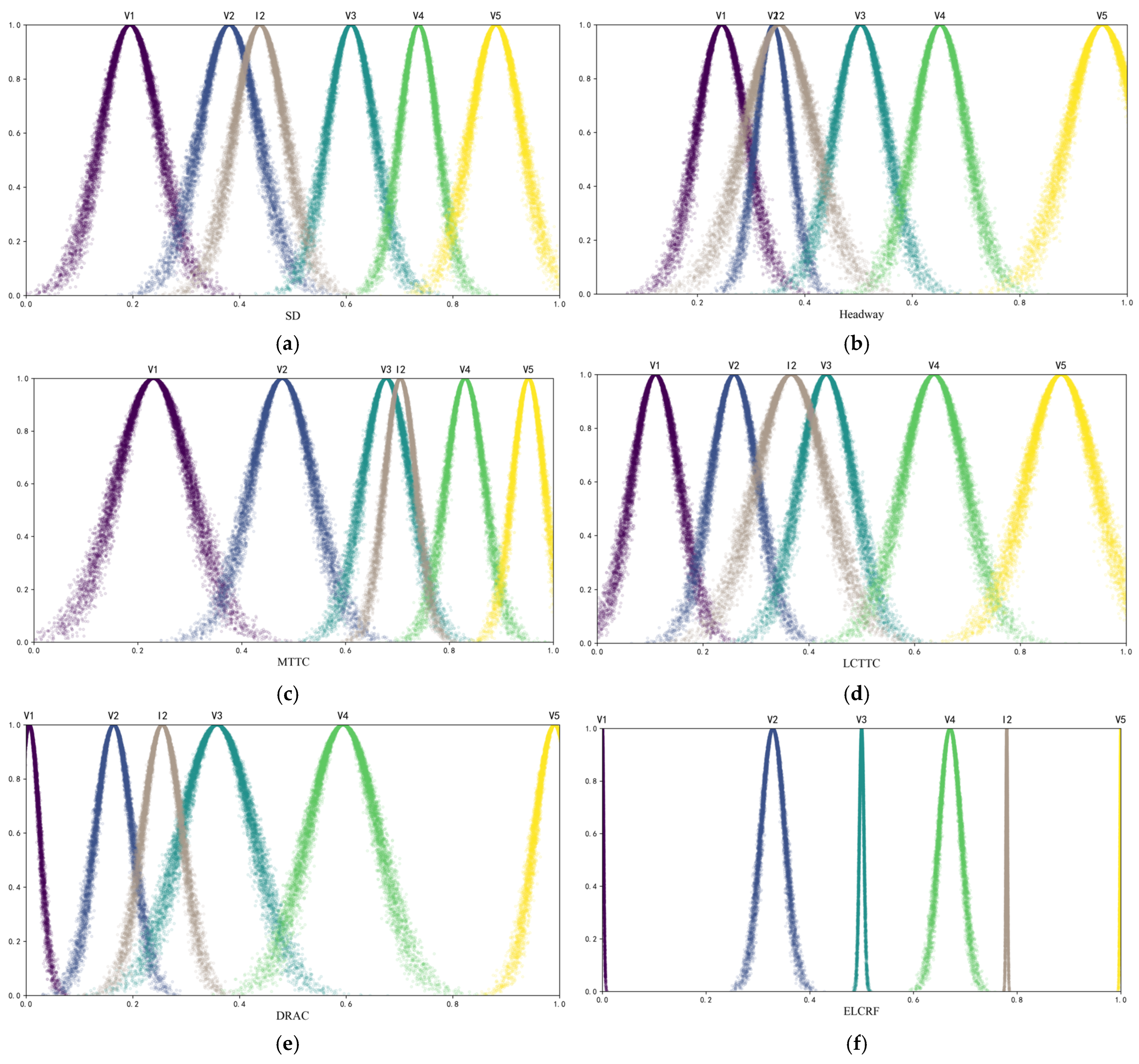
- Determination of standard cloud parameters of indicators
4.3.3. Validation of Cloud Model
4.3.4. Results Analysis
5. Conclusions
- (1)
- A novel indicator—Emergency Lane-Change Risk Frequency (ELCRF)—was developed to better capture the frequency and severity of urgent lane-changing behavior in merging areas. Together with five other SSM-based indicators, this metric contributes to a multi-dimensional safety evaluation system spanning temporal, spatial, macro, and micro perspectives.
- (2)
- A comprehensive safety evaluation model was developed by combining FCM with the cloud model. In addition, a modified game theory was employed to balance the objective weight and subjective weight of indexes, which effectively handles differences between expert judgment and data-driven results. Through a comparative case study with the fuzzy comprehensive evaluation (FCE) method, the results demonstrated that the modified cloud model is both feasible and better aligned with actual traffic dynamics.
- (3)
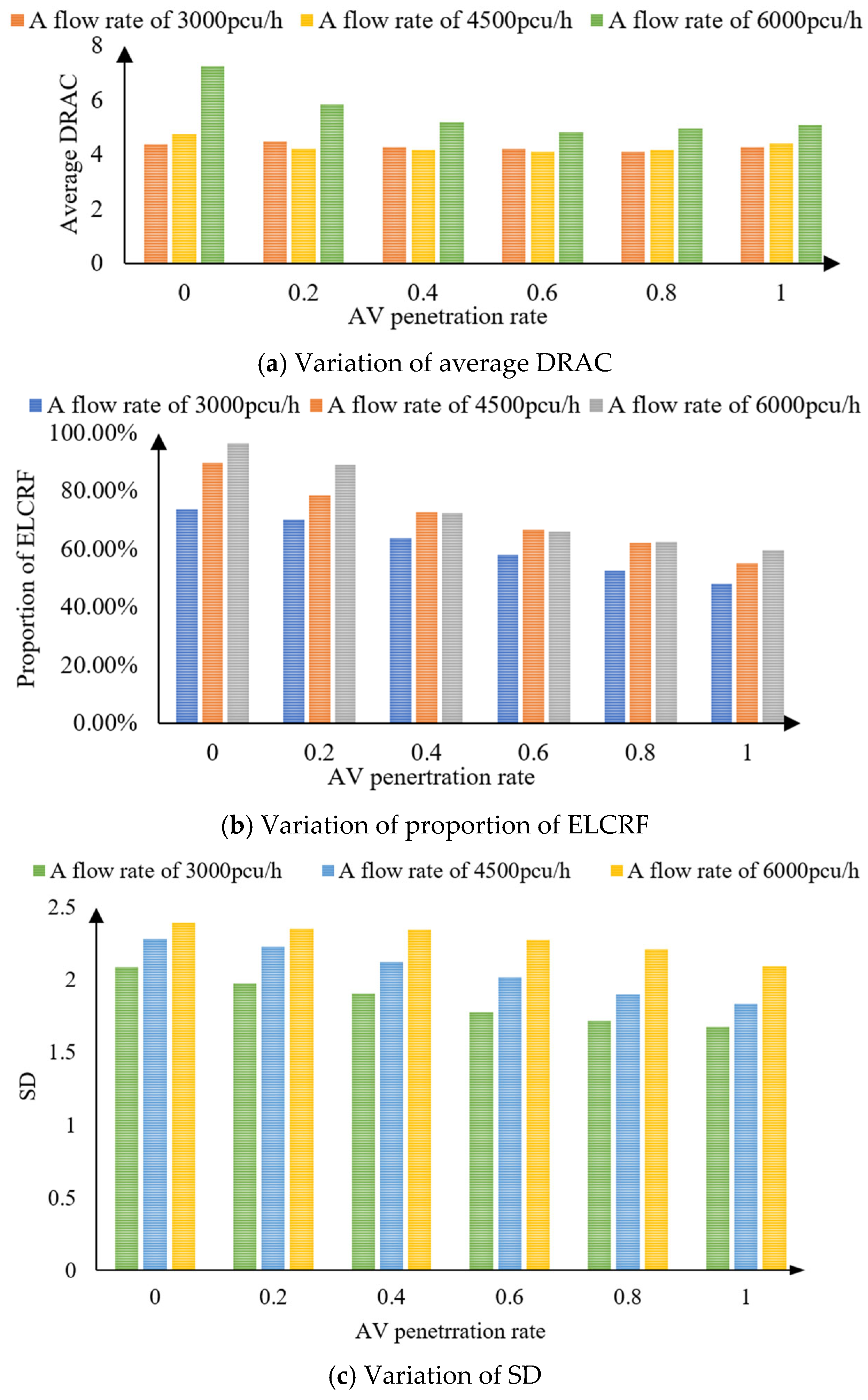
- Simulation results across various traffic scenarios indicated that increasing AV penetration rates generally lead to improved safety levels, especially under high traffic volumes. However, low AV penetration rates (less than 20%) introduce greater asymmetry, leading to unstable interactions between AVs and HDVs, which deteriorates safety. This conclusion provides valuable insight for the government to formulate the development policy of AV. Overall, the increase of flow rate and ramp flow ratio also will worsen traffic safety of mixed traffic. Therefore, necessary flow control measures under high flow and ramp flow ratio, such as ramp flow restriction and variable speed limited strategy, are very important to improve the safety of mixed traffic flow in merging areas.
- (4)
- Some valuable suggestions were put forward based on our findings, such as penetration-based strategies, flow control, V2X coordination technology, and improvement of the legal framework.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Accel | Acceleration |
| Decel | Deceleration |
| MinGap | Minimum gap |
| MaxSpeed | Maximum speed |
| Tau | Desired Time Headway (in seconds) |
Appendix A
| Scenarios | High Risk | Moderate Risk | Average Risk | Low Risk | Very Low Risk | Level |
|---|---|---|---|---|---|---|
| 3000/0.15/0.0 | 0 | 0.00002 | 0.16377 | 0.61964 | 0.21657 | 4 |
| 3000/0.15/0.2 | 0.00318 | 0.35547 | 0.24347 | 0.24461 | 0.15327 | 2 |
| 3000/0.15/0.4 | 0.0015 | 0.03613 | 0.30423 | 0.41743 | 0.24072 | 4 |
| 3000/0.15/0.6 | 0.0005 | 0.01256 | 0.43888 | 0.38292 | 0.16513 | 3 |
| 3000/0.15/0.8 | 0.00021 | 0.01421 | 0.59663 | 0.13412 | 0.25483 | 3 |
| 3000/0.15/1.0 | 0.00009 | 0.00503 | 0.60781 | 0.16811 | 0.21896 | 3 |
| 3000/0.25/0.0 | 0 | 0.00014 | 0.27854 | 0.59576 | 0.12556 | 4 |
| 3000/0.25/0.2 | 0.00209 | 0.04986 | 0.28575 | 0.52193 | 0.14036 | 4 |
| 3000/0.25/0.4 | 0.00033 | 0.00827 | 0.31954 | 0.52778 | 0.14408 | 4 |
| 3000/0.25/0.6 | 0.00007 | 0.00195 | 0.44700 | 0.40221 | 0.14877 | 3 |
| 3000/0.25/0.8 | 0.00001 | 0.00099 | 0.36416 | 0.50751 | 0.12733 | 4 |
| 3000/0.25/1.0 | 0 | 0.00522 | 0.71193 | 0.16141 | 0.12144 | 3 |
| 3000/0.35/0.0 | 0 | 0.28342 | 0.17826 | 0.40689 | 0.13143 | 4 |
| 3000/0.35/0.2 | 0.00319 | 0.35659 | 0.37505 | 0.01958 | 0.24558 | 3 |
| 3000/0.35/0.4 | 0.00097 | 0.30737 | 0.37015 | 0.1326 | 0.18890 | 3 |
| 3000/0.35/0.6 | 0.00008 | 0.28770 | 0.32532 | 0.25251 | 0.13439 | 3 |
| 3000/0.35/0.8 | 0 | 0.29621 | 0.31606 | 0.17715 | 0.21057 | 3 |
| 3000/0.35/1.0 | 0 | 0.30443 | 0.28951 | 0.25170 | 0.15436 | 2 |
| 4500/0.15/0.0 | 0.00035 | 0.44018 | 0.08797 | 0.22665 | 0.24485 | 2 |
| 4500/0.15/0.2 | 0.02067 | 0.42374 | 0.20735 | 0.22681 | 0.12144 | 2 |
| 4500/0.15/0.4 | 0.02193 | 0.42266 | 0.27557 | 0.1559 | 0.12395 | 2 |
| 4500/0.15/0.6 | 0.01644 | 0.14298 | 0.18593 | 0.51057 | 0.14408 | 4 |
| 4500/0.15/0.8 | 0.13135 | 0.14358 | 0.17496 | 0.54372 | 0.00639 | 4 |
| 4500/0.15/1.0 | 0.13266 | 0.14318 | 0.27239 | 0.44731 | 0.00445 | 4 |
| 4500/0.25/0.0 | 0.22937 | 0.17892 | 0.11608 | 0.45739 | 0.01824 | 4 |
| 4500/0.25/0.2 | 0.02271 | 0.38159 | 0.20784 | 0.38785 | 0 | 4 |
| 4500/0.25/0.4 | 0.01868 | 0.16119 | 0.41312 | 0.40700 | 0 | 3 |
| 4500/0.25/0.6 | 0.13750 | 0.14314 | 0.25321 | 0.46602 | 0.00013 | 4 |
| 4500/0.25/0.8 | 0.01038 | 0.26100 | 0.19541 | 0.46885 | 0.06436 | 4 |
| 4500/0.25/1.0 | 0.10910 | 0.13955 | 0.24762 | 0.50205 | 0.00168 | 4 |
| 4500/0.35/0.0 | 0.16097 | 0.24637 | 0.24687 | 0.34578 | 0 | 4 |
| 4500/0.35/0.2 | 0.14461 | 0.27399 | 0.27376 | 0.30763 | 0 | 4 |
| 4500/0.35/0.4 | 0.14014 | 0.14304 | 0.42543 | 0.29139 | 0 | 3 |
| 4500/0.35/0.6 | 0.02140 | 0.25990 | 0.37050 | 0.34820 | 0 | 3 |
| 4500/0.35/0.8 | 0.01635 | 0.26216 | 0.28084 | 0.44023 | 0.00042 | 4 |
| 4500/0.35/1.0 | 0.13101 | 0.14227 | 0.20379 | 0.52224 | 0.00069 | 4 |
| 6000/0.15/0.0 | 0.01047 | 0.38381 | 0.03276 | 0.57277 | 0.00019 | 4 |
| 6000/0.15/0.2 | 0.02237 | 0.53419 | 0.01905 | 0.42259 | 0.00181 | 2 |
| 6000/0.15/0.4 | 0.02931 | 0.51709 | 0.08923 | 0.36436 | 0 | 2 |
| 6000/0.15/0.6 | 0.02577 | 0.25683 | 0.28684 | 0.43051 | 0.00005 | 4 |
| 6000/0.15/0.8 | 0.13423 | 0.14492 | 0.19867 | 0.51818 | 0.00401 | 4 |
| 6000/0.15/1.0 | 0.12749 | 0.12628 | 0.33425 | 0.35687 | 0.0551 | 4 |
| 6000/0.25/0.0 | 0.02844 | 0.37918 | 0.03713 | 0.46801 | 0.08725 | 4 |
| 6000/0.25/0.2 | 0.05307 | 0.36489 | 0.26895 | 0.31309 | 0 | 2 |
| 6000/0.25/0.4 | 0.15941 | 0.27115 | 0.28626 | 0.28318 | 0 | 3 |
| 6000/0.25/0.6 | 0.16700 | 0.29141 | 0.25791 | 0.28368 | 0 | 2 |
| 6000/0.25/0.8 | 0.15194 | 0.13261 | 0.42665 | 0.28879 | 0 | 3 |
| 6000/0.25/1.0 | 0.15115 | 0.13330 | 0.31989 | 0.39459 | 0.00107 | 4 |
| 6000/0.35/0.0 | 0.11851 | 0.28892 | 0.03941 | 0.43323 | 0.11993 | 4 |
| 6000/0.35/0.2 | 0.13783 | 0.29523 | 0.28214 | 0.28480 | 0 | 2 |
| 6000/0.35/0.4 | 0.14085 | 0.26386 | 0.31172 | 0.28356 | 0 | 3 |
| 6000/0.35/0.6 | 0.14439 | 0.21567 | 0.35317 | 0.28677 | 0 | 3 |
| 6000/0.35/0.8 | 0.13301 | 0.1446 | 0.28998 | 0.42897 | 0.00344 | 4 |
| 6000/0.35/1.0 | 0.13327 | 0.14402 | 0.31009 | 0.39225 | 0.02038 | 4 |
References
- Mergia, W.Y.; Eustace, D.; Chimba, D.; Qumsiyeh, M. Exploring factors contributing to injury severity at freeway merging and diverging locations in Ohio. Accid. Anal. Prev. 2013, 55, 202–210. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Lei, L.; Bao, Y.; Wang, L. Research on safety and traffic efficiency of mixed traffic flows in the converging section of a super-freeway ramp. Sustainability 2022, 14, 13234. [Google Scholar] [CrossRef]
- Chen, P.; Ni, H.; Wang, L.; Yu, G.; Sun, J. Safety performance evaluation of freeway merging areas under autonomous vehicles environment using a co-simulation platform. Accid. Anal. Prev. 2024, 199, 107530. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Aty, M.; Ding, S. A matched case-control analysis of autonomous vs human-driven vehicle accidents. Nat. Commun. 2024, 15, 4931. [Google Scholar] [CrossRef]
- Li, T.; Han, X.; Ma, J.; Ramos, M.; Lee, C. Operational safety of automated and human driving in mixed traffic environments: A perspective of car-following behavior. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2023, 237, 355–366. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Y. Driver-automated vehicle interaction in mixed traffic: Types of interaction and drivers’ driving styles. Hum. Factors J. Hum. Factors Ergon. Soc. 2024, 66, 544–561. [Google Scholar] [CrossRef]
- Zhu, J.; Gao, K.; Li, H.; He, Z.; Monreal, C.O. Bi-level ramp merging coordination for dense mixed traffic conditions. Fundam. Res. 2024, 4, 992–1008. [Google Scholar] [CrossRef]
- Zhu, J.; Ma, Y.; Lou, Y. Multi-vehicle interaction safety of connected automated vehicles in merging area: A real-time risk assessment approach. Accid. Anal. Prev. 2022, 166, 106546. [Google Scholar] [CrossRef]
- Morando, M.M.; Tian, Q.; Truong, L.T.; Vu, H.L. Studying the safety impact of autonomous vehicles using simulation-based surrogate safety measures. J. Adv. Transp. 2018, 2018, 6135183. [Google Scholar] [CrossRef]
- Papadoulis, A.; Imprialou, M.; Feng, Y.; Quddus, M. Simulating and modelling the safety impact of connected and autonomous vehicles in mixed traffic: Platoon size, sensor error, and path choice. Machines 2024, 12, 371. [Google Scholar] [CrossRef]
- Fu, C.; Sayed, T. Multivariate Bayesian hierarchical Gaussian copula modeling of the non-stationary traffic conflict extremes for crash estimation. Anal. Methods Accid. Res. 2021, 29, 100154. [Google Scholar] [CrossRef]
- Sinha, A.; Chand, S.; Wijayaratna, K.P.; Virdi, N.; Dixit, V. Comprehensive safety assessment in mixed fleets with connected and automated vehicles: A crash severity and rate evaluation of conventional vehicles. Accid. Anal. Prev. 2020, 142, 105567. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Xie, Y.; Huang, H.; Liu, P. A review of surrogate safety measures and their applications in connected and automated vehicles safety modeling. Accid. Anal. Prev. 2021, 157, 106157. [Google Scholar] [CrossRef] [PubMed]
- Behbahani, H.; Hosseini, S.M.; Taherkhani, A.; Asadi, H.; Samerei, S.A. Proposing new methods to estimate the safety level in different parts of freeway interchanges. Adv. Civ. Eng. 2018, 2018, 8702854. [Google Scholar] [CrossRef]
- Zhu, J.; Tasic, I. Safety analysis of freeway on-ramp merging with the presence of autonomous vehicles. Accid. Anal. Prev. 2021, 152, 105966. [Google Scholar] [CrossRef]
- Wang, C.; Xu, C.; Xia, J.; Qian, Z.; Lu, L. A combined use of microscopic traffic simulation and extreme value methods for traffic safety evaluation. Transp. Res. Part C Emerg. Technol. 2018, 90, 281–291. [Google Scholar] [CrossRef]
- Yao, Z.; Hu, R.; Jiang, Y.; Xu, T. Stability and safety evaluation of mixed traffic flow with connected automated vehicles on expressways. J. Saf. Res. 2020, 75, 262–274. [Google Scholar] [CrossRef]
- Jiang, Y.; Ren, T.; Ma, Y.; Wu, Y.; Yao, Z. Traffic safety evaluation of mixed traffic flow considering the maximum platoon size of connected automated vehicles. Phys. A Stat. Mech. Its Appl. 2023, 612, 128452. [Google Scholar] [CrossRef]
- Garg, M.; Bouroche, M. Can connected autonomous vehicles improve mixed traffic safety without compromising efficiency in realistic scenarios? IEEE Trans. Intell. Transp. Syst. 2023, 24, 6674–6689. [Google Scholar] [CrossRef]
- He, Y.; Kong, Y. Traffic impact analysis of expressway accident in mixed traffic environment of connected and autonomous considering multi-factor coupling. IEEE Access 2025, 13, 57342–57353. [Google Scholar] [CrossRef]
- Hu, X.; Huang, M.; Guo, J. Feature analysis on mixed traffic flow of manually driven and autonomous vehicles based on cellular automata. Math. Probl. Eng. 2020, 2020, 7210547. [Google Scholar] [CrossRef]
- Kong, D.; Sun, L.; Chen, Y. Traffic dynamics around freeway merging area with mixed conventional vehicles and connected and autonomous vehicles. Int. J. Mod. Phys. C 2022, 33, 2250128. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, L.; Wang, X.; Jiang, C.; Ye, N. Operational characteristics of mixed-autonomy traffic flow on the freeway with on- and off-ramps and weaving sections: An rl-based approach. IEEE Trans. Intell. Transp. Syst. 2021, 23, 13512–13525. [Google Scholar] [CrossRef]
- Das, T.; Samandar, M.S.; Rouphail, N. Longitudinal traffic conflict analysis of autonomous and traditional vehicle platoons in field tests via surrogate safety measures. Accid. Anal. Prev. 2022, 177, 106822. [Google Scholar] [CrossRef]
- Zheng, L.; Ismail, K.; Sayed, T.; Fatema, T. Bivariate extreme value modeling for road safety estimation. Accid. Anal. Prev. 2018, 120, 83–91. [Google Scholar] [CrossRef]
- Wu, H. Safety Evaluation of Railway Passenger Transport Based on Improved CRITIC Cloud Model. Railw. Transp. Econ. 2024, 46, 207–214+222. [Google Scholar]
- Liu, H.; He, Y. Comprehensive Evaluation of Resilience for Qinling Tunnel Group Operation Safety System Based on Combined Weighting and Cloud Model. Sustainability 2024, 16, 3937. [Google Scholar] [CrossRef]
- Vuong, X.C.; Mou, R.F.; Vu, T.T.; Tran, V.H.; Nguyen, C.T. A safety evaluation model of intersections under mixed traffic conditions using traffic conflicts and cloud model. J. Adv. Transp. 2021, 2021, 5899673. [Google Scholar] [CrossRef]
- Sharma, A. Analyzing Crash Potential in Mixed Traffic with Autonomous and Human-Driven Vehicles. Master’s Thesis, Texas A&M University, San Antonio, TX, USA, 2019. [Google Scholar]
- Cheng, G.; Meng, F.; Lv, J.; Chen, Y.; Xi, C. Dynamic Zonal Modeling and Connectivity: Enhancing Safety and Efficiency in Merging Zones. Phys. A Stat. Mech. Appl. 2025, 664, 130470. [Google Scholar] [CrossRef]
- Arun, A.; Haque, M.; Washington, S.; Sayed, T.; Mannering, F. How many are enough?: Investigating the effectiveness of multiple conflict indicators for crash frequency-by-severity estimation by automated traffic conflict analysis. Transp. Res. Part C Emerg. Technol. 2022, 138, 103653. [Google Scholar] [CrossRef]
- Ramezanı-khansarı, E.; Nejad, F.M.; Moogeh, S. Comparing time to collision and time headway as safety criteria. Pamukkale Univ. J. Eng. Sci. 2020, 27, 669–675. [Google Scholar] [CrossRef]
- Amirgholy, M.; Yang, J.J. Decision Making and Policy Analysis in Transportation Planning; MDPI: Basel, Switzerland, 2024. [Google Scholar]
- Dong, G.; Chen, C.; Xia, H. Safety Evaluation of Road Passenger Transportation Process by Fuzzy Comprehensive Evaluation Method and Entropy Value Method. In Recent Developments in Mechatronics and Intelligent Robotics; Springer: Singapore, 2020; pp. 671–678. [Google Scholar]
- Ortíz, M.A.; Cómbita, J.P.; De la Hoz, Á.A.; De Felice, F.; Petrillo, A. An integrated approach of AHP-DEMATEL methods applied for the selection of allied hospitals in outpatient service. Int. J. Med. Eng. Inform. 2016, 8, 87. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Shen, F.; Jin, J. A novel classification approach based on integrated connection cloud model and game theory. Commun. Nonlinear Sci. Numer. Simul. 2021, 93, 105540. [Google Scholar] [CrossRef]
- Nayak, J.; Naik, B.; Behera, H.S. Fuzzy C-means (FCM) clustering algorithm: A decade review from 2000 to 2014. In Computational Intelligence in Data Mining—Volume 2: Proceedings of the International Conference on CIDM, 20–21 December 2014; Springer: New Delhi, India, 2015; pp. 133–149. [Google Scholar]
- Zeng, Y.; Wu, B.; Tian, N. Risk Assessment of Power Monitoring System Based on Cloud Model and Improved Evidence Theory. Comput. Syst. Appl. 2022, 31, 55–63. [Google Scholar]
- CJJ37-2012; Design Code for Urban Expressways. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- He, Y.; Xiang, D.; Wang, D. Traffic safety evaluation of emerging mixed traffic flow at freeway merging area considering driving behavior. Sci. Rep. 2025, 15, 10686. [Google Scholar] [CrossRef]
- Pang, M.S. Analysis and Control of Traffic Flow in the Connected Autonomous Driving Environment. Master’s Thesis, Shanghai Institute of Technology, Shanghai, China, 2023. [Google Scholar]
- Pelizza, A.; Orsini, F.; Yilmaz-Niewerth, S.; Rossi, R.; Friedrich, B. Exploring the impact of automated vehicles lane-changing behavior on urban network efficiency. In Proceedings of the 2023 8th International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Nice, France, 14–16 June 2023; pp. 1–6. [Google Scholar]
- Mintsis, E.; Koutras, D.; Porfyri, K.; Mitsakis, E.; Lücken, L.; Erdmann, J.; Flötteröd, Y.; Alms, R.; Rondinone, M.; Maerivoet, S.; et al. TransAID Deliverable 3.1—Modelling, Simulation and Assessment of Vehicle Automations and Automated Vehicles’ Driver Behaviour in Mixed Traffic—Iteration 2. Available online: https://elib.dlr.de/132647/ (accessed on 12 December 2019).
- Ding, Z.; Wu, H.; Sun, Y. Research on Time Headway Mixture Distribution Model Based on YOLOv5 + DeepSORT Detection Data. Meas. Control. Technol. 2023, 42, 56–64. [Google Scholar]
- Ma, Q.L.; Fu, B.Y.; Zeng, H.W. Fundamental diagram and stability analysis of heterogeneous traffic flow in a connected and autonomous environment. J. Transp. Inf. Saf. 2021, 39, 76–84. [Google Scholar]
- Lee, H.; Park, S.H.; Kang, M. A safety analysis based on evaluation indicators of mixed traffic flow. J. Korea Inst. Intell. Transp. Syst. 2024, 23, 42–60. [Google Scholar] [CrossRef]





| Indicator | Types of SSMs | Dimension | Scale | Time-Space | |||||
|---|---|---|---|---|---|---|---|---|---|
| Time-Based | Deceleration-Based | Energy Based | Longitudinal Dynamics | Lateral Dynamics | Macro-Level | Micro-Level | Temporal | Spatial | |
| MTTC | ✓ | ✓ | ✓ | ✓ | |||||
| LCTTC | ✓ | ✓ | ✓ | ✓ | |||||
| DRAC | ✓ | ✓ | ✓ | ✓ | |||||
| SD | ✓ | ✓ | |||||||
| Headway | ✓ | ✓ | ✓ | ✓ | |||||
| ELCRF | ✓ | ✓ | ✓ | ✓ | |||||
| Parameter | HDV | AV |
|---|---|---|
| Accel (m/s2) | 3 | 2.9 |
| Decel (m/s2) | 4 | 7.5 |
| MinGap (m) | 2 | 1.5 |
| MaxSpeed (main line) (m/s) | 22.2 | 22.2 |
| MaxSpeed (ramp) (m/s) | 11.1 | 11.1 |
| Tau (s) | 1.5 | 0.6 |
| Parameter | HDV | AV |
|---|---|---|
| LcKeepright | 1 | 1 |
| LcStrategic | 1 | 1 |
| LcCooperative | 1 | 0.9 |
| LcSpeedgain | 1 | 1 |
| Indicator | Objective Weight | Subjective Weight | Comprehensive Weight |
|---|---|---|---|
| SD | 0.076119 | 0.1477 | 0.126219 |
| MTTC | 0.033229 | 0.1887 | 0.142044 |
| Headway | 0.136975 | 0.1739 | 0.162819 |
| ELCRF | 0.575076 | 0.1580 | 0.283162 |
| LCTTC | 0.125701 | 0.1497 | 0.165105 |
| DRAC | 0.052900 | 0.1820 | 0.120651 |
| Index | High Risk | Moderate Risk | Average Risk | Low Risk | Very Low Risk |
|---|---|---|---|---|---|
| SD | (0.1946, 0.0550, 0.0055) | (0.3806, 0.0562, 0.0056) | (0.6088, 0.0454, 0.0045) | (0.7356, 0.0361, 0.0036) | (0.8806, 0.0493, 0.0049) |
| MTTC | (0.2300, 0.0721, 0.0072) | (0.4781, 0.0610, 0.0061) | (0.6785, 0.0469, 0.0047) | (0.8302, 0.0377, 0.0038) | (0.9522, 0.0309, 0.0031) |
| Headway | (0.2450, 0.0470, 0.0047) | (0.3408, 0.0319, 0.0032) | (0.5034, 0.0497, 0.0050) | (0.6514, 0.0497, 0.0050) | (0.9536, 0.0649, 0.0065) |
| ELCRF | (0.0000, 0.0024, 0.0002) | (0.3288, 0.0233, 0.0023) | (0.5000, 0.0044, 0.0004) | (0.6706, 0.0215, 0.0022) | (1.0000, 0.0016, 0.0002) |
| DRAC | (0.0059, 0.0195, 0.0020) | (0.1640, 0.0348, 0.0035) | (0.3580, 0.0685, 0.0068) | (0.5942, 0.0662, 0.0066) | (0.9908, 0.0376, 0.0038) |
| LCTTC | (0.1102, 0.0455, 0.0046) | (0.2587, 0.0454, 0.0045) | (0.4329, 0.0521, 0.0052) | (0.6368, 0.0605, 0.0061) | (0.8769, 0.0671, 0.0067) |
| Index | Evaluation Cloud Model |
|---|---|
| SD | (0.43782, 0.04932, 0.00493) |
| MTTC | (0.70533, 0.03085, 0.00309) |
| Headway | (0.35217, 0.06493, 0.00649) |
| ELCRF | (0.7799, 0.00157, 0.00016) |
| DRAC | (0.25507, 0.03762, 0.00376) |
| LCTTC | (0.36644, 0.06712, 0.00671) |
| Level | High Risk | Moderate Risk | Average Risk | Low Risk | Very Low Risk |
|---|---|---|---|---|---|
| Membership degree | 0.13783 | 0.29523 | 0.28214 | 0.2848 | 0 |
| Scenarios | Level | Scenarios | Level | Scenarios | Level |
|---|---|---|---|---|---|
| 3000/0.15/0.0 | 4 | 3000/0.25/0.0 | 4 | 3000/0.35/0.0 | 4 |
| 3000/0.15/0.2 | 2 | 3000/0.25/0.2 | 4 | 3000/0.35/0.2 | 3 |
| 3000/0.15/0.4 | 4 | 3000/0.25/0.4 | 4 | 3000/0.35/0.4 | 3 |
| 3000/0.15/0.6 | 3 | 3000/0.25/0.6 | 3 | 3000/0.35/0.6 | 3 |
| 3000/0.15/0.8 | 3 | 3000/0.25/0.8 | 4 | 3000/0.35/0.8 | 3 |
| 3000/0.15/1.0 | 3 | 3000/0.25/1.0 | 3 | 3000/0.35/1.0 | 2 |
| 4500/0.15/0.0 | 2 | 4500/0.25/0.0 | 4 | 4500/0.35/0.0 | 4 |
| 4500/0.15/0.2 | 2 | 4500/0.25/0.2 | 4 | 4500/0.35/0.2 | 4 |
| 4500/0.15/0.4 | 2 | 4500/0.25/0.4 | 3 | 4500/0.35/0.4 | 3 |
| 4500/0.15/0.6 | 4 | 4500/0.25/0.6 | 4 | 4500/0.35/0.6 | 3 |
| 4500/0.15/0.8 | 4 | 4500/0.25/0.8 | 4 | 4500/0.35/0.8 | 4 |
| 4500/0.15/1.0 | 4 | 4500/0.25/1.0 | 4 | 4500/0.35/1.0 | 4 |
| 6000/0.15/0.0 | 4 | 6000/0.25/0.0 | 4 | 6000/0.35/0.0 | 4 |
| 6000/0.15/0.2 | 2 | 6000/0.25/0.2 | 2 | 6000/0.35/0.2 | 2 |
| 6000/0.15/0.4 | 2 | 6000/0.25/0.4 | 3 | 6000/0.35/0.4 | 3 |
| 6000/0.15/0.6 | 4 | 6000/0.25/0.6 | 2 | 6000/0.35/0.6 | 3 |
| 6000/0.15/0.8 | 4 | 6000/0.25/0.8 | 3 | 6000/0.35/0.8 | 4 |
| 6000/0.15/1.0 | 4 | 6000/0.25/1.0 | 4 | 6000/0.35/1.0 | 4 |
| Method | Scenarios | High Risk | Moderate Risk | Average Risk | Low Risk | Very Low Risk | FCM Method |
|---|---|---|---|---|---|---|---|
| FCM method | 6000/0.15/0.0 | 0 | 0.28273 | 0.33944 | 0.18135 | 0.19648 | average risk |
| Cloud model | 0.01047 | 0.38381 | 0.03276 | 0.57277 | 0.00019 | low risk | |
| FCM method | 6000/0.15/0.2 | 0 | 0.41587 | 0.27713 | 0.09430 | 0.21270 | moderate risk |
| Cloud model | 0.02237 | 0.53419 | 0.01905 | 0.42259 | 0.00181 | moderate risk | |
| FCM method | 6000/0.15/0.4 | 0 | 0.36460 | 0.36382 | 0.17739 | 0.09418 | moderate risk |
| Cloud model | 0.02931 | 0.51709 | 0.08923 | 0.36436 | 0 | moderate risk | |
| FCM method | 6000/0.15/0.6 | 0 | 0.37520 | 0.26329 | 0.28351 | 0.07799 | moderate risk |
| Cloud model | 0.02577 | 0.25683 | 0.28684 | 0.43051 | 0.00005 | low risk | |
| FCM method | 6000/0.15/0.8 | 0.12807 | 0.30368 | 0.16393 | 0.40432 | 0 | low risk |
| Cloud model | 0.13423 | 0.14492 | 0.19867 | 0.51818 | 0.00401 | low risk | |
| FCM method | 6000/0.15/1.0 | 0.28300 | 0.10035 | 0.27155 | 0.31174 | 0.03336 | low risk |
| Cloud model | 0.12749 | 0.12628 | 0.33425 | 0.35687 | 0.0551 | low risk |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Xia, J. Comprehensive Evaluation on Traffic Safety of Mixed Traffic Flow in a Freeway Merging Area Based on a Cloud Model: From the Perspective of Traffic Conflict. Symmetry 2025, 17, 855. https://doi.org/10.3390/sym17060855
He Y, Xia J. Comprehensive Evaluation on Traffic Safety of Mixed Traffic Flow in a Freeway Merging Area Based on a Cloud Model: From the Perspective of Traffic Conflict. Symmetry. 2025; 17(6):855. https://doi.org/10.3390/sym17060855
Chicago/Turabian StyleHe, Yaqin, and Jun Xia. 2025. "Comprehensive Evaluation on Traffic Safety of Mixed Traffic Flow in a Freeway Merging Area Based on a Cloud Model: From the Perspective of Traffic Conflict" Symmetry 17, no. 6: 855. https://doi.org/10.3390/sym17060855
APA StyleHe, Y., & Xia, J. (2025). Comprehensive Evaluation on Traffic Safety of Mixed Traffic Flow in a Freeway Merging Area Based on a Cloud Model: From the Perspective of Traffic Conflict. Symmetry, 17(6), 855. https://doi.org/10.3390/sym17060855





