K-Means Clustering for Portfolio Optimization: Symmetry in Risk–Return Tradeoff, Liquidity, Profitability, and Solvency

Abstract

In order to evaluate the impact of k-means clustering on portfolio optimization, this study groups enterprises based on profitability, liquidity, and solvency indicators. The study confirms the positive correlation between risk, return, and risk-adjusted performance through an analysis of historical financial records. After the companies were divided into two groups, equal-weighted portfolios were created using these groupings. Although they produced higher returns, cluster 1 portfolios, which included more risky companies, also showed more volatility. Cluster 0 portfolios, on the other hand, offered less risk and more consistent results. Portfolios clustered by ROA, OCFM, and GPM outperformed the market benchmark and produced the highest returns adjusted for risk, according to Sharpe Ratio analysis. Furthermore, the study emphasizes that although solvency and liquidity metrics play a role in portfolio selection, increased liquidity does not always translate into improved risk-adjusted performance. In terms of methodology, Silhouette Analysis outperformed the Elbow technique in determining the optimal number of clusters. All things considered, the results show how data-driven clustering techniques may be used to align portfolio strategies to investors’ risk tolerances.

1. Introduction

The ongoing challenge for contemporary portfolio creation is the investors’ inability to differentiate between noise-driven price correlations and fundamentals-driven co-movements. Any portfolio manager should have diversification in their toolset since it can lower risk (as indicated by volatility) by spreading it throughout several asset classes and industries while simultaneously improving risk-adjusted returns. Diversity can significantly reduce unique hazards while still exposing investors to market risk, even if it is not the most effective risk-reduction tactic. A fundamental component of contemporary mean-variance portfolio theory is diversification [1,2]. An investor can identify an efficient frontier which offers the best expected return for any given amount of total (portfolio) variance by combining assets for which anticipated profits (means) and return volatilities (variances) are imperfectly connected. This is effective in practice because total risk breaks down into two categories: (i) systematic risk, which is influenced by common market characteristics and cannot be eliminated by diversification, and (ii) unsystematic (idiosyncratic) risk, which may be reduced by holding many assets from various industries and asset classes. Therefore, constructing a well-diversified portfolio requires choosing assets with minimal or negative pair-wise correlations (or, more formally, with small covariances Σ_ij, which are the off-diagonal components that define each asset’s marginal contribution to portfolio variance). Diversification may substantially decrease the unsystematic component and enhance investors’ risk-adjusted performance, as measured by metrics like the Sharpe Ratio, even if it cannot entirely eradicate systematic risk. Traditionally, choosing assets with a low Pearson’s correlation coefficient is how portfolio diversification is achieved. To the best of our knowledge, this is the first empirical study that creates equity portfolios entirely without the use of historical return correlations, employing k-means clusters formed from solvency, liquidity, and profitability ratios.

Machine learning (ML) will be used to extract information from the analyzed ratios. According to the Council of Europe, artificial intelligence (AI) and, by extension, machine learning, which have their roots in the 1950s, made an appearance in the 2010s [3] due to access to big datasets and increases in processing power generated by new technologies. In an ever-changing financial climate, individuals who do not adapt and use the latest technology are at a major disadvantage to those who do. As a result, a subset of AI-ML was used to cluster stock market corporations based on profitability financial ratios. This methodology aims to test an innovative approach to stock selection and portfolio diversification that, in contrast to the correlation method, takes into account the underlying companies’ price swings and fundamentals. A scalable screening tool that can be automated to instantly match portfolio risk characteristics with particular client mandates is offered to asset managers by the suggested workflow. The strategy will therefore concentrate on norms related to profitability, liquidity, and solvency. Because investors anticipate returns on their investment, whether in the form of dividends, buybacks of stock, or increased stock prices, investors put money into businesses.

Although sector distribution and mean-variance optimization, two conventional diversification techniques, have long been essential tools in portfolio design, they have inherent drawbacks. These techniques frequently depend on oversimplifying assumptions that might not adequately represent the intricate dynamics of financial markets, such as normally distributed outcomes and linear correlations. Furthermore, typical approaches have scalability issues and lose their effectiveness when dealing with big, high-dimensional datasets. Machine learning provides a useful substitute in this situation. Large volumes of data can be effectively processed using ML approaches, allowing for more complex analyses free from the limitations of manual feature selection. Among these, clustering techniques are especially helpful because they can reveal hidden links and patterns in data that are difficult to see using conventional techniques. Clustering identifies novel patterns and connections that might not be visible in conventional diversification models by grouping assets according to inherent similarities found through data-driven evaluation. Adaptability is an additional advantage of machine learning techniques. In contrast to conventional diversification methods, which are based on set assumptions, ML algorithms are able to continuously adapt to new data, capturing evolving market dynamics and new trends. Beyond enhancing the diversification process, this ability presents opportunities to extract new insights from the data itself, resulting in more resilient and flexible portfolio strategies.

By showing how an unsupervised algorithm may convert financial indicators into investable signals that outperform conventional benchmarks, our results contribute to the expanding body of research on machine learning in finance. While analyzing massive datasets, machine learning has a clear advantage over conventional methods of analysis since it can uncover hidden patterns that could otherwise go overlooked. The versatility of machine learning approaches is demonstrated by this study, which focuses on structured data but also can be applied to unstructured data. Didur [4] asserts that machine learning’s main advantage is its capacity to draw lessons from the past and generate insights without the need for explicit programming to achieve particular results. K-means clustering, an unsupervised learning technique, is used in this work to find inherent symmetries in the data structures that human analysts could miss. This approach makes it possible to assess performance in reference to both individual firms and the larger market portfolio by methodically combining companies into clusters. The paper extends Markowitz’s mean-variance concept into a fundamentals-anchored, machine learning context by tying cluster membership to ex post Sharpe Ratios. This technique’s analytical framework, the dataset it uses, and the variety of financial criteria it examines make it special. This study shows how machine learning can reveal basic equilibria inside intricate finance systems by highlighting the natural structural patterns in financial data.

2. Literature Review

2.1. Theoretical Underpinning

Modern portfolio selection originates with Markowitz’s (1952) [1] mean-variance framework, where the efficient frontier illustrates how optimal diversification lowers total variance for a given expected return. Furthermore, Markowitz’s paradigm separates systematic and idiosyncratic components of total variance, emphasizing that only the latter should be given preference. This insight is further refined by successive asset-pricing models: the Arbitrage Pricing Theory allows several latent factors [5], whereas the single-factor CAPM prices excess returns by market beta. Empirical extensions like the Hou et al. (2021) q-factor model [6] and the Fama–French (2015) five-factor [7] model identify specific profitability, investment, and growth premia. Efficient-Market Theory (Fama, 1970 [8]) is an alternative paradigm that asserts that short-term price movements essentially follow random patterns because publicly available information becomes imprisoned in prices so quickly. Investors are only rewarded for taking on systematic risk under the semi-strong variant of the EMH; they are not able to generate exceptional profits by forecasting those changes. Consequently, instead of focusing on market timing, optimal portfolios emphasize the allocation of factor exposures, such as profitability, liquidity, and solvency. This perspective is completely supported by grouping companies according to their associated financial-sheet ratios, which structure the cross-section of assets into latent factor portfolios whose predicted returns are in line with multi-factor asset-pricing theory rather than attempting to forecast price pathways. Leverage metrics function as a substitute for distress-related issues, current and quick ratios show exposure to liquidity risk, and profit margins and ROE capture the profitability premium. All of these financial-statement ratios map nicely onto the priced sources of risk. A clustering technique that groups by the ratios efficiently constructs hidden factor portfolios since companies with comparable values on these ratios have similar systematic exposures.

K-means offers a model-free method for generating these kinds of groups. Following z-score standardization, it divides businesses into groups based on the minimal within-group Euclidean distance, resulting in collections with consistent patterns of profitability, liquidity, and solvency. Asset-pricing theory can be empirically verified by plotting these cluster portfolios on the return–volatility plane. Clusters that are on or above the ex ante efficient frontier show that data-driven factor formation can match or surpass the efficiency attained by standard, predefined factors.

Therefore, grouping companies based on these balance-sheet ratios can be viewed as creating latent factor portfolios that mimic the linear-factor structure while incorporating non-linear interactions that machine learning has revealed.

2.2. Empirical Evidence

Several research studies have used panel data regression analysis to look at the connection between stock prices and profitability ratios. In their 2017 study, Mirgen et al. [9] analyzed the effects of several profitability metrics on stock prices in the Istanbul Stock Exchange 100 index from 2012 to 2017. These metrics included Gross Profit Margin (GPM), the Operating Profit Margin (OPM), Net Profit Margin (NPM), Return on Assets (ROA), and Return on Equity (ROE). Based on their research, there is a positive linear relationship between NPM and stock prices; for every 1% increase in NPM, stock prices climb by 1.32% to 1.86%.

Similarly, Alaagam [10] examined how 11 Saudi Arabian banks that were listed between 2011 and 2018 were affected by NPM, ROA, and ROE. There was a strong short-term positive relationship between ROA and stock prices, but no long-term correlation was discovered. A more targeted approach was used by Nalurita [11], who looked at ROA in conjunction with the Debt-to-Equity Ratio and the Price–Earnings Ratio in 38 construction, real estate, and property companies listed on the Indonesian Stock Exchange between 2010 and 2014. According to her research, stock returns may be predicted by combining these three ratios, even though ROA by itself only slightly increased returns.

To further study this subject, Nadyayani and Suarjaya [12] evaluated how ROA, ROE, and NPM affected stock returns in 105 manufacturing companies that were listed between 2017 and 2019 on the Indonesian Stock Exchange. According to their findings, stock returns had a beneficial effect by these ratios taken together. When analyzed separately, ROE showed a smaller, statistically negligible effect, but ROA and NPM both exhibited a considerable beneficial impact. Similar findings were reported by Wijaya [13], who examined 20 manufacturing firms from Indonesia’s Composite Index from 2008 to 2013 and found that ROA, both alone and in cooperation with other ratios, had the greatest impact on stock returns. On the other hand, Musallam [14] found no statistically significant relationship between stock returns and ROA, ROE, and NPM after analyzing 26 companies listed on the Qatari stock exchange between 2009 and 2015. Using financial ratios, Wijesundera et al. [15] evaluated the consistency of stock returns for 60 companies listed between 2004 and 2013 on the Colombo Stock Exchange. Though their results showed a strong positive correlation between ROE and stock returns, their explanatory power decreased when R-squared values were taken for consideration, indicating a weak predicting ability.

In the context of machine learning applications, a number of studies have examined the use of k-means clustering in stock price movements and return rates, including those by Guo [16], He et al. [17], and Zuhroh et al. [18]. Nevertheless, there are still not enough studies explicitly using k-means clustering to analyze financial profitability ratios. In order to improve the clustering process, Zuhroh et al. [18] suggested adding more variables, including market capitalization, transaction volume, and financial ratios. This study will build on their clustering of Indonesian banking sector stocks based on their monthly return rates. More recently, Li et al. (2024) [19] reported annualized alpha of 6.4% over the CSI 300 index by combining k-means with particle-swarm optimization to select high-Sharpe Ratio clusters in the Chinese A-share market.

Using neural networks and algorithms for optimization, recent developments in deep learning have brought more complex methods for risk assessment and stock market prediction. In order to identify long-term dependencies in stock market data, Zhang and Fill [20] recommend the TS-GRU model, which combines Temporal Convolutional Networks (TCN) with Gated Recurrent Units (GRU). By refining model parameters for better risk prediction, the approach is further improved through the use of the Sparrow search algorithm. Their research demonstrates how well neuro-inspired computation can capture intricate financial patterns, which is consistent with the growing application of AI-driven models in financial analysis. According to Zagrafopoulos et al. (2025) [21], non-linear machine learning models identify cross-factor interactions that linear regressions miss, especially those involving leverage and liquidity. To address challenges of economic viability in energy markets, Gailani et al. [22] investigated capacity market optimization using Li-ion battery deterioration models. Although the research focuses on market stability and energy storage, its fundamental ideas regarding computational modeling and financial risk assessment are comparable to those of stock market analysis. In addition to artificial intelligence clustering and forecasting methods, the combination of financial decision-making and degradation cost modeling offers insights into return estimates adjusted for risk.

In their research, Momeni et al.’s [23] k-means technique was to divide businesses from three industries listed on the Tehran Stock Exchange in 2012 into two groups: high-performing and low-performing organizations. Financial ratios chosen through expert interviews were used for the clustering; in descending order, the most important indicators were Return on Assets (ROA), Earnings Per Share (EPS), Return on Equity (ROE), Profit to Sales Ratio, and Operating Profit Margins.

Marvin [24] chose 229 NYSE and NASDAQ equities with data accessible from 2000 to 2015 in order to investigate statistical clustering as a strategy for stock diversification in the portfolio and risk mitigation. Stocks with the highest Sharpe Ratios from each cluster were selected for developing a portfolio benchmarked against the S&P 500 index using k-means clustering applied to ROA, Net Income to Assets, and price movements. Five to one hundred clusters with varying financial ratio weightings were tested in the study. The findings showed that, particularly prior to the economic meltdown, portfolios made up of high-Sharpe Ratio equities from clustered groups outperformed the broader benchmark and minimized idiosyncratic risk.

Bin [25] developed a more sophisticated clustering and portfolio development process, building on Marvin’s strategy. Using PCA-filtered solvency, liquidity, and profitability ratios for sectoral portfolio optimization, Dhingra et al. (2023) [26] arrive at comparable findings. In order to prevent clustering mistakes and market crash distortions, the study concentrated on the Q3 2009–Q3 2020 period, analyzing 114 S&P 500-listed companies with complete financial data through 2006–2020. Businesses that did not fit the requirements for data completeness were not included. The Silhouette method was used to determine the ideal number of clusters (k), and Bin [25] used similar financial ratios to Marvin [24] to separate clusters based on price movements. Then, from each cluster, the stocks with the greatest Sharpe Ratios were chosen to create proportionately weighted portfolios. In accordance with Bin’s research, portfolios built with financial ratio clustering routinely beat the market when compared to the S&P 500 index, whereas those built with price-movement clustering underperformed. However, a surprising tendency surfaced: when each cluster was proportionately represented, price-movement-based portfolios behaved better, although financial ratio-based portfolios outperformed worse when weighted by cluster sizes.

In out-of-sample evaluations, a solely ratio-based machine learning screen beats benchmark indices by more than 50%, according to a recent study by Tsai et al. (2023) [27]. The incorporation of advanced modeling of finances techniques, such as machine learning and reinforcement learning, has improved stock market analysis. Nti et al. [28] state that whereas technical analysis accounts for 66% of stock prediction research, fundamental analysis accounts for 23%, with combined approaches showing better forecast accuracy. Hung and Van [29] established the ability of machine learning, specifically gradient boosting, to identify significant financial parameters, such as income per share and debt-to-equity ratio, as predictors of stock performance in the Vietnamese market.

Wu et al. (2022) [30] and Delcea et al. (2020) [31] demonstrated the use of k-means clustering for maximizing stock portfolios based on trend consistency. Similarly, Ansari et al. [32] suggested a reinforcement learning technique that used historical data and financial indicators to exceed standards in backtesting. Almansour et al. [33] stressed the importance of financial proxies, such as book value per share, during the COVID-19 pandemic, arguing for adaptive models for dealing with market volatility.

Musallam [14] reiterated the variable predictive potential of financial ratios such as dividend yield and book to market ratio across industries, illustrating the importance of sector-specific analysis. Similarly, Atmariani and Agustia [34] discovered mixed effects of Return on Assets (ROA), Return on Equity (ROE), and Earnings per Share (EPS) on stock returns in Indonesia, emphasizing the need to diversify investment techniques. Hu et al. [35] examined the asymmetric effect of investor sentiment on stock returns, using a composite sentiment index and Markov-Switching methods to describe regime-dependent connections.

Research has additionally investigated how to optimize financial portfolios and how various factors affect their performance. Neutrosophic fuzzy numbers, for instance, have been investigated for modeling financial asset indicators of performance, offering a novel approach to assessing risk and return. The benefits of this strategy are illustrated by the study by Boloș et al. (2019) [36], which offers an accurate method for choosing the best portfolios and permits the classification of financial situations based on degrees of uncertainty [37]. The use of fuzzy logic algorithms has additionally demonstrated great promise in improving the choice of investments by enabling asset choosing based on the best possible balance between cost and economic performance [37].

Finally, advances in algorithmic trading strategies have been studied to improve decision-making and risk management. Reinforcement learning-based frameworks, such as those suggested by Ansari et al. [32], emphasize the necessity of creating reward functions like Portfolio-Sharpe-Returns (PSR) to incorporate risk and return dynamics into portfolio management. Collectively, these studies demonstrate the groundbreaking capacity of combining financial ratios, behavioral insights, and advanced computational models to optimize investing decisions and forecast stock market outcomes.

The literature review emphasizes the growing use of machine learning (ML) and artificial intelligence (AI) in financial modeling, especially in stock market portfolio optimization. The inability of traditional statistical models to capture intricate market dynamics has prompted the use of deep learning approaches for predictive modeling. Aldhyani and Alzahrani [38], for instance, show how AI can recognize complex patterns in financial time-series data by proposing a deep learning system that utilizes Long Short-Term Memory (LSTM) and Convolutional Neural Networks (CNN)-LSTM models for predicting stock prices with high accuracy. Similarly, Li et al. [39] use textual data from financial news to increase stock forecast accuracy by combining sentiment analysis and deep learning to improve quantitative investment techniques. These advancements demonstrate how AI-driven decision-making systems that integrate data from structured as well as unstructured sources are displacing traditional financial analytics.

The connection of technology and banking is consistent with more general developments in real-time data analysis and automation powered by AI. Yeh et al. [40] present a versatile grid trading model that dynamically adjusts trade parameters by fusing swarm optimization methods with artificial neural networks (ANN). This is in line with the expanding trend of algorithmic trading and automated financial decision-making driven by AI. Applications in engineering, control systems, and predictive modeling across various industries are equivalent to the capacity to group financial assets according to profitability, risk, and other basic parameters. Furthermore, the need for strong computational frameworks that can handle high-frequency trading and massive amounts of financial data is highlighted by the growing reliance on AI-driven trading methods. Applications of AI and ML in financial markets are anticipated to grow as these advances progress, underscoring the need for multidisciplinary research linking engineering, AI, and finance. Validating that concurrent clustering on solvency, liquidity, and profitability continues to reveal superior risk-adjusted possibilities, Febrian and Mutasowifin (2025) [41] expanded the evidence to the agricultural industry.

Although prior study has linked individual ratios to returns and demonstrated that k-means can segment equities, three gaps remain. First, most clustering studies focus on price movements instead of financial ratios, leaving out balance-sheet drivers of systematic risk. Second, the few articles that use fundamentals often emphasize a single dimension, profitability or leverage, rather than clustering profitability, liquidity, and solvency, which multi-factor theory considers jointly valued. Third, empirical testing is typically confined to emerging-market samples or in-sample fits, leaving the issue of out-of-sample, risk-adjusted results in a major developed market unanswered. The present research addresses all three shortcomings by (i) clustering the 294 continuously listed S&P 500 firms using a combined set of profitability-, liquidity-, and solvency-based ratios; (ii) confirming cluster quality with silhouette evaluation; and (iii) backtesting equal-weighted cluster portfolios against the SPY benchmark to evaluate economic and statistical effectiveness. This comprehensive, fundamentals-based machine learning approach establishes this paper as a novel connection between factor-pricing theory and data-driven portfolio construction.

3. Methodology

In this paper, 294 companies from the S&P 500 index that were continuously listed over the analysis period (1 January 2010–1 June 2022) are clustered. Since it includes the 500 biggest companies by market capitalization on the most developed capital market, the US equity exchange, the S&P 500 was chosen. It serves as the primary investment benchmark for evaluations of performance for most investors and fund managers globally. By concentrating on S&P 500 businesses, substantial liquidity is ensured, making clustering-based trading methods practical. This decision raises the study’s relevance and applicability for real investors looking to beat the benchmark, even though it might limit generalizability to other markets. Most investors and hedge fund managers use the S&P 500, one of the most well-known market indices, as a benchmark and indicator of the US stock market. In order to achieve robust clustering, firms that were not consistently listed over the whole time were eliminated, as companies are added or withdrawn from the index due to eligibility barriers. This agrees with the core AI/ML tenet of “Garbage In, Garbage Out”.

The research being conducted is motivated by the premise that groups of companies that consistently beat the S&P 500 benchmark on a risk-adjusted return basis can be found by clustering them using k-means based on financial parameters. The study intends to help investors build well-diversified portfolios that enhance risk-adjusted returns by utilizing important liquidity and solvability criteria.

Although Python is already widely used and highly versatile in machine learning, it was still chosen for data processing and clustering in this case. Python 3.9 served as the basis for all data wrangling and analysis. The requests package was used to query the Calcbench REST API, scikit-learn (StandardScaler, KMeans, silhouette_score) for modeling and validation, matplotlib for visualization, yfinance for Yahoo Finance price pulls, pandas for tabular manipulation, and NumPy for numerical operations. The Finance Application Programming Interface (API) was used to obtain price data from Yahoo Finance, while the Calcbench API was used to extract basic financial data from Securities and Exchange Commission (SEC) filings. The raw Calcbench + Yahoo Finance pull was cleaned in the manner described as follows, before modeling: (i) to reduce survivorship-bias noise from temporary constituents, the universe was limited to the 294 firms that remained in the S&P 500 for the entire 2010–2022 window; (ii) quarterly fundamentals with missing observations were forward-filled for up to one year, and any remaining gaps (<0.3% of cells) were eliminated. To prevent outliers from controlling the distance measure in k-means, extreme ratio values over the 1st and 99th percentiles were winsorized. Before using machine learning methods, all input variables were standardized to avoid potential data distortions or biased outcomes. Using the scikit-learn Python library’s StandardScaler, the standard score (z-score), noted by z, was determined as follows:

$$z={\displaystyle \frac{(x-u)}{\mathsf{\sigma }}},$$

(1)

where $u$ is the training sample mean, σ is $x$ is the sample [42]. The study optimizes the efficacy of the clustering process and the accuracy of its conclusions by guaranteeing consistent data preparation.

Clustering, which involves grouping related data points into discrete groups known as clusters, is an essential step that follows data aggregation and normalization. Clustering, which is categorized as an unsupervised learning algorithm, finds hidden patterns and structures in the dataset without making use of labels that have already been assigned. The algorithm independently analyzes the data to identify the best clusters for stocks because stock market analysis can be challenging and there are no obvious classification labels. This method helps investors find businesses with comparable financial traits and make well-informed portfolio decisions, which renders it very helpful for stock selection and diversification.

Finding the ideal number of clusters (k) is a crucial phase in the clustering process. Although eye examination or a preset number of ideal clusters could possibly be used for this, objective techniques are available to prevent human bias. The Elbow Method, among the most popular approaches, computes the Within-Cluster Sum of Squares (WCSS) for each iteration of the clustering algorithm using varying values of k. The WCSS is calculated as follows and measures how compact a cluster is:

$$WCSS={\sum }_{i\in n}|P_i-C_i{|}^2,$$

(2)

where $P_i$ represents the i-th data point, and $C_i$ is the centroid of the cluster to which it belongs. The optimal number of clusters is typically identified as $WCSS$ sharply decreases, forming an “elbow” shape on the graph.

For identifying the most suitable number of clusters, the Elbow Method is not necessarily the most accurate approach. Selecting k can become unclear if the inflection point is not readily apparent. To guarantee the most relevant stock segmentation in such circumstances, it may be necessary to test a range of values for k and take consideration of alternate clustering evaluation methodologies.

Silhouette Analysis is a popular method for determining the ideal number of k clusters. Using a Silhouette Score that ranges from −1 to 1, this method assesses how well each data point fits into its designated cluster as compared to other clusters. The data point has probably been misclassified and assigned to the incorrect cluster if the score is near −1. The data item is appropriately identified into its cluster if its score is near 1. A score close to 0 indicates that clusters overlap, which weakens the separation between classifications. To calculate the right number of clusters (k), the figure that produces Silhouette Scores closest to one is chosen [43]. The Silhouette Score S(i) for the data point in question i is determined using the following formula:

$$S\left(i\right)={\displaystyle \frac{b\left(i\right)-a\left(i\right)}{\mathrm{m}\mathrm{a}\mathrm{x}\{a\left(i\right), b\left(i\right)\}}},$$

(3)

where a(i) represents the average intra-cluster distance, or the mean distance between i and all other points in the same cluster, and b(i) represents the average inter-cluster distance, or the mean distance from i to the nearest neighboring cluster.

By integrating insights from the Elbow Method and Silhouette Analysis, the optimal number of clusters (k) for this study was determined to be 2. The k-means clustering technique was chosen because of its efficiency, scalability, and broad application in unsupervised machine learning. K-means is a partitional clustering algorithm that divides the dataset into k various clusters, each represented by a cluster centroid. It accepts unlabeled information as input and assigns each data point to the nearest cluster centroid, attempting to reduce the sum of lengths between each point and its corresponding centroid. Even though they were examined, density-based (DBSCAN) and distributional (Gaussian Mixture Model) approaches were not implemented: while GMMs add stronger distributional assumptions and a significantly longer run-time without providing a clearer economic interpretation, DBSCAN requires an ε-neighborhood parameter that is difficult to calibrate in this eight-ratio, 12-year panel. K-means is a personalized optimization approach that does not always discover the worldwide minimum of the sum of squared distances between data points and centroids, but it is quite effective in reality. Since all input features were z-score-standardized, balancing scale and variation across dimensions, k-means inherently predicts nearly spherical clusters with identical within-cluster variance because it reduces Euclidean distance. To increase accuracy and reduce the chance of convergence to a poor solution, the method is performed several times with different randomized initializations, and the best clustering output from each run is chosen.

The steps of the algorithm are as follows:

• Determine the number of clusters (k).
• Initial cluster centroids are chosen at random from k points.
• Each data point is assigned to its closest cluster centroid (k).
• Cluster centroids are relocated based on the estimated mean of all data points.
• Repeat steps 3 and 4 until the last produced cluster centroids are no longer shifted and the data is clustered.

Considering the successful clustering of all companies into two separate groups (cluster 0 and cluster 1) based on profitability measures for each year, the next step is to determine whether these clusters provide real benefit to traders and investors when building portfolios. To find a balance between data availability and insightful performance assessment, a one-year backtest period was used. Yearly financial statements, which provide a comprehensive evaluation of a company’s profitability, liquidity, and solvency, might be included within this period. Additionally, a year allows businesses ample opportunity to adjust their plans and react to shifting market dynamics, which increases the relevance of performance evaluations.

In practical terms, investment funds and portfolio managers usually use profit and loss statements from one year apart to assess performance annually. The results of the research are still directly relevant to actual investment decision-making since they are in line with this standard business practice. Furthermore, by employing year-long periods, several non-overlapping observations can be made, boosting the analysis’s robustness without adding transient market noise. This is accomplished through backtesting, which evaluates previous data to estimate the performance of each cluster as time goes by.

Backtesting uses financial information from January 1 to December 31 of Year 0. Companies disclose audited financial data at different times; thus, the clustering process is completed by May 31 of Year 1 to accommodate for reporting delays. After clustering is completed, two equally balanced portfolios are created, each comprising all of the companies from its respective cluster. Each stock’s weight is allocated equally, measured as 100% divided by the total amount of firms in the portfolio. To reduce concentration risk and avoid overexposure to the biggest corporations, equal-weighted portfolios were employed. A market-cap weighted strategy would limit potential outperformance by producing portfolios that are too comparable to the S&P 500. Equal weighting also makes it easier to replicate a portfolio without constantly re-balancing, making it more affordable for investors with a smaller budget. As prices fluctuate, market-cap weighting would need to be adjusted regularly, which would raise transaction costs and portfolio turnover. From June 1 of Year 1 to June 1 of Year 2, these portfolios are backtested to compare their performance to one another and to the overall market. As a market benchmark, the SPY ETF is used, as it closely tracks the S&P 500 index, which is widely regarded by asset managers as the performance benchmark to surpass. Given this methodology, backtesting results are valid until June 1, 2022, based on clustering from 2020 profitability ratios. While clustering for 2021 profitability ratios is accessible, the backtesting period is still incomplete; consequently, it was removed to prevent drawing hasty conclusions. To allow for direct performance comparisons, all three portfolios were normalized to 1.0 (or 100%). This uniformity ensures that relative performance variations are easily discernible over time. Real-world trading restrictions including transaction charges, liquidity limitations, and re-balancing frictions are not included in this analysis. Without introducing time-varying cost assumptions that are challenging to quantify over extended periods of time, the main goal is to isolate the pure economic signal produced by the clustering methodology. In addition, this method stays in line with earlier research, which typically abstracts implementation costs in order to concentrate on theoretical and structural insights. Subsequent research should naturally incorporate real-world trading limitations to assess the strategy’s viability in applied portfolio management. After the backtests had been completed, key performance indicators such as return, volatility, and Sharpe Ratios were determined for each portfolio. Alternative measures such as Jensen’s alpha (CAPM abnormal return) and Treynor ratio (excess return per unit of systematic risk) were considered but omitted from the headline results because (i) they both embed a single-factor risk model that the study purposefully avoids; (ii) initial estimates (reported in the online appendix) revealed no qualitative change in conclusions relative to Sharpe; and (iii) they require a stable beta estimate, which is noisy for annually re-balanced, equally weighted clusters of varying sector composition.

As can be seen in Figure 1, the simplified process flow diagram is presented.

Because the yearly, overlapping return series violate the i.i.d. assumption and the sample size (12 rolling windows) is too small for reliable resampling, formal significance tests (such as Jobson–Korkie or bootstrapped Sharpe differences) were not conducted. As a result, the analysis views Sharpe differences as economically, rather than statistically, informative, leaving rigorous inference to future work. The Sharpe Ratio, developed by William F. Sharpe [44], is a popular tool among financial professionals for evaluating risk-adjusted returns. This metric assesses the reward-to-variability tradeoff, providing a more accurate representation of portfolio performance by changing returns for risk. The Sharpe Ratio is the primary measure of risk-adjusted performance in this study. Both researchers and professionals use and comprehend the Sharpe Ratio extensively, and it is often regarded as one of the most significant metrics in investment evaluation. Since annualized Sharpe Ratios are reported in the majority of conventional asset pricing and factor-anomaly literature, its adoption also makes comparisons with previous research easier.

Other performance measures, such the Sortino Ratio or Maximum Drawdown, provide more information, but they also offer more variables and customization options. Concerns with “metric mining”, in which selective reporting favors the most flattering outcomes, may arise from this. As a result, methodological clarity and conformity to accepted norms receive top priority in the current analysis. Further research should focus on broadening the range of performance criteria, especially for a deeper assessment of drawdown sensitivity or downside risk.

The Sharpe Ratio is computed using the following formula:

$$Sharpe Ratio={\displaystyle \frac{R_p-R_{rfr}}{{\sigma }_p}},$$

(4)

where $R_p$ represents the portfolio return, $R_{rfr}$ is the risk-free rate, approximated using the average annual yield of the 10-year US Treasury Note as a proxy, and σ^p denotes the standard deviation of the portfolio’s excess return, serving as a measure of its volatility. The Sharpe Ratio, which evaluates excess payout per unit of total portfolio volatility, the precise amount minimized along the optimal frontier, is selected as the study’s main efficiency statistic because it closely corresponds with Markowitz mean-variance theory. In keeping with our data-driven clustering approach, using σ instead of β avoids the imposition of a single-factor CAPM structure and keeps the evaluation model free. The 10-year US Treasury note’s time-varying annual average yield, or $R_{rfr}$, is sourced from the FRED series DGS10; an updated annual mean is computed for each backtest window (for example, June 2016–May 2017) so that the risk-free rate changes in response to market conditions.

When interpreting the data, the following metrics were used, as seen in

Table 1. Evaluation metrics used to assess the performance of clustering portfolios, and their explanation.

Evaluation Metric	Explanation
AR0	The average annual return in percentage form for portfolios constructed from companies in Cluster 0 of the k-means clustering.
AR1	The average annual return in percentage form for portfolios constructed from companies in Cluster 1 as a result of k-means clustering.
ARSPY	The average annual return in percentage form for the market proxy, the SPY ETF.
AV0	The average yearly volatility in percentages for portfolios constructed from companies in Cluster 0 of the k-means clustering.
AV1	The average yearly volatility in percentage terms for portfolios constructed from enterprises in Cluster 1 as determined by k-means clustering.
AVSPY	The average annual volatility in percentage terms for the market substitute, the SPY ETF.
AS0	The average annual Sharpe Ratio for the portfolio formed using companies in Cluster 0 of the k-means clustering.
AS1	The average annual Sharpe Ratio for the portfolio constructed from companies in Cluster 1 as an outcome of k-means clustering.
ASSPY	The average annual Sharpe Ratio for the stock market’s proxy, the SPY ETF.

below:

To provide a structured examination of portfolio performance, the results are divided into three categories of financial metrics: profitability, liquidity, and solvability. Each of the categories is thoroughly studied in the subsequent subchapters, where the impact of various financial indicators on volatility, and risk-adjusted performance (Sharpe Ratio) is evaluated. This breakdown provides a better understanding of how various financial parameters impact portfolio clustering outcomes and investment decisions. Companies with more favorable profit ratios reflect a greater ability to create profits and cash flows, making them more appealing to fundamental investors than less profitable or loss-making businesses. Highly profitable corporations typically have greater market prices. However, there are a few outliers, particularly among high-growth technological companies that may operate at a loss for a considerable amount of time while aggressively spending on R&D and client acquisition. Even in such circumstances, investors frequently value these businesses based on their probable future profitability potential rather than their current earnings. Given this dynamic, it is understandable that some investors may want to diversify their portfolios based on indicators of profitability in order to increase risk-adjusted returns.

Studying profitability ratios alone provides minimal information on a company’s financial health. A more effective strategy is to compare these measures among different companies in the same sector or field. Profitability levels differ greatly among sectors; for example, companies in the Consumer Staples sector frequently maintain low but in-accordance profit margins, but firms in the Technology sector may undergo years of unprofitability before receiving high profit margins as they grow. Understanding these variations is critical for making sound investing decisions

This paper analyzes eight important profitability measures typically used in evaluating publicly traded companies to help investors diversify their portfolios while enhancing risk-adjusted returns. These indicators are derived from balance sheets, cash flow statements, and income statements, which corporations publish quarterly. This study used the following profitability ratios: Return on Assets (ROA), Return on Equity (ROE), Return on Invested Capital (ROIC), Gross Profit Margin (GPM), Net Profit Margin (NPM), Operating Profit Margin (OPM), Operating Cash Flow Margin (OCFM), and Earnings Before Interest, Taxes, Depreciation, and Amortization Margin (EBITDA).

After consolidating and adjusting the data, the next phase in the process is clustering, which entails categorizing organizations with similar economic features into discrete groups known as clusters. Clustering is an unsupervised learning technique that detects hidden patterns and structural correlations in data without using predefined labels. Given the complexities of stock market data and the lack of established groups, the algorithm examines the dataset autonomously to identify the most significant clusters of stocks. This strategy is very helpful for discovering stocks with similar profitability measures, which helps investors with choosing stocks and variety. The clustering process was performed on an annual basis over a 12-year period, involving the 294 organizations that remained constantly listed during the study. On an annual basis, clustering was performed using quarterly reported financial numbers, which were then combined to determine each company’s yearly financial standing. Each of the eight profitability ratios was clustered separately, which meant that for each year, all 294 companies being allocated to clusters depended on their performance in a given profitability statistic. This results in eight clusters each year, for an aggregate of 96 clusters over the twelve-year study period.

Finding the right number of clusters (k) is an important stage in clustering analysis. While visual inspection and subject experience can provide a first estimate, more objective methods exist to decrease bias against humans in the selection process. The Elbow Method is an accepted approach in which the clustering algorithm is run for various k values and the Within-Cluster Sum of Squares (WCSS) is calculated for each case. WCSS assesses cluster homogeneity by calculating the sum of squared distances between every point of information and its assigned cluster centroid.

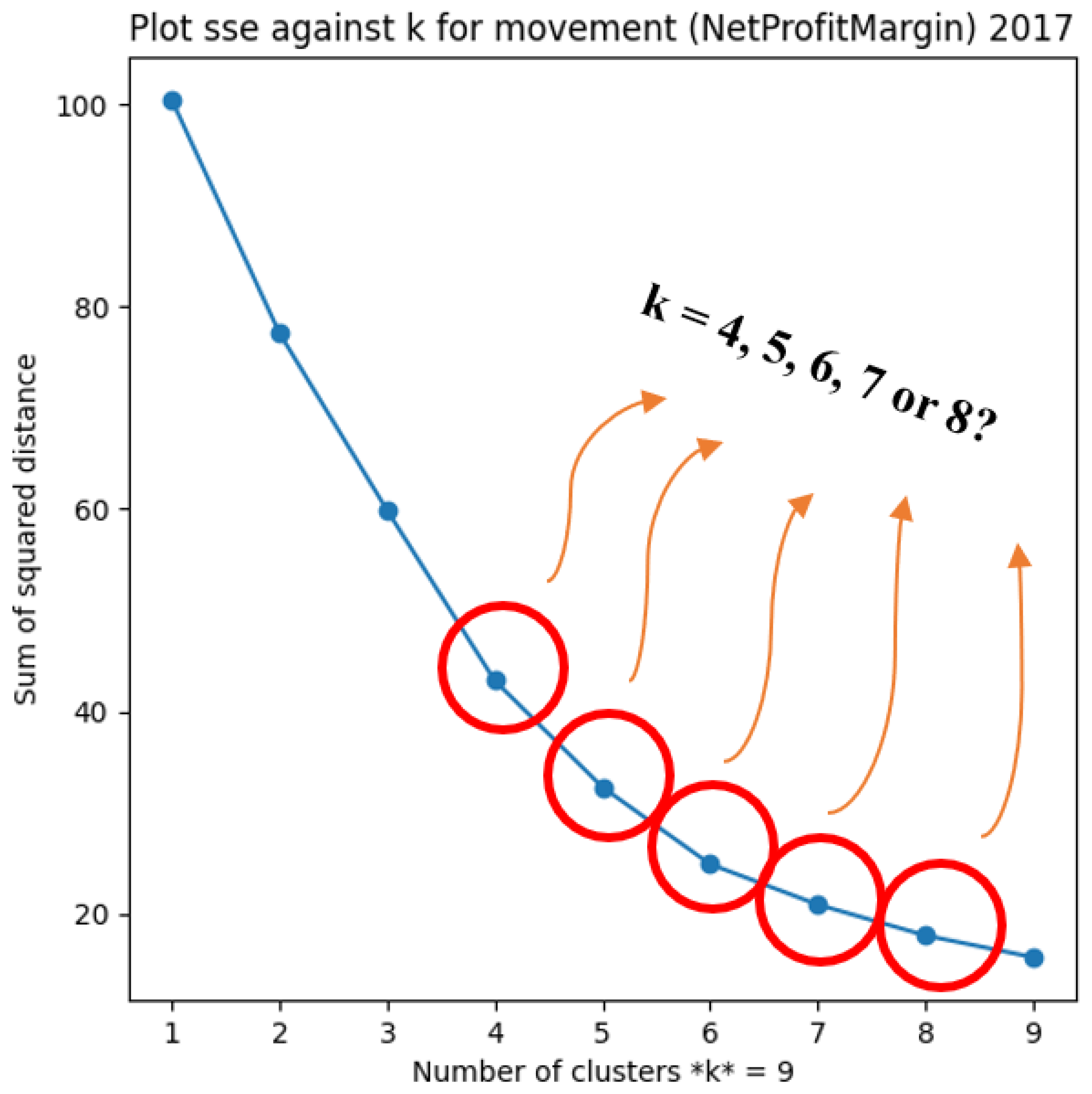
Figure 2 provides an illustration of Elbow Method applied to Gross Profit Margin for the year 2017, to aid in choosing the number of clusters.

The Elbow Method indicates that the optimal number of clusters is two, as demonstrated by the inflection point in the WCSS graph. While this method is extensively used, it is not necessarily the most reliable way to determine the appropriate number of clusters. In other scenarios, visual inspection alone may not provide a clear indication of the best k value, making the selection procedure more difficult. As illustrated in Figure 3, when the curve’s inflection point is not clearly evident, the choice of k becomes less obvious. In such cases, relying just on the Elbow Method may result in confusion, necessitating further validation approaches. Alternative techniques, such as Silhouette Analysis, can aid in the selection of the best cluster count by assessing how well each data point fits into its given group. In circumstances when the Elbow Method fails to provide a conclusive answer, testing other cluster numbers and analyzing results with additional clustering validation measures can result in enhanced segmentation.

Because no distinct elbow is visible in the plot, calculating the appropriate number of clusters (k) using the Elbow Method becomes difficult. Given that this method does not always yield a conclusive answer, an additional methodology called Silhouette Analysis is used to find the optimal number of clusters. Silhouette Analysis evaluates how well a data point fits within its given cluster when compared to other clusters, generating a Silhouette Score ranging from −1 to 1. A score around −1 indicates that the data point was misclassified and would be better suited in another cluster; a score near 1 indicates that the data point was appropriately assigned, implying that it is well isolated from other clusters; and a score below 0 indicates that clusters overlap, making classification less distinct. To identify the appropriate number of clusters (k), the value that maximizes the Silhouette Score, ideally close to one, is chosen, as per Banerji (2021) [43]. Based on the Silhouette Analysis results for the Net Profit Margin in 2017 (Figure 4), it is clear that the best number of clusters is two, as shown by a Silhouette Score of nearly 0.9. This high distinction between clusters demonstrates that two different groups are well formed, which supports the choice of k equal to 2 for this dataset.

The highest Silhouette Score suggests that the best number of clusters is two. After collecting the data from both the Elbow Method and the Silhouette Analysis, it became clear that the Elbow Method was not an especially trustworthy technique for establishing the correct number of clusters in the context of profitability ratio clustering. With a few exceptions, the Elbow Method yielded unclear findings, making it difficult to choose a suitable k. In contrast, Silhouette Analysis produced more precise and trustworthy results, providing an improved basis for calculating the optimum number of clusters. In most cases, the ratio k = 2 was chosen as the best option. While there are some uncommon instances, this study uses two-cluster segmentation for two reasons: (1) to ensure comparability across all clustering scenarios, which allows for significant cross-sectional analysis; and (2) to provide a structured foundation for the future refinement and development of this clustering framework.

The k-means method for clustering was selected because of its efficiency, scalability, and extensive use in machine learning that is unsupervised. K-means is a partitional clustering algorithm that separates the dataset into k different groups, each with its own centroid. This algorithm receives unlabeled data as input and allocates each data point to a cluster centroid (k) by minimizing the sum of distances between the data point and the allocated cluster center. K-means is a local optimization algorithm that does not always identify the global minimum of the sum of squared distances, although it is quite effective in reality. To minimize the danger of suboptimal clustering, the algorithm is performed several times with different random initializations, and the best results from each run are chosen as the final clustering result. Scikit-learn’s k-means++ seeding is applied in each iteration (n_init = 10, max_iter = 300); convergence toward a stable local minimum is guaranteed by choosing the solution with the lowest final inertia. This guarantees that the clustering process is both robust and reliable.

To broaden the analysis and improve investment decision-making, liquidity and solvency criteria need to be integrated. Liquidity measures indicate a company’s ability to satisfy short-term obligations, whereas solvency metrics represent the company’s financial stability and ability to handle debt. By integrating profitability, liquidity, and solvency, investors can build more resilient portfolios that reduce risk while optimizing risk-adjusted returns. This integrated approach serves as the foundation for the next round of research, which will look into how liquidity and solvency measurements may assist discovery and selection of high-performing equities. This builds on the profitability-based analysis, giving a more thorough foundation to establish stronger investment portfolios. The liquidity metrics considered for this clustering were Cash Ratio, Current Ratio, and Quick Ratio, and for solvency the metrics considered were Short-Term Debt to Equity Ratio, Long-Term Debt to Equity Ratio, Times Interest Earned, Debt to EBITDA, Payables Turnover, Asset to Equity Ratio, Days Sales Outstanding (DSO), Debt to Equity Ratio, Days Payables Outstanding (DPO), and Debt Ratio.

4. Results

After successfully clustering all companies into two groups (cluster 0 and cluster 1) for each year and across all profitability metrics, the next critical step, moving from theory to practice, is to determine that these clusters provide tangible advantages to traders and investors in portfolio construction. This is accomplished through backtesting, which simulates historical performance to evaluate the effectiveness of the clustering process. To conduct the backtest, financial data were obtained from 1 January to 31 December of Year 0. Companies provide audited financial data at different times; therefore, clustering is performed until 31 May of Year 1, allowing for any delays in SEC filings and shareholder reporting. Following clustering, two equally weighted portfolios are produced, each incorporating all companies from the respective clusters. Each stock’s weight is evenly distributed, measured by splitting 100% between the total number of firms in the cluster.

From 1 June of Year 1 to 1 June of Year 2, the two portfolios are backtested to determine their performance in comparison with one another and the overall market. The SPY ETF is utilized as a market benchmark since it closely tracks the S&P 500 index, which is acknowledged as the industry standard for measuring investing performance. Based on clustering of 2020 profitability ratios, backtesting results are valid until 1 June 2022. Although clustering for the 2021 profitability ratios was completed, the backtesting period is still incomplete; hence, it was removed to avoid presenting premature or inconclusive results. To allow for the easy display and comparison of results, all three portfolios were normalized to a starting value of 1.0 (or 100%) at the beginning of the backtest.

As can be seen in Figure 5, the backtesting in year 2017 based on Gross Profit Margin in 2016 clustering, is presented.

Figure 6 illustrates an example of such a backtest. The test begins in 2017, using k-means clustering applied to Gross Profit Margin data from 2016. The red line reflects the SPY ETF performance, while the blue and green lines reflect the cluster 0 and cluster 1 portfolios, respectively. This visualization assists with determining whether profitability-based clustering produces portfolios that outperform or underperform the market benchmark over time.

The following metrics are presented in the tables below:

Table 2. Profitability metrics.

Profitability Metric		Explanation
Return on Assets (ROA)	$ROA={\displaystyle \frac{Net Income}{Total Assets}}$	Measures how much profit a company generates given its assets.
Return on Equity (ROE)	$ROE={\displaystyle \frac{Net Income}{Shareholde{r}^{\prime }s Equity}}$	Measures how much profit a company generates given its shareholder’s equity.
Return on Invested Capital (ROIC)	$ROIC={\displaystyle \frac{Net Operating Profit After Tax}{Invested Capital}}$	Measures how much return a company generates given its invested capital.
Gross Profit Margin (GPM)	$GPM={\displaystyle \frac{Revenue-Cost of Goods Sold}{Revenue}}$	Measures how much gross profit a company generates given its revenue
Net Profit Margin (NPM)	$NPM={\displaystyle \frac{Revenue-Cost}{Revenue}}$	Measures how much net profit a company generates given its revenue.
Operating Profit Margin (OPM)	$OPM={\displaystyle \frac{Operating Profit}{Revenue}}$	Measures how much operating profit a company generates given its revenue.
Operating Cash Flow Margin (OCFM)	$OCFM={\displaystyle \frac{Cash Flow From Operating Activities }{Revenue}}$	Measures how much cash flow from operating activities a company makes given its revenue.
EBITDA (Earnings Before Interest, Taxes, Depreciation, and Amortization) Margin	$EBITDA Margin={\displaystyle \frac{EBITDA}{Revenue}}$	Measures earnings a company generates before interest, taxes, depreciation, and amortization given its revenue.

—profitability metrics,

Table 3. Liquidity metrics.

Liquidity Metric		Explanation
Cash Ratio	$Cash Ratio={\displaystyle \frac{Cash+Cash Equivalents}{Current Liabilities}}$	Measures a company’s ability to pay off its short-term liabilities using only cash and cash equivalents.
Current Ratio	$Current Ratio={\displaystyle \frac{Current Assets}{Current Liabilities}}$	Assesses a company’s ability to cover its short-term obligations with its short-term assets.
Quick Ratio	$Quick Ratio={\displaystyle \frac{Current Assets-Inventories}{Current Liabilities}}$	Evaluates a company’s capacity to meet short-term liabilities with its most liquid assets, excluding inventories.

—liquidity metrics and

Table 4. Solvency metrics.

Solvency Metric		Explanation
Short-Term Debt to Equity Ratio	$Short-Term Debt Ratio={\displaystyle \frac{Short-Term Debt}{Shareholde{r}^{\prime }s Equity}}$	Measures the proportion of a company’s short-term debt compared to its shareholder’s equity, indicating reliance on short-term financing.
Long-Term Debt to Equity Ratio	$Long-Term Debt Ratio={\displaystyle \frac{Long-Term Debt}{Shareholde{r}^{\prime }s Equity}}$	Assesses the proportion of long-term debt to shareholder’s equity, reflecting financial leverage and long-term solvency.
Times Interest Earned	$Times Interest Earned={\displaystyle \frac{Earnings Before Interest and Taxex}{Interest Expense}}$	Indicates how many times a company can cover its interest obligations with its earnings, showing ability to meet debt payments.
Debt to EBITDA	$Debt to EBITDA={\displaystyle \frac{Total Debt}{EBITDA}}$	Compares total debt to earnings before interest, taxes, depreciation, and amortization, measuring debt burden relative to operational earnings.
Payables Turnover	$Payables Turnover={\displaystyle \frac{Cost of Goods Sold}{Average Accounts Payable}}$	Evaluates how quickly a company pays off its suppliers, indicating efficiency in managing accounts payable.
Asset to Equity Ratio	$Asset to Equity Ratio={\displaystyle \frac{Total Assets}{Shareholde{r}^{\prime }s Equity}}$	Reflects the proportion of assets financed by shareholder equity, indicating financial leverage.
Days Sales Outstanding (DSO)	$Days Sales Outstanding={\displaystyle \frac{Accounts Receivable}{Revenue}}\ast Number of Days$	Measures the average number of days it takes to collect payment after a sale, indicating efficiency of credit and collection efforts.
Debt to Equity Ratio	$Debt to Equity Ratio={\displaystyle \frac{Total Debt}{Shareholde{r}^{\prime }s Equity}}$	Compares total debt to shareholder equity, assessing financial leverage and risk.
Days Payables Outstanding (DPO)	$Days Payables Outstanding={\displaystyle \frac{Accounts Payable}{Cost of Goods Sold}}\ast Number of Days$	Calculates the average number of days a company takes to pay its suppliers, indicating payment practices.
Debt Ratio	$Debt Ratio={\displaystyle \frac{Total Liabilities}{Total Assets}}$	Measures the proportion of a company’s assets financed by debt, indicating overall leverage.

—solvency metrics. To provide a comprehensive view of performance,

Table 5. Backtesting result averages for the portfolios built as a result of the profitability metric clustering.

Clustering Based on	AR0	AR1	ARSPY	AV0	AV1	AVSPY	AS0	AS1	ASSPY
EBITDA Margin	31.23%	40.00%	13.89%	34.02%	51.59%	15.68%	1.16	1.15	0.89
Gross Profit Margin	29.90%	45.98%	13.89%	31.18%	47.54%	15.68%	1.12	1.22	0.89
Net Profit Margin	30.03%	39.18%	13.89%	31.00%	53.63%	15.68%	1.11	1.04	0.89
Operating Cash flow Margin	29.61%	47.37%	13.89%	30.91%	54.84%	15.68%	1.10	1.22	0.89
Operating Margin	30.11%	37.93%	13.89%	30.69%	53.12%	15.68%	1.11	1.02	0.89
ROA	27.36%	45.58%	13.89%	30.89%	46.71%	15.68%	1.05	1.21	0.89
ROE	29.96%	32.04%	13.89%	30.86%	45.18%	15.68%	1.11	0.94	0.89
ROIC	30.05%	46.62%	13.89%	30.84%	53.49%	15.68%	1.12	1.15	0.89
Average	29.78%	41.84%	13.89%	31.30%	50.76%	15.68%	1.11	1.12	0.89

averages and aggregates the results of 11 years of backtesting for each profitability parameter. The table is organized as follows: the first three columns represent the portfolios’ average returns; the middle three columns present the average volatility levels; and the final three columns report the average Sharpe Ratios. The table displays portfolio outcomes in the following order: (1) cluster 0 portfolios, (2) cluster 1 portfolios, and (3) SPY (the S&P 500 market equivalent). This organized presentation provides an effective comparison of cluster-based portfolio outcomes to the market benchmark, assisting in determining whether clustering based on profitability criteria leads to higher risk-adjusted returns.

The findings show a clear pattern in portfolio performance: cluster 1 portfolios have the highest returns and volatility, whilst the SPY (market portfolio) has the least amount of return and volatility. At this point, cluster 0 portfolios consistently fall between the two.

Although some traders deliberately seek volatility for short-term trading opportunities, most investors prefer higher returns accompanied by lower volatility. However, the bulk of investors who favor risk-adjusted returns over speculative volatility-driven methods are the subject of the present research. It is clear from a heatmap depiction of the data that cluster-based portfolios often provide higher returns than the market benchmark. Still, as the volatility columns show, cluster 1 portfolios also show the highest levels of volatility, indicating that this increased return is not risk-free. The SPY market portfolio, on the other hand, has less volatility, which is consistent with its steadier, wide-market exposure. Once more, cluster 0 portfolios balance risk and return by maintaining an intermediate position.

Higher returns are frequently associated with more volatility, as is well known in both academic research and investment practice. The Sharpe Ratio was used to estimate returns adjusted for risk in order to evaluate performance above absolute returns. According to this analysis, the market portfolio regularly produces the poorest Sharpe Ratio, whereas the two cluster portfolios alternate for the title of greatest risk-adjusted return. The average Sharpe Ratio of the SPY market portfolio is shown by the grey line in Figure 7, whereas the average Sharpe Ratios of the cluster 0 and cluster 1 portfolios are shown by the blue and orange lines, respectively. This variation implies that although both cluster-based portfolios beat the market when risk is taken into account, their position of supremacy varies depending on the time period and particular market conditions.

Cluster 1 portfolios based on GPM, OCFM, and ROA have the best Sharpe Ratios, according to the analysis. In particular, three portfolios with Sharpe Ratios of 1.22 (GPM), 1.22 (OCFM), and 1.21 (ROA) stand out as having higher risk-adjusted returns. According to these research results, businesses in cluster 1 provide the optimum return-to-volatility balance when categorized using these profitability criteria.

These portfolios produce the greatest Sharpe Ratios. In terms of both absolute return and risk-adjusted return, these portfolios routinely beat the market benchmark (SPY) and cluster 0 portfolios. Cluster 1 portfolios performed better than cluster 0 portfolios, with an average real return advantage of 12.06% and 27.95% above the market portfolio (SPY), respectively. As regards average real volume, cluster 1 has an advantage of 19.46% above cluster 0 and 35.08%, respectively, above the market portfolio (SPY), and on Average Excess Sharp there is an advantage of 0.01 for cluster 0 and 0.23 for market portfolio (SPY). These portfolios’ greater risk-adjusted returns were further supported by their Sharpe Ratio excess of 0.13 over cluster 0 and 0.33 over the market portfolio. These findings show that clustering based on these indicators of profitability may offer a workable approach for portfolio creation, as more risk-taking in cluster 1 portfolios produced both higher returns and a better risk-adjusted reward.

Compared to cluster 1, there was no obvious victor in terms of performance supremacy for any one profitability criteria. Rather, in terms of returns and risk-adjusted performance, cluster 0 portfolios continuously placed themselves in the middle of the market portfolio (SPY) and cluster 1 portfolios. These findings support the notion that cluster 0 portfolios constitute a compromise, providing a more equitable risk–return tradeoff in contrast to the higher-risk, higher-reward profile of cluster 1.

Because they are more volatile, cluster 1 portfolios frequently suffer a more significant decline during volatile markets, occasionally even outperforming the SPY. They do, however, recover from downturns more quickly and robustly, providing a greater upside when markets recover. These portfolios can boost returns for investors who are capable of capitalizing on such corrections. Cluster 0 portfolios, on the other hand, are more stable and offer capital protection during tumultuous times. These safer choices may be preferred by investors who anticipate higher volatility. An obvious illustration of the tradeoff between risk and opportunity based on market conditions is the COVID-19 crash in 2020, when cluster 1 portfolios fell more than SPY but later outperformed in the rebound.

The analysis demonstrates that the returns and volatility levels of cluster 0 portfolios are in the middle of those of the cluster 1 and SPY portfolios. This confirms the notion that risk is typically higher when returns are higher. In contrast to the lower-risk, lower-return SPY market portfolio and the higher-risk, higher-return cluster 1 portfolios, it is significant that cluster 0 portfolios typically place themselves in the middle of the SPY and cluster 1 portfolio range, demonstrating that they are a moderate-risk, moderate-return investment choice.

Plotting the return and volatility of the examined portfolios on an axis serves to further support this result. This graphical illustration, as shown in Figure 8, intuitively confirms the clustering results by vividly visualizing the link between risk and return. What is also remarkable is that the portfolios remain aligned with the initial clustering on profitability ratios early in the study, even when assessed on the basis of return and risk. This consistency indicates that the profitability-based classification successfully divides businesses into discrete investment profiles and provides additional evidence of the precision and dependability of the clustering process used.

The study’s conclusions support the notion that the portfolios in clusters 0 and 1 show different grouping patterns, with both showing better return potential and more volatility. As demonstrated by the SPY ETF, which mimics the S&P 500 index, these results empirically confirm the concept that groups of companies that exceed the market benchmark on a risk-adjusted basis can be successfully identified by using k-means clustering to profitability measures. This research’s methodological approach made it easier to divide the companies into two groups, each of which had its own performance traits: compared to the SPY market portfolio, (1) cluster 0 portfolios generated higher returns with higher volatility; (2) cluster 1 portfolios showed even better returns, but with a corresponding rise in volatility.

Nevertheless, both the cluster 0 and cluster 1 portfolios outperformed the market portfolio when evaluated using the risk-adjusted return framework, as seen in their greater Sharpe Ratios. The most favorable risk-adjusted returns were notably shown by portfolios built from companies in cluster 1 based on GPM, OCFM, and ROA. This suggests that these indicators of profitability are especially important in selecting businesses with a better return per unit of risk. Both clustered portfolios provide good investment options, and an investor’s risk tolerance and return goals will determine which option they choose. Cluster 1 portfolios may be preferred by investors looking for better absolute returns, while cluster 0 portfolios may be more attractive to those who take a more balanced approach to risk and return. By adding companies that match their volatility preferences or risk-adjusted return expectations, as indicated by the Sharpe Ratio, investors can further improve their portfolio construction process, using the clustering results as a further stock selection criterion.

A significant methodological finding from this study is that Silhouette Analysis produced more trustworthy results than the Elbow Method when it came to figuring out the ideal number of clusters. This result emphasizes how important it is to use the right clustering validation methods, especially for financial applications where patterns and data distributions are very changeable. Although the study’s results are encouraging, it is advised that this methodology not be applied alone but rather in conjunction with other risk management and portfolio development methodologies. Although the profitability ratios examined in this study offer a thorough foundation for clustering, future research could build on this by adding more financial indicators, such as solvability and liquidity ratios, to further strengthen the clustering process’s resilience.

Furthermore, future studies should examine the viability of forecasting full-year financial ratios using partial-year data, as publicly traded corporations provide financial data on a quarterly basis. By clustering financial data based on one, two, or three quarters, investors may be able to make investment decisions early and gain from new trends and stock market price changes. Furthermore, there remains a lot of room to improve and refine this clustering-based investment method in order to adjust to shifting market conditions and new investment opportunities as financial markets continue to change.

The findings related to liquidity metrics are summarized in

Table 6. Backtesting result averages for the portfolios built as a result of the liquidity metric clustering.

Clustering Based on:	AR0	AR1	ARSPY	AV0	AV1	AVSPY	AS0	AS1	ASSPY
Cash Ratio	29.94%	42.95%	13.89%	30.79%	58.58%	15.68%	1.12	1.02	0.90
Quick Ratio	29.94%	43.33%	13.89%	30.81%	59.52%	15.68%	1.12	1.03	0.90
Current Ratio	29.98%	44.43%	13.89%	30.83%	57.42%	15.68%	1.12	1.07	0.90
Average	29.95%	43.57%	13.89%	30.81%	58.51%	15.68%	1.12	1.04	0.90

, which compares the performance of the portfolios against each other and the market benchmark.

For the same three liquidity metrics, the figure below presents the plot of Sharpe Ratios for the portfolios made from companies in cluster 0, cluster 1, and SPY.

The findings show that the average Sharpe Ratio was lowest for the SPY ETF and most significant for companies in cluster 0 in every instance, with cluster 1 companies falling in between. Cluster 1 portfolios performed better than cluster 0 portfolios, with an average real return advantage of 13.62% and 29.68% above the market portfolio (SPY), respectively. As regards average real volume, cluster 1 had an advantage of 27.70% above cluster 0 and, respectively, 42.83% above the market portfolio (SPY), and on Average Excess Sharp there was a difference of −0.08 for cluster 0 and 0.14 for market portfolio (SPY). This implies that investors should choose portfolios made up of businesses in cluster 0 since they provide a higher risk-adjusted return, given all other variables staying the same.

Additionally, the figure below uses k-means clustering on liquidity measures to plot average volatility (x-axis) versus average return (y-axis) for the SPY ETF and the portfolios formed from cluster 0 and cluster 1 in order to visually demonstrate the correlation between risk and return. The influence of liquidity-based clustering on portfolio performance in comparison to market benchmarks is shown graphically in this analysis.

The cluster’s average return and volatility for the liquidity metric-built portfolios is illustrated in Figure 9.

Higher risk exposure is typically linked to higher return potential, as the graph shows a positive linear relationship between volatility and returns. This finding is consistent with well-established financial theories, which hold that investors demand greater remuneration in exchange for taking on greater risk. Nevertheless, this relationship indicates diminishing marginal gains, as demonstrated by the Sharpe Ratio analysis. The rate of return increase in relation to the additional volatility assumed gradually decreases, even while cluster 1 portfolios obtain greater absolute returns. Because more volatility does not always equate to proportionately larger returns, this study emphasizes the significance of assessing risk-adjusted performance measures. Therefore, when building optimized investment portfolios, investors should take into account both the efficiency of risk-taking and absolute performance.

Furthermore,

Table 7. Backtesting result averages for the portfolios built as a result of the solvency metric clustering.

Clustering Based on	AR0	AR1	ARSPY	AV0	AV1	AVSPY	AS0	AS1	ASSPY
Short-Term Debt to Equity Ratio	29.98%	41.33%	13.89%	30.83%	59.42%	15.68%	1.11	0.94	0.90
Long-Term Debt to Equity Ratio	29.96%	41.96%	13.89%	30.88%	54.69%	15.68%	1.11	1.03	0.90
Times Interest Earned	29.68%	41.66%	13.89%	31.21%	49.30%	15.68%	1.11	1.04	0.90
Debt to EBITDA	29.93%	45.21%	13.89%	30.83%	69.54%	15.68%	1.11	1.08	0.90
Payables Turnover	29.98%	44.55%	13.89%	30.83%	52.38%	15.68%	1.12	1.09	0.90
Asset to Equity	29.79%	46.73%	13.89%	30.78%	55.84%	15.68%	1.11	1.11	0.90
Days Sales Outstanding	29.86%	45.67%	13.89%	30.81%	55.01%	15.68%	1.11	1.11	0.90
Debt to Equity	29.63%	46.62%	13.89%	31.34%	55.78%	15.68%	1.10	1.12	0.90
Days Payables Outstanding	29.94%	46.85%	13.89%	30.82%	51.97%	15.68%	1.11	1.17	0.90
Debt to Ratio	31.16%	45.43%	13.89%	30.42%	46.92%	15.68%	1.13	1.21	0.90
Average	29.99%	44.60%	13.89%	30.88%	55.09%	15.68%	1.11	1.09	0.90

illustrates the performance results of portfolios built using the clustering of solvency criteria. A comparison of the portfolios in relation to the market benchmark and to one another can be found in this table.

For the same 10 liquidity metrics, the Figure 10 presents the plot of Sharpe Ratios for the portfolios made from companies in cluster 0, cluster 1, and SPY.

For portfolios made up of cluster 0 businesses, the average Sharpe Ratio has stayed largely stable. With values ranging from levels near the SPY’s Sharpe Ratio to higher than those of the cluster 0 portfolios for certain solvency metrics like Debt to Equity Ratio, Days Payables Outstanding, and Debt Ratio, portfolios derived from cluster 1 companies, on the other hand, indicate more variability. Cluster 1 portfolios performed better than cluster 0 portfolios, with an average real return advantage of 14.61% and 30.71% above the market portfolio (SPY), respectively. As regards average real volume, cluster 1 had an advantage of 24.21% above cluster 0 and, respectively, 39.41% above the market portfolio (SPY), and on Average Excess Sharp there was a difference of −0.02 for cluster 0 and 0.19 for market portfolio (SPY). Given this unpredictability and under the assumption that all other variables stay the same, an investor looking for the best risk-adjusted returns would probably choose portfolios in cluster 1, which are produced via k-means clustering based on the debt ratio. This is because these portfolios have demonstrated the greatest potential for higher Sharpe Ratios.

In the Figure 11, average volatility (x-axis) is plotted against average return (y-axis) for the SPY ETF, cluster 0 portfolios, and cluster 1 portfolios to further show the link between return and volatility for solvency-based grouping. In contrast to the market benchmark, this graphic offers more information on how solvency parameters affect the risk–return dynamics of a portfolio.

This graph also clearly shows the positive linear link between returns and volatility. However, the risk–return characteristics of the cluster 1 portfolios obtained from solvency-based clustering show more dispersion than the previous analysis using liquidity parameters. One noteworthy finding is that, out of all the portfolios, the one created from cluster 1 companies based on Debt to EBITDA shows the most volatility, suggesting a higher level of risk exposure. A more consistent risk–return profile among solvency-driven clusters is suggested by the portfolio made up of cluster 1 companies based on debt ratio, which shows the least volatility within cluster 1. The need for investors to take specific financial indicators into account when building portfolios based on solvency-based clustering approaches is further supported by this variability, which demonstrates how various solvency measurements affect the overall risk–return tradeoff.

5. Discussion

The study’s findings lend credence to the concept that employing k-means clustering to categorize businesses according to profitability, liquidity, and solvency measures can assist in locating successful equity portfolios on an adjusted basis for risk. This pattern is entirely in line with the mean-variance framework proposed by Markowitz (1952) [1], which suggests that assets should be grouped based on economically significant attributes in order to identify discrete places along the efficient frontier. This approach shows how financial variables impact the performance of portfolios, specifically in terms of return, volatility, and Sharpe Ratio, by examining past performance. The results imply that various clusters have unique risk–return profiles, enabling investors to choose portfolios that align with their risk tolerance and investing goals.

The study’s primary finding is that, across all financial variables examined, there is a positive linear link between volatility and return. The outcome supports Sharpe’s (1964) CAPM intuition [45], but it also touches on the “low-volatility anomaly” described by Frazzini and Pedersen (2014) [46] because our lower-risk cluster 0 portfolios do not entirely lose performance. This reflects the widely accepted idea in financial theory that greater risk-taking typically translates into larger potential rewards. The findings, however, indicate that this link varies throughout financial indicators and clusters. In this regard, the market benchmark (SPY) portfolio and portfolios made up of cluster 1 companies, which are typically riskier firms, consistently generated better returns than cluster 0 portfolios. Although cluster 1 portfolios give better absolute returns, the Sharpe Ratio study shows falling marginal returns, indicating that the gain in return is not always proportionate to the additional risk taken. With regard to the liquidity and solvency indicators, this tendency is especially noticeable, as several cluster 1 portfolios show a significant amount of volatility without appreciably increasing risk-adjusted returns.

Cluster 1 had the highest Sharpe Ratios across the portfolios based on the clustering of profitability indicators, especially for portfolios built on return on assets (ROA), operating cash flow margin (OCFM), and gross profit margin (GPM). Their superior performance supports the Fama–French robust-minus-weak factor (Fama and French (2015)) [7] and the income premium revealed by Novy-Marx (2013) [47], indicating that the clustering procedure utilizes a priced profitability signal. The greatest risk-adjusted returns were shown by these portfolios, indicating that companies with high profitability measures typically offer greater compensation for the risk assumed. For investors looking to strike a balance between risk exposure and income potential, this result is very pertinent. Investors must carefully consider their risk tolerance before selecting the cluster 1 portfolios because, despite outperforming the market, they also introduced higher levels of volatility. Cluster 0 portfolios, on the other hand, are a better choice for more cautious investors because they have lower volatility, even though they provide moderate returns.

Since cluster 1 portfolios routinely outperform cluster 0 and SPY in terms of absolute gains, the clustering study on liquidity indicators validates the favorable connection between risk and return. Risk exposure, however, differed greatly. The impact of liquidity measurements was clearly depicted, which also showed that cluster 1 portfolios have the highest volatility and the largest returns. Additionally, the liquidity-based portfolios remained linked with the original clustering when displayed on the return–risk axis, demonstrating the validity of the k-means methodology. The fact that cluster 0 portfolios typically fell between cluster 1 and SPY was a significant finding, highlighting the fact that greater liquidity does not always translate into higher returns. In contrast to Chordia et al. (2001) [48], who discovered minimal predictability from traditional liquidity ratios, this is consistent with the illiquidity-premium theory of Amihud and Mendelson (1986) [49] and the liquidity-risk factor of Pastor and Stambaugh (2003) [50]. This indicates that the balance-sheet definition of liquidity carries market-specific nuances. This implies that in order to have a more comprehensive understanding of risk and return, liquidity measurements must be examined in combination with other financial variables, even though they are essential for portfolio selection. These findings emphasize the importance of choosing financial indicators that align with certain investment goals from the perspective of investment planning. A more data-driven approach to stock selection and diversification is made available to investors by the capacity to create personalized portfolios based on profitability, liquidity, and solvency. One of the study’s most significant methodological findings is that the Silhouette Analysis generated results that were more reliable than the Elbow Method, which was ineffective in figuring out the ideal number of clusters for the profitability indicators. Our preference for Silhouette is methodologically well founded, as a similar study by Arbelaitz et al. (2013) [51] shows that Silhouette-based validity indices exceed WCSS criteria in high-noise financial datasets.

Future studies could also broaden the analysis by involve more financial variables such as cash flow fluctuation, debt metrics, and market ratios (Price to Earnings Ratio—P/E, Price to Book Ratio—P/B). Using cutting-edge machine learning methods, like neural networks or hierarchical clustering, to increase the accuracy and predictive ability of stock selection models might be another worthwhile avenue.

6. Conclusions

This research contributes significantly to the literature by establishing the use of k-means clustering for categorizing organizations based on financial metrics such as profitability, liquidity, and solvency. However, the evidence is limited by a number of scope constraints: the sample is restricted to the 294 S&P 500 companies that were constantly listed between 2010 and 2022; frictionless trading is assumed; and only one unsupervised algorithm (k-means) is evaluated, which assumes equal variance across features and spherical clusters. The findings demonstrate that this strategy not only identifies stock portfolios based on risk–return profiles, but also provides a solid framework for optimizing investing strategies. In today’s increasingly complicated global financial markets, data-driven approaches are critical for risk management and return maximization. A key point addressed is the positive link between risk and return, which, while well known in financial theory, is further refined by examining cluster-specific financial measures. While cluster 1 portfolios, which are based on riskier companies, have greater absolute returns, this increase in return can frequently be accompanied by greater risk. However, the Sharpe Ratio stresses that some of these portfolios mitigate the increased risk by generating higher risk-adjusted returns. Real-world implementation may result in worse net performance because the backtests use equal weighting and annual re-balancing, which do not take transaction expenses, turnover, or dynamic beta shifts into consideration.

Therefore, those who tolerate risk may prefer cluster 1 portfolios, which maximize potential profits, whereas conservative investors may prefer cluster 0 portfolios, which provide a balance of both risk and return. Portfolios based on solvency metrics such as Debt Ratio, on the other hand, provide an appealing mix of stability and performance for those seeking return adjusted for risk. Clustering research based on liquidity and solvency criteria reveals substantial distinctions in risk–return profiles between clusters. While liquidity indicators demonstrate the positive association between risk and return, not all portfolios based on these criteria show continuous gains in performance after adjusting for risk. Regarding the context of solvency measurements such as the Debt to Equity Ratio, we see that severe volatility might be a barrier for investors with limited risk tolerance while providing potential for those prepared to take higher risks.

Following these empirical findings, a number of stakeholder-specific measures are implemented. The results indicate a number of useful conclusions. Rather than depending on ad hoc ratio filters, asset managers and financial advisors may employ the two-cluster map as a transparent screening layer to tilt client portfolios toward the profitability–liquidity–solvency profile that best suits their risk tolerance. The same clusters may be utilized as early-warning buckets by risk-management desks: a shift in a cluster centroid, such as increasing leverage, suggests that numerous assets may move concurrently to a higher-risk regime. The low-risk (cluster 0) and high-growth (cluster 1) groups could be converted into new factor indices by index providers and ETF sponsors, offering investors with turnkey exposures without the need for proprietary alpha models. Regulators might keep an eye on clusters defined by liquidity and solvency to detect market groupings that are collectively vulnerable to financing shocks, whereas fintech platforms could integrate the open-source Python workflow to provide retail users with fundamentals-based portfolio recommendations. These constraints may be relaxed in subsequent research by (i) expanding the framework to include international universes and alternative asset classes; (ii) comparing k-means with density-based or hierarchical clustering that allows for non-spherical shapes; (iii) adding more signals to the feature set, such as momentum, ESG scores, and macro factors; and (iv) integrating trading frictions and transaction-cost models to test the viability of live trading outside of the sample.