The New Gompertz Distribution Model and Applications
Abstract
1. Introduction
2. The Marshall–Olkin Power Gompertz (MOPG) Distribution
- ,
- ,
2.1. Mathematical Mixture Representation
2.2. Identifiability
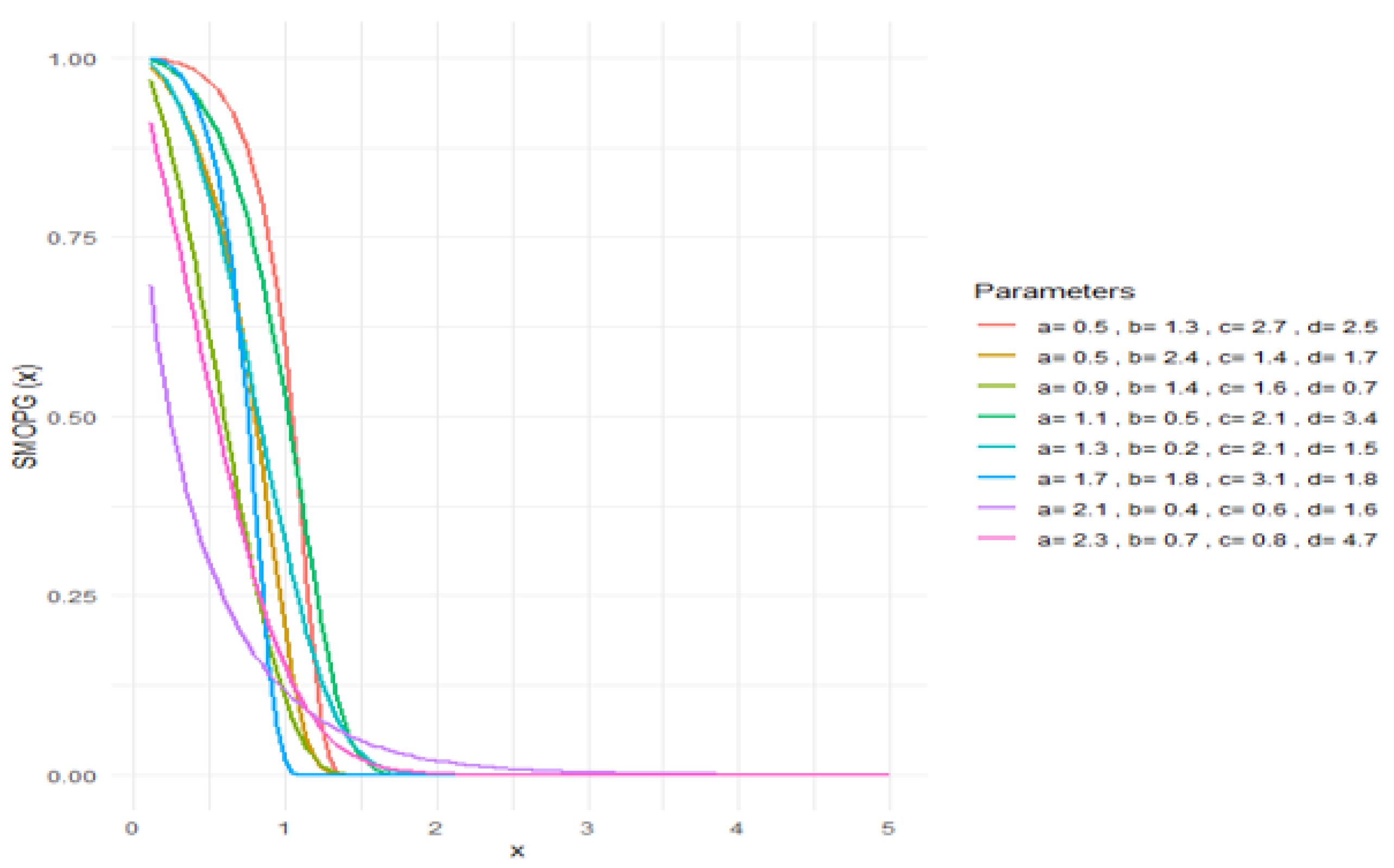
2.3. Asymptotic Findings
3. Characteristics Structure of the MOPG Distribution
3.1. Quantile Function of the MOPG Distribution
3.2. Moments
3.3. Renyi Entropy
4. Order Statistics
5. Estimation of MOPG Parameters
6. Simulation Studies
6.1. Model Fitting
6.2. Data Set 1
- 0.2070, 0.1520, 0.1628, 0.1666, 0.1417, 0.1221, 0.1767, 0.1987, 0.1408, 0.1456, 0.1443, 0.1319, 0.1053, 0.1789, 0.2032, 0.2167, 0.1387, 0.1646, 0.1375, 0.1421, 0.2012, 0.1957, 0.1297, 0.1754, 0.1390, 0.1761, 0.1119, 0.1915, 0.1827, 0.1548, 0.1522, 0.1369, 0.2495, 0.1253, 0.1597, 0.2195, 0.2555, 0.1956, 0.1831, 0.1791, 0.2057, 0.2406, 0.1227, 0.2196, 0.2641, 0.3067, 0.1749, 0.2148, 0.2195, 0.1993, 0.2421, 0.2430, 0.1994, 0.1779, 0.0942, 0.3067, 0.1965, 0.2003, 0.1180, 0.1686, 0.2668, 0.2113, 0.3371, 0.1730, 0.2212, 0.4972, 0.1641, 0.2667, 0.2690, 0.2321, 0.2792, 0.3515, 0.1398, 0.3436, 0.2254, 0.1302, 0.0864, 0.1619, 0.1311, 0.1994, 0.3176, 0.1856, 0.1071, 0.1041, 0.1593, 0.0537, 0.1149, 0.1176, 0.0457, 0.1264, 0.0476, 0.1620, 0.1154, 0.1493, 0.0673, 0.0894, 0.0365, 0.0385, 0.2190, 0.0777, 0.0561, 0.0435, 0.0372, 0.0385, 0.0769, 0.1491, 0.0802, 0.0870, 0.0476, 0.0562, 0.0138.
| Minimum | Median | Mean | Maximum | ||||
|---|---|---|---|---|---|---|---|
| 0.0138 | 0.1201 | 0.1628 | 0.1668 | 0.2064 | 0.4972 | 0.006202403 | 0.07875533 |
| Model | a | b | c | d |
|---|---|---|---|---|
| Gompertz | 2.25880 | 7.50430 | – | – |
| Power Gompertz | 10.00000 | 5.61014 | 1.54864 | – |
| Marshall–Olkin Gompertz | 2.25880 | 7.50430 | – | 1.00000 |
| Gamma | 3.84914 | 23.07735 | – | – |
| Weibull | 2.2223672 | 0.1879877 | – | – |
| Marshall–Olkin Power Gompertz | 10.00000 | 10.00000 | 2.876269 | 0.050427 |
| Model | l | AIC | BIC | A | KS | p-Value |
|---|---|---|---|---|---|---|
| Gompertz | −236.7621 | −232.7621 | −227.3431 | 2.8738 | 0.1214 | 0.07587 |
| Power Gompertz | −23.89247 | −17.89247 | −9.763883 | 2.0810 | 0.1059 | 0.16580 |
| Marshall–Olkin Gompertz | −236.7621 | −230.7621 | −222.6336 | 2.8738 | 0.1214 | 0.07587 |
| Gamma | −232.7172 | −228.7172 | −223.2981 | 1.7300 | 0.095747 | 0.26070 |
| Weibull | −227.1131 | −223.1131 | −217.6940 | 1.84045 | 0.088331 | 0.67790 |
| Marshall–Olkin Power Gompertz | −250.1612 | −242.1612 | −231.3231 | 1.5515 | 0.081044 | 0.45950 |


6.3. Data Set 2
- 0.080, 0.200, 0.400, 0.500, 0.510, 0.810, 0.900, 1.050, 1.190, 1.260, 1.350, 1.400, 1.460, 1.760, 2.020, 2.020, 2.070, 2.090, 2.230, 2.260, 2.460, 2.540, 2.620, 2.640, 2.690, 2.690, 2.750, 2.830, 2.870, 3.020, 3.250, 3.310, 3.360, 3.360, 3.480, 3.520, 3.570, 3.640, 3.700, 3.820, 3.880, 4.180, 4.230, 4.260, 4.330, 4.340, 4.400, 4.500, 4.510, 4.870, 4.980, 5.060, 5.090, 5.170, 5.320, 5.320, 5.340, 5.410, 5.410, 5.490, 5.620, 5.710, 5.850, 6.250, 6.540, 6.760, 6.930, 6.940, 6.970, 7.090, 7.260, 7.280, 7.320, 7.390, 7.590, 7.620, 7.630, 7.660, 7.870, 7.930,8.260, 8.370, 8.530, 8.650, 8.660, 9.020, 9.220, 9.470,9.740, 10.06, 10.34, 10.66, 10.75, 11.25, 11.64, 11.79,11.98, 12.02, 12.03, 12.07, 12.63, 13.11, 13.29, 13.80, 14.24, 14.76, 14.77, 14.83, 15.96, 16.62, 17.12, 17.14, 17.36, 18.10, 19.13, 20.28, 21.73, 22.69, 23.63, 25.74, 25.82, 26.31, 32.15, 34.26, 36.66, 43.01, 46.12, 79.05.
6.4. Data Set 3
- 0.0149, 0.0235, 0.0230, 0.0159, 0.0200, 0.0413, 0.0360, 0.0378, 0.0363, 0.0399, 0.0453, 0.0436, 0.0598, 0.0624, 0.0546, 0.0607, 0.0609, 0.0521, 0.0615, 0.0928, 0.2232, 0.0620, 0.0812, 0.0629, 0.0651, 0.0840, 0.1072, 0.0821, 0.0567, 0.0559, 0.0606, 0.0380, 0.0586, 0.0980, 0.0925, 0.0631, 0.1869, 0.0049, 0.0176, 0.0495, 0.1112, 0.0890, 0.0940, 0.0600, 0.0652, 0.0413, 0.0588, 0.0665, 0.0816, 0.0753, 0.0579, 0.0436, 0.0527, 0.0382, 0.0568, 0.0613, 0.0531, 0.0767, 0.0400, 0.0406, 0.0237, 0.0471, 0.0722, 0.0595, 0.0597, 0.0389, 0.0265, 0.0518, 0.0419, 0.0566, 0.0516, 0.0390, 0.0245, 0.0266, 0.0314, 0.0701, 0.0410, 0.0436, 0.0320, 0.0255, 0.0171, 0.0268, 0.0259, 0.0333, 0.0318, 0.0188, 0.0172, 0.0112, 0.0155, 0.0229, 0.0184, 0.0621, 0.0146, 0.0114, 0.0216, 0.0103, 0.0129, 0.0134, 0.0117, 0.0143, 0.0032 and 0.0054.
| Minimum | Median | Mean | Maximum | ||||
|---|---|---|---|---|---|---|---|
| 0.00320 | 0.02475 | 0.04360 | 0.04881 | 0.06145 | 0.22320 | 0.001106218 | 0.03325986 |

7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc. Lond. 1824, 115, 513–583. [Google Scholar]
- Eghwerido, J.T.; Nzei, L.C.; Agu, F.I. The alpha power Gompertz distribution: Characterization, properties, and applications. Sankhya A 2021, 83, 449–475. [Google Scholar] [CrossRef]
- Khan, M.S.; King, R.; Hudson, I.L. Transmuted Gompertz distribution: Properties and estimation. Pak. J. Statist. 2016, 32, 161–182. [Google Scholar]
- Khan, M.S.; King, R.; Hudson, I.L. Transmuted Generalized Gompertz distribution with application. J. Stat. Theory Appl. 2017, 16, 65–80. [Google Scholar] [CrossRef]
- Benkhelifa, L. The Marshall-Olkin extended generalized Gompertz distribution. J. Data Sci. 2017, 15, 239–266. [Google Scholar] [CrossRef]
- Eghwerido, J.T.; Ikwuoche, J.D.; Adubisi, O.D. Inverse odd Weibull generated family of distributions. Pak. J. Stat. Oper. Res. 2020, 16, 617–633. [Google Scholar] [CrossRef]
- Eghwerido, J.T.; Agu, F.I.; Ibidoja, O.J. The shifted exponential-G family of distributions: Properties and applications. J. Stat. Manag. Syst. 2022, 25, 43–75. [Google Scholar] [CrossRef]
- Eghwerido, J.T.; Agu, F.I. The shifted Gompertz-G family of distributions: Properties and applications. Math. Slovaca 2021, 71, 1291–1308. [Google Scholar] [CrossRef]
- Eghwerido, J.T. The alpha power Teissier distribution and its applications. Afr. Stat. 2021, 16, 2733–2747. [Google Scholar] [CrossRef]
- Thomas, J.; Zelibe, S.C.; Eyefia, E. Kumaraswamy alpha power inverted exponential distribution: Properties and applications. Istat. J. Turk. Stat. Assoc. 2019, 12, 35–48. [Google Scholar]
- Eghwerido, J.T.; Oguntunde, P.E.; Agu, F.I. The alpha power Marshall-Olkin-G distribution: Properties and applications. Sankhya A 2021, 85, 172–197. [Google Scholar] [CrossRef]
- Eghwerido, J.T.; Nzei, L.; David, I.J.; Adubisi, O.D. The Gompertz extended generalized exponential distribution: Properties and applications. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2020, 69, 739–753. [Google Scholar] [CrossRef]
- Eghwerido, J.T.; Zelibe, S.C.; Efe-Eyefia, E. Gompertz-alpha power inverted exponential distribution: Properties and applications. Thail. Stat. 2020, 18, 319–332. [Google Scholar]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Mahdavi, A.; Kundu, D. A new method for generating distributions with an application to exponential distribution. Commun. Stat. Theory Methods 2017, 46, 6543–6557. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Eghwerido, J.T.; Ogbo, J.O.; Omotoye, A.E. The Marshall-Olkin Gompertz distribution: Properties and applications. Statistica 2021, 81, 183–215. [Google Scholar]
- Smith, R.L.; Naylor, J. A comparison of maximum likelihood and Bayesian estimators for the three-parameter Weibull distribution. Appl. Stat. 1987, 36, 358–369. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 20 May 2025).
- Ahmad, A.; Ahmad, A.; Tashkandy, Y.A.; Bakr, M.E.; Mekiso, G.T.; Balogun, O.S.; Gemeay, A.M. A study on the new logarithmic-G family with statistical properties, simulations, and different data analysis. Sci. Rep. 2025, 15, 15069. [Google Scholar] [CrossRef]
- Aldeni, M.; Lee, C.; Famoye, F. Families of distributions arising from the quantile of generalized lambda distribution. J. Stat. Distrib. Appl. 2017, 4, 25. [Google Scholar] [CrossRef]
- Alsuhabi, H.; Alkhairy, I.; Almetwally, E.M.; Almongy, H.M.; Gemeay, A.M.; Hafez, E.H.; Aldallal, R.A.; Sabry, M. A superior extension for the Lomax distribution with application to COVID-19 infections real data. Alex. Eng. J. 2022, 61, 11077–11090. [Google Scholar] [CrossRef]













| d | Median | |||||
|---|---|---|---|---|---|---|
| 2.0 | 0.38290646 | 0.18260440 | 0.60828465 | 0.05890837 | 1.13072244 | |
| 0.3 | 0.08626889 | 0.02398859 | 0.23101085 | 0.39832268 | 1.40894761 | |
| 1.5 | 0.32533440 | 0.14224880 | 0.55012270 | 0.10224390 | 1.12500640 | |
| 3.8 | 0.51539840 | 0.29275530 | 0.73168760 | −0.01447590 | 1.17561930 | |
| 2.0 | 0.69465380 | 0.55485170 | 0.80740930 | −0.10709030 | 1.23305070 | |
| 0.3 | 0.44949095 | 0.32145487 | 0.59470041 | 0.06284964 | 1.19678632 | |
| 1.5 | 0.66004885 | 0.51645561 | 0.78096380 | −0.08573750 | 1.21036321 | |
| 3.8 | 0.76437790 | 0.63887820 | 0.85907320 | −0.13989610 | 1.29195260 | |
| 2.0 | 0.72626310 | 0.64195670 | 0.78649050 | −0.16659860 | 1.29606390 | |
| 0.3 | 0.56938656 | 0.46779810 | 0.66724369 | −0.01870850 | 1.19415510 | |
| 1.5 | 0.70649280 | 0.61649990 | 0.77289660 | −0.15082870 | 1.26744330 | |
| 3.8 | 0.76424170 | 0.69405750 | 0.81219430 | −0.18818410 | 1.35923060 | |
| 2.0 | 0.71073430 | 0.63393900 | 0.76490920 | −0.17271420 | 1.30399180 | |
| 0.3 | 0.56692136 | 0.47166155 | 0.65709561 | −0.02742510 | 1.19551450 | |
| 1.5 | 0.69284670 | 0.61052950 | 0.75271390 | −0.15789360 | 1.27516910 | |
| 3.8 | 0.74496270 | 0.68155030 | 0.78787210 | −0.19283950 | 1.36756710 | |
| 2.0 | 0.75280510 | 0.69001990 | 0.79634340 | −0.18102270 | 1.31790890 | |
| 0.3 | 0.63396511 | 0.55183950 | 0.70906749 | −0.04466910 | 1.20596318 | |
| 1.5 | 0.73828910 | 0.67056420 | 0.78660270 | −0.16728310 | 1.28819650 | |
| 3.8 | 0.78039500 | 0.72909600 | 0.81465070 | −0.19921000 | 1.37814290 |
| d | Mean | Variance | 3rd Moment | 4th Moment | |
|---|---|---|---|---|---|
| 2.8 | 0.7257 | 0.0385 | 0.4602 | 0.3872 | |
| 3.3 | 0.7434 | 0.0370 | 0.4872 | 0.4150 | |
| 3.8 | 0.7581 | 0.0356 | 0.5106 | 0.4394 | |
| 4.1 | 0.7660 | 0.0349 | 0.5233 | 0.4528 | |
| 2.8 | 0.6328 | 0.0191 | 0.2871 | 0.2010 | |
| 3.3 | 0.6450 | 0.0182 | 0.3008 | 0.2130 | |
| 3.8 | 0.6552 | 0.0174 | 0.3127 | 0.2233 | |
| 4.1 | 0.6605 | 0.0169 | 0.3190 | 0.2289 | |
| 2.8 | 1.0766 | 0.5835 | 3.4545 | 7.8668 | |
| 3.3 | 1.1476 | 0.6039 | 3.8893 | 8.9820 | |
| 3.8 | 1.2097 | 0.6198 | 4.2957 | 10.0442 | |
| 4.1 | 1.2436 | 0.6277 | 4.5278 | 10.6589 |
| 0.25 | 0.7302033 | 0.8835358 |
| 0.5 | 0.5347315 | 1.0056804 |
| 0.75 | 0.3757402 | 1.6979304 |
| 1.5 | 0.4124733 | −0.7010513 |
| 2 | 0.3269019 | −0.3607943 |
| 3 | 0.2431661 | −0.2232975 |
| Sample Size | Parameter | AE | Bias | Variance | MSE | RMSE |
|---|---|---|---|---|---|---|
| 50 | 1.403027 | −0.2969733 | 2.531496 | 2.619182 | 1.618389 | |
| 2.494623 | 0.8946226 | 1.680719 | 2.480732 | 1.575034 | ||
| 1.907303 | 0.007302849 | 0.3308364 | 0.3308234 | 0.5751725 | ||
| 2.028698 | 1.428698 | 132.4825 | 134.497 | 11.59729 | ||
| 100 | 1.468208 | −0.2317916 | 2.104932 | 2.158238 | 1.469094 | |
| 2.315360 | 0.7153595 | 1.446955 | 1.958405 | 1.399430 | ||
| 1.874812 | −0.02518752 | 0.1716296 | 0.1722297 | 0.4150057 | ||
| 1.272029 | 0.6720287 | 35.2335 | 35.67808 | 5.973113 | ||
| 150 | 1.460094 | −0.2399062 | 1.786332 | 1.843529 | 1.357766 | |
| 2.267850 | 0.6678498 | 1.330526 | 1.776283 | 1.332773 | ||
| 1.866607 | −0.03339264 | 0.1173131 | 0.1184046 | 0.3440998 | ||
| 0.9687776 | 0.3687776 | 19.78717 | 19.91921 | 4.463094 | ||
| 200 | 1.464602 | −0.2353983 | 1.559436 | 1.614537 | 1.270644 | |
| 2.201872 | 0.6018720 | 1.197432 | 1.559442 | 1.248776 | ||
| 1.872626 | −0.02737415 | 0.08514975 | 0.08588206 | 0.2930564 | ||
| 0.8163338 | 0.2163338 | 10.42389 | 10.46861 | 3.235523 | ||
| 250 | 1.480735 | −0.2192645 | 1.422855 | 1.470647 | 1.212702 | |
| 2.169876 | 0.5698755 | 1.162843 | 1.487368 | 1.219577 | ||
| 1.867437 | −0.03256283 | 0.06458035 | 0.06562777 | 0.2561792 | ||
| 0.6976477 | 0.09764765 | 1.399904 | 1.409159 | 1.187080 | ||
| 350 | 1.484816 | −0.2151837 | 1.484816 | 1.239795 | 1.113461 | |
| 2.113505 | 0.5135053 | 2.113505 | 1.305716 | 1.142679 | ||
| 1.877554 | −0.02244633 | 0.04777045 | 0.04826474 | 0.2196924 | ||
| 0.6388831 | 0.03888314 | 0.4958848 | 0.4972975 | 0.7051932 |
| Sample Size | Parameter | AE | Bias | Variance | MSE | RMSE |
|---|---|---|---|---|---|---|
| 50 | 1.784009 | −0.7159908 | 3.580949 | 4.092874 | 2.023085 | |
| 3.097175 | 1.297175 | 2.459885 | 4.142055 | 2.035204 | ||
| 3.591730 | 0.09173038 | 1.320104 | 1.328254 | 1.152499 | ||
| 2.354617 | 1.454617 | 111.5903 | 113.6839 | 10.66226 | ||
| 100 | 1.966794 | −0.5332061 | 3.367743 | 3.651378 | 1.910858 | |
| 2.828541 | 1.028541 | 2.337539 | 3.394967 | 1.842544 | ||
| 3.478744 | −0.02125599 | 0.7371669 | 0.7374711 | 0.8587614 | ||
| 2.019041 | 1.119041 | 93.12662 | 94.36023 | 9.713919 | ||
| 150 | 1.967338 | −0.532662 | 2.817610 | 3.100775 | 1.760902 | |
| 2.751210 | 0.9512103 | 2.143555 | 3.047927 | 1.745831 | ||
| 3.472308 | −0.02769216 | 0.4488286 | 0.4495056 | 0.6704518 | ||
| 1.156495 | 0.2564951 | 8.003632 | 8.067819 | 2.840391 | ||
| 200 | 2.056188 | −0.443812 | 2.501721 | 2.698189 | 1.642617 | |
| 2.615520 | 0.8155205 | 1.983365 | 2.648042 | 1.627281 | ||
| 3.469061 | −0.03093884 | 0.3634978 | 0.3643823 | 0.6036409 | ||
| 1.106084 | 0.206084 | 8.231363 | 8.272187 | 2.876141 | ||
| 250 | 2.099677 | −0.4003231 | 2.303136 | 2.462934 | 1.569374 | |
| 2.533784 | 0.7337842 | 1.844653 | 2.382724 | 1.543607 | ||
| 3.469258 | −0.03074175 | 0.2925736 | 0.2934602 | 0.5417196 | ||
| 1.030674 | 0.1306739 | 4.290053 | 4.306270 | 2.075156 | ||
| 350 | 2.099016 | −0.4009836 | 1.924913 | 2.085316 | 1.444062 | |
| 2.481551 | 0.681551 | 1.662466 | 2.126645 | 1.458302 | ||
| 3.462565 | −0.03743505 | 0.1944424 | 0.1958049 | 0.4424985 | ||
| 0.946022 | 0.04602195 | 1.510235 | 1.512051 | 1.229655 |
| Sample Size | Parameter | AE | Bias | Variance | MSE | RMSE |
|---|---|---|---|---|---|---|
| 50 | 0.926953 | 0.026953 | 1.563981 | 1.564393 | 1.250757 | |
| 2.010265 | 0.610265 | 1.151444 | 1.523637 | 1.234357 | ||
| 2.844973 | −0.055027 | 0.452010 | 0.454947 | 0.674498 | ||
| 0.940922 | 0.770922 | 107.8541 | 108.4268 | 10.41282 | ||
| 100 | 0.991690 | 0.091690 | 1.366354 | 1.374487 | 1.172385 | |
| 1.789751 | 0.389751 | 0.781199 | 0.932948 | 0.965893 | ||
| 2.848979 | −0.051021 | 0.247050 | 0.249604 | 0.499604 | ||
| 0.794938 | 0.624938 | 140.3078 | 140.6702 | 11.86045 | ||
| 150 | 0.982015 | 0.082015 | 1.158914 | 1.165409 | 1.079541 | |
| 1.738595 | 0.338595 | 0.676697 | 0.791208 | 0.889499 | ||
| 2.840943 | −0.059057 | 0.152653 | 0.156110 | 0.395108 | ||
| 0.407379 | 0.237379 | 19.55789 | 19.61032 | 4.428354 | ||
| 200 | 0.970217 | 0.070217 | 0.989686 | 0.994418 | 0.997205 | |
| 1.691925 | 0.291925 | 0.623786 | 0.708881 | 0.841951 | ||
| 2.846649 | −0.053351 | 0.115127 | 0.117950 | 0.343438 | ||
| 0.296755 | 0.126755 | 2.829213 | 2.844714 | 1.686628 | ||
| 250 | 0.955454 | 0.055454 | 0.833672 | 0.836580 | 0.914648 | |
| 1.675397 | 0.275397 | 0.569573 | 0.645302 | 0.803307 | ||
| 2.851899 | −0.048101 | 0.088108 | 0.090404 | 0.300672 | ||
| 0.237157 | 0.067157 | 0.275380 | 0.279835 | 0.528994 | ||
| 350 | 0.949376 | 0.049376 | 0.702748 | 0.705046 | 0.839670 | |
| 1.641489 | 0.241489 | 0.519298 | 0.577511 | 0.759941 | ||
| 2.858940 | −0.041060 | 0.059486 | 0.061160 | 0.247306 | ||
| 0.213738 | 0.043738 | 0.061174 | 0.063074 | 0.251146 |
| Minimum | Median | Mean | Maximum | ||||
|---|---|---|---|---|---|---|---|
| 0.080 | 3.348 | 6.395 | 9.366 | 11.838 | 79.050 | 110.425 | 10.50833. |
| Model | a | b | c | d |
|---|---|---|---|---|
| Gompertz | 0.106772 | 0.000001 | – | – |
| Power Gompertz | 0.093910 | 0.000001 | 1.047758 | – |
| Marshall–Olkin Gompertz | 0.106775 | 0.000001 | – | 0.999999 |
| Gamma | 1.172559 | 0.125201 | – | – |
| Weibull | 1.047835 | 9.560699 | – | – |
| Marshall–Olkin Power Gompertz | 0.006559 | 0.000001 | 1.511359 | 0.109803 |
| Model | l | AIC | BIC | A | KS | p-Value |
|---|---|---|---|---|---|---|
| Gompertz | 828.6841 | 832.6841 | 839.9882 | 1.1736 | 0.084631 | 0.3184 |
| Power Gompertz | 1084.1740 | 1090.1740 | 1098.7300 | 0.95775 | 0.069991 | 0.5575 |
| Marshall–Olkin Gompertz | 828.6841 | 834.6841 | 843.2402 | 1.1736 | 0.084636 | 0.3183 |
| Gamma | 831.7356 | 835.7356 | 841.4396 | 0.77148 | 0.073289 | 0.4975 |
| Weibull | 830.1738 | 834.1738 | 839.9778 | 0.95771 | 0.070017 | 0.5570 |
| Marshall–Olkin Power Gompertz | 820.5461 | 828.5461 | 839.9542 | 0.23751 | 0.039214 | 0.9893 |
| Model | a | b | c | d |
|---|---|---|---|---|
| Gompertz | 14.6398 | 8.0975 | – | – |
| Power Gompertz | 10.00000 | 9.60754 | 0.93220 | – |
| Marshall–Olkin Gompertz | 10.00000 | 10.00000 | – | 0.71989 |
| Gamma | 2.34571 | 48.05337 | – | – |
| Weibull | 1.578270 | 0.054556 | – | – |
| Marshall–Olkin Power Gompertz | 4.6546585 | 2.8468283 | 2.2647271 | 0.0034618 |
| Model | ℓ | AIC | BIC | A | KS | p-Value |
|---|---|---|---|---|---|---|
| Gompertz | 3.5349 | 0.11849 | 0.1140 | |||
| Power Gompertz | 3.4155 | 0.13386 | 0.05169 | |||
| Marshall–Olkin Gompertz | 3.8502 | 0.14751 | 0.02362 | |||
| Gamma | 1.8057 | 0.09030 | 0.5263 | |||
| Weibull | 1.8091 | 0.08938 | 0.3891 | |||
| Marshall–Olkin Power Gompertz | 1.5056 | 0.08811 | 0.4068 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakaş, A.M.; Bulut, F. The New Gompertz Distribution Model and Applications. Symmetry 2025, 17, 843. https://doi.org/10.3390/sym17060843
Karakaş AM, Bulut F. The New Gompertz Distribution Model and Applications. Symmetry. 2025; 17(6):843. https://doi.org/10.3390/sym17060843
Chicago/Turabian StyleKarakaş, Ayşe Metin, and Fatma Bulut. 2025. "The New Gompertz Distribution Model and Applications" Symmetry 17, no. 6: 843. https://doi.org/10.3390/sym17060843
APA StyleKarakaş, A. M., & Bulut, F. (2025). The New Gompertz Distribution Model and Applications. Symmetry, 17(6), 843. https://doi.org/10.3390/sym17060843







