An Invertible, Robust Steganography Network Based on Mamba
Abstract
1. Introduction
- We propose a invertible steganography network with stronger robustness (MRIN).
- We propose using a selective state space model (SSM) for efficient global feature modeling. By modeling with the differential equations of linear time-invariant systems, we maintain a global receptive field while reducing computational complexity to , significantly enhancing feature representation capability while ensuring lossless information transmission.
- We propose a dynamic adversarial noise training strategy, introducing a composite optimization framework that integrates fidelity constraints, adversarial games, and noise immunity, achieving dynamic balance in the steganography system through multimodal joint training.
- We introduced the Wasserstein GAN framework to establish a dynamic adversarial game, where the generator embeds secret information into the cover image through reversible transformations and the discriminator uses a multi-level wavelet convolution structure. When the game reaches Nash equilibrium, the distribution of the stego images coincides with that of natural images, achieving statistical invisibility.
2. Related Works
2.1. Image Steganography
2.2. Invertible Neural Networks
2.3. Mamba Architecture and the SSM
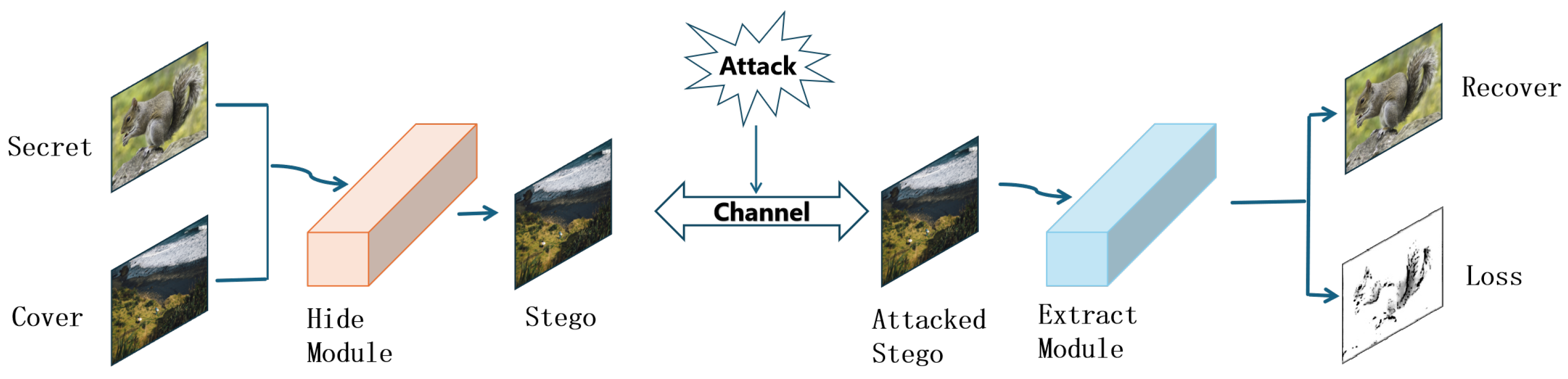
3. Proposed Method
3.1. Invertible Feature Mapping Mechanism
- 1.
- Base Case (): Apply an inverse transformation to the first level forward output :Substituting the forward equation giveswhere , verifying that the base case holds.
- 2.
- Inductive Hypothesis: Assume that the kth layer satisfies .
- 3.
- Inductive Step: For the th layer, the forward output is , and the inverse transformation is applied:Replacing and according to the forward equation givesBy the induction hypothesis, it follows that after N inverse transformations, there must be .
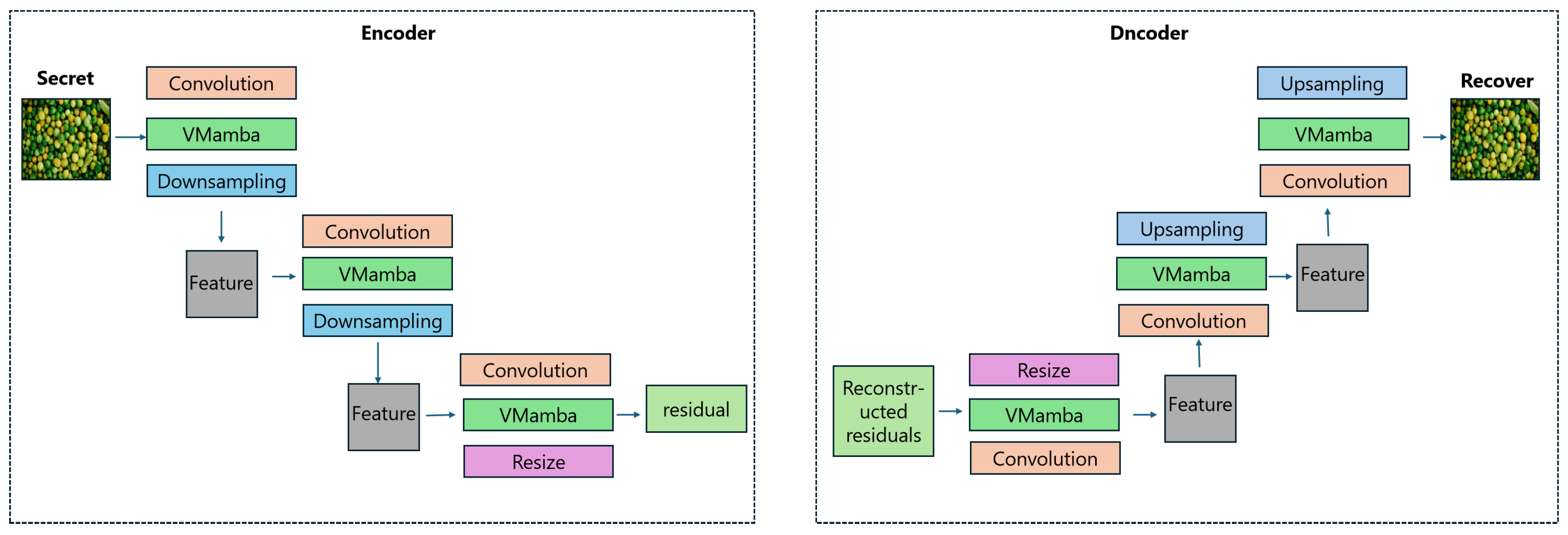
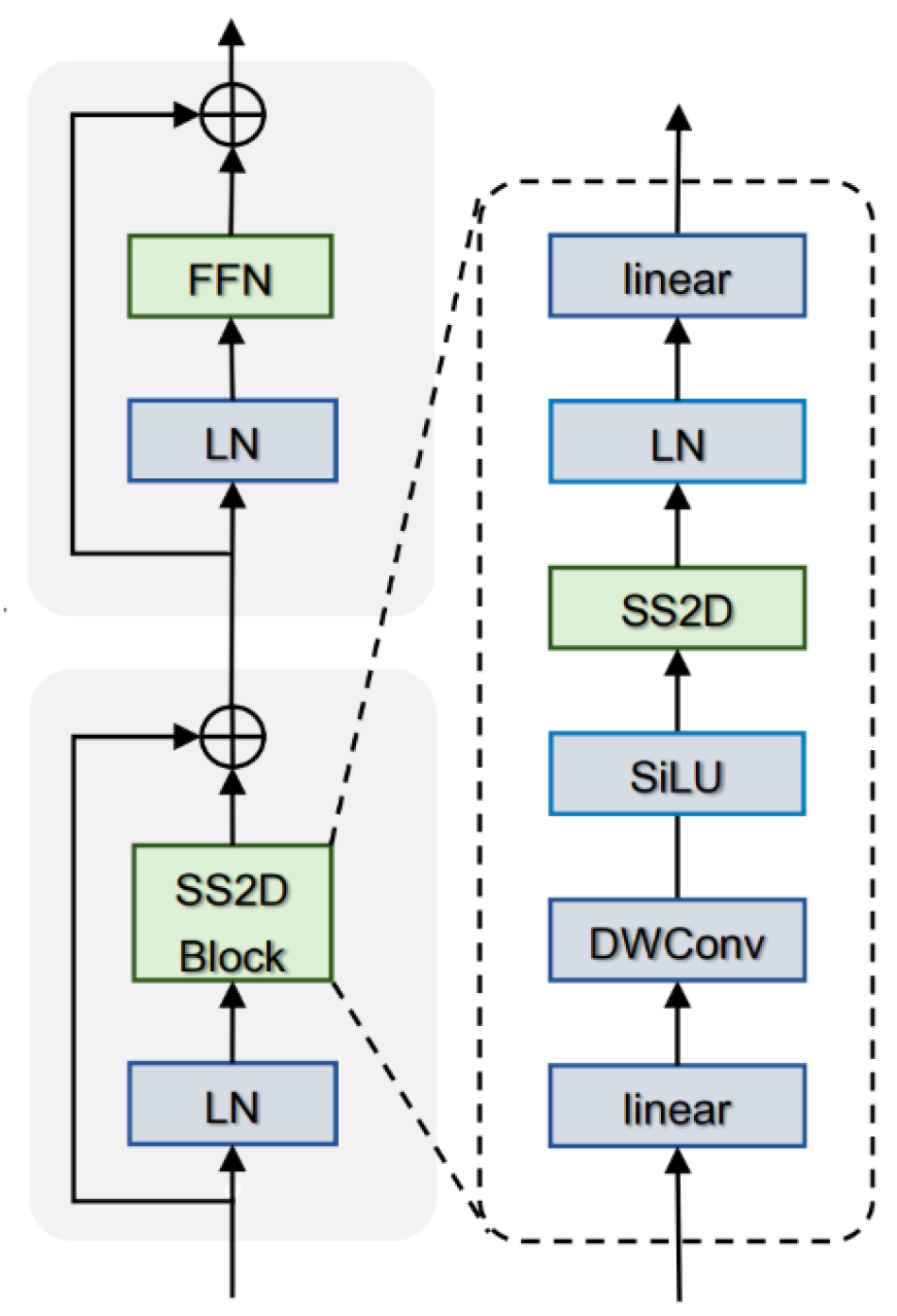
3.2. Imitation VMamba Module
- -
- The input sequence mapping , where t refers to any given time.
- -
- The latent state representation .
- -
- The predicted output sequence .
3.3. Compound Loss Optimization for Adversarial Training
4. Experiments
4.1. Datasets
4.2. Implementation Details
4.3. Evaluation Metrics
4.3.1. Structural Similarity Index
4.3.2. Peak Signal-to-Noise Ratio
4.3.3. No-Reference Image Quality Evaluation
- 1.
- Local luminance distribution modeling:
- 2.
- Texture correlation analysis:
- 3.
- Multi-scale wavelet coefficient analysis:
5. Results and Discussion
5.1. Image Hiding and Reconstruction Visualization
5.2. Quality of Information Reconstruction
5.3. Robustness Against Degradation
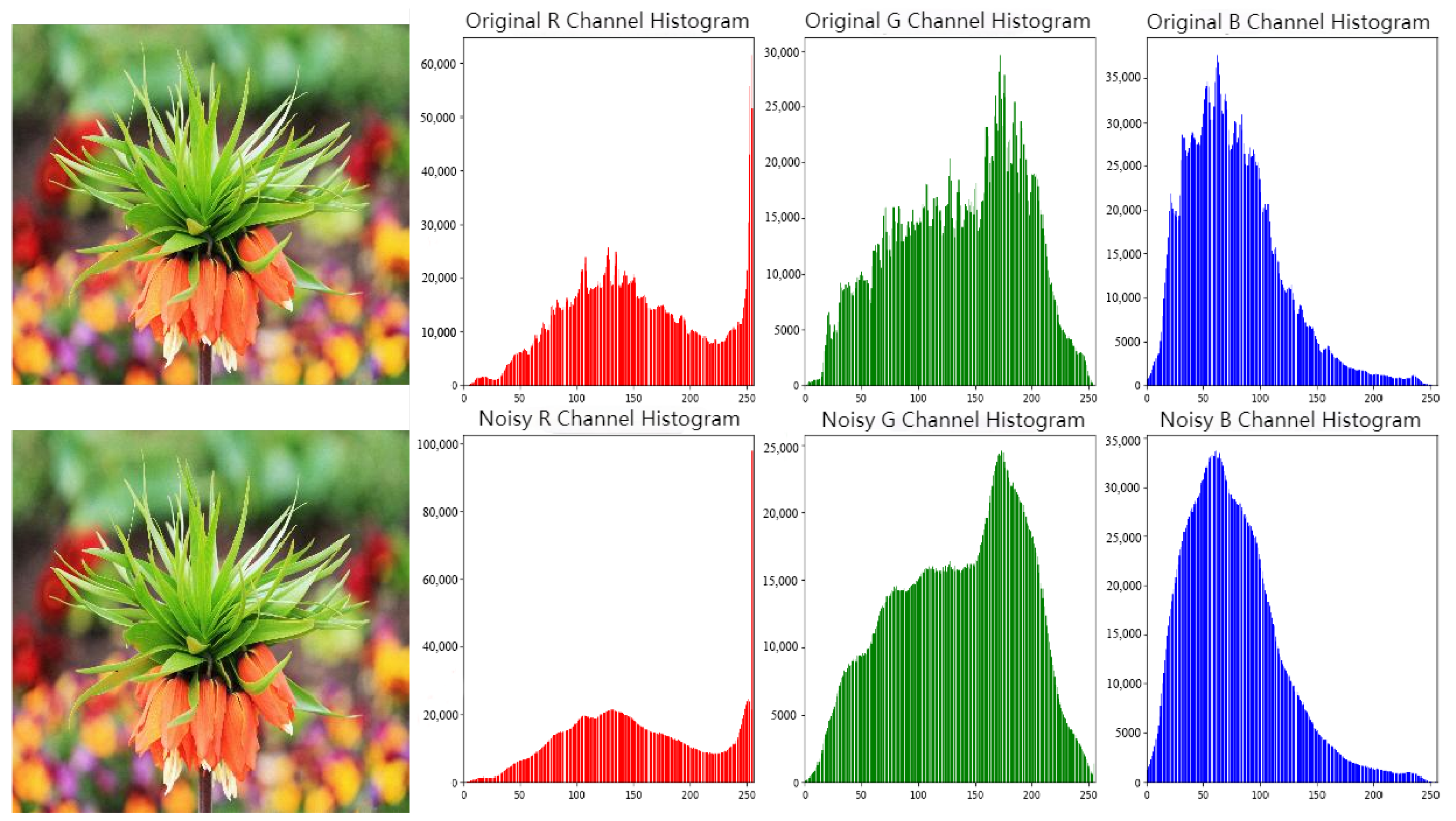
5.4. Invisibility Assessment
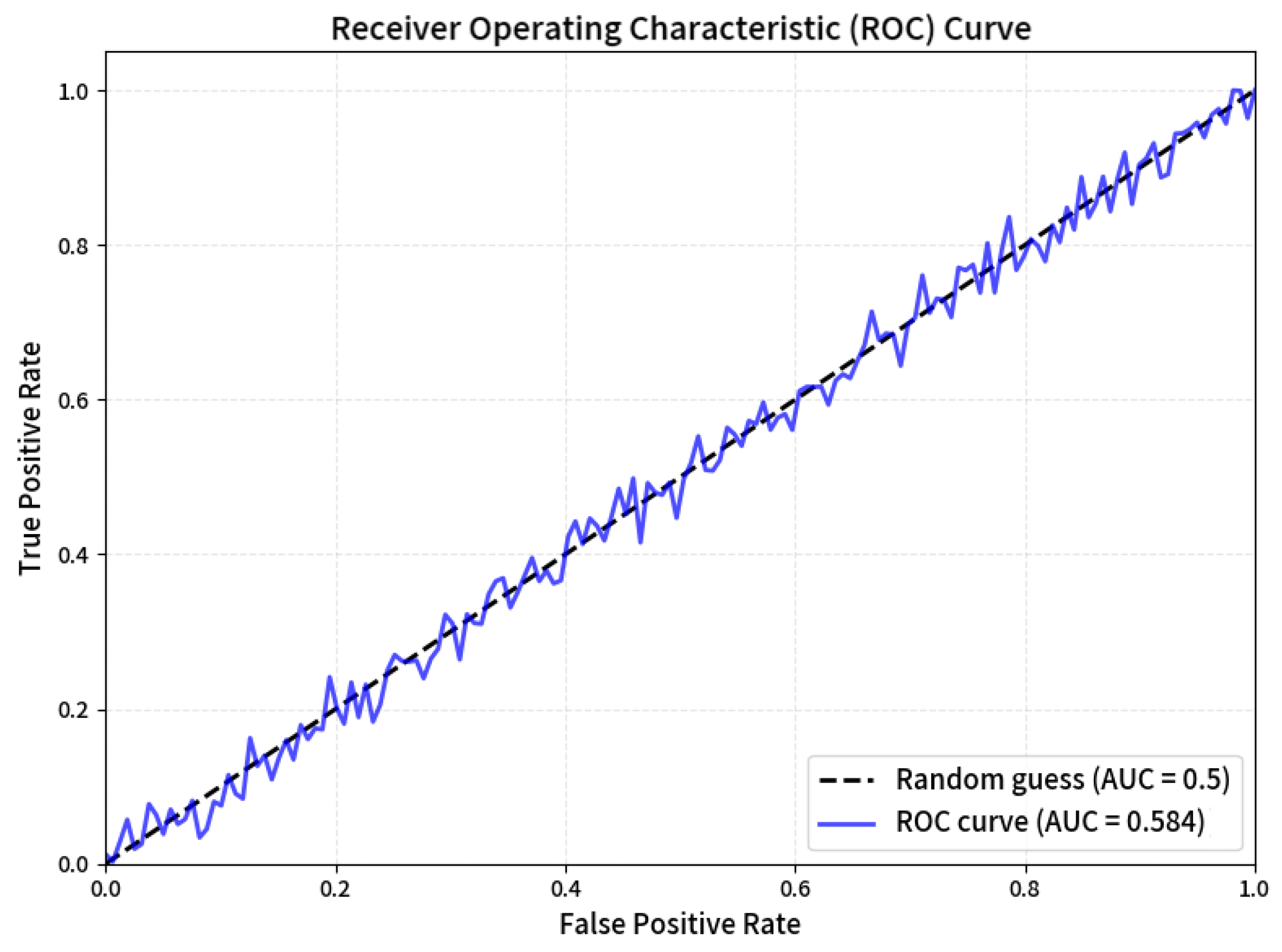
5.5. Resistance to Steganalysis
5.6. Ablation Experiment
5.7. Complexity Comparison
6. Conclusions
- Coverless steganography: Coverless steganography aims to embed secret information within a medium without modifying the cover object. The Mamba architecture could be applied to a coverless image steganography to weaken the dependence on cover images.
- Lightweight network: Researchers could further solve the problem of high memory usage and degradation of inference speed faced when dealing with long sequences.
- Multimodal steganography: In the future, an adaptive dynamic steganography system could be developed to adjust the joint concealment of text, images, and videos in real time.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheddad, A.; Condell, J.; Curran, K.; Mc Kevitt, P. Digital image steganography: Survey and analysis of current methods. Signal Process. 2010, 90, 727–752. [Google Scholar] [CrossRef]
- Baluja, S. Hiding images in plain sight: Deep steganography. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Denis, V.; Ivan, N.; Evgeny, B. Steganographic generative adversarial networks. In Proceedings of the Twelfth International Conference on Machine Vision, Amsterdam, The Netherlands, 16–18 November 2019; Volume 11433, p. 114333M. [Google Scholar]
- Shi, H.; Dong, J.; Wang, W.; Qian, Y.; Zhang, X. SSGAN: Secure steganography based on generative adversarial networks. In Proceedings of the Advances in Multimedia Information Processing–PCM 2017: 18th Pacific-Rim Conference on Multimedia, Harbin, China, 28–29 September 2017; Revised Selected Papers, Part I 18. Springer: Berlin/Heidelberg, Germany, 2018; pp. 534–544. [Google Scholar]
- Yao, Y.; Wang, J.; Chang, Q.; Ren, Y.; Meng, W. High invisibility image steganography with wavelet transform and generative adversarial network. Expert Syst. Appl. 2024, 249, 123540. [Google Scholar] [CrossRef]
- Zhang, R.; Dong, S.; Liu, J. Invisible Steganography via Generative Adversarial Networks. arXiv 2018, arXiv:1807.0857. [Google Scholar]
- Weng, X.; Li, Y.; Chi, L.; Mu, Y. High-capacity convolutional video steganography with temporal residual modeling. In Proceedings of the 2019 on International Conference on Multimedia Retrieval, Ottawa, ON, Canada, 10–13 June 2019; pp. 87–95. [Google Scholar]
- Rahim, R.; Nadeem, S. End-to-end trained CNN encoder-decoder networks for image steganography. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Zhu, J.; Kaplan, R.; Johnson, J.; Fei-Fei, L. Hidden: Hiding data with deep networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 657–672. [Google Scholar]
- Lu, S.P.; Wang, R.; Zhong, T.; Rosin, P.L. Large-capacity image steganography based on invertible neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10816–10825. [Google Scholar]
- Cheng, K.L.; Xie, Y.; Chen, Q. Iicnet: A generic framework for reversible image conversion. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual Event, 11–17 October 2021; pp. 1991–2000. [Google Scholar]
- Xu, Y.; Mou, C.; Hu, Y.; Xie, J.; Zhang, J. Robust Invertible Image Steganography. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 7865–7874. [Google Scholar] [CrossRef]
- Jing, J.; Deng, X.; Xu, M.; Wang, J.; Guan, Z. Hinet: Deep image hiding by invertible network. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 4733–4742. [Google Scholar]
- Dinh, L.; Krueger, D.; Bengio, Y. Nice: Non-linear independent components estimation. arXiv 2014, arXiv:1410.8516. [Google Scholar]
- Skodras, A.; Christopoulos, C.; Ebrahimi, T. The JPEG 2000 still image compression standard. IEEE Signal Process. Mag. 2001, 18, 36–58. [Google Scholar] [CrossRef]
- Yangjie, Z.; Jia, L.; Yan, K.; Meiqi, L. Image steganography based on generative implicit neural representation. arXiv 2024, arXiv:2406.01918. [Google Scholar]
- Mandal, P.C.; Mukherjee, I.; Paul, G.; Chatterji, B. Digital image steganography: A literature survey. Inf. Sci. 2022, 609, 1451–1488. [Google Scholar] [CrossRef]
- Mielikainen, J. LSB matching revisited. IEEE Signal Process. Lett. 2006, 13, 285–287. [Google Scholar] [CrossRef]
- Noda, H.; Niimi, M.; Kawaguchi, E. Application of QIM with dead zone for histogram preserving JPEG steganography. In Proceedings of the IEEE International Conference on Image Processing 2005, Genova, Italy, 11–14 September 2005; Volume 2, pp. II–1082. [Google Scholar] [CrossRef]
- Wang, W.; Tan, H.; Pang, Y.; Li, Z.; Ran, P.; Wu, J. A Novel Encryption Algorithm Based on DWT and Multichaos Mapping. J. Sens. 2016, 2016, 2646205. [Google Scholar] [CrossRef]
- Volkhonskiy, D.; Borisenko, B.; Burnaev, E. Generative Adversarial Networks for Image Steganography. arXiv 2017, arXiv:1703.05502. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Tang, W.; Tan, S.; Li, B.; Huang, J. Automatic steganographic distortion learning using a generative adversarial network. IEEE Signal Process. Lett. 2017, 24, 1547–1551. [Google Scholar] [CrossRef]
- Xu, G.; Wu, H.Z.; Shi, Y.Q. Structural design of convolutional neural networks for steganalysis. IEEE Signal Process. Lett. 2016, 23, 708–712. [Google Scholar] [CrossRef]
- Wu, P.; Yang, Y.; Li, X. Stegnet: Mega image steganography capacity with deep convolutional network. Future Internet 2018, 10, 54. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Duan, X.; Jia, K.; Li, B.; Guo, D.; Zhang, E.; Qin, C. Reversible image steganography scheme based on a U-Net structure. IEEE Access 2019, 7, 9314–9323. [Google Scholar] [CrossRef]
- Zhou, Y.; Luo, T.; He, Z.; Jiang, G.; Xu, H.; Chang, C.C. CAISFormer: Channel-wise attention transformer for image steganography. Neurocomputing 2024, 603, 128295. [Google Scholar] [CrossRef]
- Xiao, C.; Peng, S.; Zhang, L.; Wang, J.; Ding, D.; Zhang, J. A transformer-based adversarial network framework for steganography. Expert Syst. Appl. 2025, 269, 126391. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Guo, Y.; Liu, Z. Coverless Steganography for Face Recognition Based on Diffusion Model. IEEE Access 2024, 12, 148770–148782. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Ying, Q.; Peng, W.; Zhang, X.; Qian, Z. Establishing Robust Generative Image Steganography via Popular Stable Diffusion. IEEE Trans. Inf. Forensics Secur. 2024, 19, 8094–8108. [Google Scholar] [CrossRef]
- Peng, Y.; Hu, D.; Wang, Y.; Chen, K.; Pei, G.; Zhang, W. StegaDDPM: Generative Image Steganography based on Denoising Diffusion Probabilistic Model. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; MM ’23. pp. 7143–7151. [Google Scholar] [CrossRef]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using Real NVP. arXiv 2017, arXiv:1605.08803. [Google Scholar]
- Yang, H.; Xu, Y.; Liu, X.; Ma, X. PRIS: Practical robust invertible network for image steganography. Eng. Appl. Artif. Intell. 2024, 133, 108419. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 4–9 December 2017; NIPS’17. pp. 6000–6010. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-Time Sequence Modeling with Selective State Spaces. arXiv 2024, arXiv:2312.00752. [Google Scholar]
- Liu, Y.; Tian, Y.; Zhao, Y.; Yu, H.; Xie, L.; Wang, Y.; Ye, Q.; Jiao, J.; Liu, Y. VMamba: Visual State Space Model. In Proceedings of the Advances in Neural Information Processing Systems; Globerson, A., Mackey, L., Belgrave, D., Fan, A., Paquet, U., Tomczak, J., Zhang, C., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2024; Volume 37, pp. 103031–103063. [Google Scholar]
- Gu, A.; Dao, T.; Ermon, S.; Rudra, A.; Ré, C. HiPPO: Recurrent Memory with Optimal Polynomial Projections. In Proceedings of the Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 1474–1487. [Google Scholar]
- Wu, L.; Cheng, H.; Yan, W.; Chen, F.; Wang, M.; Wang, T. Reversible and colorable deep image steganography with large capacity. J. Electron. Imaging 2023, 32, 043006. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R. Ntire 2017 challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 126–135. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Proceedings, Part v 13. Springer: Berlin/Heidelberg, Germany, 2014; pp. 740–755. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Welstead, S.T. Fractal and Wavelet Image Compression Techniques; SPIE Press: Bellingham, WA, USA, 1999; Volume 40. [Google Scholar]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “completely blind” image quality analyzer. IEEE Signal Process. Lett. 2012, 20, 209–212. [Google Scholar] [CrossRef]
- Stamm, M.C.; Liu, K.R. Forensic detection of image manipulation using statistical intrinsic fingerprints. IEEE Trans. Inf. Forensics Secur. 2010, 5, 492–506. [Google Scholar] [CrossRef]
- Song, H.; Tang, G.; Sun, Y.; Gao, Z. Security Measure for Image Steganography Based on High Dimensional KL Divergence. Secur. Commun. Netw. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Boehm, B. StegExpose-A Tool for Detecting LSB Steganography. arXiv 2014, arXiv:1410.6656. [Google Scholar]
- Boroumand, M.; Chen, M.; Fridrich, J. Deep residual network for steganalysis of digital images. IEEE Trans. Inf. Forensics Secur. 2018, 14, 1181–1193. [Google Scholar] [CrossRef]
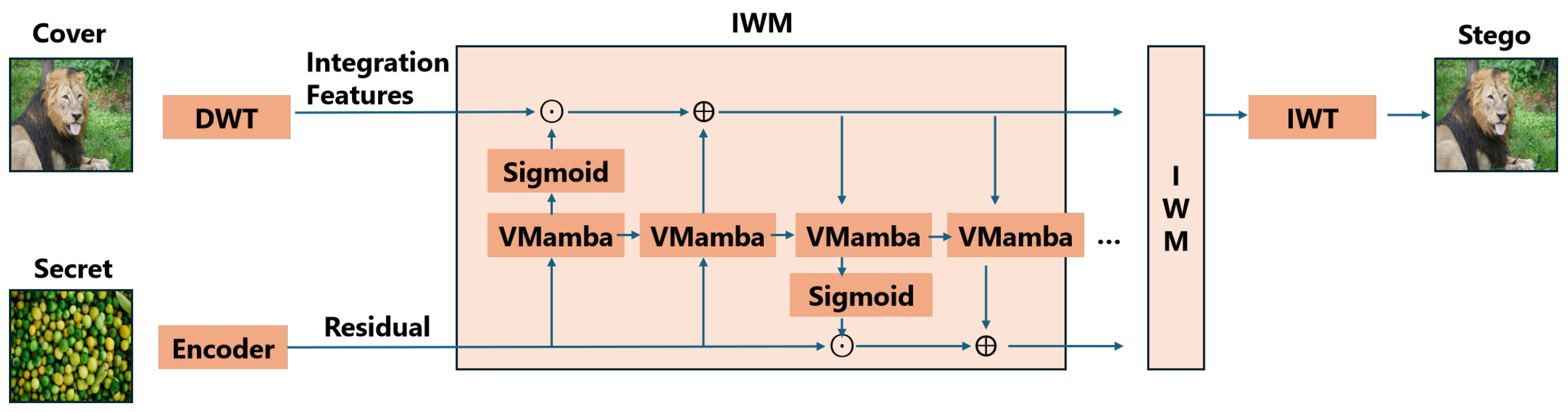
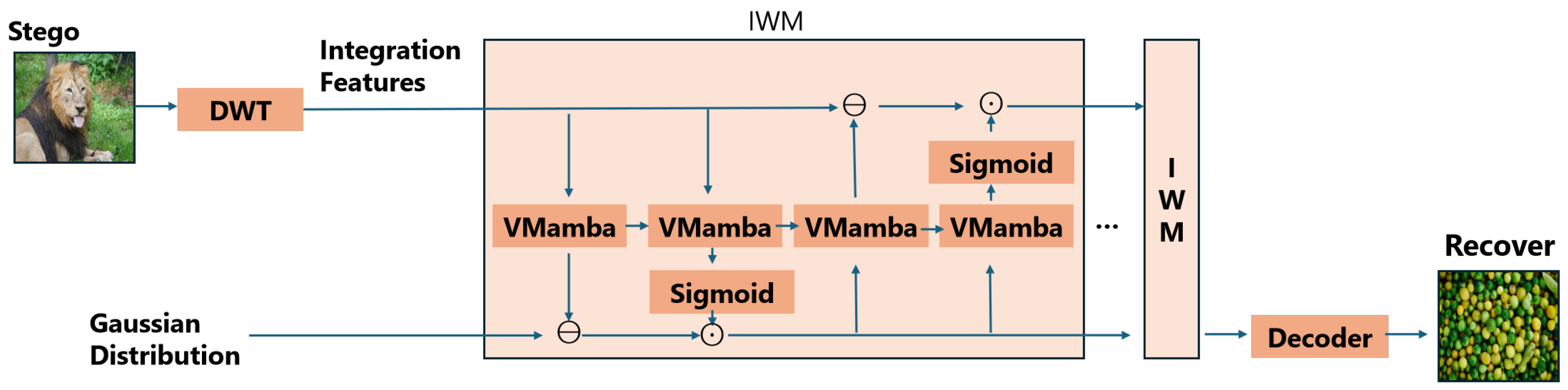





| Property | Mathematical Description | Functional Significance |
|---|---|---|
| Spatial dimensions | Maintains resolution consistency with wavelet-decomposed features. | |
| Channel composition | Preserves joint frequency representation (low + high sub-bands). | |
| Initialization condition | Inherits complete spectral information from original cover image. |
| Property | Mathematical Description | Functional Significance |
|---|---|---|
| Initialization | Maps secret image features to wavelet-compatible representation space. | |
| Channel dimension | Experimentally optimizes balance between capacity and concealment. | |
| Update mechanism | Establishes cross-layer feature feedback. Dynamically adjusts embedding intensity. |
| Symbol | Role in Transformation | Description |
|---|---|---|
| Scaling function | Adjusts weights of channels in , similar to gating in attention mechanisms. | |
| Bias injection | Provides conditionally dependent biases for to enhance expression. Encodes secret information into high-frequency components. | |
| State feedback controller | Generates a scaling factor for based on the current state of feature , thus controlling the propagation range of the steganographic trace. | |
| Residual transformation | Injects the nonlinear transformation of the current feature into the state . It deliberately introduces noise to mask secret information traces. |
| Data Type | Source | Size | Resolution | Preprocessing |
|---|---|---|---|---|
| Training set | DIV2K Train [41] | 800 images | 2K | Random flipping Random cropping Resized to pixels |
| In-domain test | DIV2K Test [41] | 100 images | 2K | Center-cropped to pixels |
| Cross-domain test | COCO [42] ImageNet [43] | 120 images 120 images | Varied | Center-cropped to pixels |
| Method | DIV2K | COCO | ImageNet | |||
|---|---|---|---|---|---|---|
| SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | |
| Baluja [2] | 0.938 | 35.88 | 0.934 | 35.01 | 0.925 | 34.13 |
| Lu-INN [10] | 0.978 | 38.82 | 0.976 | 36.36 | 0.955 | 35.38 |
| HiNet [13] | 0.993 | 46.53 | 0.985 | 41.21 | 0.986 | 41.60 |
| MRIN | 0.995 | 48.75 | 0.986 | 40.68 | 0.991 | 42.45 |
| Method | DIV2K | COCO | ImageNet | |||
|---|---|---|---|---|---|---|
| SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | |
| Baluja [2] | 0.938 | 35.88 | 0.934 | 35.01 | 0.925 | 34.13 |
| Lu-INN [10] | 0.978 | 38.82 | 0.976 | 36.36 | 0.955 | 35.38 |
| HiNet [13] | 0.992 | 46.24 | 0.985 | 40.10 | 0.981 | 40.03 |
| MRIN | 0.996 | 50.29 | 0.991 | 40.74 | 0.990 | 48.15 |
| Method | Noise Attack ( = 0.1) | Resolution Scaling (0.5×) | ||
|---|---|---|---|---|
| SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | |
| Baluja [2] | 0.814 | 27.54 | 0.768 | 26.29 |
| Lu-INN [10] | 0.861 | 30.91 | 0.812 | 29.54 |
| HiNet [13] | 0.842 | 31.18 | 0.792 | 28.42 |
| RIIS [12] | 0.876 | 29.84 | 0.825 | 29.59 |
| PRIS [35] | 0.883 | 32.14 | 0.831 | 30.72 |
| MRIN (Ours) | 0.918 | 32.74 | 0.857 | 31.63 |
| Method | QF = 95 | QF = 85 | QF = 75 | QF = 65 | ||||
|---|---|---|---|---|---|---|---|---|
| SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | |
| HiNet [13] | 0.841 | 26.98 | 0.813 | 25.43 | 0.779 | 23.29 | 0.744 | 20.07 |
| RIIS [12] | 0.845 | 29.01 | 0.827 | 28.43 | 0.806 | 28.02 | 0.753 | 27.85 |
| PRIS [35] | 0.881 | 32.84 | 0.832 | 31.13 | 0.810 | 30.09 | 0.755 | 28.14 |
| MRIN (Ours) | 0.951 | 33.14 | 0.931 | 31.82 | 0.909 | 30.63 | 0.881 | 28.44 |
| Methods | DIV2K | COCO | ImageNet |
|---|---|---|---|
| Baluja (2017) [2] | 5.43 | 5.88 | 6.12 |
| HiNet (2021) [13] | 4.87 | 5.15 | 5.34 |
| Lu-INN (2021) [10] | 4.35 | 4.62 | 4.79 |
| RIIS (2022) [12] | 3.97 | 4.53 | 4.56 |
| PRIS (2024) [35] | 3.89 | 4.03 | 4.25 |
| MRIN | 3.81 | 3.56 | 3.89 |
| Method | ACC (%) | AUC | FPR@5% | EER (%) |
|---|---|---|---|---|
| Baluja | 71.2 | 0.745 | 18.5 | 29.3 |
| HiNet | 68.5 | 0.712 | 23.7 | 32.1 |
| Lu-INN | 63.9 | 0.683 | 32.4 | 36.8 |
| RIIS | 59.6 | 0.679 | 38.5 | 40.1 |
| PRIS | 58.4 | 0.631 | 41.2 | 43.5 |
| MRIN | 55.8 | 0.584 | 47.6 | 47.5 |
| Variant Model | Generative Quality | Detection Resistance | Robustness | |||
|---|---|---|---|---|---|---|
| SSIM | PSNR (dB) | ACC (%) | AUC | Noise SSIM | Compression PSNR | |
| MRIN-M | 0.916 | 37.5 | 61.2 | 0.623 | 0.832 | 33.1 |
| MRIN-T | 0.934 | 38.8 | 59.7 | 0.642 | 0.853 | 34.5 |
| MRIN | 0.978 | 41.2 | 54.3 | 0.562 | 0.921 | 37.6 |
| Model | Resolution (Pixel) | FLOPs (G) | Memory Footprint (GB) | Reasoning Time (ms) | OOM |
|---|---|---|---|---|---|
| Transformer | 128 × 128 | 4.2 | 0.9 | 12.5 | No |
| Mamba | 128 × 128 | 2.3 | 0.5 | 6.8 | No |
| Transformer | 256 × 256 | 15.8 | 3.2 | 45.3 | No |
| Mamba | 256 × 256 | 8.7 | 1.8 | 22.1 | No |
| Transformer | 512 × 512 | 63.2 | 12.8 | 181.2 | No |
| Mamba | 512 × 512 | 34.8 | 7.2 | 88.4 | No |
| Transformer | 1024 × 1024 | 252.8 | 51.2 | - | Yes |
| Mamba | 1024 × 1024 | 139.2 | 28.8 | 353.6 | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, L.; Ren, J.; Li, J. An Invertible, Robust Steganography Network Based on Mamba. Symmetry 2025, 17, 837. https://doi.org/10.3390/sym17060837
Huo L, Ren J, Li J. An Invertible, Robust Steganography Network Based on Mamba. Symmetry. 2025; 17(6):837. https://doi.org/10.3390/sym17060837
Chicago/Turabian StyleHuo, Lin, Jia Ren, and Jianbo Li. 2025. "An Invertible, Robust Steganography Network Based on Mamba" Symmetry 17, no. 6: 837. https://doi.org/10.3390/sym17060837
APA StyleHuo, L., Ren, J., & Li, J. (2025). An Invertible, Robust Steganography Network Based on Mamba. Symmetry, 17(6), 837. https://doi.org/10.3390/sym17060837






