Canonical Effect on Quarkonium Enhancement in the Deconfined Medium
Abstract
1. Introduction
2. Theoretical Model
2.1. Heavy Quark Dynamics and Coalescence
2.2. Quarkonium Primordial Production
3. Numerical Results in Heavy-Ion Collisions
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Badyal, S.K.; Bai, Y.; Balewski, J.; et al. Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. A 2005, 757, 102–183. [Google Scholar] [CrossRef]
- Gyulassy, M.; McLerran, L. New forms of QCD matter discovered at RHIC. Nucl. Phys. A 2005, 750, 30–63. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Song, H.; Bass, S.A.; Heinz, U.; Hirano, T.; Shen, C. 200 A GeV Au+Au collisions serve a nearly perfect quark-gluon liquid. Phys. Rev. Lett. 2011, 106, 192301, Erratum in Phys. Rev. Lett. 2012, 109, 139904. [Google Scholar] [CrossRef]
- Heinz, U.; Snellings, R. Collective flow and viscosity in relativistic heavy-ion collisions. Ann. Rev. Nucl. Part. Sci. 2013, 63, 123–151. [Google Scholar] [CrossRef]
- Alver, B.; Roland, G. Collision geometry fluctuations and triangular flow in heavy-ion collisions. Phys. Rev. C 2010, 81, 054905, Erratum in Phys. Rev. C 2010, 82, 039903. [Google Scholar] [CrossRef]
- Qin, G.Y.; Wang, X.N. Jet quenching in high-energy heavy-ion collisions. Int. J. Mod. Phys. E 2015, 24, 1530014. [Google Scholar] [CrossRef]
- Pang, L.; Wang, Q.; Wang, X.N. Effects of initial flow velocity fluctuation in event-by-event (3+1)D hydrodynamics. Phys. Rev. C 2012, 86, 024911. [Google Scholar] [CrossRef]
- Van Hees, H.; Greco, V.; Rapp, R. Heavy-quark probes of the quark-gluon plasma at RHIC. Phys. Rev. C 2006, 73, 034913. [Google Scholar] [CrossRef]
- Yang, M.; Zheng, S.; Tong, B.; Zhao, J.; Ouyang, W.; Zhou, K.; Chen, B. Bottom energy loss and nonprompt J/ψ production in relativistic heavy ion collisions. Phys. Rev. C 2023, 107, 054917. [Google Scholar] [CrossRef]
- Xing, W.J.; Li, S.Q.; Cao, S.; Qin, G.Y. Bottom quark dynamics from nonprompt D0 and J/ψ production in Pb+Pb collisions at = 5.02 TeV. Phys. Rev. C 2024, 110, 024903. [Google Scholar] [CrossRef]
- Zhao, J.; Aichelin, J.; Gossiaux, P.B.; Beraudo, A.; Cao, S.; Fan, W.; He, M.; Minissale, V.; Song, T.; Vitev, I.; et al. Hadronization of heavy quarks. Phys. Rev. C 2024, 109, 054912. [Google Scholar] [CrossRef]
- Zhao, S.; He, M. Statistical production of Bc mesons in heavy-ion collisions at the LHC energy. Phys. Lett. B 2025, 861, 139283. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, K.; Chen, S.; Zhuang, P. Heavy flavors under extreme conditions in high energy nuclear collisions. Prog. Part. Nucl. Phys. 2020, 114, 103801. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Escobedo, M.A. Quantum and classical dynamics of heavy quarks in a quark-gluon plasma. J. High Energy Phys. 2018, 6, 034. [Google Scholar] [CrossRef]
- Hagedorn, R.; Redlich, K. Statistical Thermodynamics in Relativistic Particle and Ion Physics: Canonical or Grand Canonical? Z. Phys. C Part. Fields 1985, 27, 541. [Google Scholar] [CrossRef]
- Hamieh, S.; Redlich, K.; Tounsi, A. Canonical description of strangeness enhancement from p-A to Pb Pb collisions. Phys. Lett. B 2000, 486, 61–66. [Google Scholar] [CrossRef]
- Liu, Y.; Ko, C.M.; Song, T. Hot medium effects on J/ψ production in p+Pb collisions at = 5.02 TeV. Phys. Lett. B 2014, 728, 437–442. [Google Scholar] [CrossRef][Green Version]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef]
- Chen, Y.; He, M. Charged-particle multiplicity dependence of charm-baryon-to-meson ratio in high-energy proton-proton collisions. Phys. Lett. B 2021, 815, 136144. [Google Scholar] [CrossRef]
- Bai, X.; Li, G.; Zhang, Y.; Situ, Q.; Chen, X. Data-driven analysis of the beauty hadron production in pp collisions at the LHC with Bayesian unfolding. J. High Energy Phys. 2024, 11, 018. [Google Scholar] [CrossRef]
- Cao, S.; Qin, G.Y.; Bass, S.A. Energy loss, hadronization and hadronic interactions of heavy flavors in relativistic heavy-ion collisions. Phys. Rev. C 2015, 92, 024907. [Google Scholar] [CrossRef]
- Chen, B.; Wen, L.; Liu, Y. Bc+ formation from random charm and anti-bottom quarks in the quark-gluon plasma. Phys. Lett. B 2022, 834, 137448. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, L.; Liu, X.H.; Liu, Y.; Zhao, J. X(3872) production in relativistic heavy-ion collisions. Phys. Rev. C 2022, 105, 054901. [Google Scholar] [CrossRef]
- Xu, Y.; Bernhard, J.E.; Bass, S.A.; Nahrgang, M.; Cao, S. Data-driven analysis for the temperature and momentum dependence of the heavy-quark diffusion coefficient in relativistic heavy-ion collisions. Phys. Rev. C 2018, 97, 014907. [Google Scholar] [CrossRef]
- Schenke, B.; Jeon, S.; Gale, C. Elliptic and triangular flow in event-by-event (3+1)D viscous hydrodynamics. Phys. Rev. Lett. 2011, 106, 042301. [Google Scholar] [CrossRef]
- Schenke, B.; Jeon, S.; Gale, C. (3+1)D hydrodynamic simulation of relativistic heavy-ion collisions. Phys. Rev. C 2010, 82, 014903. [Google Scholar] [CrossRef]
- Shen, C.; Qiu, Z.; Song, H.; Bernhard, J.; Bass, S.; Heinz, U. The iEBE-VISHNU code package for relativistic heavy-ion collisions. Comput. Phys. Commun. 2016, 199, 61–85. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, N.; Zhuang, P. The Effect of partonic wind on charm quark correlations in high-energy nuclear collisions. Phys. Rev. Lett. 2008, 100, 152301. [Google Scholar] [CrossRef]
- Greco, V.; Ko, C.M.; Rapp, R. Quark coalescence for charmed mesons in ultrarelativistic heavy ion collisions. Phys. Lett. B 2004, 595, 202–208. [Google Scholar] [CrossRef]
- Song, T.; Berrehrah, H. Hadronization time of heavy quarks in nuclear matter. Phys. Rev. C 2016, 94, 034901. [Google Scholar] [CrossRef]
- Shi, S.; Zhao, J.; Zhuang, P. Heavy flavor dissociation in framework of multi-body Dirac equations. Chin. Phys. C 2020, 44, 084101. [Google Scholar] [CrossRef]
- Zhao, W.; Ko, C.M.; Liu, Y.X.; Qin, G.Y.; Song, H. Probing the Partonic Degrees of Freedom in High-Multiplicity p–Pb collisions at = 5.02 TeV. Phys. Rev. Lett. 2020, 125, 072301. [Google Scholar] [CrossRef]
- Zhu, X.l.; Zhuang, P.f.; Xu, N. J/psi transport in QGP and p(t) distribution at SPS and RHIC. Phys. Lett. B 2005, 607, 107–114. [Google Scholar] [CrossRef]
- Chen, B.; Hu, M.; Zhang, H.; Zhao, J. Probe the tilted Quark-Gluon Plasma with charmonium directed flow. Phys. Lett. B 2020, 802, 135271. [Google Scholar] [CrossRef]
- Chen, S.; He, M. Heavy quarkonium dissociation by thermal gluons at next-to-leading order in the Quark–Gluon Plasma. Phys. Lett. B 2018, 786, 260–267. [Google Scholar] [CrossRef]
- Zhao, X.; Rapp, R. Charmonium in Medium: From Correlators to Experiment. Phys. Rev. C 2010, 82, 064905. [Google Scholar] [CrossRef]
- Andronic, A.; Gossiaux, P.B.; Petreczky, P.; Rapp, R.; Strickland, M.; Blaizot, J.P.; Brambilla, N.; Braun-Munzinger, P.; Chen, B.; Delorme, S.; et al. Comparative study of quarkonium transport in hot QCD matter. Eur. Phys. J. A 2024, 60, 88. [Google Scholar] [CrossRef]
- Liu, Y.; Qu, Z.; Xu, N.; Zhuang, P. Rapidity Dependence of J/psi Production at RHIC and LHC. J. Phys. G 2010, 37, 075110. [Google Scholar] [CrossRef]
- Sjöstrand, T.; Ask, S.; Christiansen, J.R.; Corke, R.; Desai, N.; Ilten, P.; Mrenna, S.; Prestel, S.; Rasmussen, C.O.; Skands, P.Z. An introduction to PYTHIA 8.2. Comput. Phys. Commun. 2015, 191, 159–177. [Google Scholar] [CrossRef]
- Yan, L.; Zhuang, P.; Xu, N. Competition between J/psi suppression and regeneration in quark-gluon plasma. Phys. Rev. Lett. 2006, 97, 232301. [Google Scholar] [CrossRef] [PubMed]
- Chen, B. Thermal production of charmonia in Pb-Pb collisions at = 5.02 TeV. Chin. Phys. C 2019, 43, 124101. [Google Scholar] [CrossRef]
- Zhang, Y.f. Overview of charm production at RHIC. J. Phys. G 2008, 35, 104022. [Google Scholar] [CrossRef]
- Song, T.; Ko, C.M.; Lee, S.H. Quarkonium formation time in relativistic heavy-ion collisions. Phys. Rev. C 2015, 91, 044909. [Google Scholar] [CrossRef]
- Acharya, S.; ALICE Collaboration. Measurements of inclusive J/ψ production at midrapidity and forward rapidity in Pb–Pb collisions at sNN = 5.02 TeV. Phys. Lett. B 2024, 849, 138451. [Google Scholar] [CrossRef]
- Adare, A.; PHENIX Collaboration. J/ψ Production vs Centrality, Transverse Momentum, and Rapidity in Au+Au Collisions at =200 GeV. Phys. Rev. Lett. 2007, 98, 232301. [Google Scholar] [CrossRef]
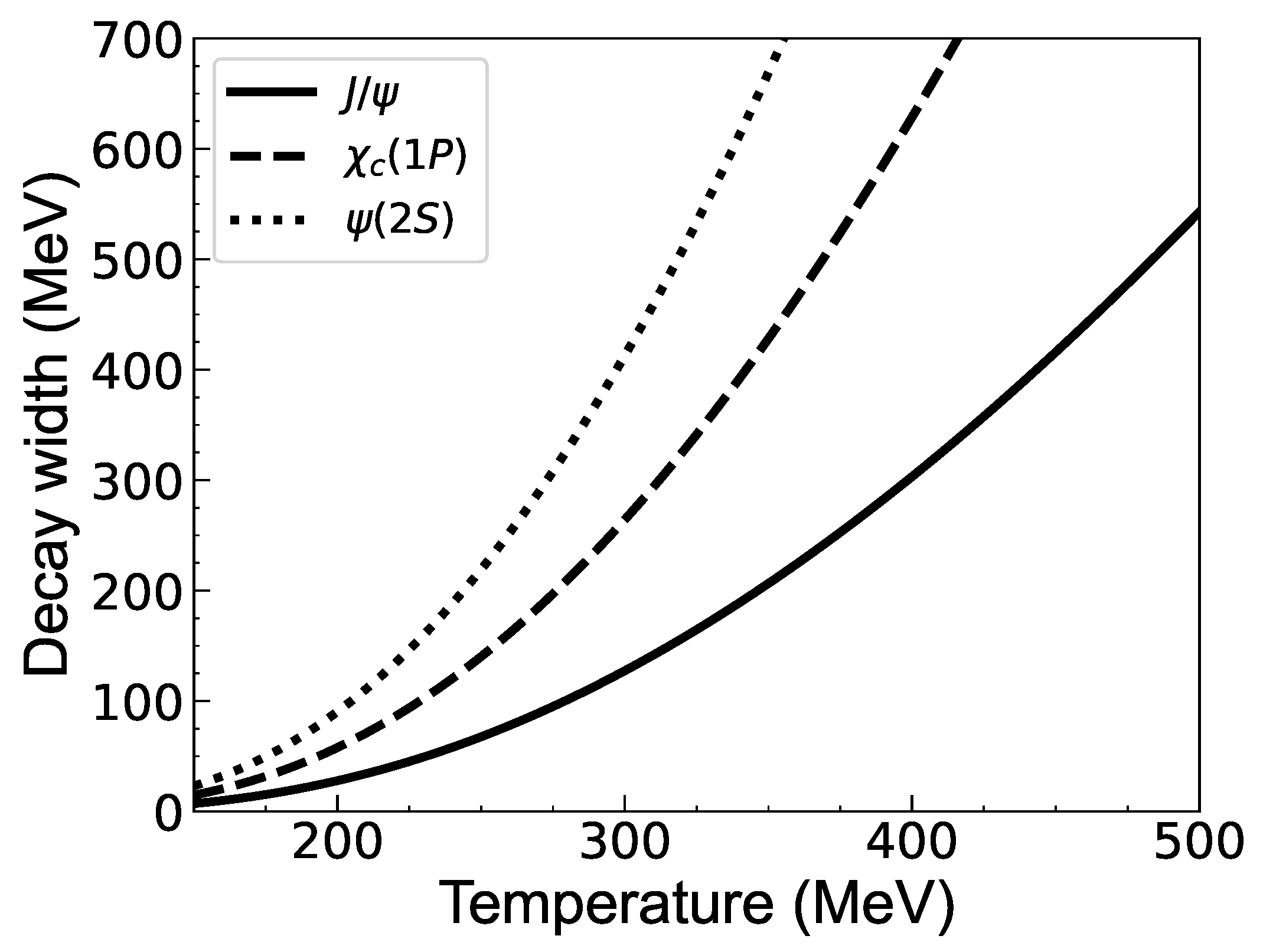
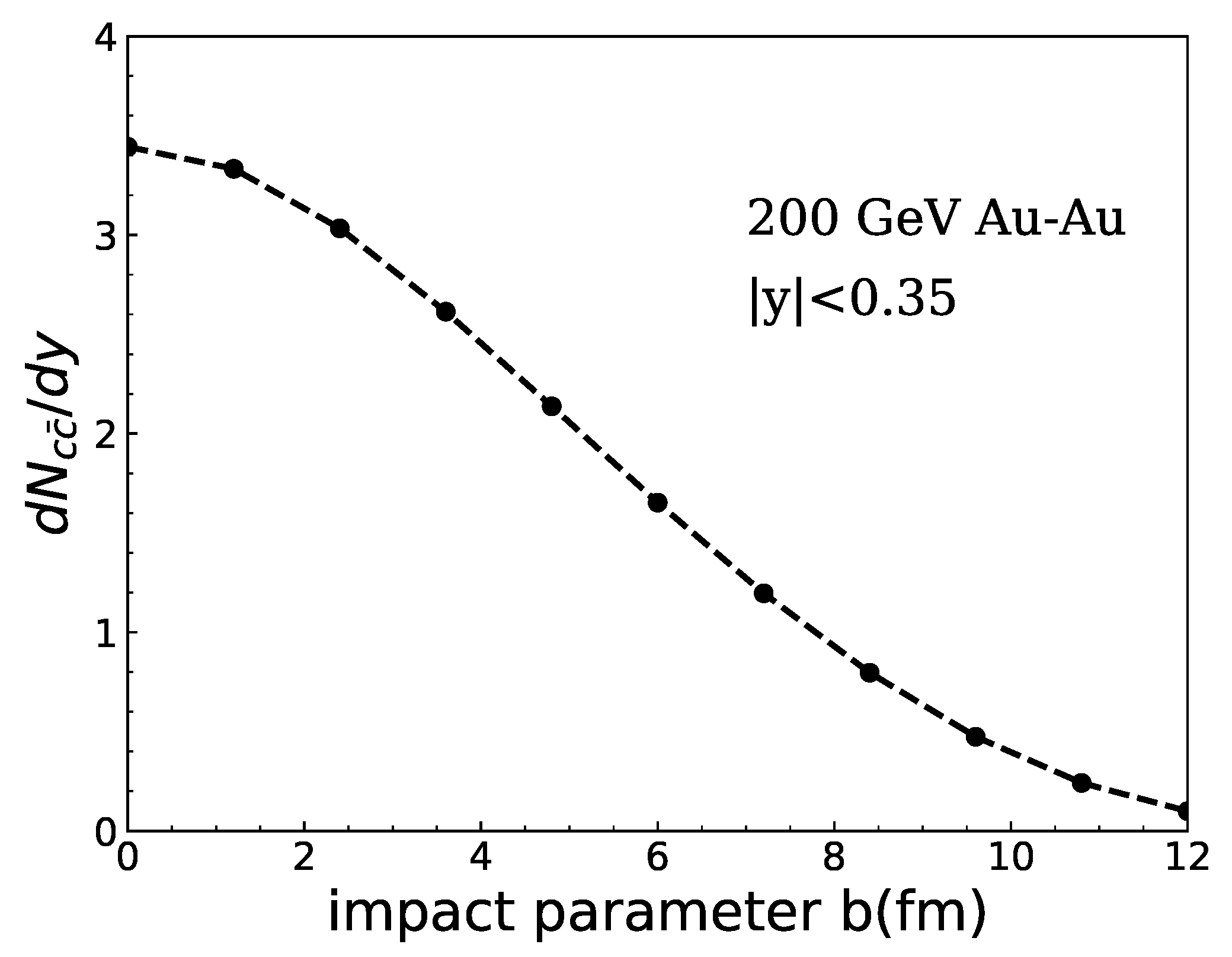

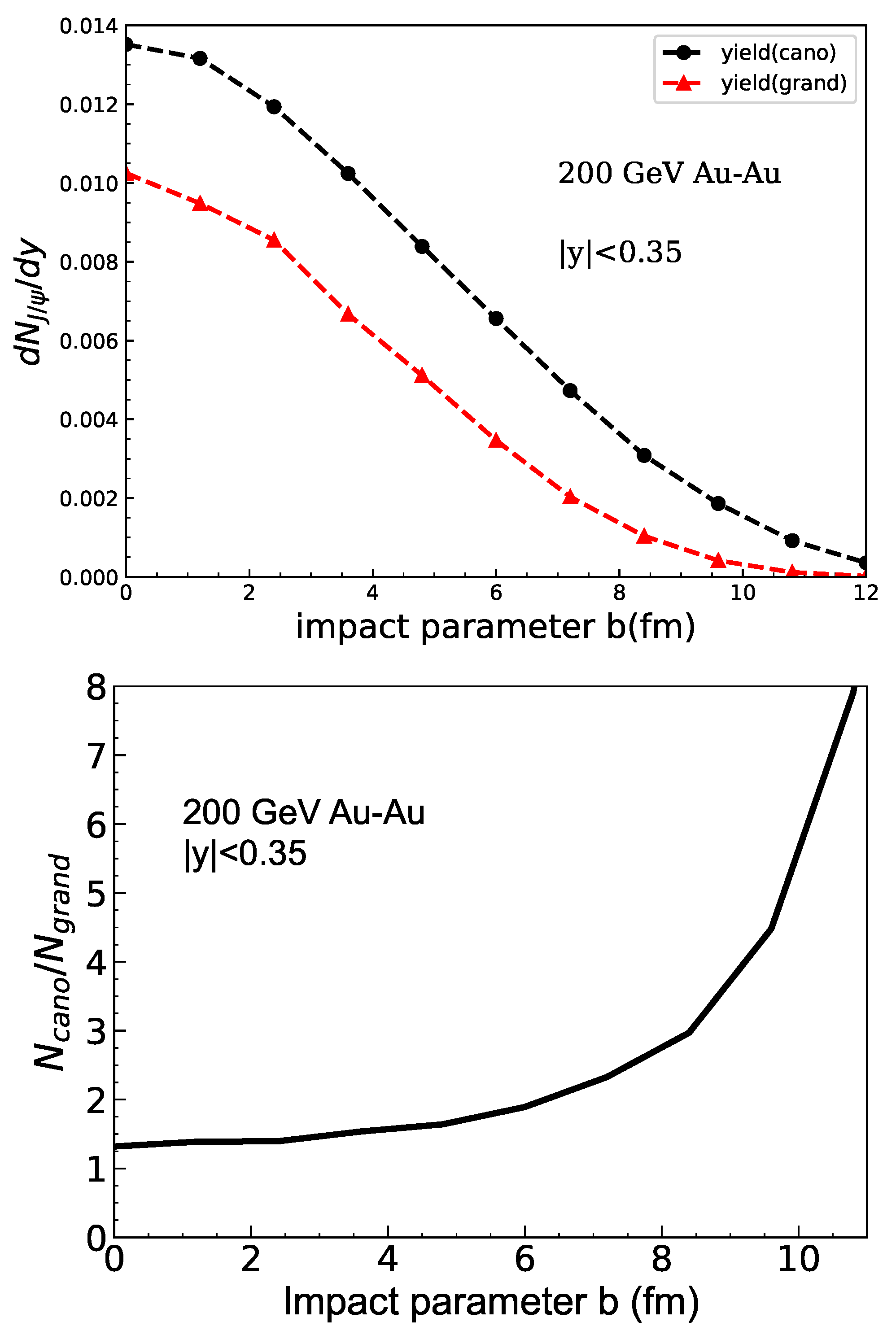
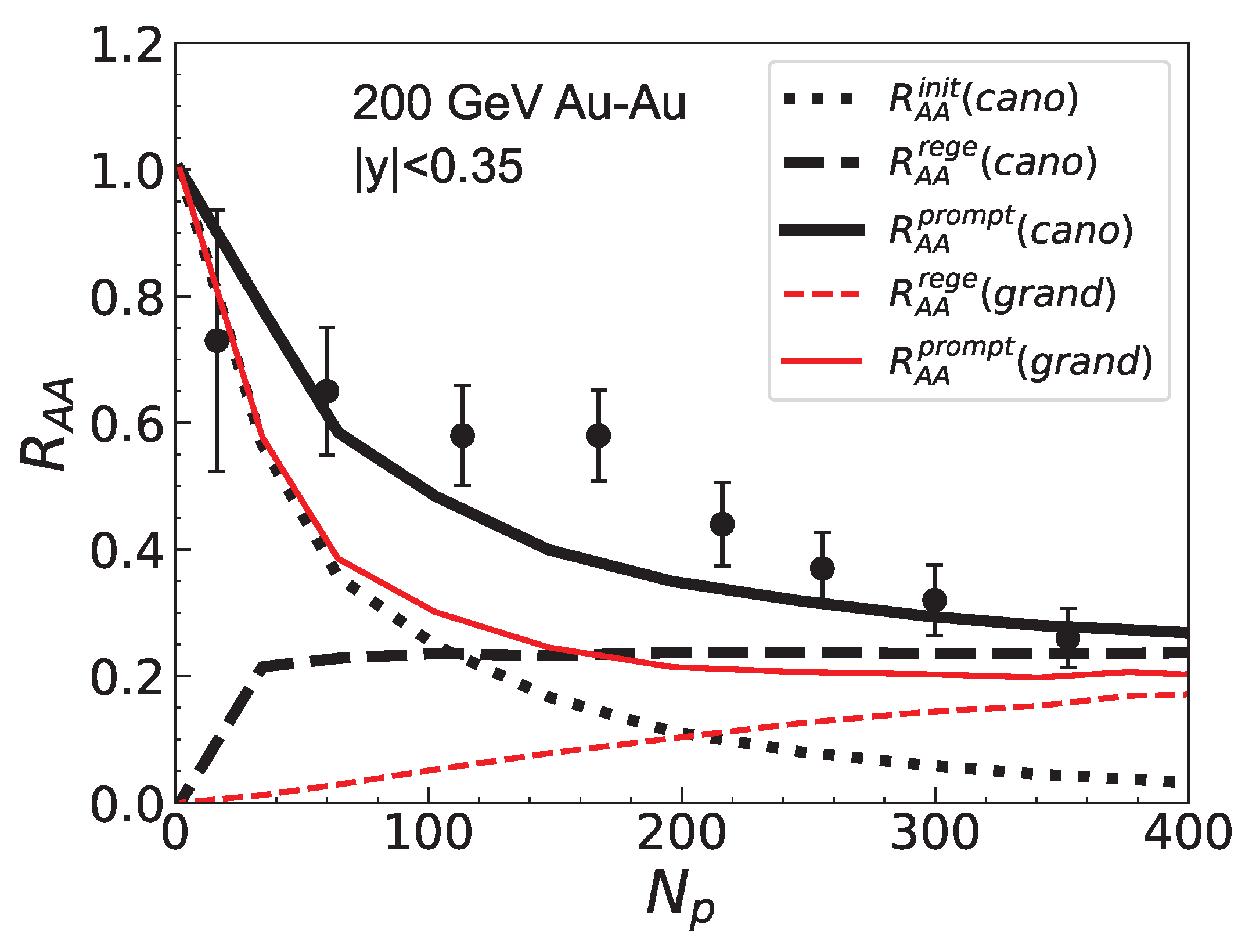
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, A.; Zheng, S.; Chen, B. Canonical Effect on Quarkonium Enhancement in the Deconfined Medium. Symmetry 2025, 17, 830. https://doi.org/10.3390/sym17060830
Zhou A, Zheng S, Chen B. Canonical Effect on Quarkonium Enhancement in the Deconfined Medium. Symmetry. 2025; 17(6):830. https://doi.org/10.3390/sym17060830
Chicago/Turabian StyleZhou, Aidan, Shiqi Zheng, and Baoyi Chen. 2025. "Canonical Effect on Quarkonium Enhancement in the Deconfined Medium" Symmetry 17, no. 6: 830. https://doi.org/10.3390/sym17060830
APA StyleZhou, A., Zheng, S., & Chen, B. (2025). Canonical Effect on Quarkonium Enhancement in the Deconfined Medium. Symmetry, 17(6), 830. https://doi.org/10.3390/sym17060830





