Study of Numerical Modeling Method for Precooling of Spherical Horticultural Produce Stacked Symmetrically in Vented Package
Abstract
1. Introduction
2. Materials and Methods
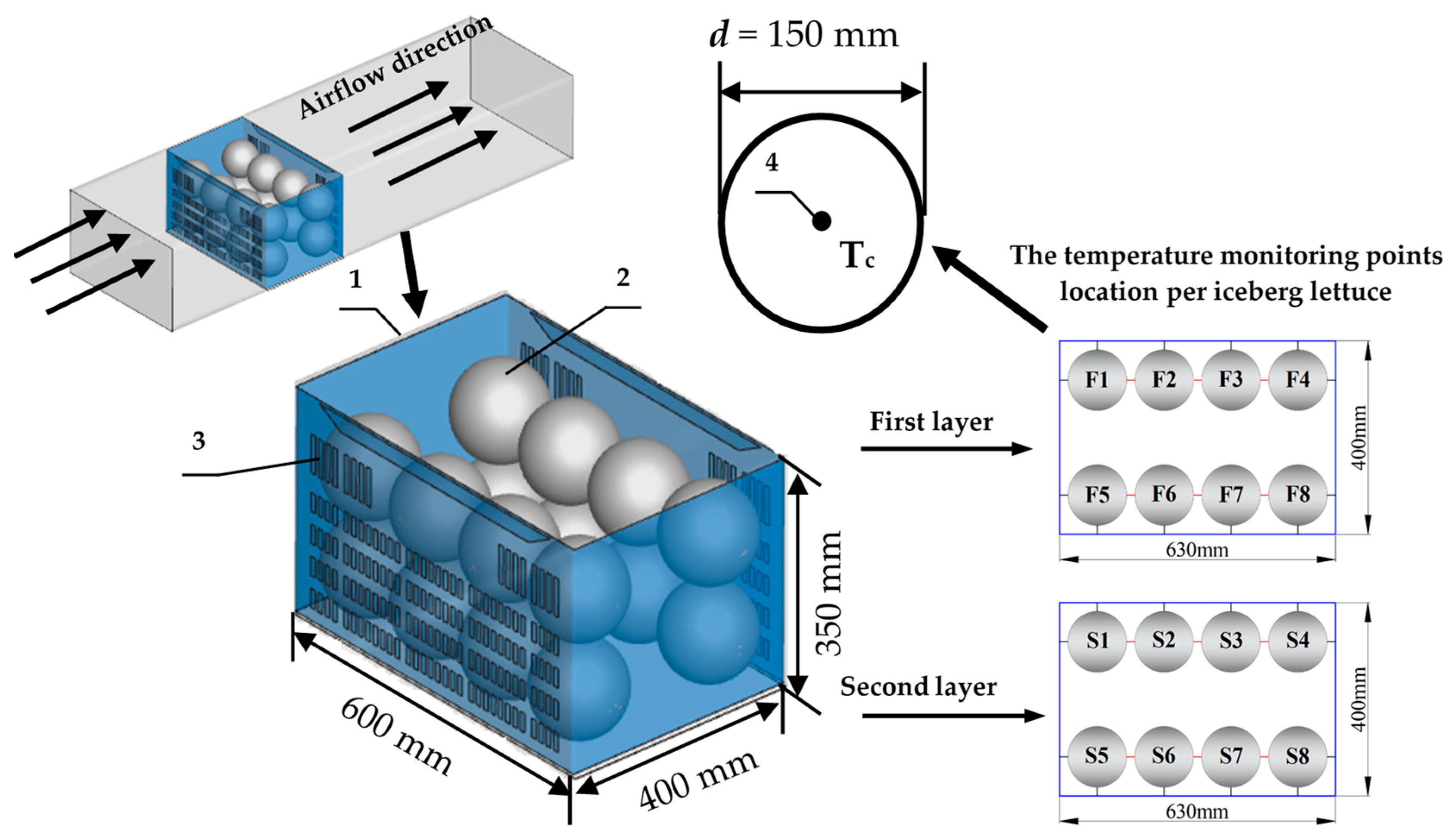
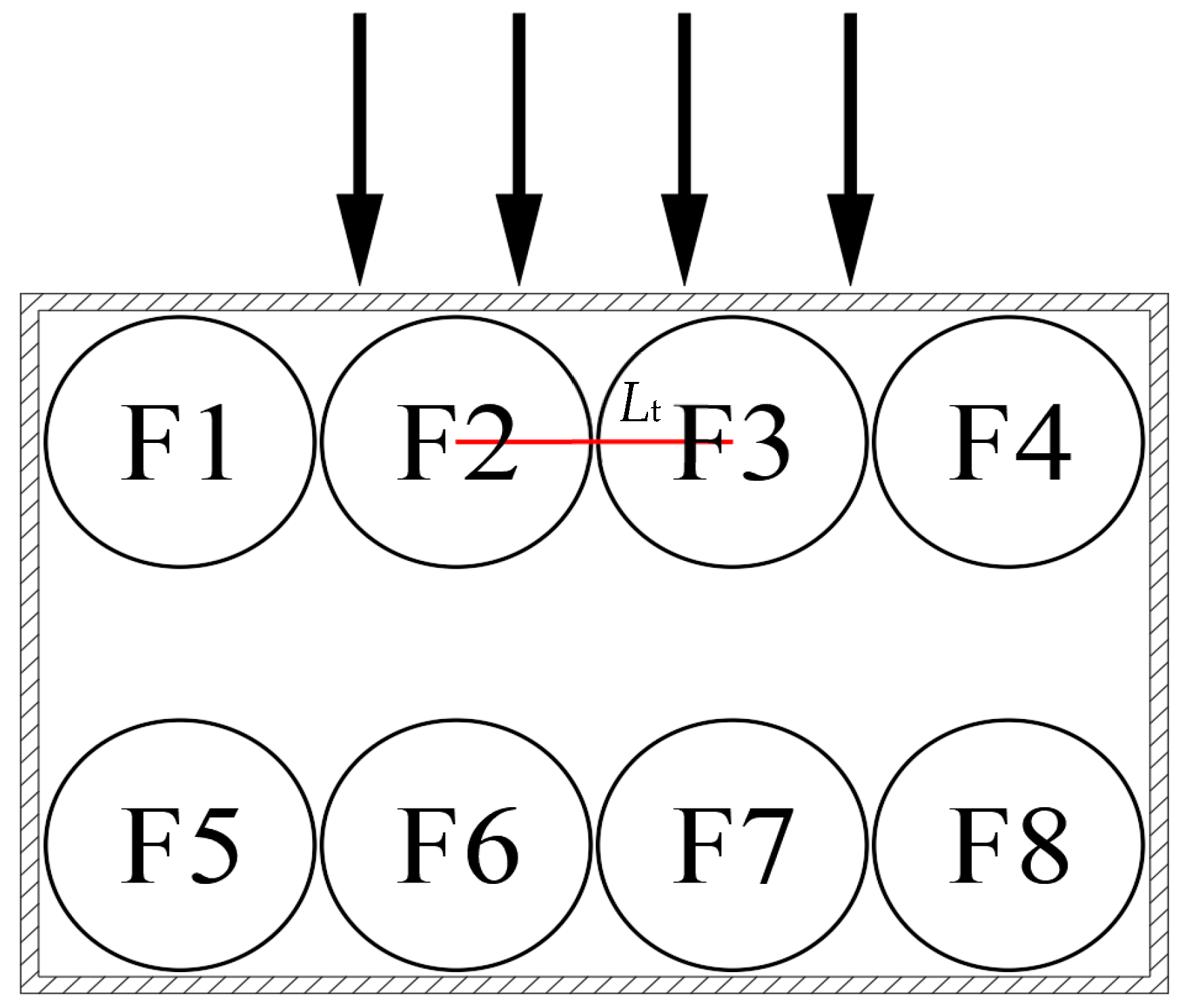
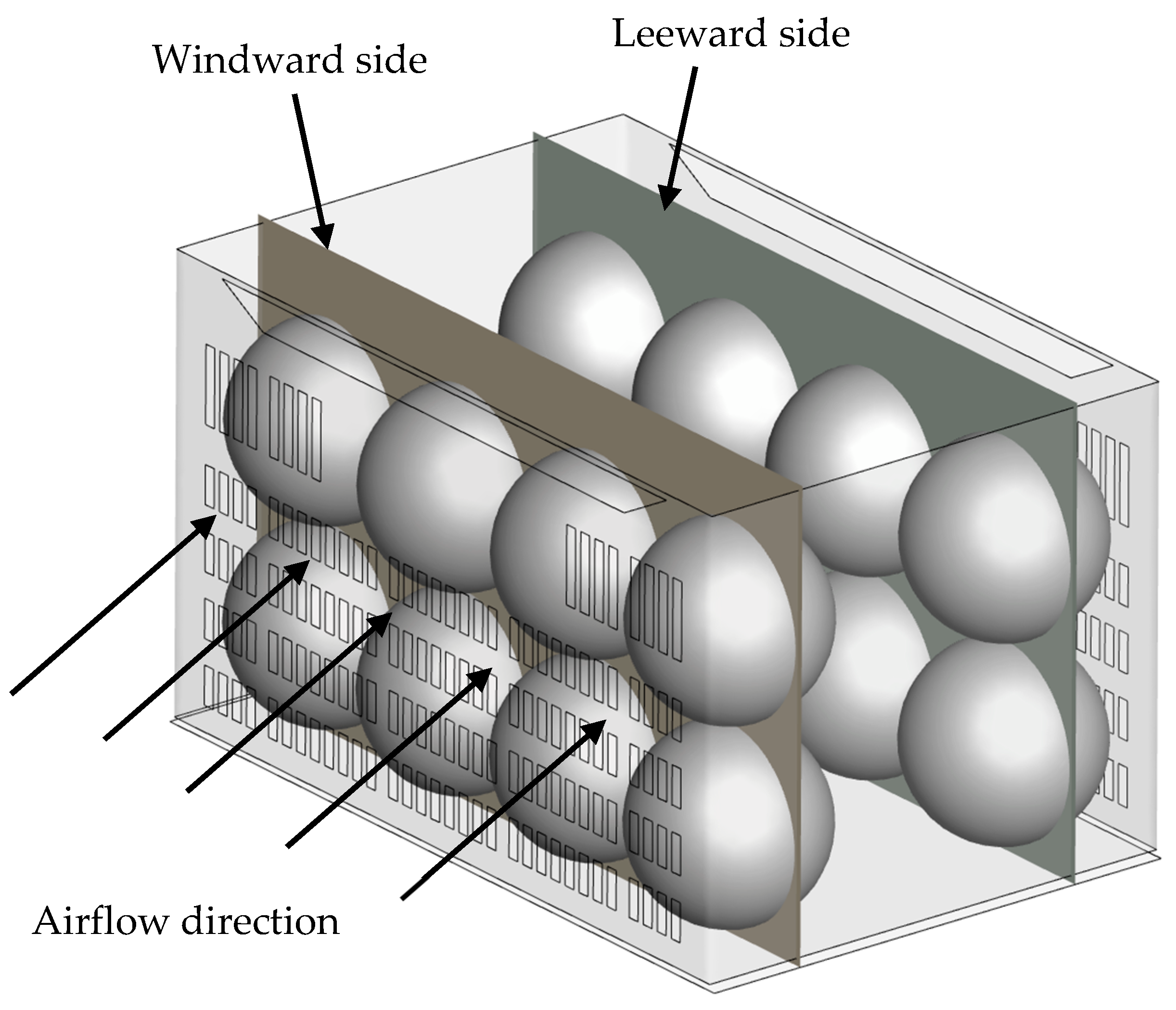
2.1. Physical Model
2.2. Experimental Designs
2.2.1. Experimental Device
2.2.2. Equipment Parameters
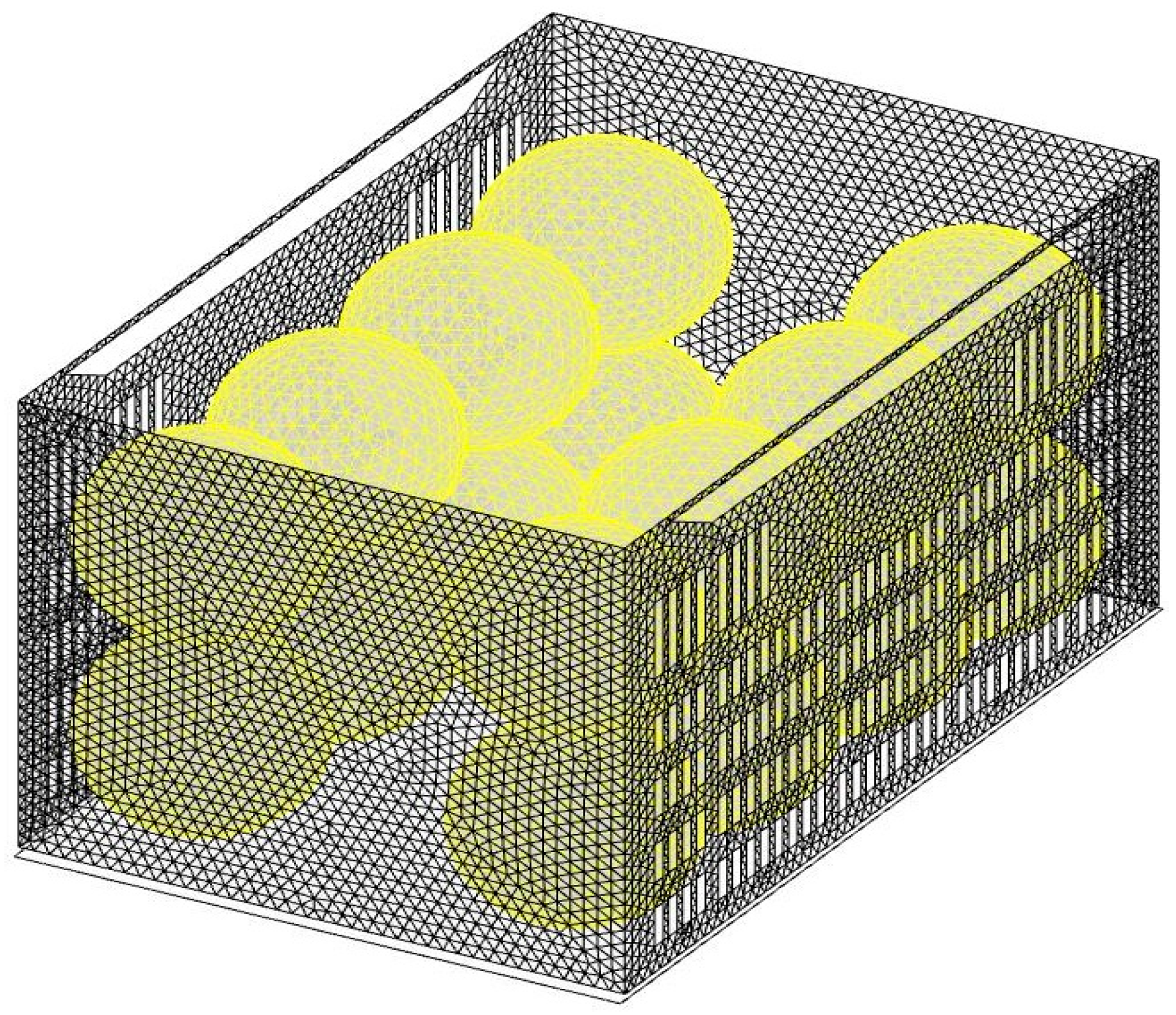
2.3. Numerical Modeling
2.3.1. Modeling Hypothesis
- Individual iceberg lettuces were geometrically idealized as homogeneous isotropic spheres with a diameter of 150 mm. The effects of product ripening or senescence on respiration and transpiration were not considered.
- The impact of radiation between iceberg lettuces, the cooling air, and the plastic crate on the simulated results was assumed to be negligible.
- Any influence of experimental instruments on airflow was not considered.
- The cooling air was regarded as Newtonian fluid and the gas medium was considered transparent in the visible range.
- The thermophysical properties of the cooling air and produce were assumed to be constant throughout the whole FAC process.
2.3.2. Governing Equations
2.4. Initial and Boundary Conditions
- Inlet boundary. The velocity-inlet boundary condition was adopted to define the airflow velocity at the inlet, which was set to 1 m s−1. The inlet cold air temperature was set to 2 °C.
- Outlet boundary. At the outlet, a fully developed flow section boundary condition was imposed, where the outlet velocity was computed based on the mass conservation equation. The other variable gradients normal to the flow direction were also set to zero at the outlet [31].
- Wall boundary. The iceberg lettuce surface and the inner and outer wall surfaces of the polymetric container were considered as no-slip wall boundary conditions, which assumed normal velocity components and normal gradients equal to zero at the boundary.
2.5. Numerical Simulation
3. Results
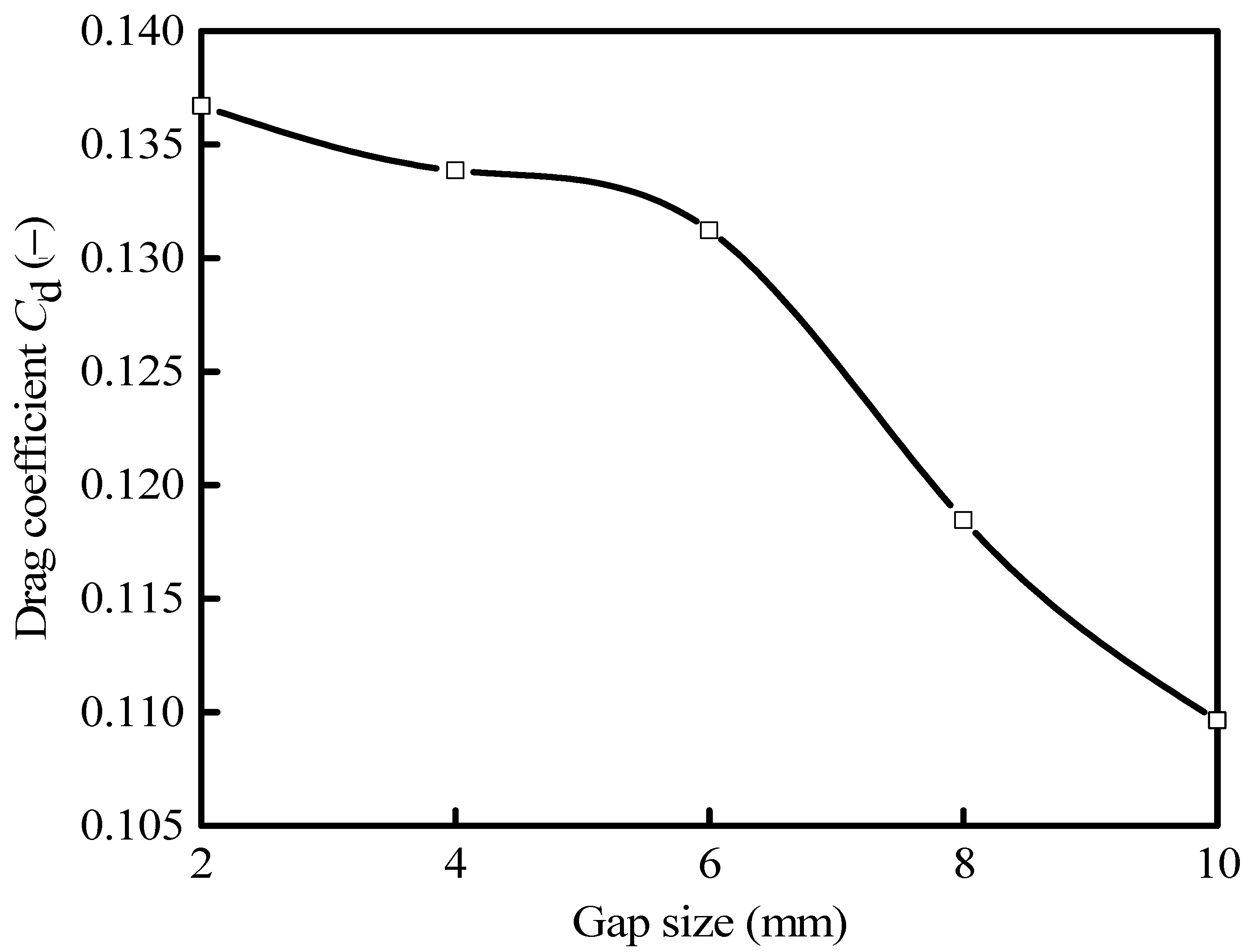
3.1. Drag Coefficient
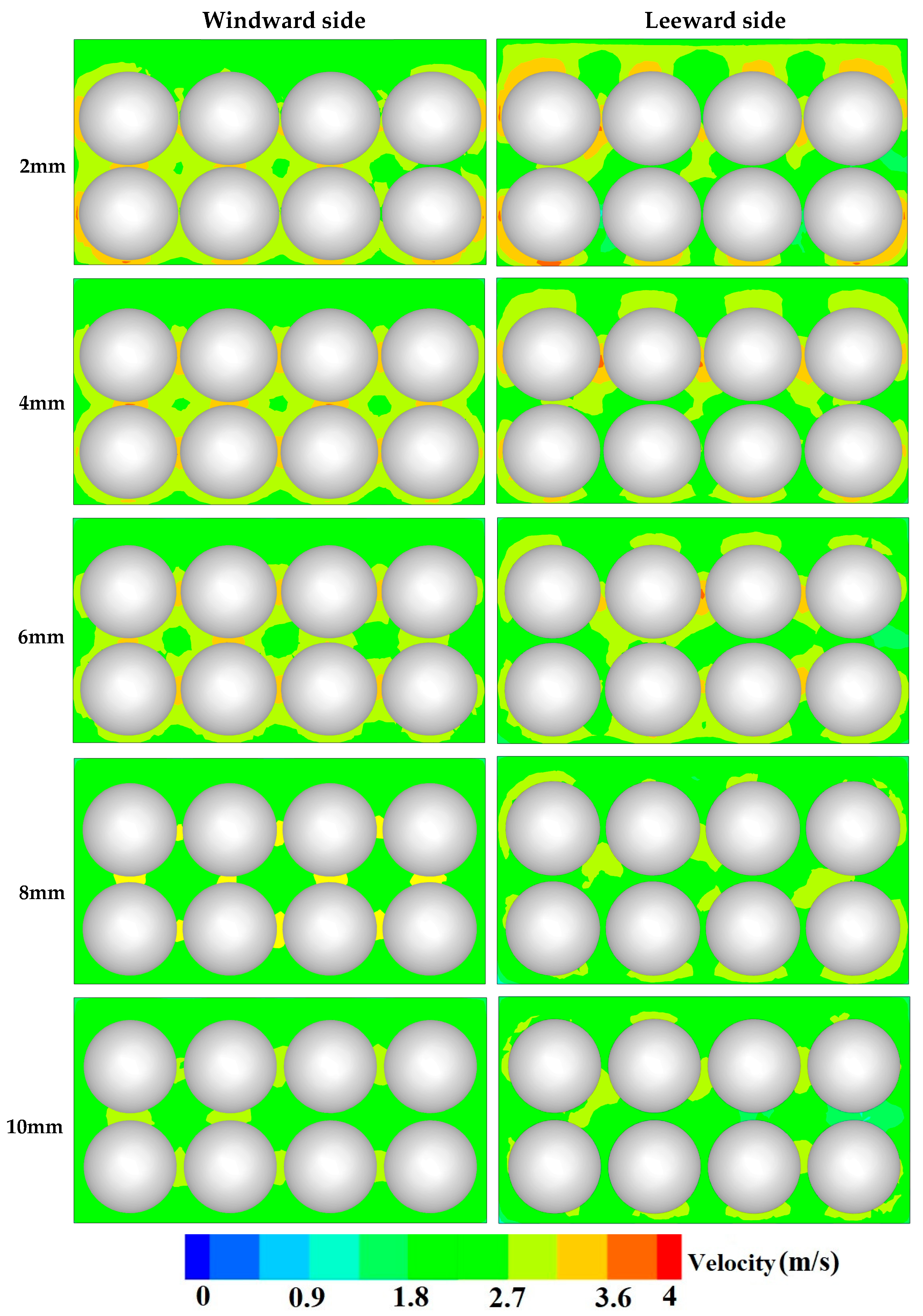
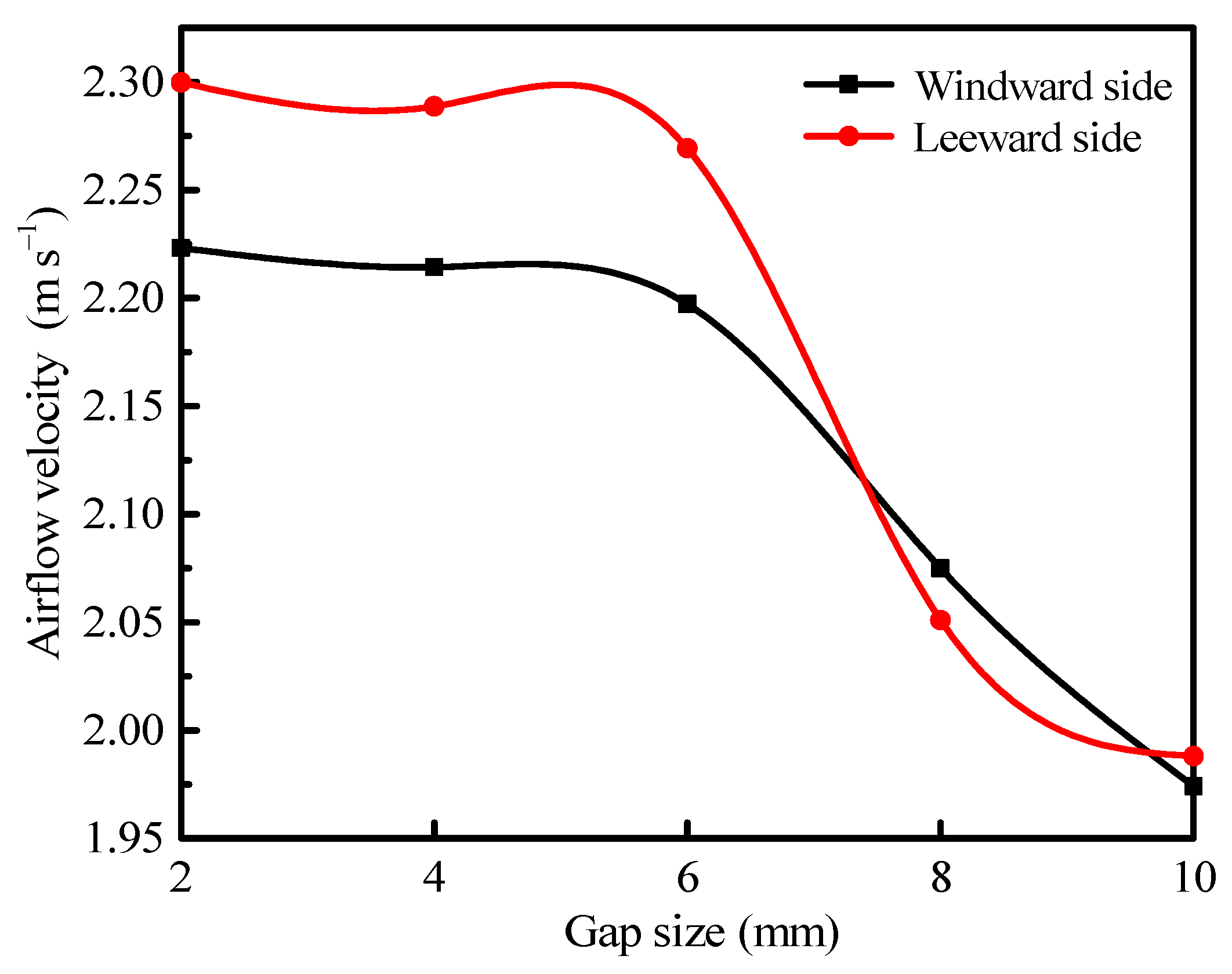
3.2. Airflow Characteristics
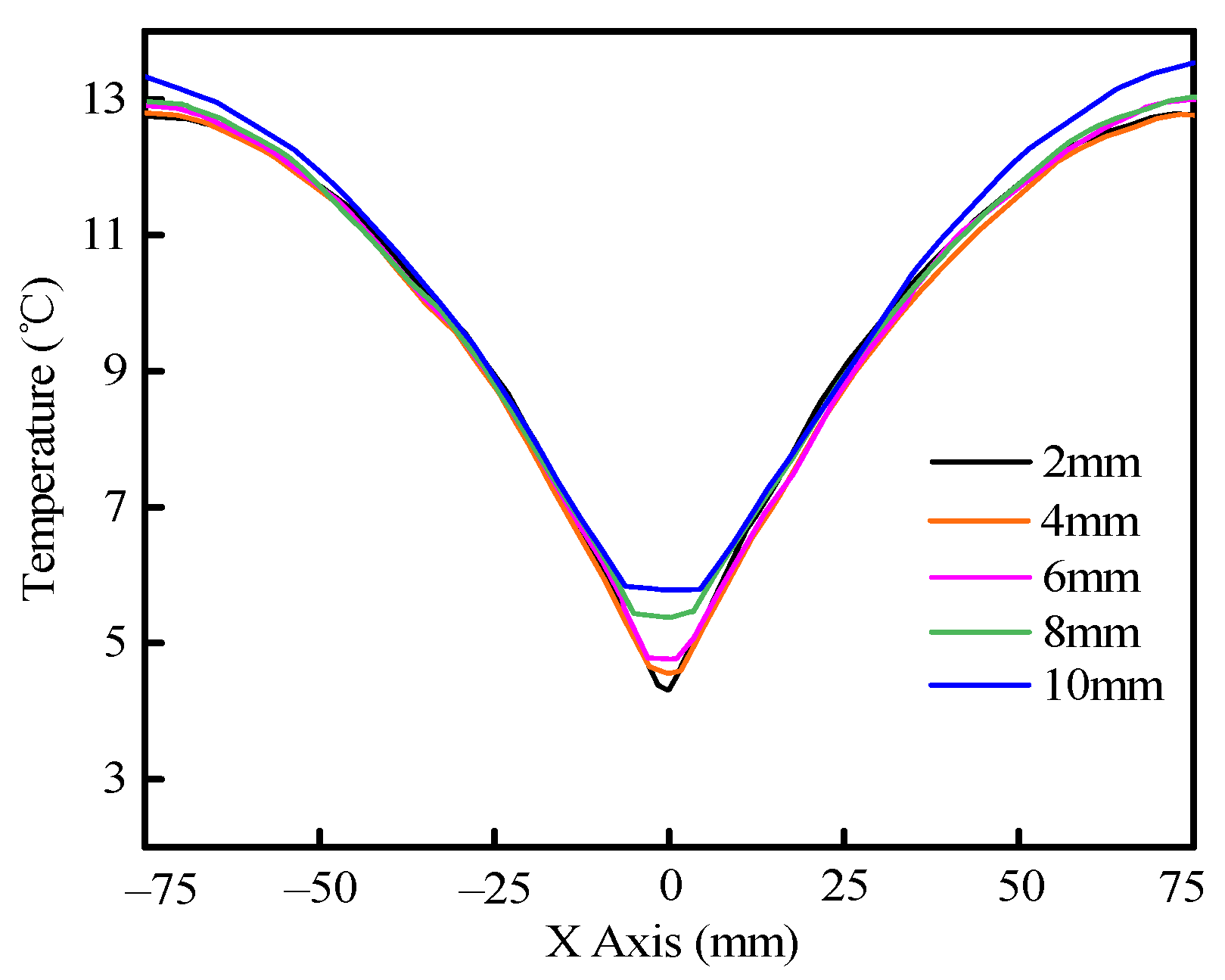
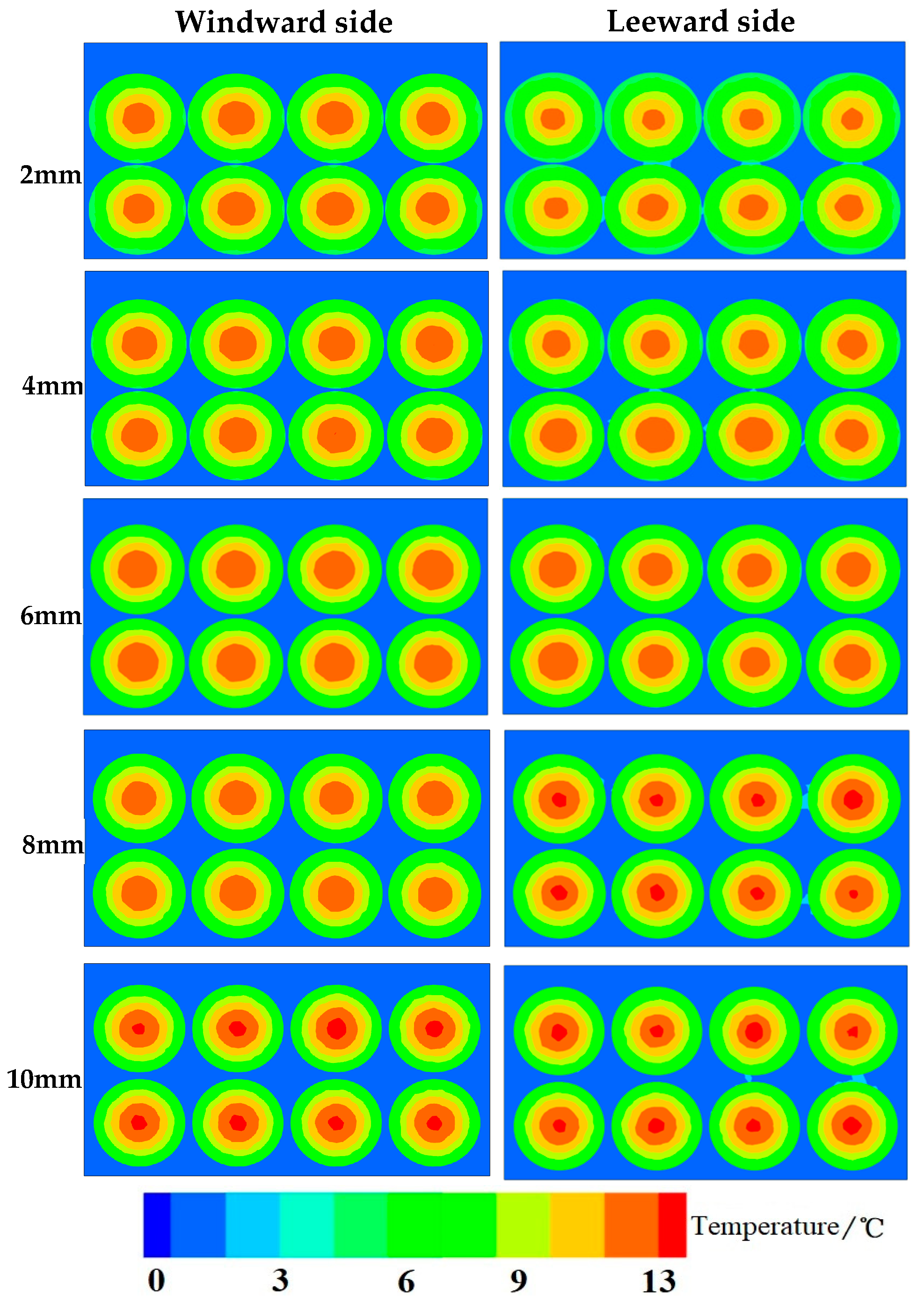
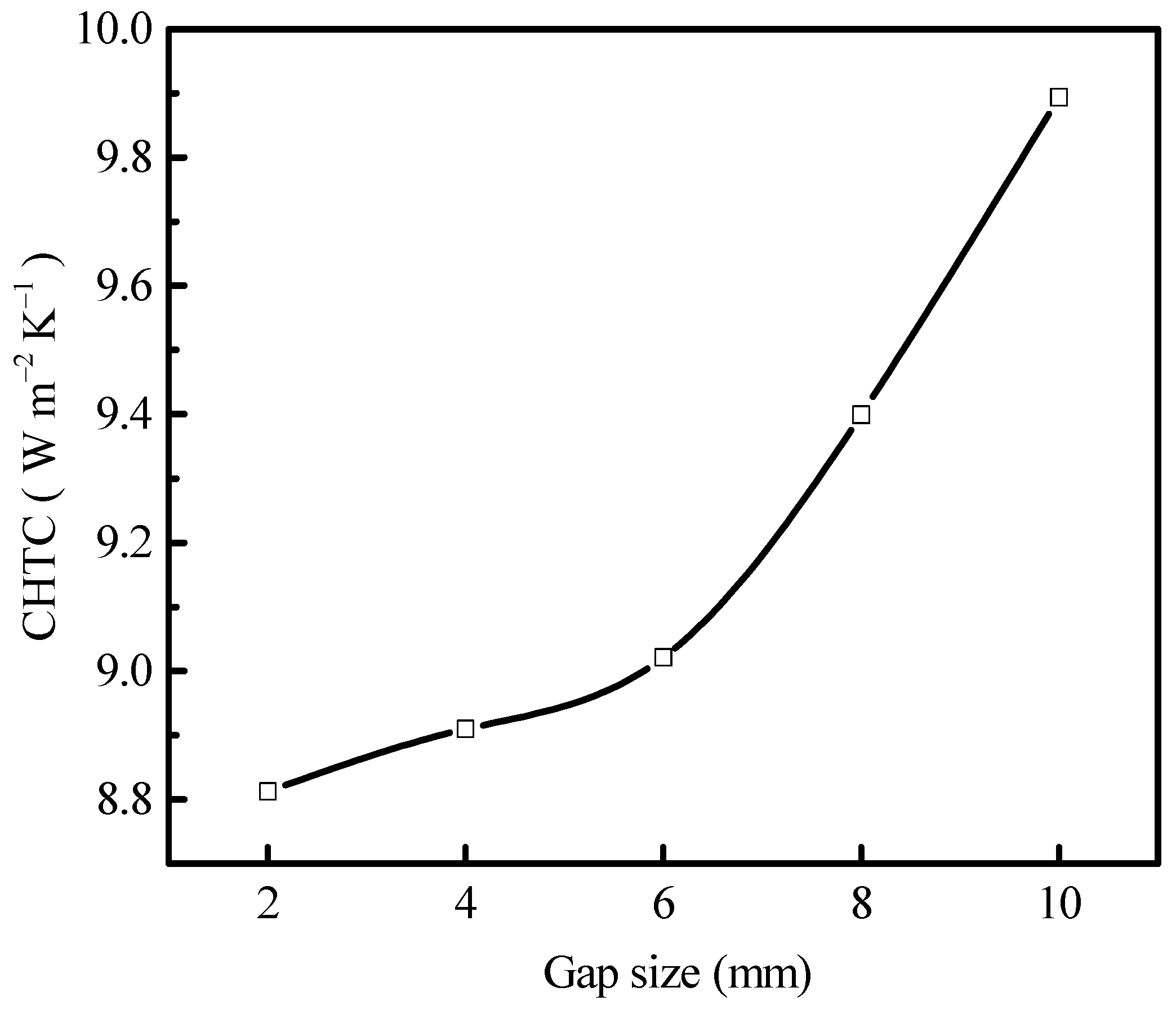
3.3. Heat Transfer Characteristics
3.4. Experimental Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, K.X.; Feng, X.L.; Tan, W.J.; Zheng, Q.H.; Zhong, W.T.; Liao, C.Y.; Liu, Y.T.; Li, S.J.; Hu, W.Z. Development of a food preservative from sea buckthorn together with chitosan: Application in and characterization of fresh-cut lettuce storage. Front. Microbiol. 2023, 14, 1080365. [Google Scholar] [CrossRef] [PubMed]
- Kim, A.N.; Kim, H.J.; Kerr, W.L.; Choi, S.G. The effect of grinding at various vacuum levels on the color, phenolics, and antioxidant properties of apple. Food Chem. 2017, 216, 234–242. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Kumar, R.; Subudhi, S. Experimental investigations of periodic airflow reversal during forced-air cooling of Apples: Impacts on cooling rate and uniformity. J. Food. Eng. 2023, 359, 111684. [Google Scholar] [CrossRef]
- Pratsanee, K.W.; Danai, B.; Pichaya, P. Extending the shelf life and qualities of baby cos lettuce using commercial precooling systems. Postharvest Biol. Technol. 2019, 150, 60–70. [Google Scholar] [CrossRef]
- Mercier, S.; Villeneuve, S.; Mondor, M.; Uysal, I. Time-temperature management along the food cold chain: A review of recent developments. Compr. Rev. Food. Sci. Food. Saf. 2017, 16, 647–667. [Google Scholar] [CrossRef]
- Han, J.W.; Badía-melis, R.; Yang, X.T.; Ruiz Garcia, L.; Qian, J.P.; Zhao, C.J. CFD simulation of airflow and heat transfer during forced-air precooling of apples. J. Food Process Eng. 2017, 40, e12390. [Google Scholar] [CrossRef]
- Castro(de), L.R.; Vigneault, C.; Cortez, L.A.B. Cooling performance of horticultural produce in containers with peripheral openings. Postharvest Biol. Technol. 2005, 38, 254–261. [Google Scholar] [CrossRef]
- Ngcobo, M.E.K.; Delele, M.A.; Opara, U.L.; Zietsman, C.J.; Meyer, C. Resistance to airflow and cooling patterns through multi-scale packaging of table grapes. Int. J. Refrig. 2012, 35, 445–452. [Google Scholar] [CrossRef]
- Han, J.W.; Zhao, C.J.; Yang, X.T.; Qian, J.P.; Fan, B.L. Computational modeling of airflow and heat transfer in a vented box during cooling: Optimal package design. Appl. Therm. Eng. 2015, 91, 883–893. [Google Scholar] [CrossRef]
- Defraeye, T.; Verboven, P.; Nicolai, B. CFD modelling of flow and scalar exchange of spherical food products: Turbulence and boundary-layer modelling. J. Food Eng. 2013, 114, 495–504. [Google Scholar] [CrossRef]
- Dehghannya, J.; Ngadi, M.; Vigneault, C. Simultaneous aerodynamic and thermal analysis during cooling of stacked spheres inside ventilated packages. Chem. Eng. Technol. 2008, 31, 1651–1659. [Google Scholar] [CrossRef]
- O’Sullivan, J.; Ferrua, M.J.; Love, R.; Verboven, P.; Nicolai, B.; East, A. Modelling the forced-air cooling mechanisms and performance of polylined horticultural produce. Postharvest Biol. Technol. 2016, 120, 23–35. [Google Scholar] [CrossRef]
- Zhao, C.J.; Han, J.W.; Yang, X.T.; Qian, J.P.; Fan, B.L. A review of computational fluid dynamics for forced-air cooling process. Appl. Energy. 2016, 168, 314–331. [Google Scholar] [CrossRef]
- Ambaw, A.; Mukama, M.; Opara, U.L. Analysis of the effects of package design on the rate and uniformity of cooling of stacked pomegranates: Numerical and experimental studies. Comput. Electron. Agr. 2017, 136, 13–24. [Google Scholar] [CrossRef]
- O’Sullivan, J.L.; Ferrua, M.J.; Love, R.; Verboven, P.; Nicolai, B.; East, A. Forced air cooling of polylined horticultural produce: Optimal cooling conditions and package design. Postharvest Biol. Technol. 2017, 126, 67–75. [Google Scholar] [CrossRef]
- Han, J.W.; Qian, J.P.; Zhao, C.J.; Yang, X.T.; Fan, B.L. Mathematical modelling of cooling efficiency of ventilated packaging: Integral performance evaluation. Int. J. Heat. Mass. Tran. 2017, 111, 386–397. [Google Scholar] [CrossRef]
- Delele, M.A.; Ngcobo, M.E.K.; Getahun, S.T.; Chen, L.; Mellmann, J.; Opara, U.L. Studying airflow and heat transfer characteristics of a horticultural produce packaging system using a 3-D CFD model. Part II: Effect of package design. J. Food Eng. 2013, 86, 546–555. [Google Scholar] [CrossRef]
- Defraeye, T.; Lambrecht, R.; Delele, M.A.; Tsige, A.A.; Opara, U.L.; Cronjé, P.; Verboven, P.; Nicolai, B. Forced-convective cooling of citrus fruit: Cooling conditions and energy consumption in relation to package design. J. Food Eng. 2014, 121, 118–127. [Google Scholar] [CrossRef]
- Wang, D.; Lai, Y.; Jia, B.; Chen, R.; Hui, X. The optimal design and energy consumption analysis of forced air pre-cooling packaging system. Appl. Therm. Eng. 2020, 165, 114592. [Google Scholar] [CrossRef]
- Berry, T.M.; Defraeye, T.; Nicolai, B.M.; Opara, U.L. Multiparameter analysis of cooling efficiency of ventilated fruit cartons using CFD: Impact of vent hole design and internal packaging. Food Bioprocess Technol. 2016, 9, 1481–1493. [Google Scholar] [CrossRef]
- Defraeye, T.; Lambrecht, R.; Tsige, A.A.; Delele, M.A.; Opara, U.L.; Cronjé, P.; Verboven, P.; Nicolai, B. Forced-convective cooling of citrus fruit: Package design. J. Food Eng. 2013, 118, 8–18. [Google Scholar] [CrossRef]
- Wang, X.F.; Fan, Z.Y.; Li, B.G.; Liu, E.H. Variable air supply velocity of forced-air precooling of iceberg lettuces: Optimal cooling strategies. Appl. Therm. Eng. 2021, 187, 116484. [Google Scholar] [CrossRef]
- Berry, T.M.; Fadiji, T.S.; Defraeye, T.; Opara, U.L. The role of horticultural carton vent hole design on cooling efficiency and compression strength: A multi-parameter approach. Postharvest Biol. Technol. 2017, 127, 62–74. [Google Scholar] [CrossRef]
- Wang, X.F.; Li, B.G.; Fan, Z.Y. Packaging Optimization and integral evaluation of cooling Efficiency of Apples. Food Sci. Technol. Res. 2019, 25, 677–686. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R.; Subudhi, S. Numerical modeling of forced-air pre-cooling of fruits and vegetables: A review. Int. J. Refrig. 2022, 145, 217–232. [Google Scholar] [CrossRef]
- Delele, M.A.; Ngcobo, M.E.; Getahun, S.T.; Chen, L.; Mellmann, J.; Opara, U.L. Studying airflow and heat transfer characteristics of a horticultural produce packaging system using a 3-D CFD model, Part I: Model development and validation. Postharvest Biol. Technol. 2013, 86, 536–545. [Google Scholar] [CrossRef]
- Ferrua, M.J.; Singh, R.P. Modeling the forced-air cooling process of fresh strawberry packages, Part III: Experimental validation of the energy model. Int. J. Refrig. 2009, 32, 359–368. [Google Scholar] [CrossRef]
- Rennie, J.T.; Tavoularis, S. Perforation-mediated modifed atmosphere pack-aging: Part I. Development of a mathematical model. Postharvest Biol. Technol. 2009, 51, 1–9. [Google Scholar] [CrossRef]
- Becker, B.R.; Misra, A.; Fricke, B.A. Bulk refrigeration of fruits and vegetables part I: Theoretical considerations of heat and mass transfer. HVAC&R Res. 1996, 2, 122–134. [Google Scholar] [CrossRef]
- Gong, Y.F.; Cao, Y.H.; Zhang, X.R. Forced-air precooling of apples: Airflow distribution and precooling effectiveness in relation to the gap width between tray edge and box wall. Postharvest Biol. Technol. 2021, 177, 111523. [Google Scholar] [CrossRef]
- Kuznik, F.; Rusaouèn, G.; Brau, J. Experimental and numerical study of a full scale ventilated enclosure: Comparison of four two equations closure turbulence models. Build. Environ. 2007, 42, 1043–1053. [Google Scholar] [CrossRef]
- Denys, A.; Pieters, J.G.; Dewettinck, K. Computational fluid dynamics analysis for process impact assessment during thermal pasteurization of intact eggs. J. Food Prot. 2005, 68, 366–374. [Google Scholar] [CrossRef] [PubMed]
- Tutar, M.; Erdogdu, F.; Toka, B. Computational modeling of airflow patterns and heat transfer prediction through stacked layers’ products in a vented box during cooling. Int. J. Refrig. 2009, 32, 295–306. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R.; Subudhi, S. Numerical modeling of periodic airflow reversal with variable air supply velocity for optimal forced-air cooling of apples. Therm. Sci. Eng. Progress. 2024, 48, 102398. [Google Scholar] [CrossRef]
- Ain, Q.T.; He, J.H.; Qiang, X.L.; Kou, Z.; Taylor, T. The two-scale fractal dimension: A unifying perspective to metabolic law. Fractals 2024, 32, 2450016. [Google Scholar] [CrossRef]

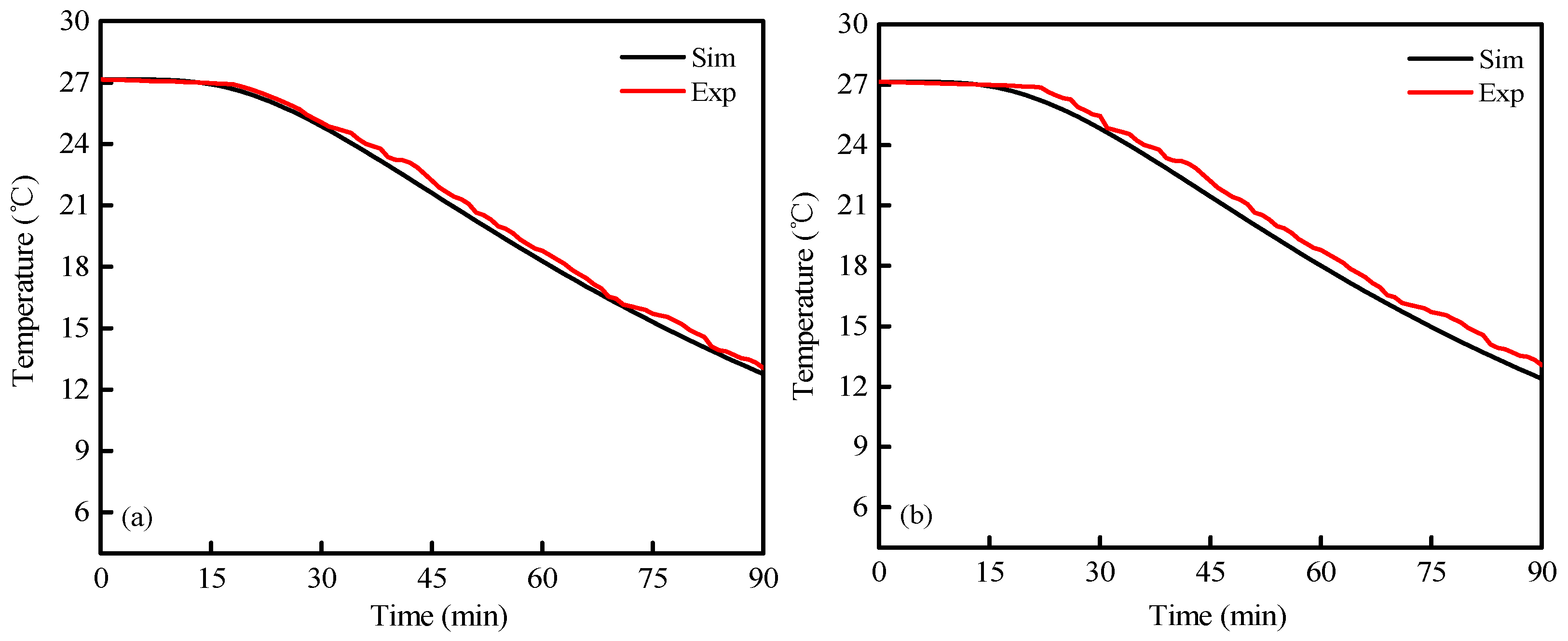
| F2 | S6 | |
|---|---|---|
| Core Temperature | Core Temperature | |
| RMSE (°C) | 0.4 | 0.6 |
| ARD (%) | 1.7 | 2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Fan, Z.; Zhu, C.; Liu, H. Study of Numerical Modeling Method for Precooling of Spherical Horticultural Produce Stacked Symmetrically in Vented Package. Symmetry 2025, 17, 810. https://doi.org/10.3390/sym17060810
Wang X, Fan Z, Zhu C, Liu H. Study of Numerical Modeling Method for Precooling of Spherical Horticultural Produce Stacked Symmetrically in Vented Package. Symmetry. 2025; 17(6):810. https://doi.org/10.3390/sym17060810
Chicago/Turabian StyleWang, Xifang, Zhongyang Fan, Chuanhui Zhu, and Hongbin Liu. 2025. "Study of Numerical Modeling Method for Precooling of Spherical Horticultural Produce Stacked Symmetrically in Vented Package" Symmetry 17, no. 6: 810. https://doi.org/10.3390/sym17060810
APA StyleWang, X., Fan, Z., Zhu, C., & Liu, H. (2025). Study of Numerical Modeling Method for Precooling of Spherical Horticultural Produce Stacked Symmetrically in Vented Package. Symmetry, 17(6), 810. https://doi.org/10.3390/sym17060810







