On the Theory of Nonlinear Landau Damping
Abstract
1. Introduction
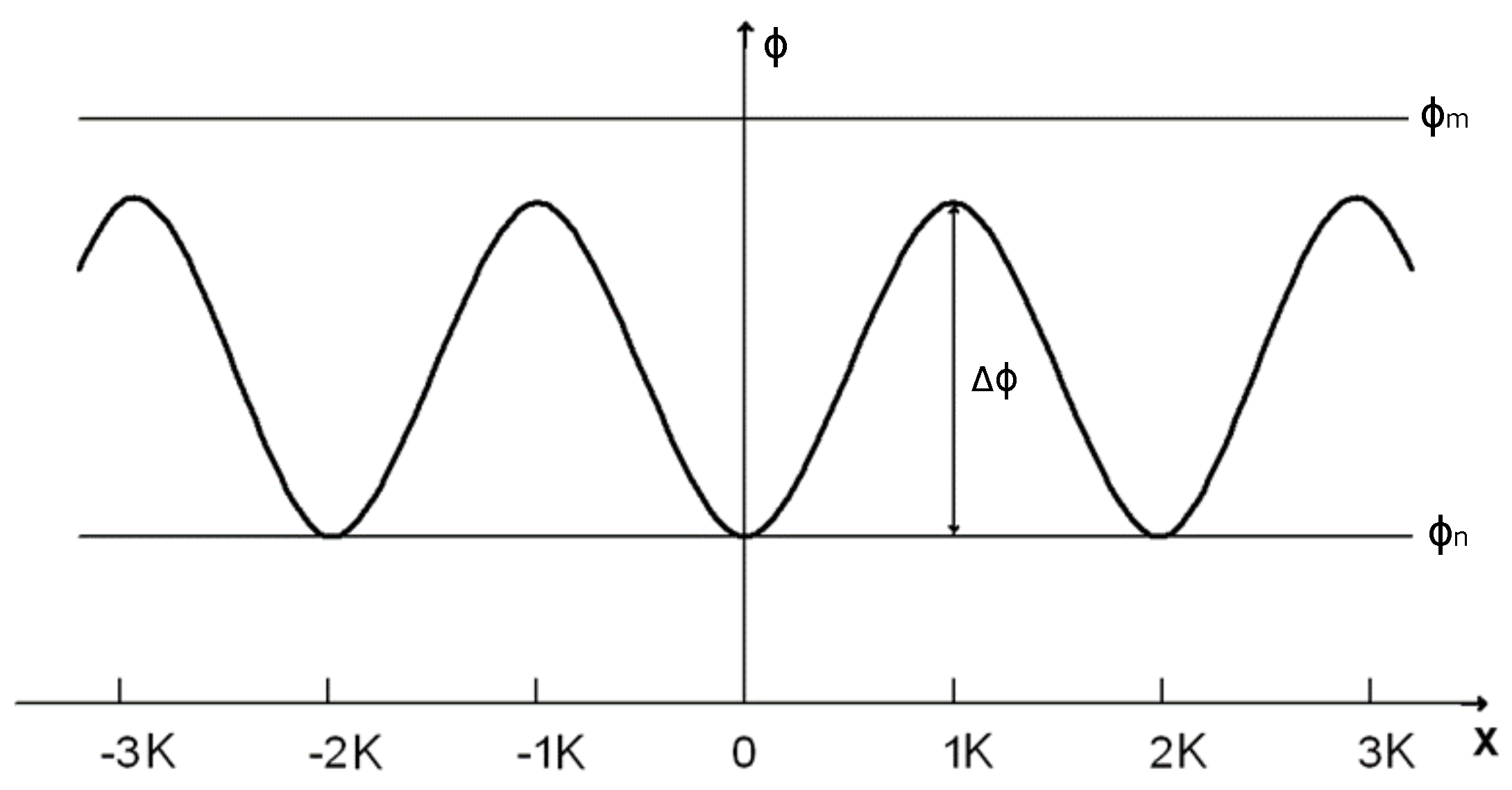
2. Exact Solution of the Vlasov Equation
3. Waves in the Weak Nonlinear Case
4. Instability of the Waves
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Landau, L. On the vibrations of the electronic plasma. J. Phys. 1946, 10, 25–34. [Google Scholar]
- Weitzner, H. Plasma oscillations and Landau damping. Phys. Fluids 1963, 6, 1123. [Google Scholar] [CrossRef]
- Weiland, J. A derivation of Landau damping from the Vlasov equation without contour integration. Eur. J. Phys. 1981, 2, 171–173. [Google Scholar] [CrossRef]
- Li, J. Initial value problem for plasma oscillations. Phys. Fluids B Plasma Phys. 1991, 3, 1158. [Google Scholar] [CrossRef]
- Sagan, D. On the physics of Landau damping. Am. J. Phys. 1994, 62, 450. [Google Scholar] [CrossRef]
- Soshnikov, V.N. Landau damping: Is it real. J. Mosc. Phys. Soc. 1996, 6, 279. [Google Scholar]
- Brodin, G. A new approach to linear Landau damping. Am. J. Phys. 1997, 65, 66. [Google Scholar] [CrossRef]
- O’Neil, T. Collisionless damping of nonlinear plasma oscillations. Phys. Fluids 1965, 8, 2255. [Google Scholar] [CrossRef]
- Shatashvili, N.L.; Tsintsadze, N.L. Nonlinear Landau damping phenomenon in a strongly turbulent plasma. Phys. Scr. Vol. T 1982, 2, 511–516. [Google Scholar] [CrossRef]
- Tsintsadze, N.; Rozina, C.; Shah, H.; Murtaza, G. Nonlinear Landau damping of transverse electromagnetic waves in dusty plasmas. Phys. Plasmas 2009, 16, 043702. [Google Scholar] [CrossRef]
- Mazitov, R.K. Damping of plasma waves. Prikl. Mech. Tech. Fiz. 1965, 6, 27. [Google Scholar] [CrossRef]
- Bernstein, I.B.; Greene, J.M.; Kruskal, M.D. Exact nonlinear plasma oscillations. Phys. Rev. 1957, 108, 546–550. [Google Scholar] [CrossRef]
- Drummond, W.E. Landau damping. Phys. Plasmas 2004, 11, 552. [Google Scholar] [CrossRef]
- Drummond, W.E. The damping of plasma waves. Phys. Plasmas 2005, 12, 092311. [Google Scholar] [CrossRef]
- Tskhakaya, D.D. A new approach to the description of plasma Langmuir waves. Phys. Plasmas 2024, 31, 112301. [Google Scholar] [CrossRef]
- Kadomtsev, B.B. Collective Phenomena in Plasma; Pergamon: Elmsford, NY, USA, 1978; § 4. [Google Scholar]
- Shafranov, V.D. Plasma Confinement in Closed Magnetic Systems; Consultants Bureau: New York, NY, USA, 1965; § 5. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Mechanics; Elsevier: Amsterdam, The Netherlands, 2005; pp. 80–83. [Google Scholar]
- Alexandrov, A.F.; Bogdankevich, L.S.; Ruchadze, A.A. Principles of Plasma Electrodynamics; Springer: Berlin/Heidelberg, Germany, 1984; pp. 78–83. [Google Scholar] [CrossRef]
- Jahnke, E.; Emde, F. Tables of Functions with Formulae and Curves; Dover: Garden City, NY, USA, 1945; pp. 41–106. [Google Scholar]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis; Cambridge University Press: Cambridge, UK, 1973; pp. 413–417. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kos, L.; Vasileska, I.; Tskhakaya, D.D. On the Theory of Nonlinear Landau Damping. Symmetry 2025, 17, 809. https://doi.org/10.3390/sym17060809
Kos L, Vasileska I, Tskhakaya DD. On the Theory of Nonlinear Landau Damping. Symmetry. 2025; 17(6):809. https://doi.org/10.3390/sym17060809
Chicago/Turabian StyleKos, Leon, Ivona Vasileska, and Davy D. Tskhakaya. 2025. "On the Theory of Nonlinear Landau Damping" Symmetry 17, no. 6: 809. https://doi.org/10.3390/sym17060809
APA StyleKos, L., Vasileska, I., & Tskhakaya, D. D. (2025). On the Theory of Nonlinear Landau Damping. Symmetry, 17(6), 809. https://doi.org/10.3390/sym17060809





