Fundamentals of Symmetry and Topology: Applications to Materials Science and Condensed Matter Physics
Abstract
1. Introduction
2. Mathematical Background for Topology and Geometry
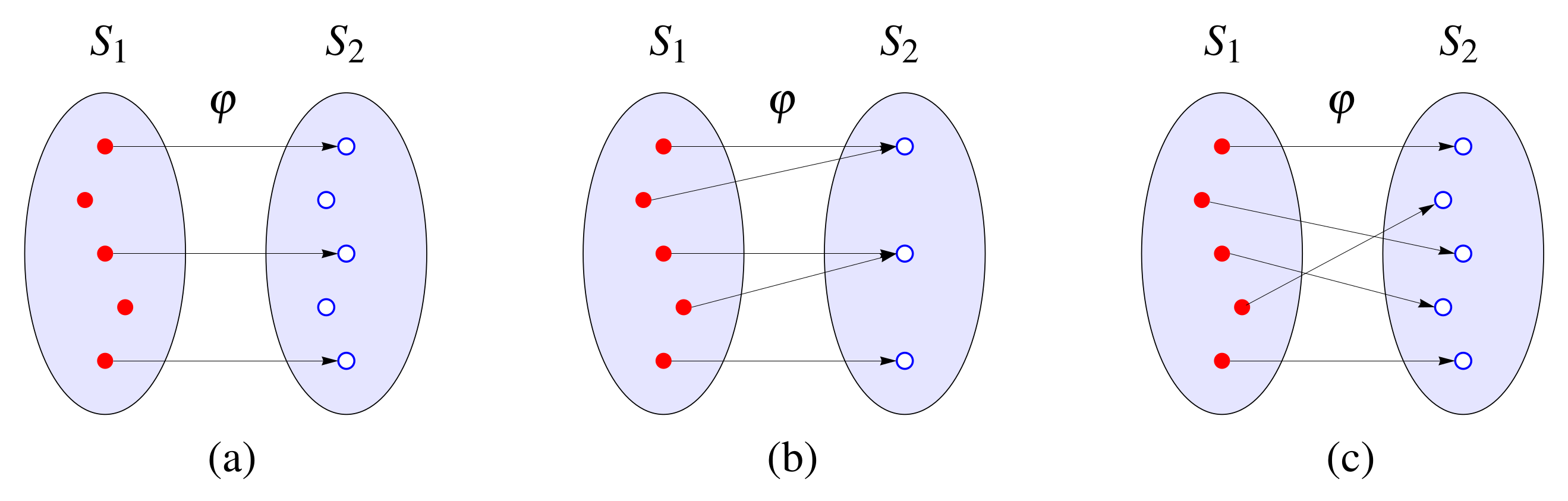
2.1. Definition
- ;
- For any , ; k can be infinite;
- For any , , k is finite.
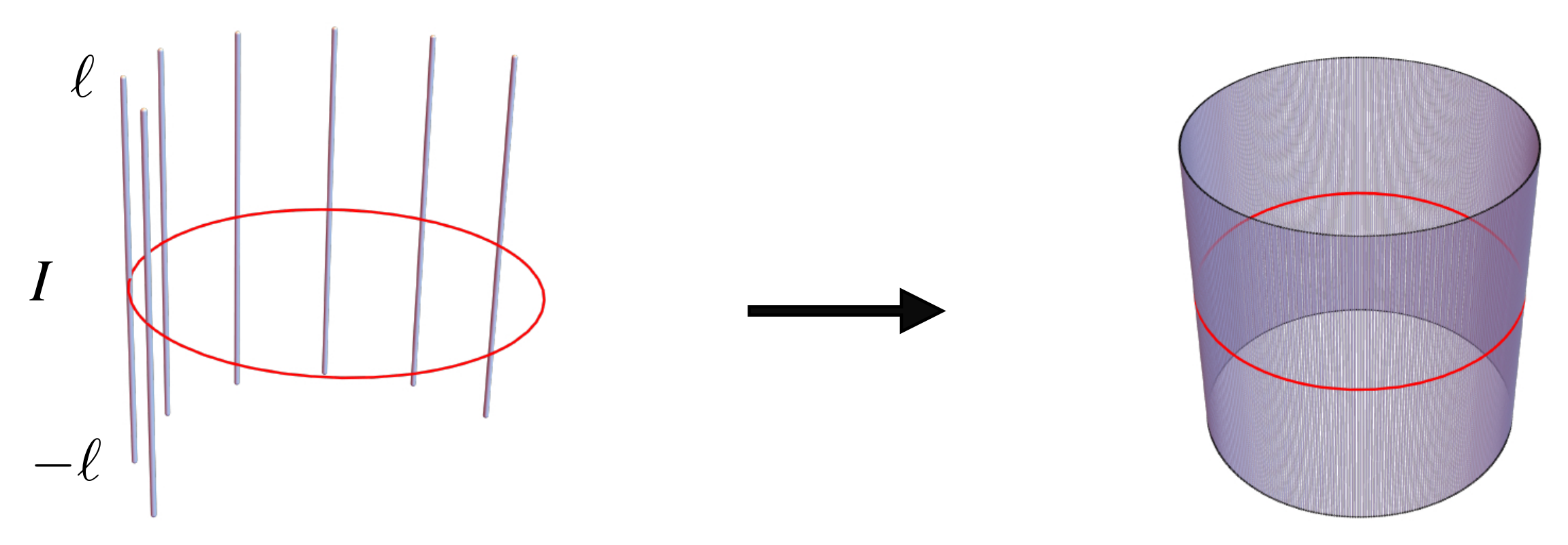
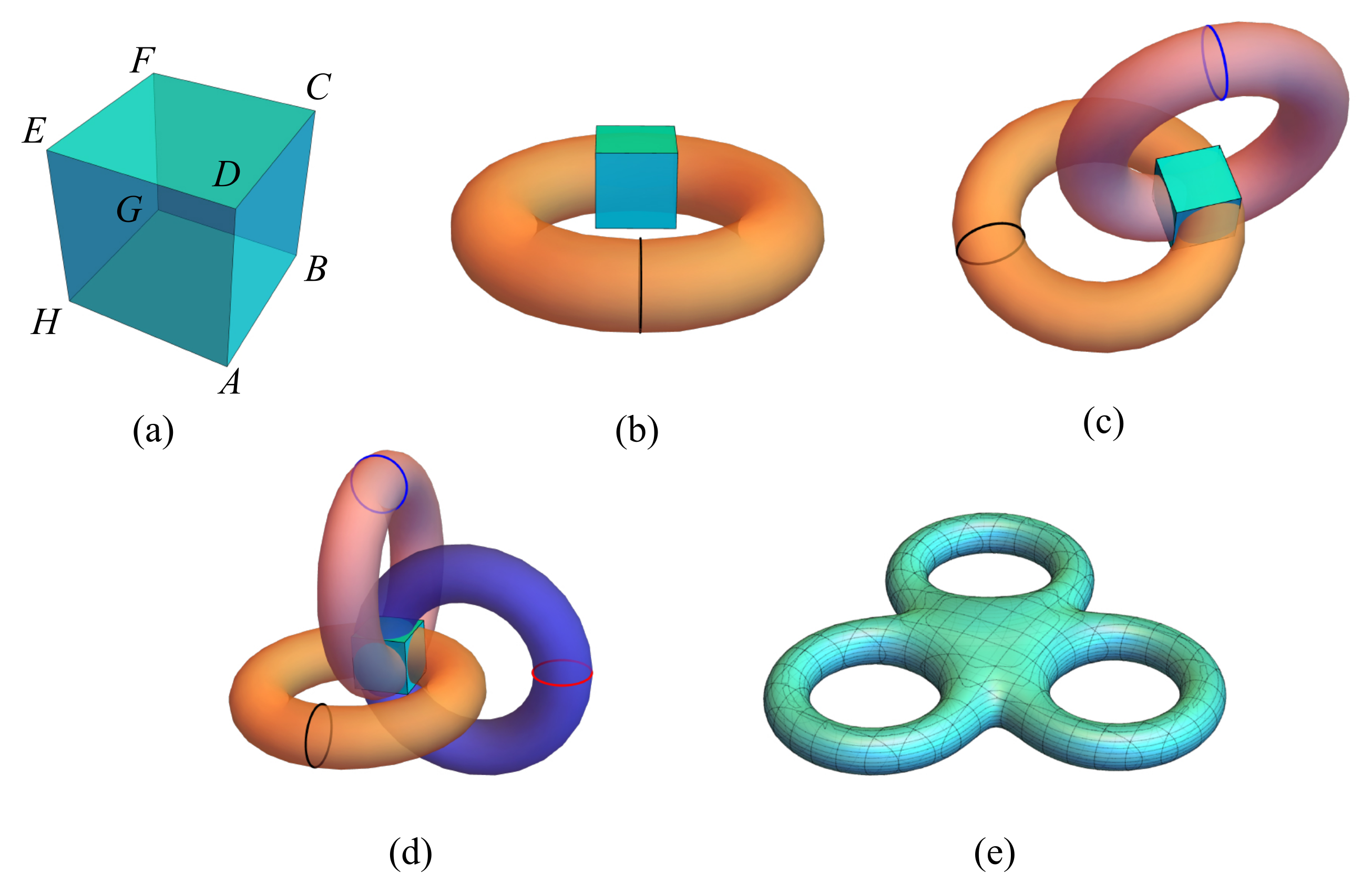
2.2. Topological Invariants
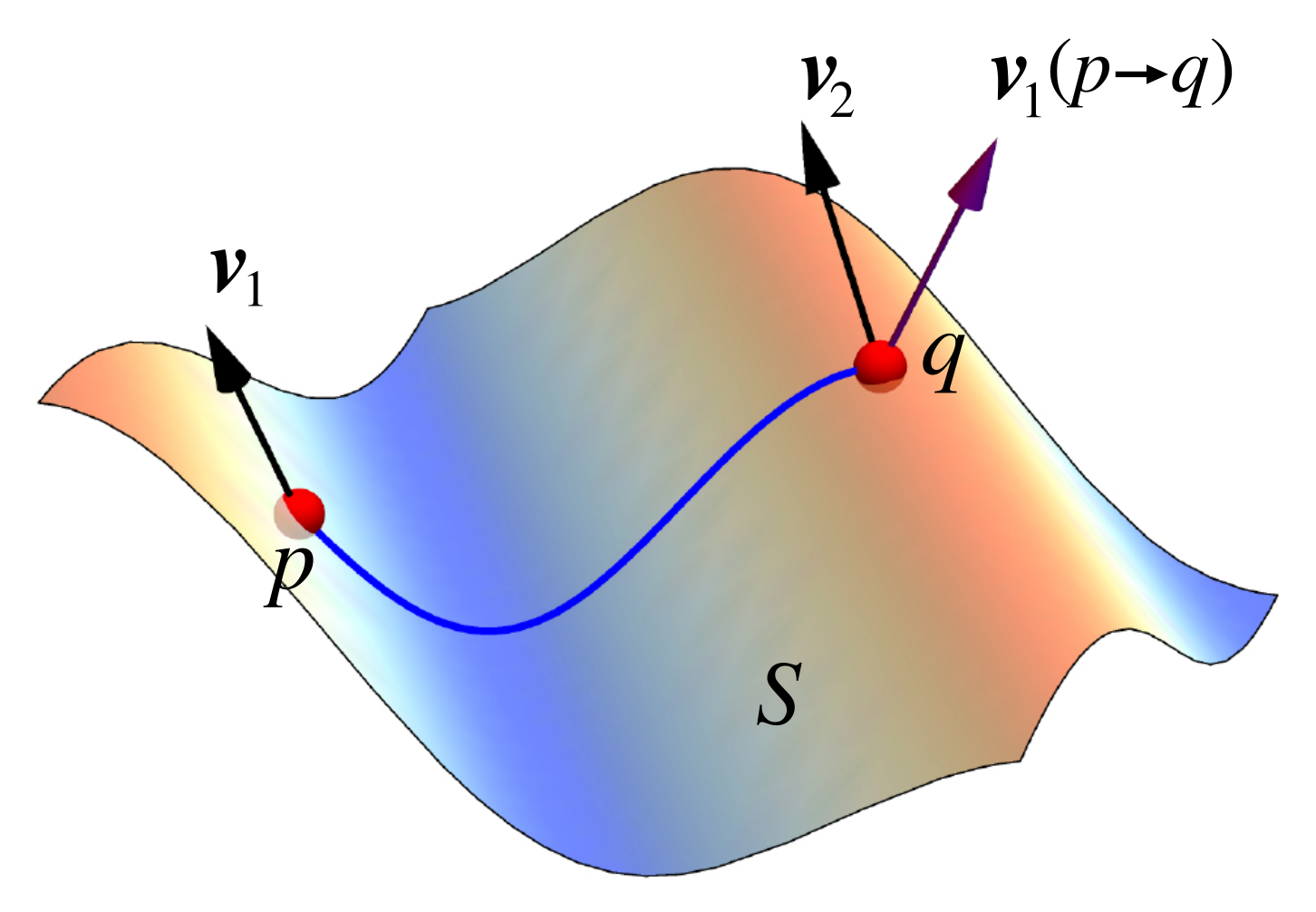
2.3. Connections
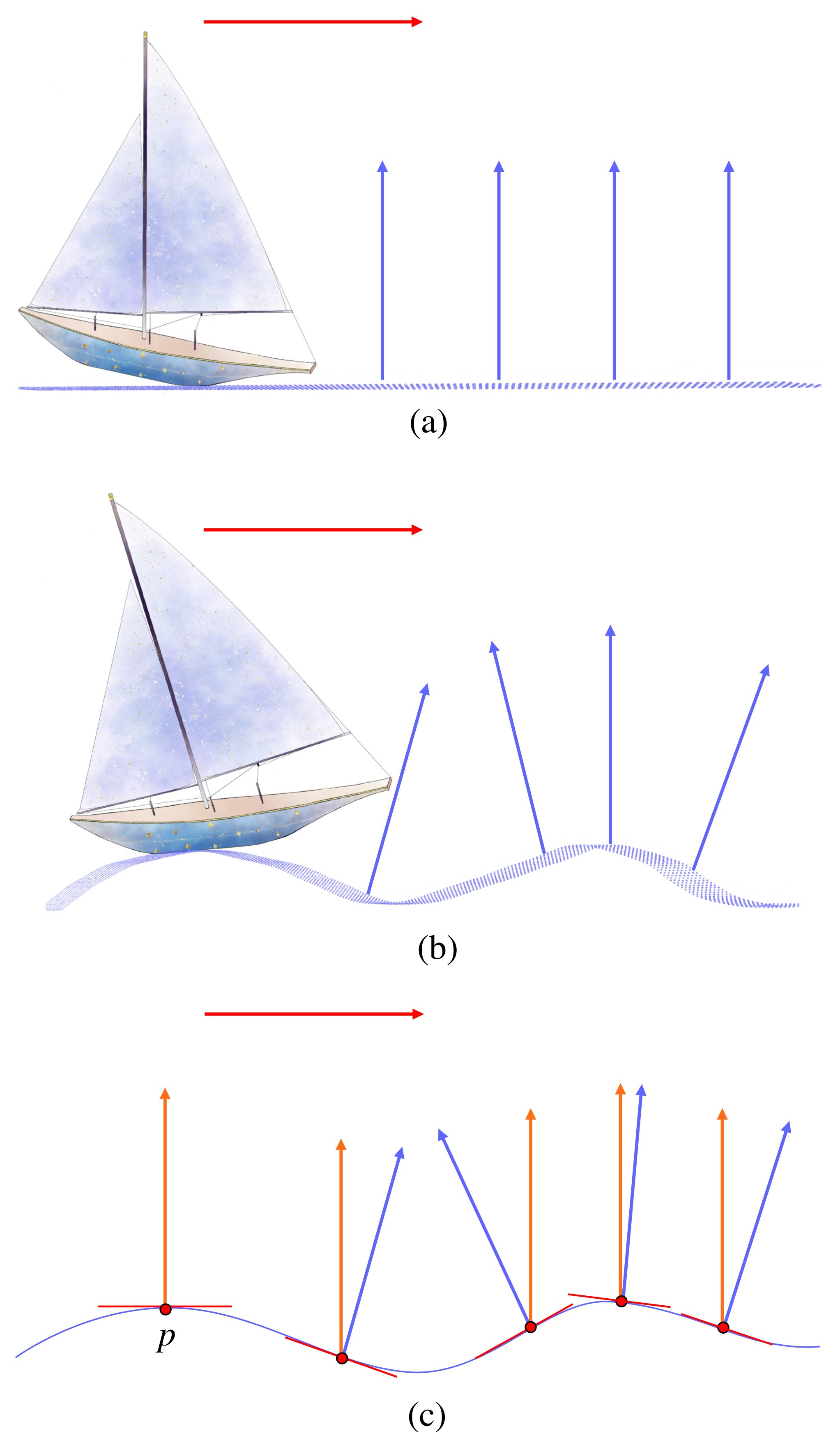
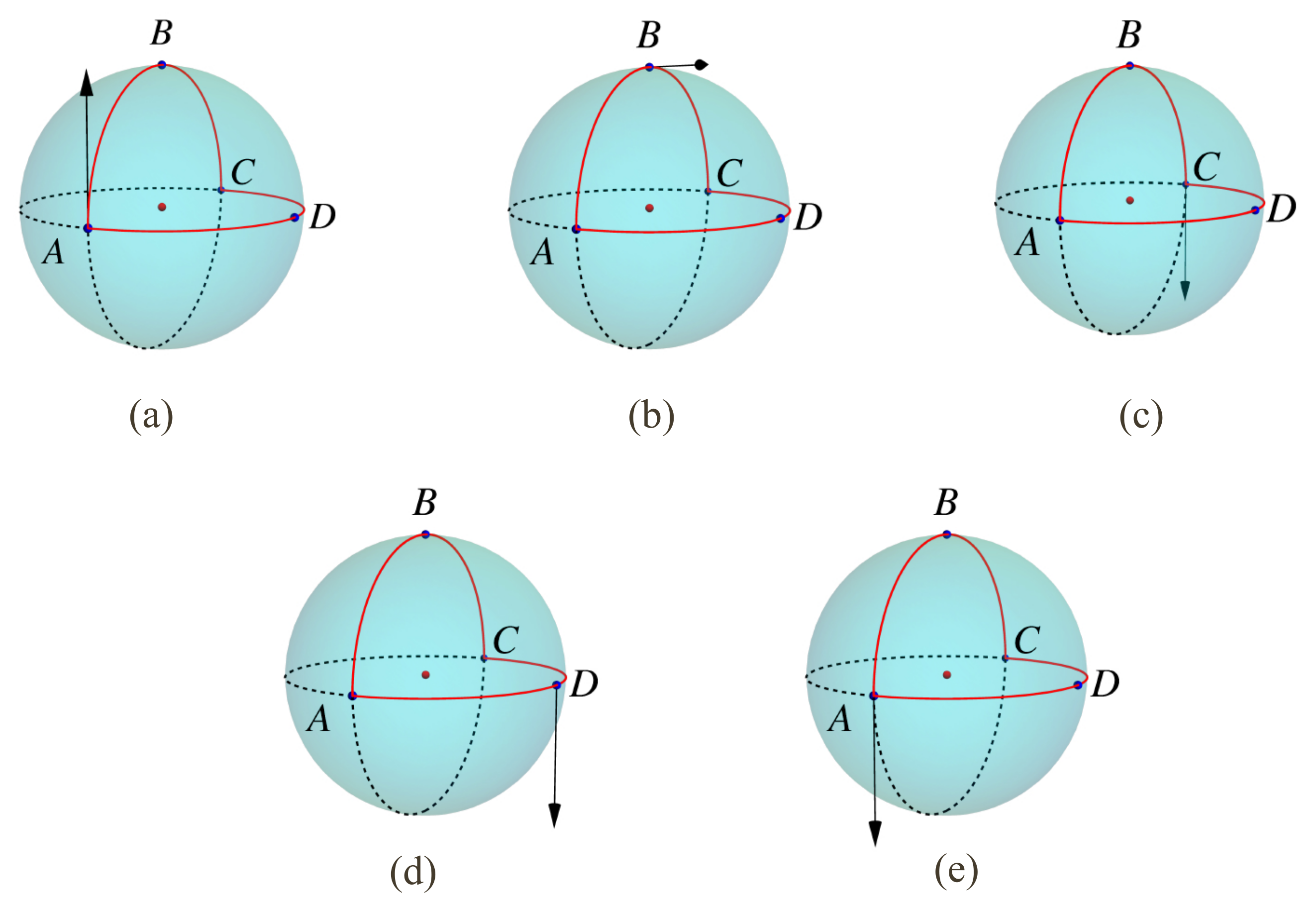
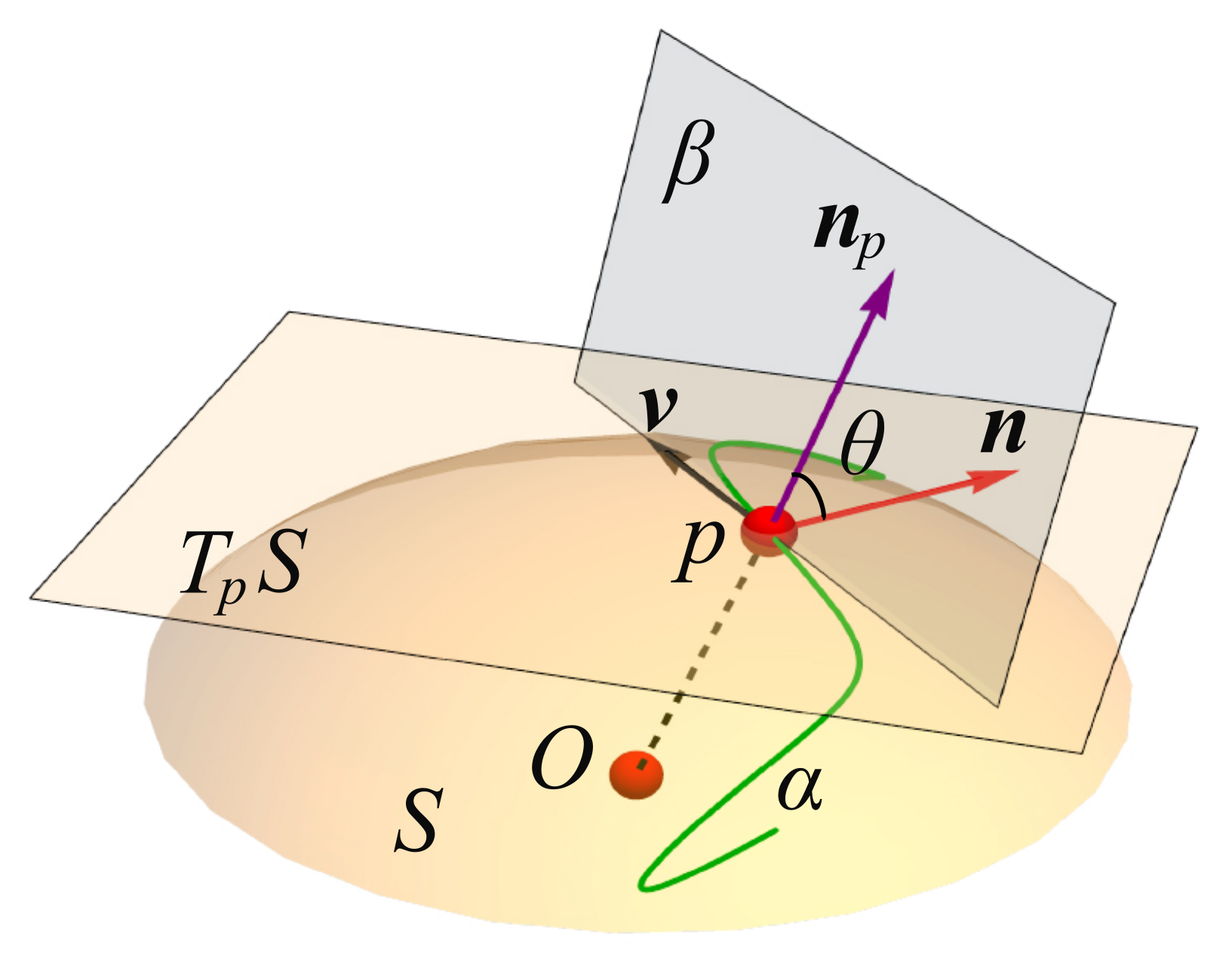
2.4. Curvature
2.5. Fiber Bundles
- E: a differentiable manifold called the total space;
- B: a differentiable manifold called the base space;
- p: a surjection called the projection;
- F: a differentiable manifold called the fiber;
- G: a Lie group called the structure group that acts on F from the left. The special case of as a structure group is addressed in the following example.
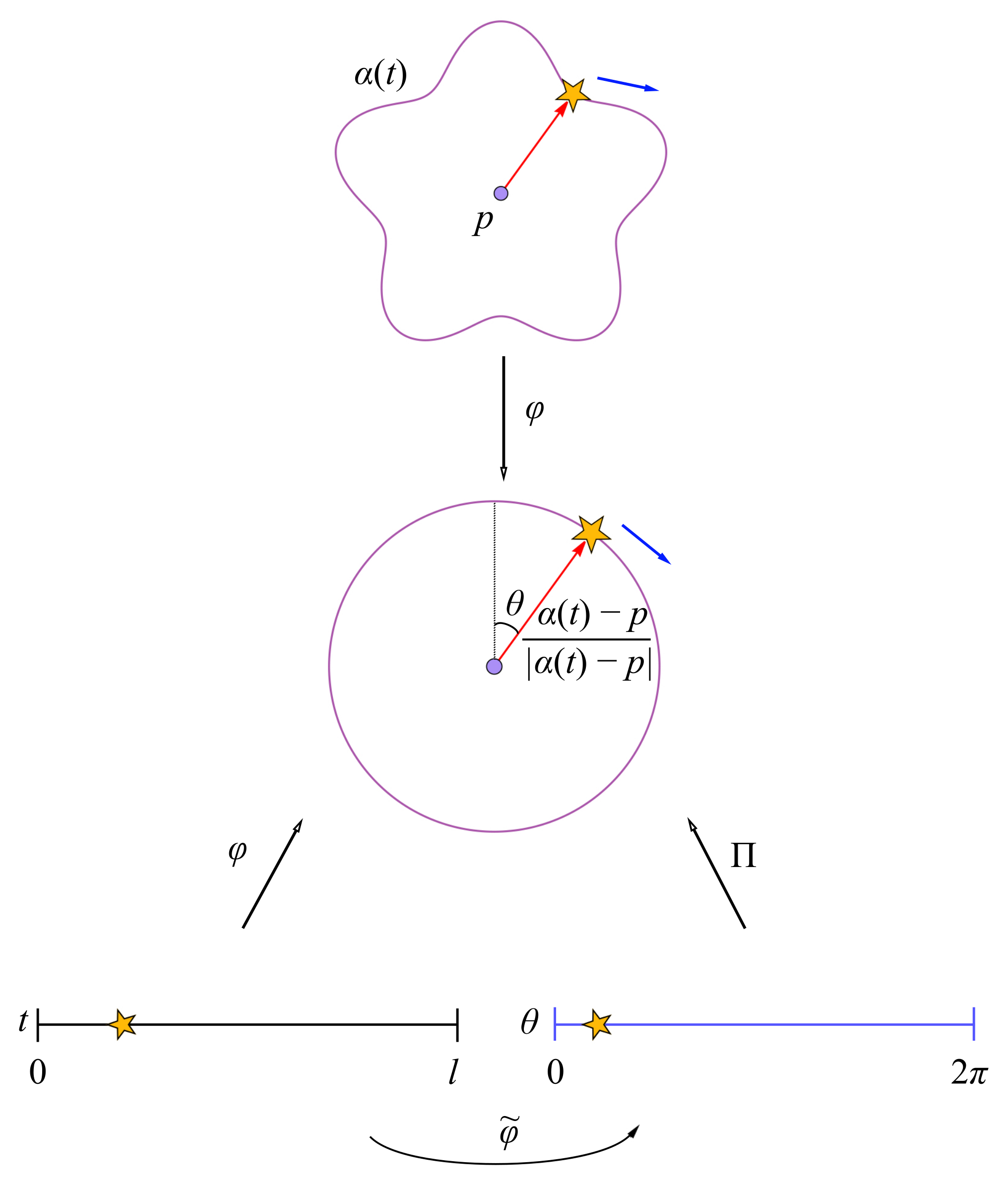
3. Triply Periodic Minimal Surfaces
3.1. Presentations of Minimal Surfaces
3.2. Martensitic Phase Transformations and the Shape-Memory Effect
3.3. Triply Periodic Minimal Surfaces and Density Functional Theory
4. Dynamical Phase and Geometric Phase
4.1. Adiabatic Evolution
4.2. Connection and Curvature: Analogy with Electromagnetism
4.3. Two-Level System
4.4. The Bulk–Boundary Correspondence
- Edge states occur at the interfaces between materials with different topological invariants (including the vacuum) with different topological invariants, such as Chern numbers and indices.
- The number of edge states is equal to the difference in topological invariants across an interface.
- Edge states take various forms, depending on the underlying topological phase and symmetries of the system.
4.5. Degenerate Energy Levels
5. Topology of Energy Bands in Crystalline Solids
6. Topological Quantum Chemistry and Band Representations
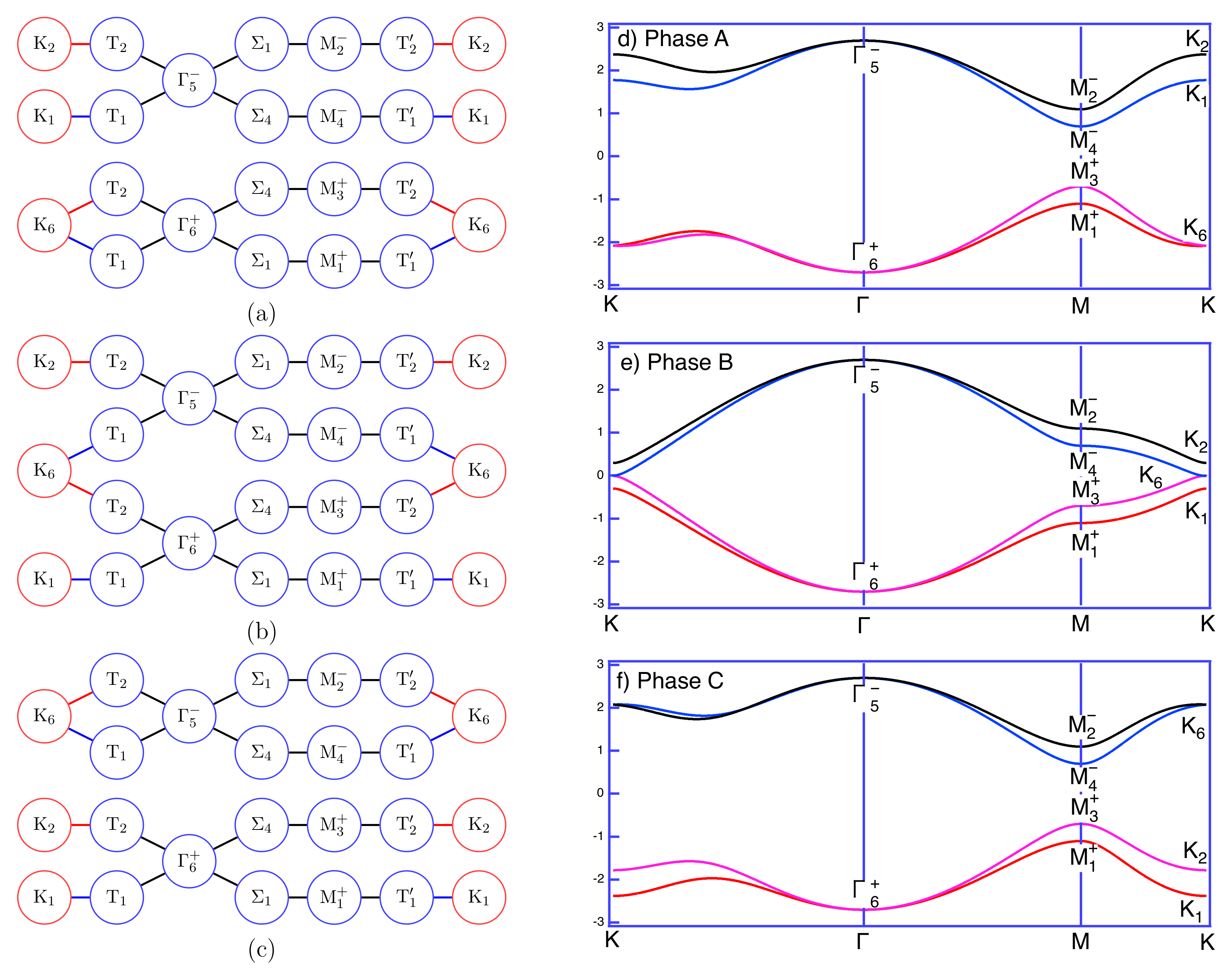
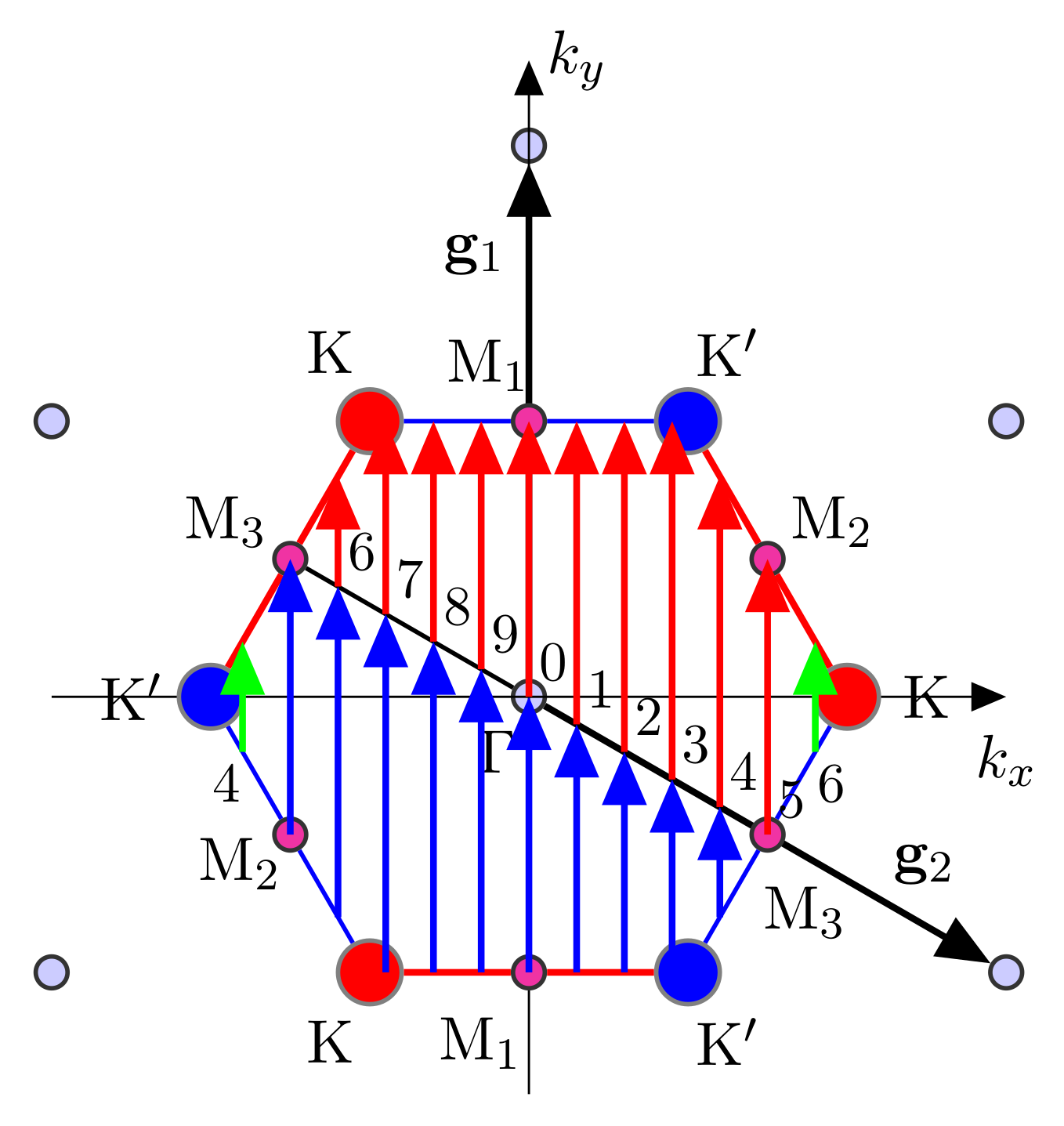
7. Band Representations, Connectivity, and Irreducibility
7.1. Projection Operators and Band Connectivity
7.2. Complex Links and Band Connectivity
7.3. Band Connectivity and Band Representations
8. Symmetry Constraints on Berry Phases and Topological Invariants
- The connected bands are invariant/irreducible, thus having IBR bases.
- The reduced tensor element of the symmetry-permitted form of the CPIBC with respect to the IBR bases is symmetry-forbidden because contractible paths should have a zero or :
9. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TPMS | Triply periodic minimal surfaces (11) |
| DFT | Density functional theory (14) |
| BCC | Body-centered cubic (14) |
| FCC | Face-centered cubic (14) |
| ZEP | Zero equipotential surface (14) |
| RMS | Root mean square (15) |
| HCP | Hexagonal close-packed (15) |
| BZ | Brillouin zone (22) |
| RD | Representation domain (22) |
| TQC | Topological quantum chemistry (24) |
| TB | Tight binding (24) |
| BR | Band representation (24) |
| EBR | Elementary band representation (25) |
| CBR | Composite band representation (25) |
| PEBR | Physical elementary band representation (25) |
| HSP | High-symmetry point (25) |
| IBR | Irreducible band representations (31) |
| CPIBC | Closed-path integral of the Berry connection (31) |
References
- Plato. Timaeus and Critias; Lee, H.D.P., Translator; Penguin: Middlesex, UK, 1971. [Google Scholar]
- Euler, L. Solutio problematis ad geometriam situs pertinentis. Comment. Acad. Sci. Petropolitanae 1741, 8, 128–140. [Google Scholar]
- James, I.M. (Ed.) History of Topology; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Cantor, G. Üeber unendliche, lineare Punktmannichfaltigkeiten. Math. Ann. 1883, 21, 545–591. [Google Scholar] [CrossRef]
- Hausdorff, F. Grundzüge der Mengenlehre; Leipzig Viet: Leipzig, Germany, 1914. [Google Scholar]
- Yang, C.N. Quantum numbers, Chern classes, and a bodhisattva. Phys. Today 2012, 65, 33–34. [Google Scholar] [CrossRef]
- Yang, C.N. Topology and gauge theory in physics. Int. J. Mod. Phys. A 2012, 27, 1230035. [Google Scholar] [CrossRef]
- Avron, J.E.; Osadchy, D.; Seiler, R. A topological look at the quantum Hall effect. Phys. Today 2003, 56, 38–42. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 1982, 49, 405–408. [Google Scholar] [CrossRef]
- Hyde, S.; Andersson, S. A cubic structure consisting of a lipid bilayer forming an infinite periodic minimum surface of the gyroid type in the glycerolmonooleat-water system. Z. Kristallogr. Cryst. Mater. 1984, 168, 213–220. [Google Scholar] [CrossRef]
- Hyde, S.; Andersson, S. Differential geometry of crystal structure descriptions, relationships and phase transformation. Z. Kristallogr. Cryst. Mater. 1985, 170, 225–240. [Google Scholar] [CrossRef]
- Hyde, S.; Andersson, S. The martensite transition and differential geometry. Z. Kristallogr. Cryst. Mater. 1986, 174, 225–236. [Google Scholar] [CrossRef]
- Andersson, S.; Hyde, S.; Larsson, K.; Lidin, S. Minimal Surfaces and Structures: From Inorganic and Metal Crystals to Cell Membranes and Biopolymers. Chem. Rev. 1988, 88, 221–242. [Google Scholar] [CrossRef]
- Anirban, A. 15 years of topological matter. Nat. Rev. Phys. 2023, 5, 267. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, S.C. Topological states of condensed matter. Nat. Mater. 2017, 16, 1062–1067. [Google Scholar] [CrossRef]
- Pariari, A.K. Atoms to Topological Electronic Materials: A Bedtime Story for Beginners. Indian J. Phys. 2021, 95, 2636–2660. [Google Scholar] [CrossRef]
- Gao, H.; Venderbos, J.W.F.; Kim, Y.; Rappe, A.M. Topological semimetals from first principles. Annu. Rev. Mater. Res. 2019, 49, 153–183. [Google Scholar] [CrossRef]
- Yan, B.; Felser, C. Topological materials: Weyl semimetals. Annu. Rev. Mater. Res. 2017, 8, 337–354. [Google Scholar] [CrossRef]
- Lv, B.Q.; Qian, T.; Ding, H. Experimental perspective on three-dimensional topological semimetals. Rev. Mod. Phys. 2021, 93, 025002. [Google Scholar] [CrossRef]
- Shen, S.Q. The family of topological phases in condensed matter. Natl. Sce. Rev. 2017, 1, 49–59. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Liu, Y. Topology optimization: A review for structural designs under static problems. Materials 2024, 17, 5970. [Google Scholar] [CrossRef]
- Ghil, M. Review article: Dynamical systems, algebraic topology and the climate sciences. Nonlin. Process. Geophys. 2023, 30, 399–434. [Google Scholar] [CrossRef]
- Garcia, M.S.; Süsstrunk, R.; Huber, S.D. Topology in nonlinear mechanical systems. Phys. Rev. Lett. 2021, 127, 076802. [Google Scholar] [CrossRef]
- Shankar, S.; Bowick, S.M.J.; Marchetti, M.C.; Vitelli, V. Topological active matter. Nat. Rev. Phys. 2022, 4, 380–398. [Google Scholar] [CrossRef]
- Gross, D.J. The role of symmetry in fundamental physics. Proc. Natl. Acad. Sci. USA 1996, 93, 14256–14259. [Google Scholar] [CrossRef] [PubMed]
- Senthil, T. Symmetry-protected topological phases of quantum matter. Annu. Rev. Condens. Matter. Phys. 2015, 6, 299–324. [Google Scholar] [CrossRef]
- Fischer, M.H.; Sigrist, M.; Agterberg, D.F.; Yanase, Y. Superconductivity and local inversion-symmetry breaking. Annu. Rev. Condens. Matter. Phys. 2023, 14, 153–172. [Google Scholar] [CrossRef]
- McGrevy, J. Generalized symmetries in condensed matter. Annu. Rev. Condens. Matter. Phys. 2023, 14, 57–82. [Google Scholar] [CrossRef]
- Nakahara, M. Geometry Topology and Physics; IOP Publishing Ltd.: West Philadelphia, PA, USA, 2003. [Google Scholar]
- Hasan, M.; Kane, C. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Qi, X.; Zhang, S. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- Murakami, S.; Hirayama, M.; Okugawa, R.; Miyake, T. Emergence of topological semimetals in gap closing in semiconductors without inversion symmetry. Sci. Adv. 2017, 3, e1602680. [Google Scholar] [CrossRef]
- Burkov, A.A. Topological semimetals. Nat. Mater. 2016, 15, 1145–1148. [Google Scholar] [CrossRef]
- Yu, R.; Weng, H.; Fang, Z.; Dai, X.; Hu, X. Topological node-line semimetal and Dirac semimetal state in antiperovskite Cu3PdN. Phys. Rev. Lett. 2015, 115, 036807. [Google Scholar] [CrossRef]
- Burkov, A.A.; Hook, M.D.; Balents, L. Topological nodal semimetals. Phys. Rev. B 2011, 84, 235126. [Google Scholar] [CrossRef]
- Mermin, N.D. The topological theory of defects in ordered media. Rev. Mod. Phys. 1979, 51, 591–648. [Google Scholar] [CrossRef]
- Michel, L. Symmetry defects and broken symmetry. Configurations Hidden symmetry. Rev. Mod. Phys. 1980, 52, 617–651. [Google Scholar] [CrossRef]
- Munkres, J. Topology; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Carmo, M. Differential Geometry of Curves and Surfaces; Dover: New York, NY, USA, 2016. [Google Scholar]
- Sethna, J.P. Frustration and curvature: Glasses and the cholesteric blue phase. Phys. Rev. Lett. 1983, 51, 2198–2201. [Google Scholar] [CrossRef]
- Rosso, R.; Virga, E.G.; Kralj, S. Parallel transport and defects on nematic shells. Contin. Mech. Thermodyn. 2012, 24, 643–664. [Google Scholar] [CrossRef]
- Brazil, R. Fighting flat-Earth theory. Phys. World 2020, 33, 35–39. [Google Scholar] [CrossRef]
- Dreshler, W.; Mayer, M.E. Fiber Bundle Techniques in Gauge Theories: Lectures in Mathematical Physics at the University of Texas at Austin: 67; Lecture Notes in Physics, 67; Springer: Berlin, Germany, 1977. [Google Scholar]
- Cayssol, J.; Fuchs, J.N. Topological and geometrical aspects of band theory. J. Phys. Mater. 2021, 4, 034007. [Google Scholar] [CrossRef]
- Fruchart, M.; Carpentier, D. An introduction to topological insulators. Comptes Rendus Phys. 2013, 14, 779–815. [Google Scholar] [CrossRef]
- Hillel, D. (Ed.) Encyclopedia of Soils in the Environment; Academic Press: Los Angeles, CA, USA, 2005. [Google Scholar]
- Schwarz, H.A. Gesammelte Mathematische Abhandlungen; American Mathematical Society: Ann Arbor, MI, USA, 1972. [Google Scholar]
- Lai, M.; Kulak, A.; Law, D.; Zhang, Z.; Meldrum, F.; Riley, D. Profiting from nature: Macroporous copper with superior mechanical properties. Chem. Commun. 2007, 34, 3547–3549. [Google Scholar] [CrossRef]
- Galusha, J.; Richey, L.; Gardner, J.; Cha, J.; Bartl, M. Discovery of a diamond-based photonic crystal structure in beetle scales. Phys. Rev. E 2008, 77, 050904. [Google Scholar] [CrossRef]
- Feng, J.; Fu, J.; Yao, X.; He, Y. Triply periodic minimal surface (TPMS) porous structures: From multi-scale design, precise additive manufacturing to multidisciplinary applications. Int. J. Extrem. Manuf. 2022, 4, 022001. [Google Scholar] [CrossRef]
- Pugliesea, R.; Graziosib, S. Biomimetic scaffolds using triply periodic minimal surface-based porous structures for biomedical applications. SLAS Technol. 2023, 28, 165–182. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhai, L. Structural optimization, compressive strength analysis, and application exploration of triply periodic minimal surfaces (TPMS) in interior design. Sci. Rep. 2025, 15, 11026. [Google Scholar] [CrossRef] [PubMed]
- Cheung, S.; Kang, J.; Lin, Y.; Goodson, K.E.; Asheghi, M.; Gu, X.W. Triply periodic minimal surfaces for thermo-mechanical protection. Sci. Rep. 2025, 15, 1688. [Google Scholar] [CrossRef]
- Gado, M.G.; Al-Ketan, O.; Aziz, M.; Al-Rub, R.A.; Ookawara, S. Triply periodic minimal surface structures: Design, fabrication, 3D printing techniques, state-of-the-art studies, and prospective thermal applications for efficient energy utilization. Energy Technol. 2024, 12, 2301287. [Google Scholar] [CrossRef]
- Felix, L.C.; Ambekar, R.; Tromer, R.M.; Woellner, C.F.; Rodrigues, V.; Ajayan, P.M.; Tiwary, C.S.; Galvao, D.S. Schwarzites and triply periodic minimal surfaces: From pure topology mathematics to macroscale applications. Small 2024, 2400351. [Google Scholar] [CrossRef]
- Fomenko, A.; Tuzhilin, A. Elements of the Geometry and Topology of Minimal Surfaces in Three-Dimensional Space; American Mathematical Society: Ann Arbor, MI, USA, 2000. [Google Scholar]
- Weierstrass, K. Mathematische Werke; Mayer & Müller: Berlin, Germany, 1903. [Google Scholar]
- Enneper, A. Analytisch-Geometrische Untersuchung. Z. Math. Phys. 1864, 9, 96–125. [Google Scholar]
- Schoen, A.H. Infinite Periodic Minimal Surfaces without Self-Intersections; Tech. Rep. TN D-5541; NASA: Washington, DC, USA, 1970. [Google Scholar]
- Osmond, F. Nomenclature in Metallography. J. Iron Steel Inst. 1902, 61, 90. [Google Scholar]
- Portella, P.D.; Helmerich, R. Adolf Martens and his contribution to materials engineering. Eng. Fail. Anal. 2014, 43, 2–10. [Google Scholar] [CrossRef]
- Hao, Y.; Zhang, L.; Chen, X.; Cai, L.; Wu, Q.; Alfè, D. Ab initio calculations of the thermodynamics and phase diagram of zirconium. Phys. Rev. B 2008, 78, 134101. [Google Scholar] [CrossRef]
- Campbell, W. Twenty-five years of metallography, 3rd Howe Memorial Award. Trans. AIME 1926, 73, 1135. [Google Scholar]
- Greninger, A.; Mooradian, V. Strain transformation in metastable beta copper-zinc and beta copper-titanium alloys. Trans. AIME 1938, 128, 337. [Google Scholar]
- Wadhawan, V. Ferroelasticity and related properties of crystals. Phase Transit. 1982, 3, 3–103. [Google Scholar] [CrossRef]
- Buehler, W.; Gilfrich, J.; Wiley, R. Effect of low-temperature phase changes on the mechanical properties of alloys near composition TiNi. J. Appl. Phys. 1963, 34, 1475–1477. [Google Scholar] [CrossRef]
- Hatcher, N.; Kontsevoi, O.; Freeman, A. Martensitic transformation path of NiTi. Phys. Rev. B 2009, 79, 020202(R). [Google Scholar] [CrossRef]
- Hatcher, N.; Kontsevoi, O.; Freeman, A. Role of elastic and shear stabilities in the martensitic transformation path of NiTi. Phys. Rev. B 2009, 80, 144203. [Google Scholar] [CrossRef]
- Mishin, Y.; Farkas, D.; Mehl, M.; Papaconstantopoulos, D. Interatomic potentials for monoatomic metals from experimental data and ab initio calculations. Phys. Rev. B 1999, 59, 3393–3407. [Google Scholar] [CrossRef]
- Wang, T.; Du, J.; Wei, S.; Liu, F. Ab-initio investigation for the microscopic thermodynamics and kinetics of martensitic transformation. Prog. Nat. Sci. Mater. 2021, 31, 121–128. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, M.; Shi, X.; Shuai, J.; Zhu, Z. Bain and Nishiyama–Wassermann transition path separation in the martensitic transitions of Fe. RSC Adv. 2021, 11, 3043. [Google Scholar] [CrossRef]
- Kibey, S.; Sehitoglu, H.; Johnson, D. Energy landscape for martensitic phase transformation in shape memory NiTi. Mater. Res. Soc. Symp. Proc. 2009, 57, 1624–1629. [Google Scholar] [CrossRef]
- Chakraborty, T.; Rogal, J.; Drautz, R. Martensitic transformation between competing phases in Ti–Ta alloys: A solid-state nudged elastic band study. J. Phys. Condens. Matter. 2015, 27, 115401. [Google Scholar] [CrossRef]
- Ghosh, P.; Arya, A.; Tewari, R.; Dey, G. Alpha to omega martensitic phase transformation pathways in pure Zr. J. Alloys Compd. 2014, 586, 693–698. [Google Scholar] [CrossRef]
- Trinkle, D.; Hatch, D.; Stokes, H.; Hennig, R.; Albers, R. Systematic pathway generation and sorting in martensitic transformations: Titanium alpha to omega. Phys. Rev. B 2005, 72, 014105. [Google Scholar] [CrossRef]
- Cowley, R. Structural phase transitions I. Landau theory. Adv. Phys. 1980, 29, 1–110. [Google Scholar] [CrossRef]
- Pallikara, I.; Skelton, J. Phase stability of the tin monochalcogenides SnS and SnSe: A quasi-harmonic lattice-dynamics study. Phys. Chem. Chem. Phys. 2021, 23, 19219. [Google Scholar] [CrossRef]
- Pallikara, I.; Kayastha, P.; Skelton, J.; Whalley, L. The physical significance of imaginary phonon modes in crystals. Electron. Struct. 2022, 4, 033002. [Google Scholar] [CrossRef]
- Kamba, S. Soft-mode spectroscopy of ferroelectrics and multiferroics: A review. APL Mater. 2021, 9, 020704. [Google Scholar] [CrossRef]
- Scott, J.F. Soft-mode spectroscopy: Experimental studies of structural phase transitions. Rev. Mod. Phys. 1974, 46, 83–128. [Google Scholar] [CrossRef]
- Tolédano, J.; Tolédano, P. The Landau Theory of Phase Transitions; World Scientific: River Edge, NJ, USA, 1987. [Google Scholar]
- Tolédano, P.; Dmitriev, V. Reconstructive Phase Transitions: In Crystals and Quasicrystals; World Scientific: River Edge, NJ, USA, 1996. [Google Scholar]
- Landau, L.; Lifshitz, E. Course of Theoretical Physics, Statistical Physics; Pergamon Press: Oxford, UK, 1980. [Google Scholar]
- Falk, F. Model free energy, mechanics, and thermodynamics of shape memory alloys. Acta Mater. 1980, 28, 1773–1780. [Google Scholar] [CrossRef]
- Falk, F. Landau theory and martensitic phase transitions. J. Phys. Colloq. 1982, 43, C4-3–C4-15. [Google Scholar] [CrossRef]
- Nesper, R.; Schnering, H. Periodische äquipotential flächen. Z. Kristallogr. 1985, 170, 138. [Google Scholar]
- Schnering, H.; Nesper, R. How nature adapts chemical structures to curved surfaces. Angew. Chem. 1987, 26, 1059–1080. [Google Scholar] [CrossRef]
- Schnering, H.; Nesper, R. Nodal surfaces of Fourier series: Fundamental invariants of structured matter. Z. Physik B Condensed Matter. 1991, 83, 407–412. [Google Scholar] [CrossRef]
- Yin, M.; Zhang, J.; Vvedensky, D.D. Density-functional theory and triply-periodic minimal surfaces. arXiv 2025, arXiv:2503.12555. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Yin, M.; Vvedensky, D.D. Shape memory effect and the topology of minimal surfaces. Symmetry 2024, 16, 1187. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Simon, B. Holonomy, the quantum adiabatic theorem, and Berry’s phase. Phys. Rev. Lett. 1983, 51, 2167–2170. [Google Scholar] [CrossRef]
- Zwanziger, J.W.; Koenig, M.; Pines, A. Berry’s phase. Annu. Rev. Phys. Chem. 1990, 41, 601–646. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.-C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef]
- Girvin, S.M.; Yang, K. Modern Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Messiah, A. Quantum Mechanics; North-Holland: Amsterdam, The Netherlands, 1962; Volume II. [Google Scholar]
- Fu, L.; Kane, C.L. Topological insulators with inversion symmetry. Phys. Rev. B 2007, 76, 045302. [Google Scholar] [CrossRef]
- Liu, G.; Gao, Z.; Zhang, B. Topological Chern vectors in three-dimensional photonic crystals. Nature 2022, 609, 925–930. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. Lectures on Quantum Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Asbóth, J.K.; Oroszlány, L.; Pályi, A. A Short Course on Topological Insulators; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Hatsugai, Y. Chern number and edge states in the integer quantum Hall effect. Phys. Rev. Lett. 1993, 71, 3697–3700. [Google Scholar] [CrossRef] [PubMed]
- Johnsen, T.; Schattauer, C.; Samaddar, S.; Weston, A.; Hamer, M.J.; Watanabe, K.; Taniguchi, T.; Gorbachev, R.; Libisch, F.; Morgenstern, M. Mapping quantum Hall edge states in graphene by scanning tunneling microscopy. Phys. Rev. B 2023, 107, 115426. [Google Scholar] [CrossRef]
- Halperin, B.I. Quantized Hall conductance, current-carrying edge states, and the existence of extended states in a two-dimensional disordered potential. Phys. Rev. B 1982, 25, 2185–2190. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Phys. Usp. 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting proximity effect and Majorana Fermions at the surface of a topological insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef]
- Wilczek, F.; Zee, A. Appearance of Gauge Structure in Simple Dynamical Systems. Phys. Rev. Lett. 1984, 52, 2111–2114. [Google Scholar] [CrossRef]
- Marcel, F.; Laurens, M. (Eds.) Topological Insulators. In Contemporary Concepts in Condensed Matter Science; Elsevier B.V.: Amsterdam, The Netherlands, 2013; Volume 6. [Google Scholar]
- Bradlyn, B.; Iraola, M. Lecture notes on Berry phases and topology. Scipost Phys. Lect. Notes 2022, 51, 51. [Google Scholar] [CrossRef]
- Bradley, C.J.; Davies, B.L. Magnetic groups and their corepresentations. Rev. Mod. Phys. 1968, 40, 359–379. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Z2 topological order and the quantum spin hall effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef] [PubMed]
- Bradlyn, B.; Elcoro, L.; Cano, J.; Vergniory, M.G.; Wang, Z.; Felser, C.; Aroyo, M.I.; Bernevig, B.A. Topological quantum chemistry. Nature 2017, 547, 298–305. [Google Scholar] [CrossRef]
- Po, H.; Vishwanath, A.; Watanabe, H. Symmetry-based indicators of band topology in the 230 space groups. Nature Commu. 2017, 8, 50. [Google Scholar] [CrossRef]
- Kruthoff, J.; de Boer, J.; van Wezel, J.; Kane, C.L.; Slager, R.-J. Topological classification of crystalline insulators through band structure combinatorics. Phys. Rev. X 2017, 7, 041069. [Google Scholar] [CrossRef]
- Wannier, G.H. The structure of electronic excitation levels in insulating crystals. Phys. Rev. 1936, 52, 191–197. [Google Scholar] [CrossRef]
- Marzari, N.; Mostofi, A.A.; Yates, J.R.; Souza, I.; Vanderbilt, D. Maximally localized Wannier functions: Theory and applications. Rev. Mod. Phys. 2012, 84, 1419–1475. [Google Scholar] [CrossRef]
- Slater, J.; Koster, G. Simplified LCAO method for the periodic potential problem. Phys. Rev. 1954, 94, 1498–1524. [Google Scholar] [CrossRef]
- Zak, J. Band representations of space groups. Phys. Rev. B 1982, 26, 3010–3023. [Google Scholar] [CrossRef]
- Cano, J.; Bradlyn, B.; Wang, Z.; Elcoro, L.; Vergniory, M.G.; Felser, C.; Aroyo, M.I.; Bernevig, B.A. Building blocks of topological quantum chemistry: Elementary band representations. Phys. Rev. B 2018, 97, 035139. [Google Scholar] [CrossRef]
- Cano, J.; Bradlyn, B. Band representations and topological quantum chemistry. Annu. Rev. Condens. Matter Phys. 2021, 12, 225–246. [Google Scholar] [CrossRef]
- Evarestov, R.A. Quantum Chemistry of Solids: The LCAO First Principles Treatment of Crystals; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Zak, J. Continuity chords of bands in solids: The diamond structure. Phys. Rev. B 1982, 25, 1344. [Google Scholar] [CrossRef]
- Bouckaert, L.; Smoluchowski, R.; Wigner, E. Theory of Brillouin zones and symmetry properties of wave functions in crystals. Phys. Rev. 1936, 50, 58–67. [Google Scholar] [CrossRef]
- Vergniory, M.G.; Elcoro, L.; Wang, Z.; Cano, J.; Felser, C.; Aroyo, M.I.; Bernevig, B.A.; Bradlyn, B. Graph theory data for topological quantum chemistry. Phys. Rev. E 2017, 95, 023310. [Google Scholar] [CrossRef]
- Zhang, J. Band representation, band connectivity and irreducibility. arXiv 2021, arXiv:2109.15219. [Google Scholar] [CrossRef]
- Po, H.C. Symmetry indicators of band topology. J. Phys. C Cond. Matt. 2020, 32, 263001. [Google Scholar] [CrossRef]
- Cano, J.; Elcoro, L.; Aroyo, M.I.; Bernevig, B.A.; Bradlyn, B. Topology invisible to eigenvalues in obstructed atomic insulators. Phys. Rev. B 2022, 105, 125115. [Google Scholar] [CrossRef]
- Bacry, H.; Michel, L.; Zak, J. Symmetry and Analyticity of Energy Bands in Solids. Phys. Rev. Lett. 1988, 61, 1005–1008. [Google Scholar] [CrossRef]
- Cano, J.; Bradlyn, B.; Wang, Z.; Elcoro, L.; Vergniory, M.G.; Felser, C.; Aroyo, M.I.; Bernevig, B.A. Topology of D disconnected elementary band representations. Phys. Rev. Lett. 2018, 120, 266401. [Google Scholar] [CrossRef]
- Elcoro, L.; Bradlyn, B.; Wang, Z.; Vergniory, M.G.; Cano, J.; Felser, C.; Bernevig, B.A.; Orobengoa, D.; de la Flor, G.; Aroyo, M.I. Double crystallographic groups and their representations on the Bilbao crystallographic server. J. Appl. Crystal. 2017, 50, 1457–1477. [Google Scholar] [CrossRef]
- Eckart, C. The application of group theory to the quantum dynamics of monatomic systems. Rev. Mod. Phys. 1930, 2, 305–380. [Google Scholar] [CrossRef]
- Koster, G. Matrix elements of symmetric operators. Phys. Rev. 1958, 109, 227–231. [Google Scholar] [CrossRef]
- Zhang, J. Symmetry constraints on topological invariants and irreducible band representations. arXiv 2024, arXiv:2408.16658. [Google Scholar] [CrossRef]
- Resta, R. Theory of electrical polarization in crystals. Ferroelectrics 1992, 136, 51–55. [Google Scholar] [CrossRef]





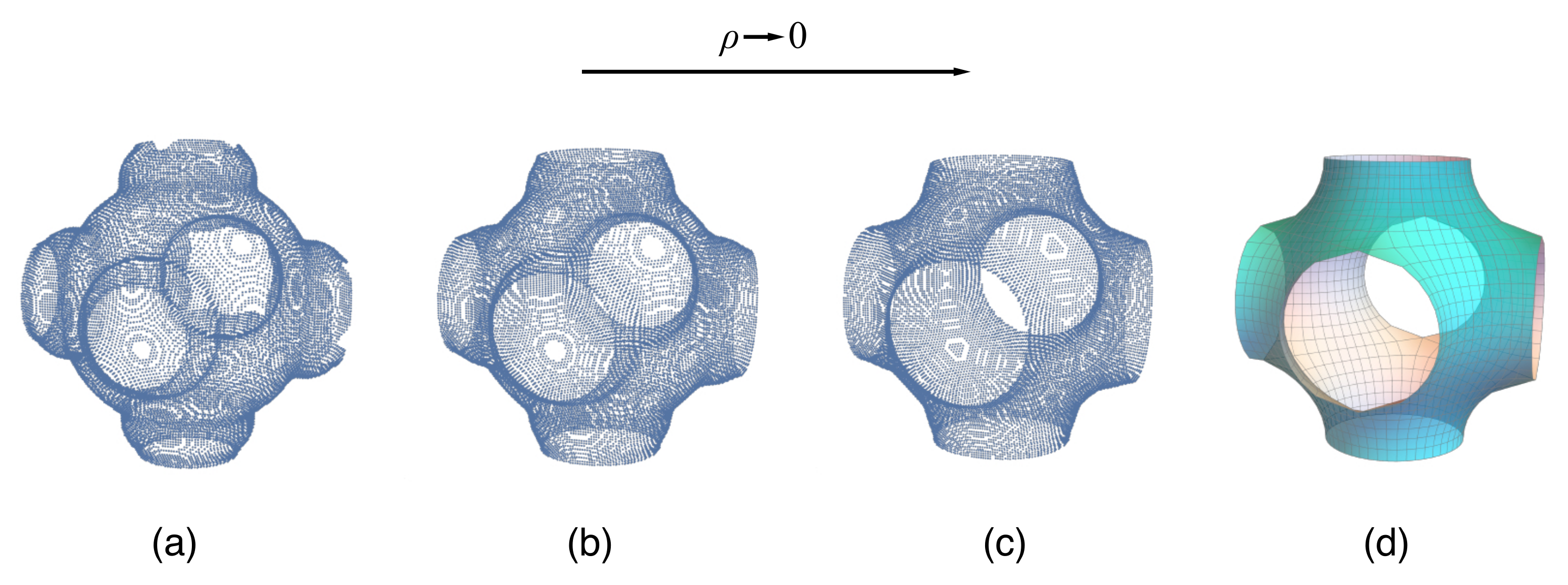

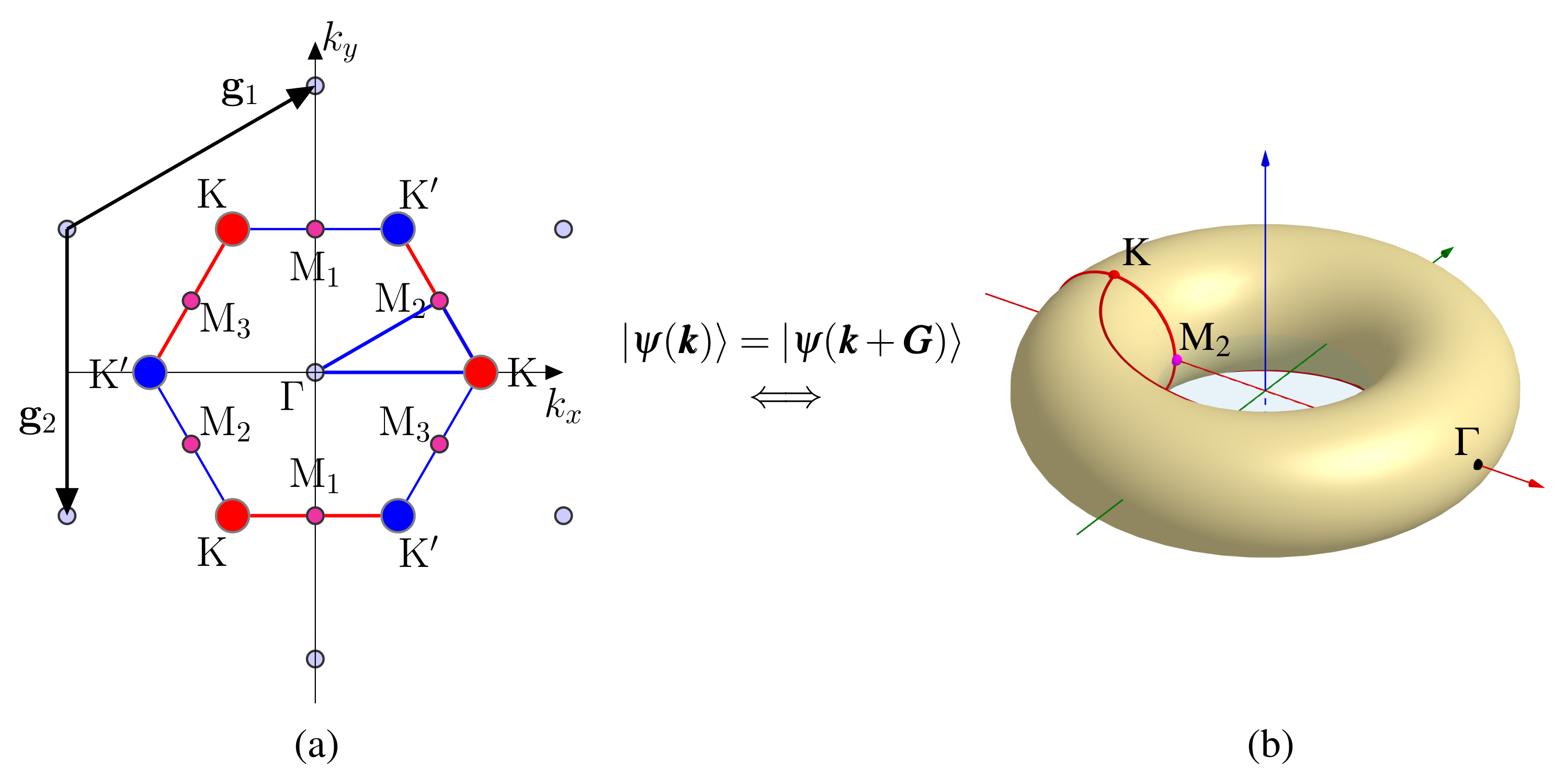
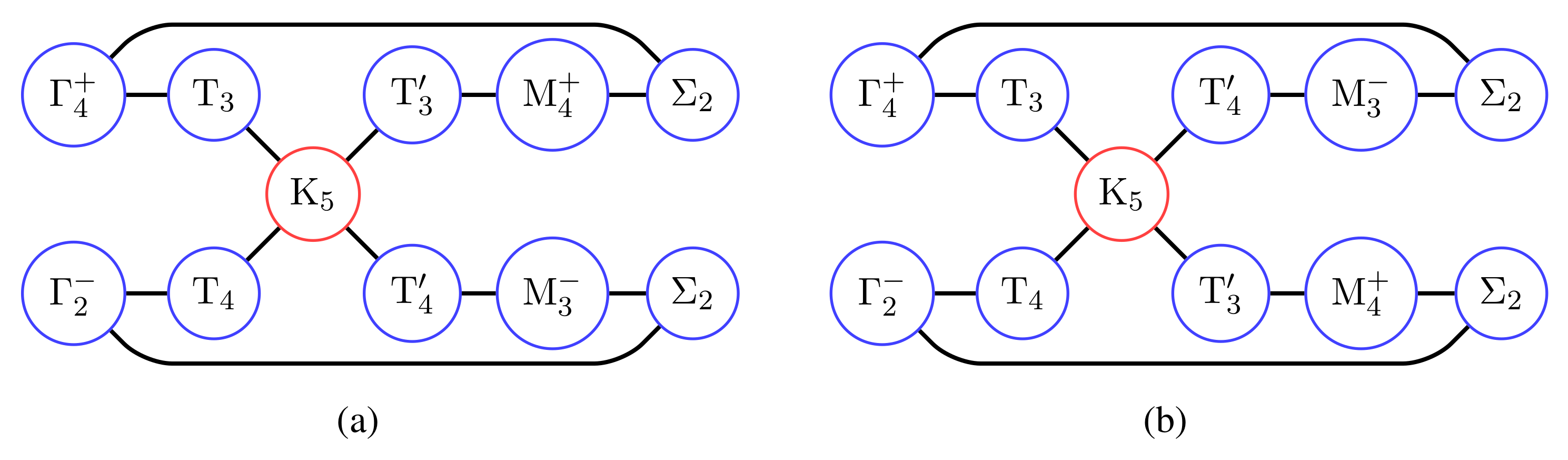
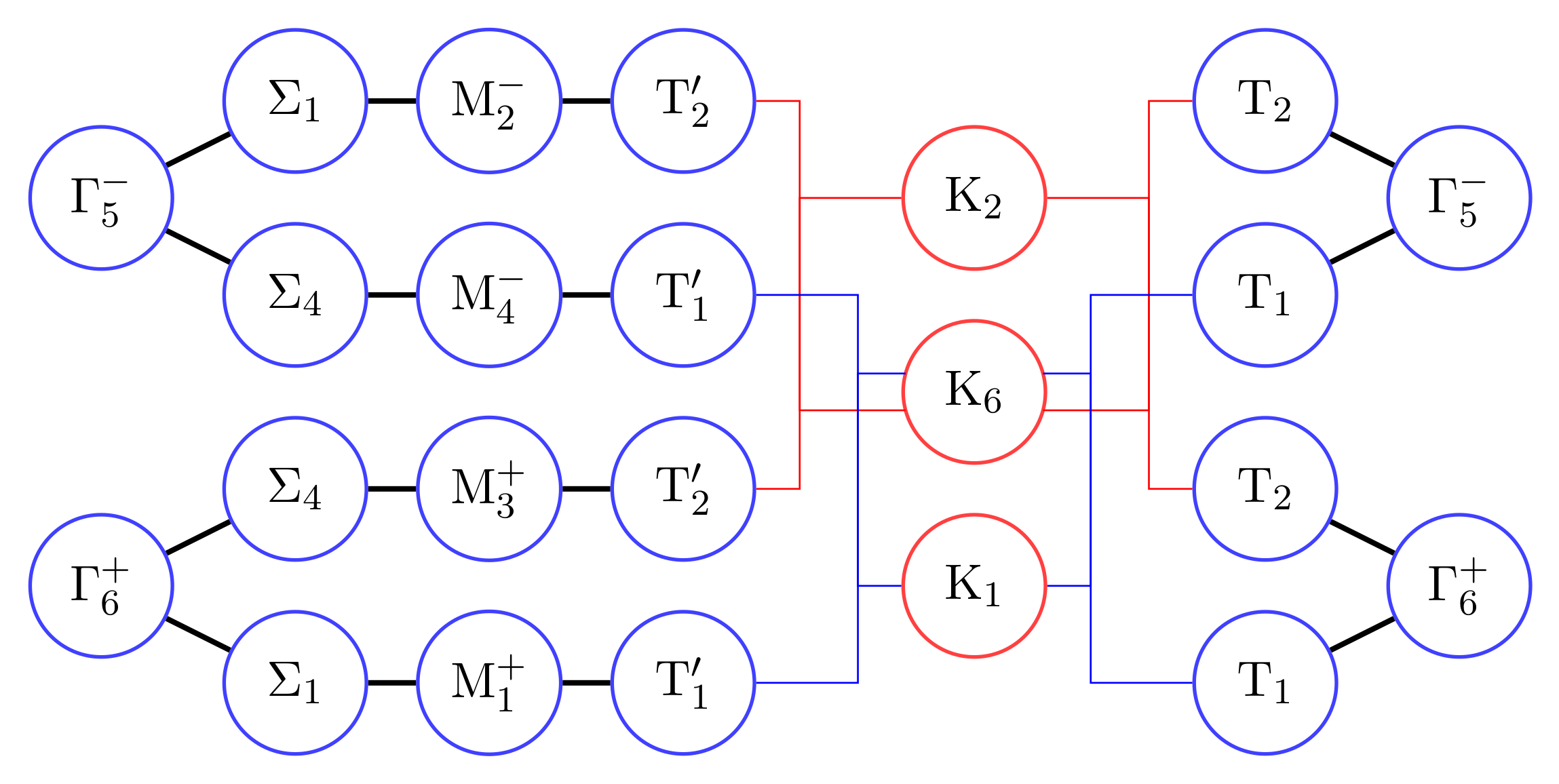
| TPMS | Space Group | Point Group | Genus |
|---|---|---|---|
| Schwarz P (P) | 3 | ||
| Schwarz D (D) | 3 | ||
| Schwarz H(H) | 3 | ||
| I-WP | 4 | ||
| -T | 4 | ||
| F-RD | 6 |
| Differential Geometry | Topological Insulators | |
|---|---|---|
| Coordinates | Local coordinates | Parameters of Hamiltonian |
| Local basis | Local vectors | Eigenvectors of Hamiltonian |
| (that span tangent space) | ||
| Measures of curvature | Parallel transport | Berry phase |
| (around closed curve) | (adiabatic change to Hamiltonian) | |
| Connection | Berry connection | |
| Local curvature | Berry curvature | |
| Topology | Winding number | Chern number |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, M.; Zhang, J.; Vvedensky, D.D. Fundamentals of Symmetry and Topology: Applications to Materials Science and Condensed Matter Physics. Symmetry 2025, 17, 807. https://doi.org/10.3390/sym17060807
Yin M, Zhang J, Vvedensky DD. Fundamentals of Symmetry and Topology: Applications to Materials Science and Condensed Matter Physics. Symmetry. 2025; 17(6):807. https://doi.org/10.3390/sym17060807
Chicago/Turabian StyleYin, Mengdi, Jing Zhang, and Dimitri D. Vvedensky. 2025. "Fundamentals of Symmetry and Topology: Applications to Materials Science and Condensed Matter Physics" Symmetry 17, no. 6: 807. https://doi.org/10.3390/sym17060807
APA StyleYin, M., Zhang, J., & Vvedensky, D. D. (2025). Fundamentals of Symmetry and Topology: Applications to Materials Science and Condensed Matter Physics. Symmetry, 17(6), 807. https://doi.org/10.3390/sym17060807






