A BiGRUSA-ResSE-KAN Hybrid Deep Learning Model for Day-Ahead Electricity Price Prediction
Abstract
1. Introduction
- In this study, we systematically solve the core challenge of asymmetry of day-ahead tariff prediction intervals under a high percentage of renewable energy grid-connectedness by constructing a symmetric adaptive prediction framework. Based on the innovative design of multi-modal feature fusion and BiGRUSA-ResSE-KAN deep learning architecture, we realize the dual balance of prediction accuracy and interval symmetry.
- A novel hybrid approach combining CEEMDAN and VMD is employed to decompose electricity price data into multi-scale components. This method reorganizes components by frequency, constructing a multi-scale matrix that effectively captures fluctuation patterns and lays a foundation for deep feature extraction.
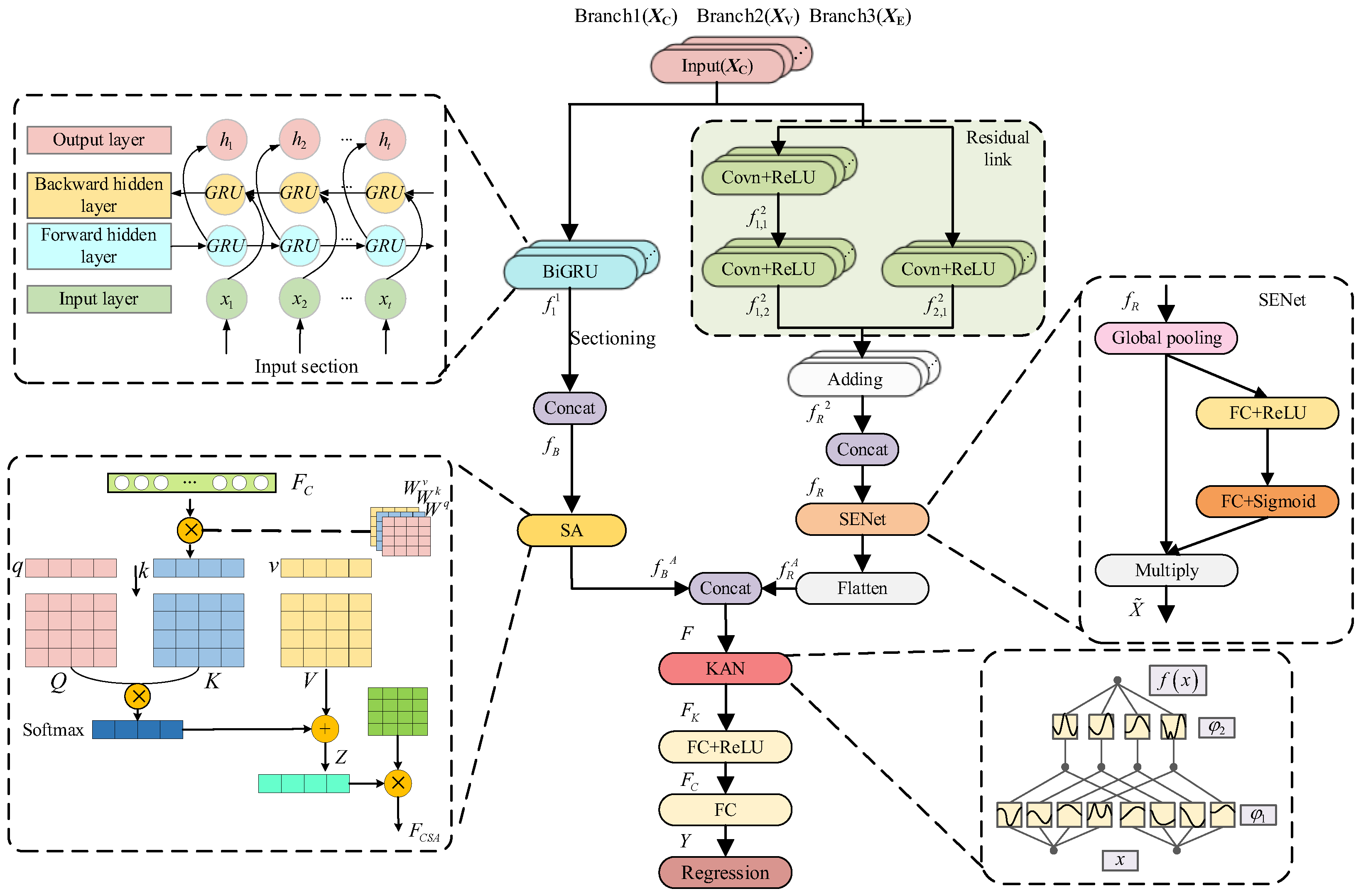
- The introduced BiGRU-SA-RESSE-KAN model innovatively integrates three branching inputs: the CEEMDAN component, the VMD component, and the exogenous variables through a unified deep learning framework. By synergizing the bidirectional gated recursive unit (BiGRU) with an attention mechanism, a residual contraction and expansion network, and KAN, the model achieves comprehensive feature fusion that captures time-dependent, nonlinear dynamics and complex patterns simultaneously.
- A dynamic sliding window mechanism with a fixed prediction target length of 24 time steps is designed to segment the multi-scale component and exogenous variable matrices. This approach not only preserves temporal continuity but also adapts to the short market cycles in electricity price datasets, enabling the model to learn long-term dependencies and generate robust 24-h-ahead predictions across diverse electricity markets.
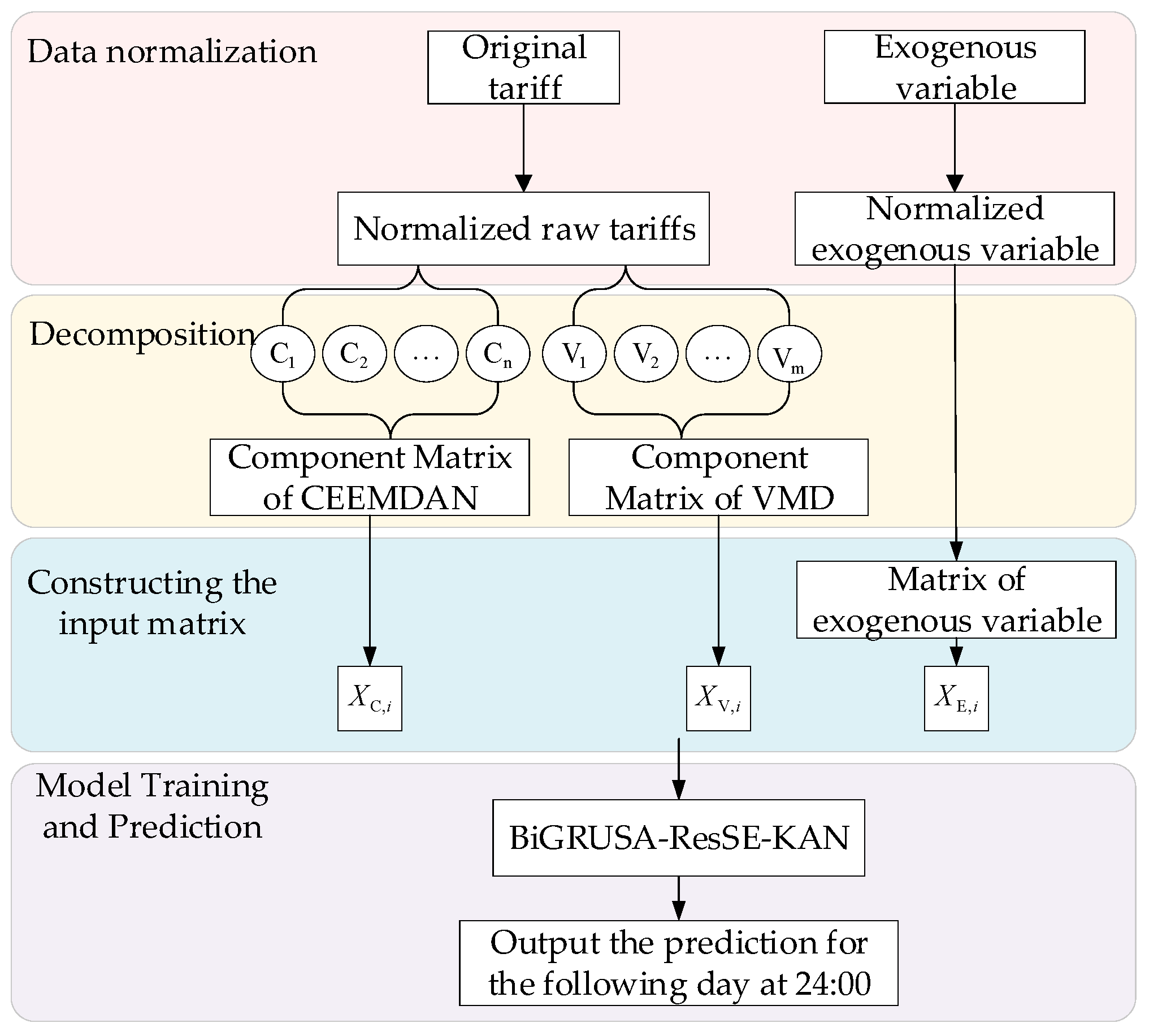
2. Forecasting Process
3. Data Preprocessing
3.1. Introduction to the Dataset
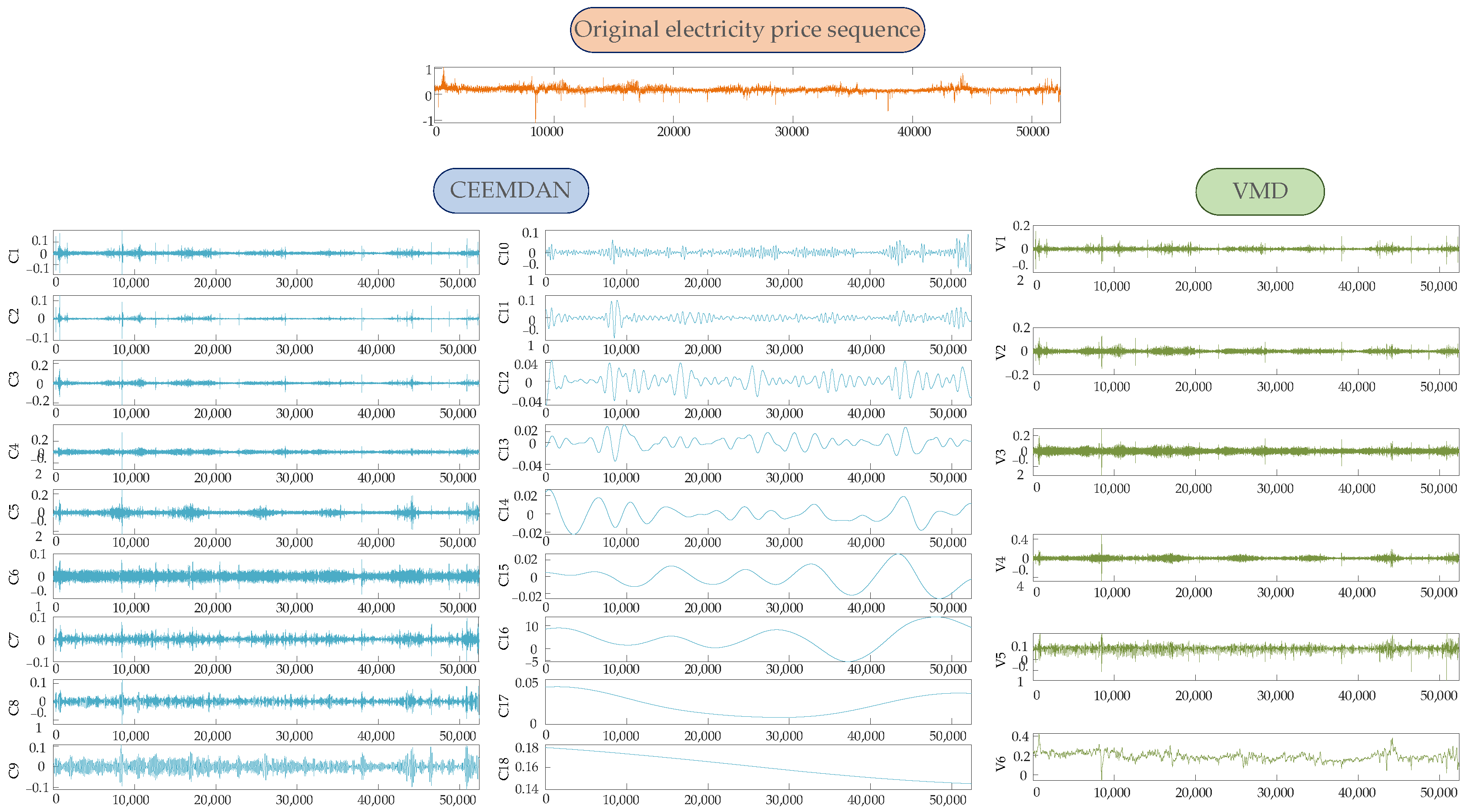
3.2. CEEMDAN
3.3. VMD
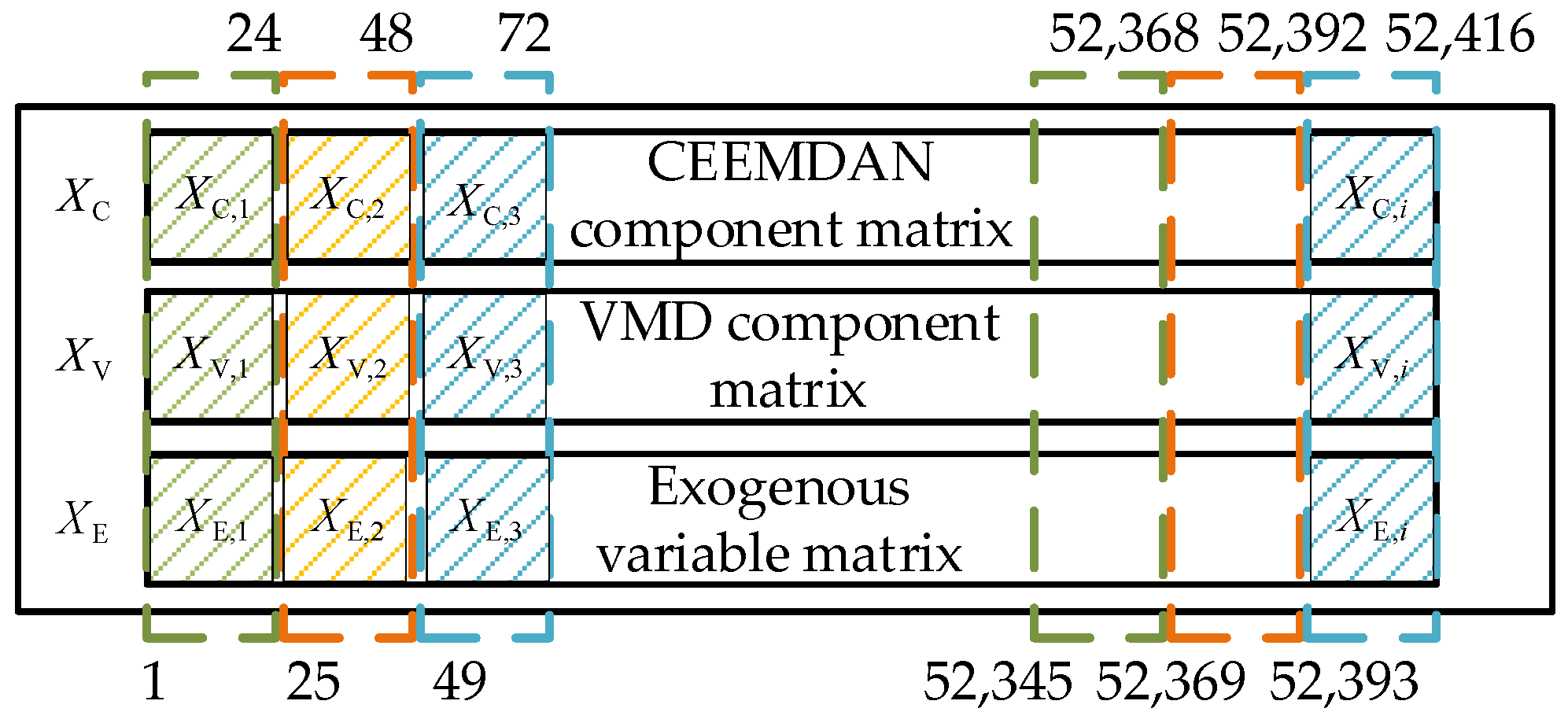
3.4. Construct the Input Matrix
4. Deep Learning Model
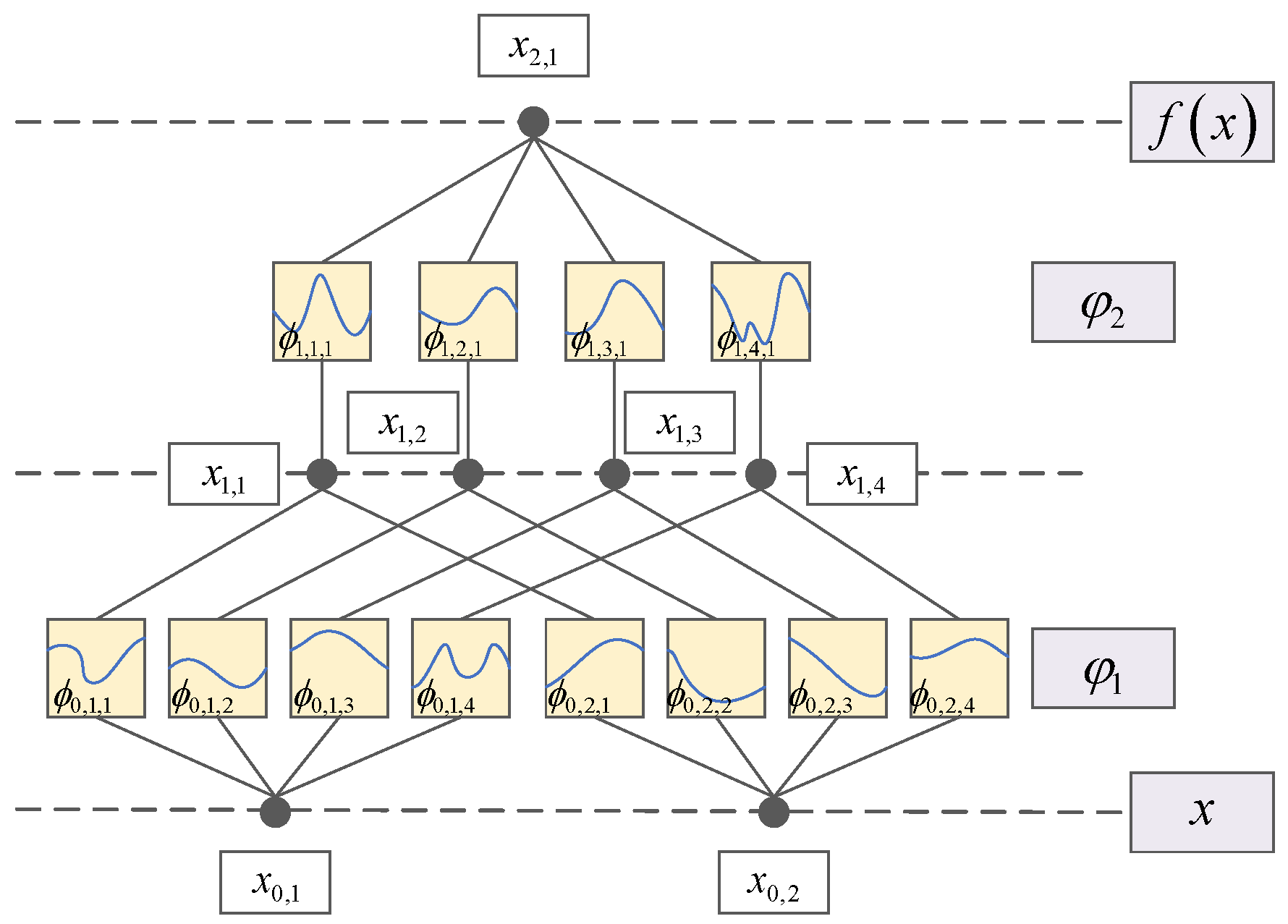
4.1. KAN
4.2. BiGRUSA-ResSE-KAN Structure
5. Experimental Verification
5.1. Platform and Model Configuration
5.2. Evaluation Index
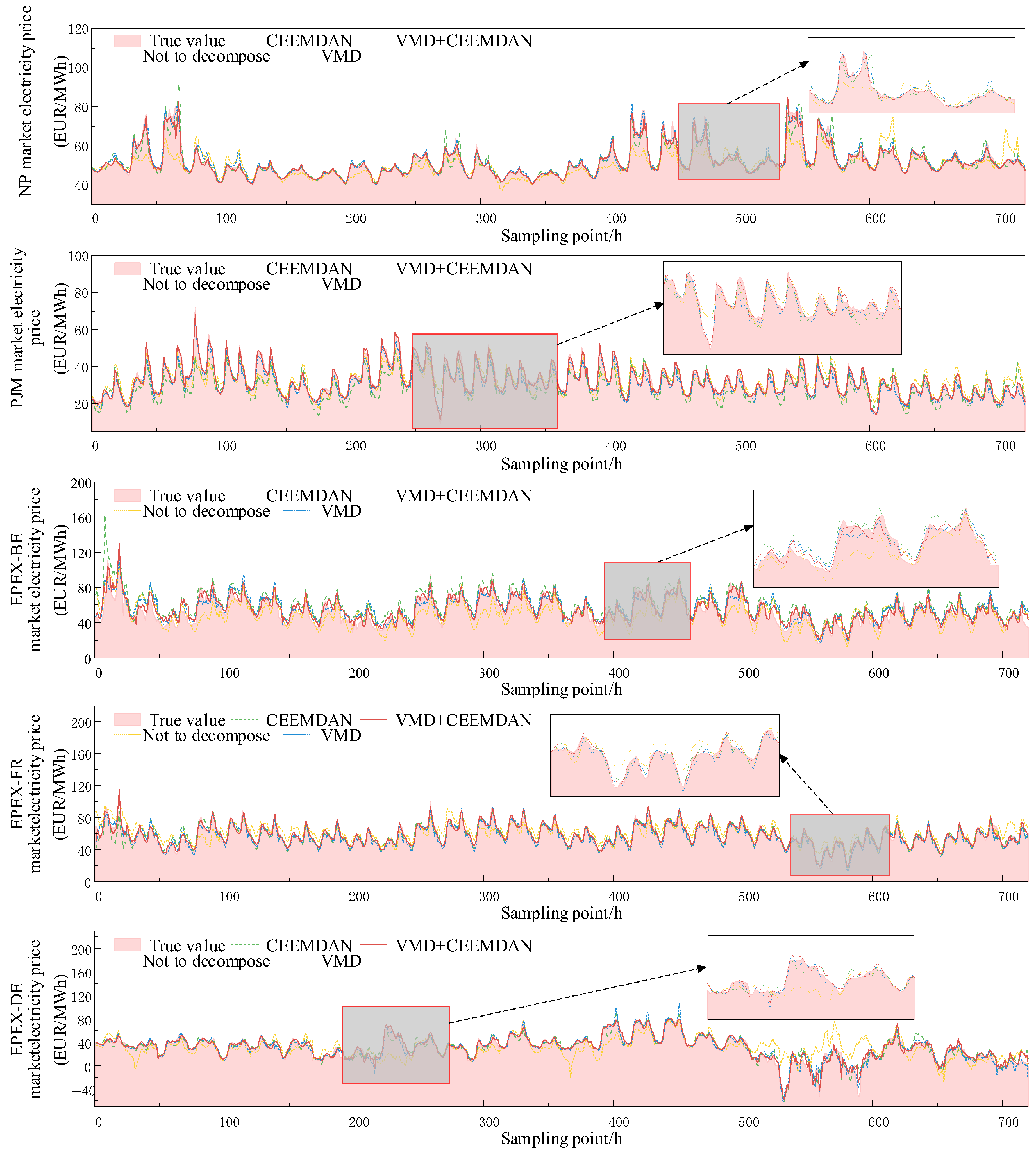
5.3. Verification Experiment of the Validity of Double Decomposition Input Matrix
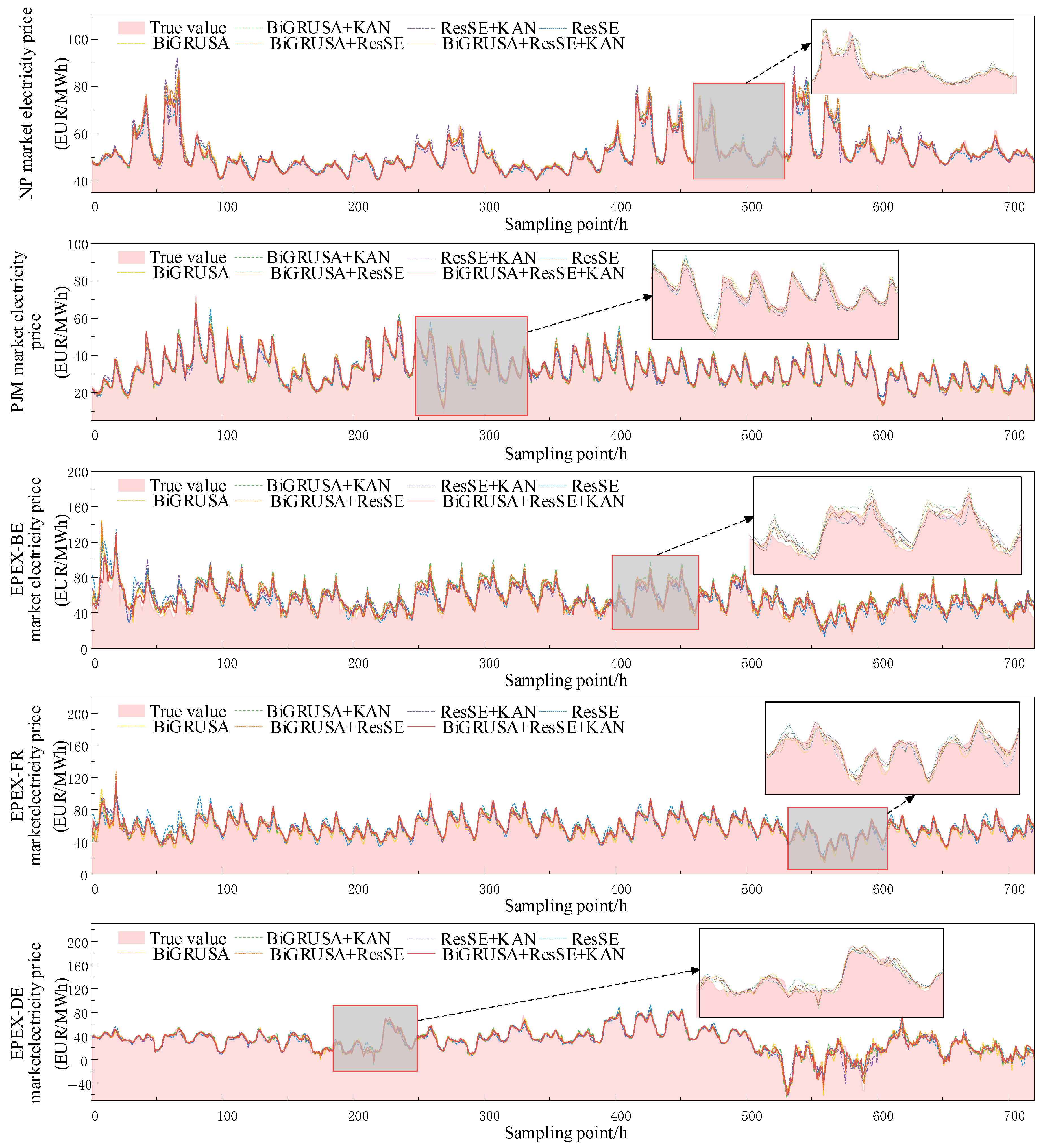
5.4. Ablation Experiment
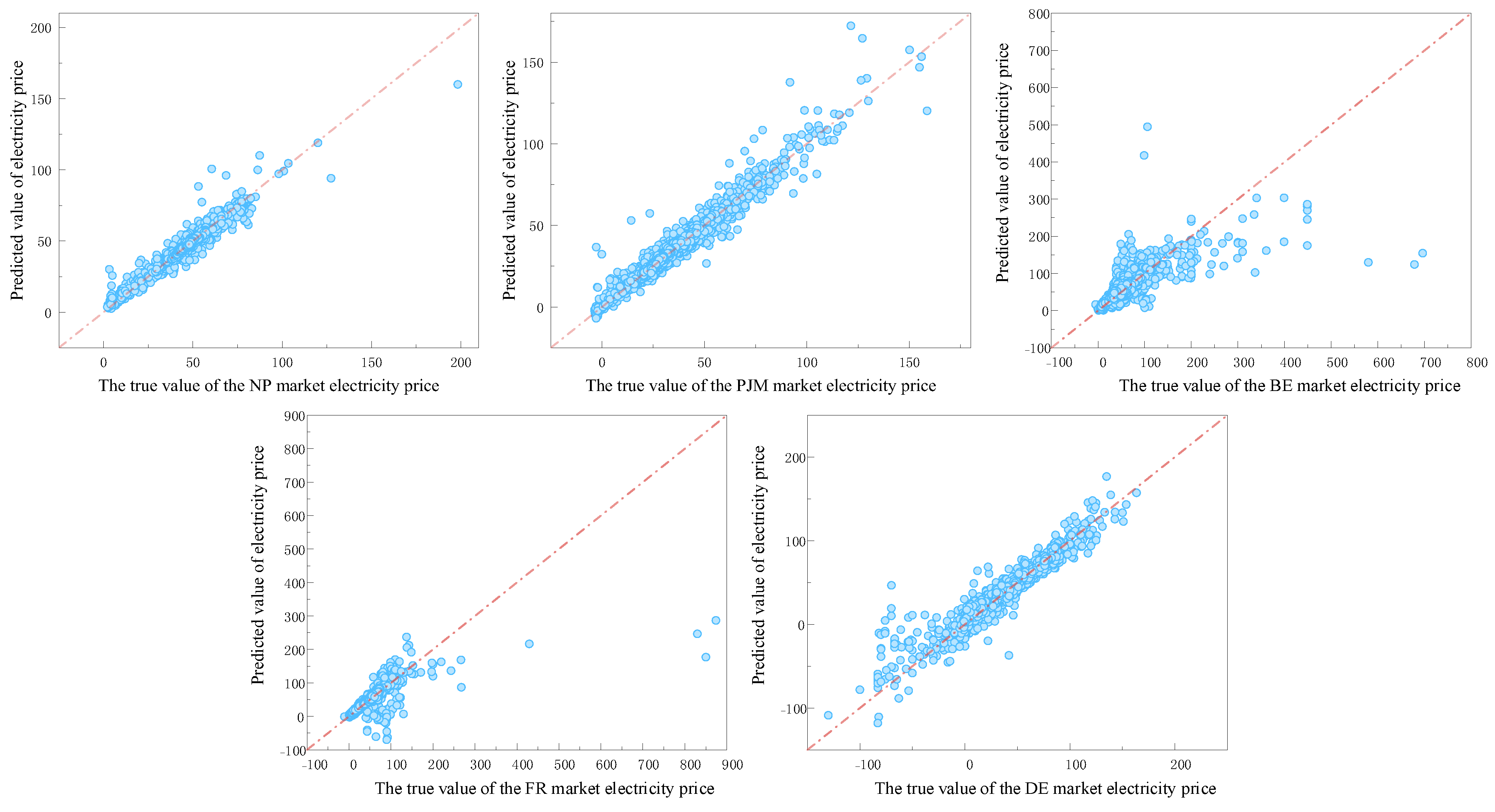
5.5. Comparison of Methods in Different Studies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, N.; Li, Y.; Huang, J.; Li, Y.; Du, E.; Li, M.; Liu, Y.; Kang, C. Carbon Measurement Method and Carbon Meter System for Whole Chain of Power System. Autom. Electr. Power Syst. 2023, 47, 2–12. [Google Scholar] [CrossRef]
- Davies, G. The European Union’s Implementation of the Paris Agreement. In Research Handbook on the Law of the Paris Agreement; Zahar, A., Ed.; Research Handbooks in Climate Law Series; Edward Elgar Publishing Ltd.: Cheltenham, UK; Northampton, MA, USA, 2024; pp. 323–342. [Google Scholar] [CrossRef]
- Handayani, K.; Anugrah, P.; Goembira, F.; Overland, I.; Suryadi, B.; Swandaru, A. Moving beyond the NDCs: ASEAN pathways to a net-zero emissions power sector in 2050. Appl. Energy 2022, 311, 118580. [Google Scholar] [CrossRef]
- Li, F.; Wang, X.; Zhang, S. Multi-period equilibrium analysis of electricity and natural gas markets with wind power bidding. In Proceedings of the 5th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 12–14 September 2020; pp. 588–594. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, X.; Zhang, P.; Pang, W.; Qu, C. Short-Term Tariff Prediction for High Penetration New Energy Electricity Market Based on Singular Spectrum Analysis and CNN-GRU Combination Model. In Proceedings of the 2024 International Conference on New Trends in Computational Intelligence (NTCI), Qingdao, China, 18–20 October 2024; pp. 166–171. [Google Scholar] [CrossRef]
- Qin, B.; Huang, X.; Wang, X.; Liling, G. Ultra-short-term wind power prediction based on double decomposition and LSSVM. Trans. Inst. Meas. Control 2023, 45, 2627–2636. [Google Scholar] [CrossRef]
- Chen, R.; Hui, W.; Da, L.; Ma, Y.; Yang, D. Ensemble Prediction of Spot Electricity Prices Using Heterogeneous Models by Integrating the RSDE Framework and KAN Algorithm. CSEE 2024, 44, 9645–9657. [Google Scholar] [CrossRef]
- Han, S.; Hu, F.; Chen, Z.; Zhang, L.; Bai, X. Day ahead market marginal price forecasting based on GCN-LSTM. CSEE 2022, 42, 3276–3286. [Google Scholar] [CrossRef]
- Ji, X.; Zeng, R.; Zhang, Y.; Song, F.; Sun, P.; Zhao, G. CNN-LSTM short-term electricity price prediction based on an attention mechanism. Power Syst. Prot. Control 2022, 50, 125–132. [Google Scholar] [CrossRef]
- Cu, Y.; Wang, K.; Zhang, L.; Liu, Z.; Liu, Y.; Mo, L. A Time Series Decomposition-Based Interpretable Electricity Price Forecasting Method. Energies 2025, 18, 664. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2024. [Google Scholar] [CrossRef]
- He, Y.; Xu, M.; Hu, Y.; Gu, H.; Xie, X.; Lei, S. Improving Day-Ahead Electricity Price Forecasting Accuracy in Australia’s National Electricity Market with Kolmogorov-Arnold Networks. In Proceedings of the International Conference of Electrical, Electronic and Networked Energy Systems, Xi’an, China, 18–20 October 2024; Springer Nature: Singapore, 2024; pp. 40–50. [Google Scholar] [CrossRef]
- Shejul, K.; Harikrishnan, R.; Kukker, A. Short-Term Electricity Price Forecasting Using the Empirical Mode Decomposed Hilbert-LSTM and Wavelet-LSTM Models. J. Electr. Comput. Eng. 2024, 2024, 4575735. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Q.; Cui, H. Short-term Multi-step Price Prediction for the Electricity Market with a High Proportion of Clean Energy and Energy Storage Based on MIC-EEMD-improved Informer. Power Syst. Technol. 2024, 48, 949–957. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, Z.; Gao, K.; Wang, P. Short-term Electricity Price Forecasting Method Based on CNN-LSTM by Random Forest and EEMD. In Proceedings of the 4th International Conference on Electrical Engineering and Control Science (IC2ECS), Nanjing, China, 27–29 December 2024; pp. 124–129. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Casillas-Pérez, D.; Salcedo-Sanz, S. Two-step deep learning framework with error compensation technique for short-term, half-hourly electricity price forecasting. Appl. Energy 2024, 353 Pt A, 122059. [Google Scholar] [CrossRef]
- Liu, H.; Shen, X.; Wei, Z.; Liu, Y.; Liu, J.; Bai, Y. Interpretable two-layer day-ahead electricity price forecast based on calibration window combination and coupled market characteristics. CSEE 2022, 44, 1272–1285. [Google Scholar] [CrossRef]
- Yin, H.; Ding, W.; Chen, S.; Zhang, Z.; Zong, Z.; Meng, A. Day-ahead electricity price forecasting of electricity market with high proportion of new energy based on LSTM-CSO model. Power Syst. Technol. 2022, 46, 472–480. [Google Scholar] [CrossRef]
- Mi, J.; Xie, X.; Luo, Y.; Zhang, Q.; Wang, J. Research on Rebar Futures Price Forecast Based on VMD—EEMD—LSTM Model. Adv. Transdiscipl. Eng. 2023, 42, 54–62. [Google Scholar] [CrossRef]
- Lago, J.; Marcjasz, G.; De Schutter, B.; Weron, R. Forecasting day-ahead electricity prices: A review of state-of-the-art algorithms, best practices and an open-access benchmark. Appl. Energy. 2021, 293, 116983. [Google Scholar] [CrossRef]
- Mutinda, J.K.; Geletu, A. Stock Market Index Prediction Using CEEMDAN-LSTM-BPNN-Decomposition Ensemble Model. J. Appl. Math. 2025, 2025, 7706431. [Google Scholar] [CrossRef]
- Gan, W.; Ma, R.; Zhao, W.; Peng, X.; Cui, H.; Yan, J.; Duan, S.; Wang, L.; Feng, P.; Chu, J. A VMD-LSTNet-Attention model for concentration prediction of mixed gases. Sens. Actuators B Chem. 2025, 422, 136641. [Google Scholar] [CrossRef]
- Hu, R.; Qiao, J.; Li, Y.; Sun, Y.; Wang, B. Medium and long term wind power forecast based on WOA-VMD-SSA-LSTM. Acta Energiae Solaris Sin 2024, 45, 549–556. [Google Scholar] [CrossRef]
- Bi, G.; Zhao, X.; Chen, C.; Chen, S.; Li, L.; Xie, X.; Luo, Z. Ultra-short-term prediction of photovoltaic power generation based on multi-channel input and PCNN-BiLSTM. Power Syst. Technol. 2022, 46, 3463–3476. [Google Scholar] [CrossRef]
- Li, C.; Liu, X.; Li, W.; Wang, C.; Liu, H.; Liu, Y.; Chen, Z.; Yuan, Y. U-kan makes strong backbone for medical image segmentation and generation. arXiv 2024, arXiv:2406.02918. [Google Scholar] [CrossRef]
- Guo, L.; Wang, Y.; Guo, M.; Zhou, X. YOLO-IRS: Infrared Ship Detection Algorithm Based on Self-Attention Mechanism and KAN in Complex Marine Background. Remote Sens. 2025, 17, 20. [Google Scholar] [CrossRef]
- Joshi, P.; Størdal, S.; Lien, G.; Mishra, D.; Haugom, E. A Comprehensive Analysis of Dropout Assisted Regularized Deep Learning Architectures for Dynamic Electricity Price Forecasting. IEEE Access 2023, 12, 177327–177341. [Google Scholar] [CrossRef]
- Olivares, K.G.; Challu, C.; Marcjasz, G.; Weron, R.; Dubrawski, A. Neural basis expansion analysis with exogenous variables: Forecasting electricity prices with NBEATSx. Int. J. Forecast. 2023, 39, 884–900. [Google Scholar] [CrossRef]
- Shi, W.; Wang, Y.F. A robust electricity price forecasting framework based on heteroscedastic temporal Convolutional Network. Int. J. Electr. Power Energy Syst. 2024, 161, 110177. [Google Scholar] [CrossRef]
| Electricity Market | Exogenous Variable 1 | Exogenous Variable 2 | Training Set | Test Set |
|---|---|---|---|---|
| NP | The day-ahead load forecast | The day-ahead wind generation forecast | 1 January 2013–26 December 2016 | 27 December 2016–24 December 2018 |
| PJM | The day-ahead system load forecast | The day-ahead zonal load forecast | 1 January 2013–26 December 2016 | 27 December 2016–24 December 2018 |
| EPEX-BE | The day-ahead load forecast in France | The day-ahead generation forecast in France | 9 January 2011–3 January 2015 | 4 January 2015–31 December 2016 |
| EPEX-FR | The day-ahead load forecast | The day-ahead generation forecast | 9 January 2011–3 January 2015 | 4 January 2015–31 December 2016 |
| EPEX-DE | The day-ahead zonal load forecast in Amprion | The day-ahead wind generation forecast | 9 January 2012–3 January 2016 | 4 January 2016–31 December 2017 |
| Dataset | Metric | Original Data | CEEMDAN | VMD | VMD + CEEMDAN |
|---|---|---|---|---|---|
| NP | rMAE | 0.587 | 0.269 | 0.193 | 0.173 |
| MAE | 2.429 | 1.111 | 0.798 | 0.732 | |
| MAPE (%) | 6.978 | 3.121 | 2.239 | 2.067 | |
| sMAPE (%) | 6.732 | 3.175 | 2.282 | 2.082 | |
| RMSE | 4.268 | 2.296 | 1.539 | 1.438 | |
| R2 | 0.841 | 0.954 | 0.979 | 0.980 | |
| PJM | rMAE | 0.822 | 0.677 | 0.332 | 0.194 |
| MAE | 5.201 | 4.280 | 2.102 | 1.224 | |
| MAPE (%) | 15.819 | 17.587 | 10.318 | 5.934 | |
| sMAPE (%) | 17.773 | 16.196 | 8.877 | 5.212 | |
| RMSE | 9.405 | 8.214 | 2.934 | 1.736 | |
| R2 | 0.496 | 0.563 | 0.932 | 0.970 | |
| EPEX-BE | rMAE | 0.873 | 0.831 | 0.707 | 0.466 |
| MAE | 8.866 | 8.445 | 7.186 | 4.730 | |
| MAPE (%) | 27.027 | 19.957 | 16.112 | 12.213 | |
| sMAPE (%) | 22.696 | 20.312 | 17.518 | 12.066 | |
| RMSE | 18.169 | 15.391 | 13.825 | 11.116 | |
| R2 | 0.461 | 0.549 | 0.636 | 0.684 | |
| EPEX-FR | rMAE | 1.203 | 0.534 | 0.435 | 0.373 |
| MAE | 8.822 | 3.916 | 3.191 | 2.736 | |
| MAPE (%) | 20.242 | 13.223 | 11.524 | 9.333 | |
| sMAPE (%) | 23.256 | 10.848 | 9.509 | 7.415 | |
| RMSE | 15.414 | 14.997 | 9.911 | 10.264 | |
| R2 | 0.483 | 0.516 | 0.713 | 0.726 | |
| EPEX-DE | rMAE | 0.835 | 0.353 | 0.233 | 0.232 |
| MAE | 7.621 | 3.222 | 2.128 | 2.113 | |
| MAPE (%) | 49.166 | 18.368 | 13.622 | 11.350 | |
| sMAPE (%) | 28.069 | 12.783 | 9.411 | 9.235 | |
| RMSE | 12.394 | 5.660 | 4.178 | 4.141 | |
| R2 | 0.639 | 0.866 | 0.926 | 0.929 |
| Dataset | Metric | BiGRUSA | BiGRUSA-KAN | ResSE | ResSE + KAN | BiGRUSA-ResSE | BiGRUSA-ResSE-KAN |
|---|---|---|---|---|---|---|---|
| NP | rMAE | 0.180 | 0.173 | 0.294 | 0.271 | 0.180 | 0.173 |
| MAE | 0.746 | 0.715 | 1.216 | 1.119 | 0.745 | 0.732 | |
| MAPE (%) | 2.125 | 2.098 | 3.485 | 3.192 | 2.099 | 2.067 | |
| sMAPE (%) | 2.174 | 2.094 | 3.502 | 3.283 | 2.153 | 2.082 | |
| RMSE | 1.424 | 1.449 | 2.142 | 1.963 | 1.459 | 1.438 | |
| R2 | 0.979 | 0.980 | 0.960 | 0.967 | 0.979 | 0.980 | |
| PJM | rMAE | 0.275 | 0.282 | 0.362 | 0.356 | 0.267 | 0.194 |
| MAE | 1.739 | 1.784 | 2.292 | 2.252 | 1.686 | 1.224 | |
| MAPE (%) | 8.132 | 7.968 | 10.450 | 9.435 | 7.569 | 5.934 | |
| sMAPE (%) | 7.148 | 7.271 | 9.574 | 9.551 | 6.893 | 5.212 | |
| RMSE | 2.770 | 2.708 | 3.530 | 3.387 | 2.696 | 1.736 | |
| R2 | 0.939 | 0.942 | 0.901 | 0.901 | 0.909 | 0.970 | |
| EPEX-BE | rMAE | 0.536 | 0.672 | 0.749 | 0.653 | 0.598 | 0.466 |
| MAE | 5.445 | 6.823 | 7.609 | 6.631 | 6.072 | 4.730 | |
| MAPE (%) | 14.911 | 15.223 | 17.018 | 15.495 | 13.467 | 12.213 | |
| sMAPE (%) | 12.969 | 16.059 | 18.438 | 15.707 | 14.210 | 12.066 | |
| RMSE | 14.102 | 13.456 | 13.831 | 13.044 | 14.117 | 11.116 | |
| R2 | 0.621 | 0.655 | 0.635 | 0.676 | 0.620 | 0.684 | |
| EPEX-FR | rMAE | 0.482 | 0.438 | 0.838 | 0.524 | 0.446 | 0.373 |
| MAE | 3.531 | 3.213 | 6.143 | 3.841 | 3.272 | 2.736 | |
| MAPE (%) | 13.848 | 13.102 | 17.963 | 11.781 | 12.411 | 9.333 | |
| sMAPE (%) | 10.107 | 8.696 | 17.806 | 11.085 | 9.401 | 7.415 | |
| RMSE | 12.104 | 12.184 | 13.711 | 10.993 | 10.354 | 10.264 | |
| R2 | 0.619 | 0.614 | 0.512 | 0.686 | 0.721 | 0.726 | |
| EPEX-DE | rMAE | 0.236 | 0.249 | 0.276 | 0.259 | 0.248 | 0.232 |
| MAE | 2.155 | 2.273 | 2.515 | 2.364 | 2.264 | 2.113 | |
| MAPE(%) | 18.892 | 13.515 | 22.554 | 18.581 | 13.213 | 11.350 | |
| sMAPE(%) | 9.290 | 9.482 | 10.676 | 10.289 | 9.666 | 9.235 | |
| RMSE | 3.905 | 4.438 | 4.394 | 4.652 | 4.326 | 4.141 | |
| R2 | 0.926 | 0.917 | 0.919 | 0.910 | 0.921 | 0.929 |
| Dataset | Metric | RNN | CNN | LSTM | GRU | LEAR Ensemble | DNN Ensemble | NBEATSx | HeTCN | BiGRUSA-ResSE-KAN |
|---|---|---|---|---|---|---|---|---|---|---|
| NP | rMAE | 1.220 | 0.490 | 1.200 | 0.400 | 0.420 | 0.400 | 0.530 | - | 0.173 |
| MAE | 7.300 | 2.020 | 7.180 | 2.410 | 1.740 | 1.670 | 1.680 | 2.040 | 0.732 | |
| MAPE (%) | 20.190 | 6.790 | 19.690 | 7.760 | 5.530 | 5.380 | - | - | 2.067 | |
| sMAPE (%) | 21.500 | 5.840 | 21.040 | 6.840 | 5.010 | 4.850 | 4.890 | 5.890 | 2.082 | |
| RMSE | 8.360 | 3.850 | 8.240 | 4.240 | 3.360 | 3.330 | 3.330 | 3.690 | 1.438 | |
| PJM | rMAE | 0.520 | 0.540 | 0.630 | 0.420 | 0.480 | 0.440 | 0.620 | - | 0.194 |
| MAE | 4.140 | 3.420 | 4.970 | 3.370 | 3.010 | 2.780 | 3.010 | 3.060 | 1.224 | |
| MAPE (%) | 33.040 | 34.950 | 45.550 | 30.750 | 30.130 | 28.660 | - | - | 5.934 | |
| sMAPE (%) | 15.880 | 13.240 | 19.460 | 12.970 | 11.980 | 11.220 | 11.910 | 11.960 | 5.212 | |
| RMSE | 6.370 | 5.700 | 6.740 | 34.940 | 5.130 | 4.640 | 5.000 | 5.420 | 1.736 | |
| EPEX-BE | rMAE | 0.590 | 0.490 | 0.580 | 0.510 | 0.600 | 0.570 | 0.750 | - | 0.466 |
| MAE | 8.090 | 6.680 | 7.880 | 7.030 | 6.140 | 5.820 | 6.170 | 6.340 | 4.730 | |
| MAPE (%) | 30.910 | 30.560 | 33.790 | 32.340 | 20.720 | 26.110 | - | - | 12.213 | |
| sMAPE (%) | 19.370 | 16.690 | 19.210 | 16.100 | 14.550 | 13.330 | 14.520 | 15.130 | 12.066 | |
| RMSE | 18.000 | 15.050 | 17.800 | 16.790 | 15.970 | 16.130 | 15.430 | 16.410 | 11.116 | |
| EPEX-FR | rMAE | 0.510 | 0.430 | 0.510 | 0.440 | 0.540 | 0.530 | 0.670 | - | 0.373 |
| MAE | 5.740 | 4.860 | 5.750 | 4.970 | 3.980 | 3.910 | 3.970 | 4.350 | 2.736 | |
| MAPE (%) | 17.310 | 18.430 | 17.560 | 18.650 | 14.680 | 14.770 | - | - | 9.333 | |
| sMAPE (%) | 16.300 | 13.410 | 16.800 | 14.110 | 11.570 | 10.980 | 11.290 | 12.770 | 7.415 | |
| RMSE | 13.160 | 12.420 | 13.190 | 12.540 | 10.680 | 11.740 | 11.080 | 12.020 | 10.264 | |
| EPEX-DE | rMAE | 0.520 | 0.430 | 0.430 | 0.430 | 0.400 | 0.380 | 0.420 | - | 0.232 |
| MAE | 6.010 | 4.960 | 4.960 | 4.990 | 3.610 | 3.440 | 3.370 | 4.420 | 2.113 | |
| MAPE (%) | 104.560 | 117.860 | 109.270 | 67.140 | 113.980 | 95.760 | - | - | 11.350 | |
| sMAPE (%) | 22.590 | 18.400 | 18.620 | 18.540 | 14.740 | 14.190 | 14.340 | 17.270 | 9.235 | |
| RMSE | 8.870 | 8.100 | 7.840 | 8.190 | 6.510 | 6.000 | 5.640 | 7.330 | 4.141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, N.; Bi, G.; Li, Y.; Wang, X.; Luo, Z.; Shen, X. A BiGRUSA-ResSE-KAN Hybrid Deep Learning Model for Day-Ahead Electricity Price Prediction. Symmetry 2025, 17, 805. https://doi.org/10.3390/sym17060805
Yang N, Bi G, Li Y, Wang X, Luo Z, Shen X. A BiGRUSA-ResSE-KAN Hybrid Deep Learning Model for Day-Ahead Electricity Price Prediction. Symmetry. 2025; 17(6):805. https://doi.org/10.3390/sym17060805
Chicago/Turabian StyleYang, Nan, Guihong Bi, Yuhong Li, Xiaoling Wang, Zhao Luo, and Xin Shen. 2025. "A BiGRUSA-ResSE-KAN Hybrid Deep Learning Model for Day-Ahead Electricity Price Prediction" Symmetry 17, no. 6: 805. https://doi.org/10.3390/sym17060805
APA StyleYang, N., Bi, G., Li, Y., Wang, X., Luo, Z., & Shen, X. (2025). A BiGRUSA-ResSE-KAN Hybrid Deep Learning Model for Day-Ahead Electricity Price Prediction. Symmetry, 17(6), 805. https://doi.org/10.3390/sym17060805






