A Novel 2D Hyperchaotic Map with Homogeneous Multistability and Its Application in Image Encryption
Abstract
1. Introduction
- (1)
- A hyperchaotic map with two positive LEs is obtained by inserting an orthorhombic feedback into a 2D system. Furthermore, we also talked about the system’s dynamic properties.
- (2)
- The unique homogeneous multistability is illustrated, in which a set of unified LEs are used to pick attractors based on the initial condition (IC).
- (3)
- Statistical analysis confirms the high stochasticity of the chaotic sequence, validating its suitability for cryptographic applications. Capitalizing on this intrinsic unpredictability, we propose a novel image encryption framework that synergizes the hyperchaotic system with a dual permutation–diffusion architecture.
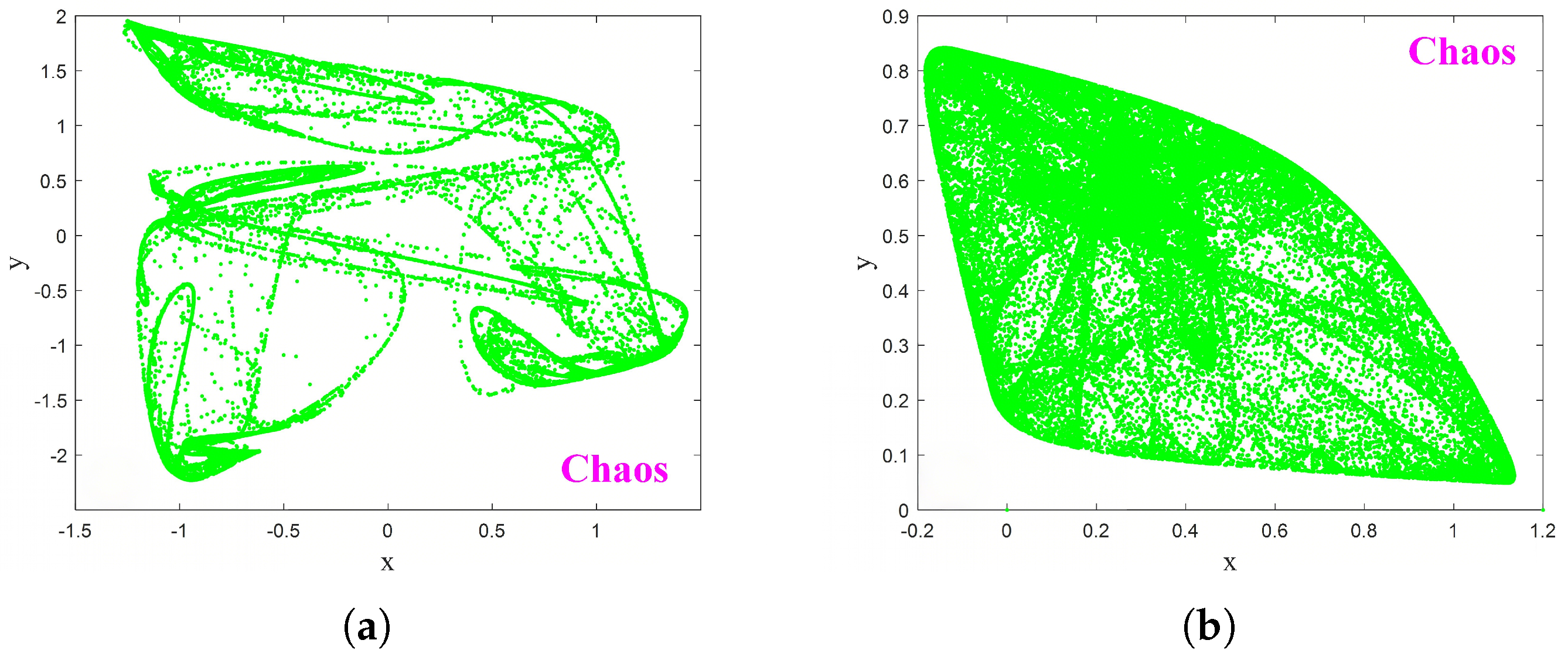
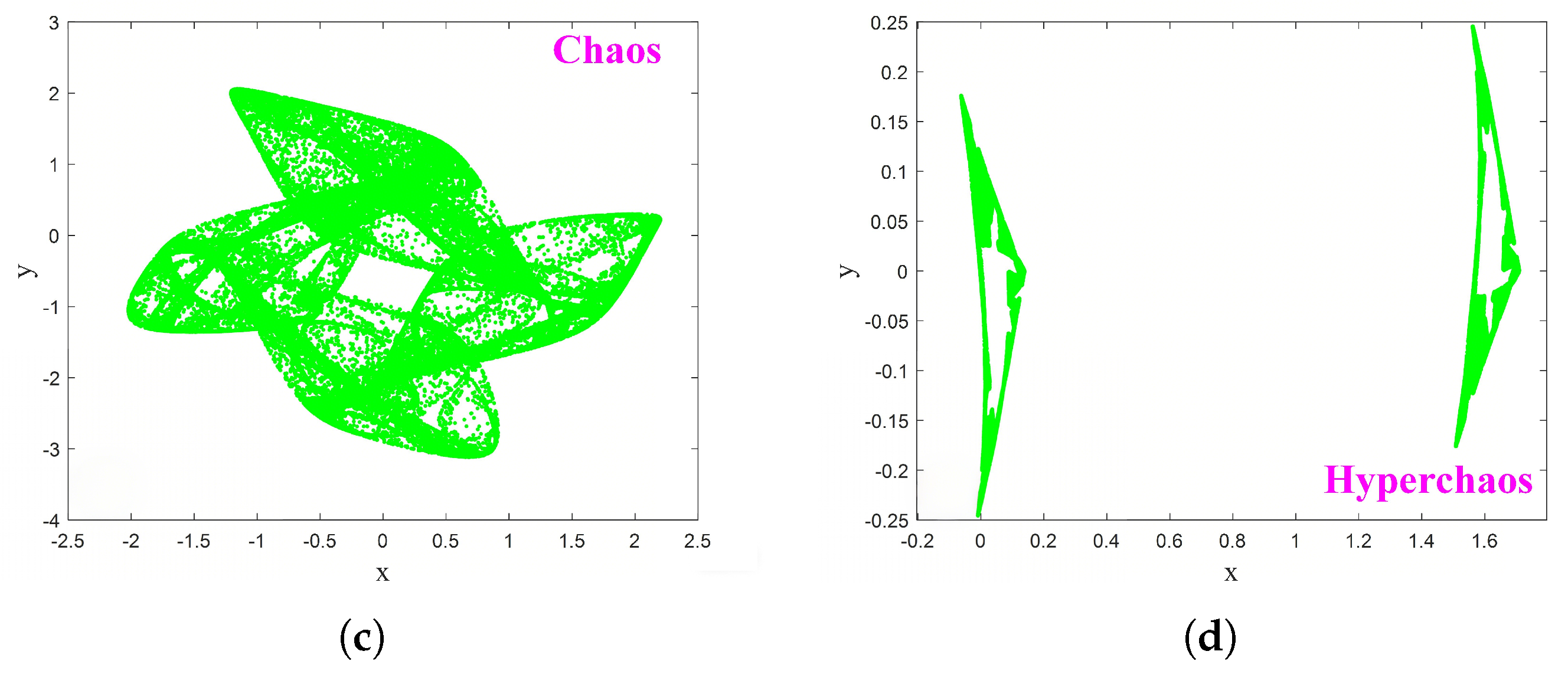
2. A Novel 2D Hyperchaotic Map and Its Basic Dynamics
2.1. A Novel 2D Hyperchaotic Map
2.2. Equilibrium Point Analysis
- Configuration 1 (, , , ):
- Fixed point: ;
- Eigenvalues: ;
- Stability: , unstable.
- Configuration 2 (, , , ):
- Fixed point: ;
- Eigenvalues: , ;
- Stability: unstable.
- Configuration 3 (, , , ):
- Fixed point: ;
- Eigenvalues: , ;
- Stability: , unstable.
- Configuration 4 (, , , ):
- Fixed point: ;
- Eigenvalues: ,;
- Stability: , unstable.
- Configs 1, 3, 4: Spectral radius violation ();
- Config 2: Positive real parts in complex conjugate pair.
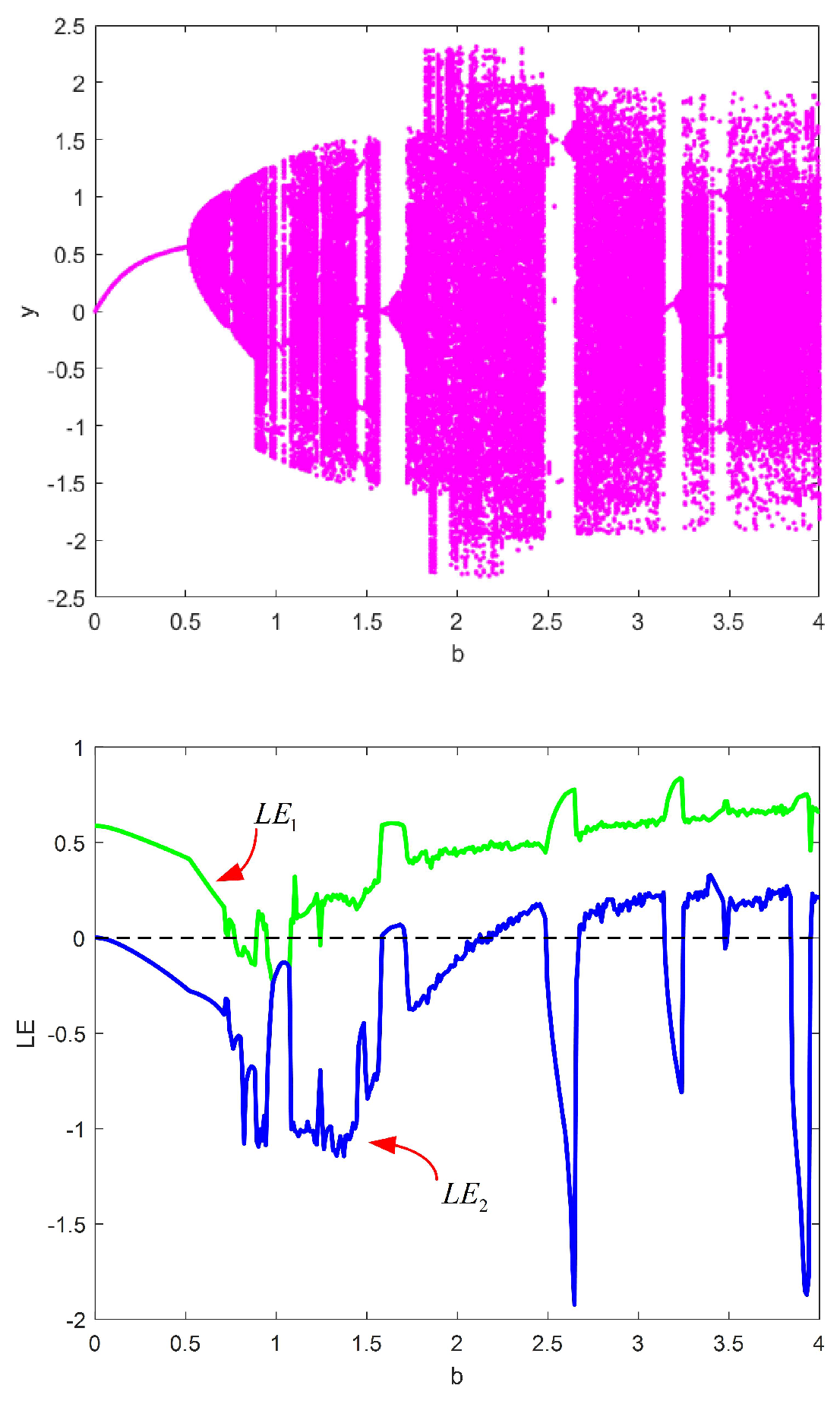
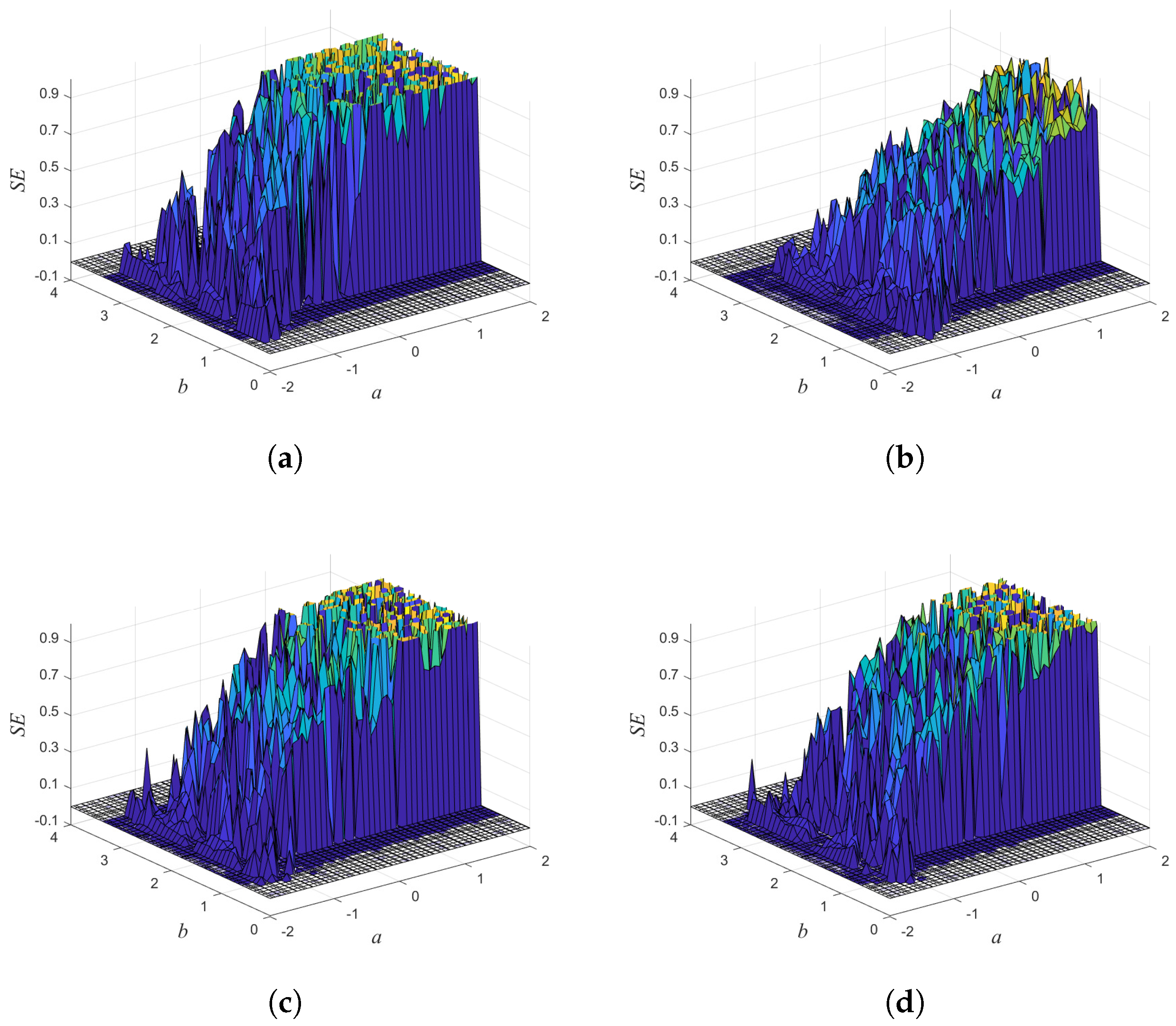
2.3. Bifurcation and LE Analysis
2.4. Sample Entropy
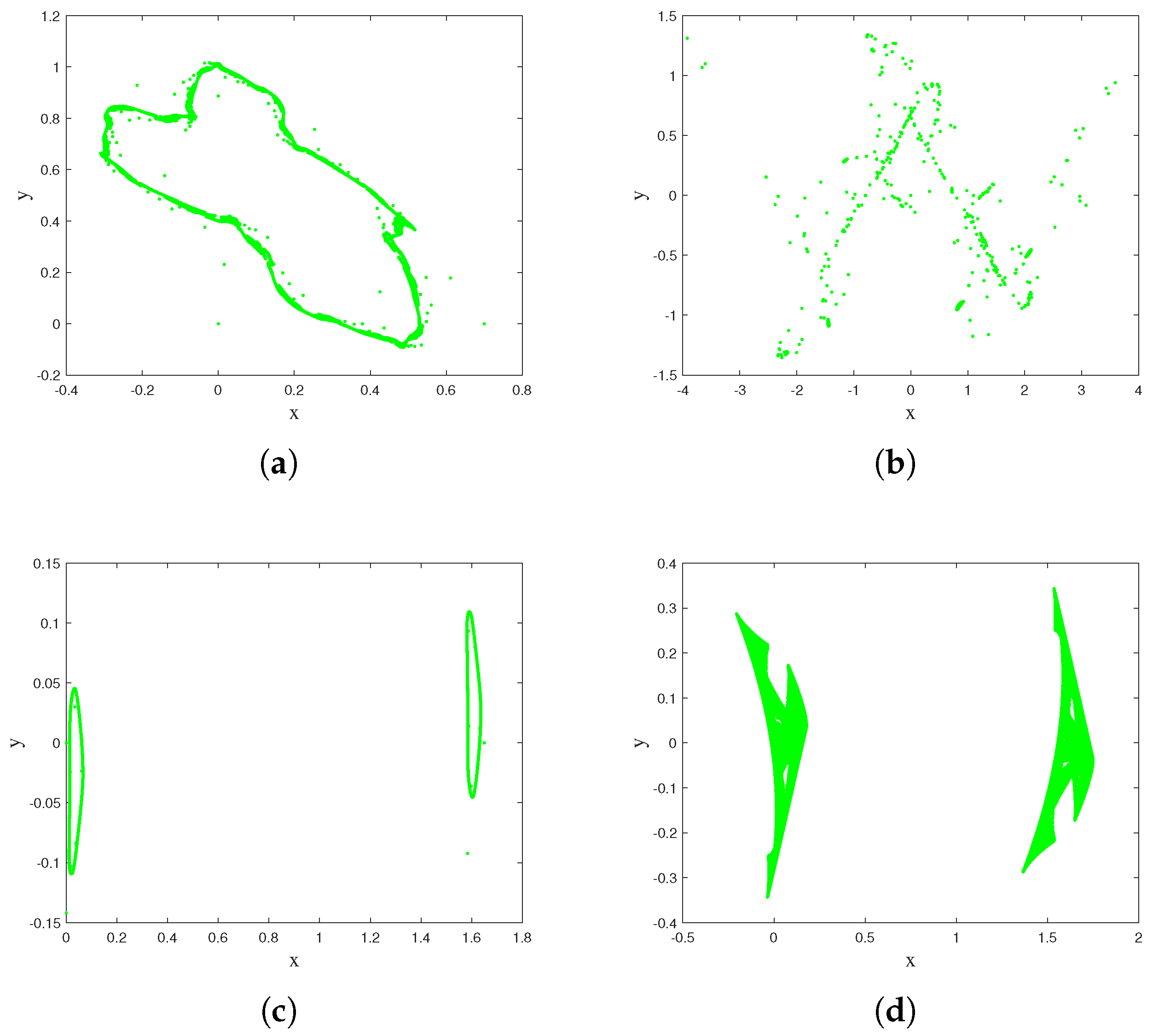
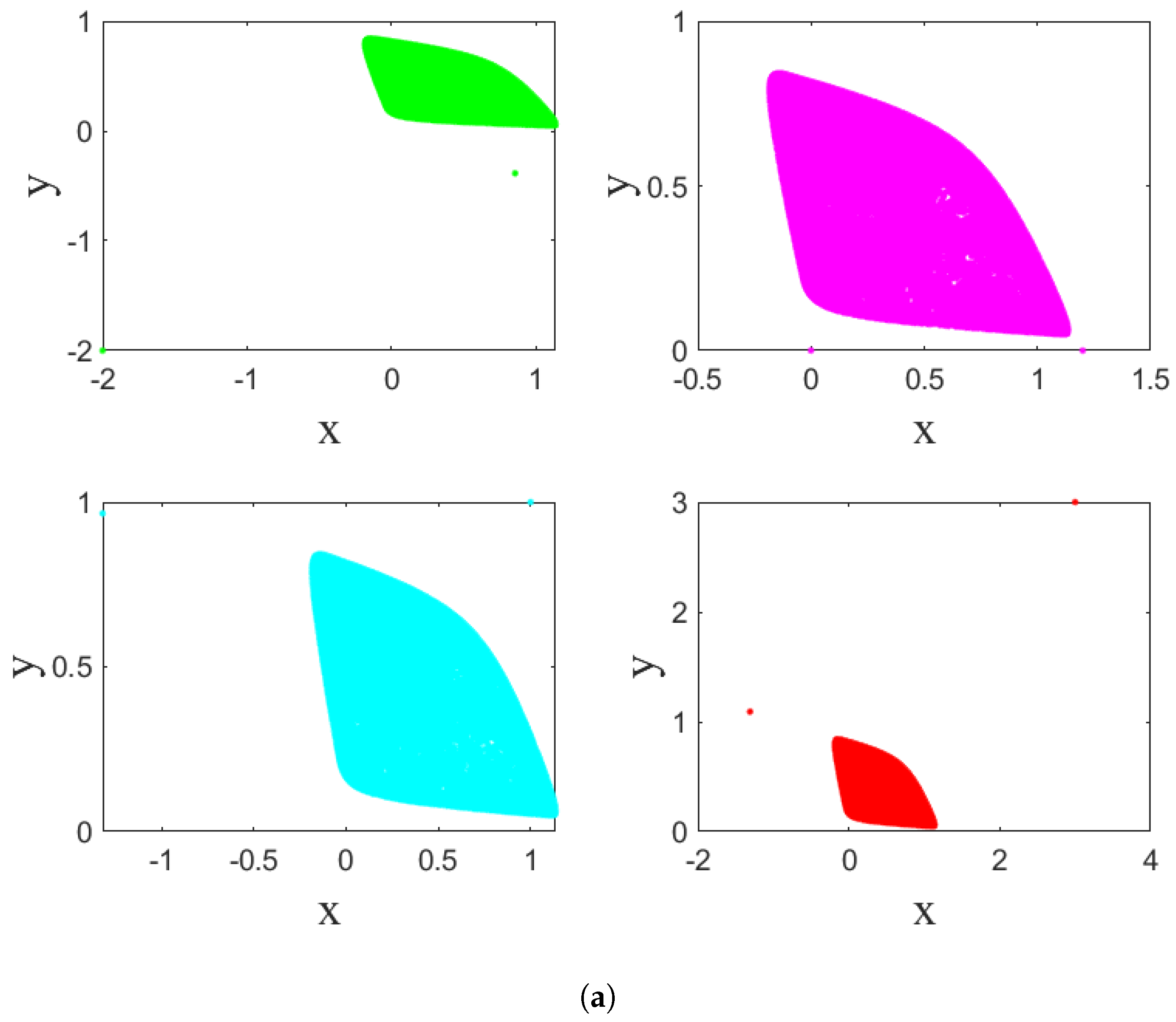
3. Homogeneous Multistability
4. A Pseudorandom Number Generator Based on the Proposed Hyperchaotic System
5. A Color Image Encryption Scheme Based on 2D Hyperchaotic System and Its Corresponding Security Analysis
5.1. A Color Image Encryption Scheme Based on 2D Hyperchaotic System
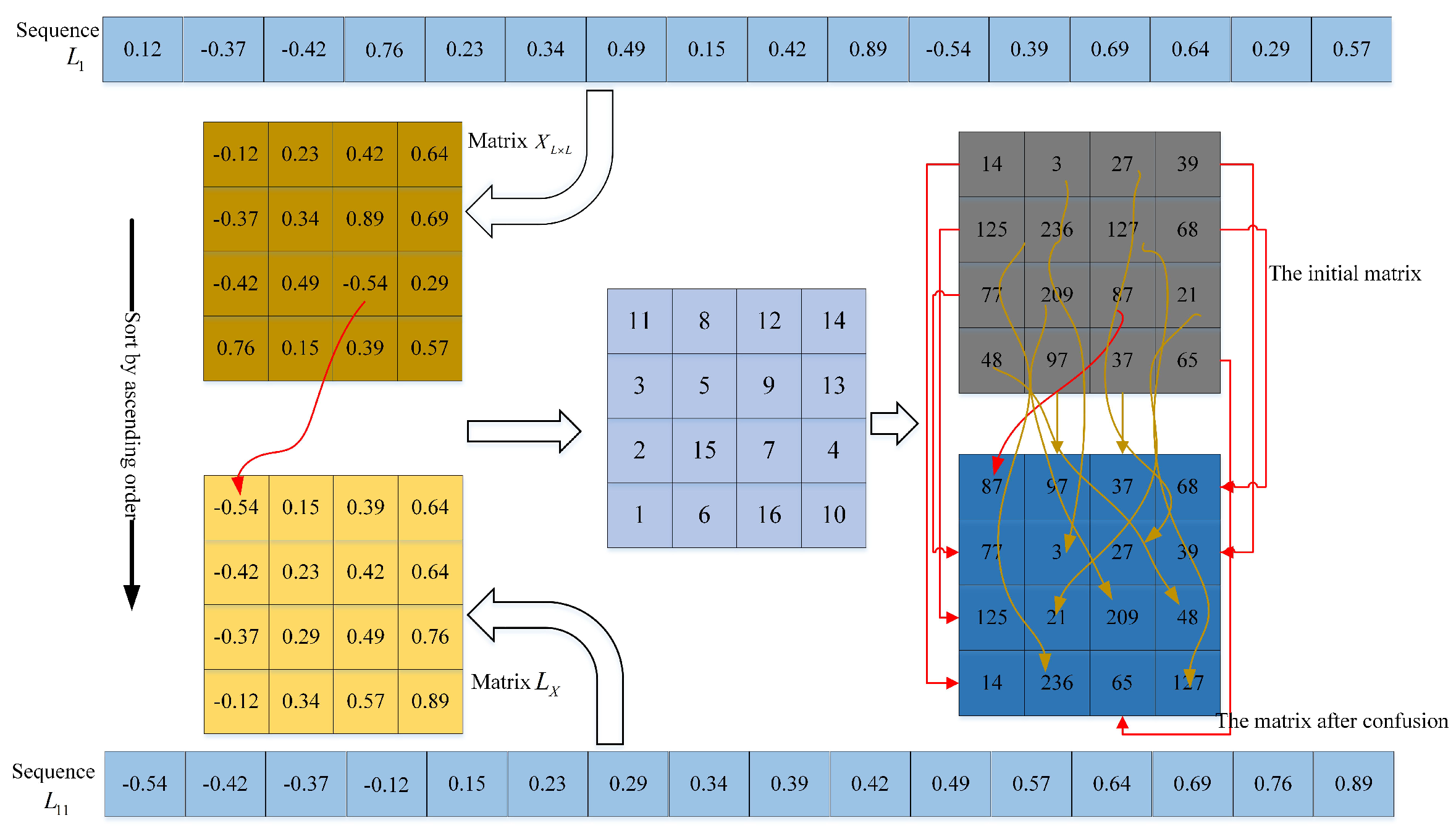
5.2. Confusion Operation
| Algorithm 1 Confusion during encryption |
| Input: the initial value {, }T of the chaotic system and the plaintext image P |
| Output: The image after confusion |
| 1. According to the size of the plaintext image given, the intercepted chaotic sequence L1, L2 is arranged in ascending order, and the new sequence obtained is recorded as L11, L22 |
| 2. L11(i) = l1(index(i)). % index is the position element of sequence L11 in sequence L1 |
| 3. Reorganize L1, L2, L11, L22 into a square matrix by column, denoted as XL×L,YL×L, LX, LY, respectively. |
| 4. For i from 1 to L do |
| 5. For j from 1 to L do |
| 6. |
| 7. |
| 8. |
| 9. Confused on color image R channel for operation |
| 10. End for |
| 11. End for |
| 12. Similarly, |
| 13. By recombining the three channels R, G and B, the image P after confusion can be obtained |
5.3. Diffusion Operation
5.4. Simulation Results
5.5. Security Analysis
5.5.1. Key Space Analysis
5.5.2. Histogram Analysis and Information Entropy
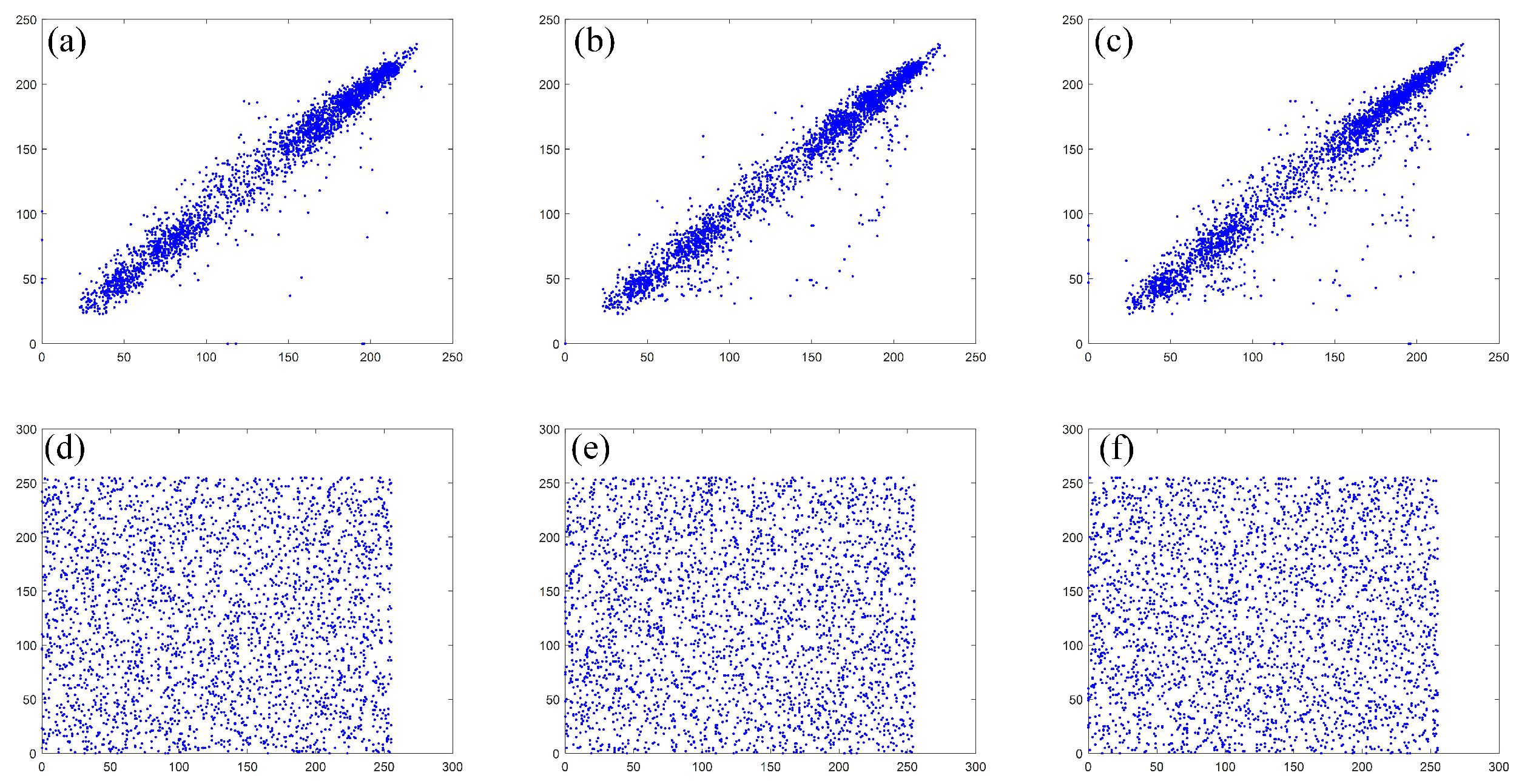
5.5.3. Correlation Analysis
5.5.4. Differential Attack
5.5.5. Time Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rakkiyappan, R.; Chandrasekar, A.; Lakshmanan, S. Effects of leakage time-varying delays in Markovian jump neural networks with impulse control. Neurocomputing 2013, 121, 365–378. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Chandrasekar, A.; Lakshmanan, S. Exponential stability of Markovian jumping stochastic Cohen-Grossberg neural networks with mode-dependent probabilistic time-varying delays and impulses. Neurocomputing 2014, 131, 265–277. [Google Scholar] [CrossRef]
- Yan, W.; Jiang, Z.; Huang, X.; Ding, Q. Adaptive Neural Network Synchronization Control for Uncertain Fractional-Order Time-Delay Chaotic Systems. Fractal Fract. 2023, 7, 288. [Google Scholar] [CrossRef]
- Deng, Y.M.; Fan, H.F.; Wu, S.M. A hybrid ARIMA-LSTM model optimized by BP in the forecast of outpatient visits. J. Ambient Intell. Humaniz. Comput. 2020, 14, 5517–5527. [Google Scholar] [CrossRef]
- Xu, G.; Xu, J.; Xiu, C.; Liu, F.; Zang, Y. Secure communication based on the synchronous control of hysteretic chaotic neuron. Neurocomputing 2017, 227, 108–112. [Google Scholar] [CrossRef]
- Wu, A.; Zeng, Z. Dynamic behaviors of memristor-based recurrent neural networks with time-varying delays. Neural Netw. 2012, 36, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Devaney, R.L. An Introduction to Chaos Dynamical Systems; Addison Wesley Publishing Company: New York, NY, USA, 1989. [Google Scholar]
- Elwakil, A.S.; Kennedy, M.P. Chua’s circuit decomposition: A systematic design approach for chaotic oscillators. J. Frankl. Inst. 2000, 337, 251–265. [Google Scholar] [CrossRef]
- Salamon, M. Chaotic electronic circuits in cryptography. In Applied Cryptography and Network Security; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef]
- Bao, B.; Hu, J.; Cai, J.; Zhang, X.; Bao, H. Memristor-induced mode transitions and extreme multistability in a map-based neuron model. Nonlinear Dyn. 2023, 111, 3765–3779. [Google Scholar] [CrossRef]
- Bao, H.; Hua, M.; Ma, J.; Chen, M.; Bao, B. Offset-control plane coexisting behaviors in two-memristor-based Hopfield neural network. IEEE Trans. Ind. Electron. 2023, 70, 10526–10535. [Google Scholar] [CrossRef]
- Li, C.; Lei, T.; Liu, Z. Offset parameter cancellation produces countless coexisting attractors. Chaos Interdiscipl. J. Nonlinear Sci. 2022, 32, 121104. [Google Scholar] [CrossRef]
- Csaba, G.; Porod, W. Coupled oscillators for computing: A review and perspective. Appl. Phys. Rev. 2020, 7, 011302. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J. Amplitude control approach for chaotic signals. Nonlinear Dyn. 2013, 73, 1335–1341. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J. Variable-boostable chaotic flows. Optik 2016, 127, 10389–10398. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C. Influences of electromagnetic radiation distribution on chaotic dynamics of a neural network. Appl. Math. Comput. 2020, 369, 124840. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Zhang, X.; Koyuncu, I.; Bonny, T.; Tuna, M.; Alçin, M.; Zhang, S.; Sulaiman, I.M.; Awwal, A.M.; et al. A novel 3D chaotic system with line equilibrium: Multistability, integral sliding mode control, electronic circuit, FPGA implementation and its image encryption. IEEE Access 2022, 10, 68057–68074. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q.; Tse, C.K. Designing n-D non-degenerate hyperchaotic systems via a simple circulant matrix. IEEE Trans. Circuits Syst. II Exp. Briefs 2024, 71, 460–464. [Google Scholar] [CrossRef]
- Wang, M.; Gu, L. Multiple mixed state variable incremental integration for reconstructing extreme multistability in a novel memristive hyperchaotic jerk system with multiple cubic nonlinearity. Chin. Phys. B 2024, 33, 020504. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, L.; Liu, Y. Design and realization of discrete memristive hyperchaotic map with application in image encryption. Chaos Solitons Fractals 2022, 165, 112781. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, W. Hidden hyperchaotic attractors in a modiffed Lorenz–Stenffo system with only one stable equilibrium. Int. J. Bifurc. Chaos 2014, 24, 1450127. [Google Scholar] [CrossRef]
- Minati, L. Simulation versus experiment in non-linear dynamical systems. Chaos Solitons Fractals 2021, 144, 110656. [Google Scholar] [CrossRef]
- Cao, W.; Cai, H.; Hua, Z. n-dimensional chaotic map with application in secure communication. Chaos Solitons Fractals 2022, 163, 112519. [Google Scholar] [CrossRef]
- Zhao, Y.; Ding, J.; He, S.; Wang, H.; Sun, K. Fully fixedpoint integrated digital circuit design of discrete memristive systems. AEU-Int. J. Electron. Commun. 2023, 161, 154522. [Google Scholar] [CrossRef]
- He, S.; Fu, L.; Yao, L.; Wu, X.; Wang, H.; Sun, K. Analog circuit of a simplified tent map and its application in sensor position optimization. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 885–888. [Google Scholar] [CrossRef]
- Yan, W.; Ding, Q. n-dimensional polynomial hyperchaotic systems with synchronization application. Eur. Phys. J. Plus 2023, 138, 915. [Google Scholar] [CrossRef]
- Cai, Z.; Sun, J. Convergence of C0 complexity. Int. J. Bifurc. Chaos 2009, 19, 977–992. [Google Scholar] [CrossRef]
- Tomcala, J. New fast ApEn and SampEn entropy algorithms implementation and their application to supercomputer power consumption. Entropy 2020, 22, 863. [Google Scholar] [CrossRef]
- Li, C.B.; Sprott, J.C.; Xing, H. Constructing chaotic systems with conditional symmetry. Nonlinear Dyn. 2016, 87, 1351–1358. [Google Scholar] [CrossRef]
- Fan, C.L.; Ding, Q. A universal method for constructing non-degenerate hyperchaotic systems with any desired number of positive Lyapunov exponents. Chaos Solit. Fractals 2022, 161, 112323. [Google Scholar] [CrossRef]
- Belazi, A.; Khan, M.; El-Latif, A.A.A.; Belghith, S. Efficient cryptosystem approaches: S-boxes and permutation-substitution-based encryption. Nonlinear Dyn. 2017, 87, 337–361. [Google Scholar] [CrossRef]
- Hua, Z.Y.; Zhou, Y.C. Design of image cipher using block-based scrambling and image filtering. Inf. Sci. 2017, 396, 97–113. [Google Scholar] [CrossRef]
- Cao, C.; Sun, K.; Liu, W. A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map. Signal Process 2018, 143, 122–133. [Google Scholar] [CrossRef]
- Lu, L.; Li, Y.; Sun, A. Parameter identification and chaos synchronization for uncertain coupled map lattices. Nonlinear Dyn. 2013, 73, 2111–2117. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015, Proceedings, Part III 18; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Wu, S.; Zhong, S.; Liu, Y. Deep residual learning for image steganalysis. Multimed. Tools Appl. 2017, 77, 10437–10453. [Google Scholar] [CrossRef]
- NIST SP 800-22 Rev. 1a; A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. NIST: Gaithersburg, MD, USA, 2010.
- Raghuvanshi, A.; Budhia, M.; Patro, K.A.K.; Acharya, B. FSR-SPD: An efficient chaotic multi-image encryption system based on flip-shift-rotate synchronous-permutation-diffusion operation. Multimed. Tools Appl. 2024, 83, 57011–57057. [Google Scholar] [CrossRef]
- NIST SP 800-131A Rev. 2; Offset Parameter Cancellation and Cryptographic Algorithm Transition Guidance. NIST: Gaithersburg, MD, USA, 2019. [CrossRef]
- Yan, X.; Hu, Q.; Teng, L. A novel color image encryption method based on new three-dimensional chaotic mapping and DNA coding. Nonlinear Dyn. 2025, 113, 1799–1826. [Google Scholar] [CrossRef]
- Acharya, B.; Sravan, J.V.; Potnuru, D.J.R.; Patro, K.A.K. MIE-SPD: A New and Highly Efficient Chaos-Based Multiple Image Encryption Technique With Synchronous Permutation Diffusion. IEEE Access 2025, 13, 3558943. [Google Scholar] [CrossRef]
- Yan, W.; Ding, Q. A controllable 3D hyperchaotic map with infinite coexisting attractors and its application to image encryption. Nonlinear Dyn. 2024, 113, 9045–9059. [Google Scholar] [CrossRef]
- Liu, C.Y.; Ding, Q. A color image encryption scheme based on a novel 3d chaotic mapping. Complexity 2020, 202, 3837209. [Google Scholar] [CrossRef]
- Hua, Z.Y.; Cheng, Y.Y.; Bao, H.; Zhou, Y.C. Two-dimensional parametric polynomial chaotic system. IEEE Trans. Cybern. 2022, 52, 4402–4414. [Google Scholar] [CrossRef]
- Xin, Y.; Wang, X. Fractal sorting matrix and its application on chaotic image encryption. Inf. Sci. 2021, 547, 1154–1169. [Google Scholar] [CrossRef]
- Xu, Q.; Sun, K.; Zhu, C. A visually secure asymmetric image encryption scheme based on RSA algorithm and hyperchaotic map. Phys. Scrpta 2020, 95, 035223. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Bao, L.; Chen, C.L.P. A new 1D chaotic map for image encryption. Signal Process 2014, 97, 3039–3052. [Google Scholar] [CrossRef]

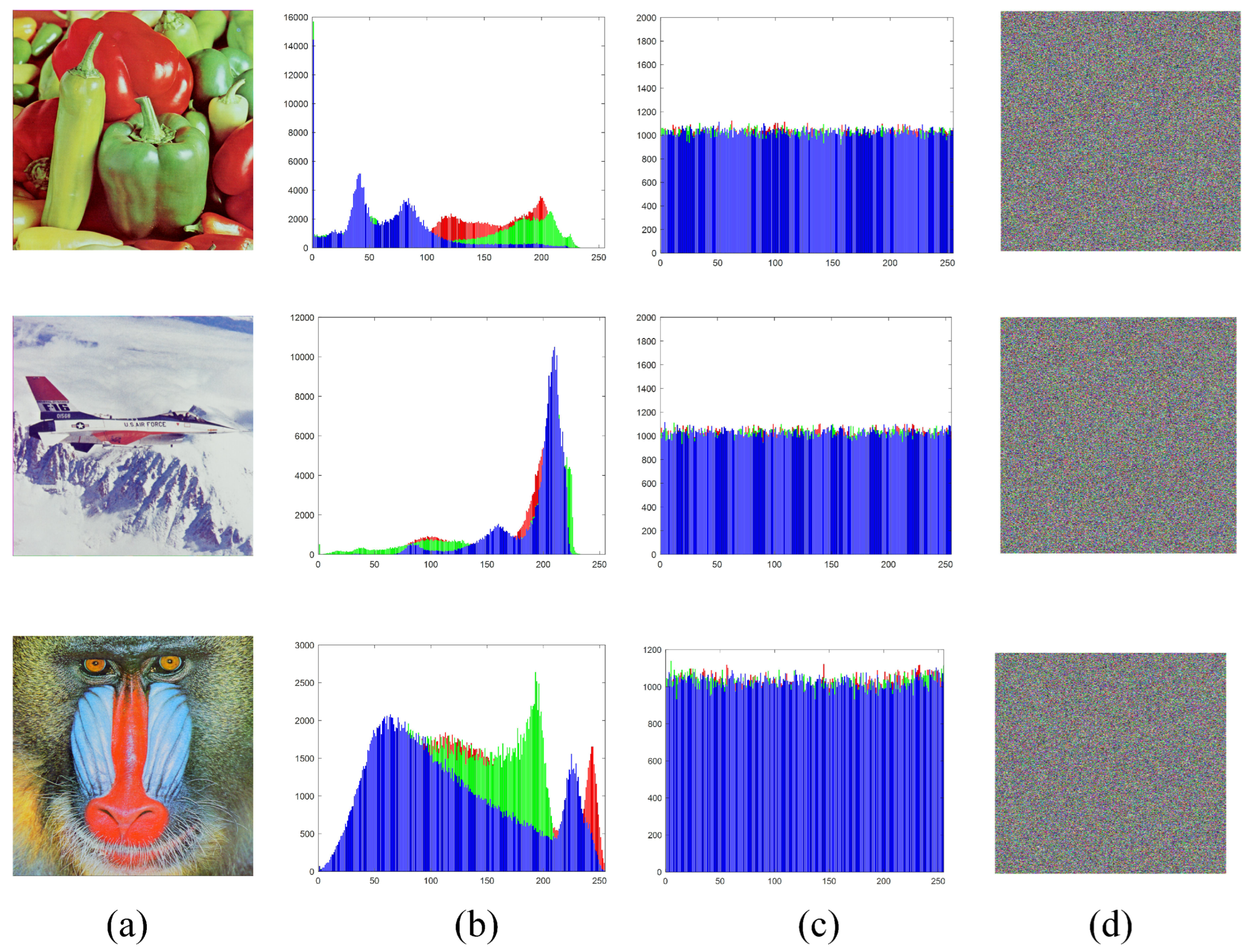
| Order | Test Suites | p-Value | Result |
|---|---|---|---|
| 1 | Frequency | 0.546821 | Pass |
| 2 | Block frequency | 0.765321 | Pass |
| 3 | Cumulative sums (forward) | 0.866744 | Pass |
| 4 | Cumulative sums (backward) | 0.123765 | Pass |
| 5 | Runs | 0.532570 | Pass |
| 6 | Longest run | 0.823465 | Pass |
| 7 | Rank | 0.972380 | Pass |
| 8 | FFT | 0.029687 | Pass |
| 9 | Non-overlapping template | 0.234758 | Pass |
| 10 | Overlapping tempUniversal | 0.166534 | Pass |
| 11 | Universal | 0.925643 | Pass |
| 12 | Approximate entropy | 0.614867 | Pass |
| 13 | Random excursions | 0.657103 | Pass |
| 14 | Random excursions variant | 0.587641 | Pass |
| 15 | Serial (forward) | 0.858761 | Pass |
| 16 | Serial (backward) | 0.762146 | Pass |
| 17 | Linear complexity | 0.714581 | Pass |
| No. | Image | R | G | B | ||
|---|---|---|---|---|---|---|
| 1 | Pepper | 274.67 | 252.17 | 246.98 | pass | pass |
| 2 | Airplane | 261.23 | 249.09 | 258.92 | pass | pass |
| 3 | Monkey | 253.18 | 250.01 | 257.98 | pass | pass |
| Encrypted Images | Pepper | Airplane | Monkey |
|---|---|---|---|
| Ref. [38] | 7.99950 | 7.99950 | 7.99940 |
| Ref. [40] | 7.99934 | 7.99932 | 7.99933 |
| Ref. [41] | 7.99940 | 7.99930 | 7.99940 |
| Ref. [42] | 7.99920 | 7.99900 | 7.99940 |
| Our scheme | 7.99923 | 7.99910 | 7.99940 |
| Pepper | Original Image | Encrypted Image | ||||
|---|---|---|---|---|---|---|
| Horizontal | Vertical | Diagonal | Horizontal | Vertical | Diagonal | |
| Ref. [43] | 0.9783 | 0.9789 | 0.9661 | 0.0031 | 0.0014 | 0.0006 |
| Ref. [44] | 0.9783 | 0.9789 | 0.9661 | −0.0041 | −0.0024 | 0.0007 |
| Ref. [45] | 0.9783 | 0.9789 | 0.9661 | −0.0023 | −0.0036 | 0.0021 |
| Ref. [46] | 0.9783 | 0.9789 | 0.9661 | 0.0019 | 0.0036 | 0.0017 |
| Our scheme | 0.9783 | 0.9789 | 0.9661 | −0.0005 | 0.0009 | 0.0010 |
| Images | NPCR(%) | UACI(%) | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| Pepper | 99.63 | 99.63 | 99.60 | 33.42 | 33.46 | 33.50 |
| Airplane | 99.65 | 99.59 | 99.63 | 33.40 | 33.28 | 33.28 |
| Monkey | 99.59 | 99.58 | 99.62 | 33.37 | 33.32 | 33.30 |
| Image | Size | Encryption Time (s) | Decryption Time (s) |
|---|---|---|---|
| Peppers | 0.202145 | 0.284039 | |
| 0.324531 | 0.385432 | ||
| 0.426432 | 0.503421 | ||
| 0.893421 | 0.983241 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Yan, W.; Dong, W.; Ding, Q. A Novel 2D Hyperchaotic Map with Homogeneous Multistability and Its Application in Image Encryption. Symmetry 2025, 17, 801. https://doi.org/10.3390/sym17050801
Huang X, Yan W, Dong W, Ding Q. A Novel 2D Hyperchaotic Map with Homogeneous Multistability and Its Application in Image Encryption. Symmetry. 2025; 17(5):801. https://doi.org/10.3390/sym17050801
Chicago/Turabian StyleHuang, Xin, Wenhao Yan, Wenjie Dong, and Qun Ding. 2025. "A Novel 2D Hyperchaotic Map with Homogeneous Multistability and Its Application in Image Encryption" Symmetry 17, no. 5: 801. https://doi.org/10.3390/sym17050801
APA StyleHuang, X., Yan, W., Dong, W., & Ding, Q. (2025). A Novel 2D Hyperchaotic Map with Homogeneous Multistability and Its Application in Image Encryption. Symmetry, 17(5), 801. https://doi.org/10.3390/sym17050801





