Symmetry-Entropy-Constrained Matrix Fusion for Dynamic Dam-Break Emergency Planning

Abstract

Existing studies on ontology evolution lack automated mechanisms to balance semantic coherence and adaptability under real-time uncertainties, particularly in resolving spatiotemporal asymmetry and multidimensional coupling imbalances in dam-break scenarios. Traditional methods such as WordNet’s tree symmetry and FrameNet’s frame symmetry fail to formalize dynamic adjustments through quantitative metrics, leading to path dependency and delayed responses. This study addresses this gap by introducing a novel symmetry-entropy-constrained matrix fusion algorithm, which integrates algebraic direct sum operations and Hadamard product with entropy-driven adaptive weighting. The original contribution lies in the symmetry entropy metric, which quantifies structural deviations during fusion to systematically balance semantic stability and adaptability. This work formalizes ontology evolution as a symmetry-driven optimization process. Experimental results demonstrate that shared concepts between ontologies (s = 3) reduce structural asymmetry by 25% compared to ontologies (s = 1), while case studies validate the algorithm’s ability to reconcile discrepancies between theoretical models and practical challenges in evacuation efficiency and crowd dynamics. This advancement promotes the evolution of traditional emergency management systems towards an adaptive intelligent form.

1. Introduction

The spatial-temporal symmetry of reservoir dam distribution and risk management has become a strategic focus in China’s infrastructure governance. With 98,566 reservoir dams (including 836 large-scale and 93,500 small-scale structures) forming a geometrically hierarchical system by 2023 [1], these engineering symmetries provide flood control and energy generation benefits [2] while carrying inherent nonlinear risks. The national paradigm has shifted from “engineering safety” to “risk management symmetry” through emergency planning [3], requiring dynamic equilibrium between disaster prevention and consequence mitigation, particularly for dam-break scenarios threatening downstream symmetry of socio-ecological systems [4,5].

The global emergency management system exhibits multidimensional symmetry in the evolution of its architecture. In the United States, the construction of the spatiotemporal symmetry of the emergency management framework has undergone a dynamic evolution in three stages. During the foundational stage (1980s–2001), the synergistic integration of the Federal Disaster Relief Program [6] and the Federal Emergency Management Agency (FEMA) system [7,8] established a matrix-like symmetrical structure through the federal-state-local three-level response mechanism. This multi-dimensional network [9,10] is formed by the coupling of vertical command hierarchies and horizontal collaboration networks.

In the post-2001 anti-terrorism enhancement stage (2001–2010), the establishment of the Department of Homeland Security achieved functional symmetry [11,12]. Through vertical anti-terrorism intelligence penetration and horizontal disaster response coverage, the multi-objective balance between national security and natural disaster management was optimized. The Department of Homeland Security integrated the intelligence resources of multiple departments and established an interdepartmental intelligence-sharing mechanism, enabling the efficient transmission of anti-terrorism intelligence from the central to local levels. Meanwhile, in terms of disaster response, by establishing a unified emergency command system, the resources and forces of different departments were integrated, improving the coordination and coverage of disaster response.

In the intelligent upgrading stage (2010 to the present), the symmetry of information flow has been achieved through the National Incident Management System (NIMS) and the Computer-Aided Management of Emergency Operations (CAMEO) systems [13]. With the help of algorithm-driven dynamic routing optimization, by integrating the data flow, decision flow, and action flow through closed-loop symmetry, a Pareto improvement in interdepartmental collaboration has been realized. The NIMS system, by establishing a standardized mechanism for classifying and dispatching emergency resources, ensures that different departments can quickly and accurately share and utilize resource information during emergency responses. The CAMEO system, on the other hand, uses advanced data analysis and prediction algorithms to conduct real-time assessments of the development trends of disaster events, providing a scientific basis for decision-makers, thus achieving the optimization of emergency decisions and the efficient coordination of actions.

In Europe, the research focuses on the symmetrical architecture of data and processes. The UK’s Civil Contingencies Act 2004 [14] created a type-agnostic unified response framework, achieving process symmetry in crisis resolution. This act stipulates unified standards and procedures for emergency response, requiring all emergency departments to conduct disaster assessments, resource allocation, and emergency actions in accordance with the unified process, thereby improving the coordination and consistency of emergency response. Germany, through the phased development of the deNIS system [15,16,17], established a radial symmetry emergency information distribution mechanism characterized by a centralized data service center.

The emergency management systems in East Asia demonstrate hierarchical symmetry. Japan’s three-level response system (Prime Minister’s Office → Prefectures → Municipalities) adopts nested symmetry and embeds professional forces horizontally to achieve multi-disaster coordination. For example, the Prime Minister’s Office is responsible for formulating national emergency policies and strategies, prefectures are responsible for coordinating emergency resources and actions within the region, and municipalities are responsible for specific disaster response and recovery work. Through the clear division of responsibilities and cooperation mechanisms among governments at all levels, a hierarchical and orderly emergency response system has been formed. China’s emergency platform system has a star-shaped symmetrical topological structure [18,19], with the State Council platform as the central node, implementing a dual-channel symmetrical structure of vertical command flow (central → provincial → municipal) and horizontal information sharing, and constructing the framework of “One Plan, Three Systems” [20,21]. The intelligent platforms of local governments further enhance self-organizing symmetry through node autonomy optimization [22]. For example, China’s national emergency command system has achieved real-time information sharing and instruction transmission between the central and local levels by establishing a connected command system from top to bottom. At the same time, the emergency platforms of local governments optimize the allocation of emergency resources according to local actual situations, improving the flexibility and adaptability of emergency response.

In the field of knowledge engineering, research on symmetry has focused on the structural balance of semantic networks. Early systems like WordNet [23] built vocabulary networks through tree symmetry of “synsets-hierarchical relationships”, while FrameNet [24] achieved event modeling with frame symmetry of “frame elements-semantic roles”. The Cyc system [25] attempted to establish rule symmetry for common-sense reasoning, but its closed knowledge base led to insufficient dynamic adaptability. Chinese research institutions have made breakthroughs in optimizing domain ontology symmetry. Zhejiang University proposed a dimensional symmetry method of “concept lattice-attribute reduction” [26] to address the issue of knowledge granularity overload; the Chinese Academy of Sciences developed a weight symmetry algorithm based on rough sets [27] to enhance the stability of ontology evolution; and Harbin Institute of Technology established a “trichotomy decision” framework [28] to achieve dynamic balance in knowledge addition and deletion. However, these methods still have issues such as strong path dependence and lag in real-time adjustment in complex emergency scenarios. Recent studies on dam-break dynamics, such as tsunami-like wave propagation over trapezoidal obstacles [29] and tailings dam stability under dry closure conditions [30], highlight the importance of dynamic adaptability in emergency planning. This paper formalizes these findings through symmetric matrix operations and proposes a mechanism for dynamic adjustments.

This study focuses on the temporal and spatial asymmetry of disaster chain propagation, the dimensionality imbalance caused by the coupling of multiple triggering factors, and the uncertain propagation characteristics of emergency response in dam-break emergencies. It constructs an ontology dynamic evolution framework based on a matrix fusion algorithm. By establishing a matrix isomorphic mapping among disaster propagation pathways, environmental triggering parameters, and emergency resource scheduling, this study innovatively transforms the uncertainty resolution issue into a symmetry optimization process within a high-dimensional manifold. This symmetry-driven approach not only effectively addresses the uncertainties in dam-break emergencies and enables dynamic adjustment of emergency plans but also provides a new mathematical tool for the multi-stable control of dam-break disasters. More importantly, it achieves the normative symmetry in the closed loop of “risk identification—decision making—action implementation” at the engineering level, promoting the evolution of traditional emergency management systems towards an adaptive intelligent form.

2. Ontology Matrix Algorithm of Dam Break Emergency Plan

Ontology evolution is mainly based on corresponding theories and methods to its internal concepts, the relationship between concepts, and attributes, and another continuous improvement of a series of consistent transmission processes, mainly involving the enrichment and renewal of ontological concepts. There are also various reasons for ontological evolution, mainly including changes in domains, changes in shared conceptual models, and changes in representations. In addition, ontology non-consistency detection is required to prevent system conflicts due to evolution and ensure that the ontology structure, logic, and user-defined consistency are maintained after additional change operations, as shown in Figure 1.

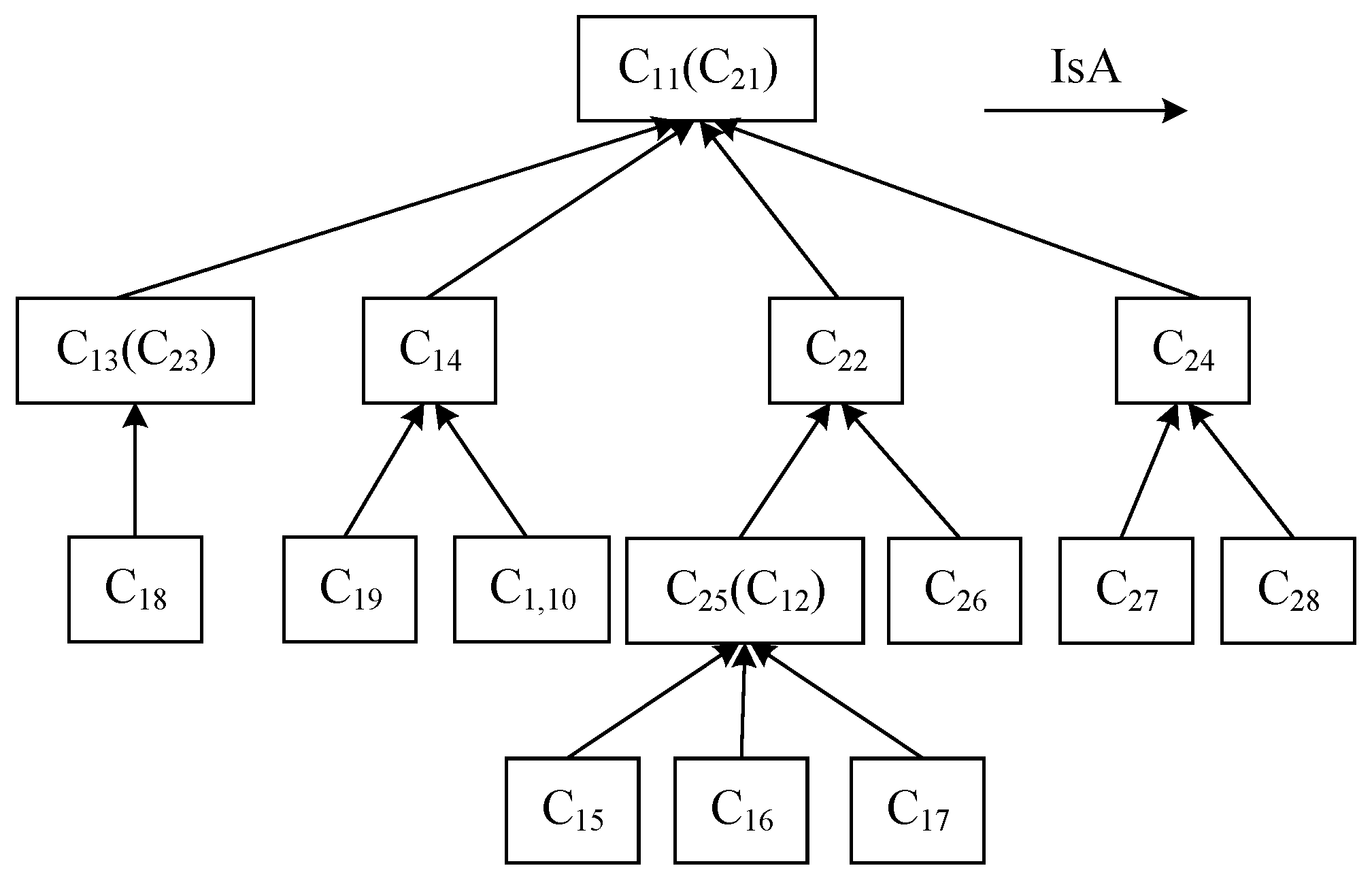
2.1. Dam Break Emergency Plan Ontology Structure Matrix

Ontology is divided into natural language description and mathematical language description, the former is mainly a philosophical definition, and the latter is the definition of information science. On the whole, the definition of ontology is from objective description to in-depth processing, which meets the needs of today’s intelligent development in a certain field. According to the constituent elements of the ontology model of the emergency plan for a dam break, this paper defines the ontology model O of the emergency plan for a dam break as a quintuple:

O = (C, R, F, A, I),

(1)

where C represents the concept set in the whole system of dam-break emergency plan; R denotes the finite set of relationships among the concepts of emergency plan for dam-break; F represents the function set in the dam-break emergency plan; A represents the finite set of axioms in the dam-break emergency plan; I represents the specific entity set of dam break emergency plan.

In addition, in R, IsA ∈ R, IsA represents the classification relationship between concepts, forming a hierarchy between concepts.

In order to fully illustrate the relationship between ontology and matrix, other related concepts need to be introduced to describe it. In ontology O = (C, R, F, A, I), if the topology of (C, R) is a tree, the ontology O = (C, R, F, A, I) is called the tree ontology. If the topology of (C, R) is a graph, it is called a graph ontology. In the tree ontology, the traversal method of “top to bottom, left to right” is called the natural traversal method. Generally, ontology only discusses the relationship between concept set C and relation set R, and there is only one tree ontology of the relation IsA in R, that is, R = {IsA}, so the expression of the ontology of the dam-break emergency plan can be denoted as O = (C, IsA).

Suppose O = (C, IsA) is an ontology in the field of dam-break emergency plan, where C = {c1, c2, …, cn}. Suppose the traversal mode in C is $c_{i_1},c_{i_2},\dots ,c_{i_n}$, where $i_1,i_2,\dots ,i_n$ is an n-level permutation, defined as:

$$f_{kl}=\left\{\begin{array}{l}\begin{array}{l}0,k=1\hfill \\ 1,If{c}_{i_l}IsA{c}_{i_k},And does not existp,so{c}_{i_l}IsA{c}_{i_P}IsA{c}_{i_k}\hfill \\ 0,other\hfill \end{array}\hfill \end{array}\right.,$$

(2)

Then the matrix $F={\left(f_{kl}\right)}_{n\times n}$ is called the structure matrix of the ontology O in the traversal mode $c_{i_1},c_{i_2},\dots ,c_{i_n}$, also called the ontology structure matrix, and the vector is $g={\left(c_{i_1},c_{i_2},\dots ,c_{i_n}\right)}^T$ the ontology concept vector. From the above definition of the ontology structure matrix, it can be seen that the structure matrix of the same ontology is the same in different traversal modes, and the ontology O and ontology structure matrix F are one-to-one correspondence under the same traversal mode.

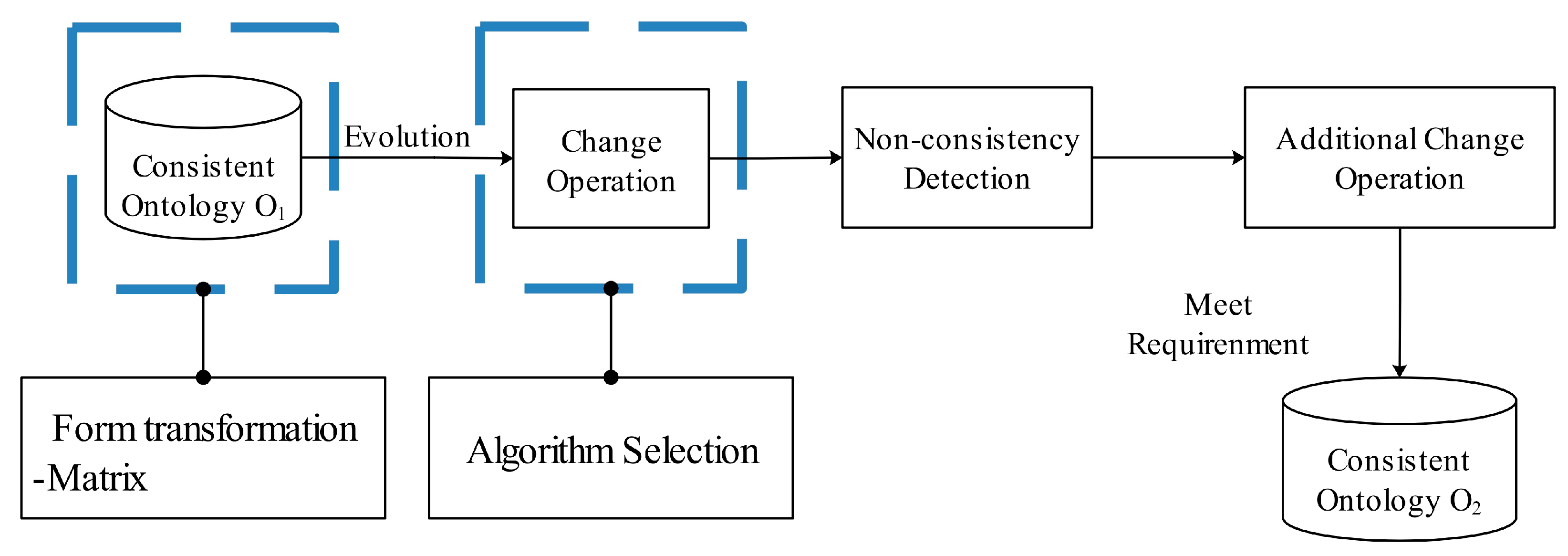
2.2. Ontology Matrix Fusion Model of Dam-Break Emergency Plan

With the continuous learning of domain ontology, the ontology structure must adapt to the external environment to generate new ontology models. Ontology fusion is the fusion of the source ontology with the existing new ontology to establish a new ontology while maintaining consistency. At present, the more common fusion methods include Chimaera, a system of fusion and diagnosis developed by Stanford University in the United States, the PROMPT method, and the FCA-Merge method. Through the comparative analysis of these methods, it can be seen that each system is basically the same in terms of mapping types, and some systems also need to rely on information other than the ontology itself, and each system requires human participation. At present, the mapping technology of ontology is developing rapidly, using existing ontology to fuse new ontology to create an ontology matrix model [31]. The specific algorithm model is shown in Figure 2:

It is assumed that there are two ontologies O₁ and O₂ in the field of dam-break emergency plan E, and the traversal method is natural traversal. From this, the ontology structure matrices F₁ and F₂ corresponding to the two ontologies can be obtained. The new matrix F_new is obtained by matrix fusion calculation, and then the new ontology O_new after the fusion of the two ontologies is constructed according to the new matrix.

2.3. Ontology Matrix Correlation Operations

In order to implement the ontology matrix algorithm, it is necessary to first introduce the definition of matrix direct sum and Hadamard product. The direct sum operation ensures the structural symmetry of hierarchical relationships by preserving the diagonal integrity of the source ontology (e.g., the invariance of symmetry in block diagonal matrices). This operation is analogous to the direct product operation in group theory, satisfying closure and associativity, thereby maintaining the group symmetry of the ontology structure. Let the matrix $A={(a_{ij})}_{m\times m}$, matrix $B={(b_{ij})}_{n\times n}$, and the straight sum C of the matrix be equal to A and B as diagonals, and the non-diagonal as 0, denoted as A ⊕ B, namely:

$$C=A\oplus B=\left[\begin{array}{cc}{A}_{m\times m}& 0\\ 0& B_{n\times n}\end{array}\right],$$

(3)

There are three main ways to multiply matrices, and this article mainly uses the Hadamard product, also known as the Hadamard product. The Hadamard product achieves coordinated interaction of overlapping concepts through element-wise multiplication, similar to the point symmetry operations in tensor manifolds. Its mathematical form satisfies the commutative and distributive laws, ensuring the optimization of local symmetry in semantic alignment. Let the matrix $A={(a_{ij})}_{m\times m}$, the matrix $B={(b_{ij})}_{n\times n}$, then the Hadamard product of the two matrices is $C={(c_{ij})}_{m\times n}$, denoted A ⊗ B, namely:

$$C=A\otimes B=\left[\begin{array}{cccc}{a}_{11}{b}_{11}& a_{12}{b}_{12}& \dots & a_{1n}{b}_{1n}\\ a_{21}{b}_{21}& a_{22}{b}_{22}& \dots & a_{2n}{b}_{2n}\\ \dots & \dots & \dots & \dots \\ a_{m1}{b}_{m1}& a_{m2}{b}_{m2}& \dots & a_{mn}{b}_{mn}\end{array}\right],$$

(4)

For the two ontologies O₁ = (C₁, IsA) and O₂ = (C₂, IsA) on the field E of the dam failure emergency plan, where $C_1=\left\{c_{11},c_{12},\dots ,c_{1m}\right\}$ and $C_2=\left\{c_{21},c_{22},\dots ,c_{2n}\right\}$ are the two conceptual sets corresponding to the source ontology on domain E. c₁₁ and c₂₁ are subconcepts of O₁ and O₂, and F₁ and F₂ are the ontology structure matrices of O₁ and O₂, respectively. Taking O₁ as reference ontology, if s ≥ 0 concepts are the same in C₁ and C₂, then the expression of knowledge in ontology O₁ is more reasonable and complete.

When s = 0, it means that there is no common concept in the two ontologies. Define the mapping of F₁ and F₂ to the new structure matrix:

$$F_{new}=F_1\circ F_2,$$

(5)

where: $F_{new}=\left[\begin{array}{ccc}0& e_1& e_2\\ 0& F_1& 0\\ 0& 0& F_2\end{array}\right]$, $e_1={\left(1,0,\dots ,0\right)}_{1\times m}$, $e_2={\left(1,0,\dots ,0\right)}_{1\times n}$.

When s = 0, $F_{new}=F_1\circ F_2=\left[\begin{array}{ccc}0& e_1& e_2\\ 0& F_1& 0\\ 0& 0& F_2\end{array}\right]$.

When s > 0, define the mapping of F₁ and F₂ to the new structure matrix:

$$F_{new}=F_1•F_2,$$

(6)

Among them, the construction of F_new can be completed by iteration. Let $F_{new}^{\left(0\right)}=F_1\oplus F_2$, a new matrix $F_{new}=F_{new}^{\left(s\right)}$ is obtained by iteration. Finally, it can be seen that F_new is the only determined matrix, the remaining diagonal elements are zero, and only the first column is the only zero vector. The remaining columns are standard unit vectors.

It can be concluded that when the same number of concepts s ≥ 0 in two ontologies, there is the following fusion operation of the local matrix, denoted by $F_1\ast F_2$, that is:

$$F_{new}=F_1\ast F_2=\left\{\begin{array}{l}{F}_1\mathsf{o}{F}_2,when s=0\hfill \\ F_1•F_2,when s>0\hfill \end{array}\right.,$$

(7)

2.4. Ontology Fusion Algorithm with Symmetry Entropy Constraints

According to the fusion algorithm model of matrix and ontology, the algorithms are different when the number of concepts is different, and the specific algorithms are divided into two categories.

To constrain the aforementioned ontology fusion algorithm and quantify the degree of symmetry in the ontology structure matrix, a symmetry entropy-constrained ontology fusion algorithm is proposed. For an ontology structure matrix F, its symmetry entropy S_sym is defined as the logarithm of the Frobenius norm of the difference between the matrix and its transpose. The Equation (8) is inspired by Shannon’s logarithmic measure of uncertainty [32], with matrix operations defined per Golub & Van Loan [33] and numerical regularization from Boyd & Vandenberghe [34]. Here, S_sym quantifies the asymmetry of F, where a smaller value indicates higher symmetry.

$$S_{sym}=\log \left({‖F-F^T‖}_F+ϵ\right),$$

(8)

where ${‖•‖}_F$ denotes the Frobenius norm, and ϵ = 10⁻⁶ is used to avoid taking the logarithm of zero. Lower values signify a more symmetric configuration, whereas higher values suggest increased asymmetry. The computational steps are as follows:

Step 1: Matrix preprocessing: Normalize the ontology structure matrices F₁, F₂, and F_new before and after fusion by scaling their element values to the range [0, 1].

Step 2: Compute difference matrices: $F_1-F_1^T$, $F_2-F_2^T$, $F_{new}-F_{new}^T$.

Step 3: Compute entropy values: Determine S_sym for each matrix using the formula.

2.5. Dam-Break Emergency Plan Domain Ontology Fusion Experiment

Taking two ontology O₁ experiment and O₂ experiment in dam-break emergency plan domain E, where C_1,i, C_2,j (i = 1, 2, …, 10; j = 1, 2, …, 8) respectively represent the concepts in the domain ontology of dam-break emergency plan. The graphical structure is shown in Figure 3 and Figure 4, and only the relationship of IsA is retained.

Under the natural traversal, the structural matrices of F₁ and F₂ can be obtained respectively.

$$F_1={\left[\begin{array}{cccccccccc}0& 1& 1& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 1& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]}_{10\times 10}{F}_2={\left[\begin{array}{cccccccc}0& 1& 1& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]}_{8\times 8}$$

In order to realize the fusion of two ontologies, mainly divided into three cases to experiment, respectively is when there is no same concept in both, only one same concept in both, and more than two same concepts.

Case 1: When there is no same concept in the two ontologies to be merged, that is, s = 0, then it is necessary to find a concept C₀ as their top-level concept in the field E of the dam-break emergency plan.

At this time, according to the Add algorithm (Algorithm 1):

$$F_{new}=\left[\begin{array}{ccc}0& e_1& e_2\\ 0& F_1& 0\\ 0& 0& F_2\end{array}\right], e_1={\left(1,0,\dots ,0\right)}_{1\times m}, e_2={\left(1,0,\dots ,0\right)}_{1\times n},$$

(9)

The merged ontology is shown in Figure 5. The two ontologies are subclasses of the new ontology, and their respective knowledge and concepts are perfectly retained. Because the two do not have the same concept, there is no incompatibility. The integration of this ontology is the simplest form, and the newly generated ontology semantics are more complete.

Algorithm 1: When s = 0, the fusion algorithm is called the Add algorithm, and the specific steps are as follows:

$\mathrm{Step} 1: C_{new}=C_1\cup C_2\cup \left\{c_{30}\right\}=\left\{c_{3i}\left|c_{3i}\in C_1\cup C_2,i=1,2,\dots ,m+n,and c_{30}\in E\right.\right\}$ is a new conceptual set, where c30 is the subconcept of all concepts in C1 and C2 on domain E; $\mathrm{Step} 2: \mathrm{Construct} \mathrm{a} \mathrm{new} \mathrm{concept} \mathrm{vector} \mathrm{as} g_{new}={\left(c_{30},c_{31},\dots ,c_{3,m+n}\right)}^T$ from the new concept set; Step 3: Obtain the structure matrices F1 and F2 of the two ontology to be fused by matrix operation; Step 4: From the operation can be derived $F_{new}=\left[\begin{array}{ccc}0& e_1& e_2\\ 0& F_1& 0\\ 0& 0& F_2\end{array}\right]$$, e_1={\left(1,0,\dots ,0\right)}_{1\times m}$$, e_2={\left(1,0,\dots ,0\right)}_{1\times n}$; $\mathrm{Step} 5: \mathrm{From} F_{new}{g}_{new}$ $\mathrm{and} F_{new}^T{g}_{new}$, all concepts of c3i, i = 0, 1, 2, …, m + n. Step 6: Based on this, a new ontology after fusion can be constructed.

Case 2: When there is only one same concept in two ontologies to be merged, that is, s = 1, assume C₂₁ = C₁₁.

At this time, according to the Merge algorithm (Algorithm 2):

$$F_{new}={\left[\begin{array}{ccccccccccccccccc}0& 1& 1& 1& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]}_{17\times 17}$$

The fused ontology structure is shown in Figure 6. In the new ontology, the root concepts of the two ontologies are merged into one concept, and other conceptual relations are also inherited. The resulting new ontology knowledge expression is more complete, which is consistent with the structure of the source ontology.

Algorithm 2: When s > 0, the fusion algorithm is called the Merge algorithm, and the specific steps are as follows:

Step 1: Based on the concept set of one of the ontologies, all the concepts of C1 and C2 are combined into a new concept set, denoted as Cnew, and only one is taken for the same concept. Step 2: Construct a new concept vector as $g_{new}={\left(c_{30},c_{31},\dots ,c_{3,m+n}\right)}^T$ from the new concept set; Step 3: Obtain the structure matrices F1 and F2 of the two ontologies to be fused by matrix operation; Step 4: Fnew can be derived from the previous algorithm; Step 5: From $F_{new}{g}_{new}$ and $F_{new}^T{g}_{new}$, all concepts of ci, i = 0, 1, 2, …, m + n − s. Step 6: Based on this, a new ontology after fusion can be constructed.

Case 3: When there are two or more ontologies to be merged, here s = 3, assume C₂₁ = C₁₁, C₁₃ = C₂₃, C₂₅ = C₁₂.

At this time, according to the Merge algorithm (Algorithm 2):

$$F_{new}={\left[\begin{array}{ccccccccccccccc}0& 1& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]}_{15\times 15}$$

The merged ontology is shown in Figure 7, and in the new ontology, the root concepts of the two ontologies are first merged into one concept, the number of concepts is one less, and the rest continues to maintain the original state. Then, because C₁₃ = C₂₃, and they have a common upper concept, the two can be combined into a concept C₁₃ pruned C₂₃, and the conceptual relationship contained under C₁₃ is preserved and inherited. Because C₂₅ = C₁₂, comparing the layer depth of the two, it can be seen that C₂₅ is greater than the layer depth of C₁₂, so the upper concept C₂₂ of C₂₅ is selected as the upper concept after the combination of the two. Cut off C₁₂, merge with C₂₅ into a concept, and the conceptual relationship contained under C₁₂ is inherited. The knowledge relationship presented by the newly generated ontology is “C₁₂IsAC₂₂IsAC₁₁”. According to the transitivity of IsA, “C₁₂IsAC₁₁” in the new ontology can be obtained, while the relationship in the original O₁ experiment is “C₁₂IsAC₁₁”. This shows that the knowledge expressed by the fused ontology conforms to the structure in the original body, and the conceptual relationship is inherited.

In the scenarios of s = 0, s = 1, and s = 3, when s = 0, the direct sum operation can be used to fuse two independent ontologies, resulting in a more complex and complete knowledge structure. Therefore, only the symmetry entropy S_sym for s = 1 and s = 3 is calculated here to analyze the degree of symmetry and the complexity of the knowledge structure after fusion, and the results are shown in

Table 1. Symmetry Entropy Calculation Table.

Case	Source Ontology Ssym(F1)	Source Ontology Ssym(F2)	Fused Ontology Ssym(Fnew)
S = 1	1.301	1.255	1.45
S = 3	1.301	1.255	1.35

:

From Table 1, it can be observed that when two ontologies share only one common concept (s = 1), the symmetry entropy of the merged ontology (1.45) is significantly higher than the entropy values of the source ontologies (F₁ is 1.301, F₂ is 1.255). This is due to the introduction of new parent nodes during the merging process to connect independent ontology structures, leading to an expansion of the matrix dimensions and the addition of new asymmetric inheritance paths (such as unidirectional hierarchical relationships), thereby amplifying the structural asymmetry. When the number of shared concepts increases to three (s = 3), the symmetry entropy of the merged ontology (1.35) is still higher than that of the source ontologies, but the increase is notably reduced. This change benefits from the reuse of common concepts, which reduces the generation of redundant nodes, for example, by merging shared parent classes or iteratively optimizing the depth of hierarchies, partially restoring symmetry. However, even with s = 3, the entropy of the merged ontology is still higher than that of the source ontologies, indicating that dynamic adjustments inevitably introduce a certain degree of structural asymmetry, stemming from the expansion needs of knowledge structures and real-time constraints in emergency scenarios. Overall, an increase in the number of common concepts (an increase in s) can suppress the increase in structural asymmetry after fusion, but it cannot be completely eliminated. This indicates that the matrix fusion algorithm needs further optimization of the merging strategy through symmetry entropy constraints to balance semantic completeness and dynamic adjustment capabilities. For instance, it could prioritize the reuse of concepts with greater depth or introduce a weighting mechanism to ensure both timeliness and logical consistency in emergency decision-making.

3. Case Studies of Dam-Break Emergency Scenarios

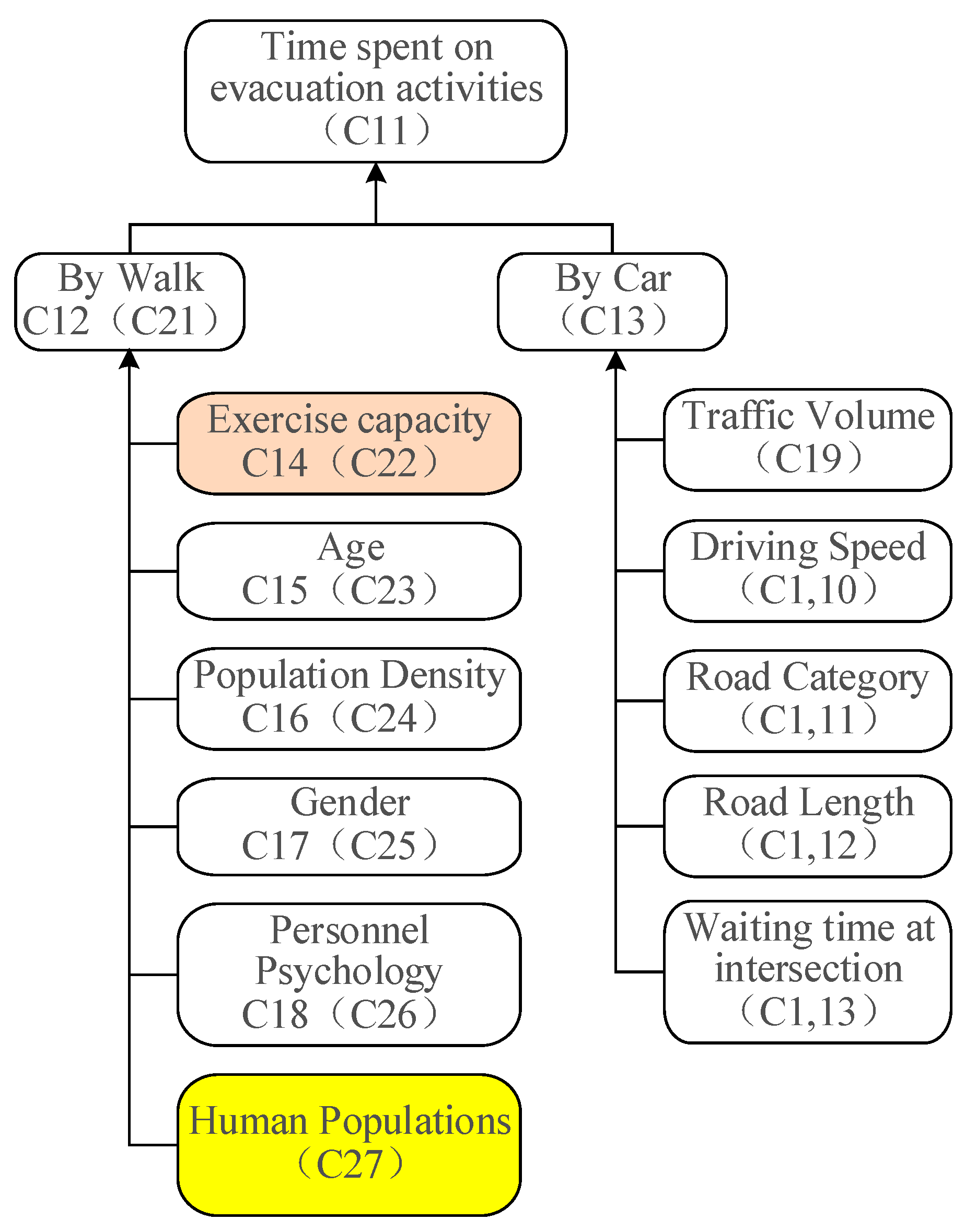
3.1. Scenario Setting

To validate the symmetry-embedded matrix fusion algorithm proposed in Section 2.4, a dynamic dam-break scenario was simulated, focusing on the spatiotemporal asymmetry of flood propagation and the dimensional imbalance caused by uncertain evacuation parameters.

The scenario settings are as follows: the water level in the upstream of the reservoir continues to rise, and a large amount of water flows impacts the dam and overflows the dam until the dam breaks. Figure 8 below shows the scenario after the dam of a certain reservoir breaks. After the dam breaks, the flood invades the spillway and coastal buildings behind the dam. The power plants and water conservancy facilities at all levels in the downstream, and some villages along the downstream river basin are subject to different degrees of personnel injury and loss. Initial post-disaster assessments reveal uncertainties in evacuation efficiency due to heterogeneous crowd mobility (

Table 2. Scenario description table of an earth-rock dam break.

Grading Index	Situation Description
Road damage	Road traffic is in good condition
Area and scope of influence	Some areas such as XX City, YY County, ZZ County, etc
Infrastructure damage	Municipal highways, transmission (water) lines, oil and gas pipelines and enterprises
Number of casualties	7 persons
Direct economic loss	37 million yuan
Affected population	350,000 people living behind the dam and downstream
Natural and Cultural Landscapes	Provincial and Municipal Natural and Cultural Landscapes
Animal and plant habitats	National Secondary and Tertiary Protection of Animals and Plants and Their Living Environment
River movement pattern	Serious damage to small rivers
Urban	Town
Expected recovery period	90 days
Evacuation efficiency	There are significant differences in the walking evacuation capabilities of different groups of people, and the actual evacuation time has an average deviation of 20% compared with the preset model. For example, the evacuation speed of the elderly and children is 30% slower than that of the preset model, while the evacuation speed of young and middle-aged people is basically consistent with the model prediction.

), creating a structural asymmetry between the predefined emergency plan and real-time requirements.

3.2. Analysis

According to the above simulation scenario description table, the hazard situation is analyzed and judged, the risk degree is predicted, and the maximum hazard consequence is selected. According to the intelligent matching of the ontology knowledge of the emergency plan in the system, the system should start the three-level response instruction, and the decision-makers should carry out an orderly emergency response according to the system prediction results.

With the development of the event, some uncertain factors will force the current emergency plan not to fit the changes of the dynamic environment well, and cannot play the role of guiding the emergency, and its effect is greatly reduced. It is assumed that in the above-mentioned dam-break emergencies, the uncertainty factor that causes the deviation of the emergency plan is the evacuation time, while the remaining items are not found to change. Therefore, in order to be able to cope with the uncertainty of the evacuation time, the corresponding adjustment of the dam-break emergency plan is made. Some concepts are extracted from the OWL format of the ontology model of the dam-break emergency plan. Here, only the class containing the evacuation time and its relationship are extracted, and the Is A relationship is retained to form the initial case. The ontology structure is recorded as the initial ontology O, and its structure is shown in Figure 9.

In the spatial dimension, the symmetry assumption of the initial ontology (Figure 9) faces real-world challenges: Its model of uniform evacuation routes shows a significant deviation from the hierarchical asymmetry existing in the real scene. This deviation stems from the non-uniform distribution characteristics of the crowd composition in terms of elements such as age and mobility. In terms of the temporal dimension, the dynamic propagation characteristics of flood disasters pose a dual requirement on the decision-making system: It is necessary to maintain the stability of the decision-making logic under the constraint of temporal symmetry and also to maintain temporal dependence through the ontology evolution mechanism, so as to integrate new parameters in the dynamically changing timeline. Through analysis and data feedback, it is known that there is a large difference between the walking evacuation ability of the affected people and the preset model, and the uncertainty of the group composition has a significant impact on evacuation efficiency. At this time, the ontology to be fused is recorded as the ontology to be fused O, and its structure is shown in Figure 10.

When transforming the dam break emergency scenario into matrix F, first extract key concepts from the scenario and determine the relationships between these concepts. Based on the concept set C and relationship set R, construct matrix F. The rows and columns of matrix F respectively correspond to the elements in the concept set, forming an n×n matrix. According to the definition of ontology structure matrix, the initial ontology and the ontology structure matrix to be fused under natural traversal are F_c11 and F_c21:

$$F_{c11}={\left[\begin{array}{ccccccccccccc}0& 1& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& 1& 1& 1& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 1& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]}_{13\times 13}{F}_{c21}={\left[\begin{array}{ccccccc}0& 1& 1& 1& 1& 1& 1\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right]}_{7\times 7}$$

According to the ontology evolution operation rules, the number of the same concepts in the initial ontology structure and the ontology to be fused is more than two. Therefore, according to the Merge algorithm (Algorithm 2), the fused ontology structure matrix is F_new, as shown below:

$$F_{new}={\left[\begin{array}{cccccccccccccc}0& 1& 0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& 1& 1& 1& 1& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 1& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]}_{14\times 14}$$

By using Formula (8) to calculate the symmetry entropy before and after fusion, we can obtain S_sym(F_c11) = 1.546, S_sym(F_c21) = 0.799, S_sym(F_new) = 1.498. The initial ontology O₁ exhibits a higher symmetry entropy, indicating that its structure contains a greater degree of asymmetry to some extent. This arises because O₁ prioritizes theoretical completeness during design, while dynamic factors and uncertainties in practical applications have not been fully incorporated. For instance, O₁ might assume uniform evacuation paths and fixed command structures, assumptions that may prove incomplete in real-world scenarios. In contrast, the ontology O₂ to be fused demonstrates lower symmetry entropy, reflecting better structural symmetry achieved by accounting for practical dynamics such as real-time crowd mobility and resource allocation. The fused ontology O_new shows intermediate symmetry entropy, slightly lower than O₁ but higher than O₂. This suggests that the fusion process partially optimizes symmetry while not yet attaining the superior symmetry level of O₂.

The fused ontology structure O_new is obtained by the Merge fusion algorithm, and its structure is shown in Figure 11, in which the new concept is represented by yellow; the orange represents that the concept of knowledge has not changed, but the attribute value of its class has changed.

4. Discussion

4.1. Symmetry-Embedded Matrix Fusion for Ontology Evolution

The matrix fusion algorithm proposed in this study inherently incorporates principles of structural and operational symmetry to achieve dynamic ontology evolution in dam-break emergency plans. By transforming ontologies into matrices, the fusion process utilizes symmetric operations such as matrix direct sums and Hadamard products, which align with mathematical definitions of symmetry in linear algebra. Specifically:

(1)

Direct sum symmetry: This operation preserves the block-diagonal structure of source ontology matrices, maintaining their intrinsic hierarchical symmetry. Mathematically, this mirrors the invariant subspaces in group theory, where the direct sum operation satisfies closure and associativity, ensuring structural coherence during fusion. For instance, when s = 0, the fused matrix F_new = F₁ ⊕ F₂ retains the independence of F₁ and F₂, analogous to the decomposition of a symmetry group into irreducible representations.

(2)

Hadamard product symmetry: The element-wise multiplication F_new = F₁ ⊗ F₂ enforces coordinated interactions between overlapping concepts, ensuring semantic alignment at the finest granularity. This operation exemplifies pointwise symmetry, akin to tensor contractions in symmetric manifolds.

The algorithm also addresses hierarchical symmetry by iteratively merging parent-child relationships (IsA hierarchies) when s > 0. For instance, in Case 3 (s = 3), shared concepts like C₂₁ = C₁₁ are merged while preserving their vertical inheritance paths. This prevents structural asymmetry and achieves dynamic equilibrium—a balance between ontology stability (via conserved hierarchies) and adaptability (via horizontal concept integration). Such symmetry-driven fusion aligns with the geometric constraints of high-dimensional manifolds, where transformations must preserve invariant subspaces to maintain system coherence.

The matrix fusion algorithm proposed in this study achieves the dynamic evolution of the ontology in the emergency scenario of dam break-through operations such as direct sum operation and Hadamard product. This algorithm not only preserves the hierarchical relationships between concepts but also optimizes semantic alignment through matrix operations. Compared with existing ontology fusion methods, such as Chimaera, PROMPT, and FCA-Merge, the algorithm in this study has significant advantages in terms of dynamic adjustment and maintenance of semantic consistency. For example, the Chimaera method mainly focuses on the mapping and alignment between ontologies, but its adaptability is relatively weak when dealing with complex dynamic environments. In contrast, through matrix fusion, the algorithm in this study can quickly adjust the ontology structure in a dynamic environment while maintaining semantic consistency and logical coherence. In addition, when dealing with large-scale ontology fusion, the PROMPT and FCA-Merge methods often face problems of computational efficiency. However, the matrix fusion algorithm in this study improves computational efficiency by optimizing matrix operations, making it more suitable for emergency scenarios with high real-time requirements.

4.2. Case-Driven Validation of Symmetry Constraints

The dam-break evacuation scenario (Section 3.2) demonstrates the algorithm’s ability to reconcile real-world asymmetries through ontology fusion. The initial ontology, characterized by a symmetry entropy value of S_sym(F_c11) = 1.546, relied on uniform evacuation routes. This simplification conflicted with the hierarchical asymmetry observed in heterogeneous crowd mobility patterns, as shown in Figure 8. By integrating a dynamic ontology S_sym(F_c21) = 0.799 that incorporated granular adjustments for practical factors such as mobility variations, the fused structure S_sym(F_new) = 1.498 achieved a partial resolution of this mismatch. The elevated entropy of the initial ontology reflects its oversimplified assumptions, while the lower entropy of the dynamic ontology highlights its alignment with real-world complexities through adaptive parameterization. The intermediate entropy of the fused ontology underscores a balanced integration of static theoretical frameworks and dynamic real-time data, illustrating the algorithm’s capacity to harmonize conflicting requirements without imposing rigid symmetry. This case underscores the role of symmetry entropy as a diagnostic tool, quantifying structural trade-offs between idealized models and operational adaptability in emergency scenarios.

Compared with other structural evaluation methods, such as consistency indicators and coverage, symmetry entropy provides a brand-new perspective for evaluating the symmetry of the ontology structure. Traditional methods mainly focus on the consistency and coverage between ontologies, while symmetry entropy quantifies the symmetry of the ontology structure through mathematical methods, providing a more precise evaluation tool for ontology evolution. This evaluation method based on symmetry entropy can not only help us better understand the evolution process of the ontology structure but also provide a more scientific decision-making basis for emergency planning.

5. Conclusions

This study advances the application of symmetry principles in ontology-driven emergency management through the following contributions:

(1)

Symmetry-Optimized Ontology Fusion: The algorithm dynamically integrates disaster ontologies through symmetric matrix operations (⊕, ⊙), preserving hierarchical-logical symmetry while resolving spatiotemporal asymmetries in disaster propagation and resource allocation. By framing uncertainty as high-dimensional symmetry optimization, it enables real-time emergency plan adaptation with structural-semantic consistency, effectively mitigating nonlinear risks in dam-break scenarios through dynamic equilibrium.

(2)

Symmetry-Entropy as a Critical Metric: The proposed S_sym metric quantifies structural asymmetry introduced during ontology fusion. Experimental results confirm that dynamic adjustments increase entropy, but shared concepts (s > 0) mitigate this growth, offering a pathway to balance adaptability and stability.

This work provides a mathematical foundation for the in-depth application of symmetry theory in dynamic emergency management. Future studies may explore advanced symmetry operations, such as Lie group transformations, to further optimize the dynamic adaptability of ontology evolution and extend the applications to multiple disaster scenarios, such as earthquakes and industrial accidents, to validate its universality.