Solving Fractional Stochastic Differential Equations via a Bilinear Time-Series Framework
Abstract
1. Introduction
2. Preliminaries
2.1. Foundations of Stochastic Differential Equations
2.2. The Background of the Fractional Differential Equations Tool
2.3. Foundations and Preliminaries of Bilinear Time-Series Models
3. Discretization: Key Results and Problem Formulation
Numerical Applications of a Class of Fractional Stochastic Differential Equations
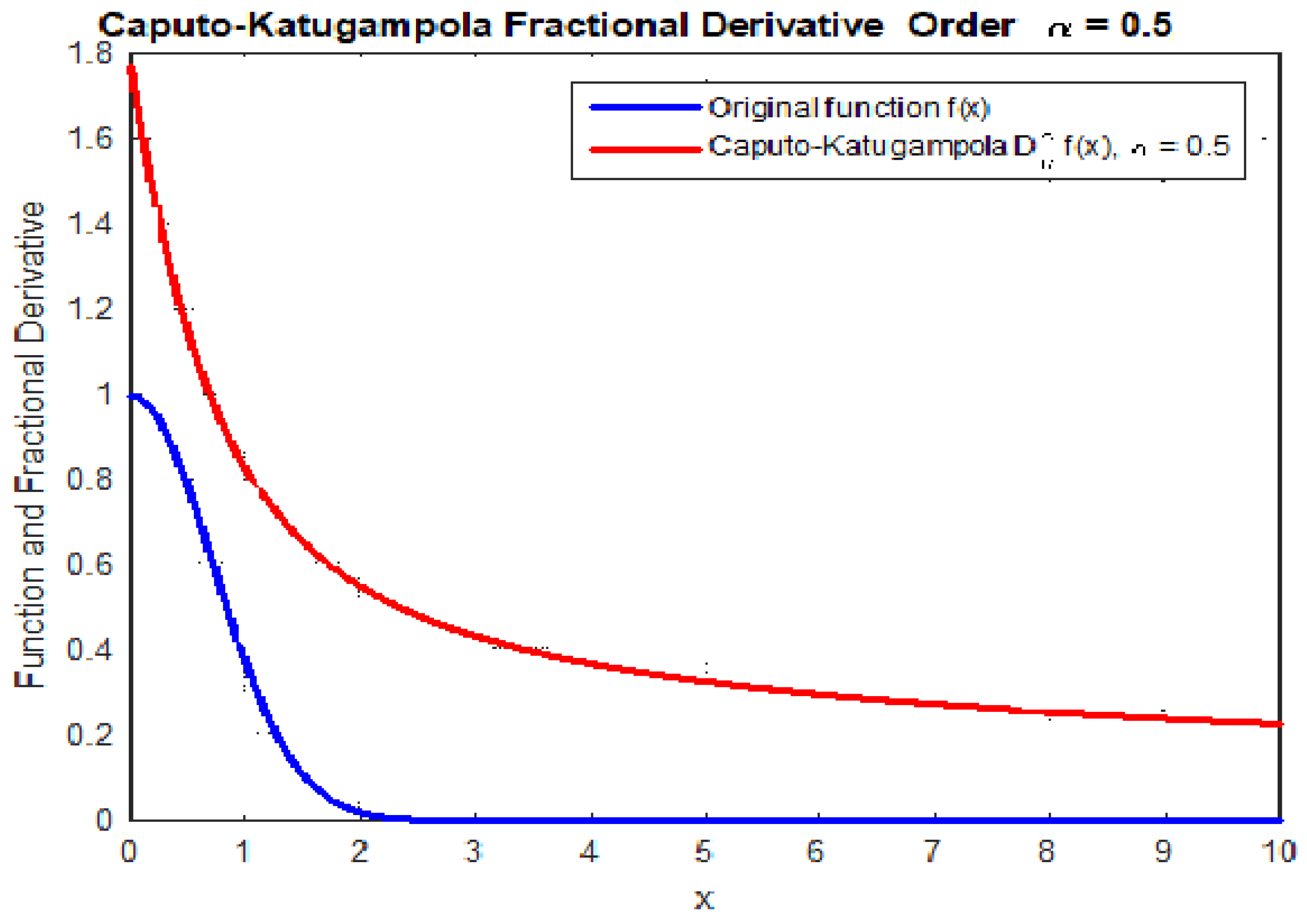
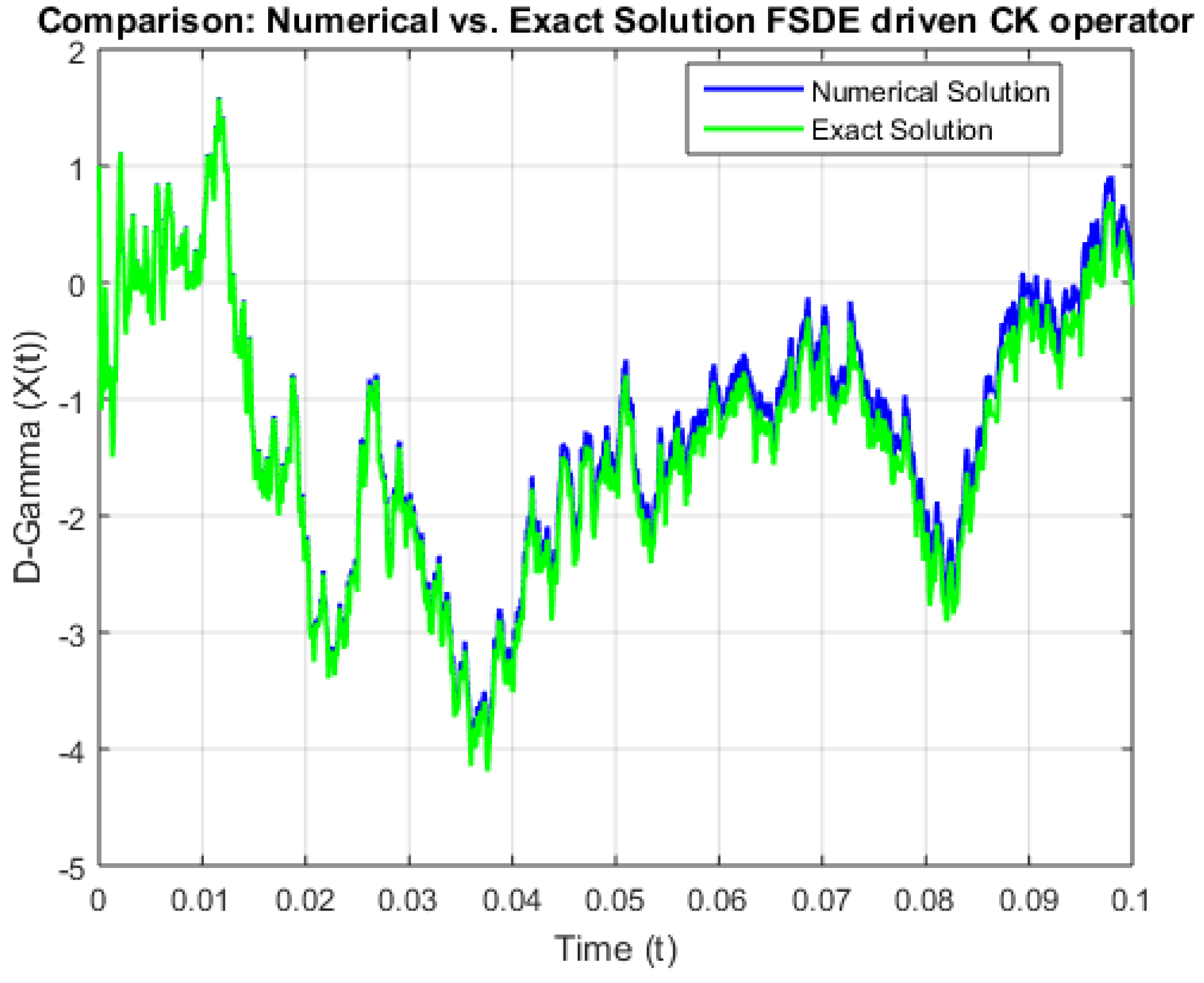
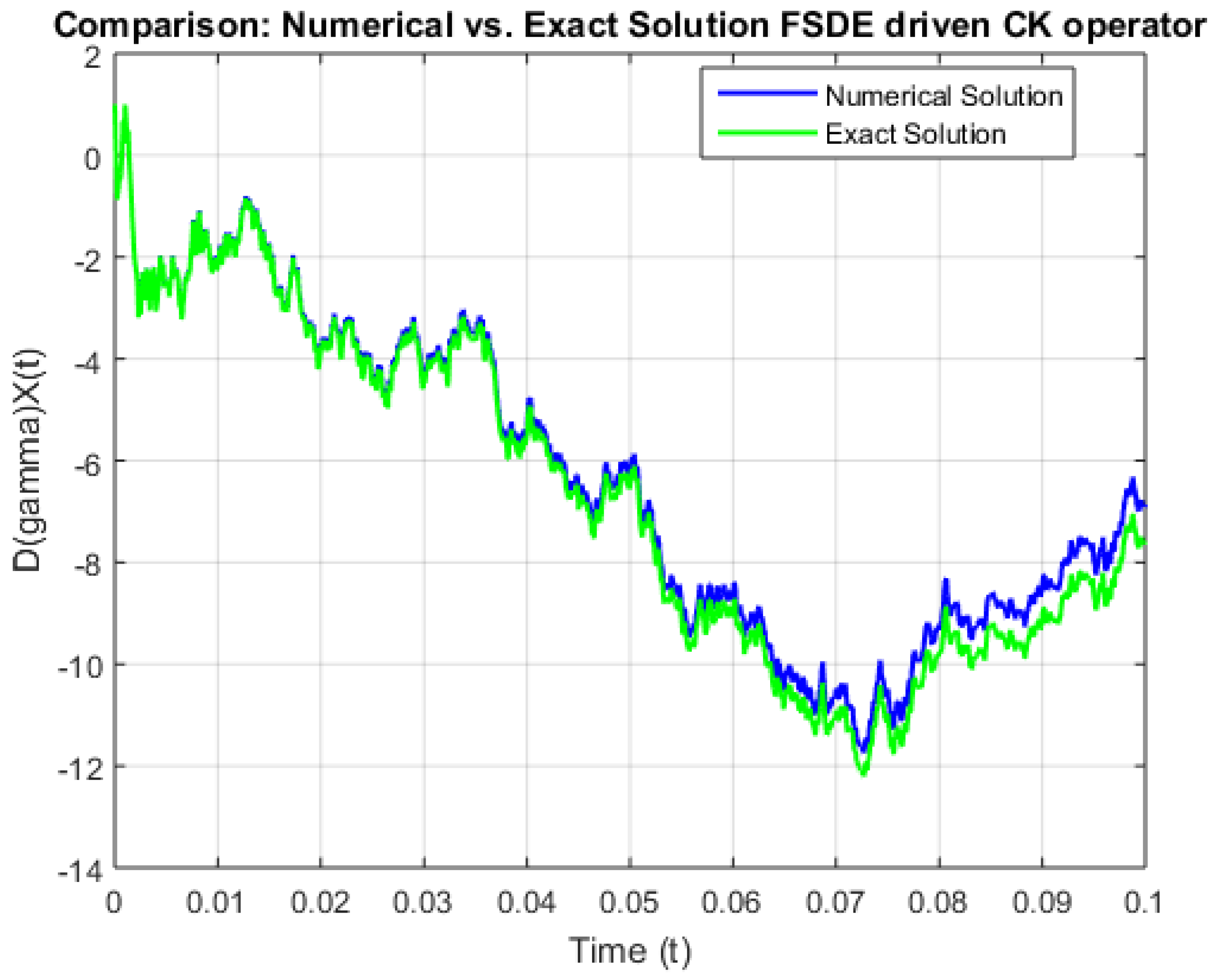
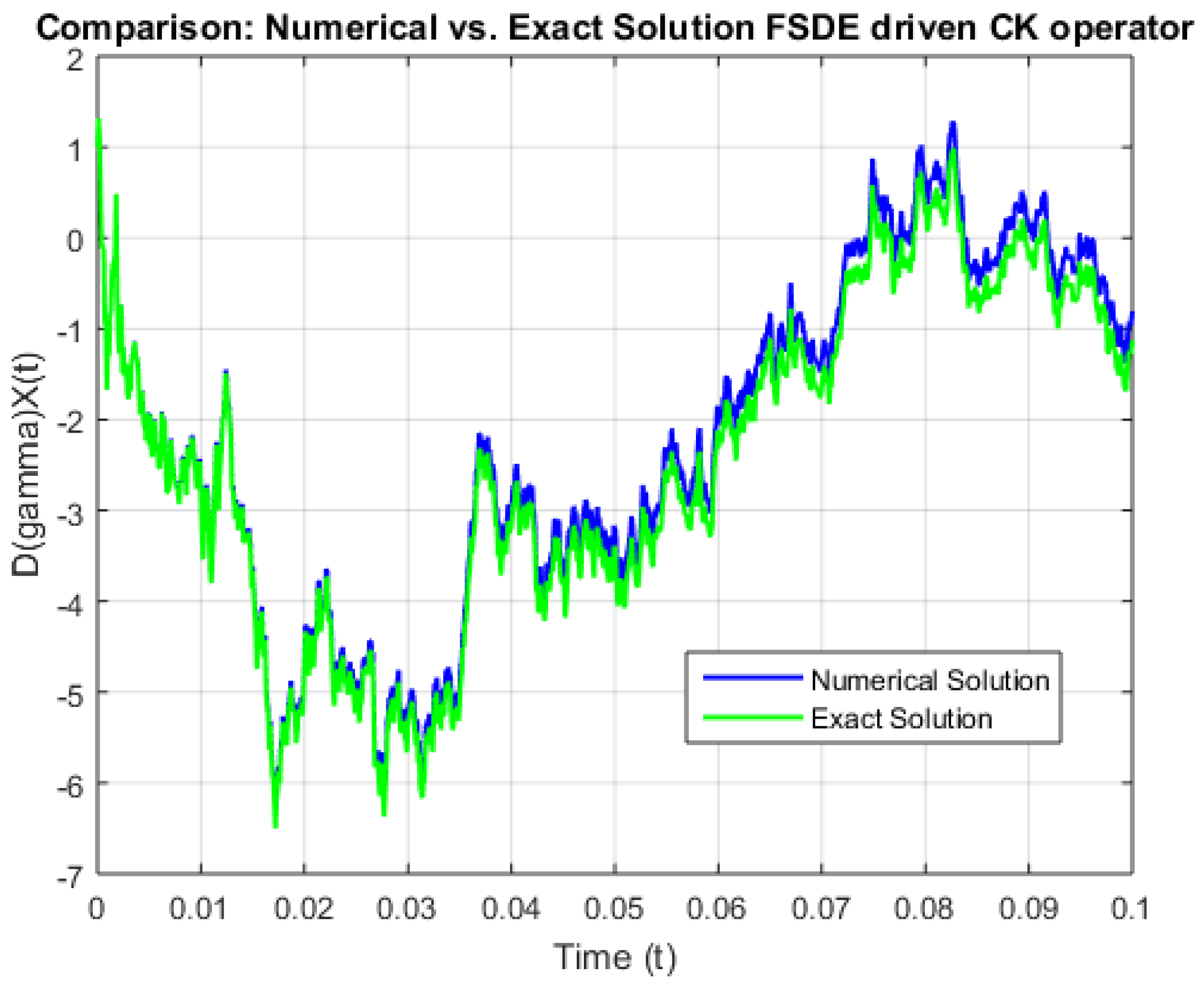
4. Numerical Illustrations and Simulation
Some Graphs Representing Convergence
5. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- Rothman, P. (Ed.) Nonlinear Time Series Analysis of Economic and Financial Data; Springer: Berlin/Heidelberg, Germany, 2012; Volume 1, pp. 1–300. [Google Scholar]
- Rao, T.S.; Gabr, M.M. An Introduction to Bispectral Analysis and Bilinear Time Series Models; Springer: Berlin/Heidelberg, Germany, 2012; Volume 24, pp. 1–224. [Google Scholar]
- Almarashi, A.M.; Daniyal, M.; Jamal, F. Modelling the GDP of KSA using linear and non-linear NNAR and hybrid stochastic time series models. PLoS ONE 2024, 19, e0297180. [Google Scholar] [CrossRef] [PubMed]
- Evans, L.C. An Introduction to Stochastic Differential Equations; American Mathematical Society: Providence, RI, USA, 2012; Volume 82. [Google Scholar]
- Bibi, A.; Merahi, F. GMM Estimation of Continuous-Time Bilinear Processes. Stat. Optim. Inf. Comput. 2021, 9, 990–1009. [Google Scholar] [CrossRef]
- Sivalingam, S.M.; Govindaraj, V. A Novel Numerical Approach for Time-Varying Impulsive Fractional Differential Equations Using Theory of Functional Connections and Neural Network. Expert Syst. Appl. 2024, 238, 121750. [Google Scholar]
- Sivalingam, S.M.; Kumar, P.; Govindaraj, V. A Novel Method to Approximate Fractional Differential Equations Based on the Theory of Functional Connections. Numer. Algorithms 2024, 95, 527–549. [Google Scholar]
- Crauel, H.; Gundlach, M. (Eds.) Stochastic Dynamics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Oksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Carriero, A.; Clark, T.E.; Marcellino, M.; Mertens, E. Addressing COVID-19 Outliers in BVARs with Stochastic Volatility. Rev. Econ. Stat. 2024, 106, 1403–1417. [Google Scholar] [CrossRef]
- Ma, W.; Jin, M.; Liu, Y.; Xu, X. Empirical Analysis of Fractional Differential Equations Model for Relationship Between Enterprise Management and Financial Performance. Chaos Solitons Fractals 2019, 125, 17–23. [Google Scholar] [CrossRef]
- Yavuz, M.; Ozdemir, N.; Okur, Y.Y. Generalized Differential Transform Method for Fractional Partial Differential Equation from Finance. In Proceedings of the International Conference on Fractional Differentiation and its Applications, Novi Sad, Serbia, 18–20 July 2016; Volume 785. [Google Scholar]
- Zhang, Z.; Karniadakis, G.E. Numerical Methods for Stochastic Partial Differential Equations with White Noise; Springer: Berlin, Germany, 2017; Volume 196. [Google Scholar]
- Ma, L.; Li, C. On Hadamard Fractional Calculus. Fractals 2017, 25, 1750033. [Google Scholar] [CrossRef]
- Alzaareer, H.; Al-Zoubi, H.; Al-Mashaleh, W. Classification of Surfaces of Finite Chen II-Type. WSEAS Trans. Math. 2025, 24, 1–7. [Google Scholar] [CrossRef]
- Badrakhan, S.; Shaban, E.A.; Oqilat, O.; Taha, J.; Doudeen, H. Efforts Towards Achieving Sustainable Development Goals in Light of National Strategy Jordan’s Vision. J. Educ. Soc. Res. 2024, 16, 1234–1245. [Google Scholar]
- Anakira, N.; Almalki, A.; Mohammed, M.J.; Hamad, S.; Oqilat, O.; Amourah, A. Analytical Approaches for Computing Exact Solutions to System of Volterra Integro-Differential Equations. WSEAS Trans. Math. 2024, 23, 400–407. [Google Scholar] [CrossRef]
- Kumar, S.; Shaw, P.K.; Abdel-Aty, A.H.; Mahmoud, E.E. A Numerical Study on Fractional Differential Equation with Population Growth Model. Numer. Methods Partial. Differ. Equ. 2024, 40, e22684. [Google Scholar] [CrossRef]
- Laiche, N.; Gasmi, L.; Halim, Z. Exploring Novel Approaches for Estimating Fractional Stochastic Processes through Practical Applications. J. Appl. Math. Inform. 2024, 42, 223–235. [Google Scholar]
- Almeida, R.; Malinowska, A.B.; Odzijewicz, T. Fractional differential equations with dependence on the Caputo–Katugampola derivative. J. Comput. Nonlinear Dyn. 2016, 11, 061017. [Google Scholar] [CrossRef]
- Su, C.-M.; Sun, J.-P.; Zhao, Y.-H. Existence and Uniqueness of Solutions for BVP of Nonlinear Fractional Differential Equation. Int. J. Differ. Equ. 2017, 2017, 4683581. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Nagy, A.M.; Al-Ajami, T.M. Numerical Solutions of Fractional Optimal Control with Caputo–Katugampola Derivative. Adv. Differ. Equ. 2021, 2021, 425. [Google Scholar] [CrossRef]
- Taroni, M.; Barani, S.; Zaccagnino, D.; Petrillo, G.; Harris, P.A. A Physics-Informed Stochastic Model for Long-Term Correlation of Earthquakes. Preprints 2024. [Google Scholar] [CrossRef]
- Liu, W.; Liu, L. Properties of Hadamard Fractional Integral and Its Application. Fractal Fract. 2022, 6, 670. [Google Scholar] [CrossRef]
- Liu, J.; Wei, W.; Wang, J.; Xu, W. Limit Behavior of the Solution of Caputo–Hadamard Fractional Stochastic Differential Equations. Appl. Math. Lett. 2023, 140, 108586. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, Y.; Wang, H.; Liu, Q. Graph Neural Stochastic Diffusion for Estimating Uncertainty in Node Classification. In Proceedings of the Forty-First International Conference on Machine Learning (ICML), Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2023. [Google Scholar]
- Laiche, N.; Gasmi, L.; Elmezouar, Z.C.; Ozer, O. The Generalized Solution of Fractional Differential Equations Sample with Brownian Motion. Int. J. Nonlinear Anal. Appl. 2024, 15, 361–371. [Google Scholar]
- Zhou, Y.; Shangerganesh, L.; Manimaran, J.; Debbouche, A. A Class of Time-Fractional Reaction-Diffusion Equation with Nonlocal Boundary Condition. Math. Methods Appl. Sci. 2018, 41, 2987–2999. [Google Scholar] [CrossRef]
- Raubitzek, S.; Mallinger, K.; Neubauer, T. Combining Fractional Derivatives and Machine Learning: A Review. Entropy 2022, 25, 35. [Google Scholar] [CrossRef] [PubMed]
- Fukushima, K.; Kamata, S. Stochastic Quantization and Diffusion Models. J. Phys. Soc. Jpn. 2025, 94, 031010. [Google Scholar] [CrossRef]
- Poongadan, S.; Lineesh, M.C. Non-Linear Time Series Prediction Using Improved CEEMDAN, SVD and LSTM. Neural Process. Lett. 2024, 56, 164. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Stochastic Problems in Physics and Astronomy. Rev. Mod. Phys. 1943, 15, 1. [Google Scholar] [CrossRef]
- Bibi, A. The L2–Structure of Subordinated Solution of Continuous-Time Bilinear Time Series. In Time Series Analysis—New Insights; IntechOpen: London, UK, 2022; pp. 1–20. [Google Scholar]
- McKean, H.P. Stochastic Integrals; American Mathematical Society: Providence, RI, USA, 2024; Volume 353. [Google Scholar]
- Bibi, A.; Merahi, F. Estimating Continuous-Time Bilinear Process with Moments Method. Nonlinear Stud. 2023, 30, 1–15. [Google Scholar]
- Cox, S.; Hutzenthaler, M.; Jentzen, A. Local Lipschitz Continuity in the Initial Value and Strong Completeness for Nonlinear Stochastic Differential Equations. Amer. Math. Soc. 2024, 296, 1481. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S.; Alabdala, A.T.; Redhwan, S.S.; Bazighifan, O.; Ali, A.H.; Iambor, L.F. Symmetrical Solutions for Non-Local Fractional Integro-Differential Equations via Caputo–Katugampola Derivatives. Symmetry 2023, 15, 662. [Google Scholar] [CrossRef]
- Ben Makhlouf, A.; Nagy, A.M. Finite-Time Stability of Linear Caputo-Katugampola Fractional-Order Time Delay Systems. Asian J. Control 2020, 22, 297–306. [Google Scholar] [CrossRef]
- Singh, J.; Gupta, A.; Baleanu, D. Fractional Dynamics and Analysis of Coupled Schrödinger-KdV Equation with Caputo-Katugampola Type Memory. J. Comput. Nonlinear Dyn. 2023, 18, 091001. [Google Scholar] [CrossRef]
- Kristensen, D. On Stationarity and Ergodicity of the Bilinear Model with Applications to GARCH Models. J. Time Series Anal. 2009, 30, 125–144. [Google Scholar] [CrossRef]
- Ray, S.S. Fractional Calculus with Applications for Nuclear Reactor Dynamics; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Rao, M.B.; Rao, T.S.; Walker, A.M. On the Existence of Some Bilinear Time Series Models. J. Time Series Anal. 1983, 4, 95–110. [Google Scholar] [CrossRef]
- Bibi, A.; Oyet, A.J. Estimation of Some Bilinear Time Series Models with Time Varying Coefficients. Stoch. Anal. Appl. 2004, 22, 355–376. [Google Scholar] [CrossRef]
- Bibi, A.; Ghezal, A. QMLE of Periodic Time-Varying Bilinear–GARCH Models. Commun. Stat. Theory Methods 2019, 48, 3291–3310. [Google Scholar] [CrossRef]
- Zeng, S.; Baleanu, D.; Bai, Y.; Wu, G. Fractional Differential Equations of Caputo-Katugampola Type and Numerical Solutions. Appl. Math. Comput. 2017, 315, 549–554. [Google Scholar] [CrossRef]
- Gohar, M.; Li, C.; Li, Z. Finite Difference Methods for Caputo–Hadamard Fractional Differential Equations. Mediterr. J. Math. 2020, 17, 194. [Google Scholar] [CrossRef]
- Herrmann, R. Fractional Calculus within the Optical Model Used in Nuclear and Particle Physics. J. Phys. G Nucl. Part. Phys. 2023, 50, 065102. [Google Scholar]
- Katugampola, U.N. Existence and Uniqueness Results for a Class of Generalized Fractional Differential Equations. arXiv 2014, arXiv:1411.5229. [Google Scholar]
- Fallahgoul, H.A.; Veredas, D.; Fabozzi, F.J. Quantile-Based Inference for Tempered Stable Distributions. Comput. Econ. 2019, 53, 51–83. [Google Scholar] [CrossRef]
- Föllmer, H.; Schied, A. Stochastic Finance: An Introduction in Discrete Time; Walter de Gruyter: Berlin, Germany, 2011. [Google Scholar]
- Hammad, M.A. Conformable Fractional Martingales and Some Convergence Theorems. Mathematics 2022, 10, 6. [Google Scholar] [CrossRef]
- Ghezal, A.; Cavicchioli, M.; Zemmouri, I. On the Existence of Stationary Threshold Bilinear Processes. Stat. Pap. 2024, 1, 1–29. [Google Scholar] [CrossRef]

| n | ES | NS | |
| 100 | 0.0345 | 0.0396 | |
| 150 | 0.0345 | 0.0351 | |
| 300 | 0.0345 | 0.0339 | |
| , and | |||
|---|---|---|---|
| n | ES | NS | |
| 1000 | 0.0345 | 0.0349 | |
| 1000 | 0.0345 | 0.0377 | |
| 1000 | 0.0345 | 0.0565 | |
| t | Exact Solution | Approximative Solution | Error |
|---|---|---|---|
| 0.10 | 0.047577 | 0.045811 | 0.001765 |
| 0.20 | 0.261076 | 0.257940 | 0.003136 |
| 0.30 | 0.567776 | 0.563707 | 0.004825 |
| 0.40 | 0.944813 | 0.939989 | 0.004825 |
| 0.50 | 1.380888 | 1.375411 | 0.005477 |
| 0.60 | 1.868874 | 1.862815 | 0.006059 |
| 0.70 | 2.403741 | 2.397151 | 0.006591 |
| 0.90 | 2.981690 | 2.974608 | 0.007082 |
| 1.00 | 3.265960 | 3.134587 | 0.131373 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkhateeb, R.; Abu Hammad, M.; AL-Shutnawi, B.; Laiche, N.; Chikr El Mezouar, Z. Solving Fractional Stochastic Differential Equations via a Bilinear Time-Series Framework. Symmetry 2025, 17, 764. https://doi.org/10.3390/sym17050764
Alkhateeb R, Abu Hammad M, AL-Shutnawi B, Laiche N, Chikr El Mezouar Z. Solving Fractional Stochastic Differential Equations via a Bilinear Time-Series Framework. Symmetry. 2025; 17(5):764. https://doi.org/10.3390/sym17050764
Chicago/Turabian StyleAlkhateeb, Rami, Ma’mon Abu Hammad, Basma AL-Shutnawi, Nabil Laiche, and Zouaoui Chikr El Mezouar. 2025. "Solving Fractional Stochastic Differential Equations via a Bilinear Time-Series Framework" Symmetry 17, no. 5: 764. https://doi.org/10.3390/sym17050764
APA StyleAlkhateeb, R., Abu Hammad, M., AL-Shutnawi, B., Laiche, N., & Chikr El Mezouar, Z. (2025). Solving Fractional Stochastic Differential Equations via a Bilinear Time-Series Framework. Symmetry, 17(5), 764. https://doi.org/10.3390/sym17050764






