Defending Graph Neural Networks Against Backdoor Attacks via Symmetry-Aware Graph Self-Distillation
Abstract
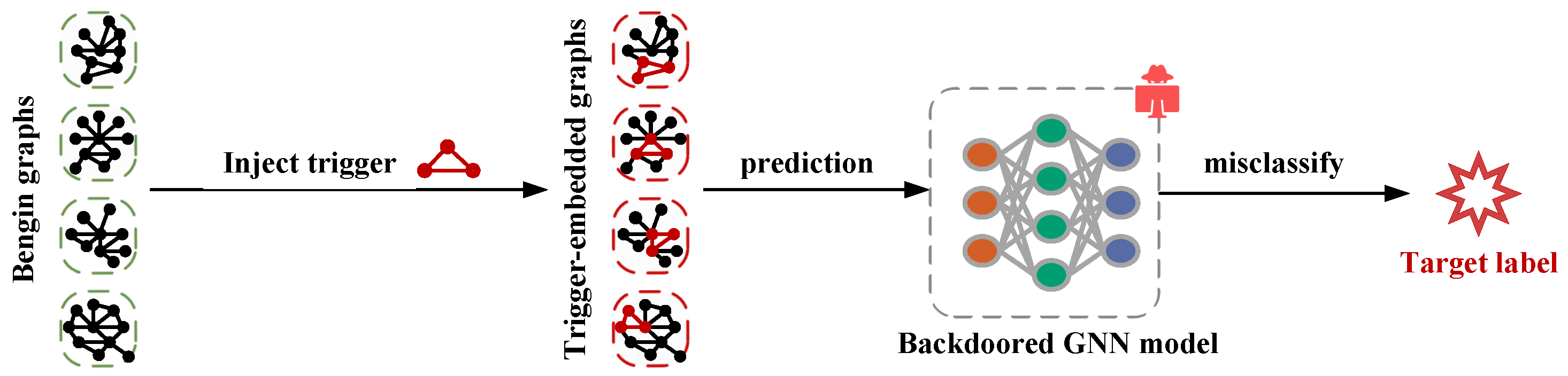
1. Introduction
- The Graph Self-Distillation Backdoor Defense (GSD-BD) sanitizes ingrained backdoor perturbations by leveraging symmetry knowledge from shallow layers to supervise deeper layers. This ensures the preservation of intrinsic structural characteristics of graph data, enhancing both model stability and adversarial robustness.
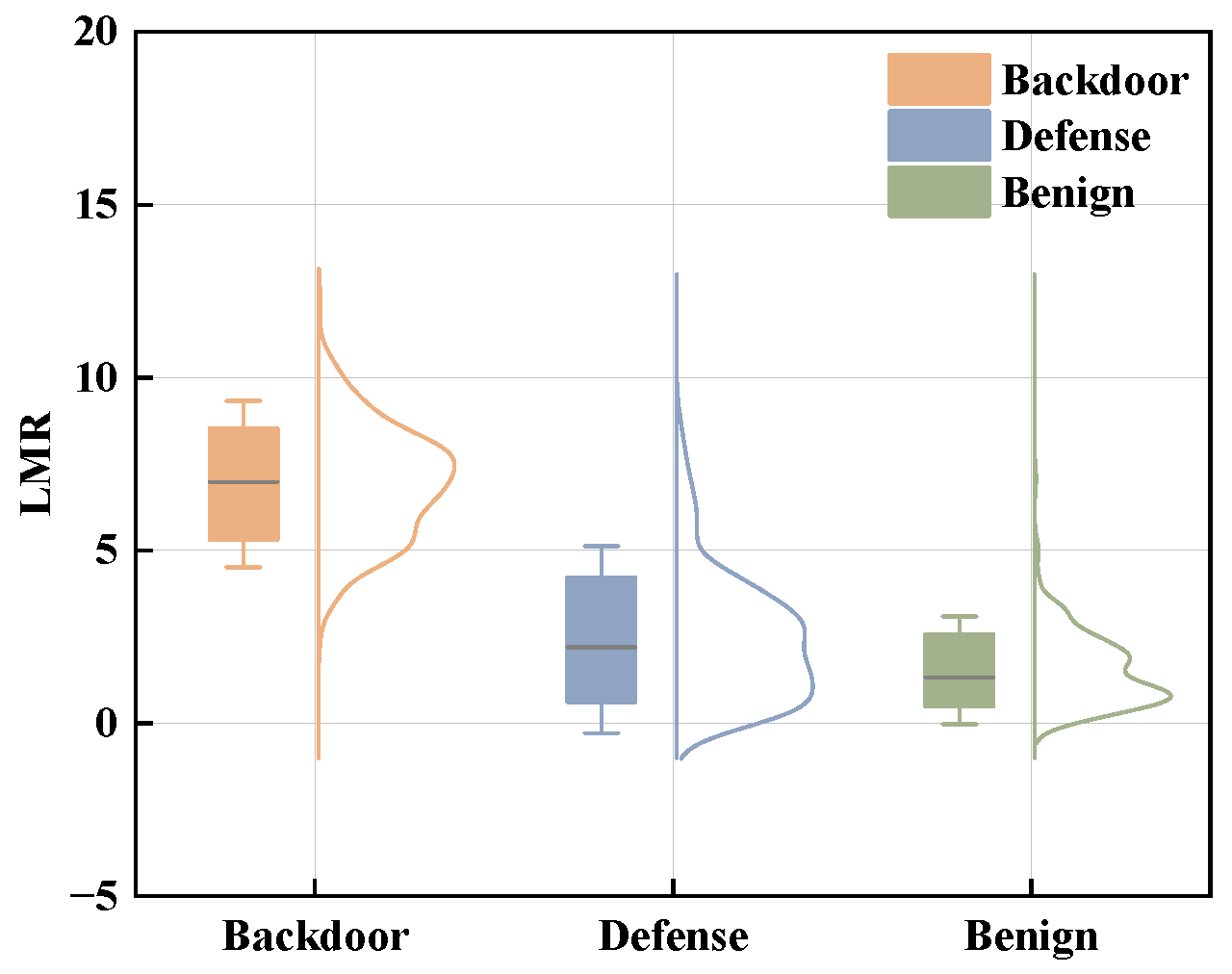
- Experimental findings reveal that backdoor attack effects can be characterized by boosting and suppression effects. Based on this, the Logit Margin Rate (LMR) is introduced as a quantitative metric to measure logit output asymmetry across GNN layers, facilitating accurate and efficient backdoor sanitization.
- The efficacy of GSD-BD is validated through comparisons with state-of-the-art graph backdoor defense methods. Experimental results demonstrate that GSD-BD achieves a superior Average Defense Rate (ADR) against various backdoor attack algorithms while preserving the sanitized model’s original benign behavior.
2. Related Works
2.1. Graph Knowledge Distillation
2.2. Backdoor Attack
2.3. Backdoor Defense
3. Preliminaries
3.1. Notations
3.2. GNN-Based Graph Classification
3.3. Backdoor Attack
3.4. The Threat Model
3.4.1. Attacker’s Capabilities and Goals
3.4.2. Defender’s Capabilities and Goals
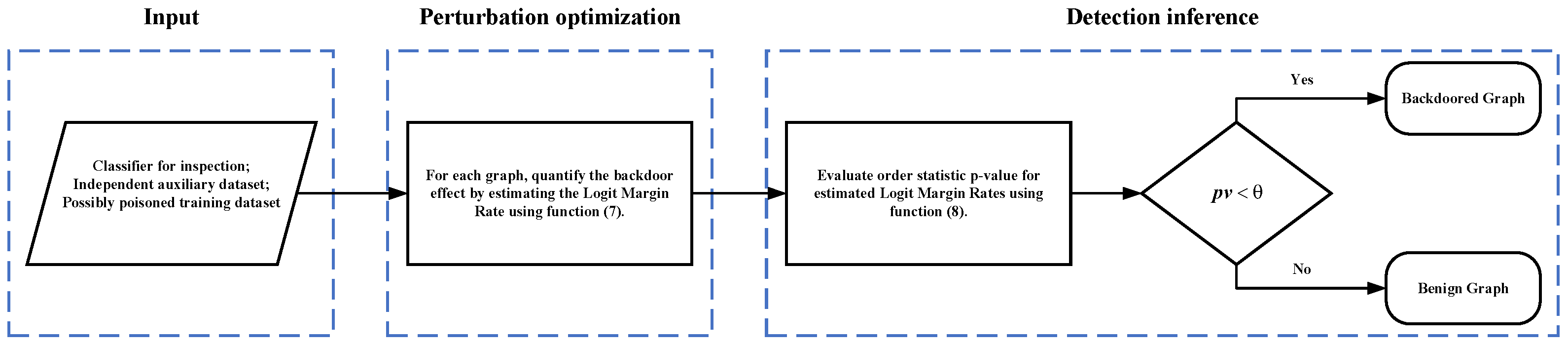
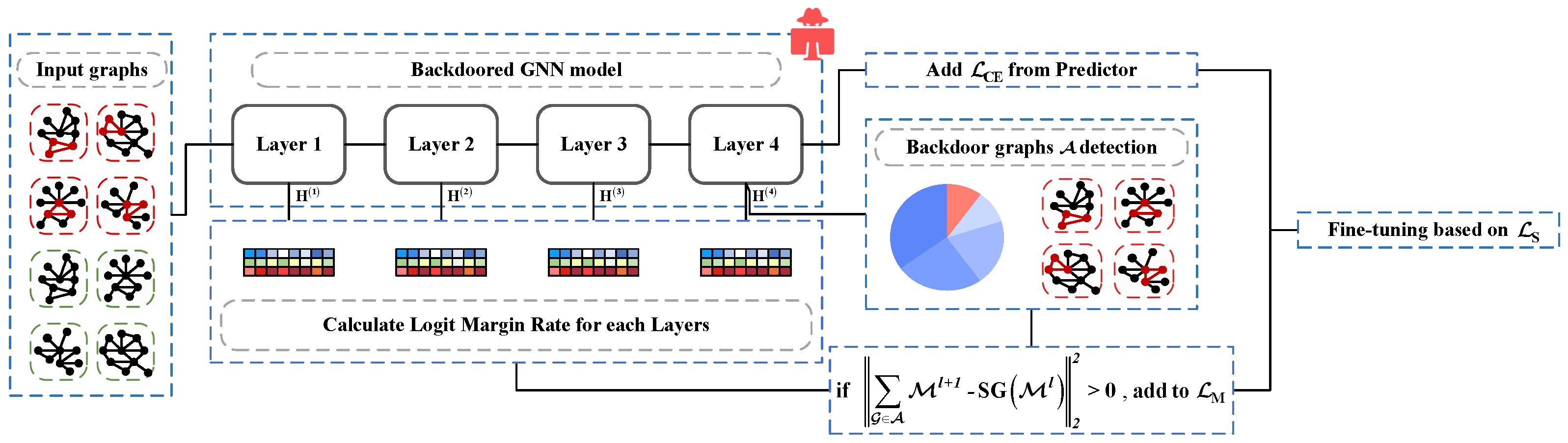
4. Methodology
4.1. Design Intuition
4.2. Quantification for Backdoor Effect
4.3. Symmetry-Aware Graph Knowledge Self-Distillation for Backdoor Sanitization
4.4. Time and Space Complexity
5. Evaluation
5.1. Experiment Setup
5.1.1. Datasets
- PROTEINS [39]: This dataset consists of proteins in which each node is represented as an amino acid, and two nodes are connected by an edge if they are less than 6 angstroms apart. The labels are determined as enzymatic or non-enzymatic.
- BITCOIN [40]: This dataset is used for graph-based detection of fraudulent Bitcoin transactions, where each node is represented as a transaction and its associated transactions, and each edge between two transactions indicates the Bitcoin currency flow between them. The labels are determined based on illicit or licit transactions.
- AIDS [41]: This dataset contains molecular compounds from the AIDS antiviral screen database. The labels are determined based on active or inactive of molecular compounds.
- NCI1 [42]: This dataset comprises chemical compounds used to inhibit cancer cells, where each graph corresponds to a chemical compound, each vertex represents an atom of the molecule, and the edges between vertices represent bonds between atoms.
5.1.2. Dataset Split and Construction
5.1.3. Baseline Defense Methods
5.1.4. Model Settings and Parameter Settings
5.1.5. Evaluation Metrics
5.2. Defense Performance
5.3. Robustness Against Different Poisoning Rates
5.4. Importance of Symmetry Knowledge Filter
5.5. Exploration for Logit Margin Rate
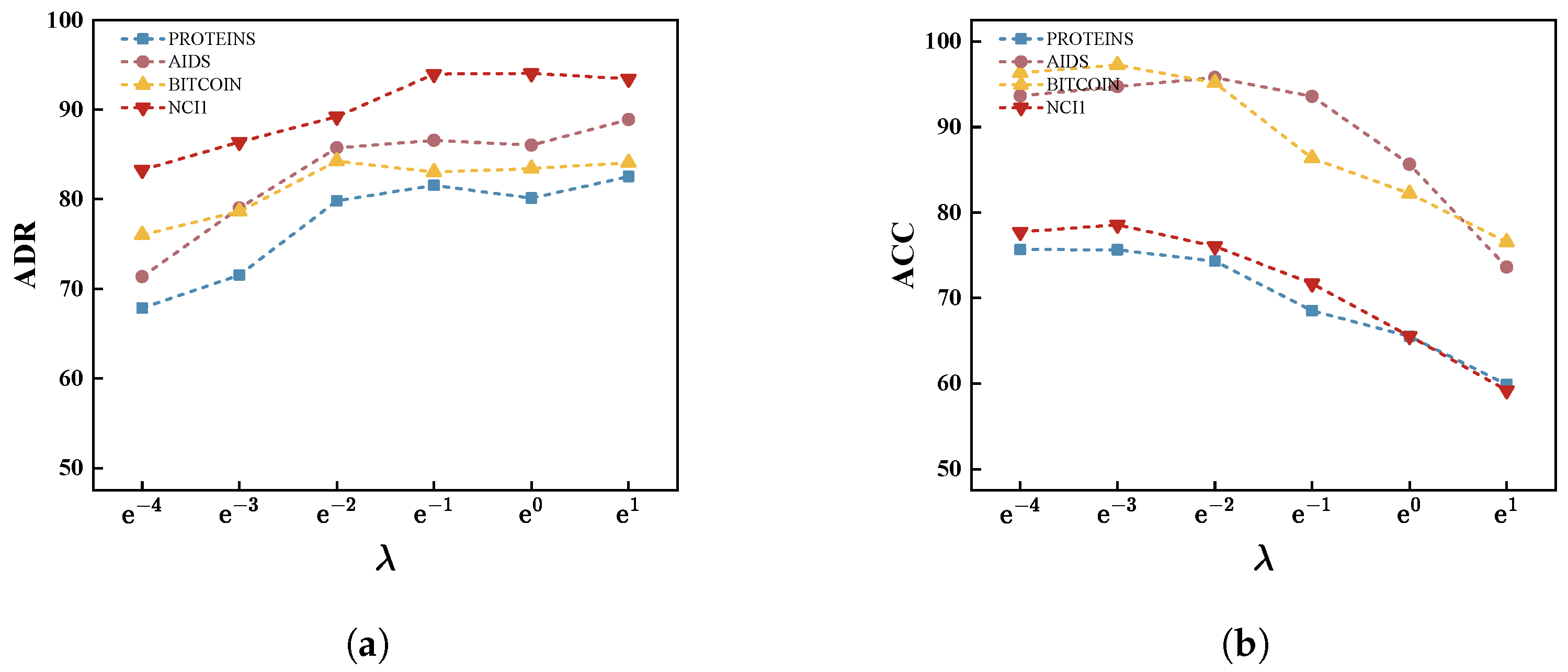
5.6. Exploration for Sanitization Loss
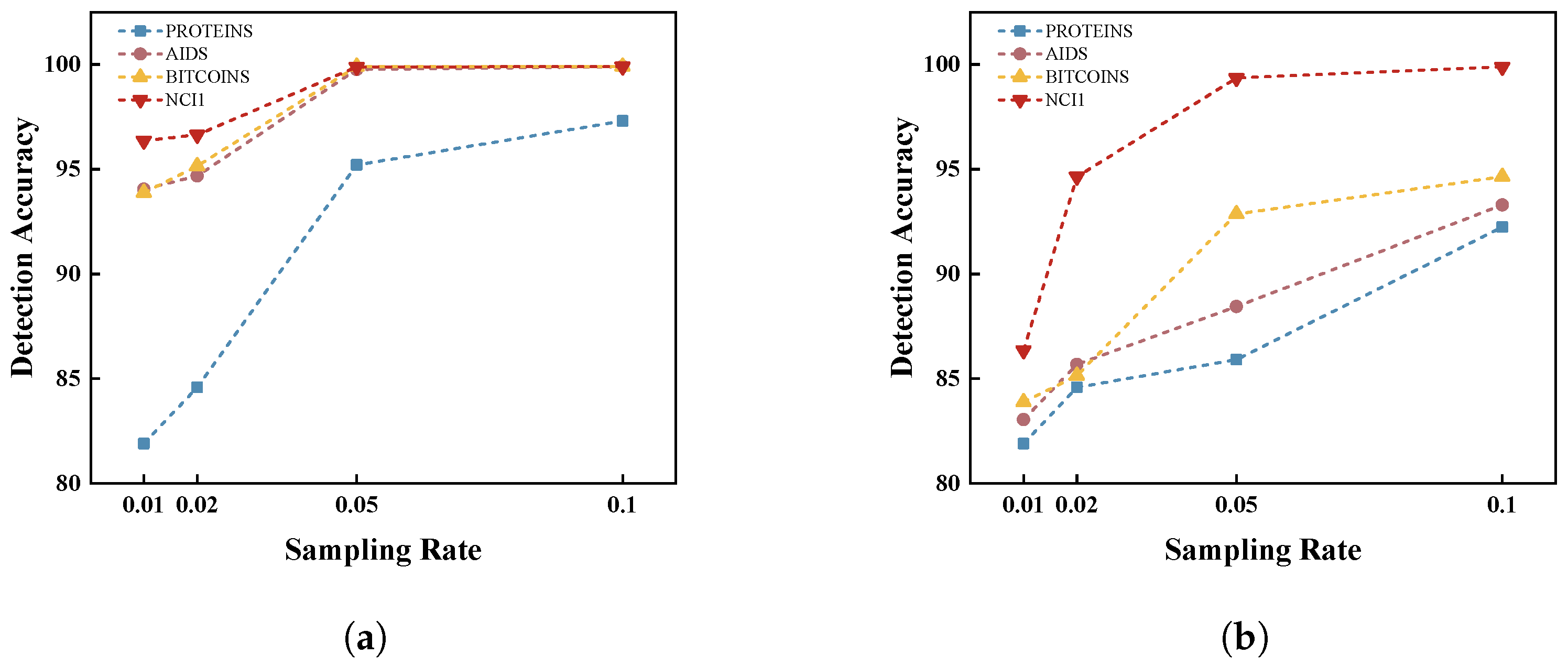
5.7. Exploration for Sampling Rate
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks? In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Qiu, J.; Tang, J.; Ma, H.; Dong, Y.; Wang, K.; Tang, J. Deepinf: Social influence prediction with deep learning. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2110–2119. [Google Scholar]
- Wang, J.; Zhang, S.; Xiao, Y.; Song, R. A Review on Graph Neural Network Methods in Financial Applications. J. Data Sci. 2022, 20, 111–134. [Google Scholar] [CrossRef]
- Kearnes, S.; McCloskey, K.; Berndl, M.; Pande, V.; Riley, P. Molecular graph convolutions: Moving beyond fingerprints. J. Comput.-Aided Mol. Des. 2016, 30, 595–608. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Liu, B.; Gomes, J.; Zitnik, M.; Liang, P.; Pande, V.; Leskovec, J. Strategies For Pre-training Graph Neural Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Hu, Z.; Dong, Y.; Wang, K.; Chang, K.W.; Sun, Y. Gpt-gnn: Generative pre-training of graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 1857–1867. [Google Scholar]
- Nassar, L.; Karray, F. Overview of the crowdsourcing process. Knowl. Inf. Syst. 2019, 60, 1–24. [Google Scholar] [CrossRef]
- Zhang, Z.; Jia, J.; Wang, B.; Gong, N.Z. Backdoor attacks to graph neural networks. In Proceedings of the 26th ACM Symposium on Access Control Models and Technologies, Virtual, 16–18 June 2021; pp. 15–26. [Google Scholar]
- Xu, J.; Xue, M.; Picek, S. Explainability-based backdoor attacks against graph neural networks. In Proceedings of the 3rd ACM Workshop on Wireless Security and Machine Learning, Miami, FL, USA, 15–17 May 2019; Association for Computing Machinery: New York, NY, USA, 2021; pp. 31–36. [Google Scholar]
- Xi, Z.; Pang, R.; Ji, S.; Wang, T. Graph backdoor. In Proceedings of the 30th USENIX Security Symposium (USENIX Security 21), Virtual, 11–13 August 2021; pp. 1523–1540. [Google Scholar]
- Zheng, H.; Xiong, H.; Chen, J.; Ma, H.; Huang, G. Motif-backdoor: Rethinking the backdoor attack on graph neural networks via motifs. IEEE Trans. Comput. Soc. Syst. 2023, 11, 2479–2493. [Google Scholar] [CrossRef]
- Dai, E.; Lin, M.; Zhang, X.; Wang, S. Unnoticeable backdoor attacks on graph neural networks. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; Association for Computing Machinery: New York, NY, USA, 2023; pp. 2263–2273. [Google Scholar]
- Wang, B.; Yao, Y.; Shan, S.; Li, H.; Viswanath, B.; Zheng, H.; Zhao, B.Y. Neural cleanse: Identifying and mitigating backdoor attacks in neural networks. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2019; pp. 707–723. [Google Scholar]
- Liu, Y.; Lee, W.C.; Tao, G.; Ma, S.; Aafer, Y.; Zhang, X. Abs: Scanning neural networks for back-doors by artificial brain stimulation. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 1265–1282. [Google Scholar]
- Li, Y.; Lyu, X.; Koren, N.; Lyu, L.; Li, B.; Ma, X. Neural Attention Distillation: Erasing Backdoor Triggers from Deep Neural Networks. In Proceedings of the International Conference on Learning Representations, Virtual, 3–7 May 2021. [Google Scholar]
- Xiang, Z.; Miller, D.J.; Kesidis, G. Detection of backdoors in trained classifiers without access to the training set. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 1177–1191. [Google Scholar] [CrossRef]
- Wang, H.; Xiang, Z.; Miller, D.J.; Kesidis, G. Mm-bd: Post-training detection of backdoor attacks with arbitrary backdoor pattern types using a maximum margin statistic. In Proceedings of the 2024 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2024; pp. 1994–2012. [Google Scholar]
- Jiang, B.; Li, Z. Defending against backdoor attack on graph nerual network by explainability. arXiv 2022, arXiv:2209.02902. [Google Scholar]
- Sui, H.; Chen, B.; Zhang, J.; Zhu, C.; Wu, D.; Lu, Q.; Long, G. DMGNN: Detecting and Mitigating Backdoor Attacks in Graph Neural Networks. arXiv 2024, arXiv:2410.14105. [Google Scholar]
- Hinton, G. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Xu, X.; Zhou, F.; Zhang, K.; Liu, S. Ccgl: Contrastive cascade graph learning. IEEE Trans. Knowl. Data Eng. 2022, 35, 4539–4554. [Google Scholar] [CrossRef]
- Feng, K.; Li, C.; Yuan, Y.; Wang, G. Freekd: Free-direction knowledge distillation for graph neural networks. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 357–366. [Google Scholar]
- Yan, B.; Wang, C.; Guo, G.; Lou, Y. Tinygnn: Learning efficient graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 1848–1856. [Google Scholar]
- Chen, Y.; Bian, Y.; Xiao, X.; Rong, Y.; Xu, T.; Huang, J. On self-distilling graph neural network. arXiv 2020, arXiv:2011.02255. [Google Scholar]
- Li, G.; Xiong, C.; Thabet, A.; Ghanem, B. Deepergcn: All you need to train deeper gcns. arXiv 2020, arXiv:2006.07739. [Google Scholar]
- Chen, W.; Wu, B.; Wang, H. Effective backdoor defense by exploiting sensitivity of poisoned samples. Adv. Neural Inf. Process. Syst. 2022, 35, 9727–9737. [Google Scholar]
- Yang, Y.; Qiu, J.; Song, M.; Tao, D.; Wang, X. Distilling knowledge from graph convolutional networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7074–7083. [Google Scholar]
- Joshi, C.K.; Liu, F.; Xun, X.; Lin, J.; Foo, C.S. On representation knowledge distillation for graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 4656–4667. [Google Scholar] [CrossRef]
- Yang, C.; Liu, J.; Shi, C. Extract the knowledge of graph neural networks and go beyond it: An effective knowledge distillation framework. In Proceedings of the Web Conference 2021, Virtual, 19—23 April 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 1227–1237. [Google Scholar]
- Wu, L.; Lin, H.; Gao, Z.; Zhao, G.; Li, S.Z. A Teacher-Free Graph Knowledge Distillation Framework with Dual Self-Distillation. IEEE Trans. Knowl. Data Eng. 2024, 36, 4375–4385. [Google Scholar] [CrossRef]
- Wang, H.; Liu, T.; Sheng, Z.; Li, H. Explanatory subgraph attacks against Graph Neural Networks. Neural Netw. 2024, 172, 106097. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, S.; Park, W.; Mao, Z.; Jin, M.; Jia, R. Adversarial Unlearning of Backdoors via Implicit Hypergradient. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Liu, K.; Dolan-Gavitt, B.; Garg, S. Fine-pruning: Defending against backdooring attacks on deep neural networks. In International Symposium on Research in Attacks, Intrusions, and Defenses; Springer: Cham, Switzerland, 2018; pp. 273–294. [Google Scholar]
- Guo, W.; Wang, L.; Xing, X.; Du, M.; Song, D. Tabor: A highly accurate approach to inspecting and restoring trojan backdoors in ai systems. arXiv 2019, arXiv:1908.01763. [Google Scholar]
- Yang, X.; Li, G.; Tao, X.; Zhang, C.; Li, J. Black-Box Graph Backdoor Defense. In International Conference on Algorithms and Architectures for Parallel Processing; Springer: Cham, Switzerland, 2023; pp. 163–180. [Google Scholar]
- Rossi, R.; Ahmed, N. The network data repository with interactive graph analytics and visualization. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- Borgwardt, K.M.; Ong, C.S.; Schönauer, S.; Vishwanathan, S.; Smola, A.J.; Kriegel, H.P. Protein function prediction via graph kernels. Bioinformatics 2005, 21, i47–i56. [Google Scholar] [CrossRef]
- Weber, M.; Domeniconi, G.; Chen, J.; Weidele, D.K.I.; Bellei, C.; Robinson, T.; Leiserson, C. Anti-Money Laundering in Bitcoin: Experimenting with Graph Convolutional Networks for Financial Forensics. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Shervashidze, N.; Schweitzer, P.; Van Leeuwen, E.J.; Mehlhorn, K.; Borgwardt, K.M. Weisfeiler-lehman graph kernels. J. Mach. Learn. Res. 2011, 12, 2539–2561. [Google Scholar]
- Chen, J.; Zhang, D.; Ming, Z.; Huang, K.; Jiang, W.; Cui, C. GraphAttacker: A general multi-task graph attack framework. IEEE Trans. Netw. Sci. Eng. 2021, 9, 577–595. [Google Scholar] [CrossRef]
- Chen, J.; Lin, X.; Xiong, H.; Wu, Y.; Zheng, H.; Xuan, Q. Smoothing adversarial training for GNN. IEEE Trans. Comput. Soc. Syst. 2020, 8, 618–629. [Google Scholar] [CrossRef]
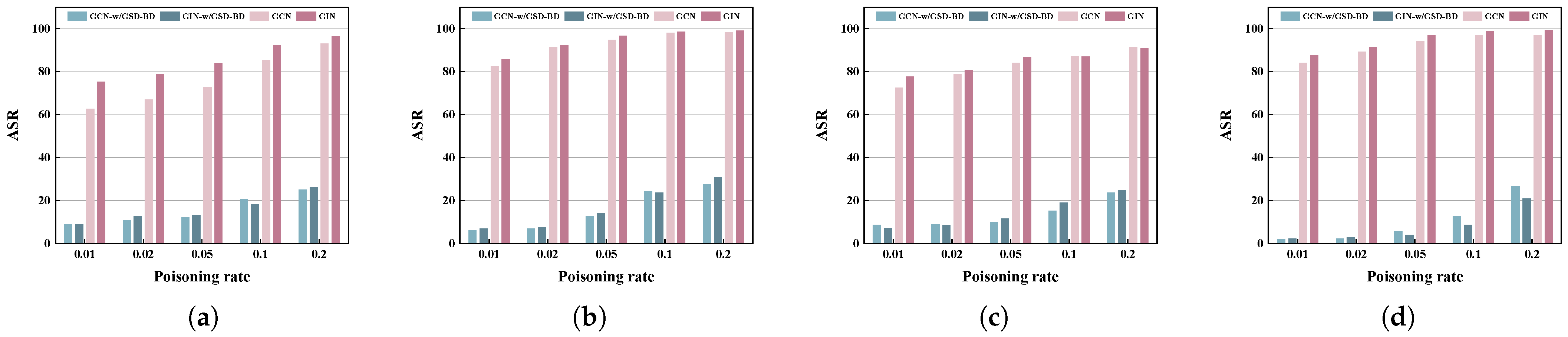

| Notations | Descriptions |
|---|---|
| Entire dataset | |
| Backdoor dataset | |
| N | Graph number of dataset |
| Graph data | |
| Trigger-embedded graph | |
| Node feature representation of a graph | |
| Adjacency matrix of a graph | |
| Identified backdoor graph set | |
| Identified benign graph set | |
| GNN model | |
| Logit output of the input graph | |
| y | Ground-truth label of a graph |
| Target label of a graph | |
| LMR for a given graph sample at layer-l |
| Datasets | # Graphs | # Classes | Avg. # Nodes | Avg. # Edges | # Graphs in Class | # Target Label |
|---|---|---|---|---|---|---|
| PROTEINS | 1113 | 2 | 39.06 | 72.82 | 663[0], 450[1] | 1 |
| BITCOIN | 1174 | 2 | 14.64 | 14.18 | 845[0], 329[1] | 0 |
| AIDS | 2000 | 2 | 15.69 | 16.20 | 400[0], 1600[1] | 1 |
| NCI1 | 4110 | 2 | 29.87 | 32.30 | 2053[0], 2057[1] | 0 |
| Model | Dataset | ACC (%) | ASR (%) | CAD () | ||||
|---|---|---|---|---|---|---|---|---|
| GBA | MIA | GTA | GBA | MIA | GTA | |||
| GCN | PROTEINS | 75.18 | 51.06 | 67.36 | 72.91 | 4.50 | 4.66 | 6.63 |
| AIDS | 97.64 | 69.42 | 73.03 | 94.75 | 4.60 | 5.01 | 4.78 | |
| BITCOIN | 97.91 | 76.53 | 74.94 | 84.11 | 6.87 | 5.43 | 8.10 | |
| NCI1 | 78.75 | 75.33 | 79.72 | 94.34 | 4.60 | 4.54 | 2.96 | |
| GIN | PROTEINS | 76.32 | 60.73 | 59.25 | 83.84 | 4.75 | 3.49 | 5.23 |
| AIDS | 98.19 | 78.94 | 81.33 | 96.67 | 4.25 | 3.87 | 3.39 | |
| BITCOIN | 96.66 | 79.06 | 82.50 | 86.67 | 4.75 | 3.24 | 3.91 | |
| NCI1 | 76.89 | 75.97 | 93.67 | 97.07 | 4.08 | 2.79 | 3.11 | |
| Dataset | Attack | ADR (%) | CAD () | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prune | Prune+LD | Exp-BD | DMGNN | GSD-BD | Prune | Prune+LD | Exp-BD | DMGNN | GSD-BD | ||
| PROTEINS | GBA | 50.58 | 51.84 | 68.56 | 69.26 | 84.84 | 6.23 | 5.97 | 4.54 | 4.25 | 3.54 |
| MIA | 41.16 | 44.76 | 71.69 | 69.63 | 84.08 | 6.31 | 6.78 | 5.17 | 5.08 | 4.37 | |
| GTA | 37.26 | 46.83 | 65.75 | 64.18 | 83.55 | 7.27 | 7.03 | 5.14 | 5.21 | 4.66 | |
| AIDS | GBA | 52.61 | 53.94 | 69.25 | 71.94 | 85.60 | 5.47 | 5.48 | 6.36 | 5.22 | 4.94 |
| MIA | 48.14 | 48.58 | 74.36 | 72.08 | 84.20 | 5.51 | 6.17 | 5.24 | 5.22 | 4.85 | |
| GTA | 36.17 | 43.37 | 63.40 | 71.14 | 86.85 | 5.53 | 6.01 | 6.19 | 4.98 | 4.06 | |
| BITCOIN | GBA | 43.45 | 48.68 | 60.28 | 70.78 | 87.39 | 7.45 | 7.03 | 6.62 | 5.58 | 3.82 |
| MIA | 48.64 | 49.10 | 66.12 | 74.65 | 85.20 | 6.61 | 7.24 | 6.49 | 5.51 | 2.25 | |
| GTA | 39.55 | 45.28 | 59.97 | 72.41 | 88.03 | 7.56 | 7.17 | 6.38 | 5.47 | 4.57 | |
| NCI1 | GBA | 43.39 | 44.28 | 69.17 | 71.16 | 93.72 | 4.76 | 5.58 | 4.71 | 4.26 | 2.35 |
| MIA | 41.24 | 41.35 | 77.53 | 79.22 | 93.56 | 5.71 | 5.58 | 4.71 | 4.74 | 2.09 | |
| GTA | 38.17 | 41.44 | 71.30 | 69.63 | 93.98 | 4.62 | 5.16 | 5.42 | 4.95 | 2.06 | |
| Dataset | Attack | ADR (%) | CAD () | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prune | Prune+LD | Exp-BD | DMGNN | GSD-BD | Prune | Prune+LD | Exp-BD | DMGNN | GSD-BD | ||
| PROTEINS | GBA | 52.33 | 52.81 | 64.93 | 71.21 | 84.80 | 6.19 | 6.63 | 5.66 | 4.47 | 3.62 |
| MIA | 39.50 | 44.05 | 67.79 | 68.14 | 86.95 | 6.28 | 6.16 | 6.08 | 4.14 | 2.94 | |
| GTA | 37.42 | 46.64 | 63.31 | 69.43 | 84.40 | 6.75 | 5.81 | 6.28 | 4.89 | 3.21 | |
| AIDS | GBA | 54.29 | 54.71 | 68.00 | 73.16 | 86.14 | 5.88 | 5.43 | 5.92 | 5.19 | 4.06 |
| MIA | 46.53 | 49.18 | 74.94 | 75.25 | 84.26 | 4.34 | 5.20 | 6.13 | 5.75 | 3.29 | |
| GTA | 41.71 | 45.22 | 64.68 | 71.14 | 85.60 | 4.13 | 4.05 | 6.36 | 4.98 | 3.32 | |
| BITCOIN | GBA | 43.33 | 45.23 | 61.36 | 71.31 | 78.34 | 6.89 | 6.17 | 6.26 | 6.36 | 3.18 |
| MIA | 45.21 | 50.17 | 66.12 | 69.36 | 85.76 | 6.34 | 4.95 | 6.19 | 5.80 | 3.79 | |
| GTA | 41.62 | 42.76 | 57.05 | 66.13 | 86.61 | 6.03 | 5.61 | 5.95 | 6.27 | 3.25 | |
| NCI1 | GBA | 40.13 | 44.87 | 64.20 | 76.16 | 93.51 | 5.41 | 5.11 | 5.00 | 5.06 | 3.22 |
| MIA | 37.71 | 41.52 | 72.44 | 72.21 | 92.21 | 5.39 | 3.69 | 4.50 | 4.64 | 2.07 | |
| GTA | 36.27 | 39.36 | 71.41 | 71.28 | 95.86 | 4.98 | 4.24 | 4.96 | 4.72 | 2.51 | |
| GCN | GIN | |||||
|---|---|---|---|---|---|---|
| Accuracy | GBA | MIA | GTA | GBA | MIA | GTA |
| PROTEINS | 95.16 | 95.36 | 90.05 | 91.21 | 95.94 | 91.06 |
| AIDS | 98.50 | 98.43 | 94.10 | 99.35 | 99.78 | 99.56 |
| BITCOIN | 99.91 | 98.18 | 96.38 | 99.87 | 99.21 | 98.94 |
| NCI1 | 99.99 | 99.84 | 99.62 | 99.99 | 99.84 | 98.83 |
| Precision | GBA | MIA | GTA | GBA | MIA | GTA |
| PROTEINS | 91.36 | 91.72 | 85.91 | 84.45 | 93.85 | 89.38 |
| AIDS | 97.67 | 96.86 | 88.44 | 92.02 | 99.56 | 99.99 |
| BITCOIN | 99.99 | 95.37 | 92.86 | 99.99 | 99.34 | 98.67 |
| NCI1 | 99.99 | 93.40 | 99.35 | 99.99 | 99.69 | 99.99 |
| Recall | GBA | MIA | GTA | GBA | MIA | GTA |
| PROTEINS | 98.89 | 98.92 | 94.72 | 97.64 | 97.94 | 92.49 |
| AIDS | 99.32 | 99.99 | 99.73 | 99.67 | 99.99 | 99.14 |
| BITCOIN | 99.83 | 99.99 | 99.89 | 99.75 | 99.08 | 99.21 |
| NCI1 | 99.99 | 96.16 | 99.89 | 99.99 | 99.99 | 99.67 |
| F1-score | GBA | MIA | GTA | GBA | MIA | GTA |
| PROTEINS | 94.97 | 95.18 | 90.10 | 90.57 | 95.85 | 90.91 |
| AIDS | 98.49 | 98.40 | 93.74 | 99.34 | 99.78 | 99.56 |
| BITCOIN | 99.91 | 97.63 | 96.25 | 99.87 | 99.21 | 98.94 |
| NCI1 | 99.99 | 94.76 | 99.62 | 99.99 | 99.84 | 99.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wan, L.; Yang, X. Defending Graph Neural Networks Against Backdoor Attacks via Symmetry-Aware Graph Self-Distillation. Symmetry 2025, 17, 735. https://doi.org/10.3390/sym17050735
Wang H, Wan L, Yang X. Defending Graph Neural Networks Against Backdoor Attacks via Symmetry-Aware Graph Self-Distillation. Symmetry. 2025; 17(5):735. https://doi.org/10.3390/sym17050735
Chicago/Turabian StyleWang, Hanlin, Liang Wan, and Xiao Yang. 2025. "Defending Graph Neural Networks Against Backdoor Attacks via Symmetry-Aware Graph Self-Distillation" Symmetry 17, no. 5: 735. https://doi.org/10.3390/sym17050735
APA StyleWang, H., Wan, L., & Yang, X. (2025). Defending Graph Neural Networks Against Backdoor Attacks via Symmetry-Aware Graph Self-Distillation. Symmetry, 17(5), 735. https://doi.org/10.3390/sym17050735





