A Study on the Influence of Disturbance Factors’ Coupling Effects on the Dynamic Response of the Symmetrical Structure Press Mechanism

Abstract

The dynamic response of symmetrical press mechanisms is severely affected by revolute clearance, translational clearance, and the elasticity of the components. Therefore, the coupling effects of disturbance factors were studied in this paper, including revolute clearance, translational clearance, and component elastic deformation; the influence of their coupling effects on the dynamic chaos characteristic are also discussed. A dynamic model of a rigid–flexible coupling mechanism with revolute clearance and translational clearance was established. Using MATLAB R2024a to solve the model, chaos identification was researched through phase diagrams, Poincaré maps, and maximum Lyapunov exponents. Under the parameters studied in this paper, the maximum Lyapunov exponents at revolute clearance A (X direction and Y direction) and translational clearance B (X direction and Y direction) were 0.0521, 0.0573, 0.3915, and −0.0287, respectively. The motion state of revolute pair A (X direction and Y direction) and translational pair B (X direction) were more prone to chaotic states; translational pair B (Y direction) was more prone to periodic motion. The influence of various factors on the dynamic response were analyzed. With the increase in driving speed and clearance value, as well as the decrease in friction coefficient, the stability of the mechanism weakened, and the vibration of the mechanism’s dynamic response intensified. This paper provides theoretical support for the establishment of precise dynamic models for multi-link symmetrical structure press mechanisms.

1. Introduction

The clearance between two relative moving members in a symmetrical structure press mechanism is inevitable, and this can cause collisions between two connecting components [1,2,3]. The collision force of the clearance will seriously affect the dynamic of the symmetrical structure press mechanism and reduce its dynamic performance. Revolute and translational pairs are the two most common types of motion pairs, so studying the coupling effect of these two types of motion pairs on mechanism dynamics is highly relevant. When the mechanism operates at a fast speed and is subjected to certain external forces, the components are prone to elastic deformation [4,5,6]. Therefore, when the mechanism is in a rapid motion state, it is necessary to comprehensively consider the coupling effects of disturbance factors, such as translational clearance, revolute clearance, and elastic deformation, and analyze the impact of their coupling effects on the mechanism’s motion state.

In recent years, the effect of revolute clearance on the dynamics of mechanisms has attracted much scholarly attention, and, therefore, research has been conducted on the dynamic performance of mechanisms with revolute pair clearance. Revolute clearance can cause inaccurate motion transmission of the mechanism, resulting in deviation between the output motion and the theoretical value, which affects the dimensional accuracy and surface quality of the machined parts. Revolute clearance can cause collisions and impacts between components, resulting in vibration and noise, which in turn affects the dynamic performance of the mechanism. Chen et al. [7] proposed a computational method for the dynamic modeling and analysis of planar multi-link mechanisms with multiple degrees of freedom and multiple clearances, and they investigated the dynamic characteristics of the planar multi-link mechanism. Li et al. [8] used the finite particle method to analyze the dynamic behavior of Bennett linkage with revolute clearance pairs. The motion of the proposed model agrees well with that of the higher-fidelity model, but the authors did not consider situations when journals and bearings are in line contact and surface contact. Wang et al. [9] established a rigid–flexible coupled multibody dynamic model of a tracked armored vehicle using the transfer matrix method for multibody systems, and they analyzed the influence of trunnion bearing clearance on the vibration characteristics of a tracked armored vehicle. The proposed method avoids the global dynamics equations of the system, keeps a high computational speed, and allows for highly formalized modeling. The proposed method successfully simplifies the modeling process but reduces the accuracy of solving problems involving a large amount of nonlinear friction. Chen et al. [10] proposed a dynamic response error and precision reliability analysis method for mechanisms with revolute clearance pairs. Fu et al. [11] proposed a compound control method for the reliability of robotic arms with clearance pairs. However, these two proposed methods involve a certain degree of subjectivity in selecting the allowable error range. In contrast, Jia et al. [12] established a dynamic response reliability model for a 4-UPS/RPS spatial parallel mechanism with clearance pairs and uncertain parameters using the metamodeling approach, significantly improving the accuracy of reliability calculations. Jiang et al. [13] proposed a precise modeling method for the nonlinear dynamics of a multi-link mechanism under the coupling effects of clearance and elastic deformation, successfully exploring the impact of component flexibility on the system’s dynamic response. However, the proposed method involves a large computational load, and the accuracy of deformation description may decrease under complex deformation conditions. Liang et al. [14] studied the dynamic characteristics of a planar R-2RRP-RRR mechanism with clearance based on the Newton–Euler method, and the validity of the dynamic model was verified through numerical calculations and multibody dynamics simulations. Chen et al. [15] analyzed the dynamic response and nonlinear characteristics of a planar six-bar mechanism, and they investigated the effect of clearance lubrication on the mechanism using the improved Pinkus–Sternlicht model. The proposed method demonstrates high numerical stability and modeling rationality, but extending it to the case of lubrication in translational pairs is more challenging. Guo et al. [6] proposed a new type of revolute clearance contact model considering surface topography. Chen et al. [16] studied the effect of impact load on the dynamics of a mechanism with clearance, and a test prototype was built. Ma et al. [17] used spectral element methodology to research the dynamics of a planar structure with clearance, and they revealed the wave propagation law in the planar structure with a rotating gap joint. Wu et al. [18] proposed a passive chaos suppression methodology. The effectiveness and correctness of the method were verified by a phase diagram, and so on. Lin et al. [19] established a nonlinear dynamics model of a mechanism with revolute clearance, and a reliability model of motion accuracy based on a strength–stress interference method was proposed. Gao et al. [20] studied a failure mechanism and the reliability of the mechanism with lubrication clearance. The applicability of the model was verified by the Monte Carlo method. Wang et al. [21] studied the influence of clearance between kinematic pairs; a degeneration and impact model of mechanical transmission mechanism was proposed. Chen et al. [22] established a dynamic model of a 3-RRRR mechanism with clearance, and simulation verification was carried out with ADMAS. Based on the Achard model, Bai et al. [23] predicted wear characteristics of clearance in the mechanism. Huang et al. [24] combined clearance with time-varying mesh stiffness, and nonlinear dynamics analysis of a gear transmission model with rotation pair clearance was carried out. Huang et al. [25] presented a monitoring method of revolute clearance that integrated dynamic and thermal image features.

A translational pair is generally used as a connection between the end effector of a mechanism and the frame. The translational clearance model is more difficult and complex compared to a revolute clearance pair, and scholars have relatively less research on it compared to revolute clearance pairs. The clearance between translational pairs causes the components to shake and jam during the movement process, affecting the smoothness of the mechanism’s motion. Due to the presence of clearance, a translational pair is prone to relative sliding and collision during motion, accelerating component wear and shortening the service life of the mechanism. Zhuang et al. [26] proposed a modeling and simulation method for a rigid multibody system with frictional translational pairs; the problem of the transitions of the contact situation of normal forces acting on sliders and the transitions of the stick–slip of the sliders in the system was formulated as a horizontal linear complementarity problem. Wang et al. [27] established a contact force model for the slider and guide rail in a three-dimensional translational pair, and they analyzed the dynamic chaotic phenomena and behavior of the three-dimensional crank–slider mechanism. This study fills the research gap regarding the clearance in three-dimensional translational pairs to some extent. Xiao et al. [28] studied the nonlinear dynamics of the crank–slider mechanism considering rod flexibility and translational pair clearance. Based on the finite element method, Zhang et al. [29] established a dynamic model of the crank–slider mechanism considering translational clearance. Combined with the numerical calculation method, Qian et al. [30] proposed a contact detection methodology, which was applied to the crank–slider mechanism with translational clearance. Wu et al. [31] studied a double crank mechanism with translational clearance, and simulation verification was carried out with ANSYS/LS-DYNA. Zheng et al. [32] presented a modeling methodology for a planar mechanism considering translational clearance, and the uncertainty problem from a stationary analysis of the mechanism was solved. Liu et al. [33] proposed a dynamic equation of a mechanism with translational clearance, and the effect of the flexibility of component and clearance lubrication on dynamic performance was analyzed. Flores and Zhuang et al. [34,35] proposed a dynamic modeling method for a rigid system with translational clearance. Liu et al. [36] researched a new tribo-dynamic coupling model of a lubricated translational joint in two-stroke marine engines to research dynamic characteristics.

In order to establish an accurate dynamic model, it is necessary to simultaneously consider the coupling effect of revolute clearance and a translational clearance pair to reveal the impact of their coupling effect on dynamics, which has attracted the attention of some researchers. However, previous studies mainly concentrated on the dynamic response of simple, four-bar, rigid-body mechanisms, and there are relatively few studies on the nonlinear characteristics of a complex flexible mechanism. Components undergo elastic deformation when subjected to force, which may result in deviations between the actual and ideal movements of the mechanism. Meanwhile, the flexible deformation of the components consumes some energy, resulting in a decrease in the energy transfer efficiency of the mechanism. Therefore, it is necessary to study the influence of component elastic deformation on mechanisms. Ting et al. [37] proposed a kinematic model to quantify the impact of joint clearance accumulation on the nominal output link position of a linkage comprising rotational and prismatic joints, and they successfully reduced complexity and computational load. Bai et al. [38] established a planar crank–slider mechanism model considering revolute and translational clearances, and its dynamics response was studied by calculation and experiment methods. Tan et al. [39], taking the crank–slider mechanism and considering mixed clearance as the research object, derived a dynamics equation based on the first type of the Lagrange multiplier method, and the dynamics response of the mechanism under four different situations was compared and analyzed. Dong et al. [40] established the dynamic equation of a flexible toggle link mechanism with the lubrication revolute and translational clearance. Jiang et al. [41] established a dynamics model with mixed clearance, and nonlinear dynamic characteristics were studied. Jiang et al. [42] compared the effects of different gap types on dynamics, and then the chaotic phenomenon, accuracy, and stability of the mechanism were studied. Chen et al. [43] analyzed the effect of mixed clearance on the dynamics of slider motor output, driving torque, contact force, and so on. Xiao et al. [44] presented a dynamic modeling method of a flexible multilink mechanism with mixed clearances. Wu and Tan et al. [45,46] used a phase diagram and bifurcation diagram to describe the nonlinear dynamics of a slider–crank mechanism with mixed clearance. Jia et al. [47] proposed a dynamic modeling method of a parallel mechanism with three-dimensional mixed clearance. Three-dimensional motion models of spherical joint clearance and rotating clearance are derived.

Previous research has mostly focused on the influence of pure revolute clearance or pure translational clearance on the dynamics of mechanisms. Due to the difficulty of coupling translational clearance, revolute clearance, and flexible component models into a multi-link mechanism and the difficulty of solving them using MATLAB, there is relatively little research on the comprehensive coupling effects of translational clearance, revolute clearance, and flexible components, as well as their coupling effects on the dynamic characteristics and chaos of complex multi-link mechanisms. Therefore, this paper has innovative and research significance for the content of the mechanism, considering the coupling effects of translational clearance, revolute clearance, and flexible components, and can more accurately predict the motion characteristics and performance of the mechanism.

The arrangement of this paper is as follows: in Section 2, mathematical motion models for translational and revolute clearances are established; in Section 3, theoretical models of rigid beam elements and flexible two elements are established; in Section 4, a dynamic model of a rigid–flexible coupled symmetrical structure press mechanism that considers both revolute and translational clearances simultaneously is established; and in Section 5, chaos identification and an analysis of the influence of various factors on the dynamics of the symmetrical structure press mechanism are studied. In Section 6, the conclusion is discussed.

2. Establishment of a Clearance Model

In the manufacturing process of mechanical parts, due to the limitations of processing technology and equipment, it is difficult to precisely process the size and shape of kinematic pair elements, resulting in clearance. In order to facilitate the assembly of the kinematic pair and ensure that the parts can be smoothly installed in the designated position, it is also necessary to leave appropriate clearance between the kinematic pair elements. Mechanical mechanisms are affected by various factors during operation, such as temperature changes, stress deformation, etc. The reserved clearance between the kinematic pair can compensate for the size changes caused by these factors, ensuring that the kinematic pair can work normally under different working conditions [48,49]. Therefore, it is necessary to study the clearance between kinematic pairs.

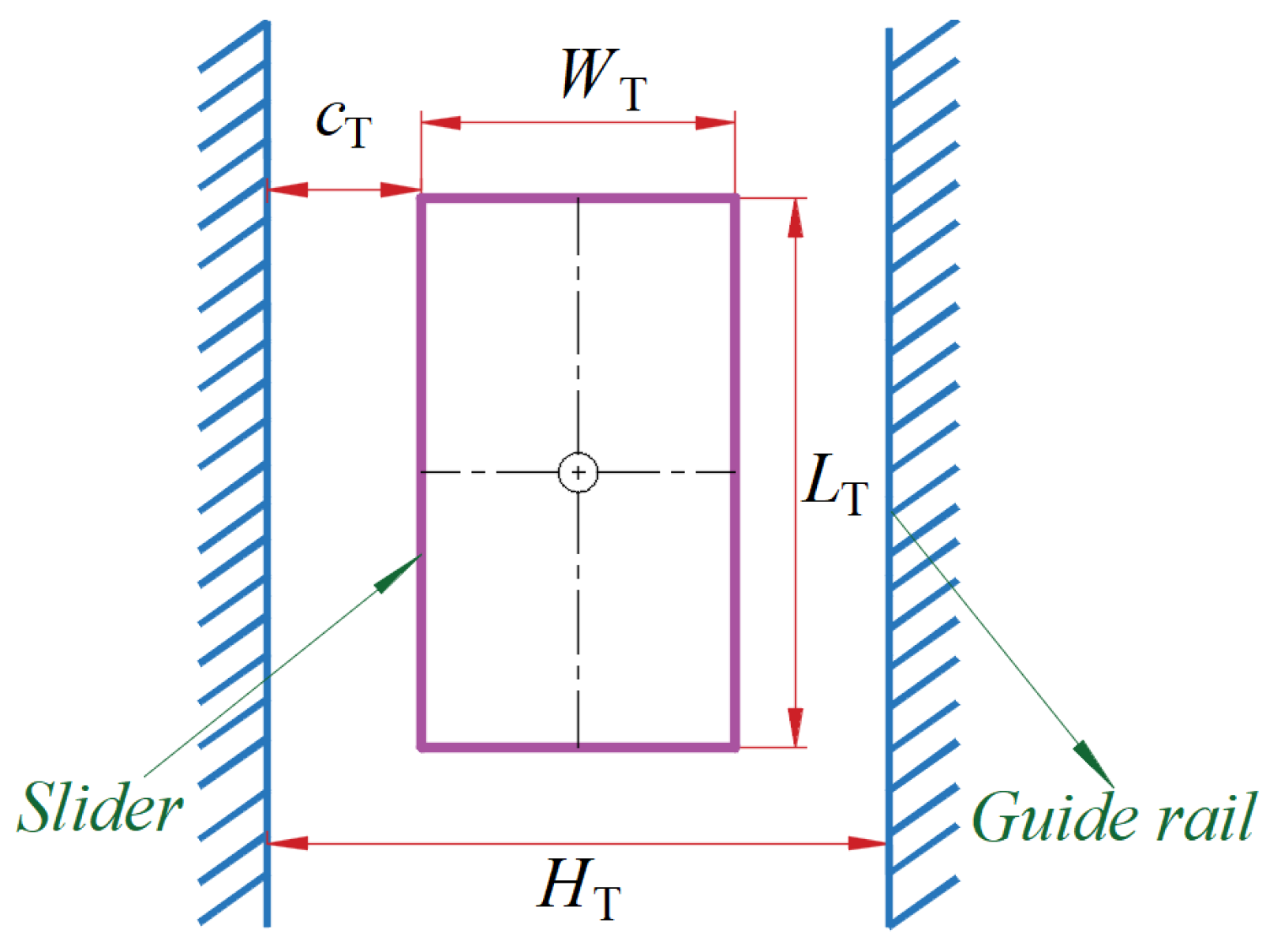
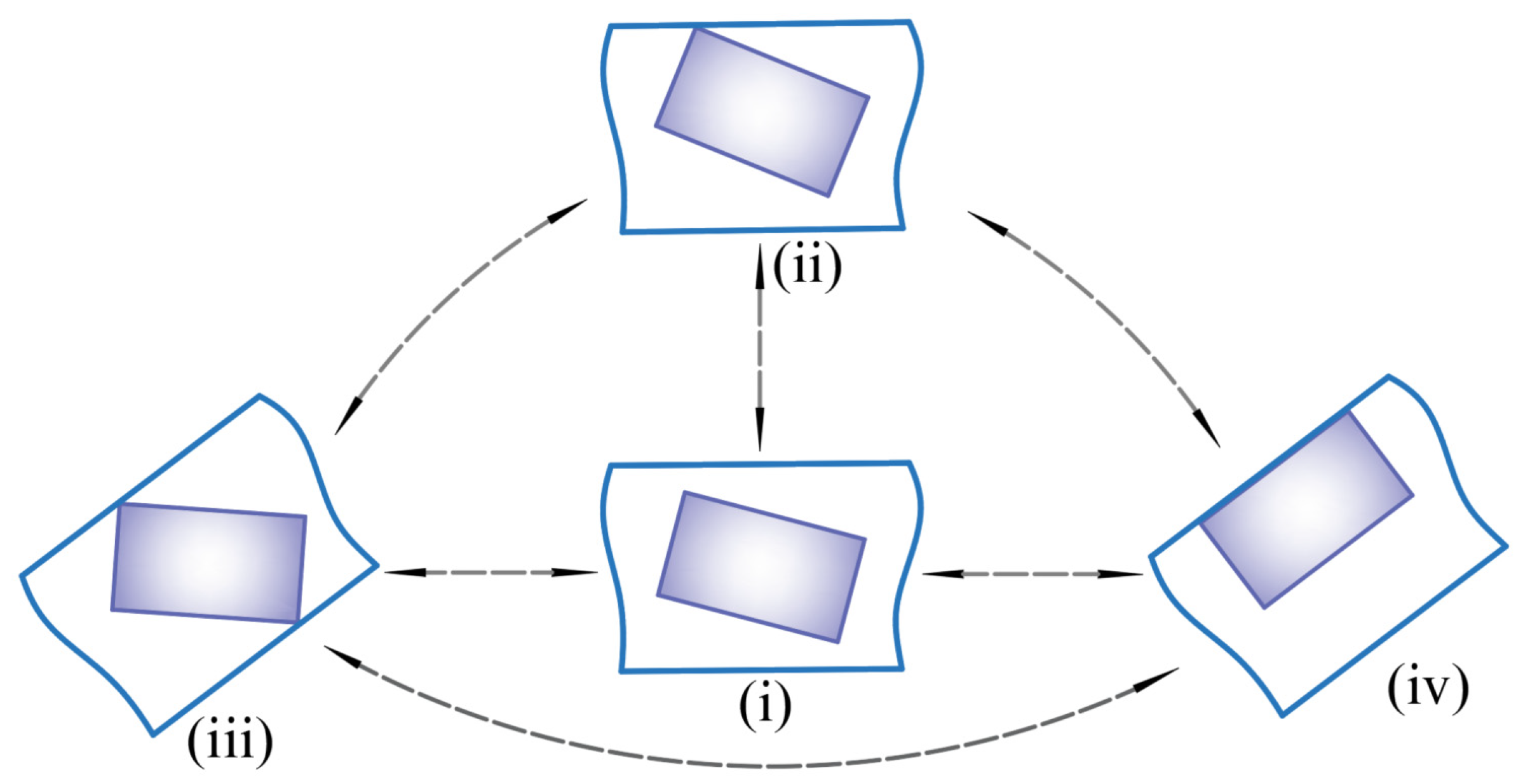
2.1. Clearance of the Translational Pair

2.1.1. Mathematical Model of Clearance of the Translational Pair

Figure 1 shows a model of clearance of the translational pair, H_T is the horizontal distance between upper and lower boundaries of the guide rail, W_T is the width of the slider, L_T is the length of the slider, and c_T is clearance size, with c_T = (H_T − W_T)/2.

Motion modes of translational clearance are mainly divided into four situations; the motion mode of translational clearance is shown in Figure 2. The slider is in a free state without any collision phenomenon, as shown in Figure 2(i); a corner of the slider collides with the guide rail surface, as shown in Figure 2(ii); the diagonal of the slider collides with the guide rail surface, as shown in Figure 2(iii); and the same side of the slider collides with the guide rail surface, as shown in Figure 2(iv).

Establishing an effective contact detection model is one of the key aspects of this study, as the clearance between the moving pair can cause contact collisions between the slider and guide rail. Figure 3 shows the contact detection model, which divides the clearance of the moving pair into two parts: slider m and guide rail n. A_m, B_m, C_m, and D_m are potential contact points on the slider, and A_n, B_n, C_n, and D_n are four corner points of the guide rail. Unit normal vector n_T is set to [1, 0]^T, and the unit horizontal vector t_T is set to [0, 1]^T. Due to the vertical placement of the guide rail, the unit normal vector is perpendicular to the guide rail. Taking the contact detection of the slider corner point A as an example, there exists a geometric relationship as follows:

$$\left\{\begin{array}{l}{\mathit{r}}_m^A={\mathit{r}}_m+T_m{s}_m^A \\ {\mathit{r}}_n^A={\mathit{r}}_n+T_n{s}_n^A \end{array}\right.$$

(1)

where r_m and r_n are position vectors of the centroid of the slider and guide rail, respectively; T_m and T_n are the transformation matrix of the slider and guide rail, respectively.

When the angle A of the slider collides with the guide rail, the judgment conditions are as follows:

$${\mathit{\delta }}_T={\mathit{r}}_n^A-{\mathit{r}}_m^A$$

(2)

When angle A of the slider collides with the guide rail, the judgment condition is as follows:

$${{\mathit{n}}_T}^{\mathrm{T}}{\mathit{\delta }}_T<0$$

(3)

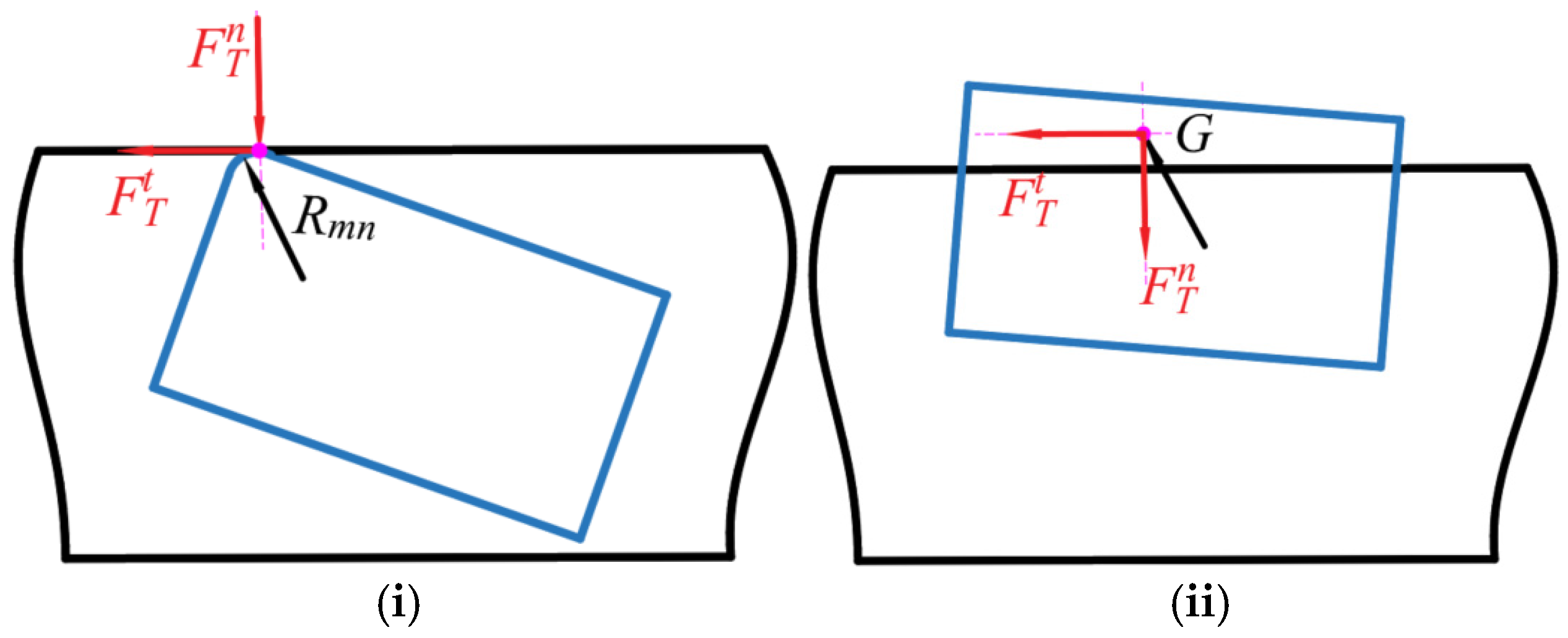
2.1.2. Collision Force Model for the Translational Clearance Pair

There are various forms of contact between guide rails and sliders. In order to improve accuracy of established model, suitable normal contact force models need to be adopted for different contact forms to measure the normal contact force. Contact mode between slider and guide rail are shown in Figure 4. For angular contact, due to the small contact area, a small fileted corner can be considered at the corner of the slider, which could be regarded as contact between a sphere and a plane, as illustrated in Figure 4i. The following contact force model considering energy dissipation effect is adopted:

$$F_T^n=K_T{{\delta }_T}^{1.5}\left(1+{\displaystyle \frac{3\left(1-c_e^2\right){\dot{\delta }}_T}{4{\dot{\delta }}_T^{\left(-\right)}}}\right)$$

(4)

$$K_T={\displaystyle \frac{4E_m{E}_n}{3\left[E_m\left(1-{\upsilon }_m^2\right)+E_n\left(1-{\upsilon }_n^2\right)\right]}}\sqrt{R_{mn}}$$

(5)

where K_T is the stiffness coefficient; c_e is the coefficient of recovery; ${\dot{\delta }}_T^{\left(-\right)}$ is initial collision velocity; ${\upsilon }_m$ and ${\upsilon }_n$ are the Poisson’s ratio; E_m and E_n are the elastic moduli, respectively; and R_mn represents radius of curvature of slider corner.

When two adjacent corners of the slider come into contact with the guideway, contact force acts on the centroid of penetration area, as illustrated in Figure 4ii. The collision force can be expressed as

$$F_T^n=K_T{\delta }_T$$

(6)

$$K_T={\displaystyle \frac{\left(T_T+L_T\right)E_m{E}_n}{0.475\left[E_m\left(1-{\upsilon }_m^2\right)+E_n\left(1-{\upsilon }_n^2\right)\right]}}$$

(7)

where $T_T$ is the thickness of the slider.

Friction, as a complex force, has a significant impact on dynamics, and selecting a reasonable friction model is crucial. A modified version of the Coulomb friction model presented by Ambrosio is used [50].

$$F_T^t=-c_f{c}_d{F}_T^n{\displaystyle \frac{v_t}{\left|v_t\right|}}$$

(8)

where c_f is the coefficient of friction, and c_d is the coefficient of correction.

$$c_d=\left\{\begin{array}{l} 0 ,\left|v_t\right|<v_0\\ {\displaystyle \frac{\left|v_t\right|-v_0}{v_1-v_0}},v_0\le \left|v_t\right|\le v_1\\ 1 ,\left|v_t\right|>v_1\end{array}\right.$$

(9)

where v₀ and v₁ are limit values of the given speed.

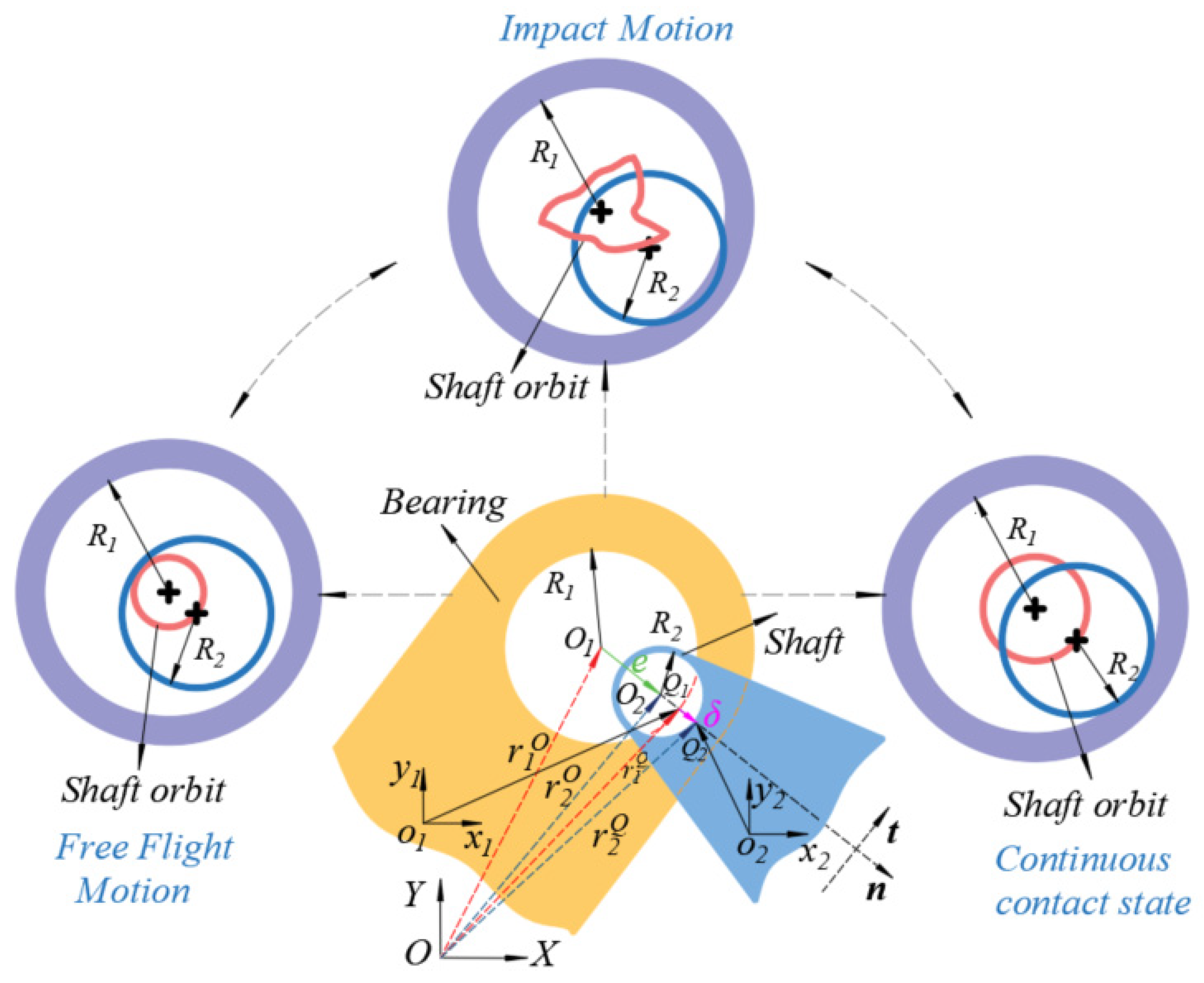
2.2. Clearance of the Revolute Pair

2.2.1. Mathematical Model of Clearance of the Revolute Pair

The clearance model of the rotating pair is shown in Figure 5. $R_1$ and $R_2$ are the bearing and shaft radius, respectively. $O_1$ and $O_2$ are the centers of the bearing and shaft, respectively. $Q_1$ and $Q_2$ are the collision points on the bearing and shaft, respectively. The eccentricity between shaft and bearing is

$$\mathit{e}={\mathit{r}}_2^O-{\mathit{r}}_1^O$$

(10)

The magnitude of eccentricity value between the shaft and bearing is

$$e=\sqrt{{\mathit{e}}^T\mathit{e}}$$

(11)

The size of embedding depth at clearance can be written as

$${\delta }_R=e-c_R$$

(12)

where $c_R$ is clearance size, $c_R=R_1-R_2$.

The unit vector of the eccentricity vector between the bearing and the shaft is

$$\mathit{n}={\displaystyle \frac{\mathit{e}}{e}}$$

(13)

Criteria for determining collisions between components in a rotating joint with clearance are as follows:

$$\left\{\begin{array}{l}{\delta }_R<0, free state\\ {\delta }_R=0, continuous contact state\\ {\delta }_R>0, collision state\end{array}\right.$$

(14)

When the shaft collides with the bearing, judgment conditions are as follows:

$${\delta }_R\left(t_n\right){\delta }_R\left(t_{n+1}\right)\le 0$$

(15)

The position vector of the collision point can be represented as

$$\left\{\begin{array}{l}{\mathit{r}}_1^Q={\mathit{r}}_1^O+R_1\mathit{n} \\ {\mathit{r}}_2^Q={\mathit{r}}_2^O+R_2\mathit{n} \end{array}\right.$$

(16)

The velocity vector at the collision point is

$$\left\{\begin{array}{l}{\dot{\mathit{r}}}_1^Q={\dot{\mathit{r}}}_1^O+R_1\dot{\mathit{n}} \\ {\dot{\mathit{r}}}_2^Q={\dot{\mathit{r}}}_2^O+R_2\dot{\mathit{n}} \end{array}\right.$$

(17)

where $\dot{\mathit{n}}$ is the first derivative of the eccentric vector unit vector, $\dot{\mathit{n}} ={\displaystyle \frac{\dot{\mathit{e}}e-\dot{e}\mathit{e}}{e^2}}$.

The velocity components of the collision point of the bearing relative to the axis in the normal and tangential directions are

$$\left\{\begin{array}{l}{v}_n={({\dot{\mathit{r}}}_2^Q-{\dot{\mathit{r}}}_1^Q)}^{\mathrm{T}}\mathit{n}\\ v_t={({\dot{\mathit{r}}}_2^Q-{\dot{\mathit{r}}}_1^Q)}^{\mathrm{T}}\mathit{t}\end{array}\right.$$

(18)

where the tangential vector t can be obtained by rotating n counterclockwise by 90°.

2.2.2. Collision Force Model of the Revolute Clearance Pair

The L-N model is widely applied in the normal collision force model at the clearance of the rotating pair, which can be written as

$$F_R^n=K_R{{\delta }_R}^{1.5}+D_R{\dot{\delta }}_R$$

(19)

where K_R is the stiffness coefficient, D_R is the damping coefficient, and ${\dot{\delta }}_R$ is the embedded depth velocity.

The stiffness coefficient and damping coefficient can be expressed as

$$K_R={\displaystyle \frac{4E_1{E}_2}{3\left[E_1\left(1-{\upsilon }_1^2\right)+E_2\left(1-{\upsilon }_2^2\right)\right]}}\sqrt{{\displaystyle \frac{R_1{R}_2}{R_1+R_2}}}$$

(20)

$$D_R={\displaystyle \frac{3\left(1-c_e^2\right){\delta }_R^{1.5}}{4{\dot{\delta }}_R^{\left(-\right)}}}$$

(21)

where ${\dot{\delta }}_R^{\left(-\right)}$ is the initial collision velocity; ${\upsilon }_1$ and ${\upsilon }_2$ represent Poisson’s ratio; and E₁ and E₂ represent elastic modulus.

Friction force at the revolute clearance also uses the modified Coulomb friction model, which is expressed in the same form as Equation (8).

3. Establishment of Beam Unit Model

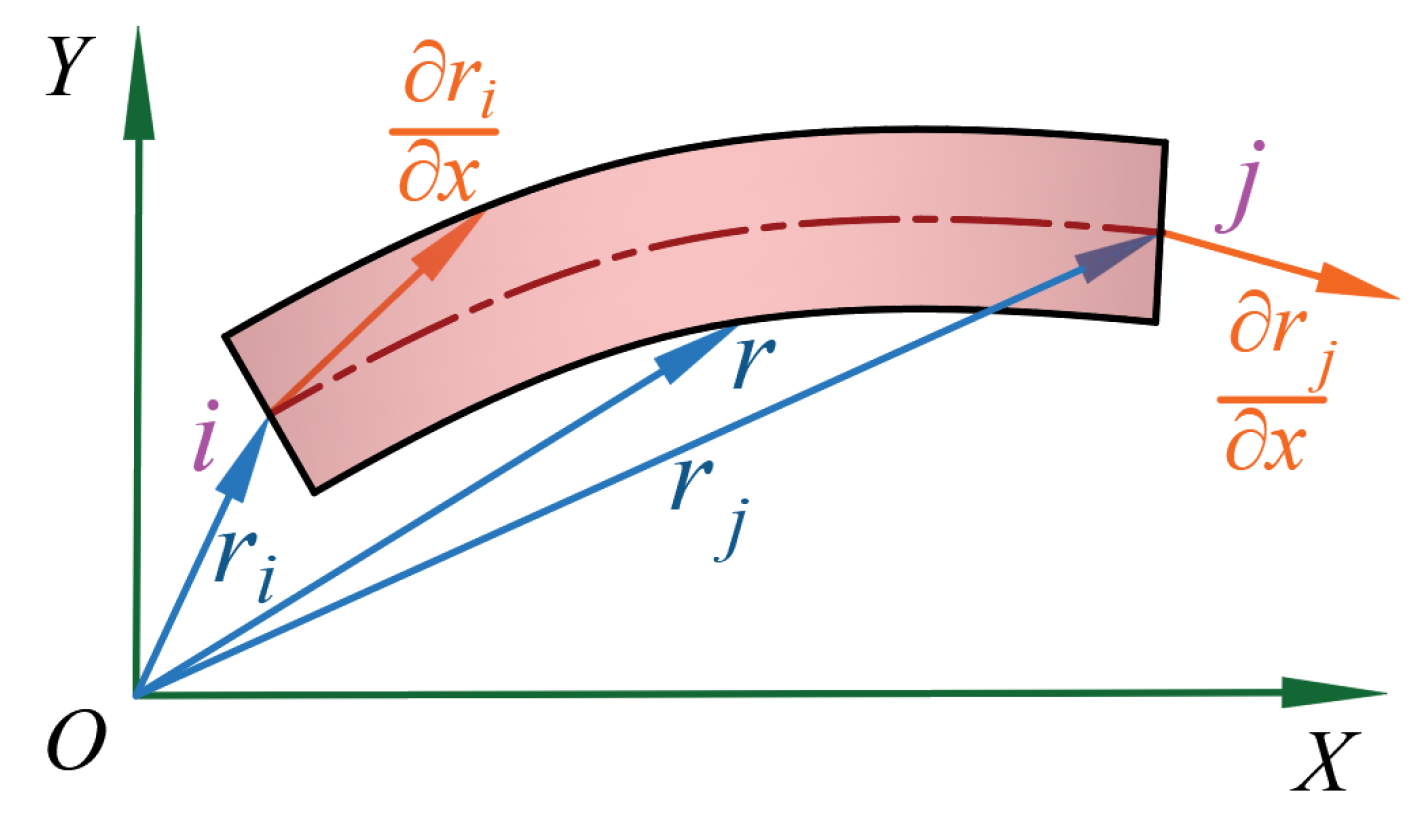
3.1. Rigid Beam Unit

The reference point coordinate method is used to model the rigid beam element. Generalized coordinate ${\tilde{\mathit{q}}}_r$ of the rigid element can be written as

$${\tilde{\mathit{q}}}_r={\left(x_r y_r {\theta }_r\right)}^{\mathrm{T}}$$

(22)

where x_r and y_r are the centroid coordinates, and θ_r is the rotation angle.

The mass matrix of the rigid beam element is

$${\tilde{\mathit{M}}}_r=\left(\begin{array}{ccc}{m}_r& & \\ & m_r& \\ & & J_r\end{array}\right)$$

(23)

where m_r and J_r represent the mass and moment of the inertia of the rigid beam element.

Gravity is simplified as a generalized force acting on the center of the mass of the element, which can be written as

$${\mathit{g}}_r={\left(\begin{array}{ccc}0& -m_{r}g& 0\end{array}\right)}^{\mathrm{T}}$$

(24)

The dynamic equation of the rigid element is

$${\tilde{\mathit{M}}}_r{\ddot{\tilde{\mathit{q}}}}_r={\mathit{g}}_r$$

(25)

3.2. Flexible Beam Unit

The flexible element is modeled by using the absolute node coordinate method, and a one-dimensional two-node element is applied to divide the flexible element. The model of the flexible beam element is shown in Figure 6. The position vector of any point could be written as

$$\mathit{r}=\left[\begin{array}{l}{r}_x\\ r_y\end{array}\right]=\left[\begin{array}{l}{a}_0+a_{1}x+a_2{x}^2+a_3{x}^3\\ b_0+b_{1}x+b_2{x}^2+b_3{x}^3\end{array}\right]=\mathit{S}{\tilde{\mathit{q}}}_f$$

(26)

where x is the local coordinates of the unit in the axial direction; S is the global shape function; and ${\tilde{\mathit{q}}}_f$ is the generalized coordinate, which can be expressed as

$$\begin{array}{ll}{\tilde{\mathit{q}}}_f& ={\left(q_{f1},q_{f2},q_{f3},q_{f4},q_{f5},q_{f6},q_{f7},q_{f8}\right)}^{\mathrm{T}}\\ & ={\left(r_{ix},r_{iy},{\displaystyle \frac{\partial r_{ix}}{\partial x}},{\displaystyle \frac{\partial r_{iy}}{\partial x}},r_{jx},r_{jy},{\displaystyle \frac{\partial r_{jx}}{\partial x}},{\displaystyle \frac{\partial r_{jy}}{\partial x}}\right)}^{\mathrm{T}}\end{array}$$

(27)

where $\left({\mathit{r}}_{ix},{\mathit{r}}_{iy}\right)$ and $\left({\mathit{r}}_{jx},{\mathit{r}}_{jy}\right)$ are position vectors of nodes i and j, $\left({\displaystyle \frac{\partial r_{ix}}{\partial x}},{\displaystyle \frac{\partial r_{iy}}{\partial x}}\right)$ and $\left({\displaystyle \frac{\partial r_{jx}}{\partial x}},{\displaystyle \frac{\partial r_{jy}}{\partial x}}\right)$ are slope vectors in the tangential direction of the axis of the flexible element.

The shape function of the flexible element is expressed as

$$\mathit{S}=\left[S_1\mathit{I},S_2\mathit{I},S_3\mathit{I},S_4\mathit{I}\right]$$

(28)

where $I$ represents a 2 × 2 unit matrix; $S_1=1-3{\xi }^2+2{\xi }^3$; $S_2=l\left(\xi -2{\xi }^2+{\xi }^3\right)$; $S_3=3{\xi }^2-2{\xi }^3$; $S_4=l\left(-{\xi }^2+{\xi }^3\right)$; and $\xi ={\displaystyle \frac{x}{l}}$; l is the length of the flexible beam element.

The absolute velocity vector can be obtained by taking the derivative of Equation (26) over time, $\dot{\mathit{r}}=\mathit{S}{\dot{\tilde{\mathit{q}}}}_f$. The kinetic energy of the flexible element is

$${\mathit{T}}_f={\displaystyle \frac{1}{2}}{\displaystyle {\int }_V\rho {\dot{\mathit{r}}}^{\mathrm{T}}\dot{\mathit{r}}dV}={\displaystyle \frac{1}{2}}{\dot{\tilde{\mathit{q}}}}_f^{\mathrm{T}}\left({\displaystyle {\int }_V\rho {\mathit{S}}^{\mathrm{T}}\mathit{S}dV}\right){\dot{\tilde{\mathit{q}}}}_f={\displaystyle \frac{1}{2}}{\dot{\tilde{\mathit{q}}}}_f^{\mathrm{T}}{\mathit{M}}_f{\dot{\tilde{\mathit{q}}}}_f$$

(29)

where ρ is density; ${\tilde{\mathit{M}}}_f$ is the constant mass matrix of the flexible element, which can be written as

$${\tilde{\mathit{M}}}_f={\displaystyle {\int }_V\rho {\mathit{S}}^T\mathit{S}dV}$$

(30)

The elastic force of a flexible element is expressed as

$${\tilde{\mathit{F}}}_f={\displaystyle \frac{\partial U_f}{\partial {\tilde{\mathit{q}}}_f}}={\displaystyle \frac{\partial \left(U_t+U_l\right)}{\partial {\tilde{\mathit{q}}}_f}}$$

(31)

where $U_f$, $U_t$, and $U_l$ are the total strain energy, bending strain energy, and axial tensile strain energy of the flexible element, respectively, for isotropic materials; $U_t$ and $U_l$ can be written as

$$U_t={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^{l}E{I}_f{\kappa }_f^2}\mathrm{d}x$$

(32)

$$U_l={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^{l}E{A}_a{\epsilon }_f^2\mathrm{d}x}$$

(33)

where E, ${\kappa }_f$, $I_f$, A_a, and ${\epsilon }_f$ are Young’s modulus, curvature of the beam element, moment of inertia of the cross-section, cross-sectional area of the beam unit, and strain of the beam element, respectively.

Bending elastic force and axial elastic force are expressed as

$${\tilde{\mathit{F}}}_t={\left({\displaystyle \frac{\partial U_t}{\partial {\tilde{\mathit{q}}}_f}}\right)}^{\mathrm{T}}=\left({\displaystyle {\int }_0^{l}E{I}_f{{\mathit{S}}^{″}}^{\mathrm{T}}{\mathit{S}}^{″}\mathrm{d}x}\right){\tilde{\mathit{q}}}_f=K_t{\tilde{\mathit{q}}}_f$$

(34)

$${\tilde{\mathit{F}}}_l={\left({\displaystyle \frac{\partial U_l}{\partial {\tilde{\mathit{q}}}_f}}\right)}^{\mathrm{T}}=\left({\displaystyle {\int }_0^{l}E{A}_a{\epsilon }_f{\mathit{S}}_f\mathrm{d}x}\right){\tilde{\mathit{q}}}_f=K_l{\tilde{\mathit{q}}}_f$$

(35)

Bending stiffness and axial stiffness are expressed as

$$K_t={\displaystyle {\int }_0^{l}E{I}_f{{\mathit{S}}^{″}}^{\mathrm{T}}{\mathit{S}}^{″}\mathrm{d}x}$$

(36)

$$K_l={\displaystyle {\int }_0^{l}EA{\epsilon }_f{\mathit{S}}_f\mathrm{d}x}$$

(37)

The strain ${\epsilon }_f$ could be simply written as

$${\epsilon }_f=\sqrt{{\left(q_{f5}-q_{f1}\right)}^2+{\left(q_{f6}-q_{f2}\right)}^2}-l$$

(38)

The generalized force of a flexible element is

$${\mathit{g}}_f=-mg{\left(0 -{\displaystyle \frac{1}{2}} 0 -{\displaystyle \frac{l}{12}} 0 -{\displaystyle \frac{1}{2}} 0 {\displaystyle \frac{l}{12}}\right)}^{\mathrm{T}}$$

(39)

The dynamic equation of a flexible beam element is

$${\mathit{M}}_f{\ddot{\tilde{\mathit{q}}}}_f+{\tilde{\mathit{F}}}_f={\mathit{g}}_f$$

(40)

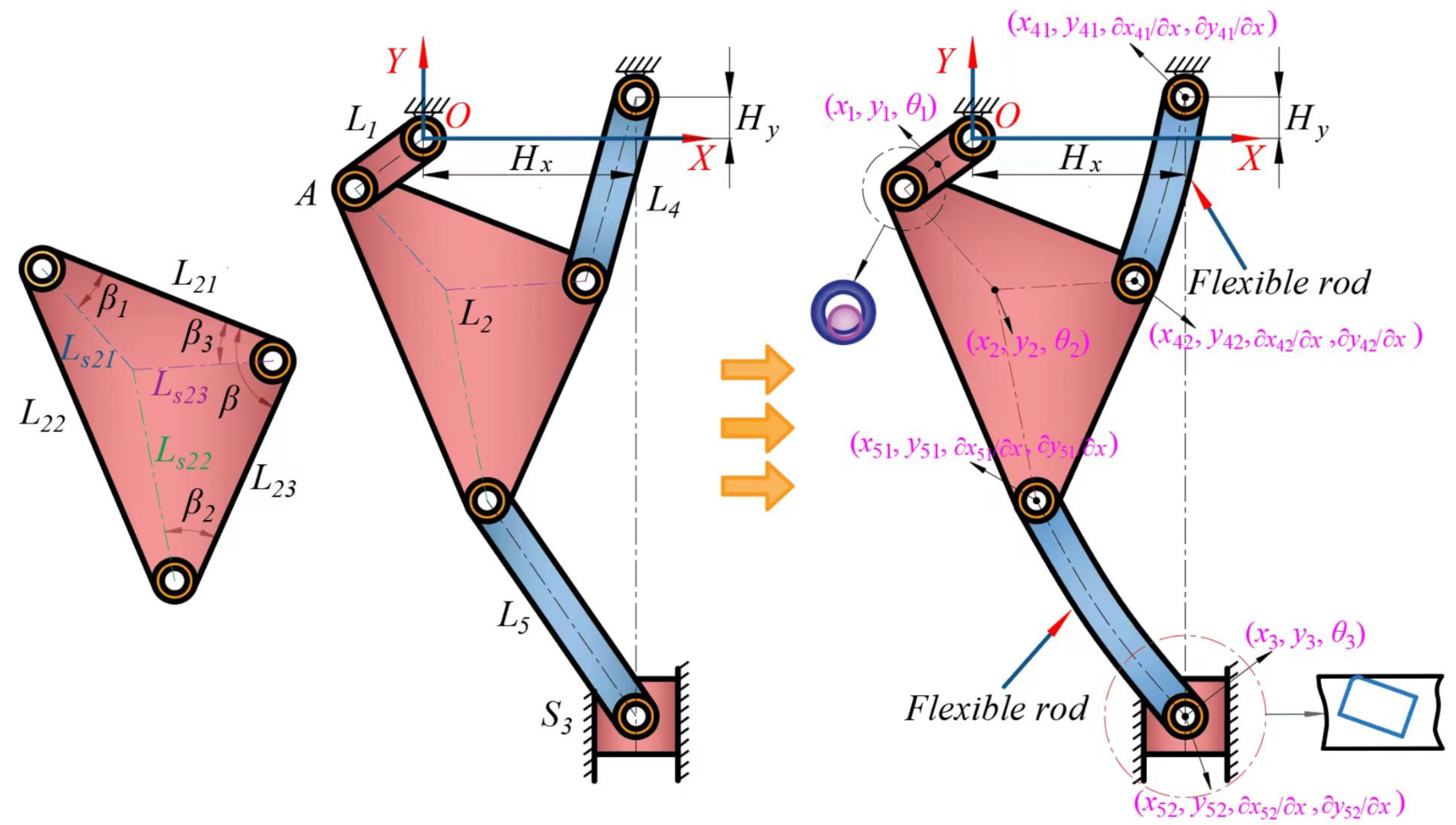
4. Rigid–Flexible Coupling Dynamic Modeling of a Mechanism with Revolute Clearance and Translational Clearance

A schematic diagram of a multilink press mechanism is shown in Figure 7, which includes crank 1, triangle plate 3, connecting rod 2, connecting rod 4, and slider. Because component 3 is a triangular plate structure that is not easily deformed during the operation of the mechanism, it is considered that link 2 and link 4 in the mechanism are flexible components, while the other components are regarded as rigid components. The revolute clearance pair at the driving component and translational clearance between the slider and guide can directly affect the driving torque and motion characteristics of the slider. Therefore, this paper focuses on the comprehensive coupling effect of rotating pair A clearance and translational clearance B on the mechanism.

The generalized coordinates of components can be written as

$$\left\{\begin{array}{c}{\mathit{q}}_1={\left(\begin{array}{ccc}{x}_1& y_1& {\theta }_1\end{array}\right)}^{\mathrm{T}}\\ {\mathit{q}}_2={\left(\begin{array}{ccc}{x}_2& y_2& {\theta }_2\end{array}\right)}^{\mathrm{T}}\\ {\mathit{q}}_3={\left(\begin{array}{ccc}{x}_3& y_3& {\theta }_3\end{array}\right)}^{\mathrm{T}}\\ {\mathit{q}}_4={\left(\begin{array}{cccccccc}{x}_{41}& y_{41}& {\displaystyle \frac{\partial x_{41}}{\partial x}}& {\displaystyle \frac{\partial y_{41}}{\partial x}}& x_{42}& y_{42}& {\displaystyle \frac{\partial x_{42}}{\partial x}}& {\displaystyle \frac{\partial y_{42}}{\partial x}}\end{array}\right)}^{\mathrm{T}}\\ {\mathit{q}}_5={\left(\begin{array}{cccccccc}{x}_{51}& y_{51}& {\displaystyle \frac{\partial x_{51}}{\partial x}}& {\displaystyle \frac{\partial y_{51}}{\partial x}}& x_{52}& y_{52}& {\displaystyle \frac{\partial x_{52}}{\partial x}}& {\displaystyle \frac{\partial y_{52}}{\partial x}}\end{array}\right)}^{\mathrm{T}}\end{array}\right.$$

(41)

The generalized coordinates of a system considering compound clearances are

$$\mathit{q}={\left(\begin{array}{cc}{\mathit{q}}_r& {\mathit{q}}_f\end{array}\right)}^{\mathrm{T}}$$

(42)

where ${\mathit{q}}_r$ is the generalized coordinate of the system’s rigid components, ${\mathit{q}}_r=\left(\begin{array}{ccc}{\mathit{q}}_1& {\mathit{q}}_2& {\mathit{q}}_3\end{array}\right)$, and ${\mathit{q}}_f$ is the generalized coordinate of flexible components, ${\mathit{q}}_f=\left(\begin{array}{cc}{\mathit{q}}_4& {\mathit{q}}_5\end{array}\right)$.

Each kinematic pair can introduce two constraint equations. Considering the presence of the clearance at rotating pair A, as well as clearance B at the translational pair, the constraints on rotating pair A and the translational pair B fail due to the presence of clearances. At this point, the constraint equation of system is

$$\mathit{\Phi }\left(\mathit{q},t\right)=\left(\begin{array}{c}{x}_1-L_{s1}\cos {\theta }_1\\ y_1-L_{s1}\sin {\theta }_1\\ x_2+L_{s23}\cos ({\theta }_2+{\beta }_3)-x_{42}\\ y_2+L_{s23}sin({\theta }_2+{\beta }_3)-y_{42}\\ x_{41}-H_x\\ y_{41}-H_y\\ x_2+L_{s22}\cos ({\theta }_2+\beta +{\beta }_2)-x_{51}\\ y_2+L_{s22}\sin ({\theta }_2+\beta +{\beta }_2)-y_{51}\\ x_{52}-H_x\\ y_{52}-y_3\\ {\theta }_1-\omega t-{303.58}^{\circ }\end{array}\right)=\mathbf{0}$$

(43)

The velocity constraint equation could be written as

$${\mathit{\Phi }}_q\dot{\mathit{q}}=-{\mathit{\Phi }}_t\equiv \mathit{\upsilon }$$

(44)

where ${\mathit{\Phi }}_q$ is the Jacobian matrix, ${\mathit{\Phi }}_t={\displaystyle \frac{\partial \mathit{\Phi }}{\partial t}}={\left(\begin{array}{cc}{\mathbf{0}}_{1\times 10}& -\omega \end{array}\right)}^{\mathrm{T}}$.

The Jacobian matrix can be represented as

$${\mathit{\Phi }}_q=\left({\mathit{\Phi }}_q^r,{\mathit{\Phi }}_q^f\right)$$

(45)

where ${\mathit{\Phi }}_q^r$ and ${\mathit{\Phi }}_q^f$ are derivative of the constraint equation with respect to generalized coordinates of rigid components and flexible components, respectively. ${\mathit{\Phi }}_q^r=\left({\displaystyle \frac{\partial \mathit{\Phi }}{\partial q_1}},{\displaystyle \frac{\partial \mathit{\Phi }}{\partial q_2}},{\displaystyle \frac{\partial \mathit{\Phi }}{\partial q_3}}\right)$, ${\mathit{\Phi }}_q^f=\left({\displaystyle \frac{\partial \mathit{\Phi }}{\partial q_4}},{\displaystyle \frac{\partial \mathit{\Phi }}{\partial q_5}}\right)$.

The acceleration constraint equation can be written as

$${\mathit{\Phi }}_q\ddot{\mathit{q}}=-{\left({\mathit{\Phi }}_q\dot{\mathit{q}}\right)}_q\dot{\mathit{q}}-2{\mathit{\Phi }}_{qt}\dot{\mathit{q}}-{\mathit{\Phi }}_{tt}\equiv \mathit{\gamma }$$

(46)

where ${\mathit{\Phi }}_{qt}={\mathbf{0}}_{11\times 25}$, ${\mathit{\Phi }}_{tt}=0_{11\times 1}$.

The dynamic model of the system could be represented as

$$\left(\begin{array}{cc}{\mathit{M}}_r& \mathbf{0}\\ \mathbf{0}& {\mathit{M}}_f\end{array}\right)\left(\begin{array}{c}{\ddot{\mathit{q}}}_r\\ {\ddot{\mathit{q}}}_f\end{array}\right)+\left(\begin{array}{c}{\left({\mathit{\Phi }}_q^r\right)}^{\mathrm{T}}\\ {\left({\mathit{\Phi }}_q^f\right)}^{\mathrm{T}}\end{array}\right)\lambda =\left(\begin{array}{c}{\mathit{G}}_r\\ {\mathit{G}}_f-{\mathit{F}}_f\end{array}\right)$$

(47)

where ${\mathit{M}}_r$ and ${\mathit{Q}}_r$ are the mass matrix and external force of rigid components for the whole system, λ is a Lagrange multiplier, and ${\mathit{M}}_f$, ${\mathit{Q}}_f$, and ${\mathit{F}}_f$ are the mass matrix, external force, and elastic force of flexible rods for the whole system, respectively.

Baumgarte proposed an algorithm that combines displacement and velocity constraints into an acceleration constraint equation to improve the stability of the solution.

$$\left(\begin{array}{ccc}{\mathit{M}}_r& \mathbf{0}& {\left({\mathit{\Phi }}_q^r\right)}^{\mathrm{T}}\\ \mathbf{0}& {\mathit{M}}_f& {\left({\mathit{\Phi }}_q^f\right)}^{\mathrm{T}}\\ {\mathit{\Phi }}_q^r& {\mathit{\Phi }}_q^f& \mathbf{0}\end{array}\right)\left(\begin{array}{c}{\ddot{\mathit{q}}}_r\\ {\ddot{\mathit{q}}}_f\\ \mathit{\lambda }\end{array}\right)=\left(\begin{array}{c}{\mathit{G}}_r\\ {\mathit{G}}_f-{\mathit{F}}_f\\ \mathit{\gamma }-2\alpha \dot{\mathit{\Phi }}-{\beta }^2\mathit{\Phi }\end{array}\right)$$

(48)

where α and β are Baumgarte feedback parameters.

5. Dynamic Response Analysis and Chaos Identification

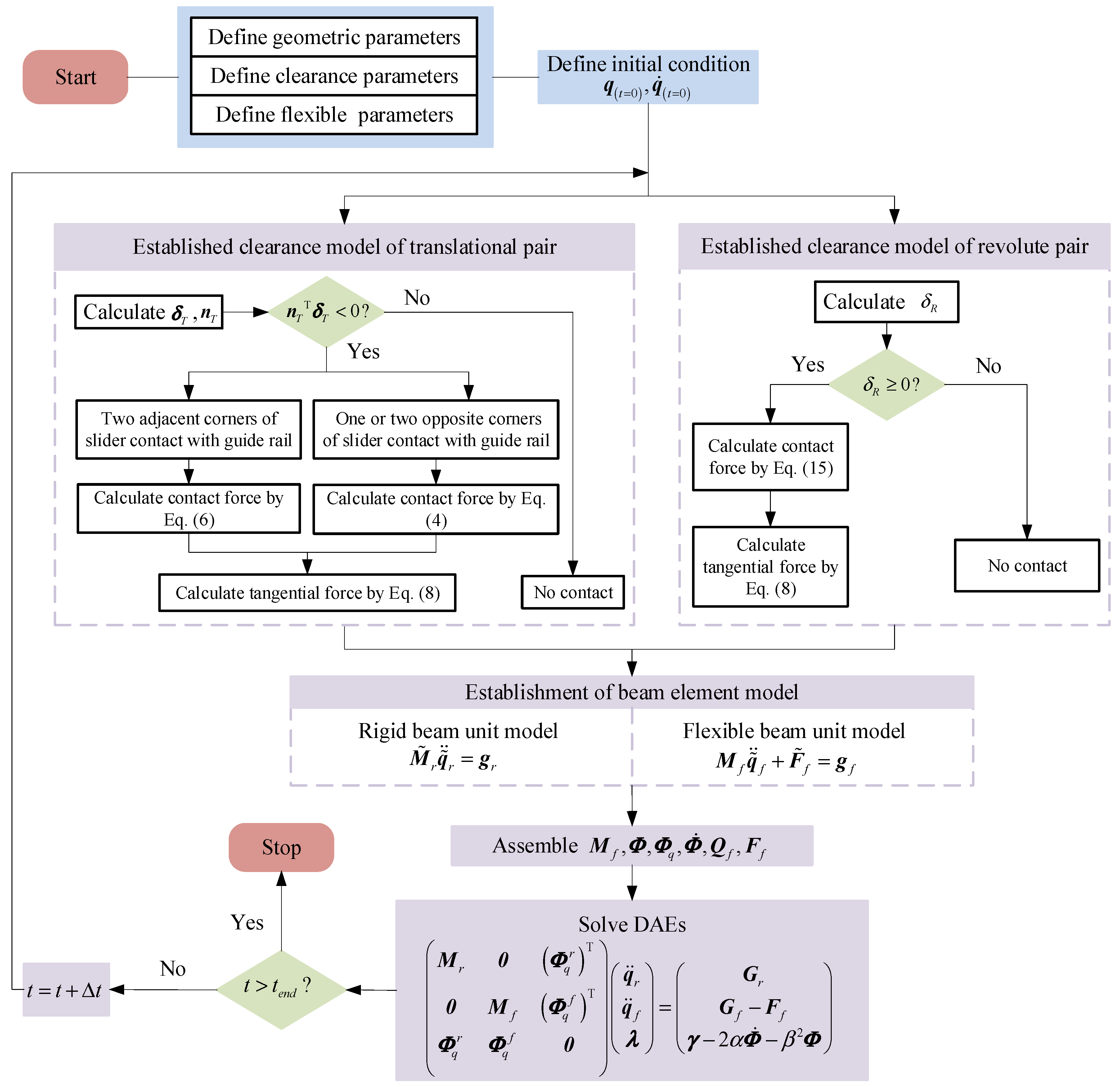
5.1. Solution of Dynamic Equations for Mechanisms with Compound Clearances

A flowchart for solving the dynamic equation with a flexible rod and compound clearances is shown in Figure 8.

5.2. Simulation Parameters

The rod length parameters of the mechanism through kinematic optimization in the early stage are obtained, and a three-dimensional model of the six-bar mechanism from SOLIDWORKS is established. Then, the SOLIDWORKS model is imported into ADAMS 2020 software for the establishment of a virtual prototype model. And the mass, moment of inertia of the rod, and cross-sectional area from the ADAMS virtual prototype model are measured; the material of the component is defined as iron. Geometric parameters of the mechanism are displayed in

Table 1. Geometric parameters of the mechanism.

Component	Length (mm)	Mass (kg)	Moment of Inertia (kg·m2)
Crank 1	75	0.738 (m1)	1.977 × 10−9 (J1)
Rod 2	584 (L2)	4.708 (m2)	546.91 × 10−9 (J2)
Rod 3	555.14 (L31)	21.483 (m3)	1348.94 × 10−9 (J3)
	985 (L32)
	473.66 (L33)
Rod 4	450 (L4)	3.663 (m4)	69.26 × 10−9 (J4)
Slider 5	150 (LT)	0.922 (m5)	1.059 × 10−9 (J5)
	100 (HT)

. Parameters of clearance and the flexible rod are displaced in

Table 2. Parameters of clearance and flexible rod.

Parameter	Value	Parameter	Value
Restitution coefficient ce	0.9 [7]	Limited speed v1/(m/s)	0.001 [7]
Elastic modulus Ei (i = 1, 2, m, n)/GPa	207 [23]	Limited speed v0/(m/s)	0.0001 [7]
Poisson’s ratio νi (i = 1, 2, m, n)	0.3 [7]	Cross-sectional area Aa/m2	0.001
Density ρ/(g/cm3)	7.85	Second moment of area If/m4	3.333 × 10−8

.

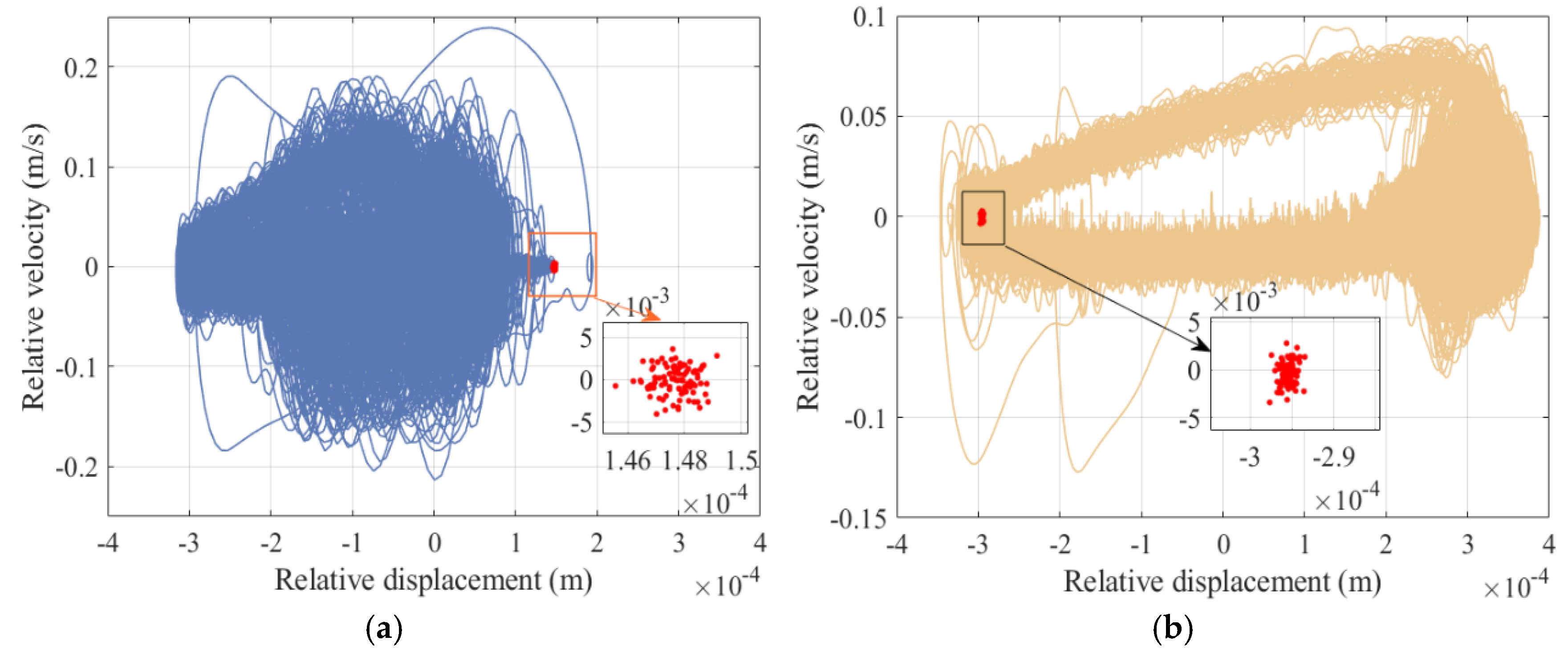
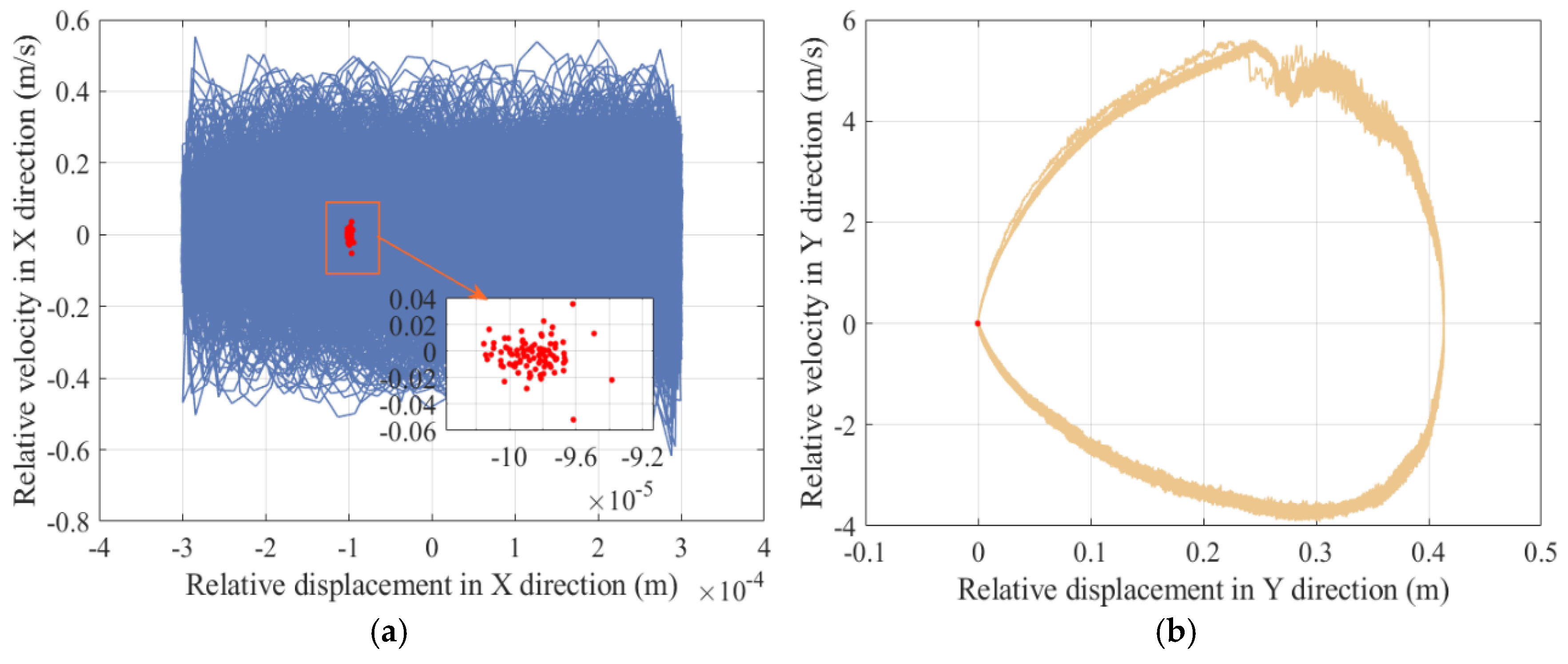
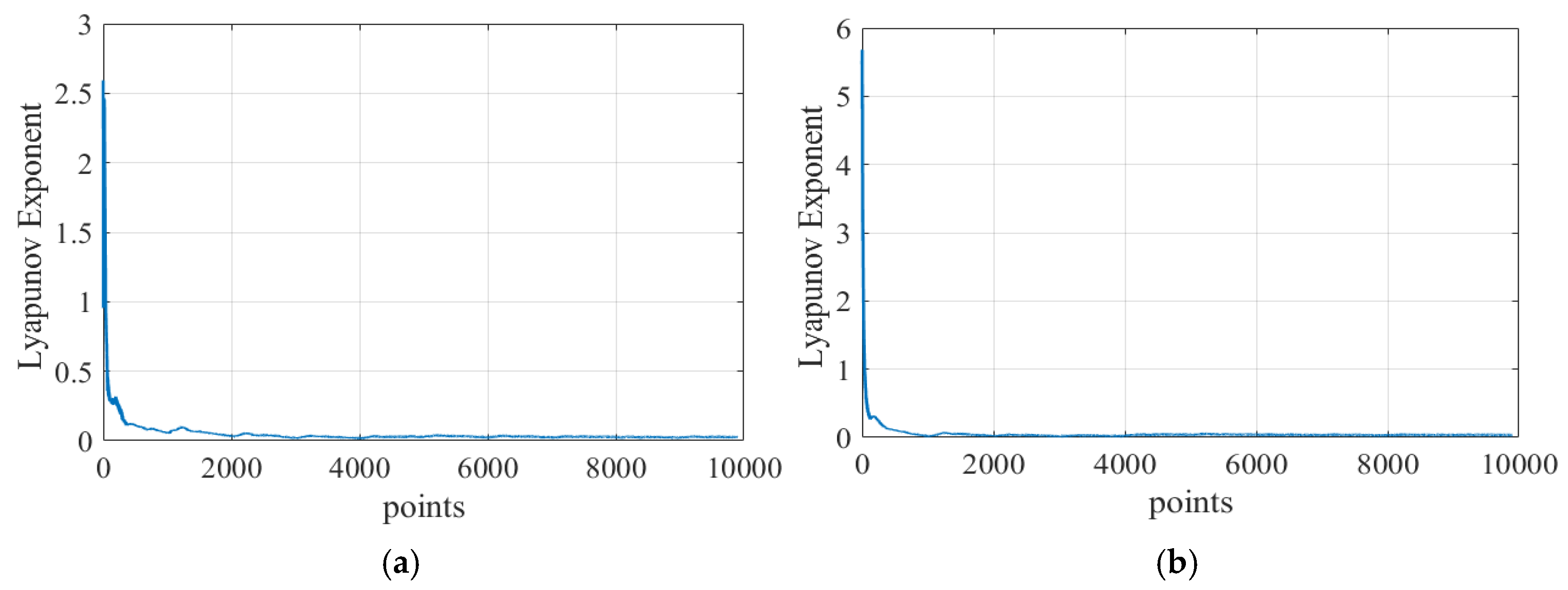
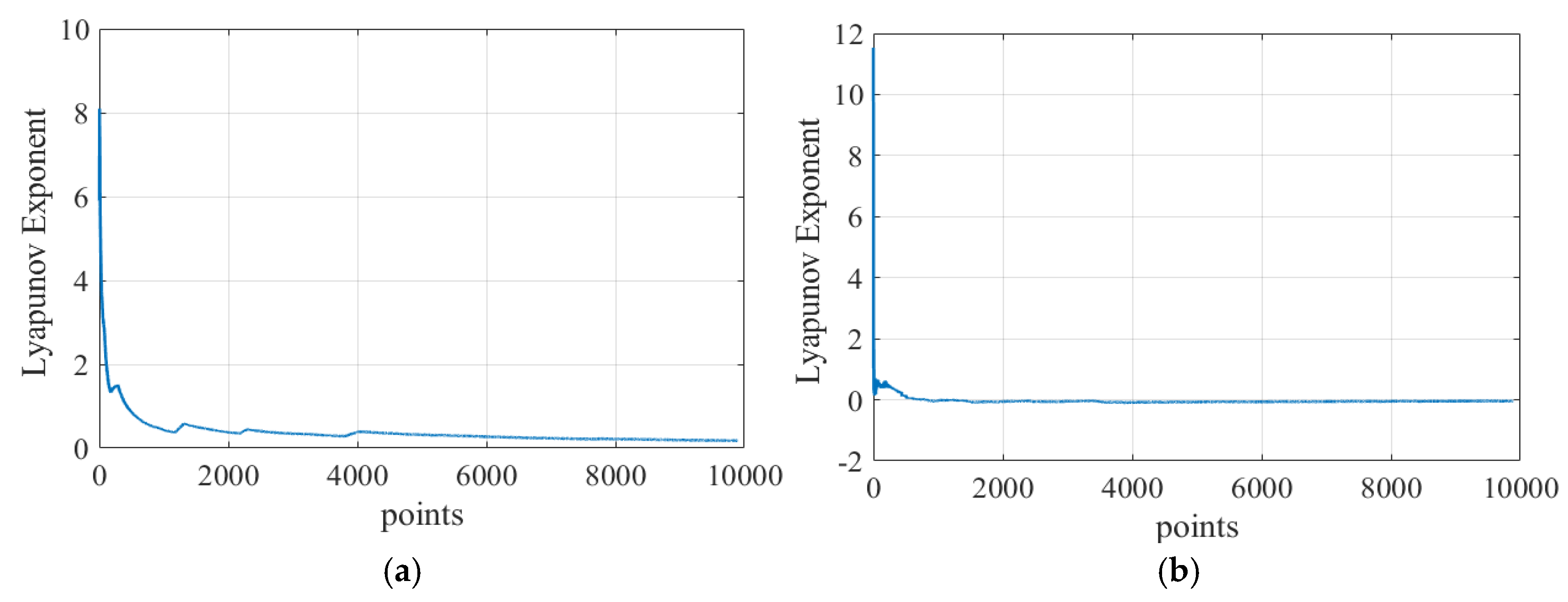
5.3. Chaos Identification

Translational and revolute pairs are common motion pairs in mechanisms, and the clearances at the motion pair can cause collisions and wear between components of motion pair, resulting in uncertainty in the motion of the mechanism. Elastic deformation of the component will cause deformation and accelerate the shaking of the mechanism. For the six-bar mechanism studied in this article, the coupling effect of clearance between rotating joints, clearance between translational pairs, and the elastic deformation of the rods are important factors that cause chaos, leading to a decrease in its stability. Therefore, it is very important to perform chaos identification on mechanisms with compound clearances and flexible components.

We selected the following parameters for simulation analysis: the driving speed of the slider 1 is 150 rpm, the friction coefficient is 0.15, and the clearance value of clearance joints B, C, and F are all set as 0.3 mm. When the mechanism operates at 100 cycles, chaos identification of the mechanism’s motion is performed based on the data from these 100 cycles. Center trajectories at the clearance are shown in Figure 9.

A phase diagram and Poincaré diagram at revolute clearance A and translational clearance B are shown in Figure 10 and Figure 11, respectively. Lyapunov exponent diagrams at revolute clearance A and translational clearance B are displayed in Figure 12 and Figure 13. When the maximum Lyapunov exponent is greater than zero, the mechanism is in a chaotic state, and when the maximum Lyapunov exponent is less than zero, the mechanism is in a periodic state. Maximum Lyapunov exponents at the clearances of revolute joint A (X direction and Y direction) and translational pair B (X direction and Y direction) are 0.0521, 0.0573, 0.3915, and −0.0287, respectively.

The maximum Lyapunov exponent at the clearances, in descending order, are translational clearance (X direction), revolute clearance (Y direction), revolute clearance (X direction), and translational clearance (Y direction). From this, it can be inferred that translational clearance (X direction) has the highest degree of chaos, while translational clearance (Y direction) has the lowest degree of chaos. Revolute pair A (X direction and Y direction) and translational pair B (X direction) are in the chaotic state, and translational pair B (Y direction) is in periodic motion.

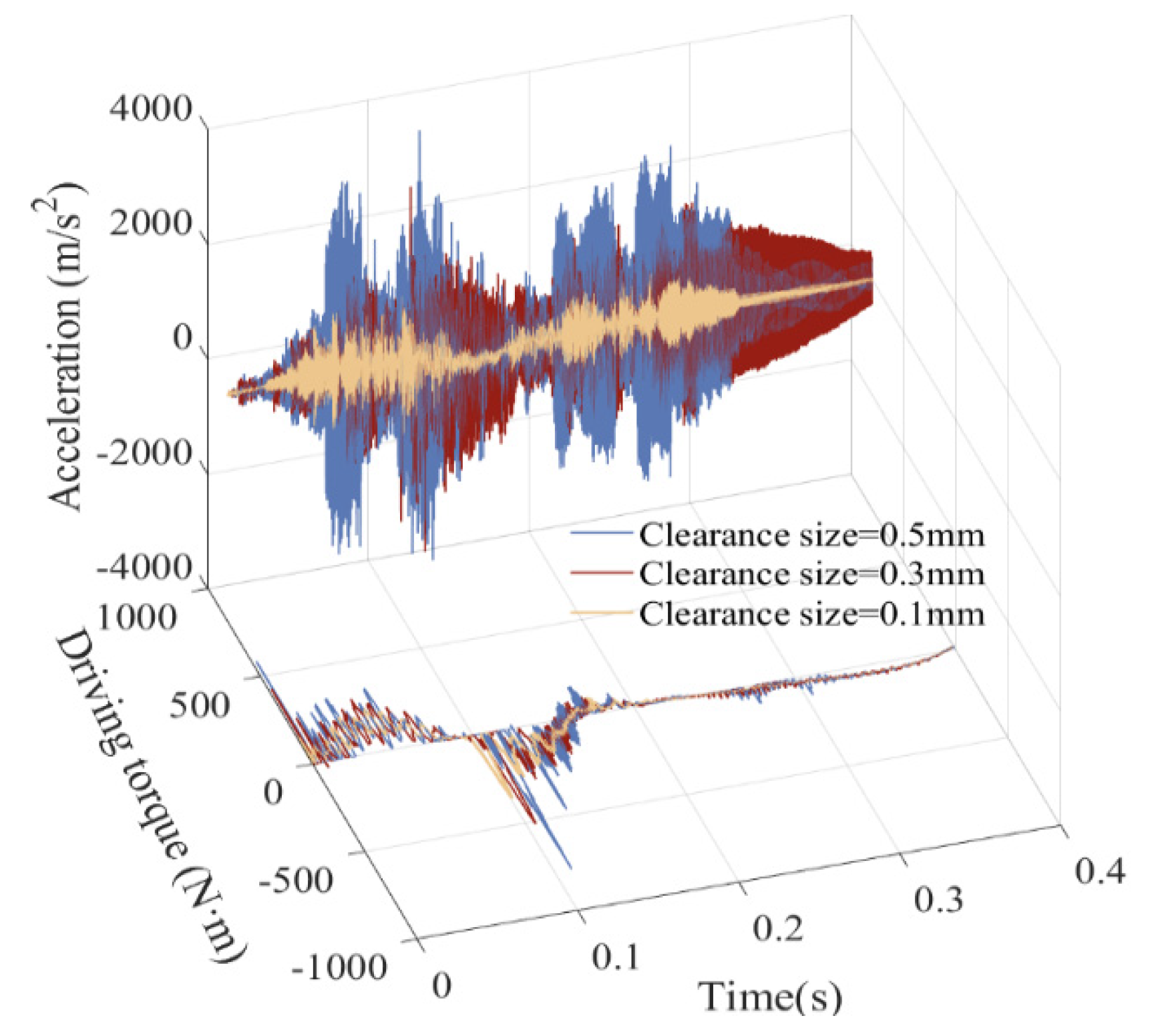
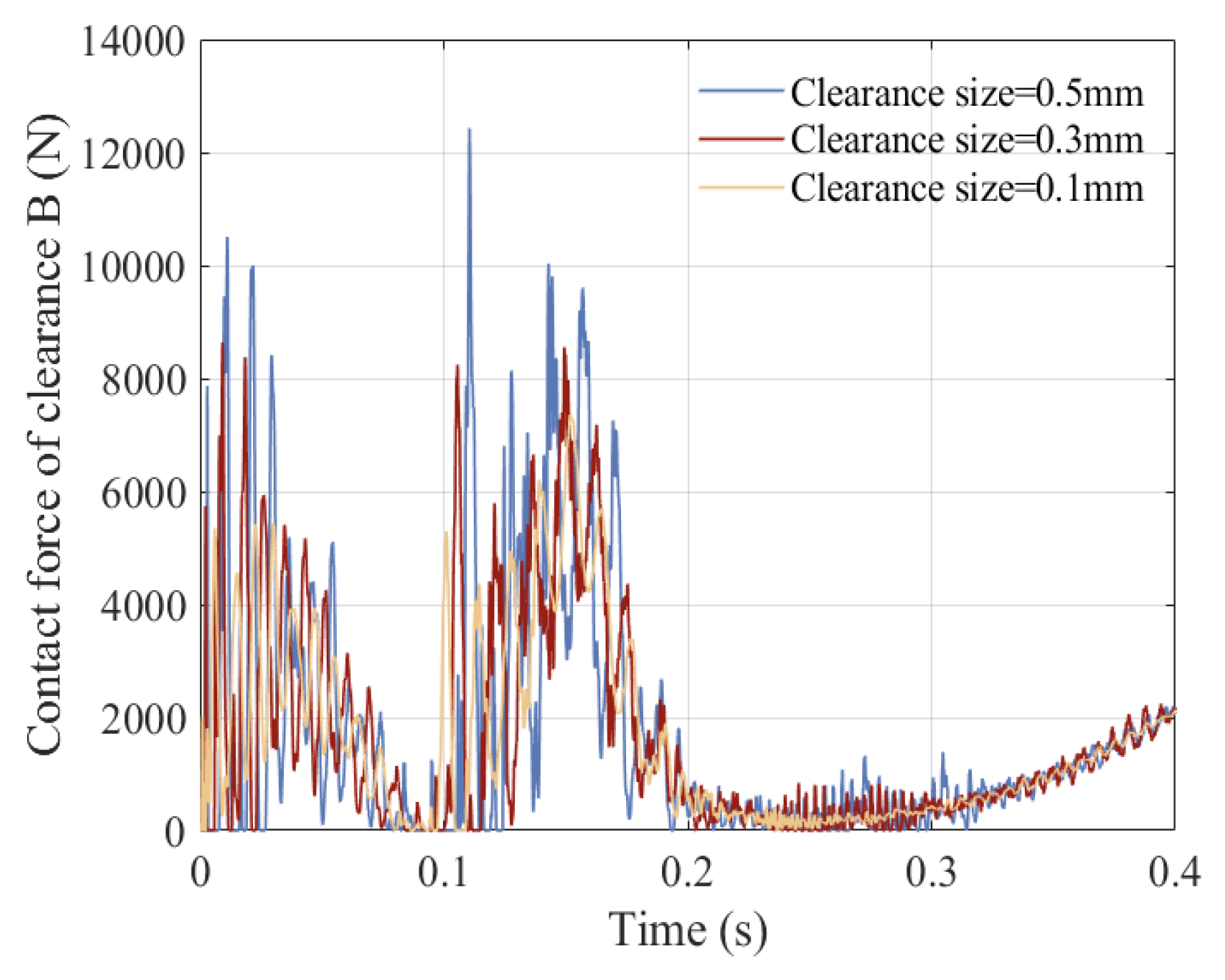
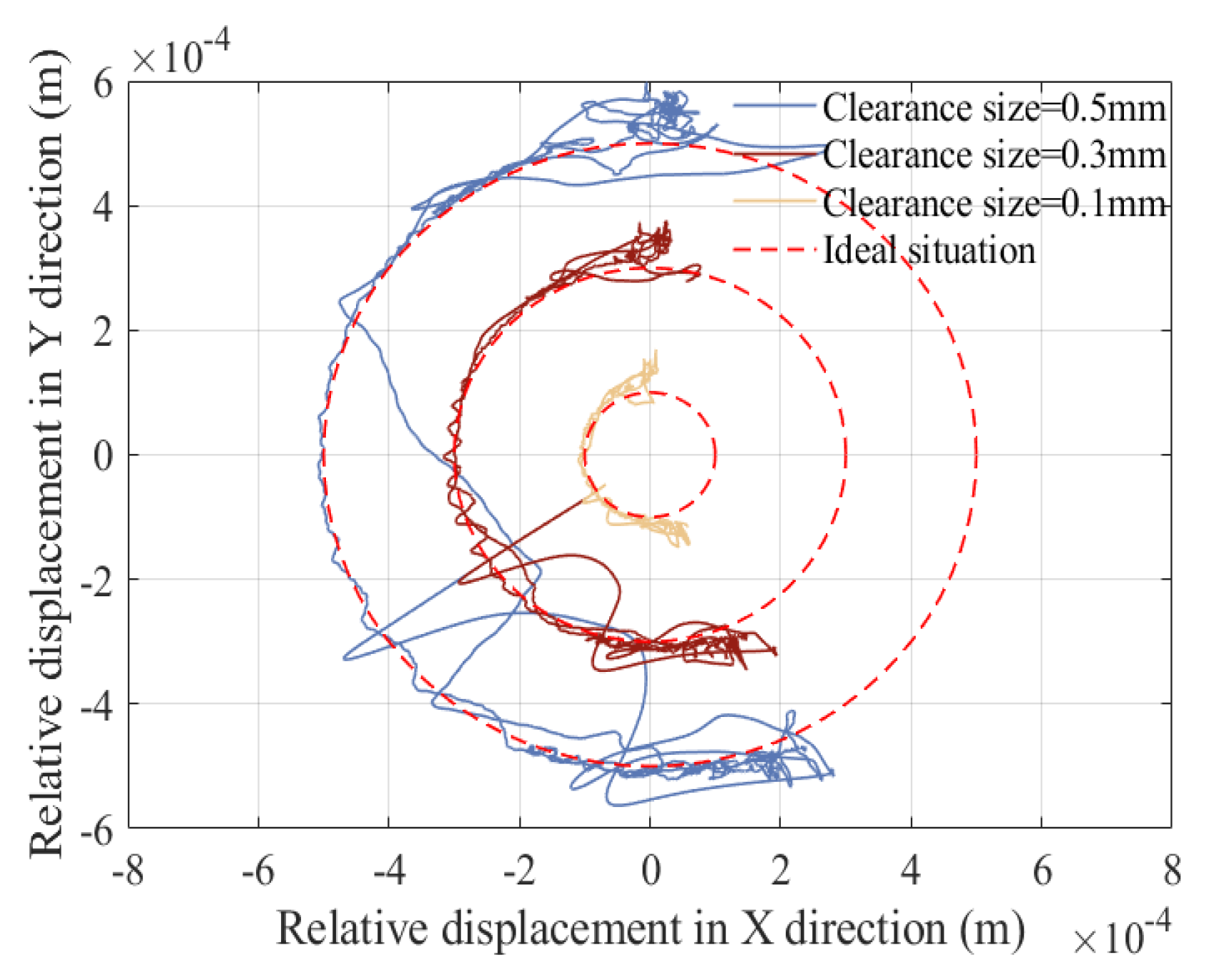
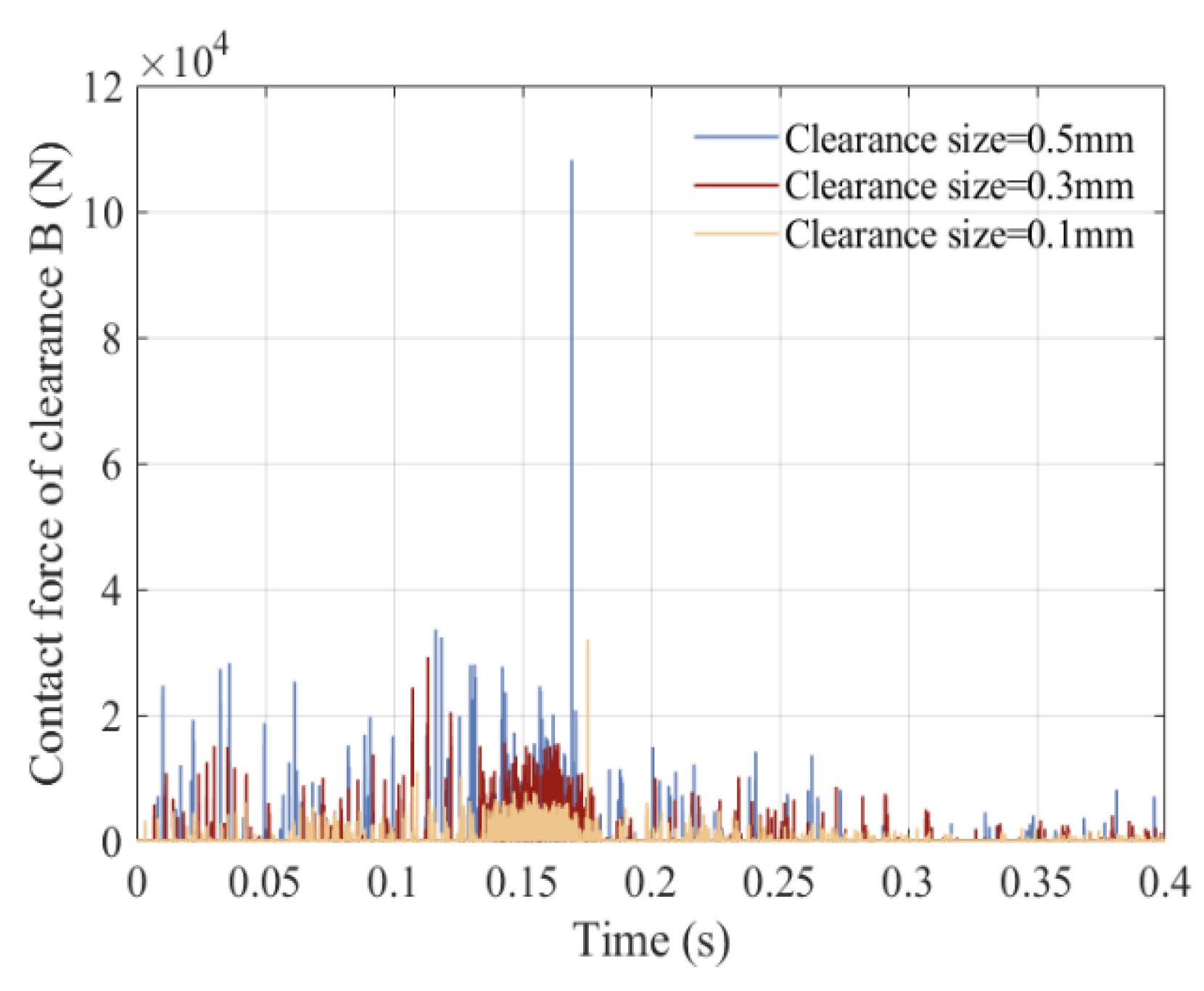
5.4. Influence of Clearance Values on the Dynamic Response

This section analyzes the influence of clearance sizes on the dynamic response of a rigid–flexible coupling six-bar mechanism with compound clearances. It is considered that clearance exists simultaneously at revolute pair A, as well as at translational pair B, and it is assumed that the three clearances have the same clearance value size. Three different clearance sizes are selected to analyze the impact of different clearance values on the mechanism, namely 0.1 mm, 0.3 mm, and 0.5 mm. The friction coefficient is set to 0.15, and the driving speed of slider 1 is set to 150 rpm. The displacement and velocity of the slider, acceleration of the slider, driving torque of crank, contact force of revolute clearance A, trajectory of revolute clearance A, contact force of revolute clearance B, and trajectory of revolute clearance B are shown in Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19.

From the displacement curve, clearance size has a relatively small impact on displacement, and the curve fluctuations are not significant. The speed curve fluctuates to a certain extent with the increase in clearance size, but there is no significant vibration peak. The acceleration, driving torque, and collision force curves at the clearances have significant vibration peaks and intense vibration frequencies, and as the clearance value increases, the response peak also increases. From the center trajectories of clearance A, the collision of clearance A in the revolute pair is mainly concentrated on the upper and lower ends. From the center trajectory of translational pair B, collision and contact between the guide rail and slider are mainly concentrated on the left guide rail, and as clearance size increases, the motion trajectory of the slider becomes more chaotic.

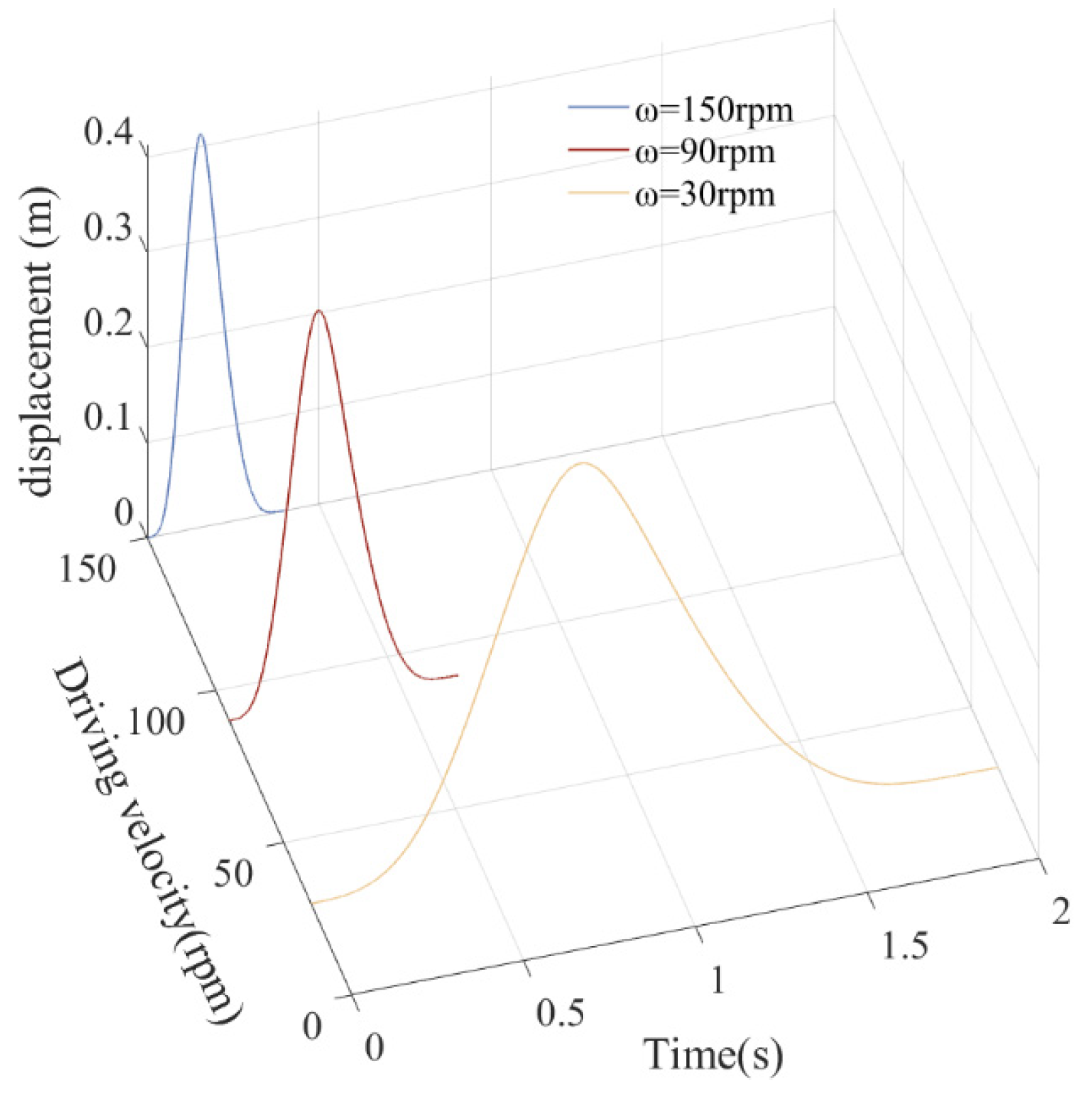
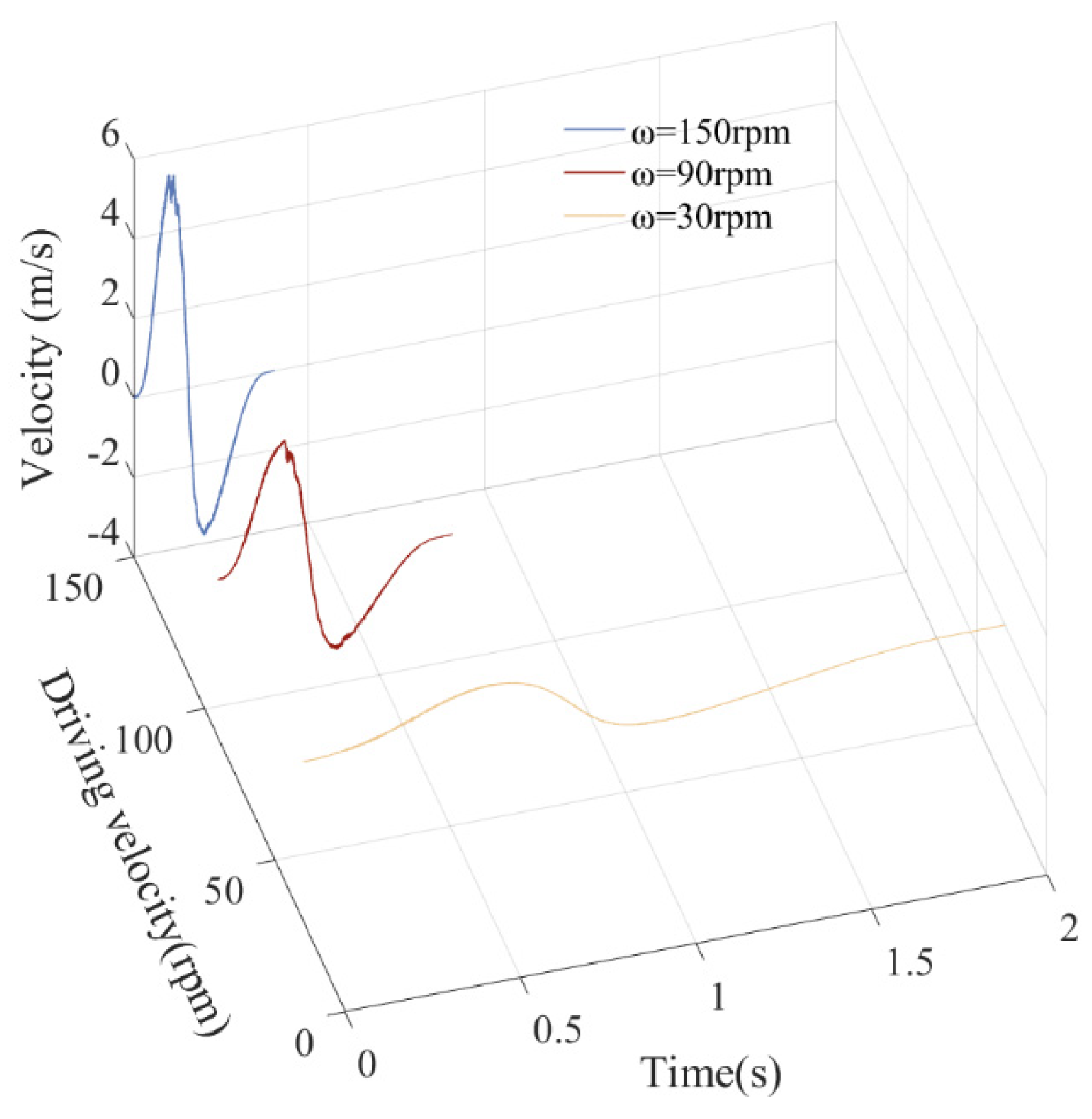
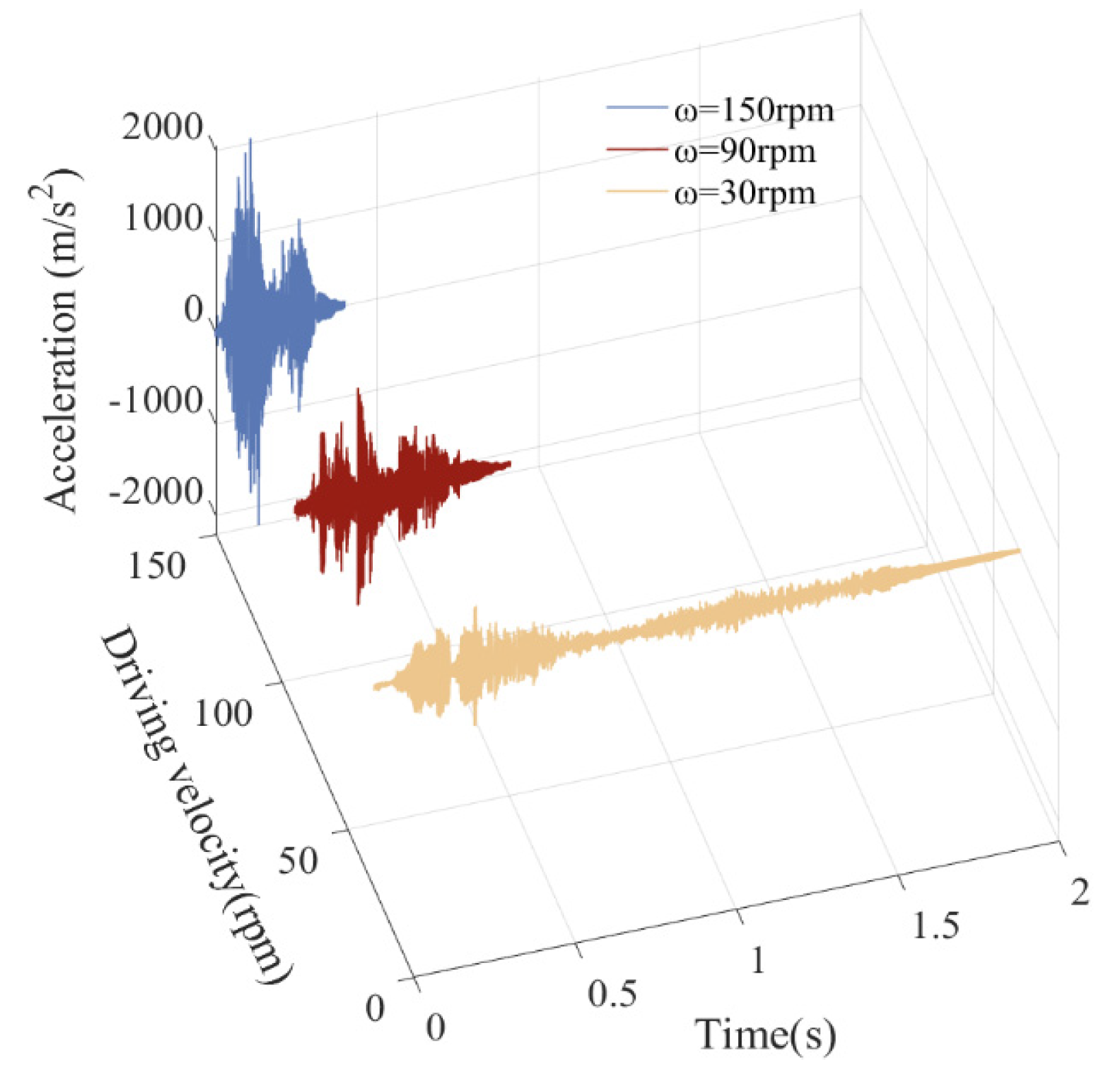
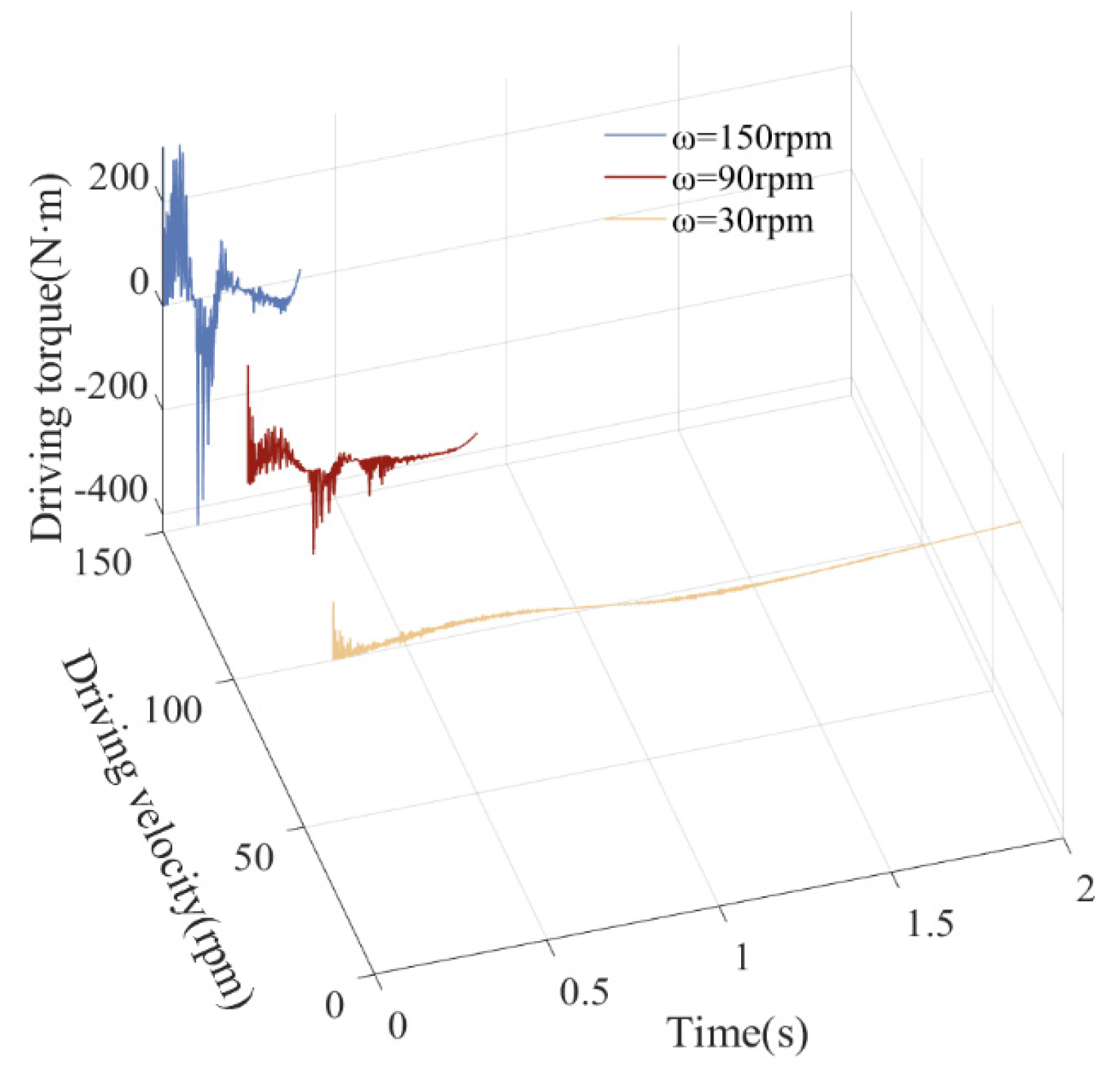
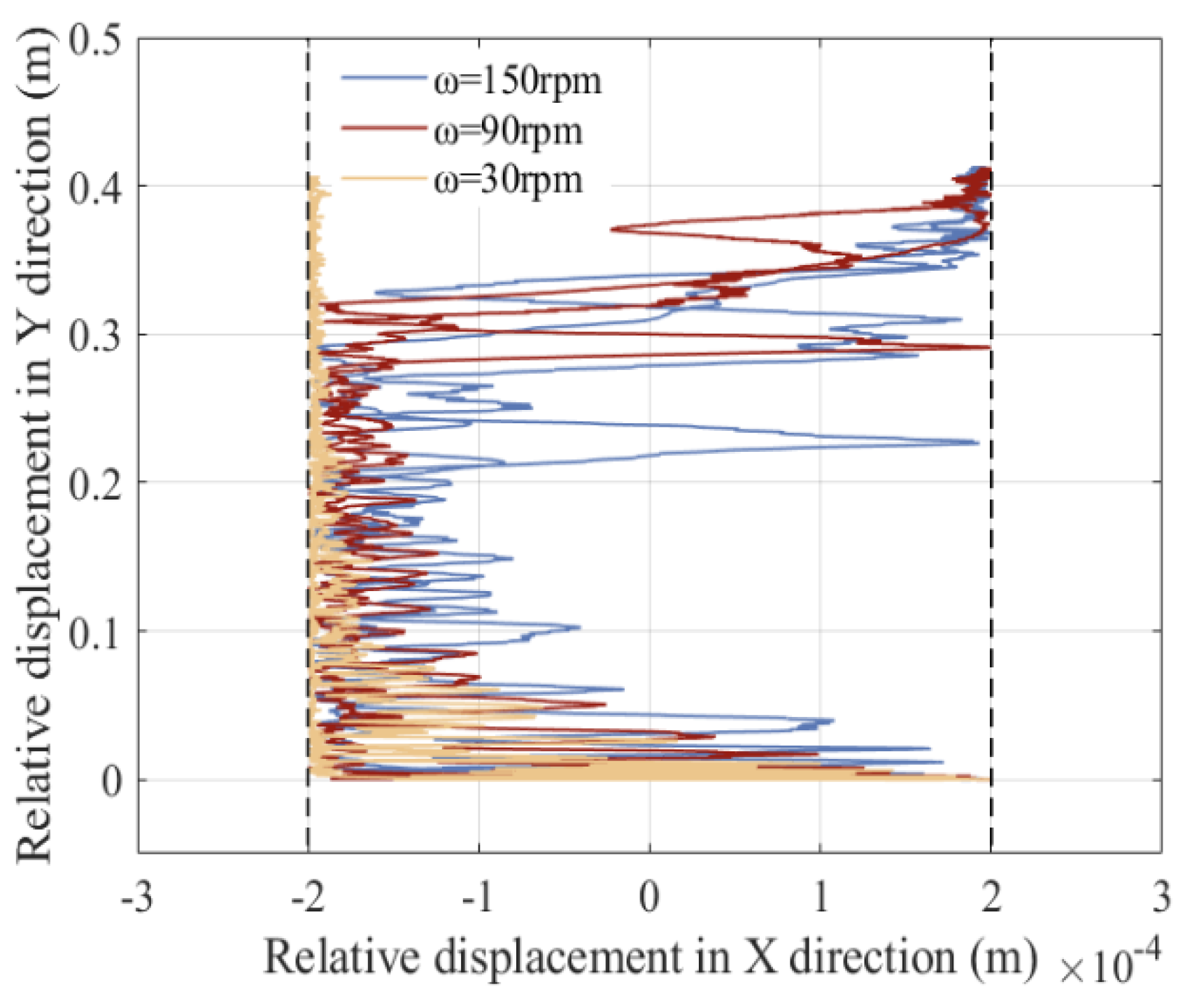
5.5. The Influence of Driving Velocities on Dynamic Response

This section analyzes the influence of driving speed on the dynamic response of a rigid–flexible coupling six-bar mechanism with compound clearances. Three different driving speeds of slider 1 are selected to analyze the impact of driving speed on the mechanism, namely 30 rpm, 90 rpm, and 150 rpm. The friction coefficient is set to 0.15, and clearance values of revolute pair clearance A and translational pair clearance B are both 0.2 mm. The displacement of the slider, velocity of the slider, acceleration of the slider, driving torque of crank, contact force of revolute clearance A, trajectory of revolute clearance A, contact force of translational pair B, and trajectory of translational pair B are displayed in Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26 and Figure 27.

From the displacement curve, there is no significant fluctuation or vibration in the displacement curve, and the effect of changes in driving speed on displacement is relatively small. From curves of speed, acceleration, driving torque, and collision force at clearance, as driving speed increases, peak dynamic response also increases, and the mechanism becomes very unstable. Due to the faster running speed of the mechanism, the impact of revolute joint A and the impact of translational pair B become more severe, the fluctuation in the response is more significant, and the peak value also increases. The center trajectory of rotating clearance and translational clearance shows that when running speed increases from 30 rpm to 90 rpm, and then to 150 rpm, the degree of confusion in the trajectory increases, and the number of collisions between elements of clearance pairs increases.

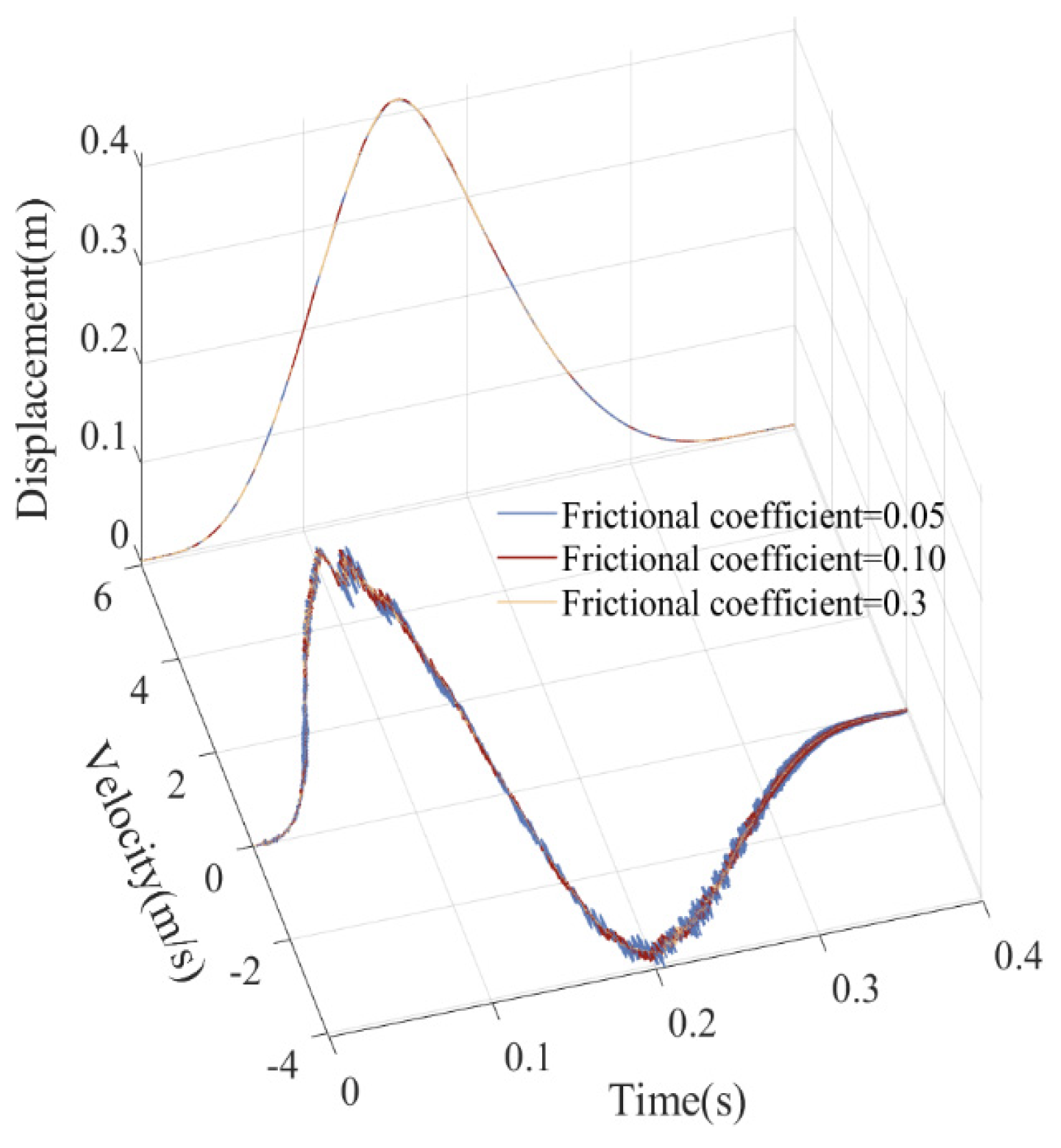
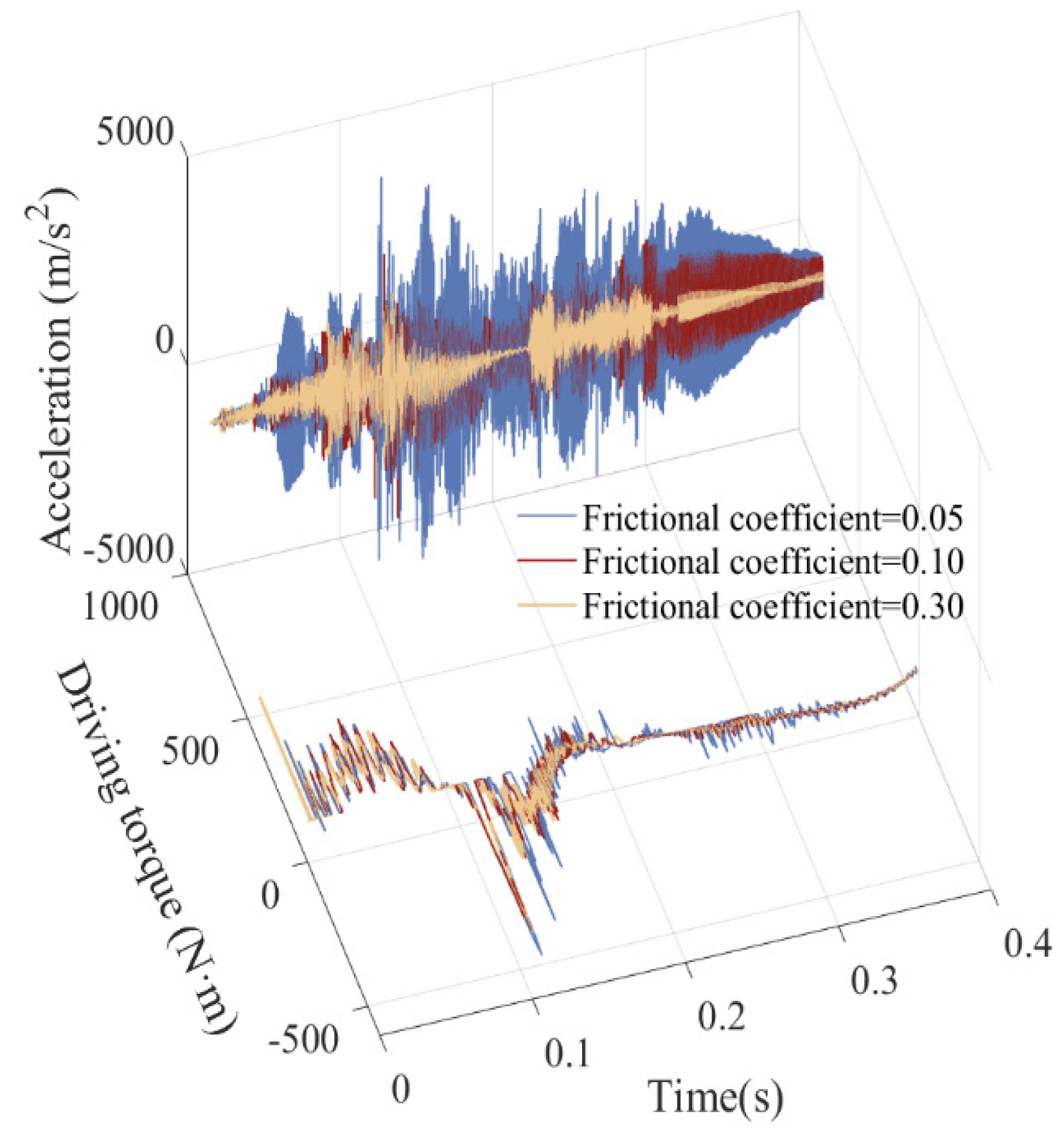
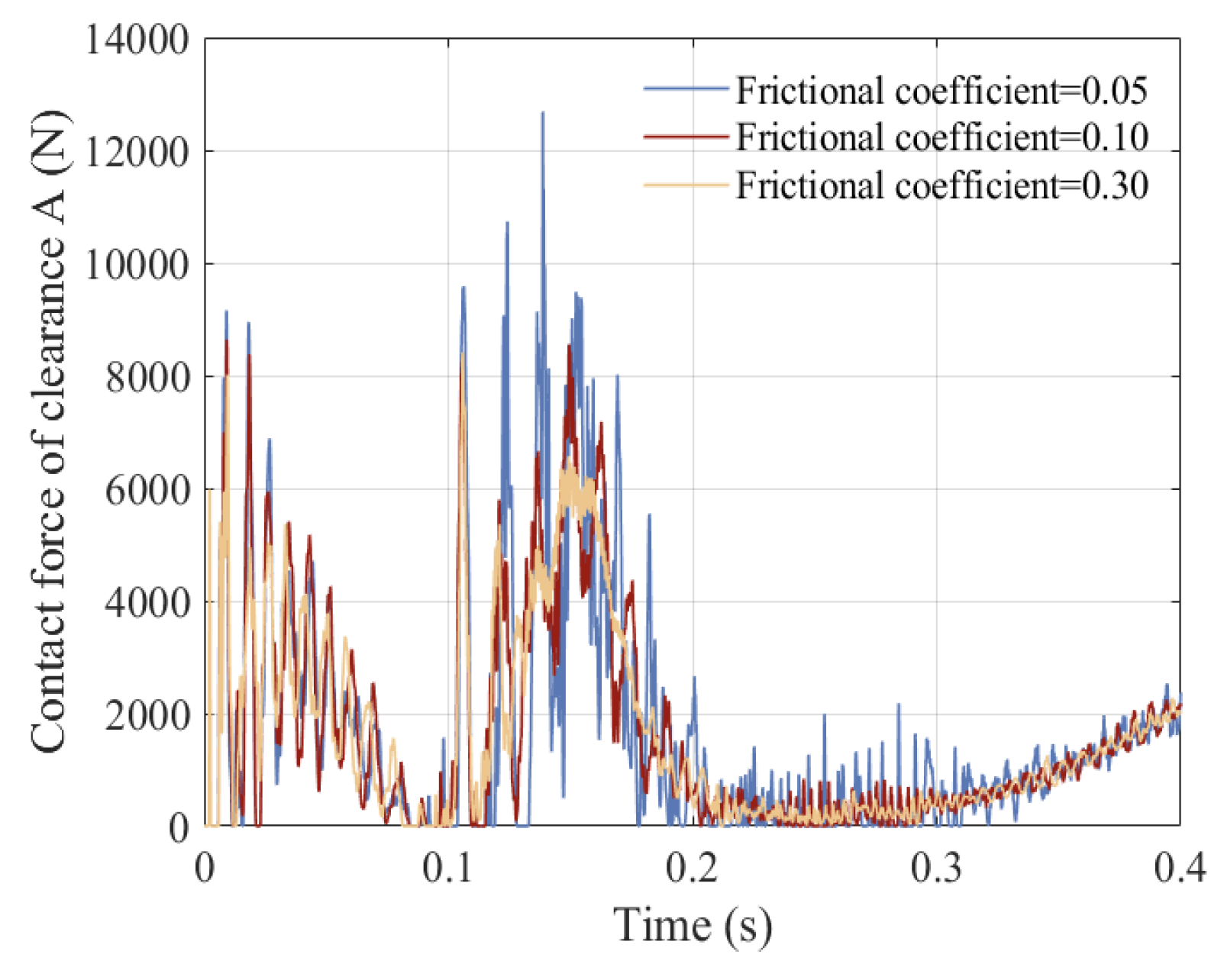
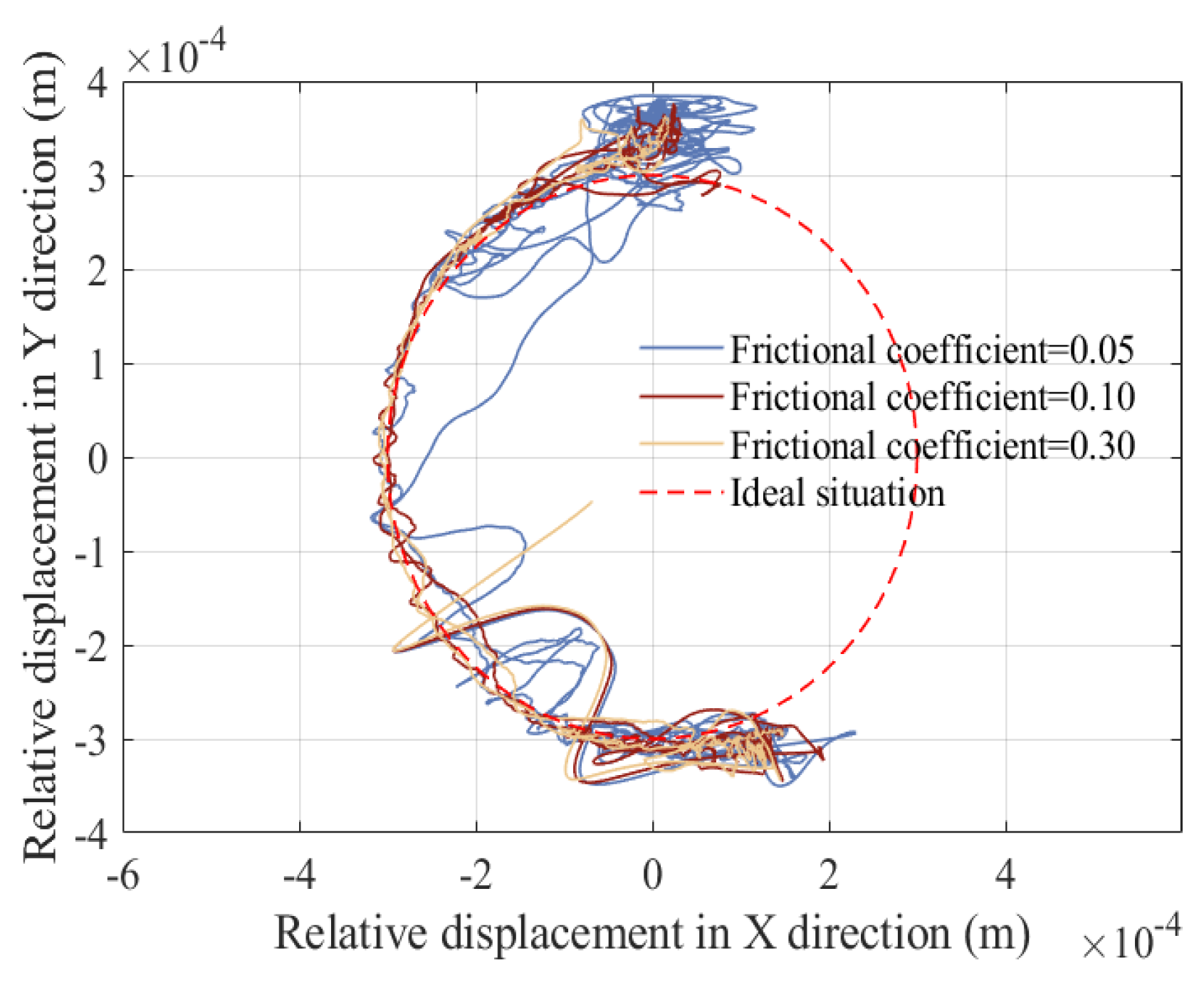
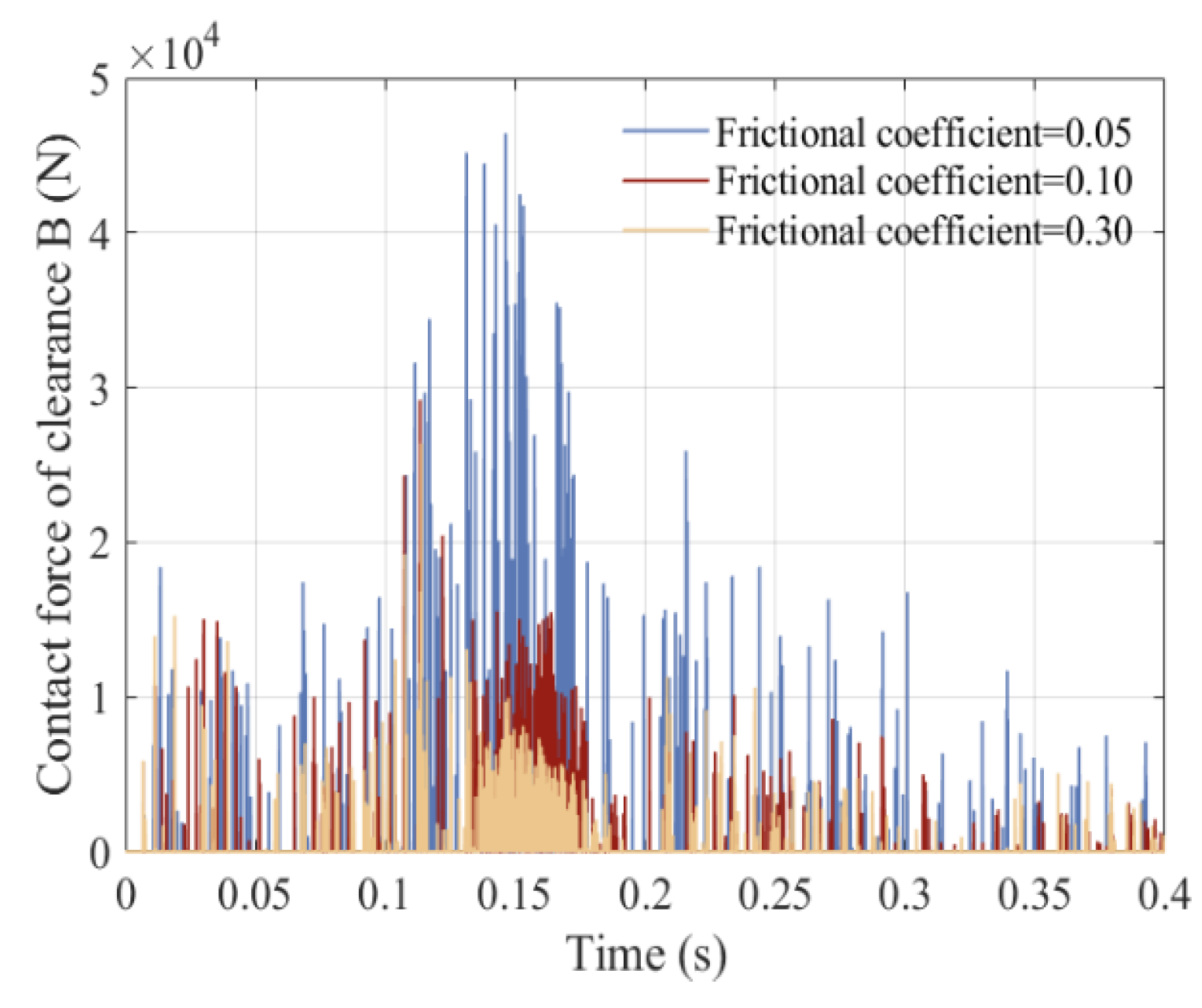
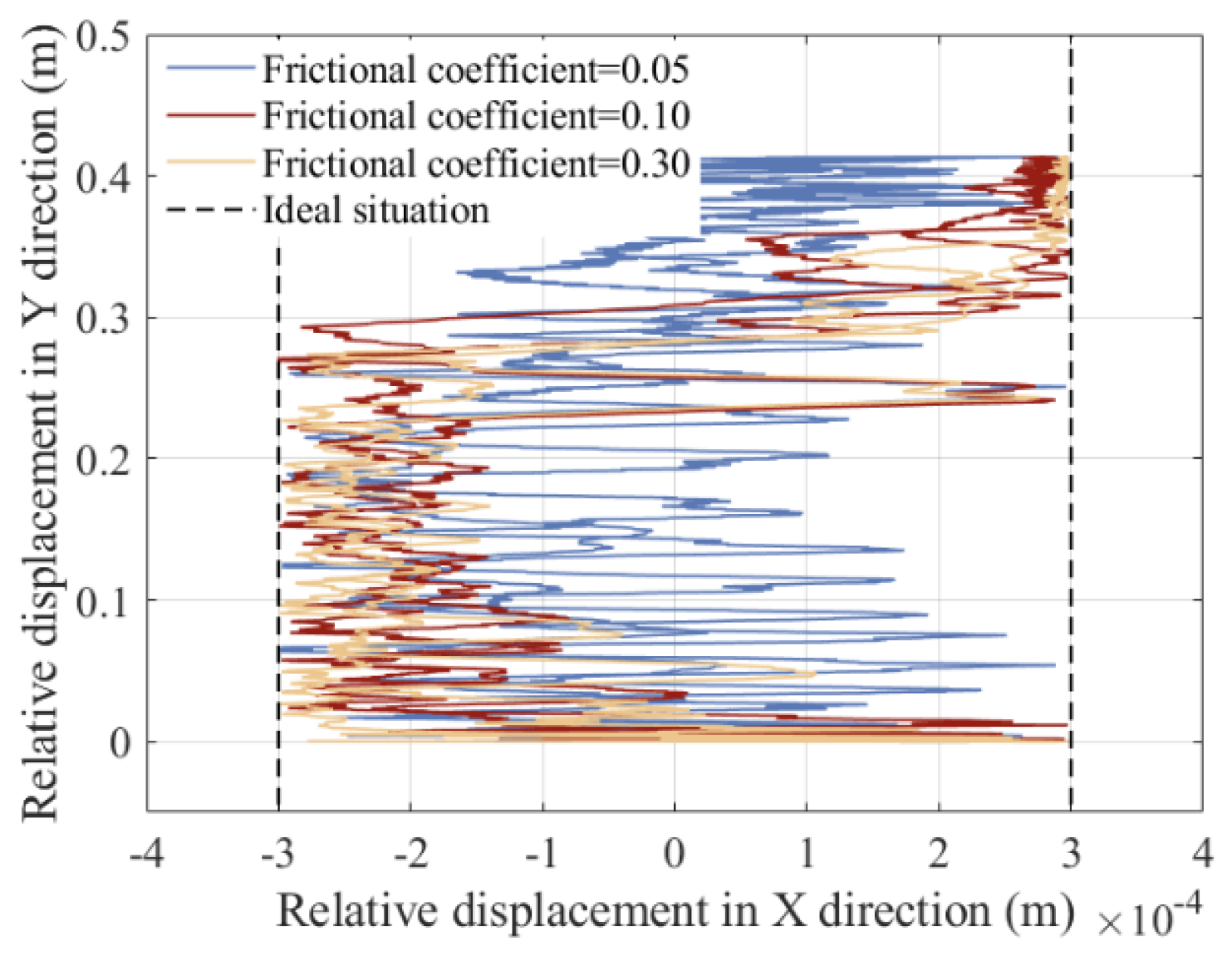
5.6. Influence of Frictional Coefficients on the Dynamic Response

Due to the presence of nonlinear factors such as clearance between revolute pairs, clearance between translational pairs, and elastic deformation, changes in the frictional coefficients of a clearance pair can also affect its operational stability. So, in order to better describe the impact of frictional coefficients on the dynamics, displacement, and velocity of the slider, the acceleration of the slider and driving torque of crank, the contact force of revolute clearance A, the trajectory of revolute clearance A, the contact force of revolute clearance B, and the trajectory of revolute clearance B changing by frictional coefficient are studied, as shown in Figure 28, Figure 29, Figure 30, Figure 31, Figure 32 and Figure 33. The three selected friction coefficients are 0.05, 0.1, and 0.3. The operating speed of the mechanism is 150 rpm, and clearance values of the revolute pair and translational pair are 0.3 mm.

Friction has a significant impact on the dynamic characteristics of a mechanism. Friction converts the mechanical energy of a system into thermal energy, causing the energy of the system to gradually dissipate, thereby changing vibration characteristics. This energy loss has a significant impact on dynamic characteristics. Increasing the friction coefficient will further increase the frictional force, causing an increase in vibration damping and a gradual decrease in amplitude, thereby reducing the system’s output power and increasing its heat loss. According to the dynamic response diagram (Figure 28, Figure 29, Figure 30, Figure 31, Figure 32 and Figure 33), as the friction coefficient increases, vibration frequency and the amplitude of the mechanism’s dynamic weaken, and the mechanism gradually exhibits a stable motion trend.

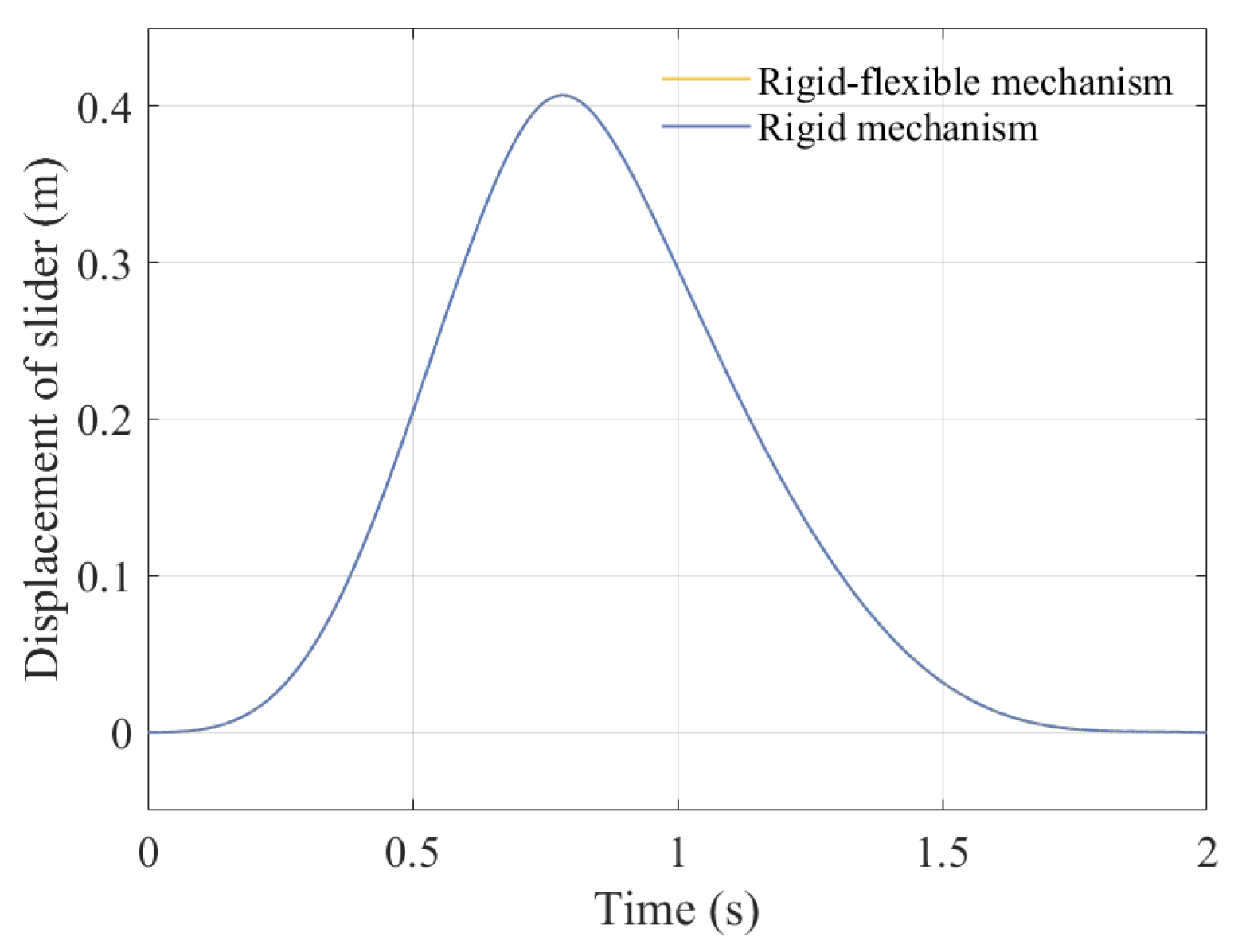
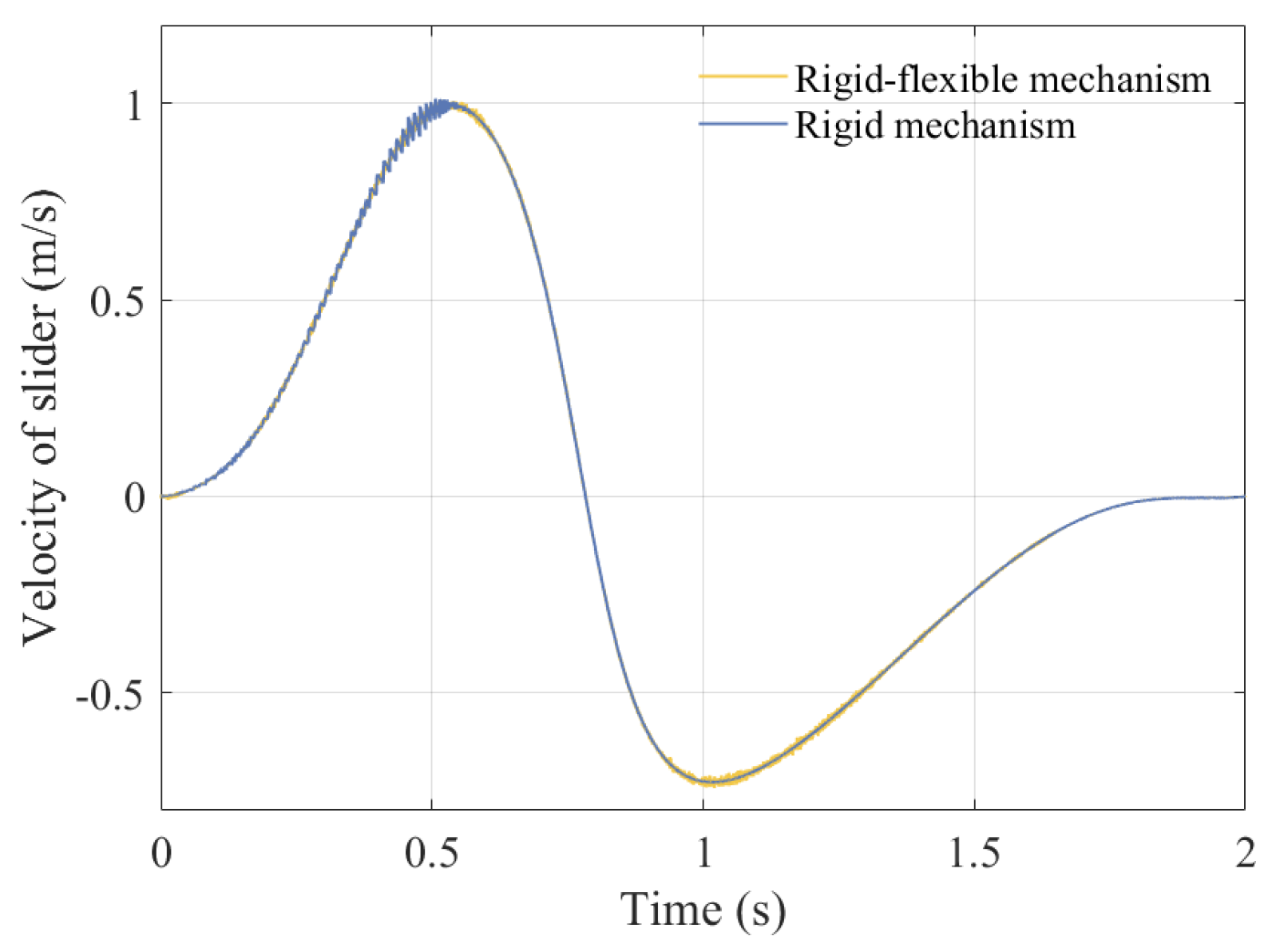
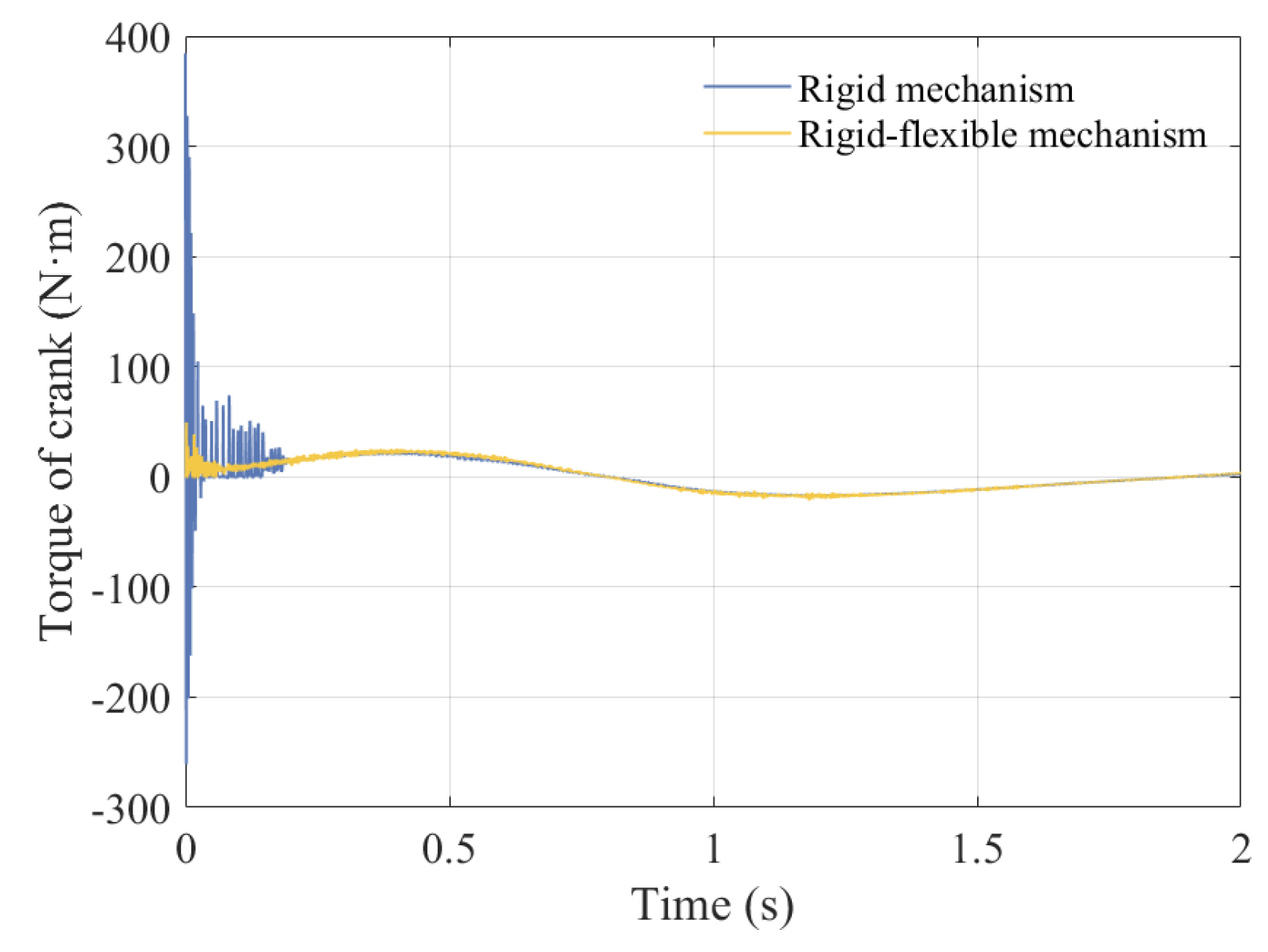
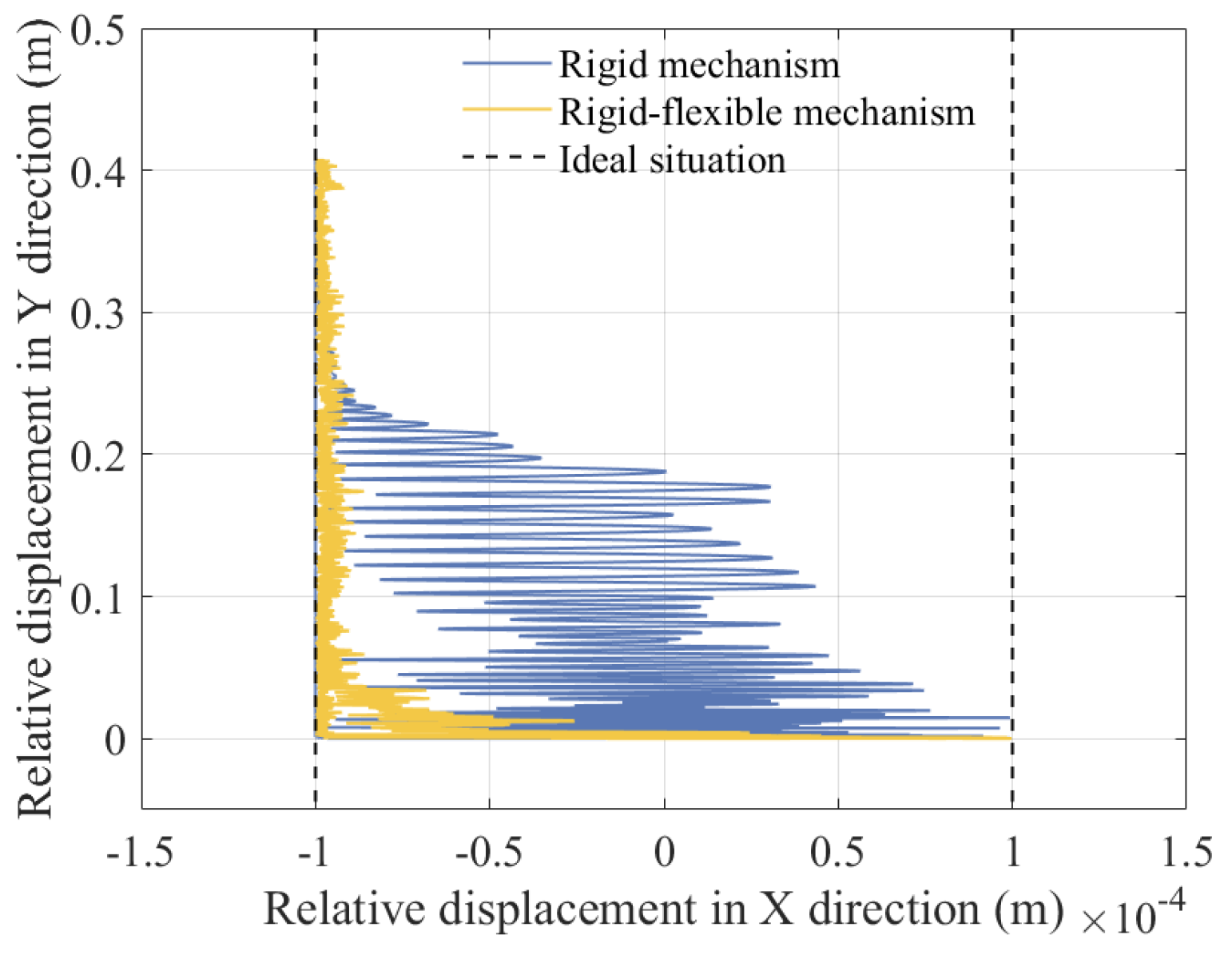
5.7. Comparison of Dynamic Response Between Rigid Mechanisms with Clearance and Rigid–Flexible Coupling Mechanisms with Clearance

The focus of this study is to simultaneously consider the coupling effects of rotating pair clearance, moving pair clearance, and component flexibility on the mechanism. Many studies have overlooked the influence of component flexibility. Therefore, this article adds a comparison of displacement, velocity, acceleration, and center trajectory between rigid mechanisms with clearance and rigid–flexible coupling mechanisms with clearance, as shown in Figure 34, Figure 35, Figure 36, Figure 37, Figure 38, and Figure 39, respectively.

From the curve of slider displacement and velocity, it can be seen that the flexibility of the component has a relatively small impact on displacement, and velocity will produce a certain amount of small vibration. According to Figure 36 and Figure 37, the elastic deformation of the component causes high-frequency vibrations in the acceleration and torque curves, but the peak values decrease. According to the center trajectory of the clearance, it is found that when considering the elastic deformation of the component, the trajectories of the shaft and slider focus on one area for high-frequency vibration. The main reason is that the components undergo elastic deformation when subjected to force, which may cause deviations between the actual motion and ideal motion of the mechanism. Meanwhile, the flexible deformation of the components will consume some energy, resulting in a decrease in the energy transfer efficiency of the mechanism.

6. Conclusions

The coupling effect of disturbance factors, such as translational clearance, revolute clearance, and component flexibility, seriously affects motion characteristics, dynamic response, and chaotic characteristics. Therefore, this paper focused on studying the impact of their coupling effects on the comprehensive performance of a symmetrical structure press mechanism.

(1)

A dynamic model of a mechanism considering multiple disturbance factors (including translational clearance, revolute clearance, and component flexibility) was established. The coupling effect between the revolute clearance, the translational clearance, and the elasticity of the components can make the motion of the mechanism unstable and produce a certain degree of vibration, and the dynamic response curve will also have certain fluctuations.

(2)

The motion state of the mechanism was quantitatively and qualitatively determined using phase diagrams, Poincaré mappings, and maximum Lyapunov exponents. It was found that revolute pair A (X direction and Y direction) and translational pair B (X direction) are more prone to chaotic states, whereas translational pair B (Y direction) is more prone to periodic motion.

(3)

The effect of various parameters on dynamics were analyzed, including friction coefficient, driving speed, and clearance value. As a result, it was found that with the increase in driving speed and clearance value, as well as the decrease in friction coefficient, the stability of the mechanism weakened, and the vibration of the mechanism’s dynamic response intensified.

This paper proposes an accurate modeling method for planar multilink symmetrical structure press mechanisms, comprehensively considering the coupling effect of revolute clearance and translational clearance, as well as flexible components. This method can more realistically and accurately describe the actual behavior of a mechanism during motion. By establishing a dynamic model of a mechanism with clearance for simulation analysis, the dynamic performance of mechanisms under different working conditions can be predicted, and potential design problems such as component wear and fatigue damage caused by clearance can be identified in advance. This can optimize the design parameters of the symmetrical structure press mechanism, improve design accuracy and reliability, and reduce product development costs and risks.