Construction Method of Compound Ground Motion Intensity Measure Based on Mutual Information Asymmetry for Engineering Seismic Fragility Analysis
Abstract
:1. Introduction
2. Compound IM Construction of Ground Motion
2.1. Candidate IMs
2.2. Mutual Information Theory
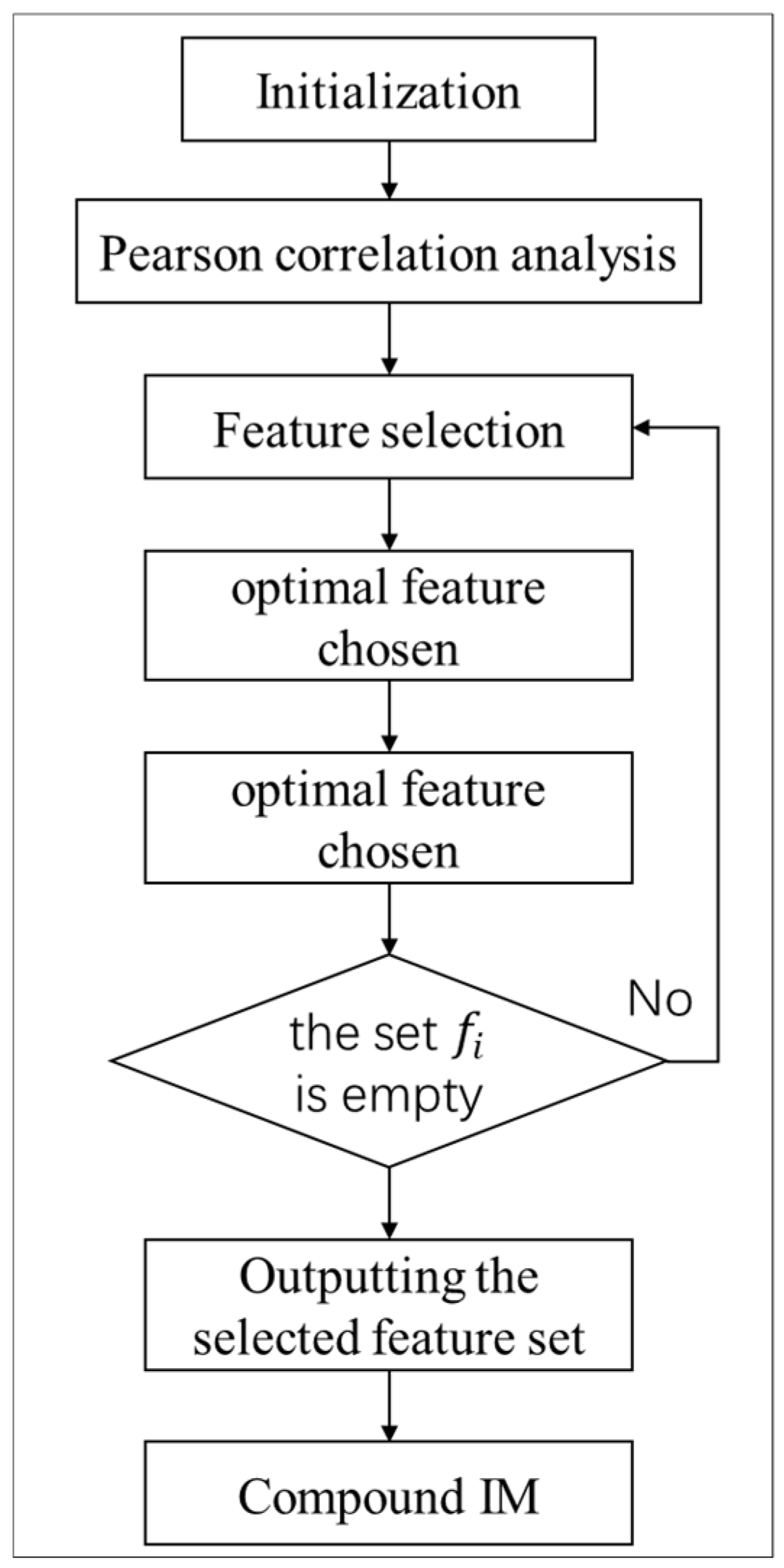
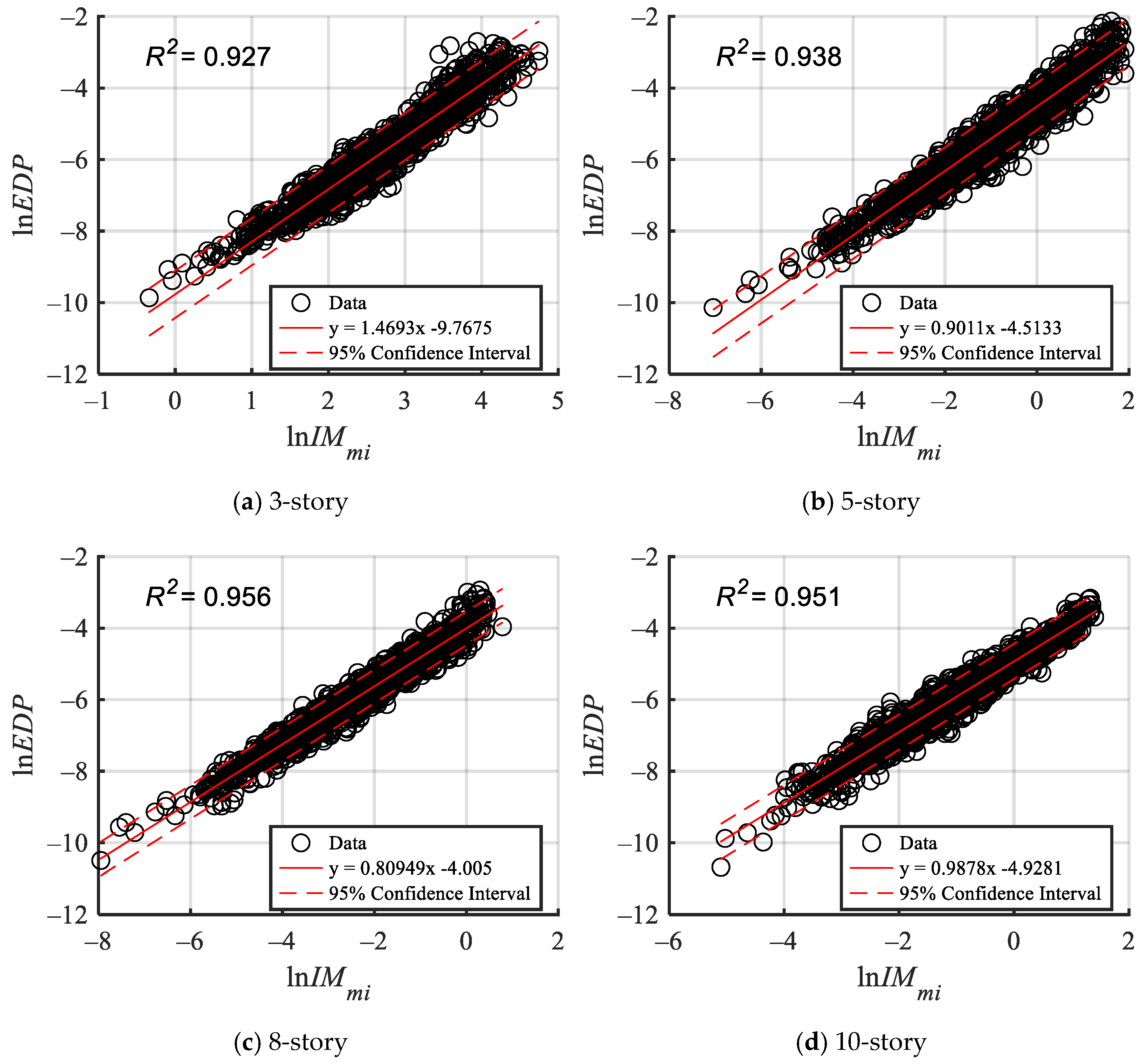
2.3. Construction of Compound Ground Motion IM
3. Seismic Record Set and Structural Model
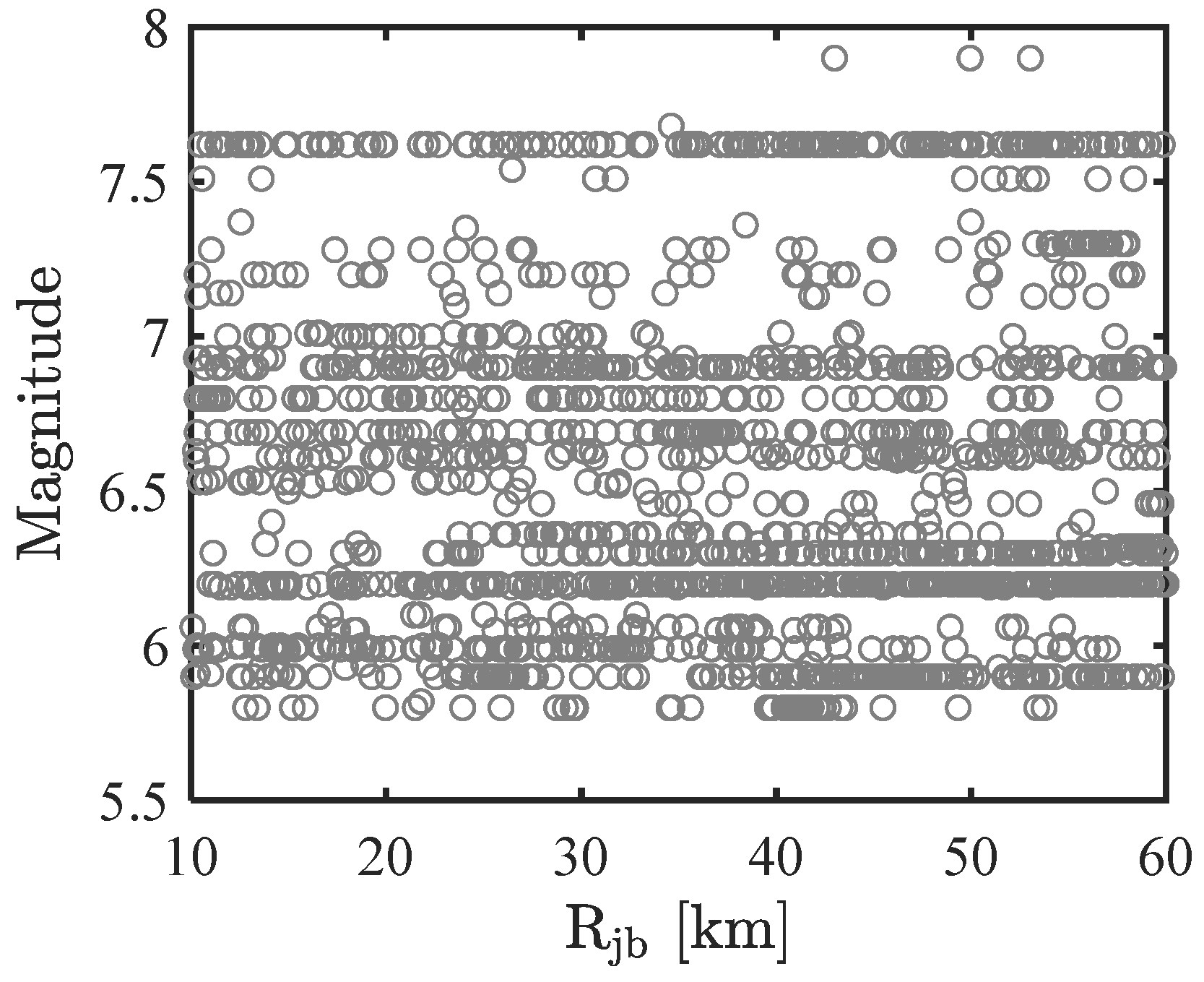
3.1. Selection of Ground Motion Record Set
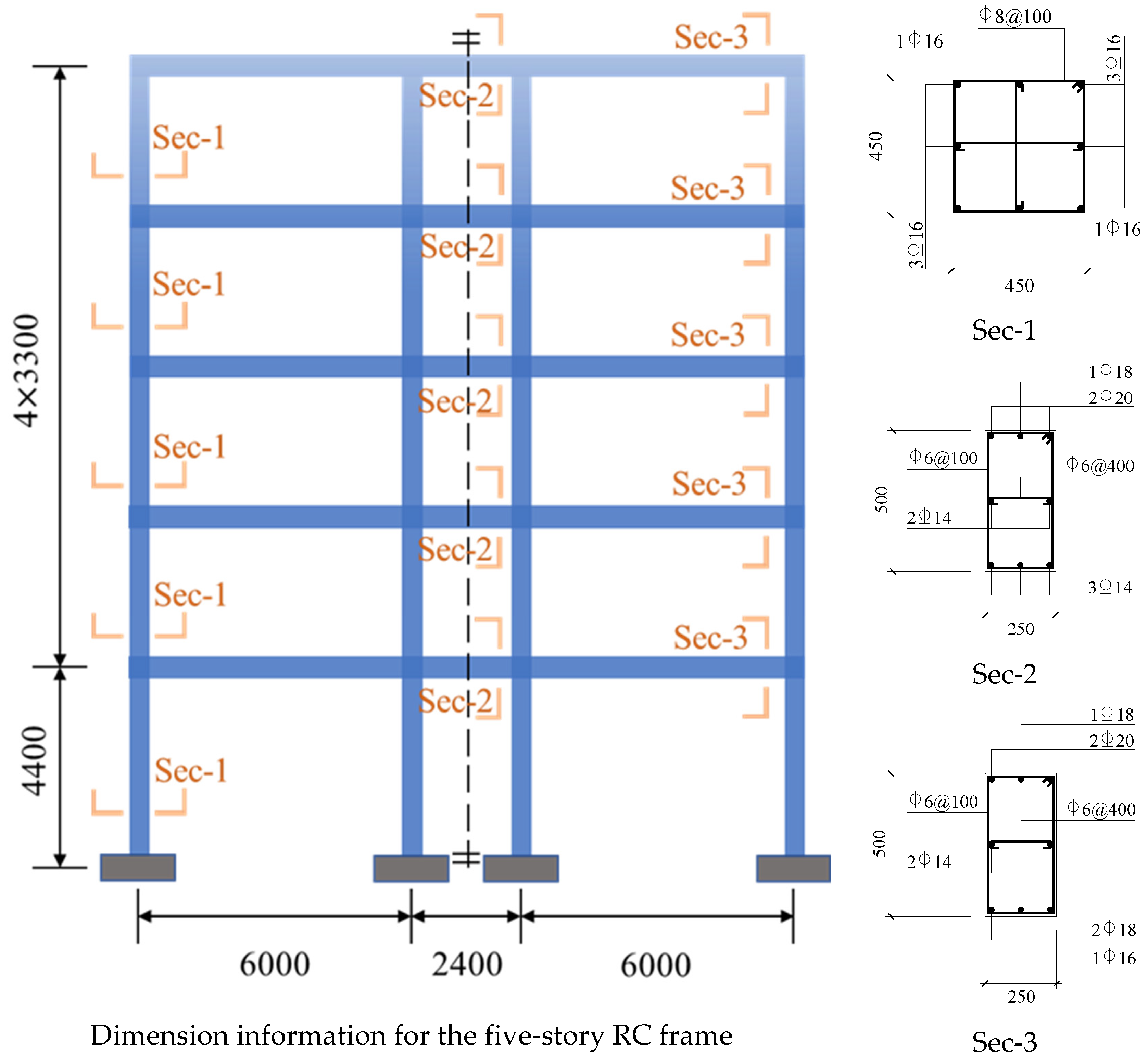
3.2. Structural Model
4. Feature Parameter Selection
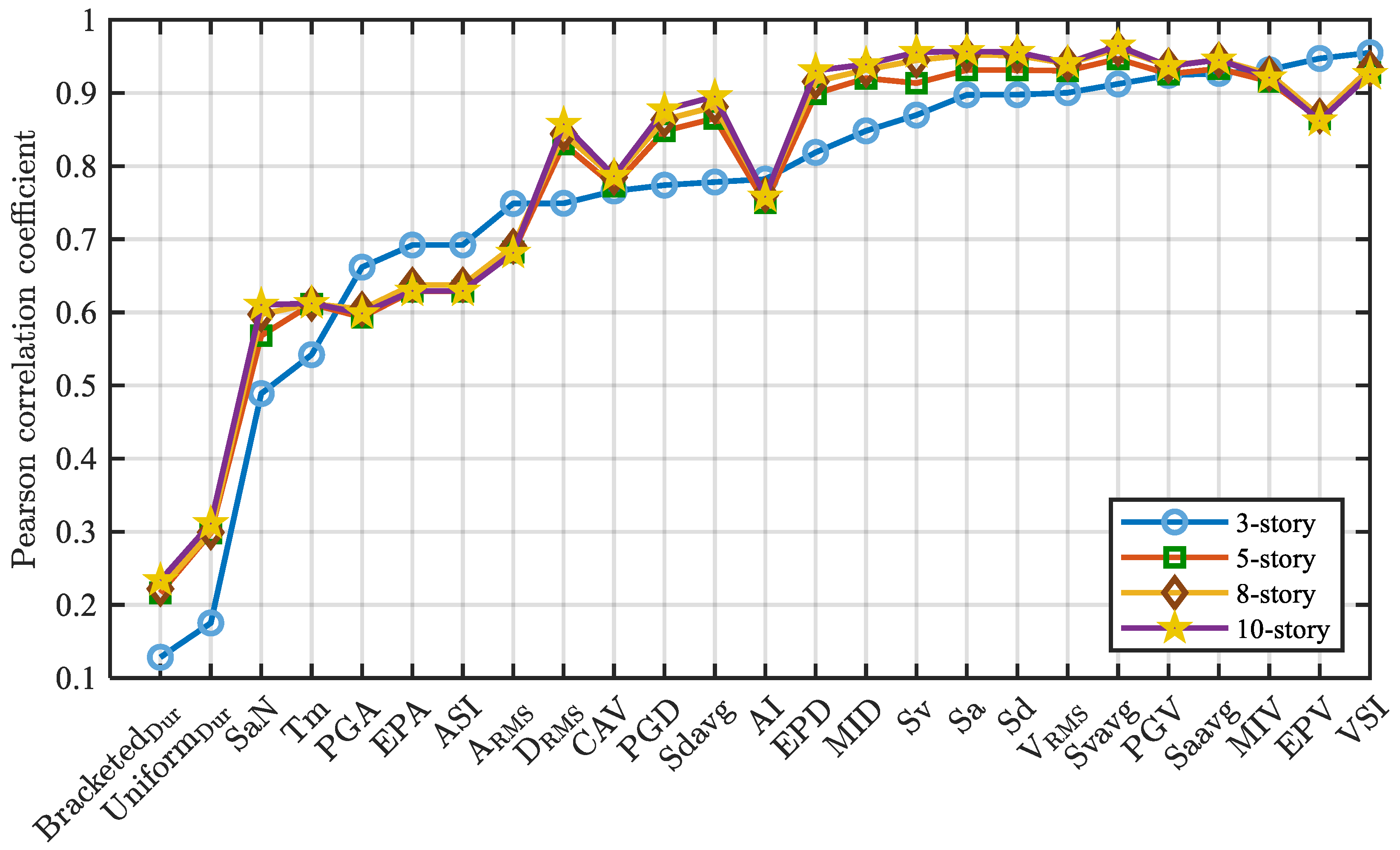
4.1. Pearson Correlation Coefficient
4.2. Multiple Regression Prediction
5. Probabilistic Seismic Fragility Analysis
5.1. Analysis Method
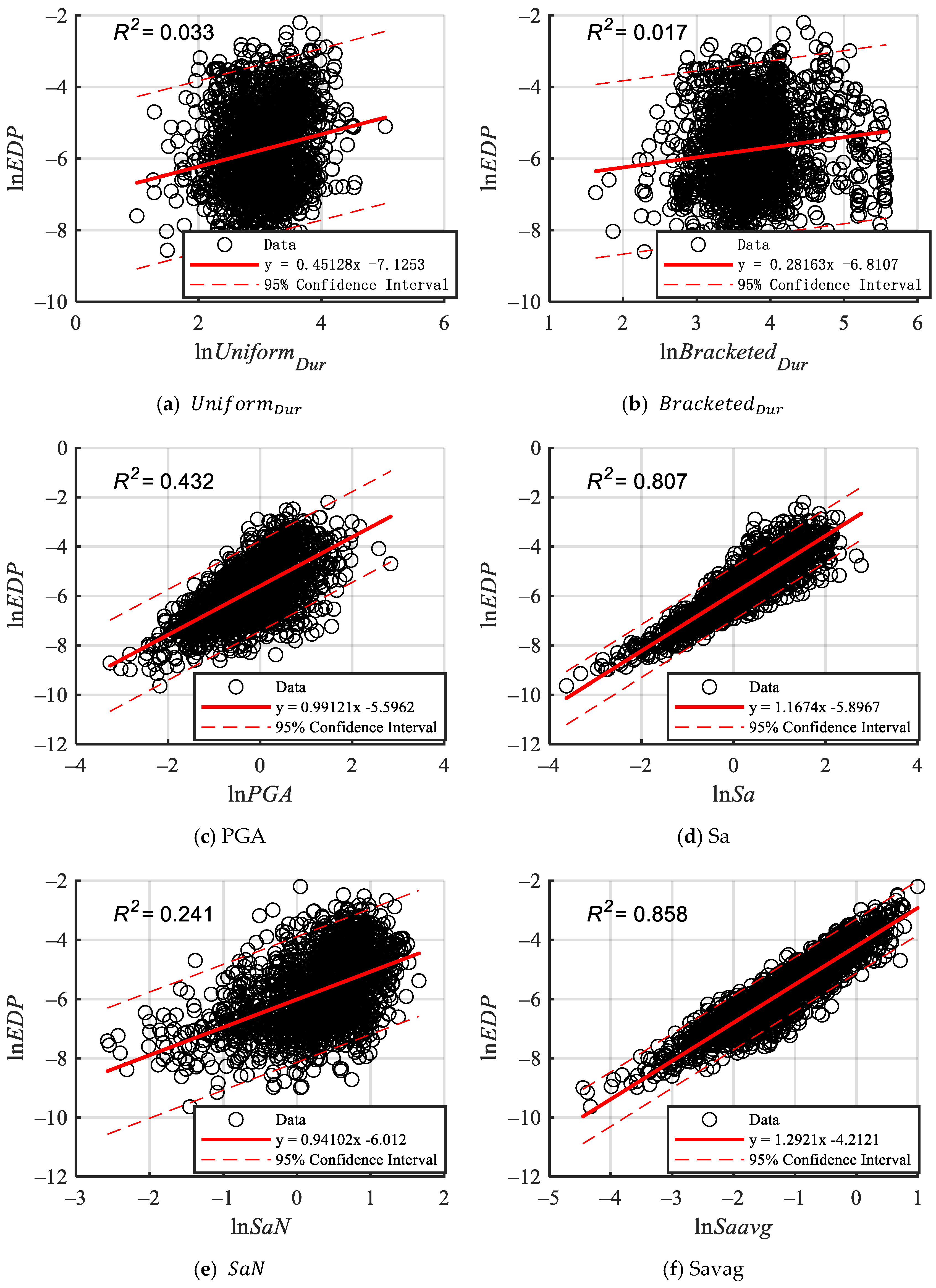
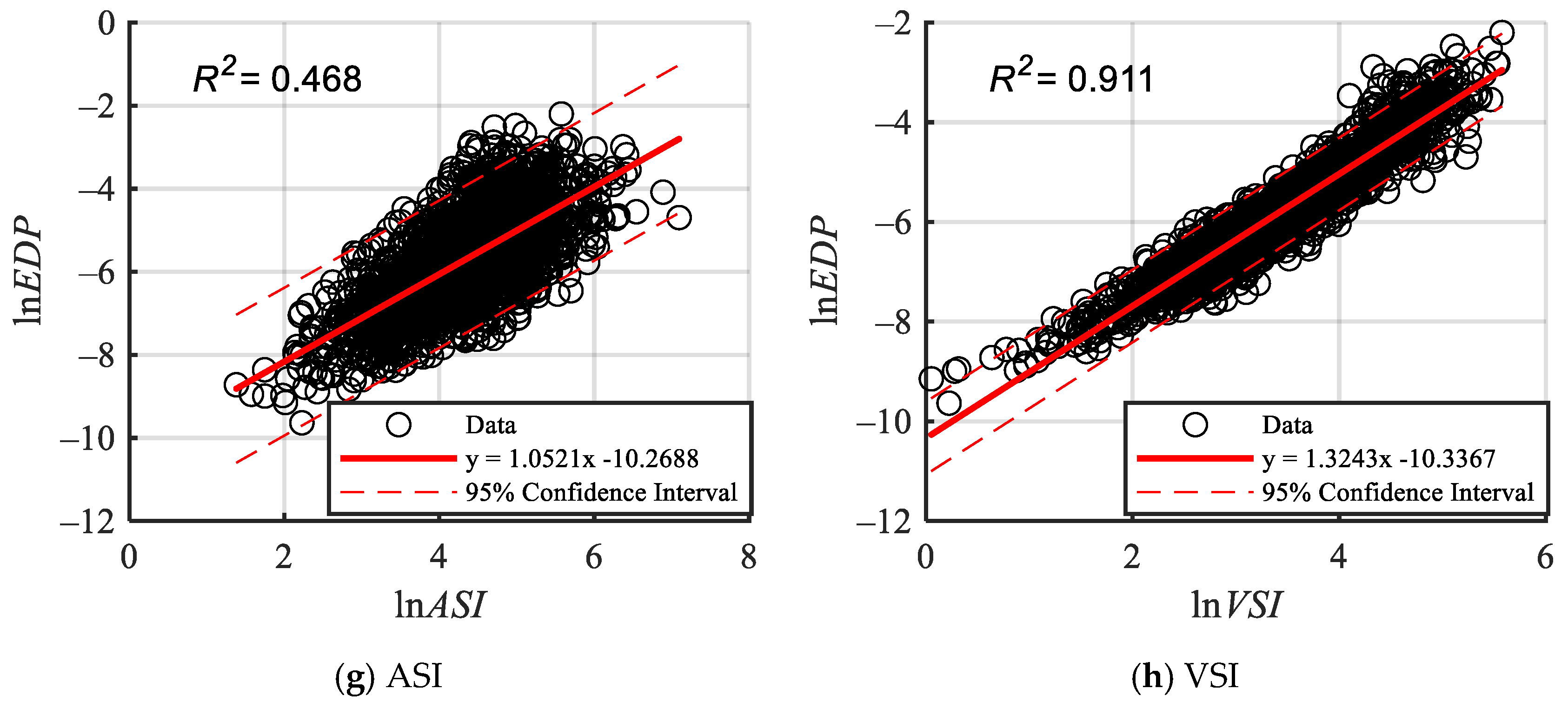
5.2. Probabilistic Seismic Demand Model
5.3. Evaluation Criteria
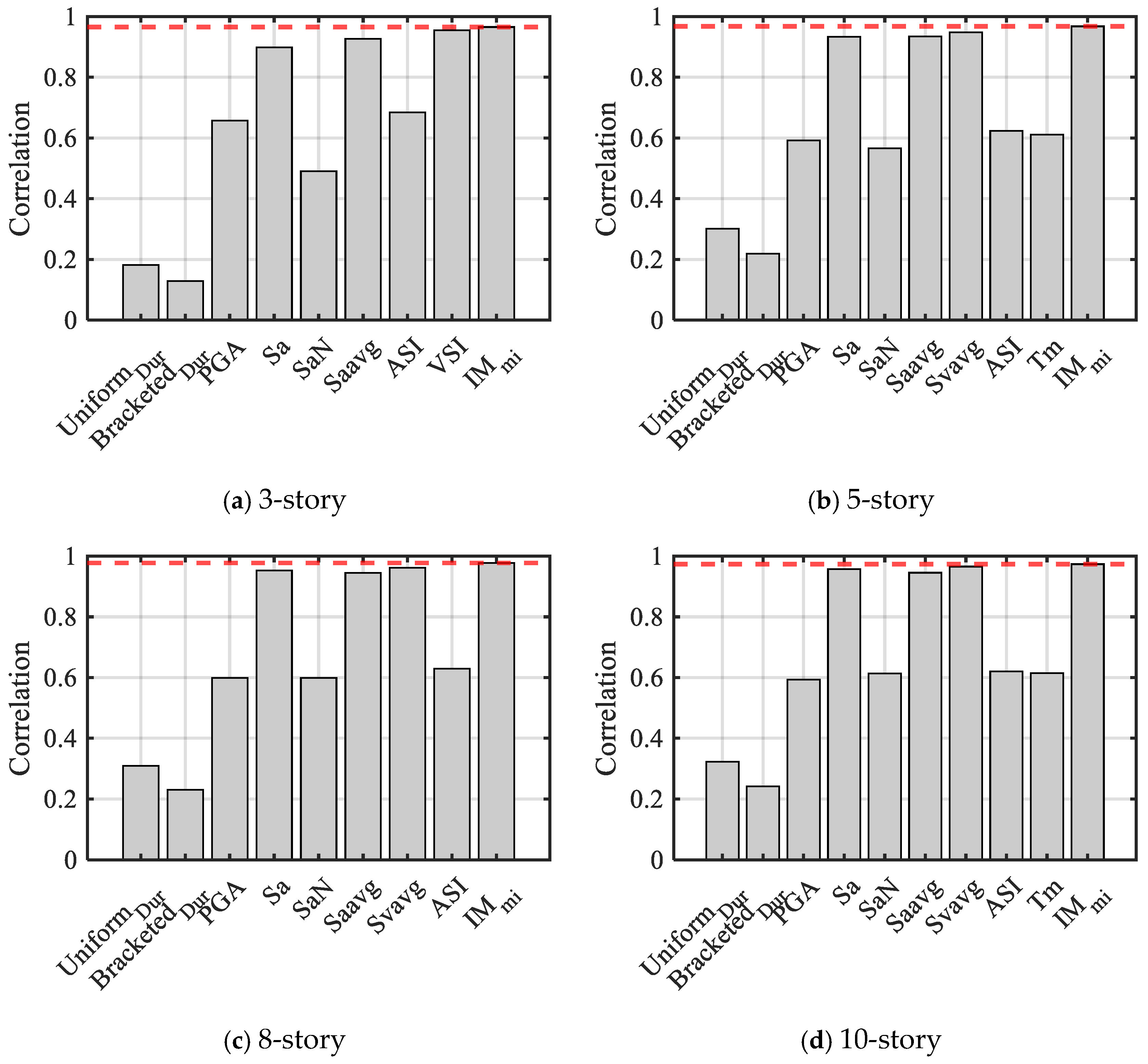
5.3.1. Correlation
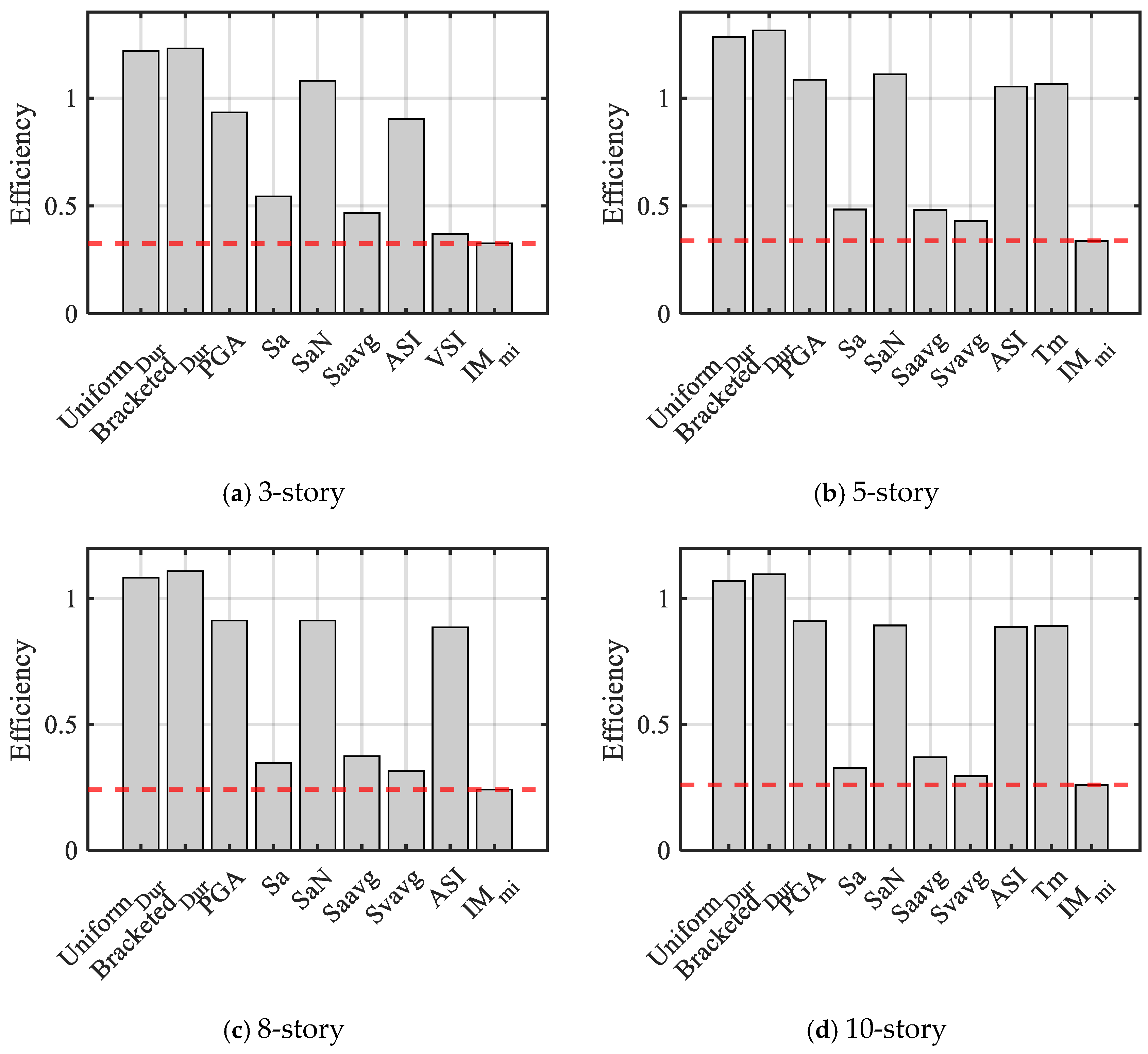
5.3.2. Efficiency
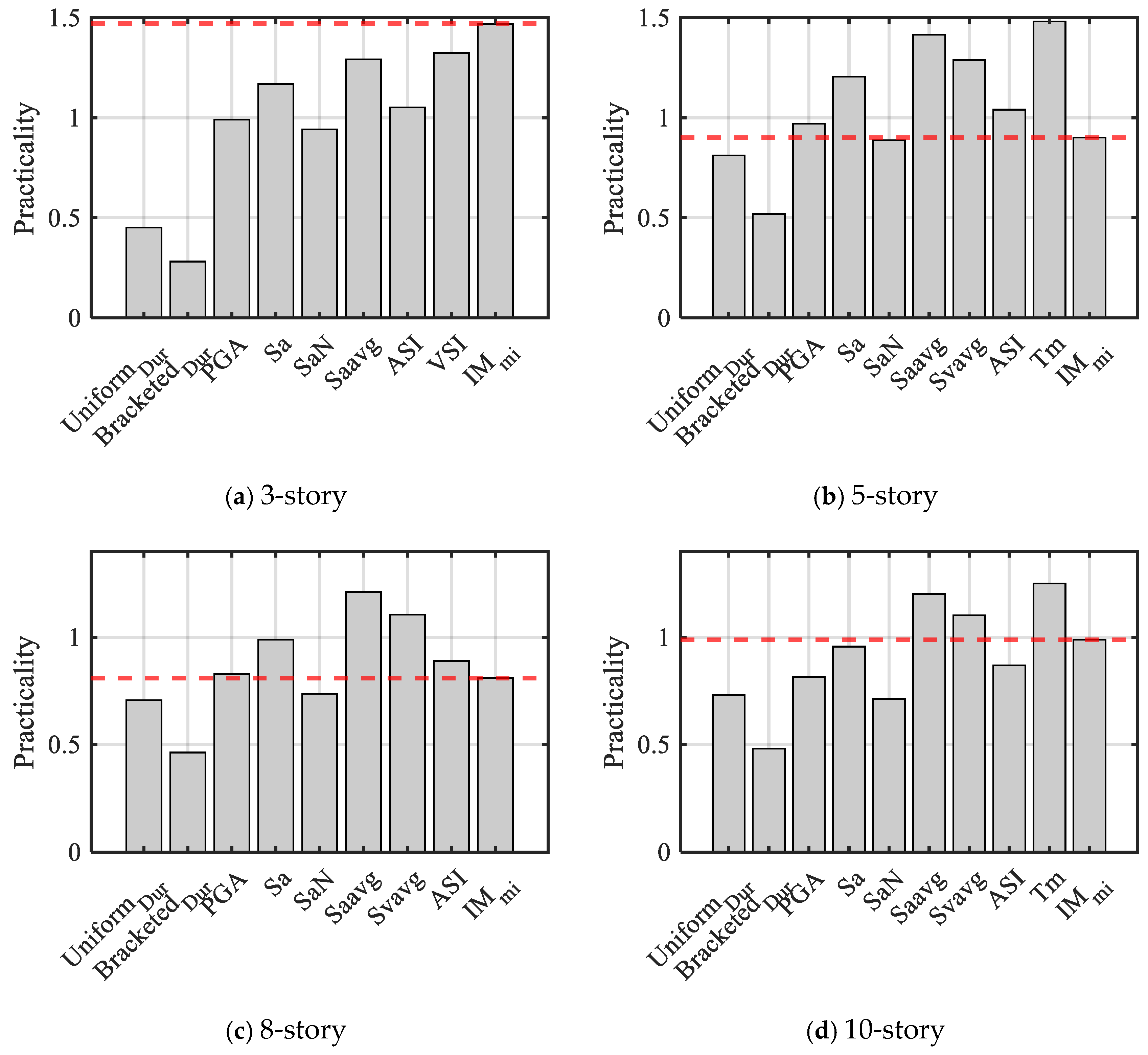
5.3.3. Practicality
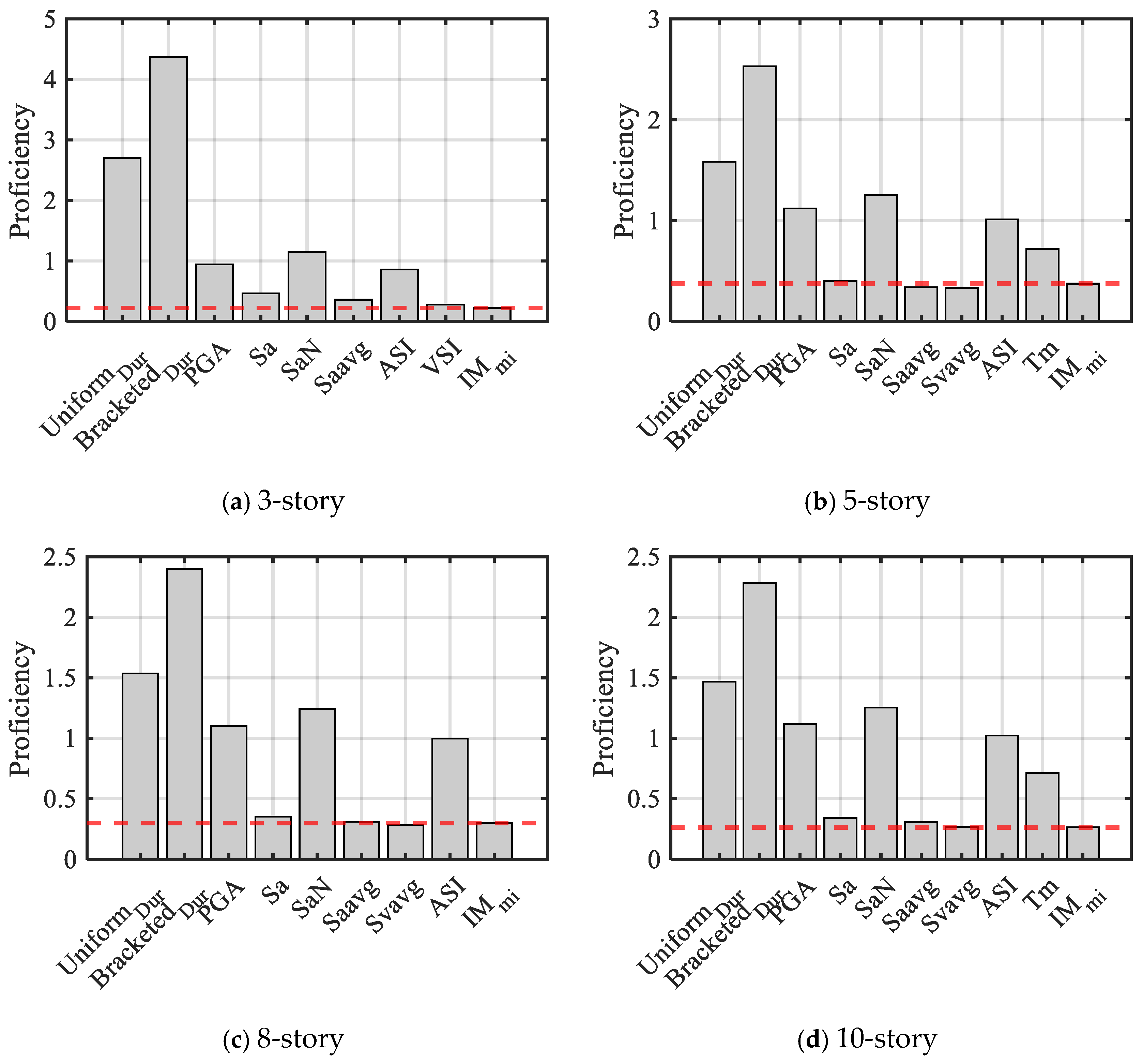
5.3.4. Proficiency
5.3.5. Sufficiency
6. Conclusions
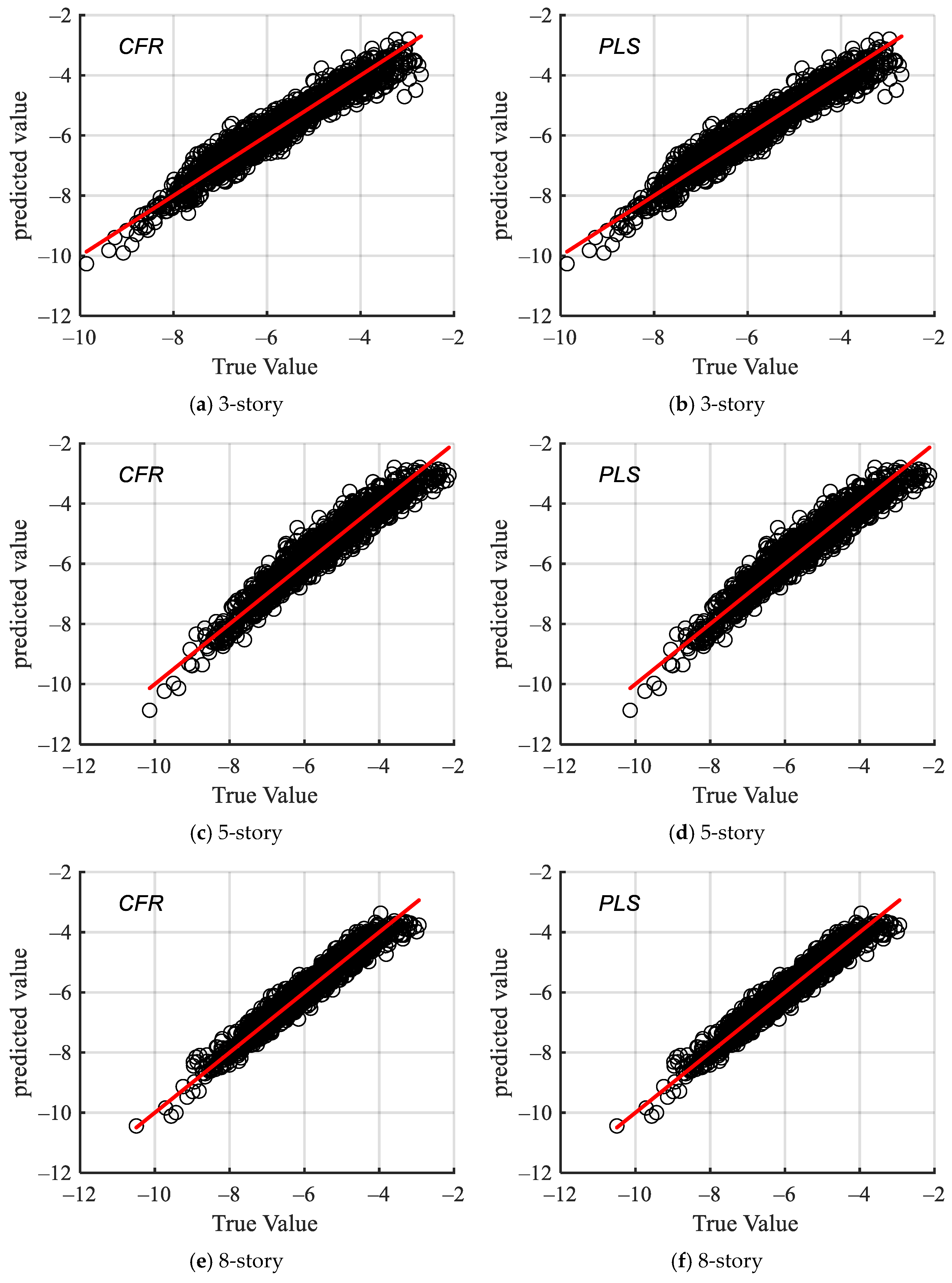
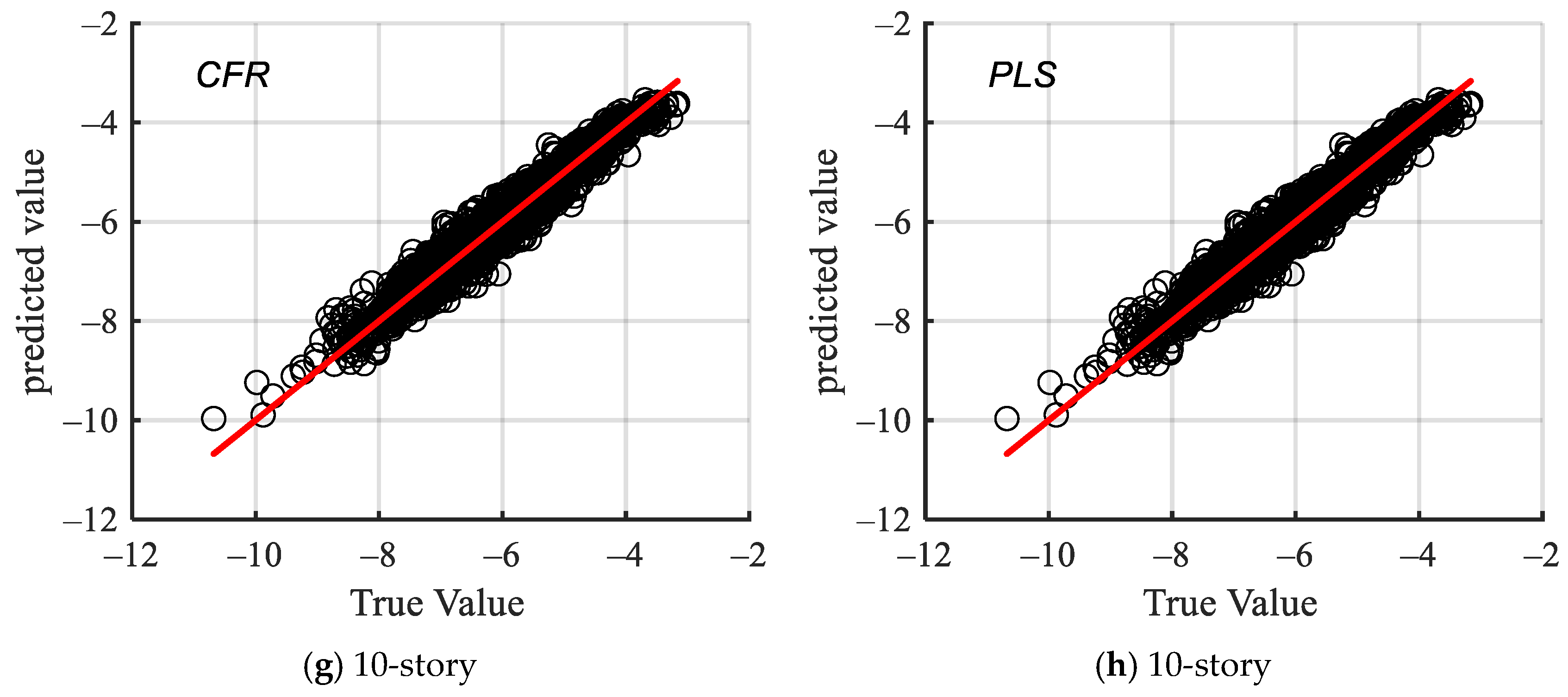
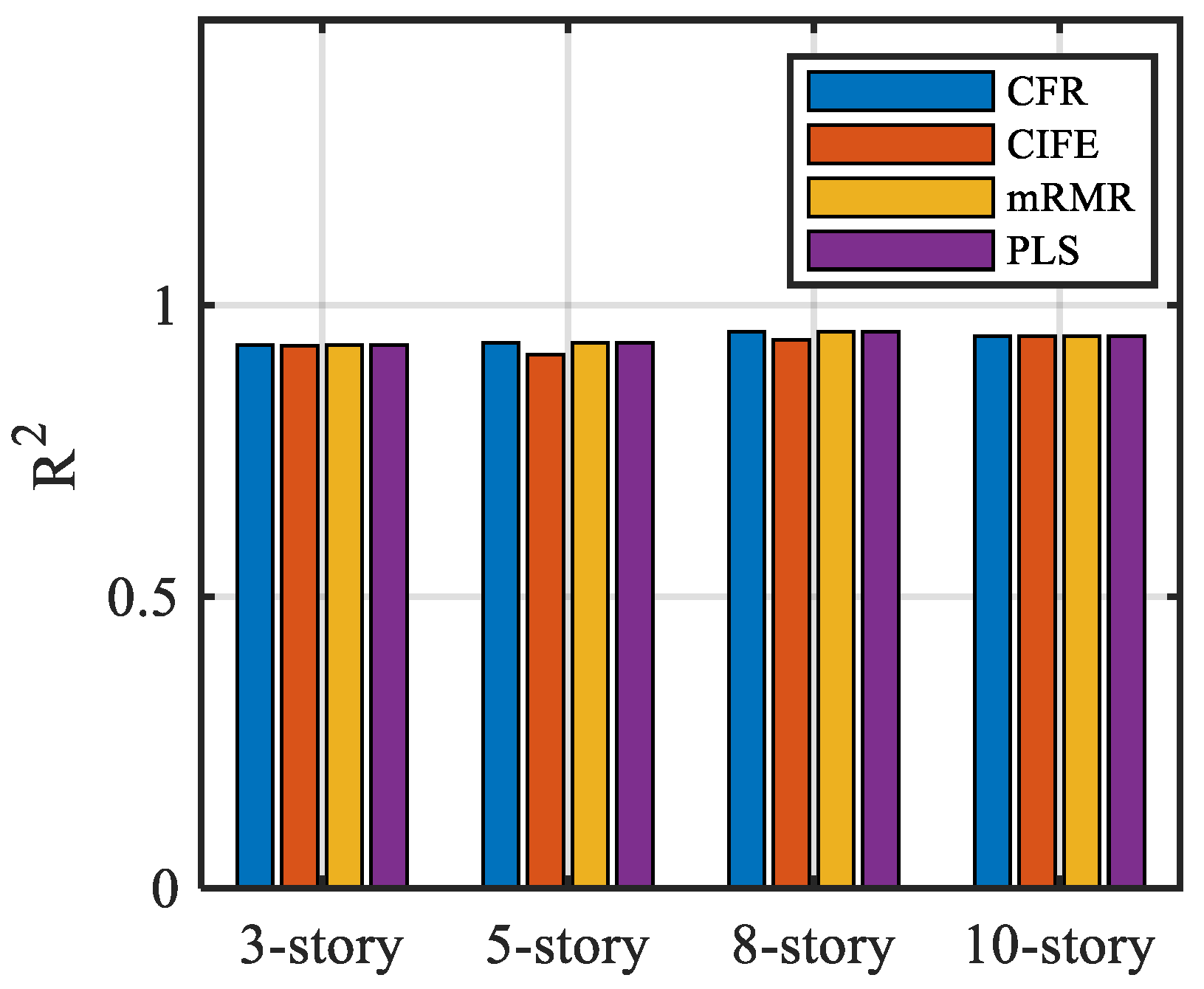
- The coefficient of determination for the multivariate linear regression model, as determined by several mutual information feature selection procedures, surpasses 0.9, indicating a strong match to the data. Comparison with the partial least squares regression model demonstrates that the features identified using mutual information metrics possess a robust capaci.y to explain seismic demand factor parameters and are suitable for analyzing structural seismic fragility.
- The probabilistic demand model was examined with linear regression analysis, utilizing compound intensity measures and various scalar intensity measures with engineering demand parameters. The goodness-of-fit results indicate that the derived from the mutual information method exceeds the other IMs, demonstrating superior fit.
- The compound IM was compared with other scalar IMs using correlation, efficiency, proficiency, and sufficiency as evaluation criteria. In general, the evaluation results indicate that the compound IM is more suitable as a ground motion intensity measure compared to other scalar IMs. The compound IM can analyze ground motion parameters more comprehensively, diminish data dispersion, and enhance predictive accuracy.
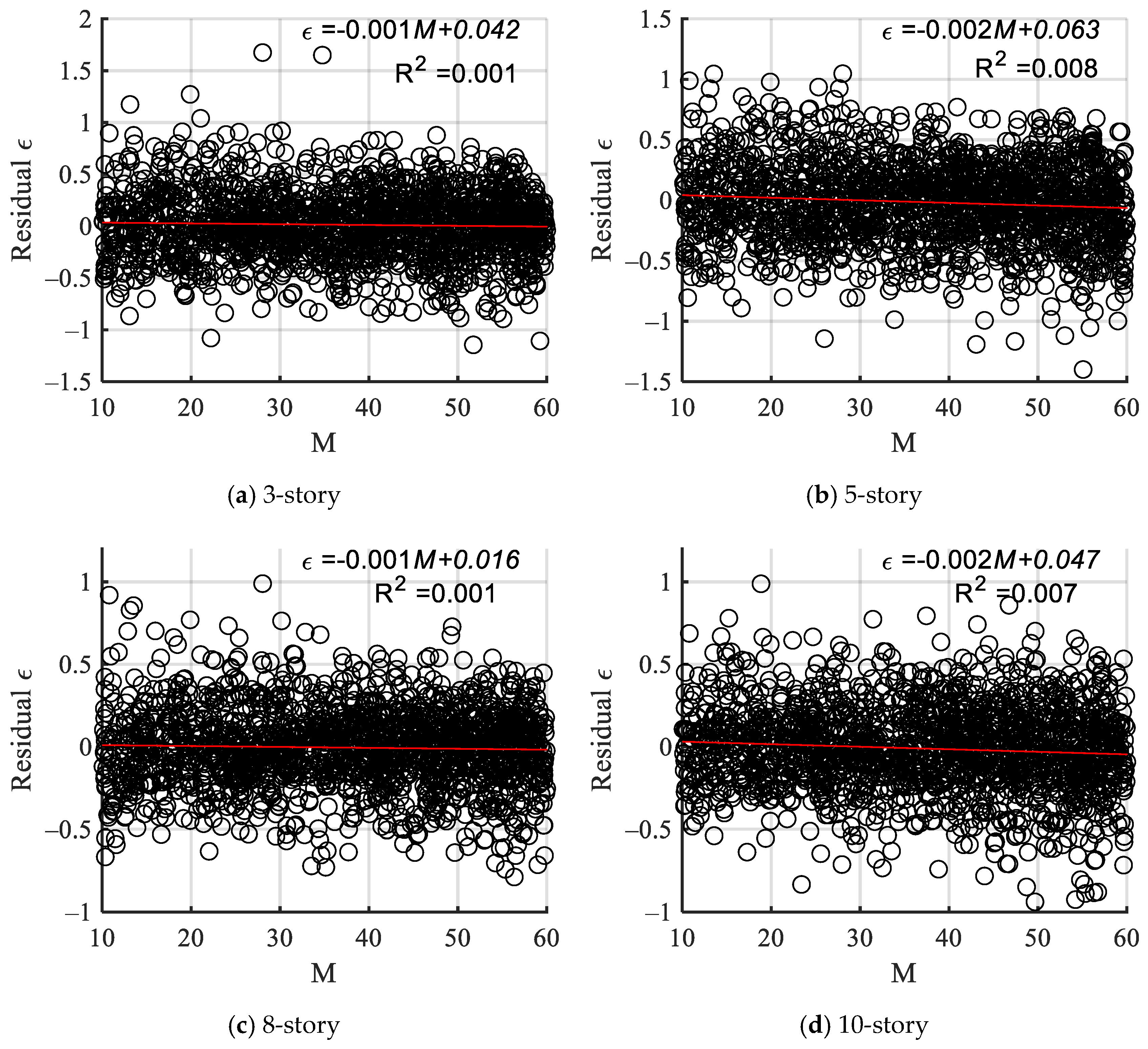
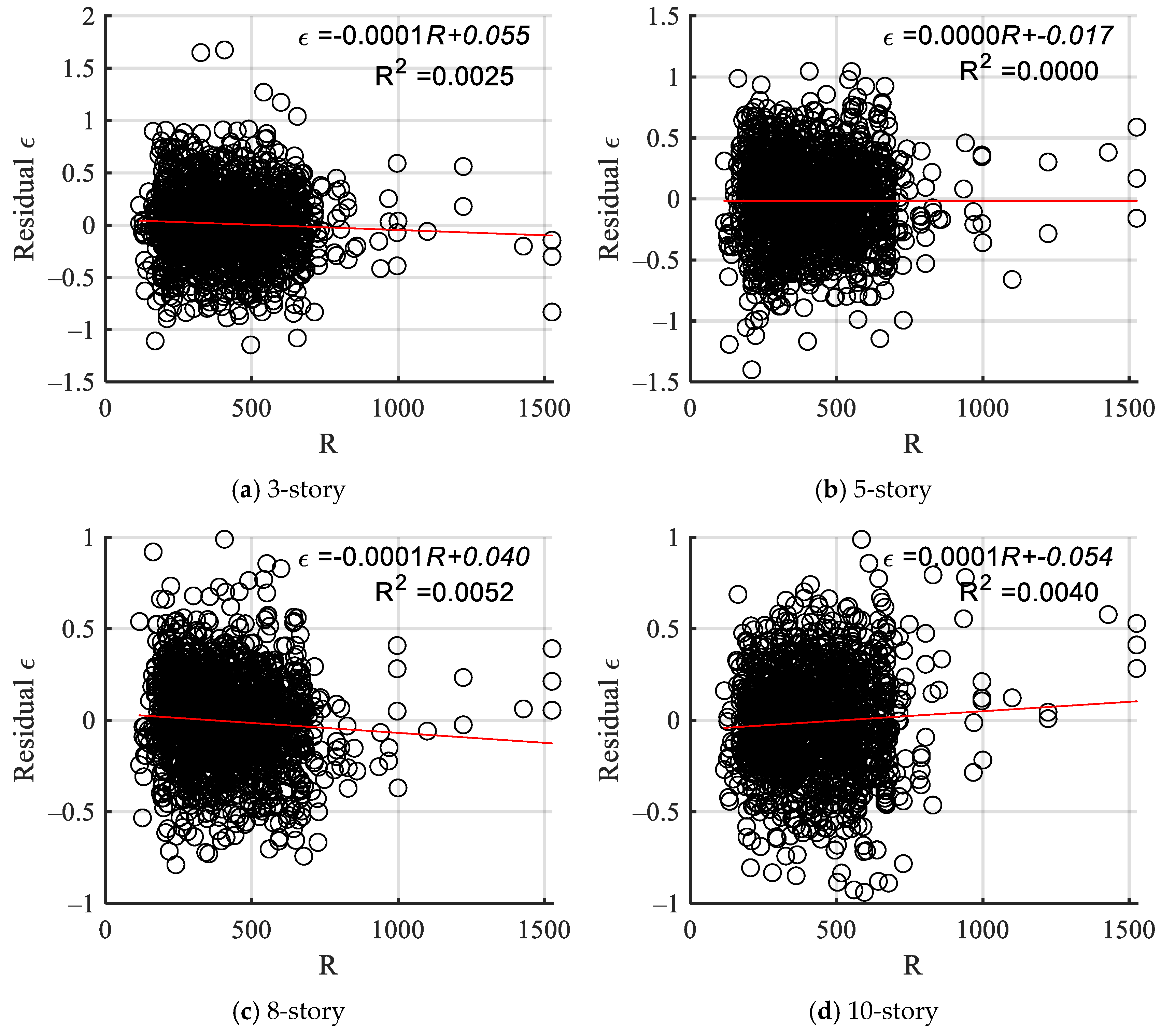
- The goodness of fit of the four structural residual results with the fitted straight line of magnitude M indicates that both magnitude M and epicenter distance R exert minimal influence on the residuals. It indicates that the compound IM is independent of magnitude and epicenter distance with good sufficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meral, E. Relationships between ground motion parameters and energy demands for regular low-rise RC frame buildings. Bull. Earthq. Eng. 2024, 22, 2829–2865. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Baker, J.W. Efficient Analytical Fragility Function Fitting Using Dynamic Structural Analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Eslamnia, H.; Malekzadeh, H.; Jalali, S.A.; Moghadam, A.S. Seismic energy demands and optimal intensity measures for continuous concrete box-girder bridges. Soil Dyn. Earthq. Eng. 2023, 165, 107657. [Google Scholar] [CrossRef]
- Du, M.; Zhang, S.R.; Wang, C.; Li, Z.; Yao, J.; Lu, T. Development of the compound intensity measure and seismic performance assessment for aqueduct structures considering fluid-structure interaction. Ocean. Eng. 2024, 311, 118838. [Google Scholar] [CrossRef]
- Yan, Y.; Xia, Y.; Yang, J.; Sun, L. Optimal selection of scalar and vector-valued seismic intensity measures based on Gaussian Process Regression. Soil Dyn. Earthq. Eng. 2022, 152, 106961. [Google Scholar] [CrossRef]
- Li, B.; Cai, Z. Effectiveness of vector intensity measures in probabilistic seismic demand assessment. Soil Dyn. Earthq. Eng. 2022, 155, 107201. [Google Scholar] [CrossRef]
- Kiani, J.; Camp, C.; Pezeshk, S. The importance of non-spectral intensity measures on the risk-based structural responses. Soil Dyn. Earthq. Eng. 2019, 120, 97–112. [Google Scholar] [CrossRef]
- Elenas, A.; Meskouris, K. Correlation study between seismic acceleration parameters and damage indices of structures. Eng. Struct. 2001, 23, 698–704. [Google Scholar] [CrossRef]
- Akkar, S.; Ozen, O. Effect of peak ground velocity on deformation demands for SDOF systems. Earthq. Eng. Struct. Dyn. 2005, 34, 1551–1571. [Google Scholar] [CrossRef]
- Sun, B.B.; Deng, M.J.; Zhang, S.R.; Wang, C.; Cui, W.; Li, Q.; Xu, J.; Zhao, X.H.; Yan, H.H. Optimal selection of scalar and vector-valued intensity measures for improved fragility analysis in cross-fault hydraulic tunnels. Tunn. Undergr. Space Technol. 2023, 132, 104857. [Google Scholar] [CrossRef]
- Shome, N.; Cornell, C.A.; Bazzurro, P.; Carballo, J.E. Earthquakes, Records, and Nonlinear Responses. Earthq. Spectra 1998, 14, 469–500. [Google Scholar] [CrossRef]
- Luco, N.; Cornell, C.A. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions. Earthq. Spectra 2007, 23, 357–392. [Google Scholar] [CrossRef]
- Eads, L.; Miranda, E.; Lignos, D.G. Average spectral acceleration as an intensity measure for collapse risk assessment. Earthq. Eng. Struct. Dyn. 2015, 44, 2057–2073. [Google Scholar] [CrossRef]
- Adam, C.; Kampenhuber, D.; Ibarra, L.F.; Tsantaki, S. Optimal Spectral Acceleration-based Intensity Measure for Seismic Collapse Assessment of P-Delta Vulnerable Frame Structures. J. Earthq. Eng. 2017, 21, 1189–1195. [Google Scholar] [CrossRef]
- Baker, J.W. Probabilistic structural response assessment using vector-valued intensity measures. Earthq. Eng. Struct. Dyn. 2007, 36, 1861–1883. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Developing efficient scalar and vector intensity measures for IDA capacity estimation by incorporating elastic spectral shape information. Earthq. Eng. Struct. Dyn. 2005, 34, 1573–1600. [Google Scholar] [CrossRef]
- Vargas-Alzate, Y.F.; Hurtado, J.E.; Pujades, L.G. New insights into the relationship between seismic intensity measures and nonlinear structural response. Bull. Earthq. Eng. 2022, 20, 2329–2365. [Google Scholar] [CrossRef]
- Baker, J.W.; Cornell, C.A. A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon. Earthq. Eng. Struct. Dyn. 2005, 34, 1193–1217. [Google Scholar] [CrossRef]
- Modica, A.; Stafford, P.J. Vector fragility surfaces for reinforced concrete frames in Europe. Bull. Earthq. Eng. 2014, 12, 1725–1753. [Google Scholar] [CrossRef]
- Marco, F.; André, R.B.; Joel, P.C.; Enrico, S.; José, I.R. Probabilistic seismic response analysis of a 3-D reinforced concrete building. Struct. Saf. 2013, 44, 11–27. [Google Scholar] [CrossRef]
- Kohrangi, M.; Bazzurro, P.; Vamvatsikos, D. Conditional spectrum bidirectional record selection for risk assessment of 3D structures using scalar and vector IMs. Earthq. Eng. Struct. Dyn. 2019, 48, 1066–1082. [Google Scholar] [CrossRef]
- Bojorquez, E.; Iervolino, I.; Reyes-Salazar, A.; Ruiz, S.E. Comparing vector-valued intensity measures for fragility analysis of steel frames in the case of narrow-band ground motions. Eng. Struct. 2012, 45, 472–480. [Google Scholar] [CrossRef]
- Kohrangi, M.; Bazzurro, P.; Vamvatsikos, D. Vector and Scalar IMs in Structural Response Estimation: Part II—Building Demand Assessment. Earthq. Spectra 2016, 32, 1525–1543. [Google Scholar] [CrossRef]
- Luis, A.P.; Yeudy, F.V.-A.; Luis, G.P.; Sergio, A.D. A drift-correlated ground motion intensity measure: Application to steel frame buildings. Soil Dyn. Earthq. Eng. 2020, 132, 106096. [Google Scholar] [CrossRef]
- Liu, T.T.; Yu, X.H.; Lu, D.G. An Approach to Develop Compound Intensity Measures for Prediction of Damage Potential of Earthquake Records Using Canonical Correlation Analysis. J. Earthq. Eng. 2020, 24, 1747–1770. [Google Scholar] [CrossRef]
- Liu, B.; Hu, J.; Xie, L. Exploratory factor analysis-based method to develop compound intensity measures for predicting potential structural damage of ground motion. Bull. Earthq. Eng. 2022, 20, 7107–7135. [Google Scholar] [CrossRef]
- Liu, T.-T.; Lu, D.-G.; Yu, X.-H. Development of a compound intensity measure using partial least-squares regression and its statistical evaluation based on probabilistic seismic demand analysis. Soil Dyn. Earthq. Eng. 2019, 125, 105725. [Google Scholar] [CrossRef]
- Sun, B.B.; Liu, W.Y.; Deng, M.J.; Zhang, S.R.; Wang, C.; Guo, J.J.; Wang, J.; Wang, J.Y. Compound intensity measures for improved seismic performance assessment in cross-fault hydraulic tunnels using partial least-squares methodology. Tunn. Undergr. Space Technol. 2023, 132, 104890. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, W.; Zhu, H.; Xie, L. Ranking method of the severest input ground motion for underground structures based on composite ground motion intensity measures. Soil Dyn. Earthq. Eng. 2023, 168, 107828. [Google Scholar] [CrossRef]
- Yong, W.; Zhi, Z.; Duofa, J.; Xiaolan, P.; Aonan, T. Machine learning-driven probabilistic seismic demand model with multiple intensity measures and applicability in seismic fragility analysis for nuclear power plants. Soil Dyn. Earthq. Eng. 2023, 171, 107966. [Google Scholar] [CrossRef]
- Bommer, J.J.; Martínez-Pereira, A. The effective duration of earthquake strong motion. J. Earthq. Eng. 1999, 3, 127–172. [Google Scholar] [CrossRef]
- Hansen, R.J. Seismic Design for Nuclear Power Plants; MIT Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Pu, W.; Wu, M.; Huang, B.; Zhang, H. Quantification of response spectra of pulse-like near-fault ground motions. Soil Dyn. Earthq. Eng. 2018, 104, 117–130. [Google Scholar] [CrossRef]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- Mackie, K.R. Fragility-Based Seismic Decision Making for Highway Overpass Bridges. Ph.D. Thesis, University of California, Berkeley, Berkeley, CA, USA, 2004. [Google Scholar]
- Applied Technology Council. Tentative Provisions for the Development of Seismic Regulations for Buildings; ATC-3-06; Applied Technology Council: Redwood City, CA, USA, 1978. [Google Scholar]
- Anderson, J.C.; Bertero, V.V. Uncertainties in Establishing Design Earthquakes. J. Struct. Eng.-Asce 1987, 113, 1709–1724. [Google Scholar] [CrossRef]
- Wu, Z.-N.; Li, Z.-Q.; Dong, Y.; Han, X.-L.; Zhang, G.; Feng, R.; Zhu, K. Seismic intensity measure selection incorporating interaction effects for damage assessment across different structural sensitive regions. Structures 2024, 67, 106917. [Google Scholar] [CrossRef]
- Thun, J.L.V.; Roehm, L.H.; Scott, G.A.; Wilson, J.A. Earthquake ground motions for design and analysis of dams. Geotech. Spec. Publ. 1988, 20, 463–481. [Google Scholar]
- Housner, G.W. Behavior of Structures During Earthquakes. J. Eng. Mech. Div. 1959, 85, 109–129. [Google Scholar] [CrossRef]
- Rathje, E.M.; Abrahamson, N.A.; Bray, J.D. Simplified Frequency Content Estimates of Earthquake Ground Motions. J. Geotech. Geoenvironmental Eng. 1998, 124, 150–159. [Google Scholar] [CrossRef]
- Chen, R.; Sun, N.; Chen, X.; Yang, M.; Wu, Q. Supervised Feature Selection With a Stratified Feature Weighting Method. IEEE Access 2018, 6, 15087–15098. [Google Scholar] [CrossRef]
- Gao, W.; Hu, L.; Zhang, P. Class-specific mutual information variation for feature selection. Pattern Recognit. 2018, 79, 328–339. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Hybridization of feature selection and feature weighting for high dimensional data. Appl. Intell. 2019, 49, 1580–1596. [Google Scholar] [CrossRef]
- Gao, W.; Hu, L.; Zhang, P. Feature redundancy term variation for mutual information-based feature selection. Appl. Intell. 2020, 50, 1272–1288. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, Y.; Zhang, X.; Chen, L. Part mutual information for quantifying direct associations in networks. Proc. Natl. Acad. Sci. USA 2016, 113, 5130–5135. [Google Scholar] [CrossRef] [PubMed]
- Dionisio, A.; Menezes, R.; Mendes, D.A. Mutual information: A measure of dependency for nonlinear time series. Phys. A Stat. Mech. Its Appl. 2004, 344, 326–329. [Google Scholar] [CrossRef]
- Hanchuan, P.; Fuhui, L.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.; Tang, X. Conditional Infomax Learning: An Integrated Framework for Feature Extraction and Fusion. In Proceedings of the Computer Vision—ECCV 2006, Graz, Austria, 7–13 May 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 68–82. [Google Scholar]
- Gao, W.; Hu, L.; Zhang, P.; He, J. Feature selection considering the composition of feature relevancy. Pattern Recognit. Lett. 2018, 112, 70–74. [Google Scholar] [CrossRef]
- Lai, Q.H.; Hu, J.J.; Xu, L.J.; Xie, L.L.; Lin, S.B. Method for Ranking Pulse-like Ground Motions According to Damage Potential for Reinforced Concrete Frame Structures. Buildings 2022, 12, 754. [Google Scholar] [CrossRef]
- Song, Z.; Li, X.; Wang, Y.; Zhou, B. Amplitude-Scaling Bias Analysis of Ground Motion Record Set in Strip Method for Structural Seismic Fragility Assessment. Buildings 2025, 15, 401. [Google Scholar] [CrossRef]
- McKenna, F.; Fenves, G.; Scott, M.; Jeremic, B. Open System for Earthquake Engineering Simulation (OpenSees); Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2000. [Google Scholar]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. Probabilistic basis for 2000 SAC Federal Emergency Management Agency steel moment frame guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef]
- Giovenale, P.; Cornell, C.A.; Esteva, L. Comparing the adequacy of alternative ground motion intensity measures for the estimation of structural responses. Earthq. Eng. Struct. Dyn. 2004, 33, 951–979. [Google Scholar] [CrossRef]
- Padgett, J.E.; Nielson, B.G.; DesRoches, R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthq. Eng. Struct. Dyn. 2008, 37, 711–725. [Google Scholar] [CrossRef]
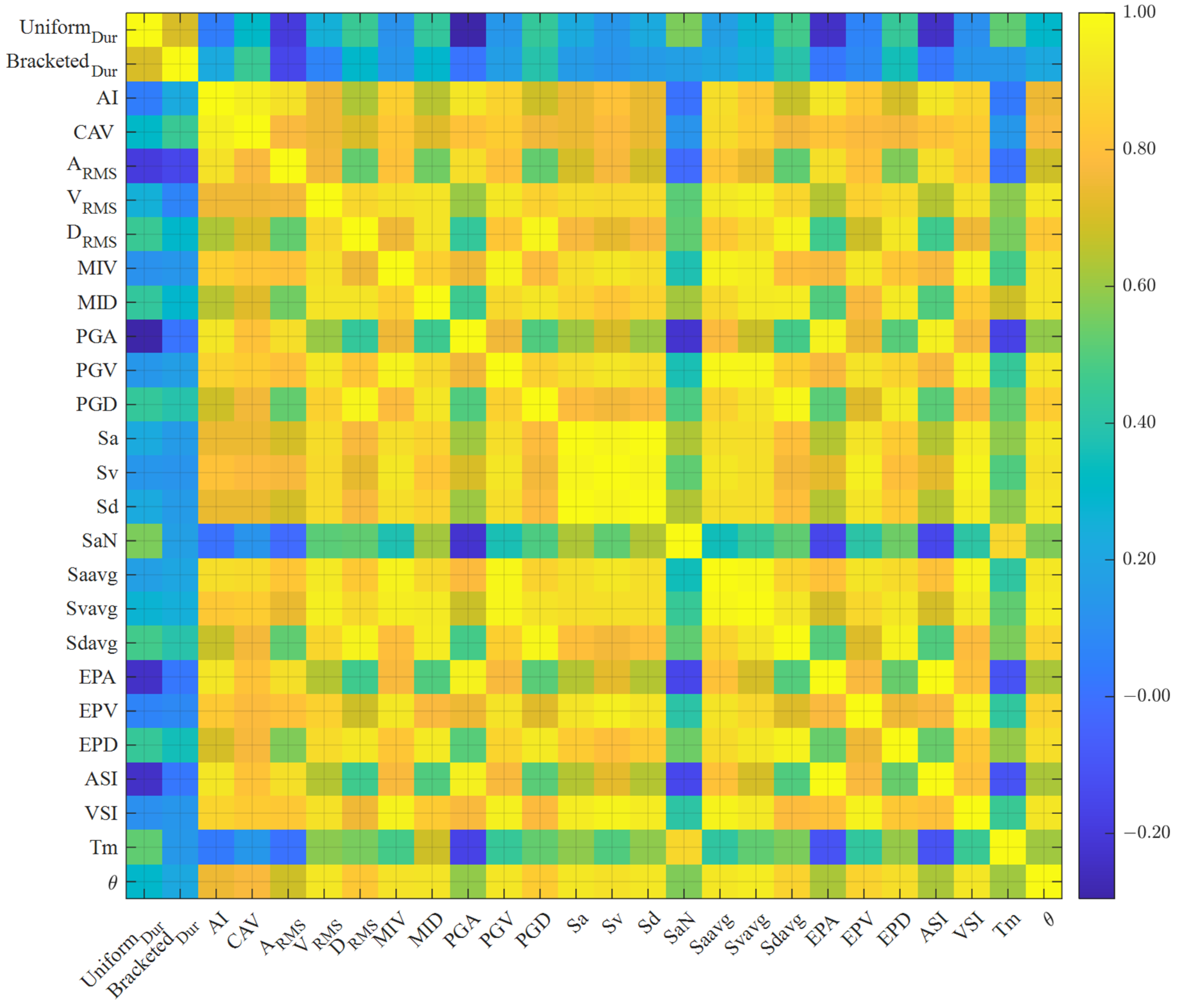
| No. | IM | Expression | Unit | Ref. | No. | IM | Expression | Unit | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Uniform _Dur | s | [32] | 14 | [12] | ||||
| 2 | Bracketed _Dur | s | [32] | 15 | [12] | ||||
| 3 | AI | [33] | 16 | SaN | /PGA | — | [34] | ||
| 4 | CAV | [35] | 17 | [36] | |||||
| 5 | [35] | 18 | [36] | ||||||
| 6 | [35] | 19 | [36] | ||||||
| 7 | [35] | 20 | EPA | [37] | |||||
| 8 | MIV | [38,39] | 21 | EPV | [36] | ||||
| 9 | MID | [39] | 22 | EPD | [36] | ||||
| 10 | PGA | [35] | 23 | ASI | [40] | ||||
| 11 | PGV | [35] | 24 | VSI | [40,41] | ||||
| 12 | PGD | [35] | 25 | s | [42] | ||||
| 13 | [12] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Li, X.; Wang, Y.; Zhou, B. Construction Method of Compound Ground Motion Intensity Measure Based on Mutual Information Asymmetry for Engineering Seismic Fragility Analysis. Symmetry 2025, 17, 699. https://doi.org/10.3390/sym17050699
Song Z, Li X, Wang Y, Zhou B. Construction Method of Compound Ground Motion Intensity Measure Based on Mutual Information Asymmetry for Engineering Seismic Fragility Analysis. Symmetry. 2025; 17(5):699. https://doi.org/10.3390/sym17050699
Chicago/Turabian StyleSong, Zhuo, Xiaojun Li, Yushi Wang, and Bochang Zhou. 2025. "Construction Method of Compound Ground Motion Intensity Measure Based on Mutual Information Asymmetry for Engineering Seismic Fragility Analysis" Symmetry 17, no. 5: 699. https://doi.org/10.3390/sym17050699
APA StyleSong, Z., Li, X., Wang, Y., & Zhou, B. (2025). Construction Method of Compound Ground Motion Intensity Measure Based on Mutual Information Asymmetry for Engineering Seismic Fragility Analysis. Symmetry, 17(5), 699. https://doi.org/10.3390/sym17050699







