Quantum Steering and Fidelity in a Two-Photon System Subjected to Symmetric and Asymmetric Phasing Interactions

Abstract

This paper examines the dynamics of quantum steering and fidelity in a two-photon system subjected to dephasing interactions, examining their behavior in Markovian and non-Markovian environments. We consider the case of identical and distinct dephasing rates with experimental parameter values to ensure that the analysis reflects realistic conditions, enhancing its relevance to practical quantum systems. Quantum steering, the ability to remotely influence a quantum state, and fidelity, a measure of initial-state preservation, are investigated for time evolution, initial-state configuration, dephasing parameters, and system characteristics. We model each photon as independently interacting with its environment and derive the time-evolved reduced-density matrix for the bipartite system, focusing on how environmental effects shape the system’s behavior. By integrating experimentally feasible parameter values, this work establishes a practical framework for tuning quantum steering and fidelity, providing valuable insights for applications in quantum information processing, such as secure communication and state preservation.

1. Introduction

Quantum correlations have gained significant attention in recent years, mainly due to their foundational role and practical applications in various fields, such as quantum computing [1], secure communications [2,3], and precision measurement [4]. These correlations, which emerge in mixed states of composite quantum systems, can take several forms [5]. Among the most well-known manifestations are entanglement [6] and Bell nonlocality [7]. More recently, a third type of quantum correlation, known as quantum steering [8,9], has generated renewed interest within the community of quantum information science [10,11]. This phenomenon has opened new theoretical and practical doors for exploration. Quantum steering refers to the ability of one party, Alice, to influence or “steer” the state of a distant party, Bob, by utilizing their shared quantum entanglement. Schrödinger [8,9] notably discussed this concept, building on earlier insights by Einstein, Podolsky, and Rosen (EPR) in their seminal 1935 paper [12]. The EPR paradox [13] highlighted the peculiar nature of steering and its connection to the concept of “spooky action at a distance”, which Einstein used to argue that quantum mechanics was incomplete. The EPR’s predictions regarding local realism were effectively challenged by Bell’s theorems [14,15], which demonstrated that no local hidden variable theory could explain all observed quantum correlations [16]. Later, Reid [17] provided the first experimental criterion for detecting quantum steering, and it was not until 2007 that this concept was rigorously formalized [10].

From a quantum information perspective [10], steering plays a crucial role in verifying the entanglement distribution in scenarios where the measurements of one party are not trusted. For example, suppose that Alice and Bob share a steerable state. In that case, Alice can convince Bob (skeptical of Alice’s trustworthiness) that their state is entangled by performing local measurements and sending classical communication [10]. Unlike entanglement, a symmetric property, steering is asymmetric: a state may be steerable from Alice to Bob but not vice versa. More recently, it has been realized that quantum steering can provide security in device-independent one-sided quantum key distribution (QKD) protocols [18], where only one party’s measurement device is trusted. This makes it less demanding than Bell-based protocols, which require complete device independence [3]. Experimentally, demonstrations of quantum steering without detection and locality loopholes are within reach [18,19,20], making quantum steering a practically useful concept in real-world applications. In addition, steering plays a vital role in other tasks, such as channel discrimination [21] and quantum tele-amplification [22]. In recent years, numerous experiments have demonstrated steering and its asymmetry [18,20,23,24,25,26,27,28,29]. Research has also focused on developing better criteria to detect steerable states and understand the distribution of steering among multiple parties [30,31,32,33,34]. However, despite substantial progress in this area, there is still a limited body of work that addresses the fundamental question of how to quantify the degree of steerability of a given quantum state [35,36,37,38,39].

Alternatively, fidelity is a crucial tool for exploring non-Markovian effects in quantum systems. It measures the closeness between a time-evolved state and a reference state, providing direct information on how environmental interactions affect quantum coherence and information loss [1]. In the realm of two-photon polarization states, fidelity facilitates the precise characterization of decoherence mechanisms, aiding in the differentiation between Markovian and non-Markovian behaviors [40]. Furthermore, fidelity-based analyses allow recognition of memory effects in structured reservoirs, making them vital for improving quantum error correction protocols and quantum memories [41]. Regardless, the study of non-Markovian dynamics in quantum systems has attracted significant attention, due to its importance in quantum information processing, quantum communication, and quantum metrology [42,43]. Unlike Markovian processes, which exhibit memoryless evolution, non-Markovian dynamics are distinguished by information backflow from the environment, resulting in revivals of quantum coherence and entanglement [44,45].

Nevertheless, the relationship between steering and fidelity lies in their roles as tools to analyze quantum correlations. Steering describes the strength and directionality of quantum correlations, while fidelity measures how well quantum states align in specific tasks. In many quantum applications, high steering often corresponds to high fidelity in producing desired outcomes. However, they address distinct properties, making their combined exploration advantageous for understanding and utilizing quantum systems. In this work, we examine the dynamics of quantum steering and fidelity in a two-photon system subjected to dephasing interactions. We examine their behavior in both Markovian and non-Markovian environments. We consider the case of identical and distinct dephasing rates with experimental parameter values to ensure that the analysis reflects realistic conditions, enhancing its relevance to practical quantum systems.

This paper is organized as follows. Section 2 explores non-Markovian dynamics in quantum systems, starting with a single-photon model and extending to two-photon interactions. The complete reduced-density matrix for two non-identical qubit systems is obtained for an open system with frequency functions characterized by a two-peak Gaussian profile. This rigorous methodology facilitates the investigation of non-Markovian phenomena over parameter regimes pertinent to experimental conditions. Section 3 examines quantum steering and fidelity, highlighting quantum steering as a reliable metric for assessing quantum correlations within the system. In Section 4, we present quantum dynamics focused on carefully selected initial photon polarization states, defined by two parameters, which preserve maximally mixed marginals while retaining practical significance for experimental contexts. Furthermore, we discuss the obtained results. The analysis is meticulously anchored within experimentally feasible parameter domains, ensuring its applicability to real-world scenarios. Section 5 details the synthesis of the findings, critical analysis, and prospective directions for subsequent investigations.

2. Non-Markovian Dynamics in Quantum Systems

This section explores non-Markovian dynamics in quantum systems, starting with a single-photon model and extending to two-photon interactions. We formulate the polarization state of a photon within the framework of an open quantum system, designating its frequency as the principal environmental degree of freedom governing system–environment interactions. The experimental configuration, rigorously detailed in [40,46,47,48,49], comprises a precisely adjustable Fabry–Pérot (FP) cavity, a high-resolution interference filter, and a bi-refringent quartz substrate. The FP cavity produces a frequency comb, filtered into a two-peaked Gaussian frequency profile $f\left(\omega \right)$:

$$f\left(\omega \right)={\displaystyle \frac{{cos}^2\varphi }{\sqrt{2\pi }\sigma }}{e}^{-{\displaystyle \frac{{(\omega -{\omega }_1)}^2}{2{\sigma }^2}}}+{\displaystyle \frac{{sin}^2\varphi }{\sqrt{2\pi }\sigma }}{e}^{-{\displaystyle \frac{{(\omega -{\omega }_2)}^2}{2{\sigma }^2}}},$$

(1)

where ${\omega }_1$ and ${\omega }_2$ are the central frequencies, $\sigma$ is the width, and $\varphi \in [0,\pi /2]$ is determined by the FP cavity’s tilt, which represents the relative weighting parameter. The profile is normalized: $\int f\left(\omega \right)d\omega =1$.

Non-Markovian dephasing arises from the photon’s interaction with frequency modes in the quartz plate, governed by the Hamiltonian [50]:

$$H^{SE}=-\int \left(n_H|H\rangle \langle H|+n_V|V\rangle \langle V|\right)\otimes \omega |\omega \rangle \langle \omega |d\omega ,$$

(2)

where $n_H$ and $n_V$ are the refractive indices for horizontal and vertical polarizations, respectively.

For an initial state ${\rho }^S\left(0\right)\otimes {\rho }^E\left(0\right)$, the photon’s time-evolved polarization state is

$${\rho }^S\left(t\right)=\mathrm{\Lambda }\left(t\right){\rho }^S\left(0\right)={\mathrm{Tr}}_E\left\{U\left(t\right){\rho }^S\left(0\right)\otimes {\rho }^E\left(0\right)U^{†}\left(t\right)\right\},$$

(3)

where $\mathrm{\Lambda }\left(t\right)$ is the quantum map, and $U\left(t\right)=exp[-i{H}^{SE}t]$. The density matrix at time t is expressed as

$${\rho }^S\left(t\right)=\left(\begin{array}{cc}{\rho }_{VV}& {\rho }_{VH}p\left(t\right)\\ {\rho }_{HV}{p}^{*}\left(t\right)& {\rho }_{HH}\end{array}\right),$$

(4)

where $p\left(t\right)$ is the dephasing factor and is the Fourier transform of the frequency distribution Equation (1); thus,

$$p\left(t\right)=e^{-{\displaystyle \frac{{\sigma }^2{(\Delta n)}^2{t}^2}{2}}}\left(e^{i{\omega }_1\Delta nt}{cos}^2\varphi +e^{i{\omega }_2\Delta nt}{sin}^2\varphi \right),\Delta n=n_V-n_H.$$

(5)

Using the Kraus procedure, we can extend the formalism to the two-photon system, which consists of two independent qubits, $S=A,B$, each interacting with its environment ($E_A,E_B$). The evolution of the reduced density matrix for each qubit is given by Equation (3), reformulated using the Kraus operators $K_{ij}^S$ [51]:

$${\rho }^S\left(t\right)=\sum _{ij}{K}_{ij}^S\left(t\right){\rho }^S\left(0\right)K_{ij}^{S†}\left(t\right).$$

(6)

Assuming subsystem independence, the total time evolution operator for the composite system $U^T\left(t\right)$ factorizes: $U^T\left(t\right)=U^A\left(t\right)\otimes U^B\left(t\right)$. The two-qubit reduced density matrix is then

$$\rho \left(t\right)=\sum _{i,j,k,l}\left(K_{ij}^A\left(t\right)\otimes K_{kl}^B\left(t\right)\right)\rho \left(0\right){\left(K_{ij}^A\left(t\right)\otimes K_{kl}^B\left(t\right)\right)}^{†}.$$

(7)

From Equations (4) and (6), we can deduce the appropriate Kraus operators for this evolution as

$$K_0^S\left(t\right)=\left(\begin{array}{cc}1& 0\\ 0& p\left(t\right)\end{array}\right),K_1^S\left(t\right)=\left(\begin{array}{cc}0& 0\\ 0& \sqrt{1-p{\left(t\right)}^2}\end{array}\right).$$

These operators satisfy the completeness relation:

$$K_0^{S†}{K}_0^S+K_1^{S†}{K}_1^S=\mathbb{I},$$

ensuring the trace-preserving property of the quantum channel. This pair of operators correctly reproduces the time-evolved density matrix via the Kraus sum. In the computational basis $\mathcal{B}=\{|1\rangle =|V_A{V}_B\rangle ,|2\rangle =|V_A{H}_B\rangle ,|3\rangle =|H_A{V}_B\rangle ,|4\rangle =|H_A{H}_B\rangle \}$, by substituting into Equation (7) and performing the tensor product, the diagonal elements of $\rho \left(t\right)$ remain unchanged, while the off-diagonal elements evolve as follows:

$$\begin{array}{ccc}\hfill {\rho }_{12}\left(t\right)& =& {\rho }_{12}\left(0\right)p_B\left(t\right),{\rho }_{13}\left(t\right)={\rho }_{13}\left(0\right)p_A\left(t\right),\hfill \\ \hfill {\rho }_{14}\left(t\right)& =& {\rho }_{14}\left(0\right)p_A\left(t\right)p_B\left(t\right),{\rho }_{23}\left(t\right)={\rho }_{23}\left(0\right)p_A\left(t\right)p_B^{*}\left(t\right),\hfill \\ \hfill {\rho }_{24}\left(t\right)& =& {\rho }_{24}\left(0\right)p_A\left(t\right),{\rho }_{34}\left(t\right)={\rho }_{34}\left(0\right)p_B\left(t\right).\hfill \end{array}$$

(8)

These equations fully characterize the two-qubit density matrix evolution, enabling a detailed investigation of non-Markovian dynamics in bipartite quantum systems.

3. Quantum Steering and Fidelity

Quantum systems are characterized by various metrics that quantify their coherence, correlations, and overlap between quantum states. In this section, we review the concepts of quantum steering and fidelity, highlighting their roles in understanding quantum dynamics and resource quantification.

3.1. Quantum Steering

The Gaussian steering measure, recently proposed in [52], is a compelling and comprehensive criterion to assess quantum steering in bipartite Gaussian states. It offers a robust alternative for quantifying quantum correlations within Gaussian modes. The essence of quantum steering lies in its ability to enable one party, $\left(b_1\right)$, to influence or steer the state of a distant party, $\left(b_2\right)$, by manipulating their shared entanglement, highlighting the nonlocal nature of quantum mechanics.

The covariance matrix describes the Gaussian quantum steering in two directions:

$$\begin{array}{cc}\hfill {\mathcal{G}}^{b_1\to b_2}& =max\left(0,\mathrm{S}\left(2{\rho }_1\right)-\mathrm{S}\left(2\rho \right)\right),\\ \hfill {\mathcal{G}}^{b_2\to b_1}& =max\left(0,\mathrm{S}\left(2{\rho }_2\right)-\mathrm{S}\left(2\rho \right)\right),\end{array}$$

(9)

where $\mathrm{S}\left(\sigma \right)={\displaystyle \frac{1}{2}}ln(det\left(\sigma \right))$ is the Rényi-2 entropy [53]. The matrices ${\rho }_{\mathbf{1}}$, ${\rho }_{\mathbf{2}}$, and ${\rho }_{\mathbf{c}}$ are $2\times 2$ block matrices. The first two matrices represent the auto-correlations, while the last one describes the cross-correlation between the two bipartite modes. Additionally, ${\rho }_c^{†}$ denotes the conjugate transpose of ${\rho }_c$, such that

$$\begin{array}{c}\hfill \rho =\left(\begin{array}{cc}{\rho }_1& {\rho }_c\\ {{\rho }_c}^{†}& {\rho }_2\end{array}\right).\end{array}$$

(10)

We can identify the following key cases:

• If ${\mathcal{G}}^{b_1\to b_2}={\mathcal{G}}^{b_2\to b_1}=0$ then no steering can be observed; this is known as no-way steering.
• If either ${\mathcal{G}}^{b_1\to b_2}>0$ or ${\mathcal{G}}^{b_2\to b_1}>0$ then one-way steering occurs, meaning that only one party can steer the other.
• If both ${\mathcal{G}}^{b_1\to b_2}>0$ and ${\mathcal{G}}^{b_2\to b_1}>0$ then two-way steering is present. However, this does not imply symmetry in the degree of steerability. The steering can be asymmetric, such that ${\mathcal{G}}^{b_1\to b_2}\ne {\mathcal{G}}^{b_2\to b_1}$. In this case, mode $b_1$ can steer mode $b_2$ and vice versa, but with possibly different strengths. The bipartite modes described by the covariance matrix $\rho$ thus exhibit directional steerability in both directions.

Remarkably, the expression ${\mathcal{I}}^{b_1<b_2}=\mathrm{S}\left(2{\rho }_1\right)-\mathrm{S}\left(2\rho \right)$ can be regarded as a form of coherent quantum information [54], where Rényi-2 entropies substitute for the more predictable von Neumann entropies.

The Gaussian steering measure possesses several important properties for mode Gaussian states:

(a) The measure ${\mathcal{G}}^{b_1\to b_2}$ is convex;

(b) The measure ${\mathcal{G}}^{b_1\to b_2}$ decreases monotonically when quantum operations are performed on the untrusted steering party $b_1$;

(c) The measure ${\mathcal{G}}^{b_1\to b_2}$ is additive;

(d) For a pure state ${\rho }^T$, we have ${\mathcal{G}}^{b_1\to b_2}=\mathcal{E}\left(\rho \right)$;

(e) For a mixed state ${\rho }^T$, the measure satisfies ${\mathcal{G}}^{b_1\to b_2}\le \mathcal{E}\left(\rho \right)$, where $\mathcal{E}\left(\rho \right)$ represents the Gaussian Rényi-2 measure of entanglement [55].

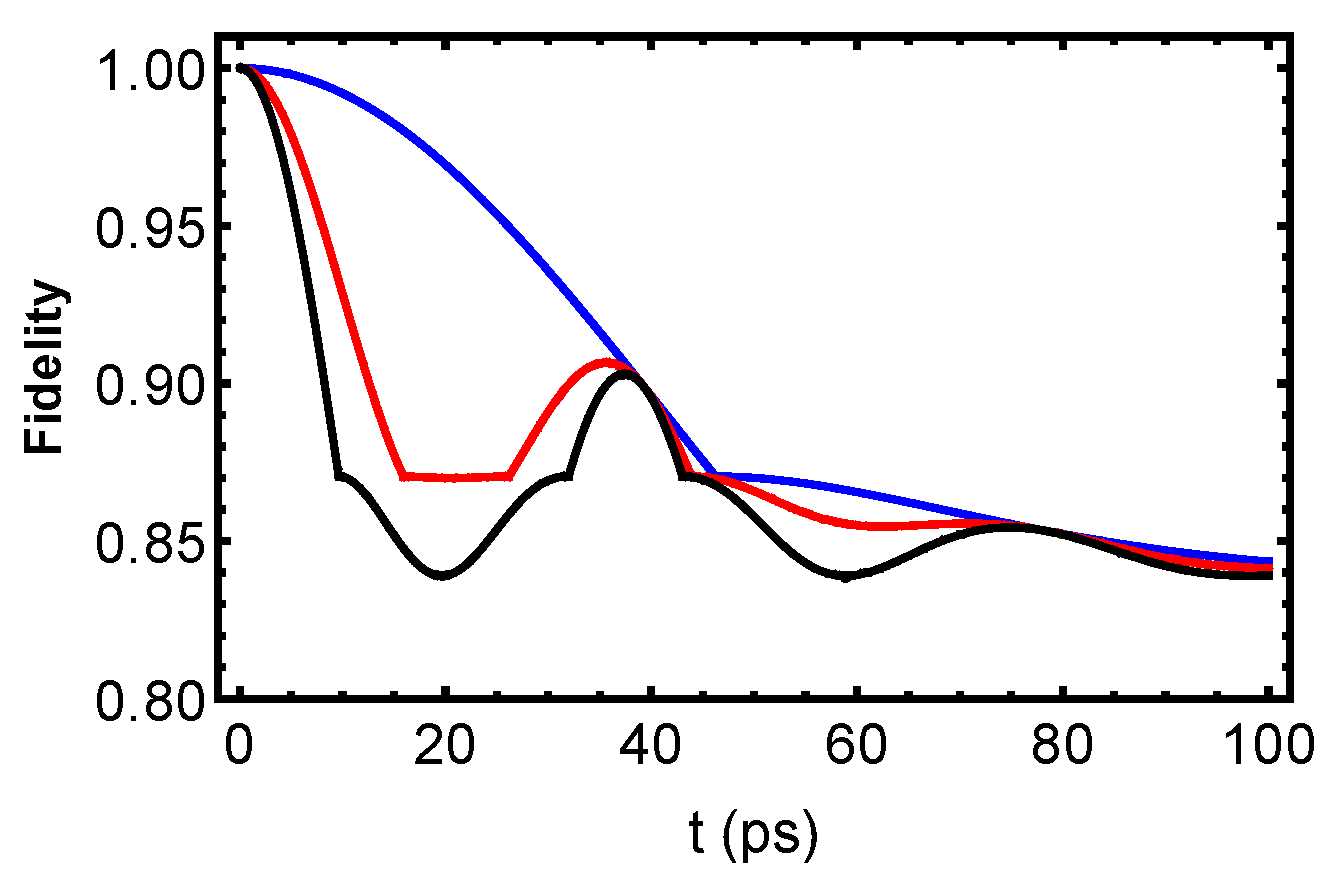
3.2. Fidelity

Fidelity quantifies the similarity between two quantum states $\rho$ and $\sigma$ and is given by

$$F(\rho ,\sigma )={\left(\mathrm{Tr}\sqrt{\sqrt{\rho }\sigma \sqrt{\rho }}\right)}^2.$$

(11)

For pure states $\rho =|\psi \rangle \langle \psi |$ and $\sigma =|\varphi \rangle \langle \varphi |$, fidelity reduces to the squared overlap:

$$F(\rho ,\sigma )={\left|\langle \psi |\varphi \rangle \right|}^2.$$

(12)

Fidelity is widely used in quantum information to benchmark the performance of quantum gates, compare quantum channels, and evaluate state reconstruction techniques [1,56]. High fidelity indicates close agreement between two states, making it a key metric in quantum communication and error correction.

4. Initial Photon States and Data Analysis

This work explores several important families of initial states that are currently interested in bipartite quantum systems. We focus on those that are experimentally feasible and hold significant promise for applications in quantum information processing. Such states play a pivotal role in the improvement of protocols such as quantum cryptography, teleportation, and entanglement-based communication [57,58,59,60,61,62]. We examine the evolution of quantum steering in these systems by utilizing canonical two-photon polarization mixed states as foundational configurations. Our discussion assumes that the two photons are initially prepared in arbitrary X-states. The density matrix of a two-photon X-state, expressed in the basis spanned by two-photon product states, takes the following general form:

$$\rho (0)=\left(\begin{array}{cccc}{\rho }_{11}\left(0\right)& 0& 0& {\rho }_{14}\left(0\right)\\ 0& {\rho }_{22}\left(0\right)& {\rho }_{23}\left(0\right)& 0\\ 0& {\rho }_{32}\left(0\right)& {\rho }_{33}\left(0\right)& 0\\ {\rho }_{41}\left(0\right)& 0& 0& {\rho }_{44}\left(0\right)\end{array}\right),$$

(13)

that is, ${\rho }_{12}\left(0\right)\equiv {\rho }_{13}\left(0\right)\equiv {\rho }_{24}\left(0\right)\equiv {\rho }_{34}\left(0\right)\equiv 0$. Equation (13) describes a quantum state provided that the unit trace and positivity conditions ${\sum }_{i=1}^4{\rho }_{ii}\left(0\right)=1$, ${\rho }_{22}\left(0\right){\rho }_{33}\left(0\right)\ge {\left|{\rho }_{23}\left(0\right)\right|}^2$, and ${\rho }_{11}\left(0\right){\rho }_{44}\left(0\right)\ge {\left|{\rho }_{14}\left(0\right)\right|}^2$ are fulfilled. In addition, X states are entangled if and only if ${\rho }_{22}\left(0\right){\rho }_{33}\left(0\right)<{\left|{\rho }_{14}\left(0\right)\right|}^2$ or ${\rho }_{11}\left(0\right){\rho }_{44}\left(0\right)<{\left|{\rho }_{23}\left(0\right)\right|}^2$. Both conditions cannot hold simultaneously.

In this framework, we introduce a class of two-parameter density matrices, as detailed in [63], which serve as useful tools for analyzing the dynamics of quantum steering:

$${\rho }_{x,y}\left(0\right)={\displaystyle \frac{1}{2}}\left(\begin{array}{cccc}x& 0& 0& x\\ 0& 1-x-y& 0& 0\\ 0& 0& 1-x+y& 0\\ x& 0& 0& x\end{array}\right),$$

(14)

where the diagonal terms ensure positivity, provided $0⩽x⩽1$ and $x-1⩽y⩽1-x$. The state depends on two parameters, x and y, determining the entangled and separable states. In addition, the ability to adjust (x,y) makes this initial state useful for real-world steering experiments [26,64,65,66,67]. Using Equations (8) and (14) as the initial state, the resulting dynamical state is

$${\rho }_{x,y}\left(t\right)={\displaystyle \frac{1}{2}}\left(\begin{array}{cccc}x& 0& 0& x{p}_A\left(t\right)p_B\left(t\right)\\ 0& 1-x-y& 0& 0\\ 0& 0& 1-x+y& 0\\ x{p}_A^{*}\left(t\right)p_B^{*}\left(t\right)& 0& 0& x\end{array}\right).$$

(15)

This evolved density matrix incorporates the time-dependent decoherence effects through the functions $p_A\left(t\right)$ and $p_B\left(t\right)$. Before investigating the evolution of quantum steering and the fidelity of the state, it is essential to analyze the key properties of the state. The functions $p_A\left(t\right)$ and $p_B\left(t\right)$, which appear in the off-diagonal elements of the density matrix, play a critical role in governing the coherence of the quantum state. Specifically, if $p_A\left(t\right)$ and $p_B\left(t\right)$ exhibit decay over time, due to noise or environmental interactions, the quantum coherence will progressively decrease, leading to decoherence. Furthermore, the behavior of $p_A\left(t\right)$ and $p_B\left(t\right)$ can provide insight into the nature of the system dynamics. For instance, revivals or oscillatory patterns in these functions may indicate non-Markovian dynamics, where information is periodically exchanged between the system and its environment. The off-diagonal elements are also pivotal in determining the entanglement properties of the system. Suppose $p_A\left(t\right)$ and $p_B\left(t\right)$ decay exponentially; the entanglement between the qubits may be lost over time. Conversely, entanglement can be temporarily restored if these functions exhibit revivals, highlighting the dynamic nature of quantum correlations. The explicit forms of $p_A\left(t\right)$ and $p_B\left(t\right)$ are intrinsically linked to the physical processes that govern the evolution of the system. Let us now examine experimentally realistic scenarios, to explore the dynamics of quantum steering and fidelity in photon-polarization states. The parameters under consideration are chosen to reflect practical experimental conditions: $\Delta n=0.01$, $\mu =1.8\times {10}^{12}$ Hz, ${\omega }_1=2.676\times {10}^{15}$ Hz (corresponding to a wavelength of approximately 704.5 nm), and ${\omega }_2=2.692\times {10}^{15}$ Hz (corresponding to a wavelength of approximately 700.3 nm). The driving time $\tau$ is determined by the relation $\tau ={\displaystyle \frac{2\pi }{\Delta \omega ·\Delta n}}$, yielding $\tau \approx 0.3927$ ps [47]. The parameter values used in our analysis are chosen to align with experimentally accessible regimes. In particular, the values of the previous parameters are motivated by those reported in recent works [68,69]. These choices ensure that our theoretical predictions are directly relevant to realistic implementations.

Figure 1 presents the time evolution of quantum steering measures, denoted ${\mathcal{G}}^{b_1\to b_2}$ and ${\mathcal{G}}^{b_2\to b_1}$, within a two-photon system subjected to dephasing interactions. These measures are evaluated for two initial state configurations with $x=0.5$: $y=0.25$ in Figure 1a and $y=-0.25$ in Figure 1b. Each subplot evaluates three distinct environmental conditions. These steering measures reveal three distinct regimes: no-way steering, where both ${\mathcal{G}}^{b_1\to b_2}$ and ${\mathcal{G}}^{b_2\to b_1}$ are zero, indicating that there is no directional influence; one-way steering, where only one measure is positive, signifying unidirectional quantum control; and two-way steering, where both measures are positive, reflecting bidirectional influence. In the Markovian regime (characterized by ${\varphi }_A={\varphi }_B=0$, shown as solid lines), the steering measures exhibit a monotonic decay, illustrating a progressive loss of quantum correlations during dynamics, eventually transitioning from two-way to no-way steering. The non-Markovian regime (dashed lines, ${\varphi }_A={\varphi }_B=\pi /8$) displays oscillatory patterns with periodic revivals of both steering measures, indicative of sustained two-way steering driven by memory effects in both subsystems. The hybrid regime (dot–dashed lines, ${\varphi }_A=0$, ${\varphi }_B=\pi /4$), where one subsystem undergoes Markovian dephasing and the other non-Markovian dynamics, shows a qualitatively similar pattern within the presented timescale. However, as seen more clearly in the extended-time analysis (Figure 1), the hybrid regime tends to exhibit reduced revival amplitudes and a gradual decay in oscillation strength, reflecting the asymmetry in environmental interactions. This supports the interpretation that full two-way memory effects are necessary to maintain strong steering dynamics over longer durations. Notably, one-way steering is absent across all scenarios, as the steering measures either remain positive symmetrically or vanish together. Adjusting the initial state parameter from $y=0.25$ to $y=-0.25$ modifies the oscillation amplitudes in non-Markovian cases, but does not fundamentally alter the steering dynamics. The pronounced asymmetry observed in two-way steering explicitly offers a strategic advantage for its exploitation. The obtained results show that quantum steering measures in a two-photon system under dephasing reveal no-way, one-way, and two-way steering regimes, with Markovian dynamics causing monotonic decay from two-way to no-way steering, while non-Markovian dynamics sustain two-way steering through oscillatory revivals. The hybrid regime shows reduced revival amplitudes, indicating how memory effects can preserve or diminish bidirectional quantum control over time. One-way steering is absent, and initial state changes affect oscillation amplitudes but not the overall steering dynamics.

Figure 2 explores the time evolution of fidelity, in terms of time t for photons initially prepared in the state given by Equation (14), with $x=0.5$ and $y=0.25$, under both Markovian and non-Markovian dynamics. At $t=0$, the fidelity $F\left(0\right)=1$ for all cases is as expected. In fact, fidelity slowly decreases with time as a result of decoherence and environmental interactions. The decay behavior depends on the nature of the dynamics. Certainly, a monotonic decay suggests Markovian dynamics, where information is irreversibly lost to the environment. However, fluctuations or partial-fidelity revivals suggest non-Markovian memory effects, where lost information is temporarily recovered. Furthermore, the parameter $\varphi$ influences the evolution of fidelity. The blue line (${\varphi }_A={\varphi }_B=0$) exhibits the highest overall fidelity, indicating stronger robustness against decoherence, while as $\varphi$ increases ($\pi /8,\pi /4$), the fidelity decays more rapidly. In addition, the presence of revivals in fidelity supports the role of non-Markovian effects. Non-Markovian dynamics allow for temporary recovery of lost quantum information, leading to oscillatory behavior in fidelity, and Markovian dynamics exhibit a smoother, irreversible decay. However, reliability quantifies the preservation of the initial quantum state. Certainly, higher fidelity values indicate stronger coherence retention, which is essential for quantum technologies, while faster fidelity decay implies greater fragility to environmental noise. In addition, the time-dependent behavior of the fidelity illustrates that adjustments of the relative weighting parameter can be used as a control mechanism. Interestingly, in the non-Markovian regime, the photons have the same dephasing, ${\varphi }_A={\varphi }_B=\pi /8$ (red line), and the fidelity evolution exhibits a rapid decrease, followed by a modest plateau, revivals, another short plateau, and final slow decay. The initial fidelity drop corresponds to the onset of decoherence due to environmental interactions. The subsequent plateau suggests a dynamically stable state in which the quantum system momentarily halts its evolution, which may be explained by the presence of a decoherence-free subspace or a temporary balance between the loss and backflow of information. Furthermore, the black line in the evolution of the fidelity, corresponding to the case of strong non-Markovianity ${\varphi }_A=0,{\varphi }_B=\pi /4$, reveals an important effect of the initial dephasing, leading to faster fidelity decay. Thus, these results illustrate that fidelity in a two-photon system, initially at $F\left(0\right)=1$, decays monotonically under Markovian dynamics due to irreversible information loss, while non-Markovian dynamics exhibit oscillatory revivals and plateaus, indicating temporary recovery of quantum information. Non-Markovian cases (${\varphi }_A={\varphi }_B=\pi /8$) show a rapid initial drop followed by revivals and plateaus, suggesting a dynamically stable state. Strong non-Markovianity (${\varphi }_A=0,{\varphi }_B=\pi /4$) leads to faster fidelity decay due to initial dephasing.

When the two-photon system undergoes dephasing interactions, the evolution of quantum steering and fidelity depends on whether the dynamics are Markovian or non-Markovian, governed by the dephasing factor given in Equation (5). Initially, at $t=0$, the system is in an entangled state (e.g., an X-state with parameters $x=0.5$, $y=0.25$), exhibiting perfect fidelity ($F=1$) and two-way steering (${\mathcal{G}}^{b_1\to b_2},{\mathcal{G}}^{b_2\to b_1}>0$), which measures the ability of one party to remotely influence another’s quantum state. In the Markovian regime, ($\varphi =0$), $p\left(t\right)=e^{i{\omega }_1\Delta nt}{e}^{-{\displaystyle \frac{{(\sigma \Delta nt)}^2}{2}}}$, leading to a steady, irreversible decay of coherences as t increases, with $p\left(t\right)\to 0$. This causes the off-diagonal elements of the density matrix (e.g., ${\rho }_{14}\left(t\right)=x{p}_A\left(t\right)p_B\left(t\right)$) to vanish, leaving only diagonal elements and transforming the quantum state into a classical, fully dephased state with no coherences. Consequently, the steering measures monotonically decrease to zero ($\mathcal{G}=0$), and the fidelity stabilizes to a value less than 1, reflecting the overlap of populations with the initial state. In contrast, the non-Markovian regime ($\varphi \ne 0$) introduces oscillatory behavior in $p\left(t\right)$, due to the interference between two frequency components (${\omega }_1$ and ${\omega }_2$), resulting in periodic revivals of steering and fidelity. These revivals indicate a temporary recovery of quantum correlations via environmental memory effects. At short times, the Gaussian decay is negligible, so steering remains robust with oscillations in the non-Markovian case, while it steadily declines in the Markovian case. In the long-time limit ($t\to \infty$), both regimes ultimately lead to $p\left(t\right)\to 0$, causing all off-diagonal elements of the density matrix to disappear. This leaves only diagonal elements, signifying a classical state without coherences, where the steering vanishes completely ($\mathcal{G}=0$) and fidelity reduces to a constant value less than 1, determined solely by the classical overlap of populations with the initial state.

5. Conclusions

In summary, we have examined quantum steering and fidelity dynamics in a two-photon system under dephasing interactions, analyzed across both Markovian and non-Markovian environments. By employing experimentally realistic parameter values, we have developed a practical framework to understand how the environment influences quantum steering and the preservation of initial quantum states. Key findings revealed that quantum steering, the ability to influence a quantum state remotely, exhibited distinct behaviors depending on the environmental context: in the Markovian environment, it underwent irreversible decay due to dephasing dominating, whereas in the non-Markovian regime, it displayed periodic recoveries driven by environmental memory effects. Similarly, fidelity, which measures the retention of the initial state, showed consistent degradation in Markovian conditions, but experienced temporary restorations in non-Markovian environments, underscoring the protective role of structured environmental interactions against coherence loss. The analysis further highlighted that steering and fidelity were sensitive to initial-state configurations and dephasing parameters, offering tunable mechanisms to control these quantum quantities. Implications of these insights are significant for quantum information processing, particularly in applications like secure communication and state preservation, where maintaining robust quantum correlations is critical. By bridging theoretical analysis with practical applications, this study may contribute to the foundation for developing applications in quantum technology through the strategic manipulation of environmental interactions and system parameters.