Abstract
This study explores the degree energy of fuzzy graphs to establish fundamental spectral bounds and characterize adjacency structures. We derive upper bounds on the sum of squared degree eigenvalues based on vertex degree distributions and formulate constraints using the characteristic polynomial of the maximum degree matrix. Furthermore, we demonstrate that the average degree energy of a connected fuzzy graph remains strictly positive. The proposed framework is applied to protein–protein interaction networks, identifying critical proteins and enhancing network resilience analysis.
Keywords:
fuzzy graph energy; eigenvalues; spectral graph theory; energy bounds; degree matrix; degree energy; maximum degree energy; minimum degree energy MSC:
05C50; 05C72; 58C40; 05C07
1. Introduction
Graph theory, originating with Euler’s seminal work on the Seven Bridges of Konigsberg in 1736, evolved into a powerful mathematical framework for modeling and analyzing interconnected systems. The core components, comprising vertices and edges, form a versatile foundation in the development of algebraic graph theory to reveal structural and functional properties of graphs through the eigenvalues of associated matrices. By analyzing matrices such as the adjacency matrix, Laplacian matrix, and normalized Laplacian matrix, spectral graph theory provides a strong framework for understanding graph topology and its implications [1,2]. Von Collatz, L. and Sinogowitz, U., in 1957, posed the problem which characterized non-singular graphs to describe the issue of all nullity greater than zero. Later, Hoffman, A. J. in 1968 introduced spectral properties of graphs by examining the interplay between spectral and graphical properties of graph G.
The seminal work of Doob in 1970 characterized certain graphs with eigenvalues by their spectra, which paved the way for the pioneering work by Cvetković, D. M., Doob, M., and Sachs, H. Later, in 1973, Fiedler, M. introduced the algebraic connectivity of graphs, which represents the second smallest eigenvalue of the Laplacian matrix and quantifies the robustness of a graph [3]. Several results concerning bounds on the eigenvalues of G were presented by Hong, Y. in 1988. Chung, F. R.’s lectures on spectral graph theory in 1996 discussed basic facts about eigenvalues and stated upper and lower bounds for graphs without loops and multiple edges. Brouwer and Haemers offered a foundational study on graph spectra, focusing on eigenvalue analysis of adjacency and Laplacian matrices [4].
The early 2000s saw a shift toward graph energy [5] and its applications. Graph energy, as introduced by Gutman, represents the sum of the absolute values of the eigenvalues of a graph’s adjacency matrix [6]. This measure has been extensively applied in chemistry, where it correlates with molecular stability [7,8]. Liu et al., in 2007, derived upper bounds for graph energy, providing insights into graph stability and resilience. Adiga and Smitha, in 2009, investigated the energy associated with maximum degrees, introducing novel metrics for graph evaluation [9]. Gutman and Oboudi proposed novel bounds on graph energy, advancing graph optimization techniques in 2020 [7]. Researchers established bounds for graph energy [10], explored estimation techniques using graph parameters such as degree sequences [11], and extended their application to specialized graph structures [12]. Filipovski and Jajcay established theoretical bounds for graph energy, enhancing the understanding of spectral properties [13]. Nagalakshmi et al., in 2024, analyzed degree energy, linking vertex degree to spectral energy distribution [14]. Concepts like maximum and minimum degree energy provide additional granularity, highlighting the energy contributions of vertices with the highest and lowest degrees, respectively [9,15]. Milovanovic et al. proposed McClelland-type upper bounds for graph energy, refining energy estimation techniques [16,17].
However, classical graph theory falls short when dealing with the inherent uncertainties and vagueness found in many real-world networks. To address this limitation, fuzzy graph theory, grounded in Zadeh’s fuzzy set theory (1965), incorporates the concept of partial membership [18]. Fuzzy graphs assign membership values in the range to both vertices and edges, allowing a more realistic representation of relationships where connections are not strictly binary. Building upon this foundation, Rosenfeld extended graph theory into the fuzzy domain [19], paving the way for fuzzy graph theory to represent imprecise relationships [20].
Fuzzy graphs and weighted graphs both assign numerical values to edges, but they differ fundamentally in interpretation and application. In a weighted graph, an edge weight represents a fixed, deterministic quantity, such as distance, probability, or interaction strength. In contrast, in a fuzzy graph, the edge membership function represents the degree of connectivity between vertices based on uncertainty, vagueness, or partial truth, rather than a fixed numerical measure.
For example, in a protein–protein interaction (PPI) network, consider two proteins and with a membership value of :
- Weighted graph interpretation: A weight might indicate an 80% probability that and interact under given biological conditions.
- Fuzzy graph interpretation: A membership value means the interaction exists to a degree of 0.8, considering multiple fuzzy factors like protein expression levels, environmental conditions, or experimental uncertainty.
The key difference is that fuzzy graphs allow operations such as fuzzy composition, intersection, and -cuts, which provide a richer framework for handling imprecise, evolving, or context-dependent relationships. Unlike weighted graphs, fuzzy graphs do not require absolute certainty in assigning values and can adapt to dynamically changing datasets, making them more suitable for complex, uncertain systems like biological networks.
The broadened view to include applications of fuzzy graphs and spectral methods in real-world contexts has paved the way for the development of spectral fuzzy graph theory. Anjali and Mathew, in 2013, analyzed the energy of fuzzy graphs as the sum of the absolute values of the eigenvalues of the adjacency matrix of the fuzzy graph [21], addressing the limitations of binary relationships in complex networks [22,23]. Akram et al. analyzed the energy of bipolar fuzzy graphs, extending spectral methods to systems with bipolar fuzziness [24]. In 2016, Vimala, S. and Jayalakshmi, P. calculated the upper and lower bounds in terms of the degree and membership values of fuzzy graphs. Kalpana et al. investigated connectedness energy in fuzzy graphs and contributed to the study of network dynamics in 2018. Al-Hawary, T. and Al-Shalaldeh, S. characterized the matrices for certain operations on fuzzy graphs and studied the energy of fuzzy graphs in 2023.
Spectral fuzzy graphs provide a powerful framework for analyzing complex systems where relationships are uncertain, imprecise, or evolving. Unlike classical graphs, which assume binary or weighted connections, fuzzy graphs incorporate membership values, making them ideal for modeling real-world networks such as biological systems, social networks, communication infrastructures, and financial markets. In protein–protein interaction (PPI) networks, spectral fuzzy graphs help identify critical proteins influencing disease progression. In cybersecurity, they enhance network anomaly detection by analyzing fuzzy connectivity patterns. Additionally, in social network analysis, they capture varying levels of influence and interaction strengths. By leveraging spectral techniques, fuzzy graphs enable deeper insights into resilience, stability, and connectivity in uncertain environments.
Recent studies have expanded fuzzy graph theory to cover perfectly regular fuzzy graphs [25], signless Laplacian energy [26], and vague fuzzy graph connectivity [27,28]. Interval-valued picture fuzzy hypergraphs aid in decision making [29]. These works highlight the field’s growing impact on real-world problems and complex networks. Shi et al. (2022) investigated picture fuzzy graphs and interval-valued quadripartitioned neutrosophic graphs, exploring their properties and real-life applications [30,31]. Rao et al. [32] focused on forcing parameters in fully connected cubic networks and explored the relationship between the planarity of graphs and the algebraic properties of symmetric and pseudo-symmetric numerical semigroups [33].
1.1. Motivation and Problem Statement
Spectral energy measures are instrumental in analyzing the structure of fuzzy graphs, where uncertainty in connectivity is modeled through membership functions. Traditional energy metrics, however, are largely based on the eigenvalues of the adjacency matrix and fail to incorporate vertex degree information, which represents the cumulative strength of local interactions. This gap limits our ability to capture critical structural and functional characteristics of fuzzy networks, particularly in scenarios where variations in edge strength play a pivotal role. In such systems, like biological or communication networks, vertex degree plays a critical role in defining stability and connectivity. To address this limitation, a degree-based energy framework for fuzzy graphs is introduced, integrating local vertex properties with global spectral characteristics. This novel energy measure is formally defined, accompanied by the derivation of analytical bounds, and its effectiveness is demonstrated in capturing robustness and resilience in complex networks such as protein–protein interaction models. This approach addresses the existing gap and provides a more comprehensive spectral tool for fuzzy graph analysis.
1.2. Novelty and Key Contributions
- 1.
- Unlike prior studies that focus on adjacency-based energy, this work defines degree energy, average degree energy, maximum degree energy, and minimum degree energy, offering a new perspective on spectral properties.
- 2.
- This work provides rigorous mathematical bounds for degree energy, strengthening the analytical framework of spectral fuzzy graphs.
- 3.
- This work integrates vertex degree information with spectral methods, enhancing insights into graph structure and resilience.
- 4.
- This is the first study to apply degree energy in fuzzy graphs to biological networks, specifically in modeling Systemic Lupus Erythematosus (SLE) PPI networks to identify critical therapeutic targets.
- 5.
- This work expands the applicability of fuzzy graph energy to network stability, resilience, and biomedical research, beyond traditional applications in social and communication networks.
1.3. Organization of the Paper
This paper is structured as follows: Section 2 covers background concepts. Section 3 defines degree energy and derives bounds for the proposed measures with examples. Section 4 derives and proves bounds for average degree energy. Section 5 addresses bounds for maximum and minimum degree energy. In Section 6, an application to model a protein–protein interaction network associated with Systemic Lupus Erythematosus (SLE) is presented to identify potential therapeutic targets. Section 7 concludes with key findings and future directions.
2. Preliminaries
A fuzzy graph consists of a non-empty vertex set V, a fuzzy vertex function , and a fuzzy edge function , satisfying the condition for all [20]. The adjacency matrix A of G is an matrix, defined as , where each entry is given by , and its eigenvalues are arranged in descending order as [21]. The spectrum of a square matrix M, denoted by , is the collection of its eigenvalues, expressed as , where each appears with multiplicity [4]. In the context of fuzzy graphs, the adjacency eigenvalues and their corresponding algebraic multiplicities collectively form the fuzzy spectrum [21]. The energy of a fuzzy graph, represented as , is given by the sum of the absolute values of its adjacency eigenvalues, formulated as [21]. Furthermore, the degree of a vertex v in a fuzzy graph is defined as , while the minimum and maximum degrees of G are, respectively, given by and [34].
Note: Throughout this section, we consider only simple, connected, undirected fuzzy graphs G. The definitions and theorems presented for energy bound, degree energy, average degree energy, maximum degree energy, and minimum degree energy are specific to this class of fuzzy graphs.
The key notations and symbols used throughout this paper are summarized in Table 1.

Table 1.
Notations and symbols.
3. Bounds on Degree Energy of Fuzzy Graph
In this section, the energy bound and the degree energy for a fuzzy graph G are defined and illustrated through examples. Additionally, theorems establishing bounds based on degree energy are proved.
Definition 1.
Energy Bound of a Fuzzy Graph.
Let be the energy of a fuzzy graph , where V is the vertex set, is the vertex membership function, and is the edge membership function.
An energy bound for G is given by the following inequality:
where and are the lower and upper bound functions, respectively, determined by the structure of G (i.e., as functions of V, σ, and μ).
Definition 2.
Degree Energy of a Fuzzy Graph.
Let G be a fuzzy graph. The sum of the membership values of the edges incident to a vertex is its degree, denoted . The matrix representing the fuzzy degree matrix of G is defined by , where
The degree spectrum of a fuzzy graph G, denoted by , consists of the eigenvalues of the degree matrix , along with their respective algebraic multiplicities . This can be represented as
The degree energy is defined as the sum of the absolute values of the degree eigenvalues weighted by their multiplicities:
Example 1.
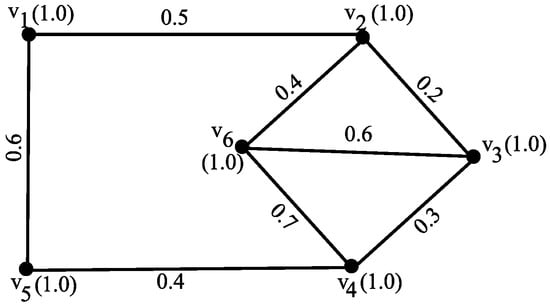

Figure 1.
Fuzzy graph G with 6 vertices demonstrating degree energy.
The degrees of the fuzzy graph are computed as follows:
The fuzzy degree matrix is given by
The characteristic equation is
The eigenvalues of the degree matrix are approximately
Therefore, the degree energy is
Let G be a fuzzy graph and let denote the degree of vertex , for . We define the following notations:
- : total number of adjacent vertex pairs with equal degrees.
- : total number of adjacent vertex pairs with unequal degrees.
- : total number of non-adjacent vertex pairs with equal degrees.
Example 2.
Consider a fuzzy graph G as shown in Figure 1. The degrees are
- Then,
Let G be a fuzzy graph consisting of n vertices, and let its degree matrix be denoted by . The subsequent theorems characterize the properties of the degree energy , including the sum of squared eigenvalues and bounds for in terms of the smallest eigenvalue and expressions involving the extremal eigenvalues.
Lemma 1.
Let be the vertex degree eigenvalues of , then
where , , and represent the total number of adjacent vertex pairs with equal degrees, adjacent vertex pairs with unequal degrees, and non-adjacent vertex pairs with equal degrees, respectively.
Proof of Lemma 1.
Let G be a fuzzy graph with n vertices, and let denote its degree matrix. The eigenvalues of are denoted as , where each eigenvalue corresponds to the degree of a vertex.
The sum of the squares of the eigenvalues of is given by
where denotes the trace of the square of . As is a diagonal matrix, its square is also diagonal, and the trace equals the sum of the squares of its diagonal entries:
where is the fuzzy degree of vertex . Hence,
To express in terms of , , and , consider the following:
- 1.
- For each pair of adjacent vertices with equal degrees (), the combined contribution to is . The total contribution from such pairs is .
- 2.
- For each pair of adjacent vertices with unequal degrees (), the combined contribution is , and summing over all such pairs gives a contribution of .
- 3.
- For each pair of non-adjacent vertices with equal degrees (), the contribution is , contributing a total of .
Combining all these, the total sum is
As the eigenvalues correspond to degrees , it follows that
□
Intuitive Explanation:
The squared sum of eigenvalues in fuzzy graphs reflects how the structure and similarity of vertex degrees contribute to the graph’s spectral properties. The expression
assigns a greater weight to adjacent vertices with equal degrees (), while adjacent vertices with unequal degrees () and non-adjacent but equally degreed vertices () have relatively lower contributions. This reflects how regularity in degree distribution affects the spectral characteristics of the fuzzy graph.
Theorem 1.
For any fuzzy graph G, if , then
Proof of Theorem 1.
The determinant of is given by the product of its eigenvalues:
Taking absolute values:
Let . Then, for all i, we have . Therefore,
This implies
Taking the n-th root on both sides gives
Thus, we conclude that □
Example 3.
Consider a fuzzy graph G as shown in Figure 1, with for all vertices , where . The vertex degree eigenvalues are found as , , , , , , and .
- , , , and confirming that .
According to Theorem 1, the value of , and . Thus, , which confirms that .
Theorem 2
(Lower and Upper Bounds for Degree Energy). Let G be a fuzzy graph. Then,
Proof of Theorem 2.
Consider a fuzzy graph with n vertices. The eigenvalues of its fuzzy degree matrix , denoted by , correspond to the degrees of the vertices. The degree energy of G, denoted by , is defined as
From the earlier result, it is known that
where , and represent the total number of adjacent vertex pairs with equal degrees, adjacent vertex pairs with unequal degrees, and non-adjacent vertex pairs with equal degrees, respectively.
As corresponds to the degrees of vertices in G, we have for all i. Thus, the maximum possible contribution to is achieved when for all i, which gives
Taking the square root yields the upper bound:
To analyze the distribution of the eigenvalues for the lower bound, consider the arithmetic mean–geometric mean (AM–GM) inequality. Let be the geometric mean of the eigenvalues. By the AM–GM inequality,
Rearranging, we obtain
Adding to both sides yields
Taking the square root gives the lower bound:
Combining the bounds, we conclude that
□
Corollary 1
(Bound on Maximum Eigenvalue). If the vertex degree eigenvalue of G is , then
Proof of Corollary 1.
Let be the eigenvalues of the fuzzy degree matrix , and let be the spectral radius.
From Lemma 1, we know that
As the maximum squared eigenvalue is at least the average,
and as it is also bounded above by the total,
Taking square roots of both bounds gives
□
Example 4.
Consider a fuzzy graph G as shown in Figure 1. From the vertex degree eigenvalues, the degree energy is given by , and the value of . The value of , where det is the determinant of G, and denotes the number of vertices.
According to Theorem 2,
implying that
According to Corollary 1, it is found that , , and . Thus, the statement
is verified.
Theorem 3
(Inequality Involving Extremal Eigenvalues). Let G be a fuzzy graph with vertices. If and are the largest and smallest eigenvalues of G, respectively, then the sum of the largest and smallest eigenvalues satisfies the following inequality:
Proof of Theorem 3.
Let be a fuzzy graph with vertices. Let the eigenvalues of the fuzzy degree matrix be , where and denote the largest and smallest eigenvalues, respectively.
From Lemma 1, the sum of the squares of the eigenvalues is
By the Cauchy–Schwarz inequality applied to the eigenvalues,
Substituting the known expression
Taking square roots on both sides,
As G has at least three vertices, the contribution of to the spectral structure is further bounded by a normalization factor reflecting the influence of the remaining eigenvalues:
This proves the desired inequality. □
Example 5.
Consider a fuzzy graph G, as shown in Figure 1, with for all vertices . The vertex degree eigenvalues are approximately and , so that . Additionally,
As , the inequality stated in the theorem holds true.
4. Bounds on Average Degree Energy of Fuzzy Graph
This section defines and explains the average degree energy of a fuzzy graph, providing illustrative examples. Furthermore, it presents and proves theorems establishing bounds based on this energy.
Definition 3.
Average Degree Energy of a Fuzzy Graph.
Consider a fuzzy graph with a symmetric fuzzy degree matrix defined as follows:
where represents the degree of vertex , computed as the total sum of the membership values of edges incident to .
The average degree energy, denoted as , is defined as the sum of the absolute values of the eigenvalues of the matrix , given by
As is a symmetric matrix with trace zero, its eigenvalues are real and sum to zero. Consequently, the eigenvalues satisfy
Example 6.
Consider a fuzzy graph G with 6 vertices as shown in Figure 1.
The average fuzzy degree matrix is represented as follows:
The average vertex degree eigenvalues are approximately
Therefore, the average degree energy is
Theorem 4.
If G is a connected fuzzy graph with a non-singular average degree matrix , then its average degree energy satisfies .
Proof of Theorem 4.
Consider a connected fuzzy graph with n vertices. The symmetric average degree matrix is defined as
where denotes the degree of vertex , computed as the sum of the membership values of the edges incident to .
As is symmetric, all its eigenvalues are real. The average degree energy of G is defined as
By assumption, is non-singular, which implies that . Hence, none of its eigenvalues are zero; that is, for all .
As all eigenvalues are real and non-zero, we have for each i. Therefore, □
Theorem 5.
Let G be a fuzzy graph with n vertices, and let be the maximum average degree among all vertices in G. Then, there exists a function such that the average degree energy is bounded above by
Proof of Theorem 5.
Let be the average degree matrix of G, with eigenvalues . The average degree energy is defined as . Let denote the spectral radius (i.e., the largest absolute eigenvalue). Then,
We now show that there exists a function such that . Consider the entries of defined as
where for all . Therefore, the maximum possible entry in is, at most, .
According to Gershgorin’s circle theorem — “Every eigenvalue of a matrix lies within at least one of its Gershgorin discs”— each eigenvalue lies within a disc centered at the diagonal entry with radius equal to the sum of the absolute values of the off-diagonal entries in the same row. As the maximum entry is, at most, , the row sum is bounded above by . Thus,
Defining , we obtain:
Hence, setting provides an upper bound for the average degree energy. □
Example 7.
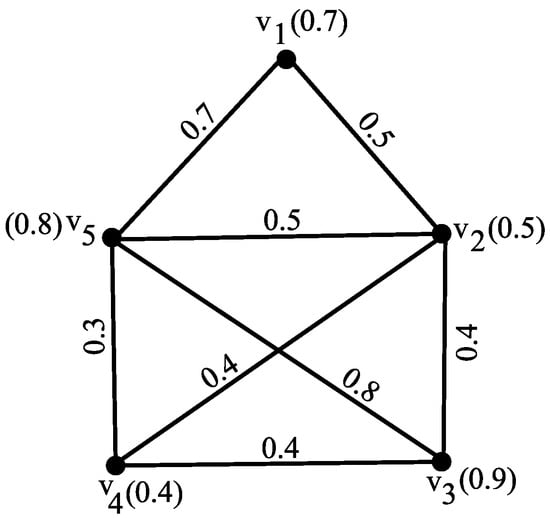
Consider the fuzzy graph G as shown in Figure 2 with vertex set , where for all , and the edge membership values are given by , , , , , , , and .

Figure 2.
Fuzzy graph G demonstrating average degree energy.
The average degrees of the vertices are , , , , and .
The average degree matrix is given by
The eigenvalues of are approximately: , , , , and . Therefore, the average degree energy is
By Theorem 4, as the average degree matrix is non-singular, we confirm that .
To verify Theorem 5, note that the fuzzy graph G has vertices and a maximum average degree .
An upper bound on the average degree energy is given by
Substituting the values: As , the inequality holds, confirming Theorem 5.
5. Bounds for Maximum Degree Energy and Maximum Degree Eigenvalue
This section defines and illustrates the concepts of maximum and minimum degree energy for fuzzy graphs using examples. Theorems providing bounds based on maximum degree energy are also proven.
Definition 4.
Maximum Degree Energy of a Fuzzy Graph.
Consider a fuzzy graph with n vertices. Let denote the degree of vertex , for . The maximum degree matrix is defined as
The characteristic polynomial of is given by
where I denotes the identity matrix of order n. The eigenvalues are arranged in descending order, with being the largest maximum degree eigenvalue, satisfying .
The maximum degree energy, denoted by , is defined as the sum of the absolute values of all eigenvalues of :
As is a real symmetric matrix with zero trace, its eigenvalues are real and satisfy
Example 8.
Consider a fuzzy graph G with six vertices, as shown in Figure 1.
The maximum degree matrix is given by
The eigenvalues of are approximately
Therefore, the maximum degree energy is
Definition 5.
Minimum Degree Energy of a Fuzzy Graph.
Consider a fuzzy graph with n vertices. Let represent the degree of vertex , for . The minimum degree matrix is defined as
The characteristic polynomial of is given by
where I denotes the identity matrix of order n. The eigenvalues are arranged in decreasing order, such that is the largest eigenvalue, satisfying .
The minimum degree energy, denoted as , is defined as the sum of the absolute values of the eigenvalues of :
As is a real symmetric matrix with zero trace, all its eigenvalues are real and their sum is zero. Therefore, we have
Example 9.
Consider a fuzzy graph G with 6 vertices, as shown in Figure 1.
The minimum fuzzy degree matrix is represented as
The minimum degree eigenvalues are approximately
Therefore, the minimum degree energy is given by
Let us define the coefficients , , and , which originate from the characteristic polynomial of the maximum degree matrix associated with a fuzzy graph, as follows:
- 1.
- Coefficient : By construction, the coefficient of in the characteristic polynomial is .
- 2.
- Coefficient : The coefficient of corresponds to . As the diagonal elements of are zero (due to the absence of self-loops), it follows that .
- 3.
- Coefficient : The second-degree coefficient in the characteristic polynomial of a real symmetric matrix A is given byAs , this simplifies toby the definition of the maximum degree matrix , we havewhere . Contributions to the summation vanish for edges with , ensuring consistency with the fuzzy graph structure.
Example 10.
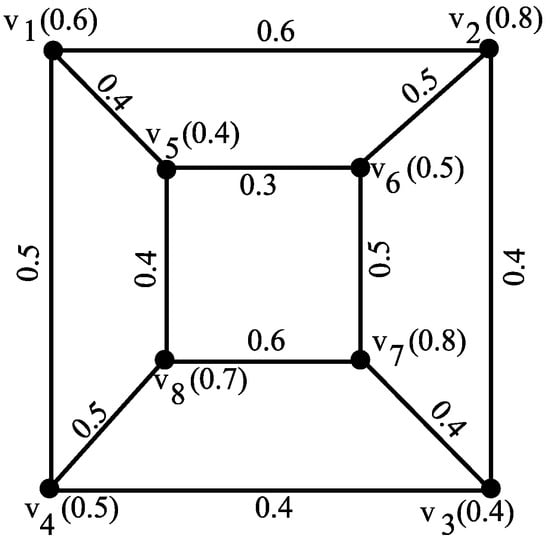

Consider a fuzzy graph G as shown in Figure 3 with vertices , where the vertex memberships are given as

Figure 3.
Fuzzy graph G depicting maximum degree energy.
Now, calculate the vertex degrees as follows:
Construct the maximum degree matrix :
To calculate for the above graph, use the following formula:
where the summation is over all unique pairs , is the degree of vertex , is the degree of vertex , is the edge membership between vertices and , and ∨ denotes the maximum operation.
Let us break down the calculation as given in Table 2.

Table 2.
Computed values of for given vertex pairs.
Therefore, the sum is
Lemma 2.
Let be a fuzzy graph and let denote its maximum degree matrix. The characteristic polynomial of is given by
where the coefficients satisfy
- ;
- ;
- .
Proof of Lemma 2.
Let be a fuzzy graph and let denote its maximum degree matrix.
- 1.
- The coefficient corresponds to the leading term in the characteristic polynomial, and it always equals 1. This follows from the definition of the characteristic polynomial:where the highest-degree term arises by multiplying all the diagonal entries of , yielding . Therefore,
- 2.
- The coefficient corresponds to the term and is given byis derived from a fuzzy graph with no self-loops, each diagonal entry satisfies for all , hence
- 3.
- The coefficient is given byis symmetric with generally non-zero off-diagonal entries, we have , implying . Specifically,so thatwhich confirms that .
□
Theorem 6.
Let be a fuzzy graph with n vertices, and let be its maximum degree matrix. Suppose the eigenvalues of are . Then, the maximum degree energy of the graph satisfies the following lower bound in terms of the second-degree coefficient of the characteristic polynomial of :
Proof of Theorem 6.
As is a real symmetric matrix, all its eigenvalues are real. By the Cauchy–Schwarz inequality,
Taking square roots gives
From spectral theory, the sum of the squares of the eigenvalues equals the trace of the square of the matrix:
Substituting,
□
Example 11.
Consider the fuzzy graph G shown in Figure 3. Let denote its maximum degree matrix. Suppose the approximate eigenvalues of are
the maximum degree energy is given by As , the lower bound on is
the actual energy exceeds the theoretical lower bound , thereby verifying the validity of the bound established by the theorem.
Corollary 2
(Upper Bound on Maximum Degree Energy). Let G be a fuzzy graph with n vertices, and let be the associated maximum degree matrix with eigenvalues . Then, the maximum degree energy satisfies the following inequality:
Proof of Corollary 2.
The result follows directly from the Cauchy–Schwarz inequality applied to the eigenvalues of . Specifically,
Taking the square root of both sides yields the desired bound:
□
Theorem 7.
Let be a fuzzy graph with n vertices, maximum degree matrix , and maximum vertex degree . Let λ be any eigenvalue of . Then .
Proof of Theorem 7.
Let . As M is a real symmetric matrix, all its eigenvalues are real. Let x be an eigenvector corresponding to the eigenvalue , so . Let k be the index such that . Considering the k-th component of the equation , we obtain
Taking absolute values and applying the triangle inequality,
, we have The inequality holds for any k; hence,
which is the maximum absolute row sum of M. As for all , and each row has at most n entries, we conclude that
□
Example 12.
Consider a fuzzy graph G with vertices, as shown in Figure 3. The eigenvalues are found to be , , , , , , , and .
and . The theorem stating holds true, as for all eigenvalues.
6. Real-World Application
In this section, spectral fuzzy graph theory is applied to model a protein–protein interaction network associated with Systemic Lupus Erythematosus (SLE) through the proposed algorithm. This algorithm helps in identifying critical proteins that influence disease mechanisms, thereby guiding the identification of potential therapeutic targets.
6.1. Protein Interactions in SLE
Proteins are the workhorses of the cell, carrying out a vast array of functions essential for life. These complex molecules are composed of amino acid chains folded into specific three-dimensional structures that dictate their function. Their roles are incredibly diverse, ranging from catalyzing biochemical reactions (enzymes) to providing structural support (structural proteins) and transporting molecules (transport proteins). Many proteins achieve their function through intricate interactions with other molecules, including other proteins, DNA, RNA, and small molecules. These interactions are highly specific and often transient, allowing for dynamic regulation of cellular processes. The precise three-dimensional structure of a protein is critical for its function and its ability to interact with other molecules. Disruptions to protein structure or interactions can have profound consequences on cellular function and overall health.
Protein–protein interactions (PPIs) are fundamental to nearly all cellular processes. Proteins rarely act in isolation; instead, they cooperate through carefully orchestrated interactions to execute complex tasks. These interactions, governed by non-covalent forces, are highly specific and often transient. Signaling pathways, for example, depend on precisely timed PPIs to transmit signals throughout the cell. Structural complexes, on the other hand, require more stable PPIs to maintain integrity. Disruptions to PPIs, whether through mutations, post-translational modifications, or environmental factors, can lead to cellular dysfunction and disease. Studying these interactions is crucial for understanding the workings of healthy cells and for identifying targets for therapeutic intervention.
Autoimmune diseases arise from a malfunctioning immune system that mistakenly attacks the body’s own tissues and organs. Instead of targeting foreign invaders like bacteria or viruses, the immune system—-specifically, autoreactive lymphocytes—recognizes self-antigens as threats, leading to chronic inflammation and tissue damage. Several factors contribute to autoimmunity, including genetic predisposition, environmental triggers, and hormonal influences. The breakdown of mechanisms that maintain self-tolerance—the ability of the immune system to distinguish self from non-self—plays a central role in initiating and perpetuating these diseases. The precise mechanisms underlying autoimmunity remain complex and not fully understood, but they often involve dysregulation of immune cell signaling pathways and interactions.
Systemic Lupus Erythematosus (SLE) is a complex autoimmune disease affecting multiple organ systems. Characterized by the production of autoantibodies against various nuclear and cytoplasmic antigens (such as DNA, RNA, and histones), SLE leads to chronic inflammation and tissue damage. The pathogenesis of SLE involves a complex interplay of genetic susceptibility, hormonal influences, and environmental factors. Dysregulation of several crucial PPIs, including those involved in immune cell activation, complement system function, and apoptotic cell clearance, contribute significantly to the disease process. The broad spectrum of autoantibodies produced in SLE highlights the complex nature of this autoimmune response. This complexity underscores the need for a multi-faceted approach to understanding and managing SLE, with ongoing research seeking to define these disease mechanisms and develop targeted therapies.
The proposed method, grounded in fuzzy graph theory, offers a robust framework for modeling protein–protein interaction (PPI) networks by addressing the inherent uncertainty and gradation in biological interactions. In PPI networks, interactions are rarely binary; instead, they exhibit varying degrees of reliability influenced by experimental noise, temporal expression changes, post-translational modifications, and cellular context. Traditional graph-theoretic models that encode interactions as crisp edges fail to capture this variability, resulting in a loss of critical biological information. Our approach assigns fuzzy membership values to vertices and edges, enabling a spectrum-based representation of interaction strength. This facilitates a more nuanced characterization of network topology and interaction dynamics. By incorporating this uncertainty into spectral metrics—such as fuzzy vertex centralities and fuzzy energy measures—our method yields biologically consistent insights that outperform deterministic models in resolving functionally relevant vertices and critical subnetworks within the PPI landscape.
6.2. Algorithm
- 1.
- Obtain interaction scores of proteins from UniProt and STRING databases and analyze the most crucial factors in the disease process.
- 2.
- Simplify the network and concentrate on their direct relationships within the SLE context.
- 3.
- Determine the vertex , where each represents a protein and represents the edges (interactions) between the vertices (proteins) and .
- 4.
- Model a fuzzy graph with from the acquired data.
- 5.
- Construct an adjacency matrix and analyze the degree of every vertex for all , and construct the maximum degree matrix .
- 6.
- Compute the eigenvalues of G associated with and proceed to calculate the maximum degree energy .
- 7.
- Perform spectral gap between the eigenvalues .
- 8.
- Analyze the largest and smallest eigenvalues to identify the strongest interactions within the network.
6.3. Spectral Fuzzy Network Analysis of SLE Protein Interactions
Analyzing protein–protein interactions (PPIs) in Systemic Lupus Erythematosus (SLE) requires a method capable of handling the inherent complexity and uncertainty of the biological system. A spectral fuzzy network approach addresses this challenge by incorporating probabilistic interaction data (from sources like UniProt and STRING) into a fuzzy network model. This allows the identification of key proteins driving the disease through analysis of the network’s spectral properties (eigenvalues, energy, spectral gap). Focusing on direct relationships simplifies the network, highlighting central proteins and strong interactions, and providing quantitative measures for objective comparison and the identification of potential therapeutic targets. This approach offers a more nuanced and targeted understanding of SLE pathogenesis than traditional methods.
6.4. Implementation in PPI Networks
Protein–protein interactions (PPIs) are fundamental to virtually all cellular processes. Understanding these interactions is crucial for deciphering complex biological mechanisms and developing targeted therapies for various diseases. Systemic Lupus Erythematosus (SLE), a complex autoimmune disease, is a prime example where unraveling the intricate web of PPIs can lead to significant breakthroughs in understanding disease pathogenesis and identifying potential therapeutic targets. This research focuses on a specific subset of proteins implicated in SLE, aiming to characterize their interaction network using advanced graph-theoretical methods.
This research investigated the protein–protein interaction (PPI) network as shown in Figure 4 associated with Systemic Lupus Erythematosus (SLE), focusing on seven key proteins frequently implicated in the disease: AHSG, IGF1, IGF2, IGFBP3, ORM1, ORM2, and SERPINA1. Interaction data and associated confidence scores were retrieved from the UniProt and STRING databases. While STRING initially provided a broader network, the analysis was narrowed to interactions exclusively among these seven proteins to isolate their direct relationships within the SLE context. This refined network was modeled as a fuzzy graph, a more appropriate representation than a traditional binary graph because it accounts for the uncertainty inherent in interaction data. The fuzzy graph of SLE is represented below.
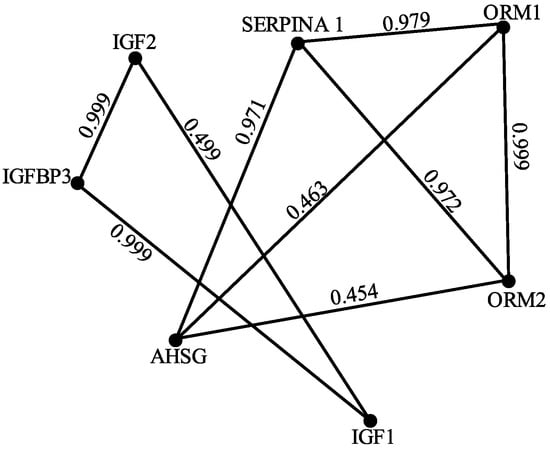
Figure 4.
PPI network of crucial proteins associated with Systemic Lupus Erythematosus.
The confidence scores from STRING served as edge weights in this fuzzy graph, quantifying the strength of each interaction. This fuzzy graph was then represented as an adjacency matrix, facilitating computational analysis using the NetworkX library in Python (version 3.10.12). The adjacency matrix is presented below.
First, we calculate the degree of each vertex in the fuzzy graph represented by the adjacency matrix . The degree of a vertex is calculated as the sum of membership values of edges incident at a particular vertex v. Now, we calculate the degrees of each protein to establish bounds on the energy. The degrees are computed as follows:
- Degree of AHSG
- Degree of IGF1
- Degree of ORM2
- Degree of ORM1
- Degree of SERPINA1
- Degree of IGF2
- Degree of IGFBP3
We prefer the maximum degree energy () over the degree energy () as the research focuses on identifying and analyzing the strongest interactions within the network, particularly when these interactions are hypothesized to be critical for network function and robustness to perturbations targeting high-degree vertices.
The maximum degree matrix is given by
The eigenvalues detailed below reveal key characteristics of the network’s connectivity and the influence of individual proteins:
Crucially, this representation allows the calculation of maximum degree energy of the network, providing a novel metric for characterizing its structure and stability, as described in the previous sections. It is given by The spectral gap between two vertices and is found to be
6.5. Comparison with Traditional Centrality Measures
To contextualize the significance of the proposed maximum degree energy (), we compare it against standard centrality metrics widely used in network analysis. These include degree centrality (), betweenness centrality (), and eigenvector centrality (), each of which captures a different aspect of vertex importance.
The fuzzy PPI network associated with Systemic Lupus Erythematosus (SLE) was modeled as described in the previous sections. The confidence scores obtained from the STRING database were used as edge weights to construct the fuzzy adjacency matrix. Subsequently, we computed the degree of each protein based on these edge weights and calculated the corresponding values. Traditional centrality measures were also computed using the NetworkX library in Python (version 3.10.12).
The following are the mathematical formulations for standard centrality measures used in network analysis for a fuzzy graph G:
- Degree Centrality (): Degree centrality quantifies the relative importance of a vertex based on the number of direct connections it has to other vertices. It is defined aswhere denotes the degree of vertex , and is the total number of vertices in the graph.
- Betweenness Centrality (): Betweenness centrality measures the extent to which a vertex lies on the shortest paths between other pairs of vertices. Formally, it is given bywhere denotes the total number of shortest paths from vertex to vertex , and is the number of those paths that pass through vertex .
- Eigenvector Centrality (): Eigenvector centrality assigns influence scores to vertices based not only on their connections, but also on the importance of the vertices to which they are connected. It is defined as the solution to the eigenvector equationwhere is the largest eigenvalue of the adjacency matrix , and the vector is the corresponding principal eigenvector.
The table below summarizes the comparative analysis.
As shown in Table 3, proteins such as SERPINA1, ORM1, and ORM2 exhibit consistently high values across all centrality metrics, including . This alignment validates the relevance of in capturing vertex influence. However, offers an added advantage: it incorporates fuzzy interaction strengths and leverages spectral properties, making it particularly well suited for biological networks characterized by uncertain or probabilistic edges.

Table 3.
Comparison of with traditional centrality measures.
By comparing with established centrality measures, we reinforce its validity and underscore its potential as a robust metric for structural analysis in fuzzy-graph-based biological networks.
6.6. Advantage over Other Methods
- 1.
- Traditional degree centrality treats all connections equally, whereas gives higher importance to strong protein interactions. Stronger interactions often indicate more biologically significant relationships, such as stable protein complexes or key regulatory mechanisms.
- 2.
- SERPINA1 has the highest , which aligns with its known involvement in immune system regulation and inflammation in SLE.
- 3.
- Unlike betweenness or eigenvector centrality, which depend on path structures, is directly derived from interaction strengths.
- 4.
- correlates well with eigenvector centrality but focuses more on local structural strength, making it a better metric for identifying functionally relevant hubs rather than just influential vertices.
- 5.
- ORM1 and ORM2 have similar eigenvector centralities, but ORM1 has a slightly higher , highlighting its relatively stronger local interactions.
- 6.
- High proteins are likely to be crucial for network stability, meaning that their perturbation (mutation, inhibition) could significantly alter network dynamics. This aligns with real-world biological findings, where proteins with strong interactions are often essential for disease progression and therapeutic targeting.
6.7. Limitations of the Study
- 1.
- By incorporating confidence scores as edge weights, ensures that stronger interactions contribute more to network energy, providing a more realistic biological insight.
- 2.
- The analysis only considered direct interactions between the selected proteins, ignoring potentially important indirect interactions.
- 3.
- The computational cost of applying this method to significantly larger PPI networks could be prohibitive, hindering its application to other complex biological systems.
- 4.
- As is derived from the spectral properties of the adjacency matrix, it provides a quantitative measure of structural stability, making it suitable for studying network resilience.
7. Results and Discussion
- 1.
- The metric () maximum degree energy, is preferred because it directly reflects the energy associated with the maximum degree of vertices in a graph. In biological networks such as protein–protein interaction (PPI) networks, proteins with high degrees are often central to key processes, influencing the overall stability and function of the system.
- 2.
- The PPI network of seven key SLE-related proteins was modeled as a fuzzy graph. STRING confidence scores were used as edge weights to represent interaction strengths. The maximum degree energy () quantified the influence of highly connected proteins.
- 3.
- The leading eigenvalue () indicated key protein dominance.
- 4.
- High-degree centrality proteins (SERPINA1, ORM1, ORM2) exhibited high values, confirming their structural importance.
- 5.
- IGF1 and IGF2 had lower betweenness centrality but comparable , revealing additional network insights.
- 6.
- The spectral gap () identified critical interaction thresholds, impacting network resilience.
- 7.
- In the context of disease, proteins associated with illness often show higher energy values due to a shift in their interaction patterns, indicating that their central roles in the network may be compromised.
8. Conclusions and Future Work
This work introduced degree-based energy measures for fuzzy graphs, including degree energy, average, maximum, and minimum degree energies, offering a refined spectral perspective by integrating vertex degree information. Sharp theoretical bounds were established and validated through rigorous proofs and illustrative examples. Application to a protein–protein interaction (PPI) network related to Systemic Lupus Erythematosus (SLE) demonstrated the practical relevance of these measures in uncovering structurally significant proteins.
One direction for future research involves extending the proposed degree-based energy measures to dynamic fuzzy graphs, thereby facilitating real-time analysis of evolving systems in biological and social networks. Another promising avenue lies in the development of efficient computational frameworks for analyzing large-scale fuzzy networks, enhancing their applicability to complex systems such as protein interactions and cybersecurity infrastructures.
Author Contributions
Conceptualization, R.C., B.R., S.P.K. and A.K.; Methodology, R.C., B.R., S.P.K. and A.K.; Software, R.C., B.R., S.P.K. and A.K.; Validation, R.C., B.R., S.P.K. and A.K.; Formal analysis, R.C., B.R., S.P.K. and A.K.; Investigation, R.C., B.R., S.P.K. and A.K.; Resources, R.C., B.R., S.P.K. and A.K.; Data curation, R.C., B.R., S.P.K. and A.K.; Writing—original draft, R.C., B.R., S.P.K. and A.K.; Writing—review & editing, R.C., B.R., S.P.K. and A.K.; Visualization, R.C., B.R., S.P.K. and A.K.; Supervision, B.R. and A.K.; Project administration, R.C. and B.R.; Funding acquisition, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Guangdong University Young Innovative Talents Program Project (No. 2024KQNCX081).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank the reviewers for their valuable suggestions in improving the quality of this paper.
Conflicts of Interest
The authors of this paper declare that they have no conflicts of interest.
References
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Macmillan: London, UK, 1976. [Google Scholar]
- Godsil, C.; Royle, G.F. Algebraic Graph Theory; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Fiedler, M. Algebraic connectivity of graphs. Czechoslov. Math. J. 1973, 23, 298–305. [Google Scholar] [CrossRef]
- Brouwer, A.E.; Haemers, W.H. Spectra of Graphs; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Gutman, I.; Ramane, H. Research on graph energies in 2019. MATCH Commun. Math. Comput. Chem. 2020, 84, 277–292. [Google Scholar]
- Brualdi, R.A. Energy of a graph. In Notes for AIM Workshop on Spectra of Families of Matrices Described by Graphs, Digraphs, and Sign Patterns; American Institute of Mathematics: Palo Alto, CA, USA, 2006. [Google Scholar]
- Gutman, I.; Oboudi, M.R. Bounds on graph energy. Discret. Math. Lett. 2020, 4, 1–4. [Google Scholar]
- Nikiforov, V. The energy of graphs and matrices. J. Math. Anal. Appl. 2007, 326, 1472–1475. [Google Scholar] [CrossRef]
- Adiga, C.; Smitha, M. On maximum degree energy of a graph. Int. J. Contemp. Math. Sci. 2009, 4, 385–396. [Google Scholar]
- Alawiah, N.; Rad, N.J.; Jahanbani, A.; Kamarulhaili, H. New upper bounds on the energy of a graph. MATCH Commun. Math. Comput. Chem. 2018, 79, 287–301. [Google Scholar]
- Ma, X. A low bound on graph energy in terms of minimum degree. MATCH Commun. Math. Comput. Chem. 2019, 81, 393–404. [Google Scholar]
- Das, K.C.; Elumalai, S. On energy of graphs. MATCH Commun. Math. Comput. Chem. 2017, 77, 3–8. [Google Scholar]
- Filipovski, S.; Jajcay, R. Bounds for the energy of graphs. Mathematics 2021, 9, 1687. [Google Scholar] [CrossRef]
- Nagalakshmi, A.R.; Shrikanth, A.S.; Kalavathi, G.K.; Sreekeshava, K.S. The degree energy of a graph. Mathematics 2024, 12, 2699. [Google Scholar] [CrossRef]
- Zangi, S.; Ghorbani, M.; Eslampour, M. On the eigenvalues of some matrices based on vertex degree. Iran. J. Math. Chem. 2018, 9, 149–156. [Google Scholar]
- Milovanovic, I.; Milovanovic, E.; Altindag, S.B.B.; Matejic, M. McClelland-type upper bounds for graph energy. MATCH Commun. Math. Comput. Chem. 2022, 88, 141–155. [Google Scholar] [CrossRef]
- Milovanovic, I.Z.; Milovanovic, E.I.; Zakic, A. A short note on graph energy. MATCH Commun. Math. Comput. Chem. 2014, 72, 179–182. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Rosenfeld, A. Fuzzy graphs. In Fuzzy Sets and Their Applications; Academic Press: New York, NY, USA, 1975; pp. 77–95. [Google Scholar]
- Mordeson, J.N.; Nair, P.S. Fuzzy Graphs and Fuzzy Hypergraphs; Physica: Heidelberg, Germany, 2012. [Google Scholar]
- Narayanan, A.; Mathew, S. Energy of a fuzzy graph. Ann. Fuzzy Math. Inform. 2013, 6, 455–465. [Google Scholar]
- Buhtani, K.; Mordeson, J.; Rosenfeld, A. On degrees of end nodes and cut nodes in fuzzy graphs. Iran. J. Fuzzy Syst. 2004, 1, 53–60. [Google Scholar]
- Gani, A.N.; Radha, K. The degree of a vertex in some fuzzy graphs. Int. J. Algorithms Comput. Math. 2009, 2, 107–116. [Google Scholar]
- Akram, M.; Sarwar, M.; Dudek, W.A. Energy of bipolar fuzzy graphs. In Graphs for the Analysis of Bipolar Fuzzy Information; Springer: Cham, Switzerland, 2021; pp. 309–347. [Google Scholar]
- Kosari, S.; Shi, X.; Kacprzyk, J.; Chen, Z.; Rashmanlou, H. A novel description of perfectly regular fuzzy graphs with application in psychological sciences. J. Mult.-Valued Log. Soft Comput. 2024, 42, 405–424. [Google Scholar]
- Romdhini, M.U.; Al-Sharqi, F.; Nawawi, A.; Al-Quran, A.; Rashmanlou, H. Signless Laplacian energy of interval-valued fuzzy graph and its applications. Sains Malays. 2023, 52, 2127–2137. [Google Scholar] [CrossRef]
- Kosari, S.; Jiang, H.; Khan, A.; Akhoundi, M. Properties of connectivity in vague fuzzy graphs with application in building university. J. Mult.-Valued Log. Soft Comput. 2023, 41, 6. [Google Scholar]
- Kosari, S.; Shao, Z.; Rao, Y.; Liu, X.; Cai, R.; Rashmanlou, H. Some types of domination in vague graphs with application in medicine. J. Mult.-Valued Log. Soft Comput. 2023, 41, 203. [Google Scholar]
- Khan, W.A.; Arif, W.; Rashmanlou, H.; Kosari, S. Interval-valued picture fuzzy hypergraphs with application towards decision making. J. Appl. Math. Comput. 2024, 70, 1103–1125. [Google Scholar] [CrossRef]
- Shi, X.; Kosari, S.; Rashmanlou, H.; Broumi, S.; Satham Hussain, S. Properties of interval-valued quadripartitioned neutrosophic graphs with real-life application. J. Intell. Fuzzy Syst. 2023, 44, 7683–7697. [Google Scholar] [CrossRef]
- Shi, X.; Kosari, S.; Talebi, A.A.; Sadati, S.H.; Rashmanlou, H. Investigation of the main energies of picture fuzzy graph and its applications. Int. J. Comput. Intell. Syst. 2022, 15, 31. [Google Scholar] [CrossRef]
- Rao, Y.; Kosari, S.; Anitha, J.; Rajasingh, I.; Rashmanlou, H. Forcing parameters in fully connected cubic networks. Mathematics 2022, 10, 1263. [Google Scholar] [CrossRef]
- Rao, Y.; Binyamin, M.A.; Aslam, A.; Mehtab, M.; Fazal, S. On the planarity of graphs associated with symmetric and pseudo-symmetric numerical semigroups. Mathematics 2023, 11, 1681. [Google Scholar] [CrossRef]
- Gani, A.N.; Ahamed, M.B. Order and size in fuzzy graphs. Bull. Pure Appl. Sci. 2003, 22, 145–148. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).