Abstract
The aim of this work is to propose an explanation of the inverse mass hierarchy of the low-lying nonet of the scalar mesons in the framework of the massless Nambu–Jona-Lasinio quark model. The proposed explanation is based on symmetry principles. The collective meson states are described via quark–antiquark pairs, whose condensates lead simultaneously to spontaneous breaking of chiral and flavour symmetry. It is shown that, due to flavour symmetry breaking, two iso-doublets of mesons play the role of Goldstone bosons. It is also proven that there exists a solution with degenerate masses of the and mesons and a zero mass of the meson.
1. Introduction
Symmetries and symmetry breaking have a fundamental role in Physics. It is known that spontaneous symmetry breaking of the chiral symmetry leads to massless Goldstone bosons, whose role is played by the pions. In the case of the spontaneous symmetry breaking of the flavour symmetry, mesons play the role of massless Goldstone bosons. Further on in this article we will call these bosons Bogoliubov–Nambu–Goldstone (BNG) bosons to highlight the legacy of Bogoliubov [1,2].
In this work, we will consider simultaneous chiral and flavour spontaneous symmetry breaking and their important role for the explanation of the mass spectrum of the low-lying scalar mesons.
The pions, consisting of quark–antiquark pairs (), have a very small mass in comparison with the other hadronic states. The smallness of the pion mass would have been a problem for their constituent quark models, however, it is well known that the small mass of the pseudoscalar pions is explained by the mechanism of spontaneous breaking of the chiral symmetry [3]. As a result of that symmetry breaking, the pions play the role of massless BNG bosons [4,5].
There exists another problem connected with the mass of the low-lying scalar mesons, namely the explanation of the inverse hierarchy mass in the low-lying scalar nonet. The constituent quark models, describing the mesons as quark–antiquark pairs, could not explain this problem. Therefore, one of the first hypotheses offering an explanation of the inverse hierarchy was the work by Jaffe [6] that proposed a diquark–antidiquark structure () for the scalar mesons. Another explanation, which preserves the quark–antiquark structure of scalar mesons [7], uses the anomaly term in dynamical chiral symmetry breaking of chiral effective theories. However, while this mechanism explains the difference between the lowest-lying scalar mesons (or ) and , it cannot explain the mass of the (or ) meson [8].
In this paper, we propose an alternative explanation for the smallness of the mass of the meson. It is based on the well-known mechanism of spontaneous symmetry breaking of flavour symmetry to isotopic symmetry. As a result of this symmetry breaking, mesons with isospin play the role of massless BNG bosons. According to us, this is a natural explanation of the small masses of the mesons, similar to the explanation for the small masses of pions. Note that isotopic symmetry cannot be spontaneously broken, as shown in [9], i.e., there exists isotopic symmetry in nature.
In Section 2, we introduce a model of self-interaction of scalar quark currents, analogous to the Nambu–Jona-Lasinio (NJL) model [10,11]. We present a quantisation of this model and derive the effective potential for the scalar mesons nonet. In Section 3, we present the minimisation of this effective potential and we obtain the mass states of the scalar mesons. In the Conclusion, we list the basic results and conclusions of this work.
2. The Model
Let us consider a chiral self-interaction of the scalar quark currents:
where, is the triplet of massless color quarks (here, the colour indices are suppressed), while are the Gell-Mann matrices. Here, and are positive constants of the self-interaction of the singlet state quark scalar current and the octet states of the quark scalar currents, respectively, and both have a dimension . We consider massless quarks, which will obtain masses due to spontaneous symmetry breaking.
It is obvious that the quantisation of this Lagrangian in perturbation theory on the dimensional constants and will result in a nonrenormalisable theory. Therefore, we will use the linearisation method of this Lagrangian developed in [12,13]. The linearisation of the Lagrangian (Equation (1)) leads to the following equivalent on the classical level Lagrangian:
where we have introduced the auxiliary fields
which will play the role of collective excitation states of the corresponding currents. Here, and are the dimensionless Yukawa coupling constants.
All the collective modes become dynamical as a result of the self-energy quantum corrections from fermion loops (Figure 1a).
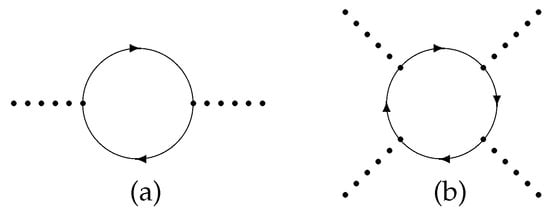
Figure 1.
(a) Radiative correction to self-energy parts; (b) Radiative correction to self-interactions.
Let us consider the self-energy quantum corrections to the scalar field :
and to the scalar fields
where p is the internal and q is the external momentum, denotes the number of colours, and
is the quadratically divergent integral, while
is a logarithmically divergent integral, which are both positive in Euclidean momentum space.
Here, we have introduced the small current mass for the quark, which will help to avoid the infrared divergences in the denominator and which will be neglected in the numerator. This kind of quark mass introduction explicitly breaks the chiral symmetry, and is called soft symmetry breaking. Such symmetry breaking does not cause extra ultraviolet divergences in the scalar particles masses. Due to the dimensionless of the Yukawa coupling constants and in the four dimensional space, there exist only two types of divergent integrals (6) and (7). The ultraviolet divergences in (6) and (7) are removed using one of the known regularisation methods.
The first terms in the last lines of Equations (4) and (5) represent the corrections to the mass terms of the scalar fields : and : . The second terms represent the kinetic parts of the scalar fields. For a correct normalisation of the scalar fields wave functions, the following requirements should be fulfilled:
Due to the dynamical origin of the kinetic terms, all the interactions in the NJL model are descried by a single dimensionless coupling constant
Another essential point of the NJL model is the generation of the self-interactions of the scalar fields; these self-interactions lead to a spontaneous dynamical breaking of the chiral symmetry. Let us denote by □ the integral on the internal momentum p, which comes from the fermionic loop in Figure 1b:
Thus, at a quantum level, due to the radiative corrections (Figure 1b) in the effective Lagrangian, local terms appear for the self-interaction of the scalar mesons with zero external momentum and corresponding symmetry factors:
Here, are totally symmetric structure constants of algebra, where the indices a, b and c obtain different values non-equal to each others.
The last expressions (11)–(17) were obtained using the normalisation condition (8), the relation between coupling constants (9), and neglecting the small current quark mass , which was introduced only to remove infrared divergencies. The normalisation condition (8) requires that the leading term in the effective Lagrangian consists only of the divergent terms of the diagrams with zero external momentum [14], depicted in Figure 1b.
Thus, the effective potential reads:
The advantage of this potential is that it depends only on one dimensionless constant and two dimensional parameters of the mass: and . This allows exact solutions of spontaneous symmetry breaking and the mass spectrum of the scalar mesons to be found, which will be presented in the next section.
3. Symmetry Breaking and Mass Spectrum of Scalar Mesons
Due to the spontaneous symmetry breaking, the scalar fields obtain non-zero vacuum expectation values. The physical vacuum must conserve the electric charge and the quark flavour. Therefore, only the scalar fields , and , which interact with the diagonal combinations of quark–antiquark flavours, can have non-zero vacuum expectation values. In order to find the minimum of the effective potential (18), we will differentiate the potential only on these degrees of freedom. The minimisation leads to the following system of equations:
Note that for , due to neutrality of vacuum expectation values. It has also been shown in [9], that the group cannot be spontaneously broken and is the right solution of the system (19), while and acquire non-zero vacuum expectation values.
Spontaneous symmetry breaking is possible only at strong coupling constants and , when the massive parameters have negative values, i.e., and . To avoid the irrational coefficients and the dimensional parameters in (19), we introduce the dimensionless variables , and . Then, the constituent quark masses can be obtained from the following relations:
The first and the third equations of the system (19) in the new dimensionless variables read:
Before solving this system, let us first find the square of the masses of the scalar meson isotriplet , :
This result shows that for non negative square masses, the vacuum expectation values of and should have the same signs. We should note that the solutions of the system (22) are invariant with respect to simultaneous sign changing of the vacuum expectation values: and . Therefore, for definiteness, we will search solutions for positive vacuum expectation values.
The solutions of the second equation of the system (22) are:
Substituting these solutions into the first equation of the system (22), the following expression is obtained:
In order to solve this equation analytically, it is necessary to square its right and left hand sides. Thus, using the substitution , a cubic equation follows:
The solutions of this equation are illustrated in Figure 2, where and .
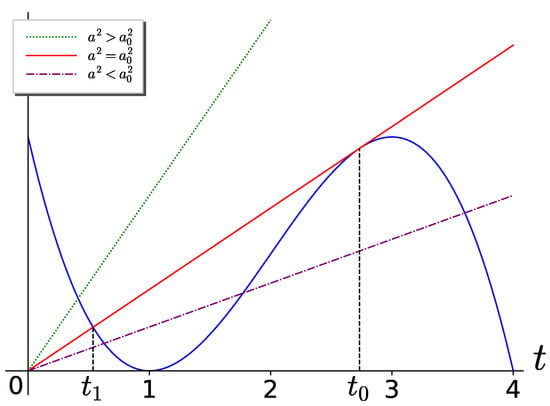
Figure 2.
The graphical illustration of solutions of the cubic Equation (26).
It is obvious from Figure 2, that three real roots exist for , where . Vice versa, for , only one real root exists. For and , we obtain only two real roots. From Equation (25), it follows that .
Let us describe all the exact solutions of Equation (26), dividing them into three intervals, such that within each interval, one single solution exists. The first case corresponds to the interval . This interval consists of two subintervals, namely and . In the first subinterval, the solution with one real root for is:
In the other subinterval, the solution for reads:
This solution corresponds to one of the three real roots of Equation (26).
In the second case, corresponding to the interval , the solution for reads:
In the third case, corresponding to the interval , the solution for reads:
Let us now calculate all the masses of the scalar meson nonet. We have already carried this out for the isotriplet (23). The squares of the masses of the scalar mesons with isospin : , ,
are equal to zero, where and the last equality follows from the third equation of the system (19) with . The fact that the squares of the masses are equal to zero for these states is a direct consequence of the Goldstone theorem [4,5].
Now let us calculate the squares of the masses of the isosinglet states with isospin , and :
From the last equation, it follows that there exists a non-trivial mixing between these states. This can be described by the non-diagonal matrix:
where , , . The diagonalisation of this matrix leads to two eigenvalues:
These correspond to the squares of the masses of the physical states and .
Let us analyse the obtained solutions (27)–(30), keeping in mind that the squares of masses of , and mesons should be non-negative. In the first case, the solutions (27) and (28), are illustrated in Figure 3. The left panel of the figure presents the solutions of Equation (24). From the panel, it is obvious that only the solution is positive. For positive x, this leads to positive masses of the scalar isotriplet . The right panel presents the reduced squares of the masses of the meson isotriplet and the two isosinglets, and . Thus, it is seen from the right panel, that this case does not correspond to physical masses, due to the unphysical pattern .
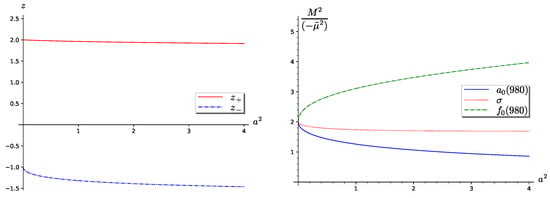
Figure 3.
The left panel presents the solutions of Equation (24). The right panel presents the reduced squares of the masses of the , , and mesons. The figure corresponds to the first case.
The second case, solution (29), is illustrated in Figure 4. The left panel of the figure presents the solutions of Equation (24). Again, only solution is positive. The right panel presents the reduced squares of the masses of the meson isotriplet and the two isosinglets. This result is more attractive from a physical point of view. Namely, for , the masses of the isotriplet and isosinglet are almost degenerate and heavy, while the meson mass tends to zero, and it equals zero for . From Equation (25), it follows that for the case , the parameter a is positive: . So, for the second case, the mass ratio . This mass ratio depends on the initial coupling constants in the Lagrangian (1) and this means that is greater than .
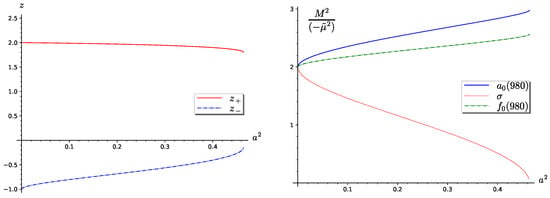
Figure 4.
The left panel presents the solutions of Equation (24). The right panel presents the reduced squares of masses of the , , and mesons. The figure corresponds to the second case.
Let us analyse the mixing at . The physical states and are defined by the states and from the following relation:
where the mixing angle is
The corresponding illustration of this mixing angle is presented in Figure 5.
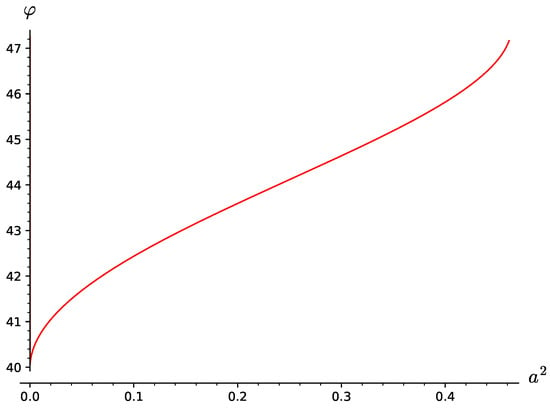
Figure 5.
The figure presents the mixing angle (in degrees) on the parameter corresponding to the second case.
The formula connecting the pure states and to the physical states and reads:
where the mixing angle is related to the mixing angle by the relation:
It is interesting to note that at point , , where . This very small angle corresponds to a nearly ideal mixing. However, contrary to the common assumption, that the meson has an almost pure state, we obtain that actually, it is the meson which has an almost pure state, while the meson is close to a state.
In the third case, solution (30), both the solutions and can be positive. Therefore, we will consider separately both cases. Figure 6 presents the solution , while in Figure 7, solution is presented. The solution is non-negative for .
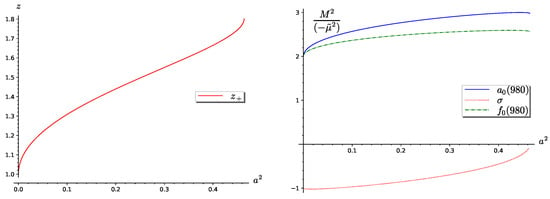
Figure 6.
The left panel presents the solution of Equation (24). The right panel presents the reduced squares of masses of the , , and mesons. The figure corresponds to the third case.
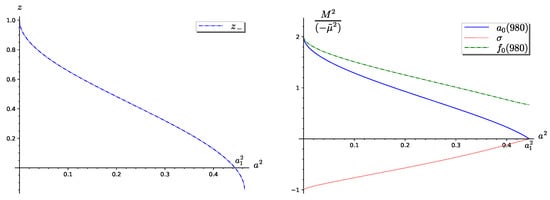
Figure 7.
The left panel presents the solution of Equation (24). The right panel presents the reduced squares of masses of , , and mesons. The figure corresponds to the third case.
However, as is seen from the right panels of these figures, the square of the mass of the meson is negative in the whole range of variation of parameter , except for point in Figure 6 and point in Figure 7, at which points the mass of the meson is zero. The first point is included in the second case, as an intermediate point between the second and third cases, and already have been considered as physical solution, while at the second point in the right panel of Figure 7, the mass of the meson is also zero, which does not correspond to a physical case. Negative values of the mass of the meson do not correspond to the minimum of the potential.
In conclusion, only the second case, illustrated in Figure 4, corresponds to a physical solution.
4. Conclusions and Discussion
In this article, we propose an explanation for the inverted mass hierarchy of the low-lying nonet of the scalar mesons. This is a new type of explanation. The explanation is provided in the framework of the quark–antiquark NJL model. In particular, the chiral symmetry is broken to , which in its turn, is broken simultaneously to . The latter type of spontaneous symmetry breaking has not been considered before. Remarkably, this type of symmetry breaking leads to the appearance of BNG bosons, which results into zero masses for the mesons. Moreover, our model suggests also a zero mass for the meson. We have also determined that the meson state consists almost completely of a quark combination. In previous studies, it was assumed that the meson consists predominantly of light quarks. We have also shown that consists predominantly of light quarks, contrary to the previous assumptions that it consists mainly of strange quarks. Thus, the experimentally observed decay of into two pions is nicely described by our model.
Future analysis should consider the realistic case of non-zero current masses. In order to explain the real mass spectrum, it is necessary to introduce explicit breaking of flavour symmetry due to non-zero current quark masses. The method for the introduction of heavy current mass of the strange quark has been developed in the framework of the chiral model with spontaneous symmetry breaking [15]. The results obtained in this work confirmed the mass value of the meson predicted in [16]. This meson was experimentally discovered 15 years later [17], with the exact predicted mass value. Such an analysis will be provided elsewhere. Here, we want only to note that during the symmetry breaking, besides pseudoscalar pions, K mesons, which contain a strange quark, also obtain zero mass.
It is known that the account for the current quark masses, in the case of dominant strange quark mass, leads to a real mass of the pseudoscalar K mesons of the order of 500 MeV. We expect that, similarly to the K mesons case, the and mesons, which contain strange quarks, will obtain masses of the same order as those of the K mesons.
Author Contributions
Conceptualization, M.C.; methodology, M.C.; software, E.C. and M.N.; formal analysis, D.K. and E.C.; writing—original draft preparation, D.K. and M.C.; writing—review and editing, D.K. and M.C.; visualization, E.C. and M.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded by Project D01-326 04.12.2023 of the Bulgarian Ministry of Education and Science and Program FNI-SU/80-10-190 and by the Bulgarian Ministry of Education and Science under the National Program Young Scientists and Postdoctoral Students—2.
Data Availability Statement
No new data were created.
Acknowledgments
E.C. was partially financially supported by Project D01-326 04.12.2023 of the Bulgarian Ministry of Education and Science. M.N. acknowledges partial support within Program FNI-SU/80-10-190 and by the Bulgarian Ministry of Education and Science under the National Program Young Scientists and Postdoctoral Students—2. The research of D.K. was partially supported by infrastructure purchased under the National Roadmap for Scientific Infrastructure, financially coordinated by the Ministry of Education and Science of the Republic of Bulgaria (Agreement D01-326/04.12.2023).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BNG | Bogoliubov–Nambu–Goldstone |
| NJL | Nambu–Jona-Lasinio |
References
- Bogoliubov, N.N. A New method in the theory of superconductivity. I. Sov. Phys. JETP 1958, 34, 41–46. [Google Scholar] [CrossRef]
- Bogoliubov, N.N. A New method in the theory of superconductivity. III. Sov. Phys. JETP 1958, 34, 51–55. [Google Scholar]
- Nambu, Y. Quasiparticles and Gauge Invariance in the Theory of Superconductivity. Phys. Rev. 1960, 117, 648–663. [Google Scholar] [CrossRef]
- Goldstone, J. Field Theories with Superconductor Solutions. Nuovo Cimento 1961, 19, 154–164. [Google Scholar] [CrossRef]
- Goldstone, J.; Salam, A.; Weinberg, S. Broken Symmetries. Phys. Rev. 1962, 127, 965–970. [Google Scholar] [CrossRef]
- Jaffe, R.L. Multi-Quark Hadrons. I. The Phenomenology of Mesons. Phys. Rev. D 1977, 15, 267. [Google Scholar] [CrossRef]
- Kuroda, Y.; Harada, M.; Matsuzaki, S.; Jido, D. Inverse Mass Hierarchy of Light Scalar Mesons Driven by Anomaly-Induced Flavor Breaking. Prog. Theor. Exp. Phys. 2020, 5, 053D02. [Google Scholar] [CrossRef]
- Naito, K.; Oka, M.; Takizawa, M.; Umekawa, T. UA(1) breaking effects on the light scalar meson spectrum. Prog. Theor. Phys. 2003, 109, 969–980. [Google Scholar] [CrossRef]
- Naydenov, M.N.; Chizhov, M.V. On the Problem of Spontaneous Isotopic Symmetry Breaking in Nambu–Jona-Lasinio Models. Phys. Part. Nucl. Lett. 2020, 17, 120–125. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Bender, C.M.; Cooper, F.; Guralnik, G.S. Path Integral Formulation of Mean Field Perturbation Theory. Ann. Phys. 1977, 109, 165. [Google Scholar] [CrossRef]
- Tamvakis, K.; Guralnik, G.S. Renormalization of Four Fermion Theories in a Mean Field Expansion. Phys. Rev. D 1978, 18, 4551. [Google Scholar] [CrossRef]
- Eguchi, T. A New Approach to Collective Phenomena in Superconductivity Models. Phys. Rev. D 1976, 14, 2755. [Google Scholar] [CrossRef]
- Chizhov, M.V.; Naydenov, M.N. Mass prediction for the last discovered member of the axial-vector nonet with quantum numbers JPC = 1+−. JETP Lett. 2020, 112, 133–137. [Google Scholar] [CrossRef]
- Chizhov, M.V. Vector meson couplings to vector and tensor currents in extended NJL quark model. JETP Lett. 2004, 80, 73–77. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Ahmed, S.; Albrecht, M.; Amoroso, A.; An, F.F.; An, Q.; Bai, J.Z.; Bai, Y.; Bakina, O.; et al. Observation of h1(1380) in the J/ψ→η′Kπ Decay. Phys. Rev. D 2018, 98, 072005. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).