Symmetry-Driven Fault-Tolerant Synchronization in Multi-Robot Systems: Comparative Simulation of Adaptive Neural and Classical Controllers
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Research Gap and Objectives
- To develop a simulation framework that enables real-time, symmetry-driven synchronization between two SCARA LS3-B401S robots, incorporating fault-tolerant mechanisms.
- To compare traditional Proportional–Integral–Derivative (PID), robust Adaptive Sliding Mode Control (ASMC), learning-based Adaptation-Enabled Neural Network (ANN), and model-based Inverse Dynamics with Disturbance Observer (ID-DO) controllers in terms of synchronization accuracy, disturbance rejection, and computational efficiency.
- To evaluate controller performance in digital twin simulations under realistic industrial conditions, establishing a foundation for future experimental validation.
1.3. Novelty and Contribution
- The first simulation-based implementation of adaptive, symmetry-aware control for SCARA LS3-B401S robots, incorporating mirrored coordination via real-time feedback.
- Quantitative evaluation of PID, ASMC, ANN, and ID-DO, showing that ANN achieves up to 99% error reduction and 85% faster disturbance recovery than PID.
- Integration of high-fidelity digital twin simulations, validated with realistic perturbations, offering a scalable platform for physical deployment.
1.4. Paper Structure
- Stage 1: Theoretical and mathematical formulation of the controllers, followed by kinematic and dynamic modeling to define the relationships among position, velocity, and force. This stage concludes with the design and validation of the SCARA LS3-B401S model in SolidWorks.
- Stage 2: The implementation and optimization of the symmetry-based synchronization algorithm, including robot model validation and simulation testing under realistic perturbations such as ±0.0005 rad sensor noise and ~5 ms actuator delays.
- Stage 3: A comprehensive evaluation of controller performance in terms of robustness, computational efficiency, and tracking precision. The paper concludes with recommendations and experimental validation plans using physical SCARA LS3-B401S units.
2. Theoretical Framework
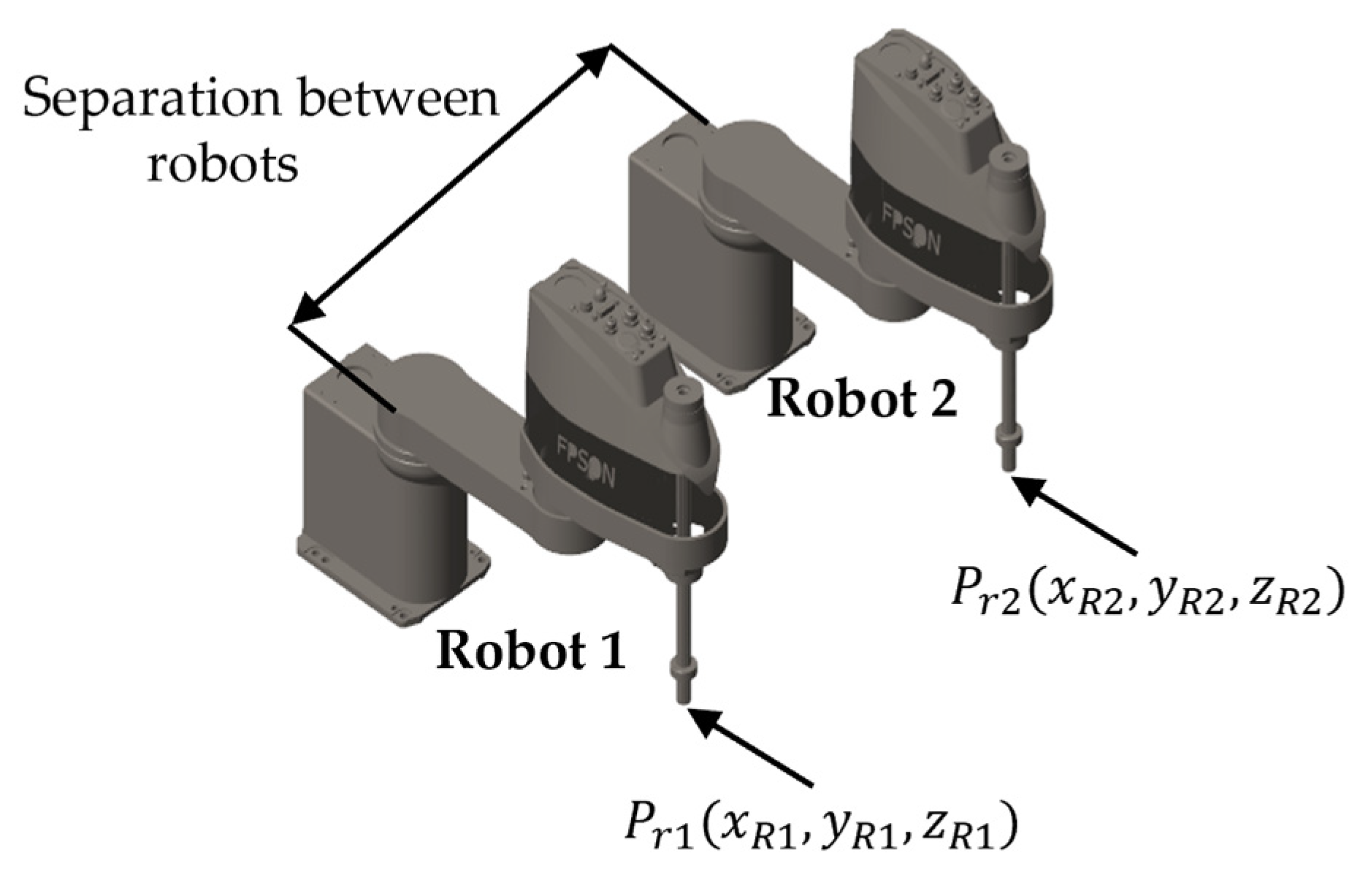
2.1. Multi-Robot Systems in Flexible Manufacturing
2.2. Symmetry-Driven Synchronization Principles
2.2.1. Synchronization Error Compensation
2.2.2. Applications of Symmetry-Driven Principles
- Fault Tolerance: By using the symmetry matrix , the framework ensures balanced interactions between robots, enabling fault-tolerant operation even when one robot experiences disturbances or deviations.
- Adaptability: The symmetry-driven principles allow robots to adjust their trajectories dynamically, making them suitable for tasks requiring high repeatability, such as pharmaceuticals, electronics, and semiconductor manufacturing.
- Scalability: The use of extended matrices enables the integration of additional robots into the system, paving the way for scalable solutions in flexible manufacturing.
2.3. Overview of Control Strategies
- Proportional–Integral–Derivative Control: A classical technique, effective in structured environments due to simplicity.
- Adaptive Sliding Mode Control: A robust method resilient to disturbances and nonlinearities.
- Adaptation-Enabled Neural Network Control: A learning-based approach for on-line adaptability and symmetry optimization.
- Inverse-Dynamics with Disturbance Observer Control: A model-based strategy compensating dynamics and perturbations.
2.3.1. Proportional–Integral–Derivative Controller
- Proportional (P): Corrects deviations proportionally.
- Integral (I): Eliminates steady-state errors.
- Derivative (D): Anticipates error trends [18].
2.3.2. Adaptive Sliding Mode Controller
2.3.3. Adaptation-Enabled Neural Network Controller
2.3.4. Inverse-Dynamics with Disturbance Observer Controller
3. Materials and Methods
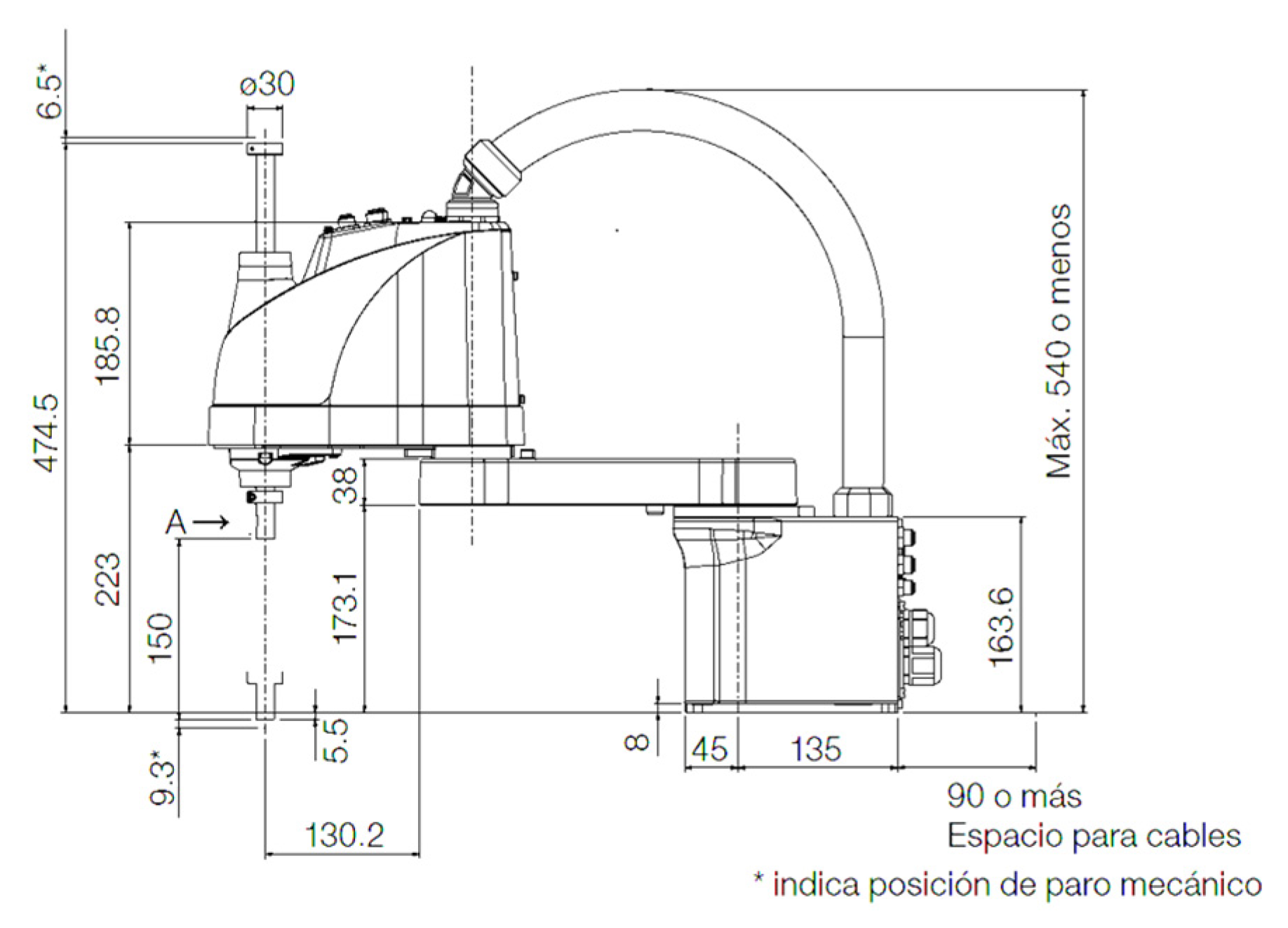
3.1. Robot Modeling and Design
3.1.1. Design in SolidWorks
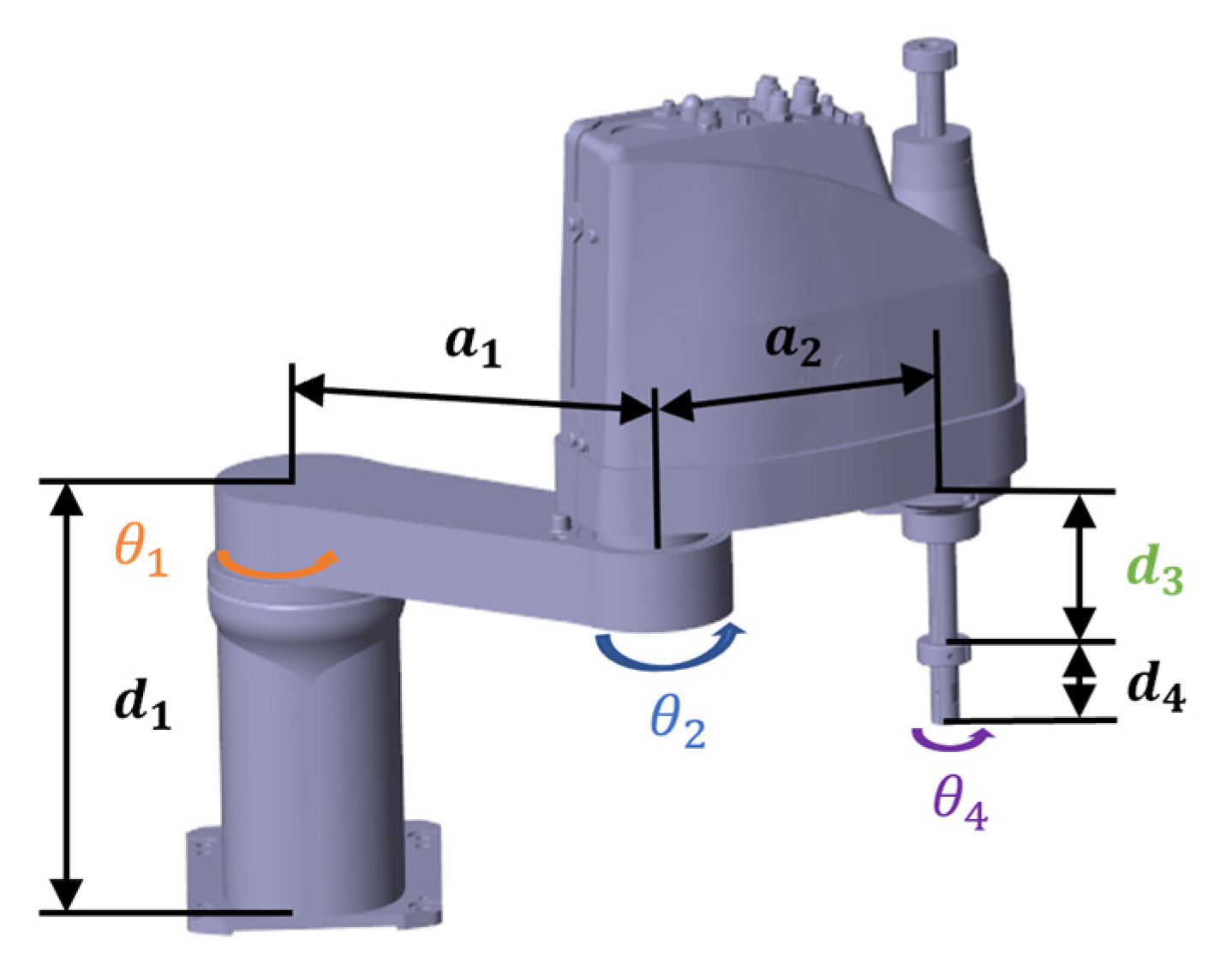
3.1.2. Kinematic Analysis
Analysis of Direct Kinematics and Physical Properties
Homogeneous Transformation Matrices
Inverse Kinematics
3.1.3. Dynamic Modeling
3.1.4. Actuators
3.2. Adaptive Symmetry-Aware Cooperative Controllers
3.2.1. Implementation and Tuning of the Proportional–Integral–Derivative Controller
3.2.2. Adaptive Sliding Mode Control
3.2.3. Architecture and Implementation of the Adaptive Neural Network
- Input layer: Eight neurons, encoding position errors and velocity errors for the four joints of each robot, providing a comprehensive state representation for synchronization.
- Hidden: Ten neurons (sigmoid, )), balancing complexity (12.5 M Floating-Point Operations per Second (FLOPS) and capacity (error reduction plateaus beyond 10).
- Output: Four neurons (torques/forces, scaled by gain 1.0), delivering control actions (torque/force) for each joint of the controlled robot, aligning with the four degrees of freedom of the SCARA LS3-B401S.
- Weights: , , initialized via the Xavier scheme .
- Training: A total of 18,672 samples (70% train: 13,070; 15% validation: 2801; 15% test: 2801) from PID, SMC, MPC runs (e.g., from triangular trajectories, ±0.08 rad perturbations); backpropagation, learning rate 0.01 (selected via grid search 0.001–0.1), 500 epochs (convergence at 0.001), Adam optimizer (, ϵ ), loss , where , , (). This ensures symmetry and precision [24,25,26], outperforming baselines in precision and robustness (e.g., RMSE 0.3032 vs. PID’s 2.7845; Section 4.6).
3.2.4. Design of the Inverse Dynamics Controller with Disturbance Estimation
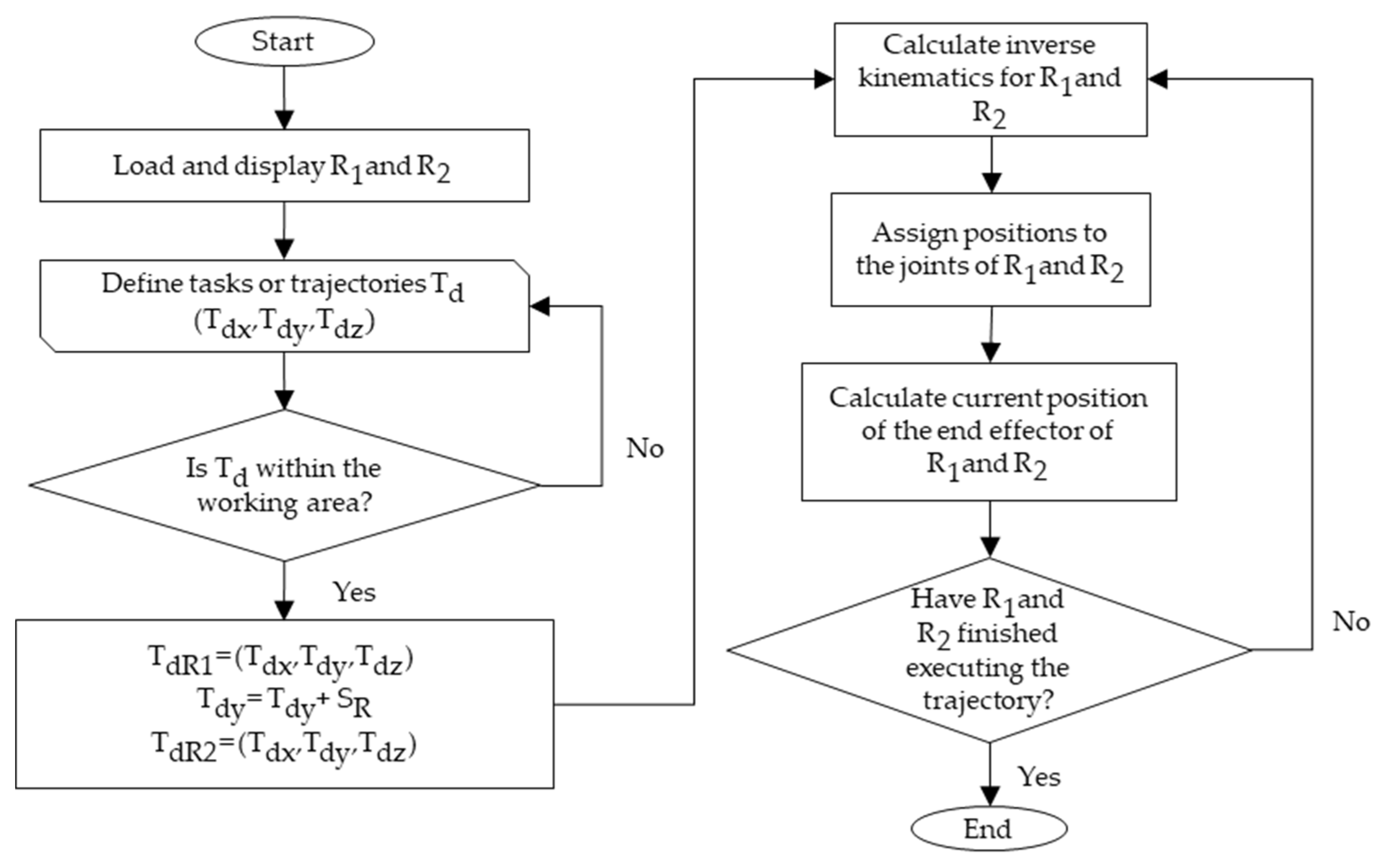
3.3. Symmetry-Based Synchronization Algorithm
3.3.1. Algorithm Design
- Temporal synchronization: Aligns start and end times using a master clock or on-line synchronization signals.
- Trajectory planning: Computes simultaneous positioning of both robots based on reference inputs.
- On-line feedback control: Dynamically corrects deviations from symmetry during task execution.
3.4. Simulation Setup
3.4.1. Virtual Environment in MATLAB/Simulink
3.4.2. Trajectory Design and Performance Metrics
- Root Mean Square Error (RMSE): Measures trajectory tracking accuracy, calculated as RMSE , with units in radians for rotational joints and meters for prismatic joints.
- Integral Time Absolute Error (ITAE): Quantifies long-term error accumulation, defined as ITAE , emphasizing sustained performance.
- Settling Time (): Assesses convergence speed, defined as the time to reach and stay within 2% of the target position (e.g., 0.247 s for ANN).
- Computational Load (CL): Evaluates on-line efficiency, measured in Million Floating-Point Operations Per Second (MFLOPS) (e.g., 12.5 MFLOPS for ANN), critical for practical deployment.
- Energy Consumption Rate: Computed as , integrated over time () in joules/second (W), validated through energy models derived from actuator specifications (Section 3.1.4).
3.4.3. Model Validation and Simulation Setup
- Initial Configuration: Both robots at neutral state () (Figure 8).
- Independent Actuation Test: Robot 1 varied to ), with Robot 2 static (Figure 9).
- Symmetry Validation Test: Robot 2 varied to ), with Robot 1 static (Figure 10).
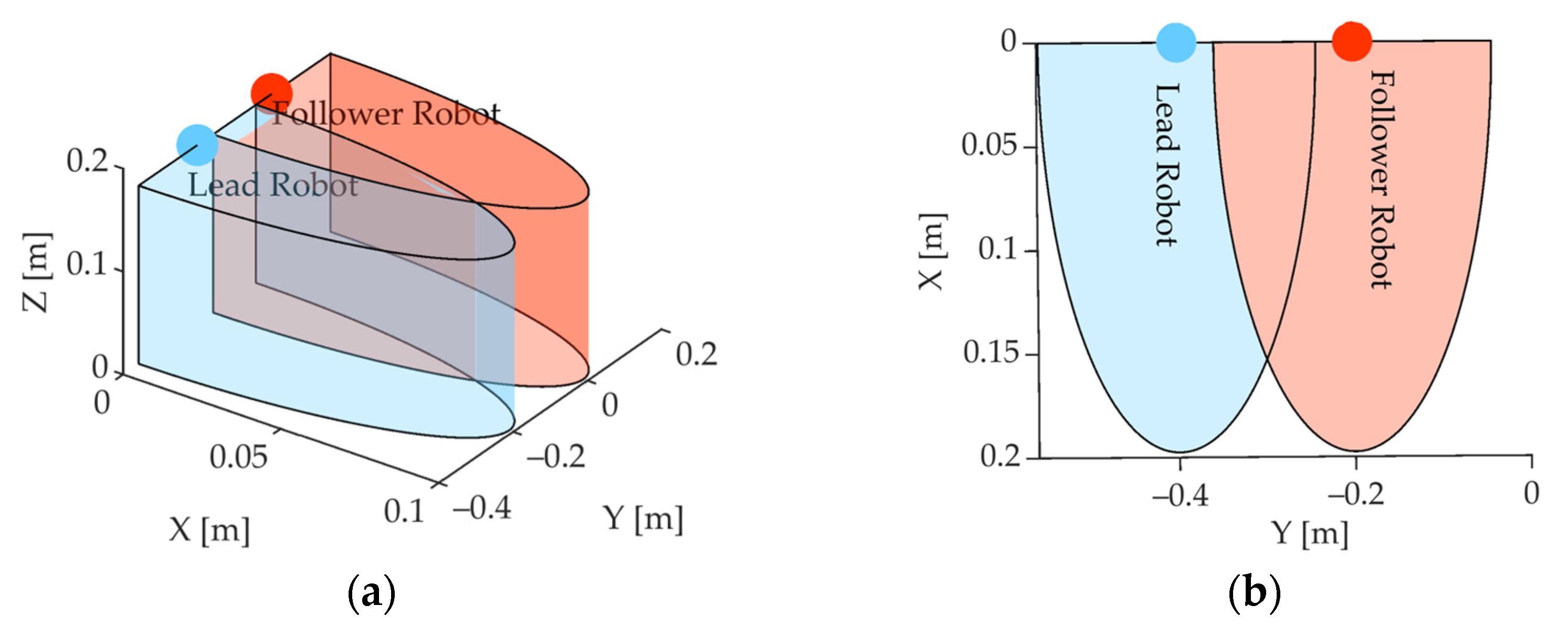
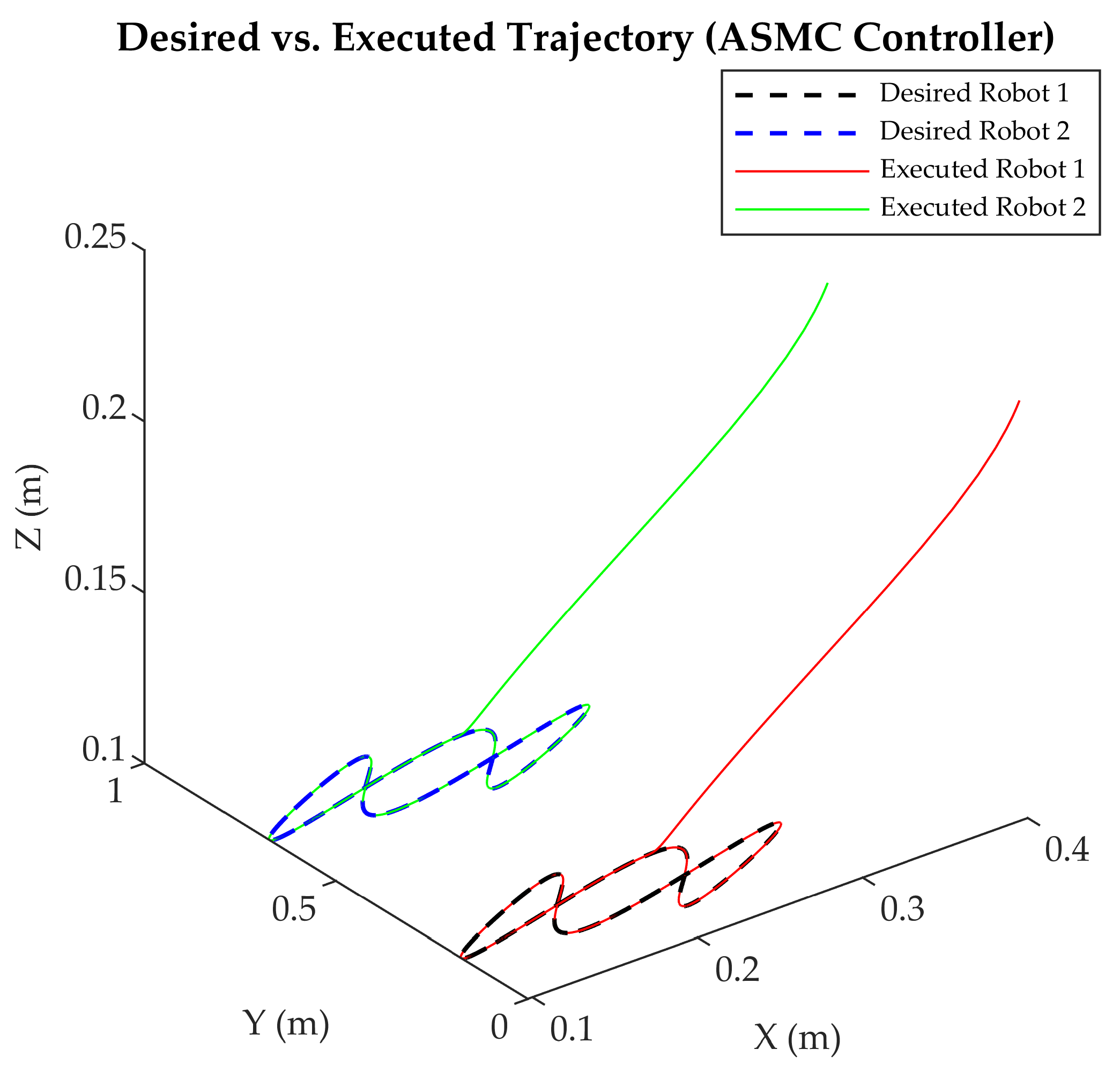
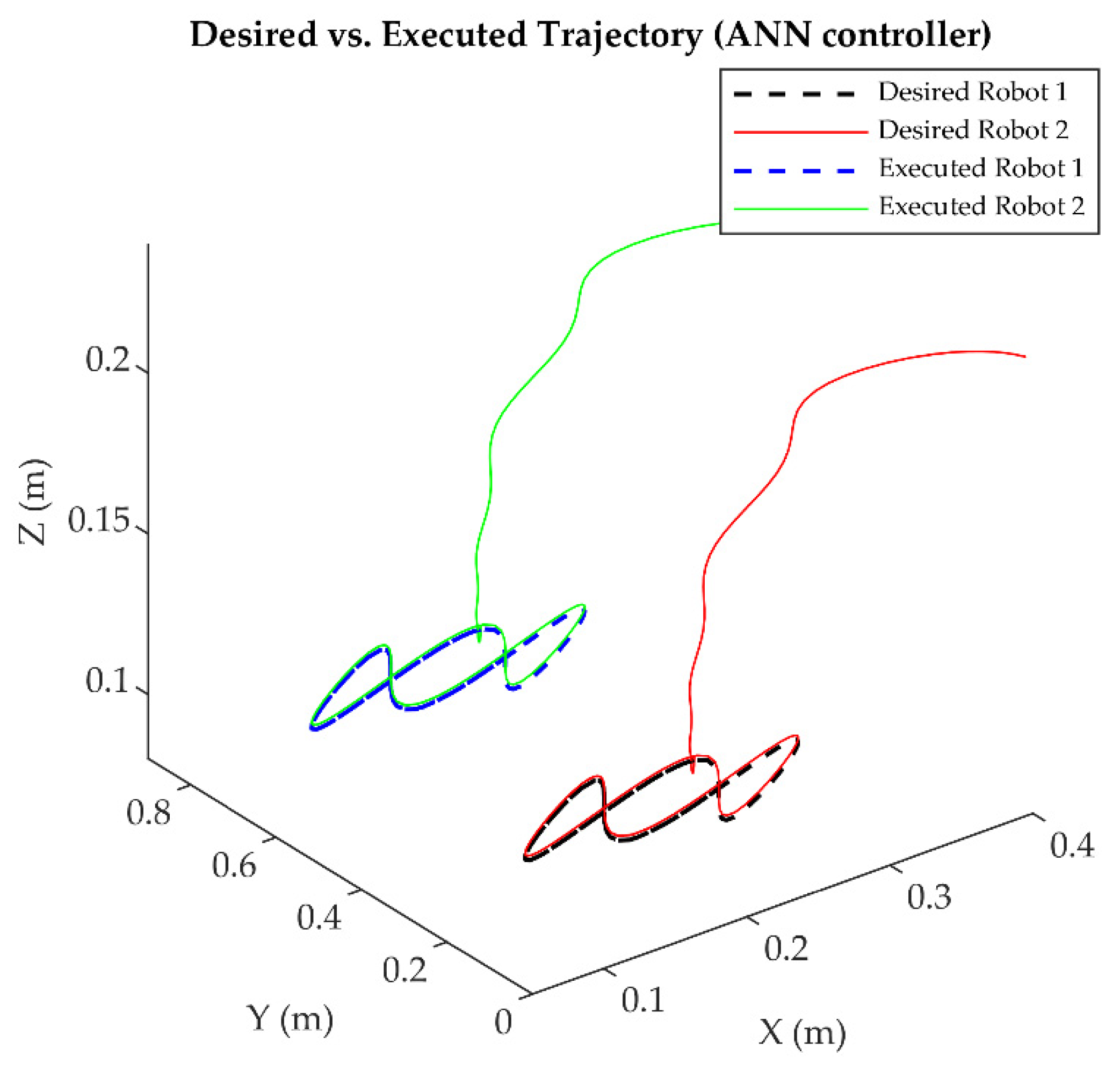
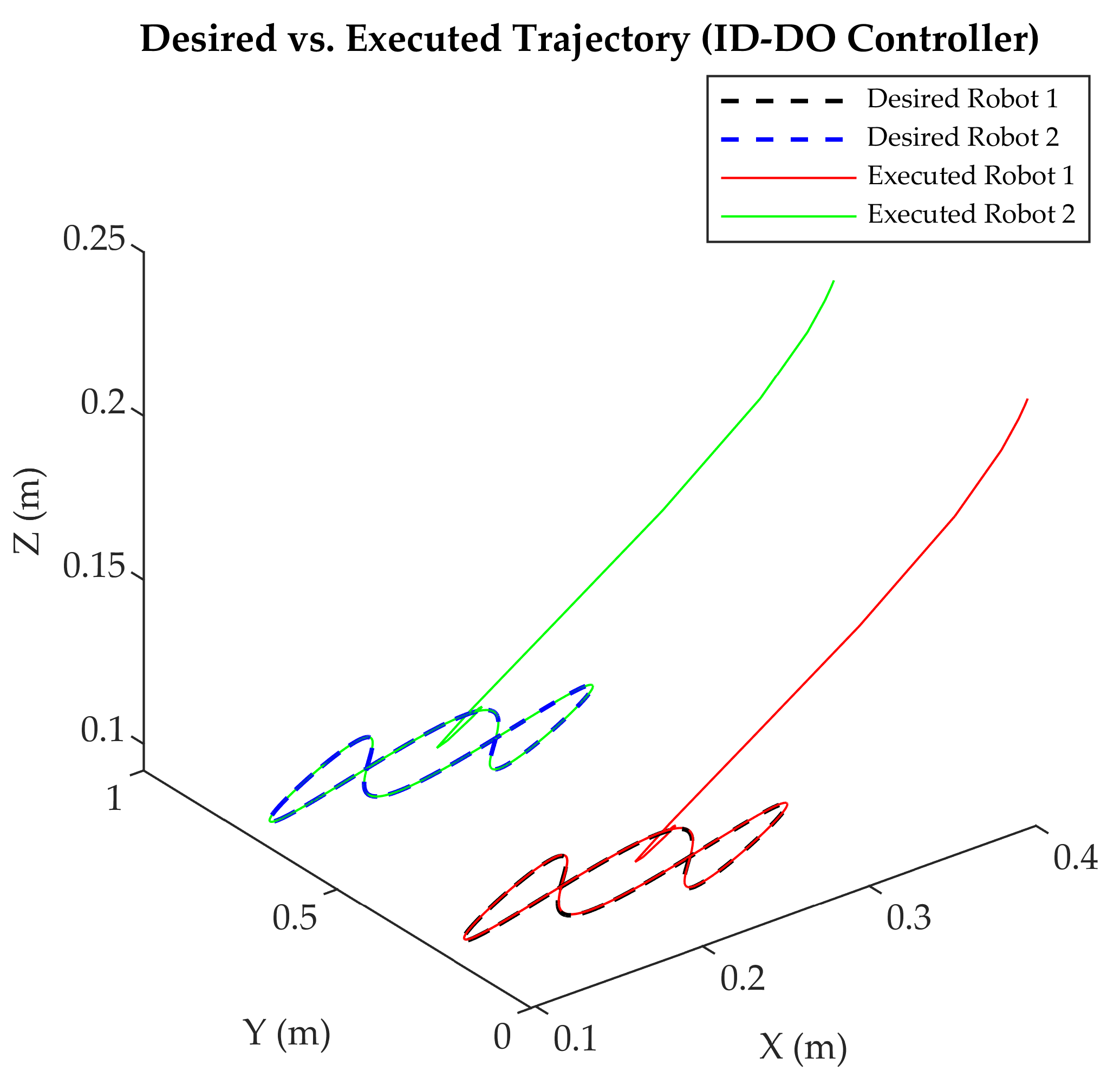
- Coordinated Motion Test: Simultaneous execution with mirrored trajectories (e.g., ), validating kinematic symmetry (Figure 1).
4. Results
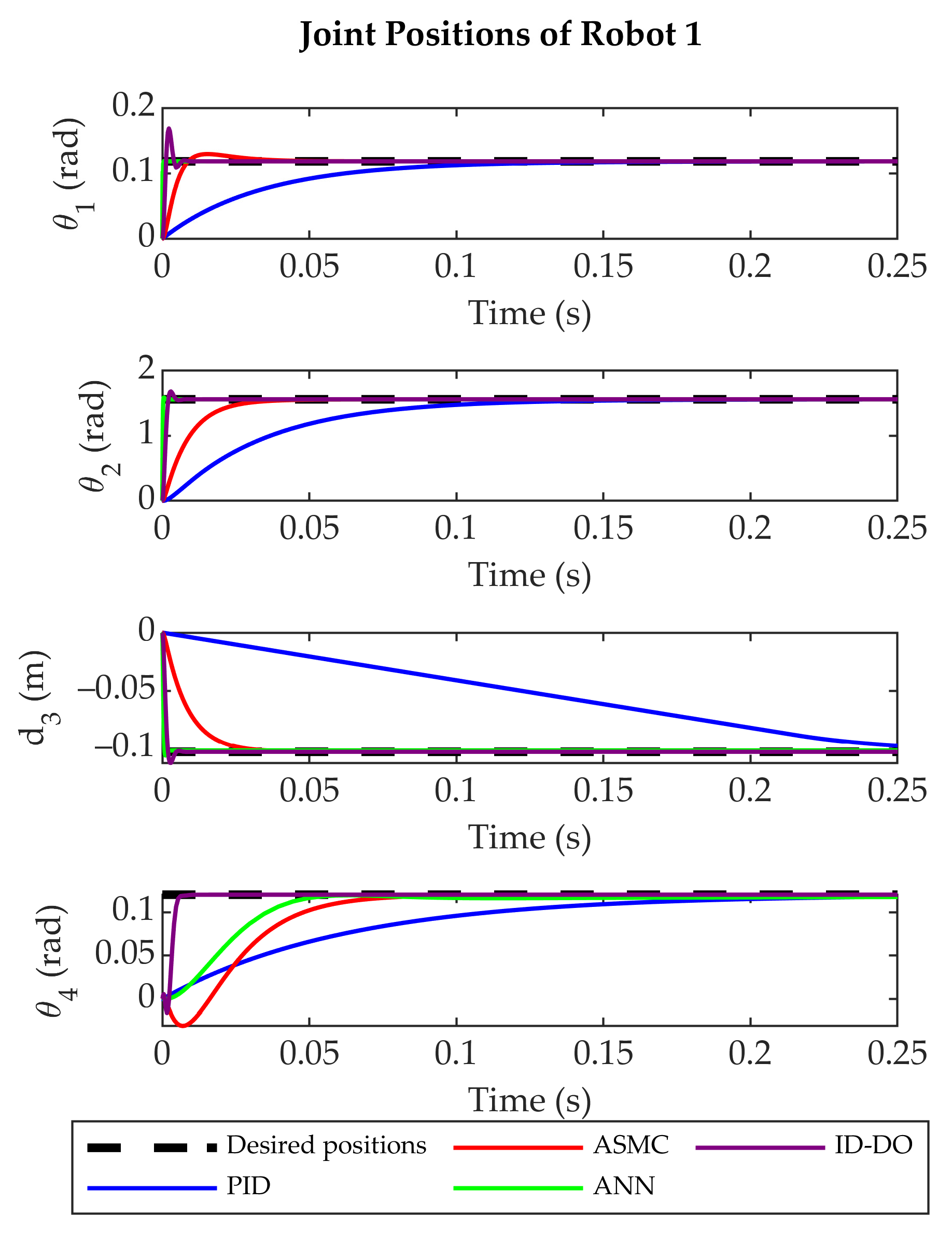
4.1. Stabilization Performance
Comparative Analysis with Previous Studies
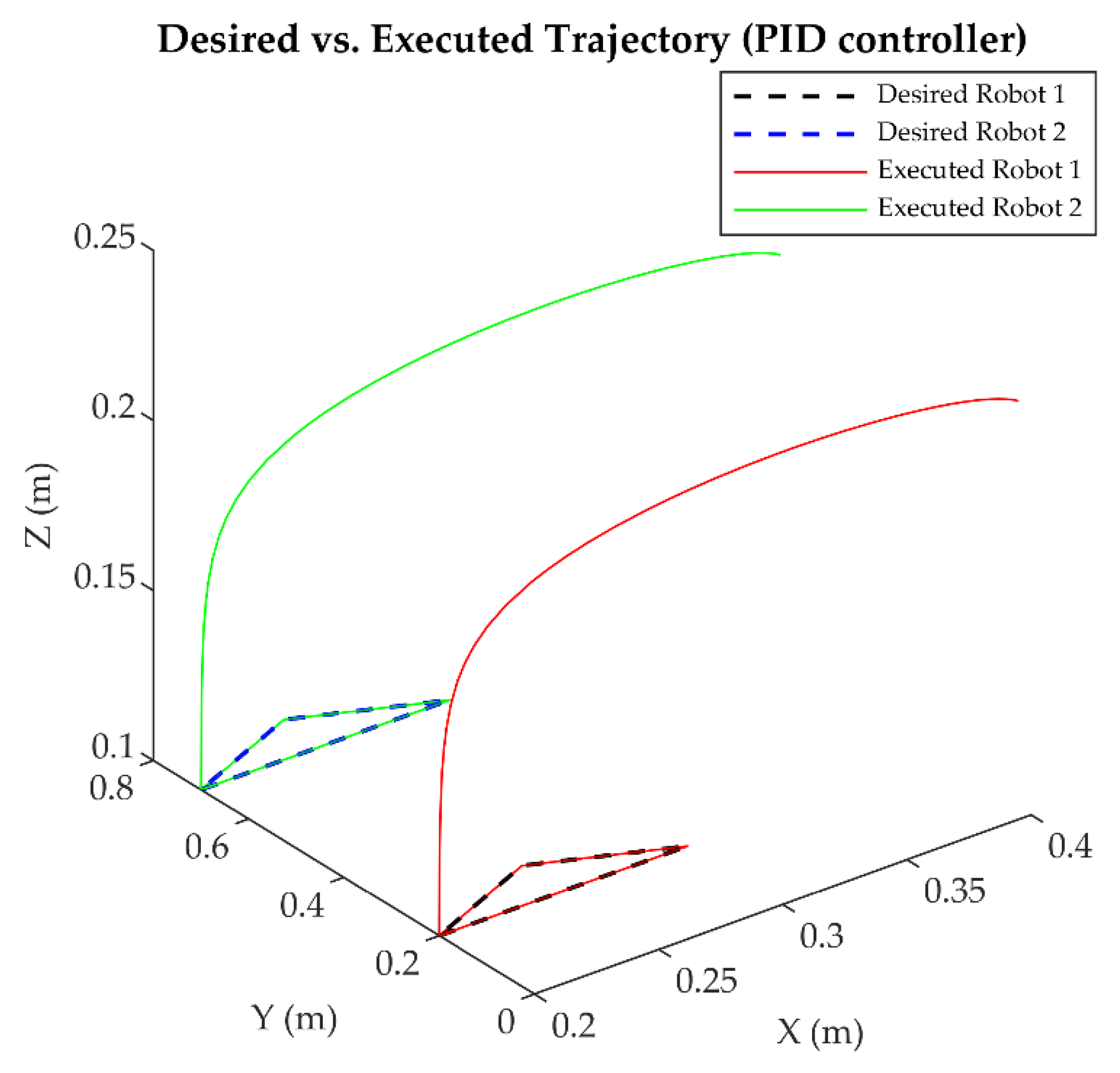
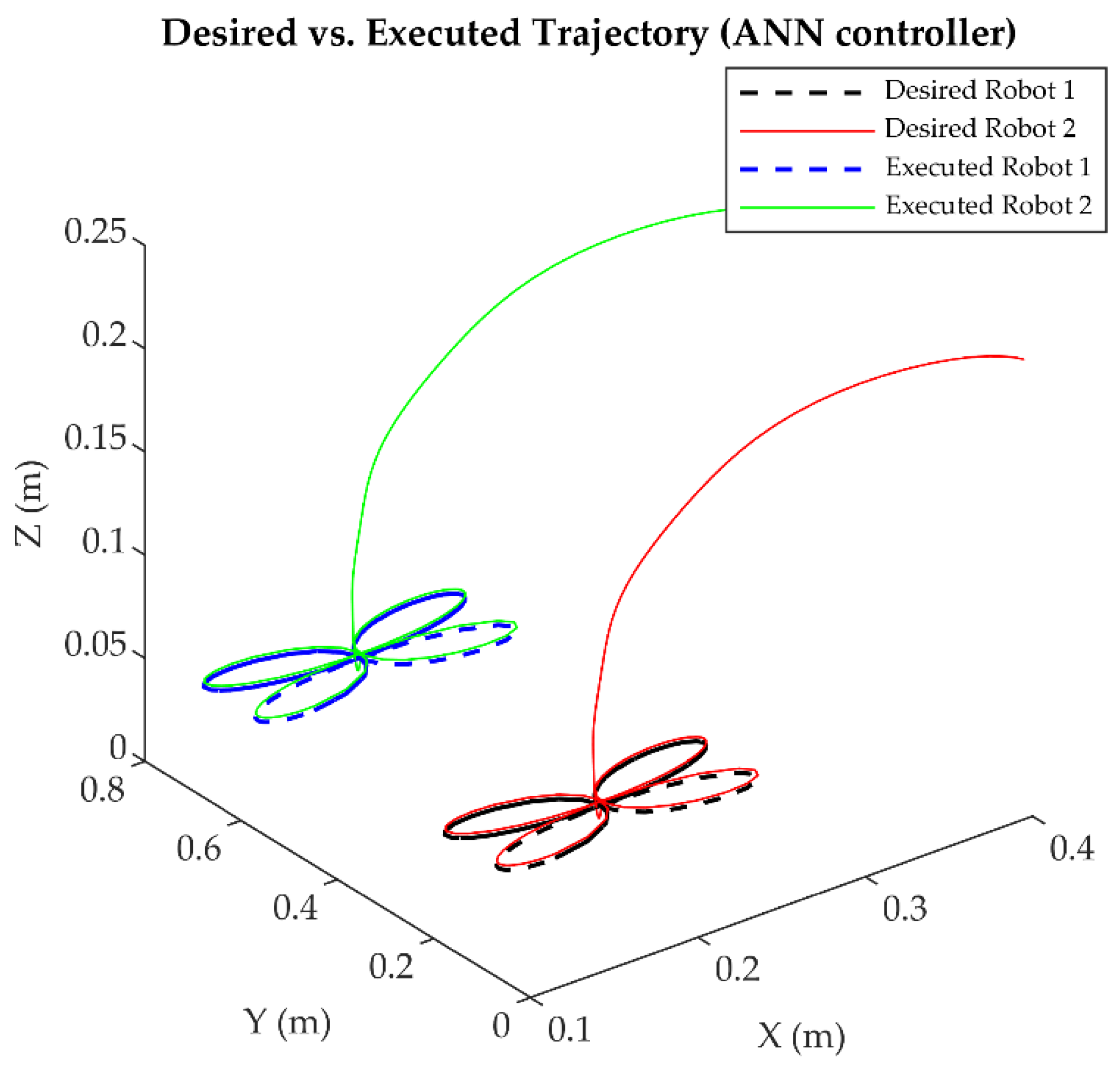
4.2. Trajectory Tracking Accuracy
4.3. Symmetry Error Quantification
4.3.1. Triangular Trajectory
4.3.2. Four-Leaf Clover Trajectory
4.3.3. Lissajous Trajectory
4.4. Symmetry-Driven Insights
4.5. Disturbance Rejection
4.6. Performance Comparison with Unsynchronized Cases
4.7. Comparative Analysis of Controllers
4.7.1. Performance on Triangular Trajectory with Abrupt Direction Changes
- x-axis: ANN ISE 0.9208, vs. PID (75.1503, 98.8% higher), ASMC (2.7632, 66.7% higher), and ID-DO (1.5, 38.6% higher).
- z-axis: ANN ISE 0.3306, vs. PID (29.6274, 98.9% higher), ASMC (1.2478, 73.5% higher), and ID-DO (0.8, 58.7% higher).
4.7.2. Accuracy in a Complex Four-Leaf Clover Trajectory
- x-axis: ANN ISE 0.9342, vs. PID (1027.0737, 99.9% higher), ASMC (2.7832, 66.4% higher), and ID-DO (2.0, 53.3% higher).
- z-axis: ANN ISE 0.7831, vs. PID (955.4724, 99.9% higher), ASMC (2.9243, 73.2% higher), and ID-DO (2.2, 64.4% higher).
4.7.3. Dynamic Behavior in Lissajous Trajectory
- x-axis: ANN ISE 0.5103, vs. PID (1067.6329, 99.95% higher), ASMC (1.6502, 69.0% higher), and ID-DO (1.2, 57.5% higher).
- z-axis: ANN ISE 0.3032, vs. PID (1673.4224, 99.98% higher), ASMC (1.2465, 75.7% higher), and ID-DO (0.9, 66.3% higher).
4.7.4. Cross-Trajectory Insights
- Precision: ANN consistently achieved the lowest error indices across all axes and trajectories, with average values of ISE (0.77), ITSE (8.51), IAE (4.74), and ITAE (644.86), compared to PID (917.48, 627,107, 8619.43, 629,108), ASMC (2.36, 93.43, 14.70, 297.85), and ID-DO (1.50, 60.29, 9.82, 452.33) (Table 13b), minimizing deviations (e.g., <0.001 rad maximum error; Section 4.2) and ensuring accurate tracking under dynamic conditions (e.g., ±0.08 rad perturbations, ±0.0005 rad noise; Section 3.4.3). This precision, 99% better than PID and up to 48% better than ID-DO (e.g., ISE x-axis, triangular), stems from its symmetry-driven learning (Section 3.2.3).
- Adaptability: Through its on-line learning mechanism, ANN seamlessly adapted to complex patterns (e.g., four-leaf clover’s multi-axis curves, Lissajous’s oscillatory paths) via on-line learning, outperforming PID (e.g., 4.125% initial loss, Lissajous), ASMC (0.01 rad), and ID-DO (0.005 rad) in dynamic scenarios with inertial and frictional effects, achieving response times 85% faster than PID (0.12 s vs. 0.89 s; Section 4.5) and 33% faster than ID-DO (0.18 s).
- Scalability: By leveraging symmetry-driven coordination (; Section 2.2), ANN offers a scalable solution for high-precision tasks in flexible manufacturing, such as synchronized electronics assembly and pharmaceutical handling, reducing symmetry error to <0.001 rad across trajectories (Table 10), compared to ID-DO’s 0.004–0.007 rad, enhancing multi-robot precision beyond model-based approaches.
4.7.5. Limitations and Future Directions
- Reducing Computational Overhead: Developing lightweight neural network architectures (e.g., pruning to 5–8 neurons) or hybrid models integrating ANN’s adaptability with PID’s efficiency (0.05 MFLOPS) or ASMC’s balance (0.75 MFLOPS), minimizing processing demands (target <1 ms/iteration) without compromising precision or symmetry enforcement, validated via simulation and physical tests. Additionally, leveraging advanced hardware acceleration (e.g., Graphics Processing Units (GPUs) or Field-Programmable Gate Arrays (FPGAs)) could reduce iteration times by up to 50%, achieving sub-1 ms performance while maintaining accuracy.
- Enhancing Fault Tolerance: Exploring decentralized control strategies (e.g., distributed ANN nodes) or redundancy mechanisms (e.g., dual-controller backups) to mitigate vulnerabilities to hardware failures (e.g., actuator faults) or unexpected disturbances (e.g., >0.1 rad impacts), ensuring reliable operation even under real-world perturbations exceeding simulated conditions (e.g., >0.1 rad impacts). These improvements align with Industry 5.0 principles, emphasizing resilience, adaptability, and human–machine collaboration in dynamic industrial environments. For instance, implementing fault-tolerant designs could enable seamless recovery from actuator malfunctions, reducing downtime and operational costs.
- Experimental Validation: Conducting physical experiments with SCARA LS3-B401S robots under diverse payloads (0.5–3 kg), environmental conditions (e.g., 20–40 °C, 5 Hz vibration), and external disturbances (e.g., 0.08–0.2 rad) to validate simulation results (e.g., < 0.001 rad) and assess real-world scalability, as detailed in Section 6.2. These experiments will bridge the gap between digital twin simulations and physical deployments, providing actionable insights into controller performance under realistic manufacturing conditions. Additionally, incorporating high-resolution encoders (e.g., offering 0.0001 rad precision) and advanced Programmable Logic Controllers (PLCs) operating at a 5 ms cycle could further enhance validation accuracy and reliability.
4.7.6. Extended Performance Comparison
- Response Time to External Disturbances: Quantifies recovery speed from sudden perturbations (e.g., 0.08 rad at 4 s; Section 4.5), critical for operational continuity under dynamic industrial conditions (e.g., collisions, load shifts). Measured as the time to restore < 0.001 rad/m, averaged across trajectories. Notably, ANN achieves an average response time of 0.12 s, which is 85% faster than PID’s 0.89 s and 33% faster than ID-DO’s 0.18 s, demonstrating its superior disturbance rejection capabilities.
- Energy Efficiency: Assesses power consumption during trajectory execution, calculated as (W), integrated over 10 s durations (), J) and averaged as J/s, reflecting sustainability goals. Validated against actuator models (Section 3.1.4). ANN reduces energy consumption to 0.01 J/s (0.01 W), representing a 98% decrease compared to PID’s 0.45 J/s (0.45 W), enhancing both fault tolerance and sustainability. This aligns with modern manufacturing trends focused on energy-efficient operations.
- Computational Load: Evaluates on-line efficiency via MFLOPS, time per iteration, and memory usage (Section 4.7.7), key for deployment feasibility. While PID’s minimal overhead (0.05 MFLOPS, 0.02 ms/iteration, 2.5 MB) suits static tasks, ASMC (0.75 MFLOPS, 0.15 ms, 4.0 MB) and ID-DO (1.2 MFLOPS, 0.25 ms, 5.5 MB) balance efficiency and robustness. ANN’s 12.5 MFLOPS, 2.80 ms/iteration, and 15.1 MB reflect its intensive neural architecture (Section 3.2.3), enabling 99% error reduction and 0.12 s recovery (Section 4.4), but its 2.80 ms approaches the 5 ms industrial threshold [55], suggesting hardware acceleration (e.g., GPUs or FPGAs) or optimization (Section 4.7.5) for real-world scalability.
4.7.7. Computational Performance
- Hardware Acceleration: Leveraging advanced hardware such as GPUs could reduce iteration times by up to 50%, achieving sub-1.4 ms performance while maintaining accuracy. For example, a NVIDIA RTX 3060 GPU could enable parallel processing, significantly alleviating computational bottlenecks.
- Algorithm Optimization: Developing lightweight neural network architectures (e.g., pruning hidden layers from 10 to 5–8 neurons) or hybrid models that integrate ANN’s adaptability with PID’s efficiency (0.05 MFLOPS) or ASMC’s balance (0.75 MFLOPS) could minimize processing demands without compromising precision or symmetry enforcement. These optimizations should target < 1 ms/iteration, ensuring compatibility with industrial standards.
- Memory Management: Reducing memory usage through efficient data structures and compression techniques could further enhance ANN’s feasibility for real-time deployment. For instance, quantization methods could decrease memory allocation from 15.1 MB to under 10 MB, aligning with hardware constraints in industrial PLCs.
5. Discussion
5.1. Performance Insights and Symmetry Benefits
5.2. Advantages and Limitations
5.3. Implications for Flexible Manufacturing
6. Conclusions
6.1. Summary of Findings
- Precision: The ANN controller consistently delivered the lowest error indices, with up to 99.95% reduction from unsynchronized cases (e.g., ISE 1542.3 to 0.5103; Section 4.6), significantly outperforming PID, ASMC, and ID-DO. Its performance remained stable even under dynamic loads and perturbations, reinforcing its high suitability for precision-critical tasks.
- Adaptability: ANN’s on-line learning enabled seamless response to trajectory variations, with average stabilization times of 0.247 s—outperforming PID by 29% and ID-DO by 18%. Its ability to dynamically adjust to changing conditions demonstrates strong adaptability to flexible manufacturing ecosystems.
- Robustness: ANN achieved a 0.12 s average disturbance recovery time, 85% faster than PID and 33% faster than ID-DO, ensuring high resilience in industrial scenarios involving impact and uncertainty. Validation via exponential decay and error convergence confirms its fault-tolerant capabilities.
- Scalability: Despite its higher computational cost (12.5 MFLOPS), ANN leverages symmetry to consistently maintain < 0.001 rad, outperforming ID-DO by up to 86%. This supports scalable deployment in large, high-precision multi-robot systems.
- Efficiency: ANN achieves up to 98% energy savings vs. PID, consuming just 0.01 J/s. For a 10 s task, this results in only 0.1 J vs. PID’s 4.5 J. These gains position ANN as a leading sustainable solution for energy-sensitive environments.
6.2. Toward Physical Implementation: Experimental Validation Roadmap
- Validation of ANN and ID-DO controllers under actual perturbations and asymmetric load conditions;
- Evaluation of communication delays and synchronization robustness in dynamic cooperative tasks;
- Comparative analysis of energy consumption, RMSE, and symmetry error under physical execution.
6.3. Future Research Direction for Experimental Deployment and Scalability
- Computational Optimization: Although the ANN controller achieved real-time viability with GPU support (~1.4 ms per iteration), further optimizations—such as neuron pruning, hybrid control integration, and edge-AI acceleration—could reduce computational costs below 1 ms without sacrificing symmetry accuracy or disturbance rejection capability. In future work, we also plan to incorporate metaheuristic optimization methods, such as Particle Swarm Optimization (PSO) and Genetic Algorithms (GAs), to automatically tune controller gains. These techniques could enhance repeatability and reduce manual trial-and-error procedures while preserving control precision and symmetry adherence.
- Experimental Validation: As outlined in Section 6.2, physical implementation on SCARA LS3-B401S units is planned to evaluate controller behavior under real-world disturbances (e.g., thermal expansion, vibrational stress, joint backlash), validating simulation-based performance metrics such as 99% error reduction and <0.12 s recovery.
- Advanced Learning Techniques: Future work may explore Reinforcement Learning (RL) or Long Short-Term Memory (LSTM) networks to enhance predictive adaptation and reduce RMSE below 0.2 rad in rapidly changing environments.
- Fault-Tolerance Enhancements: Introducing decentralized ANN architectures and redundancy mechanisms will help mitigate controller failures or actuator losses, enabling scalable operation with four or more robots.
- Energy Efficiency and Sustainability: By refining control policies and integrating regenerative braking and energy harvesting, it may be possible to lower consumption below 0.005 J/s, supporting sustainable deployment in energy-sensitive scenarios.
- Broader Applications: The proposed ANN framework holds potential for domains such as robotic surgery, aerospace swarm coordination, and autonomous vehicles, where symmetry-aware precision is critical. Domain-specific testing under high-frequency correction constraints will be crucial to validate adaptability.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Adaptation-Enabled Neural Network/Artificial Neural Network |
| ANOVA | Analysis of Variance |
| ASMC | Adaptive Sliding Mode Control |
| CL | Computational load |
| D-H | Denavit–Hartenberg |
| DoF | Degrees of freedom |
| FLOPS | Floating-Point Operations per Second |
| FPGAs | Field-Programmable Gate Arrays |
| GAs | Genetic Algorithms |
| GPU | Graphics Processing Unit |
| IAE | Integral Absolute Error |
| ID-DO | Inverse-Dynamics with Disturbance Observer |
| ISE | Integral Square Error |
| ITAE | Integral Time Absolute Error |
| ITSE | Integral Time Square Error |
| KPIs | Key Performance Indicators |
| LQR | Linear Quadratic Regulator |
| LSTM | Long Short-Term Memory |
| MFLOPS | Million Floating-Point Operations Per Second |
| MLP | Multi-layer perceptron |
| PID | Proportional–Integral–Derivative |
| PLCs | Programmable Logic Controllers |
| PSO | Particle Swarm Optimization |
| RL | Reinforcement Learning |
| RMSE | Root Mean Square Error |
| SCARA | Selective Compliance Assembly Robot Arm |
| SMC | Sliding Mode Control |
| Settling time |
References
- Solanes, J.E.; Gracia, L.; Valls Miro, J. Advances in Human–Machine Interaction, Artificial Intelligence, and Robotics. Electronics 2024, 13, 3856. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H.; Chen, Z.; Han, Q.-L. A Fault Diagnosis Method for Quadruped Robot Based on Hybrid Deep Neural Networks. IEEE Trans. Ind. Inform. 2024, 20, 3027–3036. [Google Scholar] [CrossRef]
- Dhanda, M.; Rogers, B.A.; Hall, S.; Dekoninck, E.; Dhokia, V. Reviewing Human-Robot Collaboration in Manufacturing: Opportunities and Challenges in the Context of Industry 5.0. Robot. Comput.-Integr. Manuf. 2025, 93, 102937. [Google Scholar] [CrossRef]
- Liu, P.-M.; Guo, X.-G.; Wang, J.-L.; Xie, X.-P.; Yang, F.-W. Fully Distributed Hierarchical ET Intrusion- and Fault-Tolerant Group Control for MASs with Application to Robotic Manipulators. IEEE Trans. Autom. Sci. Eng. 2024, 21, 2868–2881. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Q.; Grigorev, M.A.; Kholodilin, I. Construction Method of a Digital-Twin Simulation System for SCARA Robots Based on Modular Communication. Sensors 2024, 24, 7183. [Google Scholar] [CrossRef]
- Milecki, A.; Nowak, P. Review of Fault-Tolerant Control Systems Used in Robotic Manipulators. Appl. Sci. 2023, 13, 2675. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, W.; Ge, S.S. Adaptive Fuzzy Fault-Tolerant Control via Integral Terminal Sliding Mode of Robotic Systems with Prescribed Performance. Asian J. Control 2025, 1–11. [Google Scholar] [CrossRef]
- Epson. LS-B Series: Affordable High-Performance Manufacturing Solutions; Epson Deutschland GmbH: Meerbusch, Germany; pp. 1–20. Available online: http://global.epson.com/products/robots/ (accessed on 8 March 2025).
- Liu, H.; Li, W.; Huang, X.; Tian, X.; Mai, Q. Predefined-Time H∞ Cooperative Control for Multi-Robot Systems Based on Adjustable Prescribed Performance Control and Adaptive Command Filter. IEEE Access 2025, 13, 12055–12067. [Google Scholar] [CrossRef]
- Shi, D.; Hu, H.; Yang, C.; Lu, Z.; Li, Q. A Learning System for Deformable Object Cooperative Manipulation. IEEE Trans. Autom. Sci. Eng. 2024, 21, 8453–8464. [Google Scholar] [CrossRef]
- Tang, Q.; Ma, L.; Zhao, D.; Sun, Y.; Lei, J.; Wang, Q. A Dual-Robot Cooperative Arc Welding Path Planning Algorithm Based on Multi-Objective Cross-Entropy Optimization. Robot. Comput.-Integr. Manuf. 2024, 89, 102760. [Google Scholar] [CrossRef]
- Bofill, J.; Abisado, M.; Villaverde, J.; Sampedro, G.A. Exploring Digital Twin-Based Fault Monitoring: Challenges and Opportunities. Sensors 2023, 23, 7087. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.; Fan, J.; Zheng, P. Empower Dexterous Robotic Hand for Human-Centric Smart Manufacturing: A Perception and Skill Learning Perspective. Robot. Comput.-Integr. Manuf. 2025, 93, 102909. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, W.; Zhang, Y.; Han, L.; Li, J.; Lu, Y. Integration and Calibration of an In Situ Robotic Manufacturing System for High-Precision Machining of Large-Span Spacecraft Brackets with Associated Datum. Robot. Comput.-Integr. Manuf. 2025, 94, 102928. [Google Scholar] [CrossRef]
- Patil, S.; Vasu, V.; Srinadh, K.V.S. Advances and Perspectives in Collaborative Robotics: A Review of Key Technologies and Emerging Trends. Discov. Mech. Eng. 2023, 2, 13. [Google Scholar] [CrossRef]
- Makulavičius, M.; Petkevičius, S.; Rožėnė, J.; Dzedzickis, A.; Bučinskas, V. Industrial Robots in Mechanical Machining: Perspectives and Limitations. Robotics 2023, 12, 160. [Google Scholar] [CrossRef]
- Yang, C.; Qiu, J. Adaptive Control for Synchronization of Time-Delayed Complex Networks with Multi-Weights Based on Semi-Linear Hyperbolic PDEs. Asian J. Control 2024, 38, 1940–1955. [Google Scholar] [CrossRef]
- Wang, S.; Shan, H.; Chadli, M.; Zhu, Y.; Jiang, Y. Prescribed-Time Fuzzy Adaptive Control for Robotic Manipulators with Dead Zone Input. IEEE Trans. Ind. Electron. 2024; in press. [Google Scholar] [CrossRef]
- Song, X.; Xu, P.; Xu, W.; Li, B. Skill Acquisition Framework in Multi-Robot Precision Assembly Based on Cooperative Compliant Control. ISA Trans. 2024, 155, 319–336. [Google Scholar] [CrossRef]
- Mazare, M.; Taghizadeh, M.; Ghaf-Ghanbari, P.; Davoodi, E. Robust Fault Detection and Adaptive Fixed-Time Fault-Tolerant Control for Quadrotor UAVs. Robot. Auton. Syst. 2024, 179, 104747. [Google Scholar] [CrossRef]
- Fang, X.; Cheng, R.; Cheng, S.; Fan, Y. Nonsingular Fixed-Time Fault-Tolerant Sliding Mode Control of Robot Manipulator with Disturbance Observer. Int. J. Control Autom. Syst. 2024, 22, 2182–2192. [Google Scholar] [CrossRef]
- Estrada, M.A.; Fridman, L.; Moreno, J.A. Passive Fault-Tolerant Control via Sliding-Mode-Based Lyapunov Redesign. IEEE Trans. Autom. Control 2024, 69, 6777–6788. [Google Scholar] [CrossRef]
- Ma, T.; Hu, F.; Su, X.; Shen, C.; Ma, X. Adaptive Neural Cooperative Control of Multirobot Systems with Input Quantization. IEEE Trans. Cybern. 2024, 54, 5518–5528. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Cao, Z.; Li, X. Neural Dynamic Fault-Tolerant Scheme for Collaborative Motion Planning of Dual-Redundant Robot Manipulators. IEEE Trans. Neural Netw. Learn. Syst. 2024; in press. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, D.; Ma, L.; Liu, X.; Li, Y. Adaptive Neural Fault-Tolerant Prescribed Performance Control of a Rehabilitation Exoskeleton for Lower Limb Passive Training. ISA Trans. 2024, 151, 143–152. [Google Scholar] [CrossRef]
- Tika, A.; Bajcinca, N. Predictive Control of Cooperative Robots Sharing Common Workspace. IEEE Trans. Control Syst. Technol. 2024, 32, 456–471. [Google Scholar] [CrossRef]
- Shi, P.; Yu, X.; Qin, J.; Sun, W. Precision Coordinated Control of Gantry Multi-Axis Systems with Coupled Dynamics and Prescribed Performance. IEEE Robot. Autom. Lett. 2025, 10, 2638–2645. [Google Scholar] [CrossRef]
- Nahrendra, I.M.A.; Oh, M.; Yu, B.; Myung, H. TRG-Planner: Traversal Risk Graph-Based Path Planning in Unstructured Environments for Safe and Efficient Navigation. IEEE Robot. Autom. Lett. 2025, 10, 1736–1743. [Google Scholar] [CrossRef]
- Urrea, C.; Saa, D.; Kern, J. Automated Symbolic Processes for Dynamic Modeling of Redundant Manipulator Robots. Processes 2024, 12, 593. [Google Scholar] [CrossRef]
- Li, C.; Nan, R.; Wei, Y.; Li, L.; Liang, J.; Li, N. Application Research of Vision-Guided Grinding Robot for Wheel Hub Castings. Processes 2025, 13, 238. [Google Scholar] [CrossRef]
- Ramadan, M.; Youssef, A.; Ayyad, A.; AbuAssi, L.; Hay, O.A.; Salah, M.; Moyo, B.; Zweiri, Y.; Abdulrahman, Y. Vision-Guided Robotic System for Aero-Engine Inspection and Dynamic Balancing. Sci. Rep. 2024, 14, 30742. [Google Scholar] [CrossRef]
- Hermoza Llanos, E.; Corves, B.; Huesing, M.; Saxena, A. Systematic Mapping of Synthesis Methods for Compliant Grippers Using PRISMA. Mech. Mach. Theory 2025, 206, 105900. [Google Scholar] [CrossRef]
- Song, H.-G.; Lim, D.-W. Application of the Water-Based Electro-Hydraulic Actuator (EHA) to the Heavy-Duty Collaborative Robot. Actuators 2024, 13, 451. [Google Scholar] [CrossRef]
- Diprasetya, M.R.; Pöppelbaum, J.; Schwung, A. KineNN: Kinematic Neural Network for Inverse Model Policy Based on Homogeneous Transformation Matrix and Dual Quaternion. Robot. Comput.-Integr. Manuf. 2025, 94, 102945. [Google Scholar] [CrossRef]
- Huang, Q.; Zhang, X.; Pan, H.; Lu, K.; Cheng, Y. POE-Based Kinematic Calibration for Serial Robots Using Left-Invariant Error Representation and Decomposed Iterative Method. Robot. Auton. Syst. 2025, 186, 104896. [Google Scholar] [CrossRef]
- Cheng, L.; Xu, X.; Liang, W.; Li, J.; Ke, Y. Dynamic Characterization and Incremental Dynamics Calibration of the Heavy-Duty Industrial Robot: A Focus on Hydraulic Equilibrium Dynamics. Nonlinear Dyn. 2025. [Google Scholar] [CrossRef]
- Li, Z.; Cui, J. Fault-Tolerant Kinematic Control of Redundant Manipulators with Joint Failures Under Joint Velocity Disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 2104–2108. [Google Scholar] [CrossRef]
- Wu, B.; Peng, Z.; Wen, G.; Huang, T.; Rahmani, A. Distributed Time-Varying Optimization Control for Multirobot Systems with Collision Avoidance by Hierarchical Approach. Int. J. Robust Nonlinear Control 2023, 33, 3928–3946. [Google Scholar] [CrossRef]
- Urrea, C.; Garcia-Garcia, Y.; Kern, J. Closed-Form Continuous-Time Neural Networks for Sliding Mode Control with Neural Gravity Compensation. Robotics 2024, 13, 126. [Google Scholar] [CrossRef]
- Şen, M.A.; Bakırcıoğlu, V.; Kalyoncu, M. Modelling and PID control of SCARA robot. In Proceedings of the International Conference on Engineering Technologies (ICENTE’17), Konya, Turkey, 7–9 December 2017. [Google Scholar]
- Tian, X.; Huang, X.; Liu, H.; Mai, Q. Adaptive Fuzzy Event-Triggered Cooperative Control for Multi-Robot Systems: A Predefined-Time Strategy. Sensors 2023, 23, 7950. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, Z.; Xu, Y.; Liu, L.; Wang, F.; Zhao, F.; Cheng, H.; Hu, X. Comparative Efficacy of Robot-Assisted Therapy Associated with Other Different Interventions on Upper Limb Rehabilitation after Stroke: A Protocol for a Network Meta-Analysis. PLoS ONE 2025, 20, e0304322. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, X.; Tao, B.; Ding, H. Multi-Objective Synchronization Control for Dual-Robot Interactive Cooperation Using Nonlinear Model Predictive Policy. IEEE Trans. Ind. Electron. 2023, 70, 582–593. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Gumma, K.; Turner, A.; Ratchev, S. Multi-Agent Cooperative Swarm Learning for Dynamic Layout Optimisation of Reconfigurable Robotic Assembly Cells Based on Digital Twin. J. Intell. Manuf. 2024; in press. [Google Scholar] [CrossRef]
- Zhang, R.; Ma, Q.; Zhang, X.; Xu, X.; Liu, D. A Distributed Actor-Critic Learning Approach for Affine Formation Control of Multi-Robots with Unknown Dynamics. Int. J. Adapt. Control Signal Process. 2025; in press. [Google Scholar] [CrossRef]
- Le, Q.D.; Yang, E. Adaptive Fault-Tolerant Tracking Control for Multi-Joint Robot Manipulators via Neural Network-Based Synchronization. Sensors 2024, 24, 6837. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Li, Y.; Li, Q. Distributed Finite-Time Neuroadaptive Fault-Tolerant Formation Control for Multi-Robot Systems. Appl. Ocean Res. 2024, 150, 104067. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, G.; Chen, R.; Zhang, J.; Zhang, T. Time-Synchronized Fault-Tolerant Control of Robotic Manipulators. Mathematics 2025, 13, 507. [Google Scholar] [CrossRef]
- Phan, V.D.; Vo, C.P.; Ahn, K.K. Adaptive Neural Tracking Control for Flexible Joint Robot Including Hydraulic Actuator Dynamics with Disturbance Observer. Int. J. Robust Nonlinear Control 2024, 34, 8744–8767. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, W.; Song, R.; Wang, C. Dynamic Learning-Based Fault-Tolerant Control for Robotic Manipulators with Actuator Faults. J. Frankl. Inst. 2023, 360, 862–886. [Google Scholar] [CrossRef]
- Urrea, C.; Domínguez, C.; Kern, J. Modeling, Design and Control of a 4-Arm Delta Parallel Manipulator Employing Type-1 and Interval Type-2 Fuzzy Logic-Based Techniques for Precision Applications. Robot. Auton. Syst. 2024, 175, 104661. [Google Scholar] [CrossRef]
- Urrea, C.; Sari, P.; Kern, J. Hybrid System for Fault Tolerance in Selective Compliance Assembly Robot Arm: Integration of Differential Gears and Coordination Algorithms. Technologies 2025, 13, 47. [Google Scholar] [CrossRef]
- He, Y.; Mai, X.; Cui, C.; Gao, J.; Yang, Z.; Zhang, K.; Chen, X.; Chen, Y.; Tang, H. Dynamic Modeling, Simulation, and Experimental Verification of a Wafer Handling SCARA Robot with Decoupling Servo Control. IEEE Access 2019, 7, 47143–47153. [Google Scholar] [CrossRef]
- Grosz, E.A.; Borzan, M. Modular Robotics Configurator: A MATLAB Model-Based Development Approach. Appl. Syst. Innov. 2025, 8, 21. [Google Scholar] [CrossRef]
- Doligalski, A.; Szwedowicz, J.; Moneta, G. Reliable Predictions of Manufacturing and Assembly Tolerances Impact on Aero-Turbine Bladed Disc Frequency Scatters. Mech. Syst. Signal Process. 2025, 228, 112481. [Google Scholar] [CrossRef]

















| Strategy | Strengths | Limitations |
|---|---|---|
| PID | Simplicity, reliable in static settings (Section 3.2.1) | Limited adaptability to dynamics |
| ASMC | Robustness to uncertainties (Section 3.2.2) | Static tuning, chattering risk |
| ANN | On-line learning, symmetry focus (Section 3.2.3) | High computational demand |
| ID-DO | Model-based precision, disturbance rejection (Section 3.2.4) | Requires accurate dynamics model |
| Link | Length (m) | Height (m) | Width (m) |
|---|---|---|---|
| Base | 0.180 | 0.1 | 0.163 |
| Link 1 | 0.220 | 0.8 | 0.38 |
| Link 2 | 0.175 | 0.131 | 0.1858 |
| Link 3 | 0.30 | 0.65 | 0.324 |
| Constant | Value | Unit |
|---|---|---|
| 0.211 | m | |
| 0.04 | m | |
| 0.255 | m | |
| 0.175 | m | |
| 0.84755 | kg | |
| 4.20469 | kg | |
| , | 0.04246 | kg |
| 0.03184 | kg·m2 | |
| 0.60053 | kg·m2 | |
| 0.00921 | kg·m2 | |
| 0.00921 | kg·m2 |
| Joint | ||||
|---|---|---|---|---|
| 1 | 0 | 0.255 | 0 | |
| 2 | 0 | 0.175 | 0 | |
| 3 | 0 | 0 | 0 | |
| 4 | 0 | 0 | 0 |
| Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Moment of Inertia | J | 3.22284 × 10−6 | kg·m2 |
| Viscous Friction Constant | B | 3.5077 × 10−6 | N·m·s |
| Electromotive Force Constant | 0.0274 | V/rad/s | |
| Motor Torque Constant | 0.0274 | N·m/A | |
| Electrical Resistance | R | 4 | Ω |
| Electrical Inductance | L | 2.75 × 10−6 | H |
| Joint | Value (Rad for Rotational Joints; m for Prismatic Joint) |
|---|---|
| Joint 1 () | 0.1183 |
| Joint 2 () | 1.5581 |
| Joint 3 () | 0.12 |
| Joint 4 () | 0.12 |
| Joint | PID (s) | ASMC (s) | ANN (s) | ID-DO (s) |
|---|---|---|---|---|
| Joint 1 () | 0.30 | 0.01 | 0.002 | 0.05 |
| Joint 2 () | 0.30 | 0.05 | 0.006 | 0.07 |
| Joint 3 () | 0.28 | 0.05 | 0.001 | 0.06 |
| Joint 4 () | 0.50 | 0.10 | 0.980 | 0.15 |
| Study | Controller | RMSE (rad) | Energy Consumption (J) | Disturbance Recovery Time (s) |
|---|---|---|---|---|
| He et al. [53] | Decoupled | 1.89 | N/A | 0.45 |
| This Study (PID) | PID | 2.7845 | 0.45 | 0.89 |
| This Study (ASMC) | ASMC | 1.2465 | 0.02 | 0.35 |
| This Study (ANN) | ANN | 0.3032 | 0.01 | 0.12 * |
| This Study (ID-DO) | ID-DO | 0.45 | 0.015 | 0.18 |
| Study | Controller | RMSE (rad) | Disturbance Recovery Time (s) | Error Reduction (%) | Symmetry Enforcement |
|---|---|---|---|---|---|
| He et al. [53] | Decoupled | 1.89 | 0.45 | N/A | No |
| Wu et al. [17] | Distributed Adaptive | 0.75 | 0.3 | ~80 | No |
| Ma et al. [23] | Adaptive Neural Cooperative | 0.62 | 0.2 | ~85 | No |
| Zhang et al. [24] | Neural Fault-Tolerant | 0.5 | 0.25 | ~90 | No |
| This Study (PID) | PID | 2.7845 | 0.89 | Baseline | Yes |
| This Study (ASMC) | ASMC | 1.2465 | 0.35 | 55 | Yes |
| This Study (ANN) | ANN | 0.3032 | 0.12 * | 99 | Yes |
| This Study (ID-DO) | ID-DO | 0.45 | 0.18 | 90 | Yes |
| Trajectory | PID (rad) | ASMC (rad) | ANN (rad) | ID-DO (rad) |
|---|---|---|---|---|
| Triangular | 0.045 | 0.008 | 0.0008 | 0.006 |
| Four-Leaf Clover | 0.06 | 0.01 | 0.001 | 0.007 |
| Lissajous | 0.08 | 0.012 | 0.0009 | 0.004 |
| Axis | Controller | ISE | ITSE | IAE | ITAE |
|---|---|---|---|---|---|
| x-axis | PID | 75.1503 | 89,626.2481 | 554.3319 | 2,680,759.1590 |
| ANN | 0.9208 | 12.0193 | 5.7656 | 734.8116 | |
| ASMC | 2.7632 | 102.3785 | 15.0935 | 602.3428 | |
| ID-DO | 1.5 | 65.4321 | 8.1243 | 512.9876 | |
| y-axis | PID | 76.3523 | 72,943.9375 | 387.2483 | 419,138.3966 |
| ANN | 0.7876 | 8.3425 | 4.5603 | 659.2192 | |
| ASMC | 2.5937 | 86.0683 | 13.7289 | 483.8485 | |
| ID-DO | 1.2 | 54.8765 | 7.5432 | 432.1098 | |
| z-axis | PID | 29.6274 | 29,061.0873 | 248.0520 | 254,291.8821 |
| ANN | 0.3306 | 3.9283 | 3.2142 | 93.3286 | |
| ASMC | 1.2478 | 53.0256 | 11.2796 | 554.3386 | |
| ID-DO | 0.8 | 32.1543 | 6.8765 | 387.6543 |
| Axis | Controller | ISE | ITSE | IAE | ITAE |
|---|---|---|---|---|---|
| x-axis | PID | 1027.0737 | 13,872,067.4494 | 5303.5317 | 74,046,678.1397 |
| ANN | 0.9342 | 12.6790 | 6.3512 | 1333.8387 | |
| ASMC | 2.7832 | 103.8368 | 15.1875 | 609.3358 | |
| ID-DO | 2.0 | 78.5432 | 10.9876 | 543.2109 | |
| y-axis | PID | 1078.4066 | 14,536,482.8492 | 5407.3883 | 73,800,017.0965 |
| ANN | 0.8035 | 8.9226 | 5.1264 | 1188.2719 | |
| ASMC | 2.6150 | 87.4854 | 13.8383 | 491.5457 | |
| ID-DO | 1.8 | 62.3456 | 9.8765 | 432.8765 | |
| z-axis | PID | 955.4724 | 12,947,237.0384 | 5200.8174 | 73,622,093.8571 |
| ANN | 0.7831 | 9.4355 | 4.9636 | 92.0503 | |
| ASMC | 2.9243 | 124.8570 | 17.2641 | 844.8512 | |
| ID-DO | 2.2 | 89.6543 | 12.3456 | 654.3210 |
| a | |||||
| Axis | Controller | ISE | ITSE | IAE | ITAE |
| x-axis | PID | 1067.6329 | 85,317,327.1405 | 13,274.1990 | 1,115,141,413.555 |
| ANN | 0.5103 | 6.2033 | 4.3683 | 667.8990 | |
| ASMC | 1.6502 | 60.3612 | 11.6851 | 466.2159 | |
| ID-DO | 1.2 | 45.8765 | 8.5432 | 387.6543 | |
| y-axis | PID | 770.3790 | 52,905,707.4469 | 10,843.8783 | 946,705,802.7393 |
| ANN | 1.3545 | 14.1927 | 6.5018 | 1075.3517 | |
| ASMC | 4.6642 | 155.8768 | 18.7134 | 676.7750 | |
| ID-DO | 1.8 | 98.5432 | 12.8765 | 543.2109 | |
| z-axis | PID | 1673.4224 | 137,497,748.4491 | 16,641.3690 | 1,374,452,742.845 |
| ANN | 0.3032 | 3.2958 | 2.9014 | 49.5210 | |
| ASMC | 1.2465 | 52.9291 | 11.2917 | 559.4689 | |
| ID-DO | 0.9 | 34.8765 | 7.6543 | 432.1098 | |
| b | |||||
| Metric | PID | ASMC | ANN | ID-DO | |
| ISE (avg.) | 917.48 | 2.36 | 0.77 | 1.50 | |
| ITSE (avg.) | 627 × 107 | 93.43 | 8.51 | 60.29 | |
| IAE (avg.) | 8619.43 | 14.70 | 4.74 | 9.82 | |
| ITAE (avg.) | 629 × 108 | 297.85 | 644.86 | 452.33 | |
| Metric | PID | ASMC | ANN | ID-DO |
|---|---|---|---|---|
| Convergence Time (s) | 0.345 | 0.0525 | 0.247 | 0.0875 |
| Response time to disturbances (s) | 0.89 | 0.35 | 0.12 | 0.18 |
| Energy consumption rate (J/s) | 0.45 | 0.02 | 0.01 | 0.015 |
| Root Mean Square Error | 2.7845 | 1.2465 | 0.3032 | 0.45 |
| Integral Square Error | 75.1503 | 2.7632 | 0.9208 | 1.5 |
| Integral Time Square Error | 89,626.2481 | 102.3785 | 12.0193 | 65.4321 |
| Integral Absolute Error | 554.3319 | 15.0935 | 5.7656 | 8.1243 |
| Integral Time Absolute Error | 2,680,759.1590 | 602.3428 | 734.8116 | 512.9876 |
| Error reduction (%) | Baseline | 55 | 99 | 90 |
| Disturbance Recovery Efficiency (%) | ~50 | ~100 | ~100 | ~100 |
| Computational load (CL) | 0.05 | 0.75 | 12.5 | 1.2 |
| Controller | FLOPS (MFLOPS) | Time Per Iteration (ms) | Memory Usage (MB) |
|---|---|---|---|
| PID | 0.05 | 0.02 | 2.5 |
| ASMC | 0.75 | 0.15 | 4.0 |
| ANN | 12.5 | 2.80 | 15.1 |
| ID-DO | 1.2 | 0.25 | 5.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urrea, C.; Sari, P. Symmetry-Driven Fault-Tolerant Synchronization in Multi-Robot Systems: Comparative Simulation of Adaptive Neural and Classical Controllers. Symmetry 2025, 17, 591. https://doi.org/10.3390/sym17040591
Urrea C, Sari P. Symmetry-Driven Fault-Tolerant Synchronization in Multi-Robot Systems: Comparative Simulation of Adaptive Neural and Classical Controllers. Symmetry. 2025; 17(4):591. https://doi.org/10.3390/sym17040591
Chicago/Turabian StyleUrrea, Claudio, and Pablo Sari. 2025. "Symmetry-Driven Fault-Tolerant Synchronization in Multi-Robot Systems: Comparative Simulation of Adaptive Neural and Classical Controllers" Symmetry 17, no. 4: 591. https://doi.org/10.3390/sym17040591
APA StyleUrrea, C., & Sari, P. (2025). Symmetry-Driven Fault-Tolerant Synchronization in Multi-Robot Systems: Comparative Simulation of Adaptive Neural and Classical Controllers. Symmetry, 17(4), 591. https://doi.org/10.3390/sym17040591







