1. Introduction
The electromagnetic response of (3 + 1)D time-reversal-invariant topological insulators is described by a topological field theory akin to axion electrodynamics. The surface term, which corresponds to a (2 + 1)D Chern–Simons term, describes the anomalous Hall effect on the surface, which is the physical origin behind the topological magnetoelectric effect, a hallmark response of TIs encapsulated in the transverse Hall conductivity . The half-quantized Hall effect holds true only when the Fermi level lies within the bandgap. However, in reality, the Fermi level lies outside the gap, so it is within the finite density of states, in which case the Hall effect would not be quantized anymore. Furthermore, realistic materials often exhibit deviations from idealized theoretical predictions due to various mechanisms, such as disorder and impurity scattering, and a systematic investigation of these is fundamental for a better understanding of the topological transport. This motivates us to investigate higher-order derivative corrections to the anomalous Hall effect that may arise due to spatial variations in the fields.
Traditionally in the study of fermionic topological phases, the dependence of on frequency is taken into account at most, and the dependence on momentum is considered irrelevant or even detrimental. This idea is linked to the fact that the most common methods for calculating this conductivity, Kubo’s linear response theory and Boltzmann’s semi-classical approximation, are strictly defined for constant electric fields or at most with harmonic time dependence. However, recently in the literature, some indications have appeared that the dependence of the Hall conductivity on momentum plays a fundamental role in new phenomena of great theoretical and applied interest.
The first of these findings is related to the study of
bosonic topological phases [
1,
2,
3,
4], particularly photonic ones. As shown in these references, the existence of these new topological phases inevitably requires non-locality (i.e., dependence on momentum and frequency) of the optical parameters of the material, particularly of
. In Ref. [
1], a model is presented where the lowest-order correction in the momentum for this parameter,
, allows for the existence of topological photonic phases with Chern number
. This model was subsequently embedded in a phenomenological extension of
Chern–Simons theory in Ref. [
2]. Unlike the fermionic case, these bosonic phases have been studied little, with the additional difficulty that they have eluded experimental determination until now, unlike the former for which there has been substantial work carried out in the laboratory.
Another property of quantum Hall states where the dependence of
on momentum plays an important role is in the description of Hall viscosity. Hall viscosity, analogous to Hall conductivity, is another measurable property of these quantum states [
5,
6]. As originally defined, it is related to the system’s response to metric perturbations that can be realized through lattice vibrations. However, in Refs. [
7,
8], it has been shown that for systems where Galilean invariance holds and that are constituted by particles with an equal charge-to-mass ratio, this property can be determined solely from the electromagnetic response of the system, taking into account higher-order contributions in the momentum of the Hall conductivity. This relationship between viscosity and electromagnetic properties of the system provides a convenient alternative for the measurement of this parameter. Additionally, it has been shown that Hall viscosity is related to the so-called Wen-Zee shift, a topological property of the quantum Hall state [
9]. In Ref. [
10], we find another phenomenological proposal including higher-order derivatives in the fields, designed as an additional correction to axion electrodynamics in order to describe the response of new metamaterials. These novel metamaterials exhibit optical properties analogous to those of topological insulators, including Kerr and Faraday rotations. Notably, the presence of external sources in these materials does not lead to the emergence of dyonic charges, thereby circumventing the Witten effect.
The aim of this work is to investigate a more general response theory of (3 + 1)D topological insulators that includes corrections to the Hall conductivity due to higher-order derivative modifications as well as those due to the chemical potential. This work focuses on determining the anomalous Hall conductivity localized at the edge of the TI and associated with the electromagnetic response derived from the
-dimensional electrodynamics present there. In this way, the sought-after corrections will appear naturally from the calculation of radiative corrections generated by integrating fermionic excitations at the edge. These are encapsulated in the corresponding
-dimensional vacuum polarization tensor (VPT), which provides higher-order derivative corrections as well as modifications through the introduction of the chemical potential at zero temperature. Recalling that the usual formulation of axion electrodynamics in the
-dimensional bulk correctly describes TIs, we are interested in also showing how modifications at the edge induce a consistent extension of axion ED in the bulk, in relation to the proposal of Ref. [
10]. As expected, higher-order corrections in the momentum will depend on the metric and will not carry universal topological fermionic information. However, as we mentioned above, they will be of crucial importance for bosonic topological phases. The use of VPT calculations to incorporate additional material properties into its electromagnetic response is of a very general nature. Specifically, it has proven highly useful for determining corrections to the anomalous Hall effect in the case of a two-node Weyl semimetal with band tilt and anisotropy [
11,
12,
13].
For completeness, we review the derivation of the anomalous Hall conductivity in the presence of a chemical potential, but to the zeroth order in momentum, using the Kubo formula and the semi-classical Boltzmann approximation that includes topological modifications via the Berry phase. For the moment, both methods are unable to produce higher-order corrections in momentum, which, however, appears quite naturally in a derivative expansion of the VPT. We also investigate the impact of the corrections we have found for on the Fresnel coefficients that appear at a TI–dielectric interface. In particular, we discuss the modifications induced in the Kerr and Faraday rotations of an impinging electromagnetic wave, as well as the modifications to the magnetoelectric effect that occurs when an electric charge is placed near the insulator.
This paper is organized as follows. In
Section 2, we review the electromagnetic response of a topological insulator.
Section 2.1 deals with a review of axion electrodynamics, which is the lowest-lying order of the electromagnetic response of TIs. In
Section 2.2, we introduce the microscopic Hamiltonian for the surface states of 3D TIs and show the emergence of the half-quantized Hall effect by employing the Kubo formula and the semi-classical Boltzmann approach.
Section 3 focus on an extension of axion electrodynamics in (3 + 1) dimensions, which consistently accommodates higher-order derivative corrections appearing at the boundary, through the modified Maxwell’s equations resulting in the bulk. The basic idea is that the constant parameters encoding the magnetoelectricity of each TI in the usual case are now promoted to differential operators in the coordinates transverse to the interface, whose specific form will be determined by the radiative corrections at the interface. In
Section 4, we calculate the VPT at the insulator boundary. In
Section 4.1, we show how the microscopic Hamiltonian described in Section IIb is embedded in a (2 + 1)D Dirac theory. We note that both the dimensions of the electromagnetic coupling
f and the corresponding gauge field
in (2 + 1)D differ from their respective counterparts
e and
in (3 + 1)D. However, the product
has the same dimensions as
, allowing us to write the resulting effective electromagnetic action in terms of the electromagnetic field
in (3 + 1)D, but restricted to take values only at the interface. In this way, we can identify the resulting effective current from the (2 + 1)D calculation with the surface current
localized at the interface obtained from the modified axionic action. The derivative corrections in the transverse coordinates to the interface are subsequently identified with the radiative corrections obtained from the (2 + 1)D theory. We then calculate the effective action by integrating out the fermions in (2 + 1)D using the derivative expansion method. The result for the VPT is presented in
Section 4.2 and
Section 4.3 and contains second-order derivative corrections, which we interpret directly in terms of the surface current
, obtaining the sought-after modifications for the anomalous Hall conductivity. The extension to include finite density effects in the VPT is carried in
Section 4.4 by employing the Matsubara substitution. The final results for the corrections to the anomalous Hall conductivity are presented in
Section 4.5. These results modify the boundary conditions at the interface of the TI, as well as the Fresnel relations for an incident electromagnetic wave. In
Section 5, we discuss the effect of such modifications on Kerr and Faraday rotations, while in
Section 6, we investigate the changes induced in the magnetoelectric effect when a charge is placed near the interface of a TI and the vacuum. A summary and discussion is presented in
Section 7. For the benefit of the reader, we provide a brief summary of the derivative expansion method in
Appendix B. The remaining four appendices include some technical calculations indicated in the text.
3. Modified Axion Electrodynamics: Higher-Order Derivative Terms
Even though the calculation of the vacuum polarization effects in
dimensions naturally introduces derivative corrections in the electromagnetic fields, we need to go one step backwards to make sure that this procedure constitutes a consistent extension of the standard axion electrodynamics in the bulk. We expect that the introduction of additional derivatives in the
-term will inevitably destroy the topological features of the piecewise constant contributions previously described when
(mod
). In this way, we propose a gauge-invariant modification to the
-term in action (
1), which is valid for arbitrary magnetoelectric materials, i.e., when their constant value of the magnetoelectrical polarizability is a real arbitrary number. In this case,
’s contribution to the action is odd under time reversal. In other words, we expect the higher-derivative terms to break time-reversal symmetry and be non-topological. We propose the following extension of the
-term in action (
1):
where
is a dimensionless operator to be determined. Nevertheless, notice that any constant contribution to
, which multiplies the Pontryagin density
and is integrated over a closed surface, will produce a topological contribution related to the first Chern number of the surface.
To begin with, we obtain some general properties of the operator
and leave its detailed derivation for the next section. For an arbitrary two-dimensional interface at a given point, we choose
as the product:
where
is the coordinate parallel to the normal of the interface at that point, and
and
are the corresponding coordinates in the tangent space. The tensor structure of the Lagrangian density suggests that (
20) and action
must relate to the same equations of motion. This means that
is an even function of the derivatives such that upon integrating by parts and disregarding boundary terms, one can transform the Lagrangian densities into each other. This means that in the lowest-order derivative extension, operator
contains second-order derivatives in space and time. Finally, in the zeroth-order limit, one expects that
reduces to the original position-dependent axion angle
. The equations of motion for this model are obtained through variation in action (
1), with the axion term replaced with the generalized contribution (
20). One obtains
In addition, since we aim to describe higher-order derivative corrections to the anomalous effects on interface , function must be localized there, i.e., , where is the normal to the surface at the given point.
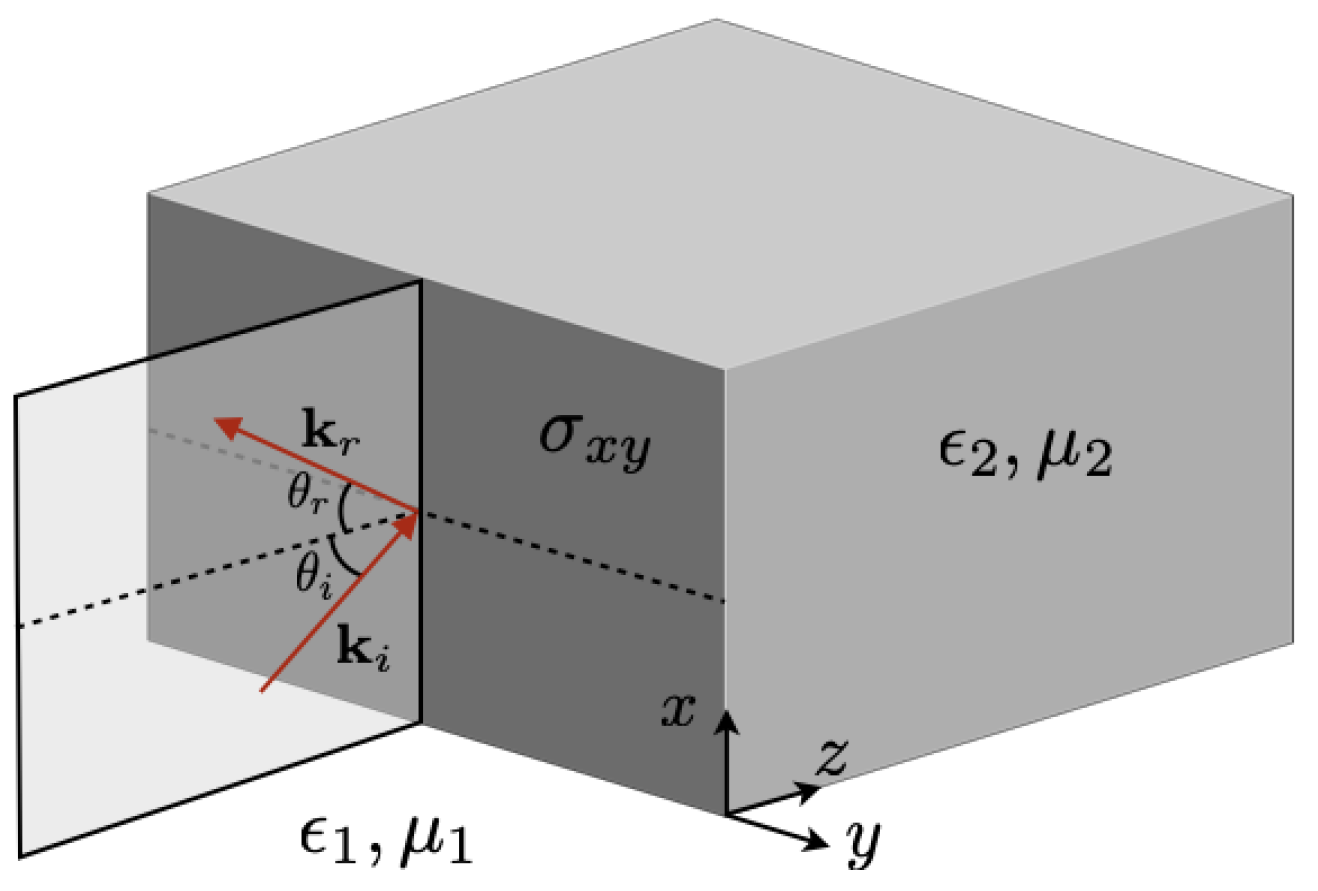
For the configuration depicted in
Figure 1, we write the coordinate dependence of operator
as
yielding
with operators
The constant contribution to these operators, due to the
, reproduces the choice
in the piecewise axion angle of
Section 2.1, which defines the topology of the phase. The notation
identifies the time plus the transverse coordinates
, such that
(with
). The constant term reproduces the surface anomalous Hall conductivity
, and the second-order derivative operator
encodes the higher-order derivative contributions at the interface, whose strength is driven by the length scales
, which are determined using the microscopic parameters of the materials. For the configuration depicted in
Figure 1, the surface current becomes
where
is the unit normal to the interface. The corresponding surface charge and current densities are
In referring to the current density
, the unit operator in each
leads to the half-quantized anomalous Hall current
. The second term includes higher-order derivatives of the electric field,
. Regarding the momentum space in the case of a topological insulator at chemical potential
, Fermi velocity
, and gap
, Equation (
27) allows us to define the following frequency–momentum transverse conductivity:
where
, and quantities
are the Fourier transforms of operators
. In the static limit
and
,
approaches the universal half-quantized value
. However, in general,
has a nontrivial dependence on the wave number
and the chemical potential
. In addition, one expects the lengths scales
to be a function of the material parameters,
,
, and
m.
For the completeness of this section and for later use, we write the modified field equations corresponding to the configuration depicted in
Figure 1, including the higher-derivative corrections, as
which yield the following boundary conditions at the interface:
The analysis above shows us that one can consistently include higher-order derivative corrections to the anomalous Hall effect, which could be related to the Hall viscosity of the fermion fluid at some limit, through an appropriate extension of the
axion electrodynamic contribution. The questions that remain open are the exact form of the operators
and the definition of the length scales
in terms of the material parameters. The next
Section 4 is devoted to answering these question in detail using methods of relativistic thermal quantum field theory in
dimensions.
5. Corrections to the Topological Kerr and Faraday Rotations
From Equation (
30), we learn that the modified Hall conductivity
in Equation (
28) determines the boundary conditions at the interface of two topological insulators. We now investigate the impact of the higher-order derivative corrections to the Hall conductivity on the reflection matrices for a topological insulator–dielectric interface. We choose our coordinates such that the interface is defined by the plane
. Let us assume that a plane wave with wave vector
impinges upon the interface from
(dielectric) towards the topological insulator occupying the region
. The semi-infinite region
(
) is characterized by the permittivity
(
), the permeability
(
), and the magnetoelectric susceptibility
(
). The interface supports a surface Hall conductivity
including derivative corrections. Let us select the plane of incidence to be the one determined by
and
. Owing to the rotational symmetry about
z, without loss of generality, we can take our coordinate system so that this plane coincides with the
plane, such that
, as shown in
Figure 4. The incident electromagnetic fields are then [
17,
18]
where
,
is the speed of light in medium 1, and
and
are the field amplitudes for TE and TM polarizations, respectively. For the reflected wave, the momentum reads
and the electromagnetic fields become
where
and
are the field amplitudes for TE and TM polarization, respectively. The transmitted wave is given by the fields inside the TI:
where
,
is the speed of light in medium 2, and
and
are the transmitted field amplitudes for TE and TM polarizations, respectively. Now we shall impose the boundary conditions (
30), which for a topological insulator–dielectric interface read
where
and the chemical potential lies in the bandgap of the TI.
Note that for a plane wave, we have , with .
Imposing the boundary conditions at
, we obtain
The solution to this system is quite simple. Defining the reflection matrix as
we find
and
. Following the same procedure, one can further calculate the transmission matrix, defined by
which becomes
At normal incidence (
), we have
and
. Therefore, the reflection matrix (
104) becomes
with
and
.
For incident light linearly polarized in the
y direction,
, the Kerr and Faraday angles are defined by
, and
, respectively. Using the Fresnel matrix, we obtain
and
respectively, where
is the ratio between the photon energy and the bandgap. Now, we shall estimate the size of this effect in a realistic experimental situation. In Ref. [
19], the authors reported the first experimental observation of the Faraday rotation angle when linearly polarized THz radiation passes through the surface of a strained HgTe 3D TI. They found a rotation angle of
rad, within an error bar estimated at
rad. Using the experimental data of Ref. [
19], with a photon energy of
meV, and an energy gap in strained HgTe of
meV [
20], from Equation (
109), one estimates a shift in the Faraday angle of
which is on the verge of the current experimental accessibility (one order of magnitude below the experimental precision). This angle shift is strictly caused by the lowest-order derivative correction to the surface anomalous Hall effect.
We observe that correction (
110) is driven by the parameter
, which is the ratio between the photon energy and the bandgap. If we increase this ratio, the angle shift could be enhanced in principle; however, the validity of the theory requires
to avoid interband transitions. This prohibits the increment in the angle shift. Other TIs, such as ZrTe
5 crystals, exhibit a large energy gap of ∼100 eV, which implies
rad, which is three orders of magnitude below the error bars. All in all, strained HgTe is the best material candidate for testing our prediction.
6. Image Magnetic Monopole
The search for magnetic monopoles has a long history in both high-energy and condensed matter physics. Up to date, this elusive particle has yet to be detected experimentally. However, the development of topological insulators provides a new platform where these kinds of magnetic excitations appear. To be precise, when the Fermi level lies within the bandgap, the surface Hall conductance is half-quantized and the electromagnetic response is described by axion electrodynamics with a quantized coefficient. If this condition is fulfilled, a point-like electric charge
q near the surface of a topological insulator induces an image magnetic monopole charge of strength [
21,
22]
If the Fermi level does not lie in the bandgap but lies within the finite density of states, the image monopole picture breaks down due to the screening effect [
23]. As we shall see in the following, applying higher-order correction terms to the surface Hall effect also implies the breakdown of the image monopole picture, even when the Fermi level lies in the bandgap.
Let us consider the geometry as shown in
Figure 5, where the left-half space (
) is occupied by a topological insulator, and the right-half space (
) is occupied by a trivial insulator. The interface, at
, supports a surface Hall conductivity
that includes derivative corrections. A point-like electric charge of strength
q is located at a distance
from the surface of a topological insulator. The field equations describing the electromagnetic response, including the surface Hall response, read
where
and
when the chemical potential lies in the bandgap of the TI. Due to gauge invariance, the fields can be written in terms of the electromagnetic potentials according to
and
, as usual. At the lowest order in
, the electromagnetic potentials are given by
in the Coulomb gauge, with the corresponding Green’s functions
These potentials can be evaluated straightforwardly. On the one hand, the electric potential is exactly the same as in Maxwell electrodynamics, since time reversal dictates a quadratic correction in
, i.e.,
which we interpret in terms of the original charge
q at
and an image electric charge of strength
at
, as usual. The magnetic part is a little more subtle. Time-reversal symmetry implies a linear response in
, which we determine in the following. We observe that the integrand
depends on the transverse Laplacian acting upon the components of the electric field parallel to the interface, which are continuous there. Therefore, using the identity
, which is also valid for the magnetic Green’s function
, one can further present the identity
Therefore, the vector potential (115) can be written as
, where
and
is the scalar potential (
118). Straightforward calculations yield
where
g is given by Equation (
111). We identify (
121) as the vector potential of a straight vortex line or Dirac string over the
z axis. The details of the calculations are relegated to
Appendix F. The zeroth-order magnetic field can then be obtained by taking the curl of Equation (
121), which yields the monopole field
, where
. Taking the curl of the full vector potential, one finds the deviation from the magnetic monopole picture as
where
is the unit dyadic.
In
Figure 5, we plot the total magnetic field
due to a point-like electric charge (marked in blue) above the topological insulator. The field strength is normalized by the magnetic field strength
. If solely the Hall conductivity is taken into account, the magnetic field lines above the surface are radially directed away from a magnetic monopole located beneath the surface (marked in red). However, in the present case, as we can see in
Figure 5, the monopole picture breaks down, since the magnetic field lines are no longer radially directed from the image point. The deviations in the field lines are apparent near the surface, while the radial behavior dominates at long distances. Our results show that, when the Fermi level lies within the gap, the image monopole picture emerges only as first-order in the electromagnetic response. Higher-order corrections yield to deviations from the magnetic monopole field.
Now, we shall estimate the size of this effect. For an electric charge of strength
(where
e is the elementary charge) in vacuum, located at a distance
µm from the TI surface and in taking
and
, the magnetic field at an observation point at
µm away is
pT [
24], which is too small to be detected directly in an experiment. For a strained HgTe, for which
meV and
m/s, Equation (
122) predicts
, which is seven orders of magnitude below the uncorrected prediction. With the present experimental precision, this field and its correction cannot be observed [
25]. However, as shown recently in Ref. [
24], integrating TIs with active metamaterials substrates can enhance the induced monopole magnetic field
by more than
times, and in our case, the correction term as well, which is proportional to
. This idea opens a new avenue for the search of the elusive monopole field and represents an interesting possibility with which to test our results as well.
7. Summary and Conclusions
The main goal of this work was to obtain higher-order corrections in the derivatives for the electromagnetic response of topological insulators (TIs) at zero temperature at finite density. The focus was on the anomalous Hall conductivity , which governs the electromagnetic response of the TI at the interface. We recover the known zeroth-order results for using both the linearized Kubo approximation and the semi-classical Boltzmann method, which incorporates anomalous transport through the inclusion of the Berry phase. Unfortunately, both methods are not capable of incorporating higher-order corrections in the derivatives in their current formulation. For this reason, we consider a third alternative based on the calculation of radiative corrections in quantum electrodynamics encoded in the vacuum polarization tensor.
We proceed in two steps, recalling that the electromagnetic behavior of topological insulators under the given conditions is well described by axion electrodynamics, with a constant piecewice axion parameter having a discontinuity at the interface, as shown in
Figure 1. To begin with, and in order to maintain the basic structure of the underlying axion electrodynamics, we propose an extension that consistently includes these corrections in the surface current
that appears at the interface of the media. At this level, the most important result is presented in Equations (
27) and (
28), where
is written in terms of differential operators in the transverse coordinates to the interface acting on the fields. This current derives from the modified axion electrodynamics in a way analogous to the standard case since the transverse operators are still localized at the interface. In momentum space, the resulting Hall conductivity is given by Equation (
28) and constitutes a direct generalization of the standard expression (
5) in terms of the newly introduced transverse operators.
The second step includes the calculation of the corrections themselves, which are naturally obtained from the radiative corrections in the coupling of fermions at the interface of the materials with the electromagnetic field described by (2 + 1)D electrodynamics. In general terms, we calculate the resulting effective electromagnetic action at the (2 + 1)D interface, which is encoded in the transverse contribution of the vacuum polarization tensor
to one-loop order, which is proportional to
. Gauge invariance provides the tensorial structure of
, which is finally characterized by the scalar
, which contains the momentum corrections. From Equations (
28) and (
45), we obtain the relation
that connects the response in axion electrodynamics with the radiative corrections at the interface from where the corrections in momentum arise.
Appendix A includes a heuristic review of the derivation of the electromagnetic effective action together with additional references.
is calculated using the derivative expansion method, which provides the local contributions to the effective action in a power series of the external momentum. With this approach, one can also select from the very beginning the required order in the series expansion. Given that the anomalous Hall effect critically depends on the position of the Fermi level
relative to the energy gap, we took into account its dependence on the calculation of
by applying the Matsubara extension to the final expression of the VPT at zero temperature. The results are indicated in Equations (
85) and (
86) for
inside the bangap and for
outside the bandgap, respectively. The corresponding expressions in terms of the anomalous Hall conductivity are given by Equations (
90) and (
91), with corrections up to the second order in the momentum.
For greater clarity, we included
Appendix B, where we provide a brief summary of the derivative expansion method, along with references [
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36], which correspond to other works that have utilized this method. The main identity of the derivative expansion is given in Equation (
51), while the explicit expansion is shown in Equation (
60). Additionally, Appendices
C,
D and
E contain detailed steps for calculating integrals and residues, which allowed us to derive the results presented in the manuscript for the polarization tensor at both zero and finite chemical potential.
As shown in Equations (
28) and (
30), the values for
determine the boundary conditions for the electromagnetic fields at the interface between two topological insulators. Keeping this in mind, we examine the implications of the calculated corrections on two well-established phenomena: firstly, the Kerr and Faraday rotations that occur when an electromagnetic wave impinges on the interface, and secondly, the ensuing magnetoelectric effect that arises when a charge is located in front of the interface.
In the first scenario, we examine an electromagnetic wave incident upon the topological insulator interface in the
-plane, as depicted in
Figure 4. By applying the boundary conditions (
100), we compute reflection matrix (
104) and transmission matrix (
106), thereby deriving the Kerr and Faraday angles expressed in (
108) and (
109) for the specific case of normal incidence and for linearly polarized light in the
y direction. In Ref. [
19], the authors reported the first experimental observation of the Faraday rotation angle when linearly polarized THz radiation passes through the surface of a strained HgTe 3D TI. They found a rotation angle of
rad, within an error bar estimated at
rad. Using the experimental data of Ref. [
19], with a photon energy of
meV and an energy gap in strained HgTe of
meV [
20], from Equation (
109), we estimate the shift in the Faraday angle
, which is on the verge of the current experimental accessibility, just one order of magnitude below the experimental precision. This angle shift is strictly caused by the lowest-order derivative correction to the surface anomalous Hall effect.
The second scenario pertains to a notable manifestation of the magnetoelectric effect in TIs, wherein the placement of an electric charge in proximity to the TI interface gives rise to the appearance of an image magnetic monopole. To be precise, when the Fermi level lies within the bandgap, the surface Hall conductance is half-quantized and the image magnetic monopole is induced [
21,
22] However, when the Fermi level lies within the finite density of states, the image monopole picture breaks down due to the screening effect [
23]. We examined the implications of the Fermi level being situated within the energy gap, while
incorporates the momentum corrections specified in Equation (
113), and found that the resultant magnetic field can no longer be interpreted in terms of an image monopole. The calculation is carried out to the first order in
and involves the derivative corrections produced by the operator
in Equation (
113), which determines the vector potential in Equation (
108) that can be rewritten as
. Here,
is the vector potential of a straight Dirac string over the
z axis yielding the original monopole field
. The shift
is reported in Equation (
122), and the total magnetic field
is plotted in
Figure 5. We see that the monopole picture breaks down, since the magnetic field lines are no longer radially directed from the image point. The deviations in the field lines are apparent near the surface, while the radial behavior dominates at long distances. Our results show that, even when the Fermi level lies within the gap, the image monopole picture emerges only at the zeroth-order momentum correction in the electromagnetic response. Higher-order corrections yield to deviations from the magnetic monopole field.
Some final comments now emphasize how our findings differ and extend the results of previous models addressing non-local corrections in non-dynamical axion electrodynamics, which are relevant to topological insulators and Weyl semimetals. These corrections can be embedded in the general higher-derivative electromagnetic Lorentz-violating modifications to Maxwell’s equations, as discussed in Refs. [
37,
38], for example. However, this phenomenological approach does not necessarily result from the effective electromagnetic response of an underlying fermionic system. While the calculation of effective electromagnetic actions in field theory has a long history and has been used in many applications, here, we focused on the above-mentioned cases relevant to condensed matter physics. In the case of the Weyl semimetals, for example, the focus is on the electromagnetic response of the bulk, and two possibilities arise: modifying Maxwell’s equations directly in a phenomenological way and deriving the electromagnetic response from the full fermionic
-D system coupled to the electromagnetic field. The latter approach yields modifications to Maxwell’s equations through radiative corrections of the effective action, including the vacuum polarization tensor in the one-loop approximation [
12,
13,
39]. For topological insulators, the corresponding axion ED introduces new dynamical effects only at the
-D interface between two media. The bulk is still described by standard Maxwell’s equations. Most higher-order derivative corrections in the literature focus on modifying only the electromagnetic
-D theory at the boundary in a phenomenological way, as, for example, in Ref. [
40]. An additional example of an alternative phenomenological proposal for a modified axion ED, this time in the bulk, is found in Ref. [
10]. Additionally, we account for effects due to the inclusion of the chemical potential, which are not considered in these studies. Our approach focuses on the
-D full fermionic system coupled to the electromagnetic field, and proceeds by calculating higher-order derivative corrections to the anomalous Hall conductivity arising from the one-loop correction to the corresponding effective electromagnetic action via the vacuum polarization tensor. We also establish a link between the theory at the boundary and at the bulk, obtaining a well-motivated modified version of the axion ED for this case.